微积分在物理竞赛中的应用

合集下载

微积分在物理中的应用举例

微积分在物理中的应用举例
微积分，作为数学中的重要分支，不仅仅是一种抽象的理论，而在现实世界中有着广泛的应用。

特别是在物理学领域，微积分的应用更是无处不在。

本文将通过几个具体的例子来说明微积分在物理中的应用。

运动学中的微积分应用
在研究物体的运动时，我们需要对其位置、速度和加速度进行分析。

而微积分正是运动学中经常使用的工具之一。

例如，对于一个运动的物体，我们可以通过微积分来求解其在不同时刻的位置，速度和加速度之间的关系。

通过对这些关系进行分析，可以更好地理解物体的运动规律。

力学中的微积分应用
在力学中，微积分可被用来分析受力物体的运动。

例如，通过对牛顿第二定律的微积分分析，我们可以得出物体在不同时间下的轨迹和速度变化。

此外，微积分还可以帮助我们计算物体受力时的加速度，从而更好地理解物体的受力情况。

热力学中的微积分应用
在研究热力学问题时，微积分同样扮演着重要角色。

例如，通过微积分可以分析热传导过程中物体温度的变化规律。

此外，微积分还可以用来解决热力学系统中的复杂方程，从而帮助我们更好地理解热力学系统的特性。

结论
通过以上几个例子，我们可以看到微积分在物理学中的重要性和广泛应用。

无论是运动学、力学还是热力学，微积分都扮演着至关重要的角色，帮助我们更好地理解和解决物理学中的问题。

因此，微积分的学习和应用对于物理学研究具有重要意义。

微积分在物理学中的应用

微积分在物理学中的应用微积分作为数学的一个基础分支，在物理学中发挥着至关重要的作用。

它不仅提供了描述物理现象的数学语言，还为解决复杂的物理问题提供了有力的工具。

本文将探讨微积分在物理学中的几个关键应用。

一、运动学分析在物理学中，运动学研究物体的运动状态和变化规律。

微积分在这里的应用主要体现在速度和加速度的概念上。

速度是位移对时间的导数，而加速度则是速度对时间的导数。

通过微积分，我们可以精确地描述物体运动的瞬时状态，进而深入理解运动的本质。

二、力学系统在力学系统中，微积分用于分析力的作用效果。

牛顿第二定律表明，物体的加速度与作用在其上的合外力成正比，这需要用到微分来描述加速度随时间的变化。

同时，通过积分可以计算出在一定时间内，物体因受力而产生的位移或速度变化。

三、电磁学电磁学是研究电荷产生电场和磁场以及这些场如何影响电荷的科学。

在电磁学中，微积分被用来描述电场和磁场的空间分布。

例如，电势差可以通过电场强度的积分得到，而电流产生的磁场则可以通过安培环路定理来计算，这涉及到对闭合路径的线积分。

四、热力学热力学是研究能量转化以及物质状态变化的学科。

在热力学中，微积分用于计算热量、功和内能等物理量的变化。

例如，通过对温度-熵图的面积积分，可以得到系统的热量变化；而对压强-体积图的面积积分，则可以得到系统对外做的功。

五、量子力学量子力学是研究微观粒子行为的基本理论。

在量子力学中，微积分用于描述波函数的时间演化和空间分布。

薛定谔方程就是一个典型的偏微分方程，它描述了量子态随时间的演变。

通过求解这个方程，可以得到粒子在不同能级的概率分布。

六、光学在光学领域，微积分用于分析光的传播和干涉现象。

波动方程描述了光波的传播特性，而通过积分方法可以解释光的干涉和衍射现象。

例如，通过计算两束光波的相位差积分，可以得到它们相遇时的干涉图样。

总结微积分在物理学中的应用广泛而深刻，它不仅是描述自然现象的语言，也是解决物理问题的工具。

微积分基础初步及其在中学物理竞赛中的应用

A
A
几何公理：两点之间直线距离最短
∫B ds 的极小值为直线 AB . A
光在均匀介质中沿直线传播
ii. 用费马原理证明折射定律
证: 通过空间两点A、B可以作无数个
平面，其中必有一个平面垂直于两种介质 n1和n2 之间的界面，OO’是它们的交线。通过A点折射到B点的入射线交界面于C点，求C点的位置。
M0
L
N
αϕ
o
AB x
tan α = lim tan ϕ = lim Δy = lim f ( x0 + x) − f ( x0 )
Δx→0
Δ x Δx → 0
Δx→0
x − x0
曲线 y = f (x)在点M0处的纵坐标 y 的增量 Δy 与横坐标
x的增量Δx之比，当Δx → 0时的极限即为曲线在M0点处
即： f ′′(x0 ) = [f ′(x)]′ x=x0
依次类推，可得三阶、四阶导数等.
导数的几何意义与物理意义
z导数的几何意义：函数 y = f (x) 在点x0处的导数等于函数所
表示的曲线L在相应点（x0,y0)处的切线斜率.
y
y = f (x)
M T
M0
L
N
αϕ
o
AB x
z导数的物理意义：变速直线运动的速率
(a) C点必在OO'上
如果有另一点C'位于线外，则对应于C’，必可在OO’线上找到它的垂足C''
因为 AC' > AC' ' C' B > C'' B AC'+C' B > AC''+C'' B 而非极小值．

高中物理竞赛讲座22(物理微积分1word)

f ( x) sgn x 1( x 0) 或 0 ( x 0) 或 1 ( x 0)
lim f ( x) B
x A
例：
lim(2 x 1 ） 3
x 2
lim
x 3
x-3 x 3 1 1 lim lim 2 x 3 x 3 x 9 ( x 3)( x 3) x3 6
2、t 时刻的瞬时速度
1 1 [v0 (t t ) a(t t ) 2 ] (v0 t at 2 ) s 2 2 vt lim lim t 0 t t 0 t
= lim
(v0 at )t v0 at t 0 t
3、 t (t t ) 平均加速度
2、t 时刻的瞬时速度
v lim
x x x [5 3(t+t ) 2(t+t )3 ] (5 3t 2t 3 ) lim t t t lim t 0 t t 0 (t t ) t t 0 t
3 6t 2
3、 t (t t ) 平均加速度
v vt t vt [3 6(t+t )2 ] (3 6t 2 ) a t t t
4、t 时刻的瞬时加速度
[3 6(t+t )2 ] (3 6t 2 ) a lim a lim 12t t 0 t 0 t
例题：加在电容器两端的电压 u u0 sin t ，求 t 时刻瞬时电流强度。提示：电容器带电量 Q CU （C 为定值），平均电流 i 量）。解： Q cu cu0 sin t
a
v [v0 a(t t )] (v0 at ) a t t
例题：变速运动的位移公式 x 5 3t 2t 3 ，则 1、 t (t t ) 内的平均速度

高中物理竞赛的知识与分类

高中物理竞赛的知识与分类物理竞赛需要哪些知识?物理竞赛力学部分需要哪些数学?首先，为了理解力学一开始的匀加速直线运动和变加速直线运动，对于一元函数的简单微积分是必不可少的，当然主要集中在多项式函数的求导和积分上，实际操作起来十分容易。

此后，当运动范围被拓展到二维，运动形式成为曲线时，矢量代数、解析几何、参数方程、斜率、曲率半径等数学概念被融入到物理模型中，用来理解抛体、圆周、一般曲线运动。

这时微积分的应用也被拓展到更为复杂的函数范围，例如三角函数。

随着运动和力的关系——牛顿第二定律的引入，我们逐渐意识到光理解运动是不够的，运动背后的机理——力的作用，以及力的效果，才是我们要研究的。

动量定理、动能定理的引入，实际上反映了力在时空的积累效果，而牛顿方程本身，也是物理学家特别喜欢的形式——微分方程。

对于矢量和微积分更综合的运用体现在一种伴随物理学发展史的特殊运动形式——简谐振动当中。

而振动在介质当中的扩散效应——波动，又引出了波动方程、波函数这一时空函数的概念。

总结下来，力学部分所需要的数学是一元函数的微积分、矢量代数、解析几何、常微分方程、对二元函数的运用。

物理竞赛热学部分需要哪些数学?虽然高中热学部分涉及气体定律和热力学第一定律的内容比较容易，一般不需要微积分，但如果深入学习，热力学过程、各种态函数(内能、熵)、热力学第二定律，那么由于热力学体系变量多，适当的偏微分基础知识是必要的。

热力学是宏观的理论，而其背后有着分子动理论作为基础，它们之间的联系是通过对大量粒子系统的统计来实现的，因此，概率统计的知识就显得十分必要了。

总结下来，热学部分所需要的数学是简单的偏微分和概率统计。

物理竞赛电磁学部分需要哪些数学?依照往年的经验，电磁学是最容易让高考学生放弃物理、竞赛学生放弃物理竞赛的困难内容。

原因是因为数学不到位，非但理解不了场的概念，而且容易产生记忆模型和公式，套例题做习题的固有思维模式，最终对于电磁学可谓是“一点没学会”!从静电场开始，如果仅仅按高中的要求来学习，对于场的理解是空洞的，仅仅是唯像的概念，对于电场线、电势、静电平衡、介质极化等概念无法做到深入掌握，那就更别提解答赛题了。

(完整版)高中物理竞赛中的高等数学

高中物理竞赛中的高等数学一、微积分初步物理学研究的是物质的运动规律，因此经常遇到的物理量大多数是变量，而要研究的正是一些变量彼此间的联系．这样，微积分这个数学工具就成为必要的了．考虑到，读者在学习基础物理课时若能较早地掌握一些微积分的初步知识，对于物理学的一些基本概念和规律的深入理解是很有好处的．所以在这里先简单地介绍一下微积分中最基本的概念和简单的计算方法，在讲述方法上不求严格和完整，而是较多地借助于直观并密切地结合物理课的需要．至于更系统和更深入地掌握微积分的知识和方法，可在通过高等数学课程的学习去完成． §1．函数及其图形1．1 函数自变量和因变量绝对常量和任意常量在数学中函数的功能是这样定义的：有两个互相联系的变量x 和y ，如果每当变量x 取定了某个数值后，按照一定的规律就可以确定y 的对应值，那么称y 是x 的函数，并记作：y =f (x )，（A ．1）；其中x 叫做自变量，y 叫做因变量，f 是一个函数记号，它表示y 和x 数值的对应关系．有时把y =f (x )也记作y =y (x )．如果在同一个问题中遇到几个不同形式的函数，也可以用其它字母作为函数记号，如ϕ(x )、ψ(x )等等．①常见的函数可以用公式来表达，例如()32y f x x ==+，212ax bx +，c x，cos2x π，ln x ，x e 等等．在函数的表达式中，除变量外，还往往包含一些不变的量，如上面出现的13 2 2e π、、、、和a b c 、、等，它们叫做常量；常量有两类：一类如13 2 2e π、、、、等，它们在一切问题中出现时数值都是确定不变的，这类常量叫做绝对常量；另一类如a 、b 、c 等，它们的数值需要在具体问题中具体给定，这类常量叫做任意常量．在数学中经常用拉丁字母中最前面几个（如a 、b 、c ）代表任意常量，最后面几个（x 、y 、z ）代表变量．当y =f (x )的具体形式给定后，就可以确定与自变量的任一特定值x 0相对应的函数值f (x 0)．例如：（1）若y =f (x )=3+2x ，则当x =-2时y =f (-2)=3+2×(-2)=-1．一般地说，当x =x 0时，y =f (x 0)=3+2x 0．（2）若()cy f x x==，则当0x x =时，00()c f x x =．1．2 函数的图形在解析几何学和物理学中经常用平面上的曲线来表示两个变量之间的函数关系，这种方法对于直观地了解一个函数的特征是很有帮助的．作图的办法是先在平面上取一直角坐标系，横轴代表自变量x ，纵轴代表因变量（函数值）y =f (x )．这样一来，把坐标为（x ，y ）且满足函数关系y =f (x )的那些点连接起来的轨迹就构成一条曲线，它描绘出函数的面貌．图A -1便是上面举的第一个例子y =f (x )=3+2x 的图形，其中P 1，P 2，P 3，P 4，P 5各点的坐标分别为：（-2，-1）、（-1，1）、（0，3）、（1，5）、（2，7），各点连接成一根直线．图A -2是第二个例子()cy f x x==的图形，其中P 1，P 2，P 3，P 4，P 5各点的坐标分别为：1(,4)4c 、1(,2)2c 、(1,)c 、(2,)2c 、(4,)4c ，各点连接成双曲线的一支．1．3 物理学中函数的实例反映任何一个物理规律的公式都是表达变量与变量之间的函数关系的．下面举几个例子．（1）匀速直线运动公式：s =s 0＋vt ．（A ．2）此式表达了物体作匀速直线运动时的位置s 随时间t 变化的规律，在这里t 相当于自变量x ，s 相当于因变量y ，s 是t 的函数．因此记作：s =s (t )＝s 0＋vt ，（A ．3）式中初始位置s 0和速度v 是任意常量，s 0与坐标原点的选择有关，v 对于每个匀速直线运动有一定的值，但对于不同的匀速直线运动可以取不同的值．图A -3是这个函数的图形，它是一根倾斜的直线．易知它的斜率等于v ．（2）匀变速直线运动公式：20012s s v t at =++，（A ．4），v =v 0＋at ．（A ．5）两式中s 和v 是因变量，它们都是自变量t 的函数，因此记作：2001()2s s t s v t at ==++，（A ．6），v =v (t )=v 0＋at ，（A ．7）图A -4a 、4b 分别是两个函数的图形，其中一个是抛物线，一个是直线．（A ．6）和（A ．7）式是匀变速直线运动的普遍公式，式中初始位置s 0、初速v 0和加速度a 都是任意常量，它们的数值要根据讨论的问题来具体化．例如在讨论自由落体问题时，若把坐标原点选择在开始运动的地方，则s 0＝0，v 0＝0，a ＝g ≈9.8M ／s 2，这时（A ．6）和（A ．7）式具有如下形式：21()2s s t gt ==,（A ．8）；v ＝v (t )＝gt ．（A ．9）；这里的g 可看作是绝对常量，式中不再有任意常量了．（3）玻意耳定律：PV ＝C ．（A ．10）上式表达了一定质量的气体，在温度不变的条件下，压强P 和体积V 之间的函数关系，式中的C 是任意常量．可以选择V 为自变量，P 为因变量，这样，（A ．10）式就可写作：()CP P V V==，（A ．11）它的图形和图A -2是一样的，只不过图中的x 、y 应换成V 、P ．在（A ．10）式中也可以选择P 为自变量，V 为因变量，这样它就应写成：()CV V P P==，（A ．12）由此可见，在一个公式中自变量和因变量往往是相对的．（4）欧姆定律：U IR =．（A ．13）当讨论一段导线中的电流I 这样随着外加电压U 而改变的问题时，U 是自变量，I 是因变量，R 是常量．这时，（A ．13）式应写作：()UI I U R==，（A ．14）；即I 与U 成正比．应当指出，任意常量与变量之间的界限也不是绝对的．例如，当讨论串联电路中电压在各电阻元件上分配问题时，由于通过各元件的电流是一样的，（A ．13）式中的电流I 成了常量，而R 是自变量，U 是因变量．于是U ＝U (R )＝IR ，（A ．15）即U 与R 成正比．但是当讨论并联电路中电流在各分支里的分配问题时，由于各分支两端具有共同的电压，（A ．13）式中的U 就成了常量，而R 为自变量，I 是因变量，于是：()UI I R R==，（A ．16）即I 与R 成反比．总之，每个物理公式都反映了一些物理量之间的函数关系，但是其中哪个是自变量，哪个是因变量，哪些是常量，有时公式本身反映不出来，需要根据所要讨论的问题来具体分析． §2．导数2．1 极限若当自变量x 无限趋近某一数值x 0（记作x →x 0）时，函数f (x )的数值无限趋近某一确定的数值a ，则a 叫做x →x 0时函数f (x )的极限值，并记作：0lim ()x x f x a →=，（A ．17）（A ．17）式中的“lim ”是英语“limit （极限）”一词的缩写，（A ．17）式读作“当x 趋近x 0时，f （x ）的极限值等于a ”．极限是微积分中的一个最基本的概念，它涉及的问题面很广．这里不企图给“极限”这个概念下一个普遍而严格的定义，只通过一个特例来说明它的意义．考虑下面这个函数：232()1x x y f x x --==-，（A ．18），这里除x ＝1外，计算任何其它地方的函数值都是没有困难的．例如当0x =时，(0)2f =，当2x =，(2)8f =，等等．但是若问x ＝1时函数值f （1）＝？，就会发现，这时（A ．18）式的分子和分母都等于0，即0(1)0f =！用0去除以0，一般地说是没有意义的．所以表达式（A ．18）没有直接给出f （1），但给出了x 无论如何接近1时的函数值来．下表列出了当x 的值从小于1和大于1两方面趋于1时f （x ）值的变化情况：从上表看，x →1时f (x )的极限值．其实计算f (x )值的极限无需这样麻烦，只要将（A ．18）式的分子作因式分解：3x 2-x -2＝(3x ＋2)(x -1)，并在x ≠1的情况下从分子和分母中将因式(x －1)消去：(32)(1)()3 2 (1)1x x y f x x x x +-===+≠-；即可看出：x 趋于1时，函数f (x )的数值趋于：3×1＋2＝5．所以根据函数极限的定义，21132lim ()lim51x x x x f x x →→--==-． 2．2 几个物理学中的实例（1）瞬时速度当一个物体作任意直线运动时，它的位置可用它到某个坐标原点O 的距离s 来描述．在运动过程中s 是随时间t 变化的，也就是说，s 是t 的函数：s ＝s (t )．函数s (t )表示的是这个物体什么时刻到达什么地方．形象一些说，假如物体是一列火车，则函数s (t )就是它的一张“旅行时刻表”．但是，在实际中往往不满足于一张“时刻表”，还需要知道物体运动快慢的程度，即速度或速率的概念．例如，当车辆驶过繁华的街道或桥梁时，为了安全，对它的速率就要有一定的限制；一个上抛体（如高射炮弹）能够达到怎样的高度，也与它的初始速率有关，等等．为了建立速率的概念，就要研究在一段时间间隔里物体位置的改变情况．假设考虑的是从t ＝t 0到t ＝t 1的一段时间间隔，则这间隔的大小为：△t ＝t 1-t 0．根据s 和t 的函数关系s （t ）可知，在t 0和t 1＝t 0+△t 两个时刻，s 的数值分别为s （t 0）和s （t 1）＝s （t 0+△t ），即在t 0到t 1这段时间间隔里s 改变了：△s ＝s （t 1）－s （t 0）＝s （t 0+△t ）－s （t 0）．在同样大小的时间间隔△t 里，若s 的改变量△s 小，就表明物体运动得慢，所以就把s ∆与t ∆之比st∆∆叫做这段时间间隔里的平均速率，用v 来表示，则00()()s t t s t s v t t+∆-∆==∆∆，（A ．19），举例说明如下．对于匀变速直线运动，根据（A ．4）式有2000001()2s t s v t at =++和2000001()()()2s t t s v t t a t t +∆=++∆++∆，22200000000000000111[()()]()()()()()12222s v t t a t t s v t at v at t a t s t t s t v v at a t t t t ++∆++∆-+++∆+∆+∆-====++∆∆∆∆；平均速率s v t ∆=∆反映了物体在一段时间间隔内运动的快慢，除了匀速直线运动的特殊情况外，st∆∆的数值或多或少与t ∆的大小有关；t ∆取得越短，s t ∆∆就越能反映出物体在0t t =时刻运动的快慢；通常就把0t ∆→时st∆∆的极限值叫做物体在t ＝t 0时刻的瞬时速率v ，即0000()()lim lim t t s t t s t sv t t ∆→∆→+∆-∆==∆∆，（A ．20）对于匀变速直线运动来说，0000001lim lim()2t t s v v at a t v at t ∆→∆→∆==++∆=+∆．这就是熟悉的匀变速直线运动的速率公式（A ．5）．（2）瞬时加速度一般地说，瞬时速度或瞬时速率v 也是t 的函数：v ＝v （t ）．但是在许多实际问题中，只有速度和速率的概念还不够，还需要知道速度随时间变化的快慢，即需要建立“加速度”的概念．平均加速度a 和瞬时加速度a 概念的建立与v 和v 的建立类似．在直线运动中，首先取一段时间间隔t 0到t 1，根据瞬时速率v 和时间t 的函数关系v （t ）可知，在t ＝t 0和t ＝t 1两时刻的瞬时速率分别为v （t 0）和v （t 1）＝v （t 0+△t ），因此在t 0到t 1这段时间间隔里v 改变了△v =v （t 0+△t ）-v （t 0）．通常把v t∆∆叫做这段时间间隔里的平均加速度，记作a ；00()()v t t v t v a t t +∆-∆==∆∆，（A ．21）举例来说，对于匀变速直线运动，根据（A ．5）式有000()v t v at =+，000()()v t t v a t t +∆=++∆．所以平均加速度为000000()()[()]()v t t v t v a t t v at v a a t t t+∆-++∆-+∆====∆∆∆（常数）．对于一般的变速运动，a 也是与t ∆有关的，这时为了反映出某一时刻速度变化的快慢，就需要取vt∆∆在0t ∆→时的极限，这就是物体在t ＝t 0时刻的瞬时加速度a ：0000()()lim lim t t v t t v t va t t∆→∆→+∆-∆==∆∆，（A ．22）（3）应用举例水渠的坡度任何排灌水渠的两端都有一定的高度差，这样才能使水流动．为简单起见，假设水渠是直的，这时可以把x 坐标轴取为逆水渠走向的方向（见图A -5），于是各处渠底的高度h 便是x 的函数：h =h （x ）．知道了这个函数，就可以计算任意两点之间的高度差．在修建水渠的时候，人们经常运用“坡度”的概念．譬如说，若逆水渠而上，渠底在100m 的距离内升高了20cm ，人们就说这水渠的坡度是0.221001000m m =，因此所谓坡度，就是指单位长度内的高度差，它的大小反映着高度随长度变化的快慢程度．如果用数学语言来表达，就要取一段水渠，设它的两端的坐标分别为x 0和x 1，于是这段水渠的长度为：△x ＝x 1-x 0．根据h 和x 的函数关系h (x )可知，在x 0和x 1=x 0+△x 两地h 的数值分别为h (x 0)和h （x 1）＝h (x 0+△x )，所以在△x 这段长度内h 改变了：△h ＝h (x 0+△x )-h (x 0)．根据上述坡度的定义，这段水渠的平均坡度为：00()()h x x h x h k x x+∆-∆==∆∆，（A ．23）前面所举例子，△x 采用了100米的数值．实际上在100米的范围内，水渠的坡度可能各处不同．为了更细致地把水渠在各处的坡度反映出来，应当取更小的长度间隔x ∆，x ∆取得越小，hx∆∆就越能精确反映出x =x 0处的坡度．所以在x =x 0处的坡度k 应是0x ∆→时的平均坡度k 的极限值，即0000()()lim lim x x h x x h x hk x x∆→∆→+∆-∆==∆∆，（A ．24）2．3 函数的变化率——导数前面举了三个例子，在前两个例子中自变量都是t ，第三个例子中自变量是x ．这三个例子都表明，在研究变量与变量之间的函数关系时，除了它们数值上“静态的”对应关系外，往往还需要有“运动”或“变化”的观点，着眼于研究函数变化的趋势、增减的快慢，即函数的“变化率”概念．当变量由一个数值变到另一个数值时，后者减去前者，叫做这个变量的增量．增量，通常用代表变量的字母前面加个“△”来表示．例如，当自变量x 的数值由x 0变到x 1时，其增量就是△x ≡x 1-x 0．（A ．25）与此对应．因变量y 的数值将由y 0＝f (x 0)变到y 1=f (x 1)，它的增量为△y ≡y 1-y 0=f (x 1)－f (x 0)＝f (x 0+△x )－f (x 0)．（A ．26）应当指出，增量是可正可负的，负增量代表变量减少．增量比00()()f x x f x y x x+∆-∆=∆∆，（A ．27）可以叫做函数在x ＝x 0到x ＝x 0+△x 这一区间内的平均变化率，它在△x →0时的极限值叫做函数y ＝f (x )对x 的导数或微商，记作y ′或f ′(x )，0000()()()lim lim x x f x x f x yy f x x x∆→∆→+∆-∆''===∆∆，（A ．28）除y '或()f x '外，导数或微商还常常写作dy dx 、df dx 、d dx等其它形式．导数与增量不同，它代表函数在一点的性质，即在该点的变化率．应当指出，函数f (x )的导数f ′(x )本身也是x 的一个函数，因此可以再取它对x 的导数，这叫做函数y ＝f (x )的二阶导数，记作y ''、()f x ''、22d y dx等；22()()()d y d dy dy f x f x dx dx dx dx '''''====，（A ．29）据此类推，则不难定义出高阶的导数来．有了导数的概念，前面的几个实例中的物理量就可表示为：瞬时速率：ds v dt =，（A ．30）；瞬时加速度：22dv d sa dt dt==，（A ．31）；水渠坡度：dh k dx =，（A ．32）．2．4 导数的几何意义在几何中切线的概念也是建立在极限的基础上的．如图A -6所示，为了确定曲线在P 0点的切线，先在曲线上P 0附近选另一点P 1，并设想P 1点沿着曲线向P 0点靠拢．P 0P 1的联线是曲线的一条割线，它的方向可用这直线与横坐标轴的夹角α来描述．从图上不难看出，P 1点愈靠近P 0点，α角就愈接近一个确定的值α0，当P 1点完全和P 0点重合的时候，割线P 0P 1变成切线P 0T ，α的极限值α0就是切线与横轴的夹角．在解析几何中，把一条直线与横坐标轴夹角的正切tan α叫做这条直线的斜率．斜率为正时表示α是锐角，从左到右直线是上坡的（见图A -7a ）；斜率为负时表示α是钝角，从左到右直线是下坡的（见图A -7b ）．现在来研究图A -6中割线P 0P 1和切线P 0T 的斜率．设P 0和P 1的坐标分别为（x 0，y 0）和（x 0+△x ，y 0+△y ），以割线P 0P 1为斜边作一直角三角形△P 0P 1M ，它的水平边P 0M 的长度为△x ，竖直边MP 1的长度为△y ，因此这条割线的斜率为：10tan MP y P M xα∆==∆．如果图A -6中的曲线代表函数y =f (x )，则割线P 0P 1的斜率就等于函数在 0x x =附近的增量比yx∆∆，切线0PT 的低斜率0tan α是10P P →时，割线P 0P 1斜率的极限值，即10100tan lim tan lim ()P P P P yf x xαα→→∆'===∆；所以导数的几何意义是切线的斜率． §3．导数的运算在上节里只给出了导数的定义，本节将给出以下一些公式和定理，利用它们可以把常见函数的导数求出来．3．1 基本函数的导数公式（1）y ＝f (x )＝C (常量)：00()()()lim lim 0x x f x x f x C C y f x x x ∆→∆→+∆--''====∆∆；（2）y ＝f (x )＝x ：000()()()()lim lim lim 1x x x f x x f x x x x x y f x x xx ∆→∆→∆→+∆-+∆-∆''=====∆∆∆；（3）y ＝f (x )=x 2：22000()()()()limlim lim(2)2x x x f x x f x x x x y f x x x x x x∆→∆→∆→+∆-+∆-''====+∆=∆∆；（4）y ＝f (x )＝x 3：33222000()()()()limlim lim[33()]3x x x f x x f x x x x y f x x x x x x x x∆→∆→∆→+∆-+∆-''====+∆+∆=∆∆；（5）y ＝f (x )＝1x ：0()()()lim x f x x f x y f x x ∆→+∆-''===∆011lim x x x x x∆→-+∆=∆ 200()11lim lim ()()x x x x x x x x x x x x x∆→∆→-+∆-===-+∆⋅∆+∆；（6）y ＝f (x )000()()()limlim x x x f x x f x y f x x ∆→∆→∆→+∆-''====∆limlimx x ∆→∆→===上面推导的结果可以归纳成一个普遍公式：当ny x =时，1n n dx y nx dx-'==，（n 为任何数），（A ．33）．例如：当1n =时，()y f x x ==，1dxy dx '==；当2n =时，2()y f x x ==，22dx y x dx '==；当3n =时，3()y f x x ==，323dx y x dx '==；当1n =-时，11()y f x x x -===，2211()(1)d y x dx x x-'==-=-；当12n =时，12()y f x x ===1212y x -'===利用（A ．33）式还可以计算其它幂函数的导数（见表A -2）．除了幂函数n x 外，物理学中常见的基本函数还有三角函数、对数函数和指数函数．现在只给出这些函数的导数公式（见表A -2）而不推导，解题时可以直接引用．3．2 有关导数运算的几个定理定理一：[()()]d du dvu x v x dx dx dx ±=±，（A ．34）．证明：00[()()]lim lim[]x x d u v u v du dvu x v x dx x x x dx dx∆→∆→∆±∆∆∆±==±=±∆∆∆．定理二：[()()]()()d du dvu x v x v x u x dx dx dx ⋅=+，（A ．35）．证明：00[()][()]u(x)v(x)v()()[()()]lim lim x x d u x u v x v x u u x v u vu x v x dx x x∆→∆→+∆+∆-∆+∆+∆∆⋅==∆∆ 0lim[()()]()()x u v du dvv x u x v x u x x x dx dx∆→∆∆=+=+∆∆．定理三：2()()()[]()[()]du dv v x u x d u x dx dx dx v x v x -=，（A ．36）．证明：000()()()[()]()[()]()()()()()[]lim lim lim()[()]()[()]()x x x u x u u x d u x u x u v x v x v u x v x u u x v v x v v x dx v x x v x v v x xv x v v x x ∆→∆→∆→+∆-+∆-+∆∆-∆+∆===∆+∆∆+∆∆ 20()()()()lim [()]()[()]x u v du dv v x u x v x u x x x dx dx v x v v x v x ∆→∆∆--∆∆==+∆．定理四：[()]d du dvu v x dx dv dx=⋅，（A ．37）．证明：00[()][()]()()[()]lim lim[]x x d u v x x u v x u v v v v v u v x dx x v x ∆→∆→+∆-+∆-∆==⋅∆∆∆00()()lim[]lim[]x x u v v v v v du dvv x dv dx∆→∆→+∆-∆=⋅=⋅∆∆ 例1．求22y x a =±（a 为常量）的导数．解：22202dy dx da x x dx dx dx=±=±=．例2．求ln x y a =（a 为常量）的导数．解：ln ln 110dy d x d a dx dx dx x x=-=-=．例3．求2y ax =（a 为常量）的导数．解：222022dy da dx x a x a x ax dx dx dx=⋅+⋅=⋅+⋅=．例4．求2x y x e =的导数．解：22222(2)xx x x x dy dx de e x x e x e x x e dx dx dx=+=⋅+⋅=+．例5．求23251x y x -=+的导数．解：2222222(32)(51)(51)(32)6(51)(32)515610(51)(51)(51)d x d x x x dy x x x x x dx dx dx x x x -++--⋅+--⋅++===+++．例6．求tan y x =的导数．解：2222sin cos cos sin sin cos cos sin (sin )1(tan )()sec cos cos cos cos d x d x x xdy d d x x x x x dx dx x xdx dx dx x x x x -⋅-⋅-======．例7．求cos()y ax b =+（a 、b 为常量）的导数．解：令v ax b =+，()cos y u v v ==，则(sin )sin()dy du dvv a a ax b dx dv dx=⋅=-⋅=-+．例8．求y =解：令21v x =-，()y u v ==2dy du dv x dx dv dx =⋅=例9．求22ax y x e -=（a 为常量）的导数．解：令v u e =，2v ax =-，则2222222(2)2(1)v ax dy dx du dvu x xu x e ax x ax e dx dx dv dx-=+⋅=+⋅⋅-=- §4．微分和函数的幂级数展开 4．1 微分自变量的微分，就是它的任意一个无限小的增量△x ．用dx 代表x 的微分，则dx =△x ．（A ．38）一函数y =f (x )的导数f ′(x )乘以自变量的微分dx 即为该函数的微分，用dy 或df (x )表示，即dy =df (x )=f ′(x )dx ，（A ．39）所以()dyf x dx'=，（A ．40）在之前曾把导数写成dydx的形式，是把它作为一个整体引入的．当时它虽然表面上具有分数的形式，但在运算时并不象普通分数那样可以拆成“分子”和“分母”两部分．在引入微分的概念之后，就可把导数看成微分dy 与dx 之商（所谓“微商”），即一个真正的分数了．把导数写成分数形式，常常是很方便的，例如，把上节定理四（A ．37）式的左端[()]d u v x dx 简写成du dx，则该式化为du du dvdx dv dx =⋅；此公式从形式上看和分数运算法则一致，很便于记忆．下面看微分的几何意义．图A -8是任一函数y ＝f (x )的图形，P 0（x 0，y 0）和P 1（x 0+△x ，y0+△y ）是曲线上两个邻近的点，P 0T 是通过P 0的切线．直角三角形△P 0MP 1的水平边0P M x =∆，竖直边1MP y =∆（见图8A -）．设0PT 与1MP 的交点为N ，则0tan MNMNNP M xPM ∠==∆，但0tan NP M ∠为切线P 0T 的斜率，它等于x =x 0处的导数f ′(x 0)，因此00()tan dy f x x NP M x MN '=∆=∠⋅∆=．所以微分dy 在几何图形上相当于线段MN 的长度，它和增量1y MP ∆=相差1NP 一段长；从上一节计算导数时取极限的过程可以看出，dy 是y ∆中正比于x ∆的那一部分，而1NP 则是正比于(△x )2以及△x 更高幂次的各项之和[例如对于函数y =f (x )＝x 3，△y ＝3x 2△x ＋3x (△x )2＋(△)3，而d y =f ′(x )△x =3x 2△x ]．当△x 很小时，（△x ）2、（△x ）3、…比△x 小得多，1NP 也就比dy 小得多，所以可以把微分dy 叫做增量y ∆中的线性主部．也就是说，若函数在x =x 0的地方像线性函数那样增长，则它的增量就是dy ．4．2幂函数的展开已知一个函数f (x )在x ＝x 0一点的数值f (x 0)，如何求得其附近的点x ＝x 0+△x 处的函数值f (x )＝f (x 0+△x )？若f (x )为x 的幂函数n x ，可以利用牛顿的二项式定理：23000000000(1)(1)(2)()()[1()]()[1()]()[1()()()]2!3!n n nn n x x x n n x n n n x f x x x x x f x f x n x x x x x ∆∆∆-∆--∆==+∆=+=+=++++⋅⋅⋅000(1)(1)()()!nmm n n n m x f x m x =-⋅⋅⋅-+∆=∑，（A ．41）此式适用于任何n （整数、非整数、正数、负数等等）．若n 为正整数，则上式中的级数在M ＝n 的地方截断，余下的项自动为0，否则上式为无穷级数．不过当△x <<x 0时，后面的项越来越小，只需保留有限多项就足够精确了．不要以为数学表达式越精确越好．如图A -9中A 、B 两点间的水平距离为l ，若将B 点竖直向上提高一个很小的距离a (a <<l)到达B ′，问AB ′之间的距离比AB 增加了多少？利用勾股定理易得距离的增加量为22l l a l ∆=+-．这是个精确的公式，但没有给出一个鲜明的印象，究竟△l 是随a 怎样变化的？若用二项式定理将它展开，只保留到最低级的非0项，则有12222221[1()1]{[1()]1}[1()1]()222a a a l a a l l l l l l l l l∆=+=+-=++⋅⋅⋅-≈=，即△l 是正比于a平方增长的，属二级小量．这种用幂级数展开来分析主要变化趋势的办法，在物理学里是经常用到的．4．3泰勒展开非幂函数(譬如s in x 、e x )如何作幂级数展开？这要用泰勒(Taylor)展开．下面用一种不太严格，但简单明了的办法将它导出．假设函数f (x )在x =x 0处的增量△f =f (x )－f (x 0)能够展成△x ＝x －x 0的幂级数：001()()()mm m f x f x a x x ∞=-=-∑，（A ．42）则通过逐项求导可得101()()m m m f x ma x x ∞-='=-∑；当x →x 0时，m ＞1的项都趋于0，于是有f ′(x 0)＝a 1；再次求导，得202()(1)()m m m f x m m a x x ∞-=''=--∑，当x →x 0时，m ＞2的项都趋于0，于是有f (x 0)＝2a 2；如此类推，一般地说，对于M阶导数有()0()!M M fx M a =；于是(A ．42)式可以写为：()000()()()()!m m m Mf x f x f x x x m ∞=-=-∑，(A ．43)．若定义第0阶导数f (0)(x )就是函数f (x )本身，则上式还可进一步简写为：()000()()()!m m m f x f x x x m ∞==-∑，(A ．44)．上述(A ．43)或(A ．44)式称为泰勒展开式，它在物理学中是非常有用的公式．下面在表A -3中给出几个常见函数在x 0＝0或1处的泰勒展开式．函数展开式收敛范围12(1)x ± 234111113113512242462468x x x x ⋅⋅⋅⋅⋅⋅±-±-±⋅⋅⋅⋅⋅⋅⋅⋅⋅1x ≤ 32(1)x ± 234331311311312242462468x x x x ⋅⋅⋅⋅⋅⋅±+±+±⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1x ≤52(1)x ± 234553531531112242462468x x x x ⋅⋅⋅⋅⋅⋅±+±+±⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1x ≤ 12(1)x -± 234113135135712242462468x x x x ⋅⋅⋅⋅⋅⋅±+±+±⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1x <32(1)x -± 234335357357912242462468x x x x ⋅⋅⋅⋅⋅⋅±+±+±⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1x < 52(1)x -±2345575795791112242462468x x x x ⋅⋅⋅⋅⋅⋅±+±+±⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1x <1(1)x -±2341x x x x ±+±+±⋅⋅⋅1x < 2(1)x -±23412345x x x x ±+±+±⋅⋅⋅1x < sin x3573!5!7!x x x x -+-+⋅⋅⋅ x <∞ cos x24612!4!6!x x x -+-+⋅⋅⋅ x <∞ tan x 35791217623153152835x x x x x +++++⋅⋅⋅ x <∞x e 23411!2!3!4!x x x x +++++⋅⋅⋅ x <∞ln(1)x + 234234x x x x -+-+⋅⋅⋅11x -<≤ ln(1)x -234()234x x x x -++++⋅⋅⋅11x -≤<§55．1几个物理中的实例（1）变速直线运动的路程大家都熟悉匀速直线运动的路程公式．若物体的速率是v ，则它在t a 到t b 一段时间间隔内走过的路程是s ＝v (t b －t a )，(A ．45)．对于变速直线运动来说，物体的速率v 是时间的函数：v ＝v (t )，函数的图形是一条曲线(见图A -10a )，只有在匀速直线运动的特殊情况下，它才是一条直线(参见图A -4b )．对于变速直线运动，(A .45)式已不适用．但是，可以把t ＝t a 到t ＝t b 这段时间间隔分割成许多小段，当小段足够短时，在每小段时间内的速率都可以近似地看成是不变的．这样一来，物体在每小段时间里走过的路程都可以按照匀速直线运动的公式来计算，然后把各小段时间里走过的路程都加起来，就得到t a 到t b 这段时间里走过的总路程．设时间间隔(t b －t a )被t ＝t 1(=t a )、t 2、t 3、…、t n 、t b 分割成n 小段，每小段时间间隔都是△t ，则在t 1、t 2、t 3、…、t n 各时刻速率分别是v (t 1)、v (t 2)、v (t 3)、…、v (t n )．若把各小段时间的速率v 看成是不变的，则按照匀速直线运动的公式，物体在这些小段时间走过的路程分等于v (t 1)△t 、v (t 2)△t 、v (t 3)△t 、…、v (t n )△t ．于是，在整个(t b -t a )这段时间里的总路程是1231()()()()()nn i i s v t t v t t v t t v t t v t t ==∆+∆+∆+⋅⋅⋅+∆=∆∑，(A ．46)．现在再看看上式的几何意义．在函数v ＝v (t )的图形中，通过t =t 1、t 2、t 3、…、t n 各点垂线的高度分别是v (t 1)、v (t 2)、v (t 3)、…、v (t n )(见图A -10b )，所以v (t 1)△t 、v (t 2)△t 、v (t 3)△t 、…、v (t n )△t 就分别是图中那些狭长矩形的面积，而1()ni i v t t=∆∑则是所有这些矩形面积的总和，即图中画了斜线的阶梯状图形的面积．在上面的计算中，把各小段时间△t 里的速率v 看做是不变的，实际上在每小段时间里v 多少还是有些变化的，所以上面的计算并不精确．要使计算精确，就需要把小段的数目n 加大，同时所有小段的△t 缩短(见图A -10c )．△t 越短，在各小段里v 就改变得越少，把各小段里的运动看成匀速运动也就越接近实际情况．所以要严格地计算变速运动的路程s ，就应对(A ．46)式取n →∞、△t →0的极限，即01lim ()ni t i n s v t t ∆→=→∞=∆∑，(A ．47)．当n 越来越大，△t 越来越小的时候，图A -10中的阶梯状图形的面积就越来越接近v (t )曲线下面的面积(图A -10d)．所以(A ．47)式中的极限值等于(t b －t a )区间内v (t )曲线下的面积．总之，在变速直线运动中，物体在任一段时间间隔(t b －t a )里走过的路程要用(A ．47)式来计算，这个极限值的几何意义相当于这区间内v (t )曲线下的面积．（2）变力的功当力与物体移动的方向一致时，在物体由位置s ＝s a 移到s ＝s b 的过程中，恒力F 对它所作的功为：A ＝F (s b －s a )（A ．48)；若力F 是随位置变化的，即F 是s 的函数：F ＝F (s )，则不能运用(A ．48)式来计算力F 的功．此时，也需要象计算变速运动的路程那样，把(s b －s a )这段距离分割成n 个长度为△s 的小段(见图A -11)：并把各小段内力F 的数值近似看成是恒定的，用恒力作功的公式计算出每小段路程△s 上的功，然后加起来取n →∞、△s →0的极限值．具体地说，设力F 在各小段路程内的数值分别为F (s 1)、F (s 2)、F (s 3)、…、F (s n )，则在各小段路程上力F 所作的功分别为F (s 1)△s 、F (s 2)△s 、F (s 3)△s 、…、F (s n )△s ，在(s b －s a )整段路程上力F 的总功A 就近似地等于1()ni i F s s =∆∑；因为实际上在每一小段路程上加F 都是变化的，所以严格地计算，还应取n →∞、△s →0的极值，即01lim ()ni t i n A F s s ∆→=→∞=∆∑，(A ．49)．同上例，这极限值应是(s b －s a )区间内F (s )下面的面积(见图A -12)．5．2定积分以上两个例子表明，许多物理问题中需要计算象(A ．47)和(A ．49)式中给出的那类极限值．概括起来说，就是要解决如下的数学问题：给定一个函数f (x )，用x ＝x 1(=a )、x 2、x 3、…、x n 、b 把自变量x 在(b －a )区间内的数值分成n 小段，设每小段的大小为△x ，求n →∞、△x →0时1()ni i f x x =∆∑的极限；通常把这类形式的极限用符号()ba f x dx ⎰来表示，即01()lim ()nbi ax i n f x dx f x x ∆→=→∞=∆∑⎰，(A ．50)；()baf x dx ⎰叫做x a =到x b =区间内()f x 对x 的定积分，()f x 叫做被积函数，b 和a 分别叫做定积分的上限和下限．用定积分的符号来表示，(A ．47)和(A ．49)式可分别写为()b at t s v t dt =⎰，(A ．51)、()bas s A F s ds =⎰，(A ．52)．在变速直线运动的路程公式(A ．51)里，自变量是t ，被积函数是v (t )，积分的上、下限分别是t b 和t a ；在变力作功的公式(A ．52)里，自变量是s ，被积函数是F (s )，积分的上、下限分别是s b 和s a ．求任意函数定积分的办法有赖于下面关于定积分的基本定理：若被积函数f (x )是某个函数Ф(x )的导数，即f (x )=Ф′(x )，则在x ＝a 到x ＝b 区间内f (x )对x 的定积分等于Ф(x )在这区间内的增量，即()()()ba f x dxb a =Φ-Φ⎰，(A ．53)．下面来证明上述定理．在a ≤x ≤b 区间内任选一点x i ，首先考虑Ф(x )在x =x i 到x =x i +△x =x i+1区间的增量△Ф(x i )=Ф(x i+1)-Ф(x i )：()()i i x x x x ∆Φ∆Φ=⋅∆∆，当0x ∆→时，可用Ф(x )的导数()d x dx Φ'Φ=代替x∆Φ∆；但按照定理的前提，Ф′(x )=f (x )，故△Ф(x i )≈Ф′(x i )△x =f (x i )△x 式中≈表示“近似等于”，若取△x →0的极限，上式就是严格的等式．把a ≤x ≤b 区间分成n －1小段，每段长△x ；上式适用于每小段．根据积分的定义和上式，有：12112100()lim[()()()]lim[()()()]bn n ax x n n f x dx f x x f x x f x x x x x --∆→∆→→∞→∞=∆+∆+⋅⋅⋅+∆=∆Φ+∆Φ+⋅⋅⋅+∆Φ⎰2132110lim{[()()][()()][()()]}()()n n n x n x x x x x x x x -∆→→∞=Φ-Φ+Φ-Φ+⋅⋅⋅+Φ-Φ=Φ-Φ因x 1＝a ，xn ＝b ，于是得(A .53)式，至此定理证毕．下面看看函数Ф(x )在f -x 图(见图A -13)中所表现的几何意义．如前所述，△Ф(x i )=Ф(x i+1)-Ф(x i )=f (x i )△x ，正是宽为△x 、高为()i i i f x x P =的一个矩形（即图13A -中的1i i i x x NP +）的面积．它和曲线段P i P i+1下面的梯形x i x i+1P i+1P i 的面积只是相差一小三角形P i NP i ＋1的面积．当△x →0时，可认为△Ф(x i )就是梯形x i x i+1P i+1P i 的面积．既然当x 由x i 变到x i+1时，Ф(x )的增量的几何意义是相应区间f -x 曲线下的面积，则Ф(x )本身的几何意义就是从原点O 到x 区间f -x 曲线下面的面积加上一个常量C ＝Ф(0)．例如Ф(x i )的几何意义是图形Ox i P i P 0的面积加C ，Ф(x i ＋1)的几何意义是图形Ox i+1P i+1P 0的面积加C ，等等．这样，△Ф(x i )=Ф(x i+1)-Ф(x i )就是：(Ox i+1P i+1P 0的面积+C )-(Ox i P i P 0的面积+C )=x i x i+1P i+1P i 的面积，而Ф(b )-Ф(a )的几何意义是：(ObP b P 0的面积+C )－(OaP a P 0的面积+C )＝abP b P a 的面积．它相当于定积分()ba f x dx ⎰的值．5．3不定积分及其运算在证明了上述定积分的基本定理之后，就可以着手解决积分的运算问题了．根据上述定理，只要求得函数Ф(x )的表达式，利用(A .53)式立即可以算出定积分()ba f x dx ⎰来，那么，给出了被积函数()f x 的表达式之后，怎样去求Ф(x )的表达式呢？上述定理说明，Ф′(x )=f (x )，所以这就相当于问f (x )是什么函数的导数．由此可见，积分运算是求导的逆运算．如果f (x )是Ф(x )的导数，可以称Ф(x )是f (x )的逆导数或原函数．求f (x )的定积分就可以归结为求它的逆导数或原函数．在上节里讲了一些求导数的公式和定理，常见的函数都可以按照一定的法则把它们的导数求出来．然而求逆导数的问题却不像求导数那样容易，而需要靠判断和试探．例如，知道了Ф(x )＝x 3的导数Ф′(x )＝3x 2，也就知道了F (x )＝3x 2的逆导数是Ф(x )＝x 3；这时，如果要问函数f (x )＝x 2的逆导数是什么，那么就不难想到，它的逆导数应该是x 3/3；这里要指出一点，即对于一个给定的函数f (x )来说，它的逆导数并不是唯一的．Ф1(x )＝x 3/3是f (x )＝x 2的逆导数，Ф2(x )＝x 3/3＋1和Ф3(x )=x 3/3－5也都是它的逆导数，因为Ф1′(x )、Ф2′(x )、Ф3′(x )都等于x 2.一般说来，在函数f (x )的某个逆导数Ф(x )上加一任意常量C ，仍旧是f (x )的逆导数．通常把一个函数f (x )的逆导数的通式Ф(x )＋C 叫做它的不定积分，并记作()f x dx ⎰，于是()()f x dx x C =Φ+⎰，(A ．54)．因在不定积分中包含任意常量，它代表的不是个别函数，而是一组函数．。

(完整word版)微积分在物理竞赛中的应用

VdV (L1 L2 ) 2x g,
dx
L1 L2
V
VdV
x (L1 L2 ) 2x gdx
0
0 L1 L2
V
2g L1 L2
(L1 L2 )x x2 .
令 x L2 , 可以求得链条滑离钉子时的速度大小
V 2L1L2 g L1 L2
再由V dx , 得到 dt
dx dt
。
小球 A 相对地的加速度
aA
a
A
aB
，取如图二所示的坐标系，
则有
a Ax
aA
cos
aB
sin 2 2(1 sin 2 )
g,
a Ay
aA sin
2sin 2 (1 sin 2 )
g.
旋转液体的液面
以等角速度 ω 旋转的液体，液面的形状如何求得？解答：
假设它的剖面是一条曲线，Y 轴是转轴，旋转面以 Y 轴为对称轴，此时在
y
m k
(V0
sin 0
mg k
)(1
kt
em
)
mg k
t.
由（3）（4）两式消去 t,得到有阻力时的轨道方程
（4）
y
(tg 0
mg kV0 cos0
)x
m2g k2
ln(1
mV0
k c os 0
)x
m2g k2
ln(1
k mV0 cos
x).
显然由于空气阻力的作用，抛体的轨道不再是简单的抛物线了，实际轨道将比理想轨
2g L1 L2
(L1 L2 )x x2
x
dx
t
0 （L1 L2）x x 2 0
积分，得到

微积分在物理解题方面的应用

形式上的应用：例：1，质点在力F= --kv 的作用下，初速为V0 开始运动，求质点运动距离。

以上在解题过程中，利用了导数的微商式dy/dx以及微分可进行四则运算的性质，将答案“凑”出来，因为对方程变形时，不需要考虑物理意义（并不是没有物理意义），这属于最基础的形式上的应用运动学中常见的微商变形：dv/dt=(dv/dw)*(dw/dt)=β*(dv/dw)dv/dt=（dv/dθ）*（dθ/dt）=w(dv/dθ)剩下的，大家可以自己在学习中总结。

微元法：数学基础：关于微分的相关概念，性质，可以自行翻阅“高数”或者“微积分”或者“数学分析”教材。

（很重要）微元法：是指将所需研究的物理对象，先微分成非常小的微元，然后研究单个微元的性质（在研究中一般会用到近似关系），找出规律，再求出整体性质的方法.微元法的一般步骤：一，写出待求量的微元表达式。

二，给出积分表达式。

三，确定积分上下限。

四，算吧= =+来来来，看看例题。

例1：求弹簧弹性势能公式例2：（变力做功）质量为m的物体以v的速度在光滑水平面上沿x正方向运动，当它到达o点是，撞击一劲度系数为k的轻弹簧，并开始受到摩擦力的作用，摩擦因数是位置的函数，可表示为μ=ax （a比较小）。

求物体第一次返回到o点时的速度。

3 求各种转动惯量杆，圆环，圆盘，圆柱等等。

4一个质量为m的圆环，其于桌面之间的动摩擦因数为μ，求当该圆环在桌面上绕着通过圆心且垂直于桌面的转轴旋转时，所受的摩擦力矩。

变：将圆环改为圆盘5一无限长直导线，均匀带电，电荷线密度为λ，(λ>0) A，B 两点到直导线的垂直距离分别为a，b，若以A点为零电势点，B点电势为（仅用场强推导）（暂时不用看）5有重物m，用缠绕在水平柱上的轻绳将其拉住缠绕了两圈，柱与绳间的摩擦因数为μ，为使得重物不下落，所用最小拉力为多大。

（备用）积分表达式的建立：一，直接利用物理量以及物理定律的微分或者导数形式，求得积分式。

微积分在高中物理中的应用

121微积分在高中物理中的应用邓圭恩微积分是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支。

它是数学的一个基础学科。

微积分是指求函数曲线的切线斜率、求函数图形的面积、求图形的体积的一种方法和过程，在高中物理概念、物理定律都包涵微积分的思想。

本文分析了微积分在高中物理的一些具体应用，目的是理解微积分思想的同时也能熟练地运用微积分来解决物理中的问题。

数学作为物理学中的重要工具，它即能准确而又简洁地表达物理概念和规律，也能为物理提供思维语言和方法。

运用数学方法解决物理问题是高中阶段学习目标之一，高中生掌握求导和积分的思想及方法，是为物理学习提供了即方便实用又强大的工具。

1微积分在高中动力学中的应用 1.1利用微积分解决变速运动问题在高中阶段，变速运动问题往往是许多同学的难点，很多变速运动问题的模型都很难建立，对许多同学甚至是教师的思维能力都是一个很大的考验。

但微积分知识和思想能帮助大家用更简洁普适的模型来解决这方面的问题，比如对于下面这一道题：例2：狐狸沿半径R 的圆轨道以恒定速率v 奔跑，在狐狸出发的同时，猎犬从圆心O 出发以相同的速率v 追击过程中，圆心、猎犬和狐狸始终连成一直线。

（1）建立相应坐标系，求出猎犬运动的轨道方程，并画出轨道曲线。

（2）判断猎犬能否追上狐狸。

这道题是一道经典的物理竞赛题，现在也是被选入许多高校的自招理论试题，其经典解法有很多，但绝大多数都复杂冗长，很多同学并不能很好的理解。

而如果我们选用微积分的方法，就会得到很容易为大家所接受，也较容易的解法了。

取圆心O 为坐标原点，从O 到狐狸的初始位置设置极轴，建立极坐标系。

我们先得到猎犬切向、径向加速度、速度与猎犬所在的r、θ的关系狐狸的圆运动角速度为：Rv dt d ==ωθ当狐狸在θ角位置时，圆心O、猎犬D 及狐狸F 共线，如图所示故猎犬的横向速度为猎犬的径向与切向速度为：r Rv dt d rv ==θθ，vRr v v v r 22221-=-=θ 径向与切向加速度为：R r R v v dtd r dt d dt dr r a 122222-⋅==+⋅=ωθθθv r a R r dt dr dr dv r dt dv dt d r d r d r r r 22222222)(-=-⋅=-=-=ωωθθ 由r R v v r d dr r22-==θθ积分：⎰⎰=-θθθ022d r R dr r 可得猎犬的轨道方程为: θ=Rr arcsin 即θsin R r =猎犬的轨道曲线如图中虚线所示。

物理竞赛数学知识——微积分

则，令，得
利润为，比遵守协议多，可见违约金至少为
[变化]成本为c，生产能力足够，价格由商家决定，而顾客根据价格是否购买。顾客购买量商家1产品的量，，购买商家2产品的量。商家的利润定义为。两商家都足理性，追求利益最大化。格有一个心理极限，只要价格低于这个极限就会购买，如果有两个商品价格都小于心理极限，则会随机购买一个。再假设所有人的心理价格是从0到M均匀分布的
例题精讲
【例2】判定下列函数在其定义域内是否有极值，求出极值并说明是否极大值、极小值。
；；；，
【答案】 1 极小：x=0,y=0
2 极小：，
3极小：，极大：
4极值：，不是极大也不是极小
4极大：
【例3】求下列函数在各自区间上的最大值和最小值（自学）
；；
【答案】 1 极值点：极小：，不在区间内。边界点；由于函数连续，有下界无上界，所以有最小值点，就在是边界取到：
B
招
不招
招
（8，8）
（10，1）
不招
（10，1）
（2，2）
[解析]
/*段子纳什均衡年轻的男性数学、物理工作者要做点成就出来，动力往往跟女人有关。纳什这家伙也不例外。纳什很有才，二十多岁就当上了教授，但是还是单身。一天他和一群狐朋狗友一起去酒吧喝酒，看见了一位漂亮mm，于是大家都想搭讪。别人都在想怎样搭讪才能成功，此时纳什的天赋表现出来了：他想，如果大家一拥而上一起搭讪，mm必然愤怒，大家都失败；如果让一个人搭讪，其他人帮腔，成功概率就会大得多，然后每次去酒吧大家轮流来，每人都有好处。由此出发他提出了著名的纳什均衡理论，大体意思是说每人都以自己利益最大化为标准，最后团体必然会形成一个稳定的策略。然后呢…然后纳什就疯了…直到几十年后他被授予了诺贝尔经济学奖才好一点。具体的情况推荐大家看《美丽心灵》，不看人生不完整*/

微积分在物理学中的应用

微积分在物理学中的应用微积分是数学的一个重要分支，它研究函数的变化和变化率，是物理学中不可或缺的工具。

微积分的应用范围广泛，尤其在物理学中，它发挥着重要的作用。

本文将介绍微积分在物理学中的几个重要应用。

一、速度和加速度的计算在物理学中，速度和加速度是描述物体运动的重要概念。

微积分可以帮助我们计算速度和加速度。

假设一个物体在时间t内的位移为s(t)，那么速度v(t)可以通过求位移函数的导数来计算，即v(t) =ds(t)/dt。

同样地，加速度a(t)可以通过求速度函数的导数来计算，即a(t) = dv(t)/dt。

微积分的求导运算可以帮助我们精确地计算速度和加速度，从而更好地理解物体的运动规律。

二、曲线的长度和曲率的计算在物理学中，我们经常需要计算曲线的长度和曲率。

微积分可以帮助我们解决这些问题。

对于一条曲线C，我们可以将其分割成无数个小线段，然后计算每个小线段的长度，再将这些长度相加，就可以得到曲线的长度。

这个过程可以通过微积分中的积分运算来实现。

同样地，曲率描述了曲线的弯曲程度，可以通过微积分中的导数运算来计算。

微积分的这些运算使得我们能够准确地计算曲线的长度和曲率，从而更好地理解曲线的性质。

三、力和功的计算在物理学中，力和功是描述物体受力和做功的重要概念。

微积分可以帮助我们计算力和功。

假设一个物体在位移s下受到力F的作用，那么力可以通过求位移函数的导数来计算，即 F = dW(s)/ds。

同样地，功可以通过力和位移的乘积来计算，即W = ∫Fds。

微积分的这些运算使得我们能够准确地计算力和功，从而更好地理解物体受力和做功的过程。

四、体积和质量的计算在物理学中，体积和质量是描述物体性质的重要概念。

微积分可以帮助我们计算体积和质量。

对于一个具有复杂形状的物体，我们可以将其分割成无数个小体积，然后计算每个小体积的大小，再将这些大小相加，就可以得到物体的体积。

同样地，质量可以通过微积分中的积分运算来计算。

宝典微积分在物理比赛中的应用

宝典微积分在物理比赛中的应用求解在立体斜面上滑动的物体的速度,,tg,一物体放在斜面上，物体与斜面间的摩擦因数,恰好满足，为斜面的倾角。

,今使物体获得一水平速度而滑动，如图一，V0求:物体在轨道上任意一点的速度V与的关,系，设为速度与水平线的夹角。

,,G解:物体在某一位置所受的力有:重力，,,,N弹力以及摩擦力。

摩擦力总是与运动速度V的方向相反，其数值ff f,,N,,mgcos,,tg,mgcos,,mgsin,,,重力在斜面上的分力为，如图二，将GG11,,,分解为两个分力:是沿轨迹切线方向的分GG11,,,力，,;,是沿G,Gsin,,mgsin,sin,G111轨迹法向的分力，,，如图三。

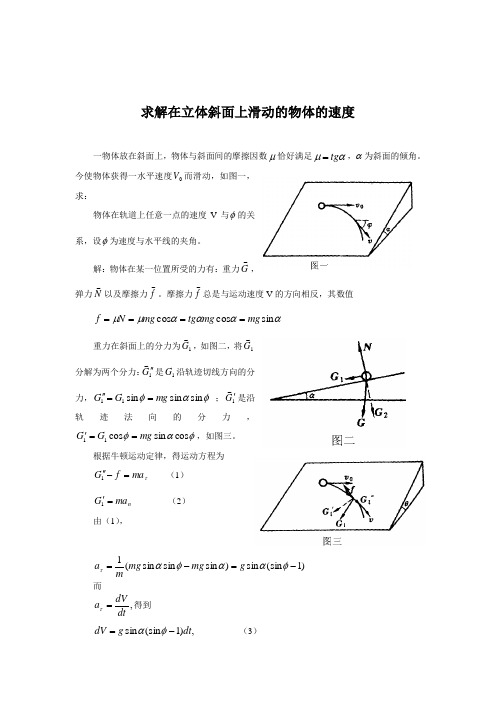
G,Gcos,,mgsin,cos,11根据牛顿运动定律，得运动方程为,,,,,,(1)G,f,ma1,,,,,,,,,,(2)G,ma1n由(1)，1a,(mgsin,sin,,mgsin,),gsin,(sin,,1) ,m而dVa,,得到 ,dt,,,,,,,,,,(3) dV,gsin,(sin,,1)dt,式中是t的函数，但是这个函数是个未知函数，因此还不能对上式积分，要设法在,,与t中消去一个变量，才能积分，注意到dS1ds,,,,,,,,,,,,,,(4) dt,,d,VVd,ds,而表示曲线在该点的曲率半径，根据(2)式， d,2V,,mgsincos,m,,,,(5) ,由式(3)(4)(5)，可得到 dV,(tg,,sec,)d,, VV,dV， ,(tg,,sec,)d,,,0V0V积分，得到V， ln,,lncos,,ln(sec,，tg,),,ln(1，sin,)V0V0 V,.，,1sin运用积分法求解链条的速度及其时间一条匀质的金属链条，质量为m，挂在一个光滑的钉子上，一边长度为，另一边长度为而且，如LL,0,L,L2211图一。

试求:链条从静止开始滑离钉子时的速度和所需要的时间。

微积分在物理学中的应用

微积分在物理学中的应用微积分是数学的一个重要分支，它研究函数的变化率和积分。

在物理学中，微积分是一种强大的工具，被广泛应用于解决各种物理问题。

本文将介绍微积分在物理学中的应用，并探讨其重要性和影响。

1. 运动学运动学是物理学的一个重要分支，研究物体的运动规律。

微积分在运动学中起着至关重要的作用。

通过微积分，我们可以求解物体的速度、加速度和位移等运动参数。

例如，当我们知道一个物体的位移随时间的变化规律时，可以通过微积分求解出其速度和加速度。

这些参数对于研究物体的运动规律和描述力学系统非常重要。

2. 力学力学是物理学的基础，研究物体受力和运动规律之间的关系。

微积分在力学中有广泛的应用。

通过微积分，我们可以求解物体受力后的运动轨迹和速度变化。

例如，在牛顿第二定律中，通过对加速度随时间的变化进行积分，可以求解出物体的速度和位移。

这些结果对于研究物体的运动和力学系统的稳定性具有重要意义。

3. 电磁学电磁学是物理学的一个重要分支，研究电荷和电磁场之间的相互作用。

微积分在电磁学中也有广泛的应用。

例如，在电场和磁场的计算中，我们需要对电荷分布和电流密度进行积分。

通过微积分，我们可以求解出电场和磁场在空间中的分布情况。

这些结果对于理解电磁现象和设计电子设备非常重要。

4. 热力学热力学是物理学的一个重要分支，研究能量转化和系统的宏观性质。

微积分在热力学中也有重要的应用。

例如，在理想气体状态方程中，通过对压强和体积随温度的变化进行积分，可以求解出气体的内能和焓等参数。

这些参数对于研究能量转化和系统平衡具有重要意义。

5. 光学光学是物理学的一个重要分支，研究光的传播和相互作用。

微积分在光学中也有广泛的应用。

例如，在光的传播和折射中，我们需要对光线的路径进行积分。

通过微积分，我们可以求解出光线在介质中的传播路径和折射角度。

这些结果对于研究光学现象和设计光学器件非常重要。

6. 量子力学量子力学是物理学的一个重要分支，研究微观粒子的行为和相互作用。

微积分在物理学中的应用

微积分在物理学中的应用微积分是数学的一个重要分支，它在物理学中有着广泛的应用。

物理学研究的是自然界中的各种现象和规律，而微积分则为我们提供了一种强大的工具，帮助我们理解和描述这些现象和规律。

本文将探讨微积分在物理学中的应用，并且通过几个具体例子来说明其重要性。

首先，微积分在物理学中的一个重要应用是对物体的运动进行描述和分析。

牛顿运动定律是经典力学的基础，而微积分则是对运动进行建模和求解的数学工具。

例如，当我们研究一个物体在一维直线上的运动时，我们可以通过微积分的方法求解物体的位移、速度和加速度之间的关系。

通过对位移-时间曲线进行微分，我们可以得到速度-时间曲线；通过对速度-时间曲线进行微分，我们可以得到加速度-时间曲线。

这样，我们就可以通过微积分来分析物体在不同时间点的位置、速度和加速度等信息。

其次，微积分在物理学中的另一个重要应用是对物体的力学性质进行研究。

力学是物理学的一个分支，研究物体的运动和相互作用。

微积分可以帮助我们理解和描述物体受力的变化和作用力的大小。

例如，当我们研究一个物体在重力场中的运动时，我们可以通过微积分的方法求解物体所受的重力和空气阻力之间的平衡关系。

通过对受力-时间曲线进行积分，我们可以得到物体的动能和势能之间的关系。

这样，我们就可以通过微积分来分析物体在不同位置和时间点的受力情况。

此外，微积分还在热力学和电磁学等领域中有着重要的应用。

热力学研究的是热能的传递和转化，而微积分可以帮助我们理解和描述热能的变化和流动。

例如，当我们研究一个物体的温度随时间的变化时，我们可以通过微积分的方法求解物体所受的热量和热容之间的关系。

通过对温度-时间曲线进行积分，我们可以得到物体的热能和热功之间的关系。

这样，我们就可以通过微积分来分析物体在不同温度和时间点的热力学性质。

在电磁学中，微积分也起着重要的作用。

电磁学研究的是电荷和电磁场之间的相互作用，而微积分可以帮助我们理解和描述电荷和电场的变化和分布。

高中物理竞赛微积分例题

高中物理竞赛微积分例题伟大的科学家牛顿，有很多伟大的成就，建立了经典物理理论，比如：牛顿三大定律，万有引力定律等；另外，在数学上也有伟大的成就，创立了微积分。

微积分学是微分学和积分学的总称。

它是一种数学思想，‘无限细分’就是微分，‘无限求和’就是积分。

无限就是极限，极限的思想是微积分的基础，它是用一种运动的思想看待问题。

微积分堪称是人类智慧最伟大的成就之一。

在高中物理中，微积分思想多次发挥了作用。

1、解决变速直线运动位移问题匀速直线运动，位移和速度之间的关系x=vt；但变速直线运动，那么物体的位移如何求解呢？例1、汽车以10m/s的速度行驶，到某处需要减速停车，设汽车以等减速2m/s2刹车，问从开始刹车到停车，汽车走了多少公里？【解析】现在我们知道，根据匀减速直线运动速度位移公式就可以求得汽车走了0.025公里。

但是，高中所谓的的匀变速直线运动的位移公式是怎么来的，其实就是应用了微积分思想：把物体运动的时间无限细分。

在每一份时间微元内，速度的变化量很小，可以忽略这种微小变化，认为物体在做匀速直线运动，因此根据已有知识位移可求；接下来把所有时间内的位移相加，即“无限求和”，则总的位移就可以知道。

现在我们明白，物体在变速直线运动时候的位移等于速度时间图像与时间轴所围图形的“面积”，即。

【微积分解】汽车在减速运动这段时间内速度随时间变化的关系，从开始刹车到停车的时间t=5s，?所以汽车由刹车到停车行驶的位移小结：此题是一个简单的匀变速直线运动求位移问题。

对一般的变速直线运动，只要结合物理知识求速度关于时间的函数，画出v－t图像，找“面积”就可以。

或者，利用定积分就可解决.v2、解决变力做功问题恒力做功，我们可以利用公式直接求出；但对于变力做功，我们如何求解呢？例2：如图所示，质量为m的物体以恒定速率v沿半径为R的竖直圆轨道运动，已知物体与竖直圆轨道间的摩擦因数为，求物体从轨道最低点运动到最高点的过程中，摩擦力做了多少功。

微元法和微积分在物理竞赛培优中的运用

微元法和微积分在物理竞赛培优中的运用摘要：在物理竞赛培优教学过程中采用微元法和微积分法拓宽学生的分析、表达和演算；提高学生创造性思维能力。

本文针对几个典型例题采用微元法和微积分法进行分析、讨论、演算和点评，从而认识到微元法和微积分法解题的关键点及数学运算的难易程度，有助于学生根据自己的数学知识采用适当的解题方法快速准确解题。

关键词：微元法；微积分；物理竞赛；培优Application OfInfinitesimal Method and Calculus In PhysicsCompetition Excellent TrainingAbstract: Infinitesimal method and calculus method are notonly applied to expand students’ ability in analysis, expression and calculation duringphysics competition excellent training, but also applied to improve students' creative thinking ability.This paper aims at adopting infinitesimal method and calculus method to analyze, discuss, calculate and comment on several typical problems, so as to realize the key points of solving problems by infinitesimal method and calculus method and the difficulty degree of mathematical operation. This is also helpful for students to solve problems quickly and accurately by using appropriate method according to their own mathematical knowledge.Key Words:Infinitesimal Method；Calculus；Physics competition；Excellent training引言物理学是一切自然学科的基础，它被公认为科学技术发展中最重要的带头学科，物理学对各种工科专业有直接或间接的支撑。

物理竞赛中的数学方法与物理方法-于强

例 4 质量为 m 的小球自 A 点以水平速度 v0 抛出，在重力和空气阻力作用下，经一段时间落到地面上。小球在运动中受到的空气阻力为 f kv ，其中 k 为正的常量，v 为小球在运动中的速度。试求解小球在任一时刻的速度。[3][4] 分析与解本题中小球除了受到重力以外还受到空气阻力，这是一个大小和方向都随着速度变化的变力，难以列方程求解。这里我们把 v0 分解为两个分速度
l 1 N sin ml 2 2 12
研究与地面的接触点 P，地面系中其加速度必沿水平方向，竖直方向加速度分量为零
an cos at sin aC
其中 an
2
l l ， at r 2 2
又根据质心动力学方程有
联立以上三式，将
mg N maC
2mgr 3 J mr 2 2mgr 3 J mr 2
条件为
u
解法二本题也可以先求出圆盘沿切向方向给甲虫的作用力，求出该力所做的功，运用动能定理求解。
对甲虫 M 受力分析如图所示，有
F mg sin mr
利用动力学方程
F mg sin
mr 2 J mg sin mg sin 2 J mr J mr 2
恰为零。根据临界条件，写能量方程临界条件：当甲虫与竖直轴夹角 / 2 时，
1 WF mgr mu 2 2
解得 u
2
2mgr 3 ，即应满足 u J mr 2
2mgr 3 J mr 2
2 寻找动力学与运动学关系，化简求导和微分运算运用求导和微分计算速度和加速度，思路清晰，不易出错。但若遇到计算量较大，或需要一定的技巧的情况时，可以寻找动力学方程和运动学关系使问题简化。 “绳拉小船”是一个常见问题，小船速度很容易求解，加速度则比较难。下面用两种方法求小船的加速度。例 2 在离水面高度为 h 的岸边，有人用绳子拉船靠岸，若人收绳的速率恒为 v0 ，试求船在离岸边距离 s 处时的加速度大小为多少？解法一本题直接利用加速度与速度的导数关系求解如下：设船速为 v ，加速度为 a ，均沿水平方向；为绳与水平面夹角，有

11年大学物理竞赛指导经典力学选例

大学物理竞赛指导-经典力学选例一．质点运动学基本内容：位置，速度，加速度，他们的微积分关系，自然坐标下切、法向加速度，*极坐标下径向速度，横向速度，直线运动，抛物运动，圆周运动，角量描述，相对运动1.运动学中的两类问题(1)已知运动方程求质点的速度、加速度。

这类问题主要是利用求导数的方法。

例1 一艘船以速率ｕ驶向码头P ，另一艘船以速率v 自码头离去，试证当两船的距离最短时，两船与码头的距离之比为： ()()ααcos :cos v v ++u u 设航路均为直线，α为两直线的夹角。

证：设任一时刻船与码头的距离为x 、y ，两船的距离为l ，则有 αc o s 2222xy y x l -+=对ｔ求导，得()()tx y t y x t y y t x x t l l d d c o s 2d d c o s 2d d 2d d 2d d 2αα--+= 将v , =-=t y u t x d d d d 代入上式，并应用0d d =tl 作为求极值的条件，则得 ααcos cos 0yu x y ux +-+-=v v()()ααc o s c o s u y u x +++-=v v由此可求得 ααc o sc o s v v ++=u u y x 即当两船的距离最短时，两船与码头的距离之比为()()ααc o s c o s v : v ++u u(2)已知质点加速度函数a ＝a (x ，v ，t )以及初始条件，建立质点的运动方程。

这类问题主要用积分方法。

例2 一质点从静止开始作直线运动，开始时加速度为a 0，此后加速度随时间均匀增加，经过时间τ后，加速度为2a 0，经过时间2τ后，加速度为3 a 0 ,…求经过时间n τ后，该质点的速度和走过的距离。

解：设质点的加速度为 a = a 0+α t∵ t = τ 时， a =2 a 0 ∴ α = a 0 /τ即 a = a 0+ a 0 t /τ ，由 a = d v /d t ，得 d v = a d tt t a a td )/(d 0000τ⎰⎰+=v v∴ 2002t a t a τ+=v由 v = d s /d t ， d s = v d t t t a t a t s tt s d )2(d d 200000τ+==⎰⎰⎰v 302062t a t a s τ+= t = n τ 时，质点的速度 ττ0)2(21a n n n +=v 质点走过的距离 202)3(61ττa n n s n += 2.相对运动例3 有一宽为l 的大江，江水由北向南流去．设江中心流速为u 0，靠两岸的流速为零．江中任一点的流速与江中心流速之差是和江心至该点距离的平方成正比．今有相对于水的速度为0v 的汽船由西岸出发,向东偏北45°方向航行，试求其航线的轨迹方程以及到达东岸的地点．解：以出发点为坐标原点，向东取为x 轴，向北取为y 轴，因流速为-y 方向，由题意可得 u x = 0u y = a (x -l /2)2＋b 令 x = 0, x = l 处 u y = 0, x = l /2处 u y ＝－u 0，代入上式定出a ＝4u 0/l 2、ｂ＝－u 0，而得 ()x x l l u u y --=204 船相对于岸的速度v (v x ，v y )明显可知是 2/0v v =xy y u +=)2/(0v v ，将上二式的第一式进行积分，有t x 20v = 还有，xy t x x y t y y d d 2d d d d d d 0v v ====()x x l l u --20042v 即 ()x x l l u x y --=020241d d v 因此，积分之后可求得如下的轨迹(航线)方程：302020032422x l u x l u x y v v +-= 到达东岸的地点(x '，y ' )为⎪⎪⎭⎫ ⎝⎛-=='='=003231v , u l y y l x l x二．质点动力学1.牛顿运动定律基本内容：牛顿运动三定律，惯性力(1)运用微积分处理力学问题：根据力函数的形式选择运动定律的形式；正确地分离变量例4 如例4图，光滑水平面上固定一半径为r 的薄圆筒，质量为m 的物体在筒内以初速率v 0沿筒的内壁逆时针方向运动，物体与筒内壁接触处的摩擦系数为μ。