牛顿-拉夫逊迭代法极坐标潮流计算C语言程序
C语言进行潮流计算

电力系统课程设计C语言潮流计算学院:电气工程班级:电092班学号:0912002020学生姓名:闵凯2013.3.7电力系统的潮流计算是对电力系统分析的最基本步骤也是最重要的步骤,是指在一定的系统结构和运行条件下,确定系统运行状态的计算,也即是对各母线(节点)电压,各元件(支路)传输电线或功率的计算。
通过计算出的节点电压和功率分布用以检查系统各元件是否过负荷,各点电压是否合理,以及功率损耗等。
即使对于一个简单的电力系统,潮流计算也不是一件简单就可以完成的事,其运算量很大,因此如果对于一个大的、复杂的电网来说的话,由于其节点多,分支杂,其计算量可想而知,人工对其计算也更是难上加难了。
特别是在现实生活中,遇到一个电力系统不会像我们期望的那样可以知道它的首端电压和首端功率或者是末端电压和末端功率,而是只知道它的首端电压和末端功率,更是使计算变的头疼万分。
为了使计算变的简单,我们就可以利用计算机,用C 语言编程来实现牛顿-拉夫逊(Newton-Raphson )迭代法,最终实现对电力系统潮流的计算。
一.用牛顿-拉夫逊迭代法进行电力系统潮流计算的相关概念1.节点导纳矩阵如图所示的电力网络,将节点i 和j 的电压用∙U i 和∙.U j 表示,它们之间的支路导纳表示为y ij ,那么有基尔霍夫电流定律可知注入接点I 的电流∙.I i (设流入节点的电流为正)等于离开节点I 的电流之和,因此有)(.00∙∙≠=≠=∙∙-==∑∑j i nij ijnij ij i U U I I y (1-1)∴ ∙≠=≠=∙∙∑∑-=U y y U I nij ij nij ij i 00 (1-2)如令ii nij ijY y=∑≠=0ij ij Y y =-则可将(1-2)改写为:∑≠=∙∙=nij ij iji U YI 1 I=1,2,…,n. (1-3)上式也可以写为: I =YU (1-4)其中Y 为节点导纳矩阵,也称为稀疏的对称矩阵,它是n×n 阶方阵。
附录_潮流计算程序

附录牛顿-拉夫逊法潮流计算程序本附录所介绍的牛顿-拉夫逊法潮流计算程序采用极坐标形式,其中所涉及的计算公式与第四章中的式(4-42)-(4-59)完全相同,计算程序框图与图4-6基本一致。
程序采用C语言编制。
为了便于初学者阅读,节点导纳矩阵和雅可比矩阵都用满阵存储而未采用稀疏技巧;但为了适当照顾使用的方便性,在输入数据中对节点编号次序不作任何要求。
下面先介绍输入文件的格式和要求,然后列出程序,最后说明潮流结果的输出。
建议读者先从原始数据的输入中了解和熟悉它们在程序中对应的变量、结构体数组及其成员的名称,然后对照图4-6和式(4-42)-(4-59)仔细和耐心地阅读程序,最好能在计算机上亲自实现和进行调试。
在调试时,可以用下面给出的对应于[例4-3]系统的输入数据,以及程序运行中得出的中间结果,逐步与[例4-3]中所给出的中间结果进行对比,从而查找错误所在并进行改正。
一、原始数据的输入程序通过“输入数据.txt”文件输入以下5个数据段。
1.信息(共6个)(1)总节点数(变量num_node)(2)线路和并联电容器总数(变量num_line)(3)变压器支路总数(变量num_tran)(4)发电机节点总数(变量num_gene)(5)负荷节点总数(变量num_load)(6)节点功率不平衡量的容许误差(变量error)2.线路和并联电容器数据(结构体数组line):每一线路或并联电容器包括5个数据I侧节点编号和J侧节点编号可以对换;线路和并联电容器之间的次序可以任意,而且允许多条线路或多个电容器并联。
3.变压器支路数据(结构体数组tran):每一变压器支路包括5个数据变压器电阻、电抗和非标准变比与两侧节点编号之间的关系服从图2-29,即电阻和电抗在1侧而非标准变比在2侧;三绕组变压器需按图2-26化成3个变压器支路,其中3侧变压器支路的非标准变比为1。
变压器支路之间的次序可以任意。
4.发电机节点数据(结构体数组gene):每一发电机节点包括5个数据对于PQ节点,节点种类为1,电压可给任意值;对于PV节点,节点种类为-1,发出无功功率可给任意值;对于平衡节点,节点种类为0,发出有功功率和发出无功功率都可给任意值。
c语言编写的牛顿拉夫逊法解潮流程序

c语言编写的牛顿拉夫逊法解潮流程序闲来无事,最近把牛拉法用c语言重写一遍,和matlab相比,c语言编写潮流程序最大的难点在于矩阵求逆,我使用的求逆方法是初等行变换法,程序段如下:#include<stdio.h>#define N 3void main(){int i,j,k;float t;float Jacob[N][N]={{1,2,2},{1,3,4},{2,3,4}};//欲进行求逆的矩阵float inv_J[N][N];//逆矩阵存储于此//初始化inv_J[N][N]for(i=0;i<N;i++)for(j=0;j<N;j++){if(i!=j)inv_J[i][j]=0;elseinv_J[i][j]=1;}//将原矩阵化简为对角阵for(i=0;i<N;i++){for(j=0;j<N;j++){if(i!=j){t=Jacob[j][i]/Jacob[i][i];for(k=0;k<N;k++){Jacob[j][k]-=Jacob[i][k]*t;inv_J[j][k]-=inv_J[i][k]*t;}}}}//原矩阵各对角元素化为1,画出逆矩阵for(i=0;i<N;i++)if(Jacob[i][i]!=1){t=Jacob[i][i];for(j=0;j<N;j++)inv_J[i][j]=inv_J[i][j]/t;}//输出逆矩阵for(i=0;i<N;i++){for(j=0;j<N;j++)printf("%9.4f",inv_J[i][j]);printf("\n");}}整个程序为://牛拉法解潮流程序#include<stdio.h>#include<math.h>#define N 4 //节点数#define n_PQ 2 //PQ节点数#define n_PV 1 //PV节点数#define n_br 5 //串联支路数void main(){void disp_matrix(float *disp_p,int disp_m,int disp_n); //矩阵显示函数float Us[2*N]={1.0,0,1.0,0,1.05,0,1.05,0}; //电压初值float Ps[N]={0,-0.5,0.2}; //有功初值float Qs[N]={0,-0.3}; //无功初值float G[N][N],B[N][N]; //各几点电导电纳struct //阻抗参数{int nl; //左节点int nr; //右节点float R; //串联电阻值float X; //串联电抗值float Bl; //左节点并联电导float Br; //右节点并联电纳}ydata[n_br]={{1,2,0,0.1880,-0.6815,0.6040},{1,3,0.1302,0.2479,0.0129,0.0129},{1,4,0.1736,0.3306,0.0172,0.0172},{3,4,0.2603,0.4959,0.0259,0.0259},{2,2,0,0.05,0,0}};float Z2; //Z^2=R^2+X^2 各串联阻抗值的平方float e[N],f[N],dfe[2*(N-1)]; //e,f存储电压的x轴分量和y轴分量,dfe存储电压修正值float mid1[N],mid2[N],dS[2*(N-1)]; //mid1、mid2存储计算雅克比行列式对角线元素的中间值,dS存储PQU的不平衡量float Jacob[2*(N-1)][2*(N-1)],inv_J[2*(N-1)][2*(N-1)]; //雅克比行列式float dPQU=1.0; //PQU不平衡量最大值int kk=0; //迭代次数int i,j,k;float t;float Pij[n_br]; //存储线路i->j的有功float Qij[n_br]; //存储线路i->j的无功float Pji[n_br]; //存储线路j->i的有功float Qji[n_br]; //存储线路j->i的无功float dPij[n_br]; //存储线路i->j的有功损耗float dQij[n_br]; //存储线路i->j的无功损耗float AA,BB,CC,DD; //存储线路潮流计算时的中间值//形成导纳矩阵--------------------------------------------------------------------------------------------------for(i=0;i<N;i++)for(j=0;j<N;j++){G[i][j]=0;B[i][j]=0;}for(i=0;i<n_br;i++){if(ydata[i].nl!=ydata[i].nr){Z2=(ydata[i].R)*(ydata[i].R)+(ydata[i].X)*(ydata[i].X);//串联阻抗等效导纳值//非对角元素G[ydata[i].nl-1][ydata[i].nr-1]=(-ydata[i].R)/Z2;B[ydata[i].nl-1][ydata[i].nr-1]=ydata[i].X/Z2;G[ydata[i].nr-1][ydata[i].nl-1]=(-ydata[i].R)/Z2;B[ydata[i].nr-1][ydata[i].nl-1]=ydata[i].X/Z2;//对角元素G[ydata[i].nl-1][ydata[i].nl-1]+=ydata[i].R/Z2;G[ydata[i].nr-1][ydata[i].nr-1]+=ydata[i].R/Z2;B[ydata[i].nl-1][ydata[i].nl-1]+=(-ydata[i].X/Z2);B[ydata[i].nr-1][ydata[i].nr-1]+=(-ydata[i].X/Z2);//并联导纳等效导纳值B[ydata[i].nl-1][ydata[i].nl-1]+=ydata[i].Bl;B[ydata[i].nr-1][ydata[i].nr-1]+=ydata[i].Br;}else{G[ydata[i].nl-1][ydata[i].nr-1]+=ydata[i].R;B[ydata[i].nl-1][ydata[i].nr-1]+=ydata[i].X;}}printf("G=\n");disp_matrix(*G,N,N);printf("B=\n");disp_matrix(*B,N,N);//分离e,ffor(i=0;i<N;i++){e[i]=Us[2*i];f[i]=Us[2*i+1];}//主程序=============================================================================== ======================while(dPQU>0.00001){//计算功率不平衡量for(i=0;i<N-1;i++){mid1[i]=0;mid2[i]=0;for(j=0;j<N;j++){mid1[i]=mid1[i]+G[i][j]*e[j]-B[i][j]*f[j];mid2[i]=mid2[i]+G[i][j]*f[j]+B[i][j]*e[j];}dS[2*i]=Ps[i]-(e[i]*mid1[i]+f[i]*mid2[i]);if(i<n_PQ)dS[2*i+1]=Qs[i]-(f[i]*mid1[i]-e[i]*mid2[i]);elsedS[2*i+1]=Us[2*i]*Us[2*i]-(e[i]*e[i]+f[i]*f[i]);}dPQU=0;for(i=0;i<2*(N-1);i++){if(dS[i]<0&&dPQU<-dS[i])dPQU=-dS[i];else if(dS[i]>0&&dPQU<dS[i])dPQU=dS[i];}if(dPQU>0.00001){kk++;//形成雅克比行列式-------------------------------------------------------------------------------------------------for(i=0;i<2*(N-1);i++)for(j=0;j<2*(N-1);j++)Jacob[i][j]=0;for(j=0;j<N-1;j++){//求H,Nfor(i=0;i<N-1;i++){if(i!=j){Jacob[2*i][2*j]=B[i][j]*e[i]-G[i][j]*f[i];Jacob[2*i][2*j+1]=-G[i][j]*e[i]-B[i][j]*f[i];}else{Jacob[2*i][2*i]=B[i][i]*e[i]-G[i][i]*f[i]-mid2[i];Jacob[2*i][2*i+1]=-G[i][j]*e[i]-B[i][j]*f[i]-mid1[i];}}//求J,Lfor(i=0;i<n_PQ;i++){if(i!=j){Jacob[2*i+1][2*j]=G[i][j]*e[i]+B[i][j]*f[i];Jacob[2*i+1][2*j+1]=B[i][j]*e[i]-G[i][j]*f[i];}else{Jacob[2*i+1][2*i]=G[i][j]*e[i]+B[i][j]*f[i]-mid1[i];Jacob[2*i+1][2*i+1]=B[i][j]*e[i]-G[i][j]*f[i]+mid2[i];}}//求R,Sfor(i=n_PQ;i<N-1;i++){if(i==j){Jacob[2*i+1][2*i]=-2*f[i];Jacob[2*i+1][2*i+1]=-2*e[i];}}}//雅克比行列式求逆-----------------------------------------------------------------------------------for(i=0;i<2*(N-1);i++)for(j=0;j<2*(N-1);j++){if(i!=j)inv_J[i][j]=0;elseinv_J[i][j]=1;}for(i=0;i<2*(N-1);i++){for(j=0;j<2*(N-1);j++){if(i!=j){t=Jacob[j][i]/Jacob[i][i];for(k=0;k<2*(N-1);k++){Jacob[j][k]-=Jacob[i][k]*t;inv_J[j][k]-=inv_J[i][k]*t;}}}}for(i=0;i<2*(N-1);i++)if(Jacob[i][i]!=1){t=Jacob[i][i];for(j=0;j<2*(N-1);j++)inv_J[i][j]=inv_J[i][j]/t;}//求电压修正值--------------------------------------------------------------------------------------------for(i=0;i<2*(N-1);i++){dfe[i]=0;for(j=0;j<2*(N-1);j++)dfe[i]-=inv_J[i][j]*dS[j];}for(i=0;i<N-1;i++){e[i]+=dfe[2*i+1];f[i]+=dfe[2*i];}}elsebreak;}//循环结束---------------------------------------------------------------------------------------------------------------//求平衡节点功率---------------------------------------------------------------------------------------------------mid1[N-1]=0;mid2[N-1]=0;for(j=0;j<N;j++){mid1[N-1]=mid1[N-1]+G[N-1][j]*e[j]-B[N-1][j]*f[j];mid2[N-1]=mid2[N-1]+G[N-1][j]*f[j]+B[N-1][j]*e[j];}Ps[N-1]=e[N-1]*mid1[N-1]+f[N-1]*mid2[N-1];Qs[N-1]=f[N-1]*mid1[N-1]-e[N-1]*mid2[N-1];for(i=n_PQ;i<N-1;i++)Qs[i]=f[i]*mid1[i]-e[i]*mid2[i];//---------------------------------------------------------------------------------------------------------------------------// 显示输出结果printf("kk=%d\n",kk);printf("P=");for(i=0;i<N;i++)printf("%9.4f",Ps[i]);printf("\nQ=");for(i=0;i<N;i++)printf("%9.4f",Qs[i]);printf("\ne=");for(i=0;i<N;i++)printf("%9.4f",e[i]);printf("\nf=");for(i=0;i<N;i++)printf("%9.4f",f[i]);printf("\n");//求线路上的潮流//计算S[i][j]for(i=0;i<n_br;i++){if(ydata[i].nl!=ydata[i].nr){Z2=(ydata[i].R)*(ydata[i].R)+(ydata[i].X)*(ydata[i].X);AA=-f[ydata[i].nl-1]*ydata[i].Bl+(e[ydata[i].nl-1]-e[ydata[i].nr-1])*ydata[i].R/Z2+(f[ydata[i].nl-1]-f[ydata[i].nr-1])*ydata[i].X/Z2;BB=-e[ydata[i].nl-1]*ydata[i].Bl-(f[ydata[i].nl-1]-f[ydata[i].nr-1])*ydata[i].R/Z2+(e[ydata[i].nl-1]-e[ydata[i].nr-1])*ydata[i].X/Z2;Pij[i]=e[ydata[i].nl-1]*AA-f[ydata[i].nl-1]*BB;Qij[i]=e[ydata[i].nl-1]*BB+f[ydata[i].nl-1]*AA;printf("S[%d][%d]=%9.4f+j%9.4f\n",ydata[i].nl,ydata[i].nr,Pij[i],Qij[i]);dPij[i]=Pij[i]+Pji[i];dQij[i]=Qij[i]+Qji[i];}}printf("\n");//计算S[j][i]for(i=0;i<n_br;i++){if(ydata[i].nl!=ydata[i].nr){Z2=(ydata[i].R)*(ydata[i].R)+(ydata[i].X)*(ydata[i].X);CC=-f[ydata[i].nr-1]*ydata[i].Br+(e[ydata[i].nr-1]-e[ydata[i].nl-1])*ydata[i].R/Z2+(f[ydata[i].nr-1]-f[ydata[i].nl-1])*ydata[i].X/Z2;DD=-e[ydata[i].nr-1]*ydata[i].Br-(f[ydata[i].nr-1]-f[ydata[i].nl-1])*ydata[i].R/Z2+(e[ydata[i].nr-1]-e[ydata[i].nl-1])*ydata[i].X/Z2;Pji[i]=e[ydata[i].nr-1]*CC-f[ydata[i].nr-1]*DD;Qji[i]=e[ydata[i].nr-1]*DD+f[ydata[i].nr-1]*CC;printf("S[%d][%d]=%9.4f+j%9.4f\n",ydata[i].nr,ydata[i].nl,Pji[i],Qji[i]);}}printf("\n");//计算dS[i][j]for(i=0;i<n_br;i++){if(ydata[i].nl!=ydata[i].nr){dPij[i]=Pij[i]+Pji[i];dQij[i]=Qij[i]+Qji[i];printf("dS[%d][%d]=%9.4f+j%9.4f\n",ydata[i].nl,ydata[i].nr,dPij[i],dQij[i]);}}printf("\n");}//主程序结束//矩阵显示函数=============================================================================== =========================void disp_matrix(float *disp_p,int disp_m,int disp_n){int i,j;for(i=0;i<disp_m;i++){for(j=0;j<disp_n;j++)printf("%9.4f",*(disp_p+i*disp_m+j));printf("\n");}printf("\n");}。
C语言潮流计算-牛顿-拉夫逊法(直角坐标)

(k )
计算平衡节点功率 S s 和线路功率
~
停止
1 / 20
程序代码如下:
#include<stdio.h> #include<stdlib.h> #include<math.h> #include<string.h> #include<conio.h> struct linetype // 线路参数 { int jiedian[2]; // 若为变压器,则 左端为“低”压侧(换算成Π型等值电路),变压器的阻抗在“低”压侧 double R,X,K,B0; }line[30]; struct Nodetype // 节点功率 { int lei; // PQ 定义 1,PV 定义 2,平衡节点 定义 3 int jie; // 节点编号 double P,Q; double y1,y2; // 初始电压 }poin[30]; int point,road; // 节点数 point 支路数 road int p1,p2; // PQ PV 节点数目 //************************************************* 自定义 函数 *************************************************************** void chargescreen() // 调节屏幕 { int mode; printf("\t 请选择界面模式: ①. 106*45 ②. 134*45\n\t>>"); a: scanf("%d",&mode); if(mode!=1 && mode!=2) { printf("\n\t 错误,请重新输入...\n\t>>"); goto a; } printf("\n\t"); system("pause"); if(mode==1) system("mode con:cols=106 lines=45"); // 调整屏幕大小 else system("mode con:cols=134 lines=45"); } void pqpv() // 统计 PQ、PV 节点 数目
Matlab及C语言在潮流计算运用

一,潮流计算算法原理:牛顿—拉夫逊法的基本原理 牛顿-拉夫逊法是一种求解非线性方程的数值解法,由于便于编写程序用计算机求解,应用较广。
下面以一元非线性代数方程的求解为例,来说明牛顿-拉夫逊法的基本思想。
设欲求解的非线性代数方程为 f(x)=o设方程的真实解为x*,则必有f(x*)=0。
用牛顿-拉夫逊法求方程真实解x*的步骤如下:首先选取余割合适的初始估值x°作为方程f(x)=0的解,若恰巧有f(x°)=0,则方程的真实解即为x*= x°若f(x°)≠0,则做下一步。
取x¹=x°+Δx°为第一次的修正估值,则 f(x¹)=f(x°+Δx°) 其中Δx°为初始估值的增量,即Δx°=x¹-x°。
设函数f(x)具有任意阶导数,即可将上式在x°的邻域展开为泰勒级数,即:f(x¹)=f(x°+Δx°)=f(x°)+f'(x°)Δx°+[f''(x°)(Δx°)2]/2+… 若所取的|Δx°|足够小,则含(Δx°)²的项及其余的一切高阶项均可略去,并使其等于零,即:f(x¹)≈f(x°)+f'(x°)Δx°=0 故得 Δx°=-f(x°)/f'(x°) 从而 x¹= x°-f(x°)/f'(x°)可见,只要f'(x°)≠0,即可根据上式求出第一次的修正估值x¹,若恰巧有f(x¹)=0,则方程的真实解即为x*=x¹。
若f(x¹)≠0,则用上述方法由x¹再确定第二次的修正估值x²。
牛顿-拉夫逊迭代法电力网潮流计算方法与程序

end
Um=conj(U');
I=Y*Um;
Sm=diag(Um)*conj(I)
form=1:N1+1
forn=1:N1+1
Smn(m,n)=U(m)*(conj(U(m))-conj(U(n)))*conj(-Y(m,n));
clear
u=sym('[u1,u2,u3]');delt=sym('[d1,d2,d3]');
G=zeros(3);
B=[-19.98,10,10;10,-19.98,10;10,10,-19.98];
Y=G+j*B;
p(1)=-1.7192;q(1)=-0.7346;p(2)=0.6661;
k=0;precision=1;
qt节点无功功率符号表达式;
pp节点有功功率不平衡值符号表达式;
qq节点无功功率不平衡值符号表达式;
uu节点电压幅值数值矩阵;
dd节点电压相角数值矩阵;
PP节点不平衡功率的数值矩阵
N1网络独立节点总数;
N2网络PV节点总数;
Sm节点功率矩阵;
Smn支路功率矩阵;
J1, J2, J节点不平衡功率雅可比符号矩阵.
end
pp(m)=p(m)-sum(pt);
end
form=1:N1-N2
forn=1:N1+1
qt(n)=u(m)*u(n)*(G(m,n)*sin(delt(m)-delt(n))-B(m,n)*cos(delt(m)-delt(n)));
end
qq(m)=q(m)-sum(qt);
牛顿拉夫逊法潮流计算

摘要本文,首先简单介绍了基于在MALAB中行潮流计算的原理、意义,然后用具体的实例,简单介绍了如何利用MALAB去进行电力系统中的潮流计算。
众所周知,电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态:各线的电压、各元件中流过的功率、系统的功率损耗等等。
在电力系统规划的设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性、可靠性和经济性。
此外,在进行电力系统静态及暂态稳定计算时,要利用潮流计算的结果作为其计算的基础;一些故障分析以及优化计算也需要有相应的潮流计算作配合;潮流计算往往成为上述计算程序的一个重要组成部分。
以上这些,主要是在系统规划设计及运行方式安排中的应用,属于离线计算范畴。
牛顿-拉夫逊法在电力系统潮流计算的常用算法之一,它收敛性好,迭代次数少。
本文介绍了电力系统潮流计算机辅助分析的基本知识及潮流计算牛顿-拉夫逊法,最后介绍了利用MTALAB程序运行的结果。
关键词:电力系统潮流计算,牛顿-拉夫逊法,MATLABABSTRACTThis article first introduces the flow calculation based on the principle of MALAB Bank of China, meaning, and then use specific examples, a brief introduction, how to use MALAB to the flow calculation in power systems.As we all know, is the study of power flow calculation of power system steady-state operation of a calculation, which according to the given operating conditions and system wiring the entire power system to determine the operational status of each part: the bus voltage flowing through the components power, system power loss and so on. In power system planning power system design and operation mode of the current study, are required to quantitatively calculated using the trend analysis and comparison of the program or run mode power supply reasonable, reliability and economy.In addition, during the power system static and transient stability calculation, the results of calculation to take advantage of the trend as its basis of calculation; number of fault analysis and optimization also requires a corresponding flow calculation for cooperation; power flow calculation program often become the an important part. These, mainly in the way of system design and operation arrangements in the application areas are off-line calculation.Newton - Raphson power flow calculation in power system is one commonly used method, it is good convergence of the iteration number of small, introduce the trend of computer-aided power system analysis of the basic knowledge and power flow Newton - Raphson method, introduced by the last matlab run results.Keywords:power system flow calculation, Newton – Raphson method, matlab目录1 绪论 (1)1.1 课题背景 (1)1.2 电力系统潮流计算的意义 (2)1.3 电力系统潮流计算的发展 (2)1.4 潮流计算的发展趋势 (4)2 潮流计算的数学模型 (5)2.1 电力线路的数学模型及其应用 (5)2.2 等值双绕组变压器模型及其应用 (6)2.3 电力网络的数学模型 (8)2.4 节点导纳矩阵 (9)2.4.1 节点导纳矩阵的形成 (9)2.4.2 节点导纳矩阵的修改 (10)2.5 潮流计算节点的类型 (11)2.6 节点功率方程 (12)2·7 潮流计算的约束条件 (13)3 牛顿-拉夫逊法潮流计算基本原理 (14)3.1 牛顿-拉夫逊法的基本原理 (14)3.2 牛顿-拉夫逊法潮流计算的修正方程 (17)3.3 潮流计算的基本特点 (20)3.4 节点功率方程 (21)4牛顿-拉夫逊法分解潮流程序 (22)4·1 牛顿-拉夫逊法分解潮流程序原理总框图 (22)4.2 形成节点导纳矩阵程序框图及代码 (23)4.2。
牛顿-拉夫逊算法(极坐标)潮流计算算例

极坐标系下的潮流计算
潮流计算
在电力系统中,潮流计算是一种常用的计算方法,用于确定在给定网络结构和参数下,各节点的电压 、电流和功率分布。在极坐标系下进行潮流计算,可以更好地描述和分析电力系统的电磁场分布和变 化。
极坐标系下的潮流计算特点
在极坐标系下进行潮流计算,可以更直观地描述电力线路的走向和角度变化,更好地反映电力系统的 复杂性和实际情况。此外,极坐标系下的潮流计算还可以方便地处理电力系统的非对称性和不对称故 障等问题。
03
CATALOGUE
极坐标系下的牛顿-拉夫逊算法
极坐标系简介
极坐标系
一种二维坐标系统,由一个原点(称为极点)和一条从极点出发的射线(称为 极轴)组成。在极坐标系中,点P的位置由一个角度θ和一个距离r确定。
极坐标系的应用
极坐标系广泛应用于物理学、工程学、经济学等领域,特别是在电力系统和通 信网络中,用于描述电场、磁场、电流和电压等物理量的分布和变化。
极坐标形式
将电力系统的节点和支路参数以极坐 标形式表示,将实数问题转化为复数 问题,简化计算过程并提高计算效率 。
02
CATALOGUE
牛顿-拉夫逊算法原理
算法概述
牛顿-拉夫逊算法是一种迭代算法,用于求解非线性方程组。在电力系统中,它 被广泛应用于潮流计算,以求解电力网络中的电压、电流和功率等参数。
准确的结果。
通过极坐标系的处理,算法 能够更好地处理电力系统的 复杂结构和不对称性,提高 了计算的准确性和适应性。
算例分析表明,该算法在处理 大规模电力系统时仍具有较好 的性能,能够满足实际应用的
需求。
展望
进一步研究牛顿-拉夫逊算法在极坐标 系下的收敛性分析,探讨收敛速度与电 力系统规模、结构和参数之间的关系, 为算法的优后的电压、电流和功 率等参数。
牛顿—拉夫逊潮流计算的程序设计

牛顿-拉夫逊法潮流计算的程序设计摘要本文,首先简单介绍了基于在MALAB中行潮流计算的原理、意义,然后用具体的实例,简单介绍了,如何利用MALAB去进行电力系统中的潮流计算。
众所周知,电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态:各母线的电压、各元件中流过的功率、系统的功率损耗等等。
在电力系统规划的设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性、可靠性和经济性。
此外,在进行电力系统静态及暂态稳定计算时,要利用潮流计算的结果作为其计算的基础;一些故障分析以及优化计算也需要有相应的潮流计算作配合;潮流计算往往成为上述计算程序的一个重要组成部分。
以上这些,主要是在系统规划设计及运行方式安排中的应用,属于离线计算范畴。
牛顿-拉夫逊法在电力系统潮流计算的常用算法之一,它收敛性好,迭代次数少,介绍了电力系统潮流计算机辅助分析的基本知识及潮流计算牛顿-拉夫逊法,最后介绍了利用matlab程序运行的结果。
关键词:电力系统潮流计算牛顿-拉夫逊法MATLABNEWTON-RAPHSON POWER FLOW CALCULATION PROGRAM DESIGNABSTRACTThis article first introduces the flow calculation based on the principle of MALAB Bank of China, meaning, and then use specific examples, a brief introduction, how to use MALAB to the flow calculation in power systems.As we all know, is the study of power flow calculation of power system steady-state operation of a calculation, which according to the given operating conditions and system wiring the entire power system to determine the operational status of each part: the bus voltage flowing through the components power, system power loss and so on. In power system planning power system design and operation mode of the current study, are required to quantitatively calculated using the trend analysis and comparison of the program or run mode power supply reasonable, reliability and economy.In addition, during the power system static and transient stability calculation, the results of calculation to take advantage of the trend as its basis of calculation; number of fault analysis and optimization also requires a corresponding flow calculation for cooperation; power flow calculation program often become the an important part. These, mainly in the way of system design and operation arrangements in the application areas are off-line calculation.Newton - Raphson power flow calculation in power system is one commonly used method, it is good convergence of the iteration number of small,introduce the trend of computer-aided power system analysis of the basic knowledge and power flow Newton - Raphson method, introduced by the last matlab run results.Keywords;power flow calculation system Newton - rafer Johnson law matlab目录牛顿-拉夫逊法潮流计算的程序设计 (I)摘要 (I)ABSTRACT (II)第一章绪论 (1)引言 (1)1.1 电力系统潮流计算的意义 (2)1.2 电力系统潮流计算的发展 (2)1.3 潮流计算的发展趋势 (3)第二章潮流计算的数学模型 (6)2.1 电力线路的数学模型及其应用 (6)2.2 等值双绕组变压器模型及其应用 (7)2.3 等值三绕组变压器模型 (9)2.4 电力网络的数学模型 (9)2.5 节点导纳矩阵 (10)2.5.1 节点导纳矩阵的形成 (10)2.5.2 节点导纳矩阵的修改 (11)2.6 潮流计算节点的类型 (11)2.7 节点功率方程 (12)2.8 潮流计算的约束条件 (13)第三章牛拉法潮流计算基本原理 (15)3.1 牛顿-拉夫逊法的基本原理 (15)3.2 牛顿-拉夫逊法潮流计算的修正方程 (17)3.3 潮流计算的基本特点 (20)3.4 节点功率方程 (21)第四章牛拉法分解潮流程序 (22)4.1 牛拉法分解潮流程序原理总框图 (22)4.2 形成节点导纳矩阵程序框图及代码 (23)4.2.1 形成节点导纳矩阵程序框图 (23)4.2.2 形成节点导纳矩阵的程序代码 (24)4.3 程序输出框图及代码 (25)4.3.1 程序输出框图 (25)4.3.2 程序输出代码 (26)4.4求取DF的程序框图及代码 (27)4.4.1 求取DF的程序框图 (27)4.4.2 求取DF的程序代码 (28)4.5 jacci矩阵求取的程序框图及代码 (29)4.5.1 jacci矩阵的程序框图 (29)4.5.2 jacci矩阵的程序代码 (30)4.6 求取DF、DE的程序框图及代码 (32)4.6.1 求取DF 、DE的程序框图 (32)4.6.2 求取DE、DF程序代码 (33)第5章实例与分析 (34)5.1 一个9节点算例 (34)5.2 变压器参数的标幺值 (36)5.3 导线参数的标幺值 (36)5.4 一个9节点电力系统的等效电路图 (37)5.5 根据算例输入相应节点的线路参数 (37)5.6 算例运行 (39)全文总结 (44)致谢 (45)英文参考资料 (46)英文翻译资料 (57)附录 (67)参考文献 (67)第一章绪论引言潮流计算是研究电力系统的一种最基本和最重要的计算,最初,电力系统潮流计算是通过人工手算的,后来为了适应电力系统日益发展的需要,采用了交流计算台。
牛顿拉夫逊潮流计算
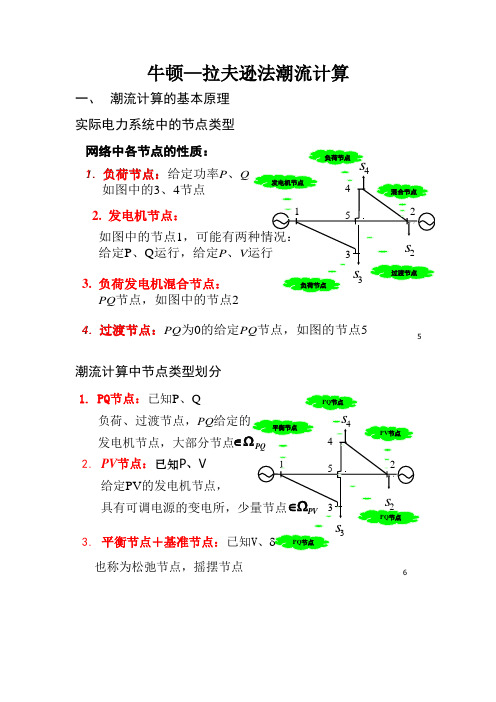
牛顿—拉夫逊法潮流计算一、 潮流计算的基本原理实际电力系统中的节点类型5二、实际电力系统中的节点类型123452s 3s 4s 过渡节点:PQ 为0的给定PQ 节点,如图的节点5网络中各节点的性质:负荷节点:给定功率P 、Q 如图中的3、4节点如图中的节点1,可能有两种情况:给定P 、Q 运行,给定P 、V 运行3. 负荷发电机混合节点:PQ 节点,如图中的节点2发电机节点负荷节点负荷节点混合节点过渡节点1. 负荷节点:2. 发电机节点:4.潮流计算中节点类型划分6三、潮流计算中节点类型的划分也称为松弛节点,摇摆节点123452s 3s 4s 平衡节点PQ 节点PQ 节点PV 节点PQ 节点PQ∈Ω1. PQ 节点:已知P 、Q负荷、过渡节点,PQ 给定的发电机节点,大部分节点PV ∈Ω给定PV 的发电机节点,具有可调电源的变电所,少量节点2.PV 节点:已知P 、V3. 平衡节点+基准节点:已知V 、δ采用极坐标,节点电压表示为()cos sin i i i i i i V V V j δδδ=∠=+节点功率将写成⎪⎪⎭⎪⎪⎬⎫-=+=∑∑==n j ij ij ij ij j i i nj ij ij ij ij j i i B G V V Q B G V V P 11)cos sin ()sin cos (δδδδ (1) 式中,ij i j δδδ=-,是i 、j 两节点电压的相角差。
方程式把节点功率表示为节点电压的幅值和相角的函数。
在有n 个节点的系统中,假定第1~m 号节点为P Q 节点,第1~1m n +-号节点为PV 节点,第n 号节点为平衡节点。
n V 和n δ是给定的,PV 节点的电压幅值11~m n V V +-也是给定的。
因此,只剩下1n -个节点的电压相角121,,,n δδδ- 和m 个节点的电压幅值12,,,m V V V 是未知量。
实际上,对于每一个P Q 节点或每一个PV 节点都可以列写一个有功功率不平衡量方程式()1(cos sin )01,2,,1ni is i is i j ij ij ij ij j P P P P V V G B i n δδ=∆=-=-+==-∑ (2)而对于每一个P Q 节点还可以再列写一个无功功率不平衡量方程式()1(sin cos )01,2,,ni is i is i j ij ij ij ij j Q Q Q Q V V G B i m δδ=∆=-=--==∑ (3)式(2)和式(3)一共包含了1n m -+个方程式,正好同未知量的数目相等,而比直角坐标形式的方程少了1n m -+个。
第三节牛顿 拉夫逊法潮流计算

∂P H11 = 1 = U1 U 2 ( −G12 sin δ12 + B12 cos δ12 ) ∂δ1 +U 3 ( −G13 sin δ13 + B13 cos δ13 ) + ... = −U1 ∑ U j (Gij sin δ ij − Bij cos δ ij )
j =2
PV节点:δi • 节点功率和支路功率(第二求解对象)
4-3 牛顿—拉夫逊法潮流计算
共2(m-1)+(n-m)=n+m-2个变量, 则需n+m-2个独立方程
节点注入功率—电压实数方程组(极坐标形式)
对节点i:
~ & S i = Pi + jQ i = U i
∑
* * Yij U j j =1
~ Si = U i
n
∑ (G
j =1 ij
− jBij U j e
)
jδ ij
e
jδ ij
= cos δ ij + j sin δ ij
∑ (G
j =1
− jBij U j cos δ ij + j sin δ ij
) (
)
4-3 牛顿—拉夫逊法潮流计算
节点注入功率—电压实数方程组(极坐标形式)
j =1
n
n
(
)
)
Qi = U i ∑ U j Gij sin δ ij − Bij cos δ ij
j =1
(
(U,δ)不是真解
∆Pi (U, δ) = Pi − U i ∑U j Gij cosδ ij + Bij sin δ ij
j =1 n
j =1
基于极坐标的牛顿-拉夫逊法潮流计算设计

摘要:电力系统潮流计算是研究电力系统稳态运行情况的一种重要的分析计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态。
在电力系统规划设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性,可靠性和经济性。
MATLAB 使用方便,有着其他高级语言无法比拟的强大的矩阵处理功能。
这样使MATLAB成为电力系统潮流计算的首选计算机语言。
牛顿-拉夫逊法是电力系统潮流计算的常用算法之一,它收敛性好,迭代次数少。
介绍了电力系统潮流计算机辅分析的基本知识及潮流计算牛顿-拉夫逊法,最后介绍了利用MATLAB制作潮流计算软件的过程。
关键词:电力系统潮流计算;牛顿-拉夫逊法;MATLABAbstract:Power Flow Calculation of Power System is an important analysis and calculation of power system steady-state operation, which according to the given operating conditions and system wiring to determine the various parts of the power system running state. In the study of power system design and the current operation mode are required Power Flow Calculation to quantitatively analyzed and compared to the program or run mode power supply reasonable, reliability and economy or not. MATLAB is easy to use, the powerful matrix processing is the other high-level language can not be compared with. This allows MATLAB to become the preferred computer language of power flow calculation.Newton Raphson power flow calculation is one of the most commonly used algorithms, which has good convergence and fewer iterations .This article describes the power flow computer assisted analysis of the basic knowledge and power flow Newton - Raphson method, Finally it describe how to use matlab GUI to make the power flow calculation software.Keywords: power flow calculation; Newton - Raphson method; matlab GUI目录前言 (4)第一章电力系统潮流计算的基本知识 (5)1.1潮流计算的定义及应用 (5)1.2 潮流计算方法的发展与前景 (5)第二章电力网络的数学模型 (6)2.1节点导纳矩阵的形成及修改 (7)2.1.1节点导纳矩阵的形成 (7)2.1.2节点导纳矩阵的修改 (9)2.2节点导纳矩阵元素的物理意义 (11)第三章牛顿—拉夫逊法潮流分布计算 (13)3.1牛顿—拉夫逊法简介 (14)3.1.1牛顿—拉夫逊法简介 (14)3.1.2牛顿—拉夫逊法的几何意义 (17)3.2牛顿—拉夫逊法计算潮流分布 (18)第四章Matlab简介及程序运算 (23)4.1 Matlab概述 (23)结论 (34)参考文献 (35)前言如今,电能已成为我国国民经济紧密联系的,不能储存的能量,它的生产、输送、分配和使用同时完成,暂态过程非常迅速,以电磁波的形式传播。
(完整)潮流计算的基本算法及使用方法

潮流计算的基本算法及使用方法一、 潮流计算的基本算法1. 牛顿-拉夫逊法1.1 概述牛顿-拉夫逊法是目前求解非线性方程最好的一种方法。
这种方法的特点就是把对非线性方程的求解过程变成反复对相应的线性方程求解的过程,通常称为逐次线性化过程,就是牛顿-拉夫逊法的核心.牛顿—拉夫逊法的基本原理是在解的某一邻域内的某一初始点出发,沿着该点的一阶偏导数——雅可比矩阵,朝减小方程的残差的方向前进一步,在新的点上再计算残差和雅可矩阵继续前进,重复这一过程直到残差达到收敛标准,即得到了非线性方程组的解。
因为越靠近解,偏导数的方向越准,收敛速度也越快,所以牛顿法具有二阶收敛特性。
而所谓“某一邻域"是指雅可比方向均指向解的范围,否则可能走向非线性函数的其它极值点,一般来说潮流由平电压即各母线电压(相角为0,幅值为1)启动即在此邻域内。
1.2 一般概念对于非线性代数方程组()0=x f即 ()0,,,21=n i x x x f ()n i ,2,1= (1-1)在待求量x 的某一个初始计算值()0x 附件,将上式展开泰勒级数并略去二阶及以上的高阶项,得到如下的线性化的方程组()()()()()0000=∆'+x x f x f (1-2)上式称之为牛顿法的修正方程式.由此可以求得第一次迭代的修正量()()()[]()()0100x f x f x -'-=∆ (1-3)将()0x ∆和()0x 相加,得到变量的第一次改进值()1x 。
接着再从()1x 出发,重复上述计算过程。
因此从一定的初值()0x 出发,应用牛顿法求解的迭代格式为()()()()()k k k x f x x f -=∆' (1-4)()()()k k k x x x ∆+=+1 (1-5)上两式中:()x f '是函数()x f 对于变量x 的一阶偏导数矩阵,即雅可比矩阵J ;k 为迭代次数。
由式(1-4)和式子(1-5)可见,牛顿法的核心便是反复形成求解修正方程式.牛顿法当初始估计值()0x 和方程的精确解足够接近时,收敛速度非常快,具有平方收敛特性.1.3 潮流计算的修正方程运用牛顿-拉夫逊法计算潮流分布时,首先要找出描述电力系统的非线性方程.这里仍从节点电压方程入手,设电力系统导纳矩阵已知,则系统中某节点(i 节点)电压方程为∑=**•⎪⎪⎪⎭⎫ ⎝⎛=nj i i j ij U S U Y 1从而得∑=**••=nj j ij i i U Y U S 1进而有()01=-+*=*•∑j nj ij i i i U Y U jQ P(1-6)式(1-6)中,左边第一项为给定的节点注入功率,第二项为由节点电压求得的节点注入功率.他们二者之差就是节点功率的不平衡量.现在有待解决的问题就是各节点功率的不平衡量都趋近于零时,各节点电压应具有的价值。
极坐标的牛顿拉夫逊法潮流计算

%主程序"PowerFlow_NR.m"function [bus_res,S_res] = PowerFlow_NR_2 % 牛顿-拉夫逊法解潮流方程的主程序[bus,line] = OpDF_; % 打开数据文件的子程序,返回bus(节点数据)和line(线路数据)回主程序[nb,mb]=size(bus);[nl,ml]=size(line); % 计算bus和line矩阵的行数和列数[bus,line,nPQ,nPV,nodenum] = Num_(bus,line); % 对节点重新排序的子程序Y = y_(bus,line); % 计算节点导纳矩阵的子程序myf = fopen('Result.m','w');fprintf(myf,'\n\n');fclose(myf); % 在当前目录下生成“Result.m”文件,写入节点导纳矩阵format longEPS = 1.0e-10; % 设定误差精度for t = 1:100 % 开始迭代计算,设定最大迭代次数为100,以便不收敛情况下及时跳出[dP,dQ] = dPQ_(Y,bus,nPQ,nPV); % 计算功率偏差dP和dQ的子程序J = Jac_(bus,Y,nPQ); % 计算雅克比矩阵的子程序UD = zeros(nPQ,nPQ);for i = 1:nPQUD(i,i) = bus(i,2); % 生成电压对角矩阵enddAngU = J \ [dP;dQ];dAng = dAngU(1:nb-1,1); % 计算相角修正量dU = UD*(dAngU(nb:nb+nPQ-1,1)); % 计算电压修正量bus(1:nPQ,2) = bus(1:nPQ,2) - dU; % 修正电压bus(1:nb-1,3) = bus(1:nb-1,3) - dAng; % 修正相角if (max(abs(dU))<EPS)&(max(abs(dAng))<EPS)breakend % 判断是否满足精度误差,如满足则跳出,否则返回继续迭代endbus = PQ_(bus,Y,nPQ,nPV); % 计算每个节点的有功和无功注入的子程序[bus,line] = ReNum_(bus,line,nodenum); % 对节点恢复编号的子程序YtYm = YtYm_(line); % 计算线路的等效Yt和Ym的子程序,以计算线路潮流bus_res = bus_res_(bus); % 计算节点数据结果的子程序S_res = S_res_(bus,line,YtYm); % 计算线路潮流的子程序myf = fopen('Result.m','a');fprintf(myf,'---------------牛顿-拉夫逊法潮流计算结果----------\n\n 节点计算结果:\n节点节点电压节点相角(角度)节点注入功率\n');for i = 1:nbfprintf(myf,'%2.0f ',bus_res(i,1));fprintf(myf,'.6f ',bus_res(i,2));fprintf(myf,'.6f ',bus_res(i,3));fprintf(myf,'.6f + j .6f\n',real(bus_res(i,4)),imag(bus_res(i,4)));endfprintf(myf,'\n线路计算结果:\n节点I 节点J 线路功率S(I,J)线路功率S(J,I) 线路损耗dS(I,J)\n');for i = 1:nlfprintf(myf,'%2.0f ',S_res(i,1));fprintf(myf,'%2.0f ',S_res(i,2));fprintf(myf,'.6f + j .6f ',real(S_res(i,3)),imag(S_res(i,3)));fprintf(myf,'.6f + j .6f ',real(S_res(i,4)),imag(S_res(i,4)));fprintf(myf,'.6f + j .6f\n',real(S_res(i,5)),imag(S_res(i,5)));endfclose(myf); % 迭代结束后继续在“Result.m”写入节点计算结果和线路计算结果程序结束bus = [1 1.00 0.00 -0.30 -0.18 1;2 1.00 0.00 -0.55 -0.13 1;3 1.10 0.00 0.50 0.00 2;4 1.05 0.00 0.00 0.00 3]line = [1 2 0.10 0.40 0.0 0.01528 0;4 2 0.08 0.40 0.0 0.01413 0;1 4 0.12 0.50 0.0 0.0192 0;3 1 0.00 0.3 0.0 0.0 -1.1]----------------------------------------牛顿-拉夫逊法潮流计算结果-------------------------------------------- 节点计算结果:节点节点电压节点相角(角度)节点注入功率1 0.984674906330845 -0.500170385513657 -0.300000000000000 - 0.180000000000000i2 0.964797665550885 -6.450305258622626 -0.550000000000000 - 0.130000000000000i3 1.100000000000000 6.732349388989963 0.500000000000000 + 0.093411003244513i4 1.050000000000000 0 0.367882692523292 + 0.264698252215732i 线路计算结果:节点I 节点J 线路功率S(I,J) 线路功率S(J,I) 线路损耗dS(I,J)1 2 0.246244-j0.014651 -0.239990+j0.010627 0.006254- j0.0040241 3 -0.500001-j0.029264 0.500000+j0.093409 -0.000001+j0.0641451 4 -0.046244-j0.136088 0.048216+j0.104522 0.001972-j0.0315662 4 -0.310010-j0.140627 0.319666+j0.160176 0.009656+j0.019549%子程序1 "OpDF_.m" 作用为打开数据文件function [bus,line] = OpDF_[dfile,pathname]=uigetfile('*.m','Select Data File'); % 数据文件类型为m文件,窗口标题为“Select Data File”if pathname == 0error(' you must select a valid data file') % 如果没有选择有效文件,则出现错误提示elselfile =length(dfile); % 读取文件字符串长度eval(dfile(1:lfile-2)); % 去除后缀,打开文件!注意!新浪博客中"eval"函数会自动加上"_r"后缀,此处的函数名是"eval"而不是"eval_r",拷贝后请去除"_r"后缀end%子程序2 "Num.m" 作用为对节点重排序,并修改相应的线路数据function [bus,line,nPQ,nPV,nodenum] = Num_(bus,line)[nb,mb]=size(bus);[nl,ml]=size(line);nSW = 0; % nSW为平衡节点个数nPV = 0; % nPV为PV节点个数nPQ = 0; % nPQ为PQ节点个数for i = 1:nb, % nb为总节点数type= bus(i,6);if type == 3,nSW = nSW + 1;SW(nSW,:)=bus(i,:); % 计算并储存平衡节点elseif type == 2,nPV = nPV +1;PV(nPV,:)=bus(i,:); % 计算并储存PV节点elsenPQ = nPQ + 1;PQ(nPQ,:)=bus(i,:); % 计算并储存PQ节点endendbus=[PQ;PV;SW]; % 对bus矩阵按PQ、PV、平衡节点的顺序重新排序nodenum=[[1:nb]' bus(:,1)];% 生成新旧节点对照表for i=1:nlfor j=1:2for k=1:nbif line(i,j)==nodenum(k,2)line(i,j)=nodenum(k,1);breakendendendend % 按排序以后的节点顺序对line矩阵重新编号%子程序3 "y_.m" 作用为计算节点导纳矩阵function Y = y_(bus,line)[nb,mb]=size(bus);[nl,ml]=size(line);Y=zeros(nb,nb); % 对导纳矩阵赋初值0for k=1:nlI=line(k,1);J=line(k,2);Zt=line(k,3)+j*line(k,4); % 读入线路参数if Zt~=0Yt=1/Zt; % 接地支路不计算YtendYm=line(k,5)+j*line(k,6);K=line(k,7);if (K==0)&(J~=0) % 普通线路: K=0Y(I,I)=Y(I,I)+Yt+Ym;Y(J,J)=Y(J,J)+Yt+Ym;Y(I,J)=Y(I,J)-Yt;Y(J,I)=Y(I,J);endif (K==0)&(J==0) % 对地支路: K=0,J=0,R=X=0Y(I,I)=Y(I,I)+Ym;endif K>0 % 变压器线路: Zt和Ym为折算到i侧的值,K在j侧Y(I,I)=Y(I,I)+Yt+Ym;Y(J,J)=Y(J,J)+Yt/K/K;Y(I,J)=Y(I,J)-Yt/K;Y(J,I)=Y(I,J);endif K<0 % 变压器线路: Zt和Ym为折算到K侧的值,K在i侧Y(I,I)=Y(I,I)+Yt+Ym;Y(J,J)=Y(J,J)+K*K*Yt;Y(I,J)=Y(I,J)+K*Yt;Y(J,I)=Y(I,J);endend%子程序4 "dPQ_.m" 作用为计算功率偏差function [dP,dQ] =dPQ_(Y,bus,nPQ,nPV) % nPQ、nPV为相应节点个数n = nPQ + nPV +1; % 总节点个数dP = bus(1:n-1,4);dQ = bus(1:nPQ,5); % 对dP和dQ赋初值PV节点不需计算dQ 平衡节点不参与计算for i = 1:n-1for j = 1:ndP(i,1) =dP(i,1)-bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3)));if i<nPQ+1dQ(i,1) = dQ(i,1)-bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3)));endendend % 利用循环计算求取dP和dQ%子程序5 "Jac_.m" 作用为计算雅克比矩阵function J = Jac_(bus,Y,nPQ)[nb,mb]=size(bus);H = zeros(nb-1,nb-1);N = zeros(nb-1,nPQ);K = zeros(nPQ,nb-1);L = zeros(nPQ,nPQ); % 将雅克比矩阵分块,即:J = [H N; K L],并初始化Qi = zeros(nb-1,1);Pi = zeros(nb-1,1);for i = 1:nb-1for j = 1:nbPi(i,1)=Pi(i,1)+bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3) ));Qi(i,1)=Qi(i,1)+bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3) ));endend % 初始化并计算Qi和Pifor i = 1:nb-1for j = 1:nb-1if i~=jH(i,j)=-bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3)));elseH(i,j)=Qi(i,1)+imag(Y(i,j))*((bus(i,2))^2);end % 分别计算H矩阵的对角及非对角元素if j < nPQ+1if i~=jN(i,j)=-bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3)));elseN(i,j)=-Pi(i,1)-real(Y(i,j))*((bus(i,2))^2);endend % 分别计算N矩阵的对角及非对角元素if i < nPQ+1if i~=jK(i,j)=bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3)));elseK(i,j)=-Pi(i,1)+real(Y(i,j))*((bus(i,2))^2);end % 分别计算K矩阵的对角及非对角元素if j < nPQ+1if i~=jL(i,j)=-bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3)));elseL(i,j)=-Qi(i,1)+imag(Y(i,j))*((bus(i,2))^2);endend % 分别计算L矩阵的对角及非对角元素endendendJ = [H N; K L]; % 生成雅克比矩阵%子程序6 "PQ_.m" 作用为计算每个节点的功率注入function bus = PQ_(bus,Y,nPQ,nPV)n = nPQ+nPV+1; % n为总节点数for i = nPQ+1:n-1for j = 1:nbus(i,5)=bus(i,5)+bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j, 3)));endend % 利用公式计算PV节点的无功注入for j =1:nbus(n,4)=bus(n,4)+bus(n,2)*bus(j,2)*(real(Y(n,j))*cos(bus(n,3)-bus(j,3))+imag(Y(n,j))*sin(bus(n,3)-b us(j,3)));bus(n,5)=bus(n,5)+bus(n,2)*bus(j,2)*(real(Y(n,j))*sin(bus(n,3)-bus(j,3))-imag(Y(n,j))*cos(bus(n,3)-b us(j,3)));end % 计算平衡节点的无功及有功注入%子程序7 "ReNum_.m" 作用为对节点和线路数据恢复编号function [bus,line] = ReNum_(bus,line,nodenum)[nb,mb]=size(bus);[nl,ml]=size(line);bus_temp = zeros(nb,mb); % bus_temp矩阵用于临时存放bus矩阵的数据k = 1;for i = 1 :nbfor j = 1 : nbif bus(j,1) == kbus_temp(k,:) = bus(j,:);k = k + 1;endendend % 利用bus矩阵的首列编号重新对bus矩阵排序并存入bus_temp矩阵中bus = bus_temp; % 重新赋值回bus,完成bus矩阵的重新编号for i=1:nlfor j=1:2for k=1:nbif line(i,j)==nodenum(k,1)line(i,j)=nodenum(k,2);breakendendendend % 恢复line的编号%子程序8 "YtYm_.m" 作用为计算线路的等效Yt和Ym,以计算线路潮流function YtYm = YtYm_(line)[nl,ml]=size(line);YtYm = zeros(nl,5); % 对YtYm矩阵赋初值0YtYm(:,1:2) = line(:,1:2); % 矩阵前两列为线路两段节点编号,后三列分别为线路等效Yt,i侧的等效Ym,j侧的等效Ymj = sqrt(-1);for k=1:nlI=line(k,1);J=line(k,2);Zt=line(k,3)+j*line(k,4);if Zt~=0Yt=1/Zt;endYm=line(k,5)+j*line(k,6);K=line(k,7);if (K==0)&(J~=0) % 普通线路: K=0YtYm(k,3) = Yt;YtYm(k,4) = Ym;YtYm(k,5) = Ym;endif (K==0)&(J==0) % 对地支路: K=0,J=0,R=X=0YtYm(k,4) = Ym;endif K>0 % 变压器线路: Zt和Ym为折算到i侧的值,K在j侧YtYm(k,3) = Yt/K;YtYm(k,4) = Ym+Yt*(K-1)/K;YtYm(k,5) = Yt*(1-K)/K/K;endif K<0 % 变压器线路: Zt和Ym为折算到K侧的值,K在i侧YtYm(k,3) = -Yt*K;YtYm(k,4) = Ym+Yt*(1+K);YtYm(k,5) = Yt*(K^2+K);endend%子程序9 "bus_res_.m" 计算并返回节点数据结果function bus_res = bus_res_(bus);[nb,mb]=size(bus);bus_res = zeros(nb,4); % bus_res矩阵储存着节点计算结果bus_res(:,1:2) = bus(:,1:2);bus_res(:,3) = bus(:,3) *180 / pi; % 相角采用角度制bus_res(:,4) = bus(:,4) + (sqrt(-1))*bus(:,5); % 注入功率%子程序10 "S_res_.m" 计算并返回线路潮流function S_res = S_res_(bus,line,YtYm)[nl,ml]=size(line);S_res = zeros(nl,5); % S_res矩阵储存着线路潮流计算结果S_res(:,1:2) = line(:,1:2); % 前两列为节点编号for k=1:nlI = S_res(k,1);J = S_res(k,2);if (J~=0)&(I~=0)S_res(k,3)=bus(I,2)^2*(conj(YtYm(k,3))+conj(YtYm(k,4)))-bus(I,2)*bus(J,2)*(cos(bus(I,3))+j*sin(bu s(I,3)))*(conj(cos(bus(J,3))+j*sin(bus(J,3))))*conj(YtYm(k,3));S_res(k,4)=bus(J,2)^2*(conj(YtYm(k,3))+conj(YtYm(k,5)))-bus(I,2)*bus(J,2)*(conj(cos(bus(I,3))+j*s in(bus(I,3))))*(cos(bus(J,3))+j*sin(bus(J,3)))*conj(YtYm(k,3));S_res(k,5)=S_res(k,3) + S_res(k,4); % 利用公式计算非接地支路的潮流elseif J==0S_res(k,3)=bus(I,2)^2*conj(YtYm(k,4));S_res(k,5)=S_res(k,3)+S_res(k,4);elseS_res(k,4)=bus(J,2)^2*conj(YtYm(k,5));S_res(k,5)=S_res(k,3)+S_res(k,4); % 利用公式计算接地支路的潮流endend。
用c语言实现牛顿拉夫逊迭代法

用c语言实现牛顿拉夫逊迭代法如何用C语言实现牛顿拉弗森迭代法[引言]牛顿拉弗森迭代法(Newton-Raphson method),又称为牛顿迭代法,是一种求解方程根的数值方法。
它是由17世纪英国物理学家伊萨克·牛顿和法国数学家约瑟夫·拉弗森独立提出的。
牛顿拉弗森迭代法通过不断逼近方程根,可以实现高精度的方程求解。
[原理]牛顿拉弗森迭代法的原理很简单,基于方程根附近的切线逼近曲线,通过不断迭代的方式逼近方程的根。
设方程的根为x0,代入方程得到曲线上的一个点(x0, f(x0))。
假设方程在x0附近可导,那么我们可以得到曲线在点(x0, f(x0))处的切线方程,即通过(x0, f(x0))和斜率f'(x0)得到切线的方程。
切线与x轴的交点即为新的近似根x1。
依此类推,我们可以采用迭代的方式不断逼近更精确的解。
具体迭代公式为:x_(n+1) = x_n - f(x_n) / f'(x_n)其中,x_n是第n次迭代得到的近似解,f(x_n)是方程在x_n处的函数值,f'(x_n)是方程在x_n处的导数值。
通过不断迭代,当两次迭代解的差值小于预设的误差范围时,我们可以认为得到了方程的近似根。
[步骤]接下来,让我们一步一步的使用C语言实现牛顿拉弗森迭代法。
步骤1:导入所需的头文件和函数声明c#include <stdio.h>#include <math.h>double f(double x); 定义方程的函数表达式double f_derivative(double x); 定义方程的导数函数表达式步骤2:实现方程和导数函数cdouble f(double x) {实现方程的函数表达式return x * x - 9;}double f_derivative(double x) {实现方程的导数函数表达式return 2 * x;}步骤3:实现牛顿拉弗森迭代法cdouble newton_raphson_method(double x0, double epsilon) { double x = x0;double difference = epsilon + 1; 初始化差值,使其大于预设的误差范围while (difference > epsilon) {double f_x = f(x);double f_derivative_x = f_derivative(x);x = x - f_x / f_derivative_x;difference = fabs(f(x));}return x;}步骤4:调用牛顿拉弗森迭代法求解方程cint main() {double x0 = 4; 初始值double epsilon = 0.0001; 误差范围double root = newton_raphson_method(x0, epsilon);printf("方程的近似根为:%lf\n", root);return 0;}[总结]通过以上步骤,我们可以使用C语言实现牛顿拉弗森迭代法来求解给定方程的根。
第4章 牛顿-拉夫逊法潮流计算

泰勒级数展开
(0) ( 0) ( 0) f 1 ( x1 − ∆ x1 , x 2 − ∆x2 ,L , xn − ∆xn ) ∂f1 ∂f1 (0) ( 0) (0) = f ( x , x , , x ) − ∆ x − L 1 1 2 1 n ∂ x ∂x 2 ( 0 ) 1 x 1 M
L
∆δ 1 ∆U 1 ∆δ 2 ∆ U 2 L ∆δ n ∆U n
∂∆Qn L J nn ∂ δn
Ø 节点的修正方程
∆P1 H 11 N 11 ∆ Q 1 J 11 L11 ∆P2 H 21 N 21 ∆Q2 = J 21 L21 L L ∆Pn H n1 N n1 Q ∆ n J n1 Ln1 H 12 N 12 L H 1n J 12 J 22 L12 L J 1n L22 J 2n H 22 N 22 L H 2n N 1n L1n N 2n L2n N nn Lnn ∆δ 1 ∆U U 1 1 ∆δ 2 ∆U 2 U 2 L ∆δ n ∆U U n n
真解 解的 初值 或估 计值
(0) (0) (0) f1 ( x1 − ∆ x1 , x 2 − ∆x2 , L , xn − ∆xn ) = 0 (0) (0) (0) f 2 ( x1 − ∆ x1 , x 2 − ∆ x 2 , L , x n − ∆ x n ) = 0 M f ( x ( 0 ) − ∆x , x ( 0 ) − ∆x , L , x ( 0 ) − ∆x ) = 0 n 1 1 2 2 n n
f (x)
4-3 n-l潮流计算

PQ节点
H2 p N2 p H2n
PV节点
H pp N pp H pn Rpp S pp Rpn Hnp Nnp Hnn Rnp Snp Rnn
2(n-m)
5
2(n-m)
2(m-1)
4-3牛顿-拉夫逊迭代法潮流计算
一、潮流计算时的修正方程式
1. 用直角坐标表示的修正方程
∂Pi H ij = ∂f j ∂Qi J ij = ∂f j
13
当j = i时:
n ∂ Pi ⎧ ⎪ H ii = ∂ δ = −U i ∑ U j ( G ij sin δ ij -Bij cos δ ij ) j =1, j ≠ i i ⎪ n ⎪ ∂ Pi N ii = U i = U i ∑ U j ( G ij cos δ ij + Bij sin δ ij ) +2 U i 2 G ii ⎪ ∂U i j =1, j ≠ i ⎪ ⎨ n ∂ Qi ⎪J = = U i ∑ U j ( G ij cos δ ij -Bij sin δ ij ) ii ⎪ ∂δ i j =1, j ≠ i ⎪ n ∂ Qi ⎪L = U i = U i ∑ U j ( G ij sin δ ij + Bij cos δ ij ) -2 U i 2 Bii ⎪ ii ∂ U j =1, j ≠ i i ⎩
17
4-4 P-Q分解法潮流计算
一、修正方程式
⎡ ΔP ⎤ ⎡ H11 1 ⎢ ΔP ⎥ ⎢ H ⎢ 2 ⎥ ⎢ 21 ⎢ ⎥ ⎢ ⎢ ⎥ ⎢ ⎢ ΔPp ⎥ ⎢H p1 ⎢ ΔP ⎥ = ⎢ Hn1 n ⎢ ⎥ ⎢ ⎢ ⎥ ⎢ ⎢ ΔQ ⎥ ⎢ J ⎢ 1 ⎥ ⎢ 11 ⎢ΔQ2 ⎥ ⎢ J21 ⎢ ⎥ ⎢ ⎣ ⎦ ⎣
牛顿拉夫逊潮流计算程序

f1 x 2 xn f 2 f 2 x 2 xn f n f n x 2 xn
f i
f1
Δ X 1 Δ X 2 Δ X n
(13)
' ' 式(13)等号右边矩阵的 x 等都是对于 X1 ,X 2 的值,这一矩阵称为雅可比(Jacobi)矩阵。
P—Q分解法潮流计算的计算机算法。
电力系统分析
1概 述
类型:
导纳法
阻抗法
牛顿-拉夫逊法(N—R法) 快速分解法( PQ分解法)
电力系统分析
2 潮流计算的基本方程
2.1节点的分类 2.2基本方程式
电力系统分析
2.1节点(bus)的分类
根据电力系统中各节点性质的不同,可把节点分成三种类型。 1.PQ节点 事先给定的是节点功率(P、Q),待求的是节点电压向量 (U、θ)。通常变电所母线都是PQ节点,当某些发电机的 出力P、Q给定时,也可作为PQ节点。PQ节点上的发电机称 之为PQ机(或PQ给定型发电机)。在潮流计算中,系统大 部分节点属于PQ节点。
2
m 1
Δ P1 e m 1 Δ Q 1 e m 1 Δ Pm e m -1 Δ Q m e m -1 Δ Pm 1 e m -1 Δ U
2
m 1
Δ P1 f m 1 Δ Q 1 f m 1 Δ Pm f m -1 Δ Q m f m -1 Δ Pm 1 f m -1 Δ U
电力系统分析
3.2牛顿-拉夫逊法潮流计算
方程式(15)和(16)具备方程组(12)的形式:
Δ W -J Δ U
(17)
Δe 1 Δf 1 Δe m Δf m ΔU Δe m 1 Δf m 1 Δe n - 1 Δf n - 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/*利用牛顿-拉夫逊迭代法(极坐标形式),计算复杂电力系统潮流,具有收敛性好,收敛速度快等优点。
所有参数应归算至标幺值下。
/*可计算最大节点数为100,可计算PQ,PV,平衡节点*//*可计算非标准变比和平行支路*/#include<stdio.h>#include<math.h>#include<stdlib.h>#define M 100 /*最大矩阵阶数*/#define Nl 100 /*迭代次数*/int i,j,k,a,b,c; /*循环控制变量*/int t,l;double P,Q,H,J; /*中间变量*/int n, /*节点数*/m, /*支路数*/pq, /*PQ节点数*/pv; /*PV节点数*/double eps; /*迭代精度*/double aa[M],bb[M],cc[M],dd[M],max, rr,tt; /*中间变量*/double mo,c1,d1,c2,d2; /*复数运算函数的返回值*/ double G[M][M],B[M][M],Y[M][M]; /*节点导纳矩阵中的实部、虚部及其模方值*/double ykb[M][M],D[M],d[M],dU[M]; /*雅克比矩阵、不平衡量矩阵*/struct jd /*节点结构体*/{ int num,ty; /* num为节点号,ty为节点类型*/double p,q,S,U,zkj,dp,dq,du,dj; /*节点有功、无功功率,功率模值,电压模值,阻抗角牛顿--拉夫逊中功率不平衡量、电压修正量*/} jd[M];struct zl /*支路结构体*/{ int numb; /*numb为支路号*/int p1,p2; /*支路的两个节点*/double kx; /*非标准变比*/double r,x; /*支路的电阻与电抗*/ } zl[M];FILE *fp1,*fp2;void data() /* 读取数据*/{int h,number;fp1=fopen("input.txt","r");fscanf(fp1,"%d,%d,%d,%d,%lf\n",&n,&m,&pq,&pv,&eps); /*输入节点数,支路数,PQ节点数,PV节点数和迭代精度*/for(i=1;i<=n;i++) /*输入节点编号、类型、输入功率和电压初值*/{fscanf(fp1,"%d,%d",&number,&h);if(h==1) /*类型h=1是PQ节点*/{fscanf(fp1,"%lf,%lf,%lf,%lf\n",&jd[i].p,&jd[i].q,&jd[i].U,&jd[i].zkj);jd[i].num=number;jd[i].ty=h;}if(h==2) /*类型h=2是pv节点*/{fscanf(fp1,",%lf,%lf,%lf\n",&jd[i].p,&jd[i].U,&jd[i].zkj);jd[i].num=number;jd[i].ty=h;jd[i].q=-1.567;}if(h==3) /*类型h=3是平衡节点*/{fscanf(fp1,",%lf,%lf\n",&jd[i].U,&jd[i].zkj);jd[i].num=number;jd[i].ty=h;}}for(i=1;i<=m;i++) /*输入支路阻抗*/fscanf(fp1,"%d,%lf,%d,%d,%lf,%lf\n",&zl[i].numb,&zl[i].kx,&zl[i].p1,&zl[i].p2,&zl[i].r,&zl [i].x);fclose(fp1);if((fp2=fopen("output.txt","w"))==NULL){printf(" can not open file!\n");exit(0);}fprintf(fp2," 电力系统潮流计算\n ");fprintf(fp2," ********** 原始数据*********\n");fprintf(fp2,"================================================================= ===============\n");fprintf(fp2," 节点数:%d 支路数:%d PQ节点数:%d PV节点数:%d 精度:%f\n",n,m,pq,pv,eps);fprintf(fp2," ------------------------------------------------------------------------------\n"); for(i=1;i<=pq;i++)fprintf(fp2," PQ节点: 节点%d P[%d]=%f Q[%d]=%f\n",jd[i].num,jd[i].num,jd[i].p,jd[i].num,jd[i].q);for(i=pq+1;i<=pq+pv;i++)fprintf(fp2," PV节点: 节点%d P[%d]=%f U[%d]=%f 初值Q[%d]=%f\n",jd[i].num,jd[i].num,jd[i].p,jd[i].num,jd[i].U,jd[i].num,jd[i].q);fprintf(fp2," 平衡节点: 节点%d e[%d]=%f f[%d]=%f\n",jd[n].num,jd[n].num,jd[n].U,jd[n].num,jd[n].zkj);fprintf(fp2," -------------------------------------------------------------------------------\n"); for(i=1;i<=m;i++)fprintf(fp2," 支路%d: 相关节点:%d,%d 非标准变比:kx=%f R=%f X=%f \n", i,zl[i].p1,zl[i].p2,zl[i].kx,zl[i].r,zl[i].x);fprintf(fp2,"=========================================================================== ===\n");}/*------------------------------------复数运算函数--------------------------------------*/double mozhi(double a0,double b0) /*复数求模值函数*/{ mo=sqrt(a0*a0+b0*b0);return mo;}double ji(double a1,double b1,double a2,double b2) /*复数求积函数a1为电压模值,a2为阻抗角,a3为导纳实部,a4为导纳虚部*/{ a1=a1*cos(b1);b1=a1*tan(b1);c1=a1*a2-b1*b2;d1=a1*b2+a2*b1;return c1;return d1;}double shang(double a3,double b3,double a4,double b4) /*复数除法求商函数*/{ c2=(a3*a4+b3*b4)/(a4*a4+b4*b4);d2=(a4*b3-a3*b4)/(a4*a4+b4*b4);return c2;return d2;}/*--------------------------------计算节点导纳矩阵----------------------------------*/void Form_Y(){for(i=1;i<=n;i++) /*节点导纳矩阵元素附初值*/ for(j=1;j<=n;j++)G[i][j]=B[i][j]=0;for(i=1;i<=n;i++) /*节点导纳矩阵的主对角线上的元素,非对地导纳加入相应的主对角线元素中(考虑非标准变比)*/for(j=1;j<=m;j++)if(zl[j].p1==i){if(zl[j].kx==1){mozhi(zl[j].r,zl[j].x);if(mo==0) continue;shang(1,0,zl[j].r,zl[j].x);G[i][i]+=c2;B[i][i]+=d2;}else{mozhi(zl[j].r,zl[j].x);if(mo==0) continue;shang(1,0,zl[j].r,zl[j].x);G[i][i]+=c2/zl[j].kx+c2*(1-zl[j].kx)/(zl[j].kx*zl[j].kx);B[i][i]+=d2/zl[j].kx+d2*(1-zl[j].kx)/(zl[j].kx*zl[j].kx);}}else if(zl[j].p2==i){if(zl[j].kx==1){mozhi(zl[j].r,zl[j].x);if(mo==0) continue;shang(1,0,zl[j].r,zl[j].x);G[i][i]+=c2;B[i][i]+=d2;}else{mozhi(zl[j].r,zl[j].x);if(mo==0) continue;shang(1,0,zl[j].r,zl[j].x);G[i][i]+=c2/zl[j].kx+c2*(zl[j].kx-1)/zl[j].kx;B[i][i]+=d2/zl[j].kx+d2*(zl[j].kx-1)/zl[j].kx;}}for(k=1;k<=m;k++) /*节点导纳矩阵非主对角线上(考虑非标准变比)的元素*/if(zl[k].kx==1){i=zl[k].p1;j=zl[k].p2;mozhi(zl[k].r,zl[k].x);if(mo==0) continue;shang(1,0,zl[k].r,zl[k].x);G[i][j]-=c2;B[i][j]-=d2;G[j][i]=G[i][j];B[j][i]=B[i][j];}else{i=zl[k].p1;j=zl[k].p2;mozhi(zl[k].r,zl[k].x);if(mo==0) continue;shang(1,0,zl[k].r,zl[k].x);G[i][j]-=c2/zl[k].kx;B[i][j]-=d2/zl[k].kx;G[j][i]=G[i][j];B[j][i]=B[i][j];}/*--------------------------输出节点导纳矩阵------------------------------*/fprintf(fp2,"\n\n ********* 潮流计算过程*********\n"); fprintf(fp2,"\n=========================================================================== ===\n");fprintf(fp2,"\n 节点导纳矩阵为:");for(i=1;i<=n;i++){fprintf(fp2,"\n ");for(k=1;k<=n;k++){fprintf(fp2,"%f",G[i][k]);if(B[i][k]>=0){fprintf(fp2,"+j");fprintf(fp2,"%f ",B[i][k]);}else{B[i][k]=-B[i][k];fprintf(fp2,"-j");fprintf(fp2,"%f ",B[i][k]);B[i][k]=-B[i][k];}}}fprintf(fp2,"\n ------------------------------------------------------------------------------\n"); }/*-------------------------------牛顿——拉夫逊-------------------------------*/void Calculate_Unbalanced_Para(){for(i=1;i<=n;i++){if(jd[i].ty==1) /*计算PQ节点不平衡量*/{t=jd[i].num;cc[t]=dd[t]=0;for(j=1;j<=n;j++){for(a=1;a<=n;a++){if(jd[a].num==j)break;}P=Q=0;P=jd[a].U*(G[t][j]*cos(jd[i].zkj-jd[a].zkj)+B[t][j]*sin(jd[i].zkj-jd[a].zkj));Q=jd[a].U*(G[t][j]*sin(jd[i].zkj-jd[a].zkj)-B[t][j]*cos(jd[i].zkj-jd[a].zkj));cc[t]+=P;dd[t]+=Q;}jd[i].dp=jd[i].p-jd[i].U*cc[t];jd[i].dq=jd[i].q-jd[i].U*dd[t];}if(jd[i].ty==2) /*计算PV节点不平衡量*/{t=jd[i].num;cc[t]=dd[t]=0;for(j=1;j<=n;j++){for(a=1;a<=n;a++){if(jd[a].num==j)break;}P=Q=0;P=jd[a].U*(G[t][j]*cos(jd[i].zkj-jd[a].zkj)+B[t][j]*sin(jd[i].zkj-jd[a].zkj));Q=jd[a].U*(G[t][j]*sin(jd[i].zkj-jd[a].zkj)-B[t][j]*cos(jd[i].zkj-jd[a].zkj));cc[t]+=P;dd[t]+=Q;}jd[i].dp=jd[i].p-jd[i].U*cc[t];jd[i].q=jd[i].U*dd[t];}}for(i=1;i<=pq;i++) /*形成不平衡量矩阵D[M]*/ {D[2*i-1]=jd[i].dp;D[2*i]=jd[i].dq;}for(i=pq+1;i<=n-1;i++){D[pq+i]=jd[i].dp;}fprintf(fp2,"\n 不平衡量为:"); /*输出不平衡量*/for(i=1;i<=pq;i++){t=jd[i].num;fprintf(fp2,"\n dp[%d]=%f",i,D[2*t-1]);fprintf(fp2,"\n dq[%d]=%f",i,D[2*t]);}for(i=pq+1;i<=n-1;i++){t=jd[i].num;fprintf(fp2,"\n dp[%d]=%f",i,D[pq+t]);}}void Form_Jacobi_Matric() /*形成雅克比矩阵*/{for(i=1;i<=pq;i++) /*形成pq节点子阵*/for(j=1;j<n;j++){ int i1=jd[i].num;int j1=jd[j].num;double Ui=jd[i].U;double Uj=jd[j].U;double zi=jd[i].zkj;double zj=jd[j].zkj;if(j<=pq) /*求j<=pq时的H、N、J、L */{if(i!=j) /*求i!=j时的H、N、J、L*/{ykb[2*i-1][2*j-1]=Ui*Uj*(G[i1][j1]*sin(zi-zj)-B[i1][j1]*cos(zi-zj)); /* H */ykb[2*i-1][2*j]=Ui*Uj*(G[i1][j1]*cos(zi-zj)+B[i1][j1]*sin(zi-zj)); /* N */ykb[2*i][2*j-1]=-ykb[2*i-1][2*j];/* J */ykb[2*i][2*j]=ykb[2*i-1][2*j-1];/* L */}else /*求i=j时的H、N、J、L*/{aa[i]=0;bb[i]=0;for(k=1;k<=n;k++){int k1=jd[k].num;H=J=0;H=jd[k].U*(G[i1][k1]*sin(jd[i].zkj-jd[k].zkj)-B[i1][k1]*cos(jd[i].zkj-jd[k].zkj));J=jd[k].U*(G[i1][k1]*cos(jd[i].zkj-jd[k].zkj)+B[i1][k1]*sin(jd[i].zkj-jd[k].zkj));aa[i]=aa[i]+H;bb[i]=bb[i]+J;}ykb[2*i-1][2*j-1]=-Ui*(aa[i]-Ui*(G[i1][i1]*sin(jd[i].zkj-jd[i].zkj)-B[i1][i1]*cos(jd[i].zkj-jd[i ].zkj))); /*H*/ykb[2*i][2*j-1]=Ui*(bb[i]-Ui*(G[i1][i1]*cos(jd[i].zkj-jd[i].zkj)+B[i1][i1]*sin(jd[i].zkj-jd[i]. zkj))); /*J*/ykb[2*i-1][2*j]=ykb[2*i][2*j-1]+2*Ui*Ui*G[i1][i1];/*N*/ykb[2*i][2*j]=-ykb[2*i-1][2*j-1]-2*Ui*Ui*B[i1][i1];/*L*/}}else /*求j>pq时的H、J */{ ykb[2*i-1][pq+j]=Ui*Uj*(G[i1][j1]*sin(zi-zj)-B[i1][j1]*cos(zi-zj)); /* H */ykb[2*i][pq+j]=-Ui*Uj*(G[i1][j1]*cos(zi-zj)+B[i1][j1]*sin(zi-zj)); /* J */}}for(i=pq+1;i<=n-1;i++) /*形成pv节点子阵*/for(j=1;j<n;j++){int i1=jd[i].num;int j1=jd[j].num;double Ui=jd[i].U;double Uj=jd[j].U;double zi=jd[i].zkj;double zj=jd[j].zkj;if(j<=pq) /*求j<=pq时的H、N */{ykb[pq+i][2*j-1]=Ui*Uj*(G[i1][j1]*sin(zi-zj)-B[i1][j1]*cos(zi-zj)); /* H */ykb[pq+i][2*j]=Ui*Uj*(G[i1][j1]*cos(zi-zj)+B[i1][j1]*sin(zi-zj)); /* N */}else /*求j>pq时的H*/{if(i!=j) /*求i!=j时的H*/ykb[pq+i][pq+j]=Ui*Uj*(G[i1][j1]*sin(zi-zj)-B[i1][j1]*cos(zi-zj)); /* H */else /*求i=j时的H*/{aa[i]=0;for(k=1;k<=n;k++){int k1=jd[k].num;H=0;H=jd[k].U*(G[i1][k1]*sin(jd[i].zkj-jd[k].zkj)-B[i1][k1]*cos(jd[i].zkj-jd[k].zkj));aa[i]=aa[i]+H;}ykb[pq+i][pq+j]=-Ui*(aa[i]-Ui*(G[i1][i1]*sin(jd[i].zkj-jd[i].zkj)-B[i1][i1]*cos(jd[i].zkj-jd[i ].zkj))); /*H*/}}}/*------------------------------输出雅克比矩阵--------------------------------*/fprintf(fp2,"\n\n 雅克比矩阵为: ");for(i=1;i<=(2*pq+pv);i++){fprintf(fp2,"\n");for(j=1;j<=2*pq+pv;j++){fprintf(fp2," %f",ykb[i][j]);}}}void Solve_Equations() /* 求解修正方程组(LU分解法)*/{double l[Nl][Nl]={0}; //定义L矩阵double u[Nl][Nl]={0}; //定义U矩阵double y[Nl]={0}; //定义数组Ydouble x[Nl]={0}; //定义数组Xdouble a[Nl][Nl]={0}; //定义系数矩阵double b[Nl]={0}; //定义右端项double sum=0;int i,j,k,s;int n;n=2*pq+pv;for(i=0; i<n; i++){for(j=0; j<n; j++){a[i][j]=ykb[i+1][j+1];}}for(i=0; i<n; i++){b[i]=D[i+1];}for(i=0; i<n; i++) /*初始化矩阵l*/{for(j=0; j<n; j++){if(i==j) l[i][j] = 1;}}for(i=0;i<n;i++) /*开始LU分解*/{ u[0][i]=(float)(a[0][i]);} /*第一步:对矩阵U的首行进行计算*/for(k=0;k<n-1;k++) /*第二步:逐步进行LU分解*/ { for(i=k+1;i<n;i++) /*对L的第k列进行计算*/{ for(s=0,sum=0;s<n;s++){ if(s!=k)sum+=l[i][s]*u[s][k];}l[i][k]=(float)((a[i][k]-sum)/u[k][k]);}for(j=k+1;j<n;j++) /*对U的第k+1行进行计算*/ { for(s=0,sum=0;s<n;s++){ if(s!=k+1)sum+=l[k+1][s]*u[s][j];}u[k+1][j]=(float)((a[k+1][j]-sum));}}y[0]=b[0] ; /*回代法计算数组Y*/for(i=1;i<n;i++){ for(j=0,sum=0;j<i;j++){ sum+=y[j]*l[i][j];}y[i]=(float)(b[i]-sum);}x[n-1]=(float)(y[n-1]/u[n-1][n-1]); /*回代法计算数组X*/for(i=n-2;i>=0;i--){ for(j=n-1,sum=0;j>i;j--){ sum+=x[j]*u[i][j];}x[i]=(float)((y[i]-sum)/u[i][i]);}for(i=1; i<=n; i++){d[i]=x[i-1];}max=fabs(d[1]); /*选出最大的修正量的值*/for(i=1;i<=n;i++)if((fabs(d[i]))>max)max=fabs(d[i]);}void Niudun_Lafuxun(){int z=1;fprintf(fp2,"\n --------------极坐标形式的牛顿-拉夫逊迭代法结果:--------------\n");do{ max=1;if((z<Nl)&&(max>=eps)){fprintf(fp2,"\n 迭代次数: %d\n",z); /*开始迭代计算*/ }Calculate_Unbalanced_Para();Form_Jacobi_Matric();Solve_Equations();for(i=1;i<=pq;i++){jd[i].zkj+=d[2*i-1];jd[i].U+=d[2*i]*jd[i].U;}for(i=pq+1;i<=n-1;i++){jd[i].zkj+=d[pq+i];}fprintf(fp2,"\n\n 输出dδ,dU: "); /*输出修正量的值*/for(c=1;c<=n;c++){for(a=1;a<=n;a++){if(jd[a].num==c)break;}fprintf(fp2,"\n");if(jd[a].ty==1)fprintf(fp2," 节点为%2d dδ=%8.5f dU=%8.5f",c,d[2*a-1],d[2*a]);if(jd[a].ty==2)fprintf(fp2," 节点为%2d dδ=%8.5f",c,d[pq+a]);}fprintf(fp2,"\n\n 输出迭代过程中的电压值: ");for(c=1;c<=n;c++){for(a=1;a<=n;a++){if(jd[a].num==c)break;}fprintf(fp2,"\n U[%d]=%f",c,jd[a].U);fprintf(fp2,"∠%f",jd[a].zkj);}fprintf(fp2,"\n\n------------------------------------------------------------------------------");z++;} while((z<Nl)&&(max>=eps)); /*判断是否达到精度要求*/}void Powerflow_Result(){int n1=jd[n].num;fprintf(fp2,"\n\n=========================================================================== ===\n\n");fprintf(fp2," ******潮流计算结果******");fprintf(fp2,"\n\n=========================================================================== ===\n\n");fprintf(fp2,"\n 各节点电压值: "); /*输出各节点的电压值*/for(c=1;c<=n;c++){for(a=1;a<=n;a++){if(jd[a].num==c)break;}fprintf(fp2,"\n U[%d]=%f",c,jd[a].U);fprintf(fp2,"∠%f",jd[a].zkj);}rr=tt=0; /*计算节点的注入功率*/for(i=1;i<=n;i++){int i1=jd[i].num;ji(jd[i].U,-jd[i].zkj,G[n1][i1],-B[n1][i1]);rr+=c1;tt+=d1;}ji(jd[n].U,jd[n].zkj,rr,tt);fprintf(fp2,"\n\n 各节点注入功率:\n");for(i=1;i<=pq;i++){int i1=jd[i].num;fprintf(fp2," PQ节点: 节点%d S[%d]=%f", i1,i1,jd[i].p); /*PQ节点注入功率*/if(jd[i].q>=0)fprintf(fp2,"+j%f\n",jd[i].q);elsefprintf(fp2,"-j%f\n",-jd[i].q);}for(i=pq+1;i<=n-1;i++){int i1=jd[i].num;fprintf(fp2," PV节点: 节点%d S[%d]=%f", i1,i1,jd[i].p); /*PV节点注入功率*/if(jd[i].q>=0)fprintf(fp2,"+j%f\n",jd[i].q);elsefprintf(fp2,"-j%f\n",-jd[i].q);}fprintf(fp2," 平衡节点: 节点%d",jd[n].num,jd[n].num); /*平衡节点注入功率*/ fprintf(fp2," S[%d]=%f",n1,c1);if(d1>=0)fprintf(fp2,"+j%f",d1);elsefprintf(fp2,"-j%f",-d1);fprintf(fp2,"\n\n 线路功率:\n");rr=tt=0;for(i=1;i<=m;i++){int i1=zl[i].p1; /*计算线路功率*/int j1=zl[i].p2;aa[i]=bb[i]=P=Q=0;for(a=1;a<=n;a++){if(jd[a].num==i1)break;}for(b=1;b<=n;b++){if(jd[b].num==j1)break;}mozhi(zl[i].r,zl[i].x);if(mo==0)continue;shang(1,0,zl[i].r,zl[i].x);ji(jd[a].U/zl[i].kx/zl[i].kx,-jd[a].zkj,c2,-d2); /*考虑非标准变比*/P+=c1;Q+=d1;ji(jd[b].U/zl[i].kx,-jd[b].zkj,c2,-d2);P-=c1;Q-=d1;ji(jd[a].U,jd[a].zkj,P,Q);fprintf(fp2," 线路%d: %d--%d 的功率为: %f",i,i1,j1,c1);if(d1>=0)fprintf(fp2,"+j%f\n",d1);elsefprintf(fp2,"-j%f\n",-d1);aa[i]+=c1;bb[i]+=d1;P=Q=0;ji(jd[b].U,-jd[b].zkj,c2,-d2); /*考虑非标准变比*/P+=c1;Q+=d1;ji(jd[a].U/zl[i].kx,-jd[a].zkj,c2,-d2);P-=c1;Q-=d1;ji(jd[b].U,jd[b].zkj,P,Q);fprintf(fp2," 线路%d: %d--%d 的功率为: %f",i,j1,i1,c1);if(d1>=0)fprintf(fp2,"+j%f\n",d1);elsefprintf(fp2,"-j%f\n",-d1);aa[i]+=c1;bb[i]+=d1;rr+=aa[i];tt+=bb[i];}fprintf(fp2,"\n\n 线路损耗功率:\n"); /*计算线路功率损耗*/for(i=1;i<=m;i++){int i1=zl[i].p1;int j1=zl[i].p2;fprintf(fp2," 线路%d损耗的功率为: %f",i,aa[i]);if(bb[i]>=0)fprintf(fp2,"+j%f\n",bb[i]);elsefprintf(fp2,"-j%f\n",-bb[i]);}fprintf(fp2,"\n\n 网络总损耗功率为: %f",rr); /*计算网络总损耗*/ if(tt>=0)fprintf(fp2,"+j%f\n",tt);elsefprintf(fp2,"-j%f\n",-tt);fprintf(fp2,"\n=========================================================================== ===\n");fprintf(fp2,"\n\n ********* 潮流计算结束*********");}void main(){printf("请仔细阅读附录里的输入文件使用说明以便于你正确输入!\n");data(); /*读取数据*/Form_Y(); /*形成节点导纳矩阵*/for(i=1;i<=pq;i++) /* U、zkj附初值*/{jd[i].U=1; jd[i].zkj=0;}for(i=pq+1;i<n;i++){jd[i].U=jd[i].U; jd[i].zkj=0;}Niudun_Lafuxun(); /*牛顿--拉夫逊迭代*/Powerflow_Result();printf("潮流计算结果存放于output.txt文件中!\n");}附录:输入文件按以下规则输入节点数,支路数,PQ节点数,PV节点数,精度节点编号,节点类型(1为PQ节点,2为PV节点,3为平衡节点)节点输入有功功率,无功功率(节点电压纵分量,横分量)支路编号,非标准变比(若没有则填1即可),相关节点,相关节点,支路电阻,支路电抗。
