二阶巴特沃斯低通滤波器 c语言
低通巴特沃斯滤波C语言实现

低通巴特沃斯滤波C语言实现巴特沃斯滤波是一种常见的信号处理滤波器,能够将高频信号从输入信号中滤除,只保留低频信号。
它在信号处理、音频信号处理、图像处理等领域有广泛的应用。
下面是一个使用C语言实现的低通巴特沃斯滤波器的例子。
首先,我们需要定义一些常量和变量来表示滤波器的参数和状态。
我们将使用一个全局变量来保存滤波器的历史输入和输出数据:```c#define FILTER_ORDER 4 // 滤波器阶数#define FILTER_CUTOFF 200 // 截止频率,单位为Hzdouble input[FILTER_ORDER + 1]; // 输入历史数据double output[FILTER_ORDER + 1]; // 输出历史数据```接下来,我们需要初始化滤波器的历史数据。
这里使用一个函数来完成初始化操作:```cvoid initFiltefor (int i = 0; i <= FILTER_ORDER; i++)input[i] = 0.0;output[i] = 0.0;}```接下来,我们需要定义一个滤波函数来实现滤波的操作。
这里使用递归计算方式来实现滤波:```cdouble filter(double x)//更新历史输入数据for (int i = FILTER_ORDER; i > 0; i--)input[i] = input[i-1];}input[0] = x;//更新历史输出数据for (int i = FILTER_ORDER; i > 0; i--)output[i] = output[i-1];}//计算输出output[0] = (input[0] + 2 * input[1] + input[2] -(0.7408 * output[1]) - (0.2042 * output[2])) /1.3403;return output[0];```在上面的代码中,我们使用了巴特沃斯低通滤波器的差分方程来实现滤波。
巴特沃斯二阶低通滤波器

MEMS 陀螺的带宽为30HZ ,从采样频率100HZ 的数据序列中消除掉30HZ 以上的噪声。
巴特沃斯函数只是在ω=0处精确地逼近理想低通特性,在通带内随着ω增加,误差愈来愈大,在通带边界上误差最大,逼近特性并不很好,但是陀螺仪的有用输出信号本就在低频段,对通带边界的滤波要求不高,因此巴特沃斯滤波器就可以满足要求。
要求巴特沃斯滤波器通带上限截止频率fc=30HZ ,阻带下限截止频率fs=80HZ ,通带最大衰减3max =A db ,阻带最小衰减为15min =A db 。
由式(1)-(4)可得巴特沃斯低通滤波器为二阶。
1110max 1.0≈-=A ε (1)49.1995.0622.30lg 110110lg 110110lg 3.05.11.01.0max min =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--A A (2) 85.01.7lg 302802lg lg 2==⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛ππc s w w (3)75.185.049.1lg 110110lg lg max min 1.01.0==⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-->c s A A w w n (4) 用302⨯⨯πs 代替121)(2++=s s s H 中的s 得到去归一化后的滤波器传递函数为式(5)所示。
6.354944.2666.35494)(2++=s s s H (5) 采用的低通滤波电路如图2所示,滤波增益为1,此电路传递函数如式(6)所示,只需将巴特沃斯滤波器的传递函数与此传递函数的系数一一对应即可以整定出滤波电路的参数。
图2 二阶低通滤波典型电路32212312112212111111)(R R C C s C R C R C R s R R C C s H +⎪⎪⎭⎫ ⎝⎛+++-= (6)式(5)与式(6)对比可得:6.3549411221=R R C C (7) 4.266111231211=++C R C R C R (8) 6.3549413221=R R C C (9) 令C 1=0.1uf ,R 2=R 1= R 3,解得R 2=R 1= R 3=6.6K ,C 2=0.6uf ,至此巴特沃斯滤波器构造完成。
二维巴特沃斯滤波器c语言

二维巴特沃斯滤波器1. 简介二维巴特沃斯滤波器是一种常用的图像处理方法,用于对图像进行频域滤波。
它基于巴特沃斯滤波器的原理,在频域中对图像进行平滑或增强。
本文将详细介绍二维巴特沃斯滤波器的原理、实现步骤以及应用案例。
2. 巴特沃斯滤波器原理巴特沃斯滤波器是一种频率域滤波器,通过调整截止频率和阶数来控制信号的频率响应。
其传输函数可以表示为:H (u,v )=11+(D (u,v )D 0)2n其中,D (u,v ) 是图像中每个点到中心点的距离,D 0 是截止频率,n 是阶数。
当 n 取不同值时,巴特沃斯滤波器可以实现不同程度的平滑或增强效果。
当 n >1 时,增加了阶数可以使得低频信号更加平坦;当 n <1 时,减小了阶数可以使得低频信号更加突出。
3. 实现步骤二维巴特沃斯滤波器的实现步骤如下:步骤 1:读取图像首先,需要从文件中读取待处理的图像。
可以使用 C 语言中的图像处理库,如 OpenCV ,来实现图像读取功能。
#include <opencv2/opencv.hpp>int main() {// 读取图像cv::Mat image = cv::imread("input.jpg", cv::IMREAD_GRAYSCALE);// 其他处理步骤...return 0;}步骤 2:进行傅里叶变换将读取的图像进行傅里叶变换,得到频域表示。
可以使用 OpenCV 提供的函数dft 来实现傅里叶变换。
#include <opencv2/opencv.hpp>int main() {// 读取图像cv::Mat image = cv::imread("input.jpg", cv::IMREAD_GRAYSCALE);// 进行傅里叶变换cv::Mat frequencyDomain;cv::dft(image, frequencyDomain, cv::DFT_COMPLEX_OUTPUT);// 其他处理步骤...return 0;}步骤 3:生成巴特沃斯滤波器根据巴特沃斯滤波器的传输函数公式,可以生成巴特沃斯滤波器的频域表示。
二阶低通滤波器c语言

二阶低通滤波器c语言摘要:I.引言- 介绍二阶低通滤波器的作用和应用- 简述本文的主要内容II.二阶低通滤波器原理- 定义二阶低通滤波器的概念- 解释二阶低通滤波器的工作原理- 说明二阶低通滤波器的性能指标III.二阶低通滤波器C 语言实现- 介绍C 语言实现二阶低通滤波器的方法- 给出二阶低通滤波器的C 语言代码- 解释代码的实现过程和原理IV.二阶低通滤波器的应用- 举例说明二阶低通滤波器在实际应用中的使用- 阐述二阶低通滤波器在各种领域的重要性V.总结- 回顾本文的主要内容- 总结二阶低通滤波器C 语言实现的优点和局限性- 提出未来可能的改进方向正文:I.引言二阶低通滤波器是一种电子滤波器,主要用于滤除信号中的高频成分,保留低频成分。
在信号处理、通信、控制等领域有着广泛的应用。
本文将详细介绍二阶低通滤波器的原理和C 语言实现方法,并探讨其应用。
II.二阶低通滤波器原理二阶低通滤波器是一种具有两个存储元件的滤波器,其传递函数可以表示为:H(s) = A / (1 + ω^2 / ωn^2)其中,A 是滤波器的幅值响应,ω是信号的角频率,ωn 是滤波器的截止角频率。
当ω > ωn 时,滤波器对信号的衰减逐渐增加,信号通过滤波器后,高频成分被滤除,低频成分得以保留。
二阶低通滤波器的性能指标主要包括:通带波动、阻带衰减、过渡带宽等。
通带波动是指滤波器在通带内,不同频率信号的衰减程度;阻带衰减是指滤波器在阻带内,对高频信号的衰减程度;过渡带宽是指滤波器从通带到阻带的过渡区域宽度。
III.二阶低通滤波器C 语言实现C 语言实现二阶低通滤波器的方法主要是通过编程实现滤波器的传递函数。
具体步骤如下:1.定义滤波器参数:包括截止角频率ωn、通带衰减A 等;2.实现滤波器传递函数:根据二阶低通滤波器的原理,编写C 语言代码实现传递函数H(s);3.设计滤波器结构:根据传递函数,设计滤波器的结构,例如采用FIR(有限脉冲响应)滤波器结构;4.编写滤波器实现函数:根据滤波器结构,编写实现函数,实现对输入信号的滤波处理。
二维巴特沃斯滤波器c语言

二维巴特沃斯滤波器c语言二维巴特沃斯滤波器:c语言巴特沃斯滤波器是数字信号处理中常用的滤波器之一,它可以用于将输入信号中的高频噪声滤除,从而得到更清晰的信号。
在本文中,我将介绍如何使用c语言实现二维巴特沃斯滤波器。
巴特沃斯滤波器是一种基于极点和零点的滤波器,使用一些预定义的参数来确定滤波器的特性。
对于二维信号,我们可以分别对其行和列进行滤波操作,即实现二维滤波。
首先,我们需要定义滤波器的参数,包括截止频率和阶数。
截止频率是指在该频率以上的信号将被滤除,而阶数则决定了滤波器的衰减速度。
在c语言中,我们可以使用结构体来定义滤波器的参数,如下所示:```ctypedef struct {float cutoff_freq; // 截止频率int order; // 阶数} ButterworthFilterParams;```接下来,我们可以编写一个函数来计算巴特沃斯滤波器的系数。
这个函数将根据给定的截止频率和阶数计算出滤波器的各个系数。
这些系数将用于滤波器的频域计算。
以下是计算系数的函数示例:```cvoid computeButterworthCoefficients(ButterworthFilterParams params, float *b,float *a) {float f = tanf(M_PI * params.cutoff_freq);float r = powf(2.0, 1.0 / params.order);// 计算系数for (int i = 0; i < params.order; i++) {float theta = M_PI * (0.5 + 2.0 * (float)i / (2.0 * params.order));a[i] = 1.0;b[i] = 1.0;b[i] *= powf(f, 2.0);a[i] *= 2.0 * r * cosf(theta) * f;b[i] *= powf(f, 2.0);a[i] /= powf(r, 2.0) + powf((f / params.cutoff_freq), 2.0);b[i] /= powf(r, 2.0) + powf((f / params.cutoff_freq), 2.0f);}}```接下来,我们需要编写一个函数来应用滤波器。
巴特沃斯滤波器c语言实现

巴特沃斯滤波器c语言实现一、巴特沃斯滤波器的原理巴特沃斯滤波器是一种常见的滤波器,用于信号处理领域。
它的特点是在通带的频率范围内具有平坦的幅频特性,而在阻带的频率范围内具有陡峭的衰减特性。
巴特沃斯滤波器的设计基于巴特沃斯函数,该函数是一种理想的滤波器幅频响应函数。
通过对巴特沃斯函数进行归一化,我们可以得到具体的巴特沃斯滤波器传递函数。
二、巴特沃斯滤波器的C语言实现下面我们将介绍如何使用C语言来实现巴特沃斯滤波器。
1. 首先,我们需要定义巴特沃斯滤波器的一些参数,包括滤波器阶数、截止频率等。
这些参数可以根据实际需求进行调整。
2. 接下来,我们需要计算巴特沃斯滤波器的传递函数的系数。
这可以通过巴特沃斯函数的表达式进行计算。
在计算过程中,我们可以使用一些数学库函数来辅助计算。
3. 然后,我们需要编写滤波器函数,该函数接受输入信号和滤波器参数作为输入,输出滤波后的信号。
在函数内部,我们可以使用巴特沃斯滤波器的传递函数来实现信号的滤波。
4. 最后,我们可以编写一个主函数来测试巴特沃斯滤波器的性能。
在主函数中,我们可以生成一个测试信号,并调用滤波器函数对该信号进行滤波。
然后,我们可以将滤波后的信号保存到文件中,以便后续的分析和处理。
三、总结本文介绍了巴特沃斯滤波器的原理和C语言实现。
巴特沃斯滤波器是一种常见的滤波器,具有平坦的幅频特性和陡峭的衰减特性。
通过使用C语言,我们可以方便地实现巴特沃斯滤波器,用于信号处理和相关领域。
通过阅读本文,读者可以了解巴特沃斯滤波器的原理和C语言实现的基本步骤。
读者可以根据自己的需求和实际情况,进行巴特沃斯滤波器的参数调整和性能优化。
希望本文对读者能够有所帮助,对巴特沃斯滤波器的理解和应用有所启发。
二阶滤波器c语言实现

二阶滤波器c语言实现二阶滤波器是一种常用的信号处理器件,它可以对输入信号进行滤波处理,去除噪声、滤波频率等。
在这篇文章中,我将介绍如何使用C语言实现一个二阶滤波器。
我们需要了解二阶滤波器的工作原理。
二阶滤波器由两个一阶滤波器级联而成,每个一阶滤波器由一个电容和一个电阻组成。
它的输入信号经过一阶滤波器后得到中间信号,再经过第二个一阶滤波器得到输出信号。
可以看出,二阶滤波器具有更强的滤波效果和更陡的滤波斜率。
在C语言中,我们可以使用差分方程来描述二阶滤波器的运算过程。
假设输入信号为x(n),输出信号为y(n),那么可以表示为:y(n) = b0 * x(n) + b1 * x(n-1) + b2 * x(n-2) - a1 * y(n-1) - a2 * y(n-2)其中,b0、b1、b2是前向系数,a1、a2是反馈系数。
这些系数决定了滤波器的特性,可以根据需要进行调整。
接下来,我们就可以使用C语言编写代码来实现二阶滤波器。
首先,我们需要定义输入和输出数组,以及系数数组。
然后,使用一个循环来遍历输入信号,按照差分方程进行计算,得到输出信号。
以下是一个简单的示例代码:```c#include <stdio.h>#define N 100 // 输入信号长度// 系数定义double b0 = 1.0;double b1 = 0.5;double b2 = 0.2;double a1 = 0.3;double a2 = 0.1;// 输入和输出数组double x[N];double y[N];int main() {// 初始化输入信号for (int i = 0; i < N; i++) { x[i] = i;}// 进行滤波计算for (int n = 2; n < N; n++) {y[n] = b0 * x[n] + b1 * x[n-1] + b2 * x[n-2] - a1 * y[n-1] - a2 * y[n-2];}// 输出滤波结果for (int i = 0; i < N; i++) {printf("%f\n", y[i]);}return 0;}```在这段代码中,我们首先定义了输入和输出数组的长度为N,然后初始化输入信号。
二阶低通滤波器c语言

二阶低通滤波器c语言(原创实用版)目录1.二阶低通滤波器的概念和原理2.二阶低通滤波器的 C 语言编程实现3.二阶低通滤波器的应用实例正文一、二阶低通滤波器的概念和原理二阶低通滤波器是一种电子滤波器,主要用于去除信号中的高频成分,保留信号的低频成分。
它主要由电容、电感和电阻组成,其中电容和电感构成了滤波器的主要部分。
二阶低通滤波器的原理是利用电容和电感之间的相互作用,使高频信号通过电容或电感时受到较大的电阻限制,从而减小信号的幅值,达到滤波的目的。
二、二阶低通滤波器的 C 语言编程实现下面是一个简单的二阶低通滤波器的 C 语言编程实现:```c#include <stdio.h>#include <math.h>// 定义滤波器参数#define R 1000 // 电阻值#define C1 100pF // 电容 1 值#define C2 300pF // 电容 2 值#define L 100uH // 电感值// 定义滤波器函数void low_pass_filter(float *input, float *output, int n) { for (int i = 0; i < n; i++) {// 计算滤波器输出float output_value = 0;for (int j = 0; j < 2; j++) {output_value += (*input * C[j]) / (C[j] * R + L); }*output++ = output_value;// 计算滤波器输入float input_value = *input;for (int j = 0; j < 2; j++) {input_value += (*output * C[j]) / (C[j] * R + L); }*input++ = input_value;}}int main() {// 定义输入信号数组float input[] = {1, 2, 3, 4, 5};int n = sizeof(input) / sizeof(input[0]);// 定义输出信号数组float output[n];// 调用滤波器函数low_pass_filter(input, output, n);// 输出滤波器结果for (int i = 0; i < n; i++) {printf("%.2f", output[i]);}return 0;}```三、二阶低通滤波器的应用实例二阶低通滤波器广泛应用于各种电子设备中,如音频处理、图像处理等。
8-二阶巴特沃什有源滤波器设计
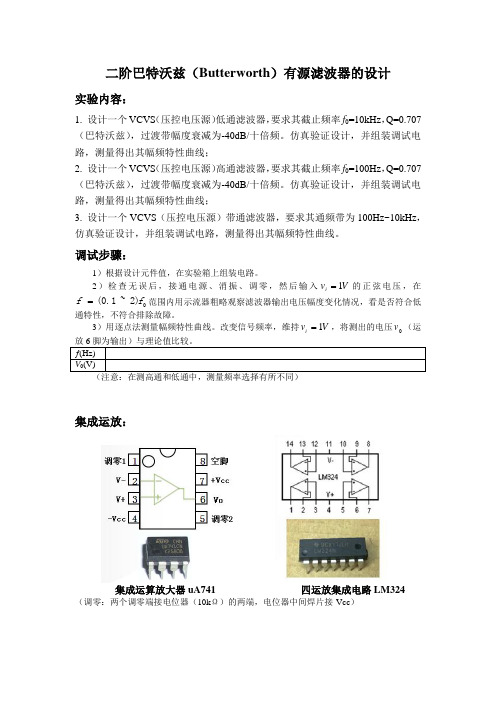
二阶巴特沃兹(Butterworth )有源滤波器的设计 实验内容:
1. 设计一个VCVS (压控电压源)低通滤波器,要求其截止频率f 0=10kHz ,Q=0.707(巴特沃兹),过渡带幅度衰减为-40dB/十倍频。
仿真验证设计,并组装调试电路,测量得出其幅频特性曲线;
2. 设计一个VCVS (压控电压源)高通滤波器,要求其截止频率f 0=100Hz ,Q=0.707(巴特沃兹),过渡带幅度衰减为-40dB/十倍频。
仿真验证设计,并组装调试电路,测量得出其幅频特性曲线;
3. 设计一个VCVS (压控电压源)带通滤波器,要求其通频带为100Hz~10kHz ,仿真验证设计,并组装调试电路,测量得出其幅频特性曲线。
调试步骤:
1)根据设计元件值,在实验箱上组装电路。
2)检查无误后,接通电源、消振、调零,然后输入V v i 1=的正弦电压,在0)2~1.0(f f =范围内用示流器粗略观察滤波器输出电压幅度变化情况,看是否符合低通特性,不符合排除故障。
3)用逐点法测量幅频特性曲线。
改变信号频率,维持V v i 1=,将测出的电压0v (运
集成运放:
集成运算放大器uA741 四运放集成电路LM324 (调零:两个调零端接电位器(10k Ω)的两端,电位器中间焊片接-Vcc )
参考电路:
1.低通滤波电路
2.高通滤波电路:
3.带通滤波电路:。
巴特沃斯滤波器c语言.docx

巴特沃斯滤波器c语言————————————————————————————————作者:————————————————————————————————日期 :1.模拟滤波器的设计1 .1 巴特沃斯滤波器的次数根据给定的参数设计模拟滤波器,然后进行变数变换,求取数字滤波器的方法,称为滤波器的间接设计。
做为数字滤波器的设计基础的模拟滤波器,称之为原型滤波器。
这里,我们首先介绍的是最简单最基础的原型滤波器,巴特沃斯低通滤波器。
由于 IIR 滤波器不具有线性相位特性,因此不必考虑相位特性,直接考虑其振幅特性。
在这里,N是滤波器的次数 , Ωc是截止频率。
从上式的振幅特性可以看出,这个是单调递减的函数 , 其振幅特性是不存在纹波的。
设计的时候,一般需要先计算跟所需要设计参数相符合的次数N。
首先,就需要先由阻带频率,计算出阻带衰减将巴特沃斯低通滤波器的振幅特性,直接带入上式,则有最后 ,可以解得次数N 为当然,这里的N 只能为正数 ,因此,若结果为小数,则舍弃小数,向上取整。
1.2 巴特沃斯滤波器的传递函数巴特沃斯低通滤波器的传递函数,可由其振幅特性的分母多项式求得。
其分母多项式根据S解开,可以得到极点。
这里,为了方便处理,我们分为两种情况去解这个方程。
当N为偶数的时候 ,这里,使用了欧拉公式。
同样的,当N为奇数的时候,同样的 ,这里也使用了欧拉公式。
归纳以上,极点的解为上式所求得的极点 ,是在 s 平面内 ,在半径为Ωc的圆上等间距的点,其数量为 2N 个。
为了使得其IIR滤波器稳定 ,那么,只能选取极点在 S 平面左半平面的点。
选定了稳定的极点之后,其模拟滤波器的传递函数就可由下式求得。
1.3 巴特沃斯滤波器的实现(C 语言 )首先 ,是次数的计算。
次数的计算,我们可以由下式求得。
其对应的 C 语言程序为[ cpp ]view plaincopy1.N= Ceil(0 .5*(log10 ( po w ( 10, Stopband_attenuation/10)-1) /2.log10 ( St opba n d/C o toff))) ;然后是极点的选择,这里由于涉及到复数的操作,我们就声明一个复数结构体就可以了。
imu 原始数据二阶低通滤波 代码

IMU(惯性测量单元)是一种用于测量和跟踪物体在空间中的运动和姿态的传感器。
它通常由加速度计、陀螺仪和磁力计等传感器组成,可以提供关于物体加速度、角速度和方向的数据。
在实际应用中,IMU的原始数据可能会受到噪音的影响,这会使得数据不够准确和稳定。
对IMU原始数据进行滤波处理是很重要的,特别是对于一些需要高精度姿态解算的应用,比如飞行器、导航系统等。
二阶低通滤波是一种常用的滤波方法,可以有效地去除高频噪音,保留信号的低频成分,从而使得数据更加平滑和稳定。
本文将介绍如何使用二阶低通滤波对IMU的原始数据进行处理,并给出相应的代码实现。
1. 确定滤波器的参数在进行二阶低通滤波之前,首先需要确定滤波器的参数,包括截止频率和采样频率。
截止频率决定了滤波器对高频噪音的抑制能力,采样频率则决定了信号的采样间隔。
2. 设计滤波器根据确定的参数,可以利用巴特沃斯滤波器设计方法设计出一个二阶低通滤波器。
该滤波器可以通过巴特沃斯滤波器的差分方程来实现,具体步骤如下:(1)计算滤波器的增益系数(2)根据增益系数计算滤波器的系数(3)利用递推算法来实现滤波器的运算3. 实现滤波器根据设计的滤波器,可以利用C语言或者其他编程语言来实现滤波器的代码。
下面是一个简单的C语言代码示例:```c#define ORDER 2 // 滤波器阶数float input[ORDER+1]; // 输入数据float output[ORDER+1]; // 输出数据float b[ORDER+1] = {0.1020, 0.2041, 0.1020}; // 滤波器系数float a[ORDER+1] = {1.0000, -0.4189, 0.6414}; // 滤波器系数void filter(float input_data){int i;for (i = ORDER; i > 0; i--) {input[i] = input[i-1];output[i] = output[i-1];}input[0] = input_data;output[0] = b[0]*input[0];for (i = 1; i < ORDER+1; i++) {output[0] += b[i]*input[i] - a[i]*output[i];}}```4. 应用滤波器将设计和实现好的滤波器应用到IMU的原始数据上,即可得到经过滤波处理后的数据。
二阶低通滤波器c语言

二阶低通滤波器c语言摘要:1.二阶低通滤波器简介2.C语言实现二阶低通滤波器的方法3.代码解析4.应用实例5.总结与展望正文:【一、二阶低通滤波器简介】二阶低通滤波器是一种常用的信号处理滤波器,其主要作用是允许低于截止频率的信号通过,而抑制高于截止频率的信号。
在众多信号处理领域,如自动控制、通信、信息处理等,二阶低通滤波器都有着广泛的应用。
【二、C语言实现二阶低通滤波器的方法】在C语言中,实现二阶低通滤波器主要依赖于数字信号处理库。
以下是一种简单的C语言实现二阶低通滤波器的方法:```c#include <stdio.h>#include <stdlib.h>#include <math.h>// 定义滤波器系数const double a0 = 1.0;const double a1 = -2.0 * a0 / (1 + sqrt(1 + a0 * a0));const double a2 = 1.0 / (1 + sqrt(1 + a0 * a0));// 滤波器函数double filter(double input, double *buffer, int size) {double output = 0.0;for (int i = 0; i < size; i++) {output += a0 * buffer[i] + a1 * buffer[i - 1] + a2 * buffer[i - 2];}return output;}int main() {// 初始化滤波器缓冲区double buffer[100];for (int i = 0; i < 100; i++) {buffer[i] = 0.0;}// 输入信号double input = 1.0;// 滤波double output = filter(input, buffer, 100);// 输出结果printf("Filtered signal: %f", output);return 0;}```【三、代码解析】上述代码中,我们定义了一个名为`filter`的函数,该函数接受一个输入信号`input`和滤波器缓冲区`buffer`,并通过计算实现对输入信号的滤波。
c语言怎样实现巴特沃斯滤波器计算公式

c语言怎样实现巴特沃斯滤波器计算公式在深度学习领域中,巴特沃斯滤波器作为一种常用的频域滤波器,可以有效地去除图像中的噪声,提高图像的质量和清晰度。
本文将围绕着C语言如何实现巴特沃斯滤波器的计算公式展开探讨。
一、巴特沃斯滤波器简介巴特沃斯滤波器是一种频域滤波器,它可以根据不同的参数配置来调整图像的频谱特征,从而实现对图像噪声的抑制和图像质量的提高。
它的数学表达式为:H(u, v) = 1 / [1 + (D(u, v) / D0) ^ (2n)]在这个公式中,H(u, v)代表的是频域域上的滤波器函数,D(u, v)代表点(u, v)到频域中心的距离,D0代表的是截止频率,n代表滤波器的阶数。
二、C语言实现巴特沃斯滤波器计算公式1. 计算频谱到中心的距离D(u, v)在C语言中,我们首先需要计算每个频率点到频域中心的距离D(u, v),这可以通过傅立叶变换的性质来实现。
我们可以使用以下代码来计算频谱到中心的距离:```cfloat D_uv(int u, int v, int M, int N) {float duv;duv = sqrt((u - M / 2) * (u - M / 2) + (v - N / 2) * (v - N / 2));return duv;}```在这个代码中,我们传入了频率点的坐标(u, v)以及图像的大小M和N,然后通过欧式距禮的计算得到了频率点到频域中心的距离。
2. 实现巴特沃斯滤波器函数H(u, v)的计算接下来,我们可以根据已经计算出来的频谱到中心的距离D(u, v)以及截止频率D0和滤波器的阶数n来计算滤波器函数H(u, v)。
以下是C语言中的实现代码:```cfloat butterworth_filter(int u, int v, int M, int N, float D0, int n) {float duv = D_uv(u, v, M, N);return 1 / (1 + pow(duv / D0, 2 * n));}```在这段代码中,我们使用了之前计算出来的频谱到中心的距离D(u, v),并结合截止频率D0和滤波器的阶数n,最终得到了滤波器函数H(u, v)的值。
c语言 2阶低通滤波器 公式

c语言 2阶低通滤波器公式2阶低通滤波器是一种常用的信号处理器件,它可以将输入信号中高频成分滤除,保留低频成分,从而实现信号的平滑处理。
在c语言中,可以通过一些公式来实现2阶低通滤波器的设计和实现。
我们需要了解一些基本概念。
在信号处理中,频率通常用赫兹(Hz)来表示,表示每秒钟的周期数。
低通滤波器是一种能够通过的频率范围较低的信号,而阻止高于该范围的信号通过的滤波器。
在设计低通滤波器时,我们需要确定一些参数,包括截止频率和滤波器的阶数。
截止频率是指信号通过滤波器后开始衰减的频率,阶数表示滤波器的复杂程度。
接下来,我们可以使用巴特沃斯滤波器设计方法来设计2阶低通滤波器。
巴特沃斯滤波器是一种常见的滤波器类型,它具有平坦的通带和陡峭的阻带。
巴特沃斯滤波器的设计步骤如下:1. 确定截止频率(fc)和采样频率(fs),截止频率是指滤波器开始衰减的频率,采样频率是指信号的采样频率。
2. 根据截止频率和采样频率计算出归一化截止频率(wc),归一化截止频率是指截止频率除以采样频率的一半。
3. 根据归一化截止频率计算出极点的实部和虚部,极点是滤波器传递函数的零点和极点的位置。
4. 根据极点的实部和虚部计算出滤波器的系数,系数是用来实现滤波器功能的参数。
在c语言中,我们可以使用以下公式来计算滤波器的系数:```Q = 1 / (2 * sin(pi * wc))alpha = sin(pi * wc) / (2 * Q)a0 = 1 + alphaa1 = -2 * cos(pi * wc)a2 = 1 - alphab0 = (1 - cos(pi * wc)) / 2b1 = 1 - cos(pi * wc)b2 = (1 - cos(pi * wc)) / 2```其中,Q表示质量因子,alpha表示极点角频率,a0、a1、a2、b0、b1、b2表示滤波器的系数。
接下来,我们可以使用这些系数来实现滤波器的功能。
二阶巴特沃斯低通滤波器阻值计算

二阶巴特沃斯低通滤波器阻值计算
二阶巴特沃斯低通滤波器的阻值计算可以通过以下步骤进行:
1. 确定滤波器的参数:首先,你需要确定滤波器的截止频率(Wn)和滤波器的类型(低通、高通、带通或带阻)。
2. 设计滤波器:在MATLAB或C语言中,可以使用butter函数来设计二阶巴特沃斯低通滤波器。
输入参数为n (滤波器阶数),Wn(归一化截止频率)和ftype(滤波器类型)。
例如,[b, a] = butter(2, Wn),其中2表示阶数为2,Wn 表示归一化的截止频率。
3. 计算阻值:二阶巴特沃斯低通滤波器的传递函数为H(jw) = b0/a0,其中b0和a0分别是滤波器的分子和分母系数。
这两个系数可以通过butter函数得到。
4. 计算阻值:阻值可以通过传递函数计算得到,阻值=1/|H(jw)|。
需要注意的是,以上步骤是基于理论计算,实际应用中可能由于电路元件的公差、温度变化等因素影响阻值,因此还需要进行实际的测量和调整。
巴特沃斯低通滤波器(C语言)

engSetVisible(ep, 0);
//mxArray *xx = mxCreateDoubleMatrix(1,N,mxREAL);
// mxArray *yy = mxCreateDoubleMatrix(1,N,mxREAL);
// memcpy(mxGetPr(xx),N*sizeof(double#34;;");
///////////////////////////////////////////////////////////
Engine *ep;
if(!(ep = engOpen(NULL)))
{
printf("open failed! please try again\n");
engEvalString(ep, "title('Butterworth analog filter prototype');");
engEvalString(ep, "grid;");
getchar();
//mxDestroyArray(xx);
// mxDestroyArray(yy);
// engClose(ep);
// memcpy(mxGetPr(yy),N*sizeof(double));
// engPutVariable(ep,"xx",xx);
//engPutVariable(ep,"yy",yy);
engEvalString(ep, "n=0:0.01:2;");
engEvalString(ep, lin);
engEvalString(ep, "plot(w,magH);");
巴特沃斯滤波器c语言

1. 模拟滤波器的设计1.1巴特沃斯滤波器的次数根据给定的参数设计模拟滤波器,然后进行变数变换,求取数字滤波器的方法,称为滤波器的间接设计。
做为数字滤波器的设计基础的模拟滤波器,称之为原型滤波器。
这里,我们首先介绍的是最简单最基础的原型滤波器,巴特沃斯低通滤波器。
由于IIR滤波器不具有线性相位特性,因此不必考虑相位特性,直接考虑其振幅特性。
在这里,N是滤波器的次数,Ωc是截止频率。
从上式的振幅特性可以看出,这个是单调递减的函数,其振幅特性是不存在纹波的。
设计的时候,一般需要先计算跟所需要设计参数相符合的次数N。
首先,就需要先由阻带频率,计算出阻带衰减将巴特沃斯低通滤波器的振幅特性,直接带入上式,则有最后,可以解得次数N为当然,这里的N只能为正数,因此,若结果为小数,则舍弃小数,向上取整。
1.2巴特沃斯滤波器的传递函数巴特沃斯低通滤波器的传递函数,可由其振幅特性的分母多项式求得。
其分母多项式根据S解开,可以得到极点。
这里,为了方便处理,我们分为两种情况去解这个方程。
当N 为偶数的时候,这里,使用了欧拉公式。
同样的,当N为奇数的时候,同样的,这里也使用了欧拉公式。
归纳以上,极点的解为上式所求得的极点,是在s平面内,在半径为Ωc的圆上等间距的点,其数量为2N个。
为了使得其IIR滤波器稳定,那么,只能选取极点在S平面左半平面的点。
选定了稳定的极点之后,其模拟滤波器的传递函数就可由下式求得。
1.3巴特沃斯滤波器的实现(C语言)首先,是次数的计算。
次数的计算,我们可以由下式求得。
其对应的C语言程序为1.N = Ceil(0.5*( log10 ( pow (10, Stopband_attenuation/10) - 1) /2. log10 (Stopband/Cotoff) ));然后是极点的选择,这里由于涉及到复数的操作,我们就声明一个复数结构体就可以了。
最重要的是,极点的计算含有自然指数函数,这点对于计算机来讲,不是太方便,所以,我们将其替换为三角函数,这样的话,实部与虚部就还可以分开来计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二阶巴特沃斯低通滤波器 c语言
二阶巴特沃斯低通滤波器是一种常用的电子滤波器,主要用于信号处理和电路设计中。
它可以有效地滤除高频信号,保留低频信号,使得输出信号更加平滑和稳定。
本文将介绍二阶巴特沃斯低通滤波器的原理和C语言实现方法。
一、二阶巴特沃斯低通滤波器原理
巴特沃斯滤波器是一种无失真滤波器,其特点是在通带中具有最大平坦度,而在阻带中具有最小衰减。
二阶巴特沃斯低通滤波器是一种二阶滤波器,可以通过调整参数来实现不同的滤波效果。
二阶巴特沃斯低通滤波器的传输函数为:
H(s) = 1 / (s^2 + s/Q + 1)
其中,s为复变量,Q为质量因子,决定了滤波器的带宽和阻带衰减。
通过调整Q的值,可以实现不同的滤波器响应。
二、C语言实现二阶巴特沃斯低通滤波器
下面是一个简单的C语言实现二阶巴特沃斯低通滤波器的代码示例:
#include <stdio.h>
#include <math.h>
#define PI 3.1415926
typedef struct
{
double a0, a1, a2; // 分子系数
double b0, b1, b2; // 分母系数
double x1, x2; // 输入延时
double y1, y2; // 输出延时
} BiquadFilter;
void BiquadFilter_init(BiquadFilter* filter, double cutoff_freq, double sample_rate)
{
double w0 = 2 * PI * cutoff_freq / sample_rate;
double alpha = sin(w0) / 2;
double a0 = 1 + alpha;
double a1 = -2 * cos(w0);
double a2 = 1 - alpha;
double b0 = (1 - cos(w0)) / 2;
double b1 = 1 - cos(w0);
double b2 = (1 - cos(w0)) / 2;
filter->a0 = b0 / a0;
filter->a1 = b1 / a0;
filter->a2 = b2 / a0;
filter->b1 = -a1 / a0;
filter->b2 = -a2 / a0;
filter->x1 = 0;
filter->x2 = 0;
filter->y1 = 0;
filter->y2 = 0;
}
double BiquadFilter_process(BiquadFilter* filter, double input) {
double output = filter->a0 * input + filter->a1 * filter->x1 + filter->a2 * filter->x2 - filter->b1 * filter->y1 - filter->b2 * filter->y2;
filter->x2 = filter->x1;
filter->x1 = input;
filter->y2 = filter->y1;
filter->y1 = output;
return output;
}
int main()
{
double cutoff_freq = 1000; // 截止频率
double sample_rate = 44100; // 采样率
BiquadFilter filter;
BiquadFilter_init(&filter, cutoff_freq, sample_rate);
double input = 0;
double output = 0;
// 生成输入信号
for (int i = 0; i < 1000; i++)
{
input = sin(2 * PI * 1000 * i / sample_rate);
// 进行滤波处理
output = BiquadFilter_process(&filter, input);
// 输出滤波结果
printf("%f\n", output);
}
return 0;
}
以上代码实现了一个简单的二阶巴特沃斯低通滤波器。
首先通过调用BiquadFilter_init函数初始化滤波器参数,然后通过BiquadFilter_process函数对输入信号进行滤波处理,得到输出信号。
在主函数中,生成了一个正弦波作为输入信号,并输出滤波结果。
三、总结
二阶巴特沃斯低通滤波器是一种常用的滤波器,可以有效地滤除高频信号,保留低频信号。
本文介绍了二阶巴特沃斯低通滤波器的原理和C语言实现方法,并给出了一个简单的代码示例。
希望本文对读者理解和应用二阶巴特沃斯低通滤波器有所帮助。
