大学物理2,15.第十五章思考题
大学物理实验课思考题参考答案

大学物理实验思考题参考答案目录一、转动惯量:二、伏安法与补偿法三、混沌思考题四、半导体PN结五、地磁场六、牛顿环七、麦克尔逊干涉仪八、全息照相九、光电效应十、声速测量十一、用电位差计校准毫安表十二、落球法测量液体的黏度十三、电子束偏转与电子比荷测量十四、铁磁材料磁化特性研究十五、光栅衍射十六、电桥十七、电位差计十八、密立根油滴十九、模拟示波器二十、金属杨氏摸量二十一、导热系数二十二、分光计二十三、集成霍尔传感器特性与简谐振动一、转动惯量:1、由于采用了气垫装置,这使得气垫摆摆轮在摆动过程中受到的空气粘滞阻尼力矩降低至最小程度,可以忽略不计。
但如果考虑这种阻尼的存在,试问它对气垫摆的摆动(如频率等)有无影响?在摆轮摆动中,阻尼力矩是否保持不变?答:如果考虑空气粘滞阻尼力矩的存在,气垫摆摆动时频率减小,振幅会变小。
(或者说对频率有影响,对振幅有影响)在摆轮摆动中,阻尼力矩会越变越小。
2、为什么圆环的内、外径只需单次测量?实验中对转动惯量的测量精度影响最大的是哪些因素?答:圆环的内、外径相对圆柱的直径大很多,使用相同的测量工具测量时,相对误差较小,故只需单次测量即可。
(对测量结果影响大小)实验中对转动惯量测量影响最大的因素是周期的测量。
(或者阻尼力矩的影响、摆轮是否正常、平稳的摆动、物体摆放位置是否合适、摆轮摆动的角度是否合适等)3、试总结用气垫摆测量物体转动惯量的方法有什么基本特点?答:原理清晰、结论简单、设计巧妙、测量方便、最大限度的减小了阻尼力矩。
二、伏安法与补偿法1、利用补偿法测量电阻消除了伏安法的系统误差,还可能存在的误差包括:读数误差、计算产生的误差、仪器误差、导线阻值的影响等或其他。
2、能利用电流补偿电路对电流表内接法进行改进:三、混沌思考题1、有程序(各种语言皆可)、K值的取值范围、图 +5分有程序没有K值范围和图 +2分只有K值范围 +1分有图和K值范围 +2分2、(1)混沌具有内在的随机性:从确定性非线性系统的演化过程看,它们在混沌区的行为都表现出随机不确定性。
大学物理(第二版)第十五章习题答案

第十五章习题15.1 解:介质中的折射率为n ,加入厚度为d 的薄膜,光程的改变为()19n d λ-=所以可以得到:1039958901011 1.530.0110n d λ--⨯⨯=+=+=⨯ 15.2 解:已知条件:6000A λ=,4m D =,垂直入射,两第五级明条纹中心之间的距离为4cm 。
2551022410m D D x d dλλ-=⨯==⨯ 双缝之间的距离:10325101046000100.610m=0.6mm 2410D d x λ---⨯⨯⨯===⨯⨯ 15.3 解:⑴ 双缝之间的距离为:0.2mm d =,缝与屏之间的距离为:1m D = 亮条纹距离零级明条纹中心的位置:D k x d λ=d xk D λ⇒=因为:4000A 8000A λ≤≤,所以可得:115d x k D λ==, 222.5d xk D λ==,即2.55k ≤≤ 第三级明纹:3310.21010106667A 13dx Dk λ--⨯⨯⨯===⨯第四级明纹:3320.21010105000A 14dx Dk λ--⨯⨯⨯===⨯ 第五级明纹:3330.21010104000A 15dx Dk λ--⨯⨯⨯===⨯ ⑵ 20mm x =,可以得到:dxk D λ=,510k ≤≤ 15k =, 33110.21020108000A 15dx Dk λ--⨯⨯⨯===⨯ 26k =,33220.21020106667A 16dx Dk λ--⨯⨯⨯===⨯ 37k =,33320.21020105714A 17dx Dk λ--⨯⨯⨯===⨯ 48k =,33440.21020105000A 18dx Dk λ--⨯⨯⨯===⨯59k =,33550.21020104444A 19dx Dk λ--⨯⨯⨯===⨯ 610k =,33660.21020104000A 110dx Dk λ--⨯⨯⨯===⨯ 15.4 解:设空气的折射率为1n ,氯气的折射率为2n ,两条光路的几何路程分别为:12,r r 。
大学物理实验思考题

力学和热学电磁学光学近代物理1. 是否可以测摆动一次的时间作周期值?为什么?答:不可以。
因为一次测量随机误差较大,多次测量可减少随机误差。
2. 将一半径小于下圆盘半径的圆盘,放在下圆盘上,并使中心一致,讨论此时三线摆的周期和空载时的周期相比是增大、减小还是不一定?说明理由。
答:当两个圆盘的质量为均匀分布时,与空载时比较,摆动周期将会减小。
因为此时若把两盘看成为一个半径等于原下盘的圆盘时,其转动惯量I0小于质量与此相等的同直径的圆盘,根据公式(3-1-5),摆动周期T0将会减小。
3. 三线摆在摆动中受空气阻尼,振幅越来越小,它的周期是否会变化?对测量结果影响大吗?为什么?答:周期减小,对测量结果影响不大,因为本实验测量的时间比较短。
实验2 金属丝弹性模量的测量1. 光杠杆有什么优点,怎样提高光杠杆测量的灵敏度?答:优点是:可以测量微小长度变化量。
提高放大倍数即适当地增大标尺距离D或适当地减小光杠杆前后脚的垂直距离b,可以提高灵敏度,因为光杠杆的放大倍数为2D/b。
2. 何谓视差,怎样判断与消除视差?答:眼睛对着目镜上、下移动,若望远镜十字叉丝的水平线与标尺的刻度有相对位移,这种现象叫视差,细调调焦手轮可消除视差。
3. 为什么要用逐差法处理实验数据?答:逐差法是实验数据处理的一种基本方法,实质就是充分利用实验所得的数据,减少随机误差,具有对数据取平均的效果。
因为对有些实验数据,若简单的取各次测量的平均值,中间各测量值将全部消掉,只剩始末两个读数,实际等于单次测量。
为了保持多次测量的优越性,一般对这种自变量等间隔变化的情况,常把数据分成两组,两组逐次求差再算这个差的平均值。
实验三,随即误差的统计规律1. 什么是统计直方图? 什么是正态分布曲线?两者有何关系与区别?答:对某一物理量在相同条件下做n次重复测量,得到一系列测量值,找出它的最大值和最小值,然后确定一个区间,使其包含全部测量数据,将区间分成若干小区间,统计测量结果出现在各小区间的频数M,以测量数据为横坐标,以频数M为纵坐标,划出各小区间及其对应的频数高度,则可得到一个矩形图,即统计直方图。
大学物理2,15.第十五章思考题

1、一束光垂直入射在偏振片上,以入射光线为轴转动偏振片,观察通过偏振片后的光强变化过程。
如果观察到光强不变,则入射光是什么光?如果观察到明暗交替变化,有时出现全暗,则入射光是什么光?如果观察到明暗交替变化,但不出现全暗,则入射光是什么光?【答案:自然光;完全偏振光;部分偏振光】详解:当一束光垂直入射在偏振片上时,以入射光线为轴转动偏振片,如果观察到通过偏振片后的光强不发生变化,入射光是由自然光;如果观察到光强有明暗交替变化,并且有时出现全暗,则入射光是完全偏振光;如果观察到光强有明暗交替变化,但不出现全暗,则入射光是部分偏振光。
2、一束光是自然光和线偏振光的混合光,让它垂直通过一个偏振片。
若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光与线偏振光的光强比值为多少?【答案:1/2】详解:设该光束中自然光和线偏振光的强度分别为I 1和I 2。
当以此入射光束为轴旋转偏振片时,透射光强度的最大值和最小值分别为21max 21I I I +=1min 21I I = 依题意有I max =5I min ,即 12121521I I I ⨯=+ 解之得2121=I I 即入射光束中自然光与线偏振光的光强比值等于1/2。
3、一束光强为I 0的自然光相继通过三个偏振片P 1、P 2、P 3后,出射光的光强为0.125I 0 。
已知P 1和P 2的偏振化方向相互垂直,若以入射光线为轴旋转P 2,要使出射光的光强为零,P 2最少要转过多大的角度?【答案:45°】详解:由于P 1和P 2的偏振化方向相互垂直,而自然光相继通过三个偏振片后的光强不等于零,说明自然光通过偏振片的顺序为P 1、P 3、P 2。
如图所示,设偏振片P 1和P 3的夹角为θ,由马吕斯定律得出射光强为 )09(cos cos 2220θθ-= I I θ2sin 820I = 由于I =0.125I 0 ,代入上式解得 45=θ要使出射光强为零,应使P 2和P 3的偏振化方向垂直,因此P 2最少要转过的角度也等于45°。
大学物理第15章习题解答

第十五章习题解答1选择题:⑴ B ;⑵ C ;⑶ B ;⑷ B 。
2填空题:⑴ 线偏振光(或完全偏振光,或平面偏振光),光(矢量)振动,偏振化(或透光轴);⑵ 完全偏振光(或线偏振光),垂直; ⑶ ; ⑷ 波动,横波;3计算题:1 自然光入射到两个重叠的偏振片上.如果透射光强为,(1)透射光最大强度的三分之一,(2)入射光强的三分之一,则这两个偏振片透光轴方向间的夹角为多少? 解:(1) max 120131cos 2I I I ==α 又 20max I I =∴ ,601I I = 故 'ο11124454,33cos ,31cos ===ααα. (2) 0220231cos 2I I I ==α ∴ 'ο221635,32cos ==αα2 投射到起偏器的自然光强度为I 0,开始时,起偏器和检偏器的透光轴方向平行.然后使检偏器绕入射光的传播方向转过30°,45°,60°,试分别求出在上述三种情况下,透过检偏器后光的强度是I 0的几倍?解:由马吕斯定律有:0o 2018330cos 2I I I ==, 0ο2024145cos 2I I I ==,0ο2038160cos 2I I I == 所以透过检偏器后光的强度分别是I 0的38,14,18倍。
3 使自然光通过两个偏振化方向夹角为60°的偏振片时,透射光强为I 1,今在这两个偏振片之间再插入一偏振片,它的偏振化方向与前两个偏振片均成30°,问此时透射光I 与I 1之比为多少?解:由马吕斯定律:ο20160cos 2I I =80I =,32930cos 30cos 20ο2ο20I I I == ∴ 194 2.25I I == 4 一束自然光从空气入射到折射率为1.40的液体表面上,其反射光是完全偏振光.试求:(1)入射角等于多少? (2)折射角为多少?解:⑴ 0tan 1.401i =,∴ 'ο02854=i⑵ οο'0903532i γ=-=5 自然光从空气中射向介质,测得布儒斯特角058i =.(1)求介质的折射率和折射角.(2)如果实验在水中进行,水的折射率为 1.33n =水,求这种情况下的布儒斯特角.(3)若介质是透明的,当光从介质射向与空气的分界面时,起偏角是多少?(4)若从空气中射向介质的是振动方向在入射面内的偏振光,仍以058i =入射,问反射光是什么性质的光?解:(1)00tan tan 58 1.6n i ===折射角:οο09032i γ=-=(2)0 1.6tan 1.2031.33i ==,ο050.26i = (3)01tan 0.6251.6i ==,ο032i = (4)无反射光。
大学物理15章习题

⼤学物理15章习题15章习题答案15-3求各图中点P 处磁感应强度的⼤⼩和⽅向。
[解] (a) 因为长直导线对空间任⼀点产⽣的磁感应强度为:()210cos cos 4θθπµ-=aIB对于导线1:01=θ,22πθ=,因此aI B πµ401=对于导线2:πθθ==21,因此02=BaIB B B πµ4021p =+= ⽅向垂直纸⾯向外。
(b) 因为长直导线对空间任⼀点产⽣的磁感应强度为:()210cos cos 4θθπµ-=aIB对于导线1:01=θ,22πθ=,因此rI a I B πµπµ44001==,⽅向垂直纸⾯向内。
对于导线2:21πθ=,πθ=2,因此rI a I B πµπµ44002==,⽅向垂直纸⾯向内。
半圆形导线在P 点产⽣的磁场⽅向也是垂直纸⾯向内,⼤⼩为半径相同、电流相同的圆形导线在圆⼼处产⽣的磁感应强度的⼀半,即rIr=,⽅向垂直纸⾯向内。
所以,rIr I r I r I r I B B B B 4244400000321p µπµµπµπµ+=++=++= (c) P 点到三⾓形每条边的距离都是a d 63=o 301=θ,o 1502=θ每条边上的电流在P 点产⽣的磁感应强度的⽅向都是垂直纸⾯向内,⼤⼩都是()a I d IB πµπµ23150cos 30cos 400000=-=故P 点总的磁感应强度⼤⼩为aIB B πµ29300==⽅向垂直纸⾯向内。
15-4在半径为R 和r 的两圆周之间,有⼀总匝数为N 的均匀密绕平⾯线圈,通有电流I ,⽅向如图所⽰。
求中⼼O 处的磁感应强度。
[解] 由题意知,均匀密绕平⾯线圈等效于通以 I NI 圆盘,设单位长度线圈匝数为nrR Nn -=建⽴如图坐标,取⼀半径为x 厚度为dx 的圆环,其等效电流为:x r R NIx j I d d d -== )(2d 2d d 000r R x xNI xIB -==µµrR r R NIr R x xNIln)(2)(2d d 0000-=-==?µµ所以⽅向垂直纸⾯向外.15-5电流均匀地流过⼀⽆限长薄壁半圆筒,设电流I =5.0A ,圆筒半径 R =m 100.12?如图所⽰。
大学物理实验思考题解答

2.用逐差法处理数据的优点是什么?
答:逐差法是物理实验中处理数据的一种常用方法,是对等间隔变化的被测物理量的数据,进行逐项或隔项相减,来获得实验结果的数据处理方法。逐差法进行数据处理有很多优点,可以验证函数的表达形式,也可以充分利用所测数据,具有对数据取平均的效果,起到减小随机误差的作用。本实验用隔项逐差法处理数据,减小了测量的随机误差。
实验三衍射光栅
【预习思考题】
1.如何调整分光计到待测状态?
答:(1)调节望远镜适合接收平行光,且其光轴垂直于仪器中心轴;
(2)平行光管能发出平行光,且其光轴垂直于仪器中心轴;
(3)载物台的台面垂直于仪器中心轴。
2.调节光栅平面与入射光垂直时,为什么只调节载物台调平螺钉b、c,而当各级谱线左右两侧不等高时,又只能调节载物台调平螺钉a?
霍尔传感器
【预习思考题】
1.写出调整霍尔式传感器的简明步ห้องสมุดไป่ตู้。
(1)按图6.2-6接线;
(2)差动放大器调零;
(3)接入霍尔式传感器,安装测微头使之与振动台吸合;
(4)上下移动测微头±4mm,每隔0.5mm读取相应的输出电压值。
2.结合梯度磁场分布,解释为什么霍尔片的初始位置应处于环形磁场的中间。
在环形磁场的中间位置磁感应强度B为零。由霍尔式传感器的工作原理可知,当霍尔元件通以稳定电流时,霍尔电压UH的值仅取决于霍尔元件在梯度磁场中的位移x,并在零点附近的一定范围内存在近似线性关系。
实验二声速的测量
【预习思考题】
1.如何调节和判断测量系统是否处于共振状态?为什么要在系统处于共振的条件下进行声速测定?
大学物理答案第15章
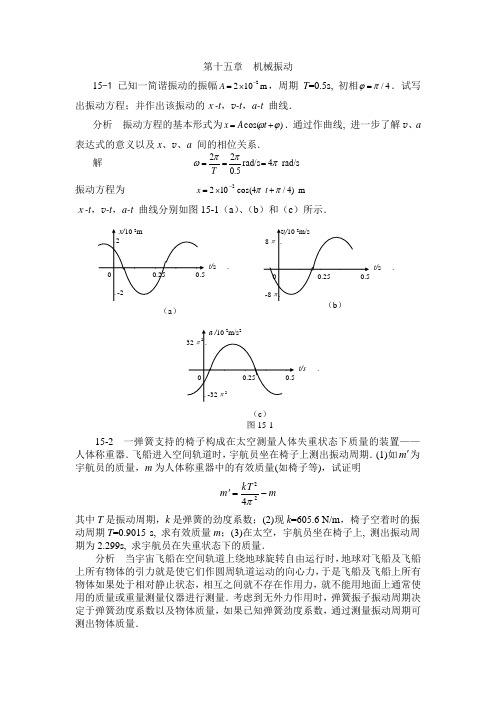
第十五章 机械振动15-1 已知一简谐振动的振幅m 1022-⨯=A ,周期T =0.5s, 初相4/πϕ=.试写出振动方程;并作出该振动的x-t ,v -t ,a-t 曲线.分析 振动方程的基本形式为)cos(ϕω+=t A x .通过作曲线, 进一步了解v 、a表达式的意义以及x 、v 、a 间的相位关系.解 rad/s 4 rad/s 5.022πππω===T振动方程为m)4/4cos(1022ππ+⨯=-t xx15-2 一弹簧支持的椅子构成在太空测量人体失重状态下质量的装置——人体称重器.飞船进入空间轨道时,宇航员坐在椅子上测出振动周期.(1)如m '为宇航员的质量,m 为人体称重器中的有效质量(如椅子等),试证明mkT m -='224π其中T 是振动周期,k 是弹簧的劲度系数;(2)现k =605.6 N/m ,椅子空着时的振动周期T =0.9015 s, 求有效质量m ;(3)在太空,宇航员坐在椅子上, 测出振动周期为2.299s, 求宇航员在失重状态下的质量.分析 当宇宙飞船在空间轨道上绕地球旋转自由运行时,地球对飞船及飞船上所有物体的引力就是使它们作圆周轨道运动的向心力,于是飞船及飞船上所有物体如果处于相对静止状态,相互之间就不存在作用力,就不能用地面上通常使用的质量或重量测量仪器进行测量.考虑到无外力作用时,弹簧振子振动周期决定于弹簧劲度系数以及物体质量,如果已知弹簧劲度系数,通过测量振动周期可测出物体质量.解 (1) 弹簧振子系统振动周期为km m T +'=π2 (1)宇航员的质量为 m kT m -='224π(2) 椅子空着时,0='m ,由(1)式得kg 66.12kg 6.605142.349015.042222=⨯⨯==πkT m(3) kg 50.68kg 66.12kg 142.34299.26.60542222=-⨯⨯=-='m kT m π15-3 一质量为0.20kg 的质点作简谐振动,其振动方程为 x =0.60cos(5t -π/2), 其中x 以m 为单位, t 以s 为单位.求:(1)质点的初速度;(2)质点在正向位移一半处所受的力.分析 物体振动速度tx d d =v , 物体所受恢复力x m ma F 2ω-==,方向指向平衡位置.解 (1)据已知)2/5(60.0π-=t x ,得t t t A tx 5cos 3)2/5sin(560.0)sin(d d =-⨯-=+-==πϕωωv当t=0时,得 v 0=3 m/s(2) 正向最大位移一半处,x =0.30 m ,所受的力为N 5.1N 3.052.022-=⨯⨯-=-==x m ma F ω方向指向平衡位置.15-4 一物体沿x 轴作简谐振动,振幅为0.12m ,周期为2s ,当t =0时,位移为0.06m ,且向x 轴正方向运动.求(1)该物体的振动方程;(2)t =0.5s 时,物体的位置、速度、加速度;(3)在x =-0.06m 处,且向x 轴负方向运动时,物体的速度、加速度,以及物体从这一位置回到平衡位置所需的时间.分析 求解振动方程的难点是确定振动物体的初相ϕ.初相取决于计时起点t =0时物体的位置和速度.确定初相可用三角函数法或旋转矢量法.解 (1) 已知振幅为A = 0.12 m ,角频率为πππω===222Trad/s ,t = 0时初始位置和初速度分别为x 0=A cos ϕ =0.06 (1)v 0=ϕωsin A - >0 (2)从(1)式得2112.006.0cos 0===Ax ϕ得 33ππϕ或-=从(2)式得0sin <ϕ,所以应取3/πϕ-=此外,由t = 0时初始位置和初速度可以确定其旋转矢量如图15-4所示,即3/πϕ-=.振动方程为m)3/cos(12.0ππ-=t x(2) t =0.5s 时, x =)3/cos(12.0ππ-t =0.104 mv m/s188.0)3/sin(12.0-=--=πππt22m/s03.1)3/cos(12.0-=--=πππt a(3) 在1x =-0.06 m 处,物体向x 轴负向运动时,设1t t =,则06.0)3/cos(11-=-=ππt A x m (3)v 1)3/sin(1ππω--=t A < 0 (4)从(3)式得 2112.006.0)3/cos(11-=-==-Ax t ππ解得 ππππππn n t 2322323/1+-+=-或 (n =0,1,2…)又从(4)式得 0)3/sin(1>-ππt 应取 ππππn t 2323/1+=- (n =0,1,2…)故 )12(1+=n tm/s 592.0 m/s 326.0211=-= a v设回到平衡位置时2t t =,则0)3/cos(22=-=ππt A x (5)v 2)3/sin(2ππω--=t A >0 (6)从(5)式得 ππππn t 2233/2+=-或ππππn t 223/2+=- (n =1,2…)从(6)式得 )3/sin(2ππ-t <0 应取 ππππn t 2233/2+=- (n =1,2…)65)12(2++=n t回到平衡位置所需时间 s 83.0s 6512==-=t t t ∆15-5 一个质点作简谐振动,其振动方程为x =0.24cos(πt /2+π/3)m ,其中x 以m 计, t 以s 计.试用旋转矢量法求出质点由初始状态运动到 x =-0.12m, v <0状态所需的最短时间.分析 根据振动方程,当0t =0时旋转矢量A 与Ox 于x =-0.12m, v <0状态时,A 32π,如图15-5所示.因此,从0t 位置转到新位置偏转3/π解 如图15-5所示, t '时刻的相位为πϕ32=A 沿逆时针方向从0t 位置转过角度3/π所需的时间为s 32231=÷ππ15-6 作简谐振动的单摆在一个周期内的几个运动状态如图15-6所示.(1)若以(a )图所示的状态为计时起点;(2)若以(b )图所示的状态为计时起点,问单摆的初相位和其它各图所示状态的相位各为何值?分析 应从本题得出的结论是: 初相与计时起点(即初始条件)有关; 相位与与计时起点无关而与振动物体的瞬时状态有关.解 (1)以图(a )状态为计时起点,t =0时m m cos θϕθθ==得0=ϕ,因此对图(b)有0)cos(=+=ϕωθθt m (1)0)sin(d d <+-=ϕωωθθt tm(2)从(1)式得 2πϕω±=+t从(2)式得 )s i n (ϕω+t >0 所以图(b)的相位应取 2)(πϕω=+t同理,对图(c) πϕω=+)(t 对图(d)3)(πϕω=+t0cos ==ϕθθm (3)0sin d d <-=ϕωθθm t(4)(3)式(4)式联立,解得 2πϕ=同理,对图(c) πϕω=+)(t 对图(d) 23)(πϕω=+t对图(a) 0)(=+ϕωt15-7 一物块在水平面上作简谐振动,振幅为0.1m ,在距平衡位置0.06m 处速度为0.4m/s ,(1)求振动周期;(2)当速度为±0.12m/s 时,位移为多少?(3)若有另一物体置于该振动物块之上,当物块运动至端点时正好滑动,问摩擦系数μ为多大?分析 当所讨论问题涉及物体正好要滑动的条件时,由于物体尚未滑动,所受摩擦力仍为静摩擦力,静摩擦力方向与物体运动趋势方向相反.解 (1)设物块的振动方程为)cos(1.0ϕω+=t x物块位于06.01=x m 时, 速度v 1= 0.4m/s, 即x 1=A )cos(ϕω+t =0.06 m (1) v 1=)sin(ϕωω+-t A =0.4 m/s (2)以上两式平方相加, 代入A =0.1m ,解得 5=ωrad/s 26.12==ωπT s(2)由 v 2=)sin(ϕωω+-t A =±0.12 得 24.0)sin( =+ϕωt971.0)(sin 1)cos(2±=+-±=+ϕωϕωt t 则位移为x 2=0.1)cos(ϕω+t =±9.7×10-2m(3)物块运动至端点时正好物体开始滑动,即最大恢复力等于最大静摩擦力,物块受力如图15-7所示,因最大静摩擦力mg F μ=f ,最大恢复力A m F 2max ω=,得mg A m μω=226.08.91.05 22=⨯==gA ωμ15-8 一个轻弹簧在60N 的拉力作用下可伸长30cm , 将一物体悬挂在弹簧下端,并在它上面放一小物体,它们的总质量为4kg , 待其静止后再把物体向下拉10cm , 然后释放. 问(1)此小物体是停在振动物体上还是离开它? (2)如果使放在振动物体上的小物体与振动物体分离, 则振幅A 需满足什么条件? 二者在何位置开始分离?分析 根据胡克定律,由弹簧在外力作用下的形变量可以求出弹簧的劲度系数.当两物体脱离接触时,它们之间的正压力等于零,以此为条件可以判断小物体是否停在振动物体上. 解 (1) 根据胡克定律,得N/m 200N/m 3.060Δ===lF k由定义得 rad/s50rad/s 4200===mk ω弹簧、物体和小物体组成一个弹簧振子系统,把物体下拉10cm 后释放,故该弹簧振子的振幅为A =0.1m .设小物体质量为m ,小物体随系统一起运动,最大加速度为A a 2ω=,小物体受力情况如图15-8所示,当达最高点时,所受物体的正压力有最小值,即Am ma F mg N 2ω==+ (1)当A =0.1m 时,得 N 2.192=-=-=kA mg A m mg F N ω 即F N > 0 ,因而小物体仍停留在振动物体上.(2) 两物体脱离接触条件为0N =F ,代入(1)式得m196.0m 508.92==='ωgA即振幅大于0.196m ,两物体将在平衡位置上方分离,分离的位置即在0.196m 处.15-9 如图15-9(a )所示,在一个倾角为θ的光滑斜面上,固连一原长为L ,劲度系数为k ,质量忽略不计的弹簧,弹簧与质量为m 的重物相连,求重物作简谐振动的平衡位置和周期.分析 平衡位置是系统所受合外力为零的位置. 在建立振动方程时,一般都把取平衡位置为坐标原点.放在斜面上的弹簧振子处于静止状态时,物体所受弹簧的弹性力与重力沿斜面向下的分量大小相等,方向相反.解 弹簧和物体组成一个弹簧振子系统.物体受力情况如图15-9(b )所示.设在平衡位置弹簧的伸长量为0x ,有0sin 0=-kx mg θ 解得 k mg x θsin 0=即处于平衡位置时弹簧长度为0x L +. 根据定义,弹簧振子系统作简谐振动的角频率为mk =ω周期为 km T π2=15-10 如图15-10(a)所示,密度计玻璃管的直径为d ,浮在密度为ρ的液体中.若在竖直方向轻轻推一下,任其自由振动,试证明:若不计液体的沾滞阻力,密度计的运动是简谐振动;设密度计的质量为m , 试求振动周期.分析 若物体运动为简谐振动,应该具有如下特征:物体所受合外力与位移成正比而方向相反,即加速度与位移成正比而方向相反;或者位移是时间的余弦F F(a) (b)图15-9函数或正弦函数.解 密度计受力分析如图15-10(b)所示.设密度计截面积为S , 当处于平衡状态时,设浸入水中部分高度为h , 浮力则为ghS F ρ=B ,有0=-ghS mg ρ(1) 取平衡位置为坐标原点,向下为x 轴正向,当密度计向下位移为x 时,有22d d )(t xm S x h g mg =+-ρ (2) 由(1)和(2)式得gxS t x m ρ-=22d d 即加速度与位移成正比而方向相反,因此运动为简谐振动,且有g m dT mg d mgS ρππρρω4 2===15-11 如图15-11,劲度系数为k 的轻弹簧上端与质量为m 的平板相连,下端与地固连.另一质量为m '的物体,从h 高处自由落下,与平板发生完全非弹性碰撞后一起运动. 若以平板开始运动为计时起点,取向下为坐标正向,求振动的周期,振幅和初相位.分析 m '与m 发生完全非弹性碰撞后一起运动,与轻弹簧组成振动系统, 平衡位置是(m '+ m )所受合外力为零的位置,并选取为坐标原点.以发生碰撞后平板开始运动为计时起点,此时平板m 的坐标就是系统的初位移0x ,碰后(m '+ m )的共同速度v 0就是系统的初速度,而且可以依据碰撞中动量守恒求出.解 m '自由下落, 以gh 2的速度与m 发生完全非弹性碰撞,设碰后m '+ m 的共同速度为v 0,方向向下,应用动量守恒定律,得)(2m m gh m +'='v 0v 0mm gh m +''=2m '、m和弹簧组成振动系统,设m '+m 所受合外力为零时,弹簧的压缩量为x ∆,此位置是系统的平衡位置,则有0Δ)(=-+'x k g m m (1)取系统的平衡位置为坐标原点,向下为x 轴正向,当m '+m 位移为x 时,有d d )()()(22tx m m x x k g m m +'=+-+'∆ (2)由(1)和(2)式得0d d 22=+'+x mm k t x且有 km m T mm k +'=+'=πω2取m '与m 相碰的瞬间为振动的初始时刻t =0,有mm gh m kmg x +''=-=2 00v即 kmg A x -==ϕcos 0 (3)mm gh m A +''=-=2sin 0ϕωv (4)(3)与(4)式联立,得振动的周期和初相位分别为)(212020gm m kh kg m x A +'+'=⎪⎭⎫ ⎝⎛+=ωvgm m kh mm x )(2tan 0+''=-=ωϕv又因ϕ , 0 , 000><v x 在第三象限,则)(2 tanarc πϕ++''=gm m kh mm15-12 弹簧下端挂一物体后,弹簧伸长量为2108.9-⨯m , 若令物体上下振动,(1)求振动周期;(2)使其在平衡位置上方0.1m 处由静止开始运动,求振幅、初相及振动方程.(3)使其在平衡位置以0.8m/s 向上的初速度开始运动,求振幅、初相及振动方程.分析 计算结果表明,同一系统在不同初始条件下的振动方程不同. 解 (1)设挂上物体达平衡时弹簧的伸长量为x ∆, 根据胡克定律和平衡条件有mgx k =∆由定义得 10===xgmk ∆ω rad/s 63.02==gx T ∆πs(2)如图15-12所示,取平衡位置为坐标原点, 向上为x 轴正向.初始条件为: t =0时, x 0=0.1m v 0=0,即1.0cos 0==ϕA x (1)0sin 0=-=ϕωA v (2) 由(1)和(2)式联立解得m 1.01.022020==⎪⎭⎫ ⎝⎛+=ωv x A0=ϕ振动方程为 t x 10cos 1.0= m(3) 初始条件为:t =0时,x 0=0 v 0=0.8,即cos 0==ϕA x (3)08.0sin 0>=-=ϕωA v (4)由(3)和(4)式联立解得A =2020⎪⎭⎫ ⎝⎛+ωv x 0.08m从(3)式得 2πϕ=或 23πϕ=从(4)式得 0sin <ϕ 所以取 23πϕ=振动方程为 )2310cos(08.0π+=t x m15-13 如图15-13(a )所示的弹簧,其一端固定在天花板上,另一端挂着质量都是1.0kg 的两个物体A 和B .当物体静止时,弹簧伸长量为2108.9-⨯m , 如果物体B 突然脱落掉下,不计弹簧质量,(1)求物体A 的振动周期;(2)若从物体B 脱落时开始计时,求物体A 的振幅、初相和振动方程.分析 虽然弹簧下悬挂着两物体,但由于物体B 脱落,振动系统实为弹簧和 物体A 组成. 据题意, 物体B 脱落之时t=0,因此物体A 的位置为系统的初始位置,且物体B 从静止状态脱落,系统初速度为0.解 物体B 脱落之前,两个物体A 和B 处于重力和弹簧的弹性力作用下的平衡状态,弹簧伸长量为m 108.9Δ2-⨯=l ,则l k mg Δ2=N/m200N/m 108.98.912Δ22=⨯⨯⨯==-lmg k物体B 脱落后,物体A 和弹簧组成弹簧振子系统,设平衡位置处弹簧伸长量为0l ,则 00=-kl mg (1) 取平衡位置为坐标原点,向下为x 轴正向,如图15-13(b )所示,当物体A 位移x 时,应用牛顿第二定律,得220d d )(tx ml x k mg =-- (2)由(1)和(2)式得22d d tx mkx =-由定义得 rad/s2100.1200===mk ω s44.02==ωπT0=t 时,物体B 脱落,有m 109.4ΔΔ200-⨯==-=-=kmg kmg l l l x即 m 109.4cos 20-⨯==ϕA x (3) 0sin 0=-=ϕωA v (4)(3)和(4) 式联立解得 2220109.4)(-⨯=+=ωv x A m从(3)式0=ϕ,满足(4)式, 所以 0=ϕ振动方程为 t x 210cos 109.42-⨯= m讨论: (1)我们现在是取向下为x 轴正向,如果取向上为正,则初相为π,振动方程有所不同.这就是解题中强调要给出坐标取向的理由.(2)如果A 、B 质量不等,例如A B m m 2=,会有不同的l Δ值,则初始条件0x 不同,将导致振动特征参量的改变.15-14 如图15-14(a )所示,一质量可忽略的盘挂在劲度系数为k 的轻弹簧之下,一质量为m 的物体自h 高处自由下落至盘中,并与盘粘在一起作简谐振动. 设m =0.1kg ,k =4.9 N/m ,h =0.3m ,若以物体刚落至盘中时为计时起点,求系统的振动方程.解 如图15-14(b), 弹簧、质量为m 的物体和盘组成振动系统.取平衡位置为坐标原点, 向上为x 轴正向.平衡时弹簧伸长为0l l-,平衡方程为)(0=--l l k mg(1)当盘的位移为x 时,应用牛顿第二定律,得220d d )(tx ml x l k mg=-+- (2)由(1)和(2)式,得 22d d tx mkx=-由定义得71.09.4===mk ω rad/s质量为m 的物体与盘相碰时, t =0,弹簧伸长量为m 2.0m 9.48.91.0k0=⨯-=-=mg x相碰时,物体下落速度为gh 2,忽略盘质量,应用动量守恒定律,碰后物与盘的共同速度方向向下,大小为m/s 3.2m/s 3.08.922=⨯⨯==gh v即 x 0=ϕcos A =0.2 m (3)ϕωsin 0A -=v <0 (4)(3)和(4)式联立解得220)(ωv +=x A =0.4 m从(3)式得21cos 0==Ax ϕ,3πϕ±=.从(4)式得0sin >ϕ,所以应取3πϕ=振动方程为 )37cos(4.0π+=t xm15-15 单摆长为l ,小球质量为m ,带有电荷+q ,悬挂在场强大小为E 、方向由左向右的均匀电场中,如图15-15(a )所示.(1)求小球处在平衡位置时悬线与竖直向下方向所成的角;(2)假设单摆对平衡位置的偏角很小,求单摆的周期.分析 由于带电小球受到均匀电场的电场力作用,合外力为零的平衡位置将与铅垂位置有一偏角.解 (1)如图15-15(b )所示, 小球受重力m g 、静电力E q 和张力F T 作用,设平衡位置偏角为0θ,则0cos 0T =-θF mgsin 0T =-qE F θmg qEarctan 0=θ (1) (2)当摆线从平衡位置偏离θ角时,与铅垂位置偏角为)(0θθ+,应用牛顿第二定律,得小球切向运动微分方程为2220200d d d )(d )sin()cos(tmltmlmg qE θθθθθθθ=+=+-+ (2)由(1)式可得0tan θmg qE =代入(2)式,得2200d d ]cos )sin(sin )[cos(cos tmlmg θθθθθθθθ=+-+应用三角函数公式,得θθθsin cos d d 022l g t-=当θ很小时,θθ≈sin,得θωθθθ222cos d d -=-=l g t表明角加速度与角位移成正比,且方向相反,因此小球作简谐振动,并得222222222 cos Eq gm ml T mlEq gm l g +=+==πθω15-16 劲度系数分别为1k 和2k 的两根弹簧串在一起,竖直地悬挂着,下面挂一质量为m 的小球,作成一个在竖直方向振动的弹簧振子.试求其振动周期.分析 这是两根弹簧串联(首尾相连)的问题.处理这类连接体问题仍要用隔离物体法.当两弹簧质量均可忽略时,无论处于运动或静止状态,两弹簧中的弹性力相等,并等于相互作用力. 解 两根串联弹簧和小球组成振动系统. 隔离物体,对小球作受力分析如图15-16所示.取平衡位置为坐标原点,向下为x 轴正向.设平衡时弹簧1的伸长量为10x ,弹簧2的伸长量为20x ,小球受力平衡方程为101=-x k mg (1)两弹簧连接处相互作用力等大而反向,即0202101=-x k x k (2)小球相对于平衡位置下移x 时,设弹簧1伸长量为1x ,弹簧2伸长量为2x ,应用牛顿第二定律,得2211d d tx mx k mg =- (3)两弹簧连接处相互作用力等大而反向,即2211x k x k =,因201021x x x x x ++=+,得 )(20102121x x x k k k x +++=代入(3)式得 22212101d d )(tx mx k k k x k mg =++- (4)由(1)和(4)式,得222121d d tx mx k k k k =+-表明加速度与位移成正比,且方向相反,因此小球作简谐振动,并得)(2 )(21212121k k k k m T k k m k k +=+=πω15-17 两弹簧劲度系数分别为1k =1N/m , 2k =3N/m .在光滑的水平面上将此二弹簧分别连接到质量为m =0.1kg 的物体的两端,弹簧的其余两端分别固定在支柱1P 及2P 上,如图15-17所示.今使物体有一向右初位移m10320-⨯=x ,向右初速度m/s10402-⨯=v ,(1)试证物体作简谐振动;(2)求振动方程(设物体在振动中,两弹簧始终处于被拉伸状态).分析 当物体运动时,两弹簧的形变量大小相同,并等于物体的位移量. 解 以物体为研究对象, 受力如图15-17所示. 设平衡时两弹簧伸长量分别为1l 、2l ,有2211l k l k = (1) 取平衡位置为坐标原点,向右为x轴正向.当物体向右位移为x 时,应用牛顿第二定律,得221122d d )( )(tx mx l k x l k =+-- (2)由(1)和(2)式得2221d d )(-tx mx k k =+由定义,得 r a d /s102rad/s 1.0421==+=mk k ω已知t =0时, m/s 1040 m 1032020--⨯=⨯=v x即 ϕcos 0A x = = m 1032-⨯ (3)v 0= ϕωsin A - >0 (4)(3)和(2)式联立,解得220)(ωv +=x A =2×10-2m从(3)式得23cos 0==Ax ϕ,6πϕ±=,从(4)式得ϕsin <0,则应取6πϕ-=所以振动方程为 m )6102cos(1022π-⨯=-t x15-18 已知某简谐振动的振动曲线如图15-18(a),试求此简谐振动的振动方程.分析 振动曲线是振动物体位移x 与时间t 的关系曲线.从振动曲线上可得出振幅和初始条件.由图15-18(a)可以看出,当t 稍大于零时,物体将向x 轴负向运动,所以物体初速度v 0< 0.由旋转矢量图可以比较容易地确定振动的角频率,即旋转矢量1s 内转过的角度便是角频率.解 由图15-18(a)看出,A = 2 m ,32πϕ=.t =1s 时的位移和速度分别为)cos(1ϕω+=t A x = 0 (1)v 1= )sin(ϕωω+-t A <0 (2)(1)式给出cos )(ϕω+t = 0,得2)(πϕω=+t ,显然满足(2)式,即为1s 时的相位.旋转矢量图如图15-18(b)所示,t =0时的旋转矢量为)0(=t A ,可以看出,1s 内A 沿逆时针方向转过的角度即角频率为rad/s61123ππππω=++=振动方程为 )32611cos(2ππ+=t xm15-19 (1)、(2)两个简谐振动的周期相同,振动曲线如图15-19.求(1)、(2)两个简谐振动的相位差. 分析 根据振动曲线可以判断指定点的相位.若两振动的相位差012>-ϕϕ,通常说,振动2的相位比振动1超前或振动1的相位比振动2落后.解 从图15-19知,振动(1)的初始条件是10cos ϕA x ==0 (1)v 0= 0sin 1>-ϕωA (2)由(1)式得 21πϕ±=由(2)式得 0sin 1<ϕ 则振动(1)的初相应取 21πϕ-=振动(2)的初始条件是20cos ϕA x = =A (3)v 0= 2sin ϕωA -=0 (4)由(3)式得02=ϕ,满足(4)式,即为振动(2)的初相.因两振动的角频率相同, 所以振动(1)与振动(2)相位差为2π-, 且振动(1)比振动(2)相位落后2π.15-20 一质量为0.1kg 的物体作振幅为0.01m 的简谐振动,最大加速度为0.042m/s .试求(1)振动的周期;(2)总的振动能量;(3)物体在何处时,其动能和势能相等?分析 作简谐振动的弹簧振子系统机械能守恒, 动能和势能都随时间周期变化且相互转换,这是系统运动过程中只有重力、弹性力等保守力作功,外力和非保守内力不作功的条件下才成立的.实际的振动系统起码要受到阻力作用, 因而必定有能量的损耗,系统机械能不守恒.解 (1)由A a m 2ω= 得s 14.3s 04.001.022===ππma A T(2)总振动能量为J102J 01.004.01.02121215-m22⨯=⨯⨯⨯===A maAm E ω(3)设动能和势能相等时, 物体距平衡位置x 远, 则 2P 21kx E =又由 mk E E E ===2k P , 21ω得 m 1007.7m 04.01.001.010235--⨯=⨯⨯⨯==mma EA x15-21 质点作简谐振动,已知振动频率为ν, 则振动动能变化的频率为多少?当其位移为振幅的一半时,其动能为总能量的几分之几?分析 只要大致勾画出k E -t 和x-t 曲线轮廓,便可得出动能变化频率与振动频率间关系.解 振动动能为)]2(2cos 1[41 )2(sin 2122222k t A m t A m E πνωπνω-==所以振动动能变化频率为ν2,k E -t 曲线如图15-21所示.当 A x 21=时, 振动势能为)21(41)2(2122p kA A k E ==此时振动动能为)21(43)21(4121222P k kA kA kA E E E =-=-= 即为总能量的3/4.15-22 两同方向简谐振动,其振动方程分别为)4110cos(106, )4310cos(1052221ππ+⨯=+⨯=--t x t x式中x 以m 为单位,t 以s 为单位.(1)求合振动的振幅和初相;(2)若另有一同方向简谐振动)10cos(10723ϕ+⨯=-t x ,问 ϕ为何值时,合振动 31x x +的振幅为最大; 又 ϕ为何值时,合振动 32x x +的振幅为最小?(3)用旋转矢量法表示(1)、(2)的结果.分析 先体会给出的两个振动方程,哪里体现了同方向?哪里体现了同频率?作两个同方向同频率振动合成,最简单的方法是旋转矢量法(不妨也尝试一下解析法),只要画出了合成矢量,简单的几何关系便给出合振动的振幅及初相.本题的另一部分是讨论振动加强减弱条件,这为后面讨论机械波、光波的干涉加强减弱作舖垫.解 (1)如图15-22,两矢量间夹角为2π所以合振动振幅m 107.81 m106522222221--⨯=⨯+=+=A A A合振动初相8484465 tanarc 0'=+=πϕ(2) 合振动A 再与第三个振动合成.据振动叠加条件, πϕϕk 21±=-时合振动有极大值,即ππϕk 243±=(k =0,1,2…)当πϕϕ)12(1+±=-k 时合振动有极小值, 即ππϕ)12(43+±=k (k =0,1,2…)15-23 有两个同方向同频率的简谐振动,其合振动的振幅为0.2m ,相位与第一振动的相位差为π61,若第一振动的振幅为1103-⨯m ,用旋转矢量法求第二振动的振幅及第一、第二两个振动的相位差.分析 本题与上题相反, 为已知合振动求分振动. 解 作旋转矢量如图15-23所示,由几何关系得m1.030cos 212122=︒-+=AA A A A再由)cos(2122122212ϕϕ-++=A A A A A 解得20)cos(1212πϕϕϕϕ=-=-15-24 示波管的电子束受到两个互相垂直的电场的作用,若电子在两个方向上的位移分别为t A x ωcos =和)cos(ϕω+=t A y .求在0=ϕ、30=ϕ、90=ϕ各种情况下,电子在荧光屏上的轨道方程,并分别说明电子沿轨道的运动方向.分析 这是两个频率相同、振动方向相互垂直简谐振动的合成. 解 轨道方程为)(sin )cos(21221221222212ϕϕϕϕ-=--+A A xy Ay Ax因 A A A ===-2112 ϕϕϕϕϕ2222sin cos 2A xy y x =-+当0=ϕ时,得x=y ,为一过原点的直线.说明电子沿直线作往返运动.当 30=ϕ时,得 222413Axy y x =-+为一椭圆,且运动方程为)30cos(cos+==t A y t A x ωω当 90=t ω时,电子位于)21,0(A -处,此后瞬间x <0, y <0,电子位于第三象限内,表明电子顺时针转动.当 90=ϕ时,得 222A y x =+ 为一圆.且运动方程为)90cos(cos+==t A y t A x ωω当0=t ω时, 电子位于)0, (A 处, 此后瞬间x >0, y <0,电子位于第四象限内, 表明电子仍顺时针转动.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、一束光垂直入射在偏振片上,以入射光线为轴转动偏振片,观察通过偏振片后的光强变化过程。
如果观察到光强不变,则入射光是什么光?如果观察到明暗交替变化,有时出现全暗,则入射光是什么光?如果观察到明暗交替变化,但不出现全暗,则入射光是什么光?【答案:自然光;完全偏振光;部分偏振光】详解:当一束光垂直入射在偏振片上时,以入射光线为轴转动偏振片,如果观察到通过偏振片后的光强不发生变化,入射光是由自然光;如果观察到光强有明暗交替变化,并且有时出现全暗,则入射光是完全偏振光;如果观察到光强有明暗交替变化,但不出现全暗,则入射光是部分偏振光。
2、一束光是自然光和线偏振光的混合光,让它垂直通过一个偏振片。
若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光与线偏振光的光强比值为多少?【答案:1/2】详解:设该光束中自然光和线偏振光的强度分别为I 1和I 2。
当以此入射光束为轴旋转偏振片时,透射光强度的最大值和最小值分别为21max 21I I I +=1min 21I I = 依题意有I max =5I min ,即 12121521I I I ⨯=+ 解之得2121=I I 即入射光束中自然光与线偏振光的光强比值等于1/2。
3、一束光强为I 0的自然光相继通过三个偏振片P 1、P 2、P 3后,出射光的光强为0.125I 0 。
已知P 1和P 2的偏振化方向相互垂直,若以入射光线为轴旋转P 2,要使出射光的光强为零,P 2最少要转过多大的角度?【答案:45°】详解:由于P 1和P 2的偏振化方向相互垂直,而自然光相继通过三个偏振片后的光强不等于零,说明自然光通过偏振片的顺序为P 1、P 3、P 2。
如图所示,设偏振片P 1和P 3的夹角为θ,由马吕斯定律得出射光强为 )09(cos cos 2220θθ-= I I θ2sin 820I = 由于I =0.125I 0 ,代入上式解得 45=θ要使出射光强为零,应使P 2和P 3的偏振化方向垂直,因此P 2最少要转过的角度也等于45°。
4、一束光强为I 0的自然光垂直穿过两个偏振片,且这两个偏振片的偏振化方向的夹角成45°角,则穿过两个偏振片后的光强是I 0的多少倍?【答案:1/4】详解:由马吕斯定律得光强为I 0的自然光垂直穿过两个偏振片后的光强为45cos 220I I =40I = 即穿过两个偏振片后的光强是I 0的1/4倍。
5、三个偏振片P 1,P 2与P 3堆叠在一起,P 1与P 3的偏振化方向相互垂直,P 2与P 1的偏振化方向间的夹角为30°。
强度为I 0的自然光垂直入射于偏振片P 1,并依次透过偏振片P 1、P 2与P 3,则通过三个偏振片后的光强是I 0的多少倍?【答案:3/32】详解:由马吕斯定律得光强为I 0的自然光垂直穿过这三个偏振片后的光强为)3090(cos 30cos 2220 -=I I 0323I = 即穿过这三个偏振片后的光强是I 0的3/32倍。
6、两个偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过。
当其中一个偏振片慢慢转动180°时,透射光强度将发生怎样的变化?【答案:光强先增加,达到最大值后又减小至零】详解:一束自然光垂直入射两个堆叠的偏振片上时没有光线通过,说明这两个偏振片的偏振化方向相互垂直。
当其中一个偏振片慢慢转动90°时,透射光强度逐渐增大到最大值。
该偏振片沿原方向继续慢慢转动90°时,透射光强度将逐渐减小到0。
因此,当其中一个偏振片慢慢转动180°时,透射光强度将先增加,达到最大值后又减小至零。
图15-327、使光强为I 0的平面偏振光先后通过两个偏振片P 1和P 2。
P 1和P 2的偏振化方向与原入射光光矢量振动方向的夹角分别是α 和90°,则通过这两个偏振片后的光强I 是多少? 【答案:α2sin 4120I 】 详解:依题意,由马吕斯定律得光强为I 0的平面偏振光先后通过这两个偏振片后的光强为)90(cos cos 220αα-= I I α2sin 4120I = 8、要使一束线偏振光通过偏振片之后振动方向转过90°,至少需要让这束光通过几块理想偏振片?在此情况下,透射光强最大是原来光强的多少倍?【答案:3;1/4】详解:由图可以看出,要使一束线偏振光通过偏振片之后振动方向转过90°,至少需要让这束光通过3块理想偏振片。
由马吕斯定律得透射光强为 )90(cos 212α-= I I )90(cos cos 22αα-= I α2sin 4I = 可见,当1sin 2=α时,透射光强最大,其值为 4max 2I I = 9、如图15-8所示,P 1、P 2为偏振化方向夹角为α 的两个偏振片。
光强为I 0的平行自然光垂直入射到P 1表面上,则通过P 2的光强等于多少?如果在P 1、P 2之间插入第三个偏振片P 3,则通过P 2的光强发生了变化。
实验发现,以光线为轴旋转P 2,使其偏振化方向旋转θ 角后,发生消光现象,从而可以推算出P 3的偏振化方向与P 1的偏振化方向之间的夹角α' 等于多少? (假设题中所涉及的角均为锐角,并且α' <α。
) 【答案:α20cos 2I ; 90)(-+αθ或)(90αθ+- 】 详解:由于P 1、P 2偏振化方向夹角为α ,因此通过P 2的光强为 α20cos 2I I =在P 1、P 2之间插入第三个偏振片后,使P 2旋转角度θ后发生消光现象,则必有P 2与P 3的偏振化方向垂直。
由于题中所涉及的角均为锐角,并且α' <α,因此得到如图所示的两种图15-8振幅投影图。
在图(a)的情况下,由几何关系得P 3与P 1的偏振化方向之间的夹角为90)(-+='αθα 在图(b )的情况下,有)(90αθα+-='1、如图15-20所示,一束自然光从空气射向一块平板玻璃,设入射角等于布儒斯特角i 0,则在界面2的反射光是不是线偏振光?如果是线偏振光, 其光矢量的振动方向如何?【答案:反射光是不是线偏振光;光矢量的振动方向垂直于入射面】详解:自然光从空气射向平板玻璃时入射角等于布儒斯特角i 0设与此对应的折射角为r 0,则必有 9000=+r i由光的折射定律得 00sin sin r n i =当光入射在平板玻璃的界面2上时,入射角等于r 0,设与此对应的折射角为r ,由光的折射定律得 r r n sin sin 0=比较两个折射定律,有r = i 0,因此90000=+=+i r r r即在界面2的反射光与折射光也是垂直的,入射角也是布儒斯特角,反射光必然是线偏振光,其光矢量的振动方向垂直于入射面。
图15-32 2P P 2 (a )P 2 (b )图15-202、如图15-21所示,如果从一池静水的表面反射出来的太阳光是线偏振光,那么太阳光的仰角大致等于多少度?该反射光的光矢量的振动方向如何?已知水的折射率为1.33。
【答案:37°;垂直于入射面】详解:由布儒斯特定律得布儒斯特角为 n i arctan 0=33.1arctan = 53=因此太阳光的仰角为 37900=-=i 仰角此时反射光光矢量的振动方向垂直于入射面。
3、自然光以60°的入射角照射在某两种介质交界面时,反射光为完全线偏振光,则折射光是什么光?折射角等于多少度?【答案:部分偏振光;30°】详解:折射光是部分偏振光。
由于反射光为完全线偏振光,因此i 0+r =90°,由此解得折射角为30900=-=i r4、某种透明介质对于空气的临界角等于45°,光从空气射向此介质时的布儒斯特角等于多少?【答案:54.7°】详解:由于这种透明介质对空气的临界角等于45°,因此这种透明介质的折射率为45sin 1sin 1==C n 2= 当光从空气射向此介质时的布儒斯特角为n i arctan 0=2arctan = 7.54=5、一束自然光从空气投射到玻璃表面上,当折射角为30°时,反射光是完全偏振光,则此玻璃板的折射率等于多少?【答案:1.73】详解:一束自然光从空气投射到玻璃表面上,当反射光是完全偏振光时,其入射角等于布儒斯特角,由于布儒斯特角与折射角的和等于90°,而折射角等于30°,因此布儒斯特角等于60°。
该玻璃板的折射率为0tan i n = 60tan ==1.73图15-216、一束平行的自然光以60°角入射到平玻璃表面上。
如果反射光是完全偏振的,则透射光的折射角是多少度?玻璃的折射率等于多少?【答案:30°;1.73】详解:由于反射光是完全偏振光,因此i 0+r =90°,由此解得折射角为30900=-=i r由布儒斯特定律得该玻璃的折射率为0tan i n = 60tan ==1.737、如图15-22所示,一束自然光入射到折射率分别为n 1和n 2的两种介质的交界面上,发生反射和折射。
测得反射光是完全偏振光,那么折射角r 的值为多少? 【答案:12arctan 2πn n -】 详解:由于反射光是完全偏振光,因此入射角是布儒斯特角。
由布儒斯特定律得 120arctan n n i = 由于这时反射光与折射光垂直,因此折射角为02πi r -=12arctan 2πn n -= 8、一束平行的线偏振光在真空中的波长为589nm ,垂直入射到方解石晶体上,晶体的光轴与表面平行,如图15-23所示。
已知方解石晶体对该单色o 光和e 光的折射率分别为1.658、1.486。
方解石晶体中寻常光的波长和非常光的波长分别等于多少?【答案:355.2 nm ;396.4 nm 】详解:方解石晶体中o 光和e 光的波长分别为o o n λλ=658.1589=)nm (2.355= ee n λλ=486.1589=)nm (4.396=1、圆偏振光通过四分之一波片后的出射光是什么偏振光?图15-22图15-23【答案:线偏振光】详解:由于形成圆偏振光的互相垂直的线偏振光的光程差为λ/4,圆偏振光通过四分之一波片后又产生了λ/4的光程差,这两个线偏振光的光程差变为λ/2,它们合成的结果为线偏振光。
2、在两个偏振化方向正交的偏振片之间平行于偏振片插入一块厚度为l 的双折射晶片,晶片对o 光、e 光的折射率分别为n o 和n e 。
晶片光轴平行于晶面且与第一偏振片的偏振化方向之间有一个夹角。
一束单色自然光垂直入射于系统,则通过第二块偏振片射出的两束光的振幅大小有什么关系?它们之间的相位差等于多少? 【答案:相等;ππ2+-λln n e o 】详解:由偏振光的干涉知识可知,这种情况下通过第二块偏振片射出的两束光的振幅大小相等。
