点的复合运动
点的复合运动

点的合成运动
y’
o’
x’
例2、直升飞机在匀速前进的军舰上降落
y
y’
o’
x’
x
o
点的合成运动
y’ x’
o’
物体的运动的描述结果与所选定的参考系有关。同一物体的运动,在不同的 参考系中看来,可以具有极为不同的运动学特征(具有不同的轨迹、速度、 加速度等)。
相对运动:未知
3、
va ve vr
大小 v1 v2
?
方向 √ √
?
vr va2 ve2 2vave cos60 3.6 m s
arcsin(ve sin 60o ) 46o12
点的合成运动
vr
求解合成运动的速度问题的一般步骤为(P180):
① 选取动点,动系和静系。
B
曲柄-滑块机构
点的合成运动
思考题 动 点:杆上A点。 动系:固连于滑块B。 定系:固连于墙面。 绝对运动? 相对运动? 牵连运动?
点的合成运动
A Bv
点的合成运动
动 点? 动参考系? 绝对运动? 相对运动? 牵连运动?
练习题1
点的合成运动
点的合成运动
点的合成运动
动 点? 动参考系? 绝对运动? 相对运动? 牵连运动?
定系的速度。
点的合成运动
基本概 念
牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
这点称为瞬时重合点或动点的牵连点。 (2)、进一步说明
牵连运动一方面是动系的绝对运动,另一方面对动点来说起 着“牵连”作用。但是带动动点运动的只是动系上在所考察的瞬 时与动点相重合的那一点,该点称为瞬时重合点或牵连点。 (3)、注 意
理论力学答案第5章点的复合运动分析
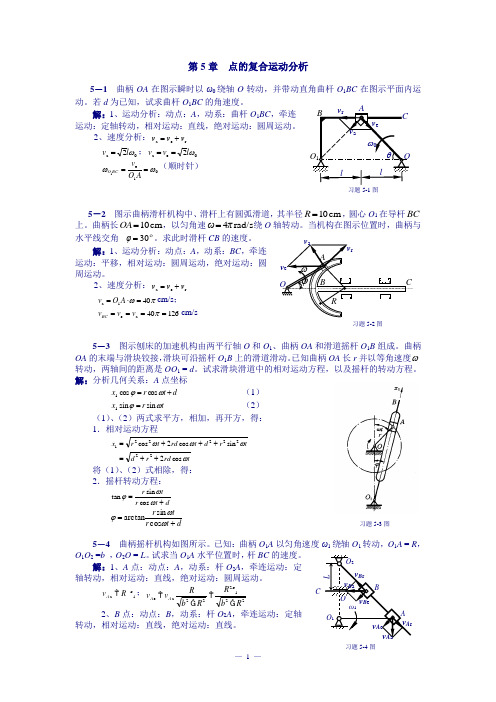
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
第4章 点的复合运动

70
例题
点的复合运动
例 题 3
3. 速度分析。
绝对速度va:va=OA · =r ω ,方 ω 向垂直于OA,沿铅垂
方向向上。
牵连速度ve:ve为所要求的未知量, 方向垂直于O1B 。 相对速度vr:大小未知,方向沿摇杆 O1B 。 应用速度合成定理
l 2 r2
72
r 2 所以可得 1 2 l r2
例题
点的复合运动
例 题 3
讨论:
若取摇杆 O1B上A点为动 点,动系固连 曲柄OA,则相 对运动轨迹是 什么曲线?
73
例题
点的复合运动
例 题 3
讨论:
若取摇杆 O1B上A点为动 点,动系固连 曲柄OA,则相 对运动轨迹是 什么曲线?
55
n
例题
点的复合运动
例 题 1
运 动 演 示
56
例题
点的复合运动
例 题 1 平动实例
相对运动轨迹
57
例题
点的复合运动
例 题 1
解: 1. 选择动点,动系与定系。
B
动点- AB的端点A 。
动系-Ox'y',固连于凸轮。
y'
定系-固连于水平轨道。
A
R φ
v0
2. 运动分析。 绝对运动-直线运动。
得船B的绝对速度和对于船A的相对速度的大小 v v2 1 , v r v1 tan cos 85
ve=v1
va=v2
例题
点的复合运动
解:由坐标变换关系
例 题 7
已知点在平面内运动,
《理论力学》第七章-点的复合运动

v0
Ra
n r
aa
a
φ
x'
O
n
arn
vr2 R
v2
Rsin2
3、速度分析
va vevr
vr
ve
sin
v
sin
4、加速度分析
aaaear arn
n
aasinaecosarn
aa
acot
v2
Rsin3
48
§7–4 牵连运动为转动的加速度合成定理
牵连运动为平动时加速度合成定理:aaaear
牵连运动为定轴平动时 aaaear是否成立?
37
§7–2 速度合成定理
va vr
应用速度合成定理
va vevr
3、速度分析。 绝对速度va: va=OA·ω=rω , 方向垂直于OA向上
牵连速度ve: ve为所要求的未知量,
方向垂直于O1B 相对速度vr: 大小未知, 方向沿摇杆O1B
38
§7–2 速度合成定理
va vr
其中 O1A l2 r2
1
第七章 点的复合运动
§7–1 复合运动的概念 §7–2 速度合成定理 §7–3 牵连运动为平动时点的加速度合成定理 §7–4 牵连运动为转动时点的加速度合成定理
2
第七章 点的复合运动
复合运动问题:研究物体相对于不同参考系 的运动之间的关系。
复合运动不是一种新的运动形式,只是
一种研究运动学问题的思路和方法。
40
§7–3 牵连运动为平动的加速度合成定理
一、绝对运动和相对运动之间的关系
z M
绝对运动方程:r r(t)
z
r (t)
r (t ) k O j
点的复合运动
r 2 l
(l 2 r 2 )1/ 2
1
ae O1 A
r 2 l
l2 r2
2
( l2 r2
1)
1
e
O1 A
r 2
l2 r2
帮助 导航 上一张
下一张
1 ak
aa aen
aet
ar
aa ae aen ar ak
aa r 2 aen O1 A2 1 r 2
ak
21vr
2r3 2l
(l 2 r 2 )3/ 2
aa cos ae ak
ae
ak
aa
cos
2r3 2l
(l 2 r 2 )3/ 2
例题
点的复合运动
例题4
第3章 点的复合运动
§3–2 点的速度合成定理
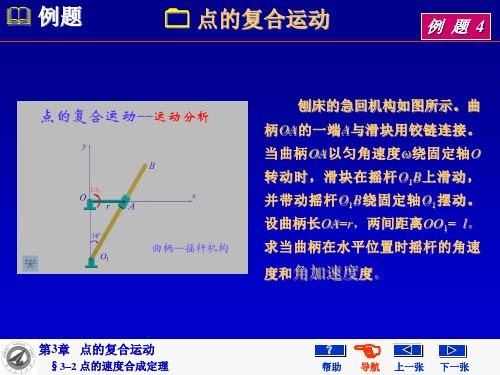
刨床的急回机构如图所示。曲 柄OA的一端A与滑块用铰链连接。 当曲柄OA以匀角速度ω绕固定轴O 转 动 时 , 滑 块 在 摇 杆 O1B 上 滑 动 , 并带动摇杆O1B绕固定轴O1摆动。 设曲柄长OA=r,两间距离OO1= l。 求当曲柄在水平位置时摇杆的角速
度和角加速度度。
帮助 导航 上一张 下一张
例题
点的复合运动
例题4
y'
x' 第3章 点的复合运动
§3–2 点的速度合成定理
解: 1. 选择动点,动系与定系。
动点-滑块 A 。
动系-O1x'y',固连于摇杆 O1B。
定系-固连于机座。 2. 运动分析。 绝对运动-以O为圆心的圆周运动。 相对运动-沿O1B的直线运动。 牵连运动-摇杆绕O1轴的摆动。
帮助 导航 上一张 下一张
例题
点的复合运动
第八章复合运动

v1
D
v2
K
θ
C E
解: 动点-刀架K
动系-纸板ABCD 绝对运动- 沿导杆的直线运动 相对运动- 牵连运动- 随纸板一起作水平向左的平动
A
F B
v1
D
v2
K
θ
C E va=v2
垂直于纸板的运动方向的直线运动
va ve v r
sin v e v1 0.385 va v2
β
ve
vay´
绝对运动-空间曲线运动
相对运动-以O为圆心的 圆周运动 牵连运动-绕z轴的定轴转动
v x´ r
va ve v r
2 2 2 1
vr= w1R
2 e 2 r
ve= Rw2
va v v R w w
ve w 2 tan vr w1
思考:甲相对于乙的速度为vr, 则能不能直接给出乙 相对于甲的速度? 例 静止的海面上有两艘舰艇A和B,分别以匀速 vA=vB=10(m/s)行驶,如图所示。A艇沿直线向东, B艇则沿以O为圆心, =100m为半径的圆弧行驶。 设在图示瞬时,=30o,s=50(m) 求: (1)B 艇相对于A艇的速度; (2)A 艇相对于B艇的速度。 解
vr 1 v r
ve1 ve '
vr 'vr ve 've v v v v ' e1 e aa lim lim r1 r t 0 t 0 t t va 'va ve1 ve vr 'vr1 lim lim lim t 0 t 0 t 0 t t t
*牵连速度、加速度:ve , ae
牵连点 相对定系的速度、加速度。
点的复合运动1

42
点的速度合成定理
动点在某瞬时的绝对速度等于它在该瞬时的牵连速 度与相对速度的矢量和。
v a ve v r
*矢量方程式,在平面问题中相当两个标量方程式; *建立了任一瞬时三个运动之间的速度关系,不能求
导,只能求得特殊位置(某瞬时)的速度.一定是以绝对
速度为对角线组成平行四边形. *牵连运动形式不限.
动等。
在复合运动的研究中,参考系(动系)的选择是问题的关
键。恰当的选择参考系,能把复杂的运动分解为若干种简
单运动,或由若干种简单运动组成各种不同的复杂运动。
15
5 动点和动系的选择
基本原则:
1.动点对动系要有相对运动。
2.动点的相对运动轨迹要明确、容易确定。 具体选择方法: 1.选择持续接触点为动点。
7
3 三种速度、加速度
*绝对速度、加速度:va , aa
动点相对定系的速度、加速度;
*相对速度、加速度:vr , ar
动点相对动系的速度、加速度; 动点的牵连点:某瞬时动系上与动点重合的点。
*牵连速度、加速度:ve , ae
牵连点 相对定系的速度、加速度。
8
4.牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
39
三种运动轨迹
设动点M在动系中沿某一曲线 AB如下
三种运动轨迹
40
刚体在定系中运动,动系固结在刚体上。
M1点——t 瞬时动系上与动点重合的点。 z' x' z M,M1 y x O
41
绝对运动轨迹
M' 相对运动轨迹
y'
r a r r M'1
r e
理论力学---第七章复合运动 (2)

3 2
y
B
ac
l
2w r l
2 3 2 2
r
3
2
wo
ac
aa
ar
A
a a a a a x e x r x c x
a
e
a
n e
x
a cos a a a e c
2 2 rl l r 2 a w 3 e 2 2 2 l r
v ' v v v v ' v a a e 1 e r r 1 l i m l i m l i m t 0 t 0 t 0 t t t
即 M’
vr’ va’ ve’
a a a a r e
M
vr
va vr1 ve M1 t+t ve1
o
t
x
2.牵连运动为转动时的加速度合成定理
应用加速度合成定理 z´
a a a e a r a C
v0
ae aC
x´
M
如以 i , j 和 k 分别表示沿坐标轴 O´x´ , O´y´ 和
O´z´的单位矢量,则M点的加速度aa可表示为
y´
ar
a a a e a r a C
2 2 v v 0 0 R wc o s f j ( c o s f j s i n f k ) 1 1 1 R R 2 w v s i n i 0 1 2
以AD杆上A点为动点,动 系固连于套筒上
例 火车 M 以等速 v0 沿子午线自南往北行驶,如图所示。
为了考虑地球的自转,设定坐标系以地心为原点,坐标轴 分别指向恒星。地球的平均半径为 R 。求火车 M 在北纬 φ 度 处的绝对加速度。
第5章点的复合运动.

第5章点的复合运动5.1复合运动中的基本概念5.2复合运动中的运动方程之间的关系5.3复合运动中的速度之间的关系一、目的要求:1、使学生了解速度和加速度的矢量式2、理解绝对运动,相对运动和牵连运动3、使学生对合成运动问题能恰当地选择动点,动系和定系,并能较正确的判定点的绝对,相对和牵连运动4、使学生掌握速度合成定理,并能较正确应用它解点的速度合成运动问题。
二、重点:绝对运动,相对运动和牵连运动的概念,速度合成定理及其应用。
难点:牵连运动,牵连点,动点,动系的选择三、学时安排:4学时四、教学准备:幻灯片五、教学过程导入新课:5.1复合运动中的基本概念一、概念:1、静参考系:固定在地球上的坐标。
2、动参考系:固定在其它相对于地球运动的参考体上的坐标,3、复杂运动:研究物体相对于不同参考系的运动,分析物体相对于不同参考系运动之间的关系,可称为复杂运动和合成运动。
实例之一:小船自左岸边A向后岸边B点运动,河水以均匀速度v运动,小船最终到到右岸的D点。
(1)动系中小船对动系来说是直线运动,从(2)静系中:动系对静系则是直线运动。
小船从A→B,C→D。
(3)同时性:先假设河水不动,则小船从A划到B:在假设人不划船,小船随河水漂流到下游D处。
实际上小船和水是同时运动的,小船动点的运动是上述两个简单运动的合成CAv图5-1 小船的复合运动图5-2车轮轮缘上点M的复合运动实例之二:研究沿地面作直线滚动的车轮轮缘上点M的运动(1)静系中:动点的轨迹是旋轮线车厢作直线运动(2)动系中:M 动点作圆周运动(3)运动的同时性,M点运动和平动是同时进行的,M点既跟随着动系一起平动,又在动系上作圆周运动。
旋轮线就是这两个运动的合成运动的轨迹,轮缘上M点的运动就是这两个简单运动的合成。
实例3:在大梁固定不动时,卷杨小车沿大梁可作直线运动,同时将吊钩上的重物A铅垂向上提升,研究重物的运动称合成运动(1)静系中:A→B(2)动系中:A →A’(3)同时性:点:A →A’小车:A→B重物既跟随动系一起向右平动,图5-3吊重物的复合运动又在动系上从下往向运动,重物的运动是两个简单运动的合成。
点的复合运动

12
MM MM M M t t t
1 1
t 0
时的极限,得
MM 1 M 1M MM lim lim lim t 0 t t 0 t t 0 t
va v e vr
13
v v v
a e
vr
va
r
ve
即在任一瞬时点的绝对速度等于其牵连速度与相对 速度的矢量和,这就是点的速度合成定理。
ve
ae
y
x` o`
A
y`
o
转轮
x
5
实例一:车刀的运动分析
动点:车刀刀尖 绝对运动:直线运动 动系:工件
相对运动:曲线运动(螺旋运动) 牵连运动:定轴转动
p4d.swf★
6
实例二:偏心轮的运动分析
动点:AB杆上的A点 绝对运动:上下直线运动 动系:偏心轮C
相对运动:C为圆心的圆周运动
牵连运动:定轴转动
第17章 点的复合运动
1
运动具有相对性,不同的观察者观察的结果不同
以地面为参考系
以盘为参考系
2
§17-1
动 点: 研究对象
点的复合运动概念
z'
x' o'
M
定参考系:(定系)
固定在地球上的坐标系Oxyz 。 动参考系: (动系) 固定在其他相对于地球运动的
z
o x
y'
y
物体上的坐标系
Oxyz
已知:OC=e , R 3e , (匀角速度)图示瞬时, OCCA 且 O,A,B三点 共线。 求:杆AB的速度。
20
解:动点:AB杆上的A点 动系:固连在偏心轮C上 绝对运动- 上下直 线运动 相对运动-以C为圆
点的复合运动

z rM
M(M') z' r' rO' x' i'
k' j' y' O' y
动点的绝对速度va,绝对加速度aa为
M va = r
(绝对导数)
x
O
+ y + x O + xi i + y j + z k =r j + z k
rM = rO + xi + yj + zk
+ y + a i k aa v rM = rO + x j + z xi + yj + z k + x + y i k +x i + y j + z k j + z
第三章 点的复合运动 动点的相对速度vr,相对加速度ar为
r d i y j z k vr =x dt
(相对导数)
§ 3.2 点的速度合成定理
z rM
M(M') z' r' rO' x' i' k' j' y' O' y
v d ar r = x i y j z k dt
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
第三章 点的复合运动
绝对导数:矢量在静参考系中观察到的对时间 的变化率。 相对导数:矢量在动参考系中观察到的对时间 的变化率。
§ 3.2 点的速度合成定理
z rM
点的复合运动的分类

点的复合运动的分类
一、直线运动:又称作线性运动,是指在限定的直线路径上,沿着一定方向和速度移动的运动。
二、角动:也称为旋转运动,是指物体围绕某一点旋转,或以一定角速度斜率运动,以该点为转轴,其轨迹是一个旋线。
三、抛物运动:指物体投掷后,在重力作用下,以匀加速度直线运动,以及水平和竖直方向上有相对应变化而称之为抛物运动。
四、径向运动:也称为近似圆周运动。
指物体在一定的轨道上以其圆心为旋转轴,以相对圆心的位置的改变不断诞生外转力。
五、螺旋运动:也称升降运动,是指一个物体水平沿螺旋线运动,由低点向高点或者高点到低点而移动,以螺旋线形式而呈现上升或下降的运动状态。
第五章 点的复合运动

aa ae a r ar
n
n
将上式向n轴投影,得
j
n
aa sinj ae cosj a r
4v 0 2 aa (ae cosj ar n )/sinj (a0 cos60 )/sin60 3R
得
3 8 v0 a A B aa ( a0 ) 3 3 R
dx' dy ' dz ' vr i ' j ' k' dt dt dt d 2 x' d 2 y' d 2 z' ar 2 i ' 2 j ' 2 k ' dt dt dt
②动系绕z轴转动,动系上与动点重合的点的速度、加速度即 牵连速度、牵连加速度:由公式(4-2-13)(4-2-14)
va ve v r wR v r 常数
即绝对运动也为匀速圆周运动,所以 2 va 2 ( Rw vr ) 2 vr 2 aa Rw 2wvr ae ar 2wvr R R R 方向指向圆心O点。
34
可见,当牵连运动为转动时,动点的绝对加速度 等于牵连加速度
速度合成定理 将建立动点的绝对 速度,相对速度和 牵连速度之间的关 系。
t→t+△t
M →M′ 也可看成:
M →M1 →M′
MM′ — 绝对轨迹 M M′ — 绝对位移 — M1M′ 相对轨迹
请看动画
M1M′ 相对位移 M M1— 牵连位移17 —
由图:
MM ' = MM1 + M 1M '
MM1 M1 M MM lim lim lim t t 0 t t 0 t t 0
解:取杆AB上的A点为动点,
清华大学理论力学lecture05A
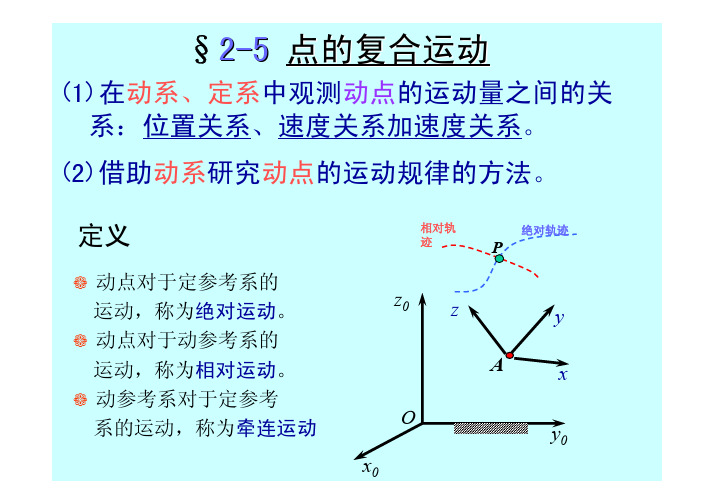
§2-5 点的复合运动(1)在动系、定系中观测动点的运动量之间的关 系:位置关系、速度关系加速度关系。
(2)借助动系研究动点的运动规律的方法。
定义动点对于定参考系的 运动,称为绝对运动。
动点对于动参考系的 运动,称为相对运动。
动参考系对于定参考 系的运动,称为牵连运动 x0 z0相对轨 迹 绝对轨迹Pz Ay x y0O绝对运动、相对运动与牵连运动 例1 动点:滑块P;定系:圆板;动系:杆 OA 绝对运动:螺旋线相对运动:沿杆直线 牵连运动:定轴转动 牵连点Pe: 动系上与动点P位置重 合的点(杆上的点) 牵连点的位置随动点的相对运动而改变。
牵连速度:牵连点的绝对速度,记为ve 。
点的复合运动公式动点的绝对速度 v a 等于动点相 对动系的相对速度 v r 与其牵连点 的速度 ve 之和。
该动系上瞬时与 动点的几何位置重合的点称为动点 的牵连点。
相对 轨迹P绝对轨迹z0z Ay x y0v a = ve + v r动点的绝对加速度 aa 等于 动点相对动系的相对加速度 ar 与其牵连点的加速度 ae 以及哥 氏加速度 aC 之和。
O x0a a = ae + a r + ac哥氏加速度 ac = 2ω × vrω动系的绝对角速度例:速度合成定理的一个启发性证明Oxyz 为定系;刚性金属丝为动系,作刚体一般运动;丝上套小环P为动点。
绝对 轨迹 相对 轨迹e e前时刻动系上与动点重合的点的绝对轨迹速度合成定理:动点的绝对速度等于其牵连速度与相对 速度的矢量和: v a = ve + v r∆r = ∆rr + ∆re⎛ ∆r ∆rr ∆re ⎞ = + lim ⎜ ⎟ t →0 ⎝ ∆t ∆t ∆t ⎠绝对 速度v a = ve + v rP的绝 对位移牵连 速度相对 速度∆rr相对 位移e牵连点的 绝对位移ee定义:在t 瞬时,动系上与动点相重合之点(牵连点) 的绝对速度称为牵连速度,记为 v e 。
理论力学-5-点的复合运动分析

5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动点相对于动系的运动,称为 动点的相对运动(relative)。动 点刀尖上P点的相对运动是在工件 圆柱面上的螺旋线(相对轨迹)运 动。 动点相对于动系的运动速度和 加速度,分别称为动点的相对速度 和相对加速度,分别用符号vr和ar 表示。
具体方法:在有的机构中,一个构件上总有一个点被另一个构件所约束。 这时,以被约束的点作为动点,在约束动点的构件上建立动系,相对运动 轨迹便是约束构件的轮廓线或者约束动点的轨道。
(3) 应用速度合成定理时,可利用速度平行四边形中的几何关系解出 未知数。也可以采用投影法:即等式左右两边同时对某一轴进行投 影,投影的结果相等。
5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动系相对于定系的运动, 称为牵连运动。图中,牵连 运动为绕Oy ' 轴的定轴转动。
5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动系上每一瞬时与动点相重 合的那一点,称为瞬时重合点,又 称为牵连点。由于动点相对于动 系是运动的,因此,在不同的瞬 时,牵连点是动系上的不同点。 动系上牵连点相对定系的运 动速度和加速度,分别称为为动 点的牵连速度和牵连加速度,分 别用符号ve和ae表示。
第5章 点的复合运动分析 5.1 点的合成运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论
第5章 点的复合运动分析
5.1 点的合成运动的基本概念
5.1 点的合成运动的基本概念
vr
q
ve OA
3 2 3e va ve tan q OA 3 3
理论力学-6-点的复合运动

相对运动(relative motion): 动点相对于动系的运动。 相对速度vr (relative velocity) 动点相对于动系的速度。 相对加速度ar (relative acceleration)
6.1 点的运动合成
z y
x
O
牵连运动 ( entrainement ) : 动系相对于定系的运动。 牵连点 P1 (瞬时重合点)
q
6.2 点的速度合成定理
例题3
6.2 点的速度合成定理
例题3
解: 动点: 杆AB上端点A 动系: 固连于凸轮
B
va ve
A
vr
q
绝对运动: 沿AB杆直线 相对运动: 沿凸轮边缘的圆周运动 牵连运动: 凸轮绕O轴的定轴转动 方程:
va =ve+ vr
3 2 3 e # 3 3
n r
O1
aa cos 60 arn 1579 0.5 1579 ae cos30 3/2 2740 cm/s 27.4 m/s
y'
z
y
x O
t 瞬时
t+t 瞬时
6.2 点的速度合成定理
动点? z' x'
定系?
动系?
y'
z
y
x O
t 瞬时
t+t 瞬时
6.2 点的速度合成定理
绝对运动? z' z x' y
牵连运动?
绝对运动轨迹
相对运动?
P'
相对运动轨迹
y'
r
r'
x
O
P,P1 t 瞬时
P1'
7-点复

O
z
ω
z M
B y
O
x
A
x
与动点相重合的点为动点在此瞬时的牵连点
(5)三种速度 三种速度: 三种速度
绝对速度(v 绝对速度 a)——动点相对于静系的速度 动点相对于静系的速度 相对速度(v 相对速度 r)——动点相对于动系的速度 动点相对于动系的速度 牵连速度(v 牵连速度 e)——牵连点的速度 牵连点的速度
例题1. 汽车以速度v 沿直线行驶雨滴M以 铅垂下落, 例题 汽车以速度 1沿直线行驶雨滴 以v2铅垂下落, 求雨滴相对于车的速度. 求雨滴相对于车的速度. 动点: 动点:雨滴 动系: 动系:汽车 V2 =Va V1
M
Vr
V1=Ve
由va = ve + vr
2 2 ∴ vr = v1 + v2
v1 tg (vr + v2 ) = v2
va= ve + vr
牵连点—凸轮与 点重和 牵连点 凸轮与A点重和的A点. 凸轮与 点重和的
绝对运动: 绝对运动:以B为圆心 l 为半径的园运动 为圆心 为半径的园运动.
va = l ωAB
解得: 解得
ω AB
ve = OAω e = ω l
阅读材料和作业
阅读材料 – P123---P129 作业 – 7-3;7-6 ; 7-14(a) 预习内容 – 第八章:刚体的平面运动
(6) 三种加速度 三种加速度: 绝对加速度(a 动点相对于静系的加速度. 绝对加速度 a)——动点相对于静系的加速度 动点相对于静系的加速度 相对加速度(a 动点相对于动系的加速度. 相对加速度 r)——动点相对于动系的加速度 动点相对于动系的加速度 牵连加速度(a 牵连点相对于静系的加速度. 牵连加速度 e)——牵连点相对于静系的加速度 牵连点相对于静系的加速度 例题7-2 图示机构中滑块 套 图示机构中滑块A套 例题 在摇杆O 上 并与曲柄O 以 在摇杆 2B上, 并与曲柄 1A以 销子连接. 销子连接.当O1A转动时通过 转动时通过 左右摆动.设 滑块A带动 滑块 带动O2B 左右摆动 设 带动 O1A长 r,以匀角速ω1转动.试 以匀角速ω 长 以匀角速 转动. 分析滑块A的运动. 分析滑块 的运动. 的运动
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.选择持续接触点为动点。
2.对没有持续接触点的问题,一般不选择接触点为动点。 根据选择原则具体问题具体分析。
§7–1 基 本 概 念
练习题1
§7–2 点的速度合成定理
速度合成定理
§7–1 基 本 概 念
三种速度 绝对速度va :动点相对于定系的速度。 相对速度vr :动点相对于动系的速度。 牵连速度ve :动系上与动点相重合的点相对于 定系的速度。
1.两种参考系
物体的运动的描述结果与所选定的参考系有关。同一物体的运动,
在不同的参考系中看来,可以具有极为不同的运动学特征(具有不同的轨 迹、速度、加速度等)。
在实际问题中,往往不仅要知道物体相对地球的运动,而且有时要知 道被观察物体相对于地面运动着的参考系的运动情况。
例如在运动着的飞机、车船上观察其他飞机、车船的运动。 在运动学中,所描述的一切运动都只具有相对的意义。在不同的参考 系中观察到的同一物体的不同运动特征之间存在着一定的联系。
解出未知数。
§7–2 点的速度合成定理 例题7-1
例7-1 军舰以20节(knot,1=1.852 km/h)的速度前进, 直升飞机一每小时18 km的速度垂直降落。求直升飞机相对 于军舰的速度。
例题 7-1
§7–2 点的速度合成定理 例题 7-1
y´
M
O1
解: 1、选择动点与动系
绝对运动: 物体相对于定参考系的运动。 相对运动: 物体相对于动参考系的运动。
牵连运动: 动参考系相对于定参考系的运动。
3. 两种运动轨迹
绝对运动轨迹:动点相对于定系的运动轨迹。 相对运动轨迹:动点相对于动系的运动轨迹。
思考题
§7–1 基 本 概 念
思考题
动 点:滑块上B点。 绝对运动? 动系:固连于曲柄OA。 相对运动? 定系:固连于机座。 牵连运动?
运动学
点的合成运动
第3章 点的复合运动
运动学
第 七
§7–1 基本概念
章
§7–2 点的速度合成定理
点
的
§7–3 牵连运动是平移时点的加
复
速度合成定理
合
§7– 4 牵连运动是定轴转动时点
运
的加速度合成定理
动
目录
§7–1 基本概念
两种参考系 三种运动 牵连点•动点和动系的选择
§7–1 基 本 概 念
在复合运动的研究中,参考系的选择是问题的关键。恰当的选择 参考系,能把复杂的运动分解为若干种简单运动,或由若干种简单 运动组成各种不同的复杂运动。
§7–1 基 本 概 念
4.牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
这点称为瞬时重合点或动点的牵连点。
(2)、进一步说明 牵连运动一方面是动系的绝对运动,另一方面对动点来说起
z' M2(m2) y'
x'
vr
M(m)
va
r ve
r1
(1)
M '(m')
r'
M1(m1)
§7–2 点的速度合成定理 va vr ve
绝对速度
相对速度
牵连速度
z' M2(m2) y'
x'
vr
M(m)
va
r ve
r1
M '(m')
r'
M1(m1)
速度合成定理
动点的绝对速度等于其相 对速度与牵连速度的矢量 和。
本章利用运动的分解、合成的方法对点的速度、加速度进行分析,研 究点在不同参考系中的运动,以及它们之间的联系。
§7–1 基 本 概 念
两种参考系
静参考系(定系或静系):在分析问题中,认定不动的参考系。 动参考系(动系):相对于静系运动着的参考系。 一般没特别说明,常以固连于地球的参考系取为静系。
2. 三种运动
A
ω0
B
O
曲柄-滑块机构
思考题
§7–1 基 本 概 念
动 点:杆上A点。
A
动系:固连于滑块B。
定系:固连于墙面。
绝对运动? 相对运动? 牵连运动?
思考题
Bv
§7–1 基 本 概 念
合成运动
由于牵连运动的存在,使物体的绝对运动和相对运动 发生了差别。 如果没有牵连运动,物体的相对运动等同于它的绝对运动。 如果没有相对运动,物体的牵连运动就是它的绝对运动。
由此可见,物体的绝对运动可以看成是牵连运动和相 对运动的合成结果。所以绝对运动也称为复合运动或合成 运动。
§7–1 基 本 概 念
几点说明
本章只研究点的复合运动理论,通过牵连运动来建立绝对运动和相 对运动之间的联系,给出这些运动特征量(轨迹、速度、加速度)之 间的关系。
必须指出在这一章,绝对运动、相对运动都是指点的运动,可能是 直线运动,也可能是曲线运动;而牵连运动是指刚体的运动,可能是 平动、定轴转动或下一章的平面运动等。
MM MM1 M1M
则有
分析其中各项
lim
t 0
MM t
va
lim MM lim MM1 lim M1M
t0 t
t0 t
t0 t
lim MM1 t0 t
lim mm1 t0 t
vm
ve
lim M1M lim MM 2
t0 t
t0 t
vr
代入(1)式可得
va vr ve
着“牵连”作用。但是带动动点运动的只是动系上在所考察的瞬 时与动点相重合的那一点,该点称为瞬时重合点或牵连点。 (3)、注 意
由于相对运动,动点在动系上的位置随时间改变,所以牵连点
具有瞬时性。
§7–1 基 本 概 念
牵连点
复ቤተ መጻሕፍቲ ባይዱ运动实例
牵连点
§7–1 基 本 概 念
5、 动点和动系的选择
基本原则: 1.动点对动系要有相对运动(动点动系不能位于同一物体上)。 2.动点的相对运动轨迹要明确、容易确定。
§7–2 点的速度合成定理
三种运动轨迹
设动点M在动系中沿某一曲线AB作相对运动,而动系本身相对定
系作某种运动,相应的运动轨迹如下
z' M2(m2) 绝对运动轨迹 y'
x'
M'(m')
相对运动轨迹
z xO
M (m) y
M1(m1)
牵连点运动轨迹
§7–2 点的速度合成定理
速度合成定理
动点M在时间△t 内的绝对位移
§7–2 点的速度合成定理
va vr ve
几点说明
牵连运动是指刚体(动系)的运动;而牵连速度是指刚体
上一点(与动点相重合的点)的速度。
速度合成定理为平面矢量方程,由此可以写出两个投
影式,所以可以求解两个未知量。
速度合成定理对任意形式的牵连运动都适用。
解 (1)选定动点、动参考系和定参考系。 题 (2)分析三种运动和三种速度。 步 (3)作出速度平行四边形。 骤 (4)利用速度平行四边形中的几何关系
