杠杆的简单计算
秤杆的原理的计算公式

秤杆的原理的计算公式
称杆由一根绳子,吊着一根硬棒组成,硬棒的一端有一个挂物钩,绳子与硬棒的交点,就在挂物钩的附近,假设:绳子与硬棒的交点为O,O的左端为L1,O的右端为L2,挂物钩在L1上L2>L1,其实就是简单的杠杆原理即:力矩平衡原理:受力大小x力臂=另一端的受力大小x相对应的力臂。
先确定秤杆的刻度,之后只要秤平了说明两边力矩相等,用砝码的重量与刻度算出此时物体的重量,再把重量与刻度对应就可以称东西了。
灵活运用“杠杆的平衡公式”。
在已知动力,阻力臂,阻力,的情况下求动力臂的长度。
并用笔画出记号。
方便下次快速称量物体重量。
更换提把,就是变更支点。
支点变更后,阻力臂缩短,动力臂加长。
所以能称更多的重量了。
物理杠杆平衡公式

物理杠杆平衡公式咱们在学物理的时候,有个特别重要的知识点,那就是杠杆平衡公式。
先来说说啥是杠杆。
就好比咱平时见到的跷跷板,还有称东西的秤杆,这都是杠杆。
杠杆平衡公式是:动力×动力臂 = 阻力×阻力臂。
这公式看着简单,可里面的门道多着呢!我记得有一次,我带着小侄子去公园玩。
公园里有那种小朋友玩的简易跷跷板。
我家小侄子非要拉着我一起玩。
这一玩,可让我对杠杆平衡公式有了更深刻的理解。
小侄子那小身板儿,一坐上去,我这边就高高的翘起来。
我就寻思,这不就是杠杆平衡嘛。
他轻,我重,但是他坐得离跷跷板中间的支点远,我离得近,所以我俩能玩得起来。
要是我俩体重差不多,坐的距离也差不多,那跷跷板就很难动起来,这不就不符合杠杆平衡公式了嘛。
再说说生活里常见的秤。
卖水果的大叔大妈用的秤,那秤杆就是个杠杆。
秤砣就是动力,被称的水果就是阻力。
秤杆上的刻度就是根据杠杆平衡公式标出来的。
咱做物理题的时候,经常会碰到这样的情况。
比如说告诉你一个杠杆,动力是多少,动力臂多长,阻力臂多长,让你算阻力是多少。
这时候,只要把数据往公式里一代,答案就出来了。
可别小看这公式,好多大工程里都用得到。
像建大桥的时候,那些起重机长长的吊臂,也是利用杠杆原理工作的。
工程师们得根据要吊起的重物重量,还有吊臂的长度,来计算需要多大的力才能吊起,这里面杠杆平衡公式就派上大用场了。
在学习杠杆平衡公式的时候,咱们得多多联系实际,这样才能真正理解它,用起来也得心应手。
别死记硬背,得明白其中的道理。
而且啊,这个公式还能让咱们明白,生活中很多事情都得讲究个平衡。
就像杠杆,两边不平衡就动不了。
咱们学习和生活也一样,得合理安排时间和精力,才能顺顺利利的。
总之,杠杆平衡公式虽然只是物理里的一个小知识点,但它的用处可大着呢。
咱们得好好学,好好用,让它帮咱们解决更多的问题!。
八年级物理杠杆

八年级物理杠杆在物理学中,杠杆是一种常见的力学工具,用以改变物体的位置或者方向。
它是由一个简单的刚性杆构成,其上有一个支点,既可以是一个固定的点,也可以是一个移动的对象。
本文将介绍杠杆的基本原理、应用以及其中涉及的相关概念。
一、杠杆的基本原理杠杆最基本的原理就是杠杆定律,即力矩平衡定律。
它可以用一个简单的公式来表示:力1 ×力臂1 = 力2 ×力臂2其中,力1、力2分别是作用在杠杆上的两个力,力臂1、力臂2分别是这两个力到支点的垂直距离。
二、一级杠杆一级杠杆是指力和支点所处位置的比例相等的杠杆。
当一级杠杆平衡时,支点两侧的力矩相等。
例如,一个横放的杠杆,支点在中间,上面施加一个力向下,下面施加一个力向上,并且两个力相等,那么杠杆就保持平衡。
这是因为力1 ×力臂1 = 力2 ×力臂2,而力臂1和力臂2是相等的。
三、二级杠杆二级杠杆是指力和支点所处位置的比例不相等的杠杆。
当二级杠杆平衡时,力矩的和为零。
例如,一个杠杆长10米,支点在一侧的2米处,上面施加一个力向下20牛顿,下面另一侧施加一个未知力,那么这两个力的乘积必须等于力臂的乘积。
即20 × 2 = 力2 × 8,解方程可得力2为5牛顿。
这样,杠杆就保持平衡。
四、三级杠杆三级杠杆是指力和支点所处位置的比例不相等的杠杆。
当三级杠杆平衡时,力矩的和为零。
例如,一个杠杆长20米,支点在一侧的3米处,上面施加一个力向下30牛顿,下面另一侧施加一个未知力,那么这两个力的乘积必须等于力臂的乘积。
即30 × 3 = 力2 × 17,解方程可得力2为5.1牛顿。
这样,杠杆就保持平衡。
五、杠杆的应用杠杆作为一种简单而有效的力学工具,广泛应用于日常生活和工程领域。
以下是一些常见的杠杆应用:1. 起重机:起重机利用杠杆的原理来提升重物。
在起重机的操作中,需要根据物体的重量和距离来选择合适的杆长和支点位置。
自制杠杆的原理

自制杠杆的原理杠杆是一种简单机械装置,用来改变力的作用效果。
它由一个支点和两个力臂组成,通过施加力在支点处产生力矩,从而实现增加力的效果。
杠杆原理是物理学的基本原理之一,它的应用广泛,可以用于各种工作中。
杠杆原理的核心概念是力矩平衡,即在杠杆上作用的力矩的总和为零。
力矩是指力对于旋转轴的作用效果,计算公式为力的大小乘以力臂的长度。
力臂是指力的作用点到旋转轴的垂直距离。
在杠杆原理中,力矩平衡可以用以下公式表示:力1乘以力臂1的长度等于力2乘以力臂2的长度。
这个公式可以写成M1=M2,其中M1和M2分别代表力1和力2的力矩。
在理解杠杆原理时,有三个主要概念需要注意。
第一个概念是支点。
支点是杠杆上的旋转轴,也是力矩计算的基准点。
在杠杆原理中,力会使杠杆绕着支点旋转。
第二个概念是力臂。
力臂是力的作用点到支点的垂直距离。
力臂越长,产生的力矩越大。
第三个概念是力。
力是杠杆上作用的物理量。
根据力臂的长度和施加的力的方向,可以计算力矩的大小。
杠杆原理的应用非常广泛。
它可以用于改变力的方向、大小和作用点。
有三种常见的杠杆形式:一级杠杆、二级杠杆和三级杠杆。
一级杠杆是最简单的杠杆形式,力和支点在杠杆中的位置相对固定。
如果力和支点在杠杆中的距离相等,那么力的方向和大小将被保持不变。
如果力和支点的距离不相等,杠杆将使力产生机械优势或劣势。
机械优势意味着使力增加,而机械劣势则意味着减小力。
二级杠杆在杠杆中增加了一个力臂。
这个额外的力臂可以增加杠杆的机械优势。
如果力1和力2的力臂方向相反,而力1的力臂长度大于力2的力臂长度,那么杠杆会产生机械优势。
这意味着用较小的力1可以产生较大的力2。
三级杠杆在杠杆中增加了两个力臂。
这个设计可以进一步增加杠杆的机械优势。
对于三级杠杆,支点通常位于杠杆的中间部分。
通过施加力在杠杆的一端,可以将力放大到杠杆的另一端。
杠杆原理在很多日常生活中的应用中都存在。
例如,钳子就是一个应用了杠杆原理的工具。
简单机械的计算公式

一、杠杆杠杆的平衡公式F 1l 1=F 2l 21、有用功: W 有=G 物h2、总功: W 总=Fs3、额外功:W 额=W 总 —W 有注意:若不计摩擦,此时只有克服杠杆自重做额外功:W 额=G 杠杆h4、机械效率二、用滑轮组竖直提升物体动滑轮的绳子段数为n1、拉力F 与物体重力G 物的关系(a )若不计动滑轮自重、绳重及摩擦:(b )若不计绳重及摩擦,(要考虑动滑轮自重G 动): 2、绳子自由端移动距离S 绳与物体上升高度h 的关系3、绳子自由端移动速度V 绳与物体上升速度V 物的关系nF = (G 物 + G 动)s 绳=nh V 绳= nnF = G物4、有用功: W 有=G 物h5、总功: W 总=Fs6、额外功:W 额=W 总 —W 有注意:此时只有动滑轮做额外功:W 额=G 动h7、机械效率(a )若不计动滑轮自重、绳重及摩擦:(b )若不计绳重及摩擦,(要考虑动滑轮自重G 动):三、用滑轮组水平拉动物体动滑轮的绳子段数为n1、拉力F 与摩擦力f 的关系:2、绳子自由端移动距离S 绳与物体移动距离S 物的关系3、绳子自由端移动速度V 绳与物体移动速度V 物的关系4、有用功: W 有=fs 物5、总功: W 总=Fs 绳6、额外功:W 额=W 总 —W 有7、机械效率:四、用斜面拉动物体1、有用功: W 有=G 物hnF =f s 绳= ns 物 V 绳= n V2、总功:W总=Fs3、额外功:W额=W总—W有=fs4、机械效率:5、计算摩擦力f方法(注意:拉力F不等于摩擦力f):(1)先根据W额=W总—W有算出额外功(2)再根据W额=fs算出摩擦力。
杠杆的简单计算
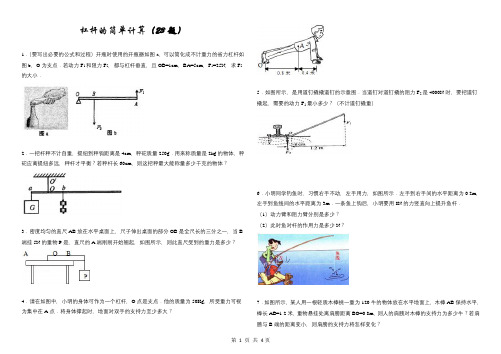
杠杆的简单计算(23题)1.(要写出必要的公式和过程)开瓶时使用的开瓶器如图a,可以简化成不计重力的省力杠杆如图b,O为支点.若动力F1和阻力F2,都与杠杆垂直,且OB=1cm,BA=5cm,F1=25N,求F2的大小.2.一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g.用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm,则这把秤最大能称量多少千克的物体?3.密度均匀的直尺AB放在水平桌面上,尺子伸出桌面的部分OB是全尺长的三分之一,当B 端挂5N的重物P是,直尺的A端刚刚开始翘起,如图所示,则此直尺受到的重力是多少?4.请在如图中,小明的身体可作为一个杠杆,O点是支点.他的质量为50Kg,所受重力可视为集中在A点.将身体撑起时,地面对双手的支持力至少多大?5.如图所示,是用道钉撬撬道钉的示意图.当道钉对道钉撬的阻力F2是4000N时,要把道钉撬起,需要的动力F1最小多少?(不计道钉撬重)6.小明同学钓鱼时,习惯右手不动,左手用力,如图所示.左手到右手间的水平距离为0.2m,左手到鱼线间的水平距离为3m.一条鱼上钩后,小明要用8N的力竖直向上提升鱼杆.(1)动力臂和阻力臂分别是多少?(2)此时鱼对杆的作用力是多少N?7.如图所示,某人用一根轻质木棒挑一重为120牛的物体放在水平地面上,木棒AB保持水平,棒长AB=1.2米,重物悬挂处离肩膀距离BO=0.8m,则人的肩膀对木棒的支持力为多少牛?若肩膀与B端的距离变小,则肩膀的支持力将怎样变化?8.如图是锅炉安全阀示意图.OA=20厘米,AB=40厘米,若锅炉在阀上产生的竖直向上的压力为30牛,在B处应挂多重的物体G?9.如图,O为杠杆AB的支点,OA:OB=2:3,物块甲和物块乙分别挂在杠杆的A、B两端,杠杆平衡,已知物块甲、物块乙的体积之比是2:1,物块甲的密度ρ甲=6×103kg/m3,物块乙的密度ρ乙是多少.10.“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1.5×103Kg,则:(1)配重体的质量应为多少Kg?(2)当滑轮移到D点时能够安全起吊重物的最大质量是多少Kg?(不计“水平臂”和滑轮重力)11.(10分)如图所示,一段粗细不均匀的木头放在地面上,用弹簧测力计竖直向上拉起细端时弹簧测力计示数为F 1,而竖直向上拉起粗端时弹簧测力计的示数为F2,则此木头的重力G是多少?F1和F2哪个大?12.如图所示,灯重30 N,灯挂在水平横杆的C端,O为杠杆的支点,水平杆OC 长2 m,杆重不计,BC长0.5 m,绳子BD作用在横杆上的拉力是多少?(已知:∠DBO=30°)13.希腊科学家阿基米德发现杠杆原理后,发出了“给我支点,我可以撬动地球”的豪言壮语.假如阿基米德在杠杆的一端施加600N的力,要搬动质量为6.0×1024kg的地球,那么长臂的长应是短臂长的多少倍?如果要把地球撬起1cm,长臂的一端要按下多长距离?假如我们以光速向下按,要按多少年?(做完该题,你有何启示?)14.小华用一根长6米、半径7.5厘米的均匀粗木棒为爸爸设计了一架能搬运柴草的简易起重机(如图所示).他把支架安在木棒的长处,每捆柴草重1000牛,为了使木棒平衡以达到省力的目的,他又在另一端吊一块配重的石头,请你算出这块配重的石头应有多重?(木棒密度0.8×103千克/米3,g取10牛顿/千克.)15.如图所示,OB为一轻质杠杆,可绕O点作自由转动,在杠杆A点和B点分别作用两个力F1和F 2(F2未画出)时,恰能使杠杆在水平位置上平衡,已知OA=1cm,OB=3cm.(1)若F1=18N,方向竖直向下,则F2的最小值是多大?(2)若F1减小为9N ,不改变(1)中F2的作用点和最小值的大小,只改变F2的方向,要使杠杆仍在水平位置平衡,则L2为多大?并在图中画出F2的方向.(2种情况)16.如图所示,要将重为G=500N,半径为r=0.5m的轮子滚上高为h=20cm的台阶,(支点为轮子与台阶的接触点O),试在图中作出阻力G的力臂L,并在图中作出所用的最小力F的示意图.这个最小力F=_________N,并且至少需要做W=_________J的功,才能将轮子滚上台阶.17.(2008•郴州)如图所示,质量为8kg,边长为5cm的正方体物块A置于水平地面上,通过细绳系于轻质杠杆BOC的B端,杠杆可绕O点转动,且CO=3BO,在C端用F=10N的力竖直向下拉杠杆,使杠杆在水平位置平衡,且细绳被拉直.(细绳重量不计,g取10N/kg)求:(1)物体A的重力G1.(2)B端细绳的拉力F拉;(3)物体A对地面的压力F压;(4)物体A对地面的压强P.18.(2005•海淀区)假期里,小兰和爸爸、妈妈一起参加了一个家庭游戏活动.活动要求是:家庭成员中的任意两名成员分别站在如图所示的木板上,恰好使木板水平平衡.(1)若小兰和爸爸的体重分别为400N和800N,小兰站在距离中央支点2m的一侧,爸爸应站在距离支点多远处才能使木板水平平衡?(2)若小兰和爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,小兰的速度是0.5m/s,爸爸的速度是多大才能使木板水平平衡不被破坏?19.如图所示,独轮车和车内的煤的总质量为90kg,可视为作用于A点.车轴为支点,将车把抬起时,作用在车把向上的力为多少?20.有一根1.5m长的杠杆,左端挂300N的物体,右端挂500N的物体,若不计杠杆重力,要使杠杆平衡,支点应在什么位置?如果两端各加100N的重物,支点应向哪端移动?移动多少?*21.(25分)如图1,一根长为20cm,横截面积为10cm2的均匀木杆用细线和弹簧测力计竖直悬挂起立,置于烧杯内水平面上方.现将烧杯竖直缓缓提升,木杆逐渐浸入水中,已知木杆的密度为ρ1=0.8×103kg/m3,水的密度为ρ0=1.0×103kg/m3(1)当弹簧测力计读数为1.2N时,求木杆浸入水中的长度.(2)继续缓慢提升烧杯,当木杆浸入水中一定深度时,开始出现倾斜,当木杆再次静止时,木杆与竖直方向成30°角,如图2所示,求木杆浸入水中的长度.(忽略木杆横截面积的影响)*22.(25分)如图所示是锅炉上保险装置的示意图,0为一可绕0点旋转的横杆(质量不计),在横杆上的B点下方连接着阀门S,阀门的底面积为3cm2,OB长度为20cm,横杆上A点处挂着重物G,OA长度为60cm.对水加热时,随着水温升高,水面上方气体压强增大.当压强增大到一定值时,阀门S 被顶开,使锅炉内气体压强减小,使锅炉内的蒸气压强减小.若要保持锅炉内、外气体的压强差为1×105Pa,试求挂在A点处的重物G为多少N?*23.(25分)某工地在冬季水利建设中设计了一个提起重物的机械,其中的一部分结构如图所示.OA是一个均匀钢管,每米长所受重力为30N;O是转动轴;重物的质量m为150㎏,挂在B处,OB=1m;拉力F作用在A点,竖直向上.为维持平衡,钢管OA为多长时所用的拉力最小?这个最小拉力是多少?(g取10N/kg)24.如图甲所示为塔式起重机简易示意图,塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装。
杠杆原理的公式计算方法

杠杆原理的公式计算方法嘿,咱今儿个就来讲讲杠杆原理的公式计算方法。
你说这杠杆原理啊,就像咱生活里的好多事儿一样,看着简单,其实里面的门道可不少呢!杠杆原理,说到底就是力和力臂的关系。
那公式呢,就是动力×动力臂=阻力×阻力臂。
这就好比是一场拔河比赛,两边的力量和距离得平衡好才行。
咱先来说说动力和阻力。
动力就是你使的劲儿,阻力呢就是你要克服的那个难事儿。
比如说你想用撬棍撬起一块大石头,你用力往下压撬棍的那个力就是动力,而大石头给撬棍的反作用力就是阻力。
你想啊,要是你劲儿使得不够大,那能撬得动大石头吗?肯定不行啊!再说说动力臂和阻力臂。
这就像是胳膊的长短一样,胳膊长的人是不是相对更容易够到远处的东西呀?动力臂长的话,你用同样的力就能产生更大的效果;阻力臂长呢,就需要你用更大的力去克服它。
那怎么运用这个公式呢?举个例子哈,你看那阿基米德不是说过嘛,给他一个足够长的杠杆,他就能撬动地球。
咱就假设真有这么个大杠杆,地球就是那个大阻力,咱要想撬动它,就得算出需要多大的动力和多长的动力臂。
你说神奇不神奇?你再想想,咱平时生活里是不是也经常用到杠杆原理啊?像开瓶器,那就是利用杠杆原理来省力的呀。
还有跷跷板,两个小朋友在上面一上一下的,不也是杠杆原理嘛。
哎呀呀,这杠杆原理可真是无处不在啊!你要是把这个搞明白了,那好多事儿都能迎刃而解啦。
就像你知道了怎么用巧劲儿去解决一个难题,而不是一味地使蛮力。
那在实际应用中,咱可得注意别把这公式给弄错了。
要是算错了,那可就麻烦啦。
就好比你本来想轻轻一撬就搞定的事儿,结果因为算错了力臂啥的,费了好大的劲儿也没弄好,那不就白折腾啦?总之啊,杠杆原理的公式计算方法虽然看起来有点复杂,但只要你用心去琢磨,多结合实际去想想,肯定能掌握得牢牢的。
以后遇到啥事儿,就可以像个小专家似的,用杠杆原理来分析分析,看看怎么能更轻松地搞定。
咋样,是不是挺有意思的呀?别小瞧这小小的杠杆原理,它能发挥的作用可大着呢!。
杠杆的工作原理

杠杆的工作原理
杠杆是一种简单机械装置,可以通过放大力量或改变力的方向,使我们能够完成更大的工作。
它的工作原理基于两个重要的因素:力和力臂。
首先,让我们来了解力。
力指的是施加在物体上的作用,可以用公式力=质量 ×加速度来计算。
力的单位是牛顿(N),它
可以被用来量化物体的重量或推拉力。
接下来,让我们来讨论力臂。
力臂是指施加力的点到杠杆支点之间的垂直距离。
力臂越大,杠杆就越容易旋转。
在杠杆中,支点是指杠杆的旋转点。
杠杆的工作原理可以通过以下的原始杠杆公式来描述:力1 ×
力臂1 = 力2 ×力臂2。
其中,力1和力2分别是施加在杠杆
两端的力,力臂1和力臂2则分别是力1和力2的力臂长度。
例如,如果我们将一个长杆平放在一个支点上,并在杆的一端施加10牛顿的力(力1),并将力臂1的长度设为1米。
如
果我们希望将杆的另一端上升,我们需要施加力2。
根据杠杆
公式,我们可以算出力2:10牛顿 × 1米 = 力2 ×力臂2。
如
果我们将力臂2的长度设置为2米,我们可以得出:力2 = 10
牛顿 × 1米 / 2米 = 5牛顿。
通过这个例子,我们可以看到杠杆可以放大或缩小施加在它上面的力。
在这种情况下,力2只有力1的一半,但我们可以通过施加较小的力在较大的距离上完成相同的工作。
杠杆的工作原理在很多日常生活中都有应用,比如开启门锁、使用钳子拧紧螺母等。
了解杠杆的原理可以帮助我们更好地利用力量,使我们的工作更加高效。
杠杆的简单计算
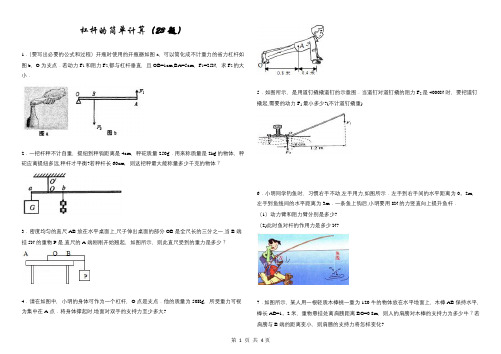
杠杆的简单计算(23题)1.(要写出必要的公式和过程)开瓶时使用的开瓶器如图a,可以简化成不计重力的省力杠杆如图b,O为支点.若动力F1和阻力F2,都与杠杆垂直,且OB=1cm,BA=5cm,F1=25N,求F2的大小.2.一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g.用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm,则这把秤最大能称量多少千克的物体?3.密度均匀的直尺AB放在水平桌面上,尺子伸出桌面的部分OB是全尺长的三分之一,当B端挂5N的重物P是,直尺的A端刚刚开始翘起,如图所示,则此直尺受到的重力是多少?4.请在如图中,小明的身体可作为一个杠杆,O点是支点.他的质量为50Kg,所受重力可视为集中在A点.将身体撑起时,地面对双手的支持力至少多大? 5.如图所示,是用道钉撬撬道钉的示意图.当道钉对道钉撬的阻力F2是4000N时,要把道钉撬起,需要的动力F1最小多少?(不计道钉撬重)6.小明同学钓鱼时,习惯右手不动,左手用力,如图所示.左手到右手间的水平距离为0。
2m,左手到鱼线间的水平距离为3m.一条鱼上钩后,小明要用8N的力竖直向上提升鱼杆.(1)动力臂和阻力臂分别是多少?(2)此时鱼对杆的作用力是多少N?7.如图所示,某人用一根轻质木棒挑一重为120牛的物体放在水平地面上,木棒AB保持水平,棒长AB=1。
2米,重物悬挂处离肩膀距离BO=0.8m,则人的肩膀对木棒的支持力为多少牛?若肩膀与B端的距离变小,则肩膀的支持力将怎样变化?8.如图是锅炉安全阀示意图.OA=20厘米,AB=40厘米,若锅炉在阀上产生的竖直向上的压力为30牛,在B处应挂多重的物体G?9.如图,O为杠杆AB的支点,OA:OB=2:3,物块甲和物块乙分别挂在杠杆的A、B两端,杠杆平衡,已知物块甲、物块乙的体积之比是2:1,物块甲的密度ρ甲=6×103kg/m3,物块乙的密度ρ乙是多少.10.“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1。
杠杆原理简单解释

杠杆原理简单解释杠杆原理也称为“杠杆平衡条件”,是分析杠杆受力平衡的定理,最早由古希腊科学家阿基米德提出。
杠杆要达到受力平衡,作用在杠杆上的两个力矩(力与力臂的乘积)必须大小相等,旋转方向相反。
也就是说,杠杆的平衡条件必须满足:动力×动力臂必须等于阻力×阻力臂,数学表达式为:F1·L1=F2·L2.式中,F1表示动力,L1表示动力臂,F2表示阻力,L2表示阻力臂。
使用杠杆时,为了省力,就应该用动力臂比阻力臂长的杠杆;如果想要省距离,就应该用动力臂比阻力臂短的杠杆。
因此使用杠杆可以省力,也可以省距离。
但是,要想省力,就必须多移动距离;要想少移动距离,就必须多费些力。
要想又省力而又少移动距离,是不可能实现的。
杠杆的支点不一定要在中间,满足以下三个点的系统,基本上就是杠杆:支点、施力点、受力点。
其中,力矩平衡公式这样写:动力×动力臂=阻力×阻力臂,即F1×L1=F2×L2.这就是一个杠杆。
杠杆有省力杠杆,也有费力杠杆,两者功能表现有所不同。
例如脚踩的打气机,手压的榨汁机,就是省力杠杆(动力臂>阻力臂);尽管省力了,但我们却要压下较大的距离,受力端只有较小的动作。
另有一种是费力杠杆。
例如路边的吊车,钓东西的钩子在整个杆的尖端,尾端是支点、中间是油压机(力矩>力臂),这就是费力的杠杆。
但费力换来的是中间的施力点只要动小距离,尖端的挂勾就会移动相当大的距离。
两种杠杆都有用处,不同的应用场景需要评估是要省力或是省下动作范围。
另外,有种机械叫轮轴,也可当作是一种杠杆的应用,只是表现上有时需要增加转动的计算。
阿基米德的名言:"假如给我一个支点,就能撬起地球!"不仅催人奋进,更有着严谨的科学根据。
杠杆原理也称为“杠杆平衡条件”,是分析杠杆受力平衡的定理,最早由古希腊科学家阿基米德提出。
杠杆要达到受力平衡,作用在杠杆上的两个力矩(力与力臂的乘积)必须大小相等,旋转方向相反。
杠杆物理的实验报告

一、实验目的1. 了解杠杆的基本原理和作用。
2. 探究杠杆平衡条件。
3. 熟悉杠杆实验的步骤和方法。
二、实验原理杠杆是一种简单机械,其基本原理是利用力矩平衡。
当杠杆处于平衡状态时,动力矩等于阻力矩,即F1L1=F2L2,其中F1为动力,L1为动力臂,F2为阻力,L2为阻力臂。
三、实验器材1. 杠杆(含支架)2. 钩码盒一套3. 弹簧测力计4. 细线5. 刻度尺四、实验步骤1. 将杠杆固定在支架上,确保杠杆水平。
2. 调节杠杆两端的螺母,使杠杆在不挂钩码时保持水平并静止,达到平衡状态。
3. 在杠杆的一端悬挂钩码,另一端悬挂弹簧测力计,记录钩码的质量和弹簧测力计的示数。
4. 逐渐增加钩码的质量,使杠杆重新达到平衡状态,记录钩码的质量、弹簧测力计的示数、动力臂和阻力臂的长度。
5. 重复步骤3和4,改变钩码的质量和位置,进行多次实验。
6. 将实验数据填入表格中。
五、实验数据实验次数 | 钩码质量(kg) | 弹簧测力计示数(N) | 动力臂(m) | 阻力臂(m)--- | --- | --- | --- | ---1 | 0.1 | 1.0 | 0.2 | 0.12 | 0.2 | 2.0 | 0.3 | 0.23 | 0.3 | 3.0 | 0.4 | 0.34 | 0.4 | 4.0 | 0.5 | 0.4六、数据分析根据实验数据,我们可以计算出每次实验的动力矩和阻力矩:实验次数 | 动力矩(N·m) | 阻力矩(N·m)--- | --- | ---1 | 0.2 | 0.12 | 0.6 | 0.43 | 1.2 | 0.94 | 2.0 | 1.6从实验数据可以看出,随着钩码质量的增加,动力矩和阻力矩逐渐增大,但始终满足动力矩等于阻力矩的平衡条件。
七、实验结论1. 杠杆的平衡条件为动力矩等于阻力矩,即F1L1=F2L2。
2. 在实验过程中,随着钩码质量的增加,动力矩和阻力矩逐渐增大,但始终保持平衡。
杠杆率计算公式举例

杠杆率计算公式举例嘿,咱来说说这杠杆率计算公式。
你知道吗,这杠杆率在金融世界里就像是个神秘的魔法数字,能揭示好多重要的信息。
比如说,它能告诉我们一家公司借了多少钱来扩大业务,是不是有点儿神奇?先来讲讲最简单也最常用的杠杆率计算公式,那就是资产负债率。
这资产负债率等于负债总额除以资产总额再乘以 100%。
比如说,有个公司,资产总额是 1000 万,负债总额是 400 万,那它的资产负债率就是 400÷1000×100% = 40%。
这 40%就代表了这家公司通过负债融资的程度。
再比如说,我之前接触过一家小创业公司,老板雄心勃勃地想要扩大规模。
他们从银行借了不少钱,买了新设备,租了更大的厂房。
我帮他们算了算杠杆率,发现已经超过了行业的平均水平。
这可把老板急坏了,天天担心资金链出问题。
还有一种杠杆率计算方法是权益乘数。
权益乘数等于资产总额除以股东权益总额。
这个数字越大,说明企业的杠杆程度越高。
给您举个例子吧,有一家制造企业,资产总额是 2000 万,股东权益总额是 800 万,那权益乘数就是 2000÷800 = 2.5。
这意味着企业每 1 元的股东权益支撑着 2.5 元的资产。
在实际生活中,杠杆率的计算可重要啦。
就像我有个朋友,他投资股票,特别喜欢研究公司的杠杆率。
有一次,他看上了一家看起来业绩不错的公司,准备重仓买入。
结果我帮他算了算杠杆率,发现这家公司的杠杆率高得吓人,负债累累。
他听了我的劝,没有盲目投资,后来那家公司真的因为债务问题股价暴跌,我朋友可算是逃过一劫。
再比如说房地产市场,很多开发商为了拿地建房,都会大量借款,这时候杠杆率就起到了关键作用。
如果杠杆率过高,一旦市场有个风吹草动,资金链就可能断裂,引发一系列的问题。
总之,杠杆率计算公式虽然看起来简单,但是背后蕴含的信息可丰富着呢。
咱们在做投资、经营决策的时候,可不能忽略了它。
希望通过这些例子,您对杠杆率计算公式能有更清楚的了解。
杠杆的动力公式

杠杆的动力公式嘿,咱们来聊聊杠杆的动力公式!在咱们的日常生活中,杠杆可是无处不在。
从小小的跷跷板,到工地上那巨大的起重机,都离不开杠杆的原理。
那啥是杠杆的动力公式呢?简单说,就是动力乘以动力臂等于阻力乘以阻力臂。
用字母表示就是:F₁×L₁ = F₂×L₂。
这就好比是一个平衡的跷跷板,两边小朋友的体重乘以他们距离跷跷板中心点的距离,得相等了,这跷跷板才能玩得起来,不然可就一头高一头低啦。
就说我上次去工地吧,看到工人们操作起重机吊起一块巨大的石板。
那起重机长长的起重臂就像一个大大的杠杆。
当时我就在想,这得需要多大的动力才能把那么重的石板吊起来啊!工人们可真是厉害,他们得精准地计算出动力和阻力,还有动力臂和阻力臂的长度,才能确保每次吊起的东西都稳稳当当,不出差错。
再想想我们家里常见的那种开瓶器。
开瓶器也是利用了杠杆原理呢。
当我们用开瓶器去开瓶盖的时候,我们手施加的力就是动力,而瓶盖给开瓶器的阻力,通过合适的动力臂和阻力臂的搭配,就能轻松把瓶盖打开。
在学习杠杆的动力公式时,很多同学一开始可能会觉得有点头疼,哎呀,这数字、这公式,咋这么复杂呢!但其实啊,只要咱们多观察观察生活中的例子,就会发现这公式其实挺简单实用的。
比如说,有一次我在家自己修椅子。
那椅子腿有点松动了,我想用个木棍把它撬起来紧一紧。
我就琢磨着,这得使多大劲,找个多长的木棍当杠杆才合适呢?这不就是在实际运用杠杆的动力公式嘛。
咱们再深入讲讲这个公式里的动力。
动力啊,就是让杠杆动起来的那个力。
就像我们推一辆车,我们使的那个劲儿就是动力。
而动力臂呢,就是动力作用点到支点的距离。
阻力和阻力臂也是同样的道理。
有时候,我们为了省力,就得把动力臂加长。
比如撬石头的时候,用一根长长的铁棍,就能比较轻松地撬起来。
但要是动力臂短,阻力臂长,那可就费力啦。
学习杠杆的动力公式,可不仅仅是为了应付考试哦。
它能让我们更好地理解这个世界,知道为啥有些东西能轻松做到,有些就特别费劲。
杠杆定理的公式

杠杆定理的公式嘿,咱来聊聊杠杆定理的公式。
你知道吗?杠杆定理这玩意儿,在咱们的生活里那可是无处不在。
就说我前几天去菜市场买菜的时候吧,看见一个卖水果的摊主用一根长长的杆子挑着一筐水果。
那杆子就像一个杠杆,摊主轻松地一抬一放,就把水果筐摆弄得服服帖帖。
杠杆定理的公式是:动力×动力臂 = 阻力×阻力臂。
用字母来表示就是 F1×L1 = F2×L2 。
这看起来简单的公式,里面可藏着大学问。
比如说,你想撬起一块大石头,可石头太重,直接搬根本搬不动。
这时候杠杆就派上用场啦。
你找一根结实的木棍,把它放在石头下面,作为杠杆。
然后在木棍靠近石头的地方用力,这就是动力作用点。
动力作用点到支点的距离就是动力臂。
而石头对木棍的压力就是阻力,阻力作用点到支点的距离就是阻力臂。
咱们再想想跷跷板,小朋友们在跷跷板上一上一下玩得可开心了。
其实跷跷板就是一个典型的杠杆。
体重重的小朋友坐在离支点近的地方,体重轻的小朋友坐在离支点远的地方,这样就能保持平衡,一起快乐玩耍。
还有开瓶器,也是利用了杠杆定理。
你握住开瓶器的手柄,用力一撬,瓶盖就开了。
手柄那部分就是动力臂,长一些,这样用较小的力就能轻松打开瓶盖。
在建筑工地上,起重机长长的起重臂也是杠杆的应用。
通过调整起重臂的长度和吊起货物的位置,就能用相对较小的力吊起很重的建筑材料。
回到学习中,理解和运用杠杆定理的公式可不简单。
做题的时候,得先搞清楚哪个是动力,哪个是阻力,再找准对应的力臂。
有时候题目里的条件不会直接告诉你,还得自己去分析、去计算。
比如说有这样一道题:有一个杠杆,动力是50 牛,动力臂是2 米,阻力臂是 1 米,求阻力是多少?这时候就可以直接套用公式啦,50×2= F2×1,算出来阻力就是 100 牛。
在实际生活里,我们也能根据杠杆定理来解决问题。
像家里的门,门轴就是支点。
当你推门或者拉门的时候,用的力和力臂的关系就符合杠杆定理。
简单机械杠杆杠杆示意图(最全版)PTT文档

则:动力臂 杠杆平衡——杠杆处于静止状态或匀速转动状态
杠杆平衡——杠杆处于静止状态或匀速转动状态
阻力臂。
§14.1 杠杆
一、杠杆(辨认杠杆、画杠杆的力臂)
1.定义:在力的作用下能饶固定点转动的硬棒叫做杠杆。
2.杠杆的七要素: 三点: 支点、动力作用点、阻力作用点 二力: 动力、阻力 二臂: 动力臂、阻力臂
二、杠杆的平衡条件(简单计算)
1.条件: 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂
2.表达式:F1L1= F2L2
或
F1 = L2 F2 L1
感谢观看
表达式: F1L1= F2L2
或
F1 = L2 F2 L1
应用
省力杠杆,即动力<阻力, 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂
省力杠杆,即动力<阻力, 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂
费力杠杆,即动力>阻力,
二、杠杆的平衡条件(简单计算)
则:动力臂 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂
费力杠杆,即动力>阻力,
杠杆的七要素 支点、动力、动力作用点、阻力、阻力作用点、动力臂、阻力臂
A
F1
O
L2
L1
B
F2
杠杆示意图
杠杆平衡——杠杆处于静止状态或匀速转动状态
L1
O
L2
F1
F2
研究杠杆的平衡条件
每个钩码重力N,每格长.
实验
次数
F1/N
L1/m
1
2
3
Байду номын сангаас
F2/N
L2/m
结论:动力 ╳ 动力臂 = 阻力 ╳ 阻力臂
定义:在力的作用下能饶固定点转动的硬棒叫做杠杆。 杠杆平衡——杠杆处于静止状态或匀速转动状态 一、杠杆(辨认杠杆、画杠杆的力臂) 杠杆平衡——杠杆处于静止状态或匀速转动状态 二、杠杆的平衡条件(简单计算) 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂 费力杠杆,即动力>阻力, 三点: 支点、动力作用点、阻力作用点 二、杠杆的平衡条件(简单计算) 省力杠杆,即动力<阻力, 支点、动力、动力作用点、阻力、阻力作用点、动力臂、阻力臂 条件: 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂 条件: 动力 ╳ 动力臂 = 阻力 ╳ 阻力臂 二、杠杆的平衡条件(简单计算) 省力杠杆,即动力<阻力,
杠杆的简单计算
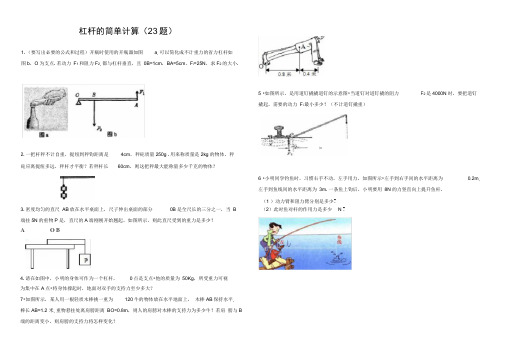
1.(要写出必要的公式和过程)开瓶时使用的开瓶器如图a ,可以简化成不计重力的省力杠杆如图b ,O 为支点.若动力 F 1和阻力F 2,都与杠杆垂直,且 0B=1cm ,BA=5cm ,F i =25N ,求F 2 的大小.6 •小明同学钓鱼时,习惯右手不动,左手用力,如图所示•左手到右手间的水平距离为 0.2m ,左手到鱼线间的水平距离为 3m .一条鱼上钩后,小明要用 8N 的力竖直向上提升鱼杆.(1 )动力臂和阻力臂分别是多少?3.密度均匀的直尺 AB 放在水平桌面上,尺子伸出桌面的部分0B 是全尺长的三分之一,当 B端挂5N 的重物P 是,直尺的A 端刚刚开始翘起,如图所示,则此直尺受到的重力是多少?A O B4.请在如图中,小明的身体可作为一个杠杆, 0点是支点•他的质量为 50Kg ,所受重力可视为集中在A 点•将身体撑起时,地面对双手的支持力至少多大? 7•如图所示,某人用一根轻质木棒挑一重为120牛的物体放在水平地面上, 木棒AB 保持水平,棒长AB=1.2 米,重物悬挂处离肩膀距离 BO=0.8m ,则人的肩膀对木棒的支持力为多少牛?若肩 膀与B 端的距离变小,则肩膀的支持力将怎样变化?杠杆的简单计算(23题)5 •如图所示,是用道钉撬撬道钉的示意图•当道钉对道钉撬的阻力 撬起,需要的动力 F i 最小多少?(不计道钉撬重)F 2是4000N 时,要把道钉2.一把杆秤不计自重,提纽到秤钩距离是 4cm ,秤砣质量250g .用来称质量是2kg 的物体,秤 砣应离提纽多远,秤杆才平衡?若秤杆长60cm ,则这把秤最大能称量多少千克的物体?~ in(2)此时鱼对杆的作用力是多少 N ?8.如图是锅炉安全阀示意图. OA=20厘米,AB=40厘米,若锅炉在阀上产生的竖直向上的压力为30牛,在B处应挂多重的物体G ?11. (10分)如图所示,一段粗细不均匀的木头放在地面上,用弹簧测力计竖直向上拉起细端时弹簧测力计示数为F1,而竖直向上拉起粗端时弹簧测力计的示数为F2,则此木头的重力G是多少?F1和F2哪个大?9. 如图,0为杠杆AB的支点,OA : 0B=2 : 3,物块甲和物块乙分别挂在杠杆的A、B两端, 杠杆平衡,已知物块甲、物块乙的体积之比是 2 : 1,物块甲的密度p甲=6X103kg/m3,物块乙的密度p乙是多少.12 .如图所示,灯重30 N,灯挂在水平横杆的C端,0为杠杆的支点,水平杆0C长2 m,杆重不计,BC长0.5 m,绳子BD作用在横杆上的拉力是多少?(已知:/ DBO=30 °10. 塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是塔吊”的简化图.OB是竖直支架, ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在0、D之间移动.已知OE=10m, OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1.5 X03Kg,则:(1 )配重体的质量应为多少Kg ?(2)当滑轮移到D点时能够安全起吊重物的最大质量是多少Kg ?(不计水平臂”和滑轮重力)13 •希腊科学家阿基米德发现杠杆原理后,发岀了给我支点,我可以撬动地球”的豪言壮语•假如阿基米德在杠杆的一端施加600N的力,要搬动质量为 6.0X1024kg的地球,那么长臂的长应是短臂长的多少倍?如果要把地球撬起1cm,长臂的一端要按下多长距离?假如我们以光速向下按,要按多少年?(做完该题,你有何启示?)14.小华用一根长6米、半径7.5厘米的均匀粗木棒为爸爸设计了一架能搬运柴草的简易起重机(如图所示).他把支架安在木棒的一长处,每捆柴草重1000牛,为了使木棒平衡以达到省力的4目的,他又在另一端吊一块配重的石头,请你算岀这块配重的石头应有多重?(木棒密度0.8X103千克/米3, g取10牛顿/千克.)15•如图所示,OB为一轻质杠杆,可绕O点作自由转动,在杠杆A点和B点分别作用两个力F1和F2 (F2未画出)时,恰能使杠杆在水平位置上平衡,已知OA=1cm,OB=3cm .(1 )若F1=18N,方向竖直向下,则F2的最小值是多大?(2)若F1减小为9N,不改变(1 )中F2的作用点和最小值的大小,只改变F2的方向,要使杠杆仍在水平位置平衡,则L2为多大?并在图中画出F2的方向.(2种情况)16. 如图所示,要将重为G=500N,半径为r=0.5m的轮子滚上高为h=20cm的台阶,(支点为轮子与台阶的接触点O),试在图中作出阻力G的力臂L,并在图中作出所用的最小力F的示意图•这个最小力F= _ _ N,并且至少需要做W= _ _ J的功,才能将轮子滚上台阶.17. (2008?郴州)如图所示,质量为8kg,边长为5cm的正方体物块A置于水平地面上,通过细绳系于轻质杠杆BOC的B端,杠杆可绕O点转动,且CO=3BO,在C端用F=10N的力竖直向下拉杠杆,使杠杆在水平位置平衡,且细绳被拉直. (细绳重量不计,g取10N/kg )求:(1)物体A的重力G1.(2)B端细绳的拉力F拉;(3)物体A对地面的压力F压;(4)物体A对地面的压强P.18 . (2005?海淀区)假期里,小兰和爸爸、妈妈一起参加了一个家庭游戏活动•活动要求是:家庭成员中的任意两名成员分别站在如图所示的木板上,恰好使木板水平平衡.(1)若小兰和爸爸的体重分别为400N和800N,小兰站在距离中央支点2m的一侧,爸爸应站在距离支点多远处才能使木板水平平衡?(2)若小兰和爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,小兰的速度是0.5m/s,爸爸的速度是多大才能使木板水平平衡不被破坏?19 .如图所示,独轮车和车内的煤的总质量为90kg,可视为作用于A点.车轴为支点,将车把抬起时,作用在车把向上的力为多少?*22 . (25分)如图所示是锅炉上保险装置的示意图, 0为一可绕0点旋转的横杆(质量不计),在横杆上的B 点下方连接着阀门 S,阀门的底面积为3cm 2, OB 长度为20cm ,横杆上A 点处挂 着重物G ,OA 长度为60cm •对水加热时,随着水温升高,水面上方气体压强增大•当压强增 大到一定值时,阀门 S 被顶开,使锅炉内气体压强减小,使锅炉内的蒸气压强减小•若要保持 锅炉内、外气体的压强差为1 X 105Pa ,试求挂在A 点处的重物G 为多少N ?20.有一根1.5m 长的杠杆,左端挂 300N 的物体,右端挂500N 的物体,若不计杠杆重力,要 使杠杆平衡,支点应在什么位置?如果两端各加 100N 的重物,支点应向哪端移动?移动多少?*21.( 25分)如图1, 一根长为20cm ,横截面积为10cm 2的均匀木杆用细线和弹簧测力计竖直 悬挂起立,置于烧杯内水平面上方•现将烧杯竖直缓缓提升,木杆逐渐浸入水中,已知木杆的 密度为p =0.8X103kg/m 3,水的密度为 p =1.0 X 103kg/m 3(1) 当弹簧测力计读数为1.2N 时,求木杆浸入水中的长度.(2) 继续缓慢提升烧杯,当木杆浸入水中一定深度时,开始出现倾斜,当木杆再次静止时,木 杆与竖直方向成30。
初三物理期中十大考点之杠杆滑轮

初三物理期中十大必考考点之杠杆、滑轮【1.考点和知识点回顾】1.杠杆分类:生活中省力、费力、等臂杠杆生活实例2.杠杆作图:(常规五要素、最小力问题,力的方向问题):常规作图注意垂直符号,最小力核心找最大力臂,动力和阻力方向应使杠杆转动方向相反。
3.杠杆简单计算:先找五要素(尤其是支点),列平衡条件,计算(注意单位换算)4.滑轮组计算(力,功,功率,机械效率等):力——受力分析;功——找力和力移动的距离;功率——找力和速度(或功和时间);机械效率——通用:η=G物/nF×100%;不计绳重和摩擦:η=G物/(G物+G动)×100%5.滑轮组绕线:限定力的方向(反画)或绳子股数n(奇动偶定)6.滑轮概念:滑轮的作用,本质和特点等。
【2.典型例题】1.杠杆分类:例题1.如图所示的生活用具中,使用时属于省力杠杆的是()A.钢丝钳剪铁钉B.食品夹子夹食品C.钓鱼竿钓鱼D.筷子夹菜例题2.在生产生活中,利用如图所示的简单机械时,一定省距离的是()A.扫帚B.斜面C.滑轮组D.羊角锤2.杠杆作图例题3.按要求作图:如图所示,一轻质杠杆在力F1、F2的作用下处于静止状态,L1是力F1的力臂,请在图中画出F2的力臂ι2和力F1的示意图。
例题4.如图,在杠杆AB上挂了一个重为G的物体。
为使杠杆在图中的位置静止。
请在杠杆上画出最小的动力F和它的方向。
3.杠杆简单计算例题5.如图,AB为能绕B点转动的均质杠杆(杠杆自重忽略不计),中点C处用细线悬挂一重物,在A端施加一个竖直向上大小为10N的拉力F,使杠杆在水平位置保持平衡,则物重G= N.若保持拉力竖直方向不变,将A端缓慢向上提升一小段距离,在提升的过程中,拉力F将(选填“增大”“不变”或“减小”)。
例题6.使用简单机械可以给人们的生活带来便利。
(1)如图甲,旗杆的顶端安装着一个滑轮,用来改变拉力的方向。
(2)如图乙,把被剪物体尽量靠近剪刀的转动轴,可减小臂,剪断物体更省力。
利用杠杆的力矩原理

利用杠杆的力矩原理杠杆是一种简单但非常有效的机械工具,它基于力矩原理实现了在实际生活中众多工作的便利。
通过适当的使用杠杆,我们可以改变力的作用方向和大小,从而提高工作效率,并减轻人力负担。
本文将介绍杠杆的力矩原理及其应用,以及它在各个领域中的重要性。
一、什么是杠杆杠杆是一个具有支点的刚性物体,它可以使我们在施加力时得到更大的作用力。
杠杆的作用原理是力矩平衡。
力矩是一个物体对于支点的转动效果的度量。
根据力矩平衡定律,当一个物体在支点处平衡时,对于静止的物体,所有作用于该物体的力矩之和等于零。
二、杠杆的原理杠杆的原理是基于力矩平衡的。
在杠杆系统中,有三个关键要素:力(F)、支点(P)和物体(O)。
力是施加在杠杆上的作用力,支点是杠杆的固定点,物体是杠杆上的负荷。
根据力矩平衡定律,力矩可以通过以下公式计算:力矩(M)= 力(F) ×力臂(r)其中,力臂是力作用线与支点的垂直距离。
当一个系统处于力矩平衡时,得出以下公式:F1 × r1 = F2 × r2其中,F1和F2分别是力1和力2的大小,r1和r2分别是力1和力2的力臂。
根据这个原理,我们可以利用不同的力臂和力的组合,以及改变力的大小,从而实现不同的工作目标和要求。
三、杠杆的应用1. 门锁门锁可以看作是一种杠杆,当我们使用钥匙旋转锁芯时,通过杠杆的力矩作用,使得门锁打开或关闭。
这种机械原理及应用在我们的日常生活中非常常见。
2. 起重机起重机是利用杠杆原理设计和构建的重要工程机械。
通过调整起重机的杠杆臂和使用不同的重物配重,起重机可以轻松地提起和放下重物,大大减轻了人力负担。
3. 梯子梯子的原理也是基于杠杆的力矩原理。
当我们使用梯子爬上高处时,梯子的支点是我们的手或脚,而杠杆臂是梯子的长度。
通过合理地使用力和力臂,我们可以保持平衡,并顺利地爬上梯子。
4. 剪刀剪刀是一种常见的工具,也是杠杆原理的应用之一。
通过剪刀的双支点和双刀片的力矩平衡,我们可以轻松地切割纸张、布料等材料。
杠杆原理公式

杠杆原理公式引言杠杆原理是一种简单而又重要的物理原理,广泛应用于工程、机械、金融等领域。
通过杠杆原理,人们可以在运用很小的力量或者输入较小的能量时,实现较大的输出效果。
本文将详细介绍杠杆原理的基本概念、公式及其应用。
一、杠杆的定义和基本原理杠杆是一种刚性物体,通常为杆状,支点称为杠杆的转动中心。
在杠杆上施加力可以改变物体的平衡或者运动状态。
杠杆的基本原理是基于力的平衡和力矩的原理。
杠杆原理的基本公式是力矩平衡公式,即\[ M_{1} = M_{2} \]其中,\(M_{1}\)表示施加在第一个力点上的力矩,\(M_{2}\)表示施加在第二个力点上的力矩。
当杠杆达到平衡状态时,这两个力矩相等。
二、杠杆原理公式根据杠杆原理,可以得到一些重要的公式。
以下是一些常用的杠杆原理公式:1. 杠杆力的平衡公式设杠杆的两个力点之间的距离为\(L\),分别施加在这两个力点上的力分别为\(F_{1}\)和\(F_{2}\),根据杠杆原理,有:\[ F_{1} \cdot L_{1} = F_{2} \cdot L_{2} \]此公式意味着通过改变力的大小或者力点的位置,可以实现力的平衡,从而实现较大的输出效果。
2. 杠杆力比例公式设杠杆的两个力点之间的距离为\(L\),分别施加在这两个力点上的力分别为\(F_{1}\)和\(F_{2}\),如果\(L_{1} > L_{2}\),则有:\[ \frac{F_{1}}{F_{2}} = \frac{L_{2}}{L_{1}} \]这个公式告诉我们,当杠杆的力点离支点越远时,所需的输入力就越小。
这也是杠杆原理能够实现较大输出效果的关键之一。
三、杠杆原理的应用杠杆原理在生活和工作中有着广泛的应用。
以下列举了一些常见的应用场景:1. 物理杠杆物理杠杆是杠杆原理应用最直观的地方之一。
根据杠杆原理,我们可以通过改变施加力的大小或者力点的位置,来实现对物体的平衡或者力的放大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杠杆的简单计算(23题)1.(要写出必要的公式和过程)开瓶时使用的开瓶器如图a,可以简化成不计重力的省力杠杆如图b,O为支点.若动力F1和阻力F2,都与杠杆垂直,且OB=1cm,BA=5cm,F1=25N,求F2的大小.2.一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g.用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm,则这把秤最大能称量多少千克的物体?3.密度均匀的直尺AB放在水平桌面上,尺子伸出桌面的部分OB是全尺长的三分之一,当B端挂5N的重物P是,直尺的A端刚刚开始翘起,如图所示,则此直尺受到的重力是多少?4.请在如图中,小明的身体可作为一个杠杆,O点是支点.他的质量为50Kg,所受重力可视为集中在A点.将身体撑起时,地面对双手的支持力至少多大?5.如图所示,是用道钉撬撬道钉的示意图.当道钉对道钉撬的阻力F2是4000N时,要把道钉撬起,需要的动力F1最小多少?(不计道钉撬重)6.小明同学钓鱼时,习惯右手不动,左手用力,如图所示.左手到右手间的水平距离为,左手到鱼线间的水平距离为3m.一条鱼上钩后,小明要用8N的力竖直向上提升鱼杆.(1)动力臂和阻力臂分别是多少?(2)此时鱼对杆的作用力是多少N?7.如图所示,某人用一根轻质木棒挑一重为120牛的物体放在水平地面上,木棒AB保持水平,棒长AB=米,重物悬挂处离肩膀距离BO=,则人的肩膀对木棒的支持力为多少牛?若肩膀与B端的距离变小,则肩膀的支持力将怎样变化?8.如图是锅炉安全阀示意图.OA=20厘米,AB=40厘米,若锅炉在阀上产生的竖直向上的压力为30牛,在B处应挂多重的物体G?9.如图,O为杠杆AB的支点,OA:OB=2:3,物块甲和物块乙分别挂在杠杆的A、B两端,杠杆平衡,已知物块甲、物块乙的体积之比是2:1,物块甲的密度ρ甲=6×103kg/m3,物块乙的密度ρ乙是多少.10.“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是×103Kg,则:(1)配重体的质量应为多少Kg?(2)当滑轮移到D点时能够安全起吊重物的最大质量是多少Kg?(不计“水平臂”和滑轮重力)11.(10分)如图所示,一段粗细不均匀的木头放在地面上,用弹簧测力计竖直向上拉起细端时弹簧测力计示数为F1,而竖直向上拉起粗端时弹簧测力计的示数为F2,则此木头的重力G是多少?F1和F2哪个大?12.如图所示,灯重30 N,灯挂在水平横杆的C端,O为杠杆的支点,水平杆OC长2 m,杆重不计,BC长 m,绳子BD作用在横杆上的拉力是多少?(已知:∠DBO=30°)13.希腊科学家阿基米德发现杠杆原理后,发出了“给我支点,我可以撬动地球”的豪言壮语.假如阿基米德在杠杆的一端施加600N的力,要搬动质量为×1024kg的地球,那么长臂的长应是短臂长的多少倍?如果要把地球撬起1cm,长臂的一端要按下多长距离?假如我们以光速向下按,要按多少年?(做完该题,你有何启示?)14.小华用一根长6米、半径厘米的均匀粗木棒为爸爸设计了一架能搬运柴草的简易起重机(如图所示).他把支架安在木棒的长处,每捆柴草重1000牛,为了使木棒平衡以达到省力的目的,他又在另一端吊一块配重的石头,请你算出这块配重的石头应有多重?(木棒密度×103千克/米3,g取10牛顿/千克.)15.如图所示,OB为一轻质杠杆,可绕O点作自由转动,在杠杆A点和B点分别作用两个力F1和F2(F2未画出)时,恰能使杠杆在水平位置上平衡,已知OA=1cm,OB=3cm.(1)若F1=18N,方向竖直向下,则F2的最小值是多大?(2)若F1减小为9N,不改变(1)中F2的作用点和最小值的大小,只改变F2的方向,要使杠杆仍在水平位置平衡,则L2为多大?并在图中画出F2的方向.(2种情况)16.如图所示,要将重为G=500N,半径为r=的轮子滚上高为h=20cm的台阶,(支点为轮子与台阶的接触点O),试在图中作出阻力G的力臂L,并在图中作出所用的最小力F的示意图.这个最小力F= _________ N,并且至少需要做W= _________ J的功,才能将轮子滚上台阶.17.(2008•郴州)如图所示,质量为8kg,边长为5cm的正方体物块A置于水平地面上,通过细绳系于轻质杠杆BOC的B端,杠杆可绕O点转动,且CO=3BO,在C端用F=10N的力竖直向下拉杠杆,使杠杆在水平位置平衡,且细绳被拉直.(细绳重量不计,g取10N/kg)求:(1)物体A的重力G1.(2)B端细绳的拉力F拉;(3)物体A对地面的压力F压;(4)物体A对地面的压强P.18.(2005•海淀区)假期里,小兰和爸爸、妈妈一起参加了一个家庭游戏活动.活动要求是:家庭成员中的任意两名成员分别站在如图所示的木板上,恰好使木板水平平衡.(1)若小兰和爸爸的体重分别为400N和800N,小兰站在距离中央支点2m的一侧,爸爸应站在距离支点多远处才能使木板水平平衡?(2)若小兰和爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,小兰的速度是s,爸爸的速度是多大才能使木板水平平衡不被破坏?19.如图所示,独轮车和车内的煤的总质量为90kg,可视为作用于A点.车轴为支点,将车把抬起时,作用在车把向上的力为多少?20.有一根长的杠杆,左端挂300N的物体,右端挂500N的物体,若不计杠杆重力,要使杠杆平衡,支点应在什么位置?如果两端各加100N的重物,支点应向哪端移动?移动多少?*21.(25分)如图1,一根长为20cm,横截面积为10cm2的均匀木杆用细线和弹簧测力计竖直悬挂起立,置于烧杯内水平面上方.现将烧杯竖直缓缓提升,木杆逐渐浸入水中,已知木杆的密度为ρ1=×103kg/m3,水的密度为ρ0=×103kg/m3(1)当弹簧测力计读数为时,求木杆浸入水中的长度.(2)继续缓慢提升烧杯,当木杆浸入水中一定深度时,开始出现倾斜,当木杆再次静止时,木杆与竖直方向成30°角,如图2所示,求木杆浸入水中的长度.(忽略木杆横截面积的影响)*22.(25分)如图所示是锅炉上保险装置的示意图,0为一可绕0点旋转的横杆(质量不计),在横杆上的B点下方连接着阀门S,阀门的底面积为3cm2,OB长度为20cm,横杆上A点处挂着重物G,OA长度为60cm.对水加热时,随着水温升高,水面上方气体压强增大.当压强增大到一定值时,阀门S被顶开,使锅炉内气体压强减小,使锅炉内的蒸气压强减小.若要保持锅炉内、外气体的压强差为1×105Pa,试求挂在A点处的重物G为多少N?*23.(25分)某工地在冬季水利建设中设计了一个提起重物的机械,其中的一部分结构如图所示.OA是一个均匀钢管,每米长所受重力为30N;O是转动轴;重物的质量m为150㎏,挂在B 处,OB=1m;拉力F作用在A点,竖直向上.为维持平衡,钢管OA为多长时所用的拉力最小?这个最小拉力是多少?(g取10N/kg)24.如图甲所示为塔式起重机简易示意图,塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装。
(动滑轮重、绳重及摩擦不计,g取10 N/kg)甲乙(1)为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越。
(2)图乙为起重机钢丝绳穿绳简化示意图,定滑轮a的作用是。
若钢丝绳能承受的最大拉力为3×104N,则能吊起货物的质量不能超过多少?(3)若将重为×104N的货物由地面沿竖直方向匀速提升30 m,再沿水平方向移动20 m,则此过程中克服货物重力做多少功?25.如图所示是一种起重机的示意图,起重机重×104N(包括悬臂),重心为P1。
为使起重机起吊重物时不致倾倒,在其右侧配有重M(重心为P2)。
现测得AB为10 m,BO为1 m,BC为4 m,CD为m。
(g取10 N/kg)(1)若该起重机将重物吊升6 m,用时50 s,则重物上升的平均速度是多少?(2)现在水平地面上有重为×104N的货箱,它与地面的接触面积是3 m2。
①若起重机不加配重,在起吊货箱时,最大可使货箱对地面的压强减少多少?②若要吊起此货箱,起重机至少需加多少牛的配重?(3)有人认为起重机的配重越重越好,这样就能吊起更重的重物。
这起重机能配8 t的配重吗?请说明理由。
26.图甲是《天工开物》中记载的三千多年前在井上汲水的桔槔,其示意图如图乙。
轻质杠杆的支点O 距左端l 1= m,距右端l 2= m 。
在杠杆左端悬挂质量为2 kg 的物体A ,右端挂边长为 m 的正方体B ,杠杆在水平位置平衡时,正方体B 对地面的压力为20 N 。
求:(1)此时杠杆左端所受拉力大小为多少牛顿? (2)正方体B 的密度为多少千克每立方米?(3)若该处为松软的泥地,能承受的最大压强为4×103Pa,为使杠杆仍在水平位置平衡,物体A 的重力至少为多少牛顿?杠杆的简单计算参考答案与试题解析一.解答题(共23小题) 1.(要写出必要的公式和过程)开瓶时使用的开瓶器如图a ,可以简化成不计重力的省力杠杆如图b ,O 为支点.若动力F 1和阻力F 2,都与杠杆垂直,且OB=1cm ,BA=5cm ,F 1=25N ,求F 2的大小.考点: 杠杆的平衡分析法及其应用。
专题: 应用题。
分析: 找出力臂,利用杠杆平衡条件F 1L 1=F 2L 2求F 2 解答: 解:L OA =L OB +L BA =1cm+5cm=6cm ∵F 1L OA =F 2L OB 求∴ 答:F 2的大小为150N点评: 找出两个力臂是关键,利用杠杆平衡条件求解. 2.一把杆秤不计自重,提纽到秤钩距离是4cm ,秤砣质量250g .用来称质量是2kg 的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm ,则这把秤最大能称量多少千克的物体? 考点: 杠杆的平衡分析法及其应用。
专题: 计算题。
分析: 根据杠杆的平衡条件:动力×动力臂=阻力×阻力臂,以O 点为支点,分别找到力与力臂,两次用平衡条件解出答案. 解答: 解:由F 1L 1=F 2L 2, (1)2kg×g×4cm=×g×L 2解得:L 2=32cm故答案为:秤砣应离提纽32cm . (2)M×g×4cm=×g×56cm 解得:M=.答:这把秤最大能称量的物体.点评: 杠杆的平衡条件是初中物理的重要内容,判断准各力对应的力臂是解对这类题的关3.密度均匀的直尺AB 放在水平桌面上,尺子伸出桌面的部分OB 是全尺长的三分之一,当B 端挂5N 的重物P 是,直尺的A 端刚刚开始翘起,如图所示,则此直尺受到的重力是多少?考点: 杠杆的平衡分析法及其应用。
