第4章 平面与平面系统 《应用光学》课件
合集下载
《应用光学第四章》PPT课件

(c) 别汉棱镜
图〔c〕为别汉棱镜,由于在这种棱镜内光轴转折5次,故在棱镜中 可以折叠很长一局部光路,可用于长焦物镜的转像
双像棱镜
z y
由四块棱镜胶合而成,其 中棱镜Ⅱ和 III的反射面
A1 A2
o
x
镀半透半反的析光膜。当
III
物点A不在光轴上时,那
么双像棱镜输出二个像点
A 1和A 2;而当物点 A移向光轴O时,双像棱
聚于焦点F上
假设M转动 角,那么反射光与光轴成2 角,经物镜L后成像于B
点,设BF = y,物镜焦距为f ,那么
y f tg 2 2 f
又tg
x / a ,上式可写y为 (2 f / a) x K x
K为光学杠杆的放大倍数
B
L
y
2
F a
f
x
4.2双平面镜系统
1.双平面镜成像 由△O1O2M,有
平面反射镜的成像原理
反射镜对虚物成实像
〔3〕镜像:由于对称性,一右手坐标系的物体,其像为左手坐标系。就像照镜 子时,你的右手只能和镜中的“你〞的左手重合一样,这种像称为镜像正对看 (沿zo/z o 看):y在x左,y 在x 右;
x
x z
O y
O
P
z
y
M
平面镜的镜像
(4〕物体旋转时,其像反方向旋转一样的角度 沿zo/z o 看: y顺时针方向转90 至 x y 逆时针方向转90 至 x 正对xo/x o 看: z顺时针方向转90 至 y,z 逆时针方向转90 至 y
平面镜成像的特点 用矢量形式表示反射镜的反射 单平面镜摆动引起光线方向旋转 平面镜在光路计算中的作用
4.2 双平面镜系统
4.2.1 4.2.2 4.2.3 4.2.4
应用光学课件-PPT

4)若视阑为长方形或正方形,其线视场按对角线计算。
5)入射窗、出射窗、视阑之间得相互共轭关系。
大家应该也有点累了,稍作休息
大家有疑问得,可以询问与交流
10
例:有一光学系统,透镜O1、O2得口径D1=D2=50mm,焦距 f1′= f2′=150mm,两透镜间隔为300mm,并在中间置一光 孔O3,口径D3=20mm,透镜O2右侧150mm处再置一光孔O4,口 径D4=40mm,平面物体处于透镜O1左侧150mm处。求该系统 得孔径光阑、入瞳、出瞳、视场光阑、入窗、出窗得位 置与大小。
两正薄透镜组L1与L2得焦距分别为100mm与50mm,通光口径 分别为60mm与30mm,两透镜之间得间隔为50mm,在透镜L2之 前30mm处放置直径为40mm得光阑,问 1)当物体在无穷远处时,孔径光阑为哪个? 2)当物体在L1前方300mm处时,孔径光阑为哪个?
4、说明: 1)物体位置改变,原孔阑可能失去控制轴上点孔径角得作用,要重复上述 三个步骤确定孔阑。
工具显微镜中(β 准确)被测物得像与刻度尺相比较,可测物之长度。
物体不论处于何位 置,发出得主光线 都不随物体位置得 移动而变化;读出 刻尺面上光斑得中 心示值,即可求出 准确得象高。
三、 象方远心光路
1、 概念: 某些大地测量仪器或投影仪器中,为了消除像平面与标尺分划刻
线面不重合而引起得测量误差,在物镜得物方焦平面上加入一个光 阑作为孔径光阑,出瞳则位于像方无穷远,称为“像方远心光路”。 2、 应用:
3)物点在无限远时,各光孔像中,直径最小者即为入瞳。入瞳对应得实际 光孔即为孔径光阑。
例:有两个薄透镜L1与L2 ,焦距分别为90mm与30mm,孔径分 别为60mm与40mm,相隔50mm,在两透镜之间,离L2为 20mm处放置一直径为10mm得圆光阑,试对L1前120mm处 得轴上物点求孔阑、入瞳、出瞳得位置与大小。
5)入射窗、出射窗、视阑之间得相互共轭关系。
大家应该也有点累了,稍作休息
大家有疑问得,可以询问与交流
10
例:有一光学系统,透镜O1、O2得口径D1=D2=50mm,焦距 f1′= f2′=150mm,两透镜间隔为300mm,并在中间置一光 孔O3,口径D3=20mm,透镜O2右侧150mm处再置一光孔O4,口 径D4=40mm,平面物体处于透镜O1左侧150mm处。求该系统 得孔径光阑、入瞳、出瞳、视场光阑、入窗、出窗得位 置与大小。
两正薄透镜组L1与L2得焦距分别为100mm与50mm,通光口径 分别为60mm与30mm,两透镜之间得间隔为50mm,在透镜L2之 前30mm处放置直径为40mm得光阑,问 1)当物体在无穷远处时,孔径光阑为哪个? 2)当物体在L1前方300mm处时,孔径光阑为哪个?
4、说明: 1)物体位置改变,原孔阑可能失去控制轴上点孔径角得作用,要重复上述 三个步骤确定孔阑。
工具显微镜中(β 准确)被测物得像与刻度尺相比较,可测物之长度。
物体不论处于何位 置,发出得主光线 都不随物体位置得 移动而变化;读出 刻尺面上光斑得中 心示值,即可求出 准确得象高。
三、 象方远心光路
1、 概念: 某些大地测量仪器或投影仪器中,为了消除像平面与标尺分划刻
线面不重合而引起得测量误差,在物镜得物方焦平面上加入一个光 阑作为孔径光阑,出瞳则位于像方无穷远,称为“像方远心光路”。 2、 应用:
3)物点在无限远时,各光孔像中,直径最小者即为入瞳。入瞳对应得实际 光孔即为孔径光阑。
例:有两个薄透镜L1与L2 ,焦距分别为90mm与30mm,孔径分 别为60mm与40mm,相隔50mm,在两透镜之间,离L2为 20mm处放置一直径为10mm得圆光阑,试对L1前120mm处 得轴上物点求孔阑、入瞳、出瞳得位置与大小。
华中科技大学 《应用光学》课程PPT——第四章 平面镜与平面系统
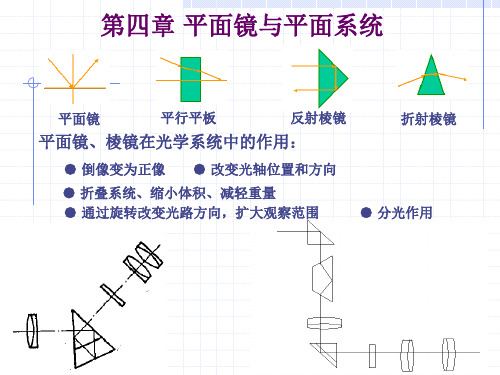
第四章 平面镜与平面系统
平面镜
平行平板
反射棱镜
折射棱镜
平面镜、棱镜在光学系统中的作用:
● 倒像变为正像 ● 改变光轴位置和方向 ● 分光作用 ● 折叠系统、缩小体积、减轻重量 ● 通过旋转改变光路方向,扩大观察范围
§ 4-1 平面镜成像特性
1. 成完善像: 物点发出的同心光束经反 射镜反射后仍成同心光束。
3)表示方法:
规定:物为左手坐标系,oz轴为光轴方向,yoz面和主截面重合, ox轴垂直于主截面,并和所有的反射面平行,通过棱镜组后的坐 标为x′y′z′ 。 原则:①光轴方向 z' 不变 ②垂直于主截面的坐标 x' 视屋脊个数而 定 ③ y‘ 坐标根据总反射次数而定, (一个屋 脊棱算两次反射)而定。奇数次反射,改 变坐标系,偶数次反射坐标系不变。
作业:
4.1,4.2,4.6,4.7,4.10,4.11,4.12
1)光线经平行板折射后,虽然方向不变,但要产生位移。 2)从点A发出的具有不同入射角的各条光线经平行板折射后,具有 不同的轴向位移值,平行板成象是不完善的。
3. 近轴光成像:
sin I1 cos I1 sin I1 1 tgI1 lim I1 0 tgI sin I1 cos I1 sin I1 n 1
2
4
6
A4
8
A5
波长一般以nm为单位。
二、玻璃的选择: 1、可用性 2、透射性 3、双折射性 4、化学稳定性 5、热特性
三、塑料光学材料: 优点:较低的质量、较高的抗冲击性,能提供更多 的形状,可塑造非球面透镜和其他复杂的形状。 缺点:较低的耐温性、耐磨性,抗化学性较差,镀 膜的附着性低,膜层的耐用性也低。
平面镜
平行平板
反射棱镜
折射棱镜
平面镜、棱镜在光学系统中的作用:
● 倒像变为正像 ● 改变光轴位置和方向 ● 分光作用 ● 折叠系统、缩小体积、减轻重量 ● 通过旋转改变光路方向,扩大观察范围
§ 4-1 平面镜成像特性
1. 成完善像: 物点发出的同心光束经反 射镜反射后仍成同心光束。
3)表示方法:
规定:物为左手坐标系,oz轴为光轴方向,yoz面和主截面重合, ox轴垂直于主截面,并和所有的反射面平行,通过棱镜组后的坐 标为x′y′z′ 。 原则:①光轴方向 z' 不变 ②垂直于主截面的坐标 x' 视屋脊个数而 定 ③ y‘ 坐标根据总反射次数而定, (一个屋 脊棱算两次反射)而定。奇数次反射,改 变坐标系,偶数次反射坐标系不变。
作业:
4.1,4.2,4.6,4.7,4.10,4.11,4.12
1)光线经平行板折射后,虽然方向不变,但要产生位移。 2)从点A发出的具有不同入射角的各条光线经平行板折射后,具有 不同的轴向位移值,平行板成象是不完善的。
3. 近轴光成像:
sin I1 cos I1 sin I1 1 tgI1 lim I1 0 tgI sin I1 cos I1 sin I1 n 1
2
4
6
A4
8
A5
波长一般以nm为单位。
二、玻璃的选择: 1、可用性 2、透射性 3、双折射性 4、化学稳定性 5、热特性
三、塑料光学材料: 优点:较低的质量、较高的抗冲击性,能提供更多 的形状,可塑造非球面透镜和其他复杂的形状。 缺点:较低的耐温性、耐磨性,抗化学性较差,镀 膜的附着性低,膜层的耐用性也低。
应用光学 ppt课件

当光线遇到障碍物时会发生光的衍射现象,从而偏离光线的直线 传播。
衍射
双折射
梯度折射率
2.2 光的独立传播定律
在光相交的区域可能发生叠加,甚至发生干涉。不管是哪一种情 况,在光离开相交区域后,光波继续沿着既定的方向向前传播,该 光波身上找不到其他光波对其产生的任何影响,此现象称为光的独 立传播定律。
1.1.2 电磁波谱
400~760nm
380~760nm 390~780nm
1nm 103 μm 106 mm 109 m
1.1.2 电磁波谱
在电磁波谱里,可见光大约在380~760nm之间,按波长从长到 短依次分别呈现红、橙、黄、绿、蓝、靛、紫等七种颜色。这七种 色光其实分界并不完全准确,因为两种色光之间的界限本身就不明 显,过渡是一种渐进的过程。
色光 红 橙 黄 绿
范围/nm 640-760 600-640 550-600 480-550
色光 蓝 靛 紫
范围/nm 450-480 430-450 380-430
1.1.3 可见光
可见光(Visible light)是波 长大约在380~760nm之间的波 段范围,由于人眼对此波段的 光线敏感,可以引起视网膜的 感光,传递到大脑后,经过大 脑处理后可以分辨出光线的颜 色及与光线相关的物体。
则光的折射定律(Snell law, refraction law of light)可以表示为
1.折射光线也在入射面内; 2.入射角和折射角正弦之比为一个常数,与入射角大小无关。
sin I sin I ' n12
其中为 n12 比例常数
2.4 光的折射定律
海市蜃楼的形成
2.5 光路可逆
光的反射定律和折射定律一个直接的应用就是光路可逆。光在空 间传播时,在光学系统中行进,无外乎有三种情况:
衍射
双折射
梯度折射率
2.2 光的独立传播定律
在光相交的区域可能发生叠加,甚至发生干涉。不管是哪一种情 况,在光离开相交区域后,光波继续沿着既定的方向向前传播,该 光波身上找不到其他光波对其产生的任何影响,此现象称为光的独 立传播定律。
1.1.2 电磁波谱
400~760nm
380~760nm 390~780nm
1nm 103 μm 106 mm 109 m
1.1.2 电磁波谱
在电磁波谱里,可见光大约在380~760nm之间,按波长从长到 短依次分别呈现红、橙、黄、绿、蓝、靛、紫等七种颜色。这七种 色光其实分界并不完全准确,因为两种色光之间的界限本身就不明 显,过渡是一种渐进的过程。
色光 红 橙 黄 绿
范围/nm 640-760 600-640 550-600 480-550
色光 蓝 靛 紫
范围/nm 450-480 430-450 380-430
1.1.3 可见光
可见光(Visible light)是波 长大约在380~760nm之间的波 段范围,由于人眼对此波段的 光线敏感,可以引起视网膜的 感光,传递到大脑后,经过大 脑处理后可以分辨出光线的颜 色及与光线相关的物体。
则光的折射定律(Snell law, refraction law of light)可以表示为
1.折射光线也在入射面内; 2.入射角和折射角正弦之比为一个常数,与入射角大小无关。
sin I sin I ' n12
其中为 n12 比例常数
2.4 光的折射定律
海市蜃楼的形成
2.5 光路可逆
光的反射定律和折射定律一个直接的应用就是光路可逆。光在空 间传播时,在光学系统中行进,无外乎有三种情况:
应用光学第4章
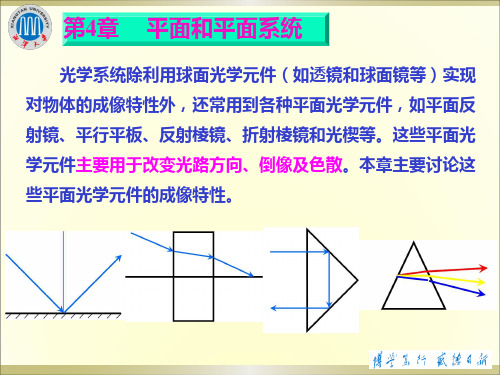
G
U2
结论2:平行平板不使物
( A2 ) A1
O1
n2 n n1
d
O2 1 n2
体放大或缩小。
光线经平行平板后方向虽然保持不变,却要 产生一定的位移,这个位移记为轴向位移ΔL′
A1F平行于GE I1 N2 EG I 2 I1 O1O2 d d ) FG FE sin(FEG) sin(N 2 EG N 2 EF ) sin(I1 I 2 ) sin(I1 I1 cos I1 cos I1 cos I1
I1
工作面 主截面
1 I 1 I 2
n
2
I2
2.偏向角的求出
sin I1 n sin I1
两式相减 n(sin I1 sin I 2 ) sin I1 sin I 2 和差化积 n sin I 2 sin I 2
sin I1 I 2 I I I I I I cos 1 2 n sin 1 2 cos 1 2 2 2 2 2
(cos cos '')i (cos cos '') j (cos cos '') k ) 2[1 (cos cos '' cos cos '' cos cos '')]
作业2.3:一玻璃球直径60mm,折射率为1.5,一束平行光 射在球上,问会聚点在什么位置?
45
最常见的是斯密特棱镜。使出射光
45
线和入射光线的夹角为45°。成 镜像,大大缩小筒长,结构紧凑。
二、 屋脊棱镜
对奇次反射的反射棱镜,为了避
U2
结论2:平行平板不使物
( A2 ) A1
O1
n2 n n1
d
O2 1 n2
体放大或缩小。
光线经平行平板后方向虽然保持不变,却要 产生一定的位移,这个位移记为轴向位移ΔL′
A1F平行于GE I1 N2 EG I 2 I1 O1O2 d d ) FG FE sin(FEG) sin(N 2 EG N 2 EF ) sin(I1 I 2 ) sin(I1 I1 cos I1 cos I1 cos I1
I1
工作面 主截面
1 I 1 I 2
n
2
I2
2.偏向角的求出
sin I1 n sin I1
两式相减 n(sin I1 sin I 2 ) sin I1 sin I 2 和差化积 n sin I 2 sin I 2
sin I1 I 2 I I I I I I cos 1 2 n sin 1 2 cos 1 2 2 2 2 2
(cos cos '')i (cos cos '') j (cos cos '') k ) 2[1 (cos cos '' cos cos '' cos cos '')]
作业2.3:一玻璃球直径60mm,折射率为1.5,一束平行光 射在球上,问会聚点在什么位置?
45
最常见的是斯密特棱镜。使出射光
45
线和入射光线的夹角为45°。成 镜像,大大缩小筒长,结构紧凑。
二、 屋脊棱镜
对奇次反射的反射棱镜,为了避
最新应用光学平面镜棱镜系统教学课件PPT教学讲义PPT

当平面镜旋转θ 角时,出射光线相对于原出射 光线将旋转2 θ 角,而且旋转的方向与镜的旋转 方向一致。
二、双平面镜的成像特性
✓θ
2θ
2θ
θ
济南大学物理学院 工程光学课件
12
证明
✓θ
β=2θ
M1
2I1 2I2
I1 I2
2
I2 I2 θ
I1
I1
M2
I1I2/2
I1I2
与入射角无关 上式恒成立
济南大学物理学院 工程光学课件
D0.33a4
(n1.516)3
D
通光口径仅有原来的1/3
D 道威棱镜
为了在一定通光口径的 条件下,减小棱镜尺寸 两个棱镜同时使用。
济南大学物理学院 工程光学课件
35
这样就组成了立方棱镜 D
D
立方棱镜的一个特点是棱镜尺寸小,通光口径大
立方棱镜的两反射面必须平行,且两反射面必须 镀膜。
立方棱镜只能工作在平行光路中
33
展开图为:
由图可求出展开长度
L AC FG D tan 600 D tan 300 4 3D
3
济南大学物理学院 工程光学课件
34
4. 立方棱镜
直角棱镜的通光口径较大,但是当采用旋转棱镜 改变光轴方向时,此时通光口径就变小了,这样 进入光学系统的光能减少,影响成像质量。
如图所示
a
由几何分析可知:
对2002年3月至2003年12 月间在我院行超声乳化人 工晶体植入手术的415例 (453眼)患者,按照民族 不同分为治疗组(维吾尔、
哈萨克族)与对照组(汉 族),治疗组共227例239 眼,对照组188例214眼。
设备及参数设置
应用光学课件完整版

由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′,则A为物点, A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
反射定律可表示为 I I ''
4. 光的折射定律
折射定律可归结为:入射光线、折射光线和投射点
的法线三者在同一平面内,入射角的正弦与折射角正弦
之比与入射角大小无关,而与两介质性质有关。对一定 波长的光线,在一定温度和压力的条件下,该比值为一
常数,等于折射光线所在介质的折射率与入射光线所在
介质折射率之比。
0 i arcsin n12 n2 2 n0
n0 =1
n0 sin i n1 cos ic n12 n22
5. 费马原理(光程极值原理)
1)光程— 光在介质中经过的几何路程l与该介质折射率n的乘积。
s=n • l
均匀介质
m层均匀介质
连续变化的非均匀介质
s=n • l=c • t
m
s
波面可分为:平面波、球面波、任意曲面波。 波面法线方向即为光传播方向。
光源
光线
波面
5. 光束— 与波面对应的法线集合。
同心光束— 波面为球面,聚于一点。 发散光束— 光线在前进方向上无相交趋势。 会聚光束— 光线在前进方向上有相交趋势。
平行光束— 波面为平面。 象散光束— 波面为曲面,不聚于一点。
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
反射定律可表示为 I I ''
4. 光的折射定律
折射定律可归结为:入射光线、折射光线和投射点
的法线三者在同一平面内,入射角的正弦与折射角正弦
之比与入射角大小无关,而与两介质性质有关。对一定 波长的光线,在一定温度和压力的条件下,该比值为一
常数,等于折射光线所在介质的折射率与入射光线所在
介质折射率之比。
0 i arcsin n12 n2 2 n0
n0 =1
n0 sin i n1 cos ic n12 n22
5. 费马原理(光程极值原理)
1)光程— 光在介质中经过的几何路程l与该介质折射率n的乘积。
s=n • l
均匀介质
m层均匀介质
连续变化的非均匀介质
s=n • l=c • t
m
s
波面可分为:平面波、球面波、任意曲面波。 波面法线方向即为光传播方向。
光源
光线
波面
5. 光束— 与波面对应的法线集合。
同心光束— 波面为球面,聚于一点。 发散光束— 光线在前进方向上无相交趋势。 会聚光束— 光线在前进方向上有相交趋势。
平行光束— 波面为平面。 象散光束— 波面为曲面,不聚于一点。
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
应用光学教学课件完整

※从上述定律可以得到光线传播的一 个重要原理—光路的可逆性原理。利 用这一原理,可以由物求像,也可以 由像求物。
• 图1-9
※光学系统 的作用之一是对物体成像,因此必须搞 清物像的基本概念和它们的关系。
※物体通过光学系统(光组)成像,光学系统(各 种光学仪器)由一系列光学零件 组成。。
※光学系统一般是轴对称的,有一条公共轴线,
全反射现象
当
一般情况下,光线射至透明介质的分界面时将发 生反射和折射现象。
光 由
由公式 n sin I n' sin I ' 可知
光
密
sin I sin I '
介 质
射
即折射光线较入射光线偏离法线
向
光
疏
sin I ' 不可能大于1,此时入射光线将不能射入
另一介质。
按照反射定律在介面上全部被反射回原介质
原点
+
-
原点
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球
心C在右为正,在左为负。
E
A
C
O +r
E
A
C
-r O
(2)物方截距L 和像方截距L’ 也以顶点O为原点,到光线
与光轴交点,向右为正,向左为负。
E
A
A’
O
C
-L
+L’
E
A
A’
O
C
-L’
-L
(3)球面间隔 d 以前一个球面的顶点为原点, 向右为正,向左为负。
(在折射系统中总为正,在反射和折反系统中才有为负的情况)
O1
O2
+d
O1
O2
• 图1-9
※光学系统 的作用之一是对物体成像,因此必须搞 清物像的基本概念和它们的关系。
※物体通过光学系统(光组)成像,光学系统(各 种光学仪器)由一系列光学零件 组成。。
※光学系统一般是轴对称的,有一条公共轴线,
全反射现象
当
一般情况下,光线射至透明介质的分界面时将发 生反射和折射现象。
光 由
由公式 n sin I n' sin I ' 可知
光
密
sin I sin I '
介 质
射
即折射光线较入射光线偏离法线
向
光
疏
sin I ' 不可能大于1,此时入射光线将不能射入
另一介质。
按照反射定律在介面上全部被反射回原介质
原点
+
-
原点
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球
心C在右为正,在左为负。
E
A
C
O +r
E
A
C
-r O
(2)物方截距L 和像方截距L’ 也以顶点O为原点,到光线
与光轴交点,向右为正,向左为负。
E
A
A’
O
C
-L
+L’
E
A
A’
O
C
-L’
-L
(3)球面间隔 d 以前一个球面的顶点为原点, 向右为正,向左为负。
(在折射系统中总为正,在反射和折反系统中才有为负的情况)
O1
O2
+d
O1
O2
《应用光学》课件

超材料与光操控技术在隐身衣、光镊、 光操控机器人等领域具有广泛的应用前 景,如实现物体隐身、微纳粒子的精确
操控等。
目前,超材料与光操控技术的研究重点 在于设计新型超材料、优化光操控效果 、提高操控精度等方面,同时也在探索
其在生物医学、能源等领域的应用。
量子光学与量子信息
量子光学是研究光的量子性质和光与物质相互作用的一门 学科,而量子信息则是利用量子力学原理进行信息处理和 传输的一门技术。
应用光学
目录
CONTENTS
• 应用光学概述 • 光学基础知识 • 光学仪器 • 光学系统设计与优化 • 现代光学技术 • 应用光学前沿研究
01 应用光学概述
应用光学的基本概念
应用光学的基本原理包括光的干涉、衍射、折射、反 射、偏振等,以及光学材料、光学元件和光学系统的 基本知识。
应用光学是研究如何将光学原理和技术应用于实际生 活和工业生产中的一门学科。它涉及到光的产生、传 播、变换、检测和应用,以及光学系统设计、光学仪 器制造和光学信息处理等领域。
光学系统优化算法
优化目标
明确优化的目标,如减小系统像差、提高成像质量或增加光学信 息量等。
优化方法
掌握常用的光学系统优化算法,如梯度优化、遗传算法、粒子群 算法等。
算法实现
具备使用编程语言实现优化算法的能力,如Python、C等。
光学系统性能评估
性能指标
结果分析
ห้องสมุดไป่ตู้
了解光学系统性能的评价指标,如分 辨率、对比度、信噪比等。
光学陀螺仪
利用光的干涉效应感知旋转角度变化,广泛应用于导航、航空、航 天等领域。
全息显示技术
3D全息投影
利用全息技术将三维图像投影到空中,无需佩戴 眼镜或头盔即可观看。
应用光学课件完整版

球面波,会聚为物体的完善象。
物象都有虚实之分: 实物— 物方实际光线直接相交而成的点。 虚物— 物方实际光线不能相交,延长线相交而成的点。 实象— 象方实际光线直接相交的点。 虚象— 象方实际光线不能直接相交,反向延长相交。 物空间— 构成物的光线所处的空间。(实物、虚物) 象空间— 构成象的光线所处的空间。(实象、虚象)
由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′,则A为物点, A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
2. 转面公式
原则:前一折射面的象为后一面的物 ,前一面的象空间为后一面的物空间
n2 = n1′, n3 = n2′ …… nk = nk-1′
3)在光学设计中有重要作用。为了设计出一定垂 轴倍率的光学系统,在物方参数nuy固定的条件下,常通 过改变像方孔径角u′的大小来改变y′的数值,使得y′与y 的比值满足系统设计的要求。
§ 2-3 共轴球面系统
探讨方法— 将光线的光路计算公式及放大率公式反复应 用于各个折射面,分别求出各面的u、 u′、l 、 l′、 β、α、γ、y、y′J、J′、Q、 Q′。 转面公式— 前后相邻面之间的基本量的转化关系。
反射定律可表示为 I I ''
物象都有虚实之分: 实物— 物方实际光线直接相交而成的点。 虚物— 物方实际光线不能相交,延长线相交而成的点。 实象— 象方实际光线直接相交的点。 虚象— 象方实际光线不能直接相交,反向延长相交。 物空间— 构成物的光线所处的空间。(实物、虚物) 象空间— 构成象的光线所处的空间。(实象、虚象)
由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′,则A为物点, A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
2. 转面公式
原则:前一折射面的象为后一面的物 ,前一面的象空间为后一面的物空间
n2 = n1′, n3 = n2′ …… nk = nk-1′
3)在光学设计中有重要作用。为了设计出一定垂 轴倍率的光学系统,在物方参数nuy固定的条件下,常通 过改变像方孔径角u′的大小来改变y′的数值,使得y′与y 的比值满足系统设计的要求。
§ 2-3 共轴球面系统
探讨方法— 将光线的光路计算公式及放大率公式反复应 用于各个折射面,分别求出各面的u、 u′、l 、 l′、 β、α、γ、y、y′J、J′、Q、 Q′。 转面公式— 前后相邻面之间的基本量的转化关系。
反射定律可表示为 I I ''
应用光学课件第四章

应用光学课件第四章
应用光学讲稿 §4-4 棱镜和棱镜的展开
在会聚光路中使用: 除了满足第一个条件外,还需满足第二个条
件:入射表面及出射表面与光轴垂直
若光轴改变90 ° ,必须∠B=∠C=45°,∠A=90°
B
A’
A
C
应用光学课件第四章
应用光学讲稿 §4-4 棱镜和棱镜的展开
若光轴改变任意角度 : A
应用光学讲稿 §4-5 屋脊面和屋脊棱镜
对屋脊面的要求:屋脊角必须严格等于90度 ,否则形成双像
90°
平行入射,平行射出
≠90°
平行入射,不平行射出
应用光学课件第四章
应用光学讲稿
§4-6 平行平板的成像性质和棱镜外形尺寸计算
一、平行玻璃板的成像性质
1、像面位置
n1=1
n1’=n2=n n2’=1
出射光线旋转方向:与反射顺序相同
出射光线的转角只 与两个平面镜的夹角有 关,而与入射光线的方 向无关,即不论入射光 线的入射角和位置如何 ,出射光线与入射光线 的夹角都不变,等于两 平面镜夹角的二倍。
P2 O2
A P1
I1
I1 O1
I2 I2
N M
B
应用光学课件第四章
应用光学讲稿 §4-3 平面镜的旋转及应用
二、双平面镜的转动
P2
在O1O2M中:
2I1 2I2
(2 I1
I
)
2
O2
两法线交于一点N,
O1NO 2
在三角形O1O2N中,利用外角定理:
I1 I2
A P1
I1
I1 O1
I2 I2
N M
B
I1 I2
