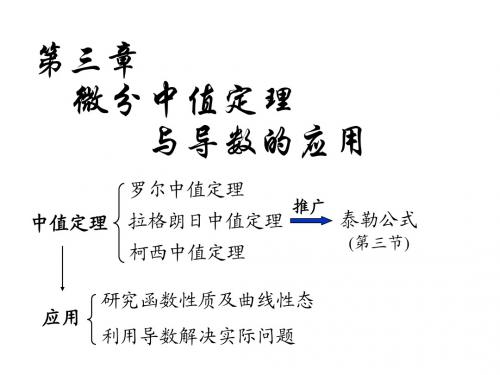
高等数学-中值定律与讲义导数的应用
高等数学第三章中值定理与导数的应用
1 0. 当 x 0 时 0 , 因此由上式得 cos
0? 问是否可由此得出 lim cos 1 x
x0
不能 !
因为 ( x) 是依赖于 x 的一个特殊的函数.
x 0 表示 x 从右侧以任意方式趋于 0 .
备用题 1. 设 f ( x) 在 [0,1] 连续, (0 ,1) 可导,且 f (1) 0 ,
f ( x0 ) 0, 即方程有小于 1 的正根
2) 唯一性 .
f ( x) 在以 x0 , x1 为端点的区间满足罗尔定理条件 , 在 x0 , x1 之间
至少存在一点
假设另有
但
矛盾, 故假设不真!
二、拉格朗日中值定理
满足: (1) 在区间 [ a , b ] 上连续
y
y f ( x)
使
f ( x) sin ln x ,
F ( x) ln x
则 f (x) , F(x) 在 [ 1 , e ] 上满足柯西中值定理条件, f (e) f (1) f ( ) , (1, e ) 因此 F (e) F (1) F ( ) 1 cos ln 即
1
分析:
例5. 试证至少存在一点 法2 令 f ( x) sin ln x sin1 ln x
使
则 f (x) 在 [ 1 , e ] 上满足罗尔中值定理条件, 因此存在 使
1 1 f ( x) cos ln x sin1 x x
内容小结
1. 微分中值定理的条件、结论及关系
3 15 4 . _____
方程
有 3 个根 , 它们分别在区间 (1, 2) , (2 , 3) , (3 , 4) 上.
第四章中值定理与导数的应用精品文档

lim
x
1 nxn
0
例5. 求 xl im exnx (n0,0).
型
解: (1) n 为正整数的情形.
原式
lim
x
nxn1
ex
罗xl imn(n21e)xxn2
罗罗xl imnne!x 0
例5. 求xl im exnx (n0,0).
费马引理
微
分 中
罗尔中值定理
值 定
拉格朗日中值定理
理
柯西中值定理
导数与差商
函数导数的定义为
f(x)lim f(xx)f(x)
x 0
x
即函数在点 x 处的导数等于 x 0时, 函数
在点 x 处的差商 f(xx)f(x) 的极限值.
x
我们常常需要从函数的导数所给出 的局部的或“小范围”性质, 推出其整体的 或“大范围”性质. 为此, 我们需要建立函 数的差商与函数的导数间的基本关系式, 这些关系式称为“微分学中值定理”.
证明 f(x 方 )0仅 程有三 ,并个 指实 出根 .根
证 f ( x ) C ( [ a ,b ] [ b ,, c ] [ c ,, d ] ) ,
又 f ( a ) f ( b ) f ( c ) f ( d ) 0 , f(x)是四次 ,在 (多 , ) 内 项可 ,式微 在[a, b],[b, c],[c, d]上运用罗尔 ,得 中值
x0
颠倒行不行 ?
解
倒数法
limxlnx limlnx
x0
x0 1
x
行 , 但繁些 .
存在一个选择 问题.
1
lim x lim(x) 0
第四章中值定理与导数的应用(全)

e e e( x 1) e x e
x
于是
e e x.
x
例2
证明 当x 0时,
x l n1 x x 1 x
证 设 f x ln1 x , 在[0, x]上应用拉格朗日中值定理
f x f 0 f x 0, 0 x
, 使得f () f () 0
证 则F(x)在[0,1]上 构造函数:令F(x)=xf(x), 满足罗尔中值定理的条件,于是在开区间(0,1) 内至少存在一点 ,使得
f () f () 0
二、拉格朗日中值定理 (Lagrange):
若f x 在 a, b 上连续,在a, b内可导,
f ( x 0 x ) f ( x 0 ) 0 x
C
从而当x 0时
f ( x 0 x ) f ( x 0 ) 0 x
x
0
根据函数f ( x)在x0可导的条件,再由极限 的保号性,便得到
f ( x 0 x ) f ( x 0 ) f ( x0 ) f ( x0 ) lim 0 x 0 x
即 5 使得f 0. , , 2 6 6
5
例2、不求导数,判断函数 f ( x ) ( x 1)( x 2)( x 3)的导数有几个 实根,以及其所在范围 。
解 显然,f (1) f (2) f (3) 0.
且f ( x)在[1,2]和[2,3]上满足罗尔定理条件。
则至少有一点 ,
a b,使得
f 0
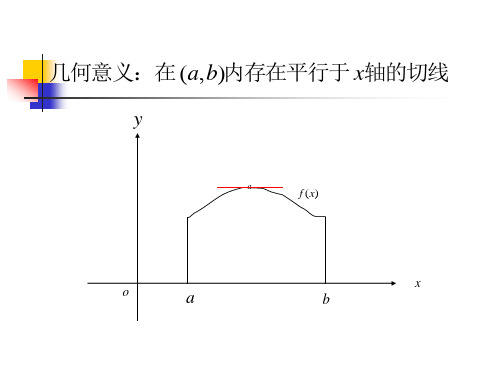
几何意义
几何上,若f x 满足罗尔定理, 则此曲线上至少存在一 点C, 过该点的切线平行于x轴如图.
第三章中值定理与导数的应用课件
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
中值定理与导数的应用(高等数学)省名师优质课赛课获奖课件市赛课一等奖课件
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
高等数学习题课(3)中值定理与导数的应用

(3)
中值定理与导数的应用
第二课 中值定理与导数应用
I. 目的要求 ⒈ 理解罗尔定理、拉格朗日定理,了解柯西定理; 会用中值定理解决诸如方程根的存在性、不等 式证明等问题; ⒉ 了解泰勒定理的条件、结论及余项,掌握函数 ex , sinx, cosx, ln(1+x), (1+x)α的麦克劳 林公式; ⒊ 熟练掌握用洛必达法则求不定型极限的方法; ⒋ 熟练掌握求函数单调区间、极值、凹凸区间、 拐点的方法,并会用其证明一些相关问题。
证:由条件易知F (x)在 [1,2]上满足罗尔定理条件, 则 (1,2),使 F(1) 0 又 F(x) 2(x 1) f (x) (x 1)2 f (x) 在 [1,1]上连续,在(1,1)内可导,且 F(1) F(1) 0 由罗尔定理, (1, 1) (1, 2) 使 F() 0 #
(a 0)有极值,试证:曲线y f (x) 在点(a, f (a))处的
切线经过坐标原点。 证:曲线 y f (x) 在 (a, f (a)) 处的切线方程为
y f (a) f (a)(x a)
即 y f (a)x [ f (a) a f (a)]
由条件 (x) 在 x a 点有极值,且易知(x)在 x a 点可导
x
2
分析:只需证明 sin x x 0 3 cos x
证:令
f
(x)
sin x 3 cos x
x
sin
1
x cos 3
x
x
,显见
f
(0)
0;
f
(x)
cos
2 3
x
1 sin
2
x
4
cos 3
x
第四章 中值定理与导数的应用

3)在(a,b)内任一点 x 处
都不等于零.
则在区间(a,b)内至少存在一点ξ,使得等式
(柯西公式) 成立. 在柯西定理中,当 F(x)=x 时,则有
,于是定理的结论变成
而这正是拉格朗日值定理的结论.因此拉格朗日中值定理是柯西中值定理的特殊情况,或者 说柯西中值定理是拉格朗日中值定理的推广.
我们先看一下柯西中值定理的几何意义,然后再证明这个定理.
7
解:1)f(x)在[0,1]上连续:
2)f(x)在(0,1)内可导(
在
(0,1)内有定义),故 f(x)满足拉格朗日中值定理的条件.
,
设
由此解得
(负根不在所给的区间内,舍去)
故取 =
,则有
成立.
即验证了拉格朗日中值定理对 f(x)=arctanx 在[0,1]上正确.
三、柯西中值定理
如果函数 f(x)和 F(x)满足条件: 1)在闭区间[a,b]上连续; 2)在开区间(a,b)内可导;
(图四) 因此它不满足条件 2),虽然满足条件 1)和 3),但定理结论不成立.从图形上看,显然没有水平 切线.
例 3. (x)=x,x∈[0,1]
函数 f(x)满足条件 1)和 2),但 f(0)≠f(1)(见图五)
(图五) 3
因此不满足条件 3),所以在(0,1)内不存在ξ,使
,也即定理的结论不成立.从图形上
看,显然也没有水平切线. (2)罗尔定理的三个条件是充分的,而不是必要的。即如果定理的三个条件不完全满足或
都不满足时,定理的结论也有可能成立.
例 4.
因为函数 f(x)在点
处不连续、不可导,
且
(见图六),
(图六) 所以 f(x)不满足罗尔定理的全部条件,但是我们可以在区间
中值定理与导数应用

嘉兴学院
10/5/2024
第四章 中值定理与导数应用
第17页
例7 证明当x [ 1 ,1]时,不等式 2
arctan x ln(1 x2 ) ln 2
4 成立.
例8 证明:若函数f (x)在(, )内 满足关系式 f (x) f (x),且f (0)=1,
则 f (x) ex.
嘉兴学院
f '() 0
嘉兴学院
10/5/2024
第四章 中值定理与导数应用
y 几何解释:
第4页
C y f (x)
o a 1
2 b x
在两端点高度相同的连续曲线弧AB上,
若除端点外处处均有不垂直于x轴的切
线存在,则此曲线弧上至少有一点C,
在该点处的切线平行于x轴.
嘉兴学院
10/5/2024
第四章 中值定理与导数应用
f (x1 x2 ) f (x2 ) f (x1)
f (x1 x2 ) f (x2 ) f (x1) f (0)
f (2 ) x1 f (1) x1 (x2 2 x1 x2 , 0 1 x1)
x1 f ( )(2 1) 0 (1 2 )
f (x1 x2 ) f (x1) f (x2 )
并求满足定理的值. 例4 证明 arcsin x arccos x
2 (1 x 1).
嘉兴学院
——证明恒等式旳一般措施
10/5/2024
第四章 中值定理与导数应用
第13页
例5 证明当x 0时, x ln(1 x) x. 1 x
例6 设 Lim f (x) K , 求 x+
Lim [ f (x a) f (x)].(a 0)
x+
嘉兴学院
中值定理与导数的应用-§3.1 中值定理

于是对于x0 x U ( x0 ) ,有 f ( x0 x) f ( x0 )
微积分 第3章 中值定理与导数的应用
3.1 中值定理
f ( x0 x ) f ( x0 ) 当 x 0 时, 0; x f ( x0 x ) f ( x0 ) 0. 当 x <0 时, x 根据函数 f ( x ) 在 x0 处可导及极限的保号性得
微积分 第3章 中值定理与导数的应用
3.1 中值定理
同理可知,方程还有两个根 2 , 3分别属于区间 2,3 及
3,4 . 因此,有且仅有三个实根,它们分别属于区间 1, 2 , 2, 3 及 3, 4 .
例3 若 f ( x )在区间 [a , b]上连续,在 ( a , b ) 内可导,且 满足 f ( x ) 0,及 f (a ) f (b) 0 , 证明方程 f ( x ) 0
三、柯西中值定理
柯西中值定理 设函数 f ( x ) 及 F ( x ) 满足条件: (1)在闭区间 [a , b] 上连续; (2)在开区间( a , b ) 内可导, 且 F ( x ) 在 ( a , b ) 内每一点处均不为零. 则在 ( a , b ) 内 至少有一点 (a b), 使得
微积分 第3章 中值定理与导数的应用
3.1 中值定理
(2)若 M m , 由于 f (a ) f (b), 所以 M 和 m 至少有一个不 等于 f ( x ) 在区间 [a , b] 端点处的函数值.不妨设 M f (a ) , 则必定在 (a, b) 有一点 使 f ( ) M . 因此任取 x [a, b] 均有 f ( x ) f ( ) , 从而由费马引理有 f ( ) 0 . 证毕
高数(微积分)中值定理和导数应用课件

微小增量公式
拉格朗日中值定理的推论
推论1:
若 f ( x ) 在 [ a ,b ] 上恒为零 , 则 f 在 [ a ,b ] 上恒 .
[证]
在 [a, b]上任意取定一点 x0
x [ a ,b ], f( x ) 在 [ x ,x ] 或 [ x ,x ] 上满足 0 0 朗日中值定理条件
(2)
M m . 此时, 由于 f (a ) f (b) , 故 M , m 之一是函
数在(a, b)内的函数值.
不妨设 M f ( ) ( a b ) . 此时, 是函数的局部 最大值点. 由费尔马引理 f ( ) 0 .
三、拉格朗日(Lagrange )定理
f ( x ) 0 0
说明:
f(x 必要条件 . 0)0是可导函数取得极值的
极值 . 点
满f 足 ( x ) 0 的 x 点 不一定 f的 是 一 函 0 0
y f(x ) 的驻点 称使 f(x 0)0的点 x 0 为函数
二、罗尔(Rolle)定理
罗尔定理 若函数 f ( x )满足下列条件: (1) 在[a, b]上连续; (2) 在 (a, b)内可导; (3) f (a) f (b) , 则在 (a, b)内至少存在一点 使得 f ( ) 0 .
故
1 ln( 1 x ) 1 .( x 0 ) 1 x x
例 4. 设 f C[0,1],在 (0,1)内可导,且 f (1) 0. 求证,存
证
在 (0,1)使得 f ( )
f ( )
.
x xf x 设 F ,显然 Fx在 [0,1] 上连续;
《高等数学B》 第四章 中值定理及导数的应用 第1节 中值定理

拉格朗日 (1736 – 1813) 法国数学家. 他在方程论, 解析函数论, 法国数学家. 他在方程论 解析函数论 及数论方面都作出了重要的贡献, 及数论方面都作出了重要的贡献 近百 余年来, 数学中的许多成就都直接或间 余年来 接地溯源于他的工作, 接地溯源于他的工作 他是对分析数学 产生全面影响的数学家之一 .
y
C M•
y = f ( x)
•
D
A•
•N
ξ1 x
o a
ξ2 b
x
分析: 证 分析: 条件中与罗尔定理相差 f (a ) = f (b) .
f (b) − f (a ) ( x − a) . 弦 AB方程为 y = f (a ) + 方程为 b−a 曲线 f ( x )减去弦 AB ,
所得曲线 a , b 两端点的函数值相等 .
(1)
f ′(ξ ) = 0 .
例如, 例如 f ( x ) = x 2 − 2 x − 3 = ( x − 3)( x + 1) .
在[−1 , 3]上连续 , 在( −1 , 3) 上可导 , 且 f ( −1) = f ( 3) = 0 , Q f ′( x ) = 2( x − 1) , 取 ξ = 1 (1 ∈ ( −1 , 3)) , f ′(ξ ) = 0 .
f (b) − f (a ) F ( x ) = f ( x ) − [ f (a ) + ( x − a )] . b−a F ( x ) 满足罗尔定理的条件 , 则在( a , b )内至少存在一点 ξ ,
作辅助函数
使得 F ′(ξ ) = 0 . 即
f (b) − f (a ) f ′(ξ ) − =0, b−a 拉格朗日中值公式 或 f (b) − f (a) = f ′(ξ )(b − a) .
高等数学第三章微分中值定理与导数的应用讲义

第三章 微分中值定理与导数的应用讲义【考试要求】1.掌握罗尔中值定理、拉格朗日中值定理并了解它们的几何意义. 2.熟练掌握洛必达法则求“0/0”、“/∞∞”、“0⋅∞”、“∞-∞”、“1∞”、“00”和“0∞”型未定式极限的方法.3.掌握利用导数判定函数的单调性及求函数的单调增、减区间的方法,会利用函数的增减性证明简单的不等式.4.理解函数极值的概念,掌握求函数的极值和最值(最大值和最小值)的方法,并且会解简单的应用问题.5.会判定曲线的凹凸性,会求曲线的拐点. 6.会求曲线的水平渐近线与垂直渐近线.【考试内容】一、微分中值定理1.罗尔定理如果函数()yf x =满足下述的三个条件:(1)在闭区间[,]a b 上连续; (2)在开区间(,)a b 内可导; (3)在区间端点处的函数值相等,即()()f a f b =,那么在(,)a b 内至少有一点ξ(ab ξ<<),使得()0f ξ'=.说明:通常称导数等于零的点为函数的驻点(或稳定点,临界点),即若0()0f x '=,则称点0x 为函数()f x 的驻点.2.拉格朗日中值定理如果函数()yf x =满足下述的两个条件:(1)在闭区间[,]a b 上连续; (2)在开区间(,)a b 内可导, 那么在(,)a b 内至少有一点ξ(ab ξ<<),使得下式(拉格朗日中值公式)成立: ()()()()f b f a f b a ξ'-=-.说明:当()()f b f a =时,上式的左端为零,右端式()b a -不为零,则只能()0f ξ'=,这就说明罗尔定理是拉格朗日中值定理的特殊情形.此外,由于拉格朗日中值定理在微分学中占有重要的地位,因此有时也称这定理为微分中值定理.3.两个重要推论(1)如果函数()f x 在区间I 上的导数恒为零,那么()f x 在区间I 上是一个常数.证:在区间I 上任取两点1x 、2x (假定12x x <,12x x >同样可证),应用拉格朗日中值公式可得2121()()()()f x f x f x x ξ'-=- (12x x ξ<<). 由假定,()0f ξ'=,所以 21()()0f x f x -=,即 21()()f x f x =.因为1x 、2x 是I 上任意两点,所以上式表明()f x 在区间I 上的函数值总是相等的,即()f x 在区间I 上是一个常数.(2)如果函数()f x 与()g x 在区间(,)a b 内的导数恒有()()f x g x ''=,则这两个函数在(,)a b 内至多相差一个常数,即()()f x g x C -=(C 为常数). 证:设()()()F x f x g x =-,则()[()()]()()0F x f x g x f x g x ''''=-=-=,根据上面的推论(1)可得,()F x C =,即()()f x g x C -=,故()()f x g x C -=.二、洛必达法则1.x a →时“0”型未定式的洛必达法则如果函数()f x 及()F x 满足下述的三个条件:(1)当x a →时,函数()f x 及()F x 都趋于零;(2)在点a 的某个去心邻域内()f x '及()F x '都存在且()0F x '≠;(3)()lim ()x a f x F x →''存在(或为无穷大),那么()()limlim()()x ax a f x f x F x F x →→'='. 说明:这就是说,当()lim ()x a f x F x →''存在时,()lim ()x a f x F x →也存在且等于()lim ()x a f x F x →'';当()lim()x af x F x →''为无穷大时,()lim ()x a f x F x →也是无穷大.2.x →∞时“”型未定式的洛必达法则 如果函数()f x 及()F x 满足下述的三个条件:(1)当x →∞时,函数()f x 及()F x 都趋于零;(2)当x X >时()f x '及()F x '都存在且()0F x '≠;(3)()lim ()x f x F x →∞''存在(或为无穷大),那么 ()()lim lim()()x x f x f x F x F x →∞→∞'='. 说明:我们指出,对于xa →或x →∞时的未定式“∞∞”,也有相应的洛必达法则. 3.使用洛必达法则求“00”型或“∞∞”型极限时的注意事项(1)使用洛必达法则之前要先判断所求极限是不是“00”型或“∞∞”型,如果不是则不能使用洛必达法则.例如:2sin lim x xx π→就不能运用洛必达法则,直接代入求极限即可,故2sinsin 22lim 2x x x ππππ→==.(2)洛必达法则可多次连续使用,也就是说,如果使用一次洛必达法则后算式仍然是“00”型或“∞∞”型,则可再次使用洛必达法则,依此类推.(3)洛必达法则是求“00”型或“∞∞”型未定式极限的一种有效方法,但最好能与其他求极限的方法结合使用,例如能化简时应尽可能先化简,可以应用等价无穷小替代或重要极限时,应尽可能应用,这样可以使运算简便.例如:求20tan lim tan x x xx x→-时,可先用~tan x x进行无穷小的等价替换,然后再用洛必达法则,故2223220000tan tan sec 1tan 1lim lim lim lim tan 333x x x x x x x x x x x x x x x →→→→---====. (4)如果求极限的式子中含有非零因子,则可以对该非零因子单独求极限(即可以先求出这部分的极限),然后再利用洛必达法则,以便简化运算.例如:求0lnsin 2limlnsin3x xx+→时,0000lnsin 2sin3cos 222sin323lim lim lim lim 1lnsin3sin 2cos333sin 232x x x x x x x x x x x x x x++++→→→→⋅⋅⋅====⋅⋅⋅,从第二步到第三步的过程中,分子上的因子cos2x 和分母上的因子cos3x 当0x +→时极限均为1,故可先求出这两部分的极限以便化简运算.(5)当洛必达法则的条件不满足时,所求极限不一定不存在,也即是说,当()lim ()f x F x ''不存在时(等于无穷大的情况除外),()lim ()f x F x 仍可能存在.例如:极限sin lim x x xx→∞+,(sin )1cos lim lim lim(1cos )1x x x x x xx x →∞→∞→∞'++==+' 极限是不存在的,但是原极限是存在的,sin sin sin limlim(1)1lim 101x x x x x x xx x x→∞→∞→∞+=+=+=+=.4.其他类型的未定式除了“00”型或“∞∞”型未定式之外,还有其他类型的未定式,如“0⋅∞”、“∞-∞”、“1∞”、“00”及“0∞”型等.对于“0⋅∞”和“∞-∞”型的未定式,处理方法为将它们直接转化成“00”或“∞∞”型;对于“1∞”、“00”及“0∞”型的未定式,处理方法为先取对数将它们转化成“0⋅∞”型,然后再转化成“00”型或“∞∞”型未定式. 三、函数单调性的判定法1.单调性判定法设函数()yf x =在[,]a b 上连续,在(,)a b 内可导,(1)如果在(,)a b 内()0f x '>,那么函数()y f x =在[,]a b 上单调增加; (2)如果在(,)a b 内()0f x '<,那么函数()y f x =在[,]a b 上单调减少.说明:① 如果把这个判定法中的闭区间改为其他各种区间(包括无穷区间),结论也成立; ② 若判定法中()f x '在(,)a b 内只有有限个点上()0f x '=,而在其余点上恒有()0f x '>(或()0f x '<),则函数()f x 在区间[,]a b 上仍然是单调增加(或单调减少)的.2.单调区间的求法设函数()f x 在定义区间上连续,除去有限个导数不存在的点外导数存在且连续,则求函数()f x 的单调性的步骤如下:(1)求出函数()f x 的定义域;(2)求出函数()f x 的导数()f x ',并令()0f x '=求出函数的驻点;此外,再找出导数不存在的点(一般是使得()f x '分母为零的点); (3)用函数()f x 的所有驻点和导数不存在的点来划分函数的定义区间,然后用单调性判定定理逐个判定各个部分区间的单调性.3.用单调性证明不等式函数()f x 的单调性还可以用来证明不等式,步骤如下:(1)将不等式的一边变为零,不等于零的一边设为()f x ,根据要证明的式子找出不等式成立的x 的范围I ; (2)求()f x 的导数()f x ',判断()f x '在上述I 范围内的符号(即正负); (3)根据范围I 的边界值与()f x '的情况,导出所需要证明的不等式即可.例如:试证明当1x>时,13x>-. 证明:原不等式即为13x -+,故令1()3f x x=-+,0x >,则2211()(1)f x xx '=-=- ,()f x 在[1,)+∞上连续,在(1,)+∞内()0f x '>,因此在[1,)+∞上()f x 单调增加,从而当1x >时,()(1)f x f >,又由于(1)0f =,故()0f x >,即130x -+>,亦即13x>-.四、函数的凹凸性与拐点1.函数凹凸性的定义设函数()f x 在区间I 上连续,如果对I 上任意两点1x 、2x ,恒有1212()()22x x f x f x f ++⎛⎫<⎪⎝⎭,那么称()f x 在I 上的图形是(向上)凹的(或凹弧);如果恒有1212()()22x x f x f x f ++⎛⎫>⎪⎝⎭,那么称()f x 在I 上的图形是(向上)凸的(或凸弧).如果函数()f x 在I 内具有二阶导数,那么可以利用二阶导数的符号来判定曲线的凹凸性,如下所示.2.函数凹凸性的判定法设函数()f x 在区间[,]a b 上连续,在(,)a b 内具有一阶和二阶导数,那么(1)若在(,)a b 内()0f x ''>,则()f x 在[,]a b 上的图形是凹的; (2)若在(,)a b 内()0f x ''<,则()f x 在[,]a b 上的图形是凸的.说明:若在(,)a b 内除有限个点上()0f x ''=外,其它点上均有()0f x ''>(或()0f x ''<),则同样可以判定曲线()y f x =在[,]a b 上为凹曲线(或凸曲线). 3.曲线的拐点的求法一般地,设()y f x =在区间I 上连续,0x 是I 的内点(除端点外I 内的点).如果曲线()y f x =在经过点00(,())x f x 时,曲线的凹凸性改变了,那么就称点00(,())x f x 为这曲线的拐点.我们可以按照下述步骤求区间I 上的连续函数()y f x =的拐点:(1)求()f x ''; (2)令()0f x ''=,解出这方程在区间I 内的实根,并求出在区间I 内()f x ''不存在的点;(3)对于(2)中求出的每一个实根或二阶导数不存在的点0x ,检查()f x ''在0x 左、右两侧邻近的符号,当两侧的符号相反时,点00(,())x f x 是拐点,当两侧的符号相同时,点00(,())x f x 不是拐点.在[,]a b 上单3.基本初等函数的微分公式说明:若要求函数()y f x =的凹凸区间,则用(2)中求出的每一个实根或二阶导数不存在的点把区间I分成若干部分区间,然后在这些部分区间上判定()f x ''的符号,若()0f x ''>,则该部分区间为凹区间,若()0f x ''<,则该部分区间为凸区间.五、函数的极值与最值1.函数极值的定义设函数()f x 在点0x 的某邻域0()U x 内有定义,如果对于去心邻域0()U x 内任一x ,有0()()f x f x <(或0()()f x f x >),那么就称0()f x 是函数()f x 的一个极大值(或极小值).函数的极大值与极小值统称为函数的极值,使函数取得极值的点称为极值点. 说明:函数的极大值与极小值概念是局部性的,如果0()f x 是函数()f x 的一个极大值,那只是就0x 附近的一个局部范围来说,0()f x 是()f x 的一个最大值,如果就()f x 的整个定义域来说,0()f x 不见得是最大值.关于极小值也类似.2.函数取得极值的必要条件设函数()f x 在0x 处可导,且在0x 处取得极值,那么0()0f x '=.说明:这也就是说,可导函数()f x 的极值点必定是它的驻点.但反过来,函数的驻点却不一定是极值点.例如,3()f x x =的导数2()3f x x '=,(0)0f '=,因此0x =是这函数的驻点,但0x=却不是这函数的极值点,所以,函数的驻点只是可能的极值点.此外,函数在它的导数不存在的点处也可能取得极值.例如,函数()f x x =在点0x =处不可导,但函数在该点取得极小值.3.判定极值的第一充分条件设函数()f x 在0x 处连续,且在0x 的某去心邻域0()U x 内可导.(1)若00(,)x x x δ∈-时,()0f x '>,而00(,)x x x δ∈+时,()0f x '<,则()f x 在0x 处取得极大值;(2)若00(,)x x x δ∈-时,()0f x '<,而00(,)x x x δ∈+时,()0f x '>,则()f x 在0x 处取得极小值;(3)若0(,)x U x δ∈时,()f x '的符号保持不变,则()f x 在0x 处没有极值.4.用第一充分条件求极值点和极值的步骤设函数()f x 在所讨论的区间内连续,除个别点外处处可导,则用第一充分条件求极值点和相应的极值的步骤如下: (1)求出导数()f x ';(2)求出()f x 的全部驻点与不可导点;(3)考查()f x '的符号在每个驻点或不可导点的左右邻近的情形,以确定该点是否为极值点;如果是极值点,进一步确定是极大值点还是极小值点; (4)求出各极值点的函数值,就得函数()f x 的全部极值.5.判定极值的第二充分条件设函数()f x 在0x 处具有二阶导数且0()0f x '=,0()0f x ''≠,那么(1)当0()0f x ''<时,函数()f x 在0x 处取得极大值; (2)当0()0f x ''>时,函数()f x 在0x 处取得极小值.说明:该极值判定条件表明,如果函数()f x 在驻点0x 处的二阶导数0()0f x ''≠,那么该驻点0x 一定是极值点,并且可按二阶导数0()f x ''的符号来判定0()f x 是极大值还是极小值.但如果0()0f x ''=,则该判定条件失效.事实上,当0()0f x '=,0()0f x ''=时,()fx 在0x 处可能有极大值,可能有极小值,也可能没有极值.例如,41()f x x =-,42()f x x =,33()f x x =这三个函数在0x =处就分别属于上述三种情况.因此,如果函数在驻点处的二阶导数为零,那么还得用一阶导数在驻点左右邻近的符号来判定.6.求()f x 在区间[,]a b 上的最值的步骤设函数()f x 在闭区间[,]a b 上连续,在开区间(,)a b 内除有限个点外可导,且至多有有限个驻点,则求()f x 在闭区间[,]a b 上的最值的步骤如下:(1)求出()f x 在(,)a b 内的驻点1x ,2x ,,m x 及不可导点1x ',2x ',,n x ';(2)计算()i f x (1,2,,i m =),()j f x '(1,2,,j n =)及 ()f a ,()f b ;(3)比较(2)中诸值的大小,其中最大的便是()f x 在[,]a b 上的最大值,最小的便是()f x 在[,]a b 上的最小值.说明:在实际问题中,往往根据问题的性质就可以断定可导函数()f x 确有最大值或最小值,而且一定在定义区间内部取得.这时如果()f x 在定义区间内部只有一个驻点0x ,那么不必讨论0()f x 是不是极值,就可以断定0()f x 是最大值或最小值.六、函数的渐近线的求法1.水平渐近线若lim()x f x a →∞=(包括lim ()x f x a →-∞=或lim ()x f x a →+∞=),则直线y a =就是函数()f x 的水平渐近线.2.垂直渐近线(或称铅直渐近线)若0lim()x x f x →=∞(包括0lim ()x x f x -→=∞或0lim ()x x f x +→=∞),则直线0x x =就是函数()f x 的垂直(铅直)渐近线.【典型例题】 【例3-1】验证罗尔定理对函数()lnsin f x x =在区间5[,]66ππ上的正确性.解:显然函数()lnsin f x x =在闭区间5[,]66ππ上连续,在开区间5(,)66ππ上可导,1()(lnsin )cos cot sin f x x x x x ''==⋅=,且5()()l n266f f ππ==-,故满足罗尔定理的条件,由定理可得至少存在一点5(,)66ππξ∈,使得()0f ξ'=,即cot 0ξ=,2πξ=即为满足条件的点.【例3-2】验证拉格朗日中值定理对函数2()482f x x x =--在区间[0,1]上的正确性.解:显然函数2()482f x x x =--在闭区间[0,1]上连续,在开区间(0,1)内可导,()88f x x '=-,根据拉格朗日中值定理可得至少存在一点(0,1)ξ∈,使得(1)(0)()(10)f f f ξ'-=-,即6(2)88ξ---=-,可得1(0,1)2ξ=∈,12ξ=即为满足条件的点.【例3-3】不求导数,判断函数()(1)(2)(3)(4)f x x x x x =----的导数有几个零点,这些零点分别在什么范围. 解:显然()f x 是连续可导的函数,且(1)(2)(3)(4)0f f f f ====,故()f x 在区间[1,2],[2,3],[3,4]上满足罗尔定理的条件,所以在区间(1,2)内至少存在一点1ξ,使得1()0f ξ'=,即1ξ是()f x '的一个零点;在区间(2,3)内至少存在一点2ξ,使得2()0f ξ'=,即2ξ是()f x '的一个零点;又在区间(3,4)内至少存在一点3ξ,使得3()0f ξ'=,即3ξ也是()f x '的一个零点.又因为()f x '是三次多项式,最多只能有三个零点,故()f x '恰好有三个零点,分别在区间(1,2),(2,3)和(3,4)内.【例3-4】证明arcsin arccos 2x x π+=,其中11x -≤≤.证明:设()arcsin arccos f x x x =+,[1,1]x ∈-, 因为()(0f x '=+=,所以()f x C =,[1,1]x ∈-.又因为(0)a r c s i n 0a r c c o s 0022f ππ=+=+=,即 2C π=,故arcsin arccos 2x xπ+=.说明:同理可证,arctan arccot 2x x π+=,(,)x ∈-∞+∞.【例3-5】求下列函数的极限.1.求 332132lim 1x x x x x x →-+--+.解:该极限为1x →时的“”型未定式,由洛必达法则可得 原式22113363lim lim 321622x x x x x x x →→-===---.2.求arctan 2lim 1x x xπ→+∞-.解:本题为x →+∞时的“00”型未定式,由洛必达法则可得原式222211lim lim 111x x x x x x→+∞→+∞-+===+-.3.求0lnsin 2lim lnsin3x xx+→. 解:该极限为0x+→时的“∞∞”型未定式,由洛必达法则可得原式0001cos 222sin 323sin 2lim lim lim 113sin 232cos33sin 3x x x x x x x x xx x+++→→→⋅⋅⋅====⋅⋅⋅.4.求 2tan lim tan 3x xx π→.解:本题为2x π→时的“∞∞”型未定式,由洛必达法则可得原式2222222sec cos 32cos3(sin 3)3lim lim lim 3sec 33cos 6cos (sin )x x x x x x x x x x x πππ→→→⋅-⋅===⋅- 22cos33sin3lim lim 3cos sin x x x x x x ππ→→-===-.5.求2tan limtan x x xx x→-. 解:该极限为0x →时的“00”型未定式,结合等价无穷小的替换,运用洛必达法则可得原式22320000tan sec 12sec tan 21lim lim lim lim 3663x x x x x x x x x x x x x x →→→→--⋅=====. 说明:此题也可这样求解(运用公式22sec1tan x x =+和等价无穷小替换来简化运算): 原式22232220000tan sec 1tan 1lim lim lim lim 3333x x x x x x x x x x x x x →→→→--=====. 6.求11lim()sin x x x→-. 解:该极限为0x →时的“∞-∞”型未定式,解决方法为先化为“1100-”型,然后通分化为“”型,故 原式20000sin sin 1cos sin lim lim lim lim 0sin 22x x x x x x x x x xx x x x →→→→---=====.7.求lim x x x +→. 解:该极限为0x +→时的“00”型未定式,解决方法为取对数化为“0ln0⋅”型,进而化为“”型,故 原式020001lim ln 1lim ln limlim ()ln 00lim 1x x x x xx x xx x x xx x e ee e e e +→+++→→→+--→=======.8.求cos limx x xx→∞+.解:原式1sin lim lim(1sin )1x x x x →∞→∞-==-,最后的极限不存在,不满足洛必达法则的条件,实际上,原式cos cos lim(1)1lim 101x x x xx x→∞→∞=+=+=+=.【例3-6】求下列函数的单调区间. 1.32()29123f x x x x =-+-.解:因2()618126(1)(2)f x x x x x '=-+=--,令()0f x '=,得11x =,22x =.用1x ,2x 将函数的定义域(,)-∞+∞分成三个区间(,1)-∞,(1,2),(2,)+∞,其讨论结果如下表所示:由上表可得,函数的单调递增区间为(,1]-∞和[2,)+∞,单调递减区间为[1,2].2.()f x = .解:函数的定义域为(,)-∞+∞,()f x '=(0x ≠),当0x =时导数不存在.将函数定义域分成两个区间(,0)-∞和(0,)+∞,讨论结果如下表所示:所以函数的单调递增区间为[0,)+∞,单调递减区间为(,0]-∞. 【例3-7】利用函数的单调性证明不等式. 1.试证当0x>时,ln(1)x x >+成立.证明:设()ln(1)f x x x =-+,则1()111xf x x x'=-=++, 因()f x 在区间[0,)+∞上连续,在(0,)+∞内可导,且 ()0f x '>, 故()f x 在区间[0,)+∞上单调增加,又因为(0)0f =,所以当0x >时,()0f x >,即ln(1)0x x -+>,也即 ln(1)x x >+成立.2.试证当1x >时,13x>-.证明:令1()(3)f x x =--,则2211()(1)f x xx '=-=-, 因()f x 在区间[1,)+∞上连续,在(1,)+∞内可导且()0f x '>, 故()f x 在区间[1,)+∞上单调增加,又因为(1)0f =,所以当1x >时,()0f x >,即1(3)0x -->,也即13x>- 成立.【例3-8】证明方程510x x ++=在区间(1,0)-内有且仅有一个实根.证明:令5()1f x x x =++,因为()f x 在闭区间[1,0]-上连续,且(1)10f -=-<,(0)10f =>,根据零点定理,()f x 在区间(0,1)内至少有一个零点.另一方面,对于任意实数x ,有4()510f x x '=+>,所以()f x 在(,)-∞+∞内单调增加,因此曲线5()1f x x x =++与x 轴至多有一个交点.综上所述,方程510xx ++=在区间(1,0)-内有且仅有一个实根.【例3-9】求下列函数的极值. 1.32()395f x x x x =--+.解:函数的定义域为(,)-∞+∞,且有2()3693(1)(3)f x x x x x '=--=+-,令()0f x '=,得驻点11x =-,23x =,列表讨论如下:由上表可得,函数的极大值为(1)10f -=,极小值为(3)22f =-.2.233()2f x x x =-.(,1]-∞-解:函数的定义域为(,)-∞+∞,且有13()1f x x-'=-=, 令()0f x '=,得驻点1x =,当0x =时()f x '不存在,驻点1x =以及不可导点0x =将定义域分成三个区间,列表讨论如下:由上表可得,函数的极大值为(0)0f =,极小值为1(1)2f =-.【例3-10】求函数32()231214f x x x x =+-+在区间[3,4]-上的最值.解:因为2()66126(2)(1)f x x x x x '=+-=+-,令()0f x '=,得 12x =-,21x =,计算(3)23f -=,(2)34f -=,(1)7f =,(4)142f =,比较上述结果可知,最大值为(4)142f =,最小值为(1)7f =.【例3-11】求下列曲线的凹凸区间和拐点. 1.43()341f x x x =-+.解:函数的定义域为(,)-∞+∞,且有32()1212f x x x '=-,2()36()3f x x x ''=-,令()0f x ''=,得10x =,223x =, 列表讨论如下:(,1]-∞-由上表可得,曲线()f x 的凹区间为(,0]-∞和2[,)3+∞,凸区间为2[0,]3,拐点为(0,1)和211(,)327.2.()f x =解:函数的定义域为(,)-∞+∞,当0x ≠时有231()3f x x -'=,532()9f x x -''=-,当0x =时,()f x '和()f x ''均不存在,但在区间(,0)-∞内,()0f x ''>,故曲线在(,0]-∞上是凹的;在区间(0,)+∞内,()0f x ''<,故曲线在[0,)+∞上是凸的.所以曲线的凹区间为(,0]-∞,凸区间为[0,)+∞,拐点为(0,0).【历年真题】 一、选择题1.(2009年,1分)若函数()y f x =满足0()0f x '=,则0x x =必为()f x 的(A )极大值点 (B )极小值点 (C )驻点 (D )拐点 解:若0()0f x '=,则0x x =必为()f x 的驻点,选(C ).2.(2009年,1分)当0x >时,曲线1sin y x x=(A )没有水平渐近线 (B )仅有水平渐近线23 x ()f x 2(,)3+∞ 0 (,0)-∞2(0,)3+-+对应拐点对应拐点凹凸凹()f x ''(C )仅有铅直渐近线 (D )既有水平渐近线,又有铅直渐近线解:由1sin1lim sin lim11x x x x x x→∞→∞==可知,1y =为曲线的水平渐近线;01lim sin 0x x x+→=,故曲线无铅直渐近线.选项(B )正确. 3.(2008年,3分)函数()ln f x x =在区间[1,2]上满足拉格朗日公式中的ξ等于(A )ln 2 (B )ln1 (C )ln e (D )1ln 2解:对函数()ln f x x =在区间[1,2]上应用拉格朗日中值定理,(2)(1)()(21)f f f ξ'-=-,即 1ln 20ξ-=,故 1ln 2ξ=.选(D ). 4.(2007年,3分)曲线33yx x =-上切线平行于x 轴的点为(A )(1,4)-- (B )(2,2) (C )(0,0)(D )(1,2)- 解:切线平行于x 轴的点即为一阶导数等于零的点.由2330y x'=-=可得,1x =±;1x =时,2y =-,1x =-时,2y =,故曲线33y x x =-上切线平行于x 轴的点为(1,2)-和(1,2)-.选项(D )正确. 5.(2007年,3分)若在区间(,)a b 内,导数()0f x '>,二阶导数()0f x ''<,则函数()f x 在该区间内(A )单调增加,曲线为凸的 (B )单调增加,曲线为凹的 (C )单调减少,曲线为凸的 (D )单调减少,曲线为凹的 解:()0f x '>可得()f x 单调增加,()0f x ''<可得曲线为凸的,故选(A ).二、填空题1.(2010年,2分)函数32()2912f x x x x =-+的单调减区间是.解:令2()618126(1)(2)0f x x x x x '=-+=--=,得驻点1x =和2x =;当1x <时,()0f x '>,当12x <<时,()0f x '<,当2x >时,()0f x '>,故函数的单调递减区间为[1,2].2.(2009年,2分)当62x ππ≤≤时,sin ()xf x x=是函数(填“单调递增”、“单调递减”).解:当6x π=时,sin36()66f ππππ==;当2x π=时,sin22()22f ππππ==;故当62x ππ≤≤时,sin ()xf x x=是单调递减函数. 3.(2009年,2分)函数32()29121f x x x x =-++在区间[0,2]上的最大值点是.解:令2()618126(1)(2)0f x x x x x '=-+=--=,得驻点1x =和2x =.比较函数值(1)6f =,(2)5f =,(0)1f =,可知,函数的最大值为(1)6f =,故函数的最大值点为1x =.4.(2007年,4分)曲线24x t y t⎧=⎨=⎩在1t =处的切线方程为.解:将1t =代入参数方程可得切点为(1,4),切线斜率11422t t t t y k tx =='===',故切线方程为42(1)y x -=-,即 22y x =+.5.(2005年,3分)x y xe -=的凸区间是.解:()(1)x x x x y xe e xe x e ----''==-=-,(1)(2)x x x y e x e x e ---''=---=-. 令 (2)0x y x e -''=-=可得,2x =,且当2x >时,0y ''>,当2x <时,0y ''<,故函数x y xe -=的凸区间是(,2]-∞.6.(2005年,3分)曲线x y x =通过(1,1)点的切线方程为.解:因ln ln ()()(ln 1)(ln 1)x x x x x x y x e e x x x '''===⋅+=+,故切线斜率1[(ln 1)]1x x k x x ==+=,所以切线方程为11(1)y x -=⋅-,即 y x =.三、应用题或综合题1.(2010年,10分)现有边长为96厘米的正方形纸板,将其四角各剪去一个大小相同的小正方形,折做成无盖纸箱,问剪区的小正方形边长为多少时做成的无盖纸箱容积最大? 解:设剪区的小正方形边长为x ,则纸盒的容积2(962)yx x =-,048x <<.2(962)2(962)(2)(962)(966)y x x x x x '=-+⋅--=--,令0y '=,可得 16x =(48x =舍去).因只有唯一的驻点,且原题中容积最大的无盖纸箱一定存在,故当剪区的小正方形边长为16厘米时,做成的无盖纸箱容积最大. 2.(2010年,10分)设函数()f x 在[0,1]上连续,并且对于[0,1]上的任意x 所对应的函数值()f x 均为0()1f x ≤≤,证明:在[0,1]上至少存在一点ξ,使得()f ξξ=.解:令()()F x f x x =-,由于()f x 在[0,1]上连续,故()F x 在[0,1]上也连续.(0)(0)0(0)F f f =-=,(1)(1)1F f =-.而对[0,1]x ∀∈,0()1f x ≤≤,故(0)0F ≥,(1)0F ≤. 若(0)0F =,即(0)00f -=,(0)0f =,则0ξ=; 若(1)0F =,即(1)10f -=,(1)1f =,则1ξ=;当(0)0F ≠,(1)0F ≠时,(0)(1)0F F ⋅<,而()F x 在[0,1]上连续,故根据零点定理可得,至少存在一点(0,1)ξ∈,使得()0F ξ=,即()0f ξξ-=,()f ξξ=.综上,在[0,1]上至少存在一点ξ,使得()f ξξ=.3.(2009年,10分)某工厂需要围建一个面积为2512m 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.问堆料场的长和宽各为多少时,才能使砌墙所用的材 料最省?解:设堆料场的宽为xm ,则长为512x m ,设砌墙周长为y ,则5122y x x=+, 令251220y x'=-=,得 2256x =,16x =(16x =-舍去).因只有一个驻点,且原题中最值一定存在,故当16x =时,函数有最小值.即当宽为16m ,长为32m 时,才能使砌墙所用的材料最省. 4.(2009年,10分)当0x >,01a <<时,1a x ax a -≤-.解:原不等式即为 10a x ax a -+-≤.设()1a f x x ax a =-+-,则(1)当1x=时,()110f x a a =-+-=,即10a x ax a -+-=成立; (2)当01x <<时,111()(1)0a a f x axa a x--'=-=->,故()f x 单调增加,可得()(1)0f x f <=,即10a x ax a -+-<成立;(3)当1x>时,111()(1)0a af x ax a a x--'=-=-<,故()f x 单调减少,可得()(1)0f x f <=,即10a x ax a -+-<成立.综上,当0x>,01a <<时,不等式10a x ax a -+-≤成立,即1ax ax a -≤-. 5.(2008年,8分)求函数233y x x =-的单调区间、极值、凹凸区间与拐点.解:函数的定义域为(,)-∞+∞. 先求单调区间和极值.令2633(2)0y x xx x '=-=-=,得驻点0x =,2x =,用驻点将整个定义域分为三个区间(,0)-∞,(0,2),(2,)+∞.当(,0)x ∈-∞时,0y '<,函数单调减少;当(0,2)x ∈时,0y '>,函数单调增加;当(2,)x ∈+∞时,0y '<,函数单调减少.故函数的单调增加区间为[0,2],单调减少区间为(,0]-∞和[2,)+∞;极小值(0)0f =,极大值(2)4f =.再求凹凸区间和拐点.令660y x ''=-=,得1x =.当(,1)x ∈-∞时,0y ''>,函数为凹的;当(1,)x ∈+∞时,0y ''<,函数为凸的,且当1x =时,2y =,故函数的凹区间为(,1]-∞,凸区间为[1,)+∞,拐点为(1,2).6.(2007年,8分)求函数11y x x =++的单调区间、极值、凹凸区间和拐点. 解:函数的定义域为(,1)(1,)-∞--+∞.先求单调区间和极值.令221(2)10(1)(1)x x y x x +'=-==++,得驻点2x =-,0x =,用驻点将整个定义域分为三个区间(,2)-∞-,(2,1)--,(1,0)-,(0,)+∞.当(,2)x ∈-∞-时,0y '>,函数单调增加;当(2,1)x ∈--时,0y '<,函数单调减少;当(1,0)x ∈-时,0y '<,函数单调减少;当(0,)x ∈+∞时,0y '>,函数单调增加.故函数的单调增加区间为(,2]-∞-和[0,)+∞,单调减少区间为[2,1)--和(1,0]-;极大值(2)3f -=-,极小值(0)1f =.再求凹凸区间和拐点.因432(1)2(1)(1)x y x x -+''=-=++,故当(,1)x ∈-∞-时,0y ''<,函数为凸的;当(1,)x ∈-+∞时,0y ''>,函数为凹的,故函数的凸区间为(,1)-∞-,凹区间为(1,)-+∞.凹凸性改变的点为1x =-,不在定义域内,故函数没有拐点.7.(2007年,8分)在周长为定值l 的所有扇形中,当扇形的半径取何值时所得扇形的面积最大?解:设扇形的半径为x ,则弧长为2lx -,设扇形的面积为y ,则由题意211(2)22y l x x x lx =-=-+.令202l y x '=-+=得,4l x =.唯一的极值点即为最大值点.故当扇形的半径为4l时,扇形的面积最大.8.(2006年,10分)求函数321y x x x =--+的单调区间、极值及凹凸区间、拐点.解:函数的定义域为(,)-∞+∞.先求单调区间和极值.令2321(31)(1)0y x x x x '=--=+-=,得驻点13x =-,1x =,用驻点将整个定义域分为三个区间1(,)3-∞-,1(,1)3-,(1,)+∞.当1(,)3x ∈-∞-时,0y '>,函数单调增加;当1(,1)3x ∈-时,0y '<,函数单调减少;当(1,)x ∈+∞时,0y '>,函数单调增加.故函数的单调增加区间为1(,]3-∞-和[1,)+∞,单调减少区间为1[,1]3-;极大值132()327f -=,极小值(1)0f =. 再求凹凸区间和拐点.令620y x ''=-=,得13x=.当1(,)3x ∈-∞时,0y ''<,函数为凸的;当1(,)3x ∈+∞时,0y ''>,函数为凹的,且当13x =时,1627y =,故函数的凸区间为1(,]3-∞,凹区间为1[,)3+∞,拐点为116(,)327.9.(2006年,10分)设函数()f x 在[0,1]上连续,且()0f x >.证明方程11()0()xxf t dt dt f t +=⎰⎰在(0,1)内有且仅有一个根.证明:先证存在性.设011()()()x xF x f t dt dt f t =+⎰⎰,[0,1]x ∈.因()f x 在[0,1]上连续,故()F x 在[0,1]上也连续,且011011(0)00()()F dt dt f t f t =+=-<⎰⎰,11(1)()0()0F f t dt f t dt =+=>⎰⎰,故由零点定理可得,至少存在一点(0,1)ξ∈使得()0F ξ=,即在(0,1)内方程至少存在一个根.再证唯一性,即证()F x 的单调性.1()()0()F x f x f x '=+>,故()F x 单调增加,所以结合上面根的存在性可知,方程011()0()xxf t dt dt f t +=⎰⎰在(0,1)内有且仅有一个根.10.(2005年,8分)已知()y f x =与2arctan 0xt y e dt -=⎰在(0,0)处切线相同,写出该切线方程并求2lim ()n nfn→∞. 解:切线斜率()22arctan arctan 02011x xtx x e k e dtx --==⎛⎫'===⎪ ⎪+⎝⎭⎰,故切线方程为01(0)y x -=⋅-,即 y x =.因()y f x =过点(0,0),故(0)0f =,且(0)1f '=,故 222()()()2lim ()lim lim 2(0)211()n n n f f n n n nf f n n n→∞→∞→∞'''===='.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品
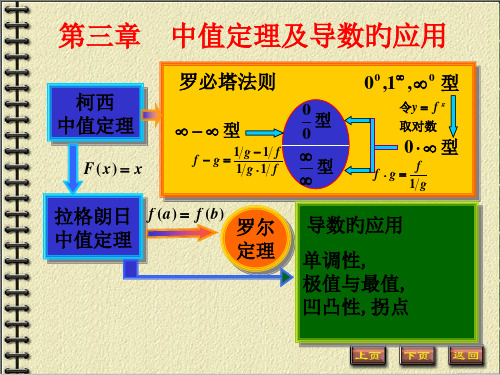
一、主要内容
Cauchy 中值定理
F(x)xபைடு நூலகம்
洛必达法则
型
f g1g1 f 1g1 f
0型 0 型
00,1,0型
令y f g 取对数
0型
f g f 1g
Lagrange 中值定理
f(a)f(b)
Rolle 定理
n0
Taylor 中值定理
常用的 泰勒公式
导数的应用
6、导数的应用
(1) 函数单调性的判定法
定理 设函数y f (x)在[a,b]上连续,(在 a,b)内 可导. 10如果在(a,b)内f (x) 0,那末函y数 f (x)在 [a,b]上单调增加; 20 如果在(a,b)内f (x) 0,那末函y数 f (x)在 [a,b]上单调减.少
(2) 函数的极值及其求法
2! 4! 6!
( 2 n )!
ln( 1 x ) x x 2 x 3 ( 1 ) n x n 1 o ( x n 1 )
23
n1
1 1 x x2 xn o(xn ) 1 x
(1 x ) m 1 mx m ( m 1) x 2 2!
m (m 1) (m n 1) x n o( x n ) n!
其 R n (中 x )f (n (n 1 )1 ())( !x x 0 )n 1(在 x 0与 x之 ) 间
常用函数的麦克劳林公式
sin x x x 3 x 5 ( 1 ) n x 2 n 1 o ( x 2 n 2 )
3! 5!
( 2 n 1)!
cos x 1 x 2 x 4 x 6 ( 1 ) n x 2 n o ( x 2 n )
定义设函数f ( x)在区间(a,b)内有定义, x0是(a,b)内 的一个点,
如果存在着点 x0的一个邻域 ,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极大值;
如果存在着点 x0的一个邻域 ,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极小值 .
f (b) F(b)
f (a) F(a)
Ff ''(())成立.
4、洛必达法则
10. 0型及 型未定式 0
定义 这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则.
20. 0 , ,00,1, 0型未定式
关键:将其它类型未定式化为洛必达法则可解决 的类型 ( 0 ), ( ) .
(3) 最大值、最小值问题
步骤:
1.求驻点和不可导点;
2.求区间端点及驻点和不可导点的函数值,比 较大小,那个大那个就是最大值,那个小那个就 是最小值; 注意:如果区间内只有一个极值,则这个极值就 是最值.(最大值或最小值)
实际问题求最值应注意:
1)建立目标函数; 2)求最值; 若目标函数只点有,唯则一该驻点 函数值即为所(求或的最最小大)值.
即f '() 0
2、拉格朗日中值定理
拉格朗日(Lagrange)中值定理 如果函数f(x) 在闭区间[a,b]上连续,在开区间(a,b)内可导,那 末在(a,b)内至少有一点(ab),使等式
f (b) f (a) f '()(ba) 成立.
有限增量公式. y f ( x 0 x ) x ( 0 1 ). 增量y的精确表达. 式
单调性,极值与最值, 凹凸性,拐点,函数 图形的描绘; 曲率;求根方法.
1、罗尔中值定理
罗尔(Rolle)定理 如果函数f (x) 在闭区间 [a,b]上连续,在开区间(a,b) 内可导,且在区间端 点的函数值相等,即f (a) f (b),那末在(a,b) 内至少有一点(a b),使得函数f (x) 在该 点的导数等于零,
驻点和不可导点统称为临界点.
定理(第一充分条件)
(1)如果x(x0 ,x0),有f'(x)0;而x(x0,x0 ),
有f'(x)0,则f(x)在x0处取得极大值.
(2)如果x(x0 ,x0),有f'(x)0;而x(x0,x0 )
有f'(x)0,则f(x)在x0处取得极小值.
(3)如果当x(x0 ,x0)及x(x0,x0 )时, f'(x)符
推论 如果函 f(x)在 数区I上 间的导数, 恒为 那末 f(x)在区I上 间是一个 . 常数
3、柯西中值定理
柯西(Cauchy)中值定理 如果函数f (x)及F(x)
在闭区间[a,b]上连续,在开区间(a,b)内可导,且F'(x)
在(a,b)内每一点处均不为零,那末在(a,b)内至少
有一点(a b),使等式
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
极值是函数的局部性概念:极大值可能小于极小 值,极小值可能大于极大值.
定理(必要条件) 设 f(x )在 点 x 0 处 具 有 导 数 ,且 在 x 0 处 取 得 极 值 ,那 末 必 定 f'(x 0 ) 0 .
定义 使导数 (即 为 方 f零 (x) 程 0的点 实 )叫根 做函 f(x)的 数驻 . 点
0
注意:洛必达法则的使用条件.
5、泰勒中值定理
泰勒(Taylor)中值定理 如果函数f(x)在含有x0 的某个开区间(a,b)内具有直到(n1)阶的导数,则 当x在(a,b)内时, f(x)可以表示为(xx0)的一 个n次多项式与一个余项Rn(x)之和:
f(x)f(x0)f(x0)(xx0)f2(!x0)(xx0)2 f(nn)(!x0)(xx0)nRn(x)
号相同,则f(x)在x0处无极值.
定理(第二充分条件)设f(x)在x0 处具有二阶导数, 且f'(x0)0, f''(x0)0, 那末 (1)当f''(x0)0时, 函数f(x)在x0 处取得极大值; (2)当f''(x0)0时, 函数f(x)在x0 处取得极小值.
求极值的步骤:
(1)求导 f(数 x); (2)求驻点, f(x即 )0方 的;程 根 (3)检查 f(x)在驻点左右的f正 (x)在 负号 该点的,判 符断 号极;值点 (4) 求极值.
