MATLAB基于BP神经网络PID控制程序

合集下载

基于bp神经网络pid控制程序

wi_1=wi;wi_2=wi;wi_3=wi;
wo=[1.0438 0.5478 0.8682 0.1446 0.1537;
0.1716 0.5811 1.1214 0.5067 0.7370;
1.0063 0.7428 1.0534 0.7824 0.6494];
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_2=y_1;y_1=yout(k);
wo_3=wo_2;
wo_2=wo_1;
wo_1=wo;
wi_3=wi_2;
wi_2=wi_1;
%wo=0.50*rands(Out,H);
wo_1=wo;wo_2=wo;wo_3=wo;
end
x=[0,0,0];
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y_1=0;y_2=0;y_3=0;
Oh=zeros(H,1); %Output from NN middle layer
for l=1:1:Out
K(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); %Getting kp,ki,kd
end
kp(k)=K(1);ki(k)=K(2);kd(k)=K(3);
Kpid=[kp(k),ki(k),kd(k)];
wi_1=wi;
error_2=error_1;
error_1=error(k);
end
figure(1);
plot(time,rin,'r',time,yout,'b');
xlabel('time(s)');ylabel('rin,yout');

MATLAB基于BP神经网络PID控制程序

MATLAB基于BP神经网络PID控制程序>> %BP based PID Controlclear all;close all;xite=0.20; %学习速率alfa=0.01; %惯性因子IN=4;H=5;Out=3; %NN Structurewi=[-0.6394 -0.2696 -0.3756 -0.7023;-0.8603 -0.2013 -0.5024 -0.2596;-1.0749 0.5543 -1.6820 -0.5437;-0.3625 -0.0724 -0.6463 -0.2859;0.1425 0.0279 -0.5406 -0.7660];%wi=0.50*rands(H,IN); %隐含层加权系数wi初始化wi_1=wi;wi_2=wi;wi_3=wi;wo=[0.7576 0.2616 0.5820 -0.1416 -0.1325;-0.1146 0.2949 0.8352 0.2205 0.4508;0.7201 0.4566 0.7672 0.4962 0.3632];%wo=0.50*rands(Out,H); %输出层加权系数wo初始化wo_1=wo;wo_2=wo;wo_3=wo;ts=20; %采样周期取值x=[0,0,0]; %比例，积分，微分赋初值u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;y_1=0;y_2=0;y_3=0;Oh=zeros(H,1); %Output from NN middle layer 隐含层的输出I=Oh; %Input to NN middle layer 隐含层输入error_2=0;error_1=0;for k=1:1:500 %仿真开始，共500步time(k)=k*ts;rin(k)=1.0;%Delay plantsys=tf(1.2,[208 1],'inputdelay',80); %建立被控对象传递函数? dsys=c2d(sys,ts,'zoh'); %把传递函数离散化? [num,den]=tfdata(dsys,'v'); %离散化后提取分子、分母yout(k)=-den(2)*y_1+num(2)*u_5;error(k)=rin(k)-yout(k);xi=[rin(k),yout(k),error(k),1];%经典增量式数字PID 的控制算式为：()(1)(()(1))()(()2(1)(2))p i d u k u k k e k e k k e k k e k e k e k =-+--++--+- BP 神经网络PID 的控制算式为：()()()333123()(1)(()(1))()(()2(1)(2))u k u k o e k e k o e k o e k e k e k =-+--++--+- x(1)=error(k)-error_1; %比例输出x(2)=error(k); %积分输出x(3)=error(k)-2*error_1+error_2; %微分输出epid=[x(1);x(2);x(3)];I=xi*wi';% 隐含层的输入，即：输入层输入*权值for j=1:1:H Oh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j))); %Middle Layer 在激活函数作用下隐含层的输出 endK=wo*Oh; %Output Layer 输出层的输入，即：隐含层的输出*权值 for l=1:1:Out K(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); %Getting kp,ki,kd 输出层的输出，即三个pid 控制器的参数endkp(k)=K(1);ki(k)=K(2);kd(k)=K(3);Kpid=[kp(k),ki(k),kd(k)];du(k)=Kpid*epid;u(k)=u_1+du(k);if u(k)>=10 % Restricting the output of controller 控制器饱和环节u(k)=10;endif u(k)<=-10u(k)=-10;end%以下为权值wi、wo的在线调整，参考刘金琨的《先进PID控制》dyu(k)=sign((yout(k)-y_1)/(u(k)-u_1+0.0000001));%Output layer 输出层for j=1:1:OutdK(j)=2/(exp(K(j))+exp(-K(j)))^2;endfor l=1:1:Outdelta3(l)=error(k)*dyu(k)*epid(l)*dK(l);endfor l=1:1:Outfor i=1:1:Hd_wo=xite*delta3(l)*Oh(i)+alfa*(wo_1-wo_2);endendwo=wo_1+d_wo+alfa*(wo_1-wo_2);%Hidden layerfor i=1:1:HdO(i)=4/(exp(I(i))+exp(-I(i)))^2;endsegma=delta3*wo;for i=1:1:Hdelta2(i)=dO(i)*segma(i);endd_wi=xite*delta2'*xi;wi=wi_1+d_wi+alfa*(wi_1-wi_2);%Parameters Update 参数更新u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k); y_2=y_1;y_1=yout(k);wo_3=wo_2;wo_2=wo_1;wo_1=wo;wi_3=wi_2;wi_2=wi_1;wi_1=wi;error_2=error_1;error_1=error(k);end%仿真结束，绘图figure(1);plot(time,rin,'r',time,yout,'b'); xlabel('time(s)');ylabel('rin,yout'); figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error'); figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u'); figure(4);subplot(311);plot(time,kp,'r');xlabel('time(s)');ylabel('kp'); subplot(312);plot(time,ki,'g');xlabel('time(s)');ylabel('ki');subplot(313);plot(time,kd,'b');xlabel('time(s)');ylabel('kd');。

基于BP神经网络的PID控制器及仿真

基于BP神经网络的PID控制器及仿真2010/5/14/11:391. 引言PID（比例-积分-微分）控制器作为最早实用化的控制器已有50多年历史，因其具有算法简单、鲁棒性好、可靠性高、直观性好等优点被广泛的应用于工业过程控制及运动控制中[1]。

常规PID控制效果的优劣，不仅仅取决于控制系统模型的精确程度，还必须调整好三个参数的关系，而这种关系不一定是简单的线性组合。

实际的工业过程及运动过程往往具有时变性、变参数、变结构等不确定性及很强的非线性，精确的数学模型难以建立，此外，常规PID还有实现在线调整困难，参数间相互影响，参数整定时间长等缺点，难以取得理想的控制效果。

随着控制理论的发展，将应用广泛的PID控制器与智能控制理论相结合[2]成为智能控制研究的新方向，神经网络算法具有逼近任意非线性表达能力，很强的自学习能力和概括推广能力，在解决高度非线性和不确定系统方面有很大的的潜能，应用神经网络，可以从复杂的PID三个参数组合中寻求最佳的线性组合，使神经网络和PID本质结合。

从而使得控制器具有较好的自适应性，实现参数的自动实时调节，适应过程的变化，提高系统了的鲁棒性和可靠性。

2. BP神经网络2.1 BP神经网络的构成及设计[3]BP神经网络是一种具有三层或三层以上的神经网络，包括输入层、隐含层、输出层，上下层之间实现全连接，而每层神经元之间无连接。

当一对学习样本提供给网络后，神经元的激活值从输入层经各中间层向输出层传播，在输出层的各神经元获得网络的输入响应。

接下来，按照减少目标输出与实际误差的方向，从输出层经过各中间层逐层修正各连接权值，最后回到输入层，这种算法即BP算法。

随着这种误差逆的传播修正不断进行，网络对输入模式响应的正确率也不断上升。

（1）输入输出层的设计输入层的设计可以根据需要求解的问题和数据表示方式确定，若输入信号为模拟波形，那么输入层可以根据波形的采样点数目撅腚输入单元的维数，也可以用一个单元输入，这是输入样本为采样的时间序列。

基于BP神经网络PID整定原理和算法步骤_精品

基于BP神经网络PID整定原理和算法步骤_精品1.收集实验数据：首先需要收集系统的输入和输出数据，包括输入变量（如温度、压力等）和输出变量（如阀门开度、电机转速等）。

同时，需要记录系统的环境条件，如温度、湿度等。

2.数据预处理：对收集到的数据进行预处理，包括数据清洗、去除异常值等。

确保数据质量的同时，也要注意保持数据的连续性和完整性。

3.构建神经网络：使用BP神经网络构建PID整定模型。

BP神经网络是一种具有前馈和反馈连接的多层感知器，可以用于解决非线性问题。

根据PID控制器的输入和输出关系，设计网络的输入层、隐含层和输出层。

4. 网络训练：使用收集到的实验数据对神经网络进行训练。

训练的目标是使网络的输出尽可能接近实际输出，从而建立输入和输出之间的映射关系。

可以使用误差反向传播算法（Backpropagation）来调整网络的权重和阈值。

5.网络评估：训练完成后，使用预留的一部分数据对网络进行评估。

通过比较网络的输出和实际输出，可以评估网络的准确性和稳定性。

如果评估结果不满意，可以进行网络调整和再训练。

6. PID参数计算：根据已经训练好的神经网络，可以使用PID整定算法计算PID参数值。

常用的PID整定算法包括Ziegler-Nichols方法、Chien-Hrones-Reswick方法等。

根据系统的响应特性和性能指标，选择合适的算法进行参数计算。

7.参数调整和优化：根据实际应用需求，对计算得到的PID参数进行调整和优化。

可以通过仿真和实验验证的方式，不断调整参数，直到满足系统的性能要求。

8.实际应用：将优化后的PID参数应用到实际控制系统中。

根据系统的特点和要求，可以进一步进行参数调整和优化。

同时，需要不断监测和评估系统的性能，并及时调整和优化PID参数。

综上所述，基于BP神经网络的PID整定原理和算法步骤主要包括数据收集、数据预处理、神经网络构建、网络训练、网络评估、PID参数计算、参数调整和优化以及实际应用等步骤。

基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计一、引言PID控制系统是目前工业控制中广泛应用的一种基本控制方法，它通过测量控制系统的偏差来调节系统的输出，以实现对控制对象的稳定控制。

然而，传统的PID控制器需要事先对系统建模，并进行参数调整，工作效果受到控制对象模型的准确性和外部干扰的影响。

而BP神经网络具有非线性映射、自适应性强、鲁棒性好等优点，可以有效地克服传统PID控制器的缺点。

因此，基于BP神经网络的PID控制系统设计成为当前研究的热点之一二、基于BP神经网络的PID控制系统设计理论1.PID控制器设计原理PID控制器是由比例环节（Proportional）、积分环节（Integral）和微分环节（Derivative）组成的控制器，其输出信号可以表示为：u(t) = Kp*e(t) + Ki*∫e(t)dt + Kd*(de(t)/dt)，其中e(t)为控制系统的输入偏差，t为时间，Kp、Ki和Kd分别为比例系数、积分系数和微分系数。

2.BP神经网络理论BP神经网络是一种前馈型神经网络，通过反向传播算法对输入信号进行学习和训练，从而得到最优的网络结构和参数。

BP神经网络由输入层、隐层和输出层组成，其中每个神经元与上、下相邻层之间的神经元互相连接，并具有非线性的激活函数。

3.基于BP神经网络的PID控制系统设计理论基于BP神经网络的PID控制系统设计的核心思想是将BP神经网络作为PID控制器的自适应调节器，根据控制对象的输入信号和输出信号之间的误差进行训练和学习，通过调整BP神经网络的权重和阈值来实现PID 控制器的参数调节，从而提高控制系统的稳定性和鲁棒性。

三、基于BP神经网络的PID控制系统设计步骤1.系统建模首先，需要对待控制对象进行建模，获取其数学模型。

对于一些复杂的非线性系统，可以采用黑箱建模的方法，利用系统的输入和输出数据进行数据拟合，获取系统的数学模型。

2.BP神经网络训练将系统的数学模型作为BP神经网络的训练集，通过反向传播算法对BP神经网络进行训练，得到最优的网络结构和参数。

基于BP神经网络PID整定原理和算法步骤

基于BP神经网络PID整定原理和算法步骤BP神经网络是一种常用的非线性拟合和模式识别方法，可以在一定程度上应用于PID整定中，提高调节器的自适应性。

下面将详细介绍基于BP神经网络的PID整定原理和算法步骤。

一、基本原理：BP神经网络是一种具有反馈连接的前向人工神经网络，通过训练样本的输入和输出数据，通过调整神经元之间的连接权重来模拟输入和输出之间的映射关系。

在PID整定中，可以将PID控制器的参数作为网络的输入，将控制效果指标作为网络的输出，通过训练网络来获取最优的PID参数。

二、算法步骤：1.确定训练数据集：选择一组适当的PID参数和相应的控制效果指标作为训练数据集，包括输入和输出数据。

2.构建BP神经网络模型：确定输入层、隐藏层和输出层的神经元数量，并随机初始化神经元之间的连接权重。

3.设置训练参数：设置学习速率、误差收敛条件和训练迭代次数等训练参数。

4.前向传播计算输出：将训练数据集的输入作为网络的输入，通过前向传播计算得到网络的输出。

5.反向传播更新权重：根据输出与期望输出之间的误差，利用误差反向传播算法来调整网络的连接权重，使误差逐渐减小。

6.判断是否达到收敛条件：判断网络的训练误差是否满足收敛条件，如果满足则跳转到第8步，否则继续迭代。

7.更新训练参数：根据训练误差的变化情况，动态调整学习速率等训练参数。

8.输出最优PID参数：将BP神经网络训练得到的最优权重作为PID 控制器的参数。

9.测试PID控制器：将最优PID参数应用于实际控制系统中，观察控制效果并进行评估。

10.调整PID参数：根据实际控制效果，对PID参数进行微调，以进一步优化控制性能。

三、应用注意事项：1.训练数据集的选择应尽量全面、充分，覆盖各种不同工况和负载情况。

2.隐藏层神经元数量的选择应根据实际情况进行合理调整，避免过拟合或欠拟合现象。

3.学习速率和训练迭代次数的设置应根据系统复杂度和训练误差的变化情况进行调整。

基于BP神经网络的PID控制器及其MATLAB仿真

（4）
（ =1，2，．．．n）
（5）
图 2 基于 BP 网络的 PID 控制框图
中国新技术新产品
- 13 -
由于输出层的神经元的活化函数不能为负数，取非负的 Sigmoid 函数：
性能指标函数为：（6）
由梯度下降法，我们取加权系数的修整量为:
（7）其中，为学习效率；为惯性系数。
（8）
这里，
未知，为表示其变化轨迹，
用符号函数
取代。
在 PID 控制器的应用中，使神经元的输出状
态对应于 PID 控制器的三个可调参数 Kp、Ki、Kd，
高新技术
中国新技术新产品 2009 NO.10
China New Technologies and Products
基于 BP 神经网络的 PID 控制器及其 MATLAB 仿真
谢利英（衡阳财经工业职业技术学院，湖南衡阳 421008）
摘要: PID 控制算法简单、应用广泛，既能消除余差，又能提高系统的稳定性,但其 P 环节、I 环节、D 环节的控制参数却参数难以整定；BP 神经网络算法具有很强的数字运算能力，因此，可通过 BP 神经网络自学习、加权系数调整，实现 PID 的最优调整，本文以小车控制为例，利用 BP 神经网络的学习能力进行 PID 参数的在线整定，并进行了 MATLAB 仿真，结果表明，利用 BP 神经网络可很快的找到 PID 的控制参数。关键词：BP 网络；PID 控制；MATLAB 仿真
行 PID 控制器的调整。通过仿真可以看出，利用
BP 神经网络进行 PID 控制，能很快得到最佳的
kp、ki、kd 值，从而有效控制被控对象，为工业
应用提供了一种快速控制手段。由于基于 BP 网络

基于BP神经网络的PID控制器的设计

基于BP神经网络的PID控制器的设计简介：PID控制器是一种常用的控制方法，可以使控制系统快速、稳定地对目标进行调节。

然而，传统的PID控制器需要依赖经验的设置参数，很难适用于非线性复杂的系统。

为了改善这一问题，本文提出了一种基于BP神经网络的PID控制器的设计方法。

一、神经网络介绍BP神经网络是一种常用的人工神经网络，通过反向传播算法进行学习和适应。

它可以用来建模非线性关系、解决分类和回归问题等。

BP神经网络由输入层、隐藏层和输出层构成，通过调整权重和偏置项，使得网络的输出接近于期望输出。

二、PID控制器的基本原理PID控制器是由比例（P）、积分（I）和微分（D）三个部分组成的，它们分别对应了系统的比例性能、整定性能和微分性能。

PID控制器的输出是由目标值与实际值之间的误差来决定的。

比例作用是根据误差的大小进行调节，积分作用是根据误差的积分值进行调节，微分作用是根据误差的变化率进行调节。

三、BP神经网络的PID控制器设计1.建立神经网络模型：确定输入层节点数、隐藏层节点数和输出层节点数。

2.确定权重和偏置项的初始值：可以使用随机数进行初始化。

3.设置训练样本集：训练样本集包括输入和输出的数据，可以根据实际情况进行设置。

4.确定学习率和训练次数：学习率决定了网络的更新速度，训练次数决定了网络的学习程度。

5.神经网络训练：使用BP算法对神经网络进行训练，通过反向传播算法调整权重和偏置项。

6.测试神经网络性能：使用测试数据对神经网络进行测试，评估其性能是否满足要求。

7.参数调整：根据测试结果对PID控制器的参数进行调整，使得神经网络对系统的控制更加精确。

四、实验结果分析通过对比传统的PID控制器和基于BP神经网络的PID控制器，可以发现基于BP神经网络的PID控制器具有更好的系统控制性能。

因为BP神经网络能够自适应地调整参数，适应非线性复杂系统的控制要求。

总结：基于BP神经网络的PID控制器是一种有效的控制方法，可以提高系统控制的精度和稳定性。

基于BP神经网络PID整定原理和算法步骤

基于BP神经网络PID整定原理和算法步骤PID（比例、积分、微分）控制是一种常用的控制算法，用于调节系统的输出使其接近期望值。

BP（Back Propagation）神经网络是一种具有强大机器学习能力的神经网络模型。

基于BP神经网络的PID整定方法结合了PID控制算法和神经网络的优点，通过神经网络的学习能力优化PID 参数的选择，提高了控制系统的鲁棒性和适应性。

以下是基于BP神经网络的PID整定原理和算法步骤：一、原理：1.神经网络模型：建立一个具有输入层、隐藏层和输出层的BP神经网络模型，其中输入层接收系统的输入信号，输出层输出控制信号的PID 参数，隐藏层的神经元通过学习调整连接权重以优化参数选择。

2.参数训练：基于反向传播算法，通过输入输出样本对神经网络进行训练，使其学习输入输出之间的映射关系。

训练过程是一个迭代过程，通过不断调整连接权重和偏置，使神经网络的输出结果逼近期望值。

3.PID原理：PID控制算法根据系统当前误差，通过比例、积分和微分项生成控制信号。

调节PID参数可以改变控制信号的响应特性，使其更好地适应控制对象的动态特性。

二、算法步骤：1.数据采集：收集系统的输入输出数据，用于训练神经网络模型。

2.数据预处理：对采集到的数据进行预处理，包括去除噪声、归一化等处理，以提高神经网络的训练效果。

3.网络构建：根据需要构建BP神经网络模型，包括输入层、隐藏层和输出层。

隐藏层的神经元数量和层数可以根据实际情况进行选择。

4.神经网络训练：将预处理后的数据输入到神经网络中，利用反向传播算法对神经网络进行训练。

根据实际需求设置训练的轮数和学习率等参数。

5.训练结果评估：通过评估神经网络的训练结果，包括误差曲线、训练时间等指标，来判断训练是否达到预期效果。

6.PID参数优化：根据神经网络的输出结果调整PID的比例、积分和微分参数。

可以通过试错法或者自适应控制方法对参数进行调整。

7.控制性能评估：利用调整后的PID参数进行控制，通过评估系统的性能指标，例如超调量、调整时间等，来判断PID参数的选择是否合理。

毕业设计(论文)_基于BP神经网络的PID控制器设计

神经网络在控制系统中的应用提高了整个系统的信息系统处理能力和适应能力，提高了系统的智能水平。此外，神经网络是由大量反映非线性本质特征的神经元互相连接而成的复杂网络系统。它具有并行计算和分布式数据处理的功能,可实时处理大量数据，具有逼近任意连续有界非线性函数的能力，对于非线性系统和不确定性系统，无疑是一种解决问题的有效途径。人工神经网络是由简单的处理单元所组成的大量并行分布的处理器，这种处理机具有存储和应用经验知识的自然特性，它与人脑的相似之处概括为两个方面：一是通过学习过程利用神经网络从外部环境中获取知识；二是内部神经元（突触权值）用来存储获取的知识信息[2]。
（2）汽车行业。汽车自动驾驶系统、保险行为分析。
（3）银行业。支票和其他文档阅览器贷款评估器。
（4）国防领域。武器操纵控制、目标跟踪、物体识别、各种新的传感器。
（5）电子领域。编码序列预测、集成电路芯片的设计、过程控制芯片、故障分析、机器视觉声音合成、非线性建模。
（6）娱乐领域。动画、特效设计、市场预测。
阶跃响应是指将一个阶跃输入加到系统上时，系统的输出。稳态误差是指系统的响应进入稳态后，系统的期望输出与实际输出之差。控制系统的性能可以用稳、准、快三个字来描述。稳是指系统的稳定性，一个系统要能正常工作，首先必须是稳定的，从阶跃响应上看应该是收敛的；准是指控制系统的准确性、控制精度，通常用稳态误差来描述，它表示系统输出稳态值与期望值之差；快是指控制系统响应的快速性，通常用上升时间来定量描述。
在模拟控制系统中，控制器最常用的控制规律是PID控制。PID的控制规律为：
（2.1）
式中， —比例系数； —积分时间常数； —微分时间常数[4]。
比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差。

基于BP算法的神经网络PID控制器设计及仿真

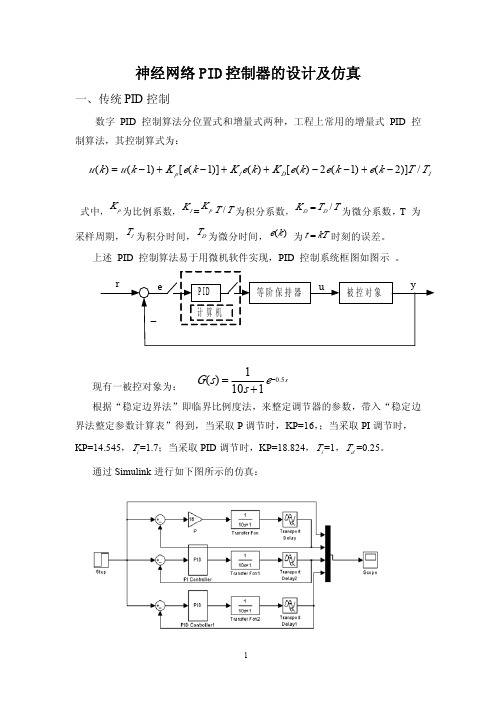
se s s G 5.01101)(−+=()(1)[(1)]()[()2(1)(2)]/p I D Iu k u k K e k K e k K e k e k e k T T =−+−++−−+−神经网络PID 控制器的设计及仿真一、传统PID 控制数字PID 控制算法分位置式和增量式两种，工程上常用的增量式PID 控制算法，其控制算式为：式中，pK 为比例系数，I K =p K /T T为积分系数，/D D K T T =为微分系数，T 为采样周期，IT 为积分时间，DT 为微分时间，()e k 为t kT =时刻的误差。

上述PID 控制算法易于用微机软件实现，PID 控制系统框图如图示。

现有一被控对象为：根据“稳定边界法”即临界比例度法，来整定调节器的参数，带入“稳定边界法整定参数计算表”得到，当采取P 调节时，KP=16，；当采取PI 调节时，KP=14.545，i T =1.7；当采取PID 调节时，KP=18.824，i T =1，d T =0.25。

通过Simulink 进行如下图所示的仿真：仿真结果如下图所示：二、基于BP算法的PID控制基于BP神经网络的PID控制系统结构如下图所示，控制器由两个部分组成：①经典的PID控制器：直接对被控对象进行闭环控制，并且KP,KI,KD三个参数为在线P,I,D整定；②神经网络NN：根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化。

即使神经网络的输出层神经元的输出状态对应于PID控制器的三个可调参数KP,KI,KD，通过神经网络的自学习、调整权系数，从而使其稳定P,I,D状态对应于某种最优控制规律下的PID控制器参数。

在这里设计的BP网络采用结构简单的三层BP神经网络，其结构如下图所示，有m个输入节点、Q个隐含层节点、3个输出节点。

输入节点对应所选的系统运行状态量，如系统不同时刻的输入量和输出量等，必要时要进行归一化K K K。

基于BP神经网络PID整定原理和算法步骤_精品

基于BP神经网络PID整定原理和算法步骤_精品1.基本原理PID控制器是一种经典的闭环控制算法，由比例项、积分项和微分项组成。

BP神经网络是一种具有自适应性的模型，可以根据输入和输出之间的关系来自动调整权重和偏置。

2.算法步骤2.1样本数据的采集在PID控制系统中，需要采集一些样本数据来训练神经网络。

可以通过试验或仿真的方式，对控制系统进行加扰动或变动目标值的操作，得到系统的输入与输出数据。

2.2数据的预处理对采集到的数据进行预处理，主要包括去除噪声、标准化等操作，使得数据更加准确和可靠。

2.3神经网络的构建根据PID控制器的结构，构建对应的BP神经网络模型。

一般来说，BP神经网络由输入层、隐含层和输出层组成。

输入层接收系统的输入数据，隐含层进行特征提取和非线性变换，输出层得到控制系统的输出。

2.4神经网络的训练将预处理后的样本数据输入到神经网络中进行训练。

训练过程中，通过调整网络的权重和偏置，使得网络的输出与期望的输出之间的误差最小化。

2.5PID参数的优化在神经网络训练完成后，可以得到最优的网络结构和权重。

根据神经网络的输出，可以得到相应的PID参数。

一般来说，比例项的参数可直接取输出层的权重，积分项和微分项的参数则可以根据网络的偏置来计算。

2.6控制系统的实时调整将优化得到的PID参数应用到实际的控制系统中。

在控制过程中，根据系统的实时反馈信号，可以通过PID控制器进行实时的调整，使得系统的响应特性达到最佳。

总结：基于BP神经网络的PID整定，通过训练神经网络来寻找最佳的PID 参数，以达到控制系统的最优响应特性。

该方法可以应用于各种复杂的控制系统中，具有很好的适应性和鲁棒性。

但需要注意的是，BP神经网络的训练过程需要较长的时间和大量的样本数据，因此在实际应用中需要进行一定的优化和加速。

MATLAB基于BP神经网络PID控制程序.pdf

MATLAB基于BP神经网络PID控制程序>> %BP based PID Controlclear all;close all;xite=0.20; %学习速率alfa=0.01; %惯性因子IN=4;H=5;Out=3; %NN Structurewi=[-0.6394 -0.2696 -0.3756 -0.7023;-0.8603 -0.XXXX -0.5024 -0.2596;-1.0749 0.5543 -1.6820 -0.5437;-0.3625 -0.0724 -0.6463 -0.2859;0.1425 0.0279 -0.5406 -0.7660];%wi=0.50*rands(H,IN); %隐含层加权系数wi初始化wi_1=wi;wi_2=wi;wi_3=wi;wo=[0.7576 0.2616 0.5820 -0.1416 -0.1325;-0.1146 0.2949 0.8352 0.2205 0.4508;0.7201 0.4566 0.7672 0.4962 0.3632];%wo=0.50*rands(Out,H); %输出层加权系数wo初始化wo_1=wo;wo_2=wo;wo_3=wo;ts=20; %采样周期取值x=[0,0,0]; %比例，积分，微分赋初值u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;y_1=0;y_2=0;y_3=0;Oh=zeros(H,1); %Output from NN middle layer 隐含层的输出I=Oh; %Input to NN middle layer 隐含层输入error_2=0;error_1=0;for k=1:1:500 %仿真开始，共500步time(k)=k*ts;rin(k)=1.0;%Delay plantsys=tf(1.2,[208 1],'inputdelay',80); %建立被控对象传递函数? dsys=c2d(sys,ts,'zoh'); %把传递函数离散化? [num,den]=tfdata(dsys,'v'); %离散化后提取分子、分母yout(k)=-den(2)*y_1+num(2)*u_5;error(k)=rin(k)-yout(k);xi=[rin(k),yout(k),error(k),1];%经典增量式数字PID 的控制算式为：()(1)(()(1))()(()2(1)(2))p i d u k u k k e k e k ke k k e k e k e k =−+−−++−−+− BP 神经网络PID 的控制算式为：()()()333123()(1)(()(1))()(()2(1)(2))u k u k o e k e k o e k o e k e k e k =−+−−++−−+− x(1)=error(k)-error_1; %比例输出x(2)=error(k); %积分输出x(3)=error(k)-2*error_1+error_2; %微分输出 epid=[x(1);x(2);x(3)];I=xi*wi';% 隐含层的输入，即：输入层输入*权值 for j=1:1:H Oh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j))); %Middle Layer 在激活函数作用下隐含层的输出endK=wo*Oh; %Output Layer 输出层的输入，即：隐含层的输出*权值 for l=1:1:OutK(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); %Getting kp,ki,kd 输出层的输出，即三个pid 控制器的参数end kp(k)=K(1);ki(k)=K(2);kd(k)=K(3);Kpid=[kp(k),ki(k),kd(k)];du(k)=Kpid*epid;u(k)=u_1+du(k);if u(k)>=10 % Restricting the output of controller 控制器饱和环节 u(k)=10; endif u(k)<=-10u(k)=-10;end%以下为权值wi 、wo 的在线调整，参考刘金琨的《先进PID 控制》dyu(k)=sign((yout(k)-y_1)/(u(k)-u_1+0.0000001));%Output layer 输出层for j=1:1:OutdK(j)=2/(exp(K(j))+exp(-K(j)))^2;endfor l=1:1:Outdelta3(l)=error(k)*dyu(k)*epid(l)*dK(l); endfor l=1:1:Outfor i=1:1:Hd_wo=xite*delta3(l)*Oh(i)+alfa*(wo_1-wo_2); endendwo=wo_1+d_wo+alfa*(wo_1-wo_2);%Hidden layerfor i=1:1:HdO(i)=4/(exp(I(i))+exp(-I(i)))^2;endsegma=delta3*wo;for i=1:1:Hdelta2(i)=dO(i)*segma(i);endd_wi=xite*delta2'*xi;wi=wi_1+d_wi+alfa*(wi_1-wi_2);%Parameters Update 参数更新u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k); y_2=y_1;y_1=yout(k);wo_3=wo_2;wo_2=wo_1;wo_1=wo;wi_3=wi_2;wi_2=wi_1;wi_1=wi;error_2=error_1;error_1=error(k);end%仿真结束，绘图figure(1);plot(time,rin,'r',time,yout,'b'); xlabel('time(s)');ylabel('rin,yout'); figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error'); figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u');figure(4);subplot(311);plot(time,kp,'r');xlabel('time(s)');ylabel('kp'); subplot(312);plot(time,ki,'g');xlabel('time(s)');ylabel('ki'); subplot(313);plot(time,kd,'b');xlabel('time(s)');ylabel('kd');。

基于BP神经网络的PID自整定程序源码

基于BP神经网络的PID自整定程序源码最近在学习神经网络，并打算设计基于BP神经网络的PID参数自整定控制器。

到处找资料，发现介绍这方面的资料不少，但都说得比较泛。

其实，大道理我们都懂，却不知道一些实际的操作问题，比如如何用MATLAB进行仿真。

看了些资料，发现现在仿真基于BP神经网络的PID控制器的方法有以下几种:1)编写代码实现。

直接编写M文件，用代码的方式来实现BP网络的权值调整，以及最终的控制器输出等。

2)将神经PID控制器编写成S函数，然后将其封装成simulink模块，直接在Simulink中搭建系统模型。

这种方式的好处是系统结构比较直观，而且不需要将被控对象用代码来表示，但S函数编写很困难，对于一般人来说好像不好掌握。

3)将神经PID控制器编写成M函数，然后同样在Simulink中搭建模块。

不过这种方法我还没看到有具体的实例，只是听人家这样说过。

%BP based PID Controlclear all;close all;xite=0.25;alfa=0.05;S=2; %Signal typeIN=4;H=5;Out=3; %NN Structureif S==1 %Step Signalwi=[-0.6394 -0.2696 -0.3756 -0.7023;-0.8603 -0.2013 -0.5024 -0.2596;-1.0749 0.5543 -1.6820 -0.5437;-0.3625 -0.0724 -0.6463 -0.2859;0.1425 0.0279 -0.5406 -0.7660]; %wi=0.50*rands(H,IN);wi_1=wi;wi_2=wi;wi_3=wi;wo=[0.7576 0.2616 0.5820 -0.1416 -0.1325;-0.1146 0.2949 0.8352 0.2205 0.4508;0.7201 0.4566 0.7672 0.4962 0.3632]; %wo=0.50*rands(Out,H); wo_1=wo;wo_2=wo;wo_3=wo;endif S==2 %Sine Signalwi=[-0.2846 0.2193 -0.5097 -1.0668;-0.7484 -0.1210 -0.4708 0.0988;-0.7176 0.8297 -1.6000 0.2049;-0.0858 0.1925 -0.6346 0.0347;0.4358 0.2369 -0.4564 -0.1324]; %wi=0.50*rands(H,IN);wi_1=wi;wi_2=wi;wi_3=wi;wo=[1.0438 0.5478 0.8682 0.1446 0.1537;0.1716 0.5811 1.1214 0.5067 0.7370;1.0063 0.7428 1.0534 0.7824 0.6494]; %wo=0.50*rands(Out,H); wo_1=wo;wo_2=wo;wo_3=wo;endx=[0,0,0];u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;y_1=0;y_2=0;y_3=0;Oh=zeros(H,1); %Output from NN middle layer I=Oh; %Input to NN middle layer error_2=0;error_1=0;ts=0.001;for k=1:1:6000time(k)=k*ts;rin(k)=1.0;%Unlinear modela(k)=1.2*(1-0.8*exp(-0.1*k));yout(k)=a(k)*y_1/(1+y_1^2)+u_1;error(k)=rin(k)-yout(k);xi=[rin(k),yout(k),error(k),1];x(1)=error(k)-error_1;x(2)=error(k);x(3)=error(k)-2*error_1+error_2;epid=[x(1);x(2);x(3)];I=xi*wi';for j=1:1:HOh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j))); %Middle Layer endK=wo*Oh; %Output Layerfor l=1:1:OutK(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); %Getting kp,ki,kdendkp(k)=K(1);ki(k)=K(2);kd(k)=K(3); Kpid=[kp(k),ki(k),kd(k)]; du(k)=Kpid*epid;u(k)=u_1+du(k);if u(k)>=10 % Restricting the output of controlleru(k)=10;endif u(k)<=-10u(k)=-10;enddyu(k)=sign((yout(k)-y_1)/(u(k)-u_1+0.0000001));%Output layerfor j=1:1:OutdK(j)=4/(exp(K(j))+exp(-K(j)))^2;delta3(j)=error(k)*dyu(k)*epid(j)*dK(j); endfor l=1:1:Outfor i=1:1:Hd_wo=xite*delta3(l)*Oh(i)+alfa*(wo_1-wo_2);endendwo=wo_1+d_wo+alfa*(wo_1-wo_2); %Hidden layerfor i=1:1:HdO(i)=4/(exp(I(i))+exp(-I(i)))^2; endsegma=delta3*wo;for i=1:1:Hdelta2(i)=dO(i)*segma(i);endd_wi=xite*delta2'*xi;wi=wi_1+d_wi+alfa*(wi_1-wi_2);%Parameters Updateu_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k); y_2=y_1;y_1=yout(k);wo_3=wo_2;wo_2=wo_1;wo_1=wo;wi_3=wi_2;wi_2=wi_1;wi_1=wi;error_2=error_1;error_1=error(k);endfigure(1);plot(time,rin,'r',time,yout,'b');xlabel('time(s)');ylabel('rin,yout'); figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error'); figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u'); figure(4);subplot(311);plot(time,kp,'r');xlabel('time(s)');ylabel('kp'); subplot(312); plot(time,ki,'g');xlabel('time(s)');ylabel('ki'); subplot(313); plot(time,kd,'b');xlabel('time(s)');ylabel('kd');。

基于BP神经网络的自整定PID控制的MATLAB程序代码

基于BP神经网络的自整定PID控制仿真在工业控制中，PID控制是工业控制中最常用的方法。

这是因为PID控制器结构简单、实现简单，控制效果良好，已得到广泛应用。

但是，PID具有一定的局限性：被控制对象参数随时间变化时，控制器的参数难以自动调整以适应外界环境的变化。

为了使控制器具有较好的自适应性，实现控制器参数的自动调整，可以采用神经网络控制的方法。

利用人工神经网络的自学习这一特性，并结合传统的PID控制理论，构造神经网络PID控制器，实现控制器参数的自动调整。

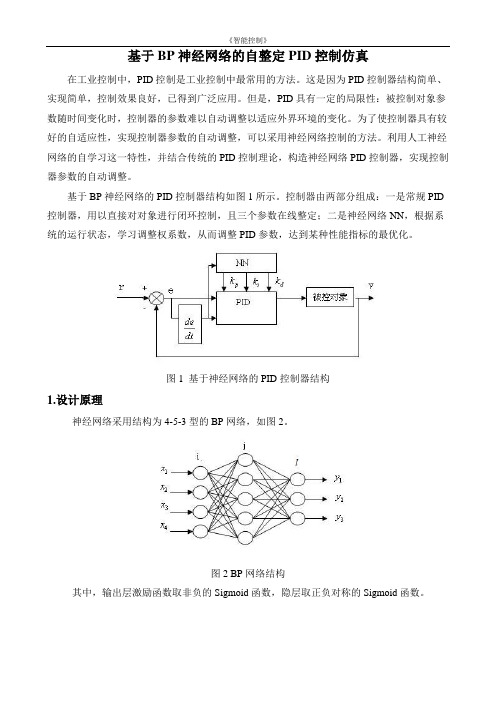
基于BP神经网络的PID控制器结构如图1所示。

控制器由两部分组成：一是常规PID 控制器，用以直接对对象进行闭环控制，且三个参数在线整定；二是神经网络NN，根据系统的运行状态，学习调整权系数，从而调整PID参数，达到某种性能指标的最优化。

图1 基于神经网络的PID控制器结构1.设计原理神经网络采用结构为4-5-3型的BP网络，如图2。

图2 BP网络结构其中，输出层激励函数取非负的Sigmoid函数，隐层取正负对称的Sigmoid函数。

被控对象为一时变非线性对象，数学模型可表示为： 2()(1)()(1)1(1)a k y k y k u k y k -=+-+- 式中，系数a(k)是慢时变的，。

为保证控制器有一定的动态跟踪能力，选定神经网络的输入层输入为[(),(1),(2),1]T in X e k e k e k =--网络的学习过程由正向和反向传播两部分组成。

如果输出层不能得到期望输出，那么转入反向传播过程，通过修改各层神经元的权值，使得输出误差信号最小。

输出层节点分别对应三个可调参数(3)1(3)2(3)3p I D O K O K O K ⎫=⎪=⎬⎪=⎭取性能指标函数为： 21()(()())2E k r k y k =-设其中：()()()r k y k e k -=若PID 控制器采用采用增量式数字PID 控制算法，则有(3)1(3)2(3)3()()(1)()()()()2(1)(2)u k e k e k O u k e k O u k e k e k e k O ⎫∂=--⎪∂⎪⎪∂=⎬∂⎪⎪∂=--+-⎪∂⎭2.网络权系数调整网络权系数的修正采用梯度下降法。

基于MATLAB的BP神经网络控制器的设计及其实验仿真

摘要虚拟设计是近年来发展起来的一个新的研究领域，智能控制虚拟实验室则是智能控制教学上的一个很好的工具。

鉴于传统实验室需要的设备，资金，场地等问题，利用虚拟实验室进行实验教学能够很大程度上的节约成本，同时用户在计算机前就能完成实验，查看实验结果，也能提高效率，节省时间。

本课题主要是建立可以进行智能控制虚拟实验，其模拟的是天煌教仪生产的“THJ-2型高级过程控制系统实验装置”。

本设计由三个主要部分构成：虚拟实验室的3D造型、智能控制实验仿真、图形用户界面（GUI）。

在具体的实现过程中，利用VRML语言完成虚拟实验室3D模型的建立；通过MATLAB的强大数据处理功能实现了BP神经网络控制实验的仿真和GUI的设计；最后利用MATLAB对系统进行封装，形成独立的可执行程序。

用户可通过封装程序界面打开GUI界面，在GUI界面中进行实验，设置参数，并能够察看系统的仿真曲线，实现虚拟实验的效果。

关键字：虚拟实验室、VRML、BP神经网络、MATLABAbstractVirtual design is developed in new area of research in recent years, Virtual Intelligent Control Laboratory is a good teaching tool of Intelligent Control Education. In view of the need for traditional laboratory equipment, funds, space and other issues, using virtual laboratory for experimental teaching in a large extent the cost savings, while people will be able to be completed the experiment to see results, but also improve efficiency, save time by using computer.The main issue is the establishment of a virtual intelligent control can be simulated laboratory equipment is “THJ-2 advanced process control system experimental” made by Tianhuang company .The design is consists of three main parts: the 3D Virtual Laboratory modeling, the simulation of intelligent control, the graphical user interfaces (GUI).The realization of the specific process, by using of VRML language to complete the virtual 3D model laboratory; through MATLAB's powerful data-processing functions to do a BP neural network control experiment simulation and make GUI design; the final, using MATLAB to let the system package to form an independent executable program. Users can open the GUI interface package interface, the GUI interface in the experiment, set parameters, and be able to see the simulation curve, the effect of virtual experiments.Keywords: Virtual Laboratory, VRML, BP neural network controller, MATLAB目录第1章引言 (1)1.1课题的研究背景及研究目地 (1)1.2虚拟实验室的介绍 (3)1.2.1 虚拟实验室的概念 (3)1.2.2 虚拟设计的技术基础 (3)1.2.3 虚拟设计的特点 (4)1.2.4虚拟设计的优点 (5)1.3课题研究的主要内容 (5)第2章VRML虚拟实验设备设计 (7)2.1 VRML技术基础知识 (7)2.1.1 VRML技术概述 (8)2.1.2 VRML文件组成 (8)2.1.3 VRML节点简介 (8)2.2实验装备简介 (11)2.3虚拟实验室的设计 (11)2.3.1 部分元件设计及程序. (11)2.3.2 由零件组成控制面板的小单元 (14)2.3.3 各控制单元组成完整的控制面板 (16)第3章神经网络理论 (17)3.1神经网络理论概述 (17)3.2 BP神经网络 (18)第4章基于MATLAB的BP神经网络控制器的设计及其实验仿真 (20)4.1基于BP神经网络控制器的设计 (20)4.2 BP-PID控制实验仿真 (23)4.2.1 MATLAB 简介. (23)4.2.2 BP-PID控制实验仿真 (24)4.3图形用户界面(GUI)的设计 (32)4.3.1MATLAB图形用户界面简介. (32)4.3.2图形用户界面实现的功能 (34)4.3.3图形用户界面的实现过程 (34)4.4系统封装 (37)4.4.1 封装目地. (37)4.4.2 MATLAB封装具体过程 (38)第5章结论 (39)参考文献 (40)致谢 (41)附录一VRML设计部分程序 (42)附录二MATLAB设计GUI程序 (46)第一章引言近些年来，迅速发展的计算机硬件技术与不断改进的计算机软件系统相匹配，使得基于大型数据集合的声音和图像的实时动画制作成为可能；人机交互系统的设计不断创新，新颖、实用的输入输出设备不断地进入市场。

基于BP神经网络整定的PID控制

１基本的ＢＰ神经网络
・
取性能指标函数为：（）（ｎｋ－ｏｔ）Ｅ』＝ｆ（）ｙｕ（）（ｉｋ
（）６
按照梯度下降法修正网络的权系数，按Ｅｋ对加权系数即（）的负梯度方向搜索调整，并附加一个使搜索快速收敛全局极小
式中，入变量的个数Ｍ取决于被控系统的复杂程度。输网络隐含层的输入、出为：输
Ｋｅｗｏｒ：ｎｒｅｔｋ，ＤｏｎｒｙｄｓＢＰｅｕａｌｎｗｏｒＰＩｃｔｏｌ
ＰＩＤ控制适用于可建立精确数学模型的确定性系统，然而
０（（＝ｎ』ｋ）
实际工业生产过程往往具有非线性、变不确定性，以建立精时难确的数学模型，实际生产中，在常规ＰＤ控制器参数往往整定不Ｉ良、能欠佳，运行工况的适应性很差。ＰＤ控制器设计中，性对在Ｉ
ｇ（）（＋ａｈｘ）ｘ：１ｔｎ（）＝
厶ｅ＋ｅ
（）５
研究了基于神经网络的控制器结构和算法的基础上，用改进共扼梯度算法对神经网络控制器参数进行在线整定。仿真结果表
明，种改进方案不仅能够提高算法在训练过程中的收敛速度，这而且训练后的神经网络具有较强的自适应和自学习能力，对控制器参数实现在线整定，从而进一步提高了控制器的性能。

基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计摘要本文主要研究一个基于神经网络的自适应PID控制系统的设计方法，利用BP神经网络对被控对象进行在线辨识和控制。

基于BP神经网络学习算法设计出两个神经网络模型：一个利用神经网络（NNM）对非线性映射的逼近能力，对被控对象进行辨识，另一个构成具有PID结构的控制器（NNC）。

通过神经网络NNM的在线学习和修正，产生对被控对象输出的预测作用，然后由网络NNC实施控制作用，从而实现对辨识对象的PID控制。

在利用神经网络对系统进行辨识时，选用白噪声信号作为系统的输入信号，以提高系统的辨识精度；另外，为了得到神经网络控制器的初始化权值，本文在自整定过程中采用常规PID控制器整定方法之一的稳定边界法。

在设计过程中运用MATLAB语言工具箱进行编程，并通过SIMULINK动态仿真工具对一阶非线性对象进行了仿真。

仿真结果表明了利用神经网络对系统进行辨识的有效性，并用经辨识所得到的输出值取代系统的实际输出值，利用神经网络NNC对系统进行控制，获得了满意的控制效果。

关键词：神经网络，BP学习算法，自适应，参数优化，辨识1 综述PID调节器从问世至今已历经了半个多世纪，在这几十年中，人们为它的发展和推广做出了巨大的努力，使之成为工业过程控制中主要的和可靠的技术工具。

近几十年来，现代控制理论迅速发展，出现了许多先进的控制算法，但到目前为止，即使在微处理技术迅速发展的今天，过程控制中大部分控制规律都未能离开PID，这充分说明PID控制仍具有很强的生命力。

过程工业控制中实际应用最多的仍是常规的PID控制算法，这是因为PID控制具有结构简单、容易实现、控制效果好和鲁棒性强等特点，且PID算法原理简明，参数物理意义明确，理论分析体系完整，为广大控制工程师所熟悉。

但在生产现场往往由于参数整定不好而使PID控制器控制效果欠佳，整定的好坏不但会影响到控制质量，而且还会影响到控制器的性能。

PID控制中一个至关重要的问题，就是控制器三参数(比例系数、积分时间、微分时间)的整定。

基于BP神经网络的PID控制器设计

基于BP神经网络的PID控制器设计1.引言在工业控制系统中，PID（比例、积分、微分）控制器被广泛应用于各种自动控制任务。

然而，传统的PID控制器在处理非线性、时变以及多输入多输出（MIMO）系统时存在一些固有的局限性。

为了克服这些问题，本文提出了基于BP神经网络的PID控制器设计方法。

2.BP神经网络BP神经网络是一种前向反馈的人工神经网络，具有强大的非线性建模能力和自适应性能。

它由输入层、隐藏层和输出层组成，每个神经元与前一层的所有神经元和后一层的所有神经元连接。

BP神经网络通过反向传播算法来训练权重和偏置，实现输入与输出之间的映射关系。

3.PID控制器PID控制器由比例项、积分项和微分项组成，具有良好的稳定性和抗干扰能力。

比例项根据控制误差与参考值的比例进行调整，积分项根据控制误差与时间的积分进行调整，微分项根据控制误差的变化率进行调整。

4.BP神经网络与PID控制器结合将BP神经网络与PID控制器相结合，可以克服传统PID控制器在处理非线性、时变和MIMO系统时的局限性。

具体而言，可以使用BP神经网络来精确建模控制对象的非线性行为，并将其应用于PID控制器中，实现自适应调节。

在实际应用中，可以按照以下步骤进行基于BP神经网络的PID控制器设计：（1）收集系统输入输出数据，并进行预处理，例如归一化处理。

（2）使用BP神经网络对控制对象进行建模。

选择适当的网络结构、激活函数和误差函数，并使用反向传播算法进行网络训练。

（3）设计PID控制器，确定比例项、积分项和微分项的权重。

（4）将BP神经网络的输出作为PID控制器的输入，进行控制操作。

根据控制误差和调节参数，调整PID控制器的输出。

（5）反复迭代并调整BP神经网络和PID控制器的参数，使系统能够快速、准确地响应控制需求。

5.实验验证为了验证基于BP神经网络的PID控制器的有效性，可以选择一个具有非线性、时变特性的控制对象进行实验。

在实验中，可以使用MATLAB或其他神经网络工具箱来实现BP神经网络，并结合传统PID控制器进行控制。

神经pid，模糊pid，常规pid的matlab比较

图4.BP神经网络PID系统输出响应曲线图6. PID 参数自适应模糊控制器系统框图图7.e，ec，Kp，Ki,Kd的隶属度函数通过不断进行仿真实验和借鉴专家经验可以得到如下的49条规则：图8.模糊PID控制系统输出曲线图9.模糊PID控制系统误差曲线图中1为常规整定PID 阶跃响应曲线，2为BP 神经网络PID 阶跃响应曲线，3为模糊自适应整定PID 阶跃响应曲线。

从曲线中以看出，三种PID控制方式中模糊PID几乎没有超调，调节时间短，控制效果最好；BP 网络PID效果次之；都比常规PID 效果好。

比较图5神经PID与图9模糊PID的误差曲线可以看出,模糊PID具有更短的学习时间。

仿真和实验结果均证明了神经网络PID 控制算法能有效地控制大时滞大惯性的温控系统，将神经网络与PID控制相结合，可以在线调整PID控制器的各个参数，减少了凭经验整定参数带来的误差，提高了温控系统的鲁棒性和自适应性。

此外，神经网络PID控制器还能有效的抑制干扰，而且对对象模型要求不高,具有较好的抗干扰性。

同时也可以进一步优化BP神经网络的结构和算法，使温度控制最终趋于最优，更好地满足实际生产对温度控制的要求。

但是由于该控制器的初始权值是随机值,控制输出在开始时波动很大,随着网络的自学习，不断调整权值控制输出来跟踪输入。

由于神经网络收敛速度慢，回到稳定状态所需时间较长，这个问题有待进一步研究解决。

，模糊PID控制响应几乎没有超调，但是响应速度较慢；在模型失配的情况下，模糊PID虽然产生了震荡，超调量也有所增加，但总体来说还能够保持稳定；在添加干扰后，系统持续产生小幅震荡，但超调量很小，系统整体还是稳定的，抗干扰能力强。

参考文献：1、陶永华.新型PID控制及其应用(第二版) [ M].北京：机械工业出版社,2002.2、杨智,朱海锋,黄以华．PID控制器设计与参数整定方法综述[ J ].化工自动化及仪表,2 005，32 ( 5 ):1-7 ．3、杨智.工业自整定P ID调节器关键设计技术综述[J].化工自动化及仪表,2000,27 ( 2 )：5-10.4、王伟,张晶涛,柴天佑.PID参数先进整定方法综述[ J ].自动化学报,2000,26 (5):347-355.5、何宏源,徐进学,金妮．PID继电自整定技术的发展综述[ J ].沈阳工业大学学报,2005,27 (4):4 09-413.6、叶岚.基于继电反馈的PI D控制器的参数整定[ D].上海:上海交通大学自动化系,2007.7、李少远.基于继电反馈的PID控制器的参数整定[D].上海：上海交通大学自动化系,2007.8、吴泽宁等.BP神经网络的改进及应用[J ].河南科学,2003-4:202 -2069、李遵基编著.热工自动控制系统[M].中国电力出版社,1997.1010、俞海斌，褚健.CFB锅炉汽包水位的专家PID控制[J].机电工程,2000（3）:103～10611、潘祥高等.模糊PID控制在工业锅炉控制系统中的应用[J].工业出版社,200412、刘金琨.先进PID 控制MA TLAB仿真M7.2 版.北京电子工业出版社,200413、薛定宇.控制系统计算机辅助设计MA TLAB 语言与应用M7.2 版．北京清华大学出版社,2006常规PID实现程序：clear all;close all;ts=10;sys=tf([1],[150,1],'inputdelay',50);dsys=c2d(sys,ts,'z oh');[num,den]=tfdata(dsys,'v');u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;u_6=0;y_1=0;y_2=0;y_3=0;error_1=0;error_2=0;ei=0;for k=1:1:1000time(k)=k*ts;yout(k)=-den(2)*y_1+num(2)*u_6;rin(k)=1;error(k)=rin(k)-yout(k);ei=ei+error(k)*ts;kp=0.03;kd=1;ki=0.004;u(k)=kp*error(k)+kd*(error(k)-error_1)/ts+ki*ei; if u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endif k==200u(k)=u(k)+1;endu_6=u_5;u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k); y_3=y_2;y_2=y_1;y_1=yout(k);error_2=error_1;error_1=error(k);endfigure(1);plot(time,rin,'b',time,yout,'r');xlabel('time(s)');ylabel('rin,yout');figure(2);plot(time,u,'r');xlabel('time(s)');ylabel('u');BP神经网络PID程序：%BP based PID Controlclear all;close all;xite=0.9;IN=4;H=5;Out=3; %NN Structurewi=[-0.6394 -0.2696 -0.3756 -0.7023;-0.8603 -0.2013 -0.5024 -0.2596;-1.0749 0.5543 -1.6820 -0.5437;-0.3625 -0.0724 -0.6463 -0.2859;0.1425 0.0279 -0.5406 -0.7660];%wi=0.50*rands(H,IN);wi_1=wi;wi_2=wi;wi_3=wi;wo=[0.7576 0.2616 0.5820 -0.1416 -0.1325;-0.1146 0.2949 0.8352 0.2205 0.4508;0.7201 0.4566 0.7672 0.4962 0.3632];%wo=0.50*rands(Out,H);wo_1=wo;wo_2=wo;wo_3=wo;x=[0,0,0];du_1=0;u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;u_6=0;y_1=0;y_2=0;Oh=zeros(H,1); %Output from NN middle layerI=Oh; %Input to NN middle layererror_2=0;error_1=0;ts=10;for k=1:1:1000time(k)=k*ts;rin(k)=1.0;%Unlinear modelyout(k)=0.9355*y_1+0.0645*u_6;error(k)=rin(k)-yout(k);xi=[rin(k),yout(k),error(k),1];x(1)=error(k)-error_1;x(2)=error(k);x(3)=error(k)-2*error_1+error_2;epid=[x(1);x(2);x(3)];I=xi*wi';for j=1:1:HOh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j))); %Middle Layer endK=wo*Oh; %Output Layerfor l=1:1:OutK(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); %Getting kp,ki,kd endkp(k)=K(1);ki(k)=K(2);kd(k)=K(3);Kpid=[kp(k),ki(k),kd(k)];du(k)=Kpid*epid;u(k)=u_1+du(k);dyu(k)=sign((yout(k)-y_1)/(du(k)-du_1+0.0001));%Output layerfor j=1:1:OutdK(j)=2/(exp(K(j))+exp(-K(j)))^2;endfor l=1:1:Outdelta3(l)=error(k)*dyu(k)*epid(l)*dK(l);endfor l=1:1:Outfor i=1:1:Hd_wo=xite*delta3(l)*Oh(i)+alfa*(wo_1-wo_2);endendwo=wo_1+d_wo+alfa*(wo_1-wo_2);%Hidden layerfor i=1:1:HdO(i)=4/(exp(I(i))+exp(-I(i)))^2;endsegma=delta3*wo;for i=1:1:Hdelta2(i)=dO(i)*segma(i);endif k==200u(k)=u(k)+1;endd_wi=xite*delta2'*xi;wi=wi_1+d_wi+alfa*(wi_1-wi_2);%Parameters Updatedu_1=du(k);u_6=u_5;u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);y_2=y_1;y_1=yout(k);wo_3=wo_2;wo_2=wo_1;wo_1=wo;wi_3=wi_2;wi_2=wi_1;wi_1=wi;error_2=error_1;error_1=error(k);endfigure(1);plot(time,rin,'r',time,yout,'b');xlabel('time(s)');ylabel('rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u');figure(4);subplot(311);plot(time,kp,'r');xlabel('time(s)');ylabel('kp');subplot(312);plot(time,ki,'g');xlabel('time(s)');ylabel('ki');subplot(313);plot(time,kd,'b');xlabel('time(s)');ylabel('kd');模糊PID程序：clear all;close all;a=newfis('fuzzpid');a=addvar(a,'input','e',[-3,3]); %Parameter e a=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','t rimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','t rimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','t rimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'input','ec',[-3,3]); %Parameter ec a=addmf(a,'input',2,'NB','zmf',[-3,-1]);a=addmf(a,'input',2,'NM','t rimf',[-3,-2,0]);a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',2,'Z','t rimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);a=addmf(a,'input',2,'PM','t rimf',[0,2,3]);a=addmf(a,'input',2,'PB','smf',[1,3]);a=addvar(a,'output','kp',[-0.3,0.3]); %Parameter kp a=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);a=addmf(a,'output',1,'NM','t rimf',[-0.3,-0.2,0]);a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);a=addmf(a,'output',1,'Z','t rimf',[-0.2,0,0.2]);a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);a=addmf(a,'output',1,'PM','t rimf',[0,0.2,0.3]);a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);a=addvar(a,'output','ki',[-0.06,0.06]); %Parameter kia=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);a=addmf(a,'output',2,'NM','t rimf',[-0.06,-0.04,0]);a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]);a=addmf(a,'output',2,'Z','t rimf',[-0.04,0,0.04]);a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);a=addmf(a,'output',2,'PM','t rimf',[0,0.04,0.06]);a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);a=addvar(a,'output','kd',[-3,3]); %Parameter kpa=addmf(a,'output',3,'NB','zmf',[-3,-1]);a=addmf(a,'output',3,'NM','t rimf',[-3,-2,0]);a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);a=addmf(a,'output',3,'Z','t rimf',[-2,0,2]);a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);a=addmf(a,'output',3,'PM','t rimf',[0,2,3]);a=addmf(a,'output',3,'PB','smf',[1,3]);rulelist=[1 1 7 1 5 1 1;1 2 7 1 3 1 1;1 3 6 2 1 1 1;1 4 6 2 1 1 1;1 5 5 3 1 1 1;1 6 4 4 2 1 1;1 7 4 4 5 1 1;2 1 7 1 5 1 1;2 2 7 1 3 1 1;2 3 6 2 1 1 1;2 4 5 3 2 1 1;2 5 5 3 2 1 1;2 6 4 43 1 1;2 7 34 4 1 1;3 1 6 1 4 1 1;3 2 6 2 3 1 1;3 3 6 3 2 1 1;3 45 3 2 1 1;3 5 4 4 3 1 1;36 3 5 3 1 1;37 3 5 4 1 1;4 1 6 2 4 1 1;4 2 6 2 3 1 1;4 3 5 3 3 1 1;4 4 4 4 3 1 1;4 5 3 5 3 1 1;4 6 2 6 3 1 1;4 7 2 6 4 1 1;5 1 5 2 4 1 1;5 2 5 3 4 1 1;5 3 4 4 4 1 1;5 4 3 5 4 1 1;5 5 3 5 4 1 1;5 6 2 6 4 1 1;5 7 2 7 4 1 1;6 1 5 4 7 1 1;6 2 4 4 5 1 1;6 3 3 5 5 1 1;6 4 2 5 5 1 1;6 5 2 6 5 1 1;6 6 27 5 1 1;6 7 1 7 7 1 1;7 1 4 4 7 1 1;7 2 4 4 6 1 1;7 3 2 5 6 1 1;7 4 2 6 6 1 1;7 5 2 6 5 1 1;7 6 1 7 5 1 1;7 7 1 7 7 1 1];a=addrule(a,rulelist);a=setfis(a,'DefuzzMethod','centroid');writefis(a,'fuzzpid');a=readfis('fuzzpid');%PID Controllerts=10;sys=tf([1],[150,1],'inputdelay',50);dsys=c2d(sys,ts,'t ustin');[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0;u_4=0.0;u_5=0.0;u_6=0.0;y_1=0;y_2=0;x=[0,0,0]';error_2=0;error_1=0;e_1=0.0;ec_1=0.0;kp0=0.0929;kd0=0.0078;ki0=0.0518;for k=1:1:1000time(k)=k*ts;rin(k)=1;%Using fuzzy inference to tunning PIDk_pid=evalfis([e_1,ec_1],a);kp(k)=kp0+k_pid(1);ki(k)=ki0+k_pid(2);kd(k)=kd0+k_pid(3);u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);if u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endif k==200u(k)=u(k)+1;endyout(k)=-den(2)*y_1+num(2)*u_6;error(k)=rin(k)-yout(k);%%%%%%%%%%%%%%Return of PID parameters%%%%%%%%%%%%%%% u_6=u_5;u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);y_2=y_1;y_1=yout(k);x(1)=error(k); % Calculating Px(2)=error(k)-error_1; % Calculating Dx(3)=x(3)+error(k); % Calculating Ie_1=x(1);ec_1=x(2);error_2=error_1;error_1=error(k);endshowrule(a)figure(1);plot(time,rin,'b',time,yout,'r');xlabel('time(s)');ylabel('rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u');。