简单的三角形网格生成程序

合集下载

图像描述中Delaunay三角形网格的快速生成方法

第３期
图像描述中Ｄｅａｎｙ三角形网格的快速生成方法ｌｕａ
焦卫东，卢朝阳，黄瑾
（安电子科技大学综合业务网理论及关键技术国家重点实验室，西西安西陕７０７）１０１
摘要：针对ＤＴ模型基图像编码方法不能实现实时编码的不足，据图像的多分辨率表示方法，用分根采层搜索的思想，出了一种基于ＭＤ或ＭＶ准则的图像描述中Ｄ网格的快速生成方法，过逐渐精细提Ｔ通
的搜索步长搜索网格节点，少了逐点搜索的次数，而节约了时间，高了运算效率．验表明，基减从提实与于ＭＤ或ＭＶ准则的一般方法相比，方法生成Ｄ网格的速度提高了近一倍，时恢复图像保持了相该Ｔ同近的质量；其他一些方法相比，相同的网格生成时间限制下，复图像的质量明显提高．与在恢
维普报（自然科学版）
Ｊ０ＵＲＮＡＬ０ＦＸＩＡＮＵＮＩ，ＳＴＹＤＩＶＥＲＩ
Ｊｎ．０７ｕ２０
Ｖｏ．４ＮＯ３１３．
第３４卷
ＡｂｔａｔＣｏｉｅｎｇｔａｌｒｆｒａｉｅｃｉｇａｐｉａｉｎｉｈｓｒｃ：ｎｓｄｒｈｅｆｉｕｅｏｅｌｔｏｄｎｐｌｃｔｏｎｔｅＤＴｏｅ－ａｅｍａｅｃｄｎｃｍｅｉｍｍｄｌｂｓｄｉｇｏｉｇｓｈｅ，ａｆｓｔｏｏｇｅｒｔｈｌｕｙＴｒａｇｕａｉｎａｔｍｅｈｄｔｎｅａｅｔｅＤｅａｎａｉｎｌｔｏｍｅｈｆｒｉｇｅｒｐｅｅｔｔｏａｅｎｔＶｒＭＤｓｏｍａｅｒｓｎａｉｎｂｓｄｏｈｅＭｏｃｉｅｉｎｉｏｏｅｙｕｉｇｔｄａｏｕｔｒｓｌｔｏｅｒｈｉｇＩｅｒｈｓｔｅｍｅｈｎｄｓｗｉｈｇａｕｌｒｔｒｏｓｐｒｐｓｄｂｓｎｈｅｉｅｆｍｌｉｅｏｕｉｎｓａｃｎ．ｔｓａｃｅｈｓｏｅｔｒｄａ－ｓｂｌｔｐｌｎｔｎｇｎｒｔｈｅｈｂｕｔｅｓｅｅｇｈｉｅｅａｉｏｆｔｅｍｓｙｗｈｉｈｔｏａｆｓａｃｉｏｎｓｉｒｄｕｅｅｂｎｅＳｉｅｏｎｃｈｅｔｔｌｏｅｒｈｎｇｐｉｔｓｅｃｄｏｎｙｏ，Ｏｔｍｃｎｂａｅｎｄｔｏｐａｉｎｌｅｆｃｅｃｐｏｅａｅｓｖｄａｈｅｃｍｕｔｔｏａｆｉｉｎｙｉｒｖｄ．ＳｉｕａｉｎｒｓｌｈｍｍｌｔｏｅｕｔｓｏｗｓｔａｈｅｐｏｏｅｅｈｄｓｖｓｈｔｔｒｐｓｄｍｔｏａｅａｍｏｔｏｅｈｌｉｅｗｈｉｅｐｎｇｆｎｌｅｏｓｒｃｅｍａｅｑａｉｙｃｍｐｒｄｗｉｈｔｅｇｎｒｌｍｅｈｓｄｌｓｎａｆｔｍｌｋｅｉｉｅｙｒｃｎｔｕｔｄｉｇｕｌｏａｅｔｈｅｅａｔｏｄｂａｅｅｔｏｈＶｒＭＤｒｔｒｏｎｔｅＭｏｃｅｉｎ，ａｈｔｉｔｌｃｎｇｔｍｏｅａｃｒｔｍａｅｒｓｎｔｔｏｎｒｔｅｓｍｅｍｅｈｉｎｄｔａｔｓｉａｅｒｃｕａｅｉｇｅｒｐｅｅａｉｎｕｄｅｈａｓｌｇｎｒｔｉｅｃｍｐｒｄｗｉｈｔｔｅｘｓｉｇｍｅｈｏ．ｅｅａｉｔｍｏａｅｔｈｅｏｈｒｅｉｔｎｔｄｓｏｎＫｅｏｄｙＷｒｓ：Ｄｅａａｒｉｌｕｎｙｔａｎｇｕａｔｏｅｈ；ｕｌｉｒｓｌｉｎｓａｃｎｇ；ｍａｅｅｅａｉｌｉｎｍｓｍｔ— ｅｏｕｔｏｅｒｈｉｉｇｅｒｐｒｓｎｔｔｏｎ

mike21fm网格生成器中文教程

MIKE21 FM网格生成器培训教程目录17简介 (1)17.1概念 (2)17.2边界定义 (3)18开始 (3)18.1介绍 (3)18.2数据位置 (4)18.3 步骤1 - 建立一个工作区域 (4)18.4步骤2 - 导入模型边界线 (5)18.5步骤3 - 编辑陆地边界线 (7)18.6 步骤4 - 定义开边界 (9)18.7步骤5 - 生成网格 (9)18.8步骤6 - 对陆地边界进行光滑处理 (10)18.9步骤7 - 网格地形插值 (12)18.10 步骤8 - 对网格进行光滑处理 (15)18.11 步骤9 - 使用多边形来控制节点密度 (15)MzGeneric.pdf手册中Mesh Generator部分17 简介网格生成器（mesh generator）为制作三角网格提供了工作平台。

创建合理的网格是模型获得可靠结果的重要条件。

基于 MIKE Zero 之上的MIKE 21 Flow Model FM, MIKE 3 Flow Model FM 和 MIKE 21 Spectral Wave Model FM,都是以三角网格为基础的。

图 17.1 全球模型的陆地/海洋边界网格的生成包括选择适当的模拟范围，确定地形网格的分辨率，考虑流场，风场和波浪场的影响，为开边界和陆地边界确定边界代码。

此外，在考虑稳定性的前提下，确定地理空间的分辨率。

生成网格文件可以使用MIKE Zero网格生成器。

网格文件是一个ASCII文件（扩展名*.mesh），其中包括地理位置信息和在网格中每一个节点的水深。

文件还包括三角形的节点连通性信息。

所有关于生成网格文件的配置信息都在网格定义文件(扩展名*.mdf) 中, 文件可以被修改和再利用。

网格生成器的功能包括从不同的外部信息源(例如. XYZ 水深点，XYZ等值线，MIKE 21矩形网格地形，MIKE C-MAP数据) 输入原始数据，或是用内置的制图工具手动创建地形数据。

三维地质构造的三角形格架式网格生成方法

ＰｔｌｕＵｎｖｒｉｆｈｎ，Ｄｏｇｉｇ２７６，ＣｉａｅｒｅｍｉｅｓｏＣｉａｏｙｔｎｙｎ５０１ｈｎ）
ＡｂｔａｔＴｅｓｍｕａｉｎｍｅｈｄｏｒｅｄｍｅｓｎｌｙｒｃｒｏｇａｉｎａｄａｃｍｕａｉｎｐｏｅｓｎｅｅｅａｅｔｒｅｄｍｅ — ｓｒｃ：ｈｉｌｔｔｏｆｈｅ — ｉｎｉａｈｄｏａｂｎｍｉｒｔｎｃｕｌｔｏｒｃｓｅｄｔｇｎｒｔｅ — ｉｎｏｔｏｏｏｈｓｏａｅｌｇｃｌｆａｗｏｋｍｅｈＴｈｅｅａｉｎｏｒｅｄｍｅｓｎｌｅｌｇｃｌａｗｏｋｍｅｈｉｂｓｄｏｔｕｔｒｄｌｃｎｉｎｌｏｏｉａｍｅｒｓ．ｇｒｅｇｎｒｔｆｈｅ — ｉｎｉａｏｏｉａｍｅｒｓａｅｎｓｒｃｕｅｍｏｅｏ — ｏｔｏｇｒｆｓｓｒｉｔＩｅｐｎｅｔｉｅｎ，ｔｅｅｉｔｇｍｅｈｇｎｒｔｎｍｅｏｓａｅａａｙｅｎｏａｅ，ａｄｏｈｓａｉｙｔｍｏｔｎｎｒｓｏｓｔｓｄｍａｄｈｘｓｉｓｅｅａｉｔｄｒｎｌｚｄａｄｃｍｐｒｄａｏｈｎｏｈｎｎｔｉｓｓａｓｓｅｆｒｂｔｉｎｕａａｅｒｓｅｅａｉｎｉｒｓｎｅ．ＴｅｃｎｔａｎｄＤｅａｎｙｔｉｎｕａｉｎａｇｒｈｉｕｅｏｓｒｃｅｇｏｏｉａｒｇｌｒｍｗｏｋｍｅｈｇｎｒｔｐｅｅｔｄａｒｆｏｓｈｏｓｒｉｅｌｕａａｇｌｔｌｏｉｍｓｄｔｃｎｔｕｔｈｅｌｇｃｌｒｏｔｓｏｔ

6节点三角形单元matlab

6节点三角形单元matlab在MATLAB中，可以使用有限元分析工具箱来创建和操作三角形有限元网格以及进行相应的计算。

下面我将从几个角度来介绍在MATLAB中如何处理6节点三角形单元。

1. 创建6节点三角形单元网格：在MATLAB中，可以使用 PDE 模型创建器 App 或者命令行函数来创建6节点三角形单元网格。

首先，你可以使用命令行函数如下创建一个简单的6节点三角形单元网格：matlab.model = createpde();geometryFromEdges(model,@()gunit);generateMesh(model,'Hmax',0.1);pdeplot(model);这段代码创建了一个 PDE 模型，使用默认的单位几何体，然后生成了一个包含6节点三角形单元的网格，并进行了绘制。

2. 定义材料属性和边界条件：一旦创建了网格，你可以定义材料属性和边界条件。

例如，你可以使用以下代码定义一个材料属性和施加边界条件：matlab.specifyCoefficients(model,'m',0,'d',1,'c',1,'a',0,'f',1);applyBoundaryCondition(model,'dirichlet','Edge',1:model.Geo metry.NumEdges,'u',0);3. 求解和后处理：接下来，可以使用 solve 函数求解模型，并使用结果进行后处理。

例如，可以使用以下代码求解模型并绘制结果：matlab.result = solvepde(model);pdeplot(model,'XYData',result.NodalSolution);这将绘制出6节点三角形单元的有限元解。

总结：在MATLAB中处理6节点三角形单元，首先需要创建网格，然后定义材料属性和边界条件，最后求解模型并进行后处理。

三角形网格生成算法的研究与应用

三角形网格生成算法的研究与应用一、引言三角网格是计算机图形学领域中最常见的图形表示方式之一。

三角形网格生成算法的出现为图形学在各个领域的应用提供了强有力的支持，如计算机辅助设计、数字娱乐、医学图像处理等等。

然而目前三角形网格的生成算法依然存在许多难点，本文将针对这些难点进行研究和分析，探讨三角形网格生成算法的研究与应用。

二、先进的三角形网格生成算法三角形网格生成算法主要分为离散型和连续型两种。

离散型算法主要是针对离散数据点进行分析和处理，是传统算法的核心。

而连续型算法则主要考虑通过合理的数值方法对连续函数进行求解得到三角形网格。

2.1 离散型算法离散型算法主要方法包括 Delaunay 三角剖分、Voronoi 图、alpha 参数、最小生成树等等。

Delaunay 三角剖分是三角形网格分割中最常见的算法之一。

该算法的核心思想是保持尽量少的单纯形边长相交。

Voronoi 图是一种基于点的分割方法，可以将平面分割成一系列多边形。

Alpha 参数是控制 Delaunay 三角剖分质量的措施之一，通过调整 alpha 参数，可以在不同场景下获得合适的 Delaunay 三角剖分。

最小生成树算法则是对点集进行聚类的一种方法，通常用于优化 Delaunay三角剖分的质量。

2.2 连续型算法连续型算法主要包括渐近线、等值线、样条曲面拟合、卷积核方法等等。

渐近线的求解方法主要是对三角形网格表面进行采样后，通过函数空间中的拟合逼近来求解渐近线。

等值线方法则是在网格表面中寻找等值线，从而实现扫描三角形网格的目的。

样条曲面拟合是利用拟合优化方法，对离散的三角形网格点进行拟合，得到连续的三角形网格。

卷积核方法则通过对三角形表面求导以及在线性空间中构建卷积核，从而求得三角形网格表面的连续性信息。

三、三角形网格生成算法在计算机图形学领域的应用三角形网格生成算法在计算机图形学领域的应用十分广泛，主要包括三维重构、曲面拟合、形状建模、虚拟现实等等。

如何进行三角网的建立与处理

如何进行三角网的建立与处理在计算机科学领域中，三角网是一种用于连接数据点的网格结构。

它由许多三角形组成，每个三角形的三个顶点都是数据点。

三角网的建立和处理是许多计算机图形学和计算机视觉任务中的基础步骤。

本文将探讨如何进行三角网的建立与处理。

一、三角网的建立三角网的建立是通过一系列步骤来生成一个包含数据点的三角网格。

以下是一个简单的流程：1. 数据预处理：首先，需要根据实际应用场景，对数据点进行预处理。

这可能包括数据清洗、数据采样和数据变换等操作，以确保数据的质量和适用性。

2. 确定边界条件：在建立三角网之前，需要确定边界条件。

边界条件可以是已知的数据点或外部提供的信息。

边界条件的选择对于生成合理的三角网格非常重要。

3. 进行三角网格的初始化：在确定边界条件后，可以开始进行三角网格的初始化。

这可以通过将数据点放置在二维平面上，并根据某种规则（如Delaunay三角剖分算法）进行三角剖分来实现。

三角剖分算法是一种常用的方法，它能够确保所有的三角形都是“良好”的，即不会出现重叠或相交的情况。

4. 优化三角网：在初始化完成后，可能需要进行一些优化来改进生成的三角网。

例如，可以使用各种算法来优化三角网的质量和形状，以满足特定的需求。

常用的优化算法包括Laplacian平滑算法和拓扑优化算法等。

二、三角网的处理一旦三角网建立完成，就可以进行各种处理操作。

以下是一些常见的三角网处理技术：1. 网格编辑：三角网的处理通常涉及在网格上进行编辑和修改。

这可以通过添加、删除或移动数据点来实现。

网格编辑技术是计算机图形学和计算机视觉任务中的重要部分，可以用于模型编辑、形变和纹理映射等应用。

2. 网格分析：通过对三角网进行分析，可以获得有关数据点之间关系的更多信息。

例如，可以计算三角形的面积、周长和法向量等属性。

这些信息在许多应用中都是有用的，如物体表面重建、拓扑分析和形状匹配等。

3. 网格变形：通过对三角网进行变形操作，可以实现形状的变化和动画效果。

简单的三角形网格生成程序(Simple+triangular+mesh+generator)

简单的三角形网格生成程序（Simple triangular meshgenerator）简单的三角形网格生成程序(Simple triangular mesh generator)Title: a triangular mesh generation procedure is simple, for beginners referenceAuthor: XURUI [3 28, 8:32]This is a simple triangle mesh generation program using advancedfront preparation method, the reference for beginners. I see Zhou Hua software download area has been empty, will initiate, hope more people can contribute to the sharing of programs. If Zhou Hua saw, hoping to take this little program to download, because here will soon be flooded.The following is the source codeProgram biliOpen (10, file='aa.map')Open (3, file='aa')Call coor0Close (10)EndSubroutine coor0Implicit real*4 (A-H, o-z)Common/nxy/nx, NY, numnod, nume, numb, MCommon /enod/ Nod1 (80000), NOD2 (80000), NOD3 (80000)Common /coor/ x (80000), y (80000)Integer n, Nod1, NOD2, NOD3C write (* *)'input = &nx; &ny; 'Open (1, file='aa.dat')Read (1 * NE)Do i=1, NERead (1 *) x (I), y (I)EnddoNs = 1C = ne (nx+ny) *2Nume = 0Nums = 0Call tricb (nume, NS, NE)Numnod = numeCall trimesh (nums, numnod, nume, 5, x, y)Call trinod (nume, NT, x, y, Nod1, NOD2, NOD3)Mtij=numnodMtik= NTWrite (10, mtij, mtik *)Write (10 '' (2f8.2) (x) (MTII), y (MTII), mtii=1, mtij)Write (10 '' (3i8) (Nod1) (MTII), NOD2 (MTII), NOD3 (MTII), mtii=1, mtik)ReturnEndC..................................................................C the following subroutines for generating triangular meshC according to circle boundary nodal pointsC trimesh generates nodal points of meshC trinod generates nodal No. of each triangleC tricb generates boundary edges according toC continuous nodal No. of circle boundaryC tricbn generates boundary edges according toC discontinuous nodal No. of circle boundary C..................................................................C trimesh (nums, numnod, numedge, MC, x, y)C trinod (numedge, NT, x, y, Nod1, NOD2, NOD3)C tricb (numedge, NS, NE)C tricbn (numedge, numnod, node) C..................................................................C nums... Starting edge... No. - 1.C numnod... Number of nodes.C numedge... Number of edges.C MC of iteration for... Modifying... Number... Nodal pointsC nt......... number of trianglesc ns. first nodal pointc i. last nodal point c..................................................................c x, y.......... document of nodal points coordinatesc nod1, nod2, nod3.... nodal document for each triangle.c node............. circle boundary nodal no. array c.................................................................. subroutine trimesh (nums, numnod, goddess, mc, x, y)c... generated new nodal points for triagle elementsc... store the nodal no. of edges() in document nod1 & nod2implicit real * 4 (a - h or - z)common / edge / nod1 (80000), nod2 (80000)dimension x *, y *), nv (100)common / tmdata / index (80000)integer edge1, edge2numb = numnodc write (*, *) is numb =, numb, x, y =c write (*, '(1x, 6f12.4)) (x (n), n = 1, numnod)c write (*, '(1x, 6f12.4)) (y (n), n = 1, numnod)c write (*, *) number =, goddess, nod1, nod2 =c write (*, '(1x, 15i5)) (nod1 (n), n = 1, 2000)c write (*, '(1x, 15i5)) (nod2 (n), n = 1, 2000)dmin = 1.e20dmax = 0.0give you 50 n = 1, 2000index (n) = 0the nod1 (n) =j = nod2 (n)d = (x (1) - x (j)) * * 2 + (y (i) - y (j)) * * 2 if (d.lt.dmin) dmin = dif (d.gt.dmax) dmax = d50 continuousdmin = sqrt (dmin)dmax = sqrt (dmax)c write (*, *), dmin, dmax = dmax, dmin,c write (*, *) index =write (*, '(1x, 15i5)) (index (n), n = 1, 2000) c... m is the middle point of n1 and n2c... m _ h is the normal vector of n1, n2 _c... h is the relative high with the bottom _ n2 n1 cccc nums = 0h = sqrt (3.0)cccc h = 1.d0100 constantnums = nums + 1write (*, *) is nums, index =, nums, index (nums) if (index (nums).gt.0) goto 2400write (*, *) is nums, god =, nums, godn1 = nod1 (nums)n2 = nod2 (nums)write (*, *) n1, n2 = n1, n2.xx1 = x (n1)yy1 = y (n1)xx2 = x (n2)yy2 = y (n2)xm = (xx1 + xx2) / 2ym = (yy1 + yy2) / 2a = xm - xx1b = ym - yy1dd = (a * a + b * b) * 4d = sqrt (dd)hh = hif (d.lt.dmin) hh = h * dmin / d if (d.gt.dmax) hh = h * dmax / d xi = xm - b * hhYH = YM + * HH写(*，*)的XH，YH =，XH，YHE = D * * 1.0e-4 HHEE = E×1.e-30NN = 0Smin =ρdmax *140我= 1，numnod中交140 n =号+ 1，数值中交我= NOD2(N)XX = X(我)YY = Y(我)S =(XX XH)* 2 +(YY YH)* 2如果(s.lt.smin)然后J =我Smin = Sendif140继续Smin = SQRT(5min)写(*，*)的J，Smin = '，J值如果(Smin CCCC。

opencascade 三角面片化算法

opencascade 三角面片化算法OpenCASCADE是一个开源的几何建模库，它提供了广泛的功能来处理3D CAD数据，包括几何形状的定义、修改、分析以及数据交换等。

在OpenCASCADE中，三角面片化（或称为网格化）是将复杂的几何形状转换为一系列三角形面的过程，这在许多应用中都是必要的，如渲染、有限元分析、碰撞检测等。

三角面片化算法在OpenCASCADE中通常涉及以下几个步骤：几何清理：在开始三角面片化之前，通常需要对输入的几何形状进行清理。

这可能包括去除小的特征、修复自相交的部分、确保曲面的连续性等。

曲面分解：复杂的几何形状可能由多个曲面组成。

三角面片化算法通常需要将这些曲面分解成更小的部分，以便单独处理。

参数化：对于每个曲面部分，算法需要找到一个参数化映射，即将曲面映射到一个二维平面上。

这样，可以更容易地在曲面上生成三角形网格。

网格生成：在参数化之后，算法会在二维平面上生成三角形网格。

这可以通过各种方法完成，如Delaunay三角剖分或其他基于边的算法。

映射回三维空间：最后，将生成的二维三角形网格映射回原始的三维几何形状。

这涉及到将每个三角形的顶点从参数空间转换回原始的三维坐标。

在OpenCASCADE中，这些步骤通常由一系列的类和函数来处理。

例如，BRepMesh_IncrementalMesh 类提供了一个增量的三角面片化算法，可以逐步地构建网格，并提供了各种参数来控制生成的网格的精度和质量。

值得注意的是，三角面片化是一个复杂的过程，可能会受到多种因素的影响，包括输入的几何形状的复杂性、所需的网格密度和精度、以及计算资源等。

因此，在选择和使用三角面片化算法时，需要根据具体的应用需求来做出权衡。

Tin三角形图的原理和应用

Tin三角形图的原理和应用概述Tin（Triangulated Irregular Network）三角形图是一种用于地理空间分析和地形建模的数据结构。

它被广泛应用于地理信息系统、计算机图形学和地质学等领域。

本文将介绍Tin三角形图的原理和应用，并说明其优势和局限性。

原理Tin三角形图是由一系列连接的三角形组成的网络。

每个三角形节点都有一个高度值，可以表示地形的高程，从而形成一个地形模型。

Tin三角形图的生成包括以下步骤：1.数据采集：首先需要收集地理空间数据，如地形高程数据、地理坐标数据等。

2.数据加密：将采集到的数据通过插值等方法进行加密，生成更密集的数据点。

3.构建拓扑关系：根据加密后的数据点，使用Delaunay三角剖分算法构建拓扑关系，生成三角形网格。

4.优化和筛选：对生成的三角形网格进行优化和筛选，确保其满足拓扑条件和几何要求。

5.存储和索引：将生成的Tin三角形图存储在数据库或文件中，并建立索引以便快速检索和查询。

应用Tin三角形图具有广泛的应用领域，下面列举几个常见的应用场景：地形建模Tin三角形图可以用于地形建模，可以根据高程数据生成真实的地形模型。

在地理信息系统中，地形建模可以用于地形分析、景观设计、地质勘探等领域。

地形分析Tin三角形图可以进行各种地形分析，如坡度分析、坡向分析、流域分析等。

这些分析可以帮助我们理解地形的特征和变化。

地质勘探Tin三角形图可以用于地质勘探，根据地形的变化和特征，可以预测矿产资源的分布、地质灾害的潜在风险等。

Tin三角形图在地质学研究中有很重要的应用价值。

计算机图形学Tin三角形图在计算机图形学中也有广泛的应用。

它可以用于建模和渲染三维物体、地形和景观等。

Tin三角形图可以提供更加真实和细致的图形效果。

优势和局限性Tin三角形图相比其他地理空间数据结构，具有以下优势：•真实性：Tin三角形图通过采集真实的高程数据和地理坐标数据来生成地形模型，具有高度的真实性。

triangle库用法

triangle库用法Triangle是一个Python库，它提供了许多用于处理三角形和计算三角形属性的函数和类。

本文将详细介绍Triangle库的使用方法，以帮助读者更好地了解如何使用这个库来处理三角形。

第一步：安装Triangle库要使用Triangle库，首先需要将其安装在您的Python环境中。

您可以通过以下命令在命令行中安装Triangle库：pip install triangle确保您已经正确安装了Python和pip，以便顺利安装Triangle库。

第二步：导入Triangle库一旦安装了Triangle库，您可以在您的Python程序中导入它，并开始使用它的功能。

要导入Triangle库，只需在程序的开头添加以下代码：pythonimport triangle现在您已经成功导入了Triangle库，并准备开始使用它的功能。

第三步：创建三角形网格Triangle库提供了一个功能强大且简单的三角形网格生成器，可以根据指定的输入数据生成三角形网格。

下面是一个示例代码片段，展示了如何使用Triangle 库生成一个简单的三角形网格：pythonimport trianglevertices = [(0, 0), (1, 0), (0, 1)] # 三角形的顶点坐标tri = triangle.triangulate({'vertices': vertices}, 'p') # 生成三角形网格print(tri['triangles']) # 打印生成的三角形在上面的示例中，我们首先定义了一个包含三角形顶点坐标的列表。

然后，我们使用`triangle.triangulate()`函数生成了一个三角形网格。

最后，我们打印出生成的三角形的列表。

第四步：计算三角形属性Triangle库不仅可以帮助我们生成三角形网格，还可以计算三角形的各种属性，如面积、周长、角度等。

三角形网格的自动生成及其局部加密技术研究

计算区域内尽可能生成正三角形，由节点间距函数控制，最后生成由疏到密的过渡三角形网格。三角形网格生成的步骤如下：（）界离散，定边界网格尺寸。据实际地形图数据，１边确根考察Ｔ程区域，根据经验进行边界离散。程工区域采用较密的网格尺寸，非计算区域可以采用较为稀疏的网格尺寸。这样能节省时间和工作量。（）界空间尺度权函数Ｅ。１得到各初始边界的空间尺度权函数。如边界ＡＡ点和Ｂ点空间２边由（）例Ｂ，
收稿日期：０１０ — ７修回日期：０１０ — ９２１－５２；２１— ６２
作者简介：阳豪（９６）女，戴１８一，湖南省人，硕士研究生，主要从事河口、海岸水动力及泥沙研究。
ＢｏｒｐｙＤＩａｇｈｏ１８一，ｍａ，ｓｒｔｄｎ．ｉｇａｈ：Ａｎ —ａ（９６）ｆｌｍａｔｕｅｔＹｅｅｅｓ
２１０２年２月
戴阳豪，等
三角形网格的自动生成及其局部加密技术研究
７９
（）４网格生成。第（）中离散后的边界开始，从２步在边界中找出长度最大的边Ａ从此处开始生成三角Ｂ，
形。生成三角形的步骤是先由ＡＢ与现有的前沿点Ｅ生成三角形，断三角形是否接近于正三角形，判是否满
第３卷第１３期
２２年２月０１

等值线算法

等值线算法：1.根据给定点生成三角形网格（具体见三角形网格生成算法），假设标量场在三角形的内部及边上满足线性分布关系。

2.根据标量场的最大值和最小值以及等值线的条数（可以设置一个缺省值比如30，用户可以改变该值），均匀划分出一系列的等值线的给定值。

3.对每一个给定值，对所有三角形单元搜索一遍。

如果这个给定值位于某三角形单元的三个顶点处的标量值的最大值和最小值之间，则必定在三角形的边上存在着两个点，这两个点的标量值等于给定值。

把这两个点连接起来就得到等值线的一部分（参见图1）。

将所有三角形单元按上述方法搜索一遍，就画出了等值线。

4.上述算法画出的等值线不够光滑，采用适当的光滑算法比如样条插值就得到光滑的等值线。

流线图算法：1.根据给定点生成三角形网格，假设矢量场在三角形的内部及边上满足线性分布关系。

2.用户可选择流线的起始点（seed）。

可以逐点选择，也可以选择一条线段，再对线段等分得到起始点。

3.起始点可能不在给定点中，这时要搜索起始点位于哪个单元（具体见搜索算法）。

通过插值可得到起始点处的矢量。

选择合适的时间步长，具体数值可以使得在该时间步长内沿矢量场方向走过的距离约等于当地网格的尺寸。

运动到下一位置后，再搜索该点位于哪个单元，插值可得到该点处的矢量，如此循环，直到点运动到边界以外或达到最大的步数（可以设成一个较大的数值如1000）。

三角形网格生成算法（Delaunay方法）：参见所附论文。

搜索算法: 搜索某个点位于哪个单元将区域分为若干子矩形区域（比如50×50），先扫描所有单元，将单元按区域归类。

对于给定点，先根据区域的坐标范围判断该点位于哪个区域。

然后扫描该区域所有单元，判断该点位于哪个单元。

判断一个点是否在一个三角形内部的方法（参见图2）：将该点与三角形的每条边分别相连，得到三个三角形，计算这三个三角形的面积，如果面积之和等于原三角形的面积，则该点在三角形内。

这三个三角形的面积和原三角形之比，就是该点的插值函数。

如何用几何画板画各种形状的网格

如何用几何画板画各种形状的网格在数学题目中，常常会见到各种图形的网格，尤其是将某几何图形衬于网格中进行研究。

几何画板是研究几何问题的必备工具，也可以用其来绘制网格。

今天来给大家介绍怎么用几何画板画各种形状的网格。

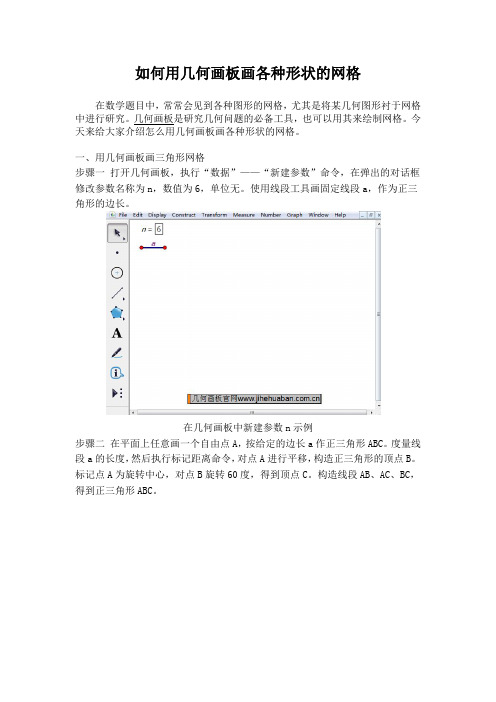
一、用几何画板画三角形网格步骤一打开几何画板，执行“数据”——“新建参数”命令，在弹出的对话框修改参数名称为n，数值为6，单位无。

使用线段工具画固定线段a，作为正三角形的边长。

在几何画板中新建参数n示例步骤二在平面上任意画一个自由点A，按给定的边长a作正三角形ABC。

度量线段a的长度，然后执行标记距离命令，对点A进行平移，构造正三角形的顶点B。

标记点A为旋转中心，对点B旋转60度，得到顶点C。

构造线段AB、AC、BC，得到正三角形ABC。

利用线段a构造正三角形ABC示例步骤三选中点A和参数n=6，此时按住“Shift键”，执行“变换”——“深度迭代”命令，在弹出的对话框作A→B，A→C的迭代，然后点击“迭代”按钮。

对点A执行深度迭代示例步骤四这样就制作完成了如下图所示的三角形网格，利用“<”、“>”键可以对参数n进行控制，增加或减少网格数量。

对三角形网格进行调整示例二、用几何画板画正方形网格步骤一打开几何画板，执行“数据”——“新建参数”命令，在弹出的对话框修改参数名称为n，数值为6，单位无。

使用线段工具画固定线段a，作为正方形的边长。

在几何画板中新建参数n示例步骤二在平面上任意画一个自由点A，按给定的边长a作正方形ABCD。

度量线段a的长度，然后执行标记距离命令，对点A进行平移，构造正方形的两个顶点B、D。

构造线段AB、AD，过点D做线段AB的平行线，过点B做平行线的垂线，交点为C，隐藏平行线和垂线，构造线段BC、CD，得到正方形ABCD。

利用线段a构造正方形ABCD示例步骤三选中点A和参数n=6，此时按住“Shift键”，执行“变换”——“深度迭代”命令，在弹出的对话框作A→B，A→C，A→D的迭代，然后点击“迭代”按钮。

ue5 三角形剖分算法

ue5 三角形剖分算法UE5是一款由Epic Games开发的游戏引擎，它提供了丰富的工具和功能，帮助开发者创作出逼真而富有创意的游戏世界。

其中一个重要的功能是三角形剖分算法，它能够将复杂的几何形状分割成由三角形组成的网格，为游戏的渲染和碰撞检测等模块提供基础支持。

三角形剖分算法是计算机图形学中一项重要的技术，它在许多应用中起着至关重要的作用。

在游戏开发中，我们需要将复杂的几何形状进行剖分，以便进行光照计算、阴影投射、碰撞检测等操作。

UE5提供了多种三角形剖分算法，以满足不同应用场景的需求。

首先，我们来介绍最常用的Delaunay三角剖分算法。

Delaunay三角剖分算法是一种基于点集的剖分方法，它的最终结果是一个无重复边且没有任何点位于三角形的外接圆内的三角网格。

在UE5中，我们可以通过调用相应的函数来进行Delaunay三角剖分，输入是一组点的坐标，输出是一个网格。

这个网格可以被用于渲染几何模型或进行碰撞检测。

除了Delaunay三角剖分算法，UE5还提供了其他一些高级的三角形剖分算法。

例如，我们可以使用Voronoi三角剖分算法来生成泰森多边形，这是一种将平面分割为由点及其最近邻点组成的多边形的方法。

泰森多边形在游戏开发中常用于创建地形、自动道路生成以及区域分割等应用。

此外，UE5还实现了一种名为Ear Clipping的三角剖分算法。

Ear Clipping算法是一种简单而高效的方法，用于对简单多边形进行剖分。

在UE5中，我们可以通过调用相应的函数来对游戏场景中的多边形进行Ear Clipping剖分，从而生成三角形网格。

在实际的游戏开发过程中，三角形剖分算法在模型导入、地形生成、物理模拟等方面都起着重要的作用。

通过合理选择和应用合适的三角形剖分算法，我们可以提高游戏的效率和表现，为玩家带来更好的游戏体验。

总而言之，UE5中的三角形剖分算法是游戏开发中不可或缺的重要技术。

无论是Delaunay三角剖分、Voronoi三角剖分还是Ear Clipping剖分，都为开发者提供了强大的工具和功能，帮助我们创建出精美而细致的游戏世界。

matlab 曲面三角剖分

一、概述Matlab是一种用于数学计算、数据分析和可视化的强大软件工具。

曲面三角剖分是在三维空间中创建曲面网格的过程，常用于工程、地质、医学等领域。

在Matlab中，曲面三角剖分可以通过多种方法实现，本文将介绍在Matlab中实现曲面三角剖分的方法和技巧。

二、Matlab中的曲面三角剖分在Matlab中，曲面三角剖分通常使用triangulation函数来实现。

该函数可以将点云数据转换为三角形网格数据，从而创建曲面的三角剖分。

在使用triangulation函数之前，我们需要准备好曲面的点云数据，可以通过手动输入或者读取外部文件获取点云数据。

三、创建点云数据1. 手动输入点云数据在Matlab中，可以使用数组或者矩阵来手动输入曲面的点云数据。

我们可以定义一个包含曲面上各个点的坐标的数组，例如:x = [0, 1, 2, 3];y = [0, 1, 2, 3];z = [0, 0, 0, 0];这些点的坐标可以表示为空间中的一个平面，通过triangulation函数，可以将这些点转换为三角形网格数据，实现曲面的三角剖分。

2. 读取外部文件获取点云数据除了手动输入外，还可以通过读取外部文件获取曲面的点云数据。

在实际应用中，曲面的点云数据通常是通过CAD软件、三维扫描仪等设备获取的。

在Matlab中，可以通过导入外部文件的方式将点云数据导入到Matlab环境中，然后使用triangulation函数进行三角剖分。

四、triangulation函数的使用一旦准备好曲面的点云数据，就可以使用triangulation函数进行曲面的三角剖分。

triangulation函数的基本语法如下:tri = triangulation(x, y, z);其中x、y、z是曲面上各个点的坐标，tri是表示三角形网格数据的三角剖分对象。

五、绘制曲面三角剖分图形在使用triangulation函数创建三角剖分对象后，可以通过plot函数将曲面的三角剖分图形绘制出来。

ue 三角面片算法

UE三角面片算法简介UE三角面片算法（UE Triangle Meshing Algorithm）是一种常用于计算机图形学和虚拟现实领域的算法，用于生成三维模型的三角面片网格。

该算法可以将复杂的几何体表示为由许多小的三角形组成的网格结构，以便更好地进行渲染、碰撞检测、动画等操作。

算法原理UE三角面片算法的核心原理是通过对输入的几何体进行三角剖分来生成三角面片网格。

以下是该算法的主要步骤：1.输入几何体：从用户处接收输入的几何体，可以是三维模型、点云或其他形式的几何数据。

2.顶点生成：根据输入的几何体，生成一组顶点。

顶点可以表示几何体的顶点、边缘或面的中心点，或者通过其他方式生成。

3.三角剖分：对生成的顶点进行三角剖分，将几何体划分为许多小的三角形。

常用的三角剖分算法有Delaunay三角剖分、Ear Clipping等。

4.网格生成：根据三角剖分的结果，生成三角面片网格。

每个三角形由三个顶点和相关的法线、纹理坐标等信息组成。

5.优化处理：对生成的网格进行优化处理，以提高渲染性能。

常见的优化方法包括顶点合并、边缘折叠、网格简化等。

6.输出结果：将生成的三角面片网格输出给渲染引擎或其他相关的应用程序进行进一步处理和展示。

应用领域UE三角面片算法在计算机图形学和虚拟现实领域有广泛的应用，主要用于以下方面：1.游戏开发：在游戏中，三角面片网格是表示场景、角色和物体的常用数据结构。

UE三角面片算法可以用于生成游戏中的地形、建筑、角色模型等。

2.可视化：在科学研究、工程设计和医学等领域，三维模型的可视化是一种重要的手段。

UE三角面片算法可以将实际数据转换为可视化的三维模型，以便更好地理解和分析。

3.虚拟现实：虚拟现实技术需要高度逼真的三维场景和物体。

UE三角面片算法可以用于生成虚拟现实环境中的三维模型，提供更真实的交互体验。

4.建筑与规划：在建筑设计和城市规划中，三维模型的生成和展示对于设计师和决策者非常重要。

python中scipy库delaunay的simplices用法

python中scipy库delaunay的simplices用法全文共四篇示例，供读者参考第一篇示例：Scipy库是一个强大的Python科学计算工具箱，其中包含了许多实用的工具和算法。

其中的delaunay模块是用来进行Delaunay三角剖分的工具，它可以将给定的点集进行三角形网格化，从而用于空间插值、地理信息系统、有限元分析等领域。

在scipy库中，delaunay模块中的simplices属性是一个用于存储Delaunay三角形网格中每个三角形顶点索引的属性。

利用这个属性，我们可以很方便地获取Delaunay三角形网格中每个三角形的顶点索引，从而进行进一步的计算和分析。

我们需要导入scipy库和相关的模块：```pythonimport numpy as npfrom scipy.spatial import Delaunay```接着，我们可以生成一个随机的二维点集，并利用Delaunay函数进行Delaunay三角剖分：现在，我们可以通过simplices属性获取Delaunay三角形网格中每个三角形的顶点索引：输出结果类似如下：```[[0 1 3][1 2 3][1 4 5][1 3 4][0 3 6][2 7 3][1 5 8][4 3 7][8 6 0][7 3 5][6 3 8][3 7 5]]```每一行表示一个三角形，其中的三个数字分别代表该三角形的三个顶点在原始点集中的索引。

通过这些顶点索引，我们可以进一步计算三角形的边长、面积、周长等属性，或者对Delaunay三角形网格进行可视化展示。

除了simplices属性之外，Delaunay对象还提供了许多其他有用的属性和方法，比如`vertex_neighbor_vertices`方法可以用来获取每个点的相邻点的索引列表，`find_simplex`方法可以用来查找给定点所在的三角形索引等等。

这些属性和方法可以帮助我们更好地理解和利用Delaunay三角剖分的结果。

接触面的一致性三角形网格生成算法

ａｏｔｍｏｃｎｏｍｎｅｔａｇｌｅｈｓｎｃｎｃｓｒｃｓｗｉｏｔｉｄｆｅａｉｐｏｅｓｓｂｉｔｅａｊｃｎｙｔｌｒｈｆｒｉｇｈｉｎｕａｍｓｅｏｔｔｕｆｅ，ｈｈｃｎａｅｖｓｒｃｓ：ｕｌｈａｅｃ — ｇｉｆｏｔｒｒｏａａｃｎｉｂｃｅｔｄｏ
域的方式来剔除非接触的网格，该方法适应各种类型的网格单
０引言
三角形网格模型在基于有限元或边界元的数值模拟领域有着广泛的应用。在热力学、学等应用中，个模型之力多
ｔｅｅｃｅｃ．Ｔｈｘｍｐｅｈｏｔｔｔｅａｇｒｔｍｓａｃｒｔｎｄｅｃｅ．ｈｆｉｎｙｉｅｅａｌｓｓｗｈａｈｌｏｉｈｉｃｕａｅａｆｉｎｔｉＫｅｒｙｗｏｄｓ：ｔｉｎｕａｓｒａｇｌｒｍｅｈ；ｃｎａｔｏｆｒｎｏｔｃ；ｃｎｏｍｉｇ；ｏｒａｐｄ；ｓａｃｉｇｖｅｌｐｅｅｒｈｎ
李国政，张云，华民，志高周黄
（中科技大学材料成形与模具技术国家重点实验室，汉４０７）华武３０４
摘要：为了简化数值模拟中三角形网格模型之间的接触问题，计了在接触面上生成一致性三角形网格的算设法。基本步骤为构造网格拓扑关系、索重叠网格、搜完善重叠网格、贝网格、拷修补边界空隙。采用面向配对顶点

cst三角形单元

cst三角形单元CST三角形单元是一种用于电磁场分析的数值计算方法，是CST公司开发的一种三角形有限元。

该方法可以在复杂情况下精确地模拟电磁场的行为，包括电场、磁场和电磁波。

如果我们能够了解和掌握这种计算方法，就可以更好地解决一些电磁学问题。

下面将详细地介绍CST三角形单元的应用步骤。

第一步：建立模型要使用CST三角形单元，必须先建立一个模型。

这个模型需要精确地反映电磁场的特性。

CST Studio软件可以帮助我们建立优质的三维模型，其中包括各种工具和功能，如绘图、几何体建模和网格划分，可以使模型设计变得更加简单和快速。

第二步：定义物理特性在模型中定义物理特性，例如材质属相、电导率、磁导率、介电常数等基本参数。

这些参数将作为计算电磁场行为的输入数据。

应该注意的是，输入参数应该与实际物理特性相对应，否则计算结果将不准确。

第三步：分区划分分区划分的目的是将模型分成更小的部分，以便更好地对电磁场进行分析。

在实际应用中，我们可以将各个部分分为相同或不同材质的部分，并对每个区域赋予相应的电磁参数。

这个过程通常需要反复修改和调整以达到最佳效果。

第四步：生成网格生成网格是CST三角形单元方法的核心步骤。

该步骤用于将分区划分的模型中的单元分割成多个三角形，以计算电磁场。

三角形的大小和形状直接影响计算过程的精度。

为了控制计算量和精度，应根据实际情况合理选择网格划分策略。

第五步：应用物理刺激在CST中，物理刺激是指电磁场交互作用的输入源。

模拟电磁场行为的过程中，必须将所感兴趣的刺激部位与正确的物理特性对应，例如，输入电压、电流、磁场等。

在实际模拟中，可以模拟不同类型的物理刺激，如正弦波形和脉冲波形。

第六步：进行分析和修改将物理刺激作为输入数据输入到模型中后，我们可以进行电磁场分析。

如果分析结果与实际情况相符，那么我们可以停止并将结果输出。

如果结果与实际情况不符，则需要重新调整模型的物理特性、网格划分等参数，并重新进行输入和分析等过程，以达到更好的精度和准确度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ee = e*1.e-30
nn = 0
smin = dmax*dmax
do 140 i=1,numnod
cccc do 140 n=nums+1,nume
cccc i = nod2(n)
xx = x(i)
yy = y(i)
s = (xx-xh)**2+(yy-yh)**2
c x,y ............... coordinate arrays of nodal points
c nod1,nod2,nod3 .... nodal No. arrays for each triangle
c node .............. circle boundary nodal No. array
c nums ....... starting edge No. - 1
c numnod ..... number of nodes
c numedge .... number of edges
c mc ......... number of iteration for modifying nodal points
nn = j
write(*,*) 'nn,smin,d =',nn,smin,d
xh = x(nn)
yh = y(nn)
write(*,*) 'xh,yh =',xh,yh
index(nums) = 2
endif
cccc do 1000 n=nums+1,nume
do 1000 n=1,nume
call trinod(nume,nt,x,y,nod1,nod2,nod3)
mtij=numnod
mtik= nt
write(10,*) mtij,mtik
write(10,'(2f8.2)')(x(mtii),y(mtii),mtii=1,mtij)
write(10,'(3i8)')(nod1(mtii),nod2(mtii),nod3(mtii),mtii=1,mtik)
c..................................................................
subroutine trimesh(nums,numnod,nume,mc,x,y)
c .... generate new nodal points for triagle elements
COMMON /TMDATA/ index(80000)
integer edge1,edge2
numb = numnod
c write(*,*) 'numb =',numb,' x,y ='
c write(*,'(1x,6f12.4)') (x(n),n=1,numnod)
c write(*,'(1x,6f12.4)') (y(n),n=1,numnod)
c trimesh generates nodal points of mesh
c trinod generates nodal No. of each triangle
c tricb generates boundary edges according to
c continuous nodal No. of circle boundary
x2 = x(k2)
y1 = y(k1)
y2 = y(k2)
dm = det(x1,x2,xm,y1,y2,ym)
dh = det(x1,x2,xh,y1,y2,yh)
if (dm*dh.gt.-ee) goto 1000
d1 = det(xm,xh,x1,ym,yh,y1)
c write(*,*) 'nume =',nume,' nod1,nod2 ='
c write(*,'(1x,15i5)') (nod1(n),n=1,nume)
c write(*,'(1x,15i5)') (nod2(n),n=1,nume)
dmin = 1.e20
dmax = 0.0
read(1,*) ne
do i=1,ne
read(1,*)x(i),y(i)
enddo
ns = 1
c ne = (nx+ny)*2
nume = 0
nums = 0
call tricb(nume,ns,ne)
numnod = nume
call trimesh(nums,numnod,nume,5,x,y)
c write(*,*) 'n =',n
if (n.eq.nums) goto 1000
k1 = nod1(n)
k2 = nod2(n)
if (k1.eq.nn .or. k2.eq.nn) goto 1000
c write(*,*) 'k1,k2 =',k1,k2
x1 = x(k1)
c nt ......... number of triangles
c ns ......... first nodal point
c ne ......... last nodal point
c..................................................................
c .... m_h is the normal vector of n1_n2
c .... h is the relative high with the bottom n1_n2
cccc nums = 0
h = sqrt(3.0)
cccc h = 1.d0
100 continue
c .... store all nodal No. of edges in arrays nod1 & nod2
implicit real*4 (a-h,o-z)
common /edge/ nod1(80000),nod2(80000)
dimension x(*),y(*),nv(100)
else
nn = k2
endif
500 continue
xh = x(nn)
yh = y(nn)
index(nums) = 4
dmin = sqrt(dmin)
dmax = sqrt(dmax)
c write(*,*) 'dmin,dmax =',dmin,dmax
c write(*,*) 'index ='
write(*,'(1x,15i5)') (index(n),n=1,nume)
c .... m is the middle point of n1 & n2
write(*,*) 'n1,n2 =',n1,n2
xx1 = x(n1)
yy1 = y(n1)
xx2 = x(n2)
yy2 = y(n2)
xm = (xx1+xx2)/2
ym = (yy1+yy2)/2
a = xm-xx1
b = ym-yy1
dd = (a*a+b*b)*4
common /enod/ nod1(80000),nod2(80000),nod3(80000)
common /coor/ x(80000),y(80000)
integer n,nod1,nod2,nod3
c write(*,*) 'input ≠&nx;&ny; '
open(1,file='aa.dat')
d2 = det(xm,xh,x2,ym,yh,y2)
if (d1*d2.gt.-ee) goto 1000
write(*,*) 'dm,dh =',dm,dh
write(*,*) 'd1,d2 =',d1,d2
write(*,*) 'n,k1,k2 =',n,k1,k2
write(*,*) 'x1,x2,y1,y2 =',x1,x2,y1,y2
do 50 n=1,nume
index(n) = 0
i = nod1(n)
j = nod2(n)
d = (x(i)-x(j))**2+(y(i)-y(j))**2
if (d.lt.dmin) dmin = d
if (d.gt.dmax) dmax = d
50 continue
标题：一个简单的三角形网格生成程序，供初学者参考
作者:xurui [3月28日,8:32]
这是一个简单的采用advanced front方法编制的三角形网格生成程序，供初学者参考。我看周华的软件下载区一直空着，就抛砖引玉一下，希望有更多的人能贡献程序共享。若周华看到后，希望能把这个小小的程序放到下载区，因为在这里很快会被淹没。
return
end
c..................................................................
c the following subroutines for generating triangular mesh