立体的投影习题集
道路工程习题第七章 立体的投影及其表面交线

步骤一:根据斜四棱锥表面的特殊位置, 补全四棱锥。
步骤二:根据点的投影性质,作出其各面 投影,并判断可见性。
淮阴工学院工程制图教研组
《道路工程制图习题集》解
分析:由图可五知棱柱和一个正垂面相交。 步骤一:根据五棱柱表面的特殊位置,补
全五棱柱。 步骤二:根据正垂面与五棱柱的棱的交点
的投影性质,作出其各面投影,并判断可 见性。
淮阴工学院工程制图教研组
《道路工程制图习题集》解
7-5求四棱柱被截后的H、 W投影图。
淮阴工学院工程制图教研组
《道路工程制图习题集》解 淮阴工学院工程制图教研组
《道路工程制图习题集》解
分析:作出半球被四个平面截断后的V、W 投影。由图可知半球被两个正平面、两个 侧平面对称截切,交线投影或其积聚投影 重合。
步骤一:根据半球表面的特殊位置,补全 半球未被切掉的轮廓线。
步骤二:根据截切与半球轮廓表面的交点 和截切面与截切面的交线的投影性质,作 出交线的各面投影。
淮阴工学院工程制图教研组
《道路工程制图习题集》解
第七章 立体的投 影及其表面交线
《道路工程制图习题集》解
7-1补全四棱柱及其表面 上点的三面投影。
淮阴工学院工程制图教研组
d' a' (c')
b'
《道路工程制图习题集》解
a"
d"
c" b"
c a
bd
淮阴工学院工程制图教研组
《道路工程制图习题集》解
分析:由图可知四棱柱四个侧面是两个铅 垂面,一个侧平面,一个正平面。A点在四 棱柱的上表面,B点在一个棱上,C点在后 表面上,D点在上表面和前表面的交线上。
工程制图基础习题集(第二版)-解答

a’’(b”)
AB是 侧垂 线
2-3 求作基本体表面上的点或线的其余两个投影
(1)
b’ c’
b”
a”
a c
2-3 求作基本体表面上的点或线的其余两个投影
(2)
e”
a”
d”
c” b”
e
c a
b
d
2-3 求作基本体表面上的点或线的其余两个投影
a”
(3)
f”
e”
d”
c”
b”
d f a
(b) e
内孔轮廓线应到顶。
3-14b 选择正确的第三视图(6)
(注意分析形体被切后和形体组合后的交线的投影)
3-14b 选择正确的第三视图(7)
(注意分析形体被切后和形体组合后的交线的投影)
应为相贯线
应为两内孔相贯且凸向大圆
等径时才为直线
3-14b 选择正确的第三视图(8)
(注意分析形体被切后和形体组合后的交线的投影)
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影 实线
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-7 求作俯视图
3-7 求作俯视图
3-8 求作左视图
3-9 画出下列各相贯线的投影 (1)
3-9 画出下列各相贯线的投影 (2)
等径圆柱的相贯 线在V面上的投 影为两条相交的 直线
3-9 画出下列各相贯线的投影_(3)
3-9 画出下列各相贯线的投影_(4)
等径圆孔的相贯 线在侧面上的投 影为两条相交的 直线
基本体的投影与表面取点习题解答
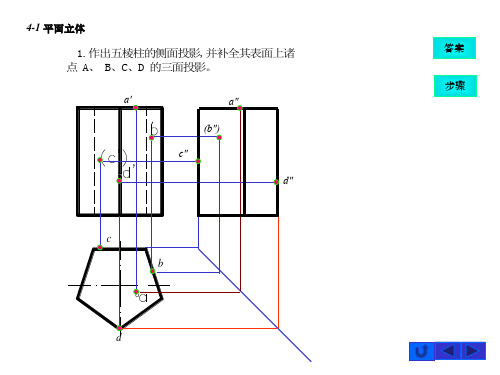
1.作出五棱柱的侧面投影,并补全其表面上诸 点 A、 B、C、D 的三面投影。
a′ ′
a″ (b″)
c″
d″
c b
d
答案 步骤
2.作出三棱锥的侧面投影,并补全其表面上
A,B的三面投影。
答案
步骤(b′)Fra bibliotekb″ a″l′
l
a
3.作出四棱台的侧面投影,并补全其表面上诸 点 A、B、C 、D、E和F的三面投影。
d′ 1′
(f′)
d″
a″
c″ (f″)
b″
e′
e″
c
a 1
b
答案 步骤
4.作出三棱锥的侧面投影,并画出属于棱锥表面 的线段LM、MN、NL的其他两投影。
m′
l′
n′
m″ l″(n″)
答案 步骤
5.作四棱锥被正垂面截断后的侧面投影,并补全截 断后的水平投影。
1′ 2′(3′) 4′
3
4
1
2
1″
3″
a″ b″
c″
b a
(c)
答案 步骤
2.作出圆锥体的水平投影,补全其表面上各点的三面投影。
b″ 1′
a″ c″ 1″
b
(a) (c)
答案 步骤
3.补全球表面上各点的三面投影。
b″ a″
c″
b
a (c)
答案 步骤
4.求 作 水 平 投 影 。
c′ d′
a
b′
a
b
c
d
d c
a
b
c″ a″
答案 步骤
5′(6′) 7′(8′)
2′
1′
9基本体的投影(习题10)

3.2 曲面立体的投影
1. 圆柱
1) 圆柱的投影
上下底圆的水平投影反 映实形,其正面和侧面 投影重影为一直线;而 圆柱面则用曲面投影的 转向轮廓线表示。
绘图步骤: (1) 先绘出圆柱的对称线、 回转轴线。 —细点划线 (2)绘出圆柱的顶面和底 面。—粗实线 (3)画出正面转向轮廓线和 侧面转向轮廓线。—粗实线
3)检查三视图确认无误。
(2)若已知三视图中的两幅图,补画第三幅图。 1)对照已知三视图中的两幅图,找全平面立体的交点并进行
编号。
2)根据投影规律,找出交点在第三幅图中的具体投影位置, 对相应点进行连线。 3)检查三视图确认无误。
3.1 平面立体的投影 1、棱柱
1)棱柱的投影
一个投影为多 边形,另外两个 投影轮廓线为矩 形。
回转体:母线绕轴旋转,形成回转面。 由回转面或回转面与平面所围成的立体 为回转体。
投影绘制的方法: (1)若已知轴测图,绘制三视图 1)找出曲面立体的特殊点。 2)根据投影规律绘制曲面立体特殊点的三面投影。 3)检查三视图确认无误。 (2)若已知三视图中的两幅图,补画第三幅图。 1)对照已知三视图中的两幅图,找全曲面立体的特殊点。 2)根据投影规律,绘制曲面立体特殊点的三面投影。 3)检查三视图确认无误。
以五棱柱的投影为例:
水平投影 正面投影 侧面投影
H
Y1
Y2
Y2 Y1 W
棱柱类立体的投影特征:
棱柱类立体的棱面在某一投影面上有积聚性。
2) 棱柱表面上的点
1’ 2’(6’) 3’(5’) 4’
(a)
7’
8’(12’) 6(12)
9’(11’) 5(11)
10’
4(10) 1(7)
第三章立体的投影4习题课

台湾 架设第一条电报线,成为中国自
出行 (1)新式交通促进了经济发展,改变了人们的通讯手段和 , 方式 转变了人们的思想观念。
(2)交通近代化使中国同世界的联系大大增强,使异地传输更为便 捷。 (3)促进了中国的经济与社会发展,也使人们的生活
多姿多彩 。
[合作探究· 提认知]
电视剧《闯关东》讲述了济南章丘朱家峪人朱开山一家, 从清末到九一八事变爆发闯关东的前尘往事。下图是朱开山 一家从山东辗转逃亡到东北途中可能用到的四种交通工具。
平行于轴线 θ = 0°
双曲线
平行于一条素线 过锥顶 θ =α 直线(三角形)
抛物线 直线
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材· 填要点] 一、铁路,更多的铁路 1.地位
铁路是
交通运输 建设的重点,便于国计民生,成为国民经济
发展的动脉。 2.出现 1881年,中国自建的第一条铁路——唐山 路建成通车。 1888年,宫廷专用铁路落成。 至胥各庄铁 开平
一、近代交通业发展的原因、特点及影响 1.原因 (1)先进的中国人为救国救民,积极兴办近代交通业,促
进中国社会发展。
(2)列强侵华的需要。为扩大在华利益,加强控制、镇压
中国人民的反抗,控制和操纵中国交通建设。
(3)工业革命的成果传入中国,为近代交通业的发展提供 了物质条件。
2.特点 (1)近代中国交通业逐渐开始近代化的进程,铁路、水运和
报先后发明。
(3)近代以来,交通、通讯工具的进步,推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年,革命党人发动武昌起义,辛亥
第四章 立体投影(第四讲)

截交线的求法: 截交线的求法:
平面立体截交线是一个封闭的平面多边形, 平面立体截交线是一个封闭的平面多边形,多边形的 封闭的平面多边形 顶点是平面立体的棱线与截平面的交点,多边形的每条边 顶点是平面立体的棱线与截平面的交点,多边形的每条边 是平面立体的棱线与截平面的交点 是平面立体的棱面与截平面的交线。 是平面立体的棱面与截平面的交线。 棱面与截平面的交线 求截交线---归根到底是求截 求截交线 归根到底是求截 平面与立体表面(或棱线) 平面与立体表面(或棱线) 一系列交线(或交点) 一系列交线(或交点)的问 题。 交线 顶点
平面与平面立体相交
应用举例(单一截平面) 应用举例(单一截平面)
例1:已知立体的正面投影和水平投影, 求其侧面投影。 ★ 形体分析和投影分析
1、根据投影,判别立体形状 、根据投影, 2、根据截平面位置,判别截断面形状 、根据截平面位置, 3、判别截平面与投影面的相对位置 、
平面与平面立体相交
(5′ 3(5′) ′ (6′ (6′) 2′ 1′
4 3
作图: 检查、 作图: ③检查、完成
检查、 (e) 检查、完成 图3-22 正四棱锥被两平面截切
平面与平面相交画法
截平面
截交线
例题2 求立体截切后的投影
4′ 5′ 1′
(3′)
3″ 6″
4″ 5″
(6′)
2″ 1″
(2′)
2
3
Ⅲ Ⅳ
1
Ⅵ
6
Ⅱ Ⅰ
4
Ⅴ
5
例题5
求立体截切后的投影
1′(2′) 3′(4′) 4″
求水平面、 (c) 求水平面、正垂面与立体的交线
图3-22 正四棱锥被两平面截切
工程制图第二版陶冶作业答案第三章基本立体的投影

P11-1 求作截切圆柱的W 面投影。
P11-2 补画截切圆柱的H 面投影,求作其W 面投影。
P11-3 求作截切圆柱的H 面投影。
P11-4 求作立体的H 面投影。
P11-5 补画截切圆锥的H 面投影,求作其W 面投影。
P11-6 求作截切圆锥的H 面投影。
P12-1 补画截切圆锥的H 面投影,求作其W 面投影。
P12-2 求作截切球的V、H 面投影。
P12-3 求作截切半球的H、W 面的投影。
P12(3-6)-1 求作穿孔圆柱体的W 面投影。
P12(3-6)-2 求作截切体的H 面投影。
P13-1 补画相交两圆柱体的V 面投影。
P13-2 求作立体的W 面投影。
P13-3 求作穿孔圆柱的W 面投影。
P13-4 半圆柱和圆台相交,补画其V、H 面投影。
P13-5 求作圆柱与圆锥相交后的H 面投影。
P13-6 求作圆柱与圆锥相交后的V 面投影。
P14-1 求作立体的H 面投影。
P14-2 完成两回转体相交的V、H 面投影。
P14-3 补画H 面投影中的漏线。
P14-4 补画V、H 面投影中的漏线。
(c') b'
a'
c (a) b
c″ (b″)
a″
P8-4 补画立体的H 面投影。
P8-5 补画立体的H 面投影。
P8-6 补画三棱台的W 面投影。
P9-1 求作圆柱的W 面投影及表面上点的其他投影。 c'
(a') b'
c″
a″ (b″)
a
c b
P9-2 求作圆柱筒的H 面投影及表面上点的其他投影。 a'
3-4.例题( 立体)

步骤: •找全特殊点 •适当的中间点 •光滑连线 •轮廓线 •可见性
1
例2:
c
若截切平面与 轴线成45°,则 椭圆的投影为圆!
45°
多平面截切圆柱体
例1:
p3´
p4´ p3 p2 p1 p4
•那些平面截切立体 •每个截断面的形状 (是否 45°?) •平面与平面的交线!
2. 必须熟悉交线的基本形式
3. 多形体相交
形体分析: 搞清哪些形体相交,交线是什么 两两求交 不完整的交线: 先整体求交,再取局部交线
3.表面交线分析
二次曲面交线的性质分析
一般为四次曲线,其 具有公共对称平面时 投影亦为四次曲线 交线在与对称平面 平行的投影面上的 投影为二次曲线
双曲线
圆球
交线分析 球心 投影分析 交线为空间曲线 投影作图 H、V面投影
求特殊点 均为未知 求中间点 光滑连接曲线 如何选择辅助面? 交线的H投影
辅助球面
归纳 1. 求交线的基本方法
利用积聚性投影 用面上取点的方法求解 辅助面法
辅助平面法 辅助球面法
利用“三面共点”的原理
二回转面的 轴线必须相交
辅助面选择原则 辅助面与二回转面交线的投影 为直线或圆 在何处作辅助面 二回转面的共有部分—交线共有
例 :求八棱柱被平面P截切后的水平投影图。
作题步骤:
① ② ③ ④ ⑤ 例1:
想清形体的形状 确定形体是如何截切的 判断截交线的边数及形状 利用面形法画图(截切平面与各棱线的交点) 补全投影图,判断可见性 例2:
5´, 6´
2´ 3´, 4´ 2″ 1″ 2 6 3 4 3″ 4″ 6″ 5″ 7″ p0´ p1´ p2´ p3´ p3 ″
人教版九年级下册数学 第29章 投影与视图 同步练习题(含答案)
人教版九年级下册数学第29章投影与视图同步练习题29.1 投影1.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是()2.小飞晚上到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定地说,广场上的大灯泡一定位于两人.3.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是() A.AB=CD B.AB≤CDC.AB>CD D.AB≥CD4.如图,如果在阳光下你的身影的方向是北偏东60°方向,那么太阳相对于你的方向是()A.南偏西60°B.南偏西30°C.北偏东60° D.北偏东30°5.如图所示,右面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是()6.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD. (1)请你在图中画出路灯灯泡所在的位置(用点P表示);(2)画出小华此时在路灯下的影子(用线段EF表示).7.如图,已知线段AB=2 cm,投影面为P,太阳光线与地面垂直.(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.29.2 三视图第1课时几何体的三视图1.下列立体图形中,主视图是圆的是()2.如图是由四个小正方体叠成的一个几何体,它的左视图是()3.如图,水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是()4.如图所示几何体的左视图是()5.将如图所示的两个平面图形绕轴旋转一周,对其所得的立体图形,下列说法正确的是()A.主视图相同B.左视图相同C.俯视图相同D.三种视图都不相同6.图中物体的一个视图(a)的名称为.7.画出如图所示圆柱的三视图.8.画出如图所示几何体三视图.9.下列四个几何体中,主视图与左视图相同的几何体有()A.1个 B.2个C.3个D.4个10.如图是一个空心圆柱体,其左视图正确的是()11.形状相同、大小相等的两个小木块放置于桌面,其俯视图如图,则其主视图是()12.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是()13.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图(从正面、左面、上面看得到的视图).14.一种机器上有一个进行转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图.15.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下列几何体中的哪一个?选择并说明理由.第2课时由三视图确定几何体1.如图是某几何体的三视图,则这个几何体是()A.棱柱 B.圆柱C.棱锥 D.圆锥2.一个几何体的三视图如图所示,这个几何体是()A.圆柱 B.棱柱C.圆锥 D.球3.如图所示,所给的三视图表示的几何体是()A.圆锥 B.正三棱锥C.正四棱锥 D.正三棱柱4.如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上方小正方体的个数,这个立体图形的左视图是()5.图中的三视图所对应的几何体是()6.已知一个正棱柱的俯视图和左视图如图,则其主视图为()7.某几何体的三视图如图所示,则组成该几何体共用了小方块()A.12块B.9块C.7块D.6块8.如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体不可能是()A.6个B.7个 C.8个 D.9个第3课时由三视图确定几何体的表面积或体积1.如图是一个几何体的三视图,根据图中提供的数据(单位: cm)可求得这个几何体的体积为()A.2 cm3B.3 cm3C.6 cm3D.8 cm32.如图是一几何体的三视图,由图中数据计算此几何体的侧面积为.(结果保留π)3.如图是某工件的三视图,求此工件的全面积.4.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积,结果为 cm2.(结果可保留根号)5.一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.6.如图是一个几何体的三视图(单位:cm).(1)写出这个几何体的名称;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个路线的最短长度.参考答案:第二十九章投影与视图29.1 投影1.B2.中间的上方.3.D4.A5.D6.解:如图所示.7.解:(1)点C为所求的投影.(2)线段CD为所求的投影,CD=2 cm.(3)线段CD为所求的投影,CD=2cos30°= 3 cm.29.2 三视图第1课时几何体的三视图1.D2.A3.D4.A5.D6.主视图.7.解:如图所示.8.解:如图所示.9. D10.B11.D12.D13.解:如图.14.解:如图.15.解:比较各几何体的三视图,考虑是否有长方形,圆及三角形即可.对于A,三视图分别为长方形、三角形、圆(含直径),符合题意;对于B,三视图分别为三角形、三角形、圆(含圆心),不符合题意;对于C,三视图分别为正方形、正方形、正方形,不符合题意;对于D,三视图分别为三角形、三角形、矩形(含对角线),不符合题意;故选A.第2课时由三视图确定几何体1.D2.A3.D4.B5.B6.D7.D8.D 提示:如图,根据左视图可以推测d=e=1,a,b,c中至少有一个为2. 当a,b,c中一个为2时,小立方体的个数为:1+1+2+1+1=6;当a,b,c中两个为2时,小立方体的个数为:1+1+2+2+1=7;当a,b,c三个都为2时,小立方体的个数为:1+1+2+2+2=8.所以小立方体的个数可能为6个、7个或8个.故选D.第3课时由三视图确定几何体的表面积或体积1.B2.10π.3.解:由三视图可知,该工件为底面半径为10 cm、高为30 cm的圆锥体.圆锥的母线长为302+102=1010(cm),圆锥的侧面积为12×20π×1010= 10010π(cm 2),圆锥的底面积为102π=100π(cm 2),圆锥的全面积为100π+10010π=100(1+10)π(cm 2).45.解:该几何体的形状是直四棱柱,由三视图知,棱柱底面菱形的对角线长分别为 4 cm ,3 cm.∴菱形的边长为(32)2+22=52(cm ),棱柱的侧面积为52×8×4=80(cm 2). 6.解:(1)圆锥.(2)表面积S =S 扇形+S 圆=πrl +πr 2=12π+4π=16π(cm 2).(3)如图将圆锥侧面展开,线段BD 为所求的最短长度.由条件,得∠BAB ′=120°,C 为弧BB ′的中点,∴BD =33(cm ).。
立体的投影习题答案

Part
03
中心投影
中心投影的定义
中心投影的定义
中心投影是一种投影方式, 其中物体通过一个固定点 (即投影中心)投射到投 影面上。
中心投影的原理
当光线通过一个固定点时, 物体的图像会呈现在该点 的对面平面上。
中心投影的特点
中心投影可以产生物体的 真实图像,且投影面与物 体的相对位置不影响图像 的形状和大小。
04
立体图形的投影
立方体的投影
01
02
03
立方体的正面投影
呈现一个正方形,其中包 含三个垂直交叉的线段, 分别代表立方体的长度、 宽度和高度。
立方体的侧面投影
呈现两个相同的长方形, 分别代表立方体的侧面和 顶面。
立方体的顶部投影
呈现一个正方形,代表立 方体的顶面。
圆柱体的投影
圆柱体的正面投影
呈现一个圆形,代表圆柱体的底面。
中心投影的应用
1 2
建筑设计
在建筑设计领域,中心投影常用于绘制建筑物的 三维效果图,以展示建筑物的外观和空间关系。
机械制图
在机械制图领域,中心投影用于绘制零件的三视 图,以准确表达零件的形状和尺寸。
3
艺术绘画
艺术家使用中心投影来创作具有立体感的画作, 通过调整光线和阴影来表现物体的立体形态。
Part
圆柱体的侧面投影
呈现一个矩形,其中包含两个平行的长方形,分 别代表圆柱体的高度和底面的宽度。
圆柱体的顶部投影
呈现一个圆形,代表圆柱体的顶面。
圆锥体的投影
圆锥体的正面投影
呈现一个等腰三角形,其中包含一个垂直的线段,代表圆锥体的 高度。
圆锥体的侧面投影
呈现一个扇形,其中包含一个弧形和两条相交的线段,分别代表圆 锥体的底面圆弧和侧面。
大学工程制图习题集答案第4章

e
b a
(c)
(d)
答案 步骤
2.作出圆锥体的水平投影,补全其表面上各点的三面投影。
e′
b″
a″
1′
c″ 1″
b
d (a)
(c) e
答案 步骤
3.补全球表面上各点的三面投影。
(f′)
(f″)
b″
(e′)
(d″)
a″
c″
b e a
d (c)
答案 步骤
4.求 作 水 平 投 影 。
c′ d ′
a
b′
4″
3″
8″
2″ 7″
答案
PW2 步骤
PW1 PW3
1.补全三面投影(形体提示:带有轴线为铅垂线和侧垂线的 个圆柱形通孔的球体)。
答案
补全三面投影(形体提示:带 有轴线为铅垂线和侧垂线 的两个圆柱形通孔的球体)。
步骤
4.求作正面投影。
步骤
感谢观看
答案
汇报人姓名
3.补全立体的 正面投影。
步骤
答案
4.补全穿孔圆柱表面交线的投影。
5.补全穿孔圆柱表面交线的投影。
步骤
答案
5.补全穿孔圆柱表面交线的投影。
4.补全穿孔圆柱表面交线的投影。
步骤
答案
4-6 立体与立体相交(二)
14.完.成完圆成柱圆与柱与圆圆锥锥相相贯贯后后的的正正面投投影影和和水水平平投投影影。。
2′
4″
3″
6″ 8″
5″
7″ 2″
64
2
1
3
答案 步骤
3.完成半圆球被截后的水平和侧面投影。
1.完成半圆球被截后的水平和侧面投影。
建筑工程制图与识图习题集

5、作图求AB的实长和倾角α 。
a'
ΔZ
b'
X
O
a ΔZ α
AB实长
b
6、作图求AB的实长和倾角ß。
AB实长
ΔY b'
ß a'
a ΔY
b
7、已知a'b'及b, ß=30º,且A在B之前,求AB实长及ab。
ß
b'
ΔY
a'
X
ΔY a
O b
8、判别两直线的相对位置 b'
a' c'
X a
a'
b'
f'
g′
d′
c'
e'
X
O
a
b g
f
d
c
e
4、求平面内ABCD内字A的另一个投影。
b′
2′
c′
4′
a′ 1′
3′
d′
X
3d
O
c
14
2
a
b
5、求三角形ABC对H面的倾角α。 b′
d′ a′
△z
e′
c′
X
b
O
d
α
a
e △z
c
6、求三角形ABC对V面的倾角β。
b′
β d′
△y e′
c′
a′
X
O
b'
c'
h'
a'
e'(f‘)
d'
(g')
X
f
O
b ch
a
g
d
第三章 基本形体—— 三视图的投影习题答案new

3-7、补绘基本形体的第三投影
(1)
(2)
班级 (3)
参考使用,交流学习 1548138554
学号
姓名
(4)
(5)
(6) 45
第三章 基本形体——补绘基本形体的第三投影 3-8、补绘基本形体的第三投影 (1)
(2)
班级
(3)
参考使用,交流学习 1548138554
学号
姓名
(4)
(5)
(6)
46
第三章 平面立体表面上的点
第三章 基本形体—— 三视图的投影 3-1、画三棱柱的投影图。
3-3、画出右下图的投影图。
3-5、画出圆台的三面投影。
班级
学号
3-2、画出六棱柱的投影图。
参考使用,交流学习 1548138554 姓名
3-4、画出半圆拱的三面投影。
3-6、画半圆拱的三面投影。
44
第三章 基本形体—— 补绘基本形体的第三投影
f'
b
cd
df
(e)
(f)
e
a
3-17、正六棱柱被正垂面 P 截断,补全截断体的 H 面投影,作出 3-18、完成平面体被平面截切后的水平投影并作出侧面投影。 截断体的 W 面投影及断面的真形。
49
第三章 平面体的截交线 3-19、补全有缺口的三棱柱的 H 面投影和 V 面投影。
班级
参考使用,交流学习 1548138554
1'
(3')
(3'')
2'
1'' 2''
3
1' 2
3-14、画出三棱柱的 V 面投影,并补全三棱柱表面上的折线 FACEDBF 的 H 面投 影及 V 面投影。
《机械制图习题集》习题答案——第2章
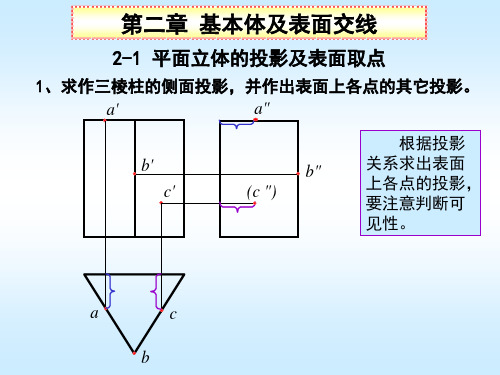
由于棱
锥体的棱面 无积聚性, 表面取点要 利用辅助线 法。
2-2 回转体的投影及表面取点
完成回转体的投影,并作出表面上各点的三面投影。
(1
)
a'
a"
b'
(b")
(b) a
回转体表面取点, 根据已知点的可见性 判断点所处的位置, 按投影关系,找出各 点的投影。
(2 )
(c') 1'
a'
b'
1" c" a"
4、完成相贯体的三视图。
1'
5'(6') 3'(4') 2' 7'(8')
1"
5" 6"
4"
3"
8"
7" 2"
4 86 21
75 3
圆锥体与圆
柱形孔正交。因 圆锥面的投影无 积聚性,利用辅 助平面求一般位 置的点。
5、完成相贯体的三视图。
1'
5'(6') 3'(4') 7'(8') 2'
1"
6"
b"
c
a
b
圆锥面的投
影无积聚性,表 面取点利用辅助 素线或辅助纬圆 法求解。底面上 的点可利用投影 关系直接求出。
(3 )
a'
b'
a" (b")
1a
圆锥台的表面
2 b
投影无积聚性,表 面上取点利用辅助
纬圆法。
(4 )
习题-第五、六、七章立体的投影 (2)

24/2012 习题
25/2012 习题
重点、难点:
1、掌握曲面立体表面取点、取线的作 图方法; 2、掌握曲面立体切割体的作图步骤; 3、掌握曲面立体切割体投影的连线原 则。
5-2 求下列各回转体的第三面投影及其表面上各点、 线的另外两个投影。 (1)
26/2012 习题
(2)
27/2012 习题
60/2012 习题
7-4 完成球、圆锥、圆柱穿孔体的投影。 (2)
61/2012 习题
切 割 体
7-4 完成球、圆锥、圆柱穿孔体的投影。 相贯体 (2)
62/2012 习题
7-4 完成球、圆锥、圆柱穿孔体的投影。 (3)
63/2012 习题
7-5 求两曲面立体相贯线 。 (1)
64/2012 习题
三、整理原轮廓线,完成作图。 3.刀与刀之间交线?
6-1 求下列各棱柱切割体的另外两面投影。 (1)
8/2012 习题
9/2012 习题
(2)
10/2012 习题
(3)
11/2012 习题
(3)
12/2012 习题
(4)
13/2012 习题
(5)
14/2012 习题
(6)
15/2012 习题
圆 柱 与 圆 柱 互 贯
7-5 求两曲面立体相贯线 。 (2) 圆 柱 与 圆 柱 互 贯
65/2012 习题
7-5 求两曲面立体相贯线 。 (3)
66/2012 习题
圆 柱 与 圆 锥 互 贯
7-5 求两曲面立体相贯线 。 (4)
67/2012 习题
圆 柱 与 半 球 互 贯
7-5 求两曲面立体相贯线 。5) (
第6章 相交立体的投影习题答案

想看立体模型?请单击这里
12
2016年1月12日星期 二11时13分8秒
6-4 画出相交立体的正面投影 (2)
作图步骤 1.画圆柱套的正面转向 轮廓素线的投影 2.求相贯线的正面投影
此题为在一直立圆柱套的 左右方向挖通一正四棱柱孔。 正四棱柱孔尺寸比圆柱套内孔 大。正四棱柱孔仅与圆柱套外 表面有交线。
6-3 画出相交立体的侧面投影
(3)
作图步骤
1.画相交立体的内、外表面 侧面转向轮廓素线的投影 2.求相贯线的侧面投影
(1)求内表面相贯线的投影 (2)求外表面相贯线的投影
①求上方相贯线的投影
②求下方相贯线的投影 此题为前后躺放一圆柱套,上方 与一内有圆柱孔的正四棱柱相贯。下 方与圆柱相贯。左右,前后均对称。 孔与孔是等径相贯,正四棱柱左右面 与躺放圆柱面相切。下方是不等径圆 柱相贯。应分别求相贯线的投影。
4
想看立体模型?请单击这里
2016年1月12日星期 二11时13分8秒
6-1 完成相交圆柱的相贯线投影
(3)
作图步骤 1.画内表面相贯线的投影
2. 画外表面相贯线的投影
由水平投影和侧面投影 可知,此题为两个内、外表 面直径相等的圆柱套正交。 内、外表面的相贯线均为椭 圆,其正面投影均为相交直 线,二者投影重合。
想看立体模型?请单击字母
16
2016年1月12日星期 二11时13分8秒
6-5 画出相交立体的正面投影 (3)
作图步骤 1.画圆柱套的侧面转向 轮廓素线的投影 2.画后面圆孔和前面拱形孔 轮廓素线的的侧面投影 3.求相贯线的侧面投影 (1)求圆孔与圆柱套内、 外表面交线的投影 (2)求拱形孔与圆柱套内、 外表面交线的投影
6-1 完成相交圆柱的相贯线投影。 (1)
《机械制图》立体的投影习题

[作图题][难度1]1、求作属于圆柱表面的点A、B、C、D 的另外两面投影。
[参考答案][作图题][难度2]2、补全正五棱柱的水平投影,并画出属于棱柱表面的点A、B及线段CD的其他两面投影。
[参考答案][作图题][难度3]3、补画出正六棱台的侧面投影,并补全属于棱台表面的线段AB、BC、CD的其他两面投影。
[参考答案][作图题][难度3]4、画出半圆柱的水平投影。
并求作属于圆柱表面的曲线AB的另外两面投影[参考答案][作图题][难度2]5、求作属于圆锥表面的点A、B、C、D的另外两面投影。
[参考答案][作图题][难度3]6、画出圆锥的侧面投影。
并求作线段SB、BC的另外两面投影。
[参考答案][作图题][难度2]7、画出圆球的水平投影和侧面投影,并求作属于圆球表面的点A、B、C、D的另外两面投影。
[参考答案][作图题][难度3]8、求作属于圆球表面的曲线段的另外两面投影。
[参考答案][作图题][难度2]9、已知属于回转体表面的点A、B的一个投影,求作另外两面投影。
[参考答案][作图题][难度3]10、画全同轴回转体的正面投影和侧面投影,并补画其水平投影。
[参考答案][作图题][难度3]11、画出侧面投影图。
[参考答案][作图题][难度4]12、补全正五棱柱的水平投影和侧面投影。
[参考答案][作图题][难度4]13、补画带切口的正三棱锥的水平投影和侧面投影。
[参考答案][作图题][难度3]14、画出圆柱体被截切后的侧面投影。
[参考答案][作图题][难度3]15、画出圆锥体被截切后的侧面投影。
[参考答案][作图题][难度3]16、画出圆球体被截切后的水平投影和侧面投影。
[参考答案][作图题][难度4]17、画出侧面投影。
[参考答案][作图题][难度3]18、求作侧面投影。
[参考答案][作图题][难度2]19、画全长方体与圆柱相交的正面投影图和水平投影图。
[参考答案][作图题][难度3]20、补全正面投影。
投影与视图技巧及练习题附答案解析

投影与视图技巧及练习题附答案解析一、选择题41)下列几何体是由个正方体搭成的,其中主视图和俯视图相同的是(.DABC ....B【答案】【解析】【分析】分别画出从几何体的上面和正面看所得到的视图,再比较即可.【详解】A,故此选项错误;、主视图,俯视图为B,故此选项正确;,俯视图为、主视图为C,故此选项错误;、主视图为,俯视图为D,故此选项错误;、主视图为,俯视图为 B.故选:【点睛】此题主要考查了简单几何体的三视图,关键是掌握所看的位置.( )2从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是.DC A B.球.棱锥.圆锥.圆柱A【答案】【解析】【分析】由主视图和左视图可得此几何体为柱体,根据俯视图是圆可判断出此几何体为圆柱.【详解】解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个圆,∴此几何体为圆柱.A.故选【点睛】此题考查利用三视图判断几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个视图确定其具体形状.( )3下面四个几何体中,俯视图是圆的几何体共有.4D3 B1 2 CA个个个...个.B【答案】【解析】B.2,,故选个共题目中的四个几何体,俯视图是圆的几何体为圆柱和球4)下面是一个几何体的俯视图,那么这个几何体是(.D C B A....B【答案】【解析】【分析】.根据各个选项中的几何体的俯视图即可解答【详解】解:由图可知,B中的图形是和题目中的俯视图看到的一样,选项B.故选:【点睛】.本题考查由三视图判断几何体,俯视图是从上向下看得到的图纸,熟练掌握是解题的关键55个相同的小正方体组成的,下列有关三视图面积的说法中正确如图所示的几何体是由.)的是(A.左视图面积最大B.俯视图面积最小C.左视图与主视图面积相等D.俯视图与主视图面积相等D【答案】【解析】【分析】利用视图的定义分别得出三视图进而求出其面积即可.【详解】解:如图所示:则俯视图与主视图面积相等.D.故选:【点睛】此题主要考查了简单组合体的三视图,正确把握三视图的定义是解题关键.6)如图所示,该几何体的主视图是(.ABCD....D【答案】【解析】【分析】从前往后看到一个矩形,后面的轮廓线用虚线表示.【详解】1个矩形,中间的轮廓线用虚线表示.该几何体为三棱柱,它的主视图是由D.故选【点睛】本题考查了简单几何体的三视图:画物体的主视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.掌握常见的几何体的三视图的画法.( )n7n的值是盒粉笔,整齐地摆在讲桌上,其三视图如图,则.小亮领来109 DBA7 8 C....A【答案】【解析】【分析】【详解】421盒,解:由俯视图可得最底层有盒,第三层有盒,由正视图和左视图可得第二层有7n7.盒,则共有的值是A.故选【点睛】本题考查由三视图判断几何体.851的小正方体搭成,下列关于这个几何体的个大小相同、棱长为.如图,一个几何体由( )说法正确的是35 AB.从左面看到的形状图的面积为.从前面看到的形状图的面积为4D3 C.三种视图的面积都是.从上面看到的形状图的面积为B【答案】【解析】.A. 4A,故从正面看第一层是三个小正方形,第二层中间一个小正方形,主视图的面积是错误;B. 3B,故从左边看第一层是两个小正方形,第二层左边一个小正方形,左视图的面积是正确;C. 4C错从上边看第一层有一个小正方形,第二层有三个小正方形,俯视图的面积是,故误;D3D.错误;,故左视图的面积是 B.故选点睛:本题考查了简单组合体的三视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图.9).如图所示,该几何体的左视图是(BA ..DC ..B【答案】【解析】【分析】.根据几何体的三视图求解即可【详解】解:从左边看是一个矩形,中间有两条水平的虚线,.故选:B【点睛】.本题考查的是几何体的三视图,熟练掌握几何体的三视图是解题的关键101?Piet Hein)发明的索玛立方块,它由四个及四个以内大小.图是数学家皮亚特海恩(2不可能是下面哪个组件的视图相同的立方体以面相连接构成的不规则形状组件组成.图)(.D CA B....C【答案】【解析】【分析】依次分析所给几何体从正面看及从左面看得到的图形是否与所给图形一致即可.【详解】12A2,符合所给图形;列正方形的个数均依次为、主视图和左视图从左往右,12B2,符合所给图形;列正方形的个数均依次为、主视图和左视图从左往右,11C2,不符合所给图形;、主视图左往右,列正方形的个数均依次为12D2,符合所给图形.、主视图和左视图从左往右,列正方形的个数均依次为C.故选【点睛】考查由视图判断几何体;用到的知识点为:主视图,左视图分别是从正面看及从左面看得到的图形.( )116个相同的立方体搭成的几何体如图所示,则它的从正面看到的图形是.由D C AB....C【答案】【解析】【分析】.观察立体图形的各个面,与选项中的图形相比较即可得到答案【详解】观察立体图形的各个面,与选项中的图形相比较即可得到答案,.C 选项为正确答案,故的图形是能够看到由图像【点睛】此题考查了从不同方向观察物体和几何体,有良好的空间想象力和抽象思维能力是解决本.题的关键12).从不同方向观察如图所示的几何体,不可能看到的是(DB CA ....B【答案】【解析】【分析】找到不属于从正面,左面,上面看得到的视图即可.【详解】1213,,解:从正面看从左往右,列正方形的个数依次为D是该物体的主视图;∴122,列正方形的个数依次为从左面看从左往右,A是该物体的左视图;∴2131,列正方形的个数依次为从上面看从左往右,,C是该物体的俯视图;∴B.没有出现的是选项B.故选13.由若干个相同的小正方体摆成的几何体的主视图和左视图均为如图所示的图形,则最)多使用小正方体的个数为(11D 10 A8 9BC个..个个.个.C【答案】【解析】【分析】.由主视图和左视图可还原该几何体每层的小正方体个数【详解】932个正方体,第二层解:由主视图可得该几何体有列正方体,高有层,最底层最多有10.1个正方体,则最多使用小正方形的个数为最多有C故选【点睛】.本题主要考查了空间几何体的三视图,由主视图和左视图确定俯视图的形状,再判断最多.的正方体个数614)如图的几何体由个相同的小正方体搭成,它的主视图是(.DB C A....A【答案】【解析】【分析】根据从正面看得到的视图是主视图,可得答案.【详解】从正面看有三列,从左起第一列有两个正方形,第二列有两个正方形,第三列有一个正方A 符合题意,形,故A.故选【点睛】本题考查了简单组合体的三视图,从正面看得到的视图是主视图.15).如图是某个几何体的三视图,该几何体是(D B A C.圆锥.三棱柱.圆柱.六棱柱C【答案】【解析】【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.【详解】解:由俯视图可知有六个棱,再由主视图即左视图分析可知为六棱柱,C.故选【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.416)个相同的小正方体搭成的,其中左视图与俯视图相同的是(.下列几何体是由D BC A....C【答案】【解析】——能反映物体的前试题分析:从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的上面形状;从物面形状;从物体的上面向下面投射所得的视图称俯视图——C左视图与俯能反映物体的左面形状.选项体的左面向右面投射所得的视图称左视图C.,故选视图都是()17.如图,这是一个机械模具,则它的主视图是BA..DC ..C【答案】【解析】【分析】.根据主视图的画法解答即可【详解】 A.不是三视图,故本选项错误;B.是左视图,故本选项错误;C.是主视图,故本选项正确;.D.是俯视图,故本选项错误C.故答案选【点睛】.本题考查了由三视图判断几何体,解题的关键是根据主视图的画法判断18“”“”是由两个找到了球体体积的计算方法.我国古代数学家刘徽用.牟合方盖牟合方盖圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几”“)牟合方盖何体是可以形成的一种模型,它的俯视图是(DB C A ....A【答案】【解析】【分析】根据俯视图即从物体的上面观察得得到的视图,进而得出答案.【详解】.该几何体的俯视图是:A.故选【点睛】此题主要考查了几何体的三视图;掌握俯视图是从几何体上面看得到的平面图形是解决本题的关键.419)个大小相同的立方块搭成的几何体,这个几何体的主视图是(.如图是由D ACB ....A【答案】【解析】【分析】.主视图:从物体正面观察所得到的图形,由此观察即可得出答案.【详解】从物体正面观察可得,.21个小正方体左边第一列有个小正方体,第二列有 A.故答案为:【点睛】本题考查三视图的知识,主视图是从物体的正面看得到的视图.20)如图所示,该几何体的俯视图是(.BA ..D C..C【答案】【解析】【分析】.根据三视图的画法即可得到答案【详解】C,解:从上面看是三个矩形,符合题意的是C.故选:【点睛】.此题考查简单几何体的三视图,明确三视图的画法是解题的关键。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a" c"
b'
a'
b"
d"(e")
c
f
b e
d
第12页
机械制图习题集
平面立体及其表面上的点和线 作左端为正垂面的凸字形侧垂柱的水平投影,并已知表面上折线的起点A的 正面投影和终点E的侧面投影,折线的水平投影成一直线,作折线的三面投影。 d' d" b' a'
e'
c'
e"
c" b" a"
D
e d(c) b(a) E C
(5)
(6)
(7)
(8) 第20页
基本体的投影
习题解答
机械制图习题集
平面立体及其表面上的点和线
a'
a"
d' c'(d') d" e' e" b" (c") e'
c'
b' (a')
b" a"
c"
d"
e" f' a f"
b' a(b)
d
e
b
c
d(e)
c(f)
第12页
机械制图习题集
平面立体及其表面上的点和线
a'
c' c" a" d' (d") b" d' f' c d b a a b'(c') e' f"
B
A
第12页
机械制图习题集
曲面立体及其表面上的点和线 s' c" b' d' e' a b c e b d s a d a' b"(a") d" e' e" f a' s" a"
c'
b'(c')
f" (f') d'
c"
e"
b"
d"
c(e)
第13页
机械制图习题集
平面与平面立体相交
1
2
3
4
第14页
机械制图习题集
平面与平面立体相交
5
6
3
4
第14页
机械制图习题集
分析曲面立体的截交线,并补全这些截断的、缺口的、穿孔的曲面立体投影
1.
2
3
4.
第15页
机械制图习题集
分析曲面立体的截交线,并补全这些截断的、缺口的、穿孔的曲面立体投影
5
6
7.
8.
第15页
机械制图习题集
分析曲面立体的截交线,并补全这些截断的、缺口的曲面立体三面投影
1
2
பைடு நூலகம்
3
4
第16页
机械制图习题集
分析曲面立体表面的交线,补全立体相贯、切割、穿孔后的投影
第17页
机械制图习题集
分析曲面立体表面的交线,补全立体相贯、切割、穿孔后的投影
3 4
第18页
机械制图习题集
由立体图画组合体三视图的徒手草图
(1)
(2)
(3)
(4)
第20页
机械制图习题集
由立体图画组合体三视图的徒手草图
