ch.2-1 内能、焓、自由能和吉布斯函数的全微分精编版
热统试题——精选推荐

热统试题2005—2006学年度第⼆学期期末考试试卷(卷)系别:物理与电⼦信息学院课程名称:热⼒学统计物理注意事项:1、教师出题时请勿超出边界线;2、学⽣答题前将密封线外的内容填写清楚,答题不得超出密封线;3、答题请⽤蓝、⿊钢笔或圆珠笔。
⼀、填空题:(每题4分,共20分)1、热⼒学第⼆定律可表为i e ds s d ds +=其中i ds 为熵产⽣,它们的取值范围是:。
2、)(KL L 为动理系数,昻萨格关系为lk kl L L =试说明其含义。
:。
3、在弱简并理想玻⾊⽓体和费⽶⽓体中,⽓体的内能为]2411[233λn g NKT U ±=,(“+”代表费⽶⽓体,“-”代表玻⾊⽓体),由此认为量⼦统计关联使费⽶粒⼦间出现作⽤,玻⾊粒⼦间出现作⽤。
4、当温度T 〈c T 时,将发⽣玻⾊---爱因斯坦凝聚,其内容为在能级E=O 有。
5、巨则分布描写的是具有确定、、的系统。
⼆、计算、证明题(共80分)1、⽤巨则分布导出单原⼦理想⽓体的物态⽅程和内能。
(20)2、试证明,在绝对零度下,⾃由电⼦的壁数为v n 41,其中V N n =是电⼦的密度,v 是平均速率。
(20)3、已知kTVp T S eW2??-??-∝,以p S ??,为⾃变量,证明2)(212)(21S p kC p SpV kT eW ?-????? ????∝,从⽽求出2)(S ?和2)(p ? (20)4、设有⼀园柱形容器,半径为 R ,⾼为L ,以⾓速度ω绕其轴线转动,容器内有⼀同轴的园柱体,半径为<<-δδ(R R) , ⾼为L ,⽤扭丝固定,两园柱之间充有⽓体,试证明,扭丝所受的⼒矩为δηωπL R G 32=由⼒矩G 可以测出⽓体的粘滞系数。
其中⽜顿粘滞定律为dx dv P xy 0η=(10)5、设粒⼦的质量为m ,带有电量e 在平衡状态下遵从麦克斯韦分布,试根据玻⽿兹曼⽅程证明在弱电场下的电导率可以表为:2τσm ne =其中0τ为驰豫时间。
统计物理课件第二章

T
a v2
实际气体的内能不仅与温度有关, 而且与体积有关。
二.焓态方程和定压热容量
H p
T
V
T V T
p
Cp
T S T
p
第一式给出了温度不变时, 系统焓随压强的变化率与物态方程 的关系,称为焓态方程。
第二式是定压热容量。
三.简单系统的 C p CV ?
同理:
窖内辐射场是各向同性和非偏振的。 内能密度也是均匀的。
辐射通量密度:
单位时间内通过单位面积,向一侧辐射的总辐射能量。
一般记为 J u 。
物理意义: 在窖璧开一小孔,电磁辐射将从小孔射出,设小孔足够小,辐射场的 平衡状态将不受到显著破坏。因此,小孔辐射反映了平衡辐射的特征。 实际上,我们研究平衡辐射就是通过小孔辐射来研究的。
辐射场
小孔辐射
可以证明:
1 Ju 4 cu
(上式中,c 为光速,u 为辐射能量密度)
证明:
由图2-4的右图可见,在d t 时 间内,一束电磁辐射通过面 积d A的辐射能量为:
cd t
u
4
d dAcos
考虑各个传播方向(见图2-4左图),可以得到投射到dA一侧的总辐射
能为:
JudtdA
cdt u ddAcos 4
T
气体经节流过程后,温度降低。
1 , 0
T
气体经节流过程后,温度升高。
1 , 0
T
气体经节流过程后,温度不变。
0 时的温度称为反转温度 1 称为反转曲线
T
例:昂尼斯物态方程:
p
nRT V
1
n V
B(T )
B(T )远小于1
p
热力学统计物理-基础题库

Q 一、选择题:(每题 3 分)下列选项正确的是().(热力学系统的平衡状态及其描述)(容易)A . 与外界物体有能量交换但没有物质交换的系统称为绝热系统。
B . 与外界物体既有能量交换又有物质交换的系统称为封闭系统。
C . 与外界物体既没有能量交换又没有物质交换的系统称为孤立系统。
D . 热力学研究的对象是单个的微观粒子。
答案:B.简单系统的物态方程的一般形式为().(物态方程)(容易)A. f ( p ,V ) = 0 ;B. f ( p ,V ,T ) = C ;C. f ( p ,V ,T ) = 0 ;D. f ( p ,V ) = C ;答案:C.下列关于状态函数的定义正确的是().(焓自由能吉布斯函数)(容易)A . 系统的焓是: H = U - pV ;B . 系统的自由能函数是: F = U + TS ;C . 系统的吉布斯函数是: G = U - TS + pV ;D . 系统的熵函数是: S = ;T答案:C.状态函数焓的全微分表达式为dH 为 ( ).(内能焓自由能和吉布斯函数的全微分)(中等)A. TdS - pdV ;B. TdS + Vdp ;C. -SdT - pdV ;D. -SdT + Vdp答案:B.内能函数的全微分表达式为dU 为 ( ). (内能焓自由能和吉布斯函数的全微分)(中等)A. TdS -pdV ;B. TdS +Vdp ;C. -SdT -pdV ;D. -SdT +Vdp答案:A.自由能函数的全微分表达式为dF 为 ( ). (内能焓自由能和吉布斯函数的全微分)(中等)A. TdS -pdV ;B. TdS +Vdp ;C. -SdT -pdV ;D. -SdT +Vdp答案:C.吉布斯函数的全微分表达式为dG 为 ( ). (内能焓自由能和吉布斯函数的全微分)(中等)A. TdS -pdV ;B. TdS +Vdp ;C. -SdT -pdV ;D. -SdT +Vdp答案:D.下列关于状态函数全微分正确的是().(内能焓自由能和吉布斯函数的全微分)(中等)A.内能: dU =TdS -pdV ;B.焓: dH =TdS -Vdp ;C.自由能: dF =-SdT +pdV ;D.吉布斯函数: dG =-SdT -Vdp ;答案:A.下面几个表达式中错误的是( ).(热量和焓)(容易).∂∂p ∂TCp =T∂TA.CVB.CV =∂U; V=∂S; V∂HC. C = ;p∂SD. ;p答案:B.下面关于热力学第零定律的表述错误的是()。
ch.2-1 内能、焓、自由能和吉布斯函数的全微分

(循环关系)
(链式关系)
(复合函数求导法)
2z 2z = xy yx
(全微分条件法)
① 基本方程记忆规则
a.函数的相邻两量为自变量,对应两量为系数。 b.箭头离开系数,取负;箭头指向系数,取正。 例如,与U相邻的两自变量分别为S和V,对应的系数为T和 p,前者箭头指向系数,后者箭头离开系数,故可写出
dU=TdS-pdV
用同样的方法,可方便的写出其他三个基本方程。
② 八个偏导数的记忆方法
由(2.1.2)式dH=TdS+Vdp ,有
H H T , V S p p S
(2.1.6)
由(2.1.3)式dF=-SdT-pdV ,有
F S , T V F p V T (2.1.7)
从四个基本方程出发,利用系数比较法,可很方便地写 出八个偏导数。例如,由dU=TdS-pdV出发,设U=U(S,V), 写出U的全微分,然后比较系数,即可得到
③ 麦氏关系的记忆方法
沿顺时针方向,例如,从S出法,S对V求导T不变,等 于p对T求导V不变。箭头都指向不变量或都离开不变量取 正,一个指向不变量,而一个离开不变量则取负,得
S V T p p T
热力学关系的记忆方法
四个基本方程,八个偏导,四个麦 氏关系。 首先,画两正交箭头,从上到下为 S→T,从左到右为P→V。 为了便于记住箭头的方向,可默读 一个英文句子: The Sun is pouring down his rays upon the Trees, and the brook is flowing from the Peak to the Valley. 然后,按顺时针方向加上E(=U)、F、 G和H。
热力学与统计物理第二章知识总结精品资料

热力学与统计物理第二章知识总结§2.1内能、焓、自由能和吉布斯函数的全微分热力学函数中的物态方程、内能和熵是基本热力学函数,不仅因为它们对应热力学状态描述第零定律、第一定律和第二定律,而且其它热力学函数也可以由这三个基本热力学函数导出。
焓:自由能:吉布斯函数:下面我们由热力学的基本方程(1)即内能的全微分表达式推导焓、自由能和吉布斯函数的全微分•焓、自由能和吉布斯函数的全微分o焓的全微分由焓的定义式,求微分,得,将(1)式代入上式得(2)o自由能的全微分由得(3)o吉布斯函数的全微分(4)从方程(1)(2)(3)(4)我们容易写出内能、焓、自由能和吉布斯函数的全微分dU,dH,dF,和dG独立变量分别是S,V;S,P;T,V和T,P所以函数U(S,V),H(S,P),F(T,V),G(T,P)就是我们在§2.5将要讲到的特性函数。
下面从这几个函数和它们的全微分方程来推出麦氏关系。
二、热力学(Maxwell)关系(麦克斯韦或麦氏)(1)U(S,V)利用全微分性质(5)用(1)式相比得(6)再利用求偏导数的次序可以交换的性质,即(6)式得(7)(2) H(S,P)同(2)式相比有由得(8)(3) F(T,V)同(3)式相比(9)(4) G(T,P)同(4)式相比有(10)(7),(8),(9),(10)式给出了热力学量的偏导数之间的关系,称为麦克斯韦(J.C.Maxwell)关系,简称麦氏关系。
它是热力学参量偏导数之间的关系,利用麦氏关系,可以从以知的热力学量推导出系统的全部热力学量,可以将不能直接测量的物理量表示出来。
例如,只要知道物态方程,就可以利用(9),(10)式求出熵的变化,即可求出熵函数。
§2.2麦氏关系的简单应用证明1. 求选T,V为独立变量,则内能U(T,V)的全微分为(1)熵函数S(T,V)的全微分为( 2)又有热力学基本方程(3)由(2)代入(3)式得(4)•(4)相比可得(5)(6)由定容热容量的定义得(7)2. 求选T 、P为独立参量,焓的全微分为(8)焓的全微分方程为(9)以T、P为自变量时熵S(T、P)的全微分表达式为(10)将(10)代入(9)得(11) (8)式和(11)式相比较得(12)(13)(14)3求由(7) (14)式得(15) 把熵S看作T,V的函数,再把V看成T,P的函数,即对上式求全微分得∴代入(15)式得由麦氏关系得(16)即得证4、P,V,T三个变量之间存在偏导数关系而可证(17)§2.3气体的节流过程和绝热膨胀过程气体的节流过程(节流膨胀)和绝热膨胀是获得低温的两种常用方法,我们利用热力学函数来分析这两种过程的性质一,气体的节流(焦耳---汤姆逊效应)1、定义:如图所示有一由绝热材料制成的管子,中间用一多孔塞(节流阀)隔开,塞子一边维持较高的压强P,另一边维持较低的压强P,在压力的作用下,气体由高压的一边经过多孔塞流向低压的一边。
内能晗自由能和吉布斯函数全微分记忆顺口溜

内能晗自由能和吉布斯函数全微分记忆顺口溜内能的全微分顺口溜:内能全微分,记清记明现在。
熵变热交与工过程表达我用它。
温度压强体积不说变化量就以du。
吉布斯函数全微分顺口溜:吉布斯全微分,内容真全面。
化学势等熵增温度压强凭借它。
迈尔关系慢慢用变化量就以dG。
在热力学中,内能和吉布斯函数是两个重要的物理量。
它们的全微分描述了系统的变化过程中的能量变化和物理性质的变化。
以下是对这两个全微分的顺口溜解释。
首先是内能,内能全微分的表达方式是dU。
内能是系统中分子的平均能量,它受到熵变、热交和功的影响。
在内能的全微分中,我们需要记住以下要点:- 系统的熵变(entropy change)和热交(heat exchange)与内能有关。
- 进行的过程可以通过表达式表示,我们用它(we use it)来描述。
-温度、压强和体积的变化通常会对内能产生影响,但在这个表达中我们不明确指出。
- 整个过程的变化量可以用du来表示,du是内能的全微分符号。
接下来是吉布斯函数,吉布斯函数全微分的表达方式是dG。
吉布斯函数是系统的自由能,在化学过程中具有重要的意义。
-吉布斯函数的全微分对系统的变化进行了全面描述。
-化学势的变化和熵的增加与吉布斯函数存在关系。
-温度、压强也与吉布斯函数有关,它们是这个表达式的关键因素。
-迈尔关系是一个重要的概念,使用它可以推导出吉布斯函数与其他物理性质之间的关系。
-整个过程的变化量可以用dG来表示,dG是吉布斯函数的全微分符号。
通过这样的顺口溜,我们可以更加容易地记住内能和吉布斯函数的全微分表达方式,并更好地理解它们在热力学中的作用和意义。
热统第二章

dG SdT Vdp (2.1.4)
强调:上式仅适合简单系统 注意它们是采用什么作为独立变量
一.麦氏关系
1.如以S.V为独立变量时, →U=U(S.V)则 与(2.1.1)比较 有
U U dU d S dV S V V S
dU TdS pdV
一.节流过程
1.实验 气体从高压的一边经多孔塞缓慢地流 到另一边 2.实验事实 气体节流后温度改变 3.实验分析 (1)为等焓过程 ∵两端维持定压 ∴外界对左边气体做功
p1
p2
V2
p2
p1
V1
绝热壁
多孔塞
→焦-汤效应(1852年)
设在左边 V1 的气体到右边后成为 V2
W1 p1V1 p1V1
∴右边气体对外界做功W2 p2V2 p2V2
该过程中外界做的净功
W W1 W2 pV 1 1 p2V2
U2 U1 W Q绝热W pV 1 1 p2V2
由热力学第一定律
即
U2 p2V2 U1 pV 1 1 H 2 H1
T p H
T )S 0 p
必有T
此时气体减少内能对外做功 同样的讨论知 必有T 绝热膨胀可以致冷,它不需预冷。
§2.4基本热力学函数的确定
热力学中,最基本的热力学函数是物态方程.内能.和熵 其它热力学函数均可由它们导出 一.选T.V为状态参量 1.物态方程 P=P(T.V) →实验测定 (2.4.1)
《热力学与统计物理》第二章 均匀物质的热力学性质

§2.2 内能、焓、自由能、吉布斯函数的全微分
本节要求: ①掌握状态函数的全微分; ②记住热力学偏导数和麦克斯韦关系。
一.状态函数的全微分
dU TdS pdV 看成是U以S,V为变量的全微分 U (S,V )
1
,得:
T V
U
T U
V
U V
T
U V
T
U
T
V
利用方法1可求出 U
V T
,连同
CV
的定义便得到
T V
U
1 CV
T
p T
V
p
CV
U T
V
U V
T
T
p T
V
p
由此可见,已知 CV 和状态方程便可求得气体的焦耳系数。
方法4.链式关系法
条件:若所求偏导数包含S,且已在分子或分母上,但 不能用热容量的定义或麦氏关系消除时,可用此法。
说明:本章在定义新的态函数和导出普遍热力学关 系时,都以P、V、T 系统为例进行。
§2.1 自由能和吉布斯函数
本节要求:①理解自由能和吉布斯函数的概念; ②理解自由能判据和吉布斯判据
一.自由能
1.定义:
对于等温条件:
引入新的热力学函数: 自由能 F U TS
有: 2.最大功原理:系统自由能的减少是在等温过程中
热力学基本方程
dU TdS pdV dH TdS Vdp dF SdT pdV dG SdT Vdp
热力学偏导数
T
U S
V
p
U V
S
热力学与统计物理学-第二章
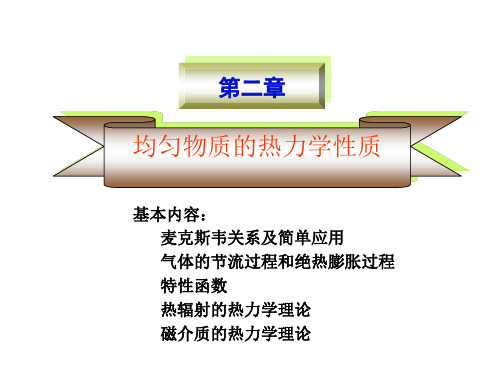
dG=-SdT+VdP
S V
P T
T P
Good Physicists Have Studied Under Very Fine Teachers
太阳照在小树上
(
S V
)T
(
p T
)V
(河流)由山峰流向山谷
照向和流向方向一致取正号,否则取负号。看对 方的分母,取自己的脚标。
T
p
T
V
( V
)S
( S
)V
;
( p )S ( S ) p
( S V
)T
(
p T
)V
;
( V T
)p
(
S p
)T
——麦克斯韦关系
Sun
太阳 peak
山峰
Tree
小树 Valley
山谷
§2-2 麦克斯韦关系的简单应用
麦克斯韦关系的应用有:
⑴用实验可测量的量(如状态方程,热容量
Summary
dU=TdS-PdV dH=TdS+VdP
P T S V V S
T V
P S
S P
G
T
P
F
H
V
S
U
dF=-SdT -PdV
S P
V T
T V
一.能态方程和定容热容量
U T p p V T T V
CV
T S T
V
第一式给出了温度不变时, 系统内能随体积的变化率与物态方程的关系,称 为能态方程;第二式是定容热容量。
第2节麦氏关系1

1 (T V
C p T
p
V )
n Cp
[T
dB dT
B]
虚线-范德瓦耳斯气体 的转换温度。
实线-氮气转换温度。
第二位力系数随温度的变化关系
B/(cm3/mol)
30
20 10
He
N2
H2
Ne
He
100 200 300 400 500 600 700 0
T/K A
-10 N2
-20
-30
3. 绝热膨胀
T (T ,V ) T T V V T V T T V
(T , p)
p
(T ,V )
V T
p 2
CV
T
T p
V
V T
2.3 气体节流过程和绝热膨胀过程
1.节流过程 A. 实验
p1
V1
p2
p1
V2
p2
B. 过程方程 Q 0
U1 P1V1 U2 P2V2
H1 H2
RT( ln p)
Hm,0 Sm,0
RT R
dT RT2
C p,m dT
x 1 RT
y Cp,mdT
=
H m,0 C p,m ln T C p,m Sm,0
RT
R
R
例二 求范氏气体的内能和熵
由范德瓦耳斯方程(1摩尔)ຫໍສະໝຸດ pa v2v
b
RT
得:
p T
v
v
R b
,T
实际气体:
(T ) 1
T
0 升温 (T ) 1
T
降温
(T ) 1 翻转温度
T
t/℃
600 致温区
2023年大学_热力学统计物理第五版(汪志诚著)课后答案下载

2023年热力学统计物理第五版(汪志诚著)课后答案下载热力学统计物理第五版(汪志诚著)内容简介导言第一章热力学的基本规律1.1 热力学系统的平衡状态及其描述1.2 热平衡定律和温度1.3 物态方程1.4 功1.5 热力学第一定律1.6 热容和焓1.7 理想气体的内能1.8 理想气体的绝热过程附录1.9 理想气体的卡诺循环1.10 热力学第二定律1.11 卡诺定理1.12 热力学温标1.13 克劳修斯等式和不等式1.14 熵和热力学基本方程1.15 理想气体的熵1.16 热力学第二定律的数学表述1.17 熵增加原理的简单应用1.18 自由能和吉布斯函数习题第二章均匀物质的热力学性质2.1 内能、焓、自由能和吉布斯函数的全微分 2.2 麦氏关系的简单应用2.3 气体的节流过程和绝热膨胀过程2.4 基本热力学函数的确定2.5 特性函数2.6 热辐射的热力学理论2.7 磁介质的.热力学2.8 获得低温的方法习题第三章单元系的相变3.1 热动平衡判据3.2 开系的热力学基本方程3.3 单元系的复相平衡条件3.4 单元复相系的平衡性质3.5 临界点和气液两相的转变3.6 液滴的形成3.7 相变的分类3.8 临界现象和临界指数3.9 朗道连续相变理论习题第四章多元系的复相平衡和化学平衡热力学第三定律 4.1 多元系的热力学函数和热力学方程4.2 多元系的复相平衡条件4.3 吉布斯相律4.4 二元系相图举例附录4.5 化学平衡条件4.6 混合理想气体的性质4.7 理想气体的化学平衡4.8 热力学第三定律习题第五章不可逆过程热力学简介5.1 局域平衡熵流密度与局域熵产生率 5.2 线性与非线性过程昂萨格关系5.3 温差电现象5.4 最小熵产生定理5.5 化学反应与扩散过程5.6 非平衡系统在非线性区的发展判据 5.7 三分子模型与耗散结构的概念习题第六章近独立粒子的最概然分布6.1 粒子运动状态的经典描述6.2 粒子运动状态的量子描述6.3 系统微观运动状态的描述6.4 等概率原理6.5 分布和微观状态6.6 玻耳兹曼分布6.7 玻色分布和费米分布……第七章玻耳兹曼统计第八章玻色统计和费米统计第九章系综理论第十章涨落理论第十一章非平衡态统计理论初步附录A 热力学常用的数学结果B 概率基础知识C 统计物理学常用的积分公式索引参考书目物理常量表热力学统计物理第五版(汪志诚著)图书目录《“十二五”普通高等教育本科国家级规划教材:热力学统计物理(第5版)》是“十二五”普通高等教育本科国家级规划教材,是作者在第四版的基础上全面修订而成的。
第二章均匀物质的热力学性质

全微分= : dH
∂H ∂S
p
dS
+
∂H ∂p
S
dp
对= 比得: T
= ∂∂HS p , V
∂H
∂p
S
求偏导的次序可以交换: ∂2H = ∂2H Cauchy-Riemann 条件 ∂p∂S ∂S∂p
∂T ∂p
S
=
∂V ∂S
p
③自由能 函数关系: F= F (T ,V =) U − TS
∂V
∂T
=p
Cp
+T
∂T p ∂T ∂V
p=
Cp
+T
∂T ∂V
p
∂p
T
∂p
T
∂p
T
例3:试证明考虑一理想气体,其熵为
S
= n σ
+
5 2
R ln U n
+
R ln V n
其中n为摩尔数,R为气体常数,U为内能,V为体积,σ为常数,
求定压和定容热容量。
解:由热力学基本方程可知熵的全微分为
(2)顶角为函数 G,H,U,F 两对自变量 {p,(-V )},{T,S}
(3)函数以直接相连的两个变量为自变量 G(T , p), H ( p, S), U (S,V ), F (T ,V )
SV pT
(4)一阶关系 dG =−SdT − (−V )dp, dH= TdS − (−V )dp,
−V
=−
∂G ∂p
T
=−
∂H ∂p
S
对广义力求偏导加负号
(5)麦克斯韦关系(二阶关系)
∂T
∂p
S
=
−
∂(−V ∂S
热力学统计物理 第二章 课件

T V
S
p S
V
S
p
T
V T
p
S V
T
p T
V
➢ 麦氏关系应用
选取T、V为状态参量,内能U的全微分为
而由
dU
U T
V
dT
U V
T
dV
dU = TdS - pdV
及以T、V为自变量时熵的全微分表达式
dS
S T
V
dT
S V
T
dV
可得
dU
T
S T
V
dT
第二章 均匀物质的热力学性质
§2.1 内能、焓、自由能和吉布斯函数的全微分
➢ 内能
热力学基本方程
dU = TdS - pdV
给出了相邻两个平衡态的内能、熵和体积之间的关系。
上式可以看作是内能U作为S、V的函数的全微分的表 达式。
内能U作为S、V的函数,其全微分为
dU
U S
V
dS
U V
S
dV
H
C p dT
V
T
V T
dp
p
H0
此式为焓的积分表达式。由U=H-pV即可求得内能。
关于熵函数,其全微分为
dS
Cp T
dT
V T
p
dp
求线积分,得
S
C
p
T
dT
V T
p
dp
S0
此式即熵的积分表达式。
为什么物态方程、内能 和熵函数是最基本的?
§2.5 特性函数
p T
V
dV
求线积分,得
S
CV T
dT
p T
2、 均物热学性质

T p
S
p S
S T T
p
1
T p
S
p
1
S
S p
T
S
S T T p T p
T p
S
S p
T
S
T p
麦氏
S p
T
V T
p
Cp
T
S T
p
V T p
Cp T
T Cp
V T
一、节流过程
1.节流过程 2.焦耳-汤姆逊效应:节流 p1 前后气体的温度发生变化.
节流阀
p1 p2
p2
3.理论分析:假设在节流过程中有一定量(M)的气体, 从左向右通过节流阀,其压强,体积,内能分别在截流前
后为:(p1,V1,U1) (p2,V2,U2).
节流过程中外界对这部分气体(M)做功(p1V1-p2V2), 而节流过程是绝热过程,则,系统从外界所吸收的热量,
S F , p F S p
T V
V T V T T V
对于吉布斯函数G=G(T,p),有
S
G ,V T p
G p
T
S p
T
V T
p
利用上述各关系式,通过数学推演得出简单系统平衡
性质的关系,并导出简单系统热力学函数一般表达式.
4
总结以上各式,即得麦克斯韦(Maxwell)关系式
T
S T
p
V p
T
S p
((TT④,,Vp分)) 母:雅可比性质1
V p
T
T
V T
p
T S T
p
T
热力学与统计物理学第二讲

讨论: 因为V不变,T 又因为CV是正的 所以,等号右边总是负的 ——表明体积膨胀时,温度总是要降低。 (在液化气体的过程中,可利用这个 特性作为降温手段) P
H )P T,( )S V S P
再利用求偏导数的次序可以交换的性质,同理可求得: (3)F(T,V) 由
T V ( )S ( )P P S
dF SdT PdV
同理可求得:
F F S P ( )V S , ( )T P; ( )T ( )V T V V T
V )P ] dP 得: T T 1 V ( )H [T( )P V ]..........( 1 ) P CP T
为描述节流过程前后气体温度随压强的变化率,引进Joule—Thomson系数
(
T )H P
代入(1)式得: 1 [ T ( V )P V ] V ( T 1 )......( 2 )
S V ) ( ) T P V T
根据麦氏关系:(
1 V 1 P 又 ( ), ( ), K T P P V V T P T
——两容量之差与物 态方程的关系
得:C P CV TV
2
KT
四、气体的节流过程和绝热膨胀
1、节流过程 实验装置: Joule—Thomson (焦耳—汤姆孙)效应: 气体经节流(膨胀)过程 而发生温度变化的现象 初态 P1(高) T1 T2 P2(底)
第二讲
第二章 均匀物质的热力学性质
一、热力学函数全微分表达式 其偏导数可以给出系统状态的热力学参量。它的微分为全微分, 并能单值地确定系统状态的函数。 例如:内能、焓、熵、自由能等 1、内能的全微分表达式 热力学函数:
热统试题库

1、 定容压强系数的表达式是 ( B )(A )0lim ()V T p T β∆→∆=∆ (B )01lim ()V T p V T β∆→∆=∆ (C ) 1()V p p T β∂=∂ (D )()V p Tβ∂=∂ 2、 体胀系数α、压强系数β、等温压缩系数T κ三者关系正确的是 ( A )(A )T P αβκ= (B )T P βακ= (C )T P καβ= (D )T P βακ=-1()P V V T α∂=∂ 1()T T V V P κ∂=-∂ 1()V P P Tβ∂=∂ 3、根据热力学第二定律,判断下列哪种说法是正确的 ( A )(A)、热量能从高温物体传到低温物体,但不能从低温物体传到高温物体。
(B)、功可以全部变为热,但热不能全部变为功。
(C)、气体能够自由膨胀,但不能自动收缩。
(D)、有规则运动的能量能够变为无规则运动的能量,但无规则运动的能量不能变为有规则运动的能量。
4、热力学第二定律的微分表达式为(dQ dS T≥) 5、热力学第一定律的数学表达式(微分)为:dUdW dQ =+ 4、关于熵的理解正确的是(?)A 系统从初态到末态,经不同的过程所得到的熵增不一样B 系统经绝热过程从初态到末态的熵增一定为0C A 和B 分别对应系统的两个不同的状态,则BB A A đQ S S T-≥⎰ D A 和B 分别对应系统的两个不同的状态,则B B A A đQ S S T -=⎰ 5、关于自由能、吉布斯函数、熵的认识不正确的是(D )A 在等温等容过程中,系统的自由能永不增加B 孤立系统的熵永不减少C 等温等压过程后,系统的吉布斯函数永不增加D 等温等压过程后,系统的自由能永不增加3.理想气体的物态方程是?4.外界简单热力学系统做功的表达式 ;对于液体表面薄膜来说,外界做功的表达式 ;对于电介质,外界做功是用来 ;对于磁介质,外界做功用来5.温度( )宏观物理参量吗?(是/不是)1、麦氏关系给出了S 、T 、P 、V 这四个变量的偏导数之间的关系,下面麦氏关系四个等式不正确的是 ( )(A )、()()S V T P V S ∂∂=-∂∂ (B )、 ()()S P T V P S∂∂=∂∂ (C )、()()T V S T V P ∂∂=∂∂ (D )、()()T P S V P T∂∂=-∂∂ 2、热力学函数U 、H 、F 、G 全微分形式不正确的是 ( )A dU TdS PdV =-B dH TdS VdP =+C dF SdT PdV =--D dF SdT VdP =--E dG SdT VdP =-+3、下述微分关系不正确的是 ( ) A ()()V T U S T T V∂∂=∂∂ B ()()T V U P T P V T ∂∂=-∂∂ C ()()P P H S T T T ∂∂=∂∂ D ()()T P H V V T P T ∂∂=-∂∂ 4、关于节流过程和绝热过程说法不恰当的是 ( )A 节流过程前后气体的自由能不变B 节流过程和绝热过程都是获得低温的常用方法C 节流过程前后气体温度随压强的变化率为[()]P P V V T V C T∂-∂ D 绝热过程中气体温度随压强的变化率为()P P T V C T∂∂ 1.写出内能、焓、自由能、吉布斯函数的全微分 、 、 、 。
求1mol理想气体的内能熵和吉布斯函数

p
T
p
T
V
T
p
Cp
T
T p T V
p
p
T
p
T
V
2
Cp
T
T V
p
p
T
19
§2.3 基本热力学函数的确定
一.选T,V为参变量 物态方程为: p=p(T,V)
S V
T
dV
pdV
T
S T
V
dT
T
S V
T
p dV
T
S T
V
dT
T
p T
V
p dV
11
比较得:
U T
V
T
S T
V
dp
S S T, p
dS
S T
p
dT
S p
T
dp
dH TdS Vdp
T
S T
p
dT
T
S p
T
dp
Vdp
T
S T
p
dT
T
S p
T
p
0
12
例二. 对于范氏气体
p
an2 V2
V
热统试题库

1、 定容压强系数的表达式是 ( )(A )0lim ()V T p T β∆→∆=∆ (B )01lim ()V T p V T β∆→∆=∆ (C ) 1()V p p T β∂=∂ (D )()V p Tβ∂=∂ 2、 体胀系数α、压强系数β、等温压缩系数T κ三者关系正确的是 ( )(A )T P αβκ= (B )T P βακ= (C )T P καβ= (D )T P βακ=-1()P V V T α∂=∂ 1()T T V V P κ∂=-∂ 1()V P P Tβ∂=∂ 3、根据热力学第二定律,判断下列哪种说法是正确的 ( )(A)、热量能从高温物体传到低温物体,但不能从低温物体传到高温物体。
(B)、功可以全部变为热,但热不能全部变为功。
(C)、气体能够自由膨胀,但不能自动收缩。
(D)、有规则运动的能量能够变为无规则运动的能量,但无规则运动的能量不能变为有规则运动的能量。
4、热力学第二定律的微分表达式为(dQ dS T≥) 5、热力学第一定律的数学表达式(微分)为:dU dW dQ =+4、关于熵的理解正确的是()A 系统从初态到末态,经不同的过程所得到的熵增不一样B 系统经绝热过程从初态到末态的熵增一定为0C A 和B 分别对应系统的两个不同的状态,则BB A A đQ S S T -≥⎰D A 和B 分别对应系统的两个不同的状态,则B B A A đQ S S T -=⎰ 5、关于自由能、吉布斯函数、熵的认识不正确的是( )A 在等温等容过程中,系统的自由能永不增加B 孤立系统的熵永不减少C 等温等压过程后,系统的吉布斯函数永不增加D 等温等压过程后,系统的自由能永不增加1.描述系统处在平衡状态的四类参量(宏观物理量)分别是什么?宏观参量彼此间是存在一定函数联系的。
2.对于简单系统,常用的参量是什么?3.理想气体的物态方程是?4.外界简单热力学系统做功的表达式 ;对于液体表面薄膜来说,外界做功的表达式 ;对于电介质,外界做功是用来 ;对于磁介质,外界做功用来5.温度( )宏观物理参量吗?(是/不是)判断题1.理想气体的内能与压强、体积有关?2.物体在等温过程中不从外界吸热?3.理想气体的等温线比绝热线陡峭4.热量不可能从低温物体流向高温物体5.不可能把从一物体吸收的热全部用来对外做功6.绝热过程中,系统的熵永不减少7.对于仅有体积变化功的系统,在等温等容下,系统的自由能永不增加8.对于仅有体积变化功的系统,在等温等压下,系统的吉布斯函数永不增加1、麦氏关系给出了S 、T 、P 、V 这四个变量的偏导数之间的关系,下面麦氏关系四个等式不正确的是 ( )(A )、()()S V T P V S ∂∂=-∂∂ (B )、 ()()S P T V P S∂∂=∂∂ (C )、()()T V S T V P ∂∂=∂∂ (D )、()()T P S V P T∂∂=-∂∂ 2、热力学函数U 、H 、F 、G 全微分形式不正确的是 ( )A dU TdS PdV =-B dH TdS VdP =+C dF SdT PdV =--D dF SdT VdP =--E dG SdT VdP =-+ 3、下述微分关系不正确的是 ( ) A ()()V T U S T T V ∂∂=∂∂ B ()()T V U P T P V T∂∂=-∂∂ C ()()P P H S T T T ∂∂=∂∂ D ()()T P H V V T P T ∂∂=-∂∂ 4、关于节流过程和绝热过程说法不恰当的是 ( )A 节流过程前后气体的自由能不变B 节流过程和绝热过程都是获得低温的常用方法C 节流过程前后气体温度随压强的变化率为[()]P P V V T V C T∂-∂ D 绝热过程中气体温度随压强的变化率为()P P T V C T∂∂ 1.写出内能、焓、自由能、吉布斯函数的全微分 、 、 、 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从四个基本方程出发,利用系数比较法,可很方便地写 出八个偏导数。例如,由dU=TdS-pdV出发,设U=U(S,V), 写出U的全微分,然后比较系数,即可得到
③ 麦氏关系的记忆方法
沿顺时针方向,例如,从S出法,S对V求导T不变,等 于p对T求导V不变。箭头都指向不变量或都离开不变量取 正,一个指向不变量,而一个离开不变量则取负,得
z
=
1 y x
z
(倒数关系)
z x
y
=
-
1
(循环关系)
x w
z
=
x y
z
y w
z
(链式关系)
x y
z
=
x y
w
+
x w
y
w y
z
(复合函数求导法)
2z = 2z xy yx
(全微分条件法)
2U V S
;
p S
V
2U
SV
利用全微分条件,上二式相等,所以有
T V
S
p S
V
将(2.1.6)的两个偏导的两边分别对S和p求导,得
T 2H
p
S
pS
;
V S
p
§2.1 内能、焓、自由能和吉布斯函数的全微分
一、4个基本方程
dU=TdS-pdV dH=TdS+Vdp dF=-SdT-pdV dG=-SdT+Vdp
(2.1.1) (2.1.2) (2.1.3) (2.1.4)
二、8个偏导数
由(2.1.1)式dU=TdS-pdV ,有
T
U S
V
由(2.1.4)式dG=-SdT+Vdp ,有
S
G T
p
,
V
G p
T
(2.1.8)
三、4个麦氏关系
由全微分条件 2 z 2 z xy yx
将(2.1.5)的两个偏导的两边分别对S和V求导,再利用 全微分条件求得
T V
S
S V
T
p T
V
将(2.1.8)的两个偏导的两边分别对p和T求导,得
S
2G
p
T
pT
;
V T
p
2G T p
利用全微分条件,上二式相等,所以有
S
p
T
V T
的量,即函数(如,U、H、F、G、S)用可以直接测 量的量(如,p、V、T、Cp、CV、α、β、κT)表达出来。
为此,我们会经常用到下面介绍的一些关系式。
设给定四个状态参量x、y、z和w,且
F(x,y,z) = 0, 而w是变量x,y,z 中任意两个的函数,则有下列等式成立:
x
y
然后,按顺时针方向加上E(=U)、F、 G和H。
① 基本方程记忆规则
a.函数的相邻两量为自变量,对应两量为系数。 b.箭头离开系数,取负;箭头指向系数,取正。 例如,与U相邻的两自变量分别为S和V,对应的系数为T和 p,前者箭头指向系数,后者箭头离开系数,故可写出
dU=TdS-pdV
用同样的方法,可方便的写出其他三个基本方程。
S p V T T V
按此方法,分别从V、T和p出发,就可得到另外三个 麦氏关系。沿逆时针方向也可得出四个麦氏关系,只不过 顺序不同而已。
(2)证明热力学恒等式的几种方法
推导和证明热力学关系是热力学部分技能训练的 重点。推导热力学关系的一般原则是:将不能直接测量
,
p
U V
S
由(2.1.2)式dH=TdS+Vdp ,有
(2.1.5)
T
H S
p
,
H
V
p
S
(2.1.6)
由(2.1.3)式dF=-SdT-pdV ,有
S
F T
V
,
p
F V
T
(2.1.7)
p
热力学关系的记忆方法
四个基本方程,八个偏导,四个麦 氏关系。
首先,画两正交箭头,从上到下为 S→T,从左到右为P→V。
为了便于记住箭头的方向,可默读 一个英文句子:
The Sun is pouring down his rays upon the Trees, and the brook is flowing from the Peak to the Valley.
2H Sp
利用全微分条件,上二式相等,所以有
T p
S
V S
p
将(2.1.7)的两个偏导的两边分别对V和T求导,得
S V
T
2F V T
;
p T
V
2F T V
利用全微分条件,上二式相等,所以有
