(完整)初一数学图形认识专项练习题

合集下载

七年级数学图形的初步认识复习测试题含答案

第四章图形初步相识复习题一、细心选一选1、以下说法正确是〔〕A、直线AB和直线BA是两条直线；B、射线AB和射线BA是两条射线；C、线段AB和线段BA是两条线段；D、直线AB和直线a不能是同一条直线2、以下图中角表示方法正确个数有〔〕A、1个B、2个C、3个D、4个3、下面图形经过折叠可以围成一个棱柱是〔〕4、经过同一平面内随意三点中两点共可以画出〔〕A、一条直线B、两条直线C、一条或三条直线D、三条直线5、假设∠A=20 o 18′，∠B=20 o 15′30〞，∠C=20.25 o，则〔〕A、∠A>∠B>∠CB、∠B>∠A>∠CC、∠A>∠C >∠BD、∠C >∠A >∠B6、如图，每个图片都是6个一样正方形组成，不能折成正方形是〔〕7、如左图所示正方体沿某些棱绽开后，能得到图形是〔〕8、以下语句正确是〔〕A.钝角与锐角差不行能是钝角；B.两个锐角和不行能是锐角；C.钝角补角肯定是锐角；D.∠α和∠β互补〔∠α>∠β〕，则∠α是钝角或直角。

9、在时刻8：30，时钟上时针和分针夹角是为〔〕西东 AD A 、85 ° B 、75° C 、70 ° D 、60° 10、假如∠α＝26°，则∠α余角补角等于〔〕 A 、20° B 、70 ° C 、110 ° D 、116°11、假如∠α＋∠β＝900，而∠β与∠γ互余，则∠α与∠γ关系为〔〕A 、互余B 、互补C 、相等D 、不能确定。

12、如右图以下说法错误是〔〕 A 、OA 方向是北偏东40° B 、OB 方向是北偏西15 ° C 、OC 方向是南偏西30° D 、OD 方向是东南方向。

13、以下说法中错误有( )(1)线段有两个端点，直线有一个端点; (2)角大小与我们画出角两边长短无关; (3)线段上有多数个点; (4)同角或等角补角相等; (5)两个锐角和肯定大于直角A ．1个B ．2个C ．3个D ．4个 14、如右图∠AOD －∠AOC ＝〔〕 A 、∠ADC B 、∠BOC C 、∠BODD 、∠COD15、如图把一个圆绕虚线旋转一周，得到几何体是( ) 二、细心填一填16. 将以下几何体分类，柱体有：，锥体有〔填序号〕。

初一数学图形的初步认识练习题及答案

一、填空题（每题3分，共30分）1、三棱柱有条棱，个顶点，个面；2、如图1，若是中点，AB=4，则DB=；3、42.79=度分秒；4、如果∠α=29°35′，那么∠α的余角的度数为；5、如图2，从家A 上学时要走近路到学校B，最近的路线为（填序号），理由是；6、如图3，OA、OB 是两条射线，C 是OA 上一点，D、E 分别是OB 上两点，则图中共有条线段,共有射线，共有个角；7.如图4，把书的一角斜折过去，使点A 落在E 点处，BC 为折痕，BD 是∠EBM 的平分线，则∠CBD＝8.如图5，将两块三角板的直角顶点重合，若∠AOD=128°，则∠BOC=；9.2：35时钟面上时针与分针的夹角为；10.经过平面内四点中的任意两点画直线，总共可以画条直线；二选择题（每题3分，共24分）7、B图3图5图412、如果与互补，与互余，则与的关系是（）A.=B.C.D.以上都不对13、对于直线，线段，射线，在下列各图中能相交的是（）A．1个B．2个C．3个D．4个16、在海上，灯塔位于一艘船的北偏东40度方向，那么这艘船位于这个灯塔的（）方向A.南偏西50度B.南偏西40度C.北偏东50度D.北偏东40度17、如右图，AB、CD交于点O，∠AOE=90°，若∠AOC：∠COE=5：4，则∠AOD等于（）A．120°B．130°C．140°D．150°18、图中(1)-(4)各图都是正方体的表面展开图，若将他们折成正方体，各面图案均在正方体外面，则其中两个正方体各面图案完全一样，他们是（）A.(1)(2)B.（2）（3）C.（3）（4）D.（2）（4）三、作图题（各7分，共21分）19、已知、求作线段AB 使AB=2a－b（不写作法，保留作图痕迹）20、按照要求，在图中画出表示下列方向的射线：(1)南偏东300(2)北偏西600(3)西南方向四、解答题（8+8+9分，共25分）21、若一个角的补角等于它的余角的4倍，求这个角的度数。

(完整)初一数学图形认识专项练习题

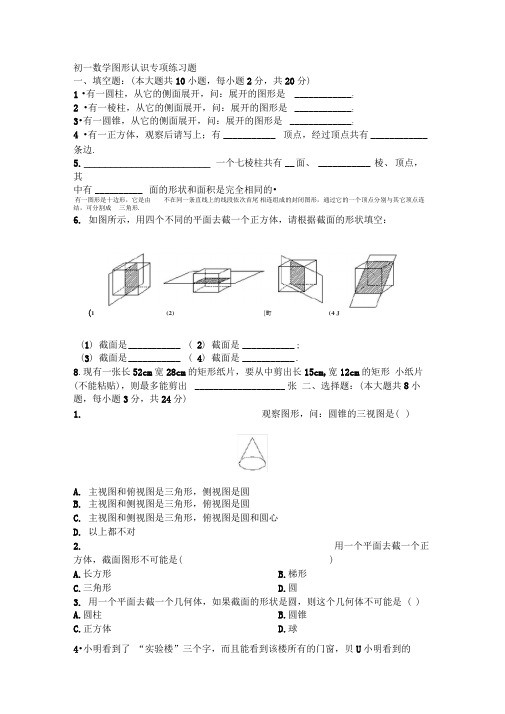
初一数学图形认识专项练习题一、填空题：(本大题共10小题，每小题2分，共20分)1•有一圆柱，从它的侧面展开，问：展开的图形是 ____________ :2•有一棱柱，从它的侧面展开，问：展开的图形是____________ :3•有一圆锥，从它的侧面展开，问：展开的图形是_____________ :4 •有一正方体，观察后请写上；有___________ 顶点，经过顶点共有____________ 条边.5.________________________ 一个七棱柱共有__ 面、___________ 棱、顶点，其中有__________ 面的形状和面积是完全相同的•有一图形是十边形，它是由不在同一条直线上的线段依次首尾相连组成的封闭图形，通过它的一个顶点分别与其它顶点连结，可分割成三角形.6.如图所示，用四个不同的平面去截一个正方体，请根据截面的形状填空：(1 (2) ｛町(4 J(1) 截面是___________ ( 2) 截面是___________ ;(3) 截面是___________ ( 4) 截面是___________ .8.现有一张长52cm宽28cm的矩形纸片，要从中剪出长15cm,宽12cm的矩形小纸片(不能粘贴)，则最多能剪出___________________ 张二、选择题：(本大题共8小题，每小题3分，共24分)1.观察图形，问：圆锥的三视图是( )A.主视图和俯视图是三角形，侧视图是圆B.主视图和侧视图是三角形，俯视图是圆C.主视图和侧视图是三角形，俯视图是圆和圆心D.以上都不对2.用一个平面去截一个正方体，截面图形不可能是( )A.长方形B.梯形C.三角形D.圆3.用一个平面去截一个几何体，如果截面的形状是圆，则这个几何体不可能是 ( )A.圆柱B.圆锥C.正方体D.球4•小明看到了“实验楼”三个字，而且能看到该楼所有的门窗，贝U小明看到的图是（）A.俯视图B.左视图C.主视图D.都有可能5.截去四边形的一个角，剩余图形不可能是（）A.三角形B.四边形C.五边形D.圆6.从下列右边备选图形中找出一个，使其经旋转后与左图完全一致的是（）三、解答题：（本大题共6小题，共56分）1.用一个平面截一个正方体，能截得五边形吗？如果行，请画出示意图.截得的这个五边形的边具有什么性质？2.图中有8块小立方块，请把它的主视图、左视图和俯视图画出来.3.下面的图是由几块小立方块组成的几何体的俯视图，小方块中的数字表示该位置小方块的个数，你能画出这个几何体的主视图和左视图吗？请动手一试，如图所示，你还能画出这些小立方块组成的几何体吗？。

(完整版)七年级数学认识三角形练习题

三角形的认识练习题一、填空（每空 3 分，共60 分）1．三角形的三边关系：①三角形随意两边之和差第三边 .第三边；②三角形随意两边之2．以下每组分别是三根小木棒的长度，用它们能摆成三角形吗？（填“能”或“不可以”）：（1）3 ㎝，4 ㎝， 5 ㎝（）（2）8 ㎝，7 ㎝，15㎝（）（3）13 ㎝，12 ㎝， 20 ㎝（）（4）5 ㎝，5 ㎝，11 ㎝（）（5）6cm, 8cm, 10cm（）（6）7cm, 7cm, 14cm（）3．在△ ABC 中，∠ A=10°，∠ B=30°，则∠ C=_________.（ 2 ）一个等腰三角形的一边是5cm ，另一边是7cm , 则这个三角形的周长是_____________cm.4．假如∠ B＋∠ C＝∠ A，那么△ ABC是三角形 .5．在△ ABC 中， AB=6 cm， AC=8 cm 那么 BC 长的取值范围是.6． ABC 中， AD 是 ABC 的中线，且 BC 10cm ，则 BD= cm.7．在 ABC 中， A 80 ，AD为 A 的均分线，则BAD=8．假如一个三角形两边上的高的交点，恰巧是三角形的一个极点，则此三角形是_____________三角形 .9．判断具备下边条件的三角形是直角三角形、锐角三角形仍是钝角三角形：（1）假如A:B:C 1: 3: 4 ，那么 ABC 是三角形；（2）假如 A B ，C 30 ，那么ABC 是三角形；（）假如 1C，那么ABC 是3 AB5三角形 .二、选择（每题 3 分，共 27 分）1．在△ ABC 中，∠ A 是锐角，那么△ ABC 是（）A 、锐角三角形B、直角三角形C、钝角三角形D、不可以确立2．△ ABC 中，若∠ A∶∠ B∶∠ C=1∶2∶3，则△ ABC 的形状是（）A 、锐角三角形B、直角三角形C、钝角三角形D、不确立3．以下是由四位同学描绘三角形的三种不一样的说法，正确的选项是()A 、由三个角构成的图形叫三角形B、由三条线段构成的图形叫三角形C、由三条直线构成的图形叫三角形D、由不在同向来线上的三条线段首尾按序相接所构成的图形叫三角形4．△ ABC 中，已知a=8, b=5，则 c 为( )A 、c=3 B、c=13 C、c 能够是随意正整数D、c 能够是大于 3 小于13 的随意数值5.下边说法中正确的选项是：（）1 / 3A、三角形的角均分线 , 中线 , 高都在三角形内B、直角三角形的高只有一条C、钝角三角形的三条高都在三角形外D、三角形起码有一条高在三角形内6.假如一个三角形的三条高线的交点恰巧是三角形的一个极点，那么这个三角形是（）A 、直角三角形B、锐角三角形C、钝角三角形D、不可以确立7．在一个三角形，若A 、直角三角形8．三角形的高线是A B 40 ，则ABC 是（B、锐角三角形C、钝角三角形（）A、线段B、垂线）D、以上都不对C、射线D、直线9. 在Rt△中，两个锐角关系是（） A、互余 B 、互补 C 、相等 D 、以上都不对三、解答题1．如图 ,在△ ABC 中 ,∠BAC=60 °,∠B=45°,AD 是△ ABC 的一条角均分线求∠ ADB的度数 . （7 分）AO2．在以下图中，分别画出三角形的三条高。

初一数学图形认识初步棱、顶点、面间数量关系(欧拉公式)练习题(含答案)

初一数学图形认识初步棱、顶点、面间数量关系（欧拉公式）练习题欧拉公式:（1）简单多面体的顶点数V、面数F及棱数E间的关系为：V+F﹣E＝2．这个公式叫欧拉公式．（2）V+F﹣E＝X（P），V是多面体P的顶点个数，F是多面体P的面数，E是多面体P的棱的条数，X（P）是多面体P的欧拉示性数．一选择题1.将正方体的面数记为f，边数记为e，顶点数记为v，则f+v﹣e＝（）A．1 B．2 C．3 D．42.一个多面体，若顶点数为4，面数为4，则棱数是（）A．2 B．4 C．6 D．83.设长方体的顶点数为v，棱数为e，面数为f，则v+e+f等于（）A．26 B．2 C．14 D．104.正多面体的面数、棱数、顶点数之间存在着一个奇妙的关系，若用F，E，V分别表示正多面体的面数、棱数、顶点数，则有F+V﹣E＝2，现有一个正多面体共有12条棱，6个顶点，则它的面数F等于（）A．6 B．8 C．12 D．205.欧拉公式中，多面体的面数F，棱数E，顶点数V之间的正确关系是（）A．F+V﹣E＝2 B．F+E﹣V＝2 C．E+V﹣F＝2 D．E﹣V﹣F＝2二填空题6.简单多面体是各个面都是多边形组成的几何体，十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）和棱数（E）之间存在一个有趣的关系式，称为欧拉公式．如表是根据左边的多面体模型列出的不完整的表.现在有一个多面体，它的每一个面都是三角形，它的面数（F）和棱数（E）的和为30，则这个多面体的顶点数V＝．7.阅读下面的材料：1750年欧拉在写给哥德巴赫的信中列举了多面体的一些性质，其中一条是，如果用V，E，F分别表示凸多面体的顶点数、棱数、面数，则有V﹣E+F＝2．这个发现就是著名的欧拉定理．根据所阅读的材料，完成：一个多面体的面数为12，棱数是80，则其顶点数为．8.阅读下面的材料：1750年欧拉在写给哥德巴赫的信中列举了多面体的一些性质，其中一条是：如果用V，E，F分别表示凸多面体的顶点数、棱数、面数，则有V﹣E+F＝2．这个发现，就是著名的欧拉定理．根据所阅读的材料，完成：一个多面体的面数为12，棱数是30，则其顶点数为．9.一个多面体的顶点数为12，棱数是30，则这个多面体的面数是．10.任意一个多面体，它的面数记为a，顶点数记为b，棱的条数记为c，则a，b，c三者之间的关系式为．11.n棱柱的面数+顶点数﹣棱数＝．12.从每个顶点出发的所有棱长相等，所有面形状、大小完全相同的正多边形的几何体称为正多面体、其面数+顶点数﹣棱数＝．13.如图，正四面体的顶点数（4）+面数（4）﹣棱数（6）＝2，仔细观察后计算，正八面体的顶点数+面数﹣棱数＝．14.瑞士著名数学家欧拉发现：简单多面体的顶点数V、面数F及棱数E之间满足一种有趣的关系：V+F﹣E＝2，这个关系式被称为欧拉公式．比如：正二十面体（如右图），是由20个等边三角形所组成的正多面体，已知每个顶点处有5条棱，则可以通过欧拉公式算出正二十面体的顶点为个．那么一个多面体的每个面都是五边形，每个顶点引出的棱都有3条，它是一个面体．15.一个多面体的面数为6，棱数是12，则其顶点数为．16.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（v）、面数（f）、棱数（e）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型：根据上面多面体模型，你发现顶点数（v）、面数（f）、棱数（e）之间存在的关系式是．17.正多面体共有五种，它们是、、、、，它们的面数f，棱数e、顶点数v满足关系式．18.图1（1）、（2）、（3）依次表示四面体、八面体、正方体．它们各自的面积数F、棱数E与顶点数V如下表,观察这些数据，可以发现F、E、V之间的关系满足等式：．三解答题19.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体模型，完成表格中的空格.（2）你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是．（3）一个多面体的面数与顶点数相同，且有12条棱，则这个多面体的面数是．20.图1至图3是将正方体截去一部分后得到的多面体．（1）根据要求将表格补充完整：（2）猜想f、v、e三个数量间有何关系；（3）根据猜想计算，若一个多面体有顶点数2018个，棱数4035条，试求出它的面数．21.观察下列多面体，并把下表补充完整．观察上表中的结果，你能发现a、b、c之间有什么关系吗？请写出发现的关系式．22.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体模型，完成表格中的空格,你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是．（2）一个多面体的面数比顶点数小8，且有30条棱，则这个多面体的面数是．（3）某个玻璃饰品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表面三角形的个数为x个，八边形的个数为y个，求x+y的值．23.观察下列多面体，并把如表补充完整．观察表中的结果，你能发现a、b、c之间有什么关系吗？请写出关系式．24.回答下列问题：（1）如图所示的甲、乙两个平面图形能折什么几何体？（2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为f，顶点个数为v，棱数为e，分别计算第（1）题中两个多面体的f+v﹣e的值？你发现什么规律？（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．25.设棱锥的顶点数为V，面数为F，棱数为E．（1）观察与发现：三棱锥中，V3＝，F3＝，E3＝；五棱锥中，V5＝，F5＝，E5＝；（2）猜想：①十棱锥中，V10＝，F10＝，E10＝；②n棱锥中，Vn＝，Fn＝，En＝；（用含有n的式子表示）（3）探究：①棱锥的顶点数（V）与面数（F）之间的等量关系：；②棱锥的顶点数（V）、面数（F）、棱数（E）之间的等量关系：E＝；（4）拓展：棱柱的顶点数（V）、面数（F）、棱数（E）之间是否也存在某种等量关系？若存在，试写出相应的等式；若不存在，请说明理由．26.如图1至图3是将正方体截去一部分后得到的多面体．（1）根据要求填写表格.（2）猜想f、v、e三个数量间有何关系；（3）根据猜想计算，若一个多面体有顶点数2018个，棱数4036条，试求出它的面数．27.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式，请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体模型，完成表格中的空格；你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是．（2）正十二面体有12个面，那它有条棱；（3）一个多面体的面数比顶点数小8，且有30条棱，则这多面体的顶点数是；（4）某个玻璃饰品的外形是简单多面体，它的外表是由三角形和八边形两种多边形拼接而成，且有48个顶点，每个顶点处都有3条棱，设该多面体表面三角形的个数为x个，八边形的个数为y个，求x+y 的值．28.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体模型，完成表格中的空格：（2）你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是．（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是．29.在对第一章“丰富的图形世界”复习前，老师让学生整理正方体截面的形状并探究多面体（由若干个多边形所围成的几何体）的棱数、面数、顶点数之间的数量关系，如图是小颖用平面截正方体后剩余的多面体，请解答下列问题：（1）根据上图完成下表.（2）猜想：一个多面体的V（顶点数），F（面数），E（棱数）之间的数量关系是；（3）计算：已知一个多面体有20个面、30条棱，那么这个多面体有个顶点．30.观察下列多面体，并把表补充完整．（1）完成表中的数据；（2）若某个棱柱由28个面构成，则这个棱柱为棱柱；（3）根据表中的规律判断，n棱柱共有个面，共有个顶点，共有条棱；（4）观察表中的结果，你发现棱柱顶点数、棱数、面数之间有什么关系吗？请直接写出来．初一数学图形认识初步棱、顶点、面间数量关系（欧拉公式）练习题参考答案与解析1.分析:根据正方体的概念和特性进行分析计算即解．解：正方体的顶点数v ＝8，棱数e ＝12，面数f ＝6．故f+v ﹣e ＝8+6﹣12＝2．故选B ．2.分析:根据欧拉公式，简单多面体的顶点数V 、面数F 及棱数E 间的关系为：V+F ﹣E ＝2，代入求出棱数．解：根据欧拉公式：V+F ﹣E ＝2，可得4+4﹣E ＝2，解得E ＝6．故选C ．3.分析:根据长方体的概念和特性进行分析计算即解．解：长方体的顶点数v ＝8，棱数e ＝12，面数f ＝6．故v+e+f ＝8+12+6＝26．故选A ．4.分析:根据题意中的公式F+V ﹣E ＝2，将E ，V 代入即解．解：∵正多面体共有12条棱，6个顶点，∴E ＝12，V ＝6，∴F ＝2﹣V+E ＝2﹣6+12＝8．故选B ．5.分析:根据欧拉公式进行解答即可．解：凸多面体的面数F 、顶点数V 和棱数E 满足如下关系：V+F ﹣E ＝2，故选A ．6.分析：直接利用V ，E ，F 分别表示凸多面体的顶点数、棱数、面数，欧拉公式为V ﹣E+F ＝2，求出答案．解：∵现在有一个多面体，它的每一个面都是三角形，它的面数（F ）和棱数（E ）的和为30，∴这个多面体的顶点数V ＝2+E ﹣F ，∵每一个面都是三角形，∴每相邻两条边重合为一条棱，∴E ＝23F ，∵E+F ＝30，∴F ＝12，∴E ＝18，∴V ＝，2+E ﹣F ＝8，故答案为8． 7.分析：直接利用欧拉公式V ﹣E+F ＝2，求出答案．解：∵用V ，E ，F 分别表示凸多面体的顶点数、棱数、面数，则有V ﹣E+F ＝2．∴V ＝E ﹣F+2，∵一个多面体的面数为12，棱数是80，∴其顶点数为：80﹣12+2＝70．故答案为：70．8.分析：直接把面数、棱数代入公式，即可求得顶点数．解：由题意可得，V ﹣30+12＝2，解得V ＝20．故答案为：209分析：根据常见几何体的结构特征进行判断．解：∵顶点数记为V ，棱数记为E ，面数记为F ，V+F ﹣E ＝2，∴12+F ﹣30＝2，解得：F ＝20．故答案为：20．10.分析：简单多面体的顶点数V 、面数F 及棱数E 间的关系为：V+F ﹣E ＝2，这个公式叫欧拉公式．解：由欧拉公式可得：a+b ﹣c ＝2．故答案为：a+b ﹣c ＝2．11.分析：根据欧拉公式，得出正多面体的面数+顶点数﹣棱数的结果．解：从每个顶点出发的所有棱长相等，所有面形状、大小完全相同的正多边形的几何体称为正多面体，其面数+顶点数﹣棱数＝2．故答案为：2．12.分析：根据欧拉公式，得出正多面体的面数+顶点数﹣棱数的结果．解：从每个顶点出发的所有棱长相等，所有面形状、大小完全相同的正多边形的几何体称为正多面体，其面数+顶点数﹣棱数＝2．故答案为2．13.分析：只需分别找出正八面体的顶点数，面数和棱数即可．解：正八面体有6个顶点，12条棱，8个面．∴正八面体的顶点数+面数﹣棱数＝6+8﹣12＝2．故答案为：2．14.分析：①设出正二十面体的顶点为n 个，则棱有25n 条．利用欧拉公式构建方程即可解决问题．②设顶点数V ，棱数E ，面数F ，每个点属于三个面，每条边属于两个面，利用欧拉公式构建方程即可解决问题．解：①设出正二十面体的顶点为n 个，则棱有25n 条．由题意F ＝20，∴n+20﹣25n ＝2，解得n ＝12．②设顶点数V ，棱数E ，面数F ，每个点属于三个面，每条边属于两个面，由每个面都是五边形，则就有E ＝25F ，V ＝35F ，由欧拉公式：F+V ﹣E ＝2，代入：F+35F ﹣25F ＝2，化简整理：F ＝12，所以：E ＝30，V ＝20，即多面体是12面体．棱数是30，面数是12，故答案为12，12．15.分析：因为多面体的面数为6，棱数是12，故多面体为四棱柱．解：根据四棱柱的概念，有8个顶点．故答案为8．16.分析：先根据四面体、长方体、正八面体，正十二面体的顶点数、面数和棱数，总结出顶点数（v ）、面数（f ）、棱数（e ）之间存在的关系式即可．解：四面体的顶点数为4、面数为4，棱数为6，则4+4﹣6＝2；长方体的顶点数为8、面数为6，棱数为12，则8+6﹣12＝2；正八面体的顶点数为6，面数为8，棱数为12，则8+6﹣12＝2；则关系式为：v+f ﹣e ＝2；故答案为：v+f ﹣e ＝2．17.分析：根据正多面体的面是正三角形，正方形，正五边形三种情况写出即可；再根据欧拉公式进行解答．解：正多面体只能有五种，用正三角形做面的正四面体、正八面体，正二十面体，用正方形做面的正六面体，用正五边形做面的正十二面体．f+v ﹣e ＝2．18.分析：根据题给图形中各图具体的面积数F 、棱数E 与顶点数V ，即可得出答案．解：根据表中所列可知：四面体有4﹣6+4＝2；八面体有8﹣12+6＝2；正方体有6﹣12+8＝2；故有F ﹣E+V ＝2．故答案为：F ﹣E+V ＝2．19.分析：（1）依据多面体模型，即可得到棱数和顶点数；（2）依据表格中的数据，即可得出顶点数（V）、面数（F）、棱数（E）之间存在的关系式；（3）依据欧拉公式进行计算，即可得到这个多面体的面数．解：（1）四面体的棱数为6；正八面体的顶点数为6；故答案为：6，6；（2）顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F﹣E＝2，故答案为：V+F﹣E＝2；（3）设这个多面体的面数是x，则2x﹣12＝2，解得x＝7，这个多面体的面数是7，故答案为：7．20.分析：（1）根据图形数出即可．（2）根据（1）中结果得出f+v﹣e＝2．（3）把数值代入f+v﹣e＝2求出即可．解：（1）填表如下：故答案为：7，8，15．（2）f+v﹣e＝2．（3）∵v＝2018，e＝4035，f+v ﹣e＝2，∴f+2018﹣4035＝2，解得f＝2019．故它的面数是2019．21.分析：只要将各个图形的顶点数、棱数、面数数一下就行；数的时候要注意：图中不能直接看到的那一部分不要遗漏，也不要重复，可通过想象计数，正确填入表内，通过观察找出每个图中“顶点数、棱数、面数”之间隐藏着的数量关系，这个数量关系用公式表示出来即可．解：填表如下，观察表中的结果，能发现a、b、c之间有的关系是：a+c﹣b＝2．22.分析：（1）观察可得顶点数+面数﹣棱数＝2；（2）代入（1）中的式子即可得到面数；（3）得到多面体的棱数，求得面数即为x+y的值．解：（1）四面体的棱数为6；正八面体的顶点数为6；关系式为：V+F﹣E＝2；（2）由题意得：F+8+F﹣30＝2，解得F＝12；（3）∵有24个顶点，每个顶点处都有3条棱，两点确定一条直线；∴共有24×3÷2＝36条棱，那么24+F﹣36＝2，解得F＝14，∴x+y＝14．故答案为：（1）6；6；V+F﹣E＝2．（2）12；（3）14．23.分析：结合三棱柱、四棱柱和五棱柱的特点，即可填表，根据已知的面、顶点和棱与几棱柱的关系，可知n棱柱一定有（n+2）个面，2n个顶点和3n条棱，进而得出答案，利用前面的规律得出a，b，c之间的关系．解：填表如下,根据上表中的规律判断，若一个棱柱的底面多边形的边数为n，则它有n个侧面，共有n+2个面，共有2n个顶点，共有3n条棱；故a，b，c之间的关系：a+c﹣b＝2．24.分析：（1）由长方体与五棱锥的折叠及长方体与五棱锥的展开图解题．（2）列出几何体的面数，顶点数及棱数直接进行计算即可；（3）设这个多面体的面数为x，根据顶点数+面数﹣棱数＝2，列出方程即可求解．解：（1）图甲折叠后底面和侧面都是长方形，所以是长方体；图乙折叠后底面是五边形，侧面是三角形，实际上是五棱锥的展开图，所以是五棱锥．（2）甲：f＝6，e＝12，v＝8，f+v ﹣e＝2；乙：f＝6，e＝10，v＝6，f+v﹣e＝2；规律：顶点数+面数﹣棱数＝2．（3）设这个多面体的面数为x，则x+x+8﹣50＝2，解得x＝22．25.分析：（1）观察与发现：根据三棱锥、五棱锥的特征填写即可；（2）猜想：①根据十棱锥的特征填写即可；②根据n棱锥的特征的特征填写即可；（3）探究：①通过列举得到棱锥的顶点数（V）与面数（F）之间的等量关系；②通过列举得到棱锥的顶点数（V）、面数（F）、棱数（E）之间的等量关系；（4）拓展：根据棱柱的特征得到棱柱的顶点数（V）、面数（F）、棱数（E）之间的等量关系．解：（1）观察与发现：三棱锥中，V3＝4，F3＝4，E3＝6；五棱锥中，V5＝6，F5＝6，E5＝10；（2）猜想：①十棱锥中，V10＝11，F10＝11，E10＝20；②n棱锥中，Vn＝n+1，Fn＝n+1，En＝2n；（用含有n的式子表示）（3）探究：①棱锥的顶点数（V）与面数（F）之间的等量关系：V ＝F；②棱锥的顶点数（V）、面数（F）、棱数（E）之间的等量关系：E＝V+F﹣2；（4）拓展：棱柱的顶点数（V）、面数（F）、棱数（E）之间也存在某种等量关系，相应的等式是：V+F﹣E ＝2．故答案为：4，4，6；6，6，10；11，11，20；n+1，n+1，2n；V＝F，V+F﹣2．26.分析：（1）根据图形数出即可．（2）根据（1）中结果得出f+v﹣e＝2．（3）代入f+v﹣e ＝2求出即可．解：（1）题1，面数f＝7，顶点数v＝9，棱数e＝14，题2，面数f＝6，顶点数v＝8，棱数e＝12，题3，面数f＝7，顶点数v＝10，棱数e＝15，故答案为：7，9，14.6，8，12，7，10，15．（2）f+v﹣e＝2．（3）∵v＝2018，e＝4036，f+v﹣e＝2，∴f+2018﹣4036＝2，f＝2020，即它的面数是2020．27.分析：（1）观察表格可以看出：顶点数+面数﹣棱数＝2，关系式为：V+F﹣E＝2；（2）根据题意得出是十二面体，得出顶点数；（3）代入（1）中公式进行计算；（4）根据欧拉公式可得顶点数+面数﹣棱数＝2，然后表示出棱数，进而可得面数．解：（1）根据题意得：四面体的棱数为6，正八面体顶点数为6，∵4+4﹣6＝2，8+6﹣12＝2，6+8﹣12＝2，∴顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F﹣E＝2；故答案为：V+F﹣E＝2；（2）正十二面体有十二个面，每个面都是正五边形，它的每个顶点处都有相同数目的棱．则它有30条棱，20个顶点；故答案是：30；（3）由（1）可知：V+F﹣E＝2，∵一个多面体的面数比顶点数小8，且有30条棱，∴V+V﹣8﹣30＝2，即V＝20，故答案是：20；（4）∵有48个顶点，每个顶点处都有3条棱，两点确定一条直线；∴共有48×3÷2＝72条棱，设总面数为F，48+F﹣72＝2，解得F＝26，∴x+y＝26．28.分析：（1）观察图形即可得出结论；（2）观察可得顶点数+面数﹣棱数＝2；（3）代入（2）中的式子即可得到面数．解：（1）观察图形，四面体的棱数为6；正八面体的顶点数为6；正十二面体的面数为12；（2）观察表格可以看出：顶点数+面数﹣棱数＝2，关系式为：V+F﹣E＝2；（3）由题意得：F﹣8+F ﹣30＝2，解得F＝20．故答案为：（1）6，6，12；（2）V+F﹣E＝2；（3）20．29.分析：（1）观察图形即可得出结论；（2）观察可得顶点数+面数﹣棱数＝2；（3）代入（2）中的式子即可得到面数．解：（1）观察图形，多面体（1）的顶点数为10；多面体（3）的面数为5；多面体（5）的棱数为12；故答案为：10，5，12；（2）观察表格可以看出：顶点数+面数﹣棱数＝2，即关系式为：V+F﹣E＝2；故答案为：V+F﹣E＝2；（3）由题意得：V+20﹣30＝2，解得V＝12．故答案为：12．30.分析：（1）结合三棱柱、四棱柱、五棱柱和六棱柱的特点，即可填表：（2）（3）根据已知的面、顶点和棱与几棱柱的关系，可知n棱柱一定有（n+2）个面，2n个顶点和3n条棱，进而得出答案；（4）利用前面的规律得出a，b，c之间的关系．解：（1）填表如下.（2）若某个棱柱由28个面构成，则这个棱柱为26棱柱；（3）根据表中的规律判断，n棱柱共有（n+2）个面，共有 2n个顶点，共有 3n条棱；（4）a，b，c之间的关系：a+c﹣b＝2故答案为：8；15，18；7；26；（n+2），2n，3n．- 11 -。

初一数学图形认识专项练习题

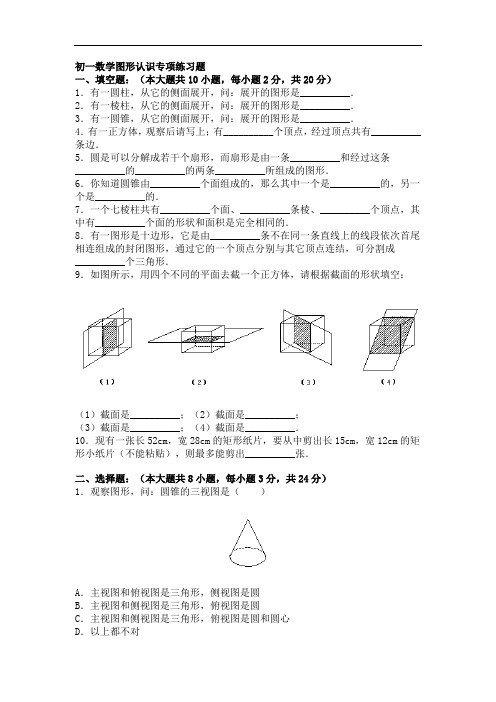
初一数学图形认识专项练习题一、填空题：（本大题共10小题，每小题2分，共20分）1．有一圆柱，从它的侧面展开，问：展开的图形是__________．2．有一棱柱，从它的侧面展开，问：展开的图形是__________．3．有一圆锥，从它的侧面展开，问：展开的图形是__________．4．有一正方体，观察后请写上；有__________个顶点，经过顶点共有__________条边．5．圆是可以分解成若干个扇形，而扇形是由一条__________和经过这条__________的__________的两条__________所组成的图形．6．你知道圆锥由__________个面组成的，那么其中一个是__________的，另一个是__________的．7．一个七棱柱共有__________个面、__________条棱、__________个顶点，其中有__________个面的形状和面积是完全相同的．8．有一图形是十边形，它是由__________条不在同一条直线上的线段依次首尾相连组成的封闭图形，通过它的一个顶点分别与其它顶点连结，可分割成__________个三角形．9．如图所示，用四个不同的平面去截一个正方体，请根据截面的形状填空：（1）截面是__________；（2）截面是__________；（3）截面是__________；（4）截面是__________．10．现有一张长52cm，宽28cm的矩形纸片，要从中剪出长15cm，宽12cm的矩形小纸片（不能粘贴），则最多能剪出__________张．二、选择题：（本大题共8小题，每小题3分，共24分）1．观察图形，问：圆锥的三视图是（）A．主视图和俯视图是三角形，侧视图是圆B．主视图和侧视图是三角形，俯视图是圆C．主视图和侧视图是三角形，俯视图是圆和圆心D．以上都不对2．用一个平面去截一个正方体，截面图形不可能是（）A．长方形B．梯形C．三角形D．圆3．用一个平面去截一个几何体，如果截面的形状是圆，则这个几何体不可能是（）A．圆柱B．圆锥C．正方体D．球4．小明看到了“实验楼”三个字，而且能看到该楼所有的门窗，则小明看到的图是（）A．俯视图B．左视图C．主视图D．都有可能5．截去四边形的一个角，剩余图形不可能是（）A．三角形B．四边形C．五边形D．圆6．用图所示的几何图形拼成的图形是（）7．如图，按照一定的规律，你认为“?”处应放的图形是（）8．从下列右边备选图形中找出一个，使其经旋转后与左图完全一致的是（）三、解答题：（本大题共6小题，共56分）1．用一个平面截一个正方体，能截得五边形吗?如果行，请画出示意图．截得的这个五边形的边具有什么性质?2．图中有8块小立方块，请把它的主视图、左视图和俯视图画出来．3．下面的图是由几块小立方块组成的几何体的俯视图，小方块中的数字表示该位置小方块的个数，你能画出这个几何体的主视图和左视图吗？请动手一试，如图所示，你还能画出这些小立方块组成的几何体吗？4．如图，将等腰三角形对折沿着中间的折痕剪开，得到两个形状和大小都相同的直角三角形，将这两个直角三角形拼在一起，使得它有一条相等的边是公有的，你能拼出多少种不同的几何图形？并请你分别说出所拼的图形的名称．5．用火柴棒拼搭等边三角形（1）用火柴棒拼搭出两个边长等于棒长的等边三角形，你有几种拼法，最少需要几根火柴棒？（2）拼6个边长等于棒长的等边三角形，看谁用的棒最少？（3）用6根火柴棒拼搭等边三角形，若允许搭成的等边三角形不在同一平面内，那么可以搭多少个？一、填空题：1．长方形2．一些有公共边的矩形拼成的图形3．扇形4．8；125．弧；弧；端点；半径6．2；平；曲7．9；21；14；2（上、下）8．10；369．正方形；正方形；长方形；长方形10．7二、选择题：1．C 2．D 3．C 4．C 5．D 6．B 7．A 8．A三、解答题：1．能截得五边形，如图，截得的这个五边形有两对对边平行．2．3．4．共可以拼出以下六种图形（（1）～（6））（1）、（3）是等腰三角形；（2）、（4）是平行四边形；（5）是长方形；（6）可以称它为筝形．5．（1）2、5 （2）12 （3）4（1）有两种情况，至少要用5根火柴棒，如图（2）；而图（1）则用6根火柴棒．（2）最少要12根火柴棒，如图（4）；图（3）用了13根．（3）若可以不在同一个平面内拼搭，可以搭4个等边三角形，如图（5）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。