高中高三立体几何试题及答案
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
2023年高考数学总复习《立体几何》附答案解析

所以 z1=0,
,故可取
, ,,
于是 < , >
,
设所成锐二面角为θ,所以 sinθ
,
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为 .
第3页共3页
第1页共3页
∴CF CC1 AA1 , ∵∠BAC=90°,
∴CD
,
在 Rt△FCD 中,tan∠FDC 맨
,
故直线 DF 与平面 ABC 所成角的正切值为 .
2.如图所示,四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形,∠BCD=60°,E 是 CD 的中点,PA⊥底面 ABCD,PA=2. (1)证明:平面 PBE⊥平面 PAB; (2)求平面 PAD 和平面 PBE 所成二面角(锐角)的正弦值.
【解答】(1)证明:如图所示,连接 BD,由 ABCD 是菱形且∠BCD=60°, 知△ABC 是等边三角形. ∵E 是 CD 的中点, ∴BE⊥CD,又 AB∥CD, ∴AB⊥BE,∴BE⊥平面 PAB, 又 BE⊂平面 PBE, ∴平面 PBE⊥平面 PAB. (2)解:在平面 ABCD 内,过点 A 作 AB 的垂线,如图所示,以 A 为原点建立空间直角
【解答】(1)证明:连接 DG、FG, 由直三棱柱的性质知,BB1∥CC1,且 BB1=CC1, ∵B1E=2EB,C1F=2FC, ∴EB∥FC,且 EB=FC, ∴四边形 BCFE 为平行四边形, ∴EF∥BC,EF=BC, ∵BD=2DA,CG=2GA, ∴GD∥BC,且 GD BC, ∴EF∥GD,且 GD EF, ∴四边形 DEFG 为梯形,即 D、E、F、G 四点共面, ∴点 G 在平面 EFD 内. (2)解:由直三棱柱的性质知,CC1⊥平面 ABC, ∵F 为 CC1 上一点, ∴点 F 在平面 ABC 上的投影为点 C, 连接 CD,则∠FDC 即为直线 DF 与平面 ABC 所成角. ∵点 D 在棱 AB 上,且 BD=2DA, ∴AD AB , ∵C1F=2FC,
高中空间立体几何经典例题精选全文完整版

可编辑修改精选全文完整版立体几何一、选择题1.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D2 2.(20XX 年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C 【答案】A3 3.(20XX 年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A4 4.(20XX 年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B .2C .2-12D .2+12【答案】C5.(20XX 年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,底面是边长为3.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A.512πB .3πC.4πD.6π【答案】B6.(20XX年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为()A.5603B.5803C.200D.240【答案】C7.(20XX年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为,m n,那么m n+=()A.8 B.9 C.10 D.11【答案】A二、填空题8.(20XX年高考北京卷(理))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________.1D1BPD1CCEBA1A【答案】2559.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2410.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-11.(20XX 年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π12.(20XX 年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______AB C1A D EF1B 1C【答案】3π三、解答题13.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值D 1 C 1 B 1A 1D C AB14.(20XX 年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,113tan 6233BC CC BC C =⋅∠==从而2333ABC S BC ∆==因此该三棱柱的体积为1336183ABC V S AA ∆=⋅==15.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))B 1 A 1C 1ACB如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF ∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF ∥平面ABC 同理:FG ∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC ∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SAB AF ⊥SB∴AF ⊥平面SBC 又∵BC ⊆平面SBC ∴AF ⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC ⊥平面SAB 又∵SA ⊆平面SAB ∴BC ⊥SA16.(20XX 年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯=而1AD C ∆中,11AC DC AD ==故132AD C S ∆= AB CSGFE所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.17.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE,在OCD ∆中,由余弦定理可得OD=由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O =,所以A O '⊥平面BCDE . (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos OH A HO A H '∠=='所以二面角ACD B '--向量法:以O 点为原点,建立空间直角坐标系O -.CO BDEA CDOBE'A图1图2C DO BE'AH则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,1,n =- 由(Ⅰ)知,(OA '=为平面CDB 的一个法向量,所以3cos ,3n OA n OA n OA'⋅'===',即二面角A CD B '--的平面角的余弦值为5.18.(20XX年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为2, 求线段AM的长.6【答案】19.(20XX年高考陕西卷(理))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,12AB AA==(Ⅰ) 证明: A1C⊥平面BB1D1D;(Ⅱ) 求平面OCB1与平面BB1D1D的夹角θ的大小.1A【答案】解:(Ⅰ) BDOAABCDBDABCDOA⊥∴⊂⊥11,,面且面;又因为,在正方形AB CD 中,BDCAACACAACABDAACOABDAC⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD中,AO = 1 . .111=∆OAOAART中,在OECAOCEAEDB1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又OOBDDDBBODDBBBD=⋂⊂⊂111111E.E,DDBBCA111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O为原点,以OC为X轴正方向,以OB为Y轴正方向.则)1,0,1()1,1,1(),10(),1(,0,1,0111-=⇒CABACB,,,,)(.由(Ⅰ)知, 平面BB1D1D的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OCOBCAn设平面OCB1的法向量为,则0,0,2122=⋅=⋅OCnOBnn).1-,1,0(法向量2=n为解得其中一个21221||||||,cos|cos212111=⋅=⋅=><=nnnnnnθ.所以,平面OCB1与平面BB1D1D的夹角θ为3π1A。
高三立体几何习题(含答案)

CBAC1B1A1高三立体几何习题一、填空题1.已知AB是球O的一条直径,点1O是AB上一点,若14OO=,平面α过点1O且垂直AB,截得圆1O,当圆1O的面积为9π时,则球O的表面积是.【答案】100p2.把一个大金属球表面涂漆,共需油漆2.4公斤.若把这个大金属球熔化制成64个大小都相同的小金属球,不计损耗,将这些小金属球表面都涂漆,需要用漆公斤.【答案】9.63.已知球的表面积为64π2cm,用一个平面截球,使截面圆的半径为2cm,则截面与球心的距离是cm【答案】234.一个圆锥与一个球体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为.【答案】4p5.一个底面置于水平面上的圆锥,若主视图是边长为2的正三角形,则圆锥的侧面积为.【答案】4p6.如图所示:在直三棱柱111ABC A B C-中,AB BC⊥,1AB BC BB==,则平面11A B C与平面ABC所成的二面角的大小为.【答案】4π二、选择题1.如图,已知圆锥的底面半径为10r=,点Q为半圆弧AB的中点,点P为母线SA的中点.若PQ与SO所成角为4π,则此圆锥的全面积与体积分别为()A.100051006,3ππB.10005100(16),3ππ+C.100031003,3ππD.10003100(13),3ππ+【答案】B2.如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么()A.S圆>S圆环 B.S圆<S圆环 C.S圆=S圆环 D.不确定3.如图所示,PAB∆所在平面α和四边形ABCD所在的平面β互相垂直,且ADα⊥,BCα⊥,4AD=,8BC=,6AB=,若tan2tan1ADP BCP∠-∠=,则动点P在平面α内的轨迹是()A.线段B.椭圆的一部分C.抛物线D.双曲线的一部分PSAQOBβαPBADC【答案】D4.在空间中,下列命题正确的是( )A .若两直线,a b 与直线l 所成的角相等,那么//a bB .空间不同的三点A 、B 、C 确定一个平面C. 如果直线//l 平面α且//l 平面β,那么//αβ D .若直线a 与平面M 没有公共点,则直线//a 平面M 【答案】D5.如图,已知直线l ⊥平面α,垂足为O ,在ABC △中,2,2,22BC AC AB ===,点P 是边AC 上的动点.该三角形在空间按以下条件作自由移动:(1)A l ∈,(2)C α∈.则OP PB +的最大值为( ) (A) 2. (B) 22. (C) 15+. (D) 10. 【答案】C6.平面α上存在不同的三点到平面β的距离相等且不为零,则平面α与平面β的位置关系为( ))(A 平行 )(B 相交)(C 平行或重合 )(D 平行或相交 【答案】D7.a b c 、、表示直线,α表示平面,下列命题正确的是( )A .若//,//αa b a ,则//αbB . 若,α⊥⊥a b b ,则α⊥aC .若,⊥⊥a c b c ,则//a bD .若,αα⊥⊥a b ,则//a b 【答案】D8.下列命题中,正确的个数是【 】① 直线上有两个点到平面的距离相等,则这条直线和这个平面平行; ② a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个; ③ 直四棱柱是直平行六面体;④ 两相邻侧面所成角相等的棱锥是正棱锥.A 、0B 、1C 、2D 、3 【答案】B9.在四棱锥ABCD V -中,1B ,1D 分别为侧棱VB ,VD 的中点,则四面体11CD AB 的体积与四棱锥 ABCD V -的体积之比为( )A .6:1B .5:1C .4:1D .3:1【答案】C三、解答题1.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)证明:11D E A D ⊥;(2)AE 等于何值时,二面角1D EC D --的大小为4π. 【答案】解:(1)在如图所示的空间直角坐标系中,11(1,0,1),(0,0,0),(0,0,1)A D D设(1,,0)([0,2])E y y ∈ 则11(1,,1),(1,0,1)D E y DA =-=…所以110D E DA ⋅=……所以11D E A D ⊥……(2)方法一:设(,,)n u v w =为平面1D CE 的一个法向量 D 1 C 1A 1AE D B 1B C Oxy zABl CαNPO由1100n CD n D E ⎧⋅=⎪⎨⋅=⎪⎩,得200v w u yv w -+=⎧⎨+-=⎩,所以(2)2u y vw v =-⎧⎨=⎩…因为二面角1D EC D --的大小为4π,所以2222(0,0,1)(,,)22cos||42(2)5u v w u v w y π⋅===++-+又[0,2]y ∈,所以23y =-,即当23AE =-时二面角1D EC D --的大小为4π2.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)当E 为AB 的中点时,求四面体1E ACD -的体积; (2)证明:11D E A D ⊥. 【答案】解:(1)1122ACE S AE BC ∆=⋅=…因为1D D ACE⊥平面,所以1111136E ACD D ACEACE V V S D D --∆==⋅=… (2)正方形11ADD A 中,11A D AD ⊥……因为11AB ADD A ⊥平面,所以1AB A D ⊥…所以11A D AD E ⊥平面…所以11D E A D ⊥……3.三棱柱111C B A ABC -中,它的体积是315,底面ABC ∆中,090=∠BAC ,3,4==AC AB ,1B 在底面的射影是D ,且D 为BC 的中点.(1)求侧棱1BB 与底面ABC 所成角的大小;(7分) (2)求异面直线D B 1与1CA 所成角的大小.(6分)【答案】解:(1)依题意,⊥D B 1面ABC ,BD B 1∠就是侧棱1BB 与底面ABC 所成的角θ 2分111111431532ABC A B C ABC V S B D B D -∆=⋅=⨯⨯⨯=4分1532B D =5分计算25=BD ,θθtan 25tan 1==BD D B , tan 3,3πθθ=∴= 7分 (2)取11C B 的中点E ,连E A EC 1,,则1ECA ∠(或其补角)为所求的异面直线的角的大小 9分 ⊥D B 1面ABC ,D B 1‖CE ,面ABC ‖面111C B A ⊥∴CE 面111C B A ,E A CE 1⊥∴ 11分33325tan 251===∠EC AE CE A 12分 所求异面直线D B 1与1CA 所成的角6π13分 D 1C 1A 1A EDB 1BC1A(第20题图)D 1C 1B 1BCDA 1A4.在如图所示的几何体中,四边形CDPQ 为矩形,四边形ABCD 为直角梯形,且90BAD ADC ∠=∠=,平面CDPQ ⊥平面ABCD ,112AB AD CD ===,2PD =.(1)若M 为PA 的中点,求证:AC //平面DMQ ;(2)求平面PAD 与平面PBC 所成的锐二面角的大小.【答案】解:(1)如图,设CP 与M 的交点为N ,连接MN .易知点N 是CP 的中点,又M 为PA 的中点,故//AC MN .…4分 于是,由MN ∉平面DMQ ,得//AC 平面DMQ .……………6分(2)如图,以点D 为原点,分别以DA DB DC 、、为x 轴,y 轴,z 轴,建立空间直角坐标系,则(0,0,0),(1,0,0),(1,1,0),(0,2,0),(0,0,2)D A B C P .易知1(0,1,0)n =为平面PAD 的一个法向量,设2(,,)n x y z =为平面PBC 的一个法向量. 则220220n BC x y n PC y z ⎧=-+=⎪⎨=-=⎪⎩2x yz y =⎧⎪⇒⎨=⎪⎩,令1y =,得2(1,1,2)n =.…………………10分 设平面PAD 与平面PBC 所成的锐二面角为θ,则12121cos 2n n n n θ==,…………………12分 故平面PAD 与平面PBC 所成的锐二面角的大小为3π.………………………………………14分5.(本题满分14分) 本题共2个小题,第1小题6分,第2小题8分. 在如图所示的直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为2的 菱形,且60,BAD ∠=︒1 4.AA =(1)求直四棱柱1111ABCD A B C D -的体积; (2)求异面直线11AD BA 与所成角的大小.【答案】解:(1)因菱形ABCD 的面积为2sin6023,AB ⋅︒= ……2分故直四棱柱1111ABCD A B C D -的体积为:12348 3.ABCD S AA ⋅=⨯=底面……6分(2)连接111BC A C 、,易知11//BC AD ,故11A BC ∠等于异面直线11AD BA 与所成角. ……8分由已知,可得111125,23,A B BC AC === ……10分 则在11A BC ∆中,由余弦定理,得222111111117cos .210A B BC AC A BC A B BC +-∠==⋅……12分 故异面直线11AD BA 与所成角的大小为7cos.10arc……14分 6.(本题满分12分)本题共2小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过11,,A C B 三点的平面截去长方体的一个角后,得到如下所示的几何体111ABCD AC D -.(1)若11A C 的中点为1O ,求求异面直线1BO 与11A D 所成角的大小(用反三角函数值表示); (2)求点D 到平面11A BC 的距离d .【答案】解:(1)按如图所示建立空间直角坐标系.由题知,可得点D(0,0,0)、(2,2,0)B 、1(0,0,3)D 、1(2,0,3)A 、1(0,2,3)C .ABCQP D M CD1A 1C 1D由1O 是11A C 中点,可得1(1,1,3)O . 于是,111(1,1,3),(2,0,0)BO A D =--=-. 设异面直线1BO 与11A D 所成的角为θ,则111111211cos 11||||211BO A D BO A D θ⋅===.因此,异面直线1BO 与11A D 所成的角为11arccos 11. (2)设(,,)nx y z =是平面ABD 的法向量. ∴110,0.n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩ 又11(0,2,3),(2,0,3)BA BC =-=-,∴230,230.y z x z -+=⎧⎨-+=⎩ 取2z =, 可得3,3,2.x y z =⎧⎪=⎨⎪=⎩即平面11BA C 的一个法向量是(3,3,2)n =. ∴||n DB d n ⋅=62211=. 7.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过1A 、1C 、B 三点的平面截去长方体的 一个角后,得到如下所示的几何体111ABCD AC D -.(1)求几何体111ABCD AC D -的体积,并画出该几何体的左视图(AB 平行主视图投影所在的平面); (2)求异面直线1BC 与11A D 所成角的大小(结果用反三角函数值表示). 【答案】解:2AB BC ==,13AA =,左视图如右图所示. (2)依据题意,有11,A D AD AD BC ,即11A D BC .∴1C BC ∠就是异面直线1BC 与11A D 所成的角. 又1C C BC ⊥,∴113tan 2C C C BC BC ∠==.∴异面直线1BC 与11A D 所成的角是3tan2arc . 8. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在直三棱柱111C B A ABC -中,已知21===AB BC AA ,AB ⊥BC . (1)求四棱锥111A BCC B -的体积; (2)求二面角111C C A B --的大小.【答案】解:(1)因为AB ⊥BC ,三棱柱111C B A ABC -是直三棱柱,所以11AB BCC B ⊥, 从而11A B 是四棱锥111A BCC B -的高. ……………………………………2分 四棱锥111A BCC B -的体积为1822233V =⨯⨯⨯=…………………………4分 (2)如图(图略),建立空间直角坐标系.则A (2,0,0),C (0,2,0),A 1(2,0,2),B 1(0,0,2),C 1(0,2,2), …………………………………………………6分 设AC 的中点为M ,,,1CC BM AC BM ⊥⊥)0,1,1(11=⊥∴BM C ,C A BM 即平面是平面A 1C 1C 的一个法向量.ABCD1A 1C 1D CBAC 1B 1A 1PSAQOB设平面A 1B 1C 的一个法向量是),,(z y x n =,)0,0,2(),2,2,2(11-=--=B A AC …8分 令z=1,解得x=0,y=1.)1,1,0(=∴n , …………………………………………9分 设法向量n 与BM 的夹角为ϕ,二面角B 1—A 1C —C 1的大小为θ,显然θ为锐角.111.3B AC C π∴--二面角的大小为………………………………………………12分9. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在正三棱柱111C B A ABC -中,已知16AA =, 三棱柱111C B A ABC -的体积为183. (1)求正三棱柱111C B A ABC -的表面积; (2)求异面直线1BC 与1AA 所成角的大小.【答案】解:(1)因为三棱柱的体积为183,16AA =,从而23334ABC S BC ∆==, 因此23BC =. ………………………2分 该三棱柱的表面积为2+=63+363423ABC S S S ∆=⋅=全侧. ………4分(2)由(1)可知23BC =因为1CC //1AA .所以1BC C ∠为异面直线1BC 与1AA 所成的角, ………8分 在Rt 1BC C ∆中,1233tan 63BC C ∠==, 所以1BC C ∠=6π. 异面直线1BC 与1AA 所成的角6π……………………………………………12分 10.如图,已知圆锥的底面半径为10r =,点Q 为半圆弧AB 的中点,点P 为母线SA 的中点.若直线PQ 与SO 所成的角为4π,求此圆锥的表面积.【答案】解:取OA 的中点M ,连接PM ,又点P 为母线SA 的中点 所以//PM OS ,故MPQ ∠为PQ 与SO 所成的角.………………………2分在Rt MPQ △中,4MPQ π∠=,PM QM =,………………………4分由点Q 为半圆弧AB 的中点知 OQ AB ⊥,在Rt MOQ △中,10,555OQ OM MQ ==⇒=故55PM =,所以105OS =,=106SA . ………………………8分 所以2S 100r ππ==底,101061006S r SA πππ=⋅=⨯⨯=侧………………10分1001006100(16)S S S πππ=+=+=+全底侧.…………………………………12分11.(本大题共有2个小题,满分14分)第(1)小题满分7分,第(2)小题满分7分. 如图,在四棱锥P ABCD -中,底面正方形ABCD 为边长为2,PA ⊥底面ABCD , E 为BC 的中点,PC 与平面PAD 所成的角为2arctan 2.(1)求异面直线AE 与PD 所成角的大小(结果用反三角函数表示); (2)求点B 到平面PCD 的距离.【答案】解:方法1,(1)因为底面ABCD 为边长为2的正方形,⊥PA 底面ABCD ,P S AQ O BMPABCD则 ⊥⇒⎪⎭⎪⎬⎫=⊥⊥CD A PA AD PA CD ADCD 平面PAD ,所以CPD ∠就是CP 与平面PAD 所成的角.………………2分在CDP Rt ∆中,由22tan ==∠PD CD CPD ,得22=PD ,…………………………3分 在PAD Rt ∆中,2=PA .分别取AD 、PA 的中点M 、N ,联结MC 、NC 、MN , 则NMC ∠异面直线AE 与PD 所成角或补角.……………4分 在MNC ∆中,2=MN ,5MC =,3NC =,由余弦定理得,()()22225310cos 10225NMC +-∠==-⋅, 所以10arccos10NMC π∠=-,………6分 即异面直线AE 与PD 所成角的大小为1010arccos .……7分(2)设点B 到平面PCD 的距离为h ,因为BCD P PCD B V V --=,…………………………9分 所以,11113232CD PD h BC CD PA ⨯⋅⋅=⨯⋅⋅,得2h =.……………………………14分 方法2,(1) 如图所示,建立空间直角坐标系,同方法1,得2=PA ,……………3分 则有关点的坐标分别为()0,0,0A ,()2,1,0E ,()0,2,0D ,()2,0,0P .………………5分 所以()2,1,0AE =,()2,2,0-=PD .设θ为异面直线AE 与PD 所成角, 则()101085202102cos =⨯-⨯+⨯+⨯=θ,所以,1010arccos =θ,即异面直线AE 与PD 所成角的大小为1010arccos.…………………………………7分 (2)因为()2,2,0-=PD ,()0,0,2=CD ,()0,2,0=BC ,设()w v u n ,,=, 则由⎩⎨⎧==⇒⎪⎩⎪⎨⎧==⋅=-=⋅w v u u CD n w v PD n 002022,………………………………………………11分 可得()1,1,0=n ,所以222n BC d n⋅===.……………………………………14分 12.(本题共有2个小题,满分14分);第(1)小题满分7分,第(2)小题满分7分.如图,在四棱锥ABCD P -中,底面ABCD 为边长为2的正方形,P ABCD EMNPAB CD Exyz PABCD⊥PA 底面ABCD , 2=PA .(1)求异面直线PC 与BD 所成角的大小; (2)求点A 到平面PBD 的距离.【答案】解:(1)联结AC 与BD 交于点M ,取PA 的中点N ,联结MN ,则CP MN //, 所以NMB ∠为异面直线PC 与BD 所成角或补角.……………………2分 在BMN ∆中,由已知条件得,5=BN ,2=BM ,3=MN ,…………5分所以222MN BM BN +=,2π=∠BMN ,所以异面直PC 与BD 所成角为2π.…7分 (或用线面垂直求异面直线PC 与BD 所成角的大小)(2)设点A 到平面PBD 的距离为h ,因为ABD P PBD A V V --=,……………9分所以,11113232BD PM h BC CD PA ⨯⋅⋅=⨯⋅⋅,得332=h .(或在MAN Rt ∆中求解)………14分 13.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.在正方体1111-ABCD A B C D 中,E 是棱1DD 的中点.(1)求直线BE 与平面11ABB A 所成的角的大小(结果用反三角函数值表示); (2)在棱11C D 上是否存在一点F ,使得1//B F 平面1A BE ,若存在,指明点F 的位置;若不存在,说明理由.【答案】解:(1)以A 为坐标原点,以射线1AB AD AA 、、分别为x y z 、、轴,建立空间 直角坐标系,如图所示.不妨设正方体1111ABCD A B C D -的棱长为a (0a >),则(,0,0),(0,,)2aB a E a ,于是(,,)2a BE a a =- 3分 根据正方体的性质,可知11DA ABB A ⊥平面,故11AD ABB A 是平面的一个法向量且AD =(0,,0)a 4分设直线BE 与平面11ABB A 所成的较为θ,则22sin 0332BE AD a BE ADa a θ===>⨯ 5分 所以2arcsin3θ=,故直线BE 与平面11ABB A 所成的角的大小为2arcsin 3. 6分(2)假设在棱11C D 上是存在一点F ,使得11//B F A BE 平面,设(,,)F x a a (其中0x a ≤≤)111(,0,0),(0,0,),(,0,),(,,0)B a A a BA a a B F x a a =-=- 8分根据(1)可知,(,,)2aBE a a =- 9分设(,,)n x y z =平面1A BE 的一个法向量,则100n BA n BE ⎧=⎪⎨=⎪⎩,即002ax az aax ay z -=⎧⎪⎨--=⎪⎩, 10分 取2z =,则(2,1,2)n =,由于直线11//B F A BE 平面,所以10B F n = 11分NPAB CDMBCDAO zxy即(,,0)(2,1,2)0x a a -=,化简得2()0x a a -+=,解得2ax = 12分 故在棱11C D 上是存在一点F ,使得11//B F A BE 平面,且点F 是棱11C D 的中点. 14分14.在正方体1111-ABCD A B C D 中,E 是棱1DD 的中点. 求直线BE 与11B A 所成的角的大小(结果用反三角函数值表示); 【答案】解:设正方体的棱长为a ,根据正方体的性质可得: 四棱锥E ABCD -的底面积2ABCD S a =,高2aED =2分21143323ABCD a V S ED a =⨯⨯=⨯=,解得2a = 5分因为11//AB A B ,所以ABE ∠即为异面直线BE 与11B A 所成角 或其补角, 8分在ABE 中,2,5,3AB AE BE ===,由余弦定理可得4952cos 02233ABE +-∠==>⨯⨯,即2arccos 3ABE ∠= 11分所以异面直线BE 与11B A 所成的较的大小为2arccos 3ABE ∠=. 12分15.(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分. 如图,在Rt AOB ∆中,6OAB π∠=,斜边4AB =,D 是AB 的中点.现将Rt AOB ∆以直角边AO 为轴旋转一周得到一个圆锥,点C 为圆锥底面圆周上的一点,且2BOC π∠=.(1)求该圆锥的全面积;(2)求异面直线AO 与CD 所成角的大小.(结果用反三角函数值表示)【答案】解:(1)在Rt AOB ∆中,2OB =,即圆锥底面半径为2圆锥的侧面积8S rl ππ==侧………………..4’故圆锥的全面积=+8+412S S S πππ==全侧底……………….6’(2)解法一:如图建立空间直角坐标系.则(0,0,23),(2,0,0),(0,1,3)A C D(0,0,23),(2,1,3)AO CD ∴=-=-………………..8’设AO 与CD 所成角为θ,则66cos 42322AO CD AO CDθ⋅-===-⋅⋅………………..10’∴异面直线AO 与CD 所成角为6arc cos4………………..12’ 解法二:过D 作//DM AO 交BO 于M ,连CM则CDM ∠为异面直线AO 与CD 所成角………………..8’ 在Rt AOB ∆中,23AO = 3DM ∴= D Q 是AB 的中点 M ∴是OB 的中点 1OM ∴=5CM ∴=在Rt CDM ∆中,515tan 33CDM ∠==,………………..10’ ED 1C 1A 1B 1CDBA15arctan3CDM ∴∠=,即异面直线AO 与CD 所成角的大小为15arctan 3……………….12’ 16.在棱长为1的正方体1111ABCD A B C D -中,点E 是棱BC 的中点,点F 是棱CD 上的动点. (1)试确定点F 的位置,使得1D E ⊥平面1AB F ;(2)当1D E ⊥平面1AB F 时,求二面角1C EF A --的大小(结果用反三角函数表示). 【答案】解:(1)如图建系,设 ),10(≤≤=x x DF 1分则)0,1,()0,21,1()1,1,0()1,0,1(),0,1,0(),0,0,1(),0,0,0(11x F E D B D B A 2分)0,1,(),1,0,1(),1,21,1(11x AF AB E D ==--=∴, 3分1111,011AB E D AB E D ⊥∴=-=⋅ 4分 由AF E D F AB E D ⊥∴⊥111,平面 5分21,01=⇒=⋅∴x AF E D 6分)0,1,21(F ∴,即F 为CD 中点时F AB E D 11平面⊥。
高三数学 数学立体几何多选题试题附解析

高三数学 数学立体几何多选题试题附解析一、立体几何多选题1.已知正方体1111ABCD A B C D -的棱长为2,点E ,F 在平面1111D C B A 内,若||5AE =,AC DF ⊥,则( )A .点E 的轨迹是一个圆B .点F 的轨迹是一个圆C .EF 21-D .AE 与平面1A BD 所成角的正弦值的最大值为153015【答案】ACD 【分析】对于A 、B 、C 、D 四个选项,需要对各个选项一一验证. 选项A :由2211||5AE AA A E =+=1||1A E =,分析得E 的轨迹为圆;选项B :由AC DBF ⊥,而点F 在11B D 上,即F 的轨迹为线段11B D ,; 选项C :由E 的轨迹为圆,F 的轨迹为线段11B D ,可分析得min ||EF d r =-; 选项D :建立空间直角坐标系,用向量法求最值. 【详解】 对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =,即点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上;故A 正确;对于B: 正方体1111ABCD A B C D -中,AC ⊥BD ,又AC DF ⊥,且BD ∩DF=D ,所以AC DBF ⊥,所以点F 在11B D 上,即F 的轨迹为线段11B D ,故B 错误;对于C:在平面1111D C B A 内,1A 到直线11B D 的距离为2,d=当点E ,F 落在11A C 上时,min ||21EF =-;故C 正确; 对于D:建立如图示的坐标系,则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上,可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =,则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1,则()1,1,1n =, 设AE 与平面1A BD 所成角为α,则:22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时,sin α2215301515=, 故D 正确故选:CD 【点睛】多项选择题是2020年高考新题型,需要要对选项一一验证.2.在长方体1111ABCD A B C D -中,4AB BC ==,18AA =,点P 在线段11A C 上,M 为AB 的中点,则( ) A .BD ⊥平面PACB .当P 为11AC 的中点时,四棱锥P ABCD -外接球半径为72C .三棱锥A PCD -体积为定值D .过点M 作长方体1111ABCD A B C D -的外接球截面,所得截面圆的面积的最小值为4π 【答案】ACD 【分析】利用线面垂直的判定定理可判断A 选项的正误;判断出四棱锥P ABCD -为正四棱锥,求出该四棱锥的外接球半径,可判断B 选项的正误;利用等体积法可判断C 选项的正误;计算出截面圆半径的最小值,求出截面圆面积的最小值,可判断D 选项的正误. 【详解】对于A 选项,因为AB BC =,所以,矩形ABCD 为正方形,所以,BD AC ⊥, 在长方体1111ABCD A B C D -中,1AA ⊥底面ABCD ,BD ⊂平面ABCD ,1BD AA ∴⊥,1AC AA A ⋂=,AC 、1AA ⊂平面PAC ,所以,BD ⊥平面PAC ,A 选项正确;对于B 选项,当点P 为11A C 的中点时,PA ===同理可得PB PC PD ===因为四边形ABCD 为正方形,所以,四棱锥P ABCD -为正四棱锥, 取AC 的中点N ,则PN 平面ABCD ,且四棱锥P ABCD -的外接球球心在直线PN上,设该四棱锥的外接球半径为R ,由几何关系可得222PN R AN R -+=, 即2288R R -+=,解得92R =,B 选项错误; 对于C 选项,2114822ACDSAD CD =⋅=⨯=, 三棱锥P ACD -的高为18AA =,因此,116433A PCD P ACD ACD V V S AA --==⋅=△,C 选项正确;对于D 选项,设长方体1111ABCD A B C D -的外接球球心为E ,则E 为1BD 的中点,连接EN 、MN ,则1142EN DD ==,122MN AD ==, E 、N 分别为1BD 、BD 的中点,则1//EN DD , 1DD ⊥平面ABCD ,EN ∴⊥平面ABCD ,MN ⊂平面ABCD ,EN MN ∴⊥,2225EM EN MN ∴=+=.过点M 作长方体1111ABCD A B C D -的外接球截面为平面α,点E 到平面α的距离为d ,直线EM 与平面α所成的角为θ,则sin 25sin 25d EM θθ==≤, 当且仅当2πθ=时,等号成立,长方体1111ABCD A B C D -的外接球半径为222126AB AD AA R ++'==,所以,截面圆的半径()()222226252r R d '=-≥-=,因此,截面圆面积的最小值为4π,D 选项正确.故选:ACD. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.3.如图,在棱长为2的正方体1111ABCD A B C D -,中,E 为棱1CC 上的中点,F 为棱1AA 上的点,且满足1:1:2A F FA =,点F ,B ,E ,G ,H 为过三点B ,E ,F 的平面BMN 与正方体1111ABCD A B C D -的棱的交点,则下列说法正确的是( )A .//HF BEB .三棱锥的体积14B BMN V -=C .直线MN 与平面11A B BA 所成的角为45︒D .11:1:3D G GC = 【答案】ABD 【分析】面面平行性质定理可得出A 正确;等体积法求得B 正确;直线MN 与平面11A B BA 所成的角为1B MN ∠,求其正切值不等于1即可得出C 错误;利用面面平行性质定理和中位线求出11,D G GC 长度即可得出D 正确. 【详解】解:对于A.在正方体1111ABCD A B C D -中平面11//ADA D 平面11BCB C , 又平面11ADA D 平面BMN HF =,平面11BCB C ⋂平面BMN BE =,有平面与平面平行的性质定理可得//HF BE ,故正确; 对于B.因为1:1:2A F FA =,所以111332B M A B ==, 又E 为棱1CC 上的中点,所以14B N =,所以1111234432B BMN N B BMV V --⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭,故正确; 对于C.由题意及图形可判定直线MN 与平面11A B BA 所成的角为1B MN ∠, 结合B 选项可得1114tan 13B N B MN B M ∠==≠,故错误; 对于D.同A 选项证明方法一样可证的11//GC B M ,因为E 为棱1CC 上的中点,1C 为棱1B N 上的中点,所以1113=22GC B M =所以11G=2D ,所以11:1:3D G GC =,故正确. 故选:ABD 【点睛】求体积的常用方法:(1)直接法:对于规则的几何体,利用相关公式直接计算;(2)等体积法:选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换;(3)割补法:首先把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算.4.已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( ) A .异面直线AC 与BD 所成角为60︒B .点A 到平面BCDC .四面体ABCDD .动点P 在平面BCD 上,且AP 与AC 所成角为60︒,则点P 的轨迹是椭圆 【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ,通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误;在四面体ABCD 中,过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心,因为所有棱长均为2,AF ==即点A 到平面BCD 的距离为3,故B 正确;设O 为正四面体的中心则OF 为内切球的半径,OA 我外接球的半径, 因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△,所以4AF OF =,即OF AO =所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确;建系如图:,A C ⎛⎛⎫⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ,则262326,,0,,AP x y AC →→⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因为cos 60AP AC AP AC →→→→⋅=,所以222324812241393972y x y +=++⨯+⨯, 即222388=33y x y +++,平方化简可得:22323400399y x y ----,可知点P 的轨迹为双曲线,故D 错误. 故选:BC .【点睛】方法点睛:立体几何中动点轨迹的求解问题,解决此类问题可采用空间向量法,利用空间向量法表示出已知的角度或距离的等量关系,从而得到轨迹方程.5.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥ B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D .设正方体棱长为1,则过点E ,F ,A 的平面截正方体所得的截面面积最大为5 【答案】AC 【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN .取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F∠==22,所以C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为6,故D 错误. 故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.6.(多选题)在四面体P ABC -中,以上说法正确的有( )A .若1233AD AC AB =+,则可知3BC BD = B .若Q 为△ABC 的重心,则111333PQ PA PB PC =++C .若0PA BC =,0PC AB =,则0PB AC =D .若四面体P ABC -各棱长都为2,M N ,分别为,PA BC 的中点,则1MN = 【答案】ABC 【分析】作出四面体P ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,1233AD AC AB =+,32AD AC AB ∴=+,22AD AB AC AD ∴-=- , 2BD DC ∴=,3BD BD DC BC ∴=+=即3BD BC ∴=,故A 正确;对于B ,Q 为△ABC 的重心,则0QA QB QC ++=,33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=即111333PQ PA PB PC ∴=++,故B 正确; 对于C ,若0PA BC =,0PC AB =,则0PA BC PC AB +=,()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+= 0CA BC PC AC ∴+=,0AC CB PC AC ∴+=()0AC PC CB ∴+=,0AC PB ∴=,故C 正确;对于D ,111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+==2MN ∴=,故D 错误.故选:ABC 【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键. (2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.7.已知棱长为1的正方体1111ABCD A B C D -,过对角线1BD 作平面α交棱1AA 于点E ,交棱1CC 于点F ,以下结论正确的是( ) A .四边形1BFD E 不一定是平行四边形 B .平面α分正方体所得两部分的体积相等 C .平面α与平面1DBB 不可能垂直D .四边形1BFDE 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E 、F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E的面积最大,,可判断D 正确. 【详解】 如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E 、F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D , 又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.8.如图,正四棱锥S -BCDE 底面边长与侧棱长均为a ,正三棱锥A -SBE 底面边长与侧棱长均为a ,则下列说法正确的是( )A .AS ⊥CDB .正四棱锥S -BCDE 的外接球半径为22a C .正四棱锥S -BCDE 的内切球半径为212a ⎛⎫- ⎪ ⎪⎝⎭ D .由正四棱锥S -BCDE 与正三棱锥A -SBE 拼成的多面体是一个三棱柱 【答案】ABD 【分析】取BE 中点H ,证明BE ⊥平面SAH 即可证AS CD ⊥;设底面中心为1O ,有1122O B O S a ==,可求得球半径为22a ;用等体积法求内切球半径即可判断;由////SA DE BC 且==SA DE BC 可知多面体是一个三棱柱.【详解】 如图所示:A 选项:取BE 中点H 连接,AH SH ,正三棱锥A SBE -中,,AH BE SH BE ⊥⊥ 又AHSH H =,所以BE ⊥平面SAH ,则BE AS ⊥,又//BE CD 所以AS CD ⊥ ,故A 正确;B 选项:设底面中心为1O ,球心为O 半径为R ,因为正四棱锥S -BCDE 外接球球心在1O S 上,所以OS OB R ==,因为,正四棱锥S -BCDE 底面边长与侧棱长均为a所以1122O B O S ==,由()22211OB O B O S OS =+- 得22222R R ⎫⎫=+-⎪⎪⎪⎪⎝⎭⎝⎭解得22R =,故B 正确; C 选项:设内切球半径为r ,易求得侧面面积为2213sin 23S a π=⋅=,由等体积法得222111432334a a a r a r ⋅=⋅+⋅⋅⋅解得4a r = ,故C 错;D 选项:取SE 中点F ,连结AF ,DF ,BF ,则BFD ∠和BFA ∠分别是D SE B --和A SE B --的二面角的平面角,由)22222221cos 2322BF DF BD BFD BF DF a ⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===-⋅⎛⎫⎪⎝⎭22222221cos 232a AF BF BA AFD AF BF ⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===⋅⎫⎪⎝⎭,故BFD ∠与BFA ∠互补,所以ASDE 共面,又因为AS AE ED SD ===,则ASDE 为平行四边形,故////AS ED BC 故正四棱锥S -BCDE 与正三棱锥A -SBE 拼成的多面体是一个三棱柱,所以D 正确 故选:ABD 【点睛】求外接球半径的常用方法:(1)补形法:侧面为直角三角形或正四面体或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;(2)利用球的性质:几何体在不同面均对直角的棱必然是球的直径;(3)定义法:到各个顶点距离均相等的点为球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.。
高三数学立体几何试题答案及解析

高三数学立体几何试题答案及解析1.已知三棱锥的三视图,则该三棱锥的体积是()A.B.C.D.【答案】B【解析】如图所示,,点P在侧面ABC的射影为O,.∴该三棱锥的体积.故选:B.【考点】由三视图求面积、体积.2.(本小题满分12分)直三棱柱中,,,分别是、的中点,,为棱上的点.(1)证明:;(2)是否存在一点,使得平面与平面所成锐二面角的余弦值为?若存在,说明点的位置,若不存在,说明理由.【答案】(1)证明见解析;(2)存在,点为中点.【解析】(1)先证明AB⊥AC,然后以A为原点建立空间直角坐标系A-xyz,则能写出各点坐标,由共线可得D(λ,0,1),所以,即DF⊥AE;(2)通过计算,面DEF的法向量为可写成,=(3,1+2λ,2(1-λ)),又面ABC的法向量=(0,0,1),令,解出λ的值即可.试题解析:(1)证明:,又,面又面以为原点建立如图所示的空间直角坐标系则,,,,设,且,即:(2)假设存在,设面的法向量为,则即:令由题可知面的法向量平面与平面所成锐二面角的余弦值为即:或(舍)当点为中点时,满足要求.【考点】1、二面角的平面角及求法;2、直线与平面垂直的性质.【方法点晴】本题考查空间中直线与直线的位置关系、空间向量及其应用,建立空间直角坐标系是解决问题的关键,属中档题.解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.3.已知正四棱锥中,,那么当该棱锥的体积最大时,它的高为()A.B.C.D.【答案】C【解析】设正四棱锥的高为,则,则,,所以四棱锥的体积,,由得,所以体积函数在区间上单调递增,在区间上单调递减,所以当时,体积有最大值,故选C.【考点】1.多面体体积;2.导数与函数最值.【方法点睛】本题主要考查本题主要考查立体几何中的最值问题,多面体体积公式、导数与函数等知识,属中档题.解决此类问题的两大核心思路:一是将立体问题转化为平面问题,结合平面几何的相关知识求解;二是建立目标函数的数学思想,选择合理的变量,利用导数、基本不等式或配方法求其最值.4.设三棱锥的三条侧棱两两互相垂直,且长度分别为,则其外接球的表面积为()A.B.C.D.【答案】B【解析】由题意可知其外接球的直径,所以外接球的表面积为.【考点】球的表面积公式.5.某几何体的三视图如图所示,则该几何体的体积为.【答案】【解析】该几何体为一个四棱锥,高为,底面为矩形,长宽分别为,因此体积为【考点】三视图6.已知是两条不同的直线,是三个不同的平面,则下列命题中正确的是()A.若B.若C.若D.若【答案】C【解析】垂直于同一平面的两个平面可能平行,也可能相交,所以A选项不正确;两个平面内存在两条平行的直线时,两平面可能相交,也可能平行,所以B选项不正确;,又,,所以C选项正确;若,则或,所以D不正确.故D正确.【考点】1线面位置关系;2面面位置关系.【易错点晴】本题主要考查的是空间点、线、面的位置关系,属于容易题.解题时一定要抓住题目中的重要字眼“真命题”,否则很容易出现错误.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形进行检验,也可作必要的合情推理.7.已知直线平面,直线平面,给出下列命题,其中正确的是()①;②;③;④A.②④B.②③④C.①③D.①②③【答案】C【解析】对①,因为直线平面,∥,则,又直线,所以,①对;对②,与的关系是:平行、相交或异面,②错;对③,因为直线平面,∥,所以,又由面面垂直的判定定理得,③对;对④,与可以平行或相交,④错,所以选C.本题可借助于长方体去判定.【考点】1.空间直线、平面的位置关系.【易错点晴】本题主要考查的是空间点、线、面的位置关系,属于中档题.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形或长方体作为载体进行检验,也可作必要的合情推理.8.利用一个球体毛坯切削后得到一个四棱锥P—ABCD,其中底面四边形ABCD是边长为1的正方形,,且,则球体毛坯体积的最小值应为()A.B.C.D.【答案】D【解析】若使得球体毛坯体积最小,则四棱锥各顶点应都在球上,由题意,将四棱锥补成一个长方体,则转化为求长方体外接球体积,长方体体对角线为外接球直径,体对角线长为,所以球的半径为,体积为.【考点】多面体的外接球.9.(2007•山东)下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④【答案】D【解析】利用三视图的作图法则,对选项判断,A的三视图相同,圆锥,四棱锥的两个三视图相同,棱台都不相同,推出选项即可.解:正方体的三视图都相同,而三棱台的三视图各不相同,圆锥和正四棱锥的,正视图和侧视图相同,所以,正确答案为D.故选D【考点】简单空间图形的三视图.10.如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为的等腰直角三角形,则该几何体的体积为_________________;表面积为________________.【答案】体积为;表面积为【解析】由题意可知三视图复原的几何体如图为四棱锥,是正方体的一部分,正方体的棱长为2;所以几何体的体积是正方体体积的一半减去,所求几何体的体积为;表面积为【考点】三视图,几何体的体积,表面积11.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为()A.B.C.D.【答案】A【解析】根据该几何体的三视图可知几何体的形状是一个长为,宽为,高为的长方体挖去一个直径为高为的圆柱,该几何体的体积为,选A.【考点】1、三视图;2、组合体的体积.12.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆千克,则共需油漆的总量为()A.千克B.千克C.千克D.千克【答案】B【解析】由三视图可知可间房由底部长宽高分别为的长方体与底面半径.母线长分别为圆锥体组合而成,所以其可刷漆的表面积为,则需要漆的总量为千克,故正确选项为B.【考点】空间几何体的表面积.13.若=(2,﹣1,0),=(3,﹣4,7),且(λ+)⊥,则λ的值是()A.0B.1C.﹣2D.2【答案】C【解析】利用(λ+)⊥⇔即可得出.解:∵=λ(2,﹣1,0)+(3,﹣4,7)=(3+2λ,﹣4﹣λ,7),(λ+)⊥,∴,∴2(3+2λ)﹣(﹣4﹣λ)+0=0,解得λ=﹣2.故选C.【考点】向量的数量积判断向量的共线与垂直.14.如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,(Ⅰ)求证:平面PED⊥平面PAC;(Ⅱ)若直线PE与平面PAC所成的角的正弦值为,求二面角A﹣PC﹣D的平面角的余弦值.【答案】(Ⅰ)证明见解析(Ⅱ)【解析】(I)由面面垂直的性质定理证出PA⊥平面ABCD,从而得到AB、AD、AP两两垂直,因此以AB、AD、AP为x轴、y轴、z轴,建立坐标系o﹣xyz,得A、D、E、C、P的坐标,进而得到、、的坐标.由数量积的坐标运算公式算出且,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是,算出、夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出=(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量,算出、的夹角余弦,再结合图形加以观察即可得到二面角A ﹣PC﹣D的平面角的余弦值.解:(Ⅰ)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥PA∴PA⊥平面ABCD结合AB⊥AD,可得分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系o﹣xyz,如图所示可得A(0,0,0)D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ)(λ>0)∴,,得,,∴DE⊥AC且DE⊥AP,∵AC、AP是平面PAC内的相交直线,∴ED⊥平面PAC.∵ED⊂平面PED∴平面PED⊥平面PAC(Ⅱ)由(Ⅰ)得平面PAC的一个法向量是,设直线PE与平面PAC所成的角为θ,则,解之得λ=±2∵λ>0,∴λ=2,可得P的坐标为(0,0,2)设平面PCD的一个法向量为=(x0,y,z),,由,,得到,令x0=1,可得y=z=﹣1,得=(1,﹣1,﹣1)∴cos<,由图形可得二面角A﹣PC﹣D的平面角是锐角,∴二面角A﹣PC﹣D的平面角的余弦值为.【考点】用空间向量求平面间的夹角;平面与平面垂直的判定;二面角的平面角及求法.15.已知正三棱锥的底面边长为,侧棱长为,则正三棱锥的体积为.【答案】【解析】∵正三棱锥的底面边长为,∴底面正三角形的高为,可得底面中心到三角形顶点的距离为,∵正三棱锥侧棱长为,∴正三棱锥的高,所以三棱锥的体积.所以答案应填:.【考点】棱柱、棱锥、棱台的体积.16.在等腰梯形中,,,,是的中点,将梯形绕旋转,得到(如图).(I)求证:;(II)求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(I)由题意容易证明四边形是平行四边形,.又为等腰梯形,,四边形是菱形,可证得,根据面面垂直的性质定理可证得平面,从而证得;(II)易证平面,以为坐标原点,建立空间直角坐标系,分别求出平面的法向量和平面的法向量,根据向量的夹角公式求得二面角的余弦值.试题解析:(I)证明:,是的中点,.又,四边形是平行四边形,.又为等腰梯形,,,四边形是菱形,,,即.平面平面,平面平面,平面.又平面,.(II)解:平面,同理平面.如图建立空间直角坐标系,设,则,,,,则,.设平面的法向量为,.设平面的法向量为,,设二面角的平面角为,,二面角的余弦值为.【考点】空间中垂直关系的证明及空间向量的应用.17.如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正(主)视图与侧(左)视图的面积的比为.【答案】【解析】因为三棱锥的主视图与左视图都是三角形, 正视图和侧视图三角形的底边长都是正方体的棱长,高都是到底面的距离(都是正方体的棱长),所以,三棱锥的主视图与左视图的面积相等,即比值为,故答案为.【考点】1、几何体的三视图;2、三角形面积公式.18.如图,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则几何体的体积为()A.B.C.D.【答案】B【解析】如图所示,该几何体是一个底面为平行四边形,高为的棱柱,体积为,故选B.【考点】几何体的体积.19.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为________.【答案】【解析】因为矩形是水平放置的一个平面图形的直观图,所以根据画直观图的基本原理知原图形是底边长为的平行四边形,其高是,因此面积是,故答案为.【考点】1、画直观图的基本原理;2、平行四边形的面积公式.20.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A.B.C.D.【答案】D【解析】由三视图知几何体是由正方体截取两个角得到,如图所示,故体积为.【考点】三视图.21.如图所示,四棱锥的底面是梯形,且,平面,是中点,.(Ⅰ)求证:平面;(Ⅱ)若,,求直线与平面所成角的大小.【答案】(I)证明见解析;(II).【解析】(I)取的中点,连结,证得,从而证得平面,根据平行四边形的性质,得,即可证明平面;(II)分别以的方向为轴的正方向,建立空间直角坐标系,求解出平面和向量,即可利用向量所成的角,得到直线与平面所成角的大小.试题解析:(Ⅰ)证明:取的中点,连结,如图所示.因为,所以.因为平面,平面,所以.又因为,所以平面.因为点是中点,所以,且.又因为,且,所以,且,所以四边形为平行四边形,所以,所以平面.(Ⅱ)解:设点O,G分别为AD,BC的中点,连结,则,因为平面,平面,所以,所以.因为,由(Ⅰ)知,又因为,所以,所以所以为正三角形,所以,因为平面,平面,所以.又因为,所以平面.故两两垂直,可以点O为原点,分别以的方向为轴的正方向,建立空间直角坐标系,如图所示.,,,所以,,,设平面的法向量,则所以取,则,设与平面所成的角为,则,因为,所以,所以与平面所成角的大小为.【考点】直线与平面垂直的判定与证明;直线与平面所成角的求解.22.如图,在三棱台中,平面平面,,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BF⊥平面ACFD;(Ⅱ)求二面角B-AD-F的平面角的余弦值.【答案】(Ⅰ)证明见解析;(Ⅱ).【解析】(Ⅰ)先证,再证,进而可证平面;(Ⅱ)方法一:先找二面角的平面角,再在中计算,即可得二面角的平面角的余弦值;方法二:先建立空间直角坐标系,再计算平面和平面的法向量,进而可得二面角的平面角的余弦值.试题解析:(Ⅰ)延长,,相交于一点,如图所示.因为平面平面,且,所以平面,因此.又因为,,,所以为等边三角形,且为的中点,则.所以平面.(Ⅱ)方法一:过点作于Q,连结.因为平面,所以,则平面,所以.所以是二面角的平面角.在中,,,得.在中,,,得.所以二面角的平面角的余弦值为.方法二:如图,延长,,相交于一点,则为等边三角形.取的中点,则,又平面平面,所以,平面.以点为原点,分别以射线,的方向为,的正方向,建立空间直角坐标系.由题意得,,,,,.因此,,,.设平面的法向量为,平面的法向量为.由,得,取;由,得,取.于是,.所以,二面角的平面角的余弦值为.【考点】线面垂直,二面角.【方法点睛】解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.证明线面垂直的关键是证明线线垂直,证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线.23.直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,则下列说法正确的是()A.c至少与a、b中的一条相交B.c至多与a、b中的一条相交C.c与a、b都相交D.c与a、b都不相交【答案】A【解析】利用空间中线线、线面、面面间的位置关系判断求解.解:由直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,知:对于B,c可以与a、b都相交,交点为不同点即可,故B不正确;对于C,a∥c,b∩c=A,满足题意,故C不正确;对于D,c与a、b都不相交,则c与a、b都平行,所以a,b平行,与异面矛盾,故D不正确;对于A,由B,C、D的分析,可知A正确故选:A.24.已知某几何体的三视图如图所示,则该几何体的体积等于()A.B.160C.D.【答案】A【解析】由三视图知该几何体是由一个直三棱柱和一个四棱锥组合的组合体,其中直三棱柱的底面为左视图,高为,故体积.四棱锥的底面为边长为的正方形,高为,所以体积,所以该几何体的体积为.故选A.【考点】1、几何体的三视图;2、几何体的体积.【方法点睛】本题主要考查三视图及空间几何体的体积,属于中档题.空间几何体体积问题的常见类型及解题策略:(1)求简单几何体的体积时若所给的几何体为柱体椎体或台体,则可直接利用公式求解;(2)求组合体的体积时若所给定的几何体是组合体,不能直接利用公式求解,则常用转换法、分割法、补形法等进行求解. (3)求以三视图为背景的几何体的体积时应先根据三视图得到几何体的直观图,然后根据条件求解.25.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为()A.1.2B.1.6C.1.8D.2.4【答案】B【解析】由题意得,即,解得,故选B.【考点】几何体的三视图及体积.26.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于()cm3A.4+B.4+C.6+D.6+【答案】D【解析】由三视图还原原几何体如图,是一个半圆柱与一个直三棱柱的组合体,半圆柱的底面半径为,高为;直三棱柱底面是等腰直角三角形(直角边为),高为.∴.故本题选D.【考点】空间几何体的三视图.27.在正方体中,是的中点,则异面直线与所成角的余弦值等于_______,若正方体边长为1,则四面体的体积为_________.【答案】;【解析】异面直线与所成角为,,.【考点】立体几何中异面直线所成角的余弦值的求法以及三棱锥的体积的求法.28.如图,在四棱锥中,底面,,,,,点为棱的中点.(1)证明:;(2)若为棱上一点,满足,求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)以点为原点建立空间直角坐标系(如图),求得,,可得,即可证结论;(2)先根据确定的位置,在求出平面的一个法向量,可证平面一个的法向量为,利用空间向量夹角余弦公式即可得结论.试题解析:(1)证明:依题意,以点为原点建立空间直角坐标系(如图),可得,,,.由为棱的中点,得.向量,,故.所以.(2)向量,,,.由点在棱上,设,.故.由,得,因此,,解得.即.设为平面的法向量,则,即.不妨令,可得为平面的一个法向量.取平面的法向量,则.易知,二面角是锐角,所以其余弦值为.【考点】1、空间直线垂直的判定;2、空间向量夹角余弦公式.29.如图,在三棱锥中,底面,且,点是的中点, 交于点.(1)求证:平面;(2)当时, 求三棱锥的体积.【答案】(1)详见解析(2)【解析】(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的证明与寻找,往往从两个方面,一是利用线面垂直性质定理转化为线线垂直,另一是结合平几条件,如本题利用等腰三角形底边中线性质得(2)求三棱锥体积,关键在于确定高,即线面垂直.由(1)得平面,因此,这样只需在对应三角形中求出对应边即可.试题解析:(1)底面,面,又因为是的中点, 面由已知平面.(2)平面,平面,而,又又平面而.【考点】线面垂直判定与性质定理,三棱锥体积【思想点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行,需转化为证明线线平行.(2)证明线面垂直,需转化为证明线线垂直.(3)证明线线垂直,需转化为证明线面垂直.30.过球表面上一点引三条长度相等的弦,且两两夹角都为60°,若球半径为,求弦的长度___________.【答案】【解析】依题意可知,这是一个正四面体的外接球. 若一个正四面体边长为,其外接球半径公式为:,即.【考点】球的内接几何体.【思路点晴】对棱相等的三棱锥,设三对棱长分别为,如下图所示三棱锥,请同学们推导其外接球半径公式,特别地,若一个正四面体边长为,其外接球半径公式为:.设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.2.若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.31.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】D【解析】由题意得,根据给定的三视图可知,原几何体表示,左侧是一个底面半径为,高为半个圆锥,几何体的右侧是一个底面为底边为,高为的等腰三角形三棱锥,其中三棱锥的高为,所以几何体的体积为,故选D.【考点】几何体的三视图及体积的计算.32.已知直线与平面平行,是直线上的一定点,平面内的动点满足:与直线成.那么点轨迹是()A.两直线B.椭圆C.双曲线D.抛物线【答案】C【解析】题意画图如下,是直线上的定点,有一平面与直线平行,平面内的动点满足的连线与成角,因为空间中过与成角的直线组成两个相对顶点的圆锥,即为平行于圆锥轴的平面,点可理解为是截面与圆锥侧面的交点,所以点的轨迹为双曲线,故选C.【考点】1、空间点、线、面的位置关系;2、圆锥曲线的定义.33.三棱锥内接于球,,当三棱锥的三个侧面积和最大时,球的体积为.【答案】【解析】由于三角形的面积公式,当时取得最大值,所以当两两垂直时,侧面积和取得最大值.此时,由于三棱锥三条侧棱两两垂直,所以可以补形为正方体,三棱锥的外接球即正方体的外接球,其直径等于正方体的体对角线即,故求的体积为.【考点】几何体的外接球.【思路点晴】设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.三棱锥三条侧棱两两垂直,且棱长分别为,则其外接球半径公式为: .34.如图,在直三棱柱中,,过的中点作平面的垂线,交平面于,则与平面所成角的正切值为()A.B.C.D.【答案】C【解析】连接,则,由直三棱柱得,因此,因此为的中点,过作于,则为与平面所成角, ,选C.【考点】线面角35.如图,在四棱锥中,底面,底面是直角梯形,(1)在上确定一点,使得平面,并求的值;(2)在(1)条件下,求平面与平面所成锐二面角的余弦值.【答案】(1)(2)【解析】(1)由线面平行的性质定理,可得线线平行,再根据平行得相似,即得比例关系:取。
高三数学立体几何试题答案及解析
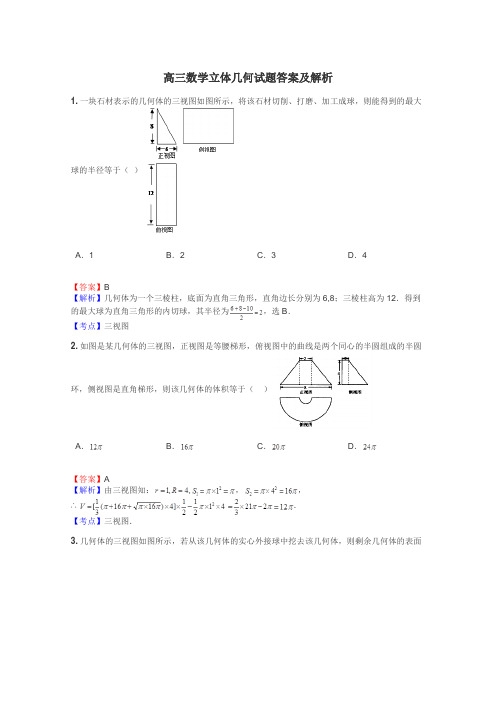
高三数学立体几何试题答案及解析1.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4【答案】B【解析】几何体为一个三棱柱,底面为直角三角形,直角边长分别为6,8;三棱柱高为12.得到的最大球为直角三角形的内切球,其半径为,选B.【考点】三视图2.如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于()A.B.C.D.【答案】A【解析】由三视图知:,,∴.【考点】三视图.3.几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)()A.133B.100C.66D.166【答案】D【解析】由三视图知,该几何体为底面半径为3,搞为8的圆柱.其外接球时半径为5的球.则剩余几何体的表面积是球的表面积与该圆柱表面积的和,即.故选D.【考点】多面体及与其外接球的关系及几何体表面积计算问题.4.(本小题满分12分)如图,已知五面体,其中内接于圆,是圆的直径,四边形为平行四边形,且平面.(1)证明:;(2)若,,且二面角所成角的正切值是,试求该几何体的体积.【答案】(1)见解析;(2)8.【解析】(1)将问题转化为证明平面,再转化为证明(由直径可证)与(由平面可证);(2)考虑建立空间直角坐标系,通过求两个法向量的夹角来确定二面角所成角的正切值,并确定的长,进而可求得几何体的体积.试题解析:(1)证明:是圆的直径,,又平面,又平面,且,平面又平面,(2)设,以所在直线分别为轴,轴,轴,如图所示则,,,由(Ⅰ)可得,平面,平面的一个法向量是设为平面的一个法向量由条件得,,即不妨令,则,,.又二面角所成角的正切值是,,得该几何体的体积是【考点】1、空间直线与直线、直线与平面的垂直的判定与性质;2、二面角;3、空间几何体的体积.【方法点睛】用空间向量处理某些立体几何问题时,除要有应用空间向量的意识外,关键是根据空间图形的特点建立恰当的空间直角坐标系.若坐标系选取不当,计算量就会增大.总之树立用数解形的观念,即用数形结合的思想解决问题,而建立空间直角坐标系通常考虑以特殊点为坐标原点(如中点、正方体的顶点),特殊直线(如有两两垂直的直线)为坐标轴来建立.5.如图,在多面体中,为菱形,,平面,平面,为的中点,若平面.(1)求证:平面;(2)若,求二面角的余弦值.【答案】(1)见解析;(2).【解析】(1)证明线面垂直,只要证明这条直线与平面内两条相交直线垂直即可,取中点,连接,可证,先证,即可证明,即可证明结论成立;(2)建立空间直角坐标系,求出平面与平面的法向量,由空间向量公式直接计算即可.试题解析:(1)取AB的中点M,连结GM,MC,G为BF的中点,所以GM //FA,又EC面ABCD, FA面ABCD,∵CE//AF,∴CE//GM,∵面CEGM面ABCD=CM,EG// 面ABCD,∴EG//CM,∵在正三角形ABC中,CM AB,又AF CM∴EG AB, EG AF,∴EG面ABF.(2)建立如图所示的坐标系,设AB=2,则B()E(0,1,1) F(0,-1,2)=(0,-2,1),=(,-1,-1),=(,1, 1),设平面BEF的法向量=()则令,则,∴=()同理,可求平面DEF的法向量 =(-)设所求二面角的平面角为,则=.【考点】1.线面垂直的判定与性质;2.空间向量的应用.【方法点睛】本题主要考查线面垂直的判定与性质、空间向量的应用,属中档题.解答空间几何体中的平行、垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间的平行、垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;求二面角,则通过求两个半平面的法向量的夹角间接求解.此时建立恰当的空间直角坐标系以及正确求出各点的坐标是解题的关键所在.6.三棱锥及其三视图中的正视图和侧视图如下图所示,,则棱的长为.【答案】.【解析】由已知三视图可知,平面,且底面为等腰三角形.在中,,边上的高为,所以.在中,由可得,故应填.【考点】1、三视图.【易错点晴】本题主要考查了空间几何体的三视图及其空间几何体的面积、体积的计算,考查学生空间想象能力和计算能力,属中档题.其解题过程中容易出现以下错误:其一是不能准确利用已知条件的三视图得出原几何体的空间形状,即不能准确找出该几何体中线线关系、线面关系,导致出现错误;其二是计算不仔细,导致结果出现错误.解决这类问题的关键是正确地处理三视图与原几何体之间的关系.7.在三棱锥中,平面为侧棱上的一点,它的正视图和侧视图如图所示,则下列命题正确的是()A.平面且三棱锥的体积为B.平面且三棱锥的体积为C.平面且三棱锥的体积为D.平面且三棱锥的体积为【答案】C【解析】∵平面,∴,又,∴平面,∴,又由三视图可得在中,为的中点,∴平面.又平面.故.故选:C.【考点】1.直线与平面垂直的判定;2.命题的真假判断与应用;3.简单空间图形的三视图.8.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于()A.B.C.D.【答案】C【解析】题设三视图是下图中几何体的三视图,由三视图中的尺寸,知其体积为,故选C.【考点】三视图与几何体的体积.9.如图,在三棱柱ABC A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:(Ⅰ)DE∥平面ABC1;(Ⅱ)B1C⊥DE.【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.【解析】(Ⅰ)取AA1的中点F,连DF,FE,根据中点易证线线平行,从而平面DEF∥平面ABC1,又因为DE平面DEF,所以B1C⊥DE;(Ⅱ)在菱形中B1C⊥BC1,又B1C⊥AB,易证B1C⊥平面ABC1,再根据面面平行的性质,得:B1C⊥平面DEF,从而证明B1C⊥DE.试题解析:(Ⅰ)如图,取AA1的中点F,连DF,FE.又因为D,E分别为A1C1,BB1的中点,所以DF∥AC1,EF∥AB.因为DF平面ABC1,AC1平面ABC1,故DF∥平面ABC1.同理,EF∥平面ABC1.因为DF,EF为平面DEF内的两条相交直线,所以平面DEF∥平面ABC1.因为DE平面DEF,所以DE∥平面ABC1.(Ⅱ)因为三棱柱ABC A1B1C1的侧面BCC1B1为菱形,故B1C⊥BC1.……9分又B1C⊥AB,且AB,BC1为平面ABC1内的两条相交直线,所以B1C⊥平面ABC1.而平面DEF∥平面ABC1,所以B1C⊥平面DEF,因为DE平面DEF,所以B1C⊥DE.【考点】1、线面平行;2、面面平行;3、线面垂直;4、三角形中位线.【方法点晴】本题主要考查的是线面平行、线线平行、线线垂直和线面垂直,属于中档题.解题时一定要注意得线线平行的常用证明方法,构造中位线和平行四边形是最常用方法.证明线面垂直的关键是证明线线垂直,证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线.10.已知,是两个不同的平面,,是两条不同的直线,则下列正确的是()A.若,,则B.若,,,则C.若,,,则D.若,,,则【答案】C.【解析】A:或者,异面,故A错误;B:根据面面垂直的判定可知B错误;C:正确;D:或,故D错误,故选C.【考点】空间中直线平面的位置关系.11.已知三条不重合的直线和两个不重合的平面,下列命题正确的是()A.若,,则B.若,,且,则C.若,,则D.若,,且,则【答案】D【解析】A.若,,则,错,有可能;B.若,,且,则,错,有可能;C.若,,则,错,有可能,或异面;D.若,,且,则,正确【考点】空间直线与平面,平面与平面的位置关系12.如图,三角形是边长为4的正三角形,底面,,点是的中点,点在上,且.(1)证明:平面平面;(2)求直线和平面所成角的正弦值.【答案】(1)证明见解析;(2).【解析】(1)由底面,可得,又,可证的平面,问题得证;(2)在第一问证明的基础上,应用面面垂直的性质定理容易作出平面的垂线,即得斜线的射影,找出角,解直角三角形可得线面角的正弦.试题解析:(1)证明∵底面,底面,∴,又,,∴平面.又平面,∴平面平面.(2)解:过点作,连结.平面平面,平面平面,平面,∴平面,∴为直线和平面所成角.∵是边长为的正三角形,∴,.又∵,∴,,∴.即直线和平面所成角的正弦值为.【考点】空间垂直关系的应用和证明,直线与平面所成的角.【方法点晴】证明面面垂直只能证明线面垂直,而要证明线面垂直就得证明线线垂直,结合题中已知的垂直条件,分析容易找到哪个平面的垂线,逐步完成证明,组织步骤时一定要思路条理;对于直线与平面所成的角遵循作—证(指)—求—答的解题步骤,应当结合条件和前面证明的结论找到平面的垂线是解题的关键,本题中在第一问证明的基础上有了平面的垂面,利用面面垂直的性质定理过直线上一点作交线的垂线即为平面的垂线,连接垂足和斜足即得射影,找到线面角后解直角三角形得解.13.一个几何体的三视图如图所示,则这个几何体的外接球表面积为()A.B.C.D.【答案】A【解析】几何体为一个三棱锥S-ABC,其中D为AC中点,且SD垂直平面ABC,BD垂直AC,则球心在SD上,设球半径为R,则外接球表面积为,选A.【考点】三视图【方法点睛】1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.14.已知正三角形的三个顶点都在半径为的球面上,球心到平面的距离为,点是线段的中点,过点作球的截面,则截面面积的最小值是_________.【答案】【解析】因为过作球的截面,当截面与垂直时,截面圆的半径最小,所以当截面与垂直时,截面圆的面积有最小值.设正三角形的外接圆圆心为,在中,,所以.在中,,所以,所以截面面积为【考点】1、多面体的外接球;2、球的截面圆性质.【方法点睛】“切”“接”问题的处理规律:①“切”的处理:解决与球的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决;②“接”的处理:把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.15.(2015•金家庄区校级模拟)如图正方形BCDE的边长为a,已知AB=BC,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:①AB与DE所成角的正切值是;②AB∥CE;③VB﹣ACE的体积是a2;④平面ABC⊥平面ADC;⑤直线EA与平面ADB所成角为30°.其中正确的有.(填写你认为正确的序号)【答案】①③④⑤【解析】①由于BC∥DE,则∠ABC(或其补角)为AB与DE所成角;②AB和CE是异面直线;③根据三棱锥的体积公式即可求VB ﹣ACE的体积;④根据面面垂直的判定定理即可证明;⑤根据直线和平面所成角的定义进行求解即可.解:由题意,AB=BC,AE=a,AD⊥平面BCDE,AD=a,AC= a①由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角∵AB=a,BC=a,AC=a,∴BC⊥AC,∴tan∠ABC=,故①正确;②由图象可知AB与CE是异面直线,故②错误.③VB﹣ACE的体积是S△BCE×AD=×a3=,故③正确;(4)∵AD⊥平面BCDE,BC⊂平面BCDE,∴AD⊥BC,∵BC⊥CD,AD∩CD=D,∴BC⊥平面ADC,∵BC⊂平面ABC,∴平面ABC⊥平面ADC,故④正确;⑤连接CE交BD于F,则EF⊥BD,∵平面ABD⊥平面BDE,∴EF⊥平面ABD,连接F,则∠EAF为直线AE与平面ABD所成角,在△AFE中,EF=,AE=a,∴sin∠EAF==,则∠EAF=30°,故⑤正确,故正确的是①③④⑤故答案为:①③④⑤【考点】命题的真假判断与应用;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.16.已知某几何体的三视图,则该几何体的体积是_______.【答案】.【解析】该几何体是一个四棱锥,底面是边长为2的正方形,高为,所以.【考点】1.空间几何体的表面积与体积;2.空间几何体的三视图与直观图.17.设三棱柱的侧棱垂直于底面,,且三棱柱的所有顶点都在同一球面上,则该球的表面积是.【答案】【解析】由题意可得:把三棱柱补成底面以2为边长的正方形,以为高的长方体,长方体的体对角线就是球的直径,所以,所以该球的表面积是;故填.【考点】空间几何体的表面积.18.某几何体的正视图与侧视图都是等腰梯形,则该几何体可以是下列几何体中的()①三棱台,②四棱台,③五棱台,④圆台.A.①②B.③④C.①③D.②④【答案】D【解析】由题意得,几何体的正视图和侧视图都是等腰梯形,则根据几何体的三视图的规则可知,该几何体可能为四棱台或圆台,故选D.【考点】空间几何体的三视图.【方法点晴】本题主要考查了空间几何体的三视图的应用,着重考查了推理和运算能力及空间想象能力,属于中档试题,解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则,还原出原几何体的形状,本题的解答中,只是给出了几何体的正视图和侧视图都是等腰梯形,从而可得这个几何体可能是四棱台或圆台.19.在直三棱柱中,,,且异面直线与所成的角等于,设.(1) 求的值;(2) 求三棱锥的体积.【答案】(1); (2)【解析】(1)由BC ∥B 1C 1可得∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角,从而∠A 1BC =60°,再由AA 1⊥平面ABC ,AB=AC ,则A 1B=A 1C ,△A 1BC 为等边三角形, 由已知可得,即可求得 (2)连接B 1C ,则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积,△的面积, 又可得平面,利用三棱锥的体积公式可求得.试题解析:(1)∵BC ∥B 1C 1,∴∠A 1BC 就是异面直线A 1B 与B 1C 1所成的角,即∠A 1BC =60°,又AA 1⊥平面ABC ,AB=AC ,则A 1B=A 1C ,∴△A 1BC 为等边三角形, 由,, ∴; (2)连接B 1C ,则三棱锥B 1–A 1BC 的体积等于三棱锥C –A 1B 1B 的体积, 即:, △的面积,又平面,所以,所以.【考点】异面直线所成的角及三棱锥的体积的求法.20. 如图,在四棱锥中,已知棱,,两两垂直,长度分别为1,2,2.若(),且向量与夹角的余弦值为.(1)求的值;(2)求直线与平面所成角的正弦值.【答案】(1);(2).【解析】(1)以为坐标原点,、、分别为、、轴建立空间直角坐标系,写出,的坐标,根据空间向量夹角余弦公式列出关于的方程可求;(2)设岀平面的法向量为,根据,进而得到,从而求出,向量的坐标可以求出,从而可根据向量夹角余弦的公式求出,从而得和平面所成角的正弦值.试题解析:(1)依题意,以为坐标原点,、、分别为、、轴建立空间直角坐标系 ,因为,所以,从而,则由,解得(舍去)或. (2)易得,,设平面的法向量, 则,,即,且,所以,不妨取,则平面的一个法向量,又易得,故,所以直线与平面所成角的正弦值为.考点: 1、空间两向量夹角余弦公式;2、利用向量求直线和平面说成角的正弦.21.如图,在四棱锥中,平面,分别是棱的中点.(1)求证:平面;(2)求证:平面平面.【答案】(1)详见解析(2)详见解析【解析】(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与证明,往往需结合平面几何条件,如本题利用三角形中位线性质定理得(2)证明面面垂直,一般利用面面垂直判定定理,即从线面垂直出发给予证明,而线面垂直的证明,需多次利用线面垂直的判定与性质定理:先由平行四边形为菱形得,再由平面得,即,从而得平面试题解析:(1)设,连结,因为,为的中点,所以,所以四边形为平行四边形,所以为的中点,所以又因为平面,平面,所以平面.(2)(方法一)因为平面,平面所以,由(1)同理可得,四边形为平行四边形,所以,所以因为,所以平行四边形为菱形,所以,因为平面,平面,所以平面因为平面,所以平面平面.(方法二)连结,因为平面,平面,所以因为,所以,因为平面,平面,所以因为为的中点,所以,由(1),所以又因为为的中点,所以因为,平面,平面所以平面,因为平面,所以平面平面.【考点】线面平行判定定理,面面垂直判定定理22.如图,网格纸上小正方形的边长为1,粗线画出的是某个几何体的三视图,则该几何体的体积为()A.B.C.D.【答案】A【解析】因为网格纸上小正方形的边长为,有三视图可知,该几何体是下面为底面半径为高为的圆柱体的一半、上面是底面半径为高为的圆锥体的一半,所以体积为,故选A.【考点】1、几何体的三视图;2、圆柱及圆锥的体积公式.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.23.已知如图所示的三棱锥的四个顶点均在球的球面上,和所在的平面互相垂直,,,,则球的体积为()A.B.C.D.【答案】C【解析】因为,,,所以的中点为的外心,连接,则,又和所在的平面互相垂直,所以平面,上的每一点到距离相等,因此正三角形的中心即是外接球球心,其半径也是外接球半径,所以球半径,求体积为,故选C.【考点】1、外接球的性质及勾股定理;2、面面垂直及球的体积公式.【方法点睛】本题主要考查外接球的性质及勾股定理、面面垂直及三棱锥外接球体积的求法,属于难题.要求外接球的表面积和体积,关键是求出求的半径,求外接球半径的常见方法有:①若三条棱两垂直则用(为三棱的长);②若面(),则(为外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径.本题是根据方法④直接找出球心并求出半径进而得到求体积的.24.四棱锥的底面是正方形,,分别是的中点(1)求证:;(2)设与交于点,求点到平面的距离【答案】(1)证明见解析;(2).【解析】(1)要证明线面垂直,一般先证明线线垂直,本题中,由于是中点,因此有,而与垂直,从而与平面垂直,结论得证;(2)要求点到平面的距离,考虑三棱锥,的面积易求(为面积的一半),另外由(1)的结论,此三棱锥以为底时,是高,体积易求,从而所求距离易得.试题解析:(1)证明:连接,由于分别是的中点,所以,又,平面,故,又为正方形,故故,故(2)连接交于点,连接,则交线为,又,故,由于分别是的中点,故为的中点,又,故为三棱锥的高又故,又设点到平面的距离为,,所以【考点】线面垂直的判断,点到平面的距离.25.某几何体的三视图如图,则该几何体的体积为()A.B.C.D.【答案】C【解析】由题意得,由几何体的三视图,知该几何体是上下底面为梯形的直棱柱,所以该几何体的体积为,故选C.【考点】几何体的三视图及几何体的体积.【方法点晴】本题主要考查了空间几何体的三视图的应用,着重考查了推理和运算能力及空间想象能力,属于中档试题,解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则,还原出原几何体的形状,本题的解答中,该几何体是上下底面为梯形的直棱柱是解答本题的关键,属于基础题.26.一个几何体的三视图如图,则这个几何体的表面积是()A.B.C.D.【答案】C【解析】由题意得,根据给定的几何体的三视图,可知,原几何体为正方体的一部分,如图所示的红线部分,是一个棱长为的正四面体,所以此几何体的表面积为,故选C.【考点】几何体的三视图与表面积.27.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.【答案】80,40【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体,,.【考点】三视图.【方法点睛】解决由三视图求空间几何体的表面积与体积问题,一般是先根据三视图确定该几何体的结构特征,再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积.28.如图,在四棱锥中,平面平面,,,,,,.(Ⅰ)求证:平面;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.【答案】(Ⅰ)见解析;(Ⅱ);(Ⅲ)存在,.【解析】(Ⅰ)由面面垂直的性质定理知AB⊥平面,根据线面垂直的性质定理可知,再由线面垂直的判定定理可知平面;(Ⅱ)取的中点,连结,以O为坐标原点建立空间直角坐标系O-xyz,利用向量法可求出直线PB与平面PCD所成角的正弦值;(Ⅲ)假设存在,根据A,P,M三点共线,设,根据BM∥平面PCD,即(为平面PCD的法向量),求出的值,从而求出的值.试题解析:(Ⅰ)因为平面平面,,所以平面.所以.又因为,所以平面.(Ⅱ)取的中点,连结.因为,所以.又因为平面,平面平面,所以平面.因为平面,所以.因为,所以.如图建立空间直角坐标系.由题意得,.设平面的法向量为,则即令,则.所以.又,所以.所以直线与平面所成角的正弦值为.(Ⅲ)设是棱上一点,则存在使得.因此点.因为平面,所以平面当且仅当,即,解得.所以在棱上存在点使得平面,此时.【考点】空间线面垂直的判定定理与性质定理;线面角的计算;空间想象能力,推理论证能力【名师】平面与平面垂直的性质定理的应用:当两个平面垂直时,常作的辅助线是在其中一个平面内作交线的垂线,把面面垂直转化为线面垂直,进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系),构造(寻找)二面角的平面角或得到点到面的距离等.29.如图,在四棱锥中,底面是菱形,,平面,,点分别为和中点.(1)求证:直线平面;(2)求三棱锥的表面积.【答案】(1)证明见解析;(2).【解析】(1)要证线面平行,一般先证线线平行,考虑到,是中点,因此取的中点,可证得且,从而得平行四边形,因此有,最终得线面平行;(2)要求三棱锥的表面积,必须求得它的各个面的面积,由平面,得,三角形和的面积可求,由题设又可证,这样就有,另两个面的面积又可求得.试题解析:(1)证明:作FM∥CD交PC于M.∵点F为PD中点,∴. ∴,∴AEMF为平行四边形,∴AF∥EM,∵,∴直线AF平面PEC.(2)连结可知,,由此;;;;因此三棱锥的表面积.【考点】线面平行的判断,多面体的表面积.30.在棱长为3的正方体中,在线段上,且,为线段上的动点,则三棱锥的体积为()A.1B.C.D.与点的位置有关【答案】B【解析】由于是定值,点到平面的距离是,因此点平面的距离是.所以三棱锥的体积,应选B.【考点】三棱锥体积的运算.31.如图,在多面体中,底面是边长为2的正方形,四边形是矩形,且平面平面,,和分别是和的中点.(1)求证:平面;(2)求.【答案】(1)证明见解析;(2).【解析】(1)运用线面平行的判定定理求证;(2)借助题设条件及转化化归的思想求解即可. 试题解析:(1)证明:设,连接,在中,因为,,所以,又因为平面,平面,所以平面.(2)因为四边形是正方形,所以,又因为平面平面,平面平面,且平面,所以平面,则到平面的距离为的一半,又因为,所以,所以.【考点】直线与平面的位置关系及棱锥公式的运用.32.如图,在三棱柱中,,,,在底面的射影为的中点,是的中点.(1)证明:平面;(2)求二面角的平面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)设为的中点,连接,依题意有,,故平面.根据分析有,故平面;(2)以的中点为原点,分别以射线为轴的正半轴,建立空间直角坐标系,利用向量法求得余弦值为.试题解析:(1)设为的中点,连接.由题意得:平面,所以.因为,所以,,故平面.由分别为的中点,得且,从而且,所以为平行四边形,故,又因为平面,所以平面.(2)方法一:作,且,连结.由,,得,由,,得与全等.由,得,因此为二面角的平面角.由,,,得,,由余弦定理得.方法二:以的中点为原点,分别以射线为轴的正半轴,建立空间直角坐标系,如图所示,由题意知各点坐标如下:,因此,,,设平面的法向量为,平面的法向量为,由,即,可取.由,即,可取,于是.由题意可知,所求二面角的平面角是钝角,故二面角的平面角的余弦值为.【考点】空间向量与立体几何.33.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,从左往右为半个圆锥,一个圆柱,一个半圆,故体积为.【考点】三视图.34.如图,在四棱柱中,底面,为线段上的任意一点(不包括两点),平面与平面交于.(1)证明:;(2)证明:平面.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)要证线线垂直,一般可证线面垂直,观察题中垂直条件,平面,则有,题中又有,从而有平面,因此结论得证;(2)要证线面平行,就是要证线线平行,直线是平面与平面的交线,因此要得平行,就要有线面平行,而这由可得平面,从而,结论得证.试题解析:(1)证明:因为平面,平面,所以.又,所以平面,而平面,所以.(2)在四棱柱中,,平面,平面,所以平面,又平面,平面与平面交于,所以,因为,所以,而平面,平面,所以平面.【考点】线面垂直的判定与性质,线面平行的判定与性质.【名师】证明线面(面面)平行(垂直)时要注意以下几点:(1)由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
高三立体几何习题(含答案)

1CBAC 1B 1A 1高三立体几何习题一、 填空题1.已知AB 是球O 的一条直径,点1O 是AB 上一点,若14OO =,平面α过点1O 且垂直AB ,截得圆1O ,当圆1O 的面积为9π时,则球O 的表面积是 .【答案】100p2.把一个大金属球表面涂漆,共需油漆2.4公斤.若把这个大金属球熔化制成64个大小都相同的小金属球, 不计损耗,将这些小金属球表面都涂漆,需要用漆 公斤.【答案】9.63.已知球的表面积为64π2cm ,用一个平面截球,使截面圆的半径为2cm ,则截面与球心的距离是 cm【答案】234.一个圆锥与一个球体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为 .【答案】4p 5.一个底面置于水平面上的圆锥,若主视图是边长为2的正三角形,则圆锥的侧面积为 .【答案】4p6.如图所示:在直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==,则平面11A B C 与平面ABC 所成的二面角的大小为 . 【答案】4π二、选择题1.如图,已知圆锥的底面半径为10r =,点Q 为半圆弧 AB 的中点, 点P 为母线SA 的中点.若PQ 与SO 所成角为4π,则此圆锥的 全面积与体积分别为( ) A .100051006,3ππ B .10005100(16),3ππ+ C .100031003,3ππ D .10003100(13),3ππ+【答案】B2.如图,取一个底面半径和高都为R 的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R 的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S 圆和S 圆环,那么( ) A .S 圆>S 圆环 B .S 圆<S 圆环 C .S 圆=S 圆环 D .不确定PSAQO B3.如图所示,PAB ∆所在平面α和四边形ABCD 所在的平面β互相垂直,且AD α⊥,BC α⊥,4AD =,8BC =,6AB =,若tan 2tan 1ADP BCP ∠-∠=,则动点P 在平面α内的轨迹是( ) A.线段 B.椭圆的一部分 C.抛物线 D.双曲线的一部分 【答案】D4.在空间中,下列命题正确的是( )A .若两直线,a b 与直线l 所成的角相等,那么//a bB .空间不同的三点A 、B 、C 确定一个平面C. 如果直线//l 平面α且//l 平面β,那么//αβ D .若直线a 与平面M 没有公共点,则直线//a 平面M【答案】D5.如图,已知直线l ⊥平面α,垂足为O ,在ABC △中,2,2,22BC AC AB ===,点P 是边AC 上的动点.该三角形在空间按以下条件作自由移动:(1)A l ∈,(2)C α∈.则OP PB +的最大值为( )(A) 2. (B) 22. (C) 15+. (D) 10.【答案】C6.平面α上存在不同的三点到平面β的距离相等且不为零,则平面α与平面β的位置关系为( ))(A 平行 )(B 相交 )(C 平行或重合 )(D 平行或相交【答案】D7.a b c 、、表示直线,α表示平面,下列命题正确的是( )A .若//,//αa b a ,则//αbB . 若,α⊥⊥a b b ,则α⊥aC .若,⊥⊥a c b c ,则//a bD .若,αα⊥⊥a b ,则//a b 【答案】D8.下列命题中,正确的个数是【 】① 直线上有两个点到平面的距离相等,则这条直线和这个平面平行; ② a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个; ③ 直四棱柱是直平行六面体;④ 两相邻侧面所成角相等的棱锥是正棱锥.A 、0B 、1C 、2D 、3 【答案】B9.在四棱锥ABCD V -中,1B ,1D 分别为侧棱VB ,VD 的中点,则四面体11CD AB 的体积与四棱锥 ABCD V -的体积之比为( ) A .6:1 B .5:1 C .4:1D .3:1【答案】CβαP B A DC A Bl C αNPO3三、解答题1.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)证明:11D E A D ⊥;(2)AE 等于何值时,二面角1D EC D --的大小为4π.【答案】解:(1)在如图所示的空间直角坐标系中,11(1,0,1),(0,0,0),(0,0,1)A D D 设(1,,0)([0,2])E y y ∈ 则11(1,,1),(1,0,1)D E y DA =-= …所以110D E DA ⋅=……所以11D E A D ⊥……(2)方法一:设(,,)n u v w =为平面1DCE 的一个法向量 由1100n CD n D E ⎧⋅=⎪⎨⋅=⎪⎩,得200v w u yv w -+=⎧⎨+-=⎩,所以(2)2u y v w v =-⎧⎨=⎩… 因为二面角1D EC D --的大小为4π,所以2222(0,0,1)(,,)22cos ||42(2)5u v w u v w y π⋅===++-+ 又[0,2]y ∈,所以23y =-,即当23AE =-时二面角1D EC D --的大小为4π2.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)当E 为AB 的中点时,求四面体1E ACD -的体积; (2)证明:11D E A D ⊥.【答案】解:(1)1122ACE S AE BC ∆=⋅=… 因为1D D ACE ⊥平面,所以1111136E ACD D ACE ACE V V S D D --∆==⋅=… (2)正方形11ADD A 中,11A D AD ⊥……因为11AB ADD A ⊥平面,所以1AB A D ⊥…所以11A D AD E ⊥平面…所以11D E A D ⊥……D 1C 1A 1A E DB 1B C Ox y zD 1C 1A 1AEDB 1B C3.三棱柱111C B A ABC -中,它的体积是315,底面ABC ∆中,090=∠BAC ,3,4==AC AB ,1B 在底面的射影是D ,且D 为BC 的中点.(1)求侧棱1BB 与底面ABC 所成角的大小;(7分)(2)求异面直线D B 1与1CA 所成角的大小.(6分)【答案】解:(1)依题意,⊥D B 1面ABC ,BD B 1∠就是侧棱1BB 与底面ABC 所成的角θ 2分111111431532ABC A B C ABC V S B D B D -∆=⋅=⨯⨯⨯=4分1532B D =5分计算25=BD ,θθtan 25tan 1==BD D B , tan 3,3πθθ=∴= 7分 (2)取11C B 的中点E ,连E A EC 1,,则1ECA ∠(或其补角)为所求的异面直线的角的大小 9分 ⊥D B 1面ABC ,D B 1‖CE ,面ABC ‖面111C B A ⊥∴CE 面111C B A ,E A CE 1⊥∴ 11分33325tan 251===∠EC AE CE A 12分 所求异面直线D B 1与1CA 所成的角6π13分4.在如图所示的几何体中,四边形CDPQ 为矩形,四边形ABCD 为直角梯形,且90BAD ADC ∠=∠= ,平面CDPQ ⊥平面ABCD ,112AB AD CD ===,2PD =.(1)若M 为PA 的中点,求证:AC //平面DMQ ;(2)求平面PAD 与平面PBC 所成的锐二面角的大小.【答案】解:(1)如图,设CP 与M 的交点为N ,连接MN .易知点N 是CP 的中点,又M 为PA 的中点,故//AC MN .…4分于是,由MN ∉平面DMQ ,得//AC 平面DMQ .……………6分 (2)如图,以点D 为原点,分别以DA DB DC 、、为x 轴,y 轴,z 轴,建立空间直角坐标系,则(0,0,0),(1,0,0),(1,1,0),(0,2,0),(0,0,2)D A B C P .易知1(0,1,0)n = 为平面PAD 的一个法向量,设2(,,)n x y z =为平面PBC 的一个法向量.则220220n BC x y n PC y z ⎧=-+=⎪⎨=-=⎪⎩2x y z y =⎧⎪⇒⎨=⎪⎩,令1y =,得2(1,1,2)n = .…………………10分 设平面PAD 与平面PBC 所成的锐二面角为θ,则12121cos 2n n n n θ== ,…………………12分1A ABCQP D M5(第20题图)D 1C 1B 1BCDA 1A故平面PAD 与平面PBC 所成的锐二面角的大小为3π.………………………………………14分5.(本题满分14分) 本题共2个小题,第1小题6分,第2小题8分. 在如图所示的直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为2的 菱形,且60,BAD ∠=︒1 4.AA =(1)求直四棱柱1111ABCD A B C D -的体积; (2)求异面直线11AD BA 与所成角的大小.【答案】解:(1)因菱形ABCD 的面积为2sin6023,AB ⋅︒= ……2分故直四棱柱1111ABCD A B C D -的体积为:12348 3.ABCD S AA ⋅=⨯=底面……6分(2)连接111BC AC 、,易知11//BC AD ,故11A BC ∠等于异面直线11AD BA 与所成角. ……8分由已知,可得111125,23,A B BC AC === ……10分则在11A BC ∆中,由余弦定理,得 222111111117cos .210A B BC AC A BC A B BC +-∠==⋅ ……12分 故异面直线11AD BA 与所成角的大小为7cos .10arc……14分6.(本题满分12分)本题共2小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过11,,A C B 三点的平面截去长方体的一个角后,得到如下所示的几何体111ABCD AC D -.(1)若11A C 的中点为1O ,求求异面直线1BO 与11A D 所成角的大小(用反三角函数值表示);(2)求点D 到平面11A BC 的距离d .【答案】解:(1)按如图所示建立空间直角坐标系.由题知,可得点D(0,0,0)、(2,2,0)B 、1(0,0,3)D 、1(2,0,3)A 、1(0,2,3)C . 由1O 是11AC 中点,可得1(1,1,3)O .于是,111(1,1,3),(2,0,0)BO A D =--=-. 设异面直线1BO 与11A D 所成的角为θ,则111111211cos 11||||211BO A D BO A D θ⋅===. 因此,异面直线1BO 与11A D 所成的角为11arccos11. (2)设(,,)n x y z = 是平面ABD 的法向量. ∴110,0.n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩又11(0,2,3),(2,0,3)BA BC =-=- ,∴230,230.y z x z -+=⎧⎨-+=⎩ 取2z =, A BC D1A 1C 1D可得3,3,2.x y z =⎧⎪=⎨⎪=⎩即平面11BAC 的一个法向量是(3,3,2)n = . ∴||n DB d n ⋅=62211=.7.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过1A 、1C 、B 三点的平面截去长方体的 一个角后,得到如下所示的几何体111ABCD AC D -.(1)求几何体111ABCD AC D -的体积,并画出该几何体的左视图(AB 平行主视图投影所在的平面); (2)求异面直线1BC 与11A D 所成角的大小(结果用反三角函数值表示).【答案】解: 2AB BC ==,13AA =,11111=2232231032ABCD A D C V V V -∴=-⨯⨯-⨯⨯⨯⨯=长方体三棱锥.左视图如右图所示. (2)依据题意,有11,A D AD AD BC ,即11A D BC . ∴1C BC ∠就是异面直线1BC 与11A D 所成的角. 又 1C C BC ⊥,∴113tan 2C C C BC BC ∠==.∴异面直线1BC 与11A D 所成的角是3tan 2arc . 8. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在直三棱柱111C B A ABC -中,已知21===AB BC AA ,AB ⊥BC . (1)求四棱锥111A BCC B -错误!未指定书签。
高中几何体试题及答案解析

高中几何体试题及答案解析试题一:立体几何基础题题目:已知一个长方体的长、宽、高分别为a、b、c,求该长方体的体积。
解析:长方体的体积可以通过其三个维度的乘积来计算,即体积V = a × b × c。
答案:V = abc。
试题二:空间向量在立体几何中的应用题目:在空间直角坐标系中,点A(1, 0, 0),点B(0, 1, 0),点C(0, 0, 1),求三角形ABC的面积。
解析:空间直角坐标系中,三角形的面积可以通过向量叉乘来求解。
设向量AB = (-1, 1, 0),向量AC = (-1, 0, 1),向量AB与向量AC 的叉乘结果为向量AB × AC = (1, -1, 1)。
该向量的模即为三角形ABC的面积的两倍。
答案:三角形ABC的面积为√3。
试题三:圆锥体的体积计算题目:已知圆锥的底面半径为r,高为h,求圆锥的体积。
解析:圆锥的体积可以通过公式V = (1/3)πr²h来计算。
答案:V = (1/3)πr²h。
试题四:球体的表面积与体积题目:已知球体的半径为R,求球体的表面积和体积。
解析:球体的表面积可以通过公式A = 4πR²来计算,球体的体积可以通过公式V = (4/3)πR³来计算。
答案:球体的表面积A = 4πR²,球体的体积V = (4/3)πR³。
试题五:旋转体的体积题目:已知圆柱的底面半径为r,高为h,求圆柱的体积。
解析:圆柱的体积可以通过公式V = πr²h来计算。
答案:V = πr²h。
结束语:通过上述试题及答案解析,我们可以看到高中几何体的计算涉及体积、面积和表面积等概念,这些计算在数学和物理等多个领域都有广泛的应用。
掌握这些基础知识对于解决更复杂的几何问题至关重要。
希望这些试题和解析能够帮助学生加深对立体几何概念的理解,并在解题过程中培养空间想象能力。
高三精选立体几何大题30题(含详细解答)
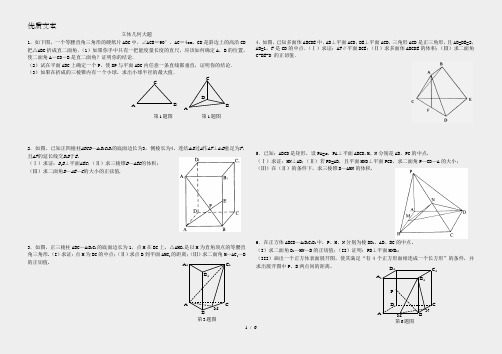
A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
高三数学立体几何试题答案及解析

高三数学立体几何试题答案及解析1..已知正四棱锥S—ABCD,底面上的四个顶点A、B、C、D在球心为O的半球底面圆周上,顶点S在半球面上,则半球O的体积和正四棱锥S—ABCD的体积之比为。
【答案】;【解析】略2.已知菱形中,,,沿对角线将折起,使二面角为,则点到所在平面的距离等于。
【答案】【解析】先设中点为,连接,然后解得,过点做的垂线,即为所求。
3.某三棱锥的三视图如下图所示,正视图、侧视图均为直角三角形,则该三棱锥的四个面中,面积最大的面的面积是.【答案】【解析】该三棱锥底面是边长为2的正三角形,面积为,有两个侧面是底边为2,高为2的直角三角形,面积为2,另一个侧面是底边为2,腰为的等腰三角形,面积为,所以面积最大的面的面积是.【考点】三视图.4.(本小题满分12分)如图,在四棱锥P –ABCD中,PA 平面ABCD,DAB为直角,AB//CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.(Ⅰ)证明:AB平面BEF:(Ⅱ)设PA =h,若二面角E-BD-C大于45 ,求h的取值范围.【答案】(Ⅰ)见解析;(Ⅱ)【解析】第一问注意将空间的垂直关系的转换掌握好即可,第二问注意应用空间向量解决二面角的问题的步骤,注意不等关系的建立.试题解析:(Ⅰ)证:由已知且为直角,故四边形是矩形,从而.又底面,∴平面平面,∵,故平面,∴,在内,分别是的中点,,∴;由此得平面.(Ⅱ)以为原点,以为轴,轴,轴正向建立空间直角坐标系,则设平面的法向量为,平面的法向量为,则,可取设二面角E-BD-C的大小为,则=,化简得,所以【考点】线面垂直的判定,二面角的问题,不等关系的建立.5.(本小题满分12分)如图,在棱长为1的正方体中,是侧棱上的一点,.(Ⅰ)试确定,使直线与平面所成角的正切值为;(Ⅱ)在线段上是否存在一个定点,使得对任意的,垂直于,并证明你的结论.【答案】(1);(2)为的中点时,满足题设的要求.【解析】本题主要考查线线平行、线面平行、线线垂直、线面垂直、线面角、空间向量法、向量的数量积等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑思维能力、计算能力.第一问,利用线面平行的性质得,利用线面垂直的判定得平面,得到为线面角,在中,列出的表达式,解出m的值;第二问,要在上找一点,使得.只需利用线面垂直的判定得,再利用线面垂直的性质得.试题解析:解法一:(1)如图:故.所以.又故在△,即.故当时,直线.(Ⅱ)依题意,要在上找一点,使得.只需设,可推测的中点即为所求的点.因为,所以即又,故.即解法二:(1)建立如图所示的空间直角坐标系,(1,则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(0,0,1).1,1), D1所以又由的一个法向量.设与所成的角为,则依题意有:,解得.故当时,直线.(2)若在上存在这样的点,设此点的横坐标为,则.……8分依题意,对任意的要使,只需对恒成立,即为的中点时,满足题设的要求【考点】线线平行、线面平行、线线垂直、线面垂直、线面角、空间向量法、向量的数量积.6.一个球的内接圆锥的最大体积与这个球的体积之比为.【答案】【解析】设球半径为R,其内接圆锥的底半径为r,高为h,作轴截面,则r2=h(2R﹣h).V=πr2h=h2(2R﹣h)=h•h(4R﹣2h)≤=•πR3.锥∵V=πR3 ∴球的内接圆锥的最大体积与这个球的体积之比为8:27.球【考点】球的体积和表面积.7.直三棱柱中,,分别是的中点,,为棱上的点.(1)证明:;(2)是否存在一点,使得平面与平面所成锐二面角的余弦值为?若存在,说明点的位置,若不存在,说明理由.【答案】(1)证明:∵,,又∵∴⊥面.又∵面,∴,以为原点建立如图所示的空间直角坐标系,则有,设且,即,则∵,所以;(2)结论:存在一点,使得平面与平面所成锐二面角的余弦值为.【解析】(1)首先根据已知条件可得出⊥面,由线面垂直的性质定理可得,然后以为原点建立如图所示的空间直角坐标系,并写出各点的坐标并设,于是由可得出点的坐标,进而由空间向量的数量积的坐标运算可得出,即可得出证明结果;(2)根据(1)中建立的空间直角坐标系中,分别求出平面与平面的法向量,然后运用即可求出所求的结果.试题解析:(1)证明:∵,,又∵∴⊥面.又∵面,∴,以为原点建立如图所示的空间直角坐标系,则有,设且,即,则,∵,所以;(2)结论:存在一点,使得平面与平面所成锐二面角的余弦值为,理由如下:由题可知面的法向量,设面的法向量为,则,∵,∴,即,令,则.∵平面与平面所成锐二面角的余弦值为,∴,即,解得或(舍),所以当为中点时满足要求.【考点】1、直线与直线垂直的判定定理;2、线面垂直的判定定理与性质定理;3、空间向量解立体几何问题的应用.【易错点睛】本题主要考查了直线与直线垂直的判定定理、线面垂直的判定定理与性质定理和空间向量解立体几何问题的应用,属中档题.解决这类空间立体几何问题最容易出现以下几处错误:其一是在运用空间向量求解立体几何问题如证明线线垂直或平行、线面垂直或平行和面面垂直等,不能结合已知条件建立适当地空间直角坐标系,进而导致错误;其二是在求解二面角问题时,不知道怎么判断这个二面角的大小,到底是锐角还是钝角,从而导致错误.8.已知是矩形,分别是线段的中点,平面.(1)求证:平面;(2)若在棱上存在一点,使得平面,求的值.【答案】(1)详见解析;(2)【解析】(1)通过证明,然后再利用线面垂直的判定定理,即可证明平面;(2)过作交于,则平面,且.再过作交于,所以平面,且,所以平面平面,进而满足题意.试题解析:(1)在矩形中,因为,点是的中点,所以.所以,即.又平面,所以,所以平面.(2)过作交于,则平面,且.再过作交于,所以平面,且.所以平面平面,所以平面,从而点满足.【考点】1.线面垂直的判定定理;2.面面平行的判定定理和性质定理.9.利用一个球体毛坯切削后得到一个四棱锥,其中底面四边形是边长为的正方形,,且平面,则球体毛坯体积的最小值应为.【答案】【解析】将四棱锥补成一个正方体,则球体毛坯体积的最小时应为正方体的外接球,此时直径为,体积为【考点】正方体外接球体积【名师】1. 某些空间几何体是某一个几何体的一部分,在解题时,把这个几何体通过“补形”补成完整的几何体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的几何问题,这是一种重要的解题策略——补形法.常见的补形法有对称补形、联系补形与还原补形.2.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.10.如图,在矩形中,,,在平面内将矩形绕点按顺时针方向旋转后得到矩形,则点到直线的距离是.【答案】.【解析】如下图所示,连结,,过作于,由题意得,,,∴,故点到直线距离为.【考点】三角恒等变形.11.(2015秋•盐城校级月考)如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点(1)求证:PE⊥BC;(2)求证:EF∥平面PAD.【答案】(1)见解析;(2)见解析.【解析】(1)证明PA⊥BC,AB⊥BC,证得CB⊥平面PAB,从而有CB⊥PE.(2)取CD的中点G,由FG是三角形CPD的中位线,可得 FG∥PD,再由举行的性质得EG∥AD,证明平面EFG∥平面PAD,从而证得EF∥平面PAD.解:(1)证明:∵侧棱PA垂直于底面,∴PA⊥BC.又底面ABCD是矩形,∴AB⊥BC,这样,CD垂直于平面PAD内的两条相交直线,∴CB⊥平面PAB,∴CB⊥PE.(2)取CD的中点G,∵E、F分别是AB、PC的中点,∴FG是三角形CPD的中位线,∴FG∥PD,FG∥面PAD.∵底面ABCD是矩形,∴EG∥AD,EG∥平面PAD.故平面EFG∥平面PAD,∴EF∥平面PAD.【考点】直线与平面平行的判定.12.如图,在直三棱柱中,底面是正三角形,点是中点,,.(Ⅰ)求三棱锥的体积;(Ⅱ)证明:.【答案】(Ⅰ);(Ⅱ)详见解析【解析】(Ⅰ)求三棱锥体积,关键在于确定高,因为面为侧面,因此可利用等体积法转移体积:,这样只需确定面上的高,由直三棱柱知侧面与底面垂直,因此过作,再由面面垂直性质定理得面,最后根据三棱锥体积公式求体积(Ⅱ)证明线线垂直,一般利用线面垂直性质与判定定理,经多次转化进行论证:取的中点E,则,再由面面垂直性质定理得面,进而;另一方面,在矩形中,由平几的相似知识可推得,因此面,试题解析:证明:(Ⅰ)过作,直三棱柱中面,面,是高=,,(Ⅱ)取的中点E,连接底面是正三角形,矩形中,中,,中,,∽,,面,【考点】三棱锥体积,线面垂直性质与判定定理13.如图,三角形是边长为4的正三角形,底面,,点是的中点,点在上,且.(1)证明:平面平面;(2)求三棱锥的体积.【答案】(1)证明见解析;(2).【解析】(1)由底面,可得,又,可证的平面,问题得证;(2)由第一问可发现存在平面的垂线,故可把三棱锥变换顶点为,用棱锥的体积公式易求其体积.试题解析:(1)证明∵底面,底面,∴,又,,∴平面,又平面,∴平面平面.(2)解:在中,则,则.【考点】空间垂直关系的应用和证明,直线与平面所成的角.【方法点晴】证明面面垂直只能证明线面垂直,而要证明线面垂直就得证明线线垂直,结合题中已知的垂直条件,分析容易找到哪个平面的垂线,逐步完成证明,组织步骤时一定要思路条理;求棱锥的体积时关键是选择恰当的顶点和底面,原则是容易找到或作出底面的垂线即棱锥的高,这样可以达到事半功倍的效果.14.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的个数是()(1) AC⊥BE;(2)若P为AA1上的一点,则P到平面BEF的距离为;(3)三棱锥A-BEF的体积为定值;(4)在空间与三条直线DD1,AB,B1C1都相交的直线有无数条.A.0B.1C.2D.3【答案】A【解析】(1)连接,,可证明平面,所以正确;(2)平面,点到平面的距离就是直线到平面的距离,正确;(3),是定值;正确(4)在上任取点,过点和直线确定平面,平面,,那么就是与三条直线都有交点的直线,因为点有无数个,所以直线也有无数条,所以正确.所以错误的有0个,故选A.【考点】1.直线与平面平行;2.线线垂直;3.棱柱的性质.15.一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为的直角三角形,俯视图是半径为的四分之一圆周和两条半径,则这个几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知几何体为圆锥的,圆锥的底面半径为1,母线长为2,∴圆锥的高为.∴.故选A.【考点】由三视图求面积、体积.16.设是两条不同的直线,是两个不同的平面,则下列命题正确的是()A.若且则B.若且则C.若D.若且则【答案】B【解析】对于A中,若且则与可能是平行的,所以不正确;对于C中,则可能,所以不正确;对于D中,若且则与可能是相交的,所以不正确,故选B.【考点】直线与平面位置关系的判定.17.如图,四棱锥P﹣ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E 为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.(Ⅰ)求证:PC⊥平面AEF;(Ⅱ)求三棱锥P﹣AEF的体积.【答案】(Ⅰ)见解析;(Ⅱ)三棱锥P﹣AEF的体积V=.【解析】(1)连结BD,交AC于O,连结OE,由PD∥平面ACE可知OE∥PD,故E为PB 中点,从而AE⊥PB,由BC⊥平面PAB可知BC⊥AE,推出AE⊥平面PBC,得到AE⊥PC,结合PC⊥EF,推出PC⊥平面AEF;(2)由勾股定理求出AE,PB,PC,根据Rt△PEF≌Rt△PCB,列出比例式求出EF,PF,代入体积公式计算.(1)证明:连结BD,交AC于O,连结OE,∵底面四边形ABCD是正方形,∴O是BD中点.∵PD∥平面ACE,PD⊂平面PBD,平面PBD∩平面ACE=OE,∴PD∥OE,∴,∴E是PB的中点.∵PA=AB,∴AE⊥PB.∵PA⊥平面ABCD,BC⊂平面ABCD,∴PA⊥BC,又AB⊥BC,PA⊂平面PAB,AB⊂平面PAB,PA∩AB=A,∴BC⊥平面PAB,∵AE⊂平面PAB,∴AE⊥BC,又PB⊂平面PBC,BC⊂平面PBC,PB∩BC=B,∴AE⊥平面PBC,∵PC⊂平面PBC,∴AE⊥PC,又EF⊥PC,AE⊂平面AEF,EF⊂平面AEF,AE∩EF=E,∴PC⊥平面AEF.(2)∵PA=AB=1,底面ABCD是正方形,∴PB=,AC=,PC=,∴PE=,AE=.∵Rt△PEF≌Rt△PCB,∴,∴PF=,EF=.∴S==.△AEF∴三棱锥P﹣AEF的体积V==.【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定.18.已知某几何体的三视图如图所示,则该几何体的体积等于()A.B.160C.D.60【答案】A【解析】试题分析:几何体如图所示,体积可看一个三棱住减一个三棱锥:.故选A.【考点】几何体的体积.19.在如图所示的多面体中,面是边长为的菱形,,,面,,且.(I)证明:平面;(II)求直线与平面所成角的正弦值.【答案】(I)见试题解析;(II)【解析】(Ⅰ)先确定四边形为平行四边形. 连接交于,连接,交于,连接,证明为平行四边形,可得,故平面;(Ⅱ)可先证明,与平面所成的角就是.再解三角形得与平面所成角的正弦为.此外也可建立坐标系,利用空间向量求解.试题解析:(Ⅰ)证明:与共面.由平面平面四边形为平行四边形连接交于,连接,交于,连接,如图所示.则,且,故为平行四边形,所以.又平面,平面,所以平面,即平面.(Ⅱ)解法一、由(Ⅰ)知,所以.因为平面平面,平面,所以点在平面内的射影落在上,故与平面所成的角就是.在中,,所以与平面所成角的正弦为.解法二、由(Ⅰ)易知,以为坐标原点,分别以直线、为、轴,建立空间直角坐标系,如图所示.则有、,,,,所以,,.设面的法向量为,由, ,得令,则所以,于是故直线与平面所成角的正弦值为【考点】线面平行;线面角的求法;空间向量的应用.20.在三棱柱中,,侧棱平面,且,分别是棱,的中点,点在棱上,且.(1)求证:平面;(2)求二面角的余弦值.【答案】(1)详见解析;(2).【解析】(1)设为的中点,连结,根据条件首先证明四边形为平行四边形,即可得到,再根据线面平行的判定即可得证;(2)根据图形特点,建立空间直角坐标系,求得两个平面的法向量后即可求解.试题解析:(1)设为的中点,连结,∵,为的中点,∴为的中点,又∵为的中点,∴,又∵为的中点,为的中点,∴,又∵,∴四边形为平行四边形,∴,又∵,∴,又∵平面,平面,∴平面;(2)建立如图所示的坐标系,∵,,分别为,的中点,,,,,,,设平面的法向量为,,,,,,不妨令,则,,∴,同理可得平面的一个法向量为,,∴二面角的余弦值为.【考点】1.线面平行的判定;2.空间向量求空间角.21.如图是一个多面体的三视图,则其全面积为()A.B.C.D.【答案】C【解析】由三视图可知几何体是一个正三棱柱,底面是一个边长是的等边三角形,侧棱长是,根据矩形和三角形的面积公式写出面积再求和.解:由三视图可知几何体是一个正三棱柱,底面是一个边长是的等边三角形,侧棱长是,∴三棱柱的面积是3××2=6+,故选C.【考点】由三视图求面积、体积.22.一个几何体的三视图如图所示,则该几何体的外接球的表面积为()A.B.C.D.【答案】B【解析】根据三视图可知该几何体为底面为等腰直角三角形,一条长为的侧棱垂直于底面的三棱锥,如下图,可把该几何体还原为直三棱柱(或长方体),从而得到几何体的外接球的半径,所以该几何体的外接球的表面积为,故选B.【考点】三视图与几何体的表面积.【方法点睛】本题主要考查了几何体的三视图与几何体的表面积,考查考生的空间想象能力,属于基础题.解答本题的关键根据给出的三视图还原出几何体,再由三视图的特征得到几何体的结构特征,同时本题考查了几何体外接球的表面积,需要把几何体补形为三棱柱或长方体,从而得到外接球的直径于几何体棱长之间的关系.23.如图,四棱柱的底面是菱形,底面,.(1)证明:平面;(2)若,求点到平面的距离.【答案】(1)证明见解析;(2).【解析】(1)欲证明平面,利用线面垂直的判定,先证和即可;(2)通过等积法求点到平面的距离.试题解析:(1)证明:因为平面,平面,是菱形,,平面,平面.(2)因为底面是菱形,,的面积为,平面,平面,,平面,到面的距离等于到面的距离,由(1)得平面.平面,,的面积为,设到面的距离为,.所以点到平面的距离为.【考点】1、直线与平面垂直的判定;2、锥体的体积;3、点到平面的距离.【方法点睛】证明线面垂直的关键是证明线线垂直,再根据线面垂直的判定定理,即证得线面垂直;证明线线垂直常用的方法是等腰三角形底边上的高线,菱形对角线互相垂直,勾股定理,线面垂直的定义.本题主要考查的是线面垂直的判定和求点到平面的距离,将求点到平面的距离转化为求锥体的的高,关键是利用等体积法求椎体的体积,进而求出点到平面的距离,属于中档题.24.已知矩形 A BCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为.【答案】【解析】设正六棱柱的底面边长为,高为,则,正六棱柱的体积,当且仅当时,等号成立,此时,可知正六棱柱的外接球的球心在是其上下点中心的连线的中点,则半径为,所以外接球的表面积为.【考点】六棱柱的性质;外接球的表面积.【方法点晴】本题主要考查了六棱柱的结构特征、棱柱外接球的的表面积的计算、基本不等式求最值等知识点的应用,其中解答中,利用正六棱柱的结构特征,外接球的球心在是其上下点中心的连线的中点,得出外接球的半径是解答本题的关键,着重考查了学生分析问题和解答问题的能力,属于基础题.25.直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,则下列说法正确的是()A.c至少与a、b中的一条相交B.c至多与a、b中的一条相交C.c与a、b都相交D.c与a、b都不相交【答案】A【解析】利用空间中线线、线面、面面间的位置关系判断求解.解:由直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,知:对于B,c可以与a、b都相交,交点为不同点即可,故B不正确;对于C,a∥c,b∩c=A,满足题意,故C不正确;对于D,c与a、b都不相交,则c与a、b都平行,所以a,b平行,与异面矛盾,故D不正确;对于A,由B,C、D的分析,可知A正确故选:A.26.如图所示的几何体中,是正三角形, 且平面, 平面,是的中点.(1)求证:;(2)若,求与平面所成角的正切值;(3)在(2)的条件下, 求点到平面的距离.【答案】(1)证明见解析;(2);(3).【解析】(1)依据题设条件运用线面垂直的性质定理推证;(2)借助题设条件运用线面角的定义找到这个角,再在三角形中求解;(3)运用体积相等建立方程求解.试题解析:(1)证明:是正在三角形,是的中点,平面,平面,平面平面.(2)连接,在直角梯形中,.在中,平面平面,故是直线与平面所成的角,在中,.(3)在四棱锥中, 底面的面积为,高.而四棱锥的底面的三条边,等腰的面积为.点到平面的距离为.【考点】空间线面的位置关系的判定和角度距离的计算.27.如图,四棱锥中,底面为平行四边形,,,,底面.(1)证明:;(2)若,求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)由余弦定理得,由勾股定理得,由线线面垂直得,从而平面,由此能证明;(2)以为原点,为轴,为轴,为轴,建立空间直角坐标系,分别求出平面的法向量和平面的法向量,由此能求出二面角的余弦值.试题解析:(1)证明:因为,,由余弦定理得.从而,故. ∵面,面,∴又, 所以平面.故.(2)如图,以为坐标原点,射线分别为的正半轴建立空间直角坐标系,则,,,,设平面的法向量为,则即因此可取.设平面PBC的法向量为,则可取则故钝二面角的余弦值为.【考点】(1)直线与平面垂直的性质;(2)二面角的平面角及其求法;(3)用空间向量求平面间的夹角.【方法点晴】本题考查异面垂直的证明,考查二面角的余弦值的求法,解题时要注意余弦定理、勾股定理、向量法的合理运用,注意空间思维能力的培养.在证明垂直的过程中,要注意线线垂直和线面垂直的相互转化,利用向量法求空间中二面角的大小,先求出面的法向量,把二面角转化为两个面所在法向量的夹角,应先判断角是钝角还是锐角,根据向量夹角公式得解.28.如图所示,已知直三棱柱中,分别是的中点,点P在线段上运动.(1)证明:无论点P在线段上的任何位置,总有AM⊥平面PNQ;(2)若AC=1,求三棱锥P-MNQ的体积.【答案】(1)证明见解析;(2).【解析】(1)建立空间直角坐标系,设出棱长,得到点的坐标,由向量数量积证得答案;(2)把三棱锥的体积转化为的体积,即的体积,则三棱锥的体积可求.试题解析:(1)证明:建立如图所示的空间直角坐标系,设,则,,,,,,再设,由,得,即,即,∴,∵,,,∴,则平面;(2)解:由(1)可知,在线段上移动时三棱锥的体积一定,由,得,到的距离为,∴,,则.【考点】(1)几何体的体积;(2)空间向量在立体几何中的应用.【一题多解】(1)连接.因为,分别是的中点,所以.所以.所以,即.①因为分别是,的中点,所以.又,所以.在直三棱柱中,平面,所以.又,所以平面,所以.②由①②及,得平面.(2)设点到平面的距离为,由可得平面.由得,易得,所以.29.如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为()A.B.C.D.【答案】C【解析】从三视图可以看出这是一个正方体上的一个四面体,如图,其中正的边长为,其外接圆的半径,同样正的外接圆的半径是,由球的对称性可知球心必在正方体的对角线上,且,该球经过六个点,设球心到平面的距离为;球心到平面的距离为,而两个平面和之间的距离为,则由球心距、垂面圆半径之间的关系可得,所以,即,又,将其代入可得,由此可得,所以,所以外接球的半径,应选C.【考点】三视图的识读和理解及几何体体积的计算.【易错点晴】本题以网格纸上的几何图形为背景,提供了一个三棱锥的几何体的三视图,要求求其外接球的半径,是一道较为困难的难题.难就难在无法搞清其几何形状,只知道是一个三棱锥(四面体)是没有任何用的.通过仔细观察不难看出这是一个正方体上的一个四面体,如图,正的边长为,其外接圆的半径,同样正的外接圆的半径是,由球的对称性可知球心必在对角线上,且经过六个点,设球心到平面的距离为;球心到平面的距离为,而两个平面和之间的距离为,则由球心距垂面圆半径之间的关系可得,所以,即,又,将其代入可得,由此可得,所以,所以外接球的半径,其中计算时可用等积法进行.30.一个几何体的三视图如图所示,则该几何体的外接球的表面积为()A.B.C.D.【答案】A【解析】几何体为一个斜放的三棱柱,底面为一个等腰直角三角形,底长为2,底上高为1;三棱柱高为3,因此外接球半径为,外接球的表面积为,选A.【考点】三视图,外接球【方法点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.31.若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和侧视图如图所示,则此几何体的表面积是A.24πB.24π+8πC.24π+4πD.32π【答案】C【解析】几何体的表面积是圆柱的侧面积与半个球的表面积、圆锥的侧面积的和.圆柱的侧面积为S1=2π×2×4=16π,半球的表面积为S2=2π×22=8π,圆锥的侧面积为S3=×2π×2×2=4π,所以几何体的表面积为S=S1+S2+S3=24π+4π.【考点】三视图,表面积.32.某几何体的三视图如图所示,则此几何体的体积是()A.B.C.D.【答案】B【解析】由三视图所提供的信息可知该几何体是一个圆台和圆柱的组合体,故其体积,应选B。
高中立体几何试题(答案)

高中立体几何试题1. 在正方体1111D C B A ABCD -中,求二面角111C BD A --的大小.解析:如图9-43,在平面B C D 11内作11BD E C ⊥,交1BD 于E .连结E A 1,设正方体棱长为a ,在△11BD A 和△11BD C 中,a D C D A ==1111,a B C B A 211==,11BD BD =a 3=,∴ △11BD A ≌△11BD C ,∵ 11BD E C ⊥,∴ 11BD E A ⊥,∴ 11EC A ∠ 二面角111C BD A --的平面角.在Rt △11D BC中,︒=∠9011B C D ,∴ 111112121BD E C BC D C ⋅=⋅,∴ a aa a E C 32321=⋅=,在△11EC A 中,==E C E A 11 a 32,a C A 211=,2132322)2(3232cos 22211-=⋅-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∠a a a a a EC A ,110 EC A ∠︒< ︒180<,︒=∠∴120 11EC A2. 如图9-50,点A 在锐二面角-MN -的棱MN 上,在面内引射线AP ,使AP 与MN 所成的∠P AM 为45°,与面所成的角为30°,求二面角-MN -的大小.解析:如图答9-44,取AP 上一点B ,作BH ⊥于H ,连结AH ,则∠BAH 为射线AP 与平面所成的角,∴ ∠BAH =30°,再作BQ ⊥MN ,交MN 于Q ,连结HQ ,则HQ 为BQ 在平面内的射影.由三垂线定理的逆定理,HQ ⊥MN ,∴ ∠BQH 为二面角-MN -的平面角.图答9-44设BQ =a ,在Rt △BAQ 中,∠BQA =90°,∠BAM =45°,∴ a AB 2=,在Rt △BAH 中∠BHA =90°,∠BAH =30°,∴ a BH 22=.在Rt △BHQ 中,∠BHQ =90°,BQ =a ,a BH 22=,∵ ∠BQH 是锐角,∴ ∠BQH =45 即二面角-MN -等于45°. 3. 如图,四棱锥P —ABCD 的底面是直角梯形,AB ∥DC ,AB ⊥BC ,且AB =21CD ,侧棱PB ⊥底面ABCD ,PC =5,BC =3,ΔPAB 的面积等于6,若平面DPA 与平面CPB 所成的二面角为α,求α.解析:平面DPA 与平面CPB 有一公共点P ,要画出它们构成的二面角的平面角必须确定它们公共交线,DA 和CB 的延长线的交点E 是它们的另一公共点.由公理二,PE 就是二面角的公共棱.有了公共棱,二面角的平面角就生了根.解 延长DA 交CB 的延长线于E ,连PE ,则PE 就是平面DPA 和平面CPB 的交线. ∵AB ∥DC ,AB ⊥BC ,∴DC ⊥BC ,PB ⊥底面ABCD.∴PB ⊥DC ,∴DC ⊥平面PCE.作CF ⊥PE 于F ,连DF 由三垂线定理得PE ⊥DF ,∴∠DFC =α.∵AB =21CD ,PC =5,BC =3,∴PB =4. S ΔPAB =6,∴AB =3,CD =6,DC AB =EC EB =21. ∴EB =3,PE =5.∵PB·EC =CF·PE ,∴CF =524.在直角ΔDCF 中,tanα=CFDC =5246=45. α=antan 45. 4. 在正方体ABCD —A 1B 1C 1D 1中,其棱长为a.(1)求证BD 1⊥截面AB 1C ;(2)求点B 到截面AB 1C 的距离;(3)求BB 1与截面AB 1C 所成的角的余弦值。
2024届新高考数学大题精选30题--立体几何含答案
大题立体几何1(2024·黑龙江·二模)如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,M是BC的中点,N是AB1的中点,P是B1C1的中点.(1)证明:MN⎳平面A1CP;(2)求点P到直线MN 的距离.2(2024·安徽合肥·二模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,M是侧棱PC的中点,侧面PAD为正三角形,侧面PAD⊥底面ABCD.(1)求三棱锥M-ABC的体积;(2)求AM与平面PBC所成角的正弦值.2024届新高考数学大题精选30题--立体几何3(2023·福建福州·模拟预测)如图,在三棱柱ABC-A1B1C1中,平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2,A1B=6.(1)设D为AC中点,证明:AC⊥平面A1DB;(2)求平面A1AB1与平面ACC1A1夹角的余弦值.4(2024·山西晋中·三模)如图,在六面体ABCDE中,BC=BD=6,EC⊥ED,且EC=ED= 2,AB平行于平面CDE,AE平行于平面BCD,AE⊥CD.(1)证明:平面ABE⊥平面CDE;(2)若点A到直线CD的距离为22,F为棱AE的中点,求平面BDF与平面BCD夹角的余弦值.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中,A1在平面ABC内的射影O在棱AC的中点处,P为棱A1B1(包含端点)上的动点.(1)求点P到平面ABC1的距离;(2)若AP⊥平面α,求直线BC1与平面α所成角的正弦值的取值范围.6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中,已知AB∥CD,∠BAD=90°,CD= 2AB,△PAB是正三角形,点M在侧棱PB上且使得PD⎳平面AMC.(1)证明:PM=2BM;(2)若侧面PAB⊥底面ABCD,CM与底面ABCD所成角的正切值为311,求二面角P-AC-B的余弦值.7(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.(1)求点H到平面ABCD的距离;(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.8(2024·重庆·模拟预测)如图,ACDE为菱形,AC=BC=2,∠ACB=120°,平面ACDE⊥平面ABC,点F在AB上,且AF=2FB,M,N分别在直线CD,AB上.(1)求证:CF⊥平面ACDE;(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若∠EAC=60°,MN为直线CD,AB的公垂线,求ANAF的值;(3)记直线BE与平面ABC所成角为α,若tanα>217,求平面BCD与平面CFD所成角余弦值的范围.9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°,使得CD 到EF 的位置,得到如图所示的几何体.(1)求证:平面ACF ⊥平面BDE ;(2)点M 为DF 上一点,若二面角C -AM -E 的余弦值为13,求∠MAD .10(2024·安徽黄山·二模)如图,已知AB 为圆台下底面圆O 1的直径,C 是圆O 1上异于A ,B 的点,D 是圆台上底面圆O 2上的点,且平面DAC ⊥平面ABC ,DA =DC =AC =2,BC =4,E 是CD 的中点,BF =2FD .(1)证明:DO 2⎳BC ;(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22,A 1B 1=12AB ,M 为BC 中点,已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ,其中λ∈0,1 .(1)求证D 1P ⊥AC ;(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37,当λ=23时,求直线DP 与平面AMC 1所成角的正弦值.12(2024·辽宁·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2,AB =1,BC =3,点E 为线段AC 的中点.(1)求证:AB 1∥平面BEC 1;(2)若∠A 1AC =π3,求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,△DCP是等边三角形,∠DCB=∠PCB=π4,点M,N分别为DP和AB的中点.(1)求证:MN⎳平面PBC;(2)求证:平面PBC⊥平面ABCD;(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD 为直角梯形,△PAD为等边三角形,AD⎳BC,AD⊥AB,AD=AB=2BC=2.(1)求证:AD⊥PC;(2)点N在棱PC上运动,求△ADN面积的最小值;(3)点M为PB的中点,在棱PC上找一点Q,使得AM⎳平面BDQ,求PQQC的值.15(2024·广东广州·模拟预测)如图所示,圆台O1O2的轴截面A1ACC1为等腰梯形,AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点,且AB=BC,P是线段BC的中点.(1)求证:C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图,三棱柱ABC-A1B1C1中,侧面BB1C1C⊥底面ABC,且AB= AC,A1B=A1C.(1)证明:AA1⊥平面ABC;(2)若AA1=BC=2,∠BAC=90°,求平面A1BC与平面A1BC1夹角的余弦值.17(2024·河北保定·二模)如图,在四棱锥P -ABCD 中,平面PCD 内存在一条直线EF 与AB 平行,PA ⊥平面ABCD ,直线PC 与平面ABCD 所成的角的正切值为32,PA =BC =23,CD =2AB =4.(1)证明:四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ,求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图,在圆锥PO 中,P 是圆锥的顶点,O 是圆锥底面圆的圆心,AC 是圆锥底面圆的直径,等边三角形ABD 是圆锥底面圆O 的内接三角形,E 是圆锥母线PC 的中点,PO =6,AC =4.(1)求证:平面BED ⊥平面ABD ;(2)设点M 在线段PO 上,且OM =2,求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形,∠DAB =60°,PA =PC ,PB =PD =210,M 是线段PC 上的点,且PC =4MC .(1)证明:PC ⊥平面BDM ;(2)点E 在直线DM 上,求BE 与平面ABCD 所成角的最大值.20(2024·湖南·二模)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形,∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积;(2)设点D 1关于平面A 1C 1D 的对称点为E ,点E 和点C 1关于平面α对称(E 和α未在图中标出),求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图,在四棱锥P-ABCD中,四边形ABCD为直角梯形,AB∥CD,∠DAB=∠PCB=60°,CD=1,AB=3,PC=23,平面PCB⊥平面ABCD,F为线段BC的中点,E为线段PF上一点.(1)证明:PF⊥AD;(2)当EF为何值时,直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1,在平行四边形ABCD中,AB=2BC=4,∠ABC=60°,E为CD 的中点,将△ADE沿AE折起,连结BD,CD,且BD=4,如图2.(1)求证:图2中的平面ADE⊥平面ABCE;(2)在图2中,若点F在棱BD上,直线AF与平面ABCE所成的角的正弦值为3010,求点F到平面DEC 的距离.23(2024·福建·模拟预测)如图,在三棱锥P-ABC中,PA⊥PB,AB⊥BC,AB=3,BC=6,已知二面角P-AB-C的大小为θ,∠PAB=θ.(1)求点P到平面ABC的距离;(2)当三棱锥P-ABC的体积取得最大值时,求:(Ⅰ)二面角P-AB-C的余弦值;(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图,在多面体ABCDPQ中,底面ABCD是平行四边形,∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点,PQ∥BC,PD⊥DC,QB⊥MD.(1)证明:∠ABQ=90°;(2)若多面体ABCDPQ的体积为152,求平面PCD与平面QAB夹角的余弦值.25(2024·浙江嘉兴·二模)在如图所示的几何体中,四边形ABCD为平行四边形,PA⊥平面ABCD,PA∥QD,BC=2AB=2PA=2,∠ABC=60°.(1)证明:平面PCD⊥平面PAC;(2)若PQ=22,求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图,在三棱锥P-ABC中,AB=4,AC=2,∠CAB=60°,BC⊥AP.(1)证明:平面ACP⊥平面ABC;(2)若PA=2,PB=4,求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图,在正三棱锥A -BCD 中,BC =CD =BD =4,点P 满足AP=λAC ,λ∈(0,1),过点P 作平面α分别与棱AB ,BD ,CD 交于Q ,S ,T 三点,且AD ⎳α,BC ⎳α.(1)证明:∀λ∈(0,1),四边形PQST 总是矩形;(2)若AC =4,求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1.在菱形ABCD 中,∠ABC =120°,AB =4,AE =λAD ,AF =λAB(0<λ<1),沿EF 将△AEF 向上折起得到棱锥P -BCDEP .如图2所示,设二面角P -EF -B 的平面角为θ.(1)当λ为何值时,三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时,∀λ∈0,1 ,平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ,n ,其中m ,n 与α的交点分别为A ,B ,AB =1,设直线m 与n 之间的夹角为π3,(1)如图1,若直线m ,n 交于点C ,求点C 到平面α距离的最大值;(2)如图2,若直线m ,n 互为异面直线,直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α,PQ ⊥n 且PQ ⊥m ,(i )求直线m ,n 与平面α的夹角之和;(ii )设PQ =d 0<d <1 ,求点P 到平面α距离的最大值关于d 的函数f d .30(2024·浙江绍兴·模拟预测)如图所示,四棱台ABCD -A 1B 1C 1D 1,底面ABCD 为一个菱形,且∠BAD =120°. 底面与顶面的对角线交点分别为O ,O 1. AB =2A 1B 1=2,BB 1=DD 1=392,AA 1与底面夹角余弦值为3737.(1)证明:OO 1⊥平面ABCD ;(2)现将顶面绕OO 1旋转θ角,旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343,此时求θ的值(θ<90°);(3)求旋转后AA 1与BB 1的夹角余弦值.大题 立体几何1(2024·黑龙江·二模)如图,已知正三棱柱ABC -A 1B 1C 1的侧棱长和底面边长均为2,M 是BC 的中点,N 是AB 1的中点,P 是B 1C 1的中点.(1)证明:MN ⎳平面A 1CP ;(2)求点P 到直线MN 的距离.【答案】(1)证明见解析(2)3【分析】(1)建立如图空间直角坐标系A -xyz ,设平面A 1CP 的一个法向量为n=(x ,y ,z ),利用空间向量法证明MN ⋅n=0即可;(2)利用空间向量法即可求解点线距.【详解】(1)由题意知,AA 1⊥平面ABC ,∠BAC =60°,而AB ⊂平面ABC ,所以AA 1⊥AB ,在平面ABC 内过点A 作y 轴,使得AB ⊥y 轴,建立如图空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (1,3,0),A 1(0,0,2),B 1(2,0,2),得M 32,32,0,N (1,0,1),P 32,32,2,所以A 1C =(1,3,-2),A 1P =32,32,0 ,MN =-12,-32,1 ,设平面A1CP 的一个法向量为n=(x ,y ,z ),则n ⋅A 1C=x +3y -2z =0n ⋅A 1P =32x +32y =0,令x =1,得y =-3,z =-1,所以n=(1,-3,-1),所以MN ⋅n =-12×1+-32×(-3)+1×(-1)=0,又MN 不在平面A 1CP 内即MN ⎳平面A 1CP ;(2)如图,连接PM ,由(1)得PM =(0,0,-2),则MN ⋅PM =-2,MN =2,PM =2,所以点P 到直线MN 的距离为d =PM 2-MN ⋅PMPM2= 3.2(2024·安徽合肥·二模)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,∠BAD =60°,M 是侧棱PC 的中点,侧面PAD 为正三角形,侧面PAD ⊥底面ABCD .(1)求三棱锥M -ABC 的体积;(2)求AM 与平面PBC 所成角的正弦值.【答案】(1)12(2)3311.【分析】(1)作出辅助线,得到线线垂直,进而得到线面垂直,由中位线得到M 到平面ABCD 的距离为32,进而由锥体体积公式求出答案;(2)证明出BO ⊥AD ,建立空间直角坐标系,求出平面的法向量,进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【详解】(1)如图所示,取AD 的中点O ,连接PO .因为△PAD 是正三角形,所以PO ⊥AD .又因为平面PAD ⊥底面ABCD ,PO ⊂平面PAD ,平面PAD ∩平面ABCD =AD ,所以PO ⊥平面ABCD ,且PO =3.又因为M 是PC 的中点,M 到平面ABCD 的距离为32,S △ABC =12×2×2×sin 2π3=3,所以三棱锥M -ABC 的体积为13×3×32=12.(2)连接BO ,BD ,因为∠BAD =π3,所以△ABD 为等边三角形,所以BO ⊥AD ,以O 为原点,OA ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则P 0,0,3 ,A 1,0,0 ,B 0,3,0 ,C -2,3,0 ,所以M -1,32,32 ,AM =-2,32,32,PB =0,3,-3 ,BC =-2,0,0 .设平面PBC 的法向量为n=x ,y ,z ,则PB ⋅n =0BC ⋅n =0,即3y -3z =0-2x =0 ,解得x =0,取z =1,则y =1,所以n=0,1,1 .设AM 与平面PBC 所成角为θ,则sin θ=cos AM ,n =AM ⋅nAM ⋅n=-2,32,32 ⋅0,1,14+34+34×1+1=3311.即AM 与平面PBC 所成角的正弦值为3311.3(2023·福建福州·模拟预测)如图,在三棱柱ABC -A 1B 1C 1中,平面AA 1C 1C ⊥平面ABC ,AB =AC =BC =AA 1=2,A 1B =6.(1)设D 为AC 中点,证明:AC ⊥平面A 1DB ;(2)求平面A 1AB 1与平面ACC 1A 1夹角的余弦值.【答案】(1)证明见解析;(2)55【分析】(1)根据等边三角形的性质得出BD ⊥AC ,根据平面ACC 1A 1⊥平面ABC 得出BD ⊥平面ACC 1A 1,BD ⊥A 1D ,利用勾股定理得出AC ⊥A 1D ,从而证明AC ⊥平面A 1DB ;(2)建立空间直角坐标系,利用坐标表示向量,求出平面A 1AB 1的法向量和平面ACC 1A 1的一个法向量,利用向量求平面A 1AB 1与平面ACC 1A 1的夹角余弦值.【详解】(1)证明:因为D 为AC 中点,且AB =AC =BC =2,所以在△ABC 中,有BD ⊥AC ,且BD =3,又平面ACC 1A 1⊥平面ABC ,且平面ACC 1A 1∩平面ABC =AC ,BD ⊂平面ABC ,所以BD ⊥平面ACC 1A 1,又A 1D ⊂平面ACC 1A 1,则BD ⊥A 1D ,由A 1B =6,BD =3,得A 1D =3,因为AD =1,AA 1=2,A 1D =3,所以由勾股定理,得AC ⊥A 1D ,又AC ⊥BD ,A 1D ∩BD =D ,A 1D ,BD ⊂平面A 1DB ,所以AC ⊥平面A 1DB ;(2)如图所示,以D 为原点,建立空间直角坐标系D -xyz ,可得A (1,0,0),A 1(0,0,3),B (0,3,0),则AA 1 =-1,0,3 ,AB=-1,3,0 ,设平面A 1AB 1的法向量为n=(x ,y ,z ),由n ⋅AA 1=-x +3z =0n ⋅AB=-x +3y =0,令x =3,得y =1,z =1,所以n=3,1,1 ,由(1)知,BD ⊥平面ACC 1A 1,所以平面ACC 1A 1的一个法向量为BD=(0,-3,0),记平面A 1AB 1与平面ACC 1A 1的夹角为α,则cos α=|n ⋅BD ||n ||BD |=35×3=55,所以平面A 1AB 1与平面ACC 1A 1夹角的余弦值为55.4(2024·山西晋中·三模)如图,在六面体ABCDE 中,BC =BD =6,EC ⊥ED ,且EC =ED =2,AB 平行于平面CDE ,AE 平行于平面BCD ,AE ⊥CD .(1)证明:平面ABE ⊥平面CDE ;(2)若点A 到直线CD 的距离为22,F 为棱AE 的中点,求平面BDF 与平面BCD 夹角的余弦值.【答案】(1)证明见解析(2)10535【分析】(1)设平面ABE 与直线CD 交于点M ,使用线面平行的性质,然后用面面垂直的判定定理即可;(2)证明BE ⊥平面CDE ,然后构造空间直角坐标系,直接用空间向量方法即可得出结果.【详解】(1)设平面ABE 与直线CD 交于点M ,连接ME ,MB ,则平面ABE 与平面CDE 的交线为ME ,平面ABE 与平面BCD 的交线为MB ,因为AB 平行于平面CDE ,AB ⊂平面ABE ,平面ABE 和平面CDE 的交线为ME ,所以AB ∥ME .同理AE ∥MB ,所以四边形ABME 是平行四边形,故AE ∥MB ,AB ∥ME .因为CD ⊥AE ,AE ∥MB ,所以CD ⊥MB ,又BC =BD =6,所以M 为棱CD 的中点在△CDE 中,EC =ED ,MC =MD ,所以CD ⊥ME ,由于AB ∥ME ,故CD ⊥AB .而CD ⊥AE ,AB ∩AE =A ,AB ,AE ⊂平面ABE ,所以CD ⊥平面ABE ,又CD ⊂平面CDE ,所以平面ABE ⊥平面CDE .(2)由(1)可知,CD ⊥平面ABME ,又AM ⊂平面ABME ,所以CD ⊥AM .而点A 到直线CD 的距离为22,故AM =2 2.在等腰直角三角形CDE 中,由EC =ED =2,得CD =2,MC =MD =ME =1.在等腰三角形BCD 中,由MC =MD =1,BC =BD =6,得BM = 5.在平行四边形ABME 中,AE =BM =5,AB =EM =1,AM =22,由余弦定理得cos ∠MEA =EM 2+AE 2-AM 22EM ·AE=-55,所以cos ∠BME =55,所以BE =BM 2+EM 2-2BM ·EM cos ∠BME =2.因为BE 2+ME 2=22+12=5 2=BM 2,所以BE ⊥ME .因为平面ABME ⊥平面CDE ,平面ABME 和平面CDE 的交线为ME ,BE 在平面ABME 内.所以BE ⊥平面CDE .如图,以E 为坐标原点,EC ,ED ,EB 分别为x ,y ,z 轴正方向,建立空间直角坐标系.则E 0,0,0 ,C 2,0,0 ,D 0,2,0 ,B 0,0,2 ,A -22,-22,2 ,F -24,-24,1.所以CD =-2,2,0 ,DB =0,-2,2 ,FB =24,24,1 .设平面BCD 的法向量为m=x 1,y 1,z 1 ,则m ⋅CD=0m ⋅DB =0,即-2x 1+2y 1=0-2y 1+2z 1=0 .则可取x 1=2,得m=2,2,2 .设平面BDF 的法向量为n =x 2,y 2,z 2 ,则n ⋅FB =0n ⋅DB=0,即24x 2+24y 2+z 2=0-2y 2+2z 2=0.取z 2=1,则n=-32,2,1 .设平面BDF 与平面BCD 的夹角为θ,则cos θ=m ⋅n m ⋅n =-3210×21=10535.所以平面BDF 与平面BCD 夹角的余弦值为10535.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC -A 1B 1C 1中,A 1在平面ABC 内的射影O 在棱AC 的中点处,P 为棱A 1B 1(包含端点)上的动点.(1)求点P 到平面ABC 1的距离;(2)若AP ⊥平面α,求直线BC 1与平面α所成角的正弦值的取值范围.【答案】(1)23913;(2)25,104.【分析】(1)以O 为原点建立空间直角坐标系,求出平面ABC 1的法向量,再利用点到平面距离的向量求法求解即得.(2)由向量共线求出向量AP的坐标,再利用线面角的向量求法列出函数关系,并求出函数的值域即可.【详解】(1)依题意,A 1O ⊥平面ABC ,OB ⊥AC (底面为正三角形),且A 1O =OB =3,以O 为原点,OB ,OC ,OA 1的方向分别为x ,y ,z 轴的正方向,建立空间直角坐标系,如图,则O (0,0,0),A (0,-1,0),B (3,0,0),C (0,1,0),A 1(0,0,3),C 1(0,2,3),AC 1 =(0,3,3),BC 1 =(-3,2,3),AA 1 =(0,1,3),由A 1B 1⎳AB ,A 1B 1⊄平面ABC 1,AB ⊂平面ABC 1,则A 1B 1⎳平面ABC 1,即点P 到平面ABC 1的距离等于点A 1到平面ABC 1的距离,设n =(x ,y ,z )为平面ABC 1的一个法向量,由n ⋅AC 1=3y +3z =0n ⋅BC 1=-3x +2y +3z =0,取z =3,得n=(1,-3,3),因此点A 1到平面ABC 1的距离d =|AA 1 ⋅n||n |=2313=23913,所以点P 到平面ABC 1的距离为23913.(2)设A 1P =λA 1B 1 ,λ∈[0,1],则AP =AA 1 +A 1P =AA 1 +λAB=(0,1,3)+λ(3,1,0)=(3λ,1+λ,3),由AP ⊥α,得AP为平面α的一个法向量,设直线BC 1与平面α所成角为θ,则sin θ=|cos ‹BC 1 ,AP ›|=|BC 1 ⋅AP||BC 1 ||AP |=|5-λ|10⋅3λ2+(1+λ)2+3=5-λ25⋅2λ2+λ+2,令t =5-λ,则λ=5-t ,t ∈[4,5],则sin θ=t 25⋅2(5-t )2+(5-t )+2=t25⋅2t 2-21t +57=125⋅2-21t+57t 2=125571t-7382+576,由t ∈[4,5],得1t ∈15,14 ,于是571t -738 2+576∈225,516,25⋅571t -738 2+576∈2105,52 ,则sin θ∈25,104,所以直线BC 1与平面α所成角的正弦值的取值范围是25,104.6(2024·重庆·模拟预测)在如图所示的四棱锥P -ABCD 中,已知AB ∥CD ,∠BAD =90°,CD =2AB ,△PAB 是正三角形,点M 在侧棱PB 上且使得PD ⎳平面AMC .(1)证明:PM =2BM ;(2)若侧面PAB ⊥底面ABCD ,CM 与底面ABCD 所成角的正切值为311,求二面角P -AC -B 的余弦值.【答案】(1)证明见解析;(2)1010.【分析】(1)连接BD 与AC 交于点E ,连接EM ,由已知得AB CD=EBED ,由线面平行的性质得PD ∥EM ,根据三角形相似可得EB ED =BM PM=12,即PM =2BM(2)设AB 的中点O ,首先由已知得PO ⊥底面ABCD ,在△PAB 中过点M 作MF ∥PO 交AB 于点F ,得MF ⊥底面ABCD ,则∠MCF 为CM 与底面ABCD 所成角,在底面ABCD 上过点O 作OG ⊥AC 于点G ,则∠PGO 是二面角P -AC -B 的平面角,根据条件求解即可【详解】(1)证明:连接BD 与AC 交于点E ,连接EM ,在△EAB 与△ECD 中,∵AB ∥CD ,∴AB CD=EBED ,由CD =2AB ,得ED =2EB ,又∵PD ⎳平面AMC ,而平面PBD ∩平面AMC =ME ,PD ⊂平面PBD ,∴PD ∥EM ,∴在△PBD 中,EB ED =BM PM=12,∴PM =2BM ;(2)设AB 的中点O ,在正△PAB 中,PO ⊥AB ,而侧面PAB ⊥底面ABCD ,侧面PAB ∩底面ABCD =AB ,且PO ⊂平面PAB ,∴PO ⊥底面ABCD ,在△PAB 中过点M 作MF ⎳PO 交AB 于点F ,∴MF ⊥底面ABCD ,∴∠MCF 为CM 与底面ABCD 所成角,∴MF CF=311,设AB =6a ,则MF=3a,∴CF=11a,BF=MF3=a,则在直角梯形ABCD中,AF=5a,而CD=12a,则AD=11a2-12a-5a2=62a,在底面ABCD上过点O作OG⊥AC于点G,则∠PGO是二面角P-AC-B的平面角,易得OA=3a,AC=66a,在梯形ABCD中,由OAOG=ACAD⇒3aOG=66a62a,得OG=3a,在Rt△POG中,PG=30a,∴cos∠PGO=OGPG=1010.7(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.(1)求点H到平面ABCD的距离;(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.【答案】(1)4(2)413【分析】(1)取AB,CD的中点M,N,证得平面ADE⎳平面MNHG,得到AE⎳GH,再由平面ABG⎳平面CDEHG,证得AG⎳EH,得到平行四边形AGHE,得到GH=AE,求得HN=4,结合HN⊥平面ABCD,即可求解;(2)以点N为原点,建立空间直角坐标系,分别求得平面BFHG和平面AGHE的法向量n =(1,3,4)和m =(1,-3,4),结合向量的夹角公式,即可求解.【详解】(1)如图所示,取AB,CD的中点M,N,连接GM,MN,HN,因为GA=GB,可得GM⊥AB,又因为平面ABG⊥平面ABCD,且平面ABG∩平面ABCD=AB,GM⊂平面ABG,所以GM⊥平面ABCD,同理可得:HN⊥平面ABCD,因为ED⊥平面ABCD,所以ED⎳HN,又因为ED⊄平面MNHG,HN⊂平面MNHG,所以ED⎳平面MNHG,因为MN⎳AD,且AD⊄平面MNHG,MN⊂平面MNHG,所以AD⎳平面MNHG,又因为AD∩DE=D,且AD,DE⊂平面ADE,所以平面ADE⎳平面MNHG,因为平面AEHG与平面ADE和平面MNHG于AE,GH,可得AE⎳GH,又由GM⎳HN,AB⎳CD,且AB∩GM=M和CD∩HN=N,所以平面ABG⎳平面CDEHG,因为平面AEHG与平面ABG和平面CDEHF于AG,EH,所以AG⎳EH,可得四边形AGHE 为平行四边形,所以GH =AE ,因为AE =AD 2+DE 2=42+12=17,所以GH =17,在直角△AMG ,可得GM =GB 2-AB 22=52-42=3,在直角梯形GMNH 中,可得HN =3+17-42=4,因为HN ⊥平面ABCD ,所以点H 到平面ABCD 的距离为4.(2)解:以点N 为原点,以NM ,NC ,NH 所在的直线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,则E (0,-4,1),F (0,4,1),G (4,0,3),H (0,0,4),可得HE =(0,-4,-3),HF =(0,4,-3),HG=(4,0,-1),设平面BFHG 的法向量为n=(x ,y ,z ),则n ⋅HG=4x -z =0n ⋅HF=4y -3z =0,取z =4,可得x =1,y =3,所以n=(1,3,4),设平面AGHE 的法向量为m=(a ,b ,c ),则m ⋅HG=4a -c =0m ⋅HE=-4b -3c =0,取c =4,可得a =1,b =-3,所以m=(1,-3,4),则cos m ,n =m ⋅n m n=1-9+161+9+16⋅1+9+16=413,即平面BFHG 与平面AGHE 所成锐二面角的余弦值413.8(2024·重庆·模拟预测)如图,ACDE 为菱形,AC =BC =2,∠ACB =120°,平面ACDE ⊥平面ABC ,点F 在AB 上,且AF =2FB ,M ,N 分别在直线CD ,AB 上.(1)求证:CF ⊥平面ACDE ;(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若∠EAC =60°,MN 为直线CD ,AB 的公垂线,求ANAF的值;(3)记直线BE 与平面ABC 所成角为α,若tan α>217,求平面BCD 与平面CFD 所成角余弦值的范围.【答案】(1)证明见解析(2)AN AF=913(3)528,255 【分析】(1)先通过余弦定理及勾股定理得到CF ⊥AC ,再根据面面垂直的性质证明;(2)以C 为原点,CA 的方向为x 轴正方向,建立如图所示空间直角坐标系C -xyz ,利用向量的坐标运算根据MN ⋅CD =0MN ⋅AF =0,列方程求解即可;(3)利用向量法求面面角,然后根据tan α>217列不等式求解.【详解】(1)AB 2=AC 2+BC 2-2AC ⋅BC ⋅cos ∠ACB =12,AB =23,AF =2FB ,所以AF =433,CF=13CA +23CB ,CF 2=19CA 2+49CB 2+49CA ⋅CB =43,AC 2+CF 2=4+43=163=AF 2,则CF ⊥AC ,又因为平面ACDE ⊥平面ABC ,平面ACDE ∩平面ABC =AC ,CF ⊂面ABC ,故CF ⊥平面ACDE ;(2)以C 为原点,CA 的方向为x 轴正方向,建立如图所示空间直角坐标系C -xyz ,由∠EAC =60°,可得∠DCA =120°,DC =2,所以C 0,0,0 ,D -1,0,3 ,A 2,0,0 ,F 0,233,0 所以AF =-2,233,0 ,CD =-1,0,3 ,设AN =λAF =-2λ,233λ,0 ,则N 2-2λ,233λ,0 ,设CM =μCD ,则M -μ,0,3μ ,MN =2-2λ+μ,233λ,-3μ ,由题知,MN ⋅CD=0MN ⋅AF =0 ⇒2λ-2-μ-3μ=04λ-4-2μ+43λ=0 ,解得λ=913,μ=-213,故AN AF=913;(3)B -1,3,0 ,设∠EAC =θ,则E 2-2cos θ,0,2sin θ ,BE=3-2cos θ,-3,2sin θ ,可取平面ABC 的法向量n=0,0,1 ,则sin α=cos n ,BE=n ⋅BEn ⋅BE =2sin θ 3-2cos θ 2+3+4sin 2θ=sin θ4-3cos θ,cos α=4-3cos θ-sin 2θ4-3cos θ,则tan α=sin θ4-3cos θ-sin 2θ>217,整理得10cos 2θ-9cos θ+2<0,故cos θ∈25,12,CF =0,23,0,CD =-2cos θ,0,2sin θ ,CB =-1,3,0 ,记平面CDF 的法向量为n 1 =x ,y ,z ,则有n 1 ⋅CD =0n 1 ⋅CF =0 ⇒-2x cos θ+2z sin θ=023y =0,可得n 1=sin θ,0,cos θ ,记平面CBD 的法向量为n 2 =a ,b ,c ,则有n 2 ⋅CD=0n 2 ⋅CB =0 ⇒-2a cos θ+2c sin θ=0-a +3b =0,可得n 2=3sin θ,sin θ,3cos θ ,记平面BCD 与平面CFD 所成角为γ,则cos γ=cos n 1 ,n 2 =33+sin 2θ,cos θ∈25,12 ,所以sin 2θ∈34,2125 ,3+sin 2θ∈152,465 ,故cos γ=33+sin 2θ∈528,255 .9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°,使得CD 到EF 的位置,得到如图所示的几何体.(1)求证:平面ACF ⊥平面BDE ;(2)点M 为DF上一点,若二面角C -AM -E 的余弦值为13,求∠MAD .【答案】(1)证明见解析(2)∠MAD =45°【分析】(1)根据面面与线面垂直的性质可得BD ⊥AF ,结合线面、面面垂直的判定定理即可证明;(2)建立如图空间直角坐标系,设∠MAD =α,AB =1,利用空间向量法求出二面角C -AM -E 的余弦值,建立方程1-sin αcos α1+sin 2α1+cos 2α=13,结合三角恒等变换求出α即可.【详解】(1)由已知得平面ABCD ⊥平面ABEF ,AF ⊥AB ,平面ABCD ∩平面ABEF =AB ,AF ⊂平面ABEF ,所以AF ⊥平面ABCD ,又BD ⊂平面ABCD ,故BD ⊥AF ,因为ABCD 是正方形,所以BD ⊥AC ,AC ,AF ⊂平面ACF ,AC ∩AF =A ,所以BD ⊥平面ACF ,又BD ⊂平面BDE ,所以平面ACF ⊥平面BDE .(2)由(1)知AD ,AF ,AB 两两垂直,以AD ,AF ,AB 所在直线分别为x ,y ,z 轴,建立空间直角坐标系,如图.设∠MAD =α,AB =1,则A 0,0,0 ,M cos α,sin α,0 ,C 1,0,1 ,E 0,1,1 ,故AM =cos α,sin α,0 ,AC =1,0,1 ,AE =0,1,1设平面AMC 的法向量为m =x 1,y 1,z 1 ,则m ⋅AC =0,m ⋅AM=0故x 1+z 1=0x 1cos α+y 1sin α=0,取x 1=sin α,则y 1=-cos α,z 1=-sin α所以m=sin α,-cos α,-sin α设平面AME 的法向量为n =x 2,y 2,z 2 ,n ⋅AE =0,n ⋅AM=0故y 2+z 2=0x 2cos α+y 2sin α=0,取x 2=sin α,则y 2=-cos α,z 2=cos α所以n=sin α,-cos α,cos α ,所以cos m ,n =1-sin αcos α1+sin 2α1+cos 2α,由已知得1-sin αcos α1+sin 2α1+cos 2α=13,化简得:2sin 22α-9sin2α+7=0,解得sin2α=1或sin2α=72(舍去)故α=45°,即∠MAD =45°.10(2024·安徽黄山·二模)如图,已知AB 为圆台下底面圆O 1的直径,C 是圆O 1上异于A ,B 的点,D 是圆台上底面圆O 2上的点,且平面DAC ⊥平面ABC ,DA =DC =AC =2,BC =4,E 是CD 的中点,BF =2FD .(1)证明:DO 2⎳BC ;(2)求直线DB 与平面AEF 所成角的正弦值.【答案】(1)证明见解析(2)68585【分析】(1)取AC 的中点O ,根据面面垂直的性质定理,可得DO ⊥平面ABC ,即可求证DO 2⎳OO 1,进而可证矩形,即可根据线线平行以及平行的传递性求解.(2)建系,利用向量法,求解法向量n =1,-12,3 与方向向量DB =(-1,4,-3)的夹角,即可求解.【详解】(1)证明:取AC 的中点为O ,连接DO ,OO 1,O 1O 2,∵DA =DC ,O 为AC 中点,∴DO ⊥AC ,又平面DAC ⊥平面ABC ,且平面DAC ∩平面ABC =AC ,DO ⊂平面DAC ,∴DO ⊥平面ABC ,∴DO ⎳O 1O 2,DO =O 1O 2,故四边形DOO 1O 2为矩形,∴DO 2⎳OO 1,又O ,O 1分别是AC ,AB 的中点,∴OO 1⎳BC ,∴DO 2⎳BC ;(2)∵C 是圆O 1上异于A ,B 的点,且AB 为圆O 1的直径,∴BC ⊥AC ,∴OO 1⊥AC ,∴如图以O 为原点建立空间直角坐标系,由条件知DO =3,∴A (1,0,0),B (-1,4,0),C (-1,0,0),D (0,0,3),∴E -12,0,32 ,设F (x ,y ,z ),∴BF =(x +1,y -4,z ),FD=(-x ,-y ,3-z ),由BF =2FD ,得F -13,43,233 ,∴AF =-43,43,233 ,∴DB =(-1,4,-3),AE =-32,0,32 ,设平面AEF 法向量为n=(x 1,y 1,z 1),则n ⋅AE=-32x 1+32z 1=0n ⋅AF =-43x 1+43y 1+233z 1=0,取n =1,-12,3 ,设直线BD 与平面AEF 所成角为θ,则sin θ=|cos <n ,DB>|=625⋅172=68585∴直线BD 与平面AEF 所成角的正弦值为68585.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22,A 1B 1=12AB ,M 为BC 中点,已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1,其中λ∈0,1 .(1)求证D 1P ⊥AC ;(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37,当λ=23时,求直线DP 与平面AMC 1所成角的正弦值.【答案】(1)证明见解析(2)241391【分析】(1)方法一运用空间向量的线性运算,进行空间位置关系的向量证明即可.方法二:建立空间直角坐标系,进行空间位置关系的向量证明即可.(2)建立空间直角坐标系,利用线面角的向量求法求解即可.【详解】(1)方法一:∵A 1B 1=12AB ,∴AA 1 ⋅AB =AA 1 ⋅AD =22×22=2.∵D 1A =-12AD-AA 1∴D 1P =D 1A +AP =1-λ AB +12λ-12AD+λ-1 AA 1∴D 1P ⋅AC =1-λ AB +12λ-12AD +λ-1 AA 1 ⋅AB +AD =1-λ AB 2+12λ-12 AD2+λ-1 AB ⋅AA 1 +λ-1 AD ⋅AA 1=81-λ +812λ-12+4λ-1 =0.∴D 1P ⊥AC ,即D 1P ⊥AC .方法二:以底面ABCD 的中心O 为原点,以OM 方向为y 轴,过O 点平行于AD 向前方向为x 轴,以过点O 垂直平面ABCD 向上方向为z 轴,建立如图所示空间直角坐标系,设正四棱台的高度为h ,则有 A 2,-2,0 ,B 2,2,0 ,C -2,2,0 ,D -2,-2,0 ,A 122,-22,h ,C 1-22,22,h ,D 1-22,-22,h ,M 0,2,0 ,AC =-22,22,0AP =1-λ 0,22,0 +12λ-22,0,0 +λ-22,22,0 =-322λ,22-322λ,λhD 1A =322,-22,-h ,D 1P =D 1A +AP =-322λ+322,-322λ+322,λh -h .故AC ⋅D 1P=0,所以D 1P ⊥AC .(2)设平面ABCD 的法向量为n=0,0,1 ,设平面AMC 1的法向量为m =x ,y ,z ,AM =-2,22,0 ,AC 1 =-322,322,h ,则有AM ⋅m=0AC 1 ⋅m=0 ,即-2x +22y =0-322x +322y +hz =0,令x =22h ,则m=22h ,2h ,3 .又题意可得cos m ,n =38h 2+2h 2+9=37,可得h =2.因为λ=23,经过计算可得P 0,0,43 ,D 1-22,-22,2 ,D 1P =2,2,43.将h =2代入,可得平面AMC 1的法向量m=42,22,3 .设直线DP 与平面AMC 1所成角的为θsin θ=cos DP ,m =8+4+42+2+16932+8+9=241391.12(2024·辽宁·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2,AB =1,BC =3,点E 为线段AC 的中点.(1)求证:AB 1∥平面BEC 1;(2)若∠A 1AC =π3,求二面角A -BE -C 1的余弦值.【答案】(1)证明见详解(2)-22【分析】(1)连接BC 1,交B 1C 于点N ,连接NE ,利用线面平行的判定定理证明;(2)由已知可知,△AA 1C 为等边三角形,故A 1E ⊥AC ,利用面面垂直的性质定理可证得A 1E ⊥底面ABC ,进而建立空间直角坐标系,利用向量法即可求二面角余弦值.【详解】(1)连接BC 1,交B 1C 于点N ,连接NE ,因为侧面BCC 1B 1是平行四边形,所以N 为B 1C 的中点,又因为点E 为线段AC 的中点,所以NE ⎳AB 1,因为AB 1⊄面BEC 1,NE ⊂面BEC 1,所以AB 1⎳面BEC 1.(2)连接A 1C ,A 1E ,因为∠A 1AC =π3,AC =AA 1=2,所以△AA 1C 为等边三角形,A 1C =2,因为点E 为线段AC 的中点,所以A 1E ⊥AC ,因为侧面ACC 1A 1⊥底面ABC ,平面ACC 1A 1∩平面ABC =AC ,A 1E ⊂平面ACC 1A 1,所以A 1E ⊥底面ABC ,过点E 在底面ABC 内作EF ⊥AC ,如图以E 为坐标原点,分布以EF ,EC ,EA 1 的方向为x ,y ,z 轴正方向建立空间直角坐标系,则E 0,0,0 ,B 32,-12,0 ,C 10,2,3 ,所以EB =32,-12,0 ,EC 1 =0,2,3 ,设平面BEC 1的法向量为m=x ,y ,z ,则m ⋅EB =32x -12y =0m ⋅EC 1=2y +3z =0,令x =1,则y =3,z =-2,所以平面BEC 1的法向量为m=1,3,-2 ,又因为平面ABE 的法向量为n=0,0,1 ,则cos m ,n =-21+3+4=-22,经观察,二面角A -BE -C 1的平面角为钝角,所以二面角A -BE -C 1的余弦值为-22.13(2024·广东广州·一模)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,△DCP 是等边三角形,∠DCB =∠PCB =π4,点M ,N 分别为DP 和AB 的中点.(1)求证:MN ⎳平面PBC ;(2)求证:平面PBC ⊥平面ABCD ;(3)求CM 与平面PAD 所成角的正弦值.【答案】(1)证明见解析;(2)证明见解析;(3)33.【分析】(1)取PC 中点E ,由已知条件,结合线面平行的判断推理即得.(2)过P 作PQ ⊥BC 于点Q ,借助三角形全等,及线面垂直的判定、面面垂直的判定推理即得.(3)建立空间直角坐标系,利用线面角的向量求法求解即得.【详解】(1)取PC 中点E ,连接ME ,BE ,由M 为DP 中点,N 为AB 中点,得ME ⎳DC ,ME =12DC ,又BN ⎳CD ,BN =12CD ,则ME ⎳BN ,ME =BN ,因此四边形BEMN 为平行四边形,于是MN ⎳BE ,而MN ⊄平面PBC ,BE ⊂平面PBC ,所以MN ⎳平面PBC .(2)过P 作PQ ⊥BC 于点Q ,连接DQ ,由∠DCB =∠PCB =π4,CD =PC ,QC =QC ,得△QCD ≌△QCP ,则∠DQC =∠PQC =π2,即DQ ⊥BC ,而PQ =DQ =2,PQ 2+DQ 2=4=PD 2,因此PQ ⊥DQ ,又DQ ∩BC =Q ,DQ ,BC ⊂平面ABCD ,则PQ ⊥平面ABCD ,PQ ⊂平面PBC ,所以平面PBC ⊥平面ABCD .(3)由(2)知,直线QC ,QD ,QP 两两垂直,以点Q 为原点,直线QC ,QD ,QP 分别为x ,y ,z 轴建立空间直角坐标系,则C (2,0,0),P (0,0,2),D (0,2,0),M 0,22,22,A (-2,2,0),CM =-2,22,22,AD =(2,0,0),DP =(0,-2,2),设平面PAD 的一个法向量n =(x ,y ,z ),则n ⋅AD=2x =0n ⋅DP=-2y +2z =0,令y =1,得n=(0,1,1),设CM 与平面PAD 所成角为θ,sin θ=|cos ‹CM ,n ›|=|CM ⋅n||CM ||n |=23⋅2=33,所以CM 与平面PAD 所成角的正弦值是33.14(2024·广东梅州·二模)如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,底面ABCD 为直角梯形,△PAD 为等边三角形,AD ⎳BC ,AD ⊥AB ,AD =AB =2BC =2.(1)求证:AD ⊥PC ;(2)点N 在棱PC 上运动,求△ADN 面积的最小值;(3)点M 为PB 的中点,在棱PC 上找一点Q ,使得AM ⎳平面BDQ ,求PQQC的值.【答案】(1)证明见解析(2)2217(3)4【分析】(1)取AD 的中点H ,连接PH ,CH ,依题意可得四边形ABCH 为矩形,即可证明CH ⊥AD ,再由PH ⊥AD ,即可证明AD ⊥平面PHC ,从而得证;(2)连接AC 交BD 于点G ,连接MC 交BQ 于点F ,连接FG ,即可得到CG AG=12,再根据线面平行的性质得到CF FM =12,在△PBC 中,过点M 作MK ⎳PC ,即可得到MKCQ=2,最后由PQ =2MK 即可得解.【详解】(1)取AD 的中点H ,连接PH ,CH ,则AH ⎳BC 且AH =BC ,又AD ⊥AB ,所以四边形ABCH 为矩形,所以CH ⊥AD ,又△PAD 为等边三角形,所以PH ⊥AD ,PH ∩CH =H ,PH ,CH ⊂平面PHC ,所以AD ⊥平面PHC ,又PC ⊂平面PHC ,所以AD ⊥PC .(2)连接HN ,由AD ⊥平面PHC ,又HN ⊂平面PHC ,所以AD ⊥HN ,所以S △ADH =12AD ⋅HN =HN ,要使△ADN 的面积最小,即要使HN 最小,当且仅当HN ⊥PC 时HN 取最小值,因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,PH ⊂平面PAD ,所以PH ⊥平面ABCD ,又HC ⊂平面ABCD ,所以PH ⊥HC ,在Rt △HPC 中,CH =2,PH =3,所以PC =CH 2+PH 2=7,当HN ⊥PC 时HN =PH ⋅CH PC =237=2217,所以△ADN 面积的最小值为2217.(3)连接AC 交BD 于点G ,连接MC 交BQ 于点F ,连接FG ,因为AD ⎳BC 且AD =2BC =2,所以△CGB ∽△AGD ,所以CG AG =BC AD=12,因为AM ⎳平面BDQ ,又AM ⊂平面ACM ,平面BDQ ∩平面ACM =GF ,所以GF ⎳AM ,所以CF FM =CG AG=12,在△PBC 中,过点M 作MK ⎳PC ,则有MK CQ =MF CF=2,所以PQ =2MK ,所以PQ =2MK =4CQ ,即PQQC=415(2024·广东广州·模拟预测)如图所示,圆台O 1O 2的轴截面A 1ACC 1为等腰梯形,AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点,且AB =BC ,P 是线段BC 的中点.(1)求证:C 1P ⎳平面A 1AB .(2)求平面A 1AB 与平面C 1CB 夹角的余弦值.【答案】(1)证明见解析(2)17【分析】(1)取AB 的中点H ,连接A 1H ,PH ,证明四边形A 1C 1PH 为平行四边形,进而得C 1P ⎳A 1H ,即可证明;(2)建立空间直角坐标系,求两平面的法向量,利用平面夹角公式求解.【详解】(1)取AB 的中点H ,连接A1H ,PH ,如图所示,因为P 为BC 的中点,所以PH ⎳AC ,PH =12AC .在等腰梯形A 1ACC 1中,A 1C 1⎳AC ,A 1C 1=12AC ,所以HP ⎳A 1C 1,HP =A 1C 1,所以四边形A 1C 1PH 为平行四边形,所以C 1P ⎳A 1H ,又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB ,所以C 1P ⎳平面A 1AB .(2)因为AB =BC ,故O 2B ⊥AC ,以直线O 2A ,O 2B ,O 2O 1分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,在等腰梯形A 1ACC 1中,AC =2AA 1=2A 1C 1=4,此梯形的高为h =AA 21-AC -A 1C 122= 3.因为A 1C 1=12AC ,A 1C 1⎳AC ,。
高中立体几何试题及答案

高中立体几何试题及答案一、选择题(每题3分,共15分)1. 空间中,如果直线a与平面α平行,那么直线a与平面α内的任意直线b的位置关系是:A. 平行B. 异面C. 相交D. 垂直2. 一个正方体的棱长为a,那么它的对角线长度为:A. a√2B. a√3C. 2aD. 3a3. 已知一个圆锥的底面半径为r,高为h,圆锥的体积是:A. πr²hB. 1/3πr²hC. 2πr²hD. 3πr²h4. 一个球的半径为R,那么它的表面积是:A. 4πR²B. 2πR²C. πR²D. R²5. 空间中,如果两个平面α和β相交于直线l,那么直线l与平面α和平面β的位置关系是:A. 平行B. 垂直C. 相交D. 包含二、填空题(每题2分,共10分)6. 空间直角坐标系中,点A(2,3,4)到原点O的距离是________。
7. 一个正四面体的每个顶点都与其它三个顶点相连,那么它的边长与高之比为________。
8. 已知一个长方体的长、宽、高分别为l、w、h,那么它的体积是________。
9. 空间中,如果一个点到平面的距离是d,那么这个点到平面上任意一点的距离的最大值是________。
10. 一个圆柱的底面半径为r,高为h,它的侧面积是________。
三、解答题(共75分)11. (15分)已知空间直角坐标系中,点A(1,2,3),B(4,5,6),点C 在平面ABC内,且AC=BC=2,求点C的坐标。
12. (20分)一个圆锥的底面半径为3,高为4,求圆锥的全面积和表面积。
13. (20分)一个长方体的长、宽、高分别为5、3、2,求其外接球的半径。
14. (20分)已知一个球的表面积为4π,求该球的体积。
答案:一、选择题1. A2. B3. B4. A5. C二、填空题6. √(1²+2²+3²)=√147. √3:18. lwh9. d+R10. 2πrh三、解答题11. 点C的坐标可以通过向量运算求得,设C(x,y,z),则向量AC=向量BC,即(1-x,2-y,3-z)=(x-4,5-y,6-z),解得x=3,y=4,z=5,所以点C的坐标为(3,4,5)。
2023全国甲卷数学立体几何18题

(1)证明见解析.
(2) 13 13
【基本思路】 (1)根据线面垂直,面面垂直的判定与性质定理可得 A1O 平面 BCC1B1 ,再由勾股定理 求出 O 为中点,即可得证; (2)利用直角三角形求出 AB1 的长及点 A 到面的距离,根据线面角定义直接可得正弦值. 【详细解析】⑴如图,
第 4 页(共 5 页)
由 CM∥A1C1,CM A1C1知四边形 A1CMC1 为平行四边形, C1M∥A1C ,C1M 平面 ABC ,又 AM 平面 ABC ,
C1M AM 则在 Rt△AC1M 中, AM 2AC,C1M A1C , AC1 (2AC)2 A1C2 , 在 Rt△AB1C1 中, AC1 (2AC)2 A1C2 , B1C1 BC 3 ,
(1)证明见解析. (2)1
【基本思路】
(1)由 A1C 平面 ABC 得 A1C BC ,又因为 AC BC ,可证 BC 平面 ACC1A1 ,从而 证得平面 ACC1A1 平面 BCC1B1 ; (2) 过点 A1 作 A1O CC1 ,可证四棱锥的高为 A1O ,由三角形全等可证 A1C AC ,从而证 得 O 为 CC1 中点,设 A1C AC x ,由勾股定理可求出 x ,再由勾股定理即可求 A1O .
AB1 (2 2)2 ( 2)2 ( 3)2 13 , 又 A 到平面 BCC1B1 距离也为 1,
所以 AB1 与平面 BCC1B1 所成角的正弦值为
1 13
13
.
13
第 5 页(共 5 页)
【详细解析】 ⑴证明:因为 A1C 平面 ABC , BC 平面 ABC , 所以 A1C BC , 又因为 ACB 90o,即 AC BC ,
高三数学立体几何试题答案及解析

高三数学立体几何试题答案及解析1.如图,设为正四面体表面(含棱)上与顶点不重合的一点,由点到四个顶点的距离组成的集合记为,如果集合中有且只有个元素,那么符合条件的点有()A.个B.个C.个D.个【答案】C【解析】分以下两种情况讨论:(1)点到其中两个点的距离相等,到另外两点的距离分别相等,且这两个距离不等,此时点位于正四面体各棱的中点,符合条件的有个点;(2)点到其中三个点的距离相等,到另外一点的距离与它到其它三点的距离不相等,此时点在正四面体各侧面的中心点,符合条件的有个点,故选C.【考点】新定义2.在等腰三角形中,点是边上异于的一点,光线从点出发,经发射后又回到原点(如图).若光线经过的中心,则等于()A.B.C.D.【答案】D;【解析】以A为原点,AB所在直线为x轴,AC所在直线为y轴建立直角坐标系,所以等腰三角形ABC的中心坐标为,因为光线从点出发,经发射后又回到原点,故点P为三角新ABC的中心在底边AB上的投影,所以AP=.3.已知三棱锥的三视图,则该三棱锥的体积是()A.B.C.D.【答案】B【解析】如图所示,,点P在侧面ABC的射影为O,.∴该三棱锥的体积.故选:B.【考点】由三视图求面积、体积.4.(本题满分12分)如图,在三棱锥底面ABC,且SB=分别是SA、SC的中点.(Ⅰ)求证:平面平面BCD;(Ⅱ)求二面角的平面角的大小.【答案】(Ⅰ)证明过程详见解析;(Ⅱ).【解析】(Ⅰ)已知SB、AB、BC两两互相垂直,故可建立空间直角坐标系如下图.根据线段长度可求出相应点的坐标,从而可推出,则,所以平面平面BCD.(Ⅱ)求出两个平面的法向量,利用法向量夹角与二面角平面角的关系求出平面角的大小.试题解析:(Ⅰ).又因,所以建立如上图所示的坐标系.所以A(2,0,0),,D(1,0,1),,S(0,0,2)易得,,,又,又又因,所以平面平面BCD.(Ⅱ)又设平面BDE的法向量为,则所以又因平面SBD的法向量为所以所以二面角的平面角的大小为.【考点】•平面与平面的垂直的证明 二面角大小的求法.5.(本小题满分12分)直三棱柱中,,,分别是、的中点,,为棱上的点.(1)证明:;(2)是否存在一点,使得平面与平面所成锐二面角的余弦值为?若存在,说明点的位置,若不存在,说明理由.【答案】(1)证明见解析;(2)存在,点为中点.【解析】(1)先证明AB⊥AC,然后以A为原点建立空间直角坐标系A-xyz,则能写出各点坐标,由共线可得D(λ,0,1),所以,即DF⊥AE;(2)通过计算,面DEF的法向量为可写成,=(3,1+2λ,2(1-λ)),又面ABC的法向量=(0,0,1),令,解出λ的值即可.试题解析:(1)证明:,又,面又面以为原点建立如图所示的空间直角坐标系则,,,,设,且,即:(2)假设存在,设面的法向量为,则即:令由题可知面的法向量平面与平面所成锐二面角的余弦值为即:或(舍)当点为中点时,满足要求.【考点】1、二面角的平面角及求法;2、直线与平面垂直的性质.【方法点晴】本题考查空间中直线与直线的位置关系、空间向量及其应用,建立空间直角坐标系是解决问题的关键,属中档题.解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.6.已知是矩形,分别是线段的中点,平面.(1)求证:平面;(2)若在棱上存在一点,使得平面,求的值.【答案】(1)详见解析;(2)【解析】(1)通过证明,然后再利用线面垂直的判定定理,即可证明平面;(2)过作交于,则平面,且.再过作交于,所以平面,且,所以平面平面,进而满足题意.试题解析:(1)在矩形中,因为,点是的中点,所以.所以,即.又平面,所以,所以平面.(2)过作交于,则平面,且.再过作交于,所以平面,且.所以平面平面,所以平面,从而点满足.【考点】1.线面垂直的判定定理;2.面面平行的判定定理和性质定理.7.已知某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】B【解析】根据三视图知几何体的下面是一个圆柱,上面是圆柱的一半,所以.故应选B.【考点】空间几何体的三视图.8.(2015•汕头二模)某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)()A.100(3+)cm2B.200(3+)cm2C.300(3+)cm2D.300cm2【答案】A【解析】本题以实际应用题为背景考查立体几何中的三视图.由三视图可知,该几何体的形状如图,它是底面为正方形,各个侧面均为直角三角形[的四棱锥,用去的铁皮的面积即该棱锥的表面积解:由三视图可知,该几何体的形状如图,它是底面为正方形,各个侧面均为直角三角形的四棱锥,用去的铁皮的面积即该棱锥的表面积,其底面边长为10,故底面面积为10×10=100,与底面垂直的两个侧面是全等的直角,两直角连年长度分别为10,20,故它们的面积皆为100,另两个侧面也是全等的直角三角形,两直角边中一边是底面正方形的边长10,另一边可在与底面垂直的直角三角形中求得,其长为=10,故此两侧面的面积皆为50,故此四棱锥的表面积为S=100(3+)cm2.故选:A【考点】由三视图求面积、体积.9.如图,在直四棱柱中,底面是边长为1的正方形,侧棱,是侧棱的中点.(1)求证:平面⊥平面;(2)求二面角的正切值.【答案】(1)见解析;(2).【解析】(1)易证得为等腰直角三角形,从而得到,又由直四棱柱的性质可得到,进而可使问题得证;(2)方法一:过点作于,过作于,则就是二面角的平面角,然后在中求得,从而求得,再在中求得,最后在中即可求得所求二面角的正切值;方法二:以为原点建立空间直角坐标系,分别求得平面与平面的一个法向量,从而利用空间夹角公式求解即可.试题解析:(1)证明:如图,在矩形中,E为中点且,,所以,所以为等腰直角三角形,所以.在直四棱柱中,因为底面是边长为1的正方形,所以平面.又因为平面,所以,所以平面又因为平面,所以平面⊥平面(2)解:方法一:因为平面,所以平面⊥平面,所以只需在平面内过点作于,而平面.如图,过作于,连接,则就是二面角的平面角.在中,,所以.在中,在中,.所以二面角的平面角的正切值大小为方法二:以为原点,,,分别为轴建立如图所示的空间直角坐标系.由题意,,,,,,,,,设平面的一个法向量为,则,同理可得,平面的一个法向量为,代入公式有:,所以二面角的平面角的正切值大小为【考点】1、空间垂直关系的判定;2、二面角.10.(2015秋•扬州期末)已知正四棱锥底面边长为,体积为32,则此四棱锥的侧棱长为.【答案】5【解析】利用体积求出正四棱锥的高,求出底面对角线的长,然后求解侧棱长.解:正四棱锥底面边长为,体积为32,可得正四棱锥的高为h,=32,解得h=3,底面对角线的长为:4=8,侧棱长为:=5.故答案为:5.【考点】棱柱、棱锥、棱台的体积;点、线、面间的距离计算.11.(2010•江苏二模)如图,在四边形ABCD中,CA=CD=AB=1,=1,sin∠BCD=.(1)求BC的长;(2)求四边形ABCD的面积;(3)求sinD的值.【答案】(1)BC=;(2);(3)【解析】(1)根据题意可分别求得AC,CD和AB,利用=1,利用向量的数量积的性质求得cos∠BAC的值,进而求得∠BAC,进而利用余弦定理求得BC的长.(2)根据(1)可求得BC2+AC2=AB2.判断出∴∠ACB=,进而在直角三角形中求得cos∠ACD的值,利用同角三角函数的基本关系气的sin∠ACD,然后利用三角形面积公式求得三角形ABC和ACD的面积,二者相加即可求得答案.(3)在△ACD中利用余弦定理求得AD的长,最后利用正弦定理求得sinD的值.解:(1)由条件,得AC=CD=1,AB=2. ∵=1,∴1×2×cos ∠BAC=1.则cos ∠BAC=.∵∠BAC ∈(0,π),∴∠BAC=.∴BC 2=AB 2+AC 2﹣2AB•ACcos ∠BAC=4+1﹣2×2×=3.∴BC=.(2)由(1)得BC 2+AC 2=AB 2. ∴∠ACB=.∴sin ∠BCD==. ∵∠ACD ∈∈(0,π),∴.∴S △ACD =×1×1×=. ∴S 四边形ABCD =S △ABC +S △ACD =.(3)在△ACD 中,AD 2=AC 2+DC 2﹣2AC•DCcos ∠ACD=1+1﹣2×1×1×=. ∴AD=.∵,∴. 【考点】解三角形的实际应用.12. (2014•阳泉二模)某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为( )A .B .3πC .D .π【答案】C【解析】由于正视图、侧视图、俯视图都是边长为1的正方形,所以此四面体一定可以放在棱长为1的正方体中,所以此四面体的外接球即为此正方体的外接球,由此能求出此四面体的外接球的体积.解:由于正视图、侧视图、俯视图都是边长为1的正方形, 所以此四面体一定可以放在正方体中, 所以我们可以在正方体中寻找此四面体. 如图所示,四面体ABCD 满足题意,所以此四面体的外接球即为此正方体的外接球,由题意可知,正方体的棱长为1,所以外接球的半径为R=,所以此四面体的外接球的体积V==.故选C.【考点】由三视图求面积、体积.13.如图,一竖立在水平对面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥表面爬行一周后回到点处,则该小虫爬行的最短路程为,则圆锥底面圆的半径等于()A.B.C.D.【答案】C【解析】作出该圆锥的侧面展开图,如下图所示:该小虫爬行的最短路程为,由余弦定理可得,∴.设底面圆的半径为,则有,∴.故C项正确.【考点】圆锥的计算,平面展开——最值问题.【方法点晴】本题主要考查了圆锥的计算及有关圆锥的侧面展开的应用,着重考查了求立体图形中两点之间的曲线段的最短线路长,解答此类问题一般应把几何体的侧面展开,展在一个平面内,构造直角三角形,从而求解两点间的线段的长度,用到的知识为:圆锥的弧长等于底面周长,本题的解答中圆锥的侧面展开图是一个三角形,此扇形的弧长等于圆锥的面周长,扇形的半径等于圆锥的母线长,体现了“化曲面为平面”的思想方法.14.已知三棱锥中,,,,,则此三棱锥的外接球的表面积为()A.B.C.D.【答案】C【解析】如图,设是的外心,是三棱锥外接球球心,则平面,由已知平面,则,,,,所以.,所以,.故选C.【考点】棱锥的外接球,球的表面积.15.如图,一个空间几何体的正视图、侧视图都是面积为,一个内角为的菱形,俯视图为正方形,那么这个几何体的表面积为()A.B.C.D.【答案】D【解析】因为一个空间几何体的正视图、侧视图都是面积为,且一个内角为的菱形,所以菱形的边长为,由三视图可得,几何体是由两个底面正方形的正四棱锥组合而成,底面边长为,侧棱长为,所以几何体的表面积为:,故选D.【考点】1、三视图;2、多面体的表面积.16.已知直三棱柱中,,侧面的面积为,则直三棱柱外接球表面积的最小值为.【答案】【解析】根据题意,设,则有,从而有其外接球的半径为,所以其比表面积的最小值为.【考点】1、几何体的外接球;2、基本不等式;3、球的体积和表面积.【方法点睛】设,则有,利用直三棱柱中,,从而直三棱柱外接球的半径为,所以其比表面积的最小值为.根据直三棱柱中,,侧面的面积为,设,,利用均值不等式,确定直三棱柱外接球的半径的最小值是关键.17.在体积为的四面体中,平面,,,,则长度的所有值为.【答案】或【解析】由题意得因此由余弦定理得:或,因此或【考点】三棱锥体积,余弦定理18.如图,正四棱锥的底面一边长为,侧面积为,则它的体积为________.【答案】【解析】设侧面三角形的高为,则,解之可得,故棱锥的高为,所以棱锥的体积为,答案应填:.【考点】正四棱锥的侧面面积和体积公式.19.如图,在正方体中分别为棱的中点,用过点的平面截去该正方体的上半部分,则剩余几何体(下半部分)的左视图为()【答案】C【解析】通过观察剩余几何体(下半部分),可以发现C图才正确,故选C.【考点】1、直观图;2、三视图.20.如图,已知三棱柱的所有棱长都是2,且.(1)求证:点在底面内的射影在的平分线上;(2)求棱柱的体积.【答案】(1)证明见解析;(2).【解析】(1)通过作图的方式先作出的射影,只需求到距离相等即是所求,利用三角形全等即可;(2)底面是等边三角形,面积容易求得,其高为,(1)可知,,,可得到,则此可求出.试题解析:(1)证明:过作平面,垂足为,作,垂足为,连接,则,,故平面,故,同理,过作,连接,则.∵,,∴,∴≌,∴,∴是的角平分线,即点在底面内的射影在的平分线上.(2)解:由(1)可知,,,在中,,∴,∴三棱柱的体积为【考点】线面垂直、几何体的体积.【易错点晴】破解线面垂直关系的技巧(1)解答此类问题的关键在于熟练把握空间垂直关系的判定与性质,注意平面图形中的一些线线垂直关系的灵活利用,这是证明空间垂直关系的基础.(2)由于“线线垂直”“线面垂直”“面面垂直”之间可以相互转化,因此整个证明过程围绕着线面垂直这个核心而展开,这是化解空间垂直关系难点的技巧所在.21.如图,梯形中,,分别是的中点,矩形所在的平面与所在的平面互相垂直,且.(1)证明:平面;(2)证明:平面;(3)若二面角为,求直线与平面所成角的大小.【答案】(1)证明见解析(2)证明见解析;(3).【解析】(1)根据平面与平面垂直的性质定理证平面,又,从而可证得平面;(2)取中点,连接,先证得为平行四边形,进而可得,再根据直线与平面平行的判定定理即可证得平面;(3)连接交于,连接,证明平面,则即为直线与平面所成角,再通过解求得的大小.试题解析:(1)平面.(2)取中点,连接,.(3)为二面角的平面角,.由(1)知,中,,,∴,∴,∴与平面成角.【考点】1、线面垂直的判定;2、线面平行的判定;3、线面角的求法.【方法点晴】本题主要考查的是线面垂直、平行判定和线面角的求法,属于中档题.证明线面垂直的方法主要有定义法,判定定理法;证明线面平行的关键是证明线线平行,证明线线平行常用的方法是利用三角形、梯形的中位线,对应线段成比例,构造平行四边形,平行线的传递性,线面垂直的性质定理,面面平行的性质定理.求线面角的一般步骤是:一作出线面角,二证明,三求线面角的大小.22.如图,在正方形中,点分别是的中点,将分别沿、折起,使两点重合于.(Ⅰ)求证:平面⊥平面;(Ⅱ)求二面角的余弦值.【答案】(Ⅰ)证明见解析;(Ⅱ).【解析】(Ⅰ)要证明面面垂直,可以先证明线面垂直,即可以先证明直线,进而可证明平面⊥平面;(Ⅱ)可以用传统方法也可以用向量方法,用传统方法时,可按照“作、算、证”的步骤,并结合余弦定理即可求二面角的余弦值.向量法关键是要建立适当的直角坐标系,并正确地求出二平面的法向量,进而可得到二面角的余弦值.试题解析:(Ⅰ)证明:连接交于,连接.在正方形中,点是的中点,点是的中点,所以,所以,因此,所以在等腰中,是的中点,且.因此在等腰中,,从而平面.又平面,所以平面平面.即平面平面.(Ⅱ)方法一:在正方形中,连接,交于.设正方形的边长为.由于点是的中点,点是的中点.所以,于是,从而,所以.于是,在翻折后的几何体中,为二面角的平面角.在正方形中,解得,,所以,在中,,由余弦定理得.所以,二面角的余弦值为.方法二:由题知两两互相垂直,故以为原点,向量方向分别为轴的正方向,建立如图的空间直角坐标系.设正方形边长为,则,所以,设为平面的一个法向量,由,得,令,得,又由题知是平面的一个法向量,所以,所以,二面角的余弦值为.【考点】1、面面垂直;2、二面角的平面角.23.如图4,在边长为4的菱形中,,点分别是边的中点,,沿将翻折到,连接,得到如图5的五棱锥,且.(1)求证:;(2)求四棱锥的体积.【答案】(1)证明见解析;(2).【解析】(1)由三角形的中位线定理,证得,再由菱形的对角线互相垂直,证得,即可得到,再由已知可得,然后利用线面垂直的判定得到答案;(2)设,连接,结合已知可得,通过解直角三角形求得平面,然后求出梯形的面积,代入棱锥的体积公式得到答案.试题解析:(1)证明:∵分别是边的中点,∴∵菱形对角线互相垂直,∴,∴∴,∵平面,平面,∴平面,∴平面,∴(2)设,连接,∵,∴为等边三角形,∴,在中,在中,,∴∵平面,平面,∴平面,∴,∴四棱锥的体积【考点】直线与平面垂直的判定;几何体的体积的计算.24.如图,棱形与正三角形的边长均为2,它们所在平面互相垂直,,且.(1)求证:;(2)若,求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)依据线面平行的判定定理,需要在平面找到一条直线与直线平行即可.因为平面平面,则过点作于,连接,证明四边形为平行四边形即可;(2)由(1)知平面,又,为等边三角形,,分别以所在直线为轴建立如图所示空间直角坐标系,分别求出平面和平面的法向量即可.试题解析:(1)如图,过点作于,连接,,可证得四边形为平行四边形,平面(2)连接,由(1),得为中点,又,为等边三角形,分别以所在直线为轴建立如图所示空间直角坐标系,则,设平面的法向量为,由即,令,得设平面的法向量为由即,令,得所以,所以二面角的余弦值是【考点】1.线面平行的判定定理;2.利用空间向量求二面角.25.一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】D【解析】由三视图可知,该几何体为半个圆柱加一个长方体的组合体,故其体积为【考点】三视图,几何体的体积26.如图所示,在三棱柱ABC—A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点.(1)证明:平面BDC1⊥平面BDC;(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.【答案】(1)证明见解析;(2).【解析】(1)由题意易证平面,再由面面垂直的判定定理即可得平面平面;(2)设棱锥的体积为,易求,三棱柱的体积为,于是可得,从而得到答案.试题解析:(1)证明:由题设知BC⊥CC1,BC⊥AC,CC1∩AC=C,所以BC⊥平面ACC1A1.又DC1⊂平面ACC1A1,所以DC1⊥BC.由题设知∠A1DC1=∠ADC=45°,所以∠CDC1=90°,即DC1⊥DC.又DC∩BC=C,所以DC1⊥平面BDC.又DC1⊂平面BDC1,故平面BDC1⊥平面BDC.(2)设棱锥B—DACC1的体积为V1,AC=1.由题意得V1=××1×1=.又三棱柱ABC—A1B1C1的体积V=1,所以(V-V1)∶V1=1∶1.故平面BDC1分此棱柱所得两部分体积的比为1∶1.【考点】平面与平面垂直的判定;棱信的结构特征;棱柱、棱锥、棱台的体积.【易错点睛】(1)两平面垂直,在一个平面内垂直于交线的直线必垂直于另一个平面.这是把面面垂直转化为线面垂直的依据.运用时要注意“平面内的直线”.(2)两个相交平面同时垂直于第三个平面,那么它们的交线也垂直于第三个平面,此性质是在课本习题中出现的,在不是很复杂的题目中要对此进行证明.27.如图1,,,过动点作,垂足在线段上且异于点,连接,沿将折起,使(如图2所示).(Ⅰ)当的长为多少时,三棱锥的体积最大;(Ⅱ)当三棱锥的体积最大时,设点分别为棱的中点,试在棱上确定一点,使得,并求与平面所成角的大小.【答案】(I);(II)是的靠近点的一个四等分点,大小为.【解析】(I)设,利用三棱锥体积公式求得体积的表达式为,利用导数或者基本不等式求出其最大值.(II)以为坐标原点建立空间直角坐标系,设,利用求出,然后利用法向量求出与平面所成角的大小为.试题解析:解析:(Ⅰ)方法一:在图1所示的中,设,则.由,知,为等腰直角三角形,所以.由折起前知,折起后(如图2),,,且.所以平面.又,所以.于是,当且仅当,即时,等号成立,故当,即时,三棱锥的体积最大.方法二:同方法一,得.令,由,且,解得.当时,;当时,.所以当时,取得最大值.故当时,三棱锥的体积最大.(Ⅱ)方法一:以为原点,建立如图所示的空间直角坐标系.由(Ⅰ)知,当三棱锥的体积最大时,.于是可得,,且.设,则,因为等价于,解得,.所以当(即是的靠近点的一个四等分点)时,. 设平面的一个法向量为,由,及,得可取.设与平面所成角的大小为,则由,可得,即.故与平面所成角的大小为.方法二:由(Ⅰ)知,当三棱锥的体积最大时,,如图b,取的中点,连结,则.由(Ⅰ)知平面,所以平面.如图c,延长至点使得,连,则四边形为正方形,所以.取的中点,连结,又为的中点,则,所以.因为平面,又平面,所以.又,所以平面.又平面,所以.因为当且仅当,而点是唯一的,所以点是唯一的.即当(即是的靠近点的一个四等分点)时,.连结,由计算得,所以与是两个共底边的全等的等腰三角形,如图d所示,取的中点,连接,则平面.在平面中,过点作于,则平面,故是与平面所成的角.在中,易得,所以是正三角形,故,故与平面所成角的大小为.【考点】空间向量与立体几何.28.如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且,.求证:(1)直线DE平面A1C1 F;(2)平面B1DE⊥平面A1C1F.【答案】(1)详见解析(2)详见解析【解析】(1)利用线面平行判定定理证明线面平行,而线线平行的寻找往往结合平面几何的知识,如中位线的性质等;(2)利用面面垂直判定定理证明,即从线面垂直出发给予证明,而线面垂直的证明,往往需要多次利用线面垂直性质定理与判定定理.试题解析:证明:(1)在直三棱柱中,在三角形ABC中,因为D,E分别为AB,BC的中点,所以,于是,又因为DE平面平面,所以直线DE//平面.(2)在直三棱柱中,因为平面,所以,又因为,所以平面.因为平面,所以.又因为,所以.因为直线,所以【考点】直线与直线、直线与平面、平面与平面的位置关系【名师】垂直、平行关系证明中应用转化与化归思想的常见类型:(1)证明线面、面面平行,需转化为证明线线平行;(2)证明线面垂直,需转化为证明线线垂直;(3)证明线线垂直,需转化为证明线面垂直;(4)证明面面垂直,需转化为证明线面垂直,进而转化为证明线线垂直.29.某四面体的三视图如图,则该四面体四个面中最大的面积是()A.B.C.D.【答案】D【解析】将该几何体放入边长为的正方体中,由三视图可知该四面体为有由直观图可知,最大面积为三角形的面积,在三角形中,所以面积故选D.【考点】1、几何体的三视图;2、三角形的面积公式.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,有时还需要将不规则几何体补形成常见几何体,来增加直观图的立体感.30.如图,在四棱锥中,是边长为的正三角形,底面.(1)求证:;(2)已知是上一点, 且平面.若,求点到平面的距离.【答案】(1)见解析;(2)1.【解析】(1)连接交于,然后利用线面垂直的性质与已知条件证得平面,由此推出,从而通过解三角形推出,进而推出平面,可使问题得证;(2)取的中点, 连接,当为的中点,根据等腰三角形的性质可推出,然后结合中位线定理推出平面,由此可求出点到平面的距离.试题解析:(1)证明:连接交于,底面,平面,则,即,即平面.(2)取的中点, 连接,当为的中点时,平面,证明如下:,由(1) 得,则,则是的中点,平面平面,平面,平面.底面点到平面的距离等于.【考点】1、空间直线与直线的位置关系;2、线面平行的判定定理;3、点到平面的距离.【方法点睛】解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间的垂直关系进行转化,转化时要正确运用相关的定理,找出足够的条件进行推理;证明线面平行时,通常利用中位定理得到线线平行,从而推出面面平行,进而推出线面平行.31.已知正三角形边长为2,将它沿高翻折,使点与点间的距离为,此时四面体的外接球的表面积为 .【答案】。
2024届高考数学专项立体几何大题含答案

立体几何大题1.空间中的平行关系(1)线线平行(2)线面平行的判定定理:平面外一直线与平面内一直线平行,则线面平行(3)线面平行的性质定理若线面平行,经过直线的平面与该平面相交,则直线与交线平行(4)面面平行的判定定理判定定理1:一个平面内有两条相交直线分别平行于另一个平面,则面面平行判定定理2:一个平面内有两条相交直线分别于另一个平面内两条相交直线平行,则面面平行(5)面面平行的性质定理性质定理1:两平面互相平行,一个平面内任意一条直线平行于另一个平面性质定理2:两平面互相平行,一平面与两平面相交,则交线互相平行6.空间中的垂直关系(1)线线垂直(2)线面垂直的判定定理一直线与平面内两条相交直线垂直,则线面垂直(3)线面垂直的性质定理性质定理1:一直线与平面垂直,则这条直线垂直于平面内的任意一条直线性质定理2:垂直于同一个平面的两条直线平行(4)面面垂直的判定定理一个平面内有一条直线垂直于另一个平面,则两个平面垂直(或:一个平面经过另一个平面的垂线,则面面垂直)(5)面面垂直的性质定理两平面垂直,其中一个平面内有一条直线与交线垂直,则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角,a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角,sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ,n 为平面α,β的法向量).9.点B 到平面α的距离d =|AB ⋅n | (n 为平面α的法向量,AB 是经过面α的一条斜线,A ∈α).2024届高考数学专项立体几何大题含答案模拟训练一、解答题1(22·23下·湖南·二模)如图,在直三棱柱ABC -A B C 中,∠ABC =120°,AB =BC =2,AC =BB ,点D 为棱BB 的中点,AE =13AC .(1)求DE 的长度;(2)求平面CDE 与平面BDE 夹角的余弦值.2(22·23下·绍兴·二模)如图,在多面体ABCDE 中,DE ⊥平面BCD ,△ABC 为正三角形,△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证:AE ⊥BC ;(2)若AE ⎳平面BCD ,求直线BE 与平面ABC 所成的线面角的正弦值.3(22·23·张家口·三模)如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,∠CBB1=60°,AB= BC=2,AC=AB1=2.(1)证明:平面ACB1⊥平面BB1C1C;(2)求平面ACC1A1与平面A1B1C1夹角的余弦值.4(22·23·湛江·二模)如图1,在五边形ABCDE中,四边形ABCE为正方形,CD⊥DE,CD=DE,如图2,将△ABE沿BE折起,使得A至A1处,且A1B⊥A1D.(1)证明:DE⊥平面A1BE;(2)求二面角C-A1E-D的余弦值.5(22·23下·长沙·三模)如图,在多面体ABCDE 中,平面ACD ⊥平面ABC ,BE ⊥平面ABC ,△ABC 和△ACD 均为正三角形,AC =4,BE =3,点F 在AC 上.(1)若BF ⎳平面CDE ,求CF ;(2)若F 是AC 的中点,求二面角F -DE -C 的正弦值.6(22·23下·湖北·二模)如图,S 为圆锥的顶点,O 是圆锥底面的圆心,△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322,AM =2MS ,AS =3,PQ 为⊙O 的一条弦,且SB ⎳平面PMQ .(1)求PQ 的最小值;(2)若SA ⊥PQ ,求直线PQ 与平面BCM 所成角的正弦值.7(22·23·深圳·二模)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA= AD=2AB,点M是PD的中点.(1)证明:AM⊥PC;(2)设AC的中点为O,点N在棱PC上(异于点P,C),且ON=OA,求直线AN与平面ACM所成角的正弦值.8(22·23下·温州·二模)已知三棱锥D-ABC中,△BCD是边长为3的正三角形,AB=AC=AD, AD与平面BCD所成角的余弦值为33.(1)求证:AD⊥BC;(2)求二面角D-AC-B的平面角的正弦值.9(22·23下·浙江·二模)如图,四面体ABCD,AD⊥CD,AD=CD,AC=2,AB=3,∠CAB=60°,E为AB上的点,且AC⊥DE,DE与平面ABC所成角为30°,(1)求三棱锥D-BCE的体积;(2)求二面角B-CD-E的余弦值.10(22·23下·襄阳·三模)如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C为矩形,∠BAC=90°,AB= AC=2,AA1=4,A1在底面ABC的射影为BC的中点N,M为B1C1的中点.(1)求证:平面A1MNA⊥平面A1BC;(2)求平面A1B1BA与平面BB1C1C夹角的余弦值.11(22·23·唐山·二模)如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,侧面ACC1A1⊥底面ABC,且AA1=AC,∠AA1C1=120°,M是CC1的中点.(1)证明:A1C⊥BM.(2)求二面角A1-BC-M的正弦值.12(22·23下·盐城·三模)如图,该几何体是由等高的半个圆柱和14个圆柱拼接而成,点G为弧CD的中点,且C,E,D,G四点共面.(1)证明:平面BDF⊥平面BCG;(2)若平面BDF与平面ABG所成二面角的余弦值为155,且线段AB长度为2,求点G到直线DF的距离.13(22·23下·江苏·三模)如图,圆锥DO中,AE为底面圆O的直径,AE=AD,△ABC为底面圆O的内接正三角形,圆锥的高DO=18,点P为线段DO上一个动点.(1)当PO=36时,证明:PA⊥平面PBC;(2)当P点在什么位置时,直线PE和平面PBC所成角的正弦值最大.14(22·23下·镇江·三模)如图,四边形ABCD是边长为2的菱形,∠ABC=60°,四边形PACQ为矩形,PA=1,从下列三个条件中任选一个作为已知条件,并解答问题(如果选择多个条件分别解答,按第一个解答计分).①BP,DP与平面ABCD所成角相等;②三棱锥P-ABD体积为33;③cos∠BPA=55(1)平面PACQ⊥平面ABCD;(2)求二面角B-PQ-D的大小;(3)求点C到平面BPQ的距离.15(22·23下·江苏·一模)在三棱柱ABC -A 1B 1C 1中,平面A 1B 1BA ⊥平面ABC ,侧面A 1B 1BA 为菱形,∠ABB 1=π3,AB 1⊥AC ,AB =AC =2,E 是AC 的中点.(1)求证:A 1B ⊥平面AB 1C ;(2)点P 在线段A 1E 上(异于点A 1,E ),AP 与平面A 1BE 所成角为π4,求EP EA 1的值.16(22·23下·河北·三模)如图,四棱锥P -ABCD 的底面ABCD 是菱形,其对角线AC ,BD 交于点O ,且PO ⊥平面ABCD ,OC =1,OD =OP =2,M 是PD 的中点,N 是线段CD 上一动点.(1)当平面OMN ⎳平面PBC 时,试确定点N 的位置,并说明理由;(2)在(1)的前提下,点Q 在直线MN 上,以PQ 为直径的球的表面积为214π.以O 为原点,OC ,OD ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O -xyz ,求点Q 的坐标.17(22·23·汕头·三模)如图,圆台O1O2的轴截面为等腰梯形A1ACC1,AC=2AA1=2A1C1=4,B为底面圆周上异于A,C的点.(1)在平面BCC1内,过C1作一条直线与平面A1AB平行,并说明理由;(2)若四棱锥B-A1ACC1的体积为23,设平面A1AB∩平面C1CB=l,Q∈l,求CQ的最小值.18(19·20下·临沂·二模)如图①,在Rt△ABC中,B为直角,AB=BC=6,EF∥BC,AE=2,沿EF将△AEF折起,使∠AEB=π3,得到如图②的几何体,点D在线段AC上.(1)求证:平面AEF⊥平面ABC;(2)若AE⎳平面BDF,求直线AF与平面BDF所成角的正弦值.19(22·23下·广州·三模)如图,四棱锥P-ABCD的底面为正方形,AB=AP=2,PA⊥平面ABCD,E,F分别是线段PB,PD的中点,G是线段PC上的一点.(1)求证:平面EFG⊥平面PAC;(2)若直线AG与平面AEF所成角的正弦值为13,且G点不是线段PC的中点,求三棱锥E-ABG体积.20(22·23下·长沙·一模)斜三棱柱ABC-A1B1C1的各棱长都为2,∠A1AB=60°,点A1在下底面ABC 的投影为AB的中点O.(1)在棱BB1(含端点)上是否存在一点D使A1D⊥AC1若存在,求出BD的长;若不存在,请说明理由;(2)求点A1到平面BCC1B1的距离.21(22·23下·长沙·三模)如图,三棱台ABC -A 1B 1C 1,AB ⊥BC ,AC ⊥BB 1,平面ABB 1A 1⊥平面ABC ,AB =6,BC =4,BB 1=2,AC 1与A 1C 相交于点D ,AE =2EB,且DE ∥平面BCC 1B 1.(1)求三棱锥C -A 1B 1C 1的体积;(2)平面A 1B 1C 与平面ABC 所成角为α,CC 1与平面A 1B 1C 所成角为β,求证:α+β=π4.22(22·23·衡水·一模)如图所示,A ,B ,C ,D 四点共面,其中∠BAD =∠ADC =90°,AB =12AD ,点P ,Q 在平面ABCD 的同侧,且PA ⊥平面ABCD ,CQ ⊥平面ABCD .(1)若直线l ⊂平面PAB ,求证:l ⎳平面CDQ ;(2)若PQ ⎳AC ,∠ABP =∠DAC =45°,平面BPQ ∩平面CDQ =m ,求锐二面角B -m -C 的余弦值.23(22·23下·湖北·三模)已知平行六面体(底面是平行四边形的四棱柱)ABCD-A1B1C1D1的各条棱长均为2,且有∠AA1D1=∠AA1B1=∠D1A1B1=60°.(1)求证:平面AA1C1C⊥平面A1B1C1D1;(2)求直线B1D与平面AA1C1C所成角的正弦值.24(22·23下·武汉·三模)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E为线段PB的中点,F为线段BC上的动点.(1)求证:平面AEF⊥平面PBC;(2)求平面AEF与平面PDC夹角的最小值.25(22·23下·黄冈·三模)如图1,在四边形ABCD中,BC⊥CD,AE∥CD,AE=BE=2CD=2,CE =3.将四边形AECD沿AE折起,使得BC=3,得到如图2所示的几何体.(1)若G为AB的中点,证明:DG⊥平面ABE;(2)若F为BE上一动点,且二面角B-AD-F的余弦值为63,求EFEB的值.26(22·23·德州·三模)图1是直角梯形ABCD,AB⎳CD,∠D=90°,AD=3,AB=2,CD=3,四边形ABCE为平行四边形,以BE为折痕将△BCE折起,使点C到达C1的位置,且AC1=6,如图2.(1)求证:平面BC1E⊥平面ABED;(2)在线段BE上存在点P使得PA与平面ABC1的正弦值为365,求平面BAC1与PAC1所成角的余弦值.27(22·23·山东·二模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⎳CD,AB⊥BC,PA =AB=BC=2,CD=4.(1)证明:AD⊥PC;(2)若M为线段PB的靠近B点的四等分点,判断直线AM与平面PDC是否相交?如果相交,求出P到交点H的距离,如果不相交,说明理由.28(22·23·黄山·三模)如图,在直角梯形ABCD中,AD⎳BC,AD⊥CD,四边形CDEF为平行四边形,对角线CE和DF相交于点H,平面CDEF⊥平面ABCD,BC=2AD,∠DCF=60°,G是线段BE上一动点(不含端点).(1)当点G为线段BE的中点时,证明:AG⎳平面CDEF;(2)若AD=1,CD=DE=2,且直线DG与平面CDEF成45°角,求二面角E-DG-F的正弦值.29(22·23·菏泽·三模)已知在直三棱柱ABC-A1B1C1中,其中AA1=2AC=4,AB=BC,F为BB1的中点,点E是CC1上靠近C1的四等分点,A1F与底面ABC所成角的余弦值为2 2.(1)求证:平面AFC⊥平面A1EF;(2)在线段A1F上是否存在一点N,使得平面AFC与平面NB1C1所成的锐二面角的余弦值为277,若存在,确定点N的位置,若不存在,请说明理由.30(22·23·福州·三模)如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=2,AB=AC=1,将△PAB绕着PA逆时针旋转π3到△PAD的位置,得到如图所示的组合体,M为PD的中点.(1)当∠BAC为何值时,该组合体的体积最大,并求出最大值;(2)当PC⎳平面MAB时,求直线PC与平面PBD所成角的正弦值.31(22·23·福州·二模)如图1,在△ABC 中,AB =AC =2,∠BAC =2π3,E 为BC 的中点,F 为AB 上一点,且EF ⊥AB .将△BEF 沿EF 翻折到△B EF 的位置,如图2.(1)当AB =2时,证明:平面B AE ⊥平面ABC ;(2)已知二面角B -EF -A 的大小为π4,棱AC 上是否存在点M ,使得直线B E 与平面B MF 所成角的正弦值为1010?若存在,确定M 的位置;若不存在,请说明理由.32(22·23·三明·三模)如图,平面五边形ABCDE 由等边三角形ADE 与直角梯形ABCD 组成,其中AD ∥BC ,AD ⊥DC ,AD =2BC =2,CD =3,将△ADE 沿AD 折起,使点E 到达点M 的位置,且BM =a .(1)当a =6时,证明AD ⊥BM 并求四棱锥M -ABCD 的体积;(2)已知点P 为棱CM 上靠近点C 的三等分点,当a =3时,求平面PBD 与平面ABCD 夹角的余弦值.33(22·23·宁德·一模)如图①在平行四边形ABCD 中,AE ⊥DC ,AD =4,AB =3,∠ADE =60°,将△ADE 沿AE 折起,使平面ADE ⊥平面ABCE ,得到图②所示几何体.(1)若M 为BD 的中点,求四棱锥M -ABCE 的体积V M -ABCE ;(2)在线段DB 上,是否存在一点M ,使得平面MAC 与平面ABCE 所成锐二面角的余弦值为235,如果存在,求出DMDB的值,如果不存在,说明理由.34(22·23·龙岩·二模)三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,AB =AC =2,侧面A 1ACC 1为矩形,∠A 1AB =2π3,三棱锥C 1-ABC 的体积为233.(1)求侧棱AA 1的长;(2)侧棱CC 1上是否存在点E ,使得直线AE 与平面A 1BC 所成角的正弦值为55?若存在,求出线段C 1E 的长;若不存在,请说明理由.35(22·23下·浙江·二模)如图,在多面体ABC-A1B1C1中,AA1⎳BB1⎳CC1,AA1⊥平面A1B1C1,△A1B1C1为等边三角形,A1B1=BB1=2,AA1=3,CC1=1,点M是AC的中点.(1)若点G是△A1B1C1的重心,证明;点G在平面BB1M内;(2)求二面角B1-BM-C1的正弦值.36(22·23下·浙江·三模)如图,三棱台ABC-A1B1C1中,A1C1=4,AC=6,D为线段AC上靠近C的三等分点.(1)线段BC上是否存在点E,使得A1B⎳平面C1DE,若不存在,请说明理由;若存在,请求出BEBC的值;(2)若A1A=AB=4,∠A1AC=∠BAC=π3,点A1到平面ABC的距离为3,且点A1在底面ABC的射影落在△ABC内部,求直线B1D与平面ACC1A1所成角的正弦值.37(22·23下·苏州·三模)如图,在三棱锥P-ABC中,△ABC是边长为62的等边三角形,且PA= PB=PC=6,PD⊥平面ABC,垂足为D,DE⊥平面PAB,垂足为E,连接PE并延长交AB于点G.(1)求二面角P-AB-C的余弦值;(2)在平面PAC内找一点F,使得EF⊥平面PAC,说明作法及理由,并求四面体PDEF的体积.38(22·23·沧州·三模)如图,该几何体是由等高的半个圆柱和14个圆柱拼接而成.C,E,D,G在同一平面内,且CG=DG.(1)证明:平面BFD⊥平面BCG;(2)若直线GC与平面ABG所成角的正弦值为105,求平面BFD与平面ABG所成角的余弦值.39(23·24上·永州·一模)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD为正三角形,且AD=2AB=4,M、N分别为PD、BC的中点,H在线段PC上,且PC=3PH.(1)求证:MN⎳平面PAB;(2)当AM⊥PC时,求平面AMN与平面HMN的夹角的余弦值.40(22·23·潍坊·三模)如图,P为圆锥的顶点,O是圆锥底面的圆心,AC为底面直径,△ABD为底面圆O的内接正三角形,且边长为3,点E在母线PC上,且AE=3,CE=1.(1)求证:PO∥平面BDE;(2)求证:平面BED⊥平面ABD(3)若点M为线段PO上的动点.当直线DM与平面ABE所成角的正弦值最大时,求此时点M到平面ABE的距离.立体几何大题1.空间中的平行关系(1)线线平行(2)线面平行的判定定理:平面外一直线与平面内一直线平行,则线面平行(3)线面平行的性质定理若线面平行,经过直线的平面与该平面相交,则直线与交线平行(4)面面平行的判定定理判定定理1:一个平面内有两条相交直线分别平行于另一个平面,则面面平行判定定理2:一个平面内有两条相交直线分别于另一个平面内两条相交直线平行,则面面平行(5)面面平行的性质定理性质定理1:两平面互相平行,一个平面内任意一条直线平行于另一个平面性质定理2:两平面互相平行,一平面与两平面相交,则交线互相平行6.空间中的垂直关系(1)线线垂直(2)线面垂直的判定定理一直线与平面内两条相交直线垂直,则线面垂直(3)线面垂直的性质定理性质定理1:一直线与平面垂直,则这条直线垂直于平面内的任意一条直线性质定理2:垂直于同一个平面的两条直线平行(4)面面垂直的判定定理一个平面内有一条直线垂直于另一个平面,则两个平面垂直(或:一个平面经过另一个平面的垂线,则面面垂直)(5)面面垂直的性质定理两平面垂直,其中一个平面内有一条直线与交线垂直,则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角,a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角,sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ,n 为平面α,β的法向量).9.点B 到平面α的距离d =|AB ⋅n | (n 为平面α的法向量,AB 是经过面α的一条斜线,A ∈α).模拟训练一、解答题1(22·23下·湖南·二模)如图,在直三棱柱ABC -A B C 中,∠ABC =120°,AB =BC =2,AC =BB ,点D 为棱BB 的中点,AE =13AC .(1)求DE 的长度;(2)求平面CDE 与平面BDE 夹角的余弦值.【答案】(1)393(2)34【分析】(1)在△ABC 中,用余弦定理可得到AC =23,在△ABE 中,用余弦定理可得BE =233,即可求得DE =DB 2+BE 2=393;(2)以B 为原点,分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立空间直角坐标系,求出平面CDE 与平面BDE 的法向量,即可求解【详解】(1)因为在直三棱柱ABC -A B C 中,∠ABC =120°,AB =BC =2,在△ABC 中,由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC=22+22-AC 22×2×2=-12,解得AC =23,则AE =13AC =233,在△ABE 中,由余弦定理得cos ∠BAE =AB 2+AE 2-BE 22AB ⋅AE =22+233 2-BE 22×2×233=32,解得BE =233,又AC =BB =23,所以BD =12BB =3,因为BB ⊥平面ABC ,BE ⊂平面ABC ,所以BB ⊥BE ,在直角三角形DBE 中,DE =DB 2+BE 2=(3)2+233 2=393;(2)因为AE =BE =233,所以∠ABE =∠BAE =30°,则∠CBE =∠ABC -∠ABE =120°-30°=90°,则BE ,BC ,BB 两两互相垂直,以B 为原点,分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立如下图所示的空间直角坐标系:设平面CDE 的法向量为n =x ,y ,z ,由n ⋅CD =x ,y ,z ⋅0,-2,3 =-2y +3z =0n ⋅CE =x ,y ,z ⋅233,-2,0 =233x -2y =0 ,得z =233y x =3y,令y =3,得平面CDE 的一个法向量为n =3,3,2 ;平面BDE 的一个法向量为m =0,1,0 .设平面CDE 与平面BDE 夹角的大小为θ,则cos θ=m ⋅n m n =0,1,0 ⋅3,3,2 1×4=34,故平面CDE 与平面BDE 夹角的余弦值为34.2(22·23下·绍兴·二模)如图,在多面体ABCDE 中,DE ⊥平面BCD ,△ABC 为正三角形,△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证:AE ⊥BC ;(2)若AE ⎳平面BCD ,求直线BE 与平面ABC 所成的线面角的正弦值.【答案】(1)证明见解析(2)63【分析】(1)由线面垂直的性质定理和判定定理即可证明;(2)法一:由分析可知,∠EBH 就是直线BE 与平面ABC 所成的线面角,设∠AFD =α,当α<90°时,O 与D 重合,可得A ,E 两点重合,不符合题意,当α>90°时,求出EH ,BE ,即可得出答案;法二:建立空间直角坐标系,求出直线BE 的方向向量与平面ABC 的法向量,由线面角的向量公式代入即可得出答案.【详解】(1)设F 为BC 中点,连接AF ,EF ,则由△ABC 为正三角形,得AF ⊥BC ;DE ⊥平面BCD ,且△BCD 为等腰直角三角形,计算可得:BE =CE =2,∴EF ⊥BC .EF ∩AF =F ,EF ,AF ⊂面AEF ,于是BC ⊥面AEF ,AE ⊂面AEF ,从而BC ⊥AE .(2)法一:由(1)可知,过点E 作EH ⊥AF ,垂足为H ,则∠EBH 就是直线BE 与平面ABC 所成的线面角.当AE ⎳平面BCD 时,可得A 到平面BCD 的距离为 2.设∠AFD =α,所以AF ⋅sin α=2,可得sin α=63,当α<90°时,cos α=33,不妨设A 在底面BCD 射影为O ,则FO =1,此时O 与D 重合,可得A ,E 两点重合,不符合题意,舍去;当α>90°时,FO =1,此时O 在DF 的延长线上,作EH ⊥AF ,由于AODE 为矩形,可得AE =DO =2,AE ∥OD ,可得sin ∠EAH =63,可得EH =263.于是sin ∠EBH =EH BE=63.法二:建立如图坐标系,可得F 0,0,0 ,B 1,0,0 ,C -1,0,0 ,D 0,1,0 ,E 0,1,2 ,A 0,a ,b由AF =3,解得a 2+b 2=3,又∵AE ⎳平面BCD ,令n =0,0,1 ,可得AB ⋅n =0,解得b =2,a =±1.当a =1时A ,E 重合,所以a =-1,此时A 0,-1,2 .不妨设平面ABC 的法向量为m =x ,y ,z ,则CB ⋅m =0CA ⋅m =0代入得x -y +2z =02x =0 ,令z =1,则y =2,所以m =0,2,1 .由于BE =-1,1,2 ,不妨设所成角为θ,则sin θ=∣cos BE ,m |=63.3(22·23·张家口·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C 为菱形,∠CBB 1=60°,AB =BC =2,AC =AB 1=2.(1)证明:平面ACB 1⊥平面BB 1C 1C ;(2)求平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值.【答案】(1)证明见解析;(2)57.【分析】(1)利用面面垂直的判定定理进行证明;(2)利用垂直关系建立空间直角坐标系,用向量法进行求解.【详解】(1)如图,连接BC 1,交B 1C 于O ,连接AO .因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为BC 1的中点.又AC =AB 1=2,故AO ⊥B 1C .又AB =BC =2,且∠CBB 1=60°,所以CO =1,BO =3,所以AO =AC 2-CO 2=1.又AB =2,所以AB 2=BO 2+AO 2,所以AO ⊥BO .因为BO ,CB 1⊂平面BB 1C 1C ,BO ∩CB 1=O ,所以AO ⊥平面BB 1C 1C .又AO ⊂平面ACB 1,所以平面ACB 1⊥平面BB 1C 1C .(2)由(1)知,OA ,OB ,OB 1两两互相垂直,因此以O 为坐标原点,OB ,OB 1,OA 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系O -xyz ,则A (0,0,1),B (3,0,0),C (0,-1,0),C 1(-3,0,0).故CC 1 =(-3,1,0),CA =(0,1,1),CB =(3,1,0).设n =(x 1,y 1,z 1)为平面ACC 1A 1的一个法向量,则有n ⋅CC 1 =0n ⋅CA =0 ,即-3x 1+y 1=0y 1+z 1=0 ,令x 1=1,则n =(1,3,-3).设m =(x 2,y 2,z 2)为平面ABC 的一个法向量,则有m ⋅CA =0m ⋅CB =0,即y 2+z 2=03x 2+y 2=0 ,令x 2=1,则m =(1,-3,3).因为平面A 1B 1C 1∥平面ABC ,所以m =(1,-3,3)也是平面A 1B 1C 1的一个法向量.所以cos <n ,m > =n ⋅m n m=1-3-3 7×7=57.所以平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值57. 4(22·23·湛江·二模)如图1,在五边形ABCDE 中,四边形ABCE 为正方形,CD ⊥DE ,CD =DE ,如图2,将△ABE 沿BE 折起,使得A 至A 1处,且A 1B ⊥A 1D .(1)证明:DE ⊥平面A 1BE ;(2)求二面角C -A 1E -D 的余弦值.【答案】(1)证明见解析(2)63【分析】(1)由已知易得DE ⊥BE ,即可证明线面垂直;(2)建立空间直角坐标系,用坐标公式法求解即可.【详解】(1)由题意得∠BEC =∠CED =π4,∠BED =π2,DE ⊥BE ,又A 1B ⊥A 1D ,A 1E ∩A 1D =A 1,A 1E ,A 1D ⊂面A 1ED ,所以A 1B ⊥面A 1ED ,又DE ⊂面A 1ED ,则DE ⊥A 1B ,又DE ⊥BE ,A 1B ∩BE =B ,A 1B ⊂平面A 1BE ,BE ⊂平面A 1BE ,所以DE ⊥平面A 1BE .(2)取BE 的中点O ,可知BE =2CD ,OE =CD ,由DE ⊥BE ,且CD ⊥DE 可得OE ⎳CD ,所以四边形OCDE 是平行四边形,所以CO ∥DE ,则CO ⊥平面A 1BE ,设BE =2,以点O 为坐标原点,OB ,OC ,OA 1所在直线为坐标轴建立空间直角坐标系,如图,则A 1(0,0,1),E (-1,0,0),B (1,0,0),C (0,1,0),D (-1,1,0),EA 1 =(1,0,1),EC =(1,1,0),ED =(0,1,0),设平面A 1EC 的一个法向量为n 1 =(x 1,y 1,z 1),则n 1 ⋅EA 1 =0n 1 ⋅EC =0 ,即x 1+z 1=0x 1+y 1=0 ,取x 1=1,则n 1 =(1,-1,-1),设平面A 1ED 的一个法向量为n 2 =(x 2,y 2,z 2),则n 2 ⋅E 1A =0n 2 ⋅ED =0 ,即x 2+z 2=0y 2=0 ,取x 2=1,则n 2 =(1,0,-1),所以cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2=63,由图可知,二面角C -A 1E -D 为锐角,所以面角C -A 1E -D 的余弦值为63.5(22·23下·长沙·三模)如图,在多面体ABCDE 中,平面ACD ⊥平面ABC ,BE ⊥平面ABC ,△ABC 和△ACD 均为正三角形,AC =4,BE =3,点F 在AC 上.(1)若BF ⎳平面CDE ,求CF ;(2)若F 是AC 的中点,求二面角F -DE -C 的正弦值.【答案】(1)CF =1(2)8517【分析】(1)记AC 中点为M ,连接DM 、BM ,依题意可得DM ⊥AC ,根据面面垂直的性质得到DM ⊥平面ABC ,如图建立空间直角坐标系,求出平面CDE 的法向量,设F a ,0,0 ,a ∈2,-2 ,依题意可得BF ⋅n =0求出a 的值,即可得解;(2)依题意点F 与点M 重合,利用空间向量法计算可得.【详解】(1)记AC 中点为M ,连接DM 、BM ,△ACD 为正三角形,AC =4,则DM ⊥AC ,且DM =2 3.所以DM ⊥平面ABC ,又△ABC 为正三角形,所以BM ⊥AC ,所以BM =23,如图建立空间直角坐标系,则B 0,23,0 ,C -2,0,0 ,D 0,0,23 ,E 0,23,3 ,所以CD =2,0,23 ,CE =2,23,3 ,设平面CDE 的法向量为n =x ,y ,z ,则n ⋅CD =2x +23z =0n ⋅CE =2x +23y +3z =0,令x =3,则z =-3,y =-32,则n =3,-32,-3 ,设F a ,0,0 ,a ∈-2,2 ,则BF =a ,-23,0 ,因为BF ⎳平面CDE ,所以BF ⋅n =3a +-23 ×-32+0×-3 =0,解得a =-1,所以F 为CM 的中点,此时CF =1.(2)若F 是AC 的中点,则点F 与点M 重合,则平面FDE 的一个法向量可以为m =1,0,0 ,设二面角F -DE -C 为θ,显然二面角为锐角,则cos θ=m ⋅n m ⋅n=332+-32 2+-3 2=651,所以sin θ=1-cos 2θ=1-651 2=8517,所以二面角F -DE -C 的正弦值为8517.6(22·23下·湖北·二模)如图,S 为圆锥的顶点,O 是圆锥底面的圆心,△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322,AM =2MS ,AS =3,PQ 为⊙O 的一条弦,且SB ⎳平面PMQ .(1)求PQ 的最小值;(2)若SA ⊥PQ ,求直线PQ 与平面BCM 所成角的正弦值.【答案】(1)22(2)3010【分析】(1)作出辅助线,找到符合要求的PQ ,并利用垂径定理得到最小值;(2)在第一问基础上,得到当PQ 取得最小值时,SA ⊥PQ ,并建立空间直角坐标系,利用空间向量求解线面角.【详解】(1)过点M 作MH ⎳SB 交AB 于点H ,过点H 作PQ ⊥AB ,此时满足SB ⎳平面PMQ ,由平面几何知识易知,PQ =2r 2-d 2,当弦心距d 最大时,d =OH ,弦长最短,即PQ 取得最小值,因为AM =2MS ,AS =3,所以AH =2HB ,因为AC ⊥BC ,AC =BC =322,由勾股定理得AB =322⋅2=3,故AH =2,HB =1,连接OQ ,则OQ =32,由勾股定理得HQ =OQ 2-OH 2=94-14=2,所以PQ =2HQ =22;(2)连接OS ,则OS ⊥平面ACB ,因为PQ ⊂平面ACB ,故OS ⊥PQ ,而SA ⊥PQ ,OS ∩SA =S ,所以PQ ⊥平面AOS ,即有PQ ⊥AB .以O 为坐标原点,过点O 且平行PQ 的直线为x 轴,OB 所在直线为y 轴,OS 所在直线为z 轴,建立空间直角坐标系,则P -2,12,0 ,Q 2,12,0 ,B 0,32,0 ,C 32,0,0 ,M 0,-12,3 ,设平面BCM 的法向量为m =x ,y ,z ,则m ⋅CB =x ,y ,z ⋅-32,32,0 =-32x +32y =0m ⋅MB =x ,y ,z ⋅0,2,-3 =2y -3z =0,令x =1,则y =1,z =233,故m =1,1,233,设直线PQ 与平面BCM 所成角的大小为θ,则sin θ=cos PQ ,m =PQ ⋅m PQ ⋅m =22,0,0 ⋅1,1,233 22×1+1+43=3010.故直线PQ与平面BCM所成角的正弦值为30 10.7(22·23·深圳·二模)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA= AD=2AB,点M是PD的中点.(1)证明:AM⊥PC;(2)设AC的中点为O,点N在棱PC上(异于点P,C),且ON=OA,求直线AN与平面ACM所成角的正弦值.【答案】(1)证明见解析(2)1510【分析】(1)由等腰三角形的性质可得AM⊥PD,由面面垂直的性质可得CD⊥平面PAD,则CD⊥AM,所以由线面垂直的判定可得AM⊥平面PCD,从而可得结论;(2)以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,利用空间向量求解即可.【详解】(1)证明:因为PA=AD,点M是PD的中点,所以AM⊥PD.因为PA⊥平面ABCD,PA⊂平面PAD,所以平面PAD⊥平面ABCD,因为四边形ABCD为矩形,所以CD⊥AD,因为平面PAD∩平面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面PAD,所以CD⊥AM,因为PD∩CD=D,PD,CD⊂平面PCD,所以AM⊥平面PCD,因为PC⊂平面PCD,所以AM⊥PC.(2)解:由题意可得AB,AD,AP两两垂直,设AB=1,如图,以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2),22所以AM =0,22,22 ,AC =1,2,0 ,设平面ACM 的法向量为n =x ,y ,z ,则AM ⋅n =22y +22z =0AC ⋅n =x +2y =0,令y =-1可得x =2,z =1,所以平面ACM 的一个法向量n =2,-1,1 .PC =1,2,-2 ,设N x N ,y N ,z N ,PN =λPC =λ,2λ,-2λ (0<λ<1),即x N ,y N ,z N -2 =λ,2λ,-2λ ,所以N λ,2λ,2-2λ .又O 12,22,0 ,ON =OA =32,所以λ-12 2+2λ-22 2+(2-2λ)2=34,化简得5λ2-7λ+2=0,解得λ=25或λ=1(舍去).所以AN =25,225,325,设直线AN 与平面ACM 所成的角为θ,则sin θ=n ⋅AN n ⋅AN=3252+1+1×425+825+1825=1510,所以直线AN 与平面ACM 所成角的正弦值为1510.8(22·23下·温州·二模)已知三棱锥D -ABC 中,△BCD 是边长为3的正三角形,AB =AC =AD ,AD 与平面BCD 所成角的余弦值为33.(1)求证:AD ⊥BC ;(2)求二面角D -AC -B 的平面角的正弦值.【答案】(1)证明见解析(2)223【分析】(1)取BC 的中点E ,连接AE ,DE ,证明BC ⊥平面ADE ,即可得证;(2)取正三角形BCD 的中心O ,连接OA ,从而可得OA ⊥平面BCD ,则∠ODA 即为AD 与平面BCD 所成角的平面角,进而可得AB =AC =AD =3,取AC 中点为H ,连接DH ,BH ,则DH ⊥AC ,BH ⊥AC ,故∠BHD 即为二面角D -AC -B 的平面角,解△BDH 即可得解.【详解】(1)取BC 的中点E ,连接AE ,DE ,因为△BCD 是边长为3的正三角形,所以DE ⊥BC ,又AE ∩DE =E ,AE ,DE ⊂平面ADE ,所以BC ⊥平面ADE ,因为AD ⊂平面ADE ,所以AD ⊥BC ;(2)取正三角形BCD 的中心O ,连接OA ,则点O 在DE 上,且OD =23DE ,由AB =AC =AD ,△BCD 是正三角形,得三棱锥A -BCD 为正三棱锥,则OA ⊥平面BCD ,故∠ODA 即为AD 与平面BCD 所成角的平面角,又AD 与平面BCD 所成角的余弦值为33,所以OD AD =3×32×23AD=33,即AB =AC =AD =3,即三棱锥A -BCD 是正四面体,取AC 中点为H ,连接DH ,BH ,则DH ⊥AC ,BH ⊥AC ,故∠BHD 即为二面角D -AC -B 的平面角,在△BDH 中,BH =DH =332,BD =3,则cos ∠BHD =BH 2+DH 2-BD 22⋅BH ⋅DH =274+274-92×332×332=13,所以sin ∠BHD =1-cos 2∠BHD =223,所以二面角D -AC -B 的平面角的正弦值223.9(22·23下·浙江·二模)如图,四面体ABCD ,AD ⊥CD ,AD =CD ,AC =2,AB =3,∠CAB =60°,E 为AB 上的点,且AC ⊥DE ,DE 与平面ABC 所成角为30°,(1)求三棱锥D -BCE 的体积;(2)求二面角B -CD -E 的余弦值.【答案】(1)答案见解析;(2)答案见解析.【分析】(1)取AC 中点F ,可证明AC ⊥平面DEF ,得平面ABC ⊥平面DEF ,DE 在平面ABC 内的射影就是直线EF ,∠DEF 是DE 与平面ABC 所成的角,即∠DEF =30°,由正弦定理求得∠FDE ,有两个解,在∠FDE =60°时可证DF ⊥平面ABC ,在∠FDE =120°时,取FE 中点H 证明DH ⊥平面ABC ,然后由棱锥体积公式计算体积;(2)建立如图所示的空间直角坐标系,用空间向量法求二面角.【详解】(1)取AC 中点F ,连接FE ,FD ,因为AD =CD ,所以DF ⊥AC ,又AC ⊥DE ,DE ∩DF =D ,DE ,DF ⊂平面DEF ,所以AC ⊥平面DEF ,而FE ⊂平面DEF ,所以AC ⊥FE ,由AC ⊥平面DEF ,AC ⊂平面ABC 得平面ABC ⊥平面DEF ,因此DE 在平面ABC 内的射影就是直线EF ,所以∠DEF 是DE 与平面ABC 所成的角,即∠DEF =30°,AD =CD ,AC =2,因此DF =12AC =1,在△DEF 中,由正弦定理EF sin ∠FDE =DF sin ∠DEF 得1sin30°=3sin ∠FDE ,sin ∠FDE =32,∠FDE 为△DEF 内角,所以∠FDE =60°或120°,S △ABC =12AB ×AC ×sin ∠BAC =12×3×2×sin60°=333,S △CBE =BE BAS △ABC =3-23×332=32,若∠FDE =60°,则∠DFE =90°,即DF ⊥FE ,AC ∩FE =F ,AC ,FE ⊂平面ABC ,所以DF ⊥平面ABC ,V D -BCE =13S △BCE ⋅DF =13×32×1=36;若∠FDE =120°,则∠DFE =30°,DF =DE =1,取EF 中点H ,连接DH ,则DH ⊥EF ,因为平面ABC ⊥平面DEF ,平面ABC ∩平面DEF =EF ,而DH ⊂平面DEF ,所以DH ⊥平面ABC ,DH =DF sin ∠DFE =1×sin30°=12,所以V D -BCE =13S △BCE ⋅DF =13×32×12=312;(2)若∠FDE =60°,以FA ,FE ,FD 为x ,y ,z 轴建立如图所示的空间直角坐标系F -xyz ,则D (0,0,1),C (-1,0,0),A (1,0,0),E (0,3,0),AE =(-1,3,0),EB =12AE =-12,32,0 ,所以B 点坐标为-12,332,0 ,CD =(1,0,1),CB =12,332,0 ,CE =(1,3,0),设平面DBC 的一个法向量是m =(x 1,y 1,z 1),则m ⋅CD =x 1+z 1=0m ⋅CB =12x 1+332y 1=0,取y 1=-1,则x 1=33,z 1=-33,即m =(33,-1,-33),设平面DEC 的一个法向量是n =(x 2,y 2,z 2),则n ⋅CD =x 2+z 2=0n ⋅CE =x 2+3y 2=0,取y 2=-1,则x 2=3,z 2=-3,即m =(3,-1,-3),cos m ,n =m ⋅n m n =9+1+955×7=19385385,所以二面角B -CD -E 的余弦值是19385;若∠FDE =120°,以FA 为x 轴,FE 为y 轴,过F 且平行于HD 的直线为z 轴建立如图所示的空间直角坐标系F -xyz ,FH =12FE =32,则D 0,32,12 ,C (-1,0,0),A (1,0,0),E (0,3,0),AE =(-1,3,0),EB =12AE =-12,32,0 ,所以B 点坐标为-12,332,0 ,CD =1,32,12 ,CB =12,332,0 ,CE =(1,3,0),设平面DBC 的一个法向量是m =(x 1,y 1,z 1),则m ⋅CD =x 1+32y 1+12z 1=0m ⋅CB =12x 1+332y 1=0,取y 1=-1,则x 1=33,z 1=-53,即m =(33,-1,-53),设平面DEC 的一个法向量是n =(x 2,y 2,z 2),则n ⋅CD =x 2+32y 2+12z 2=0n ⋅CE =x 2+3y 2=0,取y 2=-1,则x 2=3,z 2=-3,即m =(3,-1,-3),cos m ,n =m ⋅n m n =9+1+15103×7=25721721,所以二面角B -CD -E 的余弦值是25721721.10(22·23下·襄阳·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C 为矩形,∠BAC =90°,AB =AC =2,AA 1=4,A 1在底面ABC 的射影为BC 的中点N ,M 为B 1C 1的中点.(1)求证:平面A 1MNA ⊥平面A 1BC ;(2)求平面A 1B 1BA 与平面BB 1C 1C 夹角的余弦值.【答案】(1)证明见解析(2)23015【分析】(1)利用线面垂直和面面垂直的判定定理证明;(2)利用空间向量的坐标运算求面面夹角的余弦值.【详解】(1)如图,∵A 1N ⊥面ABC ,连AN ,则AN ⊥A 1N ,又AB =AC =2,∴AN ⊥BC ,又AN ∩BC =N ,A 1N ⊂面A 1BC ,BC ⊂面A 1BC ,于是AN ⊥面A 1BC ,又AN ⊂面A 1MN ,,所以面A 1BC ⊥面A 1MNA .(2)由(1)可得,以NA ,NB ,NA 1 为x ,y ,z 轴,建系如图,∠BAC =90°,AB =AC =2,BC =22则A (2,0,0),B (0,2,0),C (0,-2,0),因为AA 1=4,AN =2,所以A 1N =14,则A 1(0,0,14),因为NB 1 =NB +BB 1 =NB +AA 1 =0,2,0 +-2,0,14 =-2,2,14 ,所以B 1-2,2,14 ,设平面A 1BB 1的一个法向量为m =(x ,y ,z ),因为A 1B =(0,2,-14),B 1B =(2,0,-14),所以A 1B ⋅m =2y -14z =0B 1B ⋅m =2x -14z =0 ,令y =7,则x =7,z =1,所以m =(7,7,1),设平面BCC 1B 1的一个法向量为n =(a ,b ,c ),因为BC =(0,-22,0),BB 1 =(-2,0,14),所以BC ⋅n =-22b =0BB 1 ⋅n =-2a +14c =0,令a =7,则b =0,c =1,所以n =(7,0,1),设平面A 1BB 1与平面BCC 1B 1夹角为θ,则cos θ=cos <m ,n >=m ⋅n m n=7+0+17+7+1×7+0+1=23015,所以平面A 1BB 1与平面BCC 1B 1夹角的余弦值为23015.11(22·23·唐山·二模)如图,在三棱柱ABC -A 1B 1C 1中,△ABC 是等边三角形,侧面ACC 1A 1⊥底面ABC ,且AA 1=AC ,∠AA 1C 1=120°,M 是CC 1的中点.(1)证明:A 1C ⊥BM .(2)求二面角A 1-BC -M 的正弦值.【答案】(1)证明见解析(2)45【分析】(1)根据菱形的性质、结合面面垂直的性质,线面垂直的判定定理进行证明即可;(2)建立空间直角坐标系,运用空间向量夹角公式进行求解即sk .【详解】(1)取AC 的中点O ,连接OM ,OB ,AC 1.在三棱柱ABC -A 1B 1C 1中,由AA 1=AC ,得四边形ACC 1A 1为菱形,所以A 1C ⊥AC 1,易知OM ∥AC 1,则A 1C ⊥OM .由△ABC 是等边三角形,知OB ⊥AC ,又平面ACC 1A 1⊥平面ABC ,平面ACC 1A 1∩平面ABC =AC ,OB ⊂平面ABC ,知OB ⊥平面ACC 1A 1,则OB ⊥A 1C ,又OB ∩OM =O ,OB ,OM ⊂平面OBM ,得A 1C ⊥平面OBM ,又BM ⊂平面OBM ,故A 1C ⊥BM ..(2)连接OA 1,因为侧面ACC 1A 1为菱形,∠AA 1C 1=120°,则∠A 1AC =60°,则△A 1AC 为等边三角形,所以A 1O ⊥AC ,又由(1)易知OA 1,OB ,AC 两两垂直,故以O 为坐标原点,分别以OB ,OC ,OA 1 的方向为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系.不妨设AB =2,则O 0,0,0 ,B 3,0,0 ,C 0,1,0 ,A 10,0,3 ,C 10,2,3 ,BA 1 =-3,0,3 ,BC =-3,1,0 ,CC 1 =0,1,3 ,。
2024届全国高考数学真题分类专项(立体几何)汇编(附答案)

2024届全国高考数学真题分类专项(立体几何)汇编1.(2024年新课标全国Ⅰ卷)已知圆柱和圆锥的底面半径相等,侧)A .B .C .D .2.(2024年新课标全国Ⅱ卷)已知正三棱台111ABC A B C -的体积为523,6AB =,112A B =,则1A A 与平面ABC 所成角的正切值为( )A .12 B .1 C .2 D .33.(2024年高考全国甲卷数学(理))已知甲、乙两个圆台上、下底面的半径均为1r 和2r ,母线长分别为()212r r -和()213r r -,则两个圆台的体积之比=V V 甲乙.4.(2024年新课标全国Ⅰ卷)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,2PA AC ==,1,BC AB =.(1)若AD PB ⊥,证明://AD 平面PBC ;(2)若AD DC ⊥,且二面角A CP D --的正弦值为7,求AD .5.(2024年新课标全国Ⅱ卷)如图,平面四边形ABCD 中,8AB =,3CD =,AD =90ADC ︒∠=,30BAD ︒∠=,点E ,F 满足25AE AD = ,12AF AB =,将AEF △沿EF 对折至PEF !,使得PC =.(1)证明:EF PD ⊥;(2)求面PCD 与面PBF 所成的二面角的正弦值.6.(2024年高考全国甲卷数学(理))如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形ADEF 均为等腰梯形,//,//BC AD EF AD ,4,2AD AB BC EF ====,ED FB ==M为AD 的中点.(1)证明://BM 平面CDE ; (2)求二面角F BM E --的正弦值.参考答案1.(2024年新课标全国Ⅰ卷)已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高,则圆锥的体积为( )A .B .C .D .【详细详解】设圆柱的底面半径为r而它们的侧面积相等,所以2ππr r =即=,故3r =,故圆锥的体积为1π93⨯=.故选:B.2.(2024年新课标全国Ⅱ卷)已知正三棱台111ABC A B C -的体积为523,6AB =,112A B =,则1A A 与平面ABC 所成角的正切值为( ) A .12B .1C .2D .3【详细详解】解法一:分别取11,BC B C 的中点1,D D ,则11AD A D =可知11111662222ABC A B C S S =⨯⨯==⨯= 设正三棱台111ABC A B C -的为h ,则(11115233ABC A B C V h -==,解得h = 如图,分别过11,A D 作底面垂线,垂足为,M N ,设AM x =,则1AA DN AD AM MN x =--=-,可得1DD ==结合等腰梯形11BCC B 可得22211622BB DD -⎛⎫=+ ⎪⎝⎭,即()221616433x x +=++,解得x = 所以1A A 与平面ABC 所成角的正切值为11tan 1A MA ADAM?=; 解法二:将正三棱台111ABC A B C -补成正三棱锥-P ABC ,则1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,因为11113PA A B PA AB ==,则111127P A B C P ABC V V --=, 可知1112652273ABC A B C P ABC V --==,则18P ABC V -=, 设正三棱锥-P ABC 的高为d,则116618322P ABC V d -=⨯⨯⨯=,解得d =,取底面ABC 的中心为O ,则PO ⊥底面ABC,且AO = 所以PA 与平面ABC 所成角的正切值tan 1POPAO AO∠==. 故选:B.3.(2024年高考全国甲卷数学(理))已知甲、乙两个圆台上、下底面的半径均为1r 和2r ,母线长分别为()212r r -和()213r r -,则两个圆台的体积之比=V V 甲乙. 【详细详解】由题可得两个圆台的高分别为)12h r r ==-甲,)12h r r ==-乙,所以((212113143S S h r r V h V h S S h +-====+甲甲甲乙乙乙.4.(2024年新课标全国Ⅰ卷)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,2PA AC ==,1,BC AB =.(1)若AD PB ⊥,证明://AD 平面PBC ; (2)若AD DC ⊥,且二面角A CP D --的正弦值为7,求AD . 【详细详解】(1)(1)因为PA ⊥平面ABCD ,而AD ⊂平面ABCD ,所以PA AD ⊥, 又AD PB ⊥,PB PA P = ,,PB PA ⊂平面PAB ,所以AD ⊥平面PAB , 而AB ⊂平面PAB ,所以AD AB ⊥.因为222BC AB AC +=,所以BC AB ⊥, 根据平面知识可知//AD BC , 又AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC .(2)如图所示,过点D 作DE AC ⊥于E ,再过点E 作EF CP ⊥于F ,连接DF , 因为PA ⊥平面ABCD ,所以平面PAC ⊥平面ABCD ,而平面PAC 平面ABCD AC =, 所以DE ⊥平面PAC ,又EF CP ⊥,所以⊥CP 平面DEF , 根据二面角的定义可知,DFE ∠即为二面角A CP D --的平面角,即sin 7DFE ∠=,即tan DFE ∠= 因为AD DC ⊥,设AD x =,则CD =2DE =,又242xCE -=,而EFC 为等腰直角三角形,所以2EF=,故22tan DFE∠==x =AD =5.(2024年新课标全国Ⅱ卷)如图,平面四边形ABCD 中,8AB =,3CD =,AD =,90ADC ︒∠=,30BAD ︒∠=,点E ,F 满足25AE AD = ,12AF AB =,将AEF △沿EF 对折至PEF !,使得PC =.(1)证明:EF PD ⊥;(2)求面PCD 与面PBF 所成的二面角的正弦值.【详细详解】(1)由218,,52AB AD AE AD AF AB ====, 得4AE AF ==,又30BAD ︒∠=,在AEF △中,由余弦定理得2EF =,所以222AE EF AF +=,则AE EF ⊥,即EF AD ⊥, 所以,EF PE EF DE ⊥⊥,又,PE DE E PE DE =⊂ 、平面PDE , 所以EF ⊥平面PDE ,又PD ⊂平面PDE , 故EF ⊥PD ;(2)连接CE ,由90,3ADC ED CD ︒∠===,则22236CE ED CD =+=,在PEC 中,6PC PE EC ===,得222EC PE PC +=,所以PE EC ⊥,由(1)知PE EF ⊥,又,EC EF E EC EF =⊂ 、平面ABCD , 所以PE ⊥平面ABCD ,又ED ⊂平面ABCD ,所以PE ED ⊥,则,,PE EF ED 两两垂直,建立如图空间直角坐标系E xyz -,则(0,0,0),(0,0,(2,0,0),(0,E P D C F A -, 由F 是AB的中点,得(4,B ,所以(4,(2,0,PC PD PB PF =-=-=-=-,设平面PCD 和平面PBF 的一个法向量分别为111222(,,),(,,)n x y z m x y z ==,则11111300n PC x n PD ⎧⋅=+-=⎪⎨⋅=-=⎪⎩,222224020m PB x m PF x ⎧⋅=+-=⎪⎨⋅=-=⎪⎩ ,令122,y x ==11220,3,1,1x z y z ===-=,所以(0,2,3),1,1)n m ==- ,所以cos ,m nm n m n ⋅===设平面PCD 和平面PBF 所成角为θ,则sin θ== 即平面PCD 和平面PBF所成角的正弦值为65.6.(2024年高考全国甲卷数学(理))如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形ADEF 均为等腰梯形,//,//BC AD EF AD ,4,2AD AB BC EF ====,ED FB ==M 为AD 的中点.(1)证明://BM 平面CDE ; (2)求二面角F BM E --的正弦值.【详细详解】(1)因为//,2,4,BC AD EF AD M ==为AD 的中点,所以//,BC MD BC MD =,四边形BCDM 为平行四边形,所以//BM CD ,又因为BM ⊄平面CDE ,CD ⊂平面CDE ,所以//BM 平面CDE ;(2)如图所示,作BO AD ⊥交AD 于O ,连接OF ,因为四边形ABCD 为等腰梯形,//,4,BC AD AD =2AB BC ==,所以2CD =, 结合(1)BCDM 为平行四边形,可得2BM CD ==,又2AM =, 所以ABM 为等边三角形,O 为AM中点,所以OB =又因为四边形ADEF 为等腰梯形,M 为AD 中点,所以,//EF MD EF MD =, 四边形EFMD 为平行四边形,FM ED AF ==,所以AFM △为等腰三角形,ABM 与AFM △底边上中点O 重合,OF AM ⊥,3OF ==,因为222OB OF BF +=,所以OB OF ⊥,所以,,OB OD OF 互相垂直,以OB 方向为x 轴,OD 方向为y 轴,OF 方向为z 轴,建立O xyz -空间直角坐标系,()0,0,3F,)()(),0,1,0,0,2,3BM E,()(),BM BF ==,()2,3BE = ,设平面BFM 的法向量为()111,,m x y z =,平面EMB 的法向量为()222,,n x y z =,则00m BM m BF ⎧⋅=⎪⎨⋅=⎪⎩,即1111030y z ⎧+=⎪⎨+=⎪⎩,令1x =113,1y z ==,即)m = ,则00n BM n BE ⎧⋅=⎪⎨⋅=⎪⎩,即222220230y y z ⎧+=⎪⎨++=⎪⎩,令2x =,得223,1y z ==-,即)1n =-,11cos ,13m n m n m n ⋅===⋅,则sin ,m n =故二面角F BM E --的正弦值为13.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,点P 是棱 AD 上一点,且AP =a
3,过B 1,D 1,P 的平面交底面ABCD
于PQ ,Q 在直线CD 上,则PQ =________.
2.如图,在直四棱柱ABCD -A 1B 1C 1D 1中,∠ADC =90°, 且AA 1=AD =DC =2,M ∈平面ABCD , 当D 1M ⊥平面A 1C 1D 时,DM =________.
3.如图,在底面是矩形的四棱锥P -ABCD 中,P A ⊥平面ABCD ,P A =AB =2,BC =4,E 是PD 的中点.
(1)求证:平面PDC ⊥平面P AD ; (2)求点B 到平面PCD 的距离;
4.如图,PO ⊥平面ABCD ,点O 在AB 上,EA ∥PO ,四边形ABCD 为直角梯形,BC ⊥AB ,BC =CD =BO =PO ,EA =AO =12CD .
(1)求证:BC ⊥平面ABPE ;
(2)直线PE 上是否存在点M ,使DM ∥平面PBC ,若存在,求出点M ; 若不存在,说明理由.
5.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F
分别为DD1、DB的中点.
(1)求证:EF∥平面ABC1D1;
(2)求证:EF⊥B1C;
(3)求三棱锥B1-EFC的体积.
6.如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离.
1.
22
3
a ∵B 1D 1∥平面ABCD ,平面B 1D 1P ∩平面ABCD =PQ ,∴B 1D 1∥PQ , 又B 1D 1∥BD ,∴BD ∥PQ ,设PQ ∩AB =M ,∵AB ∥CD ,∴△APM ∽△DPQ ,
∴
PQ PM =PD
AP
=2,即PQ =2PM , 又△APM ∽△ADP ,∴PM BD =AP AD =13,∴PM =1
3BD ,
又BD =2a ,∴PQ =22
3
a .
2.[答案] 22 ∵DA =DC =DD 1且DA 、DC 、DD 1两两垂直,故当点M 使四边形ADCM 为正方形时,D 1M ⊥平面A 1C 1D ,∴DM =2 2.
(2)过A 作AF ⊥PD ,垂足为F .
在Rt P AD 中,P A =2,AD =BC =4,PD =42+22=25,
AF ·PD =P A ·AD ,∴AF =2×425=455,即点B 到平面PCD 的距离为45
5.
4.[解析] (1)∵PO ⊥平面ABCD ,
BC ⊂平面ABCD ,∴BC ⊥PO ,
又BC ⊥AB ,AB ∩PO =O ,AB ⊂平面ABP ,PO ⊂平面ABP ,∴BC ⊥平面ABP , 又EA ∥PO ,AO ⊂平面ABP ,∴EA ⊂平面ABP ,∴BC ⊥平面ABPE . (2)点E 即为所求的点,即点M 与点E 重合.
取PO 的中点N ,连结EN 并延长交PB 于F ,∵EA =1,PO =2,∴NO =1, 又EA 与PO 都与平面ABCD 垂直,
∴EF ∥AB ,∴F 为PB 的中点,∴NF =1
2
OB =1,∴EF =2,
又CD =2,EF ∥AB ∥CD ,∴四边形DCFE 为平行四边形,∴DE ∥CF , ∵CF ⊂平面PBC ,DE ⊄平面PBC ,∴DE ∥平面PBC .∴当M 与E 重合时即可. 5. (1)证明:连结BD 1,在△DD 1B 中,E 、F 分别为D 1D ,DB 的中点,则EF ∥D 1B ,又EF ⊄平面ABC 1D 1,D 1B ⊂平面ABC 1D 1,∴EF ∥平面ABC 1D 1.
(2)证明:∵B 1C ⊥AB ,B 1C ⊥BC 1,AB ∩BC 1=B , ∴B 1C ⊥平面ABC 1D 1,
又BD 1⊂平面ABC 1D 1,∴B 1C ⊥BD 1, 又EF ∥BD 1,∴EF ⊥B 1C .
(3)解:∵CF ⊥BD ,CF ⊥BB 1,∴CF ⊥平面BDD 1B 1, 即CF ⊥平面EFB 1,且CF =BF = 2
∵EF =1
2BD 1=3,B 1F =BF 2+BB 12=(2)2+22=6,B 1E =B 1D 12+D 1E 2=
12+(22)2=3,
∴EF 2+B 1F 2=B 1E 2,即∠EFB 1=90°, ∴VB 1-EFC =VC -B 1EF =13·S △B 1EF ·CF
=13×12·EF ·B 1F ·CF =13×12
×3×6×2=1. 6.[解析] (1)∵PD ⊥平面ABCD ,BC ⊂平面ABCD ,∴PD ⊥BC .
由∠BCD =90°知,BC ⊥DC ,
∵PD ∩DC =D ,∴BC ⊥平面PDC ,∴BC ⊥PC . (2)设点A 到平面PBC 的距离为h , ∵AB ∥DC ,∠BCD =90°,∴∠ABC =90°, ∵AB =2,BC =1,∴S △ABC =1
2
AB ·BC =1,
∵PD ⊥平面ABCD ,PD =1,∴V P -ABC =13S △ABC ·PD =1
3,
∵PD ⊥平面ABCD ,∴PD ⊥DC ,∵PD =DC =1,∴PC =2, ∵PC ⊥BC ,BC =1,∴S △PBC =12PC ·BC =2
2
,
∵V A -PBC =V P -ABC ,∴13S △PBC ·h =1
3
,∴h =2,∴点A 到平面PBC 的距离为 2.。
