中北大学离散数学第六章格和布尔代数分析
合集下载
离散数学第6章 格与布尔代数

设c是a∧b 的任一下界,即c ≤ a,c ≤ b 则 c∧a=c, c∧b=c c∧(a∧b)=(c∧a)∧b=c∧b=c ∴c ≤ a∧b 故 a∧b是a和b的最大下界
6-1 格的概念
5)下面证明 a∧b=aa∨b=b 若a∧b=a 则 a∨b=(a∧b)∨b=b 反之,若a∨b=b 则 a∧b=a∧(a∨b)=a
b用a∨b代替(∵两式中b是相互独立的) ∴a∨(a∧(a∨b))=a 即 a∨a=a. (2)格的等价定理:〈A,∨,∧〉代数系统,∨.∧满足交换性, 结合性,吸收性,则A上存在偏序关系≤,使〈A,≤〉是一个格
从格可引出代数系统〈A,∨,∧〉; 而从满足三个条件的〈A,∨,∧〉也可导出格〈A,≤〉 证明见书:(格中⑻⑼⑾三个性质很重要,决定了格)
(11) 要证 a≤a∨(a∧b) 第一式显然成立
a∨(a∧b)≤a
a≤a
a∧b≤a
∴a∨(a∧b) ≤a
∴a=a∨(a∧b)
6-1 格的概念
6、格的等价原理:格〈A,≤〉 (1)引理6-1.1:〈A,∨,∧〉代数系统,若∨, ∧满足吸收性,
则∨, ∧满足幂等性 证:a,b∈A. a∨(a∧b)=a a∧(a∨b)=a.
第六章 格与布尔代数
格论是近代数学的一个重要分支,由它所引出的布尔 代数在计算机科学中有很多直接应用。
格的概念 分配格 有补格 布尔代数 布尔表达式
6-1 格的概念
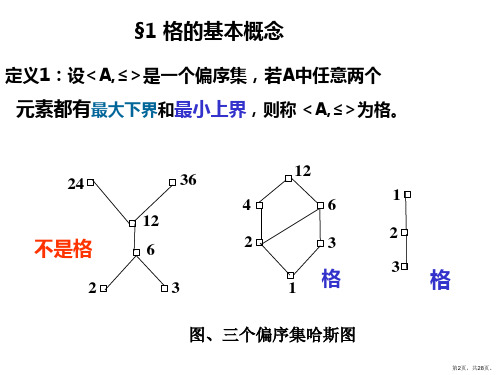
1、回忆偏序集〈A,≤〉,≤偏序关系:满足自反性,反对称性, 传递性。有限集合上的偏序集可用哈斯图来表示:
COV (A) {a,c, b,c, c, d, d,e, d, f }
∧也易求得 ∴ A,∨,∧〉是格〈A,|〉 诱导的代数系统
6-1 格的概念
6-1 格的概念
5)下面证明 a∧b=aa∨b=b 若a∧b=a 则 a∨b=(a∧b)∨b=b 反之,若a∨b=b 则 a∧b=a∧(a∨b)=a
b用a∨b代替(∵两式中b是相互独立的) ∴a∨(a∧(a∨b))=a 即 a∨a=a. (2)格的等价定理:〈A,∨,∧〉代数系统,∨.∧满足交换性, 结合性,吸收性,则A上存在偏序关系≤,使〈A,≤〉是一个格
从格可引出代数系统〈A,∨,∧〉; 而从满足三个条件的〈A,∨,∧〉也可导出格〈A,≤〉 证明见书:(格中⑻⑼⑾三个性质很重要,决定了格)
(11) 要证 a≤a∨(a∧b) 第一式显然成立
a∨(a∧b)≤a
a≤a
a∧b≤a
∴a∨(a∧b) ≤a
∴a=a∨(a∧b)
6-1 格的概念
6、格的等价原理:格〈A,≤〉 (1)引理6-1.1:〈A,∨,∧〉代数系统,若∨, ∧满足吸收性,
则∨, ∧满足幂等性 证:a,b∈A. a∨(a∧b)=a a∧(a∨b)=a.
第六章 格与布尔代数
格论是近代数学的一个重要分支,由它所引出的布尔 代数在计算机科学中有很多直接应用。
格的概念 分配格 有补格 布尔代数 布尔表达式
6-1 格的概念
1、回忆偏序集〈A,≤〉,≤偏序关系:满足自反性,反对称性, 传递性。有限集合上的偏序集可用哈斯图来表示:
COV (A) {a,c, b,c, c, d, d,e, d, f }
∧也易求得 ∴ A,∨,∧〉是格〈A,|〉 诱导的代数系统
6-1 格的概念
《离散数学及其应用》魏雪丽第6章 格与布尔代数

6.1.1 格的概念(lattices) 格的概念( ) 虽然偏序集合的任何子集的上确界、 虽然偏序集合的任何子集的上确界、下确界并不一 定都存在,但存在,则必唯一, 定都存在,但存在,则必唯一,而格的定义保证了 任意两个元素的上确界、下确界的存在性。 任意两个元素的上确界、下确界的存在性。因此我 们通常用a∨b表示 ,b}的上确界,用a∧b表示 , 表示{a, 的上确界 的上确界, 表示{a, 们通常用 ∨ 表示 ∧ 表示 b}的下确界,即 的下确界, 的下确界 a∨b=LUB{a,b}(Least upper bound), ∨ ( ) a∧b=GLB{a,b}(Greatest lower bound), ∧
LUB{a, b} = LUB{a, b}, GLB{a, b} = GLB{a, b}
L B L B
为此我们考察下面的例子。 为此我们考察下面的例子。 如图6.1.4), 取 【例6.1.4】设〈A,≤〉是一个格 如图 】 , 〉是一个格(如图
B1 = {b, d , h}, B2 = {a, b, d , h}, B3 = {a, b, d , f } B4 = {c, e, g , h}, B5 = {a, b, c, d , e, g , h},
计算机科学与技术学院
第6章 格和布尔代数 章
6.1.1 格的概念(lattices) 格的概念( )
表示正整数集, ”表示Z 上整除关系, (3)设Z+表示正整数集,“|”表示 +上整除关系,那么 ) 〈 Z+ ,|〉为格,其中并、交运算即为求两正整数最小公倍数 〉为格,其中并、 和最大公约数的运算, 和最大公约数的运算,即 m∨n=LCM(m,n) m∧n=GCD(m,n), ∨ = ( ) ∧ = ) 由〈 Z+ ,|〉所诱导的代数系统为〈 Z+ , ∨,∧ 〉。 〉所诱导的代数系统为〈 (4)任一全序集〈A, 〉是一个格。因为 a,b ∈A, )任一全序集〈 , 是一个格。 , ∀
格与布尔代数课件2
= {y | y≤x1} ∩{y | y≤x2} = f(x1) ∧2 f(x2) f (x1∨1x2) = f (max{x1,x2}) = {y | y≤max{x1,x2}}
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f,使得对 x1,x2 A, 有f(x1∨1x2)=f(x1)∨2f(x2),f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律:a∨(a∧b) = a、a∧(a∨b) = a
证明:幂等律 ∵ a≤a,∴ a是a的上界,而a∨a是a的最小上界, ∴a∨a≤a ,又 ∵ a≤a ∨a,
由反对称性得:a∨a = a 由对偶原理得,a∧a = a
第15页,共28页。
证明:吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a, a∨(a ∧ b)≤a
解:< I+ , D>是格 ∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大上界等于a、b的最大公约数。
第3页,共28页。
< P(S) , > 是格
∵子集关系是偏序关系,对a,b P(S),
a、b的最小上界等于a∪b,
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2,>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1:,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f,使得对 x1,x2 A, 有f(x1∨1x2)=f(x1)∨2f(x2),f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律:a∨(a∧b) = a、a∧(a∨b) = a
证明:幂等律 ∵ a≤a,∴ a是a的上界,而a∨a是a的最小上界, ∴a∨a≤a ,又 ∵ a≤a ∨a,
由反对称性得:a∨a = a 由对偶原理得,a∧a = a
第15页,共28页。
证明:吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a, a∨(a ∧ b)≤a
解:< I+ , D>是格 ∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大上界等于a、b的最大公约数。
第3页,共28页。
< P(S) , > 是格
∵子集关系是偏序关系,对a,b P(S),
a、b的最小上界等于a∪b,
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2,>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1:,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}
离散数学格与布尔代数优秀课件

于是有 a∨(b∧c) ≤(a∨b)∧(a∨c) 。
由对偶原理得 a∧(b∨c)≥ (a∧b)∨(a∧c) 。
即 (a∧b)∨(a∧c)≤ a∧(b∨c) 。
b c d
由<A,≤>诱导的代数系统。B是A的
非空子集,如果∧
a
和∨在B上封闭,则 称<B, ≤>是<A, ≤>
b
c b
d
e
f e
的子格。
g
a
e
c
a
b f
c
g
d
<C,≤>是<A,≤>的子格。 <A,≤>
<B,≤> <C,≤>
而<B,≤>不是. b∧c=dB, (运算规则要从格<A,≤>中找)
二. 格的对偶原理
界,所以 a∨c≤b∨d。 类似可证 a∧c≤b∧d。 推论:在一个格中,任意 a,b,c∈A,如果b≤c,则
a∨b≤a∨c,a∧b≤a∧c。 此性质称为格的保序性。
3. ∨和∧都满足交换律。即 a∨b=b∨a,a∧b=b∧a 此性质由运算∨和∧的定义直接得证。
4. ∨和∧都满足幂等律。即 a∨a=a a∧a=a 证明:由性质1, a≤a∨a (再证a∨a≤a)
P’: a∨b≥a
{a,b}的最大下界≤a {a,b}的最小上界≥a
三. 格的性质
<A,∨,∧>是由格<A,≤>诱导的代数系统。a,b,c,d∈A 1. a≤a∨b b≤a∨b a∧b≤a a∧b≤b
此性质由运算∨和∧的定义直接得证。 2.如果a≤b,c≤d,则 a∨c≤b∨d,a∧c≤b∧d。 证明:如果a≤b,又b≤b∨d,由传递性得 a≤b∨d, 类似由c≤d, d≤b∨d,由传递性得 c≤b∨d, 这说明b∨d是 {a,c} 的一个上界,而a∨c是 {a,c} 的最小上
离散数学格与布尔代数

<L, > <L, , *>
§7.1 格
例 < P(S) , >是格 表示为<P(S), , * > 又可表示为< P(S) ,∪,∩>
例 <Z+,≤>,或 <Z+,|> <Z+, , * > <Z+, LCM,GCD>
§7.2 格——代数系统
格〈L,≤〉中自然存在两个运算 和 * ,从而 派生出一个代数系统〈L,,*〉
6
<S15,|>,
2
2019/10/5
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/5
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
并、交 运算的性质
定理1 设〈L,≤〉是一个格,并运算与交运算 * 满足 如下性质:
L1 a a = a
a*a=a
(幂等律)
L2 a b = b a a * b = b * a (交换律)
L3 (a b) c = a (b c)
§7.1 格
例 < P(S) , >是格 表示为<P(S), , * > 又可表示为< P(S) ,∪,∩>
例 <Z+,≤>,或 <Z+,|> <Z+, , * > <Z+, LCM,GCD>
§7.2 格——代数系统
格〈L,≤〉中自然存在两个运算 和 * ,从而 派生出一个代数系统〈L,,*〉
6
<S15,|>,
2
2019/10/5
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/5
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
并、交 运算的性质
定理1 设〈L,≤〉是一个格,并运算与交运算 * 满足 如下性质:
L1 a a = a
a*a=a
(幂等律)
L2 a b = b a a * b = b * a (交换律)
L3 (a b) c = a (b c)
第六章 格与布尔代数

21
4. 格的半分配律
格中一般地不满足分配律
定理6-1.5:设<A, ≼>是一个格,对任意的a,b,c,d∈A,都有 (1) a∨( b∧c) ≼ (a∨b)∧( a∨c) (2) (a∧b)∨( a∧c) ≼ a∧( b∨c) 证明:(1)因为a≼a∨b,a≼a∨c, 所以a∧a≼(a∨b)∧(a∨c) 又a=a∧a,故a≼(a∨b)∧(a∨c) 又因b≼a∨b,c≼a∨c,所以由保序性 b∧c≼(a∨b)∧(a∨c) 故(a∨b)∧(a∨c)是a和b∧c的上界, 所以a∨(b∧c)≼(a∨b)∧(a∨c)
由(3)(4)式 a∨a=a, ∨满足等幂性。 同理可证:∧都满足等幂性。
2
回顾
1. 极大(极小)元: B⊆A,b∈B,B中无元素x满足b≺x (x≻b)。 不一定存在;若存在也不一定唯一。 2. 最大(最小)元: a B⊆A,b∈B,B中每一元素x都满足x≼b (b≼x)。 不一定存在;若存在也不一定唯一。 3. 上界(下界 ): B⊆A,a∈A,B中每一元素x有x≼a (a≼x)。 不一定存在;若存在也不一定唯一。 4. 最小上界、最大下界。不一定存在;若存在则必唯一。
24
四、格的代数结构
根据前面的讨论: 格<A, ≼>可以诱导出具有结合律、交换律、吸收律的两个 代数运算∨和∧的代数系统<A,∨,∧> 。
反之,什么样的代数系统<A,*, °> 可确定一个格。 一个代数系统<A,*, °>,如果运算*和°满足结合律、交 换律、吸收律,则可诱导出一个格<A, ≼>,其中偏序 ≼ 定 义为:a ≼b ⇔ a°b=a, 或 a ≼b ⇔ a*b=b
例:<I+, |>是偏序集。 最小上界:两个元素的最小公倍数; 最大下界:两个元素的最大公约数。 <I+, |>是格.
离散数学-格和布尔代数

的次序图如下
-1 的次序图如下
6 2 1 3 2
1 3 6
若 < L; > 是一个偏序集,则对于任意元素 l1, l2, l3 L,有以 下六个关系式成立: l1 l1 若 l1 l2,l2 l1,则 l1 = l2 若 l1 l2,l2 l3,则 l1 l3 l1 l1 若 l1 l2,l2 l1,则 l1 = l2 (7-1) (7-2) (7-3) (7-1) (7-2)
60以上说明与格一样布尔代数也是一个代数系统该代数系统可取交换律分配律同一律和互补律作为公二元运算是一元运算若这些运算满足交换律分配律同一律和互补律则称称作集合代数它是一个布尔代数
第二部分 抽象代数
0
第七章
格和布尔代数
格是 Birkhoff (1884 - 1944) 在 20 世纪 30 年代提出的,格的提出 以子集为背景。 历史上最初出现的格是英国数学家 George Boole 于 1854 年提出 的,是他在研究命题演算中发现的,通常称为布尔格或布尔代 数。 格和布尔代数的理论成为计算机硬件设计和通讯系统设计中的 重要工具。格论是计算机语言的指称语义的理论基础。格是一 种特殊的偏序集,也可以看作是有两个二元运算的代数系统, 布尔代数是一种特殊的格。在保密学、开关理论、计算机理论 和逻辑设计以及其他一些科学和工程领域中,都直接应用了格 与布尔代数。 1
7.2 格及其性质
一、格的定义
定义7-5 设 < L; > 是一个偏序集,如果 L 中任意两个元素都 存在着最大下界和最小上界,则称 < L; > 是格。 由于每对元素的最大下界和最小上界唯一,故引入记号: l1 l2 = glb(l1, l2),l1 l2 = lub(l1, l2), 其中 和 均可看作是集合 L 上的二元运算,分别称为交和并。 注:若 < L; > 是一个格,则意味着 < L; > 也是一个形为 < L; , > 的代数系统,其中 和 是 L 上的两个二元运算, 对于任意 l1, l2 L,l1 l2 表示在偏序 “ ” 意义下,l1 和 l2 的最小上界,l1 l2 表示 l1 和 l2 的最大下界。
离散数学布尔代数

一个非零元素b,至少存在一个原子a,使得a ≤ b。 1
证明:若b本身就是一个原子,则b ≤ b,得证。c
df
若b不是原子,肯定存在b1,使得0 ≤ b1 ≤ b, a
be
若b1是原子,则定理得证;
0
否则,若b1不是原子,则必存在b2,使得0 ≤ b2 ≤ b1 ≤ b
∵<A, ≤>是一个有全下界的有限格,
定理1:对于布尔代数中任意两个元素 a, b,必定有
(1) ( a ) = a, (2) a∨b = a∧b , (3) a∧b = a∨b
3
❖ 布尔代数
定义3:设<A,∨1,∧1, - > 和<B,∨2,∧2, ~ >是两个布尔代数, 如果存在A到B的双射 f,对于a,bA,有
f (a∨1b) = f (a) ∨2 f (b)
2、对a,bA,有 f (a∧b) = f (a)∩f (b)
9
❖ 格与布尔代数
定理3 ( Stone表示定理 ) :
设<A,∨,∧, - >是由有限布尔格<A, ≤>所诱导的一个有 限布尔代数,S是布尔格<A, ≤>中的所有原子的集合,则 < A,∨,∧, - >< P(S),∪,∩, ~ >同构。 分析:要证两个代数系统同构,分为以下几步:
1、找一个双射函数 f: A P(S)
∴a ≤ c ,又∵a ≤ c, ∴a ≤ c ∧ c,即 a ≤ 0,
这与a是原子相矛盾, ∴假设错
∴b ∧ c = 0,由引理1得: b≤c ∴b=c,即:b= a1∨a2∨... ∨ak
7
❖ 格与布尔代数
证明(2):设b的另一种表示形式为 b = aj1∨aj2∨... ∨ajt 其中aj1,aj2,……,ajt是A中原子。∵b是 aj1,aj2,……,ajt 的最小上界, ∴有aj1≤b, aj2≤b,…,ajt≤b,而a1,a2,……,ak是A中满足 a j ≤b的所有原子, {aj1,aj2,…,ajt}是{a1,a2,…,ak}的子集,即 |{aj1,aj2,…,ajt}|<=|{a1,a2,…,ak}|, 即:t ≤ k。(下面证 t < k 是不可能的)
离散数学格的概念

其中 I+ 是正整数,D是整除关系,A={a,b,c} Sn ={n的所有因子}如:S6={1,2,3,6}、S12={1,2,3,4,6,12}、 解:< I+ , D>是格
∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大下界等于a、b的最大公约数。
❖ 基本概念
< B2 , D >是否 < S30 , D >的子格?
30
6
30
10
6 15
2
3
10
15
1 ∨1 2 3 6 11236 22266
2
53
5
∧1 2 3 6
1
11111
21212
说明:
33636 66666
31133 61236
(1) 子格必是格。
运算∨和∧在B1上封闭,B1 S30 且B1 ≠Ø, ∴ < B1, D >是 < S30 , D >的子格; 同理可证< B2 , D >是 < S30 , D >的子格
例:A={a, b, c }, < P(A) , > 所诱导的代数系统为?
< P(A),∪,∩>
❖ 基本概念
定义3:设<A,≤ >是一个格,由其所诱导的代数系统为 <A,∨,∧>。设BA且B ≠Ø ,如果运算∨和∧在B上封闭, 则称<B,≤ > 是<A,≤ >的子格。
❖ 基本概念
例2:B1 = {1,2,3,6} , B2 = {5,10,15,30} ,< B1, D >和
离散数学
❖ 格与布尔代数 1 格的概念
∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大下界等于a、b的最大公约数。
❖ 基本概念
< B2 , D >是否 < S30 , D >的子格?
30
6
30
10
6 15
2
3
10
15
1 ∨1 2 3 6 11236 22266
2
53
5
∧1 2 3 6
1
11111
21212
说明:
33636 66666
31133 61236
(1) 子格必是格。
运算∨和∧在B1上封闭,B1 S30 且B1 ≠Ø, ∴ < B1, D >是 < S30 , D >的子格; 同理可证< B2 , D >是 < S30 , D >的子格
例:A={a, b, c }, < P(A) , > 所诱导的代数系统为?
< P(A),∪,∩>
❖ 基本概念
定义3:设<A,≤ >是一个格,由其所诱导的代数系统为 <A,∨,∧>。设BA且B ≠Ø ,如果运算∨和∧在B上封闭, 则称<B,≤ > 是<A,≤ >的子格。
❖ 基本概念
例2:B1 = {1,2,3,6} , B2 = {5,10,15,30} ,< B1, D >和
离散数学
❖ 格与布尔代数 1 格的概念
离散数学讲义(第6章)

18
6-2 分配格(续)
定理:如果在一个格中交运算对并运算可分配,则并运算 对交运算一定可分配。反之亦然。
定理:每个链是分配格。
定理:设〈A, ≤ 〉为一个分配格,则对任意的a,b,c A,如果有a b = a c且a b = a c,则b=c。
19
6-2 分配格(续)
定义:设〈A,,〉是由格〈A, ≤ 〉所诱导的代数系统。 如果对任意的a,b,cA,当b ≤ a时,有: a (b c) = b (a c) 则称〈A, ≤ 〉是模格。
5
6-1 格的概念(续)
偏序集但不是格
e d f
格
c a b
6
6-1 格的概念(续)
代数系统
设〈A, ≤ 〉是一个格,如果在A上定义两个二元运 算和,使得对于任意的a,bA,ab等于a和b的最小 上界,ab等于a和b的最大下界,那么就称〈A, , 〉 为由格〈A, ≤ 〉所诱导的代数系统。二元运算, 分 别称为并运算和交运算。
定理:分配格一定是模格。
21
6-3 有补格
定义:设〈A, ≤ 〉是一个格,如果存在元素aA,对 任意的xA,都有a ≤ x, 则称a为格〈A, ≤ 〉的全下界。记作 0。 定义:设〈A, ≤ 〉是一个格,如果存在元素bA,对 任意的xA,都有x ≤ b, 则称b为格〈A, ≤ 〉的全上界。记作 1。
{a,b} {a,b} {a,b} {a,b} {a,b}
{b} {a,b}
6-4 布尔代数(续)
定理:对布尔代数中的任意两个元素a,b,有
(a ) a
ab a b
a b ab
定义:具有有限个元素的布尔代数称为有限布尔代数。
26
离散数学第六章

6.1.6 循环群和置换群
§循环群 在循环群G=<a>中, 生成元a的阶与群G的阶是一样 的. 如果a是有限阶元, |a|=n, 则称G为n阶循环群. 如 果a是无限阶元, 则称G为无限阶循环群. 例如: <Z,+>是无限阶循环群; <Z6,>是n阶循环群. 注意:(1) 对9 无限阶循环群G=<a>, G的生成元是a和a-1; (2) 对n阶循环群G=<a>=<e,a,…,an-1>,G的生成元是at 当且仅当t与n互素, 如12阶循环群中, 与12互素的数 有1、5、7、11. 那么G的生成元有a1=a、a5、a7、 a11. (3) N阶循环群G=<a>, 对于n的每个正因子d, G恰好有 一个d阶子群H=<an/d>.
6.1.3 子群
例如, 群<Z6,>中由2生成的子群包含2的各次 幂, 20=e=0, 21=2, 22=22=4, 23=222=0, 所 以由2生成的子群:<2>={0,2,4}.
对于Klein四元群G={e,a,b,c}来说, 由它的每个 元素生成的子群是 <e>={e}, <a>={e,a}, <b>={e,b}, <c>={e,c}
6.1.6 循环群和置换群
§循环群
定义6.7 在群G中, 如果存在aG使得 G={ak|kZ} 则称G为循环群, 记作G=<a>,称a为G的生成元. ☆ 循环群必定是阿贝尔群, 但阿贝尔群不一定 是循环群. 证明: 设<G,*>是一个循环群, 它的生成元是a, 那么,对于任意x,yG, 必有r,sZ, 使得 x=as,y=at, 而且x*y=as*at=as+t=at*as=y*x 由此可见<G,*>是一个阿贝尔群. 例如,<Z,+>是一个循环群, 其生成元是1或-1.
格和布尔代数

15
定义6-1.4 设<A1,≼1>和<A2,≼2>都是格,由它们
分别诱导的代数系统为<A1,1,1>和<A2,2,2>,
如果存在一个从A1到A2的映射f, 使得对于任意的
a,b∈A1,有 f(a1b)=f(a)2f(b) f(a1b)=f(a)2f(b) 则称f为从<A1,1,1 >到<A2,2 ,2 >的格同态, 亦可称<f(A1),≼2>是<A1,≼1>的格同态象。 此外,当f是双射时,则称f为从<A1,1,1 >到 <A2,2,2 >的格同构,亦称<A1,≼1> 和<A2,≼2>
20
定理6-2.1 如果在一个格中交运算对于并运算可 分配,则并运算对交运算也一定是可分配的。 定理6-2.2 每个链都是分配格。 定理6-2.3 设<A,≼>是一个分配格,那么,对于 任意的a,b,cA,如果有 a∧b=a∧c 和 成立,则必有 b=c。 a∨b=a∨c
证明: (a∧b)∨c=(a∧c)∨c=c (吸收律)
例:设A为非空集合,则<P(A),,,~,,A>是布 尔代数。对应的偏序关系是包含关系()。
设S是命题公式的集合,则<S,∨,∧, , F, T>是 布尔代数,对应的偏序关系是蕴含关系()。
28
定理6-4.1 对于布尔代数中任意两个元素a,b,必 定有:
11
推论 设<A,≼>是一个格,对任意a,b,c∈A,如 果b ≼ c,则a b ≼ a c, a b ≼ a c。 (格的保序性) 证: 因为a≤a, b≤c,由定理6-1.2可知, a b ≼ a c, a b ≼ a c 。
定义6-1.4 设<A1,≼1>和<A2,≼2>都是格,由它们
分别诱导的代数系统为<A1,1,1>和<A2,2,2>,
如果存在一个从A1到A2的映射f, 使得对于任意的
a,b∈A1,有 f(a1b)=f(a)2f(b) f(a1b)=f(a)2f(b) 则称f为从<A1,1,1 >到<A2,2 ,2 >的格同态, 亦可称<f(A1),≼2>是<A1,≼1>的格同态象。 此外,当f是双射时,则称f为从<A1,1,1 >到 <A2,2,2 >的格同构,亦称<A1,≼1> 和<A2,≼2>
20
定理6-2.1 如果在一个格中交运算对于并运算可 分配,则并运算对交运算也一定是可分配的。 定理6-2.2 每个链都是分配格。 定理6-2.3 设<A,≼>是一个分配格,那么,对于 任意的a,b,cA,如果有 a∧b=a∧c 和 成立,则必有 b=c。 a∨b=a∨c
证明: (a∧b)∨c=(a∧c)∨c=c (吸收律)
例:设A为非空集合,则<P(A),,,~,,A>是布 尔代数。对应的偏序关系是包含关系()。
设S是命题公式的集合,则<S,∨,∧, , F, T>是 布尔代数,对应的偏序关系是蕴含关系()。
28
定理6-4.1 对于布尔代数中任意两个元素a,b,必 定有:
11
推论 设<A,≼>是一个格,对任意a,b,c∈A,如 果b ≼ c,则a b ≼ a c, a b ≼ a c。 (格的保序性) 证: 因为a≤a, b≤c,由定理6-1.2可知, a b ≼ a c, a b ≼ a c 。
离散数学讨论课(群环格域布尔代数)

图像的边缘 .
算法见pdf 文件
格 论:L为非空集合,+和。是L上的两个二院运算,如果他们满足交换
律、结合律、吸收律,则代数系统(L,+,。)为格,也称作代数格。 交换律:a+b=b+a,a。b=b。a
结合律:(a+b)+c=a+(b+c), (a。b)。c=a。(b。c)
吸收律:a+ (a。b)=a,a。(a+b)=a
环论和格论
环 的 基 本 定 义 整环 域
格 的 基 本 定 义 分配格 有界格
补格
布尔代数
环 的 定 义:设有代数系统(R,+,。),若满足以下条件:
(1)、(R,+)为可换群;(即满足交换律、结合律、存在零元、 负元) (2)、(R,。)为半群;(即满足结合律) (3)、运算。对+满足分配律,即对任意a,b,c∈R,存在
的一些基本概念(如:时域和频域信号空间的群同
构关系) (3)、椭圆曲线密码的应用等
组合群论在密码学中的应用 用群论的基础知识理解信号处理中的一些基本 概念(如:时域和频域信号空间的群同构关系)
椭圆曲线密码的应用
椭圆曲线密 码的应用
无线网络操作模式由 3 部分组成 : ① 移动用户。 能从一个代理范围移动到另一个代理范围 ; ②地点固定的代理。 它如同一个调停机构 , 协调移动用户和服务器之间的通信服务 ; ③ 服务器。 当移动用户从一个地区到另一个地区时 , 它能选择一个合适的代理 , 实现与服务器和 其它移动用户之间的通信。为了保证用户的合法接入和信息的安全传输 , 一般需要 做到如下 5 点: 【1】访问控制。确保接入用户合法。此过程可以通过移动用户的 MAC 地址和用户 的相关信息来实现。 【2】身份认证。确保对方为其所声称的用户及数据的完整性 , 通过数字签名技术实 现。 【3】不可否认性。确保其发出的信息事后无法抵赖 , 通过数字签名实现。 【4】数据完整性。防止信息被截获后数据被更改重新发送 , 通过消息认证码 ( MAC ) 和数字签名来实现。 【5】保密性。信息在传输中即使被截获 , 因截获者无法破解而毫无意义。通过数据 的加密来实现。 密码应用中常使用的两类椭圆曲线为定义在有限域 GF ( p ) 上的素曲线和在有限域 GF(2n )上的二元曲线。素曲线计算不需二元曲线所要求的位混淆运算 , 对软件应用 而言 , 最好使用素曲线 ;而对硬件应用而言 , 则最好使用二元曲线 , 它可用很少的门 电路来得到快速且功能强大的密码体制 。
离散数学讨论课(群环格域布尔代数)

整 环: (R,+,。)为环,它有单位元素且是可换环,无零因子,
则称(R,+,。)是一个整环。
域:设环(R,+,。)满足下列条件: (1)、R至少有两个元素 (2)、(R,。)有单位元素 (3)、(R,。)是可换的 (4)、除零元外,其余元素均存在逆元素(a∈R的逆元可记作a-1)
环论在计算机领域的应用: (1)、广义圆环论在可持续发展中
群论在计算机领域的应用: (1)、组合群论在密码学中的应用 (2)、用群论的基础知识理解信号处理中
的一些基本概念(如:时域和频域信号空间的群同 构关系)
(3)、椭圆曲线密码的应用等
组合群论在密码学中的应用 用群论的基础知识理解信号处理中的一些基本 概念(如:时域和频域信号空间的群同构关系)
椭圆曲线密码的应用
如果半群还满足交换律,则称其为可换半群。
单 元 半 群:设有一个代数系统(S, 。)其中“。”是二元运算,它
满足结合律,并且存在单位元素,则此代数系统叫做单元半群。即 对S内任意元素a,b,c有
(a。b)。c= a。(b。c) 且存在1∈S有1.a=a。1=a。 如果单元半群还满足交换律,则称其为可换单元半群。
d ∈ {0, 1, 2, ⋯ , n - 1}
用户的公开密钥定义为 Q 点:
Q = dG
设要加密的明文数据为 M , 将 M 划分为一些较小的数据块 , M = [ m 1 , m 2 , ⋯ , m t ] 。 式中 : 0 ≤ mi< n 。用户 A 将数据 mi 加密发送给 B , 加密过程如下:
【1】用户 A 查公钥库 PKDB, 查到用户 B 的公开密钥 QB 。
【2】用户 A 选择一个随机数 dA , 且 dA ∈ { 0,1, 2, ⋯ , n - 1} 。 【3】用户 A 计算点 X 1: (x 1 , y 1)=dAG 。 【4】用户 A 计算点 X 2: (x 2 , y 2) =dAQB , 如果分量 x 2 = 0, 则转【2】。 【5】用户 A 计算 C = mi x 2 mod n 。 【6】用户 A 发送加密数据 ( X1 , C ) 给用户 B 。 解密过程:
则称(R,+,。)是一个整环。
域:设环(R,+,。)满足下列条件: (1)、R至少有两个元素 (2)、(R,。)有单位元素 (3)、(R,。)是可换的 (4)、除零元外,其余元素均存在逆元素(a∈R的逆元可记作a-1)
环论在计算机领域的应用: (1)、广义圆环论在可持续发展中
群论在计算机领域的应用: (1)、组合群论在密码学中的应用 (2)、用群论的基础知识理解信号处理中
的一些基本概念(如:时域和频域信号空间的群同 构关系)
(3)、椭圆曲线密码的应用等
组合群论在密码学中的应用 用群论的基础知识理解信号处理中的一些基本 概念(如:时域和频域信号空间的群同构关系)
椭圆曲线密码的应用
如果半群还满足交换律,则称其为可换半群。
单 元 半 群:设有一个代数系统(S, 。)其中“。”是二元运算,它
满足结合律,并且存在单位元素,则此代数系统叫做单元半群。即 对S内任意元素a,b,c有
(a。b)。c= a。(b。c) 且存在1∈S有1.a=a。1=a。 如果单元半群还满足交换律,则称其为可换单元半群。
d ∈ {0, 1, 2, ⋯ , n - 1}
用户的公开密钥定义为 Q 点:
Q = dG
设要加密的明文数据为 M , 将 M 划分为一些较小的数据块 , M = [ m 1 , m 2 , ⋯ , m t ] 。 式中 : 0 ≤ mi< n 。用户 A 将数据 mi 加密发送给 B , 加密过程如下:
【1】用户 A 查公钥库 PKDB, 查到用户 B 的公开密钥 QB 。
【2】用户 A 选择一个随机数 dA , 且 dA ∈ { 0,1, 2, ⋯ , n - 1} 。 【3】用户 A 计算点 X 1: (x 1 , y 1)=dAG 。 【4】用户 A 计算点 X 2: (x 2 , y 2) =dAQB , 如果分量 x 2 = 0, 则转【2】。 【5】用户 A 计算 C = mi x 2 mod n 。 【6】用户 A 发送加密数据 ( X1 , C ) 给用户 B 。 解密过程:
《格和布尔代数》课件

第二部分:格的基础知识
有限格和无限格
介绍有限格和无限格的概念, 讨论其特点和应用。
笛卡尔积和格的同构
解释格的笛卡尔积以及同构 关系,揭示它们在格理论中 的重要性。
原子性和可分性
详细阐述格的原子性和可分 性,论述它们在实际问题中 的应用价值。
第三部分:布尔代数
1
ቤተ መጻሕፍቲ ባይዱ
3.2 布尔代数运算
2
系统阐述布尔代数的与、或、非运算,
总结格和布尔代数的重要性及其在学术和实
多研究和应用探索,促进学科的发展与创新。
践中的潜力,并对未来的研究方向进行展望。
《格和布尔代数》PPT课 件
本《格和布尔代数》PPT课件将带您深入了解格和布尔代数的基础知识、运 算规则以及其在现实世界中的重要应用。全方位解析格和布尔代数,帮助您 掌握这一重要数学领域的核心概念与技巧。
第一部分:引言
什么是格和布尔代数?探讨格和布尔代数的定义、特性和相关领域应用,以 及其在数学、计算机科学和工程中的重要性。
以及相关的异或和置位运算。
3
3.1 布尔代数的起源和发展
探索布尔代数的历史渊源与发展轨迹, 重点介绍George Boole对其的贡献。
3.3 布尔代数的完备性和最小化
讲解布尔代数的完备性定理、最小化方 法和卡诺图的应用。
第四部分:格和布尔代数的应用案例
逻辑电路设计
展示格和布尔代数在逻辑电路设 计中的重要应用,以及其在计算 机工程领域的意义。
程序设计中的控制流分析
阐述格和布尔代数在程序设计中 的控制流分析应用,帮助程序员 编写高效的代码。
数据库查询优化
探究格和布尔代数在数据库查询 优化中的关键作用,提高查询效 率和性能。
格与布尔代数(离散数学)

定理6-1.4 设<A,∨,∧>是一个代数系统,其中 ∨,∧都是二元运算且满足交换律、结合律和吸收律,
哈尔滨理工大学本科生课程
离 散 数 格与分配格 学
计算机系
第六章 格与布尔代数
这一章将介绍另一类代数系统,这就是格。
格论大体上是在1935年左右形成的,它不仅是
代数学的一个分支,而且在近代解析几何,半
序空间等方面也都有重要的作用。我们在这里
只介绍格的一些基本知识以及几个具有特别性
质的格——分配格、有补格。
则<T,≤>是 <S,≤>的一个子格。
解 对于任意的x,yT,必有x≤a 和y≤a, 所以x∨y≤a,x∧y≤a 而 x∨yS,x∧yS 故x∨yT,x∧yT
因此<T,≤>是 <S,≤>的一个子格。
同样地,可以证明,如果取Q={x|xS且a≤x},
则<Q,≤>也是 <S,≤>的一个子格。
4. 上界、下界 定义3-12.7:设<A,≤>是一偏序集,对于BA,如有a∈A,
且对任意元素x∈B,都有x≤a,则称a为B的上界。同理,对
任意元素x∈B,都有a≤x,则称a为B的下界。 5. 上确界、下确界 定义3-12.8:设<A,≤>是一偏序集且BA,a是B的任一上 界,若对B的所有上界y均有a≤y,则称a是B的最小上界(上
二、知识点
1 .格的概念,偏序集上的并运算、 偏序集上的交运算。
2.分配格、有补格; 3.布尔代数、Stone表示定理及其推 论,布尔表达式、布尔函数、开关代数的 概念。
三、要求
1.识记 根据哈斯图识别是否是格,分配格、有补格, 模格,布尔格、布尔代数。 2.领会
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:(反证法)设有两个全上界a和b,则由定义 a≤b,且b≤a,由“≤”的反对称性, a=b。
[定义]设<L,≤>是一个格,格中存在全上界和全下 界,则称该格为有界格。
16
§6.3 有补格
[定理]如果<L,≤>是有界格,全上界和全下界分别 是1和0,则对任意元素aL,有: a1=1a=1 ,a1=1a=a, a0=0a=a ,a0=0a=0。
证明:因为1≤a1, 又因(a1)L且1是全上界,∴a1≤1, ∴ a1=1。由交换律:1a=a1=1。 因为a≤a,a≤1,∴a a≤a1,即:a≤a1, 又a1≤a, ∴ a1=a。仿此可得另两式。
17
§6.3 有补格
[定义]设<L,≤>是一个有界格,对于L中的一个元素 a,如果存在bL,使得ab=1和ab=0,则称元素 b是元素a的补元。
6
§6.1格的概念
(2)对格<L,≤>中任意a和b,有a≤ab及ab≤a。 (3)<L,≤>是格。对任意a,b,c,dL,如a≤b,
c≤d,则ac≤ bdபைடு நூலகம் ac≤bd
(4)(交换律)交和并运算是可交换的。 (5)(结合律)交和并运算是可结合的。
7
§6.1 格的概念
(6)(幂等律)对L中每一个a,有aa=a,aa=a。
2
§6.1 格的概念
1.偏序集合格
L,
[定义]格是一个偏序集合
,其中每一对元素
a,b L都拥有一个最小上界和最大下界。通常用
a b表示a和b的最大下界,用 a b 表示a和b的最 小上界。即:
GLB{a,b} a b ——称为元素a和b的保交运算,
LUB{a,b} a b——称为元素a和b的保联运算。
3
§6.1 格的概念
例:以下均为偏序集合格(D为整除关系,Sn为n的因 子集合)。
4
§6.1 格的概念
2.代数系统格 [定义]设 L, 是一个格,如果在A上定
义两个二元运算和,使得对于任意的a,bA, ab等于a和b的最小上界,ab等于a和b的最大 下界,那么就称<L, ,L,> 为由格 所诱导的代数系统。
13
§6.2 分配格
[定理]每个链均是分配格。 证明:设<L,≤>是链。对任意a,b,cL (1)若a≤b或a≤c,则 a (b c) = a,
(a b) (a c)=a 即: a (b c) = (a b) (a c) (2)若a≥b且a≥c,则 a (b c) = b c,
第六章 格和布尔代数
§6.1 格的概念 §6.2 分配格 §6.3 有补格 §6.4* 布尔代数
1
第六章 格和布尔代数
教学目的及要求: 深刻理解和掌握格与布尔代数的基本概念和基本 运算。 教学内容: 格的概念、分配格、有补格、布尔代数、布尔表 达式。 教学重点:格、布尔代数、布尔表达式。 教学难点:布尔代数、布尔表达式。
9
§6.2 分配格
讨论定义: (1)定义中的两式互为对偶式。 (2)如<L,≤>非为分6配. 格,则有下面的分配不等式:
a (b c) ≤ (a b) (a c) a (b c) ≥ (a b) (a c) 以及模不等式: a≤ca (b c) ≤ (a b) c
10
§6.2 分配格
(7)(吸收律)对L中任意a,b,有
a(ab)=a
a(ab)=a。
8
§6.2 分配格
对格所定义的代数系统<L,,>,其运算和不一 定满足分配律。
[定义]设<L,,>是由<L,≤>所诱导的代数系统。 如果对任意的a,b,cL,满足: a (b c)=(a b) (a c) 及 a (b c)=(a b) (a c) 则称<L,≤>是分配格。
讨论定义: (1)∵ 和是可交换的,∴补元是相互的。 (2)0 1 0 1 0 0,0 1 1 1 0 1,在有界格 中,1和0互为补元; (3)由定义可知L中一个元素的补元不一定唯一;
例:
18
§6.3 有补格
[定义]在一个有界格中,如果每个元素都至少有一 个补元素,则称此格为有补格。
讨论定义: (1)在有补格中,每一个元素一定存在补元(不一
定是一个补元); (2)有补格一定是有界格,而有界格不一定是有补
格。请看下例:
19
§6.3 有补格
[定义]在一个有界格中,如果每个元素都至少有一 个补元素,则称此格为有补格。
讨论定义: (1)在有补格中,每一个元素一定存在补元(不一
定是一个补元); (2)有补格一定是有界格,而有界格不一定是有补
[定义]如对L中任意a,b,c有: a≤ca (b c) = (a b) c
则称<L,≤>为模格。 例:
11
§6.2 分配格
[定理]如果格中交对并是分配的,那么并对交也是 分配的,反之亦然。
证明:已知a(bc)=(ab)(ac) (ab)(ac)=((ab)a)((ab)c) =a((ab)c) =a((ac)(bc)) =(a(ac))(bc) =a(bc)
(a b) (a c)= b c 即:a (b c) = (a b) (a c)。得证。
14
§6.3 有补格
[定义]设<L,≤>是一个格,如果存在元素aL,对 于任意的x L,都有: a≤x 则称a为格<L,≤>的全下界,记格的全下界为0。
例:
15
§6.3 有补格
[定理]如果格<L,≤>有全上界(全下界),那么它 是唯一的。
5
§6.1 格的概念
3.格的主要性质: (1)格的对偶原理 设<L,≤>是格,“≤”的逆关系“≥”与L组成的偏
序集 <L, ≥>也是格。两者互为对偶。前者的GLB,LUB 恰好是后者的LUB,GLB。如有关于<L,≤>的有效 命题,将“≤”换成“≥”,“”换成“”, “”换成 “”,便能得到<L, ≥>的有效命题。 反之亦然。
即:并对交也是分配的。
12
§6.2 分配格
[定理]分配格是模格。 证明:由于a (b c) = (a b) (a c) (1)若a≤c,则a c=c,代入上式得
a (b c) = (a b) c (2)若a (b c) = (a b) c,则
a≤ a (b c) = (a b) c≤c,即: a≤c ∴分配格是模格
[定义]设<L,≤>是一个格,格中存在全上界和全下 界,则称该格为有界格。
16
§6.3 有补格
[定理]如果<L,≤>是有界格,全上界和全下界分别 是1和0,则对任意元素aL,有: a1=1a=1 ,a1=1a=a, a0=0a=a ,a0=0a=0。
证明:因为1≤a1, 又因(a1)L且1是全上界,∴a1≤1, ∴ a1=1。由交换律:1a=a1=1。 因为a≤a,a≤1,∴a a≤a1,即:a≤a1, 又a1≤a, ∴ a1=a。仿此可得另两式。
17
§6.3 有补格
[定义]设<L,≤>是一个有界格,对于L中的一个元素 a,如果存在bL,使得ab=1和ab=0,则称元素 b是元素a的补元。
6
§6.1格的概念
(2)对格<L,≤>中任意a和b,有a≤ab及ab≤a。 (3)<L,≤>是格。对任意a,b,c,dL,如a≤b,
c≤d,则ac≤ bdபைடு நூலகம் ac≤bd
(4)(交换律)交和并运算是可交换的。 (5)(结合律)交和并运算是可结合的。
7
§6.1 格的概念
(6)(幂等律)对L中每一个a,有aa=a,aa=a。
2
§6.1 格的概念
1.偏序集合格
L,
[定义]格是一个偏序集合
,其中每一对元素
a,b L都拥有一个最小上界和最大下界。通常用
a b表示a和b的最大下界,用 a b 表示a和b的最 小上界。即:
GLB{a,b} a b ——称为元素a和b的保交运算,
LUB{a,b} a b——称为元素a和b的保联运算。
3
§6.1 格的概念
例:以下均为偏序集合格(D为整除关系,Sn为n的因 子集合)。
4
§6.1 格的概念
2.代数系统格 [定义]设 L, 是一个格,如果在A上定
义两个二元运算和,使得对于任意的a,bA, ab等于a和b的最小上界,ab等于a和b的最大 下界,那么就称<L, ,L,> 为由格 所诱导的代数系统。
13
§6.2 分配格
[定理]每个链均是分配格。 证明:设<L,≤>是链。对任意a,b,cL (1)若a≤b或a≤c,则 a (b c) = a,
(a b) (a c)=a 即: a (b c) = (a b) (a c) (2)若a≥b且a≥c,则 a (b c) = b c,
第六章 格和布尔代数
§6.1 格的概念 §6.2 分配格 §6.3 有补格 §6.4* 布尔代数
1
第六章 格和布尔代数
教学目的及要求: 深刻理解和掌握格与布尔代数的基本概念和基本 运算。 教学内容: 格的概念、分配格、有补格、布尔代数、布尔表 达式。 教学重点:格、布尔代数、布尔表达式。 教学难点:布尔代数、布尔表达式。
9
§6.2 分配格
讨论定义: (1)定义中的两式互为对偶式。 (2)如<L,≤>非为分6配. 格,则有下面的分配不等式:
a (b c) ≤ (a b) (a c) a (b c) ≥ (a b) (a c) 以及模不等式: a≤ca (b c) ≤ (a b) c
10
§6.2 分配格
(7)(吸收律)对L中任意a,b,有
a(ab)=a
a(ab)=a。
8
§6.2 分配格
对格所定义的代数系统<L,,>,其运算和不一 定满足分配律。
[定义]设<L,,>是由<L,≤>所诱导的代数系统。 如果对任意的a,b,cL,满足: a (b c)=(a b) (a c) 及 a (b c)=(a b) (a c) 则称<L,≤>是分配格。
讨论定义: (1)∵ 和是可交换的,∴补元是相互的。 (2)0 1 0 1 0 0,0 1 1 1 0 1,在有界格 中,1和0互为补元; (3)由定义可知L中一个元素的补元不一定唯一;
例:
18
§6.3 有补格
[定义]在一个有界格中,如果每个元素都至少有一 个补元素,则称此格为有补格。
讨论定义: (1)在有补格中,每一个元素一定存在补元(不一
定是一个补元); (2)有补格一定是有界格,而有界格不一定是有补
格。请看下例:
19
§6.3 有补格
[定义]在一个有界格中,如果每个元素都至少有一 个补元素,则称此格为有补格。
讨论定义: (1)在有补格中,每一个元素一定存在补元(不一
定是一个补元); (2)有补格一定是有界格,而有界格不一定是有补
[定义]如对L中任意a,b,c有: a≤ca (b c) = (a b) c
则称<L,≤>为模格。 例:
11
§6.2 分配格
[定理]如果格中交对并是分配的,那么并对交也是 分配的,反之亦然。
证明:已知a(bc)=(ab)(ac) (ab)(ac)=((ab)a)((ab)c) =a((ab)c) =a((ac)(bc)) =(a(ac))(bc) =a(bc)
(a b) (a c)= b c 即:a (b c) = (a b) (a c)。得证。
14
§6.3 有补格
[定义]设<L,≤>是一个格,如果存在元素aL,对 于任意的x L,都有: a≤x 则称a为格<L,≤>的全下界,记格的全下界为0。
例:
15
§6.3 有补格
[定理]如果格<L,≤>有全上界(全下界),那么它 是唯一的。
5
§6.1 格的概念
3.格的主要性质: (1)格的对偶原理 设<L,≤>是格,“≤”的逆关系“≥”与L组成的偏
序集 <L, ≥>也是格。两者互为对偶。前者的GLB,LUB 恰好是后者的LUB,GLB。如有关于<L,≤>的有效 命题,将“≤”换成“≥”,“”换成“”, “”换成 “”,便能得到<L, ≥>的有效命题。 反之亦然。
即:并对交也是分配的。
12
§6.2 分配格
[定理]分配格是模格。 证明:由于a (b c) = (a b) (a c) (1)若a≤c,则a c=c,代入上式得
a (b c) = (a b) c (2)若a (b c) = (a b) c,则
a≤ a (b c) = (a b) c≤c,即: a≤c ∴分配格是模格
