离散数学第11章 格与布尔代数
格与布尔代数课件2
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f,使得对 x1,x2 A, 有f(x1∨1x2)=f(x1)∨2f(x2),f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律:a∨(a∧b) = a、a∧(a∨b) = a
证明:幂等律 ∵ a≤a,∴ a是a的上界,而a∨a是a的最小上界, ∴a∨a≤a ,又 ∵ a≤a ∨a,
由反对称性得:a∨a = a 由对偶原理得,a∧a = a
第15页,共28页。
证明:吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a, a∨(a ∧ b)≤a
解:< I+ , D>是格 ∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大上界等于a、b的最大公约数。
第3页,共28页。
< P(S) , > 是格
∵子集关系是偏序关系,对a,b P(S),
a、b的最小上界等于a∪b,
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2,>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1:,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}
离散数学课件13.4布尔代数

有限布尔代数的表示定理
定理13.11 若B是有限布尔代数,则 B含有2n个元(n∈N), 并且B与<P(S),∩,∪,~,,S>同构, 其中S是一个n元集合.
举例
格S12,gcd.lcm是布尔代数吗? 解: S12={1,2,3,4,6,12}的元素个数6, 不是2的整数幂, 故不是布尔代数. 不难看出2没有补元,因为 2∨x=lcm(2,x)=12当且仅当 x=12, 而12的补元是1而不是2.
例
集合代数<P(S),∩,∪,~,,S>是 布尔代数.
开关代数<{0,1},∧,∨,¬,0,1>是 布尔代数,其中∧为与运算,∨为或 运算, ¬为非运算.
布尔代数有以下性质.
定埋13.10 设<B,∧,∨,',0,1>是布尔代数, 则有:
a∈B,(a’)’=a(双重否定律), a,b∈B, (a∨b)'=a'∧b'
布尔格、布尔代数
定义13.12 如果格<L,∧,∨,0,1>是有 补分配格,则称L为布尔格,也叫做布 尔代数. 由于布尔代数L中的每个元都有唯一 的补元,求补运算也可以看成是L中的 一元运算. 因此,布尔代数L可记为<L,∧,∨,',0,1>, 其中'表示求补运算.
布尔代数的等价定义
定义13.13(公理化定义): 有两个二元运算的代 数B,*, 称为布尔代数,如果对任意元素 a,b,cB,成立
•此类布尔表达式可用带3个基本元件的电路来实 现.3个基本元件是:
①反相器
x
x’
②与门
x xy
y
③或门
x xy
y
实例之一
•实例1: 三人委员会表决某个提案,如有两张赞 成票即获通过,实现上述过程的表决机器的控制 电路如下图所示:
离散数学定义列表

A.定义1.简单命题/原子命题、复合命题2.定义1.1:否定式、否定联结词3.定义1.2:合取式、合取联结词4.定义1.3:析取式、析取联结词定义1.4:蕴含式、前件、后件、蕴含联结词;规定19.4、20.45.定义1.5:等价式、等价联结词;规定6.联结词的定义(真值表)表1.1、优先级7.命题常项、命题变项(不是命题)、合式公式8.定义1.6:原子命题公式、公式、子公式9.定义1.7:公式层次10.定义1.8:赋值/解释、成真赋值、成假赋值11.定义1..9:真值表12.定义1..10:重言式/永真式、矛盾式/永假式、可满足式13.哑元************************重点:命题逻辑等值演算***************15.等值演算、置换规则4.116.定义2.2:文字、简单析取式、简单合取式17.定义2.3:析取范式、合取范式、范式18.定义2.4:极小项、极大项定义2.5:主析取范式、主合取范式********************************一阶逻辑**********************19.个体词、个体常项、个体变项、个体域/论域、全总个体域20.谓词、谓词常项、谓词变项、n元谓词、0元谓词量词、全称量词、存在量词全称蕴含、存在合取P71 5.3********************************集合代数**********************21.定义6.1:子集、包含22.定义6.2:相等23.定义6.3:真子集定义6.4:空集P139 124.n元集、m元子集、(单元集)25.定义6.5:幂集公式:26.定义6.6:全集27.定义6.7:并集、交集、相对补集、不交28.定义6.8:对称差集29.定义6.9:绝对补集30.定义6.10:广义并31.定义6.11:广义交幂等律、结合律、交换律、分配律、同一律、零律、排中律、矛盾律、吸收律、德摩根律、双重否定律eg6.8,P108 36****************************重点:二元关系***********************32.定义7.1:有序对/序偶33.定义7.2:笛卡尔积性质P11134.定义7.3:二元关系/关系P139 735.定义7.4:从A到B的二元关系、A上的二元关系、空关系36.定义7.5:A上的全域关系(E)、恒等关系(I)、小于等于关系(L)、整除关系(D)、包含关系(R)37.关系矩阵(x行,y列)、关系图38.定义7.6:定义域、值域、域39.定义7.7:逆关系40.定义7.8:右复合(左复合)41.定义7.9:R在A上的限制、A在R下的像42.定义7.10:关系的n次幂定义7.11:自反、反自反定义7.12:对称、反对称定义7.13:传递43.定义7.15:等价关系(性质)P142 32(4)、4144.定义7.16:等价类45.定义7.17:商集46.定义7.18:划分、划分块 P134 eg7.1847.定义7.19:偏序关系(性质)48.定义7.20:小于、可比49.定义7.21:全序关系/线序关系50.定义7.22:偏序集P13551.定义7.23:偏序集中顶点的覆盖关系(为画哈斯图)P143 43(2)***************************函数*******************************53.定义8.1:函数54.定义8.2:函数相等55.定义8.3:从A到B的函数P171 6(8)(9)56.定义8.4:从A到B的函数的集合B A57.定义8.5:A1在ƒ下的像、函数的像、完全原像定义8.6:满射、单射、双射/一一映射P173 2558.定义8.7: 常函数、恒等函数、单调递增、单调递减、严格单调递减、特征函数、自然映射59.反函数(双射)*************************代数系统*****************************60.定义9.2:一元运算定义9.3:可交换/交换律定义9.4:可结合/结合律定义9.5:幂等律、幂等元61.定义9.6:可分配/分配律62.定义9.7:吸收律63.定义9.8:左单位元(右单位元)、单位元/幺元64.定义9.9:左零元(右零元)65.定义9.10:左逆元(右逆元)、逆元、可逆66.定义9.11:消去律、左消去律(右消去律)注意P183 eg9.667.定义9.12:代数系统/代数、特异元素/代数常数68.定义9.13:具有相同的构成成分/同类型69.定义9.14:子代数系统/子代数、平凡的子代数、真子代数(函数对子集封闭)70.定义9.15:积代数、因子代数************************************群与环***************************************半群与群都是具有一个二元运算的代数系统71.定义 10.1:半群()、幺半群/独异点()、群()72.有理数加群、整数加群、实数加群、复数加群、四元群、子代数、语言73.定义 10.2:有限群、无限群、平凡群、交换群/Abel群74.定义 10.3:n次幂75.定义 10.4:(元素的)阶/周期、k阶元、无限阶元***********************************格与布尔代数**********************************格与布尔代数是具有两个二元运算的代数系统定义11.1:格(偏序集定义的)P22176.幂集格、子群格77.定义11.2:对偶命题、格的对偶原理78.定义11.3:格(代数系统定义的)79.定义11.4:子格80.定义11.5:分配格81.定义11.6:全上界、全下界82.定义11.7:有界格83.定义11.8:补元84.定义11.9:有补元定义11.10:布尔格/布尔代数(有补分配格)85.定义11.11:布尔代数(代数系统定义)86.定义11.12:原子**********************************14.图的基本概念********************************87.无序积A&B88.定义14.1:无向图、顶点集、顶点/结点、边集、无向边/边89.定义14.2:有向图、无向边/边90.(P294)图、阶、n阶图;零图、平凡图;空图;标定图、非标定图;基图;端点、关联、关联次数、环、相邻;始点、终点、孤立点;邻域、闭邻域、关联集、后继元集、先驱元集91.定义14.3:平行边、重数、多重图、简单图92.定义14.4:度数/度、出度、入度、最大度、最小度、悬挂顶点、悬挂边、偶度(奇度)顶点93.度数列、可图化的、可简单图化的,出度列、入度列94.定义14.6:n阶无向完全图/n阶完全图、n阶有向完全图、n阶竞赛图95.定义14.7:k-正则图96.定义14.8:母图、真子图、生成子图、导出的子图97.定义14.10:删除边e、删除E’、删除顶点v、删除V‘、边的收缩、新加边删点边不留,删边点还在98.定义14.11:通路、始点、终点、长度、回路、简单通路、简单回路、初级通路/路径、初级回路/圈、奇圈、偶圈、复杂通路、复杂回路99.定义14.12:连通、连通图、非连通图100.定义14.13:连通分支、连通分支数101.定义14.14:短程线、距离102.定义14.15:点割集、割点103.定义14.16:边割集/割集、割边/桥104.定义14.21:弱连通图/连通图、单向连通图、强连通图105.定义14.22:二部图/二分图/偶图,完全二部图定义14.23:无向图关联次数、关联矩阵定义14.24:有向图关联矩阵定义14.25:邻接矩阵定义14.26可达矩阵**********************************15.欧拉图与哈密顿图****************************106.定义15.1:欧拉通路、欧拉回路、欧拉图、半欧拉图107.定义15.2:哈密顿通路、哈密顿回路、哈密顿图、半哈密度图**********************************16.树*****************************************108.定义16.1:无向树/树、森林、平凡树、树叶、分支点109.定义16.2:生成树、树枝、弦、余树110.定义16.:5:权、最小生成树111.避圈法(Kruskal算法)B.定理1.定理2.1:简单析取式是重言式的充要条件;简单合取式是矛盾式的充要条件2.定理2.2:析取范式(矛盾式)、合取范式(重言式)3.定理2.3:范式存在定理4.定理2.4:极小项和极大项关系5.定理2.5:主析、主合存在并唯一6.定理6.1:子集是一切集合的子集推论:空集是唯一的7.定理7.1:逆关系性质8.定理7.2:复合结合律、逆9.定理7.3:关系与恒等关系复合10.定理7.4:复合分配律注意交11.定理7.5:限制和像的分配律注意像的交12.定理7.6:有穷集上只有又穷多个不同的二元关系13.定理7.7:关系的幂性质14.定理7.8:有穷集A上的关系R的幂序列R0,R1,R2等是一个呈现周期性变化的序列15.定理7.9:五大性质16.定理7.14:等价关系的性质17.定理8.1:函数的复合(关系的右复合)推论1:函数复合结合律推论2:ƒ:A→B,g:B→C,则ƒ。
离散数学 格与布尔代数共89页

66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
离散数学 格与布尔代数
21、没有人陪你走一辈子,所以你要 适应孤 独,没 有人会 帮你一 辈子, 所以你 要奋斗 一生。 22、当眼泪流尽的时候,留下的应该 是坚强 。 23、要改变命运,首先改变自己。
24、勇气很有理由被当作人类德性之 首,因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 放上一 段时间 ,以便 让别一 只脚能 够再往 上登。
离散数学格与布尔代数

§7.1 格
例 < P(S) , >是格 表示为<P(S), , * > 又可表示为< P(S) ,∪,∩>
例 <Z+,≤>,或 <Z+,|> <Z+, , * > <Z+, LCM,GCD>
§7.2 格——代数系统
格〈L,≤〉中自然存在两个运算 和 * ,从而 派生出一个代数系统〈L,,*〉
6
<S15,|>,
2
2019/10/5
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/5
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
并、交 运算的性质
定理1 设〈L,≤〉是一个格,并运算与交运算 * 满足 如下性质:
L1 a a = a
a*a=a
(幂等律)
L2 a b = b a a * b = b * a (交换律)
L3 (a b) c = a (b c)
离散数学-格和布尔代数

的次序图如下
-1 的次序图如下
6 2 1 3 2
1 3 6
若 < L; > 是一个偏序集,则对于任意元素 l1, l2, l3 L,有以 下六个关系式成立: l1 l1 若 l1 l2,l2 l1,则 l1 = l2 若 l1 l2,l2 l3,则 l1 l3 l1 l1 若 l1 l2,l2 l1,则 l1 = l2 (7-1) (7-2) (7-3) (7-1) (7-2)
60以上说明与格一样布尔代数也是一个代数系统该代数系统可取交换律分配律同一律和互补律作为公二元运算是一元运算若这些运算满足交换律分配律同一律和互补律则称称作集合代数它是一个布尔代数
第二部分 抽象代数
0
第七章
格和布尔代数
格是 Birkhoff (1884 - 1944) 在 20 世纪 30 年代提出的,格的提出 以子集为背景。 历史上最初出现的格是英国数学家 George Boole 于 1854 年提出 的,是他在研究命题演算中发现的,通常称为布尔格或布尔代 数。 格和布尔代数的理论成为计算机硬件设计和通讯系统设计中的 重要工具。格论是计算机语言的指称语义的理论基础。格是一 种特殊的偏序集,也可以看作是有两个二元运算的代数系统, 布尔代数是一种特殊的格。在保密学、开关理论、计算机理论 和逻辑设计以及其他一些科学和工程领域中,都直接应用了格 与布尔代数。 1
7.2 格及其性质
一、格的定义
定义7-5 设 < L; > 是一个偏序集,如果 L 中任意两个元素都 存在着最大下界和最小上界,则称 < L; > 是格。 由于每对元素的最大下界和最小上界唯一,故引入记号: l1 l2 = glb(l1, l2),l1 l2 = lub(l1, l2), 其中 和 均可看作是集合 L 上的二元运算,分别称为交和并。 注:若 < L; > 是一个格,则意味着 < L; > 也是一个形为 < L; , > 的代数系统,其中 和 是 L 上的两个二元运算, 对于任意 l1, l2 L,l1 l2 表示在偏序 “ ” 意义下,l1 和 l2 的最小上界,l1 l2 表示 l1 和 l2 的最大下界。
离散数学布尔代数

一个非零元素b,至少存在一个原子a,使得a ≤ b。 1
证明:若b本身就是一个原子,则b ≤ b,得证。c
df
若b不是原子,肯定存在b1,使得0 ≤ b1 ≤ b, a
be
若b1是原子,则定理得证;
0
否则,若b1不是原子,则必存在b2,使得0 ≤ b2 ≤ b1 ≤ b
∵<A, ≤>是一个有全下界的有限格,
定理1:对于布尔代数中任意两个元素 a, b,必定有
(1) ( a ) = a, (2) a∨b = a∧b , (3) a∧b = a∨b
3
❖ 布尔代数
定义3:设<A,∨1,∧1, - > 和<B,∨2,∧2, ~ >是两个布尔代数, 如果存在A到B的双射 f,对于a,bA,有
f (a∨1b) = f (a) ∨2 f (b)
2、对a,bA,有 f (a∧b) = f (a)∩f (b)
9
❖ 格与布尔代数
定理3 ( Stone表示定理 ) :
设<A,∨,∧, - >是由有限布尔格<A, ≤>所诱导的一个有 限布尔代数,S是布尔格<A, ≤>中的所有原子的集合,则 < A,∨,∧, - >< P(S),∪,∩, ~ >同构。 分析:要证两个代数系统同构,分为以下几步:
1、找一个双射函数 f: A P(S)
∴a ≤ c ,又∵a ≤ c, ∴a ≤ c ∧ c,即 a ≤ 0,
这与a是原子相矛盾, ∴假设错
∴b ∧ c = 0,由引理1得: b≤c ∴b=c,即:b= a1∨a2∨... ∨ak
7
❖ 格与布尔代数
证明(2):设b的另一种表示形式为 b = aj1∨aj2∨... ∨ajt 其中aj1,aj2,……,ajt是A中原子。∵b是 aj1,aj2,……,ajt 的最小上界, ∴有aj1≤b, aj2≤b,…,ajt≤b,而a1,a2,……,ak是A中满足 a j ≤b的所有原子, {aj1,aj2,…,ajt}是{a1,a2,…,ak}的子集,即 |{aj1,aj2,…,ajt}|<=|{a1,a2,…,ak}|, 即:t ≤ k。(下面证 t < k 是不可能的)
离散数学格与布尔代数

6
<S15,|>,
2
2019/10/12
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/12
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
Input A B Cin
00 0 00 1 01 0 01 1 10 0 10 1 11 0 11 1
Output S Cout
00 10 10 01 10 01 01 11
S A BCin A BCin A BCin A BCin
Cout A B Cin A B Cin A B Cin A B Cin
§7.2 格——代数系统
证〈L,≤〉为要求的格
a,b∈L,(a * b)* a = a*(a * b)=(a * a)*b=a*b,
故a*b≤a,
L3
L1
同理a*b≤b,因此a*b是{a,b}的下界,
又设c是{a,b}的任一下界,即c≤a,c≤b,则a * c=c,b * c=c,于是(a * b)* c=a *(b * c)=a * c=c,即c≤a * b, 所以a * b是{a,b}的最大下界,即a * b=inf{a,b},
离散数学格的概念

∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大下界等于a、b的最大公约数。
❖ 基本概念
< B2 , D >是否 < S30 , D >的子格?
30
6
30
10
6 15
2
3
10
15
1 ∨1 2 3 6 11236 22266
2
53
5
∧1 2 3 6
1
11111
21212
说明:
33636 66666
31133 61236
(1) 子格必是格。
运算∨和∧在B1上封闭,B1 S30 且B1 ≠Ø, ∴ < B1, D >是 < S30 , D >的子格; 同理可证< B2 , D >是 < S30 , D >的子格
例:A={a, b, c }, < P(A) , > 所诱导的代数系统为?
< P(A),∪,∩>
❖ 基本概念
定义3:设<A,≤ >是一个格,由其所诱导的代数系统为 <A,∨,∧>。设BA且B ≠Ø ,如果运算∨和∧在B上封闭, 则称<B,≤ > 是<A,≤ >的子格。
❖ 基本概念
例2:B1 = {1,2,3,6} , B2 = {5,10,15,30} ,< B1, D >和
离散数学
❖ 格与布尔代数 1 格的概念
离散数学中的布尔代数知识点介绍

离散数学中的布尔代数知识点介绍离散数学是计算机科学和数学中的一个重要分支,而布尔代数则是离散数学中的一个基础概念。
布尔代数是一种逻辑推理和计算的数学体系,其基本概念和运算规则直接应用于计算机计算和逻辑设计中。
一、布尔代数的基本概念布尔代数有两个基本元素:命题和逻辑操作符。
命题是关于真(True)和假(False)的陈述,可以用字母或其他符号表示。
逻辑操作符包括与(AND)、或(OR)、非(NOT)三种基本运算符,用于对命题进行逻辑运算。
二、布尔代数的基本运算规则1. 与运算(AND):只有当两个命题都为真时,与运算的结果才为真。
用符号“∧”表示,例如命题A∧B表示“命题A和命题B都为真”。
2. 或运算(OR):只要两个命题中有一个为真,或运算的结果就为真。
用符号“∨”表示,例如命题A∨B表示“命题A或命题B为真”。
3. 非运算(NOT):将命题的真值取反,即将真变为假,将假变为真。
用符号“¬”表示,例如¬A表示“命题A的取反”。
三、布尔代数的重要性布尔代数在计算机科学和逻辑设计中具有重要的应用。
布尔代数提供了一种形式化的工具,可以对逻辑关系和计算过程进行精确的描述和处理。
利用布尔代数的运算规则,可以进行逻辑推理、逻辑运算和逻辑设计。
布尔代数为计算机的基本运算提供了理论基础,是计算机科学不可或缺的一部分。
四、布尔代数的应用领域1. 逻辑电路设计:布尔代数的基本运算规则可以用于逻辑门电路的设计与分析。
逻辑门电路由与门、或门、非门等基本门电路组成,通过布尔代数的运算规则可以进行电路的优化和逻辑设计。
2. 程序设计与算法分析:布尔代数在程序设计和算法分析中具有重要地位。
利用布尔代数的运算规则,可以对程序的逻辑关系进行抽象和分析,确保程序的正确性和可靠性。
3. 数据库查询与管理:布尔代数可用于数据库查询和管理中的条件表达式构建。
通过布尔代数的运算规则,可以对数据库数据进行选择、过滤和计算,实现对数据的高效管理与查询。
离散数学必备知识点总结

总结离散数学知识点第二章命题逻辑1.→,前键为真,后键为假才为假;<—>,相同为真,不同为假;2.主析取范式:极小项(m)之和;主合取范式:极大项(M)之积;3.求极小项时,命题变元的肯定为1,否定为0,求极大项时相反;4.求极大极小项时,每个变元或变元的否定只能出现一次,求极小项时变元不够合取真,求极大项时变元不够析取假;5.求范式时,为保证编码不错,命题变元最好按P,Q,R的顺序依次写;6.真值表中值为1的项为极小项,值为0的项为极大项;7.n个变元共有n2个极小项或极大项,这n2为(0~n2-1)刚好为化简完后的主析取加主合取;8.永真式没有主合取范式,永假式没有主析取范式;9.推证蕴含式的方法(=>):真值表法;分析法(假定前键为真推出后键为真,假定前键为假推出后键也为假)10.命题逻辑的推理演算方法:P规则,T规则①真值表法;②直接证法;③归谬法;④附加前提法;第三章谓词逻辑1.一元谓词:谓词只有一个个体,一元谓词描述命题的性质;多元谓词:谓词有n个个体,多元谓词描述个体之间的关系;2.全称量词用蕴含→,存在量词用合取^;3.既有存在又有全称量词时,先消存在量词,再消全称量词;第四章集合1.N,表示自然数集,1,2,3……,不包括0;2.基:集合A中不同元素的个数,|A|;3.幂集:给定集合A,以集合A的所有子集为元素组成的集合,P(A);4.若集合A有n个元素,幂集P(A)有n2个元素,|P(A)|=||2A=n2;5.集合的分划:(等价关系)①每一个分划都是由集合A的几个子集构成的集合;②这几个子集相交为空,相并为全(A);6.集合的分划与覆盖的比较:分划:每个元素均应出现且仅出现一次在子集中;覆盖:只要求每个元素都出现,没有要求只出现一次;第五章关系1.若集合A有m个元素,集合B有n个元素,则笛卡尔A×B的基数2种不同的关系;为mn,A到B上可以定义mn2.若集合A有n个元素,则|A×A|=2n,A上有22n个不同的关系;3.全关系的性质:自反性,对称性,传递性;空关系的性质:反自反性,反对称性,传递性;全封闭环的性质:自反性,对称性,反对称性,传递性;4.前域(domR):所有元素x组成的集合;后域(ranR):所有元素y组成的集合;5.自反闭包:r(R)=RUI;x对称闭包:s(R)=RU1-R;传递闭包:t(R)=RU2R U3R U……6.等价关系:集合A上的二元关系R满足自反性,对称性和传递性,则R称为等价关系;7.偏序关系:集合A上的关系R满足自反性,反对称性和传递性,则称R是A上的一个偏序关系;8.covA={<x,y>|x,y属于A,y盖住x};9.极小元:集合A中没有比它更小的元素(若存在可能不唯一);极大元:集合A中没有比它更大的元素(若存在可能不唯一);最小元:比集合A中任何其他元素都小(若存在就一定唯一);最大元:比集合A中任何其他元素都大(若存在就一定唯一);10.前提:B是A的子集上界:A中的某个元素比B中任意元素都大,称这个元素是B的上界(若存在,可能不唯一);下界:A中的某个元素比B中任意元素都小,称这个元素是B的下界(若存在,可能不唯一);上确界:最小的上界(若存在就一定唯一);下确界:最大的下界(若存在就一定唯一);第六章函数2种不同的关系,有m n种不同的函数;1.若|X|=m,|Y|=n,则从X到Y有mn2.在一个有n个元素的集合上,可以有22n种不同的关系,有n n种不同的函数,有n!种不同的双射;3.若|X|=m,|Y|=n,且m<=n,则从X到Y有A m n种不同的单射;4.单射:f:X-Y,对任意x,2x属于X,且1x≠2x,若f(1x)≠f(2x);1满射:f:X-Y,对值域中任意一个元素y在前域中都有一个或多个元素对应;双射:f:X-Y,若f既是单射又是满射,则f是双射;5.复合函数:fºg=g(f(x));6.设函数f:A-B,g:B-C,那么①如果f,g都是单射,则fºg也是单射;②如果f,g都是满射,则fºg也是满射;③如果f,g都是双射,则fºg也是双射;④如果fºg是双射,则f是单射,g是满射;第七章代数系统1.二元运算:集合A上的二元运算就是2A到A的映射;2. 集合A上可定义的二元运算个数就是从A×A到A上的映射的个数,即从从A×A到A上函数的个数,若|A|=2,则集合A上的二元运算的个数为2*22=42=16种;3. 判断二元运算的性质方法:①封闭性:运算表内只有所给元素;②交换律:主对角线两边元素对称相等;③幂等律:主对角线上每个元素与所在行列表头元素相同;④有幺元:元素所对应的行和列的元素依次与运算表的行和列相同;⑤有零元:元素所对应的行和列的元素都与该元素相同;4.同态映射:<A,*>,<B,^>,满足f(a*b)=f(a)^f(b),则f为由<A,*>到<B,^>的同态映射;若f是双射,则称为同构;第八章群1.广群的性质:封闭性;半群的性质:封闭性,结合律;含幺半群(独异点):封闭性,结合律,有幺元;群的性质:封闭性,结合律,有幺元,有逆元;2.群没有零元;3.阿贝尔群(交换群):封闭性,结合律,有幺元,有逆元,交换律;4.循环群中幺元不能是生成元;5.任何一个循环群必定是阿贝尔群;第十章格与布尔代数1.格:偏序集合A中任意两个元素都有上、下确界;2.格的基本性质:1) 自反性a≤a 对偶: a≥a2) 反对称性a≤b ^ b≥a => a=b对偶:a≥b ^ b≤a => a=b3) 传递性a≤b ^ b≤c => a≤c对偶:a≥b ^ b≥c => a≥c4) 最大下界描述之一a^b≤a 对偶avb≥aA^b≤b 对偶avb≥b5)最大下界描述之二c≤a,c≤b => c≤a^b对偶c≥a,c≥b =>c≥avb6) 结合律a^(b^c)=(a^b)^c对偶av(bvc)=(avb)vc7) 等幂律a^a=a 对偶ava=a8) 吸收律a^(avb)=a 对偶av(a^b)=a9) a≤b <=> a^b=a avb=b10) a≤c,b≤d => a^b≤c^d avb≤cvd11) 保序性b≤c => a^b≤a^c avb≤avc12)分配不等式av(b^c)≤(avb)^(avc)对偶a^(bvc)≥(a^b)v(a^c)13)模不等式a≤c <=>av(b^c)≤(avb)^c3.分配格:满足a^(bvc)=(a^b)v(a^c)和av(b^c)=(avb)^(avc);4.分配格的充要条件:该格没有任何子格与钻石格或五环格同构;5.链格一定是分配格,分配格必定是模格;6.全上界:集合A中的某个元素a大于等于该集合中的任何元素,则称a为格<A,<=>的全上界,记为1;(若存在则唯一)全下界:集合A中的某个元素b小于等于该集合中的任何元素,则称b为格<A,<=>的全下界,记为0;(若存在则唯一)7.有界格:有全上界和全下界的格称为有界格,即有0和1的格;8.补元:在有界格内,如果a^b=0,avb=1,则a和b互为补元;9.有补格:在有界格内,每个元素都至少有一个补元;10.有补分配格(布尔格):既是有补格,又是分配格;11.布尔代数:一个有补分配格称为布尔代数;第十一章图论1.邻接:两点之间有边连接,则点与点邻接;2.关联:两点之间有边连接,则这两点与边关联;3.平凡图:只有一个孤立点构成的图;4.简单图:不含平行边和环的图;5.无向完全图:n个节点任意两个节点之间都有边相连的简单无向图;有向完全图:n个节点任意两个节点之间都有边相连的简单有向图;6.无向完全图有n(n-1)/2条边,有向完全图有n(n-1)条边;7.r-正则图:每个节点度数均为r的图;8.握手定理:节点度数的总和等于边的两倍;9.任何图中,度数为奇数的节点个数必定是偶数个;10.任何有向图中,所有节点入度之和等于所有节点的出度之和;11.每个节点的度数至少为2的图必定包含一条回路;12.可达:对于图中的两个节点v,j v,若存在连接i v到j v的路,则称i vi与v相互可达,也称i v与j v是连通的;在有向图中,若存在i v到j v的j路,则称v到j v可达;i13.强连通:有向图章任意两节点相互可达;单向连通:图中两节点至少有一个方向可达;弱连通:无向图的连通;(弱连通必定是单向连通)14.点割集:删去图中的某些点后所得的子图不连通了,如果删去其他几个点后子图之间仍是连通的,则这些点组成的集合称为点割集;割点:如果一个点构成点割集,即删去图中的一个点后所得子图是不连通的,则该点称为割点;15.关联矩阵:M(G),m是i v与j e关联的次数,节点为行,边为列;ij无向图:点与边无关系关联数为0,有关系为1,有环为2;有向图:点与边无关系关联数为0,有关系起点为1终点为-1,关联矩阵的特点:无向图:①行:每个节点关联的边,即节点的度;②列:每条边关联的节点;有向图:③所有的入度(1)=所有的出度(0);16.邻接矩阵:A(G),a是i v邻接到j v的边的数目,点为行,点为列;ij17.可达矩阵:P(G),至少存在一条回路的矩阵,点为行,点为列;P(G)=A(G)+2A(G)+3A(G)+4A(G)可达矩阵的特点:表明图中任意两节点之间是否至少存在一条路,以及在任何节点上是否存在回路;A(G)中所有数的和:表示图中路径长度为1的通路条数;2A(G)中所有数的和:表示图中路径长度为2的通路条数;3A(G)中所有数的和:表示图中路径长度为3的通路条数;4A(G)中所有数的和:表示图中路径长度为4的通路条数;P(G)中主对角线所有数的和:表示图中的回路条数;18.布尔矩阵:B(G),v到j v有路为1,无路则为0,点为行,点为列;i19.代价矩阵:邻接矩阵元素为1的用权值表示,为0的用无穷大表示,节点自身到自身的权值为0;20.生成树:只访问每个节点一次,经过的节点和边构成的子图;21.构造生成树的两种方法:深度优先;广度优先;深度优先:①选定起始点v;②选择一个与v邻接且未被访问过的节点1v;③从v出发按邻接方向继续访问,当遇到一个节点所1有邻接点均已被访问时,回到该节点的前一个点,再寻求未被访问过的邻接点,直到所有节点都被访问过一次;广度优先:①选定起始点v;②访问与v邻接的所有节点1v,2v,……,k v,这些作为第一层节点;③在第一层节点中选定一个节点v为起点;1④重复②③,直到所有节点都被访问过一次;22.最小生成树:具有最小权值(T)的生成树;23.构造最小生成树的三种方法:克鲁斯卡尔方法;管梅谷算法;普利姆算法;(1)克鲁斯卡尔方法①将所有权值按从小到大排列;②先画权值最小的边,然后去掉其边值;重新按小到大排序;③再画权值最小的边,若最小的边有几条相同的,选择时要满足不能出现回路,然后去掉其边值;重新按小到大排序;④重复③,直到所有节点都被访问过一次;(2)管梅谷算法(破圈法)①在图中取一回路,去掉回路中最大权值的边得一子图;②在子图中再取一回路,去掉回路中最大权值的边再得一子图;③重复②,直到所有节点都被访问过一次;(3)普利姆算法①在图中任取一点为起点v,连接边值最小的邻接点2v;1②以邻接点v为起点,找到2v邻接的最小边值,如果最小边值2比v邻接的所有边值都小(除已连接的边值),直接连接,否则退回1v,1连接v现在的最小边值(除已连接的边值);1③重复操作,直到所有节点都被访问过一次;24.关键路径例2 求PERT图中各顶点的最早完成时间, 最晚完成时间, 缓冲时间及关键路径.解:最早完成时间TE(v1)=0TE(v2)=max{0+1}=1TE(v3)=max{0+2,1+0}=2TE(v4)=max{0+3,2+2}=4TE(v5)=max{1+3,4+4}=8TE(v6)=max{2+4,8+1}=9TE(v7)=max{1+4,2+4}=6TE(v8)=max{9+1,6+6}=12 最晚完成时间TL(v8)=12TL(v7)=min{12-6}=6TL(v6)=min{12-1}=11TL(v5)=min{11-1}=10TL(v4)=min{10-4}=6TL(v3)=min{6-2,11-4,6-4}=2TL(v2)=min{2-0,10-3,6-4}=2TL(v1)=min{2-1,2-2,6-3}=0 缓冲时间TS(v1)=0-0=0TS(v2)=2-1=1TS(v3)=2-2=0TS(v4)=6-4=2TS(v5=10-8=2TS(v6)=11-9=2TS(v7)=6-6=0TS(v8)=12-12=0关键路径: v1-v3-v7-v825.欧拉路:经过图中每条边一次且仅一次的通路;欧拉回路:经过图中每条边一次且仅一次的回路;欧拉图:具有欧拉回路的图;单向欧拉路:经过有向图中每条边一次且仅一次的单向路;欧拉单向回路:经过有向图中每条边一次且仅一次的单向回路;26.(1)无向图中存在欧拉路的充要条件:①连通图;②有0个或2个奇数度节点;(2)无向图中存在欧拉回路的充要条件:①连通图;②所有节点度数均为偶数;(3)连通有向图含有单向欧拉路的充要条件:①除两个节点外,每个节点入度=出度;②这两个节点中,一个节点的入度比出度多1,另一个节点的入;度比出度少1;(4)连通有向图含有单向欧拉回路的充要条件:图中每个节点的出度=入度;27.哈密顿路:经过图中每个节点一次且仅一次的通路;哈密顿回路:经过图中每个节点一次且仅一次的回路;哈密顿图:具有哈密顿回路的图;28.判定哈密顿图(没有充要条件)必要条件:任意去掉图中n个节点及关联的边后,得到的分图数目小于等于n;充分条件:图中每一对节点的度数之和都大于等于图中的总节点数;29.哈密顿图的应用:安排圆桌会议;方法:将每一个人看做一个节点,将每个人与和他能交流的人连接,找到一条经过每个节点一次且仅一次的回路(哈密顿图),即可;30.平面图:将图形的交叉边进行改造后,不会出现边的交叉,则是平面图;31.面次:面的边界回路长度称为该面的次;32.一个有限平面图,面的次数之和等于其边数的两倍;33.欧拉定理:假设一个连通平面图有v个节点,e条边,r个面,则v-e+r=2;34.判断是平面图的必要条件:(若不满足,就一定不是平面图)设图G是v个节点,e条边的简单连通平面图,若v>=3,则e<=3v-6;35.同胚:对于两个图G1,G2,如果它们是同构的,或者通过反复插入和除去2度节点可以变成同构的图,则称G1,G2是同胚的;36.判断G是平面图的充要条件:图G不含同胚于K3.3或K5的子图;37.二部图:①无向图的节点集合可以划分为两个子集V1,V2;②图中每条边的一个端点在V1,另一个则在V2中;完全二部图:二部图中V1的每个节点都与V2的每个节点邻接;判定无向图G为二部图的充要条件:图中每条回路经过边的条数均为偶数;38.树:具有n个顶点n-1条边的无回路连通无向图;39.节点的层数:从树根到该节点经过的边的条数;40.树高:层数最大的顶点的层数;41.二叉树:①二叉树额基本结构状态有5种;②二叉树内节点的度数只考虑出度,不考虑入度;③二叉树内树叶的节点度数为0,而树内树叶节点度数为1;④二叉树内节点的度数=边的总数(只算出度);握手定理“节点数=边的两倍”是在同时计算入度和出度的时成立;⑤二叉树内节点的总数=边的总数+1;⑥位于二叉树第k层上的节点,最多有12 k个(k>=1);⑦深度为k的二叉树的节点总数最多为k2-1个,最少k个(k>=1);⑧如果有n个叶子,2n个2度节点,则0n=2n+1;42.二叉树的节点遍历方法:先根顺序(DLR);中根顺序(LDR);后根顺序(LRD);43.哈夫曼树:用哈夫曼算法构造的最优二叉树;44.最优二叉树的构造方法:①将给定的权值按从小到大排序;②取两个最小值分支点的左右子树(左小右大),去掉已选的这两个权值,并将这两个最小值加起来作为下一轮排序的权值;③重复②,直达所有权值构造完毕;45.哈夫曼编码:在最优二叉树上,按照左0右1的规则,用0和1代替所有边的权值;每个节点的编码:从根到该节点经过的0和1组成的一排编码;。
离散数学 第11讲 布尔代数

三、有限布尔代数的结构
引理2: 设<B,∨,∧, ′, 0,1>是有限布尔代数, 则 (1) 任意b,c∈B, 有b∧c'=0当且仅当b ≤ c; (2) 对于B中任一原子a和任一非零元素b, a≤b 和a≤b'两式中有且仅 有一式成立。 (2)证明: 先证a ≤ b 和a ≤ b'两式不可能同时成立. 假如a ≤ b 和a ≤ b'同时 成立, 就有a ≤ b∧b'=0, 这与a是原子相矛盾。 再证a ≤ b 和a ≤ b'两式中必有一式成立. 因为a∧b ≤ a, a是原子, 所以只能是a∧b=0或a∧b=a. 若a∧b=0,则 a∧(b')'=0, 由(1)得a ≤ b'; 若a∧b=a, 得a≤b. 命题得证.
a∧b=0。
定理2的证明: (反证法) 假如a∧b≠0, 令a∧b=c, 若a, b是原子且a∧b≠0, 则 0<c≤ a 0<c ≤ b c < a 时与a为原子相矛盾. c=a时, 结合0 < c ≤ b 得0 < a< b,与b为原子相矛盾.所以a∧b=0.
三、有限布尔代数的结构
引理1: 设<B,∨,∧, ′, 0, 1>是一有限布尔代数, 则对于B中任一非 零元素b, 恒有一原子a∈B, 使a≤b。 证明: 任取b∈B且b≠0. 若b为原子, 有b≤b, 则命题已得证。 若b不是原子, 则必有b1∈B, 使得0 < b1 < b。 若b1不是原子,存在b2使0<b2<b1<b,对b2重复上面的讨论。 因为B有限,这一过程必将中止,上述过程产生的元素序列满足 0 < …<b2 < b1 < b 即存在br, br为原子,且0 < br < b, 否则此序列无限长。
离散数学格与布尔代数ppt课件

精选ppt
14
定理11.2
(3) 证明<S,≤>构成格。 即证明a∨b=ab,a∧b=a*b 。
a,b∈S 有 a(ab)=(aa)b=ab
说明 通过规定运算及其基本性质可以给出格的定义。
精选ppt
12
定理11.2
(1)证明在S中*和运算都适合幂等律。 a∈S,由吸收律得 a*a = a*(a(a*a)) = a
同理有 aa=a。
(2)在S上定义二元关系R, a,b∈S 有 <a,b>∈R ab=b
下面证明R在S上的偏序。
根据幂等律, a∈S都有aa=a,即<a,a>∈R,
6
例11.3
例11.3 设G是群,L(G)是G的所有子群的集合。即 L(G)={ H|H≤G }
对任意的H1,H2∈L(G),H1∩H2也是G的子群,而<H1∪H2>是由 H1∪H2生成的子群(即包含着H1∪H2的最小的子群)。 在L(G)上定义包含关系,则L(G)关于包含关系构成一个格, 称为G的子群格。 易见在L(G)中,H1∧H2就是H1∩H2,H1∨H2就是<H1∪H2>。
(1)交换律 a,b∈L 有
a∨b=b∨a
a∧b=b∧a
(2)结合律 a,b,c∈L 有
(a∨b)∨c=a∨(b∨c) (a∧b)∧c=a∧(b∧c)
(3)幂等律 a∈L 有
a∨a=a
a∧a=a
(4)吸收律 a,b∈L 有
a∨(a∧b)=a
a∧(a∨b)=a
精选ppt
9
定理11.1
(1)a∨b和b∨a分别是{a,b}和{b,a}的最小上界。 由于{a,b}={b,a},所以a∨b=b∨a。 由对偶原理,a∧b=b∧a得证。
离散数学格与布尔代数

证明:⑴ 因 a≤a∨b,a≤a∨c 所以 a ≤(a∨b)∧(a∨c)
又因 b∧c≤b≤ a∨b,b∧c≤c≤ a∨c
所以 b∧c ≤(a∨b)∧(a∨c)
于是有 a∨(b∧c) ≤(a∨b)∧(a∨c) 。
由对偶原理得 a∧(b∨c)≥ (a∧b)∨(a∧c) 。
即 (a∧b)∨(a∧c)≤ a∧(b∨c) 。
第二页,共87页
7-1 格 (Lattice)
一 . 基本概念
1. 格的定义
<A,≤>是偏序集,如果任何a,b∈A,使得{a,b}都有最大
下界和最小上界,则称<A,≤>是格。
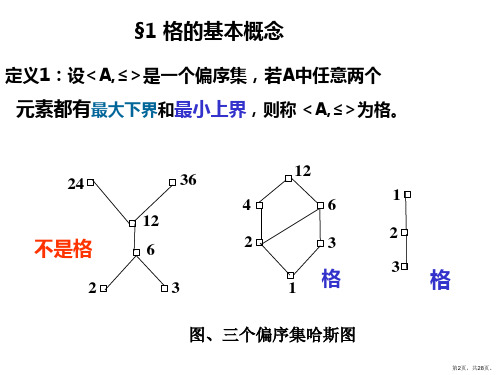
右图的三个偏 序集, <A,≤>不是格, 因为{24,36} 无最小上界。
<B,≤><C,≤>
。 。 24
36
。 30
2。
。 12 6。
离散数学格与布尔代数
第一页,共87页
2.B的最小元与最大元 y是B的最小元y∈B∧x(x∈By≤x) y是B的最大元y∈B∧x(x∈Bx≤y) {2,3,6}的最小元:无 最大元: 6 B如果有最小元(最大元), 则是唯一的。 3.B的下界与上界
。 。 24
36
。 12
6。 2。 3。
1。
y是B的下界y∈A∧x(x∈By≤x)
a∧1b=a f(a∧1b)=f(a) 即 f(a)∧2f(b)=f(a) 而 f(a)∧2f(b) ≤2f(b) 所以 f(a)≤2f(b). 3. 格同构的保序性 定理:设两个格为<A1,≤1>和<A2, ≤2> ,f是A1到A2的双射,则f是
<A1,≤1> 到<A2, ≤2>的格同构,当且仅当 对任意a,b∈A1,a≤1b f (a)≤2f(b) 证明:令<A1,∨1,∧1>和 <A2,∨2,∧2>是格<A1,≤1> 和 <A2, ≤2>诱导的代数系统,
离散数学--十一章格与布尔代数

离散数学--⼗⼀章格与布尔代数格的定义与性质:布尔代数是计算机逻辑设计的基础,它是由格引出的。
格⼜是从偏序集引出的。
所以我们先回顾⼀下偏序集中的⼀些概念。
偏序集简单来说就是集合A中有⾃反,反⾃反,传递的关系具体可以看第七章我们结合Hasse图看如下关系:假如 A={1,2,3,6,12,24,36} 且有如下关系如果:B={2,3,6}最⼤|⼩元定义:y是B的最⼩元⇔∃y∈B∧∀x(x∈B→y≤x)y是B的最⼤元⇔∃y∈B∧∀x(x∈B→x≤y)最⼤|⼩元是唯⼀的(类⽐函数的最值)⽽极⼤|⼩元不唯⼀B最⼤元6 ,最⼩元⽆B中Hasse图的最底(顶)层,且这⼀层只有⼀个点才能是最⼩(⼤)元极⼤|⼩元定义:y是B的极⼩元⇔∃y∈B∧¬∃x(x∈B∧x≤y)y是B的极⼤元⇔∃y∈B∧¬∃x(x∈B∧y≤x)这⾥⾯B的极⼩元是 {2,3},极⼤元是 {6}B中Hasse图的最底(顶)层,则是极⼩(⼤)元上下界定义:y是B的下界⇔∃y∈A∧∀x(x∈B→y≤x)y是B的上界⇔∃y∈A∧∀x(x∈B→x≤y)⽐如 B上界 {12,24,36} 下界 {1}Hasse图中B的最底(顶)层,包括这⼀层和这⼀层下⾯(上⾯)的所有元素构成的集合则是下(上)界确界定义:B的上确界(最⼩上界)下确界(最⼤下界)就是上界的min,下界的max结合Hasse 图理解若B={2,3,6} 有如上图的关系格讲这么多终于到格的定义了其实只要⼀个偏序集中任意⼦集都有上下确界就是格了莫名很简洁暗⽰判断格要疯狂枚举格诱导的代数系统交并运算设<A, ≤>是格,在A上定义⼆元运算∨和∧为:∀a,b∈Aa∨b=LUB {a,b} |{a,b}的最⼩上界.Least Upper Bounda∧b=GLB {a,b} |{a,b}的最⼤下界.Greatest Lower Bound称<A,∨,∧>是由格<A,≤>诱导的代数系统. (∨-并,∧-交)就是⽤符号定义了上下确界⽽已并且有:设<L, ≼>是格则有运算∨和∧适合交换律、结合律、幂等律和吸收律<==> 设<S, ∗, ◦ >是代数系统, ∗和◦是⼆元运算, 如果∗和◦满⾜交换律、结合律和吸收律, 则<S, ∗,◦>构成格.注意⼀下吸收率就好了:a∨(a∧b) = a, a∧(a∨b) = a各种格分配格如果交并还满⾜分配率就叫分配格有界格如果B是A时仍有上下确界则此时的格为有界格,这个确界分别称为全上|下界⼀般将全上界记为1 ,全下界记为0,⼀般将有界格L记为<L,∧,∨,0,1>.有限格L={a1,a2,…,an}是有界格, 则a1∧a2∧…∧an是L的全下界, a1∨a2∨…∨an是L的全上界.0是关于∧运算的零元,∨运算的单位元;1是关于∨运算的零元,∧运算的单位元.有补格有补元的格称为有补格a∧b = 0 和 a∨b = 1成⽴, 则称b是a的补元在任何有界格中, 全下界0与全上界1互补对于⼀般元素, 可能存在补元, 也可能不存在补元. 如果存在补元, 可能是惟⼀的, 也可能是多个补元.对于有界分配格, 如果元素存在补元, ⼀定是惟⼀的⼦群格没有特别懂对⼀个群先找出它的所有⼦群⽐如Z12 <0>,<1>,<2>,<3> ,<6>就是所有⼦群|也满⾜格的定义?也是⼦格然后再画所有⼦群(⼦格)的Hasse图就⾏了布尔代数本质上就是⼀个集合如果⼀个格是有补分配格, 则称它为布尔格或布尔代数. 布尔代数标记为<B,∧,∨,′, 0, 1>, ′为求补运算这⾥⾯的 ' 的运算规律相当于 ‘否’(a' )' =a∀a,b∈B, (a∧b)′ = a′∨b′, (a∨b) ′= a′∧b′(0∧b)∨(a∧0) = 0∨0 = 0(1∨b′)∧(a′∨1) = 1∧1 = 1(a∧b)∧(a′∨b′) = (a∧b∧a′)∨(a∧b∧b′)注意⼀下:Sn代表 n的因⼦所构成的集合|别到时候不知道⽐如 s6={1,2,3,6}。
《格和布尔代数》课件

第二部分:格的基础知识
有限格和无限格
介绍有限格和无限格的概念, 讨论其特点和应用。
笛卡尔积和格的同构
解释格的笛卡尔积以及同构 关系,揭示它们在格理论中 的重要性。
原子性和可分性
详细阐述格的原子性和可分 性,论述它们在实际问题中 的应用价值。
第三部分:布尔代数
1
ቤተ መጻሕፍቲ ባይዱ
3.2 布尔代数运算
2
系统阐述布尔代数的与、或、非运算,
总结格和布尔代数的重要性及其在学术和实
多研究和应用探索,促进学科的发展与创新。
践中的潜力,并对未来的研究方向进行展望。
《格和布尔代数》PPT课 件
本《格和布尔代数》PPT课件将带您深入了解格和布尔代数的基础知识、运 算规则以及其在现实世界中的重要应用。全方位解析格和布尔代数,帮助您 掌握这一重要数学领域的核心概念与技巧。
第一部分:引言
什么是格和布尔代数?探讨格和布尔代数的定义、特性和相关领域应用,以 及其在数学、计算机科学和工程中的重要性。
以及相关的异或和置位运算。
3
3.1 布尔代数的起源和发展
探索布尔代数的历史渊源与发展轨迹, 重点介绍George Boole对其的贡献。
3.3 布尔代数的完备性和最小化
讲解布尔代数的完备性定理、最小化方 法和卡诺图的应用。
第四部分:格和布尔代数的应用案例
逻辑电路设计
展示格和布尔代数在逻辑电路设 计中的重要应用,以及其在计算 机工程领域的意义。
程序设计中的控制流分析
阐述格和布尔代数在程序设计中 的控制流分析应用,帮助程序员 编写高效的代码。
数据库查询优化
探究格和布尔代数在数据库查询 优化中的关键作用,提高查询效 率和性能。
布尔代数

任何有限布尔代数的基数为2n, n是自然数。
设B是有限代数系统,A是B中所有原子的集合。 则:B≅P(A), ∴|B|=|P(A)|=2|A|
等势的布尔代数系统均同构
设B1和B2是有限布尔代数,且|B1|=|B2|;A1,A2分别是相应 的原子的集合。由同构关系的传递性,只需证明: P(A1)≅P(A2)。
则称ϕ是B1到B2的同态映射。(若ϕ是双射,则是同构)
其实,上述3个等式不是独立的。
(2)+(3)⇒(1): ϕ(a∨b)=ϕ(((a∨b)')')= -ϕ((a∨b)')= -ϕ(a'∧ b')= -(ϕ(a')⋂ϕ(b'))= -(-ϕ(a)⋂-ϕ(b))=ϕ(a)⋃ϕ(b) 同理:(1)+(3)⇒(2)
有限布尔代数的表示定理的证明
ϕ: B → P(A), ∀x∈B, ϕ(x)=T(x)是同态映射。
ϕ(x∧y) = T(x∧y) = {b|b∈A, b≼x∧y} = {b|(b∈A, b≼x)且 (b∈A, b≼y)} = {b|b∈A,b≼x}⋂{b|b∈A,b≼y} = T(x)⋂T(y) = ϕ(x)⋂ϕ(y) 令x=a1 ∨ a2 ∨ … ∨ an , y=b1 ∨ b2 ∨ … ∨ bm 。 则x ∨ y= a1 ∨ … ∨ an ∨ b1 ∨ … ∨ bm , 显然:ϕ(x∨y) = T(x∨y) = T(x)⋃T(y) = ϕ(x) ⋃ ϕ(y) 设x'是x在B中的补元。注意: ϕ(x)⋃ϕ(x')=ϕ(x ∨ x')=ϕ(1)=A 且 ϕ(x)⋂ϕ(x')=ϕ(x ∧ x')=ϕ(0)=∅ ∴ϕ(x') = ∼ϕ(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:一般说来, 格中的∨和∧运算不满足分配律.
5
格作为代数系统的定义
定理11.4 设<S,∗,◦>是具有两个二元运算的代数系统, 若对于 ∗和◦运算适合交换律、结合律、吸收律, 则可以适当定义S中 的偏序 ≼,使得 <S,≼> 构成格, 且a,b∈S 有 a∧b = a∗b, a∨b = a◦b. 证明省略. 根据定理11.4, 可以给出格的另一个等价定义. 定义11.3 设<S, ∗, ◦ >是代数系统, ∗和◦是二元运算, 如果 ∗和◦满足交换律、结合律和吸收律, 则<S, ∗,◦>构成格.
11
有界分配格的补元惟一性
定理11.7 设<L,∧,∨,0,1>是有界分配格. 若L中元素 a 存在 补元, 则存在惟一的补元. 证 假设 c 是 a 的补元, a∨c = 1, a∧c = 0, 又知 b 是 a 的补元, 故 a∨b = 1, a∧b = 0 从而得到 a∨c = a∨b, a∧c = a∧b, 由于L是分配格. b=b ∧ (b∨a) = b ∧ (c∨a )= (b ∧ c)∨ (b ∧ a )= (a∨c ) ∧c=c 注意: 在任何有界格中, 全下界0与全上界1互补. 对于一般元素, 可能存在补元, 也可能不存在补元. 如果 存在补元, 可能是惟一的, 也可能是多个补元. 对于有界 分配格, 如果元素存在补元, 一定是惟一的. 12
8
有界格的性质
定理11.6 设<L,∧,∨,0,1>是有界格, 则a∈L有 a∧0 = 0, a∨0 = a, a∧1 = a, a∨1 = 1
注意: 有限格L={a1,a2,…,an}是有界格, a1∧a2∧…∧an是L的全下 界, a1∨a2∨…∨an是L的全上界. 0是关于∧运算的零元,∨运算的单位元;1是关于∨运算的 零元,∧运算的单位元.
1
实例
例2 判断下列偏序集是否构成格,并说明理由. (1) <P(B), >,其中P(B)是集合B的幂集. (2) <Z, ≤>,其中Z是整数集,≤为小于或等于关系. (3) 偏序集的哈斯图分别在下图给出.
(1) 幂集格. x,y∈P(B),x∨y就是x∪y,x∧y就是x∩y. (2) 是格. x,y∈Z,x∨y = max(x,y),x∧y = min(x,y), 图2 (3) 都不是格. 可以找到两个结点缺少最大下界或最小上界
3
Байду номын сангаас
格的性质:序与运算的关系
定理11.3 设L是格, 则a,b∈L有 a ≼ b a∧b = a a∨b = b
可以用集合的例子来验证 幂集格
<P(B), >,其中P(B)是集合B的幂集. 幂集格. x,y∈P(B),x∨y就是x∪y,x∧y就是x∩y.
4
格的性质:保序
定理11.4 设L是格, a,b,c,d∈L,若a ≼ b 且 c ≼ d, 则 a∧c ≼ b∧d, a∨c ≼ b∨d 证 a∧c ≼ a ≼ b, a∧c ≼ c ≼ d 因此 a∧c ≼ b∧d. 同理可证 a∨c ≼ b∨d 例4 设L是格, 证明a,b,c∈L有 a∨(b∧c) ≼ (a∨b)∧(a∨c). 证 由 a ≼ a, b∧c ≼ b 得 a∨(b∧c) ≼ a∨b 由 a ≼a, b∧c ≼ c 得 a∨(b∧c) ≼ a∨c a∨(b∧c) ≼ (a∨b)∧(a∨c) (注意最大下界)
7
有界格的定义
定义11.6 设L是格, (1) 若存在a∈L使得x∈L有 a ≼ x, 则称a为L的全下界 (2) 若存在b∈L使得x∈L有 x ≼ b, 则称b为L的全上界 说明: 格L若存在全下界或全上界, 一定是惟一的. 一般将格L的全下界记为0, 全上界记为1. 定义11.7 设L是格,若L存在全下界和全上界, 则称L 为有界 格, 一般将有界格L记为<L,∧,∨,0,1>.
2
格的性质:算律
定理11.1 设<L, ≼>是格, 则运算∨和∧适合交换律、结合律、 幂等律和吸收律, 即 (1) a,b∈L 有 a∨b = b∨a, a∧b = b∧a (2) a,b,c∈L 有 (a∨b)∨c = a∨(b∨c), (a∧b)∧c = a∧(b∧c) (3) a∈L 有 a∨a = a, a∧a = a (4) a,b∈L 有 a∨(a∧b) = a, a∧(a∨b) = a
(1) L1中 a 与 c 互为补元, 其中 a 为全下界, c为全上界, b 没有 补元. (2) L2中 a 与 d 互为补元, 其中 a 为全下界, d 为全上界, b与 c 也互为补元. (3) L3中a 与 e 互为补元, 其中 a 为全下界, e 为全上界, b 的补 元是 c 和 d ; c 的补元是 b 和 d ; d 的补元是 b 和 c ; b, c, d 每个元素都有两个补元. (4) L4中 a 与 e 互为补元, 其中 a 为全下界, e 为全上界, b 的补 元是 c 和 d ; c 的补元是 b ; d 的补元是 b .
6
11.2 分配格、有补格与布尔代数
定义11.5 设<L,∧,∨>是格, 若a,b,c∈L,有 a∧(b∨c) = (a∧b)∨(a∧c) a∨(b∧c) = (a∨b)∧(a∨c) 则称L为分配格. 注意:可以证明以上两个条件互为充分必要条件 实例
L1 和 L2 是分配格, L3 和 L4不是分配格. 称 L3为钻石格, L4为五角格.
9
有界格中的补元及实例
定义11.8 设<L,∧,∨,0,1>是有界格, a∈L, 若存在b∈L 使得 a∧b = 0 和 a∨b = 1 成立, 则称b是a的补元. 注意:若b是a的补元, 那么a也是b的补元. a和b互为补元.
例7 考虑下图中的格. 针对不同的元素,求出所有的补元.
10
解答
11.1 格的定义与性质
定义11.1 设<S, ≼>是偏序集,如果x,yS,{x,y}都有最小上 界和最大下界,则称S关于偏序≼作成一个格. (偏序关系 P126) 求{x,y} 最小上界和最大下界看成 x 与 y 的二元运算∨和∧, 例1 设n是正整数,Sn是n的正因子的集合. D为整除关系,则 偏序集<Sn,D>构成格. x,y∈Sn,x∨y是lcm(x,y),即x与y的 最小公倍数. x∧y是gcd(x,y),即x与y的最大公约数.
