离散数学第十五章 格与布尔代数(简)
离散数学中的布尔函数和布尔代数

离散数学是一门研究离散结构和离散对象的数学学科,它在计算机科学等领域扮演着重要的角色。
布尔函数和布尔代数是离散数学中的重要概念之一,它们在逻辑电路设计、计算机编程等方面具有广泛的应用。
布尔函数是一种将布尔域上的值映射为布尔域上的值的函数。
布尔域上的值只有两个:真和假。
布尔函数的输入和输出都是布尔值。
布尔函数可以通过真值表、函数表达式或者逻辑电路图表示。
常见的布尔运算有与运算、或运算、非运算等。
布尔函数可以定义在不同的布尔变量上,而布尔变量可以取真或假两个值。
通过组合不同的布尔运算,可以构造出复杂的布尔函数。
布尔代数是研究布尔函数性质和运算规则的代数系统。
布尔代数的基本操作有与运算、或运算、非运算等。
与运算、或运算和非运算是布尔函数的基本运算,在布尔代数中具有特殊的性质。
例如,与运算满足交换律、结合律和分配律;或运算满足交换律、结合律和分配律;非运算满足德摩根定律。
布尔代数还有很多其他的运算规则,如吸收律、零元律、幂等律等。
这些运算规则可以用来简化布尔函数,使其更加简洁明了。
布尔函数和布尔代数在逻辑电路设计中起着重要的作用。
逻辑电路是一种基础的电子电路,用来完成逻辑运算。
布尔函数可以用来描述逻辑电路的功能,布尔代数可以用来简化逻辑电路。
通过布尔函数和布尔代数可以设计出各种复杂的逻辑电路,如逻辑门、多路选择器、时序电路等。
逻辑电路在计算机硬件中广泛应用,是计算机工作的基础。
因此,研究布尔函数和布尔代数不仅有助于理解离散数学的基本概念,也对计算机科学和工程领域有着重要的实际意义。
此外,布尔函数和布尔代数在计算机编程中也具有重要的应用。
计算机程序是一系列指令的集合,通过执行这些指令实现特定的功能。
布尔函数可以用来描述程序中的条件和逻辑关系,判断某个条件是否成立,从而确定程序的执行路径。
布尔代数可以用来简化程序的逻辑表达式,使程序更加高效和可读。
在编程语言中,布尔变量和布尔运算是基础数据类型和基本运算符之一,它们与布尔函数和布尔代数密切相关。
11%20布尔代数与格ppt

19
在格中定义运算
在格中可以定义如下的运算:
“保联”:x,yS, x⋁y=lub{x,y}
“保交”:x,yS, x⋀y=glb{x,y}
20
偏序格的例子
({1,2,3,4,6,8,12,16,24,48}, | )
x⋀y=gcd(x,y), x⋁y=lcm(x,y) x⋀y=x⋂y, x⋁y=x⋃y x⋀y=min{x,y}, x⋁y=max{x,y}
9
布尔恒等式(1)
等 式 x=x x+x = x xx = x x+0 = x x1 = x x+1 = 1 x0 = 0 x+y = y+x xy = yx 名 称 双重补律 幂等律 同一律
支配律
交换律
10
布尔恒等式(2)
等 式 x+(y+z)=(x+y)+z x (yz)=(xy) z x+(yz)=(x+y)(x+z) x (y+z)=xy +x z ( x y) = x + y (x+y) = x y x+(xy)=x x (x+y)=x x + x =1 x x =0 名 称 结合律 分配律 德摩根律 吸收律 补律
29
a*b即{a,b}的最大下界
注意:a◦b=b 当且仅当 a*b=a,因此aRb a*b=a
a*b即{a,b}的下界
(a*b)*a=a*(a*b)=(a*a)*b=a*b, (a*b)Ra (a*b)*b=a*(b*b)=a*b,(a*b)Rb
a*b即{a,b}的最大下界
格与布尔代数课件2
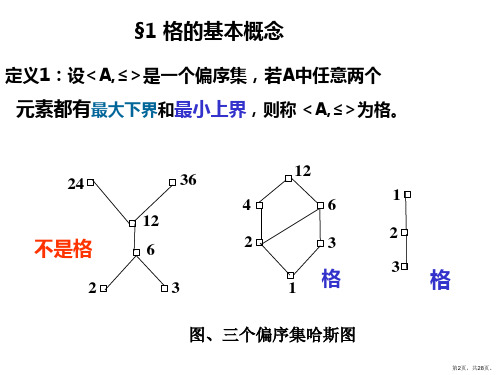
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f,使得对 x1,x2 A, 有f(x1∨1x2)=f(x1)∨2f(x2),f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律:a∨(a∧b) = a、a∧(a∨b) = a
证明:幂等律 ∵ a≤a,∴ a是a的上界,而a∨a是a的最小上界, ∴a∨a≤a ,又 ∵ a≤a ∨a,
由反对称性得:a∨a = a 由对偶原理得,a∧a = a
第15页,共28页。
证明:吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a, a∨(a ∧ b)≤a
解:< I+ , D>是格 ∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大上界等于a、b的最大公约数。
第3页,共28页。
< P(S) , > 是格
∵子集关系是偏序关系,对a,b P(S),
a、b的最小上界等于a∪b,
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2,>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1:,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}
离散数学 格与布尔代数共89页

66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
离散数学 格与布尔代数
21、没有人陪你走一辈子,所以你要 适应孤 独,没 有人会 帮你一 辈子, 所以你 要奋斗 一生。 22、当眼泪流尽的时候,留下的应该 是坚强 。 23、要改变命运,首先改变自己。
24、勇气很有理由被当作人类德性之 首,因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 放上一 段时间 ,以便 让别一 只脚能 够再往 上登。
(优选)第篇格与布尔代数

第2式证明由对偶原理从上式直接可得。
定理15-1.6 设<A, >是一个格,那么,对于任意的 a,bA, 都有:
ab(a∧b)=a(a∨b)=b
ab(a∧b)证明思路:
(1)先证 ab (a∧b)=a
由ab和a a ,根据定理15-1.2得 a a∧b
又根据a∧b的定义, 有
a∧b a
由二元关系的反对称性得 :
(优选)第篇格与布尔代数
通常用a∨b 表示{a,b}的上确界,用a∧b 表示{a, b}的下确界,∨和∧分别称为保联(join)和保交(meet) 运算。由于对任何a,b,a∨b及a∧b都是A 中确定 的成员,因此 ∨,∧均为A上的运算。
例3 设S={a,b} , (S) ={, {a},{b},{a,b}} 由格< (S), >诱导的代数系统为< (S),∨,∧> 。 其中∨为集合的并运算和∧为集合的交运算。
a∧b = a
(2) 再证 (a∧b)=a ab
设a∧b=a,则a =a∧bb ,这就证明了
(a∧b)=a ab
综合(1)和(2)得: ab(a∧b)
定理15-1.7 设<A, >是一个格,那么,对于任意的
a,b,cA, 都有: aca∨(b∧c) (a∨b)∧c
证明思路: (1)先证 ac a∨(b∧c) (a∨b)∧c 根据定理15-1.6有 ac (a∨c)=c 根据定理15-1.5有a∨(b∧c)(a∨b)∧(a∨c)
可以证明,若<A,>是格,则<A,R>也是格。 称R是的逆关系。记为。
格对偶原理可以叙述为:设P是对任意格都真的命题, 如果在命题P中把换成 ,∨换成∧,∧换成∨,就
离散数学格与布尔代数优秀课件

于是有 a∨(b∧c) ≤(a∨b)∧(a∨c) 。
由对偶原理得 a∧(b∨c)≥ (a∧b)∨(a∧c) 。
即 (a∧b)∨(a∧c)≤ a∧(b∨c) 。
b c d
由<A,≤>诱导的代数系统。B是A的
非空子集,如果∧
a
和∨在B上封闭,则 称<B, ≤>是<A, ≤>
b
c b
d
e
f e
的子格。
g
a
e
c
a
b f
c
g
d
<C,≤>是<A,≤>的子格。 <A,≤>
<B,≤> <C,≤>
而<B,≤>不是. b∧c=dB, (运算规则要从格<A,≤>中找)
二. 格的对偶原理
界,所以 a∨c≤b∨d。 类似可证 a∧c≤b∧d。 推论:在一个格中,任意 a,b,c∈A,如果b≤c,则
a∨b≤a∨c,a∧b≤a∧c。 此性质称为格的保序性。
3. ∨和∧都满足交换律。即 a∨b=b∨a,a∧b=b∧a 此性质由运算∨和∧的定义直接得证。
4. ∨和∧都满足幂等律。即 a∨a=a a∧a=a 证明:由性质1, a≤a∨a (再证a∨a≤a)
P’: a∨b≥a
{a,b}的最大下界≤a {a,b}的最小上界≥a
三. 格的性质
<A,∨,∧>是由格<A,≤>诱导的代数系统。a,b,c,d∈A 1. a≤a∨b b≤a∨b a∧b≤a a∧b≤b
此性质由运算∨和∧的定义直接得证。 2.如果a≤b,c≤d,则 a∨c≤b∨d,a∧c≤b∧d。 证明:如果a≤b,又b≤b∨d,由传递性得 a≤b∨d, 类似由c≤d, d≤b∨d,由传递性得 c≤b∨d, 这说明b∨d是 {a,c} 的一个上界,而a∨c是 {a,c} 的最小上
第5篇ch15格与布尔代数

设对任意的a,bA1, a1bf(a)2f(b)
设 a∧1b=c,则 c1a, c1b ,
于是 f(a∧1b)=f (c) ,f(c)2f(a) , f(c)2f(b)
故有 f(c)2f(a)∧2f(b)
令 则
ff((ac))∧22ff((db))=,ff((dd))2f(a) , f(d)2f(b)
所以 b∧c=b∧c∧b∧c (a∨b)∧(a∨c) (2)
再对(1)式和(2)式应用定理15-1.2得 a∨(b∧c) (a∨b)∧(a∨c)
第2式证明由对偶原理从上式直接可得。
定理15-1.6 设<A, >是一个格,那么,对于任意的a,bA,
都有: ab(a∧b)=a(a∨b)=b
ab(a∧b)证明思路:
故有 d1a ,d1b,于是 d1a∧1b ,即 d1c,
所以 f(d)2f(c)
因此 f(d)=f(c) 即 f(a∧1b)=f(a)∧2f(b)
类似地可证: f(a∨1b)=f(a)∨2 f(b) 格同构证毕。
15-2 分配格
定义15-2.1 设<A,∨,∧> 是由格<A, >是所诱导的
代数系统。如果对任意的a,b,c A,满足: a∧(b∨c)= (a∧b)∨(a∧c) a∨(b∧c)= (a∨b)∧(a∨c)
则称< A, > 是分配格 。
例1: 集合:S={a,b,c}
格: <(S), > 代数系统: <(S), ∪,∩> 结论:<(S), > 是一个分配格。
例2:不是分配格的例子。 例3:利用两个“特殊五元素非分配格”的结论。
定理15-2.1 如果在一个分配格中交运算对于并运算可分 配,则并运算对于交运算也一定是可分配的。反之亦然。
离散数学格与布尔代数

§7.1 格
例 < P(S) , >是格 表示为<P(S), , * > 又可表示为< P(S) ,∪,∩>
例 <Z+,≤>,或 <Z+,|> <Z+, , * > <Z+, LCM,GCD>
§7.2 格——代数系统
格〈L,≤〉中自然存在两个运算 和 * ,从而 派生出一个代数系统〈L,,*〉
6
<S15,|>,
2
2019/10/5
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/5
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
并、交 运算的性质
定理1 设〈L,≤〉是一个格,并运算与交运算 * 满足 如下性质:
L1 a a = a
a*a=a
(幂等律)
L2 a b = b a a * b = b * a (交换律)
L3 (a b) c = a (b c)
离散数学-格和布尔代数

的次序图如下
-1 的次序图如下
6 2 1 3 2
1 3 6
若 < L; > 是一个偏序集,则对于任意元素 l1, l2, l3 L,有以 下六个关系式成立: l1 l1 若 l1 l2,l2 l1,则 l1 = l2 若 l1 l2,l2 l3,则 l1 l3 l1 l1 若 l1 l2,l2 l1,则 l1 = l2 (7-1) (7-2) (7-3) (7-1) (7-2)
60以上说明与格一样布尔代数也是一个代数系统该代数系统可取交换律分配律同一律和互补律作为公二元运算是一元运算若这些运算满足交换律分配律同一律和互补律则称称作集合代数它是一个布尔代数
第二部分 抽象代数
0
第七章
格和布尔代数
格是 Birkhoff (1884 - 1944) 在 20 世纪 30 年代提出的,格的提出 以子集为背景。 历史上最初出现的格是英国数学家 George Boole 于 1854 年提出 的,是他在研究命题演算中发现的,通常称为布尔格或布尔代 数。 格和布尔代数的理论成为计算机硬件设计和通讯系统设计中的 重要工具。格论是计算机语言的指称语义的理论基础。格是一 种特殊的偏序集,也可以看作是有两个二元运算的代数系统, 布尔代数是一种特殊的格。在保密学、开关理论、计算机理论 和逻辑设计以及其他一些科学和工程领域中,都直接应用了格 与布尔代数。 1
7.2 格及其性质
一、格的定义
定义7-5 设 < L; > 是一个偏序集,如果 L 中任意两个元素都 存在着最大下界和最小上界,则称 < L; > 是格。 由于每对元素的最大下界和最小上界唯一,故引入记号: l1 l2 = glb(l1, l2),l1 l2 = lub(l1, l2), 其中 和 均可看作是集合 L 上的二元运算,分别称为交和并。 注:若 < L; > 是一个格,则意味着 < L; > 也是一个形为 < L; , > 的代数系统,其中 和 是 L 上的两个二元运算, 对于任意 l1, l2 L,l1 l2 表示在偏序 “ ” 意义下,l1 和 l2 的最小上界,l1 l2 表示 l1 和 l2 的最大下界。
离散数学布尔代数

一个非零元素b,至少存在一个原子a,使得a ≤ b。 1
证明:若b本身就是一个原子,则b ≤ b,得证。c
df
若b不是原子,肯定存在b1,使得0 ≤ b1 ≤ b, a
be
若b1是原子,则定理得证;
0
否则,若b1不是原子,则必存在b2,使得0 ≤ b2 ≤ b1 ≤ b
∵<A, ≤>是一个有全下界的有限格,
定理1:对于布尔代数中任意两个元素 a, b,必定有
(1) ( a ) = a, (2) a∨b = a∧b , (3) a∧b = a∨b
3
❖ 布尔代数
定义3:设<A,∨1,∧1, - > 和<B,∨2,∧2, ~ >是两个布尔代数, 如果存在A到B的双射 f,对于a,bA,有
f (a∨1b) = f (a) ∨2 f (b)
2、对a,bA,有 f (a∧b) = f (a)∩f (b)
9
❖ 格与布尔代数
定理3 ( Stone表示定理 ) :
设<A,∨,∧, - >是由有限布尔格<A, ≤>所诱导的一个有 限布尔代数,S是布尔格<A, ≤>中的所有原子的集合,则 < A,∨,∧, - >< P(S),∪,∩, ~ >同构。 分析:要证两个代数系统同构,分为以下几步:
1、找一个双射函数 f: A P(S)
∴a ≤ c ,又∵a ≤ c, ∴a ≤ c ∧ c,即 a ≤ 0,
这与a是原子相矛盾, ∴假设错
∴b ∧ c = 0,由引理1得: b≤c ∴b=c,即:b= a1∨a2∨... ∨ak
7
❖ 格与布尔代数
证明(2):设b的另一种表示形式为 b = aj1∨aj2∨... ∨ajt 其中aj1,aj2,……,ajt是A中原子。∵b是 aj1,aj2,……,ajt 的最小上界, ∴有aj1≤b, aj2≤b,…,ajt≤b,而a1,a2,……,ak是A中满足 a j ≤b的所有原子, {aj1,aj2,…,ajt}是{a1,a2,…,ak}的子集,即 |{aj1,aj2,…,ajt}|<=|{a1,a2,…,ak}|, 即:t ≤ k。(下面证 t < k 是不可能的)
离散数学格与布尔代数

6
<S15,|>,
2
2019/10/12
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/12
§7.1 格
例 设Z+为正整数集合,对于a,b Z+,关系“≤”定义为: a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格,
Input A B Cin
00 0 00 1 01 0 01 1 10 0 10 1 11 0 11 1
Output S Cout
00 10 10 01 10 01 01 11
S A BCin A BCin A BCin A BCin
Cout A B Cin A B Cin A B Cin A B Cin
§7.2 格——代数系统
证〈L,≤〉为要求的格
a,b∈L,(a * b)* a = a*(a * b)=(a * a)*b=a*b,
故a*b≤a,
L3
L1
同理a*b≤b,因此a*b是{a,b}的下界,
又设c是{a,b}的任一下界,即c≤a,c≤b,则a * c=c,b * c=c,于是(a * b)* c=a *(b * c)=a * c=c,即c≤a * b, 所以a * b是{a,b}的最大下界,即a * b=inf{a,b},
离散数学格的概念

∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大下界等于a、b的最大公约数。
❖ 基本概念
< B2 , D >是否 < S30 , D >的子格?
30
6
30
10
6 15
2
3
10
15
1 ∨1 2 3 6 11236 22266
2
53
5
∧1 2 3 6
1
11111
21212
说明:
33636 66666
31133 61236
(1) 子格必是格。
运算∨和∧在B1上封闭,B1 S30 且B1 ≠Ø, ∴ < B1, D >是 < S30 , D >的子格; 同理可证< B2 , D >是 < S30 , D >的子格
例:A={a, b, c }, < P(A) , > 所诱导的代数系统为?
< P(A),∪,∩>
❖ 基本概念
定义3:设<A,≤ >是一个格,由其所诱导的代数系统为 <A,∨,∧>。设BA且B ≠Ø ,如果运算∨和∧在B上封闭, 则称<B,≤ > 是<A,≤ >的子格。
❖ 基本概念
例2:B1 = {1,2,3,6} , B2 = {5,10,15,30} ,< B1, D >和
离散数学
❖ 格与布尔代数 1 格的概念
离散数学中的布尔代数知识点介绍

离散数学中的布尔代数知识点介绍离散数学是计算机科学和数学中的一个重要分支,而布尔代数则是离散数学中的一个基础概念。
布尔代数是一种逻辑推理和计算的数学体系,其基本概念和运算规则直接应用于计算机计算和逻辑设计中。
一、布尔代数的基本概念布尔代数有两个基本元素:命题和逻辑操作符。
命题是关于真(True)和假(False)的陈述,可以用字母或其他符号表示。
逻辑操作符包括与(AND)、或(OR)、非(NOT)三种基本运算符,用于对命题进行逻辑运算。
二、布尔代数的基本运算规则1. 与运算(AND):只有当两个命题都为真时,与运算的结果才为真。
用符号“∧”表示,例如命题A∧B表示“命题A和命题B都为真”。
2. 或运算(OR):只要两个命题中有一个为真,或运算的结果就为真。
用符号“∨”表示,例如命题A∨B表示“命题A或命题B为真”。
3. 非运算(NOT):将命题的真值取反,即将真变为假,将假变为真。
用符号“¬”表示,例如¬A表示“命题A的取反”。
三、布尔代数的重要性布尔代数在计算机科学和逻辑设计中具有重要的应用。
布尔代数提供了一种形式化的工具,可以对逻辑关系和计算过程进行精确的描述和处理。
利用布尔代数的运算规则,可以进行逻辑推理、逻辑运算和逻辑设计。
布尔代数为计算机的基本运算提供了理论基础,是计算机科学不可或缺的一部分。
四、布尔代数的应用领域1. 逻辑电路设计:布尔代数的基本运算规则可以用于逻辑门电路的设计与分析。
逻辑门电路由与门、或门、非门等基本门电路组成,通过布尔代数的运算规则可以进行电路的优化和逻辑设计。
2. 程序设计与算法分析:布尔代数在程序设计和算法分析中具有重要地位。
利用布尔代数的运算规则,可以对程序的逻辑关系进行抽象和分析,确保程序的正确性和可靠性。
3. 数据库查询与管理:布尔代数可用于数据库查询和管理中的条件表达式构建。
通过布尔代数的运算规则,可以对数据库数据进行选择、过滤和计算,实现对数据的高效管理与查询。
离散数学第十五章格与布尔代数简

例:找出下图所示哈斯图的偏序集的子集 {a,b,c},{j,h}和{a,c,d f}的下界和上界。
解: {a,b,c}的上界是e,f,j,h,它唯 一的下界是a。 {j,h}没有上界,它的下界是 a,b,c,d,e,f。 {a,c,d f}的上界是f,h,j,它的 下界是a。
例 在上图所示偏序集中,如果{b,d,g}的最 大下界和最小上界存在,求出这个最大下界和最 小上界。
从上讨论中,可知两格互为对偶。互为对偶 的两个<L,≤>和<L,≥>有着密切关系,即格<L,≤> 中交运算正是格<L,≥>中的并运算,而格 <L,≤>中的并运算正是格<L,≥>中的交运算。 因此,给出关于格一般性质的任何有效命题,把 关系≤换成≥(或者≥换成≤),交换成并,并换成 交,可得到另一个有效命题,这就是关于格的对 偶性原理。
⑤ <B,,, ',0,1>是有补分配格,满足 (CD-1) (ab)'=a'a',(ab)'=a'b' (德·摩 根律)
(CD-2) a≤ba'b=1ab'=0b'≤a' 注意,上述公式并非都是独立的,可从中选 出一些公式作为基本公式,用它们推出其余的公 式,而且可以用基本公式定义布尔代数。
定义15.2.1 设<B,,, '>是一代数结构,其中
由于有补分配格中,每个元素a都有唯一的补 元 a' , 因 此 可 在 L 上 定 义 一 个 一 元 运 算 — 补 运 算 “ ' ”。这样,有补分配格可看作具有两个二元运 算和一个一元运算的代数结构,习惯上称它为布 尔代数,记为<B,,,',0,1>,其中B=L。
第15章 格与布尔代数PPT课件
2020/11/1413Fra bibliotek对偶原理
对于格<L, ≤ >的任何命题,将保联运算与保交运 算分别换成对偶格<L, ≥>的保交运算和保联运算, 将命题中的“ ≤ ”换成对偶格<L, ≥>中的 “≥”,得到的一个关于对偶格<L, ≥>中的命题, 称这个命题为对偶命题。
容易证明,关于格<L, ≤ >的任何真命题,其对应 的对偶命题在对偶格<L, ≥>中也是真命题,把这 个原理称为对偶原理。
a ≤ b ac ≤ bc
(13)分配不等式:
a (b*c) ≤ (ab) * (ac);
a* (bc)≥(a*b) (a*c)
2020(/111/144 )模不等式:
17
定义15.2.3
设代数系统<L, , >是一个格,S L,若S满足: (1)S≠Φ; (2)运算和对子集S都是封闭的; 则称<S, , >是<L, , >的子格,简称S是L的 子格。
(j)中2元素子集{e, f}不存在最小上界,
(k)中2元素子集{a, b}不存在最大下界,
(l)中2元素子集{d, e}不存在最大下界。
2020/11/14
8
定义15.2.2
设<L, ∧, ∨>是具有两个二元运算的代数系统, 如果运算∧和∨满足交换律、结合律和吸收律,则 称<L, ∧, ∨>为格。 把由代数系统定义的格称为代数格。
第15章 格与布尔代数
1 偏序格与代数格
2 集合格的的表性示质方法 3 子格与格同态
4
布尔代数
2020/11/14
1
偏序格
比较右边两个哈 斯图的不同?
离散数学布尔代数与逻辑

离散数学布尔代数与逻辑离散数学是数学的一个分支,研究离散的、离散的结构和离散的现象。
而布尔代数是离散数学的重要组成部分,是代数学中关于二元关系的理论。
同时,与布尔代数密切相关的是逻辑学,研究命题的真值、论证的正确性以及推理的方法。
一、布尔代数基础布尔代数是一种逻辑代数,它使用逻辑运算符号和变量,描述和分析命题逻辑关系。
在布尔代数中,变量只有两个取值,即真(用1表示)和假(用0表示)。
布尔代数的基本运算包括逻辑与、逻辑或和逻辑非。
逻辑与表示当且仅当两个变量都为真时,结果为真;逻辑或表示当至少有一个变量为真时,结果为真;逻辑非表示当某个变量为真时,结果为假,反之亦然。
在布尔代数中,可以使用真值表来描述和分析布尔函数的取值情况。
布尔函数是指由布尔代数运算符组成的表达式,它接受一个或多个输入变量,并产生一个输出变量。
布尔函数在逻辑电路设计、计算机科学、编程等领域中有广泛的应用。
通过真值表分析布尔函数的取值规律,可以优化逻辑电路的设计和布尔函数的运算。
二、逻辑学与命题逻辑逻辑学是研究推理和论证的科学,其中命题逻辑是逻辑学的一个重要分支。
命题逻辑的基本概念是命题,它是陈述句,可以被判断为真或假。
命题逻辑使用逻辑连接词和命题变量来组成复合命题,并通过逻辑运算符来描述复合命题之间的关系。
逻辑连接词包括逻辑与、逻辑或、逻辑非、蕴涵和等价。
逻辑与表示两个命题同时为真时,复合命题为真;逻辑或表示两个命题至少有一个为真时,复合命题为真;逻辑非表示命题的否定,即真变为假,假变为真;蕴涵表示如果第一个命题为真,则第二个命题为真,否则为假;等价表示两个命题具有相同的真值。
逻辑学通过推理规则和推理方法来分析和判断复合命题的真假。
其中包括代入规则、假言推理、拒取否定、双重否定等推理规则。
通过应用这些推理规则,可以推导出逻辑上正确的结论,并解决实际问题中的逻辑推理和决策问题。
三、离散数学中的应用离散数学是计算机科学和信息技术的基础学科,广泛应用于计算机算法、数据结构、数据库、图论等领域。
《格和布尔代数》课件

第二部分:格的基础知识
有限格和无限格
介绍有限格和无限格的概念, 讨论其特点和应用。
笛卡尔积和格的同构
解释格的笛卡尔积以及同构 关系,揭示它们在格理论中 的重要性。
原子性和可分性
详细阐述格的原子性和可分 性,论述它们在实际问题中 的应用价值。
第三部分:布尔代数
1
ቤተ መጻሕፍቲ ባይዱ
3.2 布尔代数运算
2
系统阐述布尔代数的与、或、非运算,
总结格和布尔代数的重要性及其在学术和实
多研究和应用探索,促进学科的发展与创新。
践中的潜力,并对未来的研究方向进行展望。
《格和布尔代数》PPT课 件
本《格和布尔代数》PPT课件将带您深入了解格和布尔代数的基础知识、运 算规则以及其在现实世界中的重要应用。全方位解析格和布尔代数,帮助您 掌握这一重要数学领域的核心概念与技巧。
第一部分:引言
什么是格和布尔代数?探讨格和布尔代数的定义、特性和相关领域应用,以 及其在数学、计算机科学和工程中的重要性。
以及相关的异或和置位运算。
3
3.1 布尔代数的起源和发展
探索布尔代数的历史渊源与发展轨迹, 重点介绍George Boole对其的贡献。
3.3 布尔代数的完备性和最小化
讲解布尔代数的完备性定理、最小化方 法和卡诺图的应用。
第四部分:格和布尔代数的应用案例
逻辑电路设计
展示格和布尔代数在逻辑电路设 计中的重要应用,以及其在计算 机工程领域的意义。
程序设计中的控制流分析
阐述格和布尔代数在程序设计中 的控制流分析应用,帮助程序员 编写高效的代码。
数据库查询优化
探究格和布尔代数在数据库查询 优化中的关键作用,提高查询效 率和性能。
§8.5 布 尔 代 数(离散数学)

结论1 设e1,…,en为布尔代数B的一组基底, 则对于 i∈{1,…,n}, ei≠0。 证明: 用反证法。若有ei = 0,则一方面, ei = 0e1 + 0e2 + …+0ei + …+ 0en, 另一方面, ei = 0e1 + 0e2 + …+1ei + …+ 0en, 而ei∈B,且表示方法不唯一。这与定义中任意 a∈B,都可唯一地表示为α 1e1+α 2e2+… +α nen 矛盾。因此,ei≠0,i=1,…,n。
定理8.5.2 设(B,· ,+,¯ ,0,1)是布尔代数。 于是,B的子集S是B的子代数的充要条件是S在运 算· ,+,¯ 下是封闭的。 证明: 必要性。若S是B的子代数,则显然S在 · ,+,¯ 之下是封闭的。 充分性。若S在· ,+,¯ 下封闭,则任取a∈S,于 是有 a ∈S,a+ a = 1∈S, a· = 0∈S a 即S包含0,1。又因S在运算· ,+,¯ 之下封闭, S中元素也是B中元素,而B是布尔代数,故S中 元素对于运算· ,+,¯ 满足公理H1~H4,所以 (S,· ,+,¯ ,0,1)是布尔代数,由定义,S是 B的子代数。
于是有 ei = b+c =(α 1+β1)e1+…+(α n+βn)en 由基底的性质,则必有 α j+βj = 0 (j≠i, j = 1,…,n) α i+βi = 1 亦即: α j =βj= 0(j≠i, j=1,…,n), α i = 1或者βi= 1。 若α i = 1,则b = ei,矛盾。 若βi= 1,则c = ei,即 b i= ei,所以 e 0 =(b b )ei = b( b ei)= bei = b 矛盾。所以ei是极小元素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
② <B,,>是分配格,满足
(D-1) a(bc)=(ab)(ac),
a(bc)=(ab)(ac) (分配律)
(D-2) (ab=ac)∧(ab=ac)b=c (可约律) (D-3) (ab)(bc)(ca)=(ab)(bc)(ca)
③ <B,,, ',0,1>是有界格,满足
例:找出下图所示哈斯图的偏序集的子集 {a,b,c},{j,h}和{a,c,d f}的下界和上界。
解: {a,b,c}的上界是e,f,j,h,它唯 一的下界是a。 {j,h}没有上界,它的下界是 a,b,c,d,e,f。 {a,c,d f}的上界是f,h,j,它的 下界是a。
例 在上图所示偏序集中,如果{b,d,g}的最 大下界和最小上界存在,求出这个最大下界和最 小上界。 解: {b,d,g}的上界是g,h,故它的 最小上界是g。 {b,d,g}的下界是a,b,故它的 最大下界是b。
定理15.1.8 设<L,≤>是有补分配格,对任意 a,bL,则 ① (a')'=a ② (ab)'=a'b' ③ (ab)'=a'b' 后两式称为格中德· 摩根律。
定理15.1.9 a,bL,有
设<L,≤>是有补分配格,对任意
a≤bab'=0 a'b=1 格同态,格直积等概念可以接下来定义和研 究,但这里不打算这样做,因为如此进行会相对 较繁,而是将格作为一个代数结构而引入它们。
定义15.1.4 设<L,≤>是有界格,对于aL,存 在bL,使得 ab=0,ab=1 称b为a的补元,记为a'。 由定义可知,若b是a的补元,则a也是b的补 元,即a与b互为补元。 显然,0'=1和1'=0。 一般说来,一个元素可以有其补元,未必唯 一,也可能无补元。
定理15.1.6 设<L,≤>是有界分配格,若aL,
例 以下是偏序集<P(X), >的哈斯图。
{a,b} {a} {a,b} {a} {b} {a} ø ø (a) X={a}时 (b) X={a,b} ø (c) X={a,b,c} {b} {c} {a,c} {b,c} {a,b,c}
利用哈斯图,可以很方便的解决我们在学习 偏序集中的一些问题: 例 偏序集<S,≤>,其中 S={2,4,5,10,12,20,25},≤ 是整除关系,求此偏序集 的极大元和极小元。 解:作出哈斯图,从图中 看出,12,20和25是极大 元,2和5是极小元。
注意:并非每个偏序集都是格。如, 设A={2,3,6,8}, ―整除”关系R={‹2,2›,
‹2,6›, ‹2,8›, ‹3,3›, ‹3,6›, ‹6,6›, ‹8,8›}是A上的一
个偏序关系,则<A,R>是一个偏序集,但不
是格。因为23不存在,68也不存在。
例 确定下图中每个哈斯图表示的偏序集是 不是格。
(B-1) 0≤a≤1
(B-2) a0=a,aa=a (幺律)
(B-3) a1=1,a0=0
(零律)
④ <B,,, ',0,1>是有补格,满足
(C-1) aa'=1,aa'=0
(C-2) 1'=0,0'=1
(互补律)
⑤ <B,,, ',0,1>是有补分配格,满足
(CD-1) (ab)'=a'a',(ab)'=a'b'
等同于<L,≥>中GLB {a,b},<L,≤>中GLB{a,b}等
同于<L,≥>中的LUB{a,b}。若L是有限集,这些性 质易从偏序集及其对偶的哈斯图得到验证。
从上讨论中,可知两格互为对偶。互为对偶 的两个<L,≤>和<L,≥>有着密切关系,即格<L,≤>
中交运算正是格<L,≥>中的并运算,而格
解: 在a)和c)中的哈斯图表示的偏序集是格。因为每个偏序 集中每对元素都有最小上界和最大下界。 b)所示的哈斯图的偏序集不是格,例如元素b和c没有最 小上界。只要注意到d,e,f中每一个都是上界,但这3个元素 的任何一个关于这个偏序集中的序都不小于其它两个。
格的对偶性原理是成立的: 令<L,≤>是偏序集,且<L,≥>是其对偶的偏序 集。若<L,≤>是格,则<L,≥>也是格,反之亦然。 这是因为,对于L中任意a和b,<L,≤>中LUB{a,b}
显然盖住关系是唯一确定的, 盖住关系是“≤” 的子集。盖住关系的关系图称哈斯(Hasse)图, 它 实际上偏序关系是经过如下简化的关系图: 1. 省略关系图中的每个结点处的自环, 这是 因为偏序关系“≤”是自反的。 2. 若x<y且y盖住x, 将代表y的结点放在代表x 的结点之上, 并在x与y之间连线, 省去有向边的箭 头, 使其成为无向边。
a(ab)=a
定理15.1.3
设<L,≤>是格,对任意a,b,cL,
有
①若a≤b和c≤d,则ac≤bd,ac≤bd。
②若a≤b,则ac≤bc,ac≤bc。
③c≤a和c≤b c≤ab
④a≤c和b≤c ab≤c
定理15.1.4
有
设<L,≤>是格,对任意的a,b,cL,
a(bc)≤(ab)(ac)
若x<y 但y不盖住x, 则省去x与y之间的连线。
例 A = {1, 2, 3, 4, 5, 6, 8, 10, 12, 16, 24}, 偏序 关系是A上的整除关系“≤”, 画出偏序集<A, ≤> 的哈斯图。 我们先画出关系图。 注意图中,并没有 画出所有关系,否 则画面更显凌乱。 按照哈斯图的画法, 去掉一部分,结果 如左图。
根律)
(德· 摩
(CD-2) a≤ba'b=1ab'=0b'≤a' 注意,上述公式并非都是独立的,可从中选 出一些公式作为基本公式,用它们推出其余的公 式,而且可以用基本公式定义布尔代数。
定义15.2.1 设<B,,, '>是一代数结构,其中 和是B上的二元运算,'是B上的一元运算。 0,1B。若对任意a,bB,有
③ ab=aab=b
亦即 a≤bab=bab=a
定理15.1.2 设<L,≤>是格,对任意a,bL,有 ① aa=a, bb=b (等幂律)
② ab=ba,
ab=ba
(交换律)
(结合律)
③ a(bc)=(ab)c, ④ a(ab)=a,
a(bc)=(ab)c (吸收律)
定理15.1.5 设<L,≤>是有限格,其中 L={a1,a2,·,an},则<L,≤>是有界格。 · ·
定义15.1.3 有
设<L,≤>是格,对任意的a,b,cL,
① a(bc)=(ab)(ac) ② a(bc)=(ab)(ac) 则称<L,≤>为分配格,称①和②为格中分配 律。
若L是有限集合,称<L,≤>为有限格。
显然,对于ab,有: ①ab≤a和ab≤b,则表明ab是a和b的下界。 ②若c≤a和c≤b,则c≤ab,这表明ab是a和b 的最大下界。 对于ab,有: ①a≤ab和b≤ab,则表明ab是a和b的上界。 ②若a≤c,且b≤c,则ab≤c,这表明ab是a 和b的最小上界。
15.1 格(laቤተ መጻሕፍቲ ባይዱtice)
–
1.格作为偏序集
定义15.1.1 设<L,≤>是一个偏序集,若对任 意a,bL,存在 最大下界(GLB)和最小上界(LUB), 则称<L,≤>为格。 用ab表示GLB{a,b},ab表示LUB{a,b}, 并称和分别为L上的交(或积)和并(或和) 运算。这样我们由偏序关系定义了两种二元运算。
第十五章 格与布尔代数
15.1 格 – 15.2 布尔代数
–
在介绍格之前,对于我们在前面学过的偏序, 我们要补充两个内容: 1. 哈斯图 2. 最小上界与最大下界
1.哈斯图
为了更清楚地描述偏序集合中元素间的层次 关系, 也为了更快、更有效地画出偏序关系的简化 图, 下面介绍“盖住”的概念。
定义 在偏序集<A, ≤>中, 对x, yA, x≤y且x y, 且 A中无任何其它元素z, 满足x≤z且z≤y, 称y盖 住x, 或称x是y的直接前趋, y是x的直接后继。盖住 关系记作cov(A) = {(x, y) | x, yA且y盖住x}。
(ab)(ac)≤a(bc) 通常称上二式为格中分配不等式。
–
3.特殊的格
定义15.1.2 设<L,≤>是格,若L中有最大元和 最小元,则称<L,≤>为有界格。由于最大元存在必 唯一,故一般把格中最大元记为1,最小元记为0。 由定义可知,对任意aL,有 ① 0≤a≤1 ② a0=0, a0=a ③ a1=a, a1=1 由此可知,0是<L,≤>关于的零元,关于的 幺元;1是<L,≤>关于的幺元,关于的零元
例 设n为正整数,Sn为n的正因子的集合, ≤为整除关系,则<Sn,≤>构成格。
因为x,y∈Sn, xy就是x,y的最小公
倍数,xy是x,y的最大公约数。
例 幂集P(A)上的包含关系定义了一个 偏序关系,P(A)中任意两个元素x,y,有
xy =x∪y
xy =x∩y
因此,<P(A), >是一个格。
–
4.格是代数结构
前面我们已知,有补分配格是一个代数结构, 叫做布尔代数;反之,由代数结构也可以导出格。 定义15.1.7 设<L,,>是一代数结构,其中 和是L上满足交换律、结合律和吸收律的二元运 算,且对任意a,bL,定义偏序关系≤如下: a≤bab=a 则<L,≤>是格,称<L,≤>为代数结构<L,,> 所诱导的偏序集确立的格。
