4.1 有理数指数幂
湘教版高中数学必修第一册课后习题 第4章 幂函数、指数函数和对数函数 4.1.1--4.1.2

第4章 幂函数、指数函数和对数函数4.1 实数指数幂和幂函数4.1.1 有理数指数幂 4.1.2 无理数指数幂必备知识基础练1.(天津滨海新区高一期中)下列运算正确的是( ) A.a 2·a 3=a 6 B.(3a)3=9a 3 C.√a 88=aD.(-2a 2)3=-8a 62.若a<0,则化简a √-1a得( ) A.-√-a B.√-a C.-√aD.√a3.(福建福州三中高一期中)已知x 2+x -2=3,则x+x -1的值为( ) A.√5B.1C.±√5D.±14.(112)0-(1-0.5-2)÷(278)23的值为( )A.-13B.13C.43D.735.若√4a 2-4a +1=1-2a,则a 的取值范围是 .关键能力提升练6.(河北张家口张垣联盟高一联考)将根式√a √a √aa(a>0)化简为指数式是( ) A.a -18B.a 18C.a -78D.a -347.已知x 2+x -2=2√2,且x>1,则x 2-x -2的值为( ) A.2或-2 B.-2 C.√6D.28.(多选题)下列根式与分数指数幂的互化正确的是( ) A.-√x =(-x )12B.√y 26=y 12(y<0)C.x-13=√x3(x≠0)D.[√(-x )23]34=x 12(x>0)9.若a>0,b>0,则化简√b 3a√a2b6的结果为 .10.化简:(2-a)[(a-2)-2(-a )12]12= . 11.化简求值:(1)0.125-13−(98)0+[(-2)2]32+(√2×√33)6;(2)(5116)0.5+√(-10)2-2√3×√276-4π0÷(34)-1.学科素养创新练12.(黑龙江大庆实验中学高一期末)已知实数x 满足3×16x +2×81x =5×36x ,则x 的值为 . 答案:1.D a 2·a 3=a 5,故A 错误;(3a)3=27a 3,故B 错误;√a 88=|a|={a ,a ≥0,-a ,a <0,故C错误;(-2a 2)3=-8a 6,故D 正确.故选D.2.A ∵a<0,∴a √-1a=-√a 2×√-1a=-√a 2(-1a)=-√-a .故选A.3.C 由(x+x -1)2=x 2+x -2+2=5,可得x+x -1=±√5.故选C.4.D 原式=1-(1-22)÷(32)2=1-(-3)×49=73.故选D.5.(-∞,12] ∵√4a 2-4a +1=√(2a -1)2=|2a-1|=1-2a,∴2a-1≤0,即a≤12.6.A√a √a √aa=a 12+14+18-1=a -18,故选A.7.D (方法1)∵x>1,∴x 2>1. 由x -2+x 2=2√2,可得x 2=√2+1, ∴x 2-x -2=√2+1-√2+1=√2+1-(√2-1)=2.(方法2)令x 2-x -2=t,① ∵x -2+x 2=2√2,②∴由①2-②2,得t 2=4.∵x>1,∴x 2>x -2, ∴t>0,于是t=2,即x 2-x -2=2,故选D. 8.CD 对于选项A,因为-√x =-x 12(x≥0), 而(-x )12=√-x (x≤0),所以A 错误;对于选项B,因为√y 26=-y 13(y<0),所以B 错误; 对于选项C,x-13=√x3(x≠0),所以C 正确;对于选项D,[√(-x )23]34=x 2×13×34=x 12(x>0),所以D 正确.9.1 √b 3a√a 2b 6=√b 3a(a 2b 6)12=√b 3a ab 3=1. 10.(-a )14由已知条件知a≤0, 则(a-2)-2=(2-a)-2,所以原式=(2-a)[(2-a)-2·(-a )12]12=(2-a)(2-a)-1(-a )14=(-a )14.11.解(1)根据指数幂与根式的运算,化简可得0.125-13−(98)0+[(-2)2]32+(√2×√33)6=[(2)-3]-13−(98)0+(22)32+(212×313)6=2-1+8+(212)6(313)6=2-1+8+8×9 =81.(2)由分数指数幂及根式的运算,化简可得(5116)0.5+√(-10)2-2√3×√276-4π0÷(34)-1=[(32)4]0.5+10-2√3×(33)16-4×34=94+10-2√3×√3-3 =94+10-6-3=134.12.0或12因为3×16x +2×81x =5×36x ,所以3×24x +2×34x =5×(2×3)2x ,则3×24x +2×34x =5×22x ×32x ,所以3×24x +2×34x -5×22x ×32x =0,即(3×22x -2×32x )(22x -32x )=0,所以3×22x -2×32x =0,或22x -32x =0,解得x=12或x=0.。
实数指数幂和幂函数 教学设计-高一上学期数学湘教版(2019)必修第一册

《实数指数幂和幂函数》教学设计 4.1.1有理数指数幂一.课程标准认识有理数指数幂mna 含义,掌握指数幂的运算性质.二.教学目标1.理解根式的概念及性质,掌握分数指数幂的运算性质;2.能够熟练的进行分数指数幂与根式的互化.三、教学重点:根式的概念及n 次方根的性质;分数指数幂的意义及运算性质;分数指数幂与根式的互化.四、教学难点:n 次方根的性质;分数指数幂的意义及分数指数幂的运算. 五、教学过程一、创设情境,引入课题 1. 平方根和和立方根. 2.正整数指数幂的运算性质 二、归纳探索,形成概念 1. n 次方根若一个(实)数x 的n 次方,(2)n N n ∈≥等于a ,即n x a =,就说x 是a 的n 次方根。
那么如何表示n 次方根呢?我们分n 为奇数和n 为偶数两种情况来分别讨论n 次方根的表示方法。
例如,2=2=-;33x =-时,有x =若23x =,则x =43x =,则x =(1)当n 为奇数时,a ()a R ∈的n当a >00;当a =00;当a <00.(2)当n 为偶数时,a 的n 次方根有两个,它们互为相反数,即:其中正的n 0a <时, a 的n 次方根不存在。
(3)0的n 次方根为0=0. 2.根式,(2)n N n ∈≥,n 叫作根指数,a 叫作被开方数.a =,问题3:n 与aa =是否一直成立?你能举出那些例子?7...===-7...=== 由此我们可得到1。
当na =。
2。
当na =。
问题4:那么,n 又能化简成什么呢?一直成立吗?预案:n a =,根据定义易知成立。
3.分数指数幂问题5:m a 表示什么含义(当m 为正整数的时候)?当指数为正整数时候,指数的运算都有哪些运算性质? 答:m 个a 相乘。
,,(,0)(),()m n m n mm n nm n mn m m ma a a a a m n a aa a ab a b +-==>≠== 在这里,m n 均为正整数。
人教版高中数学必修第一册 4.1指数【课件】

指数
1.掌握有理数指数幂 (a>0,且a≠1,m,n为整数,
课标定位
素养阐释
且n>0)的概念,理解有理数指数幂的运算性质.
2.掌握根式的概念,能进行分数指数幂与根式的
互化.
3.了解指数幂的拓展过程,掌握指数幂的运算性
质.
4.感受数学抽象与逻辑推理的过程,提升数学运
算素养.
自主预习·新知导学
式.
【变式训练 1】 (1) (-) =
;
(2)使等式 (-)( -)=(3-a) + 成立的实数 a 的取值范
围是
.
解析:(1) (-) =-2;
(2)因为
(-)( -)
=
(-) ( + )=|a-3|· + =(3-a) + ,
- ≤ ,
(-) =3.
4.根式的性质
根据 n 次方根的意义,可得( )n=a.
(1)当 n 为奇数时, = a ;
,
≥
,
(2)当 n 为偶数时, =|a|=
-, < .
5.下列说法正确的有
① -=3;
③ =±3;
.(只填序号)
②64 的 6 次方根是±2;
以上解答过程中都有哪些错误?出错的原因是什么?你如何改
正?你如何防范?
提示:错解中使用根式的性质不当导致错误,应注意根式性质
成立的条件.
正解: ( + ) +
(- )=1+ +|1- |=1+ + -1=2 .
21-22版:4.1.1 第一课时 有理数指数幂(创新设计)

A.R C.12,+∞
B.-∞,21∪12,+∞ D.-∞,21
解析 将分数指数幂化为根式,可知需满足1-2x>0,
解得 x<21.
01 02 03 04 05 06 07 08 09 10 11 12 13 14
索引
3.(多选题)下列说法:①16 的 4 次实数方根是 2;②4 16的运算结果是±2;③当 n
///////
【例 3】 化简:(1)5x-23y21·-14x-1y12·-65x13y-16(其中 x>0,y>0);
4
(2)0.064-13--780+(-2)3-3+16-0.75. 解 (1)原式=5×-14×-65x-23+(-1)+13·y12+12-16=2254x-43y56.
(2)原式=0.4-1-1+(-2)-4+2-3=52-1+116+18=2176.
索引
题型二 根式与分数指数幂的互化
【例2】 将下列根式化为分数指数幂的形式:
(1)3 a a(a>0);(2)
1
;(3)( 4
22
b-3)-3(b>0).
3 x(5 x2)2
解 (1)原式= 3
1
a·a2=
3
3
a2=
3
31
a4=a4.
(2)原式=
3
1=
x·x252
3
1=
4
x·x5
3 1x59=(x195)13=x135=x-35.
(a-b)2+5 (a-b)5=|a-b|+(a-b)=02, (aa≤ -bb, ),a>b.
01 02 03 04 05 06 07 08 09 10 11 12 13 14
有理数指数幂

13 6
a 5 a9
9 5
1
6
b13
3.用分数指数幂表示下列各式 (1) a 1 (2) 5 4
3 2
b
解: 2 3 a2 a 3 (1) 4 1 (2) 5 4 b 5
b
4.求值 1 (1) 492 1 (2)32 5 解: 1 (1) 492 (2) 32 1
n 次根试 二、
1、 次根式的概念
如果一个数的n次方等于a(n>1且n∈N*),那 么这个数叫做a的n次方根。即:若xn=a,则x叫 n 做a的n次方根,其中n>1且n∈N*。式子 a 叫 做根式,这里n叫做根指数,a叫做被开放数。
n
2.根式的性质
1、当n为奇数时,正数的n次方根是一个 正数,负数的n次方根是一个负数,a的n 次方根用符号 n a 表示。 2、当n为偶数时,正数的n次方根有两个, 它们互为相反数,这时,正数的正的n次 n 方根用符号 a 表示,负的n次方根用符号 n a 表示。正负两个 n次方根可以合作为 (a>0 )。 n a 4、负数没有偶次方根。 5、零的任何次方根都是零。
课堂练习
计算: (1) 0.013
3 2 ( ) (2) 2
(3)(3a )
2 2
解答
(1)
1 3 0.01 ( ) 100 3 10 6 1000000 100
3
(2) (3)
3 2 2 2 4 ( ) ( ) 2 3 9
4.1.1有理数指数幂(课件)-高一数学(湘教版2019必修第一册)

算法则进行运算,而引入分数指数的概念就可以大大简化根式运算.
当 > 0,, ∈ 且 ≥ 2时,规定 = ,
这样就有
24
4
2
= 2 = 4, 6
1
33
=3
3
−6
=3
1
2
−
=
1
3
=
1
=
−
.
3
,方便多了.
1
−2
= 5,求下列各式的值:
(1) + −1 ;(2)2 + −2 ;(2)
1
2
解:将 +
1
−2
3
3
−
2 − 2
1
1
−
2 − 2
.
= 5两边同时平方,得: + −1 + 2 = 5.
(1) + −1 = 5 − 2 = 3;
(2)将 + −1 两边同时平方,得:2 + −2 + 2 = 9.∴2 + −2 = 7.
∙ = + ,( ) = ,() = .
下面,我们把整数指数幂推广到有理数指数幂.
新知探索——根式
若一个(实)数的次方( ∈ , ≥ 2)等于,即 = ,则称是的次
方根.
当是奇数时,数的次方根记作 .
当 > 0时, > 0;当 = 0时, = 0;当 < 0时, < 0.
1
−2
1 −3
125 −2
;(3)( ) ;(4)( ) 3 .
《有理数指数幂》中职数学基础模块上册4.1ppt课件2【语文版】

(2)(a) a
(3)(ab) a b
课后作业:
• 练习册4.1
编者语
• 要如何做到上课认真听讲?
•
我们都知道一个人的注意力集中时间是有限的,一节课45分钟如何保持时时刻刻都能认真听讲不走神呢?
•
1、往前坐
•
坐的位置越靠后,注意力就越难集中。老师不会注意到你的事实可以让你不再紧张,放心去做别的事情。坐在后面,视线分散,哪怕你是在看老师,如果有人移动,你的视线就会飘到那个同学的后脑勺上去,也就无法集中注意力。 而且,坐在后面很
③(5 23)5 23 8 ④ 2
⑤4(3)4 | 3 | 3
整数指数幂
正整数指数幂:
a2 aa
a3 aaa
指数
幂
an a a ......a
底数
n个
运算法则:(1)aman amn
(2)(am)n anm (3)aamn amn (m n,a 0)
(3)正数的奇次方根是一个正数,负数
的奇次方根是一个负数。都记为 n a 。
根式性质
由n次根式的意义,可得
1. ( n a )n a
a
2. n an a
n是奇数 n是偶数
3.n 0 0
即:n a n 与n an 不一定相等
例1
5 ①(4 5)4
②(3 5)3 5
•
低着头,心情就放松了,但那种放松对学习一点好处也没有,之所以会放松,就是因为觉得即便是自己开小差,老师也不知道。如果你往前看,不时地和老师眼神交会一下,注意力必然会集中起来。和老师眼神交汇的那种紧张感会让你注意力集中,并充
实地听完整堂课。
教案 高教版《数学》(基础模块)——4.1有理数指数幂(2)

4.1有理数指数幂(2)——实数指数幂【教学目标】知识目标:1、掌握实数指数幂的运算法则;2、通过几个常见的幂函数,了解幂函数的图像特点。
能力目标:1、正确进行实数指数幂的运算;2、培养学生的计算技能;3、通过对幂函数图形的作图与观察,培养学生的计算工具使用能力与观察能力。
【教学重点】实数指数幂的运算法则,有理数指数幂的运算。
【教学难点】有理数指数幂的运算。
【教学设计】1、在复习整数指数幂的运算中,学习实数指数幂的运算;2、通过学生的动手计算,巩固知识,培养计算技能;3、通过“描点法”作图认识幂函数的图像,通过利用软件的大量作图,总结图像规律;4、通过知识应用巩固有理数指数幂的概念。
【课时安排】2课时。
(90分钟)【教学过程】一、实数指数幂 1、复习导入整数指数幂,当*n ∈N 时,na = ; 规定当0a ≠时,0a = ; n a -= ; 分数指数幂:mna = ;0a ≠时,m na-= 。
其中*m n n ∈N 、且>1。
当n 为奇数时,a ∈R ;当n 为偶数时,0a。
例1、将下列各根式写成分数指数幂:(2.例2、将下列各分数指数幂写成根式:(1)3465-;(2)232.3()2、扩展:整数指数幂的运算法则为: (1) m n a a ⋅= ; (2) ()nm a= ;(3) ()nab = 。
其中()m n ∈Ζ、运算法则同样适用于有理数指数幂的情况3、概念当p 、q 为有理数时,有p q p q a a a +⋅=; ()qp pq a a =; ()pp p ab a b =⋅运算法则成立的条件是,出现的每个有理数指数幂都有意义。
说明:可以证明,当p 、q 为实数时,上述指数幂运算法则也成立。
4、典型例题例1、计算下列各式的值:(1)130.125; (2分析 (1)题中的底为小数,需要首先将其化为分数,有利于运算法则的利用;(2)题中,首先要把根式化成分数指数幂,然后再进行化简与计算。
4.1.1指数课件(人教版)

(a ) a (a 0, r , s Q
R)
r S
rs
(a b) a b (a 0, b 0, r Q
R)
r
r
r
完成课本109页习题
根式与分数指数幂的互化
1.正数的正分数指数幂的意义:
m
n
a a
n
m
(a 0, m , n N , 且n 1)
分母为根指数
2.正数的负分数指数幂的意义:
a
m
n
1m 1 (a 0, m , n N , 且n 1)
n m
n
a
a
a
p
3.规定0的正分数指数幂为0,0的负分数指数幂没有意义.
(2)( )
81
2
3
2.用分数指数幂的情势表示下列各式(其中a>0):
3
(1)a a
2
2
3
(2) a a
3.计算下列各式(式中字母都是正数)
2
3
1
2
1
2
1
3
1
6
5
6
(1)(2a b )(6a b ) (3a b )
(3)
1
4
3
8 8
(2)( m n )
分数指数幂运算技能
1.有括号先算括号里的,无括号先进行指数运算
( + )
5
2
3
−2
=
1
3
m
n
分数指数幂
整数指数幂
a a a
r
s
r s
有理数指数幂
(a 0, r , s Q)
4.1.1有理数指数幂课件-2023-2024学年高一上学期数学湘教版(2019)必修第一册

二、新知探究|根式
1.若 2 = ,那么叫作的 平方根 ;
记作: = ± ,
3
2.若 = ,那么叫作的 立方根 ; 记作: =
3
3.若 4 = ,那么叫作的 4次方根 ; 记作: = ± 4
5
4.若 = , 那么 叫作 的5次方根
;记作: =
− =
− , 当 > 时.
二、新知探究|有理数指数幂
分数指数幂:
当a > 0,m, n ∈ N且n ≥ 2时,规定:
=
,
1
=
−
二、新知探究|有理数指数幂
在 > 0时,对于∀, ∈ 仍有以下运算法则:
∙ = +
( ) =
3
3
3
2
2 =_______;
32 =_______;
3
5
3
(−2) =_______;
-2
4
2
(−3) =_______;
3
5
5
2 =_______;
2
2
24 =_______;
由此你能得出 的值吗?
性质2.
=
,
,
为奇数;
为偶数
4
(−2)5 =_______;
-2
(−2)4 =_______;
(3) ∙ =
=
∙ = ∙ =
三、典例精析|有理数指数幂
例4、计算下列各式
有理数指数幂ppt课件

例 2 求值:
(1)16
3 4
;(2)
25
1 2
;(3)
1 3
3
;(4) 125 64
3 2
解: 3
(1)164
3
24 4
43
24
23
8;
1
(2) 25 2
1
52 2
21
52
51 1 5
(3) 1 3 3
3 1 3 33 27
2
(4) 125 3 64
2
53 3
43
32 1
53
32
43
52 1 16
4.1.1 有理数指数幂
湘教版(2019)必修第一册
学习目标
1.了解根式及其性质. 2.了解分数指数幂的意义 3.能利用实数指数幂的运算性质进行指数运算.
学习重点
根式的概念, 分式指数冥的概念及运算法则
学习难点
根式概念和分式指数幂的理解,根式与分式指数幂的互化, 根式、分数指数幂及其运算法则的综合应用.
解析:对于
A,原式
1
(3a)3 3
0.3a1
3a 10 3
a
10a2
(a
0) ,故
A
正确;
1 2 1 2 1 1 1 1
对于
B,原式
a3
1
b3
1
a3
b3
1
a3
1
b3
1
a3
1
b3
(a, b
0)
,故
B
正确;
a3 b3
a3 b3
对于 C,原式
1
1
1
(2 2 3)2 (3 2 2)2 2 [(2 2 3)2 ]2 (3 2 2)2 2 (2 2 3)(3 2 2) 1 ,故 C
有理数指数幂--参考教案
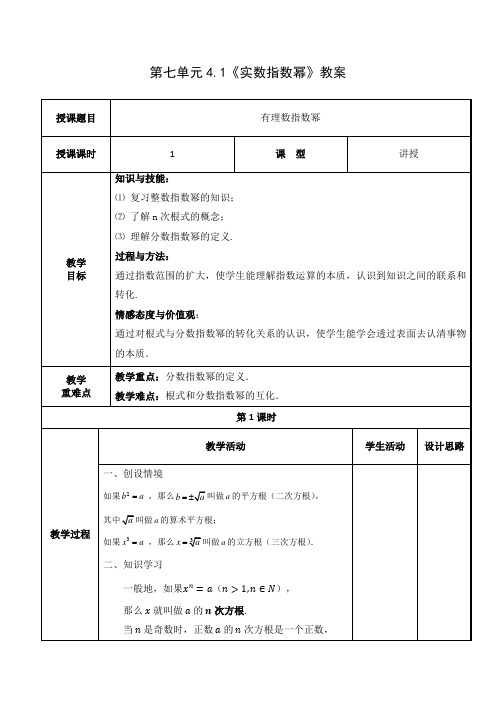
这时, 的 次方根用符号 表示.
例如,
当 是偶数时,正数 的 次方根有两个,
两数互为相反数.
这时,正数 的正的 次方根用符号 表示,
负的 次方根用符号- 表示.
正的 次方根与负的 次方根可以合并写成 .例如,
负数没有偶次方根.
的任何次方根都是 ,记为 .
形如 的式子叫作根式,
(4) ;(5)81的4次方根.
解(1) ;(2) ;
(3) ;(4) ;
(5)因为 ,所以81的4次方根是 ,即
例2化简(1) ;(2) .
解(1) ;
(2) .
例3将下列根式用分数指数幂表示(式中字母均为正实数).(1) ;(2) ;(3) .
解(1) ;
(2) ;
(3) .
例4化简
(1) ;(2) ;
第七单元4.1《实数指数幂》教案
授课题目
有理数指数幂
授课课时
1
课型
讲授
教学
目标
知识与技能:
⑴ 复习整数指数幂的知识;
⑵ 了解n次根式的概念;
⑶ 理解分数指数幂的定义.
过程与方法:
通过指数范围的扩大,使学生能理解指数运算的本质,认识到知识之间的联系和转化.
情感态度与价值观:
通过对根式与分数指数幂的转化关系的认识,使学生能学会透过表面去认清事物的本质.
解(1) ;
(2) .
四、课堂练习
1 填空题
(1)16的4次方根为;
(2) ;
(3)-13的5次方根表示为.
2计算
(1) ;(2) ;(3) ;(4) ;(5) ;(6) .
3用分数指数幂表示下列根式.
有理数指数幂

解析 (1)
(2)
3
4
3+
4
4
(3-3)4 (a≤1);
(1 − )4 .
根据根式的性质化简,注意被开方数的符号.
(3-3)4 =|3a-3|=3|a-1|=3-3a.
3+
4
(1 − )4 =a+|1-a|=
1, ≤ 1,
2-1, > 1.
课前预学
课堂导学
方法总结:根式化简求值解题思路:解决根式的化简问题,首先要分清根式为奇次根式还是
方法总结:指数幂运算的常用技巧:(1)有括号先算括号里的,无括号先进行指数运
算.(2)负指数幂化为正指数幂的倒数.(3)底数是小数,先要化成分数;底数是带分数,
要先化成假分数,然后要尽可能用幂的形式表示,便于用指数幂的运算性质.
提醒:化简的结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
(3)(ab)r=
(a>0,b>0,r∈Q).
有理数指数幂的运算性质的理解与巧记
(1)有理数指数幂的运算性质是由整数指数幂的运算性质推广而来的,可以
用文字语言叙述:①同底数幂相乘,底数不变,指数相加;②幂的幂,底数不变,指数
相乘;③积的幂等于幂的积.
(2)有理数指数幂的运算性质中幂指数运算法则遵循:乘相加,除相减,幂相乘.
课前预学
课堂导学
问题 2: 问题 1 中没有 a<b<0 的限制条件,根号内的式子还能“穿墙”吗?
答案
能,但要注意讨论.
问题 3: ( a)n 中实数 a 的取值范围是任意实数吗?
答案 不一定,当 n 为大于 1 的奇数时,a∈R;
语文版中职数学基础模块上册4.1《有理数指数幂》教案

有理数指数幂教案一、条件分析1.学情分析在上个单元中,学生学习了函数的概念、表示方法、单调性、奇偶性,对函数有了初步的认识,但是还远远不够,函数是个大家庭,需要我们继续深入学习已到达实际运用的目的。
对于这个章节的内容,学生在初中已经学过,加之初数内容的补充,学生对这方面的知识掌握起来比较容易,难点在于对八个公式的记忆可能混淆,因此在学习本章节的内容时应多做练习巩固所学知识。
2.教材分析本节内容由整数指数幂、n次根式、分数指数幂构成,这三个内容环环相扣,层层递进,所以,在学习这个章节的内容时,应注意知识的内在联系。
二、三维目标知识与技能目标A层:1. 理解有理数指数幂的概念;2. 识记正整数指数幂的运算法则;3. 识记分数指数幂的运算法则;4. 理解n次方根、n次算术根的概念。
B层:1. 理解有理数指数幂的概念;2. 识记正整数指数幂的运算法则;3. 识记分数指数幂的运算法则。
C层:1. 识记正整数指数幂的运算法则;2. 识记分数指数幂的运算法则。
过程与方法目标讲授法、练习法、游戏法。
在学习有理数指数运算时通过竞答游戏激发学生学习兴趣,通过练习加深学生对所学知识的巩固。
情感态度和价值观目标通过对有理数指数幂的探究,培养学生观察、归纳、抽象的能力和语言表达能力;通过学习有理数指数幂的知识,让学生明白,对于问题的解决,我们可以采用多种方法,其中有效的方法是转化,把不熟悉的问题转化成我们所熟悉的问题就能轻松解决。
三、教学重点有理数指数幂的运算法则四、教学难点n次方根与n次算术根的区别和联系五、主要参考资料:中等职业教育课程教材数学基础模块(上)、学生学习指导用书、教学参考书。
六、教学进程:故事导入:谣言的力量某人听到一则谣言后一小时内传给两人,以后他没有再传给别人.而那两人同样在一小时内每人又分别传给另外的两人。
如此下去,一昼夜能传遍一个千万人口的大城市吗?能?还是不能?请注意,一小时内,一个人只传给两个人,一昼夜只有24小时,一个千万人口的大城市能传遍吗?只凭直觉,是很难正确判断的。
教案 高教版《数学》(基础模块)——4.1有理数指数幂(1)

4.1有理数指数幂(1)——分数指数幂【教学目标】知识目标:1、复习整数指数幂的知识;2、 了解n 次根式的概念;3、理解分数指数幂的定义。
能力目标:1、掌握根式与分数指数幂之间的转化;2、会利用计算器求根式和分数指数幂的值;3、培养学生观察、分析问题的能力;培养学生严谨的思维和科学正确的计算能力。
【教学重点】分数指数幂的定义及运算性质,运用有理数指数幂性质 进行化简、求值。
【教学难点】对分数指数幂概念的理解,根式和分数指数幂的互化。
【教学设计】1、通过复习二次根式而拓展到n 次根式,为分数指数幂的介绍做好知识铺垫;2、复习整数指数幂知识以做好衔接;3、利用课件介绍分数指数幂的概念,字母动感闪耀强化位置关系;4、加大学生动手计算的练习,巩固知识;5、小组讨论、学习计算器的使用,培养计算工具使用技能。
【课时安排】2课时。
(90分钟)【教学过程】一、根式1、在初中时,我们已经把指数幂推广到了零指数和负整数指数幂,大家来回忆一下: a 0= (a ≠0),a -n= (a ≠0,n ∈N) 并且满足如下运算法则:(1) ),,0(Z n Z m a a a a n m n m ∈∈≠=⋅+ (2) ()()Z n Z m a a a mn nm ∈∈≠=,,0(3) ()()Z n b a b a ab n n n∈≠≠=,0,0例如:(师生共同完成)(1) 10001.011.011.022===- (2) a 3a -2=a 3-2=a (3)(2a -2)-3=2-3a(-2)(-3)=681a2.我们学习了n 次根式,知道当n a 有意义时,有下列性质:(1)a a nn =)((2)⎩⎨⎧=)(|,|)(,为偶数;为奇数n a n a a n n利用这个运算性质,引导学生得出下列各式: (1)362=332)2(=22=362, (2)5103=552)3(=32=5103,(3)32a =3332)(a =32a由此,可得出式子:362=362,5103=5103,32a =32a 。
4.1.1有理数指数幂4.1.2无理数指数幂课件高一上学期数学

式的性质进行化简;化简( ) 时,关键是明确 是否有意义,只要 有意
n
义,则( )n=a.
2.在对根式进行化简时,若被开方数中含有字母参数,则要注意字母参数的
取值范围,即确定 中 a 的正负,再结合 n 的奇偶性给出正确结果.
探究点三
指数幂的简单计算
【例3】 计算:
2
(1)
A.1个
B.2个
C.3个
D.0个
2+1
9
;④ -2 .其中无意义的有( A )
探究点二
根式的化简(求值)
【例2】 求下列各式的值:
5
6
(1)( -) +( - )6(b>a);
5
解 原式=a-b+b-a=0.
(2) 2 -2 + 1 − 2 + 6 + 9(-3<x<3).
=
73
33
=
343
.
27
(x>0);
解 原式=
5
6
3
34 4
74
1 2 1
+ 2 3 6
3 -1
5
3 -1
5
=x.
-1
;
-1
=
5 5 -1
6 3
=
5 -1 6
- 6 =-5.
1
3
(6)0.064 −
解
1
4
0
7
+(23)-3 +16-0.75+|-0.01|2 ;
8
1
3
1
1
-4
-1
3 -3
新教材2021-2022学年湘教版必修第一册 4.1.1 有理数指数幂 作业

课时跟踪检测(二十二) 有理数指数幂[A 级 根底稳固]1.假设4a -2+(a -4)0有意义,那么a 的取值范围是( )A .[2,+∞)B .[2,4)∪(4,+∞)C .(-∞,2)∪(2,+∞)D .(-∞,4)∪(4,+∞)解析:选B 由题意可知,a -2≥0且a -4≠0,∴a 的取值范围是a ≥2且a ≠4,应选B.2.化简4m 6(m <0)的结果为( )A .m mB .m -mC .-m mD .-m -m解析:选D ∵m <0,∴4m 6=-m 3=-m -m .应选D.3.假设(1-2x )-34有意义,那么x 的取值范围是( )A .(-∞,+∞)B.⎝⎛⎭⎫-∞,12∪⎝⎛⎭⎫12,+∞ C.⎝⎛⎭⎫12,+∞D.⎝⎛⎭⎫-∞,12 解析:选D ∵(1-2x )-34=14〔1-2x 〕3,∴1-2x >0,得x <12. 4.计算(2a -3b -23)·(-3a -1b )÷(4a -4b -53)得( )A .-32b 2 B .32b 2 C .-32b 73 D .32b 73 解析:选A 原式=-6a -4b 134a -4b -53=-32b 2. 5.(多项选择)以下各式中一定成立的有( )A.⎝⎛⎭⎫n m 7=n 7m 17B.12〔-3〕4=33 C.4x 3+y 4=(x +y )34 D.39=33解析:选BDA 中应为⎝⎛⎭⎫n m 7=n 7m -7;12〔-3〕4=1234=33,B 正确;C 中当x =y =1时,等式不成立;D 正确.应选B 、D.6.有以下说法: ①3-125=5;②16的4次方根是±2; ③481=±3;④〔x +y 〕2=|x +y |.其中,正确的有________.(填序号)解析:n 为奇数时,负数的n 次方根是一个负数,3-125=-5,故①错误;16的4次方根有两个,为±2,故②正确;481=3,故③错误;〔x +y 〕2是正数,故〔x +y 〕2=|x +y |,故④正确.答案:②④7.假设〔2a -1〕2=3〔1-2a 〕3,那么实数a 的取值范围为________. 解析:〔2a -1〕2=|2a -1|,3〔1-2a 〕3=1-2a .因为|2a -1|=1-2a ,故2a -1≤0,所以a ≤12. 答案:⎝⎛⎦⎤-∞,12 8.a >0,将a 2a ·3a 2表示成分数指数幂,其结果是________. 解析:a 2a ·3a 2=a 2a ·a 23=a 2a 53=a 2a 53×12=a 2·a -56=a 2-56=a 76. 答案:a 769.求以下各式的值:(1) 3+22+3-22;(2) 5+26- 6-42+ 7-4 3.解:(1)法一:原式=〔2〕2+22+1+〔2〕2-22+1=〔2+1〕2+〔2-1〕2=2+1+2-1=2 2. 法二:令x =3+22+ 3-22,两边平方得x 2=6+29-8x >0,所以x =2 2. (2)原式=〔3+2〕2- 〔2-2〕2+〔2-3〕2=3+2-(2-2)+2-3=2 2. 10.计算:(1)⎝⎛⎭⎫-127-13+-12-10(5-2)-1+π0; (2)823-⎝⎛⎭⎫12-2+⎝⎛⎭⎫1681-34-(2-1)0. 解:(1)⎝⎛⎭⎫-127-13-12-10(5-2)-1+π0=-3+105-105-20+1=-22.(2)根据分数指数幂的定义,得823=(23)23=22=4,⎝⎛⎭⎫12-2=22=4,⎝⎛⎭⎫1681-34=⎣⎡⎦⎤⎝⎛⎭⎫234-34=⎝⎛⎭⎫23-3=278.从而原式=4-4+278-1=198. [B 级 综合运用]11.如果a =3,b =384,那么a ⎣⎡⎦⎤⎝⎛⎭⎫b a 17n -3=________. 解析:a ⎣⎡⎦⎤⎝⎛⎭⎫b a 17n -3=3⎣⎡⎦⎤⎝⎛⎭⎫384317n -3 =3[(128)17]n -3=3×2n -3.答案:3×2n -3 12.化简以下各式: (1)3xy 26x 5·4y 3(x >0,y >0);(2)(x 23·y 14·z -1)·(x -1·y34·z 3)-13 (x >0,y >0,z >0). 解:(1)原式=x 13y 23x 56y 34=x 13-56y 23-34=x -12y -112.(2)原式=(x 23y 14z -1)·(x 13y -14z -1)=x 23+13·y 14-14·z -1-1=xz -2.。
4.1 指数运算(精讲)(原卷版)--人教版高中数学精讲精练必修一

6
;
1
1
(2) 4x 2 3x 2
y 3
y
3 3
;
(3) a 3 a a .
2.(2023 春·河北石家庄·高一校考阶段练习)计算下列各式的值.
(1)
1
0.064 3
3
16 4
1 9
0
4
81
(2)
25 9
1
8 3 27
Hale Waihona Puke (πe)011 2
4
(3)
3π
1 3
π
22
2
2 1 5
1
A. 6 y2 y3 ( y 0 )
B.
3
x4
4
1 x
3
(
x
0
)
C.
1
x3
3
x
(
x
0)
3
D.
3
x2
2
x(
x
0
)
【例
1
3-2】(2023·高一课时练习)已知 a 2
1
a2
3 ,求下列各式的值:
(1) a a1 ;
a2 a2 2 (2) 3 3 .
a2 a 2 3
【例 3-3】(2023 云南)计算下列各式:
(1)
1 2
0
22
2
1 4
1 2
0.010.5
;
(2)
2
7 9
0.5
0.12
2
10 27
2 3
3
π0
37 48
;
(3) a b 2 3 4a1b 12a4b2c a,b, c 0 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)12 的 4 次方根可以表示为 ,
其中根指数为 ,被开方数为 ;
(3)-7 的 5 次方根可以表示为
,
其中根指数为 ,被开方数为 ;
(4)8 的平方根可以表示为
,
其中根指数为 ,被开方数为 .
问题引入
1
思考 将整数指数幂的概念进行推广: 42 =
新知探究
概念
m
a n n am
说 其中 m、n N且n >1,
如果x2=5,则x= 5 ;x叫做5的 平方根 . 如果x3=8,则x= 2 ;x叫做8的 立方根 . 如果x3=-8,则x= 2 ;x叫做8的 立方根 .
归 如果x2 a,那么x叫做a的平方根二次方根,表示为x a; 纳 如果x3 a,那么x叫做a的立方根三次方根,表示为x 3 a.
思 如果xn=a (n∈ N 且n>1),那么x叫做a的
1
3
a 5.
5 a3
典型例题
例3计算:
1
8-13; 2
25 9
3 2
;3
a
1 2
b
a
3 2b2Fra biblioteka,b
0
.
解:1
-1
83
=
1
= 1;
38 2
2
25 9
-3
2
=
5 3
2
-
3 2
=
5 3
-3
=
27 ; 125
3
a
1 2
b
a
3 2
b
2
=
a
1 2
+
3 2
b1+2
=
a2b3.
4
(1) a 7 ;
3
(2) a 5 ;
(3)
3
a2
.
4
解:(1)a7
7
3
a4 ;(2)a5
5
a3
;
(3)a
3 2
1
.
2 a3
典型例题
例 2 将下列各根式写成分数指数幂的形式: (1) 3 x2 ; (2) 3 a4 ; (3) 1 .
5 a3
2
3
解:1 3 x2 =x3; 2 3 a4 a4; 3
考 根,表示为x=
.
次方
新知探究
概念
一般地,如果xn=a(n∈N 且n>1),那么 x叫做a的 次方根.
1 当n为偶数时,正数a的n次方根有两个,表示
为 x n a 。,其中 n a 叫做的n 次算术根.
例如:x4 81,则x 4 81,读作:81的四次方根.
新知探究
2 当n为奇数时,实数 a的n次方根只有一个,
6
1 4
3 2
;
(6)
3
3 8
1 3
;
(7)
2
10 27
2 3
.
归纳小结
学习了哪些内容? 重点和难点各是什么? 采用了怎样的学习方法? 你是如何进行学习的? 你的学习效果如何?
布置作业
阅读 教材章节4.1
作
业
书写 教材习题一
思考 寻找有理数指数幂在生活中
的应用
3. ab m a mbm . 积的乘方,等于积的每个因式分别 乘方,再把所得的幂相乘。 m, n Z . a 指数书写格式: m + b
小测验
1
0
23= 8 ; 32 = 9 ; 2 = 1 ;
2 3
4
=
16 81
;
1 5
2
=
25
;
问题引入
如果x2=9,则x= 3 ;x叫做9的 平方根 .
第四章 指数函数与对数函数
4.1 有理数指数幂
复习回顾
正整数指数幂的定义
an a a a a(n个a相乘).
负整数、零指数幂的定义
an
1 an
a
0, n N ;
a0 1a 0.
复习回顾
整数指数幂的运算性质
1.a m a n a mn ; 同底数的幂相乘,底数不变指数相加。
2. a m n a mn ; 幂的乘方,底数不变指数相乘。
记作 x n a 。
例如:x5 32,则x 5 32,读作:-32的五次方根.
3 负数没有偶次方根;零的n次方根是零.
新知探究
归纳
若xn
a,则x
n
a , 当n为偶数且a
0时;
n a,当n为奇数, a R.
零的n次方根是零.
新知探究
概念
形如 n a ( n N+且n 1)的式子叫做a 的 n 次根式, 其中 n 叫做根指数,a 叫做被开方数.
a n
1 n a
n N+且n 1
性 质
a 2当n为奇数时,n an
a, a 0 当n为偶数时,n an a a, a 0.
典型例题
(2)25的算术平方根, ( 3 ) 81 的 4 次 算 术 根 ,
巩固练习
填空:
(1)25 的 3 次方根可以表示为
,
其中根指数为 ,被开方数为 ;
巩固练习 1.将下列各根式写成分数指数幂的形式:
(1) 4 6; (2) 5 73 ; (3) 1 ; (4) 3 52 ; 43
(5) 2 2 ; (6) 3 1 ; (7) 4 a b3 .
a
2.计算:
(1)27
2 3
;
(2)32
3 5
;
(3)
6
1 4
1 2
;
(4)
2
1 4
1 2
(5)
a 0.
明
概念
m
an
1
n am
说 其中 m、n N且n >1,
a 0.
明
注: 0的正分数指数幂等于0, 0的负分数指数幂没有意义
复习回顾
有理数指数幂的运算性质
1.a m a n a mn ;
2. a m n a mn ;
3. ab m a mbm .
m, n Q.
典型例题
例 1 将下列各分数指数幂写成根式的形式
