一元案例分析

合集下载

法律案例_一元钱(3篇)

第1篇案例背景在我国，法律与道德一直是社会管理的两把利剑。

而在日常生活中，法律与道德的冲突时有发生。

本案例即是一起因一元钱引发的诉讼，它不仅涉及到法律问题，更折射出诚信在现代社会的重要性。

案情简介2019年，某市居民李某在乘坐公交车时，不小心将一张一元纸币掉落在座位上。

当时车上人流量较大，李某并未察觉。

下车后，李某发现钱不见了，于是返回车上寻找。

在询问司机和周围乘客无果后，李某无奈之下选择了报警。

经过调查，警方发现，捡到钱的是同车的一名乘客张某。

张某承认捡到了李某的一元钱，并表示愿意归还。

然而，在归还过程中，张某却以各种理由拖延时间，甚至试图与李某协商分成。

李某对此感到十分气愤，认为张某的行为有失诚信，于是将张某告上法庭。

案件审理在法庭上，李某和张某分别陈述了自己的观点。

李某认为，张某捡到钱后应当主动归还，而不是拖延时间，更不能试图与当事人分成。

张某的行为违背了社会诚信原则，应当受到法律的制裁。

张某则辩称，自己捡到钱后已经主动归还，只是在归还过程中与李某发生了争执。

至于分成一事，张某表示只是开玩笑，并无恶意。

法庭审理过程中，法官对双方进行了调解。

然而，由于双方意见分歧较大，调解未能成功。

最终，法庭依法进行了判决。

法院判决法院经审理认为，张某捡到李某的一元钱后，应当主动归还，这是其作为公民应尽的义务。

张某在归还过程中拖延时间，并试图与李某分成，其行为违背了社会诚信原则，损害了李某的合法权益。

因此，法院判决张某返还李某一元钱，并赔偿李某精神损失费500元。

案例分析本案例中，张某捡到李某的一元钱，虽然金额不大，但却引发了法律诉讼。

这充分说明了诚信在现代社会的重要性。

首先，诚信是社会道德的基本要求。

在我国，诚信被视为“立身之本”、“处世之道”。

张某捡到钱后，本应主动归还，这是其应尽的社会责任。

然而，他却试图拖延时间，并试图与李某分成，其行为显然违背了诚信原则。

其次，诚信是维护社会公平正义的基石。

张某的行为不仅损害了李某的合法权益，也破坏了社会公平正义。

源于生活，用于生活——“一元一次方程的应用复习”教学案例分析

案例评析２０２２年５月下半月㊀㊀㊀源于生活,用于生活一元一次方程的应用复习教学案例分析◉上海市嘉定区娄塘学校㊀陈欢欢㊀㊀摘要:数学来源于生活又服务于生活．在教学中,从学生熟悉的现实生活出发,由生活情境引出具体的一元一次方程的应用的数学问题,在解决不同类型问题的过程中,引导学生找出问题中已知量与未知量间的等量关系,构建数学模型,运用方程的思想解决问题,从而培养学生分析问题和解决问题的能力,提高学生的数学核心素养．关键词:生活情境;一元一次方程的应用;数学建模;方程思想１引言«新课程标准»要求:根据具体问题中的数量关系,经历形成方程模型,解方程和运用方程解决实际问题的全过程,体会方程是刻画现实世界的一个有效的数学模型．在解决一元一次方程的应用问题时,由于问题的数量关系比较隐蔽,方程的建模思想又是学生初步接触,所以,寻找已知量与未知量之间的等量关系对学生来说还较为困难．为了突破这个难点,让学生能够进一步掌握列一元一次方程解应用题的方法和步骤,也为以后学习二次方程㊁分式方程的应用打下基础,笔者精心设计了一元一次方程的应用复习．在教学中,以学生身边的实际问题贯穿整个教学环节,让学生在活动中感受数学与生活的联系,感悟数学的价值,提高学生学以致用的能力,激发学生学习的积极性[１]．２联系生活实际,引出问题五一假期,小杰和小丽两家人相约一起去杭州游玩,在游玩过程中碰到了各种各样的实际问题,今天就由我们班的各位大侠相助一番．课堂教学中创设生活情境,设计一系列游玩过程中的数学问题,激发学生学习兴趣,通过课堂探究,使学生主动参与到解决问题的实际中,将数学知识和情感教育相结合,将现实生活㊁数学应用融为一体,使课堂教学洋溢着浓浓的生活气息和数学趣味[１]．３经历探究活动,研究问题数学源于生活,又用于生活．学生一起探究去杭州游玩前㊁游玩时遇到的一些储蓄㊁行程㊁和差倍分㊁盈亏等问题,在解决问题的过程中,学会找到问题中的等量关系,建立方程模型．场景一(出发前):小杰妈妈和小丽妈妈要去银行取些现金,以备不时之需．探究１:小杰妈妈选择储蓄的银行的年利率是２．２５％,取出时刚好存期满二年,取出的人民币为５２２５元．假如不计算利息税,请同学们利用所学过的知识,算一算,小杰妈妈在银行存入的本金是多少?师:问题中给出的已知量和未知量各是什么?生１:已知量是年利率㊁期数㊁本利和;未知量是本金．师:很好,那已知量与未知量之间存在着怎样的等量关系?生２:本利和＝本金＋本金ˑ利率ˑ期数．师:同学们是否还记得列方程解应用题的一般步骤是什么?生３:设未知数(元)㊁列方程㊁解方程㊁检验并作答．师:那么探究１如何设?列出的方程是什么?生４:设小杰妈妈在银行存入的本金是x元,则x＋x ２．２５％ˑ２＝５２２５．师:回答得很棒．通过解方程得到x＝５０００,检验正确后再作答．师:刚才我们运用了什么数学思想帮助小杰妈妈解决了她的问题?齐:方程的数学思想．师生总结:通过对实际问题的分析,找到已知量与未知量的等量关系,再设合适的未知数构建方程,解出方程的解,然后验证解的合理性并作答,从而解决实际问题．６３Copyright©博看网. All Rights Reserved.２０２２年５月下半月㊀案例评析㊀㊀㊀㊀根据实际情境,设计了出发前储蓄存款的问题,通过师生互动,问题环环相扣,引发学生深入思考,根据已知量和未知量找到等量关系构建方程,体会并总结方程的思想．练习:小丽妈妈在银行存了３０００元,年利率为２．７５％,存款到期后取出的人民币为３３３０元,问小丽妈妈的这笔存款存期为几年通过探究１的变式练习,学生巩固所学,从中体验成功,获得学习的自信．场景二(出发过程):取好钱,收拾好行李,小杰和小丽两家人打算从嘉定自驾去杭州．探究２:小杰一家,若提早出门,以８０k m /h 的速度行驶,可比预定的时间早到１５m i n ;若晚出门,路上较堵,以６０k m /h 的速度行驶,则比预定时间晚到０．５h ．求嘉定与杭州之间的距离?师:问题中给出的已知量和未知量各是什么?生１:已知量是早出门的速度㊁提早时间㊁晚出门的速度㊁迟到的时间;未知量是路程．师:还有没有其他的未知量?生２:预定时间也是未知量．师:有两个未知量怎么办?生３:一个未知量用来设未知数,另一个未知量用来找等量关系．师:很好,你能找到已知量与未知量之间存在着怎样的等量关系吗小组讨论并在学习单上列出方程．师:哪位同学说下自己的解题思路?生４:由预定时间相同,得等量关系为,路程８０＋提早时间＝路程６０－迟到时间．师:方程如何列?生５:设从嘉定到杭州的路程为x k m ,则x ８０＋１５６０＝x６０－０．５．师:非常好,同学们还有其他方法吗?生６:由路程相同,找到等量关系,(预定时间－提早时间)ˑ早出门的速度＝(预定时间＋迟到时间)ˑ晚出门的速度．设预定时间为y h ,则(y －１５６０)ˑ８０＝(y ＋０．５)ˑ６０．师:在列方程解应用题时,可直接设元也可以间接设元,关键要找准等量关系．问题中出现两个未知量时,一个未知量用来设未知数,另一个未知量用来找等量关系．通过小组合作讨论,在探究的过程中得到两种解题思路,一题多解,拓宽学生思维,体验建立方程模型解决问题的一般过程,从而提高对方程建模解决实际问题的应用价值的认识．这样的教学组织,有利于学生数学抽象㊁推理㊁建模的学科素养悄然形成与发展．练习:小杰一家离开嘉定６０k m 后,小丽一家才从同一地点沿同一路线出发,小杰一家开车行驶速度为８０k m /h ,小丽一家开车行驶的速度为１００k m /h,那么小丽一家需要多长时间可以追上小杰一家?小组讨论交流解决实际生活中的追击问题,通过画图来帮助找到等量关系从而列出方程．场景三(游玩景区):两家人到达杭州,休息一晚后,第二天一起去了西溪国家湿地公园进行游玩．探究３:景区成人票价每张８０元,学生享受５折优惠,３人以上可参加团购价每张５０元,小杰和小丽两家共７人,如果他们按团购价购买门票,比按正常购买门票共少花９０元,请问两家中共有几个学生?师:问题中有哪些等量关系?生１:学生票价＝成人票价ˑ５０％;学生人数＋成人人数＝７;正常购买门票的花费－团购门票的花费＝９０．师:总的等量关系是什么?生２:正常购买门票的花费－团购门票的花费＝９０,即学生票价ˑ学生人数＋成人票价ˑ成人人数－团购价ˑ总人数＝９０．师:根据找到的等量关系,请同学们在学习单上列出方程并求解．学生通过帮助小杰和小丽解决在游玩过程中遇到了购买门票问题,学会找出问题中的所有等量关系,理清思路,找准总的等量关系列出方程,进一步体验方程建模解决问题的过程,进一步掌握运用方程解决实际问题的一般过程和基本步骤,培养分析问题㊁解决问题的能力,增强方程应用意识．随后,小杰和小丽两家人来到游客服务中心,在门口发现旅游海报上宣传:微信扫二维码答旅游安全题,满分奖西溪摇橹船票 ,小杰想试一试,就扫了二维码开始答题．练习:试题由５０道选择题组成,选对一题得２分,不选得０分,选错倒扣１分．小杰最终得分８５分,那么小杰选对了多少道题?学生独立思考并在学习单上完成练习,探究解决竞赛题的问题．场景四(丝绸城购物):赏玩西溪湿地的风景后,小杰和小丽两家人决定第三天去购物,买些杭州的特产,所以大家一起来到了杭州中国丝绸城游玩．小丽妈７３Copyright ©博看网. All Rights Reserved.案例评析２０２２年５月下半月㊀㊀㊀妈进了一家正在搞五一大促销活动的服装店,看上了一件有杭绣的丝绸旗袍．探究４:这件旗袍的原价是８８０元,按照７折出售,服装店可获得１０％的利润,则这件旗袍成本价是多少师:通过问题分析,哪位同学可以帮助小丽妈妈算一算这件旗袍的成本?生:由已知量原价和折扣,可以算出现价为８８０ˑ７０％＝６１６,再找到等量关系:现价－成本＝盈利,设这件旗袍的成本是x 元,则列出方程为６１６－x ＝１０％x ,就可以解出成本x 了．师:思路很清楚,回答得非常棒,你帮助小丽妈妈解决了她的难题,好样的!经过之前的探究学习,学生进一步掌握了列方程解应用题的步骤及方法,可以独立思考分析探究４的问题,找到问题中的等量关系,再次运用方程建模的思想解决盈亏问题,提高了分析问题和解决问题的能力．４通过实际应用,深化问题在杭州中国丝绸城游玩的过程中,小杰和小丽看到了漂亮的古风扇(团扇和折扇),想到再过一个月就是六一儿童节了,每逢这个时候,学校就会举行爱心义卖活动,而古风扇款式新颖又符合季节需求,肯定好卖,所以两人不约而同地购买了一批古风扇作为义卖品．讨论:古风扇的批发价格都是一把８元,两人共购买了２０把,购买的团扇与折扇之比是２ʒ３．(１)那么两人购买的团扇㊁折扇各是多少把?(２)两人打算先按照进价的５０％标价出售,当卖出１５把古风扇的时候,为加快卖出的速度,打折将剩余的扇子全部卖出．如果想要盈利６８元,问最后剩余的扇子打几折出售?学生先独立思考,再小组合作讨论交流解题思路,在学习单上完成后,由小组代表给大家讲解．此题设置了比例和盈亏的问题,包含的等量关系多,对前面探究问题进行了深化,找到总的等量关系是关键,然后逐步拆解为单一的等量关系,从而建立方程求解,提升数学的思维水平,提高数学建模的能力．将各项探究活动与学生的现实生活结合起来,让他们从自己的世界出发,用心去感受生活中的问题,用所学数学知识探究生活中的问题,不仅可以培养学以致用的意识,提高分析问题和解决问题的能力,而且通过在问题情境中融入杭州的人文风貌及特产,培养了学生热爱生活的情感,体现了数学学科的德育价值．５案例分析５．１联系生活实际,强化学以致用生活中处处有数学,平时要善于用数学的眼光捕捉生活中的问题,运用数学的思维思考㊁分析和解决现实问题,增强学以致用的意识,提高生活实践的能力．在教学中设计合适的问题情境,不仅可以使课堂生动有趣,激发学生学习数学的兴趣,还可以让学生在解决储蓄存款㊁行程㊁比例㊁盈亏等不同类型的现实问题的过程中,体悟方程思想㊁提升数学建模思想和数学应用意识[２]．５．２注重建模过程,发展核心素养教学的每个环节都是围绕着生活中的实际问题展开的,在具体情境中抽象出数学问题,学生在用数学符号建立方程的探究活动中,体验抽象过程㊁分析等量关系㊁思考解决方法㊁构建方程模型㊁体悟方程思想㊁感悟学以致用的价值．在教学中,营造轻松愉悦的学习氛围,注重培养学生主动探究㊁合作交流意识,锻炼学生数学表达能力,提高学生的数学核心素养．５．３强调以生为本,注重学生发展课堂立足于学生的学 ,从单一的学生独立学习变为独立学＋小组合作学＋师生一起学的多元学习方式,鼓励学生多观察㊁多思考㊁多讨论,通过小组合作㊁教师引导,帮助学生提升自主探究和主动学习的能力,培养学生合作意识和交流能力,提高学生分析问题和解决问题的能力．授人以鱼,不如授人以渔 [３],教会学生列一元一次方程解决生活实际问题的方法,不仅达到了学以致用的目的,还培养了学生学习数学的兴趣和解决问题的能力．参考文献:[１]熊有辉．在实践活动中让学生学会解决问题优化应用题教学案例[J ]．文理导航,２０１９(３３):１７．[２]刘春妮,舒萍,莫慧琼等．数学课堂教学注重发展学生应用意识的案例研究[J ]．广西教育,２０１５(４):４５Ｇ４８．[３]周雪梅．一元二次方程的应用课堂教学案例分析[J ]．新课程,２０２０(３７):１１０．Z８３Copyright ©博看网. All Rights Reserved.。

一元线性回归案例

例8. 集装箱吞吐量与外贸额
2001-2006年中国集装箱吞吐量增长与外贸额增长的弹性分析.以Y表示集装箱吞吐量 (百万标准箱),X表示外贸额(百亿美元). OLS回归方程为 Y=3.7667+0.509X (2.06) (31.78) t (5)=2.776 n=6 R^2=0.996
0.1
例8. 集装箱吞吐量与外贸额
例8. 集装箱吞吐量与外贸额
2001-2007年中国集装箱吞吐量增长与外贸额增长的弹性分析.以Y表示集装箱吞吐量增长率(%),X表示外贸额增长率(%). OLS回归方程为 Y=18.449+0.3155X (2.3982) (1.078) t (5)=2.015 n=7 R^2=0.1887
0.1
例4. 考试分数与出勤率
假如期末考试的分数(score)取决于出勤率 (attend)和影响考试成绩的其他无法观测因素（如学生能力等）： score= β1+β2 attend+u 许多不加分析的回归发现：这一回归中β2 〈0，即分数与出勤率负相关. 这一模型在什么情况下满足均值独立条件？除非学生学习能力、学习攻击、年龄及其他因素与出勤率无关，但这几乎不可能.
例3. 静态菲利普斯曲线
时间序列数据令inf(t)表示年通货膨胀率,unem(t)表示事业率, 下列菲利普斯曲线假定了一个不变的自然失业率和固定的通货膨胀率预期. Inf(t)=β1+β2 unem(t)+u 依据1948-1996年美国经济数据, OLS回归方程为 Inf(t)=1.42+0.468 unem(t) (1.72) (0.289) n=49 R^2=0.053
例5. 学校的数学成绩与学校午餐项目

一元线性回归分析案例

求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为 172cm的女大学生的体重。
解：1、选取身高为自变量x，体重为因变量y，作散点图：
2、由散点图知道身高和体重有比较好的线性相关关系，因此可以用线性回归方程刻画它们之间的关系。
第17页/共39页
课题：选修2-3 8.5 回归分析案例
分析：由于问题中要求根据身高预报体重，因此选取身高为自变量，体重为因变量．
再冷的石头，坐上三年也会暖 !
1. 散点图；
2.回归方程： yˆ 0.849x 85.172 身高172cm女大学生体重 yˆ = 0.849×172 - 85.712 = 60.316(kg)
本例中, r=0.798>0.75．这表明体重与身高有很强的线性相关关系，从而也表明我们建立的回归模型是有意义的。
xi2
2
nx
,......(2)
i 1
i 1
其中x
1 n
n i 1
xi ,
y
1 n
n i 1
yi .
(x, y) 称为样本点的中心。
第8页/共39页
课题：选修2-3 8.5 回归分析案例
再冷的石头，坐上三年也会暖 !
1、回归直线方程
1、所求直线方程叫做回归直线方程；
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
然后，我们可以通过残差 e1, e2 , , en 来判断模型拟合的效果，
判断原始数据中是否存在可疑数据，这方面的分析工作称为残差分析。
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
编号 1
2
3
4
5

一元钱的法律案例(3篇)

第1篇一、案情简介2019年5月，原告李某与被告张某因一笔一元钱的交易发生纠纷。

具体案情如下：原告李某与被告张某系邻居，双方关系较为融洽。

2019年4月，李某向张某借款一元钱，用于购买生活用品。

张某答应借款，并表示一元钱不必归还。

然而，在5月，李某因故急需用钱，便向张某索要一元钱。

张某以各种理由推脱，拒绝归还。

李某遂将张某诉至法院，要求张某归还一元钱及相应利息。

二、法院审理法院受理本案后，依法组成合议庭，对本案进行了审理。

在审理过程中，原告李某提交了以下证据：1. 借款凭证，证明李某曾向张某借款一元钱。

2. 证人证言，证明张某曾答应不归还该借款。

被告张某对原告李某提交的证据提出异议，认为：1. 借款凭证系伪造，李某与张某之间不存在一元钱的借款关系。

2. 证人证言不可信，证人与李某有利害关系，证言存在虚假成分。

法院经审理认为：1. 原告李某提供的借款凭证虽然存在瑕疵，但足以证明双方之间存在一元钱的借款关系。

2. 证人证言虽然存在争议，但结合其他证据，可以认定证人证言的真实性。

综上所述，法院认为原告李某与被告张某之间存在一元钱的借款关系，被告张某应依法归还借款。

至于利息，由于双方未约定，法院依法支持原告李某的诉讼请求。

三、判决结果法院判决如下：1. 被告张某应于判决生效之日起十日内归还原告李某一元钱。

2. 本案诉讼费用由被告张某承担。

四、案例分析本案涉及一元钱的借款纠纷，看似微不足道，实则体现了法律对小额债务的保护。

1. 法律保护小额债务。

本案中，虽然借款金额仅为元，但法院仍然依法受理并作出判决，体现了法律对小额债务的保护。

这有助于维护社会公平正义，促进社会和谐稳定。

2. 证据在诉讼中的重要性。

本案中，原告李某提供了借款凭证和证人证言作为证据，虽然证据存在瑕疵，但法院依法认定证据的真实性，支持了原告的诉讼请求。

这提醒我们在日常生活中，要注重收集和保存证据，以便在发生纠纷时维护自己的合法权益。

3. 诚信为本。

一元钱官司案例

一元钱官司案例在生活中，我们常常会听到一些离奇的官司案例，有的让人啼笑皆非，有的让人唏嘘不已。

而今天，我要向大家介绍的是一起关于一元钱的官司案例。

这个案例发生在一个小城市的法院里。

原告小王和被告小李是一对邻居，他们之间因为一元钱发生了纠纷。

原来，小王在小李的店里买了一瓶饮料，付了一元钱，但是小王认为他给的是两元钱，而小李却坚持只收到了一元钱。

于是，小王将小李告上了法庭。

在庭审过程中，小王拿出了他的钱包，里面果然只有一元钱的零钱，但是他却坚称自己是给了两元钱。

而小李则拿出了他的收银记录，上面清清楚楚地写着小王购买饮料付了一元钱。

法官在听取了双方的陈述后，表示这个案子实在是太小了，不值得耗费法院的时间和精力。

但小王却坚持要维护自己的权益，他认为这是一起明显的消费欺诈行为。

而小李则表示自己只是按照实际收到的钱数开具了收据，并没有任何欺诈行为。

最终，法官做出了判决，他认为小王在没有充分证据的情况下，无法证明自己给了两元钱，因此无法成立欺诈的指控。

同时，法官也提醒小李在以后的经营中要注意细节，以免引起不必要的麻烦。

这个案例看似微不足道，但却反映了我们在日常生活中可能会遇到的一些小矛盾。

有时候，我们可能会因为一点小事而产生矛盾，但是在处理这些矛盾时，我们需要冷静客观地分析问题，不要因为一时的冲动而走上法庭。

毕竟，法院的资源是有限的，我们应该将宝贵的司法资源留给那些真正需要帮助的人。

同时，这个案例也提醒我们在日常生活中要保持良好的信誉和诚信，不管是作为消费者还是商家，都应该遵守交易规则，避免因为一些小事而引发不必要的争端。

只有在大家都能够理性地处理问题，才能够构建一个更加和谐的社会环境。

最后，希望大家能够从这个案例中吸取教训，避免因为一元钱而走上法庭，让我们共同努力，营造一个更加和谐美好的社会。

一元一次方程的应用(储蓄问题)案例分析

《一元一次方程的应用：（储蓄问题）》案例分析“以学生的发展为本”，是通过转变学生的学习方式和教师的教学方式，培养学生创新精神和实践能力。

要求数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础上。

教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在动手实践、自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动的经验。

现就《一元一次方程的应用：（储蓄问题）》的教学实践谈一点看法：一、设计意图本课时根据学生已有的学习经验和生活经验，选取教材一元一次方程的应用例题二（储蓄问题）。

这课题虽是学生所熟悉的，但由于学生缺乏实际的操作而显得有些纸上谈兵。

为了让学生所学知识真正用于生活，也为了让学生明白数学知识是来源于生活，因而在教学准备中，让学生自己去收集有关储蓄信息，让学生了解到银行的储蓄业务并不只是我们所见到的一般储蓄。

在教学的引入过程中，着重复习储蓄计算中的几个基本量以及它们的等量关系，为以后遇到的基本量发生变化而等量关系不变的教学任务打下基础。

在教学过程中抓住列方程解应用题的一般步骤进行教学，通过审题，抓住已知量、未知量，理清数量关系，为进一步开展思维活动提供依据。

二、教学设计课题：生活中的数学————储蓄学习目标1、理解利率问题中的本金、利息等概念；2、掌握利率问题的基本关系，掌握分析数量关系和列方程的方法。

3、继续体验方程概念模型在应用问题求解中的有效刻画。

教学重点经历分析、探究的过程，学会用一元一次方程解决有关储蓄计算的实际问题教学难点经历分析、探究的过程，学会用一元一次方程解决有关储蓄计算的实际问题，列出方程课型新授课时1教师活动环节学生活动修改教师用多媒体展示本课教学目标，并适当介绍. 目标导学学生齐读，明确学习目标，布置自主学习任务请问这张存单给你哪些信息？你对哪条信息比较有兴趣？本金：利息：利息＝本息和：1、小明把5000元按一年期的定期储蓄存入银行，年利率为1.98%，到期后可得利息（）元。

一元钱的法律官司案例(3篇)

第1篇案情简介：在某市，张三和李四因一元钱引发了一场法律官司。

事情起因于一次偶然的街头偶遇。

张三是一位拾荒者，李四则是一位经营小卖部的商人。

一天，张三在街头拾得一张一元纸币，正当他准备将这张纸币收入囊中时，李四突然出现，声称这张纸币是他丢的。

双方争执不下，最终演变成了一场官司。

这场官司不仅引起了社会各界的广泛关注，也引发了关于拾金不昧、诚信和法律的深刻讨论。

案件经过：1. 争执发生：张三在街头拾得一张一元纸币，准备收入囊中时，被李四发现。

李四声称这张纸币是他不小心丢的，要求张三归还。

2. 拒绝归还：张三认为，这张纸币是他在街头拾到的，没有义务归还给李四。

双方争执不下，情绪逐渐升级。

3. 报警处理：无奈之下，双方选择报警。

警方到场后，对双方进行了调解，但双方仍然坚持自己的观点。

4. 提起诉讼：调解无效后，李四决定将张三告上法庭，要求法院判决张三归还一元钱。

5. 法院审理：法院受理了此案，并依法进行了审理。

法庭辩论：在法庭上，双方展开了激烈的辩论。

李四的诉求：李四认为，根据《中华人民共和国物权法》的规定，拾得遗失物应当归还失主。

他声称，这张一元纸币是他不小心丢的，张三没有归还的义务。

张三的辩解：张三则认为，他是在街头拾得这张一元纸币的，没有义务归还给李四。

他主张，根据《中华人民共和国拾得遗失物处理办法》的规定，拾得遗失物应当上交有关部门，而不是直接归还给失主。

法院判决：经过审理，法院认为，本案中，张三在街头拾得一张一元纸币，但没有将纸币上交有关部门，而是私自保留。

根据《中华人民共和国拾得遗失物处理办法》的规定，张三的行为构成不当得利。

因此，法院判决张三归还一元钱给李四。

同时，法院也指出，张三的行为虽然构成不当得利，但考虑到其拾荒者的身份和生活困难，法院决定对张三免予刑事处罚。

案例分析：本案中，一元钱引发了法律官司，反映了我国法律在维护公民权益方面的严谨性和公正性。

以下是对本案的几点分析：1. 拾得遗失物的处理：根据《中华人民共和国物权法》和《中华人民共和国拾得遗失物处理办法》的规定，拾得遗失物应当上交有关部门，而不是直接归还给失主。

著名的一元钱法律案例(3篇)

第1篇一、案例背景2019年，我国某市消费者李女士在某超市购物时，发现一款标价为9.9元的水果沙拉，结账时却被告知实际价格为10元。

李女士认为超市存在欺诈行为，遂要求超市退还一元差价。

超市则辩称，9.9元是活动价格，10元是正常价格，不存在欺诈。

双方协商未果，李女士将超市诉至法院，要求超市退还一元差价并承担诉讼费用。

二、案件焦点本案的焦点在于消费者权益保护法中关于欺诈行为的认定，以及一元差价是否构成欺诈。

三、法院判决法院经审理认为，消费者权益保护法规定，经营者不得利用虚假宣传、虚假价格等手段，欺骗、误导消费者。

本案中，超市在标价上存在误导消费者的情况，使得消费者在不知情的情况下支付了额外的一元费用，构成欺诈。

因此，法院判决超市退还李女士一元差价，并承担诉讼费用。

四、案例分析1.消费者权益保护法中的欺诈行为认定消费者权益保护法是我国消费者权益保护的基本法律，其中关于欺诈行为的认定，主要依据以下两点：（1）经营者故意隐瞒商品或服务的真实情况，误导消费者。

（2）经营者利用虚假宣传、虚假价格等手段，欺骗、误导消费者。

本案中，超市在标价上存在误导消费者的情况，使得消费者在不知情的情况下支付了额外的一元费用，符合消费者权益保护法中关于欺诈行为的认定。

2.一元差价是否构成欺诈在本案中，一元差价虽然数额不大，但已构成欺诈。

原因如下：（1）一元差价虽小，但足以误导消费者。

消费者在购物时，往往会关注商品的价格，一元差价的存在使得消费者在不知情的情况下支付了额外费用，导致消费者权益受损。

（2）一元差价是超市故意设置的。

超市在标价上故意设置一元差价，目的是为了误导消费者，从而达到增加销售额的目的。

这种行为违反了诚实信用原则，属于欺诈行为。

五、启示本案给我们的启示如下：1.消费者在购物时，要关注商品的价格，避免因小失大。

2.经营者要诚信经营，遵守法律法规，不得利用欺诈手段误导消费者。

3.消费者权益保护法为消费者提供了法律保障，消费者在权益受损时，要学会运用法律武器维护自己的合法权益。

一元一次方程与实际应用案例分析及教学反思

一元一次方程与实际应用案例分析及教学反思一元一次方程是初中数学中的重要知识点之一，其核心概念是变量的一次幂。

它不仅是数学学科中的基础，也是实际生活中常见的一种数学模型。

本文将通过分析实际应用案例，探讨一元一次方程在实际问题中的应用，并对教学过程进行反思和总结。

一、实际应用案例分析1. 例题一：小明骑自行车去超市，第一段骑行路程以每小时15公里的速度骑行，之后又以每小时12公里的速度骑行，总共花费时间3小时。

求小明骑行的总路程。

解析：设小明骑行的总路程为x公里，则根据题意，可以列出方程：x/15 + x/12 = 3通过解这个方程，可以得到小明骑行的总路程为36公里。

2. 例题二：某商场进行促销活动，打折力度为原价的30%。

现在有一件原价为300元的商品，问打折后的价格是多少？解析：设打折后的价格为x元，则根据题意，可以列出方程：0.7 * 300 = x通过解这个方程，可以得到打折后的价格为210元。

以上两个例题展示了一元一次方程在实际问题中的应用。

通过将实际问题转化为方程，可以利用数学方法解决问题，使得解题变得简单明了。

二、教学反思在教学一元一次方程时，我发现学生对于实际应用的理解和运用存在一些困难。

为了提高学生的学习效果，我在教学中采取了以下措施：1.提供实际案例：我在教学中增加了更多的实际应用案例，让学生通过解决实际问题来理解一元一次方程的意义和作用。

以生活中的例子为基础，引导学生思考，提高他们对于实际问题的抽象和建模能力。

2.操练训练：除了讲解概念和案例分析，我还加强了对一元一次方程的操练训练，包括解方程的方法和技巧。

通过大量的练习，学生可以加深对知识点的理解和记忆，并提高解题的能力。

3.启发式教学：我鼓励学生在解决问题时积极思考和探索，引导他们形成独立解决问题的思维习惯。

将学生分成小组，让他们自己找到解决问题的思路和方法，并鼓励他们与小组成员分享解题思路，激发合作学习的动力。

通过以上教学反思，我发现学生的学习兴趣和动力有所提高，他们对于一元一次方程的理解和应用能力也得到了明显的提升。

一元钱的官司法律案例(3篇)

第1篇一、案件背景原告：张某，男，35岁，某市居民。

被告：李某，男，32岁，某市居民。

案情简介：张某与李某系邻居，两家相邻而居。

2019年6月，张某在自家门口放置了一堆废纸箱，准备出售。

李某路过时，见状便表示要购买。

双方协商一致，以一元钱的价格成交。

然而，李某在支付一元钱后，并未将废纸箱带走。

张某多次催促，李某以各种理由推脱。

无奈之下，张某将李某诉至法院，要求李某支付一元钱并搬走废纸箱。

二、法院审理1. 争议焦点本案的争议焦点在于：一元钱买卖合同是否有效？李某是否应当履行合同义务，支付一元钱并搬走废纸箱？2. 法院判决法院经审理认为，本案中，张某与李某就废纸箱的买卖达成了一致意见，且双方均表示同意以一元钱的价格成交。

根据《中华人民共和国合同法》第二条的规定：“合同是平等主体之间设立、变更、终止民事权利义务关系的协议。

”本案中，张某与李某的买卖行为符合合同的基本特征，双方签订的买卖合同合法有效。

关于李某是否应当履行合同义务，法院认为，根据《中华人民共和国合同法》第六十条的规定：“当事人应当按照约定全面履行自己的义务。

”本案中，李某在支付一元钱后，未按照约定履行合同义务，构成违约。

因此，李某应当承担违约责任，支付一元钱并搬走废纸箱。

三、案例分析1. 合同法的基本原则本案中，法院判决李某支付一元钱并搬走废纸箱，体现了合同法的基本原则，即平等、自愿、公平、诚实信用。

在合同关系中，双方当事人应当遵循诚实信用原则，全面履行合同义务。

2. 法律的威慑力本案中，张某以一元钱为诉讼标的，看似微不足道，实则体现了法律的威慑力。

一元钱官司虽小，却警示了社会大众，任何违反合同义务的行为都将受到法律的制裁。

3. 诚信的维护本案中，李某在支付一元钱后，未按照约定履行合同义务，违背了诚信原则。

法院判决李某支付一元钱并搬走废纸箱，不仅维护了张某的合法权益，也彰显了诚信的价值。

四、启示1. 合同意识的重要性本案提醒我们，在日常生活中，要树立合同意识，自觉遵守合同法规定，维护自身合法权益。

一元线性回归模型案例

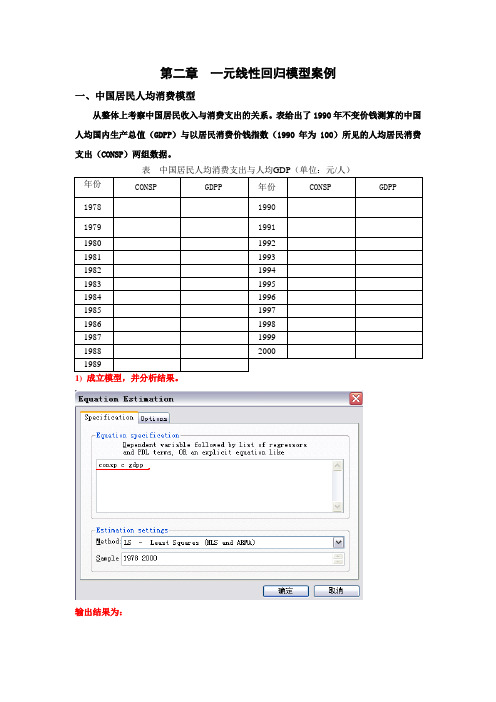
第二章一元线性回归模型案例一、中国居民人均消费模型从整体上考察中国居民收入与消费支出的关系。

表给出了1990年不变价钱测算的中国人均国内生产总值（GDPP）与以居民消费价钱指数（1990年为100）所见的人均居民消费支出（CONSP）两组数据。

表中国居民人均消费支出与人均GDP（单位：元/人）年份CONSP GDPP年份CONSP GDPP19781990197919911980 19921981 19931982 19941983 19951984 19961985 19971986 19981987 19991988 200019891) 成立模型，并分析结果。

输出结果为：对应的模型表达式为：=+201.1070.3862CONSP GDPP20.9927,2859.23,0.55===R F DW从回归估量的结果能够看出，拟合度较好，截距项和斜率项系数均通过了t查验。

中国人均消费增加10000元，GDP增加3862元。

二、线性回归模型估量表给出黑龙江省伊春林区1999年16个林业局的年木材采伐量和相应砍木剩余物数据。

利用该数据（1）画散点图；（2）进行OLS回归；（3）预测。

表年剩余物y林业局名年木材剩余物y t（万m3）年木材采伐量x t（万m3）乌伊岭东风新青红星五营上甘岭友好翠峦乌马河美溪大丰南岔带岭朗乡桃山双丰合计（1）画散点图先输入横轴变量名，再输入纵轴变量名得散点图（2）OLS估量弹出方程设定对话框取得输出结果如图：由输出结果能够看出，对应的回归表达式为：ˆ0.76290.4043t t yx =-+20.9129,146.7166, 1.48R F DW === （3）x=20条件下模型的样本外预测方式第一修改工作文件范围将工作文件范围从1—16改成1—17确信后将工作文件的范围改成包括17个观测值，然后修改样本范围将样本范围从1—16改成1—17打开x的数据文件，利用Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改成17—17，即只预测x=20时的y的值。

一元线性规划及先关分析案例

3
层次分析法和德尔菲法
哈尔滨城市综合承载力评价指标体系构建
城市综合承载力的评价实质上就是判定该城市现有的承载力能否支撑目前
的人口规模及人类各种经济社会活动的规模和强度。衡量城市综合承载力需
要考虑以下几个方面： 1)环境承载力2)资源承载力3)基础设施承载力4)生态系统承载力5)安全承载力6)公共服务承载力7)科学技术承载力8)社会文化承载力通过德尔菲法和参考已有的研究成果等初步确立了1个一级指标，8个二级指标，49个三级指标，本次参与德尔菲法的专家组由15位专家组成，包括住建部城市建设司人员3人、城乡规划司人员2人、哈尔滨城乡规划局人员4人、哈尔滨市政府人员2人、哈尔滨社会研究所人员4人，所有专家都具有多年的工作经历和丰富的实践经验，充分了解城市发展历程和城市发展动力所在。应用sPss软件对城市综合承载力评价指标进行相关性检验等一系列优化处
5.采用时间尺度分析的方法，提取交通流的时间一尺度耦合特征考虑到每个网格站点的负载量，得到时间一尺度耦合元线性回归
基于一元线性回归分析的公路工程企业定额消耗量推算方法研究
在公路工程施工过程中影响人工消耗量的因素很多，大致可以分为生产条件方面、技术条件方面、组织条件方面三类。而这些影响条件根据其影响因素变化规律的不同又可分为连续性因素和间断性因素。连续性影响因素的特点是影响因素对于人工消耗的影响变化是呈连续性渐变的。对于此类问题而言，一元线性回归分析方法是一种很好的分析影响因素带来影响大小的方法。
3.在上述网络模型分析的基础上，采用 Small—World模型模拟交通拥堵在复杂路网中的动态演进过程，如图。
1
线性回归
基于线性规划的城市交通流优化调度模型
4.在上述交通路网模型构建的基础上，进行交通流信息特征提取，信息特征提取之前，采用线性规划方案，对交通网络路网结构进行线性分割，分割结果，如图

案例分析：《我在马路边捡到一元钱》

案例分析：《我在马路边捡到一元钱》（最新版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如托班教案、小班教案、中班教案、大班教案、幼儿游戏、教育资料、幼儿管理、计划总结、家园教育、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this store provides various types of classic sample essays, such as nursery school lesson plans, small class lesson plans, middle class lesson plans, large class lesson plans, children's games, educational materials, child management, plan summary, home education, other sample essays, etc. Learn about the different formats and writing styles of sample essays, so stay tuned!案例分析：《我在马路边捡到一元钱》最进一段时间孩子们对以前的儿童歌曲特别感兴趣，很多小朋友经常聚到一起边表演边唱，根据孩子们近期的喜好，我从网上下载了很多我们儿时的歌曲给他们听孩子们听得津津有味。

一元与20元的心理学案例

一元与20元的心理学案例
经济学家苏必克(Martin Shubik)在20世纪70年代初期曾拿一元在他的课堂上拍卖，即把一元作为拍品来拍卖。

每个人都可以出价，不设底价，出价最高者可以得到一元，同时要支付所出价的金额。

同时拍卖有个附带规则，就是每个出价的人要支付自己所喊出的最高金领。

例如我喊出九十五分，另一个人喊一元钱，那我就要付出九十五分钱，组得不到一元钱。

经过多轮竞拍过后最终的结果很是出人意料，在实验当中，有人为了竞标到这一元钱，竟出价到二十元。

有的朋友可能会想这是小孩子闹着玩的不足为信，从经济收益面考虑那有那么傻的人呢!可事实是就有人利用相同的原理在在酒会.上将1000元拍到了2050元。

同时这样的例子有很多哦!
有人不解为什么会这样子呢?难道人们疯啦。

事实是不同的研究分析显示，竞标者起初认为，他们可以赚到一元钱。

在场的人也都这么想，所以参与竞标。

当竞标金额出到一元钱时，每个人的想法都变为要减少自己的损失。

只是单纯想要赢得竞标，就算买贵了也没关系另作他算。

我们发现不论是什么样的动机，受益的人始终只有一个就是实验的发起者。

我们试想一下赌输了而继续赌博的人是否和这个参与竞拍的人
想法很相似呢?还有当我们与别人发生冲突和争执时是否总想战胜对方，最后两败俱伤是不是也是这样的心理机制呢?。

案例：一元线性回归模型实现

一元线性回归模型：案例分析下面用一个实例对本章内容作一简单回顾。

我们将收集中国财政收入和国内生产总值在1978~2006年间的历史数据，然后建立两者的一元线性回归模型，并用最小二乘法对其中的参数进行估计，最后对模型进行一些必要的检验。

一、中国财政收入和国内生产总值的历史数据由经济学等相关学科的理论我们知道，国内生产总值是财政收入的来源，因此财政收入在很大程度上由国内生产总值来决定。

为了考察中国财政收入和国内生产总值之间的关系，我们收集了中国财政收入和国内生产总值在1978~2005年间的历史数据，如表 2.4.1所示。

表2.4.1中国财政收入和国内生产总值数据表单位：亿元年份财政收入(Y) 国内生产总值(X) 年份财政收入(Y) 国内生产总值(X)1978 1132 3624 1992 3483 266521979 1146 4038 1993 4349 345611980 1160 4518 1994 5218 466701981 1176 4860 1995 6242 607941982 1212 5302 1996 7408 711771983 1367 5957 1997 8651 789731984 1643 7207 1998 9876 844021985 2005 8989 1999 11444 896771986 2122 10201 2000 13395 992151987 2199 11955 2001 16386 1096551988 2357 14922 2002 18904 1203331989 2665 16918 2003 21715 1358231990 2937 18598 2004 26396 1598781991 3149 21663 2005 31628 183868我们以X为横轴，Y为纵轴将这些数据的描绘在二维坐标图上，得到如下的散点图(图2.4.1 )。

一元钱的法律案例(3篇)

第1篇一、案件背景甲、乙双方系邻居，关系较好。

2019年6月，甲因资金周转困难，向乙借款一万元。

乙考虑到双方关系，同意借款，并约定借款期限为一个月，到期后甲应立即归还本金及利息。

双方在借款时签订了借款合同，约定利息为月利率2%。

二、案件经过借款到期后，甲未能按时归还本金及利息。

乙多次催促，甲以各种理由推脱。

乙无奈之下，将甲诉至人民法院，要求甲归还借款本金及利息。

在庭审过程中，甲辩称，其确实曾向乙借款一万元，但实际借款金额只有九千元，乙在起诉时夸大了借款金额。

同时，甲认为，自己并非故意拖欠借款，而是由于个人原因导致资金紧张，无法按时归还。

乙则提交了借款合同、银行转账记录等证据，证明双方借款金额为一万元，并提供了多次催款记录，证明其已尽到催款义务。

三、法院判决法院经审理认为，甲、乙双方签订的借款合同合法有效，双方均应按照合同约定履行义务。

关于借款金额，法院认为，乙提交的证据足以证明双方借款金额为一万元，甲的辩称缺乏事实依据，不予采信。

关于借款利息，法院认为，双方约定的月利率为2%，未超过《中华人民共和国合同法》规定的上限，应予以支持。

关于甲是否故意拖欠借款，法院认为，甲虽存在个人原因导致资金紧张，但其未能按照合同约定按时归还借款，已构成违约。

综上，法院判决甲归还乙借款本金一万元及利息，利息按照月利率2%计算，自借款之日起至实际归还之日止。

四、案例分析本案涉及民间借贷纠纷，以下是对本案的法律分析：1. 民间借贷合同的法律效力根据《中华人民共和国合同法》规定，民事主体之间设立、变更、终止民事权利义务关系的协议，适用合同法的规定。

本案中，甲、乙双方签订的借款合同合法有效，双方应按照合同约定履行义务。

2. 借款金额的认定在借款纠纷中，借款金额的认定至关重要。

本案中，乙提交了借款合同、银行转账记录等证据，足以证明双方借款金额为一万元。

甲的辩称缺乏事实依据，法院不予采信。

3. 借款利息的计算根据《中华人民共和国合同法》规定，当事人可以约定利息，但不得超过国家规定的利率上限。

一元线性回归模型案例

一元线性回归模型案例一元线性回归是统计学中常用的一种回归分析方法，用于研究一个自变量和一个因变量之间的线性关系。

在本文中，我们将通过一个实际案例来介绍一元线性回归模型的应用和分析过程。

案例背景：假设我们是某家电商平台的数据分析师，我们希望通过用户的年龄来预测其在平台上的消费金额。

我们收集了100位用户的年龄和其在平台上的消费金额的数据，现在我们希望利用一元线性回归模型来分析这些数据，以便更好地了解用户消费行为。

数据分析：首先，我们需要对收集到的数据进行初步的分析。

我们可以使用散点图来观察年龄和消费金额之间的关系。

通过观察散点图，我们可以初步判断年龄和消费金额之间是否存在线性关系，以及线性关系的方向和强度。

模型建立：在确认了年龄和消费金额之间存在线性关系后，我们可以建立一元线性回归模型。

模型的基本形式为，Y = β0 + β1X + ε，其中Y表示因变量（消费金额），X表示自变量（年龄），β0和β1分别表示截距和斜率，ε表示误差项。

我们需要通过最小二乘法来估计β0和β1的值，从而建立回归方程。

模型评价：建立回归模型后，我们需要对模型进行评价。

我们可以通过计算回归方程的拟合优度R^2来评价模型的拟合程度，R^2的取值范围为0到1，值越接近1表示模型拟合得越好。

此外，我们还可以利用残差分析来检验模型的假设是否成立，以及检验模型的稳健性和可靠性。

预测分析：最后，我们可以利用建立的回归模型进行预测分析。

通过输入不同年龄的值，我们可以利用回归方程来预测用户在平台上的消费金额。

预测分析可以帮助电商平台更好地了解不同年龄段用户的消费特点，从而制定针对性的营销策略和服务方案。

结论：通过以上一元线性回归模型的应用分析，我们可以得出结论，用户的年龄和在平台上的消费金额之间存在一定的线性关系，通过建立回归模型，我们可以对用户的消费金额进行预测和分析。

这对于电商平台来说具有重要的参考价值，可以帮助平台更好地了解用户消费行为，从而提升用户体验和增加销售额。

一元线性回归模型案例分析

一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。

居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长，而且这也是人民生活水平的具体体现。

改革开放以来随着中国经济的快速发展，人民生活水平不断提高，居民的消费水平也不断增长。

但是在看到这个整体趋势的同时，还应看到全国各地区经济发展速度不同，居民消费水平也有明显差异。

例如，2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元，最高的上海市达人均10464元，上海是黑龙江的2.35倍。

为了研究全国居民消费水平及其变动的原因，需要作具体的分析。

影响各地区居民消费支出有明显差异的因素可能很多，例如，居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。

为了分析什么是影响各地区居民消费支出有明显差异的最主要因素，并分析影响因素与消费水平的数量关系，可以建立相应的计量经济模型去研究。

二、模型设定我们研究的对象是各地区居民消费的差异。

居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。

而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。

所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。

因为研究的目的是各地区城市居民消费的差异，并不是城市居民消费在不同时间的变动，所以应选择同一时期各地区城市居民的消费支出来建立模型。

因此建立的是2002年截面数据模型。

影响各地区城市居民人均消费支出有明显差异的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入，其他因素虽然对居民消费也有影响，但有的不易取得数据，如“居民财产”和“购物环境”；有的与居民收入可能高度相关，如“就业状况”、“居民财产”；还有的因素在运用截面数据时在地区间的差异并不大，如“零售物价指数”、“利率”。

法律案例_一元钱(3篇)

第1篇一、案件背景2018年10月，某市居民张某在一家超市购物时，因支付方式发生纠纷，导致其与超市工作人员李某发生争执。

争执的焦点是一元钱硬币的支付问题。

张某声称在结账时支付了一元硬币，但李某却坚称张某并未支付。

双方争执不下，最终导致张某情绪激动，与李某发生肢体冲突。

事后，张某因涉嫌故意伤害被警方控制，而李某也因故意伤害他人被起诉。

二、案件经过1. 张某支付一元硬币的认定根据超市监控录像显示，张某在结账时确实支付了一元硬币。

但李某坚称张某并未支付，而是故意找茬。

李某表示，在结账过程中，张某并未将硬币投入收银机，而是将硬币放在收银台上。

李某认为这是张某故意为之，企图诬陷自己。

2. 双方争执升级在争执过程中，张某情绪激动，指责李某故意讹诈。

李某则反驳称自己并无过错，双方争执升级。

在争执过程中，张某情绪失控，与李某发生肢体冲突，导致李某受伤。

3. 张某被警方控制事发后，张某因涉嫌故意伤害被警方控制。

警方对超市监控录像进行了调查，确认张某确实支付了一元硬币。

同时，警方也了解到李某在争执过程中存在过错，但未构成故意伤害。

4. 李某被起诉李某因故意伤害他人被起诉。

在法庭审理过程中，李某辩称自己并未故意伤害张某，而是张某先动手打了自己。

但根据监控录像和证人证言，法院认定李某在争执过程中存在过错，构成故意伤害。

三、法律解析1. 一元硬币支付的认定在本案中，张某支付一元硬币的事实得到了超市监控录像的证实。

根据《中华人民共和国合同法》第四十一条规定：“当事人应当按照约定履行自己的义务。

当事人没有约定或者约定不明确的，按照交易习惯履行。

”在本案中，张某在结账时支付了一元硬币，已履行了支付义务，超市应当认可。

2. 故意伤害的认定根据《中华人民共和国刑法》第二百三十四条规定：“故意伤害他人身体的，处三年以下有期徒刑、拘役或者管制。

”在本案中，李某在争执过程中存在过错，但未构成故意伤害。

因为李某的行为并未导致张某受到严重伤害，且李某在争执过程中也受到了伤害。