SPC计算公式

合集下载

SPC常用公式汇总

R X - ChartnX d R X X X R X nnX X X X c x C ni in//1......).12min max 121∧∧∧===-==++=∑σσσ的标准差估计值：的标准差估计值：每个子组均值和极差：XCLX X=中心线：算图中心线和管制界限计).2 ∑==+++=ki i KX KKX XX X 1211......RA X LCLRA X UCLXX**22-=+=下管制界限：上管制界限：∑==+++==ki iKR RKKR R R R CL R 1211......).3中心线：算图中心线和管制界限计RD LCLRD UCLRR**34==下管制界限：上管制界限：SX - Chart()nX c s X n xXs X nnX XX X c xc ki k ni in//11......).142,121∧∧∧===--==++=∑∑σσσ的标准差估计值：的标准差估计值：组内标准差：每个子组均值标准差：∑==+++==ki iKX XKKX XX X CL X 1211......).2中心线：算图中心线和管制界限计sA X LCLsA X UCLXX**33-=+=下管制界限：上管制界限：∑==+++==ki iKR SKKS S S S CL S 1211......).3中心线：算图中心线和管制界限计sB LCLsB UCLRR**34==下管制界限：上管制界限：R X -~Chart样本值：)(...2,1,样本容量n i X i =子组中位数：当数据升序排列时，()个元素的值；式样本中第O XO如果n 是奇数；如果n 是偶数；n=子组中元素数量；k,用于确定平均中位数和平均极差的子组数量；子组极差：min max X X R -= 每个子组内的极差；平均中位数：∑==++=ki i k X kk x x x X 121~1~......~~~平均极差：kR R R R k......21++=控制图特征：中心线控制线xCL x~~= R A X UCLx*~~2~+=R A X L C L x*~~2~-=RCL R =RD UCLR*4=RD LCLR*3=X-MR Chart单值：；单值k i X i ,......,1,=单值的平均值：kx x x X k......21++=移动极差：差；；当前值和之前值的极k i x x MR i i i ,......,2,1=-=-平均移动极差：∑=-=-++=ki ikMR k k MR MR MR MR 221111......X 的标准差估计值：2/d R c=∧σ控制图特征：中心线控制限X CLX= R E X U C L X *2+= RE X LCLX*2-=RCL R = R D U C L R *4=R D L C L R *3=P Chart单值： ninp p i i =其中：量；发现的不合格项目的数被检验零件数量；::i i np n 单值的平均值：子组的数量其中=+++++=k n n n np np np p kk;...........2121；相等；其中所有的i kn kp p p p ;......21+++=控制图特征：中心线控制限p CLp=()ip n p p p U C L i -+=13()ip n p p p LCLi--=13如果样本大小（n ）恒定，控制限：()np p p UCLp-+=13()np p p L C L p --=13当样本大小变化时，如果75.0≥ii n n 最大值最小值，则控制限不变；控制限：()np p p UCLp-+=13()np p p L C L p --=13制程能力指数计算公式单边规格计算公式： 1、稳定制程能力指数：=-=-=∧266d RLSL USL LSLUSL C cp σ∧-=cXUSL CPU σ3 ∧-=cLSLX CPL σ3[]CPL CPU MIN C pk 或=2、不稳定能力指数：pp LSLUSL P σ6-=16)167.910...()167.98()167.99()167.98(1)(222212--+-+-+-=--=∑=n x xni ipσpX USL PPU σ3-=pX LSL PPL σ3-=[]PPLPPU MIN P pk 或=双边规格计算公式：()Papk CCC ⨯-=1其中Ca: 制程准确度，越小越好！Cp: 制程精确度，越大越好！2/规格容许值规格中心值制程平均值-=a C2/T CLS X C a -=X:制程平均值； CLS: 规格中心值；LSL USL T -=-==规格下限规格上限容许规格值888888888888432⨯⨯⨯=⨯⨯=⨯=2222121211)(...)()()(...x x x x x x x xx x x xn ni inni i-++-+-=-+++=∑∑==。

SPC控制图计算公式

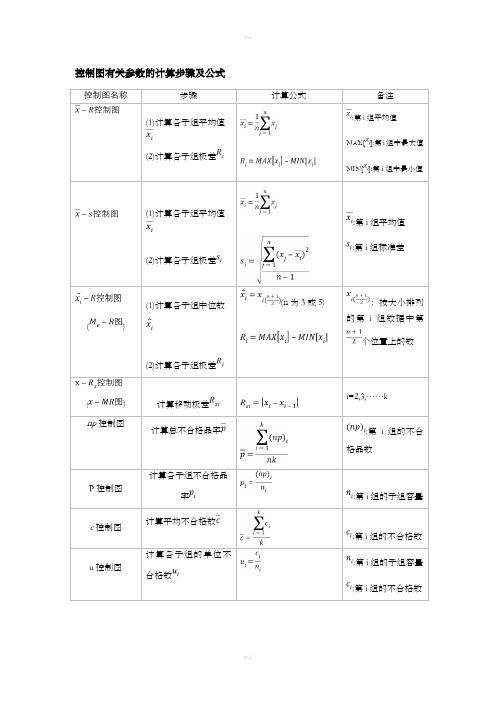
控制图有关参数的计算步骤及公式控制图名称步骤计算公式备注(1)计算各子组平均值(2)计算各子组极差:第i组平均值MAX[]:第i组中最大值MIN[]:第i组中最小值(1)计算各子组平均值(2)计算各子组极差:第i组平均值:第i组标准差()(1)计算各子组中位数(2)计算各子组极差(n为3或5)：按大小排列的第i组数据中第个位置上的数()计算移动极差i=2,3,……knp控制图计算总不合格品率:第i组的不合格品数P控制图计算各子组不合格品率:第i组的子组容量c控制图计算平均不合格数:第i组的不合格数u控制图计算各子组的单位不合格数:第i组的子组容量:第i组的不合格数控制图中控制限的计算控制图名称中心线（CL ）上、下控制限（UCL 与LCL ）备注CL==UCL=LCL=①当LCL 为负值时，取0为自然下限 ②,,,,,,查控制图系数表RCL==UCL= LCL=CL==UCL= LCL=sCL==UCL= LCL=CL==UCL= LCL= RCL==UCL= LCL=()xCL==UCL= LCL=CL==UCL=3.267 LCL=0P 图CL=UCL=LCL=np 图CL=nUCL= LCL=c图CL==UCL= LCL=u图CL=UCL= LCL=。

SPC控制图计算公式

( )
计算移动极差
i=2,3,……k
np控制图
计算总不合格品率
:第i组的不合格品数
P控制图
计算各子组不合格品率
:第i组的子组容量
c控制图
计算平均不合格数
:第i组的不合格数
u控制图
计算各子组的单位不合格数
:第i组的子组容量
:第i组的不合格数
控制图有关参数的计算步骤பைடு நூலகம்公式
控制图中控制限的计算
控制图名称
中心线（CL）
CL= =
UCL=3.267
LCL=0
P图
CL=
UCL=
LCL=
np图
CL=n
UCL=
LCL=
c图
CL= =
UCL=
LCL=
u图
CL=
UCL=
LCL=
控制图名称
步骤
计算公式
备注
(1)计算各子组平均值
(2)计算各子组极差
:第i组平均值
MAX[ ]:第i组中最大值
MIN[ ]:第i组中最小值
(1)计算各子组平均值
(2)计算各子组极差
:第i组平均值
:第i组标准差
( )
(1)计算各子组中位数
(2)计算各子组极差
(n为3或5)
：按大小排列的第i组数据中第个位置上的数
上、下控制限（UCL与LCL）
备注
CL= =
UCL=
LCL=
当LCL为负值时，取0为自然下限
, , , , , , 查控制图系数表
R
CL= =
UCL=
LCL=
CL= =
UCL=
LCL=
s
CL= =

SPC控制图计算公式

控制图有关参数的计算步骤及公式控制图名称步骤计算公式备注(1)计算各子组平均值(2)计算各子组极差:第i组平均值MAX[]:第i组中最大值MIN[]:第i组中最小值(1)计算各子组平均值(2)计算各子组极差:第i组平均值:第i组标准差()(1)计算各子组中位数(2)计算各子组极差(n为3或5) ：按大小排列的第i组数据中第个位置上的数() 计算移动极差i=2,3,……knp控制图计算总不合格品率:第i组的不合格品数P控制图计算各子组不合格品率:第i组的子组容量c控制图计算平均不合格数:第i组的不合格数u控制图计算各子组的单位不合格数:第i组的子组容量:第i组的不合格数控制图中控制限的计算控制图名称中心线（CL）上、下控制限（UCL与LCL）备注CL==UCL=LCL=①当LCL为负值时，取0为自然下限②,,,,,,查控制图系数表RCL==UCL=LCL=CL==UCL=LCL=sCL==UCL=LCL=CL==UCL=LCL=RCL==UCL=LCL=()xCL==UCL=LCL=CL==UCL=3.267LCL=0P图CL=UCL=LCL=np图CL=nUCL=LCL=c图CL==UCL= LCL=u图CL=UCL= LCL=。

SPC各值计算公式

SPC各值计算公式SPC（统计过程控制）是一种统计方法，用于检测和控制过程的稳定性和变异性。

SPC各值计算公式包括控制图参数和过程能力指数等。

以下是常见的SPC各值计算公式及其解释：1.控制图参数：a.X̄控制图上的中心线是过程的平均值的估计量。

计算公式为：X̄=ΣX/n，其中X是测量值的总和，n是样本大小。

b. R 控制图上的极差线是过程的极差的估计量。

计算公式为：R = Xmax - Xmin，其中Xmax和Xmin是样本中最大值和最小值。

c.S控制图上的标准偏差线是过程的标准偏差的估计量。

计算公式为：S=√(Σ(X-X̄)²/(n-1))，其中Σ(X-X̄)²是样本值与平均值的差的平方的总和。

d.UCL控制图上的上限控制限是过程的可接受上限。

计算公式为：UCL=X̄+3S，其中3是标准差的倍数，用于确定上限控制限。

e.LCL控制图上的下限控制限是过程的可接受下限。

计算公式为：LCL=X̄-3S，其中3是标准差的倍数，用于确定下限控制限。

2.过程能力指数：a.Cp过程能力指数是衡量过程发生误差在可接受范围内的能力。

计算公式为：Cp=(USL-LSL)/(6σ)，其中USL和LSL是规范上限和下限，σ是标准偏差的估计量。

b. Cpk 过程能力指数是衡量过程发生误差在可接受范围内的能力，同时考虑了过程的中心线偏移。

计算公式为：Cpk = min((USL - X̄) /(3σ), (X̄ - LSL) / (3σ))，其中USL和LSL是规范上限和下限，X̄是过程的平均值的估计量，σ是标准偏差的估计量。

c. Cpm 过程能力指数是衡量过程发生误差在可接受范围内的能力，同时考虑了过程的中心线偏移和过程的极差。

计算公式为：Cpm = (USL - LSL) / (6√((ΣR/n)² + σ²))，其中USL和LSL是规范上限和下限，ΣR/n是极差均值的估计量，σ是标准偏差的估计量。

SPC所有公式详细解释及分析

SPC所有公式详细解释及分析SPC（统计过程控制）是一种通过统计方法对产品或过程的变化进行控制的质量管理工具。

它以数据为基础，通过收集、分析和解释数据，帮助确定过程是否稳定、符合规范，并提供改进措施。

在SPC中，有一些重要的公式用于计算和分析数据，下面将介绍其中一些常用的公式及其详细解释和分析。

1. 平均值（Mean）：平均值是统计数据的中心点，通过计算数据的总和除以数据的个数得到。

平均值用于评估过程的中心位置，并对过程的稳定性进行评估。

2. 中位数（Median）：中位数是将数据按照大小顺序排列后，排在中间位置的数值，它能够反映数据的集中趋势。

与平均值相比，中位数对异常值的影响较小，更适用于非正态分布的数据。

3. 标准差（Standard Deviation）：标准差是数据分布离散程度的度量，用于描述数据的波动性。

标准差越大，表示数据越分散；标准差越小，表示数据越集中。

标准差可以帮助确定过程是否稳定，是否存在特殊因素影响。

4. 变异系数（Coefficient of Variation）：变异系数是标准差除以平均值的比值，用于比较不同数据集的离散性。

较小的变异系数表示数据越稳定，较大的变异系数表示数据集的离散性较大。

5. 极差（Range）：极差是数据的最大值和最小值之间的差别，用于评估数据的波动范围。

较大的极差表示数据集的波动性较大，较小的极差表示数据集的波动性较小。

6. 四分位数（Quartiles）：四分位数是将数据按大小顺序排列后，将数据分为四等份的数值。

第一四分位数是中位数的前一半数据的中位数，第二四分位数即中位数，第三四分位数是中位数之后的一半数据的中位数。

四分位数可以帮助了解数据的分布情况。

7. 直方图（Histogram）：直方图使用柱状图形象地展示数据的分布情况。

通过将数据按照一定的区间划分，并统计每个区间内的数据个数，可以直观地了解数据的分布情况。

8. 管理图（Control Chart）：管理图是SPC最重要的工具之一，它通过将数据的统计量（如平均值、标准差等）绘制在图表上，并与控制限进行比较，用于监控过程的稳定性。

计算公式集合

SPC计算公式表二------计算PpK導體電阻計算公式：實測:1M試樣導體電阻值讀取：R t=（R步進盤+R滑盤）×倍率20℃1KM導體電阻換算公式R 20=Rt×254.5/(234.5+t)×1000/L （單位：Ω/KM）注：L為試樣長度/M，R t為試樣實測電阻值/Ω，t為測試時溫度/℃導體電阻率換算公式：ρ=3.14×R t×d2/4L 或者ρ= R t×S×K（單位：Ω•mm2/M）注：L為試樣長度/M，R t為試樣實測電阻值/Ω，d為導體直徑/mm，S為導體截面積，K為測試時溫度/℃導體截面積和絞合外徑：S=d*d*n*0.7854 d：為銅線直徑，n: 為銅線根數；束絞絞合外徑：D=√n *d*1.155 D：為絞合外徑，d：為銅線直徑，n: 為銅線根數；同心絞絞合外徑：D=(1+2n)*d n:為導體自內到外的層數，d：為銅線直徑；最小絕緣厚度係數：0.0254；如：UL要求7mil minimum at any point.即：0.0254*7=0.1778約等於0.18mm；抗漲強度：P=F/A （單位：kgf/mm2） P：為抗漲強度，F：為實測拉力值，A：為截面積；P单位为kgf/mm2(拉断F为kgf,截面积A为mm2)P=F/A*1428.6 （單位：PSI） P：為抗漲強度，F：為實測拉力值，A：為截面積；P单位PSI (拉断力F为磅,截面积A为inch2)1kgf=2.2lbsF；P单位为Mpa（拉断力F为N，截面积S为mm2，1Mpa=144.83183PSI）伸长率=（L2-L1)/L1*100%管状试样截面积A=0.7854×(OD2-D2)OD为管状绝缘体直径(单位mm)；D为导体直径,单位mm.(绞式导体可采公式D=1.155×√N×d进行计算)；A单位为mm2,換算成inch2则乘以0.00155即。

Spc应用计算公式(超全)

SPC所有公式详细解释及分析SPC统计制程管制计量值管制图： Xbar-R(平均-全距)、Xbar-S(平均-标准差)、X-MR(个别值-移动全距)、EWMA、CUSUM等管制图。

计数值管制图：不良率p、不良数np、良率1-p、缺点数c、单位缺点数u等管制图。

常用分析工具：直方图、柏拉图、散布图、推移图、%GRR...等。

公式解说制程能力指数制程能力分析制程能力研究在于确认这些特性符合规格的程度，以保证制程成品不符规格的不良率在要求的水准之上，作为制程持续改善的依据。

制程能力研究的时机分短期制程能力研究及长期制程能力研究，短期着重在新产品及新制程的试作、初期生产、工程变更或制程设备改变等阶段；长期以量产期间为主。

制程能力指针 Cp 或 Cpk 之值在一产品或制程特性分配为常态且在管制状态下时，可经由常态分配之机率计算，换算为该产品或制程特性的良率或不良率，同时亦可以几 Sigma 来对照。

计数值统计数据的数量表示缺点及不良(Defects VS. Defectives)缺点代表一单位产品不符要求的点数，一单位产品不良可能有一个缺点或多个缺点，此为计点的品质指针。

例如描述一匹布或一铸件的品质，可用每公尺棉布有几个疵点，一铸件表面有几个气孔或砂眼来表达，无尘室中每立方公尺含微粒之个数，一片PCB有几个零件及几个焊点有缺点，一片按键有几个杂质、包风、印刷等缺点，这些都是以计点方式表示一单位产品的特性值。

不良代表一单位产品有不符要求的缺点，可能有一个或一个以上，此将产品分类为好与坏、良与不良及合格与不合格等所谓的通过－不通过(Go-NoGo)的衡量方式称为计件的品质指针。

例如单位产品必须以二分法来判定品质，不良的单位产品必须报废或重修，这是以计件方式来表示一单位产品的特值。

每单位缺点数及每百万机会缺点数(DPU VS. DPMO)一单位产品或制程的复杂程度与其发生缺点的机会有直接的关系，越复杂容易出现缺点；反之越简单越不容易出现缺点。

SPC计算公式和判定准则

SPC计算公式和判定准则SPC（Statistical Process Control，统计过程控制）是一种通过统计方法对过程进行监控和控制来确保产品质量的方法。

SPC包含了一系列的计算公式和判定准则，用于对过程数据进行分析和判断。

本文将介绍SPC的常用计算公式和判定准则。

一、计算公式1. 平均值（X－bar）和范围（R）控制图的计算公式：平均值控制图：X-bar = (X1 + X2 + ... +Xn)/n范围控制图：R = Xmax - Xmin2.方差（S）控制图的计算公式：方差控制图：S = √((∑(xi - x̄)²)/(n-1))其中，xi为单个数据点，x̄为平均数，n为样本个数。

3.标准差（σ）控制图的计算公式：标准差控制图：σ = √((∑(xi - x̄)²)/n)其中，xi为单个数据点，x̄为平均数，n为样本个数。

4. 标准分数（Z-score）的计算公式：标准分数：Z=(X-μ)/σ其中，X为观测值，μ为总体平均值，σ为总体标准差。

5.概率（P）的计算公式：概率：P=1-Z其中，Z为标准分数。

二、判定准则SPC通过控制图上的控制限来进行判定，一般包括控制线和规范线。

常用的判定准则有以下几种：1.控制线：控制线用于界定过程是否处于统计控制状态。

一般有上限控制线（UCL）和下限控制线（LCL）。

当数据点超过控制线时，表明过程处于非随机状态，可能存在特殊原因。

2.规范线：规范线用于界定过程是否处于规范状态。

一般有上限规范线（USL）和下限规范线（LSL）。

当数据点超过规范线时，表明产品或过程不符合规格要求。

3.判定准则：SPC根据运行趋势和控制限来进行判定，常见判定准则包括：-单点超出控制限：当单个数据点超出控制限时，可能存在特殊原因，需要进行调查和纠正。

-一组连续点趋势逐渐上升或下降：当连续的数据点呈增加或减少的趋势时，表明过程可能不稳定，需要进行调查和纠正。

SPC计算公式及参数

1)計量值管制圖(X-R﹑X-Rm)的計算公式﹕
類別
-R
X-Rm
平均值（個別值）
管制圖
【（X）Leabharlann 制圖】管制上限管制中心線
管制下限
全距（移動全距）
管制圖
【R（Rm）管制圖】
管制上限
D4*
管制中心線
管制下限
D3*
2)計量值管制圖之常數對照表﹕
樣本數值（n）
A2
D3
D4
E2
2
1.880
0
3.267
1.128
0.184
1.816
2.970
1.010
10
0.308
0.223
1.777
3.078
0.975
16
0.212
0.363
1.637
3.532
0.849
註：X-Rm管制圖查計量值管制圖之常數對照表時，查n＝2之數值。
3)計數值管制圖的計算公式﹕
類別
nP
P
C
U
管制
上限
管制
中心線
管制
下限
A平均值﹕ ＝（X1＋X2＋…＋Xn）/n;
2.660
3
1.023
0
2.574
1.693
1.772
4
0.729
0
2.282
2.059
1.457
5
0.577
0
2.114
2.326
1.290
6
0.483
0
2.004
2.534
1.184
7
0.419
0.076
1.924
2.704

SPC计算公式和判定准则

SPC计算公式和判定准则SPC（Statistical Process Control，统计过程控制）是一种用于监测和控制过程稳定性的方法，通过对过程进行统计分析和监测，可以及时发现过程中的变异，从而采取相应的控制措施，提高过程的稳定性和可控性。

本文将介绍SPC的计算公式和判定准则，以帮助读者了解如何应用SPC进行过程监控和控制。

1. SPC计算公式SPC计算公式是用于计算各种统计指标和控制图的数学公式，下面是常用的SPC计算公式。

1.1 均值（Mean）均值是一组数据的平均值，用于表示过程的中心位置。

计算均值的公式如下：均值公式均值公式其中，mu 表示均值，n 表示数据的数量，x_i 表示第i 个数据。

1.2 极差（Range）极差是一组数据的最大值和最小值之差，用于表示过程的变异程度。

计算极差的公式如下：极差公式极差公式其中，R 表示极差，x_{\text{max}} 表示数据的最大值，x_{\text{min}} 表示数据的最小值。

1.3 标准偏差（Standard Deviation）标准偏差是一组数据的离均差平方和的平均值的平方根，用于表示过程的稳定性。

计算标准偏差的公式如下：标准偏差公式标准偏差公式其中，sigma 表示标准偏差，n 表示数据的数量，x_i 表示第i 个数据，\bar{x} 表示数据的均值。

2. SPC判定准则SPC判定准则用于判断一个过程是否处于稳定状态，常用的判定准则有以下几种。

2.1 均值控制图（Mean Control Chart）均值控制图用于监测过程均值是否稳定。

常用的均值控制图有Xbar-R 控制图和 Xbar-S 控制图。

•Xbar-R 控制图：对应的是过程均值和极差的统计指标。

当连续 n 个点全部落在中心线（均值线）的上方或下方时，表示过程中有特殊原因的变异，需要采取相应措施进行调整。

•Xbar-S 控制图：对应的是过程均值和标准偏差的统计指标。

当连续 n 个点全部落在中心线（均值线）的上方或下方时，表示过程中有特殊原因的变异，需要采取相应措施进行调整。

SPC计算公式和判定准则

SPC计算公式和判定准则
PPT文档演模板
2020/10/31
SPC计算公式和判定准则
常用统计量
1. Mean:(平均值) 2. Max:(最大值) 3. Min:(最小值) 4. Range:(Max－ Min最大跨距) 5. StdDev标准差 6. Cp:(过程能力指数) 7. Cr:(过程能力比值 ) 8. k:(偏移系数 ) 9. Cpu:(上限过程能力指数 ) 10. Cpl:(下限过程能力指数 ) 11. Cpk:(过程能力指数 ) 12. Cpm:(目标能力指数) 13. Zu(Cap) :(规格上限SIGMA水平) 14. Zl(Cap) :(规格下限SIGMA水平) 15. Fpu(Cap): (超出规格上限机率)
•CP=(40.5-39.5)/(6*0.4)=1/2.4=0.42
•7、Cr:(过程能力比值 ) •例:产品规格为(40±0.5),产品标准差为0.4,试计算Cr
•Cr=(6*0.4)/(40.5-39.5)=2.4
PPT文档演模板
SPC计算公式和判定准则
计算公式
• 8、k:(偏移系数 )
•评价产品检验结果偏离规格中心程度的质量指标!
•例:产品规格为(40±0.5),产品均值为40.2,产品标准差为0.4试计算Cpk; •Cpk =Min(0.25,0.58)=0.25 •或Cpk =0.42*(1-0.4)=0.25
• 12、Cpm:(目标能力指数)
•例:产品规格为(40±0.5),目标值为40.2,产品均值为40.2,产品标准差为0.4试计算 Cpm;
PPT文档演模板
SPC计算公式和判定准则
演讲完毕，谢谢听讲!
再见，see you again

【SPC控制图计算公式】 SPC控制图的计算公式有哪些？

SPC控制图的计算公式有哪些？导语：SPC控制图是对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图。

问世数十年来，SPC控制图在众多现代化工厂中得到了普遍应用，通过其计算公式，凭借其强大的分析功能，为工厂带来丰厚的实时收益。

控制图对生产过程的关键质量特性值进行测定、记录、评估并监测过程是否处于控制状态的一种图形方法。

根据假设检验的原理构造一种图，用于监测生产过程是否处于控制状态。

它是统计质量管理的一种重要手段和工具。

那么，SPC控制图的计算公式有哪些？下面我们就详细介绍：图示：SPC控制图的计算公式有哪些？常规休哈特控制图包括计量控制图四种和计数控制图四种计量SPC控制图四种：均值—极差控制图(Xbar—R)、均值—标准差控制图(Xbar—Rs)、中位数—极差控制图(Xmed—R，也有写成X-MR的)、单值—移动极差控制图(x—Rs)；计数SPC控制图四种：不合格品率控制图(P)、不合格品数控制图(Pn)、缺陷数控制图(C)、单位缺陷数控制图(U)。

1．Xbar-R控制图是最常用的基本SPC控制图。

它适用于各种计量值(适用样品数小于10以下的抽样分析）。

Xbar控制图主要用于观察分布的均值变化；R控制图用于观察分布的分散情况或变异度的变化，而Xbar—R控制图则将两者联合运用，以观察分布的变化。

2．Xbar—S控制图(适用样品数大于10以下的抽样分析）。

与Xbar—R控制图相似，只是用标准差图(s图)代替极差图(R图)。

极差计算简便，故R图得到广泛应用，但当样本容量较大时，应用极差估计总体标准差的效率降低，需要用s图来代替R图。

3．Xmed—R控制图与Xbar—R控制图相比，只是用中位数代替均值图。

由于中位数的计算比均值简单，所以多用于需在现场把测定数据直接记入控制图的场合。

4．x—Rs控制图多用于：对每一个产品都进行检验，采用自动化检查和测量的场合；取样费时、检验昂贵的场合；样品均匀，多抽样也无太大意义的场合。

SPC控制图计算公式

控制图有关参数的计算步骤及公式控制图名称步骤计算公式备注(1）计算各子组平均值(2)计算各子组极差：第i组平均值MAX［］：第i组中最大值MIN[］：第i组中最小值（1)计算各子组平均值（2)计算各子组极差：第i组平均值：第i组标准差(）(1)计算各子组中位数（2）计算各子组极差（n为3或5) ：按大小排列的第i组数据中第个位置上的数（）计算移动极差i=2，3，……knp控制图计算总不合格品率：第i组的不合格品数P控制图计算各子组不合格品率：第i组的子组容量c控制图计算平均不合格数：第i组的不合格数u控制图计算各子组的单位不合格数：第i组的子组容量:第i组的不合格数控制图中控制限的计算控制图名称中心线（CL ）上、下控制限（UCL 与LCL ）备注CL==UCL=LCL=①当LCL 为负值时,取0为自然下限 ②，,,，,，查控制图系数表RCL==UCL= LCL=CL==UCL= LCL=sCL==UCL= LCL=CL==UCL= LCL=RCL==UCL= LCL=(）xCL== UCL=LCL=CL==UCL=3.267 LCL=0 P 图CL=UCL=LCL=np 图 CL=nUCL= LCL= c 图 CL==UCL=LCL= u 图CL=UCL=LCL=。

SPC计算公式跟判定准则

SPC计算公式跟判定准则SPC（Statistical Process Control，统计过程控制）是一种用统计学方法来监控和控制工业过程的方法。

它基于对过程进行统计分析，以确定该过程是否稳定，并且是否产生了超出规定范围的偏差。

SPC可以帮助企业实时监控过程，及时发现和纠正偏差，从而提高产品质量和生产效率。

在SPC中，有两个重要的概念：过程的中心线（Center Line，CL）和过程的控制限（Control Limits，CLs）。

中心线代表过程的平均水平，通过对样本数据进行测量和计算得出。

控制限则是在中心线周围设定的上下限，用于判断过程是否处于统计控制之中。

1.过程平均值计算公式：过程平均值（X̄）= (x1 + x2 + x3 + ... + xn) / n其中，x1、x2、x3...xn表示各个样本数据的值，n表示样本的数量。

2.样本标准差计算公式：样本标准差（S）= sqrt(((x1 - X̄)^2 + (x2 - X̄)^2 + (x3 -X̄)^2 + ... + (xn - X̄)^2) / (n-1))其中，sqrt表示平方根。

判定准则：SPC的判定准则主要是基于正态分布的特性，对数据进行判断和控制。

常见的判定准则包括：1.样本数据是否处于过程控制限内：如果样本数据的值都处于过程的控制限范围内，表示过程处于统计控制之中。

2.过程是否稳定：通过监控过程的均值和标准差的变化，判断过程是否稳定。

如果均值和标准差变化较小，则表示过程稳定。

3.是否存在特殊因素：当样本数据出现连续的、显著的趋势变化或者超出控制限，可能表示过程受到了特殊因素的影响，需要进行进一步的调查和改进。

4.是否存在异常点：如果样本数据中存在偏离正态分布的异常值，可能表示过程存在异常情况，需要进行分析和处理。

总结：SPC通过计算和分析过程的平均值和标准差，来判断过程是否处于统计控制之中，并识别可能存在的问题。

通过对过程进行持续监控和改进，可以提高产品的质量和生产的效率。

SPC公式

附件B：SPC公式P图p̅= 不合格品总数检验单元总数n = 每一次检验单元的总数UCL P= P̅+3√p̅ (1−p̅)n LCL p= p̅–3√p̅ (1−p̅ )n使用p图时，每次检验的样本量（n）固定或变化均可用。

当n变化时，UCL p 和LCL p都需要重新计算。

LCL p必须大于或等于0，不可小于0。

np 图n p̅=不合格品总数检验单元总数n = 每一次检验单元的总数UCL np= n p̅+3√np̅ (1−p̅)UCL np= n p̅–3√np̅ (1−p̅)使用np图时，每次检验的样本量（n）必须是固定才可用。

当n变化时，UCL np 和LCL np都要重新计算。

LCL np必须大于或等于0，不可小于0。

C图c̅= 缺陷总数检验单元总数UCL c= c̅+3√c̅LCL c= c̅－3√c̅使用c图时，每次的检验单元数量必须是固定才可用。

LCL c必须大于或等于0，不可小于0。

u图u̅= 缺陷总数检验单元总数n = 每一次检验单元的总数UCL u= u̅+√u̅/n LCL u= u̅－√u̅/n使用u图时，每次的检验单元数量（n）是变动的。

当n发生变化时，UCL u和LCL u必须重新计算。

LCL u必须大于或等于0，不可小于0。

均值（X-bar）控制图X̅= 子组样本均值UCL x= X̿+ A2﹡R̅LCL x= X̿ - A2﹡R̅X̿ = 所有子组均值的总和子组总数UCL X= x̿ + A3﹡s̅LCL X= X̿ - A3﹡S̅极差（R）控制图R = 子组样本极差R̅ = 所有子组极差的总和子组总数UCL R = D4﹡R̅LCL R = D3﹡R̅标准差（S）控制图S = 子组样本标准差s̅= 所有子组标准差的总和子组总和UCL S = B4﹡s̅LCL s = B3﹡s̅Xbar & R, Xbar & S图计算因子过程能力/过程性能指数Cp/Pp Pc/PrCp/Pp= 工程容忍度自然容忍度Pc/Pr=自然容忍度工程容忍度Cp= USL−LSL 6σcalcPc=6σest USL−LSLPp=USL−LSL 6σcalcPr=6σcalcUSL−LSLσest = R̅/d 2 σcalc =√∑(X−X ̅)2nCpmσCpm =√∑(X−Nom)n−1Cpm=USL−LSL 6∗σCpmCpkZ u =USL−X ̿σestZ L =X ̿−LSL σestCpk =Min （ Z u /3，Z L /3）PpkZ u =USL−X ̿σcalcZ L =X ̿−LSL σcalcPpk=Min （Z u /3，Z L /3）标准值（Tgt ）当 X ̿≥ NOM 时: 当 X ̿ > NOM 时:Tgt= X̿−LSL NOM−LSLTgt =USL−X̿USL−NOM中位数-极差控制图公式X ̃ = 子组样本中位数 X ̃̃ = 所有样本中位数的中位数 UCL x = X ̃ + A 5R ̃ LCL x = X ̃ - A 5R ̃ R = 子组样本极差R̃ = 所有子组样本极差的中位数 UCL R = D 4R ̃ LCL R = D 3R ̃中位数-极差图计算因子三向控制图公式组间均值（X-bar）图̅̅̅̅̅UCL = X̿+ E2MR̅̅̅̅̅LCL = X ̿-E2MR组间移动极差（MR）图̅̅̅̅̅UCL = D4MR̅̅̅̅̅LCL = D3MR组内极差（R）图UCL = D4R̅LCL = D3R̅三向控制图公式计算因子k表示移动极差的子组大小，n表示X测量值的子组大小。

SPC各值计算公式

SPC各值计算公式SPC（统计过程控制）是一种用于监控和改进过程稳定性的方法。

它使用统计分析和控制图来识别过程中的变异性，并采取措施来减少非随机变异。

SPC中使用的一些关键参数和计算公式如下：1.平均值（X̄）：平均值是一组数据的总和除以数据个数。

它用于衡量过程的中心位置。

平均值的计算公式如下：X̄=(X1+X2+X3+...+Xn)/n2.极差（R）：极差是一组数据中最大值和最小值之间的差异。

它用于衡量过程的不稳定性。

极差的计算公式如下：R = Xmax - Xmin3.标准差（S）：标准差是一组数据与其平均值之间的离散程度。

它用于衡量过程的变异性。

标准差的计算公式如下：S=√[(Σ(Xi-X̄)²)/(n-1)]4.各类控制限：控制限用于判断过程是否处于统计控制之内。

常见的控制限有上限（UCL）和下限（LCL）。

根据数据的分布情况，控制限可以分为以下几种类型：-3σ控制限（常用控制限）：UCL=X̄+3SLCL=X̄-3S-2σ控制限：UCL=X̄+2SLCL=X̄-2S-1σ控制限：UCL=X̄+SLCL=X̄-S-S控制限：UCL=X̄+A2RLCL=X̄-A2RA2为常数，需要查找A2值表。

5.控制图中的数据点标记：控制图中的数据点通常使用特殊的标记，用于表示超出控制限的点。

常见的标记有以下几种：-O：超出3σ控制限-X：超出2σ控制限-*：超出1σ控制限以上是SPC中常用的一些计算公式和参数。

使用这些公式可以计算过程的平均值、极差、标准差以及相关的控制限，从而进行过程的监控和改进。

掌握这些公式可以帮助人们有效地进行SPC的应用和分析。

SPC计算公式

SPC计算公式1. 简介SPC（Statistical Process Control）是一种通过对过程数据进行统计分析来控制和监督生产过程的方法。

SPC计算公式是SPC方法中最为重要的一部分，它能够帮助我们从数据中获取有用的信息，判断过程的稳定性和能力，并采取相应的措施来改善生产过程。

2. SPC计算公式SPC计算公式主要包括均值（平均值）、标准差和过程能力指数。

2.1 均值计算公式均值是一组数据的平均数，它用来表示数据的集中趋势。

均值的计算公式如下：均值= ΣX / n其中，ΣX表示所有数据的总和，n表示数据的个数。

2.2 标准差计算公式标准差是一组数据的离散程度的度量，它用来表示数据的分散程度。

标准差的计算公式如下：标准差= √(Σ(X - 均值)² / n)其中，Σ(X - 均值)²表示所有数据与均值之差的平方和，n表示数据的个数。

2.3 过程能力指数计算公式过程能力指数是用来评估生产过程能否满足指定要求的一个指标。

过程能力指数的计算公式如下：过程能力指数 = (USL - LSL) / (6 * 标准差)其中，USL表示上限规格限，LSL表示下限规格限，标准差表示生产过程的标准差。

3. 使用示例下面通过一个简单的例子来说明SPC计算公式的使用。

假设有一个生产过程需要控制产品的重量，产品的重量应该在10g 到20g之间。

我们从生产过程中随机抽取了10个样本，得到的数据如下：12.3, 11.8, 13.2, 12.7, 11.5, 12.9, 14.1, 10.9, 13.4, 11.7首先，我们计算均值：均值 = (12.3 + 11.8 + 13.2 + 12.7 + 11.5 + 12.9 + 14.1 + 10.9 + 13.4 + 11.7) / 10 = 12.76然后，我们计算标准差：标准差= √((12.3-12.76)² + (11.8-12.76)² + (13.2-12.76)² + (12.7-12.76)² + (11.5-12.76)² + (12.9-12.76)² + (14.1-12.76)² + (10.9-12.76)² + (13.4-12.76)² + (11.7-12.76)² / 10) = 0.81最后，我们计算过程能力指数：假设上限规格限（USL）为20g，下限规格限（LSL）为10g，过程能力指数 = (20 - 10) / (6 * 0.81) = 2.47通过对上述计算公式的运用，我们得到了该生产过程的均值、标准差和过程能力指数，从而能够更好地了解和控制生产过程。

SPC计算公式

SPC常用公式汇总

SPC控制图计算公式

SPC控制图计算公式

SPC控制图计算公式

SPC各值计算公式

SPC所有公式详细解释及分析

计算公式集合

Spc应用计算公式(超全)

SPC计算公式和判定准则

SPC计算公式及参数

SPC计算公式和判定准则

SPC计算公式和判定准则

【SPC控制图 计算公式 】 SPC控制图的计算公式有哪些？

SPC控制图计算公式

SPC计算公式跟判定准则

SPC公式

SPC各值计算公式

SPC计算公式

【SPC控制图计算公式】 SPC控制图的计算公式有哪些？