大学物理第十章波动第3节 波的能量能流密度
合集下载
第三节 波动过程的能量和波强度

A1 A2
平面波在媒质不吸收的情况下, 各处振幅相同。
8
2. 球面波 一个周期内通过两个球面的能量分别为
W1 I1S1T A122u 4π r12 T / 2
W2 I2S2T A222u 4π r22 T / 2
介质不吸收能量
S2
S1
W1 W2
A1r1 A2r2
• r1 r2
dx
Ox
x
说明
(1) 为介质吸收系数,与介质的性质及
波的频率有关。
(2) 波的强度随传播距离按指数衰减。
11
u
I wuTS wu TS
I 1 A2 2u
2
udt
S
写成矢量形式为
I wu
7
三、平面波和球面波的振幅(介质不吸收能量)
1. 平面波
一个周期内通过两个面的能量分别为
W1 I1S1T A122uST / 2
u
W2 I2S2T A222uST / 2
介质不吸收能量 W1 W2
S1 S2
v
y t
A
sin[
(t
x u
)
0 ]
l T1
y
y
T2
(1) 线元的动能
O
x x
Wk
1 2
mv2
1 2
x A2 2
sin
2[(t
x u
)
0
]
在波的传播过程中,由原长△x 变成△l,
形变为△l -△x ,线两端受张力T=T1=T2。 张力做的功等于线元的势能
Wp T (l x)
2
l (x)2 (y)2 x[1 ( y )2 ]1/2 x
5
2. 能量密度w 单位体积介质中波的能量。
大学物理 波的能量能流密度
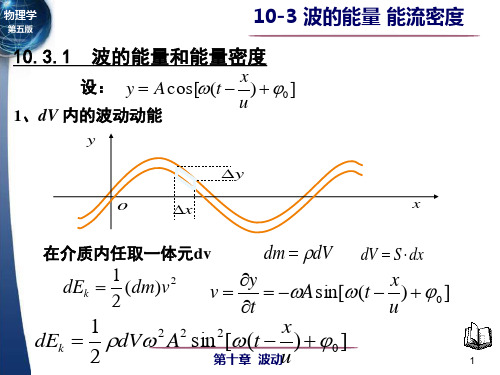
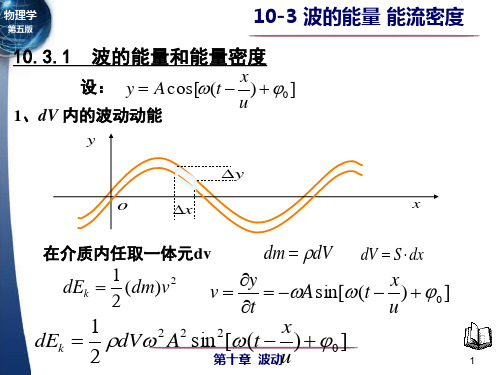
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明:w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说,不断从波源方向的介质中吸收能
量,又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式,且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中,产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
10-3 波的能量能流密度

平均能量密度
一个周期内能量密度的平均值。 一个周期内能量密度的平均值。
第十章 波动
5
物理学
第五版
1010-3 波的能量 能流密度
1 T 1 T x 2 2 2 w = ∫ wdt = ∫0 ρA ω sin ω( t − u )dt T 0 T T 1 x 2 2 2π ρA ω ∫0 sin ( t − )dt = T =π ω T T u T 1 1 x π 2 2 2 2 2π w = ρA ω = ρA ω ∫0 sin ( t − )d( t ) π T u T 2
1 A2ω2 x 2 = YSdx sin [ω(t − )] 2 2 u u
1 x 2 2 2 Wp = ρ A ω sin [ω(t − )]∆V = W k 2 u
第十章 波动
3
物理学
第五版
1010-3 波的能量 能流密度 体积中质点的总能量: 考虑 ∆V 体积中质点的总能量:
2 2 2
x W = Wk +Wp= ρA ω sin ω( t − )∆V u 说明: 说明:
∫
π
0
sin 2 θ ⋅ dθ = π 2
第十章 波动
6
物理学
第五版
1010-3 波的能量 能流密度 二、波的能流和能流密度 波的能流和能流密度
u
∆S
能流: 能流:单位时间内通过介质中某一 截面的能量。 截面的能量。 p = wu∆S 平均能流:在一个周期内能流的平均值。 平均能流:在一个周期内能流的平均值。
物理学
第五版
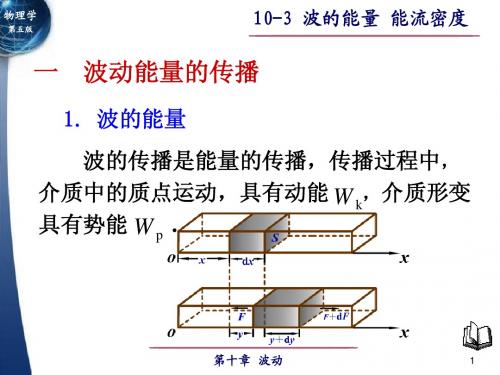
一、波的能量 波的能量
1010-3 波的能量 能流密度
波动是振动状态的传播过程, 波动是振动状态的传播过程,伴随着振动能量 的传播。 的传播。 振动动能 + 形变势能 = 波的能量 以纵波为例: 以纵波为例:
10-3 波的能量能流密度

I LI = lg I0
贝尔( 贝尔(B)
I LI = 10 lg I0
分贝( 分贝( dB )
16
第十章 波动Байду номын сангаас
物理学
第五版
几种声音近似的声强、声强级和响度 几种声音近似的声强、 声源
引起痛觉的声音 摇滚音乐会 交通繁忙的街道 通常的谈话 耳语 树叶的沙沙声 引起听觉的最弱声音
声强W/m2 声强级dB
第五版
1010-3 波的能量 能流密度
讨 论
x d W = ρ d VA ω sin ω (t − ) u
2 2 2
(1)在波动传播的介质中,任一体积元的 )在波动传播的介质中, 动能、势能、 动能、势能、 总机械能均随x, t 作周期性变 且变化是同相位 同相位的 化,且变化是同相位的. 体积元在平衡位置时,动能、 体积元在平衡位置时,动能、势能和总机 械能均最大. 械能均最大 体积元的位移最大时,三者均为零 体积元的位移最大时,三者均为零.
第十章 波动
21
物理学
第五版
1010-3 波的能量 能流密度 试题练习
C
第十章 波动
22
物理学
第五版
1010-3 波的能量 能流密度
B
第十章 波动
23
物理学
第五版
1010-3 波的能量 能流密度
第十章 波动
24
物理学
第五版
1010-3 波的能量 能流密度
位移最大时,能量最小 位移最大时 能量最小
第十章 波动
x x
6
物理学
第五版
1010-3 波的能量 能流密度 体积元的总机械能
x dW = dWk + dWp = ρdVA ω sin ω (t − ) u
3波的能量 能流密度
dW
dWk
dWp
dVA2 2
sin 2 (t
x) u
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
讨 论 (1)介质中,任一体积元的动能、势能、总
机械能均随 x,t 作周期性变化,且变化是同相位的。
dW
2dWp
2dWk
dVA22 sin2 (t
x) u
体积元在平衡位置时,动能、势能和总机械能均 最大。因为 y Acos(t x )余弦为零,正弦达到最大。
P wuS
u
2、平均能流: P wuS
3、能流密度 ( 波的强度 )
通过垂直于波传播方向
S udt
的单位面积的平均能流。
I P w幅的平方、角频率的平方、
波速以及介质密度成正比。
波动
2、能量密度:单位体积介质中的波动能量
w dW A2 2 sin 2 (t x)
dV
u
3、平均能量密度:能量密度在一个周期内
的平均值:
w 1 T wdt 1 2 A2
T0
2
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
二、能流和能流密度
1、能流:单位时间内垂直通过某一面积的能量.
3、波的能量 能流密度
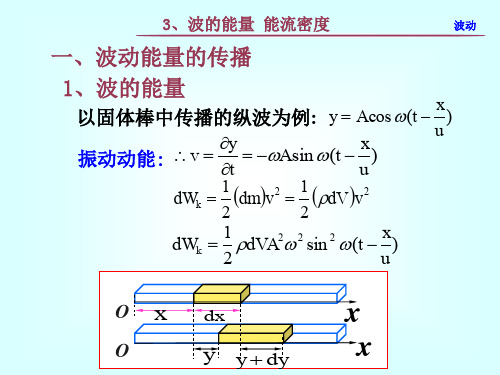
波动
一、波动能量的传播
1、波的能量
以固体棒中传播的纵波为例:
y Acos(t x )
u
振动动能: v y Asin(t x )
t
u
dWk
1 2
dmv 2
1 2
dV
v 2
dWk
大学物理-波的能量 能流密度

2πr2
)
(1
2πr1
)
如果2 1即相干波源S1、S2同位相
则
2π
r1
r2
2π
r1 r2 称为波程差(波走过的路程之差)
水
的 衍
波 的 衍
射
射
19
三 波的干涉
1 波的叠加原理 波传播的独立性:两列波在某区域相遇
后再分开,传播情况与未相遇时相同,互不 干扰.
波的叠加性:在相遇区,任一质点的振 动为二波单独在该点引起的振动的合成.
20
2 波的干涉
频率相同、振动 方向平行、相位相同 或相位差恒定的两列 波相遇时,使某些地 方振动始终加强,而 使另一些地方振动始 终减弱的现象,称为 波的干涉现象.
波是如何传播的? 传播又有什么现象? 这些现象有什么规律?
一 惠更斯原理
介质中波动传播到的各点都可以看作是 发射子波的波源,而在其后的任意时刻,这 些子波的包络就是新的波前.
ut
平
球
面
面
R1
O
R2
波
波
18
二 波的衍射
波在传播过程中遇到障碍物,能绕过障 碍物的边缘,在障碍物的阴影区内继续传播.
波
一 波动能量的传播
1 波Байду номын сангаас能量
波的传播是能量的传播,传播过程中,
介质中的质点运动,具有动能
W
,介质形变
k
具有势能 W p .
1
以棒dW中k 哪哪传12播里里d的m最最v纵大小2 波,?12为例dV分v析2 波y 动A能co量s的(t 传ux播) .
v y Asin(t x )
t
u
振动动能
大学物理-波的能量能流密度

04
电磁波中的能量传播
电磁波概述
电磁波定义
电磁波是由电场和磁场交替变化而产生 的一种波动现象,可以在真空中或物质 中传播。
VS
电磁波分类
根据频率和波长的不同,电磁波可分为无 线电波、红外线、可见光、紫外线、X射线、 γ射线等。
电磁波中电场和磁场能量关系
电场能量
电磁波中电场能量与电场强度的平方成正比,即$W_e = frac{1}{2} epsilon_0 E^2$,其中 $epsilon_0$为真空介电常数,$E$为电场强度。
行波
与驻波不同,行波是向前传播的波形 。在行波中,质点的振动方向与波的 传播方向垂直(横波)或平行(纵波 )。行波传递能量和动量。
02
能量传播与能流密度
能量传播方式
机械波
通过介质中质点的振动和相互作用传播能量,如声波、水波 等。
电磁波
通过电场和磁场的交替变化传播能量,如光波、无线电波等 。
能流密度定义及表达式
磁场能量
电磁波中磁场能量与磁场强度的平方成正比,即$W_m = frac{1}{2} mu_0 H^2$,其中 $mu_0$为真空磁导率,$H$为磁场强度。
总能量
电磁波的总能量等于电场能量和磁场能量之和,即$W = W_e + W_m$。
电磁波中能量传播特点
01
能流密度矢量
电磁波中的能量传播可以用能流密度矢量$vec{S}$来描述 ,其方向垂直于电磁波的传播方向,大小等于单位时间内 通过单位面积的能量。
光学领域应用
光的传播
01
光波的能量能流密度决定了光的亮度、颜色和温度等特性,是
光学研究的基础。
激光技术
Hale Waihona Puke 02激光具有高能量能流密度的特点,被广泛应用于切割、焊接、
10-3 波的能量能流密度

第十章 波动
14
10-3 波的能量 能流密度 例题4 一个点波源位于o点,以o点为中心作两个同心 球面,它们的半径分别为R1和R2,在两个球面上分别取 相等的面积∆S1, ∆S2,则通过它们的平均能流之比为:
P1 P2
第十章 波动
15
10-3 波的能量 能流密度
能流密度 ( 波的强度 )I:
例题1 一平面简谐机械波在弹性介质中传 播,下述各结论哪个正确? 选择( D ) (A)介质质元的振动动能增大时,其弹性势 能减小,总机械能守恒. (B)介质质元的振动动能和弹性势能都作周期 性变化,但两者相位不相同.
(C)介质质元的振动动能和弹性势能的相位在 任一时刻都相同,但两者数值不同.
(D)介质质元在其平衡位置处弹性势能最大.
第十章 波动
17
10-3 波的能量 能流密度
例题6 一平面简谐波,频率为300Hz,波速为340m/s ,在截面积为3.00×10-2m2的管内空气中传播,若在10 秒内通过截面的能量为2.70×10-2J,求:
(1)通过截面的平均能流; (2)波的平均能流密度; (3)波的平均能量密度。
第十章 波动
10-3 波的能量 能流密度
一
波动能量的传播
1 波的能量
波的传播是能量的传播,传播过程中, 介质中的质点运动,具有动能 W k,介质形变 具有势能 W p .
第十章 波动
1
10-3 波的能量 能流密度
以棒中传播的纵波为例分析波动能量的传播.
O O
x
dx
y
y dy
x x
如上图所示,以距棒的左端为x处有一段长为dx的体积元, 若该棒的密度为ρ,截面积为S,则dV=Sdx. 当波传播到该体积元时,若它的左端发生位移y,则右端 位移为y+dy.这表明该体积元不仅发生运动,还产生了 形变,说明它既有动能也有势能。
14
10-3 波的能量 能流密度 例题4 一个点波源位于o点,以o点为中心作两个同心 球面,它们的半径分别为R1和R2,在两个球面上分别取 相等的面积∆S1, ∆S2,则通过它们的平均能流之比为:
P1 P2
第十章 波动
15
10-3 波的能量 能流密度
能流密度 ( 波的强度 )I:
例题1 一平面简谐机械波在弹性介质中传 播,下述各结论哪个正确? 选择( D ) (A)介质质元的振动动能增大时,其弹性势 能减小,总机械能守恒. (B)介质质元的振动动能和弹性势能都作周期 性变化,但两者相位不相同.
(C)介质质元的振动动能和弹性势能的相位在 任一时刻都相同,但两者数值不同.
(D)介质质元在其平衡位置处弹性势能最大.
第十章 波动
17
10-3 波的能量 能流密度
例题6 一平面简谐波,频率为300Hz,波速为340m/s ,在截面积为3.00×10-2m2的管内空气中传播,若在10 秒内通过截面的能量为2.70×10-2J,求:
(1)通过截面的平均能流; (2)波的平均能流密度; (3)波的平均能量密度。
第十章 波动
10-3 波的能量 能流密度
一
波动能量的传播
1 波的能量
波的传播是能量的传播,传播过程中, 介质中的质点运动,具有动能 W k,介质形变 具有势能 W p .
第十章 波动
1
10-3 波的能量 能流密度
以棒中传播的纵波为例分析波动能量的传播.
O O
x
dx
y
y dy
x x
如上图所示,以距棒的左端为x处有一段长为dx的体积元, 若该棒的密度为ρ,截面积为S,则dV=Sdx. 当波传播到该体积元时,若它的左端发生位移y,则右端 位移为y+dy.这表明该体积元不仅发生运动,还产生了 形变,说明它既有动能也有势能。
10-3波的能量 能流密度

1 波能量
以固体棒中传播的纵波为例:
y Acos(t x )
u
dWk
1 2
dmv2
1 2
dV
v2
v y Asin(t x )
t
u
振动动能:
dWk
1 2
dVA2 2 sin 2 (t
x) u
Ox O
dx
x
y y dy
x
理学院 物理系
大学物理
P wuS
u
2 平均能流: P wuS
3 能流密度 ( 波的强度 )I:
通过垂直于波传播方向 的单位面积的平均能流.
S udt
I P wu S
I 1 A2 2u
2
理学院 物理系
w dW A2 2 sin 2 (t x)
dV
u
3 平均能量密度:能量密度在一个周期内
的平均值:
w 1 T wdt 1 2 A2
T0
2
Ox O
dx
x
y y dy
x
理学院 物理系
大学物理
§10-3 波的能量 能流密度
二 能流和能流密度
1 能流:单位时间内垂直通过某一面积的能量.
大学物理
§10-3 波的能量 能流密度
一平面简谐波沿x轴正方向传播,速度为u,已知t'时刻的波 形曲线如图所示,x1处质点位移为零,求: (1)原点O处质点的振动方程 (2)该简谐波的波函数
y
u
O
x1
x
-A
理学院 物理系
大学物理
§10-3 波的能量 能流密度
§10-3 波的能量 能流密度
10-3+波的能量能流密度
W p = Wk
第十章 波动
等于最大值
3
物理学
第五版
1010-3 波的能量 能流密度
注意: 注意: 谐振子 Wk max ⇒ W p min 系统能量守恒 内的能量不守恒 ∆V内的能量不守恒! 内的能量不守恒! 导致差异的原因——势能来源不同 导致差异的原因 势能来源不同 偏离平衡位置dy 谐振子 ——偏离平衡位置 偏离平衡位置 波 ——相邻质点相对位移 相邻质点相对位移dy/dx 相邻质点相对位移 波
P = wuS v u
udt
S
7
物理学
第五版
1010-3 波的能量 能流密度
注意:理想介质不吸收能量, 注意:理想介质不吸收能量,即在传播过 程中能量无损耗, 程中能量无损耗,因此通过不同波面的平均能 流相同, 流相同,即
P = P2 1
对平面波: 对平面波: S1 = S 2
1 2 2 P = ρA ω us 2
w=
1 T ρ A 2 ω 2 sin 2 ω ( t − x )d是常数 2
第十章 波动
5
物理学
第五版
1010-3 波的能量 能流密度
二
能流和能流密度
能流: 能流:单位时间内垂直通过某一面积的 能量. 能量 P = wuS 平均能流: 平均能流:
P = wuS
1 x 2 2 2 = (ρ ∆ V ) A ω sin ω( t − ) 2 u
第十章 波动
2
两者时时相等
物理学
第五版
1010-3 波的能量 能流密度
体积元Δ 的总能量 体积元ΔV的总能量
x W = W k + W p = ρ ∆ VA ω sin ω( t − ) u
波动-3-波的能量

1 w= T
∫
T
0
x 1 2 2 2 ρA ω sin [ω (t − )]dt = u T
∫
π
0
ρ
A2ω 2
•平均能量密度与振幅平方、频率平方和质量密度均 平均能量密度与振幅平方、
成正比。 成正比。
4
1 2 2 = ρA ω 其中 T = π ω 2
∫
π
ω
sin2 θ ⋅ dθ
0
sin 2 θ ⋅ dθ = π 2
研 究 的 类 : 分
20000Hz
* 声的
声 的
*
声的 波的
。为听觉 , 的 ;声 , 声的 。 声的 的 ; 声波的 ,为 。 于听觉 , 是 机械 。
9
• 声压 媒质中有声波传播时的压力 压强 与 媒质中有声波传播时的压力(压强 压强)与
无声波传播时的静压力之差称为声压。 无声波传播时的静压力之差称为声压。 稀疏区声压为负,稠密区声压为正值。 稀疏区声压为负,稠密区声压为正值。 由于疏密的周期性,声压也是周期变化。 由于疏密的周期性,声压也是周期变化。
∆w = u ⋅ ∆t ⋅ ∆S ⋅ w
w 为截面所在位置的能量密度
所以,能流为: 所以,能流为:
∆S
v u
u∆t ∆w x 2 2 2 P= = u ⋅ ∆S ⋅ w = u∆Sρω A sin [ω(t − )] ∆t u
单位:焦耳 秒 单位:焦耳/秒,瓦,J•s-1,W 显然能流是随时间周期性变化的。 显然能流是随时间周期性变化的。但它总为正值
设在弹性媒质中有一平面余弦纵波, 为密度, 设在弹性媒质中有一平面余弦纵波,ρ为密度
y = A cos( ω t + ϕ 0 −
10-3波的能量能流密度

反射波与入射波在同一介质中, 反射波与入射波在同一介质中,传播 的速度是相同的, 的速度是相同的,因而在同一时间内 行进的距离是相等的; 行进的距离是相等的;而折射波与入 射波在不同的介质中传播, 射波在不同的介质中传播,波速是不 同的, 同的,因而在同一时间内行进的距离 是不等的。 是不等的。据此可以解释波的反射与 折射现象。 折射现象。
二、能流与能流密度 1、能流 、 定义: 定义:单位时间内通过介质中某一面积
的能量称为通过该面积的能流
x P=w uS=uSρ A ω sin t − u
2 2 2
平均能流 P =w uS= 1 uSρ A 2ω 2 2、平均能流密度 、平均能流密度——描述能流的空间分布和方向 描述能流的空间分布和方向 定义:通过与波的传播方向垂直的单位面积的平均能流, 定义:通过与波的传播方向垂直的单位面积的平均能流, 称为平均能流密度, 称为平均能流密度,又称为波的强度。 v v 1 2 2v -2 单位: I = w u = ρA ω u 单位:W·m 2
4、用惠更斯原来解释波的反射和折射 、用惠更斯原来解释波的反射 反射和
反射波与入射波在同一介质中, 反射波与入射波在同一介质中,传播 的速度是相同的, 的速度是相同的,因而在同一时间内 行进的距离是相等的; 行进的距离是相等的;而折射波与入 射波在不同的介质中传播, 射波在不同的介质中传播,波速是不 同的, 同的,因而在同一时间内行进的距离 是不等的。 是不等的。据此可以解释波的反射与 折射现象。 折射现象。
Y
能量 极小
X
极小 极大
2、波的能量密度 、 定义: 定义:单位体积介质中的能量就是能量密度
dE x 2 2 2 w= =ρ A ω sin t − dV u
二、能流与能流密度 1、能流 、 定义: 定义:单位时间内通过介质中某一面积
的能量称为通过该面积的能流
x P=w uS=uSρ A ω sin t − u
2 2 2
平均能流 P =w uS= 1 uSρ A 2ω 2 2、平均能流密度 、平均能流密度——描述能流的空间分布和方向 描述能流的空间分布和方向 定义:通过与波的传播方向垂直的单位面积的平均能流, 定义:通过与波的传播方向垂直的单位面积的平均能流, 称为平均能流密度, 称为平均能流密度,又称为波的强度。 v v 1 2 2v -2 单位: I = w u = ρA ω u 单位:W·m 2
4、用惠更斯原来解释波的反射和折射 、用惠更斯原来解释波的反射 反射和
反射波与入射波在同一介质中, 反射波与入射波在同一介质中,传播 的速度是相同的, 的速度是相同的,因而在同一时间内 行进的距离是相等的; 行进的距离是相等的;而折射波与入 射波在不同的介质中传播, 射波在不同的介质中传播,波速是不 同的, 同的,因而在同一时间内行进的距离 是不等的。 是不等的。据此可以解释波的反射与 折射现象。 折射现象。
Y
能量 极小
X
极小 极大
2、波的能量密度 、 定义: 定义:单位体积介质中的能量就是能量密度
dE x 2 2 2 w= =ρ A ω sin t − dV u
大学物理- 波的能量能流密度
T
1 P T
0
1 2 2 wSudt wSu A u s 2
第十章 波动
6
物理学
第五版
3、平均能流密度 (又叫波强)I
10-3 波的能量 能流密度
通过垂直于波传播方向的单位面积的平 均能流. P I w u s
1 2 2 I A u 2
可见波强 (瓦/米2)
10-3 波的能量 能流密度
(5)声压:
在声波传播的空间里,某一点在某一瞬时的压强P与没有 声波时的静压强P0之差dP=P- P0,叫做该点该瞬时的声压。
第十章 波动
10
物理学
第五版
10-3 波的能量 能流密度
因空气波为疏密波,故声压可正、可负,其单位为“帕斯 卡”。
可以证明:声压的振幅
( z u
频率低于20Hz的机械波(如地震、火山爆发、陨石落地、 雷暴等发出…) (1)声强: 1 2 2 I A u 指声波的波强,即声波的平均能流密度 2 (2) 声强级:
以人耳刚能听到的声强 则声强级
IL lg
I 0 10 12 w
m 2为标准,
I I (贝尔) 10lg (分贝 dB) I0 I0
1 y 1 x 2 2 2 E p dV G dV A sin (t ) 0 2 x 2 u
第十章 波动
2
2
物理学
第五版
3、dV内的总波动能量
10-3 波的能量 能流密度 x 2 2 2 dE dE k dE p ( dV ) A sin [ (t ) 0 ] u 以上讨论说明:
y
① 在同一体元dV 内, dEk 、 dEp 是同步的。
1 P T
0
1 2 2 wSudt wSu A u s 2
第十章 波动
6
物理学
第五版
3、平均能流密度 (又叫波强)I
10-3 波的能量 能流密度
通过垂直于波传播方向的单位面积的平 均能流. P I w u s
1 2 2 I A u 2
可见波强 (瓦/米2)
10-3 波的能量 能流密度
(5)声压:
在声波传播的空间里,某一点在某一瞬时的压强P与没有 声波时的静压强P0之差dP=P- P0,叫做该点该瞬时的声压。
第十章 波动
10
物理学
第五版
10-3 波的能量 能流密度
因空气波为疏密波,故声压可正、可负,其单位为“帕斯 卡”。
可以证明:声压的振幅
( z u
频率低于20Hz的机械波(如地震、火山爆发、陨石落地、 雷暴等发出…) (1)声强: 1 2 2 I A u 指声波的波强,即声波的平均能流密度 2 (2) 声强级:
以人耳刚能听到的声强 则声强级
IL lg
I 0 10 12 w
m 2为标准,
I I (贝尔) 10lg (分贝 dB) I0 I0
1 y 1 x 2 2 2 E p dV G dV A sin (t ) 0 2 x 2 u
第十章 波动
2
2
物理学
第五版
3、dV内的总波动能量
10-3 波的能量 能流密度 x 2 2 2 dE dE k dE p ( dV ) A sin [ (t ) 0 ] u 以上讨论说明:
y
① 在同一体元dV 内, dEk 、 dEp 是同步的。
波的能量能流密度

1.波动的动能
以固体棒中传播的纵波为例分析波动能量的传播.
O O
波函数
x
dx
x
y dy
y
x
x y x y A cos ( t ) v A si n ( t ) t u u
•质元的动能
1 1 2 dWk dm v dV v 2 2 2
1 x 2 2 2 dWk dVA si n ( t ) 2 u
① 任一时刻介质元的动能等于势能,且相位相同,与振动系 统的动能与势能总有π/2相位差不同。 ② 振动系统的机械能守恒,而波动过程中,能量不守恒。波 动过程中,沿波的传播方向,介质元不断地通过振动由后面的 质元获得能量,又不断地把能量传播给前面的质元,波是能量 传递的一种形式。 ③ 在平衡位置时质元具有最大动能和势能,在最大振幅处动 能和势能为零。在回到平衡位置时从相邻质元吸收能量,离开 时放出能量。
1 x 2 2 2 dWk dWp dVA si n ( t ) 2 u 表明:质元的总能量随时间作周期性变 3.波动的能量 化,时而达到最大值,时而为零 x dW dWk dWp dVA2 2 si n2 ( t ) u 4.结论 意味着:在由波传播的细棒中有能量在传播
2.波动的势能
弹性势能 O
1 2 dWP k dy 2
F l E S l
F
弹性模量
x
dx
O
y y dy
u E
x x
ES l l
1 1 dy 2 2 dWP k dy ESdx( ) 2 2 dx
SE k dx
1 dy 2 y A si n ( t x ) 2 u dV ( ) x u u 2 dx 1 x 2 2 2 dVA si n ( t ) 2 u
10-3 波的能量能流密度

波传播速度 u 与介质性质有关 (a)纵波与弹性介质的体积变化有关, (a)纵波与弹性介质的体积变化有关,而 纵波与弹性介质的体积变化有关 液体,气体只有体变弹性, 液体,气体只有体变弹性,故气体和液体只 能传播与体积变化有关的纵波。 能传播与体积变化有关的纵波。
u= k
ρ
(纵波) 纵波)
ρ 式中k为体积模量, 为介质密度。 式中k为体积模量, 为介质密度。
设体积为V,压强为P 设体积为V,压强为P V,压强为 的液体或气体, 的液体或气体,受外力压缩 V →V′ ∆V →V′ −V , P + ∆P 压强增加量P ∆ ∆V ∆V P 有关系式 ∆P = −k P V′ V ∆P V k 体积模量 k = − ∆V(u = ρ ) P + ∆P V (b)固体中能产生切变 固体中能产生切变、 (b)固体中能产生切变、体变和长度变化 等弹性形变, 等弹性形变,所以固体中既能传播横波又能 传播纵波。 传播纵波。
F E=− s ∆l l
(u =
E
ρ
)
F
s
∆l
l
三、波的能量 1、波动过程是能量传播的过程 、
以棒中传播的简谐纵波为例) (以棒中传播的简谐纵波为例)
1 x 2 2 2 ∴dWk = ρdV • A ω sin ω(t − ) 2 u
当波传播到某质元 dm 时,该质点要振动 1 具有动能 dWk = dmv2 s 2 o x 其中 dm = ρdV x dx y + dy 振动速度 s ∂y x v= = −Aω sin ω(t − ) o ∂t u x
A0 r0 r y= cos ω (t − ) r u
第十章 波动
r1
12
物理学
u= k
ρ
(纵波) 纵波)
ρ 式中k为体积模量, 为介质密度。 式中k为体积模量, 为介质密度。
设体积为V,压强为P 设体积为V,压强为P V,压强为 的液体或气体, 的液体或气体,受外力压缩 V →V′ ∆V →V′ −V , P + ∆P 压强增加量P ∆ ∆V ∆V P 有关系式 ∆P = −k P V′ V ∆P V k 体积模量 k = − ∆V(u = ρ ) P + ∆P V (b)固体中能产生切变 固体中能产生切变、 (b)固体中能产生切变、体变和长度变化 等弹性形变, 等弹性形变,所以固体中既能传播横波又能 传播纵波。 传播纵波。
F E=− s ∆l l
(u =
E
ρ
)
F
s
∆l
l
三、波的能量 1、波动过程是能量传播的过程 、
以棒中传播的简谐纵波为例) (以棒中传播的简谐纵波为例)
1 x 2 2 2 ∴dWk = ρdV • A ω sin ω(t − ) 2 u
当波传播到某质元 dm 时,该质点要振动 1 具有动能 dWk = dmv2 s 2 o x 其中 dm = ρdV x dx y + dy 振动速度 s ∂y x v= = −Aω sin ω(t − ) o ∂t u x
A0 r0 r y= cos ω (t − ) r u
第十章 波动
r1
12
物理学
§10.4 波的能量 平均能流密度

一平面简谐波的频率为 300 Hz。波速为 340 m·s-1,在截面积为 3.0×10-2 m2 的管 内空气中传播,若在10s内通过该面的能量为 2.7×10-2 J。则波强(能流密度)为
(1)9.0×10 –2 w·m-2 ;
(2)2.7×10-3 J·s-1。
结束选择
请在放映状态小下议点链击你接认1为是对的答案
一平面简谐波的频率为 300 Hz。波速为 340 m·s-1,在截面积为 3.0×10-2 m2 的管 内空气中传播,若在10s内通过该面的能量为 2.7×10-2 J。则波强(能流密度)为
(1)9.0×10 –2 w·m-2 ;
(2)2.7×10-3 J·s-1。
结束选择
三、波的反射和透射
若Z1,Z2相差无几,则主要是透射; Ai
平均能流密度 (波的强度 ):
u
通过垂直于波传播方向的单
位面积的平均能流.
I P u 1 A2 2u
S
2
u
S
I 1 A2 2u
2
应用
⑴平面波 若媒质不吸收能量, 显然:
I1S1 I2S2 , S1 S2 , I1 I2
1 2
2 A12V
1 2
2 A22V ,
A1
A2
⑵球面波 若媒质不吸收能量, 显然:
对于“流动着”的能量,要由能量密度和能 流密度两个概念来描述。
一、波的能量分布
以固体中传播的横波为例分析波动能量的传播.
取一微小体元dV: 位移:y Acos (t x )
u
振动速度:
v y Asin (t x )
t
u
体元动能: dEk
1 2
dVv2
1 2
(1)9.0×10 –2 w·m-2 ;
(2)2.7×10-3 J·s-1。
结束选择
请在放映状态小下议点链击你接认1为是对的答案
一平面简谐波的频率为 300 Hz。波速为 340 m·s-1,在截面积为 3.0×10-2 m2 的管 内空气中传播,若在10s内通过该面的能量为 2.7×10-2 J。则波强(能流密度)为
(1)9.0×10 –2 w·m-2 ;
(2)2.7×10-3 J·s-1。
结束选择
三、波的反射和透射
若Z1,Z2相差无几,则主要是透射; Ai
平均能流密度 (波的强度 ):
u
通过垂直于波传播方向的单
位面积的平均能流.
I P u 1 A2 2u
S
2
u
S
I 1 A2 2u
2
应用
⑴平面波 若媒质不吸收能量, 显然:
I1S1 I2S2 , S1 S2 , I1 I2
1 2
2 A12V
1 2
2 A22V ,
A1
A2
⑵球面波 若媒质不吸收能量, 显然:
对于“流动着”的能量,要由能量密度和能 流密度两个概念来描述。
一、波的能量分布
以固体中传播的横波为例分析波动能量的传播.
取一微小体元dV: 位移:y Acos (t x )
u
振动速度:
v y Asin (t x )
t
u
体元动能: dEk
1 2
dVv2
1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 波动
7
物理学
第五版
10-3 波的能量 能流密度
能量密度:单位体积介质中的波动能量 dW x 2 2 2 w A sin (t ) dV u 平均能量密度:能量密度在一个周 期内的平均值 1 T 1 2 2 w wdt A T 0 2 O O
x
dx
y
y dy
P I wu S 1 I A2 2u 2
u — 介质 “特性阻
抗”
第十章 波动
P wuS
u
udt
S
11
物理学
第五版
10-3 波的能量 能流密度
dB 疼痛界限
声
强 级
音乐范围 语音范围听觉界限声Fra bibliotek范围频率
Hz
12
声 阈
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
第十章 波动
x x
8
物理学
第五版
10-3 波的能量 能流密度
1T 1 w w d t 2 A2 适用于各种弹性波 T 0 2
w
2 A2y
u
能量“一堆一 堆”地传播
w A 0
2
x
y 0 处, w wmax , y A 处, w 0 ,
第十章 波动
9
物理学
第五版
10-3 波的能量 能流密度
二
能流和能流密度
波的传播 → 能量传播 → 能流
能流:单位时间内垂直通过某一面积 的能量.
P wu S
平均能流(波的功率):
u
P w uS
udt
第十章 波动
S
10
物理学
第五版
10-3 波的能量 能流密度
能流密度 ( 波的强度 )I: 通过垂直于波传播方向的单位面积 的平均能流.
A0 r0 r y cos (t ) r u
第十章 波动
r1
14
x x
4
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
x dW p dVA si n ( t ) u 体积元的总机械能
2 2 2
x dW dWk dWp dVA sin (t ) u
2 2 2
O O
x
dx
y
y dy
x x
5
第十章 波动
物理学
第五版
物理学
第五版
10-3 波的能量 能流密度
一
波动能量的传播
1 波的能量 波的传播是能量的传播,传播 过程中,介质中的质点由不动到动, 具有动能 W k ,媒质形变具有势能 W p .
第十章 波动
1
物理学
第五版
10-3 波的能量 能流密度
以固体棒中传播的纵波为例分析波动能量 的传播. 1 x 1 2 2 dWk dm v dV v y A cos (t ) u 2 2 y x v A sin (t ) t u 1 x 2 2 2 振动动能 dWk dVA sin (t ) 2 u
O O
x
dx
y
y dy
x x
2
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
1 2 弹性势能 dWp k dy 2 F l E为杨氏模量 根据胡克定理 E S l
ES 整理后得到 F l kl k为劲度系数 l
此处 k SE dx O O
x
dx
y
y dy
1 利用 I u 2 A2 和能量守恒,可以证明, 2
对无吸收媒质,有: 平面波
A 常数
1 球面波 Ar 常 数 , A r 1 柱面波 A r 常 数 , A r r ——介质中质点到波源的距离
第十章 波动
13
物理学
第五版
10-3 波的能量 能流密度
例 证明球面波的振幅与离开其波源的 距离成反比,并求球面简谐波的波函数. 证 介质无吸收,通过两个球面的平均 能流相等. w1uS1 w2uS2 1 1 2 2 2 2 2 2 A u 4 π r A u 4 π r 即 1 1 2 2 2 2 A1 r2 s1 r s2 2 A2 r1
x x
3
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
弹性势能 1 1 dy 2 2 dWp k dy ES dx( ) 2 2 dx 1 2 dy 2 u dV ( ) 2 dx 1 x 2 2 2 dVA sin (t ) 2 u
O O
x
dx
y
y dy
讨 论
10-3 波的能量 能流密度
x dW dWk dWp dVA sin ( t ) u
2 2 2
1 x 2 2 2 dW p dVA si n ( t ) 2 u 1 x 2 2 2 dWk dVA sin ( t ) 2 u
(1)在波动传播的介质中,任一体积元的动能、势能、 总机械能均随t作周期性变化,且变化是同相位的。 体积元在平衡位置时,动能、势能和总机械能均最大; 体积元的位移最大时,三者均为零。
第十章 波动
6
物理学
第五版
10-3 波的能量 能流密度
振动系统: Ek Ep ,Ek Ep const. 系统与外界无能量交换。 dWk dWp ,dWk dWp const. 波动体积元: x 2 2 2 dWk dW p dVA si n ( t ) u 每个质元都与周围媒质交换能量。 (2)在平面简谐波中,同一体积元每时每刻都具 有相同的动能和势能,每一体积元都在不断地接 收和放出能量因此任一体积元的机械能不守恒。 这是参与波动的体积元不同于孤立振动系统的一 个重要特点。波动是能量传递的一种方式。
7
物理学
第五版
10-3 波的能量 能流密度
能量密度:单位体积介质中的波动能量 dW x 2 2 2 w A sin (t ) dV u 平均能量密度:能量密度在一个周 期内的平均值 1 T 1 2 2 w wdt A T 0 2 O O
x
dx
y
y dy
P I wu S 1 I A2 2u 2
u — 介质 “特性阻
抗”
第十章 波动
P wuS
u
udt
S
11
物理学
第五版
10-3 波的能量 能流密度
dB 疼痛界限
声
强 级
音乐范围 语音范围听觉界限声Fra bibliotek范围频率
Hz
12
声 阈
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
第十章 波动
x x
8
物理学
第五版
10-3 波的能量 能流密度
1T 1 w w d t 2 A2 适用于各种弹性波 T 0 2
w
2 A2y
u
能量“一堆一 堆”地传播
w A 0
2
x
y 0 处, w wmax , y A 处, w 0 ,
第十章 波动
9
物理学
第五版
10-3 波的能量 能流密度
二
能流和能流密度
波的传播 → 能量传播 → 能流
能流:单位时间内垂直通过某一面积 的能量.
P wu S
平均能流(波的功率):
u
P w uS
udt
第十章 波动
S
10
物理学
第五版
10-3 波的能量 能流密度
能流密度 ( 波的强度 )I: 通过垂直于波传播方向的单位面积 的平均能流.
A0 r0 r y cos (t ) r u
第十章 波动
r1
14
x x
4
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
x dW p dVA si n ( t ) u 体积元的总机械能
2 2 2
x dW dWk dWp dVA sin (t ) u
2 2 2
O O
x
dx
y
y dy
x x
5
第十章 波动
物理学
第五版
物理学
第五版
10-3 波的能量 能流密度
一
波动能量的传播
1 波的能量 波的传播是能量的传播,传播 过程中,介质中的质点由不动到动, 具有动能 W k ,媒质形变具有势能 W p .
第十章 波动
1
物理学
第五版
10-3 波的能量 能流密度
以固体棒中传播的纵波为例分析波动能量 的传播. 1 x 1 2 2 dWk dm v dV v y A cos (t ) u 2 2 y x v A sin (t ) t u 1 x 2 2 2 振动动能 dWk dVA sin (t ) 2 u
O O
x
dx
y
y dy
x x
2
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
1 2 弹性势能 dWp k dy 2 F l E为杨氏模量 根据胡克定理 E S l
ES 整理后得到 F l kl k为劲度系数 l
此处 k SE dx O O
x
dx
y
y dy
1 利用 I u 2 A2 和能量守恒,可以证明, 2
对无吸收媒质,有: 平面波
A 常数
1 球面波 Ar 常 数 , A r 1 柱面波 A r 常 数 , A r r ——介质中质点到波源的距离
第十章 波动
13
物理学
第五版
10-3 波的能量 能流密度
例 证明球面波的振幅与离开其波源的 距离成反比,并求球面简谐波的波函数. 证 介质无吸收,通过两个球面的平均 能流相等. w1uS1 w2uS2 1 1 2 2 2 2 2 2 A u 4 π r A u 4 π r 即 1 1 2 2 2 2 A1 r2 s1 r s2 2 A2 r1
x x
3
第十章 波动
物理学
第五版
10-3 波的能量 能流密度
弹性势能 1 1 dy 2 2 dWp k dy ES dx( ) 2 2 dx 1 2 dy 2 u dV ( ) 2 dx 1 x 2 2 2 dVA sin (t ) 2 u
O O
x
dx
y
y dy
讨 论
10-3 波的能量 能流密度
x dW dWk dWp dVA sin ( t ) u
2 2 2
1 x 2 2 2 dW p dVA si n ( t ) 2 u 1 x 2 2 2 dWk dVA sin ( t ) 2 u
(1)在波动传播的介质中,任一体积元的动能、势能、 总机械能均随t作周期性变化,且变化是同相位的。 体积元在平衡位置时,动能、势能和总机械能均最大; 体积元的位移最大时,三者均为零。
第十章 波动
6
物理学
第五版
10-3 波的能量 能流密度
振动系统: Ek Ep ,Ek Ep const. 系统与外界无能量交换。 dWk dWp ,dWk dWp const. 波动体积元: x 2 2 2 dWk dW p dVA si n ( t ) u 每个质元都与周围媒质交换能量。 (2)在平面简谐波中,同一体积元每时每刻都具 有相同的动能和势能,每一体积元都在不断地接 收和放出能量因此任一体积元的机械能不守恒。 这是参与波动的体积元不同于孤立振动系统的一 个重要特点。波动是能量传递的一种方式。
