基本初等函数及其应用.docx
基本初等函数及函数的应用

(2) log0.31.8 , log0.32.7; (3) log3 , log20.8. (4) log67, log76;
小 结 比较大小的方法
(1) 利用函数单调性(同底数) (2) 利用中间值(如:0,1.) (3) 变形后比较
(4) 作差比较
N
对数运算性质如下:
如果a>0,且a≠1,M>0,ห้องสมุดไป่ตู้>0 ,那么:
(1)
log a (M N ) log a M log a N ;
M (2) log log a M log a N ; a N
(3)
log a M n log a M (n R).
n
几个重要公式
n (1) log am b log a b m log c b (2) log a b (换底公式) log c a 1 (3) log a b log b a
是R上的增函数
是R上的减函数
比较两个幂的形式的数大小的方法:
(1) 对于底数相同指数不同的两个幂的大小 比较,可以利用指数函数的单调性来判断.
(2) 对于底数不同指数相同的两个幂的大 小比较,可以利用比商法来判断.
(3) 对于底数不同也指数不同的两个幂的 大小比较,则应通过中间值来判断.常用1和0.
(1)正数的分数指数幂: 当a 0, m, n N , n 1时,规定
a a
n
m n
m
a (2)零的正分数指数幂为零,零
,a
m n
1
n m
的负分数指数幂没有意义
(3)常用公式
第2讲基本初等函数及其应用(原卷版)

第2讲 基本初等函数及其应用目录第一部分:知识强化第二部分:重难点题型突破突破一:指数与对数运算突破二:基本初等函数的图象与性质突破三:函数的零点及其应用角度1:确定函数零点的个数或范围角度2:根据函数零点求参数的取值范围突破四:函数模型应用第三部分:冲刺重难点特训第一部分:知识强化1、函数的零点与方程的根之间的联系(1)函数()y f x =的零点就是方程()0f x =的实数根,也就是函数()y f x =的图象与x 轴的交点的横坐标,即方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点.(2)函数()()()F x f x g x =-的零点就是方程()()f x g x =的根,即函数()y f x =的图象与函数()y g x =的图象交点的横坐标.2、确定函数零点的常用方法:①直接解方程法;②利用零点存在性定理;③数形结合,利用两个函数图象的交点求解.A.B.C.D.()⊆f x[],m n D60C.一杯茶泡好后置于室80C、65C,给出三个茶温(单位:C)关于茶泡好后(0T at b a;③=+<.根据生活常识,从这三个函数模型中选择一个,模拟茶温T(单位:C)关(单位:分钟)的关系,并依此计算该杯茶泡好后到饮用至少需要等待的时间为x f x,则(f1)()000x x >,若关于的解,且 0x ∈cos m x 在区间A .B .C .D .2,00x x -⎧>,则满f .(湖北省鄂西北六校(宜城、枣阳、曾都、襄州、南漳、河口)1%,一年后是.可以计算得到,一年后的“进步”A .9B .10C .11D .12。
第2讲 基本初等函数的性质及应用

答案:(1)-
1 2
3 3
(2)2
二轮·数学
热点二 比较函数值的大小
1 1 【例 2】 (1)(2014 辽宁卷)已知 a= 2 ,b=log2 ,c= log 1 ,则( 3 2 3
1 3
)
(A)a>b>c (B)a>c>b (C)c>a>b (D)c>b>a
解析:(1)a= 2 <20=1,即 0<a<1,
列不等式正确的是( (A)x1>x2 (B)x1<x2 (C)x1+x2<0 (D)x1+x2>0
)
3 x 1 3x 1 解析:(2)由 f(-x)=-2x+sin(-x)+ x =-(2x+sin x+ x )=-f(x), 3 1 3 1
得函数 f(x)是奇函数,
3x 1 设 g(x)=2x+sin x,h(x)= x 3 1
-x -x
在坐标系中,作出函数 f(x)=x-a,g(x)=2 的图象, 当 x>0 时,g(x)=2 <1, x 所以如果存在 x>0,使 2 (x-a)<1,则有-a<1, 即 a>-1,故选 D.
二轮·数学
(2)当 0<x≤
1 x 时,4 <logax,则 a 的取值范围是( 2
当 a<1 时,有 3a-1≥1,所以 a≥
a
2 2 ,所以 ≤a<1. 3 3
当 a≥1 时,有 2 ≥1.所以 a≥0,所以 a≥1. 综上,a≥
2 .故选 C. 3
二轮·数学
4.(2015天津卷,理7)已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函 数.记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( (A)a<b<c (C)c<a<b (B)a<c<b (D)c<b<a
基本初等函数的运算和意义word资料12页

必修1 第二章 基本初等函数(Ⅰ)〖2.1〗指数函数【2.1.1】指数与指数幂的运算(1)根式的概念①如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 次方根用符号n a 表示;当n 是偶数时,正数a 的正的n 次方根用符号n a 表示,负的n 次方根用符号n a -表示;0的n 次方根是0;负数a 没有n 次方根.②式子n a 叫做根式,这里n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:()nn a a =;当n 为奇数时,nn a a =;当n 为偶数时,(0)|| (0) nna a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:(0,,,mn m na a a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质(4)指数函数函数 名称 指数函数定义 函数(0xy a a =>且1)a ≠叫做指数函数图象1a > 01a <<xa y =y(0,1)1y =x a y =y(0,1)1y =定义域 R值域 (0,)+∞过定点 图象过定点(0,1),即当0x =时,1y =.奇偶性 非奇非偶单调性 在R 上是增函数在R 上是减函数函数值的 变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对 图象的影响在第一象限内,a 越大图象越高;在第二象限内,a 越大图象越低.〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)xa x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈④log a NaN =⑤log log (0,)b na a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质(5)对数函数 函数 名称 对数函数定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a > 01a <<定义域 (0,)+∞值域 R过定点 图象过定点(1,0),即当1x =时,0y =.奇偶性 非奇非偶单调性 在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的 变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对图象的 影响在第一象限内,a 越大图象越靠低;在第四象限内,a 越大图象越靠高.x yO(1,0)1x =log a y x =xyO (1,0)1x =log a y x=(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y fx -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域; ②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数.〖2.3〗幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.(2)幂函数的图象 (3)幂函数的性质①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当qpα=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则qpy x =是奇函数,若p 为奇数q 为偶数时,则qpy x =是偶函数,若p 为偶数q 为奇数时,则q py x =是非奇非偶函数.⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上方,若1x >,其图象在直线y x =下方.〖补充知识〗二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便.(3)二次函数图象的性质①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--. ②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2b a -+∞上递增,当2bx a=-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2ba -+∞上递减,当2bx a=-时,2max 4()4ac b f x a -=.③二次函数2()(0)f x ax bx c a =++≠当240b ac ∆=->时,图象与x 轴有两个交点11221212(,0),(,0),||||||M x M x M M x x a ∆=-=. (4)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=- ③判别式:∆ ④端点函数值符号.①k <x 1≤x 2 ⇔ ⎩⎨⎧△=b 2-4ac ≥0af (k )>0-b 2a>kxy1x 2x 0>a O•ab x 2-=0)(>k f kxy1x 2x O•ab x 2-=k<a 0)(<k f②x 1≤x 2<k ⇔ ⎩⎨⎧△=b 2-4ac ≥0af (k )>0-b 2a<kxy1x 2x 0>a O•ab x 2-=k 0)(>k f xy1x 2x O•ab x 2-=k<a 0)(<k f③x 1<k <x 2 ⇔ af (k )<0)(<k f xy1x 2x 0>a O•kxy1x 2x O•k<a 0)(>k f④k 1<x 1≤x 2<k 2⇔ ⎩⎪⎨⎪⎧△=b 2-4ac ≥0a >0f (k 1)>0f (k 2)>0k 1<-b 2a<k 2或⎩⎪⎨⎪⎧△=b 2-4ac ≥0a <0f (k 1)<0f (k 2)<0k 1<-b 2a<k 2x y1x 2x 0>a O ••1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O•<a 1k •2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔ f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合x y1x 2x 0>a O ••1k2k 0)(1>k f 0)(2<k fxy1x 2x O•<a 1k •2k 0)(1>k f 0)(2<k f⑥k 1<x 1<k 2≤p 1<x 2<p 2⇔ ⎩⎪⎨⎪⎧a >0f (k 1)>0f (k 2)<0f (p 1)<0f (p 2)>0或⎩⎪⎨⎪⎧a <0f (k 1)<0f (k 2)>0f (p 1)>0f (p 2)<0此结论可直接由⑤推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上)最小值① 若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a=-③若2bq a->,则()m f q =最大值 ① 若02b x a -≤,则()M f q = ②02b x a->,则()M f p =(Ⅱ)当0a <时(开口向下)最大值①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2bM f a=- ③若2b q a ->,则()M f q =最小值①若02b x a -≤,则()m f q = ②02b x a->,则()m f p =. x>O -=f (p) f (q)()2b f a -x>O-=f (p)f(q)()2b f a -x>O-=f(p) f (q)()2b f a-x >O -=f(p)f (q) ()2b f a -g 0x x>O -=f (p) f(q) ()2b f a -0x g x<O-=f(p)f(q) ()2b f a -x<O -=f (p) f (q) ()2b f a -x<Of (q) ()2bf a-第1讲 §2.1.1 指数与指数幂的运算 ¤学习目标:理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握根式与分数指数幂的互化,掌握有理数指数幂的运算. ¤知识要点: 1. 若n x a =,则x 叫做a 的n 次方根,记为n a ,其中n >1,且n N *∈. n次方根具有如下性质: (1)在实数范围内,正数的奇次方根是一个正数,负数的奇次方根是一个负数;正数的偶次方根是两个绝对值相等、符号相反的数,负数的偶次方根没有意义;零的任何次方根都是零.(2)n 次方根(*1,n n N >∈且)有如下恒等式:()n n a a =;,||,n n a n a a n ⎧=⎨⎩为奇数为偶数;np n mp m a a =,(a ≥0).2. 规定正数的分数指数幂:mn m na a = (0,,,1a m n N n *>∈>且); 11m nm nmna aa-==.¤例题精讲:【例1】求下列各式的值:(1)3n nπ-()(*1,n n N >∈且); (2)2()x y -.【例2】已知221na =+,求33n nn na a a a --++的值.【例3】化简:(1)211511336622(2)(6)(3)a b a b a b -÷-; (2)3322114423()a b ab b a b a⋅(a >0,b >0); (3)243819⨯.【例4】化简与求值:(1)642642++-; (2)11111335572121n n +++⋅⋅⋅++++-++.第2讲 §2.1.2 指数函数及其性质(一)¤学习目标:理解指数函数的概念和意义,能借助计算器或计算机画出具体指数函数的图像,探索并理解指数函数的单调性与特殊点,掌握指数函数的性质.¤知识要点:1. 定义:一般地,函数(0,1)x y a a a =>≠且叫做指数函数(exponential function ),其中x 是自变量,函数的定义域为R .2. 以函数2x y =与1()2x y =的图象为例,观察这一对函数的图象,可总结出如下性质:定义域为R ,值域为(0,)+∞;当0x =时,1y =,即图象过定点(0,1);当01a <<时,在R 上是减函数,当1a >时,在R 上是增函数. ¤例题精讲:【例1】求下列函数的定义域:(1)132xy -=; (2)51()3xy -=; (3)1010010100x x y +=-.【例2】求下列函数的值域:(1)2311()3x y -=; (2)421x x y =++【例3】(05年福建卷.理5文6)函数()x b f x a -=的图象如图,其中a 、b 为常数,则下列结论正确的是( ).A .1,0a b ><B .1,0a b >>C .01,0a b <<>D .01,0a b <<<【例4】已知函数23()(0,1)x f x a a a -=>≠且.(1)求该函数的图象恒过的定点坐标;(2)指出该函数的单调性.第3讲 §2.1.2 指数函数及其性质(二)¤学习目标:在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型.x <O -=f (p) f (q) ()2b f a -0x g x <O -=f (p)f (q) ()2bf a-gx掌握指数函数的性质及应用.¤知识要点:以函数2x y =与1()2x y =的图象为例,得出这以下结论: (1)函数()y f x =的图象与()y f x =-的图象关于y 轴对称.(2)指数函数(0,1)x y a a a =>≠且的图象在第一象限内,图象由下至上,底数由下到大. ¤例题精讲:【例1】按从小到大的顺序排列下列各数:23,20.3,22,20.2.【例2】已知21()21x x f x -=+. (1)讨论()f x 的奇偶性; (2)讨论()f x 的单调性.【例3】求下列函数的单调区间:(1)223x x y a +-=; (2)10.21x y =-.第4讲 §2.2.1 对数与对数运算(一)¤学习目标:理解对数的概念;能够说明对数与指数的关系;掌握对数式与指数式的相互转化,并能运用指对互化关系研究一些问题.¤知识要点:1. 定义:一般地,如果x a N =(0,1)a a >≠,那么数 x 叫做以a 为底 N 的对数(logarithm ).记作log a x N =,其中a 叫做对数的底数,N 叫做真数2. 我们通常将以10为底的对数叫做常用对数(common logarithm ),并把常用对数10log N 简记为lg N在科学技术中常使用以无理数e=2.71828……为底的对数,以e 为底的对数叫自然对数,并把自然对数log e N 简记作ln N3. 根据对数的定义,得到对数与指数间的互化关系:当0,1a a >≠时,log b a N b a N =⇔=.4. 负数与零没有对数;log 10a =, log 1a a = ¤例题精讲:【例1】将下列指数式化为对数式,对数式化为指数式:(1)712128-=; (2)327a =; (3)1100.1-=; (4)12log 325=-; (5)lg0.0013=-; (6)ln100=4.606.【例2】计算下列各式的值:(1)lg0.001; (2)4log 8; (3)ln e . 【例3】求证:(1)log n a a n =; (2)log log log a a a MM N N-=. 【例4】试推导出换底公式:log log log c a c bb a=(0a >,且1a ≠;0c >,且1c ≠;0b >). 第5讲 §2.2.1 对数与对数运算(二)¤学习目标:通过阅读材料,了解对数的发现历史以及对简化运算的作用;理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;理解推导这些运算性质的依据和过程;能较熟练地运用运算性质解决问题.¤知识要点:1. 对数的运算法则:log ()log log a a a M N M N =+g ,log log log aa a MM N N=-,log log n a a M n M =,其中0,1a a >≠且,0,0,M N n R >>∈. 三条法则是有力的解题工具,能化简与求值复杂的对数式.2. 对数的换底公式log log log b a b N N a =. 如果令b =N ,则得到了对数的倒数公式1log log a b b a=. 同样,也可以推导出一些对数恒等式,如log log n n a a N N =,log log m n a a nN N m=,log log log 1a b c b c a =gg 等. ¤例题精讲:【例1】化简与求值:(1)221(lg 2)lg2lg5(lg 2)lg212++-+g ;(2)2log (4747)++-. 【例2】若2510a b ==,则11a b+= . (教材P 83 B 组2题)【例3】 (1)方程lg lg(3)1x x ++=的解x =________;(2)设12,x x 是方程2lg lg 0x a x b ++=的两个根,则12x x g 的值是 .【例4】(1)化简:532111log 7log 7log 7++; (2)设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅=g g g g g ,求实数m 的值.第6讲 §2.2.2 对数函数及其性质(一)¤学习目标:通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;能借助计算器或计算机画出具体对数函数的图像,探索并了解对数函数的单调性与特殊点.¤知识要点:1. 定义:一般地,当a >0且a ≠1时,函数a y=log x 叫做对数函数(logarithmic function). 自变量是x ; 函数的定义域是(0,+∞).2. 由2log y x =与12log y x =的图象,可以归纳出对数函数的性质:定义域为(0,)+∞,值域为R ;当1x =时,0y =,即图象过定点(1,0);当01a <<时,在(0,)+∞上递减,当1a >时,在(0,)+∞上递增.¤例题精讲:【例1】比较大小:(1)0.9log 0.8,0.9log 0.7,0.8log 0.9; (2)3log 2,2log 3,41log 3. 【例2】求下列函数的定义域:(1)2log (35)y x =-;(2)0.5log (4)3y x =-. 【例3】已知函数()log (3)a f x x =+的区间[2,1]--上总有|()|2f x <,求实数a 的取值范围. 【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.第7讲 §2.2.2 对数函数及其性质(二)¤学习目标:掌握对数函数的性质,并能应用对数函数解决实际中的问题. 知道指数函数y =a x 与对数函数y =log a x 互为反函数. (a > 0, a ≠1)¤知识要点:1. 当一个函数是一一映射时, 可以把这个函数的因变量作为一个新函数的自变量, 而把这个函数的自变量新的函数的因变量. 我们称这两个函数为反函数(inverse function ). 互为反函数的两个函数的图象关于直线y x =对称.2. 函数(0,1)x y a a a =>≠与对数函数log (0,1)a y x a a =>≠互为反函数.3. 复合函数(())y f x ϕ=的单调性研究,口诀是“同增异减”,即两个函数同增或同减,复合后结果为增函数;若两个函数一增一减,则复合后结果为减函数. 研究复合函数单调性的具体步骤是:(i )求定义域;(ii )拆分函数;(iii )分别求(),()y f u u x ϕ==的单调性;(iv )按“同增异减”得出复合函数的单调性.¤例题精讲:【例1】讨论函数0.3log (32)y x =-的单调性.【例2】(05年山东卷.文2)下列大小关系正确的是( ). A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<【例3】指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象有何关系?【例4】2019年10月12日,我国成功发射了“神州”六号载人飞船,这标志着中国人民又迈出了具有历史意义的一步.已知火箭的起飞重量M 是箭体(包括搭载的飞行器)的重量m 和燃料重量x 之和.在不考虑空气阻力的条件下,假设火箭的最大速度y 关于x 的函数关系式为:[ln()ln(2)]4ln 2(0)y k m x m k =+-+≠其中. 当燃料重量为(1)e m -吨(e 为自然对数的底数, 2.72e ≈)时,该火箭的最大速度为4(km/s ).(1)求火箭的最大速度(/)y km s 与燃料重量x 吨之间的函数关系式()y f x =;(2)已知该火箭的起飞重量是544吨,是应装载多少吨燃料,才能使该火箭的最大飞行速度达到8km/s ,顺利地把飞船发送到预定的轨道?第8讲 §2.3 幂函数¤学习目标:通过实例,了解幂函数的概念;结合函数y=x, y=x 2, y=x 3, y =1/x ,y=x 1/2 的图像,了解它们的变化情况.知识要点:第 11 页 1. 幂函数的基本形式是y x α=,其中x 是自变量,α是常数. 要求掌握y x =,2y x =,3y x =,1/2y x =,1y x -=这五个常用幂函数的图象.2. 观察出幂函数的共性,总结如下:(1)当0α>时,图象过定点(0,0),(1,1);在(0,)+∞上是增函数.(2)当0α<时,图象过定点(1,1);在(0,)+∞上是减函数;在第一象限内,图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象,在第一象限内,直线1x =的右侧,图象由下至上,指数α由小到大. y 轴和直线1x =之间,图象由上至下,指数α由小到大. ¤例题精讲: 【例1】已知幂函数()y f x =的图象过点(27,3),试讨论其单调性.【例2】已知幂函数6()m y x m Z -=∈与2()m y x m Z -=∈的图象都与x 、y 轴都没有公共点,且2()m y x m Z -=∈的图象关于y 轴对称,求m 的值.【例3】幂函数m y x =与n y x =在第一象限内的图象如图所示,则( ).A .101n m -<<<<B .1,01n m <-<<C .10,1n m -<<>D .1,1n m <->【例4】本市某区大力开展民心工程,近几年来对全区2a m 的老房子进行平改坡(“平改坡”是指在建筑结构许可条件下,将多层住宅平屋面改建成坡屋顶,并对外墙面进行整修粉饰,达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为),且每年平改坡面积的百分比相等. 若改造到面积的一半时,所用时间需10年. 已知到今年为止,平改坡剩余面积为原来的22. (1)求每年平改坡的百分比;(2)问到今年为止,该平改坡工程已进行了多少年?(3)若通过技术创新,至少保留24a m 的老房子开辟新的改造途径. 今后最多还需平改坡多少年? 第9讲 第二章 基本初等函数(Ⅰ) 复习¤学习目标:理解掌握指数函数、对数函数和幂函数的性质、图象及运算性质. 突出联系与转化、分类与讨论、数与形结合等重要的数学思想、能力. 通过对指数函数、对数函数等具体函数的研究,加深对函数概念的理解.¤例题精讲:【例1】若()(0,1)x f x a a a =>≠且,则1212()()()22x x f x f x f ++≤. 【例2】已知函数2()(0,0)1bx f x b a ax =≠>+. (1)判断()f x 的奇偶性; (2)若3211(1),log (4)log 422f a b =-=,求a ,b 的值. 【例3】(01天津卷.19)设a >0, ()x x e a f x a e=+是R 上的偶函数. (1)求a 的值; (2)证明()f x 在(0,)+∞上是增函数.【例4】已知1992年底世界人口达到54.8亿.(1)若人口的平均增长率为1.2%,写出经过t 年后的世界人口数y (亿)与t 的函数解析式;(2)若人口的平均增长率为x %,写出2019年底世界人口数为y (亿)与x 的函数解析式. 如果要使2019年的人口数不超过66.8亿,试求人口的年平均增长率应控制在多少以内?。
基本初等函数-78页word资料

一、指数函数(Exponential Function )(一)分数指数幂的相关运算 1. 计算:(1)14100.7533270.064()8160.018-----+++;(2)1312122)21(])21[(++---÷47.(3))31()3)((656131212132b a b a b a ÷-(4)23221)32()833()8.7()412(-+---(5)36231232⨯⨯ 解:(1) 原式=14313342334221[()]1[(2)][(2)][()]510----+++=5111143121681080-+++=;(2)原式=12131421)22⨯÷1111)22-+=2. 化简:(1)3332332313421428a a b b ab a b a a ⨯⎪⎪⎭⎫ ⎝⎛-÷++-; (2) )].)(1[())((1443333-----++÷-+a a a a a a a a解:(1) 原式=111111333333332112133333[()(2)]224a a b a ba a ab b a --÷⨯++=111211211333333333211211333333(2)(24)242a a b a a b b aa a a ab ba b-++⨯⨯=++-;(2) 原式66441()[(1)()]a a a a a a ---=-÷++-2323441[()()][(1)()]a a a a a a ---=-÷++-2244441111()(1)[(1)()]1()()()a a a a a a a a a a a a a a a a-------=-++÷++-=-+÷-=+3. 已知),0(56>-=a a x则xx xx aa a a ----33的值为_____________ 变式1:已知32121=+-xx ,则=+-2323xx变式2:已知13x x -+=,求下列各式的值: (1)1122x x -+; (2)1122x x -- 4. (1)若31)31(33-=-x x ,则使之成立的x 的取值范围为 (2)若.5)5()25)(5(2+-=--x x x x ,则使之成立的x 的取值范围为 5. 计算下列各式(式中字母都是正数) (1)211511336622(2)(6)(3)a b a b a b -÷-;(2)31884()m n -6. 计算下列各式:(1)()43512525÷-;(2)()0322>⋅a aa a7. 计算下列各式:(1)44y x y x --; (2)2222(2)()a a a a --++÷+(3)111113131313132---+++++-x xx x x x x x8. (2010年珠海质检)某种细胞在培养过程中正常情况下,时刻t (单位:分钟)与细胞数n(单位:个)的部分数据如下:t 最接近于________分钟.1000 9. 若函数2x b y x -=+在(),4(2)a b b +<-上的值域为()2+∞,,则____b a =116先定单调性,由函数图像可得2,4a b =-=-10. 已知集合{}{}2293,20x ax Ax B x x bx -===+-=,且{}2,A B=-I 试求实数,a b 的值及集合A B U11. 若方程42334115x -⋅-=的解为0x ,则0x = .1412. 2=3(1)a +的值. ()3311312222(1)()1a a a a a a a ---+=+=++-. 因为11222a a --=,所以111222()26a a a a --+=-+=,而112122()28a a a a --+=++=,所以1122a a -+=所以()3(1)61a +=-=.13. 251126331428a b b b a a ⎛⎫⎛⎫⎛⎫ ⎪⨯-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭2ab14. 等式y xy y x 2432-=成立的y x ,的条件是15. 已知0132=+-a a ,则_______))(1())((1443333=-++-+----a a a a a a a a 3(先化简,再求值)16. 我们知道,对任意正整数n 和正数a ,若1>a ,则1>n a ;若1<a ,则1<na ,探索并证明:对任意的正有理数nm,n ma 与1之间的关系如何?(反证法)(二)指数函数的概念1. 已知指数函数经过点(3,)π,求(0),(1),(3)f f f -的值 (三)指数函数的图像1. 下图是底数分别为5,6,31,21的指数函数的图像,请具体指出 2. 将函数21()3x y =图象的左移2个单位,再下移1个单位所得函数的解析式 __________3. 画出函数1()2x y =的草图4. 画出函数()|31|x f x =-的图象,并利用图象回答: (1)()f x 的单调区间是什么?(2)k 分别为何值时,方程|3x–1|=k 无解?只有一解?有两解?5. (2)xy a =-在定义域内是减函数,则a 的取值范围是6. 若方程|31x-|=k 有一解,则k =7. 当a ≠0时,函数y =ax +b 和y =b ax 的图象只可能是变式1:当0<a <1,b <-1时,函数y =a x +b 的图象必不经第 象限 变式2:若函数y =a x +b 的图象不经第过第一象限,则实数a,b 的取值范围是___________变式3:函数(01)x y a b a =+<<的图象与x 负半轴相交于一点,则b 的取值范围为变式4:如果函数f (x )=a x +b -1(a >0且a ≠1)的图象经过第一、二、四象限,不经过第三 象限,那么一定有________.① 0<a <1且b >0 ② 0<a <1且0<b <1 ③ a >1且b <0 ④ a >1且b >08. 函数x a x f )1()(2-=在R 上是减函数,则a 的取值范围是 9. 在下列图象中,二次函数y =ax 2+bx +c 与函数y =(ab)x 的图象可能是10. 若直线2y a =与函数11(01)x y a a a =-+>≠且的图像有两个公共点,则实数a 的取值范围是11. 给定函数 ①2x y =, ②1)21(+=x y , ③|2|2x x y -=,④xx y 1+=,其中在区间(0,1)上单调递减的函数 序号是12. 如图所示的是某池塘中的浮萍蔓延的面积(2m )与时间t (月) 的关系:t y a =,有以下叙述: ① 这个指数函数的底数是2; ② 第5个月时,浮萍的面积就会超过230m ; ③ 浮萍从24m 蔓延到212m 需要经过1.5个月; ④ 浮萍每个月增加的面积都相等;⑤ 若浮萍蔓延到22m 、23m 、26m 所经过的 时间分别为1t 、2t 、3t ,则123t t t +=.其中正确的是 .(填写正确命题的序号)1、2、513. 已知函数⎩⎨⎧>+-+≤=+.0,95)23(,0,)(1x a x a x a x f x 在R 上递增,则a 的取值范围21 0 y/m 2t/2 3 8 1 4为_______14. 已知实数a,b 满足等式ba⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛3121,下列五个关系式:① 0<b<a;② a<b<0;③ 0<a<b; ④ b<a<0; ⑤ a=b ,其中不可能成立的关系式有_________个 15. 已知函数221,0,()2,xx f x x x x ⎧->⎪=⎨--⎪⎩≤0.若方程()()=0g x f x m =-有三解,则实数m 的取值范围是 ____________ 16. 已知方程155x a=-有负根,则实数a 的取值范围 17.(2004年江苏高考题)若618.03=a ,[]=∈+∈k Z k k k a 则,,1,___________18. 已知函数()()()f x x a x b =--(其中a b >)的图象如下面右图所示,则函数()x g x a b =+的图象是A .B .C .D .19. 函数y =2|x |的定义域为[a ,b ],值域为[1,16],当a 变动时,函数b=g (a )的图象可以是 _________f20. 已知函数(),(0,1)x f x a b a a =+>≠.(1)若()f x 的图像如图(1)所示,求,a b 的值; (2)若()f x 的图像如图(2)所示,求,a b 的取值范围;(3)在(1)中,若|()|f x m =有且仅有一个实数解,求出m 的范围.(1) (2)21. 若直线2a y =与函数1(0,1)x y a a a =->≠的图像有两个公共点,则a 的取值范围为 _____. (0,1)(1,2)U22. 观察相关的函数图象,对下列命题的真假情况进行判断:① x x =10有实数解;②210x x =有实数解;③ 210x x >在()+∞,0上恒成立; ④ x x -=10有两个相异实数解. 其中真命题的序号为________. 2,3 23. 为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y (毫克)与时间t (小时)成正比;药物释放完毕后,y 与t 的函数关系式为116t ay -⎛⎫= ⎪⎝⎭(a 为常数),如图所示.据图中提供的信息,回答下列问题:(I )从药物释放开始,每立方米空气中的含药量y 时间t (小时)之间的函数关系式为;(II )据测定,当空气中每立方米的含药量降低到0.25毫克 以下时,学生方可进教室,那么, 药物释放开始,至少需 要经过小时后,学生才能回到教室.答案:(I )()()1101000.1 10.116t t t y t -≤≤⎧⎪⎪=⎨⎛⎫>⎪ ⎪⎪⎝⎭⎩(II )0.6解析:(I )由题意和图示,当00.1t ≤≤时,可设y kt =(k 为待定系数),由于点()0,1,1在直线上,10k ∴=;同理,当0.1t >时,可得0.11110.101610aa a -⎛⎫=⇒-=⇒=⎪⎝⎭(II )由题意可得10.254y ≤=,即得110400.1t t ⎧≤⎪⎨⎪≤≤⎩或110111640.1t t -⎧⎛⎫⎪≤ ⎪⎨⎝⎭⎪>⎩1040t ⇒≤≤或0.6t ≥,由题意至少需要经过0.6小时后,学生才能回到教室.23. 已知函数12)(1-=-x x f (1)作出函数)(x f y =的图象;(2)若c b a <<,且)()()(c f b f a f >>,求证:422<+c a . 提示:由题易知:1<a ,对c 进行1≤c 和1>c 的分类. (四)指数函数的性质 1. 求下列函数的定义域(1)1218x y -= (2)y =(3)27)2()(--=xa x f (1,0≠>a a )2. 求下列函数的值域(1)1()[1,2]2x y x =∈-;(2)3x y -=变式: 1()[1,2]2x y x =∈-;21()[1,2]2x y x =∈-;211()[1,2]2x x y x -+=∈-思考1:1(0,1)1x x a y a a a -=>≠+的值域怎么求?思考2:(0,1)x xx x a a y a a a a---=>≠+的定义域、值域、奇偶性和单调性怎么研究?思考3:已知函数22x x y b a +=+(a 、b 是常数且a >0,a ≠1)在区间[-32,0]上有y max =3,y min =52,则a +b =3. 已知函数21()21x x f x -=+(1)判断函数()f x 的奇偶性;(2)求证函数()f x 在(,)x ∈-∞+∞上是增函数拓展:已知函数1()1x xa f x a -=+(01)a a >≠且 (1)判断函数的奇偶性;(2)求函数()f x 的值域;(3)判断并证明函数()f x 的单调性变式:已知函数()13xxe f x ae +=-是定义域上的奇函数.(1)求实数a 的值; (2)求函数()f x 的值域.解:(1)因为()f x 是奇函数,所以()()0f x f x -+=恒成立,即11033x x x xe e ae ae--+++=--, 化简得()()130x e a +-=,解得3a =. (2)由()()113331x x x x e e f x e e ++==--,设11xxe t e +=-,则11x t e t -=+,因为101x t e t -=>+,所以11t t <->或.所以函数()f x 的值域为11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭U .变式:(2009年高考山东卷改编)函数y =e x +e -xe x -e -x的图象大致为________.4. 已知m x f x +-=132)(是奇函数,则常数m 的值为 5. 若指数函数xa y =在[-1,1]上的最大值与最小值的差是1,则底数a =变式1:解不等式222135x x x x a a -+-+>变式2:定义:区间[]()1212,x x x x <的长 为21x x -.已知函数||2x y =的定义域为[],a b ,值域为[]1,2,则区间[],a b 的长度的最大值与最小值的差为_________. 6. 求函数221()3x x y -=的值域及单调区间. 变式1:函数y =0.252122+-x x 的值域是____________ 单调递增区间是______________变式2:函数y =22)21(++-x x 为增函数的区间是7. 设21()2521,x x f x -=-⨯+ 求它的最小值 变式1:若函数()f x 在区间2,42a a⎡⎤--⎣⎦上是奇函数,则a 的值为_____变式1:已知函数y =4x -3·2x +3的值域为[7,43],试确定x 的取值范围.变式2:已知910390x x-⋅+≤,求函数111()4()242x x y -=-⋅+的最大值和最小值.变式3:函数221x x y a a =+-(01)a a >≠且在[]-1,1上最大值为14,则a 的值为________8. 函数2()f x x bx c =++的对称轴为直线1x =-,且(0)3f =,比较()()x x f b f c 与的大小. 变:2()(1)(1),(0)3,()()________x x f x x bx c f x f x f f b f c =-++=-=满足且则与的大小关系为思考题:若0,0a b >>,且a b c +=,求证:(1) 当1r >时,r r r a b c +<;(2)当1r <时,r r r a b c +>9. (2010年黑龙江哈尔滨模拟)若a >1,b <0,且a b +a -b =22,则a b -a-b的值等于________.变式:已知定义域为R 的函数f (x )=-2x +b2x +1+a 是奇函数.(1) 求a ,b 的值;(2) 若对任意的t ∈R,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,求k 的取值范围.10. 已知093109≤+⋅-xx,求函数2)21(4411+-⎪⎭⎫⎝⎛=-x x y 的最大值和最小值.1,211. 已知函数()23x x f x a b =⋅+⋅,其中常数,a b 满足0ab ≠ (1)若0ab >,判断函数()f x 的单调性; (2)若0ab <,求(1)()f x f x +>时x 的取值范围 12. 函数()221()4x xf x -=的值域为 . (]04,(五)指数函数的综合问题1. (2013年梁丰高一数学10月月考)设函数()(01)x x f x ka a a a -=->≠且是定义域为R 的奇函数. (1)求k 的值;(2)若(1)0f >,试判断函数单调性(不需证明),并求不等式0)4()2(22>-++x f x x f 的解集;(3)若[)223(1),()2()1,2x x f g x a a m f x -==+-⋅+∞且在上的最小值为2-,求实数m 的值.2. (苏州2013年期初检测)对于函数()f x ,若在定义域内存在实数x ,满足()()f x f x -=-,则称为“局部奇函数”(I )已知二次函数()()224f x ax x a a R =+-∈,试判断()f x 是否为“局部奇函数”,并说明理由;(II )若()2x f x m =+是定义在区间[]1,1-上的“局部奇函数”,求实数m的取值范围;(III )若()12423x x f x m m +=-⋅+-为定义域为R 上的“局部奇函数”,求实数m 的取值范围;3. 设4()42x x f x =+,若0<a<1,求(1)()(1)f a f a +-的值;(2)求122012()()()201320132013f f f +++L L 的值(倒序相加法) 一般性推广:求121()()()n f f f n n n-+++L L 的值4. 已知定义域为R 的函数121()2x x f x a +-=+是奇函数. (1)求a 的值; (2)求证:()f x 在R 上是增函数;(3)若对任意的t R ∈,不等式2(1)(1)0f mt f mt ++->恒成立,求实数m 的取值范围.5. 定义在D 上的函数()f x ,如果满足:对任意x D ∈,存在常数0M >,都有|()|f x M ≤成立,则称()f x 是D 上的有界函数,其中M 称为函数()f x 的上界.已知函数12()12xxg x -=+x x a x f 421)(+⋅+=.(1)当1a =时,求函数()f x 在(0,)+∞上的值域,并判断函数()f x 在(0,)+∞上是否为有界函数,请说明理由;(2)求函数()g x 在[0,1]上的上界T 的取值范围;(3)若函数()f x 在(,0]-∞上是以3为上界的函数,求实数a 的取值范围. 6. 已知函数x x ax f 22)(+=,且)(x f 为奇函数. (Ⅰ) 求a 的值;(Ⅱ) 定义:若函数0),0(,)(>>+=x a xa x x g ,则函数)(x g 在],0(a 上是减函数,在),[+∞a 是增函数.设2)1()()(+--=x f x f x F ,求函数)(x F 在]1,1[-∈x 上的值域.解:(Ⅰ)函数f (x )的定义域为R , ∵)(x f 为奇函数,∴f (0)=0,∴1+a=0,a=-1 ……………3分(Ⅱ) 2)1()()(+--=x f x f x F =22122221221211++=++----x x x x x x…………3分 设2x t=,则当]1,1[-∈x 时,1[,2]2t ∈, ……………3分∴1122y t t=++∵当1[2t ∈时,函数1122y t t=++单调递减;当2]t ∈时, 函数1122y t t=++单调递增; ……………2分 ∴当2=t 时,y 的最小值为22+ 当21=t 时,417=y ,当2=t 时,27=y ,y 的最大值为417 ……………2分∴函数)(x F 在]1,1[-∈x 上的值域是⎥⎦⎤⎢⎣⎡+417,22 ……………1分7. 定义在D 上的函数()f x ,如果满足:对任意D x ∈,存在常数0M >,使得|()|f x M ≤成立,则称()f x 是D 上的有界函数, 其中M 称为函数()f x 的上界. 已知函数()421xxf x p --=+⋅+, 12()12x xq g x q -⋅=+⋅.(1)当1p =时, 求函数()f x 在(),0-∞上的值域, 并判断函数()f x 在(),0-∞上是否为有界函数, 请说明理由;(2)若(0,2q ∈, 函数()g x 在[]0,1上的上界是()H q , 求()H q 的取值范围;(3)若函数()f x 在[)0,+∞上是以3为上界的有界函数, 求实数p 的取值范围.解:(1)值域为()3+∞,,故不存在常数0M >, 使得|()|f x M ≤对任意(),0x ∈-∞恒成立,所以函数()f x 在(),0-∞上不为有界函数;(2)122()11212x x xq g x q q -⋅==-+⋅+⋅,[][]0,1,21,2x x ∈∴∈,函数在定义域上单调递减则()g x 的值域为121,121q q q q ⎡⎤--⎢⎥++⎣⎦,当(0,2q ∈时, 112112q qq q -->++ 所以1()1qg x q -≤+对于[]0,1x ∈恒成立,则()H q 的取值范围是1,1q q ⎡⎫-+∞⎪⎢+⎣⎭(3)转化为不等式恒成立问题2-313t pt ≤++≤在(]0,1t ∈上恒成立,求得[]5,1p ∈-8. 已知函数()()1131242x x f x x λ-=-+-≤≤. (1)若32λ=时,求函数()f x 的值域;(2)若函数()f x 的最小值是1,求实数λ的值.解:(1)由()211()2()322x x f x λ=-⋅+,设1()2x t =,得()2123,,24g t t t t λ⎡⎤=-⋅+∈⎢⎥⎣⎦. (1)当32λ=时,()2233133(),,2244g t t t t t ⎡⎤=-+=-+∈⎢⎥⎣⎦, 当14t =时,()g t 的最大值为137()416g =;当32t =时,()g t 的最小值为3(2)4g =,所以函数()f x 的值域为337,416⎡⎤⎢⎥⎣⎦. (2)由()()2213,,24g t t t λλ⎡⎤=-+-∈⎢⎥⎣⎦,① 当14λ<时,()min 1491()4162g t g λ==-,令4911162λ-=,得338λ=,不符合;② 当2λ>时,()min (2)74g t g λ==-,令741λ-=,得32λ=,不符合;③ 当124λ≤≤时,()2min ()3g t g λλ==-,令231λ-=,得λ=.综上所述,λ=.9. 已知定义域为[]0,1的函数()f x 同时满足以下三个条件: ① 对任意的x ∈[]0,1,总有()0f x ≥;② (1)1f =;③ 若120,0x x ≥≥,且121x x +≤,则有1212()()()f x x f x f x +≥+成立,则称()f x 为“友谊函数”.(1)若已知()f x 为“友谊函数”,求(0)f 的值;(2)函数()21x g x =-在区间[]0,1上是否为“友谊函数”?给出理由; (3)已知()f x 为“友谊函数”,假设存在[]00,1x ∈,使得[]0()0,1f x ∈且0[()]f f x x =,求证:00()f x x =10. 已知函数)(22)(R a ax f xx ∈-=,将)(x f y =的图象向右平移两个单位,得到)(x g y =的图象.(1)求函数)(x g y =的解析式;(2)若方程a x f =)(在[]1,0上有且仅有一个实根,求a 的取值范围; (3)若函数)(x h y =与)(x g y =的图象关于直线1=y 对称,设)()()(x h x f x F +=,已知a x F 32)(+>对任意的()+∞∈,1x 恒成立,求a 的取值范围.11. 已知函数)(x f 时定义在[]1,1-上的奇函数,当()1,0∈x 时,142)(+=x xx f ,且)1()1(f f =-.(1)求)(x f 在[]1,1-上的解析式; (2)求证:当()1,0∈x 时,.21)(<x f12. 如图,过原点O 的直线与函数y =2x 的图象交于A ,B 两点,过B 作y 轴的垂线交函数y =4x 的图象于点C ,若AC 平行于y 轴,则点A 的坐标是__________.变式:如图,过原点O 的直线与函数y =2x 的图象交于A ,B 两点,过B A ,作y 轴的垂线分别交函数y =4x 的图象于点D C ,. (1)求证:D C O ,,三点共线; (2)当y AD //轴时,求点A 的坐标.13. (1990年高考)设nan n x f x x x x +-++++=)1(321lg )(Λ,其中a 是实数,n 是任意给定的正整数,且2≥n . 如果)(x f 在(]1,∞-∈x 时有意义,则实数a 的取值范围是___________. 21->a14. (2003年复旦大学保送生)设n a a a a ,,,,321Λ是各不相同的正整数,2≥a .求证:21111321<⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛an aaaa a a a Λ. 16.已知12()|31|,()|39|(0),x x f x f x a a x R =-=⋅->∈,且112212(),()()()(),()()f x f x f x f x f x f x f x ≤⎧=⎨>⎩ (1)当a =1时,求()f x 的解析式;(2)在(1)的条件下,若方程0)(=-m x f 有4个不等的实根,求实数m 的范围;(3)当29a ≤<时,设2()()f x f x = 所对应的自变量取值区间的长度为l (闭区间[m ,n ]的长度定义为m n -),试求l 的最大值. 解: (1)当1a =时,2()|39|x f x =-.故⎪⎩⎪⎨⎧<-≥-=0,310,13)(1x x x f x x ⎪⎩⎪⎨⎧<-≥-=2,392,93)(2x x x f xx易知当5log 3=x 时)()(21x f x f = 所以⎪⎪⎩⎪⎪⎨⎧<-<≤-<≤-≥-=0,315log 0,1325log ,392,93)(33x x x x x f x x xx (5)分(2)m x f =)(,可画出=y )(x f 和m y =的图像,由数形结合可知,当)1,0(∈m 时方程0)(=-m x f 有4个不等的实根 ……………9分 (3)当39log x a≥时,因为390x a ⋅-≥,310x ->, 所以由21()()(39)(31)(1)380x x x f x f x a a -=⋅---=--≤,解得38log 1x a ≤-, 从而当3398log log 1x a a ≤≤-时,2()()f x f x = 当390log x a≤<时,因为390x a ⋅-<,310x -≥,所以由21()()(93)(31)10(1)30x x x f x f x a a -=-⋅--=-+≤,解得310log 1x a ≥+, 从而当33109log log 1x a a≤<+时,2()()f x f x = 当0x <时,因为21()()(93)(13)8(1)30x x x f x f x a a -=-⋅--=-->, 从而2()()f x f x = 一定不成立 综上得,当且仅当33108[log ,log ]11x a a ∈+-时,2()()f x f x =, ……………14分 故33381042log log log [(1)]1151l a a a =-=+-+- 从而当2a =时,l 取得最大值为312log 5……………16分 指数的历史n 个相同的因数a 相乘,即43421Λna a a ⋅,记作na ,叫作a 的n 次幂,这时n 叫做指数.本来,幂的指数总是正整数,后来随着数的扩充,指数的概念也不断发展.正整数指数幂,特别是与面积、体积的计算联系紧密的平方和立方的概念,在一些文明古国很早就有了.我国汉代曾有人提出过负整数指数的概念,可惜未曾流传开来.15世纪末,法国数学家休凯引入了零指数概念.17世纪英国的瓦利士在他的《无穷小》算术中提出了负指数,他写道:“平方指数倒数的数列111,,,149L 的指数是-2,立方指数倒数的数列Λ,271,81,11的指数是-3,两项逐项相乘,就有了‘五次幂倒数’的数列Λ,2431,321,11它的指数显然是(-2)+(-3)=-5.同样,‘平方根倒数’的数列Λ,31,21,11的指数是Λ,21-”这是一个巨大的进步,不过瓦利士没有真正使用21322,2,2---的指数符号.分数指数幂最早在奥力森的《比例算法》中出现,他使用的符号不简洁.现在的分数指数和负指数是牛顿创设的.牛顿在1676年6月13日写信给莱布尼兹说:“因为当代数学家将aaaa aaa aa ,,等写成432,,a a a ,所以我将3,a a 写成2321,a a ;又将Λ,1,1,1aaaaa a 写成123,,,a a a ---L ”.牛顿还首先使用任意实数指数.18世纪以后,人们发现复数bi a +还可用三角式)sin (cos θθi r +即指数式θi re 表示,从而得到了一般复数指数的概念.1679年莱布尼兹写信给荷兰数学家惠更斯讨论方程24=-x x x ,b x z z x =+,c z x z x =+,这是引入变指数的开始.指数概念形成以后,欧拉才把对数建立在指数的逆运算的基础上,这就是现行教科书中广泛采用的方法.补充:指数函数x e 是一个十分重要的函数,高等数学里许多公式都少不了它,我们甚至发现衣服洗干净的程度,复利的计算都离不开它. 二、对数函数(Logarithm Function ) (一)对数的相关运算1. 已知,3log ,2log n m a a ==则.________2=+n m a2. 若)3(log )1(x x --有意义,则实数x 的取值范围是_________.3. 若03lg 2)(lg 2=--x x ,则.________=x4. 若0)](log [log log 2221=x ,则实数._________=x5. 设方程lg(42)lg 2lg 3x x x +=+的解是_____6. (08浙大自主招生)设,P Q 满足91216log log log ()p q p q ==+,求qp的值 52(二)对数的运算性质1. 计算:()22lg 50lg 2lg 25lg ++=________________2. 计算:()3253ln 125.025log-++e=________________3. 设,,,a b c R +∈且346a b c ==,(1)求证:ba c 2111=-;(2)比较cb a 6,4,3的大小.变式:已知)1,0(53≠>==k k k n m ,且211=+nm ,则=k .4. 已知72p =,75q =,则lg2用,p q 表示为 .pp q+ 4. 已知lg18,lg108m n ==,则lg375_________=5. 任何一个正实数m 的常用对数可以写成如下形式:lg m a b =+,这里[),0,1a Z b ∈∈,这时我们把a 叫lg m 的首数,把b 叫做lg m 的尾数,如果lg x 的首数为n ,2lg x 与1lgx的尾数相等,则此时_______x = 解:21lg -lg3lg 33(,01)x x n b n Z b x==+∈≤<, 所以30,1,2b =,得120,,33b =,故1233=10,10,10n n n x ++6. 对于0a >,1a ≠,下列命题中,正确命题的个数是________. ①若M N =,则log log a a M N =; ②若log log a a M N =,则M N =; ③若22log log a a M N =,则M N =; ④若M N =,则22log log a a M N =7. 给定函数1,4()2(3),4xx f x f x x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪+<⎩,则2(log 3)_____f = 8. 已知函数212log ,0()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,则实数a 的取值范围是______9.已知函数f (x )=a log 2x +b log 3x +2,且f (12010)=4,则f (2010)的值为________10. 在不考虑空气阻力的情况下,火箭的最大速度v m/s 和燃料的质量Mkg ,火箭(除燃料外)的质量m kg 的函数关系是v =2000·ln(1+M /m ).当燃料质量是火箭质量的________倍时,火箭的最大速度可达12 km/s.11. 已知函数22()log 4x f x x=-,若()()2f a x f a x b ++-=对于满足||x ( a ,4 a )的一切x 恒成立,则(a ,b )为___________.(2,1)12.(2013年苏锡常镇四市高三数学二模附加题23题) 已知()1nf n n =+,设[()]n x f n =,1[()]n y f n +=,比较x x 与y y 的大小. 13. 已知2log =y x ,则x y -的取值范围为 .()1-00+4⎡⎫∞⎪⎢⎣⎭U ,, 14. (1)写出对数的换底公式并证明;(2)已知62p =,65q =,试用,p q 表示80log 18.解:(1)对数的换底公式:log log log c a c NN a=,其中01a a >≠且,01c c >≠且,0N >.证明:设log a t N =,则t a N =,两边同时取以c 为底的对数,得log log t c c a N =, 即log log c c t a N =,所以log log c c Nt a=,得证.(2)因为62p =,65q =,所以66log 2,log 5p q ==.()6668066666log 362log 182log 22log 18log 80log 5log 16log 54log 24p q p÷--====+++.15. 已知集合A 是函数()2lg 1y x ax a ⎡⎤=-++-⎣⎦的定义域,B 是不等式311x x +≤的解集.(1)若集合A 中恰有两个正整数解,求实数a 的取值范围; (2)若A B =∅I ,求实数a 的取值范围. 16. 1324lg 293- 1217. 设C a log ,C b log 是方程0132=+-x x 的两根,则Cba log 的值为________.55±18. 若13log 2=a ,15log 3=b ,则_______59=+b a . 7 19. 已知)(log log )(log log 2882m m =,则=m 22log ________. 27 20. 若y x y x y x lg lg 2lg )2lg()lg(++=++-,则yx的值为________. 2 21. 若b a <<<10,比较)1(>n a n 与a b log 的大小.22. 若,3010.02lg ≈估计1002的大小.(参考数据:3.1102.11.0<<) 若4771.03lg ≈,估计10003的大小.(参考数据:3.1102.11.0<<) 23. 已知,10001112.0,10002.11==b a 则._______11=-ba 1 24. 求值:.________)lg(lg 2)lg(lg 2100=+a a 2 25. 换底公式源于对数的概念,所以用好概念,也能解决问题,试着利用定义解决下列问题: (1)证明:1log log =⋅a b b a ;(2)解关于x 的方程:5)2(log )2(log 224=+++x x(3)解关于x 的方程:1)1(log )1(log 3168=+-+x x26. 已知a =3log 2,则54log 12用含有a 的代数式表示为__________. 27. 求值:.______32log 9log 38=⋅28. 方程05lg 7lg )5lg 7(lg 2=⋅+++x x 的两根是βαlg ,lg ,则._______=αβ 29. 当10<<x 时,分别比较以下两组式子的大小: (1))1lg(x -和)1lg(x +; (2))1(log x a -和)1(log x a +30. 若z y x 324243432log log log log log log log log log ==,则._______=++z y x 31. 已知x x f 26log )(=,则.______)8(=f32. 设16log log 8log 4log 4843=⋅⋅m ,则m 的值为_________.33. 已知函数()13log )12a x f x x a =+++-(0,1a a >≠),如果()3log 5f b =(0,1b b >≠),那么13log f b ⎛⎫ ⎪⎝⎭的值是 .(三)对数函数的图像与性质 1. 求下列函数的定义域(1)y =log 2(x 2+2x +5) (2)y =log 31(-x 2+4x +5)(3) y =log a (-x 2-x ) (0<a <1) (4)3)1log(1)(-+=x x f (5)2312log )(--=x x x f(6)4322)1(log )(-=x x f思考1:已知函数)23lg()(2+-=x x x f 的定义域是F, 函数)2lg()1lg()(-+-=x x x g 的定义域是N,确定集合F 、N 的关系?思考2:已知集合P ={x|12≤x ≤3},函数f(x)=log 2(ax 2-2x+2)的定义域为Q.(1)若Q 为实数集R ,求a 的取值范围;(2)若P ∩Q =12,23⎡⎫⎪⎢⎣⎭,P ∪Q =(]2,3-,求实数a 的值.思考3:若函数y =lg(x 2+ax +1)的定义域为R ,实数a 的取值范围为 .变式:已知函数y =lg(x 2+ax +1)的值域为R ,则a 的取值范围是 . 2. 已知函数0),2lg()(>-+=a xax x f (1)求函数)(x f 的定义域;(2)若对任意的[)+∞∈,2x ,恒有0)(>x f ,求实数a 的取值范围.答案:(1)当10≤<a 时,)(x f 的定义域为()+∞,0;当1>a 时,)(x f 的定义域为()()+∞-+--,1111,0a a Y ;(2)()+∞,23. 函数()lg(23)x x f x =-的定义域为 .(,0)-∞ 2. 求下列函数的值域1.(1)]2,1[log )(2∈=x x x f (2)]2,1[log )(∈=x xx f a(3)2log )(22+=x x f (4)y =log 31(-x 2+4x +5)(5)y =log 2(x 2+2x +5) (6)21log )(22+=x x f 2. 已知集合{}20A x x x x =-∈,R ≤,设函数2x f x a -=+()(x A ∈)的值域为B ,若B A ⊆,则实数a 的取值范围是 3.(1)若1x 31log)1x (log 2122-≤+,求函数f(x)= 1423x x +--+的值域. (2)设M ={x |1422log 3log 2x x +≤},求函数()22log 28x xf x =⋅()(log ),x M ∈的最值及其相应的x 的值.(3)函数)2(log log 2x x y x +=的值域是(4)已知f (x )=log 3x +2,x ∈[1,9],则函数y =[f (x )]2+f (x 2)的最大值是________.4. 在函数()1f x gx =的图象上有三点A 、B 、C ,横坐标依次是1,,1(2).m m m m -+>(1)试比较(1)(1)2()f m f m f m -++与的大小; 函数的凹凸性(2)求△ABC 的面积()S g m =的值域. 0⎛⎝,5. 函数1122|log 2||log y x =+ 的值域为___________.3. 对数函数的图像问题1. x y a log =,x y b log =,x y c log =,的图象如图所示,那么a,b,c 的大小关系是_______变式1:已知0)3(log )3(log <-<-=ππn m y ,m,n 为不等于1的正数,则n 、m 、1的关系为 变式2:(10浙江)设函数的集合211()log (),0,,1;1,0,122P f x x a b a b ⎧⎫==++=-=-⎨⎬⎩⎭,平面上点的集合11(,),0,,1;1,0,122Q x y x y ⎧⎫==-=-⎨⎬⎩⎭,则在同一直角坐标系中,P 中函数()f x 的图象恰好..经过Q 中两个点的函数的个数是_____6______(图像平移与变换) 变式3:画出函数图像:ln 1x y e x -=--2. 方程20x x +=的实数根为a , 1.1log x x =的实数根为b ,12log x x =的实数根为c ,则实数,,a b c 的大小关系为_______________3. 已知不等式2log 0x a x -<,当10,2x ⎛⎫∈ ⎪⎝⎭上恒成立,则实数a 的取值范围为______4. 已知函数()lg f x x =, 若0a b <<, ()(),f a f b =则+2a b 的取值范围是________5. 已知031log 31log >>b a ,则,0,1a b ,的大小关系为________________ 6. 0x 是x 的方程)10(log <<=a x a a x 的解,则a x ,1,0这三个数大小关系是_______7. 当x ∈[n ,n +1),(n ∈N )时,f (x )=n -2,则方程f (x )=log 2x 根的个数是________.8. (2010年福建厦门模拟)已知lg a +lg b =0,则函数f (x )=a x与函数g (x )=-log b x 的图象 可能是________.9. 若a >1且0<b <1,则不等式a log b (x -3)>1的解集为________. 10. 若10a b >>>,则下列式子成立的是 . 1、2、5 (1)11()()22a b <; (2)55a b >; (3)2log ()0a b ->; (4)log 2log 2a b > (5)a b b a a b a b >. 11. 已知)1(log )(2+=x x f ,且,)()(xx f x g =)3(),2(),1(g c g b g a ===,则c b a ,,从大到小....的顺序是 .a b c >> 12. 已知函数33()3,()log 2,()log x f x x g x x h x x x =+=+=+的零点依次为,,a b c ,则,,a b c 的大小关系是 .a b c <<13.作出下列函数的图象:(1)log (01)a y x a a =>≠且;(2)log (01)a y x a a =>≠且; (3)2log 1y x =-;(4)12log y x =14. 函数()lg(2)1f x x x =⋅+-的图象与x 轴的交点个数有____个 215. 若函数1log )(2-=ax x f 的图象的对称轴是2=x ,则非零实数a 的值为_______.16. 已知函数⎪⎩⎪⎨⎧>+-≤<=.10,621,100,lg )(x x x x x f 若c b a ,,互不相等,且)()()(c f b f a f ==,则abc 的取值范围是_________. ()12,1017. 已知函数⎪⎩⎪⎨⎧≥-<-=.1,2,1,12)(x x x x f x 若c b a ,,互不相等,且)()()(c f b f a f ==,则c b a 222++的取值范围是_________. ()6,418. 若)1(log )(<<=a a x x f a ,)41(),2(),31(f p f n f m ===,则p n m ,,从小到大的顺序为__________.19. 若函数f (x )=log 2|ax -1|(a >0),当x ≠12时,有f (x )=f (1-x ),则a =________. 20. 4. 单调性1. 求函数)2(log 22x x y +=的单调递增区间;2.求函数122log (- 2)y x x =+的单调递减区间;3. 已知函数)3(log )(22a ax x x f +-=在区间[)∞+,2上是增函数,则实数a 的取值范围是 .4. 已知y =a log (2-ax )在[0,1]上是x 的减函数,则a 的取值范围是_________5. 若定义在区间(-1,0)内的函数)1(log )(2+=x x f a 满足0)(>x f ,则a的取值范围为 6. 若2log 13a<,则实数a 的取值范围是_____________ 7. 设函数()log a f x x =在()-0∞,上单调递增,则(1)(2)f a f +与的大小关系为_______8. 函数log a y x =在区间[)2+∞,上恒有1y >,则实数a 的取值范围是___________变式1:已知函数x x g a log )(=,其中a 为不等于1的正数,若10<<a ,且函数在区间]1,2[--上总有2||≤y ,则a 的取值范围为___________ 变式2:已知函数()lg()(10)x x f x a b a b =->>>. (1)求()f x 的定义域;(2)若()f x 在()1,+∞上递增且恒取正值,求,a b 满足的关系式.9. 已知函数(=log (1)(01)x a f x a a a ->≠), (1)求函数()f x 的定义域;(2)解不等式:()1f x >10. 函数())2(log 2x x f -=的定义域是______;单调减区间是_______;值域是______11. 比较下列数的大小 1.72(lg ),(lg )n n (分类讨论)变式: 1.524log 5,2,log 15的大小顺序从小到大依次为________________ (1)mn 1.0log 11log 1.0++m n )0(>>n m (2) 2)(log x a2log x a )1(a x <<12. 已知函数f (x )在),0[+∞上是减函数,g (x )=-f (|x |),若g (lg x )<g (1),则x 的取值范围是_____变式:已知)(x f 是定义在R 上的偶函数,且在),0[+∞上为增函数,0)31(=f ,则不等式0)(log 81<x f 的解集为13. 已知函数f (x )=log 3x 2+ax +bx,x ∈(0,+∞),,a b R ∈,f (x )同时满足下列三个条件:(1) 在(0,1]上是减函数,(2) 在[1,+∞)上是增函数,(3) f (x )的最小值是1,则=______a b + 14. 已知函数f (x )=lgkx -1x -1(k ∈R 且k >0).若函数f (x )在[10,+∞)上是单调增函数,则实数k 的取值范围为____________15. 若)21(log )(2+-=ax ax x f a 在]23,1[上恒正,则实数a 的取值范围是 .203⎛⎫ ⎪⎝⎭,16. 函数f(x)=(31)4(1)log (1)a a x a x x x -+<⎧⎨≥⎩在R 不是单调函数......,则实数a 的取值范围是 .()11011+73⎛⎫⎡⎫∞ ⎪⎪⎢⎝⎭⎣⎭U U ,,, 17. 已知函数3()log 3mx f x x -=+ (1)判断()f x 的奇偶性并证明;(2)若()f x 的定义域为[],αβ(0βα>>), 判断并证明()f x 在定义域上的单调性;18. 已知()lg f x x =,若()()f a f b =,则______ab = 19. 若12>>>a b a ,试比较b a alog ,abb log ,a b log ,b a log 的大小 20. 设偶函数()b x x f a +=log 在()+∞,0上是单调减函数,则()2-b f 与()1+a f 的大小关系是21. 若10<<a ,函数()()22log 2-⋅-=x x a a a x f ,则使()0<x f 的x 的取值范围____22. 设0≥x ,0≥y ,且212=+y x ,则函数()148log 221++y xy 的最大值为 023. 已知集合{||21|1}A x x =->,集合||log |,[,],1}a B y y x x m n a ==∈>,若R B C A =,且n m -的最小值为12,则a = . 2 24. 已知函数)11(11lg)(<<-+-=x xxx f ,函数)(x g 的图象与函数21--=x y 的图象关于y 轴对称,设)()()(x g x f x F +=. (1)求函数)(x F 的解析式及定义域;(2) 试问在函数)(x F 的图象上是否存在两个不同的点A 和B ,使直线AB 恰好与y 轴垂直?若存在,求出A 和B 的坐标;若不存在,请说明理由. (单调递减)25. 已知函数)1(log )(2+-=x ax x f a ,其中0>a 且1≠a . (1)当21=a 时,求函数)(x f 的值域;(2)当)(x f 在区间⎥⎦⎤⎢⎣⎡23,41上为增函数时,求实数a 的取值范围.[)+∞⎥⎦⎤⎝⎛,231,92Y 26. 已知)1,0(log )(≠>=a a x x f a ,当210x x <<时,试比较)2(21x x f +与2)()(21x f x f +的大小.(写出比较过程).27. 已知函数).32(log )(25.0+-=ax x x f(1)若)(x f 的值域为(]1,-∞-,试求实数a 的值;(2)若)(x f 在区间(]1,-∞-上是增函数,求实数a 的取值范围. 5. 奇偶性1. 函数))(1(log 22R x x x y ∈++=的奇偶性为2. 若函数)2(log )(22a x x x f a ++=是奇函数,则a =3. 设()()lg 101xf x ax =++是偶函数,()42x x bg x -=是奇函数,a b +值为_________4. 已知函数()13log )12a xf x x a =++-(0,1a a >≠),如果()3log 5f b =(0,1b b >≠),那么13log f b ⎛⎫ ⎪⎝⎭的值是 . -35. 设,,a b R ∈且2,a ≠若定义在区间(),b b -内的函数()1lg 12axf x x+=+是奇函数,则a b +的取值范围是 . ⎥⎦⎤⎝⎛--23,2(四)对数函数的综合应用 1、已知函数xxa x f +-=1lg)(, (1)若)(x f 为奇函数,求a 的值;(2)若)(x f 在(-1,5]内有意义,求a 的取值范围; (3)在(2)的条件下,判断并证明)(x f 的单调性. 解:(1)1=a ;(2)5>a(3)当5>a 时,f(x)在定义域上为减函数 由5,01>>+-a xxa ,得f(x)定义域为(-1,a ),令a x x <<<-211 2211211lg 1lg)()(x x a x x a x f x f +--+-=-221111lg x a x x x a -+⋅+-=122111lg x x x a x a ++⋅--= ∵a x x <<<-211 ∴021>->-x a x a 01112>+>+x x ∴11111221>++>--x x ,x a x a ,∴1111221>++⋅--x x x a x a ,∴011lg 1221>++⋅--x x x a x a∴0)()(21>-x f x f ,即)()(21x f x f >∴)(1x f 在(-1,a)为减函数 2、解(Ⅰ)因为()lga x f x a x-=+,由0a xa x ->+,得||||a x a -<<. 所以()f x 的定义域关于原点对称. 又因为()lglg ()a x a xf x f x a x a x+--==-=--+所以函数()f x 是奇函数.(Ⅱ)当0a >时,则()f x 的定义域为(,)a a -,设12a x x a -<<<. 则2121212121()()()()lglg lg ()()a x a x a x a x f x f x a x a x a x a x ---+-=-=+++- 2121221221()lg ()a x x a x x a x x a x x -+-=-+-因为0a >,12x x <,所以2112()()a x x a x x ->- 即2212211212()()0a x x a x x a x x a x x -+->-+->,2121221221()01()a x x a x x a x x a x x -+-<<-+-,所以2121221221()lg 0()a x x a x x a x x a x x -+-<-+-.故21()()f x f x <,所以函数()f x 是减函数.当0a <时,同上可得21()()f x f x >,函数()f x 是增函数.(Ⅲ)因为0a >,且()()10f x g x =,所以()a xg x a x-=+(a x a -<<). 所以探究()y g x =与2y x =-交点个数,即探究方程2a xx a x-=-+在(,)a a -上根个数.亦即方程2(1)30x a x a +--=在(,)a a -上根的个数. 令2()(1)3h x x a x a=+--,因为对称轴12a x -=,22(1)12101a a a a ∆=-+=++,由0∆>得5a >或5a <-,又()20h a a -=-<,()2(2)h a a a =-.当2a >时,则()0h a >,12aa a --<<,方程2(1)30x a x a +--=有一个实根.当123a ≤≤时,则()0h a ≤,12aa a --<<,方程2(1)30x a x a +--=无实根.当103a <<时,则()0h a <,12aa ->,方程2(1)30x a x a +--=无实根.3、已知函数9()log (91)x f x kx =++(k ∈R )是偶函数. (1)求k 的值;(2)若函数()y f x =的图象与直线12y x b =+没有交点,求b 的取值范围; (3)设()94()log 33x h x a a =⋅-,若函数()f x 与()h x 的图象有且只有一个公共点,求实数a 的取值范围.(1) 因为()y f x =为偶函数,所以,()()x f x f x ∀∈-=-R , 即 99log (91)log (91)x x kx kx -+-=++对于x ∀∈R 恒成立. 于是9999912log (91)log (91)log log (91)9xx x x xkx x -+=+-+=-+=-恒成立,而x 不恒为零,所以12k =-.(2) 由题意知方程911log (91)22x x x b +-=+即方程9log (91)x x b +-=无解.令9()log (91)x g x x =+-,则函数()y g x =的图象与直线y b =无交点.因为99911()log log 199xx x g x ⎛⎫+==+ ⎪⎝⎭任取1x 、2x ∈R ,且12x x <,则12099x x <<,从而121199x x>.。
第2讲 基本初等函数的性质及应用

第2讲基本初等函数的性质及应用基本初等函数的有关运算1.若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=e x,则g(x)等于( D )(A)e x-e-x (B)(e x+e-x)(C)(e-x-e x) (D)(e x-e-x)解析:因为f(x)+g(x)=e x, ①所以f(-x)+g(-x)=e-x,所以f(x)-g(x)=e-x, ②①-②得g(x)=,故选D.2.若函数f(x)=则f(f(10))等于( B )(A)lg 101 (B)2 (C)1 (D)0解析:f(f(10))=f(lg 10)=f(1)=12+1=2.故选B.3.(2015安徽卷)lg+2lg 2-()-1= .解析:lg+2lg 2-()-1=lg+lg 4-()-1=lg 10-2=-1.答案:-1比较函数值的大小4.已知a=,b=,c=(),则( C )(A)a>b>c (B)b>a>c(C)a>c>b (D)c>a>b解析:因为0<log43.6<1,所以b=<5,而又log23.4>1,log3>1,所以a=>5,c=()==>5,所以a>b,c>b.因为log23.4>log33.4>log3,所以a>c.所以a>c>b,故选C.5.(2015广州一模)已知log2a>log2b,则下列不等式一定成立的是( C )(A)> (B)log2(a-b)>0(C)()a<()b(D)2a-b<1解析:由log2a>log2b,得a>b>0,则选项A,D不成立,选项B不一定成立,对于选项C,()a<()b<()b,故选C.6.设函数f(x)=e x+x-2,g(x)=ln x+x2-3.若实数a,b满足f(a)=0,g(b)=0,则( A )(A)g(a)<0<f(b) (B)f(b)<0<g(a)(C)0<g(a)<f(b) (D)f(b)<g(a)<0解析:因为函数f(x)=e x+x-2在R上单调递增,且f(0)=1-2<0,f(1)=e-1>0,所以f(a)=0时a∈(0,1).又g(x)=ln x+x2-3在(0,+∞)上单调递增,且g(1)=-2<0,所以g(a)<0.由g(2)=ln 2+1>0,g(b)=0得b∈(1,2),又f(1)=e-1>0,且f(x)=e x+x-2在R上单调递增,所以f(b)>0.综上可知,g(a)<0<f(b).7.(2015杭州一检)设函数f(x)=e|ln x|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( C )(A)x2f(x1)>1 (B)x2f(x1)=1(C)x2f(x1)<1 (D)x2f(x1)<x1f(x2)解析:f(x)==由x1≠x2且f(x1)=f(x2),得x1,x2中一个大于1、一个小于1,且x1x2=1,若x1>1,则f(x1)=x1,x2f(x1)=1;若0<x1<1,则x2>1,f(x1)=,x 2f(x1)=>1,故选C.8.已知函数f(x)=若存在x1,x2,当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)的取值范围是.解析:作出函数f(x)的图象,由图知所以x1f(x2)=(-)·=(-)2-∈[,),即x1f(x2)的取值范围是[,).答案:[,)求参数的取值(范围)9.(2015福建卷)若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是.解析:当x≤2时,f(x)=-x+6,f(x)在(-∞,2]上为减函数,所以f(x)∈[4,+∞).当x>2时,若a∈(0,1),则f(x)=3+log a x在(2,+∞)上为减函数,f(x)∈(-∞,3+log a2),显然不满足题意,所以a>1,此时f(x)在(2,+∞)上为增函数,f(x)∈(3+log a2,+∞),由题意可知(3+log a2,+∞)⊆[4,+∞),则3+log a2≥4,即log a2≥1,所以1<a≤2.答案:(1,2]一、选择题1.下列函数中,不满足f(2x)=2f(x)的是( C )(A)f(x)=|x| (B)f(x)=x-|x|(C)f(x)=x+1 (D)f(x)=-x解析:若f(x)=|x|,则f(2x)=|2x|=2|x|=2f(x),若f(x)=x-|x|,则f(2x)=2x-|2x|=2(x-|x|)=2f(x),若f(x)=x+1,则f(2x)=2x+1≠2f(x),若f(x)=-x,则f(2x)=-2x=2f(x),故选C.2.(2015河南郑州市第二次质量预测)若正数a,b满足2+log2a=3+log3b=log6(a+b),则+的值为( C )(A)36 (B)72 (C)108 (D)解析:设2+log2a=3+log3b=log6(a+b)=x,则a=2x-2,b=3x-3,a+b=6x.所以+===22×33=108.故选C.3.(2015上饶市一模)函数f(x)=-|x-|的图象为( D )解析:函数f(x)的定义域为(0,+∞),当0<x<1时,f(x)=+(x-)=x;当x≥1时,f(x)=x-(x-)=,故选D.4.(2015烟台二模)f(x)=则f(f(-1))等于( D )(A)-2 (B)2 (C)-4 (D)4解析:f(-1)=-()=2>0,所以f(f(-1))=f(2)=3+log22=3+1=4.故选D.5.(2015慈溪市、余姚市联考)函数f(x)=x2lg的图象( B )(A)关于x轴对称 (B)关于原点对称(C)关于直线y=x对称(D)关于y轴对称解析:因为f(x)=x2lg,所以其定义域为(-∞,-2)∪(2,+∞),所以f(-x)=x2lg=-x2lg=-f(x),所以函数为奇函数,所以函数的图象关于原点对称,故选B.6.(2015信阳二检)若函数f(x)=2++sin x在区间[-k,k](k>0)上的值域为[m,n],则m+n等于( D )(A)0 (B)1 (C)2 (D)4解析:f(x)=2++sin x,设h(x)=+sin x,得h(-x)=-h(x),函数h(x)是奇函数,则h(x)的值域为关于原点对称的区间.当-k≤x≤k时,设-p≤h(x)≤p,则m=2-p,n=2+p,得m+n=4,故选D.7.已知x=ln π,y=log52,z=,则( D )(A)x<y<z (B)z<x<y(C)z<y<x (D)y<z<x解析:x=ln π>ln e=1,y=log52<log55=1,又log25>2,所以y<.又z==,所以<z<1.所以y<z<x,故选D.8.(2015山东卷)设函数f(x)=若f(f())=4,则b等于( D )(A)1 (B)(C)(D)解析:f(f())=f(3×-b)=f(-b),当-b<1,即b>时,3×(-b)-b=4,解得b=(舍去).当-b≥1,即b≤时,=4,解得b=.故选D.9.(2015石家庄市调研)已知函数f(x)=|lo x|,若m<n,有f(m)=f(n),则m+3n的取值范围是( D )(A)[2,+∞) (B)(2,+∞)(C)[4,+∞) (D)(4,+∞)解析:因为f(x)=|lo x|,若m<n,有f(m)=f(n),所以lo m=-lo n,所以mn=1,因为0<m<1,n>1,所以m+3n=m+在m∈(0,1)上单调递减.当m=1时,m+3n=4,所以m+3n>4.10.(2015河南郑州市第一次质量预测)设函数f1(x)=x,f2(x)=log2015x,a i=(i=1,2,…,2015),记I k=|f k(a2)-f k(a1)|+|f k(a3)-f k(a2)|+…+|f k(a2015)-f k(a2014)|,k=1,2,则( A )(A)I1<I2(B)I1=I2(C)I1>I2(D)无法确定解析:因为I1=|f1(a2)-f1(a1)|+|f1(a3)-f1(a2)|+…+|f1(a2015)-f1(a2014)|=|a2-a1|+|a3-a2|+…+|a2015-a2014|=|-|+|-|+…+|-|=++…+=.I2=|f2(a2)-f2(a1)|+|f2(a3)-f2(a2)|+…+|f2(a2015)-f2(a2014)|=|log2015-log2015|+|log2015-log2015|+…+|log2015-log2015|=|log20152-log20151|+|log20153-log20152|+…+|log20152015-log20152014| =log20152-0+log20153-log20152+…+1-log20152014=1-0=1.所以I1<I2.11.(2015烟台一模)已知函数f(x)=a|log2x|+1(a≠0),定义函数F(x)=给出下列命题:①F(x)=|f(x)|;②函数F(x)是偶函数;③当a<0时,若0<m<n<1,则有F(m)-F(n)<0成立;④当a>0时,函数y=F(x)-2有4个零点.其中正确命题的个数为( D )(A)0 (B)1 (C)2 (D)3解析:因为函数f(x)=a|log2x|+1(a≠0),定义函数F(x)=所以|f(x)|=|a|log2x|+1|,所以F(x)≠|f(x)|,①不对.因为F(-x)==F(x),所以函数F(x)是偶函数,故②正确.因为当a<0时,若0<m<n<1,所以|log2m|>|log2n|,所以a|log2m|+1<a|log2n|+1,即F(m)<F(n)成立,故F(m)-F(n)<0成立,所以③正确.因为f(x)=a|log2x|+1(a≠0),定义函数F(x)=所以x>0时,F(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以x>0时,F(x)的最小值为F(1)=1,故x>0时,F(x)与y=2有2个交点.因为函数F(x)是偶函数,所以x<0时,F(x)与y=2有2个交点.故当a>0时,函数y=F(x)-2有4个零点.所以④正确.二、填空题12.(2015广东省揭阳市二模)已知幂函数y=f(x)的图象过点(3,),则lo f(2)的值为.解析:设f(x)=xα,则f(3)=3α=,解得α=-1,所以f(x)=x-1,f(2)=,所以lo f(2)=lo=1.答案:113.(2015北京卷)2-3,,log25三个数中最大的数是.解析:因为2-3==,=≈1.732,而log 24<log25,即log25>2,所以三个数中最大的数是log25.答案:log2514.(2015肇庆二模)已知函数f(x)=在R上不是单调函数,则实数a的取值范围是.解析:当函数f(x)在R上为减函数时,有3a-1<0且0<a<1且(3a-1)×1+4a≥log a1,解得≤a<;当函数f(x)在R上为增函数时,有3a-1>0且a>1且(3a-1)×1+4a≤log a1,解得a无解;所以当函数f(x)在R上为单调函数时,有≤a<.所以当函数f(x)在R上不是单调函数时,有a>0且a≠1且a<或a≥,即0<a<或≤a<1或a>1.答案:(0,)∪[,1)∪(1,+∞).15.函数y=x2(x>0)的图象在点(a k,)处的切线与x轴的交点的横坐标为a k+1,其中k∈N*,若a1=16,则a1+a3+a5的值是.解析:因为y′=2x,所以k=y′=2a k,所以切线方程为y-=2a k(x-a k),令y=0,得x=a k,即a k+1=a k,所以{a k}是以首项为16,公比为的等比数列,所以a k=16×()n-1,所以a1+a3+a5=16+4+1=21.答案:21。
基本初等函数及函数的应用
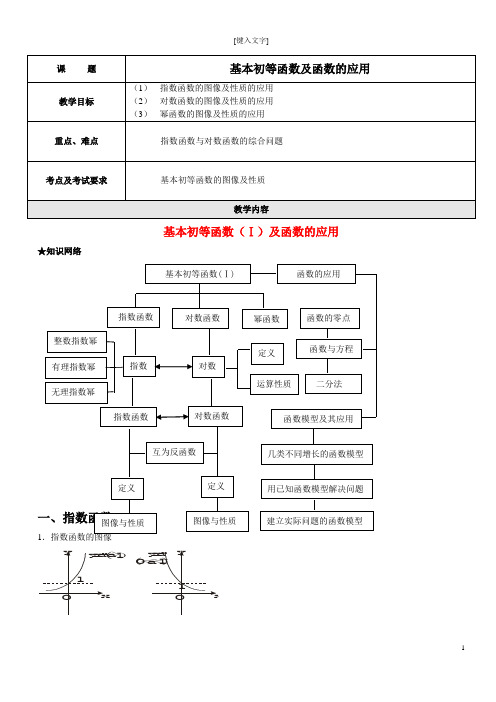
基本初等函数(Ⅰ)及函数的应用★知识网络1a > )1(02.底数互为倒数的两个指数函数的图像关于y 轴对称.例如:指数函数的图像x a y =与)1,0(≠>=-a a a y x的图象关于y 轴对称3.指数函数的性质:定义域:R ; 值域:(0,+∞);过点(0,1);即x=0时,y=1.当a >1时,在R 上是增函数;当0<a <1时,在R 上是减函数.4.利用复合函数的单调性判断形如)(x f a y =的函数的单调性:若1>a ,则)(x f y =的单调增(减)区间,就是)(x f a y =的单调增(减)区间;若10<<a ,则)(x f y =的单调增(减)区间,就是)(x f a y =的单调减(增)区间;5.指数型的方程和不等式的解法(Ⅰ)形如b a b a b a x f x f x f <>=)()()(,,的形式常用“化同底”转化为利用指数函数的单调性解决,或“取对数”等方法;(Ⅱ)形如02=++C Ba a xx 或)0(02≤≥++C Ba ax x的形式,可借助于换元法转化为二次方程或不等式求解。
考点1 指数幂的运算1. (湛江市09届统考)计算:100.256371.5()86-⨯-+ 2.=-⋅63a a ————————考点2 指数函数的图象及性质的应用 题型1:由指数函数的图象判断底数的大小 3.下图是指数函数(1)y=a x ,(2)y=b x ,(3)y=c x ,(4)y=d x 的图像,则a 、b 、c 、d 与1的大小关系是( ) A .a b c d <<<<1; B .b a d c <<<<1; C .a b c d <<<<1;D .b a c d <<<<1 [名师指引] 1的妙用题型2:解简单的指数方程4. 方程33131=++-xx的解是_________题型3:利用函数的性质解题5.不等式1622<-+x x的解集是___________6.(广东恩城中学09年模拟)不论a 为何正实数,函数12x y a +=-的图象一定通过一定点,则该定点的坐标是_________7.(广东广雅中学09届月考)已知函数()()()f x x a x b =--(其中a b >)的图象如下面右图所示,则函数()x g x a b =+的图象是( )A .B .C .D .8.(08年安徽改编)若函数(),()f x g x 分别是R 上的奇函数、偶函数,且满足()()xf xg x e -=,则)3(f 、)0(g 、)2(f 的大小关系为——————————考点3 与指数函数有关的含参数问题9.(广州六校09届联考)已知函数()22x x af x =-, 将()y f x =的图象向右平移两个单位, 得到()y g x =的图象.(1) 求函数()y g x =的解析式;(2) 若函数()y h x =与函数()y g x =的图象关于直线1y =对称, 求函数()y h x =的解析式;二. 对数及对数函数1.对数的概念如果ab=N (a >0,a≠1),那么b 叫做以a 为底N 的对数,记作logaN=b ab=N ⇔logaN=b (a >0,a ≠1,N >0). 2.对数的运算性质loga (MN )=logaM+logaN. loga N M=logaM -logaN.logaM n =nlogaM.(M >0,N >0,a >0,a ≠1)3.对数换底公式:logb N =bN a a log log (a >0,a ≠1,b >0,b ≠1,N >0).4.对数函数的图像及性质①函数y=loga x (a >0,a≠1)叫做对数函数,其中x 是自变量,图像如下a <11))②对数函数的性质:定义域:(0,+∞); 值域:R ; 过定点(1,0)当a >1时,在(0,+∞)上是增函数;当0<a <1时,在(0,+∞)上是减函数。
基本初等函数、函数与方程及函数的应用

2<0,f(1)=e-1>0,所以f(a)=0时a∈(0,1).又g(x)=ln x+
x2-3在(0,+∞)上单调递增,且g(1)=-2<0,所以g(a)<0.
由g(2)=ln 2+1>0,g(b)=0得b∈(1,2),又f(1)=e-1>0,且
f(x)=ex+x-2在R上单调递增,所以f(b)>0.综上可知,
在零点的个数进行判断,如2013年重庆T6,天津T7,湖南T5等.
4.利用零点(方程实根)的存在求相关参数的值或取值范围.
5.对函数实际应用问题的考查,题目大多以社会生活为背景,
函数的实际应用 设问新颖、灵活,而解决这些问题所涉及的数学知识、思想方法都
问题
是高中教材和课标中所要求掌握的概念、公式、法则、定理等.
个零点分别位于区间(a,b)和(b,c)内.
答案:A
3.(2013·天津高考)函数f(x)=2x|log0.5x|-1的零点个数为
A.1
B.2
()
C.3
D.4
解析:函数f(x)=2x|log0.5x|-1的零点个数即为函数y=
|log0.5x|与y=
1 2x
图像的交点个数.在同一直角坐标系中作出
函数y=|log0.5x|与y=21x的图像,易知有2个交点. 答案:B
4.(2013·湖南高考)函数f(x)=2ln x的图像与函数g(x)=x2-4x+
5的图像的交点个数为
()
A.3
B.2
C.1
D.0
解析:由已知g(x)=(x-2)2+1,所以其顶点为(2,1),又f(2)
=2ln 2∈(1,2),可知点(2,1)位于函数f(x)=2ln x图像的下
人教B版高中数学必修一第三章《基本初等函数I》讲解与例题+综合测试(7份).docx

3.4函数的应用(II)QJy I (.Hl / H?S li IJHi E \ J I \ L \1.函数模型所谓数学模型是指对客观实际的特征或数量关系进行抽象概括,用形式化的数学语言表述一种数学结构.数学模型剔除了事物中一切与研究目标无木质联系的各种属性,在纯粹状态下研究数量关系和空间形式,函数就是重要的数学模型,用函数解决方程问题,使求解变得容易进行,这是数学模型间的相互转换在发挥作用.而用函数解决实际问题,则体现了数学模型是联系数学与现实世界的桥梁.本节涉及的函数模型有:⑴指数函数模型:y=G//+c(b>0, bHl, aHO),当b>\, d>0时,其增长特点是随着自变量的增大,函数值增大的速度越来越快,常形象地称为指数爆炸.(2)对数函数模型:y=mlog(l x+n(m^O f a>0, aHl),当aAl,加>0时,其增长的特点是随着自变量的增大,函数值增大的速度越来越慢.(3)帚函数模型:y=a-x n+b(a^O),其中最常见的是二次函数模型y=ax2+bx~\~c(a0), 当d>0时,其特点是随着自变量的增大,函数值先减小,后増大.在以上几种函数模型的选择与建立时,要注意函数图彖的直观运用,分析图象特点,分析变量x的范围,同时还要与实际问题结合,如取整等.【例1 — 1】据报道,全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度,设2012年的冬季冰雪覆盖面积为加,从2012年起,经过兀年后,北冰洋冬季冰雪覆盖面积),与x的函数关系式是()A. ^=0.9550 -mB. >,=(l-O.O55O)-mC. y=0.9550_x-/?zD. y=(l-O.O55O_v)-/n解析:设每年的冰雪覆盖面积减少率为d.・・・50年内覆盖面积减少了5%,1・・・(1—a)5°=l—5%,解得0=1 — 0.9550.1 △・••从2012年起,经过x年后,冰雪覆盖面积尸加1一(1一0.95巧F二加095込答案:A【例1一2】某公司为应对金融危机的影响,拟投资100万元,有两种投资可供选择:一种是年利率1%,按单利计算,5年后收回本金和利息;另一种是年利率3%,按每年复利一次计算,5年后收回本金和利息.哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?(结果精确到0.01万元)分析:这是一个单利和复利所获得收益多少的比较问题.可先按单利和复利讣算5年后的本利和分别是多少,再通过比较作答.解:本金100万元,年利率1%,按单利计算,5年后的本利和是100X(l + l%X5) = 105(万元).本金100万元,年利率3%,按每年复利一次计算,5年后的本利和是100X(1 + 3%『a 115.93(万元).由此可见按年利率3%每年复利一次投资要比按年利率1%单利投资更有利,5年后多得利息约10.93万元.谈重点利息的计算利息分单利和复利两种.单利是只有木金牛息,利息不再牛息,而复利是把前一期的本利 和作为本金再牛息,两种情况要注意区分.我国现行定期储蓄中的自动转存业务类似复利计•息的储蓄,如某人存入本金。
基本初等函数讲义(全)

基本初等函数讲义(全)一、一次函数一次函数可以表示为y=kx+b(k不等于0),其中k表示斜率,b表示截距。
当k大于0时,函数图像随着x的增大而增大,当k小于0时,函数图像随着x的增大而减小。
当b大于0时,函数图像在y轴上方,当b小于0时,函数图像在y轴下方。
当b等于0时,函数图像经过原点。
二、二次函数1)二次函数有三种解析式形式:一般式、顶点式和两根式。
一般式为f(x)=ax^2+bx+c(a不等于0),顶点式为f(x)=a(x-h)^2+k(a不等于0),两根式为f(x)=a(x-x1)(x-x2)(a不等于0)。
2)求二次函数解析式的方法有三种情况:已知三个点坐标时,宜用一般式;已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式;若已知抛物线与x轴有两个交点,且横线坐标已知时,选用两根式求f(x)更方便。
3)二次函数的图像是一条抛物线,对称轴方程为x=-b/2a,顶点坐标为(-b/2a。
-Δ/4a)。
当a大于0时,抛物线开口向上,函数在(-∞。
-b/2a)上递增,在[-b/2a。
+∞)上递减,最小值为f(-b/2a);当a小于0时,抛物线开口向下,函数在(-∞。
-b/2a]上递增,在[-b/2a。
+∞)上递减,最大值为f(-b/2a)。
三、幂函数1)幂函数可以表示为y=x^α,其中x为自变量,α是常数。
2)所有的幂函数在(0.+∞)都有定义,并且图像都通过点(1,1)。
四、指数函数1)根式的概念是指,如果xn=a,a属于实数,x属于实数,n大于1,且n属于正整数,那么x叫做a的n次方根。
2)正数的正分数指数幂的意义是,a的n次方根的正分数指数幂等于a的n次方。
正数的负分数指数幂没有意义。
非奇非偶函数指的是在定义域为(0.+∞)上的减函数。
对于loga x,当x>1时,函数值递增;当x<1时,函数值递减;当x=1时,函数值为0.在第一象限内,a越大,函数图像越靠低;在第四象限内,a越大,函数图像越靠高。
