断裂力学综述
材料的断裂力学分析

材料的断裂力学分析在材料科学和工程领域中,断裂力学是一门研究材料在外力作用下如何发生破坏的学科。
通过断裂力学的分析,我们可以了解材料在正常使用条件下的破坏原因,以及如何提高材料的断裂韧性和强度。
本文将对材料的断裂力学进行详细分析。
1. 断裂力学的基本概念在了解材料的断裂力学之前,我们需要了解几个基本概念。
1.1 断裂断裂是指材料在外部应力作用下发生破坏、分离的过程。
断裂可以分为韧性断裂和脆性断裂两种类型。
韧性断裂是指材料在破坏之前会出现塑性变形,具有一定的延展性;而脆性断裂是指材料在外力作用下迅速发生破坏而不发生明显的塑性变形。
1.2 断裂韧性断裂韧性是指材料抵抗断裂破坏的能力。
一个具有高断裂韧性的材料可以在外力作用下发生一定程度的塑性变形,从而使其拉伸长度增加。
1.3 断裂强度断裂强度是指材料在破坏前能够承受的最大应力。
断裂强度可以通过拉伸实验等方式进行测定。
2. 断裂力学的分析方法断裂力学的分析方法主要有线弹性断裂力学和非线弹性断裂力学两种。
2.1 线弹性断裂力学线弹性断裂力学假设材料在破坏前的行为是线弹性的,并且材料的破坏是由于应力达到了一定的临界值所引起的。
在线弹性断裂力学中,断裂过程可以通过应力强度因子和断裂韧性来描述。
2.2 非线弹性断裂力学非线弹性断裂力学考虑了材料在破坏前的非线性行为,如塑性变形、蠕变等。
非线弹性断裂力学可以更准确地预测材料的破坏行为,但其计算复杂度较高。
3. 断裂力学的应用断裂力学在材料科学和工程中具有广泛的应用。
3.1 破坏分析通过断裂力学的分析,我们可以确定材料在受力状态下的破坏原因,从而改进材料的设计和制备工艺。
例如,在航空航天领域,对材料的断裂力学进行精确分析可以提高飞行器的安全性和可靠性。
3.2 材料评估通过断裂力学的测试和分析,我们可以评估材料的断裂韧性和强度,为材料的选择和应用提供依据。
这对于许多行业来说是至关重要的,如汽车制造、建筑工程等。
3.3 研发新材料断裂力学的理论和实验研究对于开发新的高性能材料具有重要意义。
第十讲--断裂力学

纹长 可计算线性解BC部
分,称为等效裂纹长度。
等效模型法:以等效裂纹长度代替裂纹原长对应力强度因子进行修正。
等效裂纹长度和应力强度因子
令按等效裂纹长度计算的应力场在r = R-ry(B点)的应力等于σys,则
:应力松驰后的应力强度因子
σys:y方向屈服应力,σys =σs(平面应力),(平面应变)
长度Δa,扩展部分各点的位移
则释放的能量为
II型和III型裂纹
,
μ:剪切弹性模量
平面应力,平面应变
6.脆性断裂的K准则
KI= KIC
临界应力:(剩余强度)
临界裂纹长度:
KC:平面应力断裂韧度
KIC:平面应变断裂韧度
板厚增加到一定值后,断裂韧度由KC(平面应力断裂韧度)降低至一稳定值KIC(平面应变断裂韧度)。
裂纹尖端应力强度子
平面应变
k =
平面应力
2)滑开型(II型)裂纹尖端应力和位移场
3)撕开型(III型)裂纹尖端应力和位移场
4.应力和位移场的一般形式
,
1)r ( 0,σij ( ((应力奇异性)
2)应力强度因子是代表应力场强度的物理量
σ:名义应力;Y:形状系数
5.应力强度因子和能量释放率的关系
设图示I型裂纹扩展一微小
在平面应力条件下,裂纹尖端有较大范围的塑性变形,线弹性断裂力学K准则不适用(塑性区较小时,经修正后仍可用K准则)。
7.裂纹尖端塑性区的形状和尺寸
a.平面应力情况
主应力
应用Von Mises屈服条件
得出裂纹尖端塑性区的形状
b.平面应变情况
裂纹尖端塑性区的形状
,
考虑塑性区内塑性变形引起的应力松驰后的塑性区修正为
断裂力学在桥梁工程领域中的应用综述

断裂力学在桥梁工程领域中的应用综述摘要:带裂缝工作是桥梁结构最为普遍的状态。
施工工艺,外界荷载以及收缩徐变等因素都会造成桥梁结构产生大量裂纹。
裂纹的存在状态,发展规律均会影响桥梁结构的安全性能。
正因为如此,越来越多的学者利用断裂力学理论针对桥梁结构进行承载能力,耐久性等方面的分析研究。
在此背景下,介绍了断裂力学面向的问题,以及断裂力学在钢桥疲劳寿命预测、结构焊接以及混凝土桥梁领域的应用,并指出现有研究存在的缺陷。
关键词:断裂力学;桥梁工程;疲劳寿命;焊接;混凝土开裂;综述1断裂力学基本理论断裂力学是固体力学的一门分支,主要研究材料和结构内部裂纹的发展规律,包括:裂纹的起裂条件,裂纹的发展规律以及裂纹发展的临界状态。
断裂力学中将裂纹分为三种类型,分别为I型裂纹(张开型)、II型裂纹(滑开型)以及III型裂纹(撕开型),如图1所示。
(a)I型裂纹(b)II型裂纹(c)III型裂纹图1 三种基本裂纹类型应力强度因子K表征了裂纹尖端区域应力场奇异性的强度,其值与裂纹体的几何形状和受荷情况有关。
Ⅰ型、Ⅱ型和Ⅲ型裂缝的应力强度因子算式为:(1)(2)(3)对于某一确定材料,总存在一个临界强度因子K C。
当某一裂纹的应力强度因子K 达到K C时,认为裂纹发生失稳。
2基于断裂力学的钢桥疲劳寿命预测钢结构问世后的很长一段时间内,大量工程人员普遍采用基于S-N曲线的评判方法针对钢结构的疲劳寿命进行预测。
伴随着断裂力学的逐步发展成熟,研究人员认为断裂力学能够很好的揭示结构内部裂纹的发展规律,线弹性断裂力学开始被普遍应用于钢桥梁结构疲劳寿命预测领域。
早在1963年,Paris 等就提出等幅疲劳荷载作用条件下,钢结构疲劳裂纹的扩展速率与应力强度因子幅度之间存在相关性。
经过进一步的研究,Paris 等于1963年提出著名的Paris 公式,其公式的基本形式为:(4)式中ΔK为应力强度因子幅度,C、m均为与钢结构材料特性有关的常数。
边界元法在断裂力学中综述

边界元法在断裂力学中的研究综述摘要:边界元法在域内采用基本解,只在边界上进行离散,代数方程组的未知数少,对应力变化剧烈的地方能得到较好计算结果。
本文简要介绍了国内外利用边界元法研究断裂力学中裂纹问题的现状,并对研究中的一些关键问题进行了探讨。
关键词:边界元法;裂纹;断裂力学;特殊单元法引言在断裂力学中,由于裂纹尖端附近的应力场存在奇异性,以致直接应用常规数值方法分析断裂力学问题的效果往往较差,因此需要结合断裂力学的特点发展更有效的数值计算方法.边界元法是在经典的积分方程的基础上,吸收了有限元法的离散技术而发展起来的计算方法[1]。
边界元法在域内采用基本解,只在边界上进行离散,因此实际上是将问题降维处理,如果是各维尺度相近的大型问题,代数方程组的未知数将按指数规律减少,这无疑将大大减少准备工作、存贮量与机时[1]。
另外,计算误差只来源于边界,区域内由解析公式计算,这就具有解析-数值计算的特点,有较高精度,对应力变化剧烈的地方能得到较好的结果,在边界上也能保持其精度,这些是有限元法所做不到的。
这些特点,对边界元法应用在线弹性断裂力学问题上的应用是很有利的。
本文首先对边界元法在断裂力学中研究现状作一简介,在此基础上提出研究中存在的一些关键问题进行了初步探讨。
1.边界元法在断裂力学中研究现状断裂力学研究的裂纹问题关键是确定应力强度因子(sif)。
应力强度因子(sif)通常用来表征裂纹尖端附近区域应力场的强弱,通过它可以把构件几何形状、裂纹形状、尺寸及应力联系起来,并以它为基础来定义材料断裂的临界参数,从而把裂纹对构件断裂的影响进行定量计算。
用边界元解决裂纹问题,一般可以归纳为以下几个关键步骤:1)、建立边界积分方程;2)、选择单元模式;3)、处理裂纹尖端及其他边界奇异性;4)、实施数值或精确积分;5)、解最终线性代数方程组;6)、计算应力强度因子[2]。
要得到精确程度可信的应力强度因子值,这些关键步骤中更为重要的是正确模拟裂纹尖端附近区域位移和应力的变化规律。
断裂力学总结

断裂力学学习报告姓名:zx 学号:xxxxxxxx一、绪论(1)传统强度理论是在假定材料无缺陷、无裂纹的情况下建立起来的,认为只要满足r []σσ≤,材料将处于安全状态。
其中:[]σ——用安全系数除失效应力得到的许用应力;r σ——为相当应力,它是三个主力学按照一定顺序组合而成的,按照从第一强度理论到第四强度强度理论的顺序,相应的应力分别为1121233134()r r r r σσσσμσσσσσσ==-+=-=但是许多事实表明,材料受应力远小于设计应力,材料仍然被破坏。
使许多力学工作者迷惑不解,于是投入对其研究,最终发现所有材料并不是理想的,材料中含有大大小小、种类各异的裂纹,于是产生了对裂纹地研究。
断裂力学从客观存在裂纹出发,把构件看成连续和和间断的统一体,从而形成了这门新兴的强度学科。
(2)断裂力学的任务是:1. 研究裂纹体的应力场、应变场与位移场,,寻找控制材料开裂的物理参量;2. 研究材料抵抗裂纹扩展的能力——韧性指标的变化规律,确定其数值与及测定方法;3. 建立裂纹扩展的临界条件——断裂准则;4. 含裂纹的各种几何构件在不同荷载作用下,控制材料开裂的物理参量的计算。
(3)断裂力学的研究方法是:假设裂纹已经存在,从弹性力学或弹塑性力学的基本方程出发,把裂纹当作边界条件,考察裂纹顶端的应力场、应变场和位移场,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
(4)断裂力学的几个基本概念:根据裂纹受力情况,裂纹可以分为三种基本类型:1. 张开型(I 型)裂纹受垂直于裂纹面的拉应力作用,裂纹上下两表面相对张开,如上图a 所示;2. 滑开型(II 型),又称平面内剪切型裂纹受平行于裂纹面而垂直于裂纹前缘OO ’的剪应力作用,裂纹上下两表面沿x 轴相对滑开,如上图b 所示;3. 撕开型(III 型),又称出平面剪切型或反平面剪切型裂纹受既平行于裂纹面又平行于裂纹前缘的剪应力作用,裂纹上下两表面沿z 轴相对错开,如上图c 所示.上述三种裂纹中I 型最为危险.而我们主要也是研究I 型裂纹,因为只要确定了I 型裂纹是安全的,则其它两种裂纹也是安全的。
断裂力学概述 2

第一章线弹性断裂力学线弹性断裂力学研究对象是线弹性裂纹固体,认为裂纹体内各点的应力应变关系是线性的。
金属材料中,严格的线弹性断裂问题几乎不存在,因为裂纹的扩展总伴随有裂纹尖端的苏醒变形。
但理论和实践都证明,只要塑性区尺寸远小于裂纹的尺寸,经适当修正,用线性理论分析不会产生太大误差。
对于低韧高强度钢,或处于低温条件下工作的构件,往往在断裂前裂纹尖端的塑性区尺寸较小,可用线弹性断裂理论进行分析。
一裂纹及其对强度的影响1.1裂纹分类1.按几何特征a 穿透裂纹: 通常把裂纹延伸到构件厚度一半以上的都视为穿透裂纹。
b 表面裂纹c 深埋裂纹2.按裂纹力学特征张开型裂纹裂纹受垂直于裂纹面的拉应力,是裂纹面产生张开位移滑开型裂纹裂纹受平行于裂纹面且垂直于裂纹前缘的剪应力,裂纹在平面内滑开撕开型裂纹裂纹受平行于裂纹面且平行于裂纹前缘的剪应力,裂纹相对错开复合型裂纹裂纹同时受正应力和剪应力的作用,或裂纹与正应力成一角度,这是就同时存在和,或和,称为复合型裂纹,实际裂纹体中裂纹可能是两种或两种以上基本型的组合。
1.2 裂纹对材料强度的影响带裂纹弹性体受力后,在裂纹尖端区域产生局部应力集中。
但是这种集中是局部性的,离开裂纹尖端稍远处应力分布趋于正常。
裂纹尖端区域应力集中程度与裂纹尖端的曲率半径有关,裂纹越尖锐应力集中程度越高。
这种应力集中必然导致材料的实际断裂强度远低于材料理论断裂强度。
二、能量释放率理论2.1 格瑞菲斯理论(Griffith)二十世纪二十年代初,英国学者Griffith最先应用能量法对玻璃、陶瓷等脆性材料进行了断裂分析,成功解释了“为什么玻璃等材料的实际断裂强度比用分子结构理论所预期的强度低得多”的问题。
Griffith研究如图厚度为t的薄平板。
两端施加均不载荷,处于平行状态并固定两端,构成能量封闭系统,板内总应变能为U0,板内开一长为2a的贯穿裂纹,裂纹处形成上下两个自由表面,作用在两表面的拉应力消失,同时两表面产生张开位移,拉应力做负功,使应变能减小到U0-U。
断裂力学
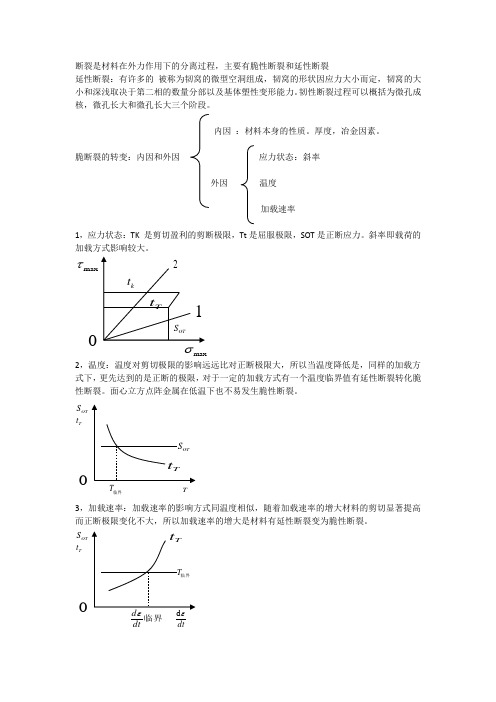
断裂是材料在外力作用下的分离过程,主要有脆性断裂和延性断裂延性断裂:有许多的 被称为韧窝的微型空洞组成,韧窝的形状因应力大小而定,韧窝的大小和深浅取决于第二相的数量分部以及基体塑性变形能力。
韧性断裂过程可以概括为微孔成核,微孔长大和微孔长大三个阶段。
内因 :材料本身的性质。
厚度,冶金因素。
脆断裂的转变:内因和外因 应力状态:斜率 外因 温度加载速率1,应力状态:TK 是剪切盈利的剪断极限,Tt 是屈服极限,SOT 是正断应力。
斜率即载荷的加载方式影响较大。
2,温度:温度对剪切极限的影响远远比对正断极限大,所以当温度降低是,同样的加载方式下,更先达到的是正断的极限,对于一定的加载方式有一个温度临界值有延性断裂转化脆性断裂。
面心立方点阵金属在低温下也不易发生脆性断裂。
3,加载速率:加载速率的影响方式同温度相似,随着加载速率的增大材料的剪切显著提高而正断极限变化不大,所以加载速率的增大是材料有延性断裂变为脆性断裂。
O T TS t d dtεd d t临界O T TS t TT 临界maxτm axσ0断裂机制:第一类是由材料屈服为主的塑性破坏,第二类是一裂纹失稳扩展的断裂破坏。
缺陷对两类破坏都有重要影响,但是机制不同。
塑性破坏而言缺陷主要影响了结构的有效承载面积,破坏的临界条件主要有塑性极限载荷控制。
裂纹失稳扩展的断裂而言缺陷引起的局部应力应变场对结构强度起主导作用。
高强材料:断裂时,裂纹端部发生很小的的屈服:线弹性断裂力学理论。
含有裂纹的材料 延性材料:断裂时裂纹端部发生很大的屈服:弹塑性断裂力学理论。
完全塑性材料:断裂时构件整体发生均匀屈服:塑性材料断裂力学。
剩余强度:含有裂纹的结构在使用过程中任意时刻所具有的承载能力就被称为剩余强度。
所有的断裂理论的落脚点都是比较剩余强度和设计强度的大小。
能量分析:英国物理学家Griffith,在1921年首次提出了裂纹扩展时能量释放的概念。
找他的理论解释,裂纹的上下表面形成导致了应变能的释放。
断裂力学的发展与研究现状

断裂力学的发展与研究现状一、断裂力学概述断裂力学是一门研究材料或结构在断裂过程中力学行为的学科。
它专注于理解材料的微观结构和性能,以及在外力作用下材料裂纹萌生、扩展和断裂的机制。
断裂力学在工程应用中具有非常重要的意义,因为材料的断裂会直接导致灾难性的后果。
二、断裂力学的发展自20世纪60年代以来,断裂力学得到了迅速的发展。
这个领域的研究可以分为两个主要方向:线性断裂力学和非线性断裂力学。
1. 线性断裂力学:线性断裂力学研究裂纹在材料中扩展的规律,其理论基础主要是弹性力学和塑性力学。
这个方向的主要目标是预测裂纹扩展的速率,以及裂纹对材料性能的影响。
2. 非线性断裂力学:非线性断裂力学研究裂纹在非线性材料中扩展的规律。
这种材料的行为会随着裂纹的扩展而改变,因此需要使用更复杂的模型来描述。
非线性断裂力学的研究对于理解复合材料、金属、陶瓷等材料的断裂行为非常重要。
三、断裂力学的研究现状当前,断裂力学的研究主要集中在以下几个方向:1. 疲劳裂纹扩展研究:疲劳裂纹扩展是工程结构中最常见的断裂形式之一。
这个方向的研究主要关注疲劳裂纹的萌生和扩展机制,以及如何预测疲劳寿命。
2. 复合材料断裂研究:复合材料由于其各向异性和非线性特性,其断裂行为比金属材料更为复杂。
这个方向的研究主要关注复合材料的分层、脱层、破碎等行为,以及如何优化复合材料的结构设计。
3. 微裂纹扩展研究:微裂纹在材料中广泛存在,其对材料的性能和安全性具有重要影响。
这个方向的研究主要关注微裂纹的萌生、扩展和聚集机制,以及如何检测和预防微裂纹的产生。
4. 跨尺度断裂力学研究:这个方向的研究关注在不同尺度(如微观、介观和宏观)下材料的断裂行为。
它涉及到材料在不同尺度下的物理性质,以及不同尺度之间的相互作用。
这种跨尺度的方法有助于更全面地理解材料的断裂行为。
四、未来研究方向与挑战随着科学技术的发展,断裂力学仍面临许多新的挑战和研究机会。
未来几年,以下几个方向可能会成为研究的热点:1. 高性能计算与模拟:随着计算机技术的发展,高性能计算和模拟已经成为解决复杂工程问题的关键工具。
断裂力学总结

失稳扩展
可以止裂
若材料的表面自由能是常数,则有:
失稳扩展
可以止裂
第二章应力பைடு நூலகம்度因子
2.1裂纹的几种基本型
断裂发生时在裂纹端点要释放出多余的能量,因此,裂端区的应力场和应变场必然与此裂端的能量释放率有关。若裂端应力应变场的强度足够大,断裂即可发生,反之则不发生。
图4-2
等于 时,则 ,当 时, 趋近于 值,得 ;当 时, 得: ,最后得到 。
4.2裂纹张开位移CTOD及J积分
裂纹张开位移是指一个理想裂纹受载荷时,其裂纹表面间的距离。对I型裂纹来说,线弹性断裂力学给出 。若用Irwin塑性区修正,真正裂纹长度被有效裂纹长度所取代,此时原点移动到有效裂纹的端点,以 代替 , 代替 ,可得小范围屈服修正时 ,利用能量释放率 与 的关系有:
考虑带有裂纹的弹性体,在拉伸载荷作用下,若裂纹仍然维持静止,则此弹性体所储存的总应变能 要比在没有裂纹时所储存的总应变能 大,两者之差用 表示。由于没裂纹时的总应变能 与裂纹长度无关,故有:
1.2能量平衡理论的应用
按照热力学的能量守恒定律,在单位时间内,外界对于系统所做功的改变量,应等于系统储存应变能的该变量,加上动能的改变量,再加上不可恢复消耗能地改变量。假设 为外界对系统所做的功, 为系统储存的应变能, 为裂纹总面积, 为表面能,则断裂发生的临界条件为: 此式为带裂纹物体的断裂判据。按照线性弹性力学的原理,在外力拉伸下,因裂纹扩展而引起的功的变化量 ,将等于两倍的总应变能的变量 ,因此能量释放率在给定外力拉伸的情形下,有:
现以I型单边裂纹为例,来说明柔度法的原理。一块很长的矩形板,如图3-3,
断裂力学论文

中国矿业大学断裂力学课程报告课程总结及创新应用XXX2014/5/7班级:工程力学XX班学号:0211XXXX断裂力学结课论文一、学科简介1、学科综述结构的破坏控制一直是工程设计的关键所在。
工程构件中难免有裂纹,从而会产生应力集中、结构失效等问题。
裂纹既可能是结构零件使用前就存在的,也可能是结构在使用过程中产生的。
但裂纹的存在并不意味着构件的报废,而是要求我们能准确地预测含裂纹构件的使用寿命或剩余强度。
针对脆性材料的研究已有完善的弹性理论方法,并获得了广发的应用。
但对于工程中许多由韧性较好的中、低强度金属材料制成的构件,往往在裂纹处先经历大量的塑性变形,然后才发生断裂破坏或失稳等。
这说明,韧性好的金属材料有能力在一定程度上减弱裂纹的危险,并可以增大结构零件的承载能力或延长器使用寿命,这也是韧性材料的优点所在。
但与此同时,这给预测强度的力学工作者带来了更复杂的问题,即不可逆的非塑性变形,这也是开展工程构架弹塑性变形的原因之一。
因而,裂纹的弹塑性变形研究具有广泛的工程背景和重要的理论意义。
作为研究裂纹规律的一门学科,即断裂力学,它是50年代开始蓬勃发展起来的固体力学新分支,是为解决机械结构断裂问题而发展起来的力学分支,被广泛地应用于航海、航空、兵器、机械、化工和地质等诸多领域,它将力学、物理学、材料学以及数学、工程科学紧密结合,是一门涉及多学科专业的力学专业课程。
断裂力学有微观断裂力学与宏观断裂力学之分。
一方面,需要深入到微观领域弄清微观的断裂机理,才能深入了解宏观断裂的现象。
另一方面,宏观断裂力学仍然没有发展完善,尤其是在工程实际中的应用还远未成熟,即使平面弹塑性断裂力学也依然有许多亟待解决的问题。
2、断裂力学研究的主要问题1、多少裂纹和缺陷是允许存在的?2、用什么判据来判断断裂发生的时机?3、研究对象的寿命图和估算?如何进行裂纹扩展率的测试及研究影响裂纹扩展率的因素。
4、如何在既安全又能避免不必要的停产损失的情况下安排探伤检测周期。
断裂力学简介

115第六章 断裂力学简介及材料典型强韧化机制§6.1 断裂的基本概念§6.1.1 断裂力学的产生和发展断裂是构件破坏的重要形式之一,影响材料断裂的因素很多,如构件的形状及尺寸,载荷的特征与分布,构件材料本身的状态及应用的环境如温度、腐蚀介质等,当然更重要的还有材料本身的强度水平。
为了防止构件的断裂或变形失效,传统的安全设计思想主要立足于外加载荷与使用材料的强度级别的选用,根据常规的强度理论,只要构件服役应力与材料的强度满足⎪⎪⎩⎪⎪⎨⎧=21m axK K s b σσσ(6- 1)则认为使用是安全的。
其中ζmax 为构建所承受的最大应力;ζ b,ζs 分别为材料的强度极限和屈服强度,K 1与K 2分别为按强度极限与按屈服强度取用的安全系数。
安全系数是一个大于1的数,其含义为扣除了材料中对强度有影响的诸因素对强度可能造成的损害作用,应当说这种考虑问题的出发点是合理的,也应当是行之有效的,因而多年来这种设计思想在工程设计中发挥了重要作用,而且还会继续发挥其重要作用。
关于断裂力学的最早理论可以追溯到1920年,为了研究玻璃、陶瓷等脆性材料的实际强度比理论强度低的原因,Griffith 提出了在固体材料中或在材料的运行过程中存在或产生裂纹的设想,计算了当裂纹存在时,板状构件中应变能的变化进而得出了一个十分重要的结果。
ζca =常数 (6- 2)其中,ζc 是断裂扩展的临界应力;a 为断裂半长度。
该理论非常成功地解释了玻璃等脆性材料的开裂现象,但应用于金属材料并不成功,又由于当时金属材料的低应力破坏事故并不突出,所以在很长一段时间内未引起人们的重视。
1949年E.Orowan 在分析了金属构件的断裂现象后对Griffith 公式提出了修正,他认为产生断裂所释放的应变能不仅能转化为表面能,也应转化为裂纹前沿的塑性应变功,而且由于塑性应变功比表面能大得多,以至于可以不考虑表面能的影响,其提出的公式为:ζca =212⎪⎭⎫⎝⎛λEU =常数 (6- 3)Orowan 公式虽然有所进步,但仍未超出经典的Griffith 公式的范围,而且同表面能一样,形变功U 也是难以测量的,因而该式仍难以实现工程上的的应用。
断裂力学概述

断裂力学是近几十年才发展起来的一支新兴学科 ,它从宏观的连续介质力学角度出发 ,研究含缺陷或裂纹的物体在外界条件(荷载、温度、介质腐蚀、中子辐射等)作用下宏观裂纹的扩展、失稳开裂、传播和止裂规律。
断裂力学应用力学成就研究含缺陷材料和结构的破坏问题 ,由于它与材料或结构的安全问题直接相关 ,因此它虽然起步晚 ,但实验与理论均发展迅速 ,并在工程上得到了广泛应用。
例如断裂力学技术已被应用于估算各种条件下的疲劳裂纹增长率、环境问题和应力腐蚀问题、动态断裂以及确定试验中高温和低温的影响 ,并且由于有了这些进展 ,在设计有断裂危险性的结构时 ,利用断裂力学对设计结果有较大把握。
断裂力学研究的方法是:从弹性力学方程或弹塑性力学方程出发 ,把裂纹作为一种边界条件 ,考察裂纹顶端的应力场、应变场和位移场 ,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
用弹性力学的线性理论研究含裂纹体在荷载作用下的力学行为和失效准则的工程学科成为线弹性断裂力学。
在分析中,可认为材料是线弹性的,并且不考虑裂纹尖端极小范围内的屈服问题。
研究含裂纹体的力学行为可以从两种观点出发,即从能量平衡观点和从裂纹尖端应力场强度的观点进行研究。
按裂纹的受力特点和位移特点,可以把它们抽象化为张开型、滑移型和撕开型三种基本类型,任何形式的裂纹,都可以看成上述三种基本类型的组合。
从应力场强度的观点研究裂纹体的力学行为和失效准则。
Ⅰ型和Ⅱ型的脆断问题归结为平面问题下含裂纹的线弹性体的线弹性力学分析,先选取满足双调和方程和边界条件的应力函数,极坐标系原点选在裂纹尖端,把裂纹看作一部分边界,就可以用弹性力学的方法求得裂纹体的应力场和位移场。
求出的应力函数为Williams应力函数,得到极坐标下应力分量表达式,通过物理方程和几何方程得到几何分量表达式。
按远场的边界条件不同可分别求出Ⅰ型和Ⅱ型的裂纹尖端领域的应力场和位移场。
Ⅲ型问题为反平面应力问题,xy方向位移为零,只有z方向位移且是xy的函数,只有两个应变分量和两个应力分量,解一个平衡方程得Ⅲ型裂纹尖端领域的应力场合位移场。
断裂力学综述

断裂力学概述关键词:断裂力学;现状;阶段性问题;发展趋势中文摘要:本文主要介绍了断裂力学的4个方面,包括对断裂力学的简单介绍,相关的理论和方法,现阶段存在的问题及技术关键,发展趋势。
英文摘要:Four aspects of fracture mechanics are referred in this paper, including brief introduction about fracture mechanics, related theories and methods, problems and key technologies existing at the present stage, and the development.1.引言断裂力学是近几十年才发展起来了的一门新兴学科,主要研究承载体由于含有一条主裂纹发生扩展(包括静载及疲劳载荷下的扩展)而产生失效的条件。
断裂力学应用于各种复杂结构的分析,并从裂纹起裂、扩展到失稳过程都在其分析范围内。
由于它与材料或结构的安全问题直接相关,因此它虽然起步晚,但实验与理论均发展迅速,并在工程上得到了广泛应用。
断裂力学研究的方法是:从弹性力学方程或弹塑性力学方程出发,把裂纹作为一种边界条件,考察裂纹顶端的应力场、应变场和位移场,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
2.国内外相关研究现状目前,断裂力学总的研究趋势是:从线弹性到弹塑性;从静态断裂到动态断裂;从宏观微观分离到宏观与微观结合;从确定性方法到概率统计性方法。
所以就断裂力学本身而言,根据研究的具体内容和范围,它又被分为宏观断裂力学(工程断裂力学)和微观断裂力学(属金属物理范畴)。
宏观断裂力学又可分为弹性断裂力学(它包括线性弹性断裂力学和非线性弹性断裂力学)和弹塑性断裂力学(包括小范围屈服断裂力学和大范围屈服断裂力学及全面屈服断裂力学)。
工程断裂力学还包括疲劳断裂、蠕变断裂、腐蚀断裂、腐蚀疲劳断裂及蠕变疲劳断裂等工程中重要方面。
断裂力学概述

断裂力学是近几十年才发展起来的一支新兴学科 ,它从宏观的连续介质力学角度出发 ,研究含缺陷或裂纹的物体在外界条件(荷载、温度、介质腐蚀、中子辐射等)作用下宏观裂纹的扩展、失稳开裂、传播和止裂规律。
断裂力学应用力学成就研究含缺陷材料和结构的破坏问题 ,由于它与材料或结构的安全问题直接相关 ,因此它虽然起步晚 ,但实验与理论均发展迅速 ,并在工程上得到了广泛应用。
例如断裂力学技术已被应用于估算各种条件下的疲劳裂纹增长率、环境问题和应力腐蚀问题、动态断裂以及确定试验中高温和低温的影响 ,并且由于有了这些进展 ,在设计有断裂危险性的结构时 ,利用断裂力学对设计结果有较大把握。
断裂力学研究的方法是:从弹性力学方程或弹塑性力学方程出发 ,把裂纹作为一种边界条件 ,考察裂纹顶端的应力场、应变场和位移场 ,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
用弹性力学的线性理论研究含裂纹体在荷载作用下的力学行为和失效准则的工程学科成为线弹性断裂力学。
在分析中,可认为材料是线弹性的,并且不考虑裂纹尖端极小范围内的屈服问题。
研究含裂纹体的力学行为可以从两种观点出发,即从能量平衡观点和从裂纹尖端应力场强度的观点进行研究。
按裂纹的受力特点和位移特点,可以把它们抽象化为张开型、滑移型和撕开型三种基本类型,任何形式的裂纹,都可以看成上述三种基本类型的组合。
从应力场强度的观点研究裂纹体的力学行为和失效准则。
Ⅰ型和Ⅱ型的脆断问题归结为平面问题下含裂纹的线弹性体的线弹性力学分析,先选取满足双调和方程和边界条件的应力函数,极坐标系原点选在裂纹尖端,把裂纹看作一部分边界,就可以用弹性力学的方法求得裂纹体的应力场和位移场。
求出的应力函数为Williams应力函数,得到极坐标下应力分量表达式,通过物理方程和几何方程得到几何分量表达式。
按远场的边界条件不同可分别求出Ⅰ型和Ⅱ型的裂纹尖端领域的应力场和位移场。
Ⅲ型问题为反平面应力问题,xy方向位移为零,只有z方向位移且是xy的函数,只有两个应变分量和两个应力分量,解一个平衡方程得Ⅲ型裂纹尖端领域的应力场合位移场。
材料断裂力学简述

材料断裂力学简述断裂力学是研究含裂纹物体的强度和裂纹扩展规律的科学。
它是固体力学的一个分支,又称裂纹力学,萌芽于20世纪20年代A.A.格里菲斯对玻璃低应力脆断的研究。
其后,国际上发生了一系列重大的低应力脆断灾难性事故,如第二次世界大战期间, 美国建造了2000多艘全焊接的货轮和油轮,据统计在1943~1965年期间断为两截的有20艘。
50年代,北极星导弹固体燃料发动机壳体的实验发射和耐压试验时多次因破裂而爆炸。
压力容器、大电机转子、桥梁等也发生过很多脆断事故。
这些都促进了断裂研究工作和线弹性断裂力学的形成。
通过断裂力学分析,可以确定裂纹的容许尺寸、评定零件和构件的承载能力,估算其使用寿命,从而提出零件和构件的损伤容限设计方法。
传统的材料力学和结构力学都假设材料为不包含裂纹的连续体,并比较工作应力和许用应力来判断强度。
然而机械零件和构件,特别是大型铸件和锻件,难免有裂纹或类裂纹缺陷的存在。
断裂力学在零件和裂纹的尺寸、载荷与材料力学性能三者之间建立了定量的关系,从而可以根据试样的断裂力学试验数据,推测带裂纹机械零件和构件的抗断裂能力。
由于断裂力学兴起的年代较晚,所涉及的学科较多,现在仍处于发展阶段,因此无论其研究的对象、方法或其分类都尚未完全定型,人们认为它不仅仅是固体力学的一个分支,而且也是工程技术科学或材料科学的一个分支。
但目前断裂力学总的研究趋势是:从线弹性到弹塑性;从静态断裂到动态断裂;从宏观微观分离到宏观与微观结合;从确定性方法到概率统计性方法。
所以就断裂力学本身而言,根据研究的具体内容和范围,它又被分为宏观断裂力学(工程断裂力学)和微观断裂力学(属金属物理范畴)。
根据所研究的裂纹尖端附近材料塑性区的大小,可将断裂力学分为线弹性断裂力学和弹塑性断裂力学;根据所研究的引起材料断裂的载荷性质,可将断裂力学分为断裂静力学和断裂动力学。
断裂力学的主要任务是求得各类材料的断裂韧度;确定物体在给定外力作用下是否发生断裂,即建立断裂准则;研究载荷作用过程中裂纹扩展规律;研究在腐蚀环境和应力同时作用下物体的断裂(即应力腐蚀)问题。
(完整word)岩石的损伤力学及断裂力学综述

岩石的断裂力学及损伤力学综述摘要:论述了国内外断裂力学及损伤力学的学科发展历程,总结了岩体断裂力学损伤力学的研究内容、研究特点以及岩石力学专家们一些年来所取得的主要成果,并简单介绍了断裂力学损伤力学在岩土工程中的实际应用.最后,通过对岩石破坏的断裂—损伤理论的阐述,指出了综合考虑损伤与断裂的破坏理论是能更好地反映岩石实际破坏过程的一种新的理论, 可在以后的理论研究和实际工程中得以更为广泛的应用。
关键词:岩石断裂力学损伤力学应用1 引言岩石的破坏过程总是伴随着损伤(分布缺陷)和裂纹(集中缺陷)的交互扩展, 这种耦合效应使得裂纹尖端附近区域材料必然具有更严重的分布缺陷。
岩石的破坏, 如脆性断裂和塑性失稳,虽然有突然发生的表面现象,但是,从材料损伤的发生、发展和演化直到出现宏观的裂纹型缺陷, 伴随着裂纹的稳定扩展或失稳扩展,是作为过程而展开的。
经典的断裂力学广泛研究的是裂纹及其扩展规律问题。
物体中的裂纹被理想化为一光滑的零厚度间断面。
在裂纹的前缘存在着应力应变的奇异场,而裂纹尖端附近的材料假定同尖端远处的材料性质并无区别。
象裂纹这样的缺陷可称它为奇异缺陷,因此经典断裂力学中物体的缺陷仅仅表现为有奇异缺陷的存在。
而损伤力学所研究的是连续分布的缺陷,物体中存在着位错、微裂纹与微孔洞等形形色色的缺陷,这些统称为损伤.从宏观来看,它们遍布于整个物体.这些缺陷的发生与发展表现为材料的变形与破坏。
损伤力学就是研究在各种加载条件下,物体中的损伤随变形而发展并导致破坏的过程和规律。
事实上,物体中往往同时存在着奇异缺陷和分布缺陷。
在裂纹(奇异缺陷)附近区域中的材料必然具有更严重的分布缺陷,它的力学性质必然不同于距离裂纹尖端远处的材料.因此, 为了更切合实际, 就必须把损伤力学和断裂力学结合起来, 用于研究物体更真实的破坏过程。
2 断裂力学2。
1 断裂力学学科发展“断裂力学”指的是固体力学的一个重要分支,该学科要在假定裂纹存在的条件下,寻求裂纹长度、材料抗裂纹增长的固有阻力、以及能使裂纹高速扩展从而导致结构失效的应力之间的定量关系[]1。
断裂力学概述及其应用

断裂力学概述及应用定义:断裂力学(fracture mechanics) 是为解决机械结构断裂问题而发展起来的力学分支,它将力学、物理学、材料学以及数学、工程科学紧密结合,是一门涉及多学科专业的力学专业课程。
起源:1957年,美国科学家G.R.Irwin提出应力强度因子的概念, 线弹性断裂理论的重大突破,应力强度因子理论作为断裂力学的最初分支——线弹性断裂力学建立起来。
发展:现代断裂理论大约是在1948—1957年间形成,它是在当时生产实践问题的强烈推动下,在经典Griffith理论的基础上发展起来的,上世纪60年代是其大发展时期。
我国断裂力学工作起步至少比国外晚了20年,直到上世纪70年代,断裂力学才广泛引入我国,一些单位和科技工作者逐步开展了断裂力学的研究和应用工作。
从上世纪五十年代中期以来,断裂力学发展很快,目前线性理论部分已比较成熟,在工程方面,已广泛应用于宇航、航空、海洋、兵器、机械、化工和地质等许多领域。
分类:断裂力学的类型分为:线性断裂力学、弹塑性断裂力学、断裂动力学。
研究的内容包括了:裂纹的起裂条件、裂纹在外部载荷和(或)其他因素作用下的扩展过程、裂纹扩展到什么程度物体会发生断裂。
1.线性断裂力学:应用线弹性理论研究物体裂纹扩展规律和断裂准则。
1921年格里菲斯通过分析材料的低应力脆断,提出裂纹失稳扩展准则格里菲斯准则。
1957年G.R.欧文通过分析裂纹尖端附近的应力场,提出应力强度因子的概念,建立了以应力强度因子为参量的裂纹扩展准则。
线弹性断裂力学可用来解决脆性材料的平面应变断裂问题,适用于大型构件(如发电机转子、较大的接头、车轴等)和脆性材料的断裂分析。
实际上,裂纹尖端附近总是存在塑性区,若塑性区很小(如远小于裂纹长度),则可采用线弹性断裂力学方法进行分析。
2.弹塑性断裂力学:应用弹性力学、塑性力学研究物体裂纹扩展规律和断裂准则,适用于裂纹体内裂纹尖端附近有较大范围塑性区的情况。
断裂力学报告

目录一、断裂力学的基本概念 (2)Griffith断裂判据 (2)能量平衡理论 (3)应力强度因子··········错误!未定义书签。
裂纹问题的三种基本类型··········错误!未定义书签。
利用应力强度因子提出的断裂判据 (4)J积分 (5)J积分简介 (5)J积分断裂判据 (5)J积分的物理意义 (6)二、冻土断裂力学在挡墙基础稳定性分析中的应用 (6)冻土断裂力学判据 (6)挡墙基础强度和稳定性分析 (6)三、个人小结 (8)参考文献: (8)断裂力学G、K、J断裂判据及其应用通过对断裂力学的学习,我们知道断裂力学作为一门新兴的学科,由于生产实践、工程设计等方面的需要,已成为固体力学的一个重要组成部分。
目前断裂力学已广泛应用于宇航与航空工程、化学工程、机械工程、核能工程、造船等各个部门。
近年来,对岩石这类地质材料的破坏过程与机理的研究也应用了断裂力学的方法和理论,可见断裂力学的发生与发展也是以生产与工程实践的需要为动力的。
在本文总共分两部分,一部分为断裂力学的基本概念,一部分为一断裂力学的实例。
一、 断裂力学的基本概念1.1 Griffith 断裂判据我们知道研究断裂的目的主要是防止构件断裂,这个任务长期以来人们已经积累了丰富的经验,建立了许多强度理论条件:⎪⎪⎪⎩⎪⎪⎪⎨⎧→→→=≤在交变应力作用下对塑形材料对脆性材料nn n r ss bb σσσσσ][ 式中:→σ根据外载计算的工作应力;→][σ许用应力;b σ、s σ、→r σ由实验得到的不同材料的极限强度、屈服极限、持久极限; b n 、s n 、→r n 对应于b σ、s σ、r σ的安全系数;但是对于有裂纹的物体上述强度理论已经不再适用,为此本世纪二十年代英国著名的科学家Griffith ,提出了能量释放(energy release)的观点,以及根据这个观点而建立的断裂判据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
断裂力学概述关键词:断裂力学;现状;阶段性问题;发展趋势中文摘要:本文主要介绍了断裂力学的4个方面,包括对断裂力学的简单介绍,相关的理论和方法,现阶段存在的问题及技术关键,发展趋势。
英文摘要:Four aspects of fracture mechanics are referred in this paper, including brief introduction about fracture mechanics, related theories and methods, problems and key technologies existing at the present stage, and the development.1.引言断裂力学是近几十年才发展起来了的一门新兴学科,主要研究承载体由于含有一条主裂纹发生扩展(包括静载及疲劳载荷下的扩展)而产生失效的条件。
断裂力学应用于各种复杂结构的分析,并从裂纹起裂、扩展到失稳过程都在其分析范围内。
由于它与材料或结构的安全问题直接相关,因此它虽然起步晚,但实验与理论均发展迅速,并在工程上得到了广泛应用。
断裂力学研究的方法是:从弹性力学方程或弹塑性力学方程出发,把裂纹作为一种边界条件,考察裂纹顶端的应力场、应变场和位移场,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
2.国内外相关研究现状目前,断裂力学总的研究趋势是:从线弹性到弹塑性;从静态断裂到动态断裂;从宏观微观分离到宏观与微观结合;从确定性方法到概率统计性方法。
所以就断裂力学本身而言,根据研究的具体内容和范围,它又被分为宏观断裂力学(工程断裂力学)和微观断裂力学(属金属物理范畴)。
宏观断裂力学又可分为弹性断裂力学(它包括线性弹性断裂力学和非线性弹性断裂力学)和弹塑性断裂力学(包括小范围屈服断裂力学和大范围屈服断裂力学及全面屈服断裂力学)。
工程断裂力学还包括疲劳断裂、蠕变断裂、腐蚀断裂、腐蚀疲劳断裂及蠕变疲劳断裂等工程中重要方面。
如今在断裂力学研究方法中,又引入可靠性理论,称为概率断裂力学,使断裂力学的研究内容更加丰富,也使断裂力学的理论得到进一步的发展和完善,并在工程实际中发挥出越来越大的指导作用。
(1)格里菲斯理论为研究材料内部含有裂纹对材料强度有多大影响,上世纪20年代的格里菲斯首先研究了含裂纹的玻璃强度,并得出断裂能量的关系:S G γ2=这就是著名的格里菲斯断裂判据,其中G 为裂纹尖端能量释放率,γs 是表面自由能(材料每形成单位裂纹面积所需能量)。
由此关系可得格里菲斯裂纹应力和裂纹尺寸关系:()为裂纹长度a a Es πγσ2=若S G γ2>,裂纹将扩展;若S G γ2<,裂纹不会扩展;若S G γ2=,为极限状态。
又,若裂纹扩展,且0>da dG ,可以确定为失稳扩展;若裂纹扩展,且0<dadG ,则裂纹止裂。
(2)应力强度因子K裂纹顶端区域弹性应力场强度因子的简称。
是线弹性力学中反映裂纹顶端区域弹性应力场强弱的力学参数,以符号K I 表示。
对裂纹顶端附近区域应力场的研究可知:靠近裂纹顶端的应力,在趋近于裂纹顶端处,其数值以某种方式趋向于无穷大,即具有奇异性。
因此,不能用此处应力来衡量其强度。
而K I 值能反映裂纹顶端区域弹性应力场的强度,它的数值大小与所受荷载的大小、裂纹尺寸及几何形状有关,格里菲斯裂纹的数学表达式为: a K I πσ=其中,σ为应力,a 为裂纹长度,按裂纹扩展的三种形式有K I 、K II 、K III ,分别表示I 型,II 型和III 型裂纹的应力强度因子。
其中,对于I 性裂纹:()为平面应力E E K G I 2=注:应力强度因子适用于裂纹尖端塑性区比K 场区小几倍,也比裂纹长度小几倍。
如韧性材料。
(3)J 积分1968年由赖斯(J .R .Rice )提出。
它反映裂纹顶端由于大范围屈服而产生的应力、应变集中程度。
J 积分的定义是:⎰Γ⎪⎭⎫ ⎝⎛∂∂⋅-=ds x u T Wdy J 用于研究平面问题。
它代表与裂纹扩展有关的能量。
式中右侧第一项是与应变能有关的能量,其中W 是应变能的密度(即单位体积应变能)。
在弹塑性情况下,为单调加载过程中试件各处体元所接受的应力变形功密度(包括弹性应变能和塑性变形功)。
第二项是ds 上面力分量;ds 是路径Γ上的弧元。
J 积分有以下各性质:1)J 积分与路径无关2)J 积分能决定裂纹顶端弹塑性应力应变场3)J 积分与形变功功率有如下关系:∇⎪⎭⎫ ⎝⎛∂∂-=a U B J 1 式中,B 为试件厚度,U 为试件的形变功,∇为给定位称。
上式是J 积分得以实验测定的基础。
(4)阻力曲线断裂力学中表示裂纹在材料中发生稳定扩展行为的曲线(下图所示)。
纵坐标为裂纹扩展的阻力,用J 积分、CTOD 的δ或应力强度因子K 表示,横坐标为裂纹扩展量△a 。
裂纹未扩展时曲线与纵轴重合,一旦扩展则△a ≠0,曲线便偏离纵轴,拐点即为起裂点。
再后面表示稳定扩展过程。
当曲线上某点的切线能通过水平负轴上表示裂纹长度的点时,表示将发生失稳扩展。
失稳时裂纹扩展推动力与裂纹扩展阻力随裂纹尺寸的变化率相同,不需加载裂纹即会自行快速扩展而断裂。
阻力曲线可以用试样测试,可用于确定起裂值(δi 或J IC )或条件起裂值( δ0.005或J 0.005等),也可用以预测构件中裂纹发生亚临界扩展的过程。
(5)数值计算方法随着断裂力学研究的日益深入,需要求解的问题日趋复杂化和多样化,使得如何建立高效、高精度的计算方法成为学者们研究的热点。
由于计算机科学、计算数学和力学等学科的不断发展,用于解决断裂力学问题的数值计算方法不断涌现,从早期的有限差分法、有限元法、边界元法到现在的无网格法、数值流形法、小波数值法、非连续变形分析等,它们正成为推动断裂力学研究不断发展的重要工具。
1)有限元法:在有限元解的情况下,通过应力恢复、误差估计和新网格自动划分,进而再进行有限元求解,重复这一过程直至得到满意的有限元解。
另外,随机分析是断裂力学发展的一个重要方向,也是结构可靠性评估的基础。
随机有限元法在有限元法的基础上,采用随机参数来描述工程实际问题,主要研究内容包括随机变分原理、随机有限元控制方程的建立及其求解。
2)边界元法:这是继有限元法之后发展起来的一种求解力学问题的数值方法。
其构成包含如下三个主要部分:①基本解的特性及其应用;②离散化和边界单元的选取;③叠加法与求解技术。
这种方法的优点是应用Guass定理使问题降阶,将三维问题化为二维问题,将二维问题化为一维问题,使数据的准备大为简化,网格的划分和重新调整更为方便,最后形成的代数方程组的规模也小得多。
3)无网格法:也叫无单元法。
该方法将整个求解域离散为独立的节点,而无须将节点连成单元,它不需要划分网格,从而克服了有限元法在计算过程中要不断更新网格的缺陷。
计算过程中可以实时跟踪裂纹尖端区域进行局部细化,将连续的裂纹扩展过程看作多个线性增量,每一个增量内裂纹扩展角根据应力强度因子确定。
通过在裂纹尖端细化节点引入外部基函数提高计算精度。
4)数值流形法:该方法的基本思想是将微分几何的流形原理引入材料分析,以拓扑流形与微分流形为基础,同时吸收有限元中插值函数构造方法与非连续变形分析中块体运动学理论两方面的优势,把连续和非连续变形力学问题统一起来。
5)小波数值法:该方法利用了小波具有的良好局部化特性,用小波函数对位移场进行逼近,建立了小波数值计算格式,模拟了裂纹尖端的奇异性问题并求解出裂纹尖端的应力强度因子。
3.现阶段存在的问题及技术关键上述方法或理论均源于格里菲斯的断裂理论,是建立在奇异性基础上的,即均基于裂纹顶端应力与应变为无限大的模式展开的。
Inglis数学尖裂纹模型的弹性力学解释断裂理论的基础。
这种数学尖裂纹上下表面间距为零,裂纹顶端曲率半径也为零,因而有弹性力学求出的应力分量在裂纹顶端处为无限大,这种现象称为奇异性。
奇异性理论一直延续至今,但奇异性断裂力学在物理上存在本质的缺陷,这主要表现在两方面:其一,在实际中发现的裂纹其上下表面间距和裂纹顶端曲率半径都是有限值,且不等于零;其二,实际裂纹,即使在裂纹顶端,应力与应变均为有限值,不存在所谓的应力与应变的奇异性。
这样,基于数学尖裂纹和应力奇异性的物理量缺乏坚实的物理基础。
为了完善理论,呈现非奇异性,可以采用比较符合真实情形的半圆形顶端的钝裂纹(或切口)模型,但钝裂纹的曲率半径的测量需要用金相的方法测出,这就需要金相断裂力学的发展。
4.未来的发展趋势弹塑性断裂力学虽取得了一些进展,但仍有许多尚待深入研究的问题,它是当前断裂力学的主要研究方向之一。
断裂动力学,对于线性材料还有待完善;对于非线性材料,尚处于研究初期,是断裂力学的又一主要研究方向。
随着对断裂问题的深入研究及数学工具的方便使用,断裂力学理论会日益成熟,断裂力学应用会日渐广泛。
对于数值计算方法,其未来的发展趋势为:跨尺度的断裂力学数值计算方法、并行数值计算方法、解析法与数值法的结合、多种计算方法的有机结合于融合、数据处理自动化。
参考文献:[1] 王自强,陈少华.高等断裂力学[M].科学出版社,2009[2] 范天佑.断裂理论基础[M].北京:科学出版社,2003[3]黄克智.弹塑性断裂力学的一个重要进展[J].力学与实践,1993,(1):1-7[4] 康颖安.断裂力学的发展与研究现状[J].湖南工程学院,2006,(1):39-42[5] 辛德臣.浅谈断裂力学的创立与发展[J].大庆师范学院学报,2005,(4):50-52[6] 单丙娟.浅谈断裂力学的发展与研究现状[J].内蒙古石油化工,2007,(7):55-56[7] 冒小萍,郎福元,柯显信.断裂力学的数值计算方法的研究现状与展望[J].商丘师范学院学报,2004,(2):20-24[8] 李健康等.断裂分析中的随机有限元方法[J].固体力学学报,2001,(1):85-88[9] 杨庆生,杨卫.断裂过程单的有限元模拟[J].计算力学学报,1997,(4):407-412。
