排列与组合、二项式定理精选课件PPT
合集下载
排列、组合、二项式定理精选教学PPT课件
当我们爱自己的孩子的时候，可曾想过，我们把爱孩子的十分之一去爱母亲，她就足矣，往往这一点也做不到，说句心里话，我们欠母亲的无法补偿，更无法用语言表达。 我有这两位母亲，虽然我的人生很不幸，但我有她们给我的无私的爱，我永远是幸福的，她们对我的爱我永存心里。在美国西雅图的一所著名教堂里，有一位德高望重的牧师――戴尔·泰勒。有一天，他向教会学校一个班的学生们先讲了下面这个故事。 那年冬天，猎人带着猎狗去打猎。猎人一枪击中了一只兔子的后腿，受伤的兔子拼命地逃生，猎狗在其后穷追不舍。可是追了一阵子，兔子跑得越来越远了。猎狗知道实在是追不上了，只好悻悻地回到猎人身边。猎人气急败坏地说：“你真没用，连一只受伤的兔子都追不
数有多少？
5×5=25
练习2
1.某段铁路上有12个车站，共需准备多少种普通客票？
P122
2.某段铁路上有12个车站，问有多少种不同的票价？
C122
3.用3，5，7，9四个数字，一共可组成多少个没有重 复数字的正整数
P41 P42 P43 P44
练习3
1.在(1+x)10的展开式中，二项式系数最大为 C150 ；
名称
排列
组合
一个~ ~~数
从n个不同元素中取出m个元 素，按一定的顺序排成一列
所有排列的个数
从n个不同元素中取出m个元 素，把它并成一组
所有组合的个数
符号
种数 公式 关系
性质
Pnm
C
m n
Pnm
Pnm
n(n 1) (n m
n! (n m)! Pnn n!
1)
0!
1
排列、组合、二项式定理
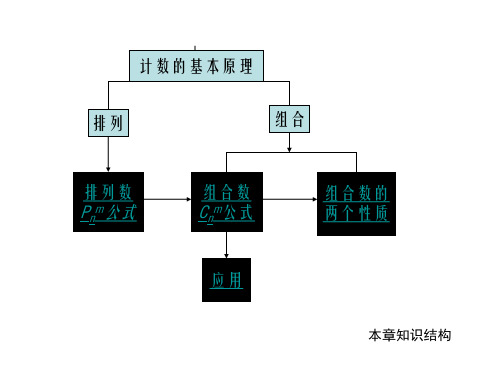
知识结构网络图：
排列与组合
二项式定理
数有多少？
5×5=25
练习2
1.某段铁路上有12个车站，共需准备多少种普通客票？
P122
2.某段铁路上有12个车站，问有多少种不同的票价？
C122
3.用3，5，7，9四个数字，一共可组成多少个没有重 复数字的正整数
P41 P42 P43 P44
练习3
1.在(1+x)10的展开式中，二项式系数最大为 C150 ；
名称
排列
组合
一个~ ~~数
从n个不同元素中取出m个元 素，按一定的顺序排成一列
所有排列的个数
从n个不同元素中取出m个元 素，把它并成一组
所有组合的个数
符号
种数 公式 关系
性质
Pnm
C
m n
Pnm
Pnm
n(n 1) (n m
n! (n m)! Pnn n!
1)
0!
1
排列、组合、二项式定理
知识结构网络图：
排列与组合
二项式定理
人教版中职数学(拓展模块)3.1《排列、组合与二项式定理》ppt课件1
所有组合的个数叫做组合数,用符号 Cnm表示.
组合与组合数
(3)组合数计数公式.
Cnm =⑥
Anm Amm
=⑦ n(n 1)(n 2) (n m 1) .
m!
n!
=⑧ m!(n m)! .
规定 Cn0 =1. (4)组合数的两个性质.
(ⅰ)
Cnm
=
C nm n
;
(ⅱ)
Cm n 1
=
Cnm
+ Cnm1
一、两个原理
3.分类和分步的区别 分类：完成一件事同时存在n类方法，每一类 都能独立完成这件事，各类互不相关.分步：完成一 件事须按先后顺序分n步进行，每一步缺一不可， 只有当所有步骤完成，这件事才完成.
一、两个原理
练习1： 书架上放有3本不同的数学书，5本 不同的语文书，6本不同的英语书．
（1）若从这些书中任取一本，有多少种不同的
二、 排列与排列数
(3)排列数计算公式.
Anm
=n(n-1)(n-2)…(n-m+1)=⑤
n!
(n m()其! 中m≤n).
(ⅰ)若m=n，排列称为全排列，记
=1·2·3·…·(n-1)·n=n!(称为n的阶乘)；
Ann (ⅱ)规定0!＝1.
组合与组合数
从n个不同元素中，取出m(m≤n)个不同元素组 成一组，叫做从n个不同元素中取出m个元素的一 个组合.
位整数（各位上的数字允许重复）？
解：要组成一个三位数，需要分成三个步骤：
第一步确定百位上的数字，从1～4这4个数字中任选一个数 字，有4种选法； 第二步确定十位上的数字，由于数字允许重复，共有5种选 法；
第三步确定个位上的数字，仍有5种选法．根据乘法原理， 得到可以组成的三位整数的个数是 N=4×5×5=100．
组合与组合数
(3)组合数计数公式.
Cnm =⑥
Anm Amm
=⑦ n(n 1)(n 2) (n m 1) .
m!
n!
=⑧ m!(n m)! .
规定 Cn0 =1. (4)组合数的两个性质.
(ⅰ)
Cnm
=
C nm n
;
(ⅱ)
Cm n 1
=
Cnm
+ Cnm1
一、两个原理
3.分类和分步的区别 分类：完成一件事同时存在n类方法，每一类 都能独立完成这件事，各类互不相关.分步：完成一 件事须按先后顺序分n步进行，每一步缺一不可， 只有当所有步骤完成，这件事才完成.
一、两个原理
练习1： 书架上放有3本不同的数学书，5本 不同的语文书，6本不同的英语书．
（1）若从这些书中任取一本，有多少种不同的
二、 排列与排列数
(3)排列数计算公式.
Anm
=n(n-1)(n-2)…(n-m+1)=⑤
n!
(n m()其! 中m≤n).
(ⅰ)若m=n，排列称为全排列，记
=1·2·3·…·(n-1)·n=n!(称为n的阶乘)；
Ann (ⅱ)规定0!＝1.
组合与组合数
从n个不同元素中，取出m(m≤n)个不同元素组 成一组，叫做从n个不同元素中取出m个元素的一 个组合.
位整数（各位上的数字允许重复）？
解：要组成一个三位数，需要分成三个步骤：
第一步确定百位上的数字，从1～4这4个数字中任选一个数 字，有4种选法； 第二步确定十位上的数字，由于数字允许重复，共有5种选 法；
第三步确定个位上的数字，仍有5种选法．根据乘法原理， 得到可以组成的三位整数的个数是 N=4×5×5=100．
排列、组合 和二项式定理幻灯片PPT
组合
组合数的概念和推导 组合数公式 组合数性质
CnmCnnm C n m 1C n mC n m 1
kCnk nCnk1
C k k C k k 1 C k k 2 C n k C n k 1 1
计数综合问题
先选后排
7.从3名男生和3名女生中，选出3名分别担 任语文、数学、英语的课代表，要求至少 有1名女生，则选派方案共有（ ）
其中能被5整除的四位数共有
个
二维：有5有0，有5无0，无5有0
主元：个位为0，个位为5（再根据需要细 分，选0与不选0）
在6名内科医生和4名外科医生中，内科主 任和外科主任各一名，现在要组成人医疗 小组送医下乡，依下列条件各有多少种方 法：
既有内科医生又有外科医生（间接考察）
既有主任又有外科医生
排列数应用
组合 组合数
组合数应用
二项式定理
教学内容
不仅有着许多直接应用，还是学习概率理 论的准备知识，而且由于其思维方法的新 颖性与独特性，因此它也是培养学生思维 能力的不可多得的好素材；作为初中多项 式乘法公式的推广——二项式定理，不仅 使前面组合等知识的学习得到强化，而且 与后面概率中的二项分布有着密切联系。
排列、组合 和二项式定理 幻灯片PPT
本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！
知识结构
分类计数原理、分步计数原理
排列 排列数
3．展开式的每一项由若干个a和若干个b的乘积 构成，a和b的个数之和等于n，它可以表示为ankbk．
中职数学21.1排列组合与二项式ppt课件
解： ( 3x 3 2)100 的展开式的通项公式为：
Tr1
Cr 100
•
100r
3x •
32
r
100r
r
3 2
•
23
•
Cr 100
•
x100r
100 2
r
,
r 3
r 0，1，2， ，100
均为整数时,T为有理数. 有理项即
r为6的倍数,且0 r 100.
整数次幂项
即r为0, 6,12,,96,展开式中共有17项有理项.
五、二项式定理：
将(a+b)n展开 （a+b）n=(a b)( ab)(ab)
n个
计算(a+b)n展开式的二项式系数并填入下表
n
(a+b)n展开式的二项式系数
1 11
2 121
3 1331
4 14641
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
对称性
(a+b)1 (a+b)2 (a+b)3 (a+b)4 (a+b)5 (a+b)6
解:（1＋ 1 )4 x
1
C41
(
1 x
)
C42
(
1 x
)2
C43
(
1 x
)3
C44
(
1 x
)4
1
4 x
6 x2
4 x3
1 x4
.
注：1）注意对二项式定理的灵活应用
2）注意区别二项式系数与项的系数的概念
二项式系数为 Cnr ；
项的系数为：二项式系数与数字系数的积
排列与组合、 二项式定理的应用PPT优秀课件
所以符合题意的不同取法种数为 C104(4C64+6+3)=141.
方法二, 在四面体中取定一个面,
记为, 那么取不同不共面的4个点, 可
分为四类：
第一类, 恰有3个点在 上, 这时该
3点必然不在同一条棱上, 因此, 4个点 的不同取法数为4(C633)=68.
第二类，恰有2个点在α上，可分两 种情况：①该2点在同一条棱上，这时4 个点的不同取法数为4C32(C42-3)=27; ② 该2点不在同一条棱上，这时4个点的不 同取法数为(C62-3C32)(C42-1)=30.
(4) 安排甲、乙和丙3人以外的其他4 人，有A44种排法；由于甲、乙要相邻, 故再把甲、乙排好, 有A22种排法, 最后把 甲、乙排好的这个整体与丙分别插入原 先排好的4人的空档中有A52种排法, 这样, 总共有A44 A22 A52=960种不同排法.
(5) 从7个位置中选出4个位置把男 生排好, 则有A74种排法; 然后再在余下 的3个空位置中排女生, 由于女生要按 身体高矮排列, 故仅有一种排法, 这样 总共有A74 840种不同排法.
[评注] 排列问题中，部分元素 相邻的问题可用“视一法”解；部分 元素不相邻的问题可用“插入法”解， 部分元素定序的问题也可用“插入法” 解.
[例5] 按以下要求分配6本不同的书, 各有几种分法？
(1) 平均分给甲、乙、丙三人，每人 2本；
(2) 平均分成三份，每份2本； (3) 甲、乙、丙三人一人得1本，一 人得2本，一人得3本；
4×3×2×2×2=96种；若区域4与区域6
不栽同一种花，则区
域2、3两块中有1种栽
5
法，总共有4×3×2× 6 1 4
1×1=24，所以一共有
方法二, 在四面体中取定一个面,
记为, 那么取不同不共面的4个点, 可
分为四类：
第一类, 恰有3个点在 上, 这时该
3点必然不在同一条棱上, 因此, 4个点 的不同取法数为4(C633)=68.
第二类，恰有2个点在α上，可分两 种情况：①该2点在同一条棱上，这时4 个点的不同取法数为4C32(C42-3)=27; ② 该2点不在同一条棱上，这时4个点的不 同取法数为(C62-3C32)(C42-1)=30.
(4) 安排甲、乙和丙3人以外的其他4 人，有A44种排法；由于甲、乙要相邻, 故再把甲、乙排好, 有A22种排法, 最后把 甲、乙排好的这个整体与丙分别插入原 先排好的4人的空档中有A52种排法, 这样, 总共有A44 A22 A52=960种不同排法.
(5) 从7个位置中选出4个位置把男 生排好, 则有A74种排法; 然后再在余下 的3个空位置中排女生, 由于女生要按 身体高矮排列, 故仅有一种排法, 这样 总共有A74 840种不同排法.
[评注] 排列问题中，部分元素 相邻的问题可用“视一法”解；部分 元素不相邻的问题可用“插入法”解， 部分元素定序的问题也可用“插入法” 解.
[例5] 按以下要求分配6本不同的书, 各有几种分法？
(1) 平均分给甲、乙、丙三人，每人 2本；
(2) 平均分成三份，每份2本； (3) 甲、乙、丙三人一人得1本，一 人得2本，一人得3本；
4×3×2×2×2=96种；若区域4与区域6
不栽同一种花，则区
域2、3两块中有1种栽
5
法，总共有4×3×2× 6 1 4
1×1=24，所以一共有
高中数学 排列、组合、二项式定理 组合 (初始课件)
组合的定义
• 一般地，从n个不同元素中,任取m（m《n） 个元素合成一组,叫做从n个不同元素中取 出m个元素的一个组合.
你能说说排列与组合之间的联系与 区别吗？
• 相同点：两者都是从n个不同元素中取出m 个元素
• 不同点：排列与元素的顺序有关，组合与 元素的顺序无关
判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e}，则集合A的含有3个元素的子集有 多少个? 组合问题 (2)某铁路线上有5个车站，则这条铁路线上共需准备多少种 车票? 排列问题 有多少种不同的火车票价？ 组合问题 组合是选择的结果，排列 (3)10名同学分成人数相同的数学和英语两个学习小组 ,共有 是选择再排序的结果. 多少种分法? 组合问题 (4)10人聚会，见面后每两人之间要握手相互问候,共需握手 多少次? 组合问题
内容
描述
课件名称
组合
课程内容
组合的定义及其特点
教学设计
激趣导入：通过具体例子组合的定义。 知识新授：通过实例归纳总结组合特征，得出组合的 定义。 课堂练习：通过一小题巩固 课堂小结：总结
Байду номын сангаас
组合
主讲教师：栾小敏
探究
• 问题1：从甲、乙、丙3名同学中选出2名参 加一项活动，其中1名同学参加上午的活动， 另1名同学参加下午的活动，有多少种不同 的选法？ • 问题2：从甲、乙、丙3名同学中选出2名去 参加一项活动，有多少种不同的选法？
思考
• 这两个问题有什么联系与区别？ • 都是两名同学去参加活动 • 不同的是问题1有顺序，问题2没有顺序
• 问题1：从3名同学中选出2名：甲乙，甲丙， 乙丙
• 而且还要将他们按照“上午在前，下午在 后”的顺序排列。
高中数学 排列、组合、二项式定理 二项式定理 (初始课件)
引出定理，总结特征
(a b) C a C a
n 0 n n 1 n
n 1
bC a
2 n r
n 2
b
2 n
C a
r n
n r
b C b
n n
二项展开式定理:
一般地，对于nN*，有：
(a b) C a C a
n 0 n n 1 n
n 1
bC a
系数
C4
0
C4
1
C4
2
C4
3
C4
4
(a+b)4 ＝ C40 a4 ＋C41 a3b ＋C42 a2b2 ＋C43 ab3 ＋C44 b4
将(a+b)n展开的结果又是怎样呢？ 发现规律： 对于（a+b）n=
(a b)(a b) (a b)
n个
的展开式中an-rbr的系数是在n个括号中，恰有r个 r 括号中取b(其余括号中取a)的组合数 C n .那么， 我们能不能写出(a+b)n的展开式？
r 1 n
二项展开式定理: n 0 n 1 n 1 r n r r n n (a b) Cn a Cn a b Cn a b Cn b
1.项数规律： 展开式共有n+1个项 2.二项式系数规律：
(n N )
C 、C 、C 、 、C
0 n 1 n 2 n
n n
3.指数规律：
（1）各项的次数和均为n； （2）二项和的第一项a的次数由n逐次降到0， 第二项b的次数由0逐次升到n.
单三步
小结
• 二项式定理是初中多项式乘法的延伸，又 是后继学习概率的基础，要理解和掌握好 展开式的规律，利用它对二项式展开，进 行相应的计算与证明。
排列组合与二项式定理PPT课件
(1)C0n＋Cn1
＋
…＋
Crn＋…
＋
Cnn＝ 2n；
C0n＋
Cn2
＋
…＝
Cn1
＋
C
3 n
＋…＝2n－1.
(2) 应 用 “ 赋 值 法 ” 可 求 得 二 项 展 开 式 中 各项 系 数 和 为
f(1)．“奇数(偶次)项”系数和为12[f(1)＋f(－1)]，“偶数(奇次)
项”系数和为12[f(1)－f(－1)]．
第18讲 │ 要点热点探究
要点热点探究
► 探究点一 计数原理及其应用
例1(1)在任意两个正整数m和n间定义某种运算，用⊗表 示运算符号，并规定，当m和n都为奇数或都为偶数时，m⊗n ＝m＋n；当m和n中有一个为奇数，另一个为偶数时，m⊗n ＝mn，设集合M＝{(a，b)|a⊗b＝36，a、b∈N＋}，则集合M 中共有________个元素；
第18讲 │ 要点热点探究
41 【解析】 一类：当 m、n 都为奇数时，由 m＋n＝36， 可知 m＝1,3,5，…，35，相应的 n 随之确定，共有 18 个不同 数对(a，b)；
二类：当 m 和 n 都为偶数时，由 m＋n＝36，可知 m＝ 2,4,6，…，34，相应的 n 随之确定，共有 17与D”看成一个整体，故有2A
3 4
＝
48种涂法．
故不同的涂法共有24＋48＝72种，选A.
【点评】 本题的涂色问题是一类典型应用两个计数原理解决的 计数问题，在高考中多次出现这类问题，解决的基本思路有两条：一 是按照颜色的种类进行分类；二是按区域一个一个地涂色．在具体填 涂的过程中应用计数原理，找到问题的解决方案．
第18讲 │ 要点热点探究
【点评】 分清是分类还是分步，是决定用分类计算原理 还是分步计算原理的必要条件；分类时标准统一，做到不重不 漏．分步时程序清晰，做到独立、完整．如果题目中既要用到 分类计数原理，又要用到分步计数原理，一般应遵循“先分 类，再分步”的原则．
《排列组合二项式》PPT幻灯片PPT
①取三个元素：有 C12·C12·C12＝8(种)； ②取四个元素：先从±1，±2，±3 三组中选取一组 C13， 再从剩下的两组中选两个元素 C12·C12，故共有 C13·C12·C12＝ 12(种)； ③取五个元素：C56＝6(种)； ④取六个元素：1 种． 由分类计数原理，共有 8＋12＋6＋1＝27(种)．
答案 C
【变式训练】
1．某次活动中，有30个人排成6行5列，现要从中选出 3人进展礼仪表演，要求这3人任意2人不同行也不同列，那 么不同的选法种数为________(用数字作答)．
解析 其中最先选出的一个有30种方法，此时这个人 所在的行和列不能再选人，还剩一个5行4列的队形，选第二 个人有20种方法，此时该人所在的行和列不能再选人，还剩 一个4行3列的队形，此时第三个人的选法有12种，根据分步 乘法计数原理，总的选法种数是30×20×12＝7 200.
义域中可能包含的元
素，分类讨论确定其定义域．
[规范解答] (1)若选甲，则有 A12A24种排法； 若不选甲，则有 A34种排法，则共有 A12A24＋A34＝48(种)． (2)分别由 x2＋1＝2，x2＋1＝5，x2＋1＝10 解得 x＝±1， x＝±2，x＝±3，由函数的定义，定义域中元素的选取分四 种情况：
③各二项式系数的和 a．C0n＋C1n＋C2n＋…＋Ckn＋…＋Cnn＝2n； b．C0n＋C2n＋…＋C2nr＋…＝C1n＋C3n＋…＋C2nr＋1＋…
＝12·2n＝2n－1.
自主学习导引
真题感悟
1．(2012·安徽)(x2＋2)x12－15 的展开式的常数项是
A．－3
B．－2
C．2
D．3
解析 第一个因式取 x2，第二个因式取x12得：1×C15(－
答案 C
【变式训练】
1．某次活动中，有30个人排成6行5列，现要从中选出 3人进展礼仪表演，要求这3人任意2人不同行也不同列，那 么不同的选法种数为________(用数字作答)．
解析 其中最先选出的一个有30种方法，此时这个人 所在的行和列不能再选人，还剩一个5行4列的队形，选第二 个人有20种方法，此时该人所在的行和列不能再选人，还剩 一个4行3列的队形，此时第三个人的选法有12种，根据分步 乘法计数原理，总的选法种数是30×20×12＝7 200.
义域中可能包含的元
素，分类讨论确定其定义域．
[规范解答] (1)若选甲，则有 A12A24种排法； 若不选甲，则有 A34种排法，则共有 A12A24＋A34＝48(种)． (2)分别由 x2＋1＝2，x2＋1＝5，x2＋1＝10 解得 x＝±1， x＝±2，x＝±3，由函数的定义，定义域中元素的选取分四 种情况：
③各二项式系数的和 a．C0n＋C1n＋C2n＋…＋Ckn＋…＋Cnn＝2n； b．C0n＋C2n＋…＋C2nr＋…＝C1n＋C3n＋…＋C2nr＋1＋…
＝12·2n＝2n－1.
自主学习导引
真题感悟
1．(2012·安徽)(x2＋2)x12－15 的展开式的常数项是
A．－3
B．－2
C．2
D．3
解析 第一个因式取 x2，第二个因式取x12得：1×C15(－
排列组合二项式定理复习ppt中小学教学课件
闻,由同狱鲁思蒂谦笔录成书《马可.波
罗游记》, 此书盛道东方之富庶和文明,
深受大众喜爱和传诵. 后来，他获释后
回到威尼斯. 1324年，马可·波罗70岁。
当年去世，葬於威尼斯的圣．多雷玆教
堂
。
( 威尼斯） 帕米尔高原
波 斯
（大都）
河西走廊
吐鲁番
楼兰古城
玉门关
敦煌
秦陵兵马俑
大雁塔
真真假假
马可·波罗一行经过长途跋涉，来到了繁华的 楼兰城，见到了美丽的楼兰姑娘。
D 10
3．1 3 32 399 被4除所得的系数为（ A ）
A．0 B．1
C．2
D．3
二填空题
1(05湖南 ) (1 x) (1 x)2 (1 x)3 (1 x)6 展开式中x2 的系数是___3_5__________
2 20012000 被22除所得的余数为 1 。
3 已知 (x 1)6 (ax 1)2 展开式中的 x3 系数是56，
例1：1993年全国高考题：同室4人各写1张贺年卡，先集
中起来，然后每人从中各拿1张别人送出的贺年卡，则4张
贺年卡不同的分配方式有（ ）
A．6种
B．9种
C．11种
D．23种
解法1：设四人A，B，C，D写的贺年卡分别是a，b，c，d， 当A拿贺年卡b，则B可拿a，c，d中的任何一个，即B拿a， C拿d，D拿c或B拿c，D拿a，C拿d或B拿d，C拿a，D拿c， 所以A拿b时有三种不同分配方法．同理，A拿c ，d时也各
3×3×3×3=81
1.排列和组合的区别和联系：
名称
排列
组合
一个~
从n个不同元素中取出m个元 素，按一定的顺序排成一列
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当中间数为 3 时，有 2×3＝6 种；
本 当中间数为 4 时，有 4×5＝20 种；
目 开
当中间数为 6 时，有 5×6＝30 种；
关 当中间数为 7 时，有 6×7＝42 种；
当中间数为 8 时，有 7×8＝56 种；
当中间数为9时，有8×9＝72种．
内科医生都至少有 1 人的选派方法种数是________．(用数
本 字作答)
讲 栏
(2)(2013·浙江)将 A、B、C、D、E、F 六个字母排成一排，
目 开
且 A、B 均在 C 的同侧，则不同的排法共有________种．(用
关 数字作答)
解析 (1)分三类：①选 1 名骨科医生，
则有 C13(C14C35＋C24C25＋C34C15)＝360(种)．
Tr＋1＝Crnan－rbr，r＝0,1,2，…，n，其中 Crn叫做二项式系数．
(3)二项式系数的性质
①对称性：与首末两端“等距离”两项的二项式系数相等，
即 Cn0＝Cnn，Cn1＝Cnn－1，…，Crn＝Cnn－r，….
主干知识梳理
专题六 第1讲
n
②最大值：当
n
为偶数时，中间的一项的二项式系数 C
2 n
取得
n 1
最大值；当 n 为奇数时，中间的两项的二项式系数C n 2 ，
n 1
本 讲
C n 2 相等，且同时取得最大值．
栏
目 ③各二项式系数的和
开
关 a．C0n＋C1n＋C2n＋…＋Crn＋…＋Cnn＝2n；
b．Cn0＋C2n＋…＋C2nr＋…＝C1n＋Cn3＋…＋C2nr＋1＋… ＝12·2n＝2n－1.
当相同的数字是 1 时，共有 C13C13个，
由分类计数原理知共有“好数”C13＋C13C13＝12 个．
答案 (1)96 (2)12
热点分类突破
专题六 第1讲
考点二 排列与组合
例 2 (1)(2013·重庆)从 3 名骨科、4 名脑外科和 5 名内科医生
中选派 5 人组成一个抗震救灾医疗小组，则骨科、脑外科和
本
讲 三个、四个、五个字母这 4 类计算，再考虑右侧情况．
栏
目 开
主干知识梳理
专题六 第1讲
(3)组合数的性质
①Cmn ＝Cnn－m；
②Cmn＋1＝Cmn ＋Cmn －1.
3．二项式定理
本 讲
(1)定理：(a＋b)n＝C0nan＋C1nan－1b＋Cn2an－2b2＋…＋Crnan－rbr
栏 目
＋…＋Cnnbn(r＝0,1,2，…，n)．
开 关
(2)二项展开式的通项
本 讲
公式是
A
m n
＝
n(n
－
1)(n
－
2)…(n
－
m
＋
1)
或
写
成
A
m n
＝
栏
n！
目 开
n－m！.
关 (2)组合：从 n 个不同元素中，任取 m(m≤n)个元素并成一
组，叫做从 n 个不同元素中取出 m 个元素的一个组合．从
n 个不同元素中取出 m 个元素的组合数公式是 Cmn ＝nn－1n－m2！…n－m＋1或写成 Cmn ＝m！nn！ －m！.
开
关
热点分类突破
专题六 第1讲
(1)在航天员进行的一项太空实验中，先后要实施6 个程序，其中程序A只能出现在第一步或最后一步，程序B和 本 C实施时必须相邻，则实验顺序的编排方法共有________
讲
栏 种．
目
开 (2)如果把个位数是1，且恰有3个数字相同的四位数叫作“好
关
数”，那么在由1,2,3,4四个数字组成的重复数字的四位数 中，“好数”共有________个．
数为________．
热点分类突破
专题六 第1讲
本题主要考查分类计数原理与分步计数原理的简
本 讲
单应用，解题的关键是合理分类，正确分步．
栏
目
开
关
热点分类突破
专题六 第1讲
解析 (1)无重复的三位数有：A39＋A21A29＝648 个． 则有重复数字的三位数有：900－648＝252 个． (2)分 8 类，当中间数为 2 时，有 1×2＝2 种；
本 讲 栏 目 开 关
专题六 第1讲
第 1 讲 排列与组合、二项式定理
【高考考情解读】
本 讲
高考中对两个计数原理、排列、组合往往通过实际问题进行综
栏 目
合考查，经常与概率问题相结合，出现在解答题中，难度中等；
开 关
对于二项式定理的考查，难度较小．
主干知识梳理
专题六 第1讲
1．分类计数原理和分步计数原理 如果每种方法都能将规定的事件完成，则要用分类计数原
热点分类突破
专题六 第1讲
考点一 两个计数原理
例1 (1)(2013·山东改编)用0,1，…，9十个数字，可以组成有
本 讲
重复数字的三位数的个数为________．
栏 目
(2)如果一个三位正整数“a1a2a3”满足a1<a2且a3<a2，则称
开 关
这样的三位数为凸数(如120,343,275)，那么所有凸数的个
故共有2＋6＋12＋20＋30＋42＋56＋72＝240种．
答案 (1)252
(2)240
热点分类突破
专题六 第1讲
(1)在应用分类计数原理和分步计数原理时，一般
先分类再分步，每一步当中又可能用到分类计数原理．
本 讲
(2)对于复杂的两个原理综合使用的问题，可恰当列出示意图
栏 目
或表格，使问题形象化、直观化．
本
讲 理将方法种数相加；如果需要通过若干步才能将规定的事
栏
目 件完成，则要用分步计数原理将各步的方法种数相乘．
开 关
主干知识梳理
专题六 第1讲
2．排列与组合
(1)排列：从 n 个不同元素中，任取 m(m≤n)个元素，按照
一定的顺序排成一列，叫做从 n 个不同元素中取出 m 个元
素的一个排列．从 n 个不同元素中取出 m 个元素的排列数
②选 2 名骨科医生，则有 C23(C14C25＋C24C15)＝210(种)；
③选 3 名骨科医生，则有 C33C14C15＝20(种)．
热点分类突破
专题六 第1讲
∴骨科、脑外科和内科医生都至少有 1 人的选派方法种数是 360＋210＋20＝590.
(2)分类讨论：A、B 都在 C 的左侧，且按 C 的左侧分别有两个、
热点分类突破
专题六 第1讲
解析 (1)首先安排 A 有 2 种方法；
第二步在剩余的 5 个位置选取相邻的两个排 B，C，有 4 种排
法，而 B，C 位置互换有 2 种方法；
本 讲
第三步安排剩余的 3 个程序，有 A33种排法，共有 2×4×2×A33
栏 目
＝96 种．
开 关
(2)当相同的数字不是 1 时，有 C31个；