推荐-浙江省2018年五校联考试数学参考答案 精品
浙江省衢州市五校联盟2024-2025学年高一上学期期中联考数学试题

B. m = 2
C. m = 1或 m = 2
D. m 不存在
4.函数 y =
4 - x2 的定义域是( x
)
A. [ -2,2]
B. (-2, 2)
C.[-2,0) U (0, 2] D.[-4,0) È (0, 4]
5.设函数
f
(x)
=
æ çè
1 2
öx(x-a) 在区间 (0,1)
÷ø
a 上单调递增,则
x x2 + x -12 £ 0
,B
=
ìíx î
x
3 +1
£
1üý þ
.
(1)判断 2 是否为集合 B 中的元素,并说明理由;
(2)若全集U = R ,求 A Ç B , A È (ðU B) .
16.已知函数 f ( x) = x2 - 2ax - 3 .
(1)若 f ( f (-1)) = -3 ,求 a 的值;
C.{Æ,{0},{1}}
D.{Æ,{0},{1},{0,1}}
2.设 x Î R ,则“ x < 1”是“ x2 < 1 ”的( )
A.充分不必要条件 C.充要条件
B.必要不充分条件 D.既不充分也不必要条件
3.已知幂函数 f (x) = (m2 - 3m + 3)x m-1 为偶函数,则( )
A. m = 1
的取值范围是(
)
A. [ -2, 0)
B.(-¥, 0]
C. (0, 2]
D.[2, +¥)
6.若
x
£
2
,则函数
f
(x)
=
1 2x +
1
2018-2019学年浙江省台州市温岭市五校联考八年级(上)期中数学试卷
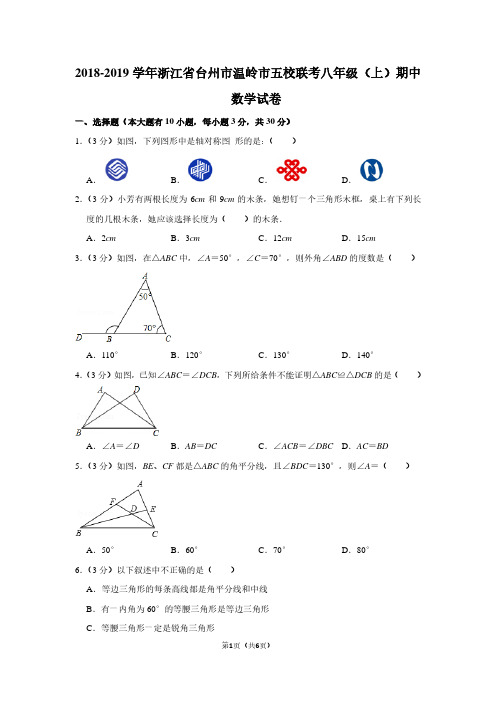
2018-2019学年浙江省台州市温岭市五校联考八年级(上)期中数学试卷一、选择题(本大题有10小题,每小题3分,共30分)1.(3分)如图,下列图形中是轴对称图形的是:()A.B.C.D.2.(3分)小芳有两根长度为6cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为()的木条.A.2cm B.3cm C.12cm D.15cm3.(3分)如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是()A.110°B.120°C.130°D.140°4.(3分)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD5.(3分)如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A=()A.50°B.60°C.70°D.80°6.(3分)以下叙述中不正确的是()A.等边三角形的每条高线都是角平分线和中线B.有一内角为60°的等腰三角形是等边三角形C.等腰三角形一定是锐角三角形D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,如果两个角不相等,那么它们所对的边也不相等7.(3分)等腰三角形一腰上的高与另一腰的夹角为60°,则顶角的度数为()A.30°B.30°或150°C.60°或150°D.60°或120°8.(3分)在平面直角坐标系中,点A的坐标为(4,0),使△OAB是等腰三角形,此时,点B的坐标不可能是()A.(0,4)B.(2,4)C.(4,4)D.(4,2)9.(3分)如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC =BE,则∠B的度数是()A.45°B.60°C.50°D.55°10.(3分)如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=4,将∠ACB平移使其顶点C与I重合,则图中阴影部分的周长为()A.9B.8C.6D.4二、填空题(本大题6小题,每小题3分,共18分)11.(3分)已知在△ABC中,∠C=∠A+∠B,则△ABC的形状是.12.(3分)若正多边形的一个内角等于120°,则这个正多边形的边数是.13.(3分)若点P(a+2,3)与点Q(﹣1,b+1)关于y轴对称,则a+b=.14.(3分)如图,DE是△ABC边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD 的周长为.15.(3分)如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,第2018个三角形的底角度数是.16.(3分)有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,﹣1,8,这称为第一次操作;做第二次同样的操作后也产生一个新数串:3,3,6,3,9,﹣10,﹣1,9,8,相继依次操作下,则从数串:3,9,8开始操作第100次时所产生的那个新数串的所有数之和是.三、解答题(本大题共8小题,17-19小题每小题6分,20-22小题每小题6分,23-24小题10分,共52分)17.(6分)已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:△ABC≌△DEF.18.(6分)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).19.(6分)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处.求∠1+∠2的度数.20.(6分)如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.21.(7分)小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.(1)请用a表示第三条边长.(2)问第一条边长可以为7m吗?请说明理由.22.(7分)如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD 于E,交BA的延长线于F.(1)求证:△ABD≌△ACF;(2)若BD平分∠ABC,求证:CE=BD;(3)若D为AC上一动点,∠AED如何变化,若变化,求它的变化范围;若不变,直接写出它的度数.23.(7分)问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);(1)特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为.24.(7分)已知△ABC在平面直角坐标系中的位置如图所示,直线l过点M(3,0)且平行于y轴.(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标.(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求P1P2的长.(用含a的代数式表示)(3)通过计算加以判断,PP2的长会不会随点P位置的变化而变化.2018-2019学年浙江省台州市温岭市五校联考八年级(上)期中数学试卷参考答案一、选择题(本大题有10小题,每小题3分,共30分)1.C;2.C;3.B;4.D;5.D;6.C;7.B;8.D;9.C;10.B;二、填空题(本大题6小题,每小题3分,共18分)11.直角三角形;12.6;13.1;14.28cm;15.()2017×75°;16.520;三、解答题(本大题共8小题,17-19小题每小题6分,20-22小题每小题6分,23-24小题10分,共52分)17.;18.;19.;20.;21.;22.;23.1;24.;。
2025届浙江省杭州市五校联盟高三第二次联考数学试卷含解析

2025届浙江省杭州市五校联盟高三第二次联考数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.运行如图所示的程序框图,若输出的值为300,则判断框中可以填( )A .30i >?B .40i >?C .50i >?D .60i >?2.已知x ,y R ∈,则“x y <”是“1xy <”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件3.若不等式22ln x x x ax -+对[1,)x ∈+∞恒成立,则实数a 的取值范围是( )A .(,0)-∞B .(,1]-∞C .(0,)+∞D .[1,)+∞4.等比数列{}n a 的各项均为正数,且384718a a a a +=,则3132310log log log a a a +++=() A .12 B .10 C .8 D .32log 5+5.已知集合{}22|A x y x ==-,2{|}10B x x x =-+≤,则A B =( )A .[12]-,B .[2]-,C .(2]-,D .2,2⎡-⎣6.给出下列三个命题:①“2000,210x x x ∃∈-+≤R ”的否定;②在ABC 中,“30B ︒>”是“3cos 2B <”的充要条件; ③将函数2cos2y x =的图象向左平移6π个单位长度,得到函数π2cos 26y x ⎛⎫=+ ⎪⎝⎭的图象. 其中假命题的个数是( )A .0B .1C .2D .37.将函数()sin(2)3f x x π=-()x R ∈的图象分别向右平移3π个单位长度与向左平移n (n >0)个单位长度,若所得到的两个图象重合,则n 的最小值为( )A .3πB .23πC .2πD .π8.已知函数()ln ln(3)f x x x =+-,则( )A .函数()f x 在()0,3上单调递增B .函数()f x 在()0,3上单调递减C .函数()f x 图像关于32x =对称D .函数()f x 图像关于3,02⎛⎫ ⎪⎝⎭对称 9.已知,x y 满足001x y x y x -⎧⎪+⎨⎪⎩,则32y x --的取值范围为( ) A .3,42⎡⎤⎢⎥⎣⎦ B .(1,2] C .(,0][2,)-∞+∞ D .(,1)[2,)-∞⋃+∞10.已知等差数列{}n a 中,若5732a a =,则此数列中一定为0的是( )A .1aB .3aC .8aD .10a11.如图,在平面四边形ABCD 中,满足,AB BC CD AD ==,且10,8AB AD BD +==,沿着BD 把ABD 折起,使点A 到达点P 的位置,且使2PC =,则三棱锥P BCD -体积的最大值为( )A .12B .122C .23D .16312.函数||1()e sin 28x f x x =的部分图象大致是( ) A . B .C .D .二、填空题:本题共4小题,每小题5分,共20分。
推荐-浙江省2018年五校联考理数学参考答案 精品

浙江省2018年五校联考试题数学(理工类)答案11.()⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛<-⎪⎭⎫ ⎝⎛≥-21121122x x x 12. (]9,∞- 13.1- 14.()2,0 三、解答题:本大题共6小题,每小题14分,共84分。
解答应写出文字说明,证明过程或演算步骤。
15.解:设()11,y x =,()22,y x =………………………………………………(2分) 则023211=+-=y x c a ;423222-=+-=y x c b ;………………………………………………(6分) 82121=+=y x ;42222=+=y x .………………………………………………(10分)解得⎩⎨⎧==6211y x ,或⎩⎨⎧-=-=6211y x ,对应的b 分别为⎩⎨⎧-==2022y x ,或⎩⎨⎧==1322y x ,分别代入()2,32-=+=n m ,解得6,4±=-=m n ……………(14分)16.解:()()cos 1sin sin 4f x a x x b x a b π⎛⎫=+++=+++ ⎪⎝⎭……………(2分)(Ⅰ)当1a =时,()14f x x b π⎛⎫==+++ ⎪⎝⎭∴当()22242k x k k Z πππππ-≤+≤+∈时,()f x 是增函数,∴函数()f x 的单调增区间为()32,244k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦……………(8分) (Ⅱ)由0x π≤≤得5444x πππ≤+≤∴sin 14x π⎛⎫≤+≤ ⎪⎝⎭………………………………………………(10分)∵0a <∴当sin 14x π⎛⎫+= ⎪⎝⎭时,()f x 取最小值33a b ++=……………(※)当sin 4x π⎛⎫+= ⎪⎝⎭时, ()f x 取最大值4,即4b =将4b =代入(※)式得1a =5a b +=(14分) 17.解:1)3P =31………………………………………………(4分) 2)由于第n 次到顶点A 是从D C B ,,三个顶点爬行而来,从其中任何一个顶点到达A 的概率都是31,而第1-n 次在顶点A 与小虫在D C B ,,是对立事件. 因此,第n 次到顶点A 的概率为()1131--=n n P P ………………(8分)即⎪⎭⎫⎝⎛--=--4131411n n P P ………………………………………(11分) ⎭⎬⎫⎩⎨⎧-∴=41,11n P P 是以43411=-P为首项,公比为31-的等比数列, ()N n n P n n ∈≥+⎪⎭⎫⎝⎛-=∴-,2 4131431………………………………(14分) 18.(Ⅰ)取1CC 的中点G ,则DG 为AE 在面1DC 内的射影,11D F DG AE D F ⊥∴⊥ 又1AD AE A D F ⋂=∴⊥面ADE ………………………………(5分) (Ⅱ)不成立………………………………(7分) 设1CC 、F D 1与平面ADE 的交点分别为G 、H, 在菱形11C CDD 中,可得DG DD ⊥1 又 平面⊥ABCD 平面11C CDD ,且平面⋂ABCD 平面11C CDD =CD ,CD AD ⊥1DD AD ⊥∴,因此AED DD 平面⊥1所以1DHD ∠为直线ADE F D 与平面1所成的角………………………………(10分) 在菱形11C CDD 内,因为CD C 1∠=060,所以01120=∠DE D可求得a F D 271=,所以1475arccos1=∠F D D , 在H DD Rt 1∆中,211π=∠+∠HD D H DD ,∴1DHD ∠=1475arcsin所以直线ADE F D 与平面1所成的角为1475arcsin.………………………(14分) 19.解:(1)设(0,),(,0)P b M a ,则,PF PM bk b k a=-=-201PF PM PM PF k k a b ⋅=∴⋅=-∴=-2(,0)M b ∴-,又PM PN =,即P 为MN 的中点,2(,2)N b b ∴因此,N 的轨迹方程为:24y x =,其轨迹为以(1,0)F 为焦点的抛物线………………………………………………(6分)(2)设:l y kx b =+,与24y x =联立得:20(*)4k y y b -+= 设1122(,),(,)A x y B x y ,则12y y 、是(*)式的两根,且124b y y k=由4OA OB ⋅=-得:12124x x y y +=-,即221212124,844y y y y y y ⋅+=-∴=-482bb k k∴=-∴=-………………………(10分) 因此,直线方程可写为:2(2)y kx k k x =-=- (*)式可化为:21212420,84k y y k y y y y k--=∴+==-而AB ⎡=⎣ 即:22116(1)(2)30k k ≤++≤ 令211x k =+,解得211125141122x k k k ≤≤∴≤≤∴-≤≤-≤≤或 ………………………(14分) 20.证明:(1) 0)1()1(==-f f ,v u v f u f -≤-)()( ∴()()()x x f x f x f -=-≤-=111由此可得:()x x f x -≤≤-11………………………(5分) (2)若01≤<≤-v u ,则由v u v f u f -≤-)()(,得1)()(≤-≤-u v v f u f ,同理,若10≤<≤v u ,则由v u v f u f -≤-)()(, 得1)()(≤-≤-u v v f u f ………………………………(9分)若101<≤<≤-v u ,则()()()()11)()(f v f f u f v f u f +---=- ()()()()()1111-+--≤-+--≤v u f v f f u f =()u v v u --=-++21110≤<≤v u ,1≥-∴u v ,因此()12≤--u v()()1≤-∴v f u f综上所述,对任意的]1,1[,-∈v u ,都有1)()(≤-v f u f ………(14分)。
浙江省2018年五校联考数学试题最终稿学参考答案

1 5
13. 26 2 34 ,
125 2 3
17. 4 33
三、解答题:本大题共 5 小题,共 74 分.解答应写出文字说明、证明过程或演算步骤. 18. (本题满分 14 分) 解:(Ⅰ)由 (b c) a (2
2 2
2)bc得
b 2 c 2 a 2 2bc,
km 1 x ,解得 xQ 1 k2 k
…………………………9 分
由 PB : y kx m 联立 OQ : y
∴ PQ 1 k
2
km 4k 1 k2 m
∴ S OPQ
PQ OQ 2
m 1 km 4k 1 k2 …………………………12 分 2 2 1 k 1 k2 m
EG EF sin
o
…………………15 分
方法(体积法)作,则由面面可得面 2 PE BF PBF , 由解得点到面距离从而 VP ACD VD PAC , D PAC h
ABCD, 3 , 2
PE
ABCD
sin
h 3 AD 4
20. (本小题满分 15 分)
xx 1 ' g x x ln x , 可得: f x 0 x 1 解: (Ⅰ)设 x 2x x 所以是增函数,得即欲证成立 g x g x .g 1 0, (5分) L L
2
x 1 ln x x 1 x ' x (Ⅱ)① f x ln x 0 x 1 2 2 2 2 x x 1 ln x x 1 ln x
当 k 1 时取等号
浙江省五校联考2018年高考模拟数学理科试卷及答案解析

浙江省五校联考2018年高考模拟数学理科试卷(总分:150分 时间:120分钟)一、选择题:本题共12小题,每小题5分,共60分. 1. 已知集合(){},|1A x y y x ==-,(){},|1B x y y x ==-+,则A B =I( )A.∅B.{}1C.{}0,1D.(){}1,02.已知复数z= 201821i i++(i 为虚数单位),则复数z 的共轭复数....在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x 、y 的 值分别为( )A. 7、8B. 5、7C. 8、5D. 7、74. 设向量a ,b 满足,()3-=g a a b ,则a 与b 的夹角为5若123)(23++-=x x a x x f 在区间⎪⎭⎫⎝⎛3,21上有极值点,则实数的取值范围是( )A. B. C. D.6. 执行如图所示的程序框图,若输出的57S =,则判断框内应填入的条件是( ) A .4k > B .5k > C.6k > D .7k >7. 已知ABCD 为正方形,其内切圆I 与各边分别切于E ,F ,G ,H ,连接EF ,FG ,GH ,HE .现向正方形ABCD 内随机抛掷一枚豆子,记事件A :豆子落在圆I 内,事件B :豆子落在四边形EFGH 外,则(|)P B A =( )A .14π-B .4π C .21π-D .2π8. 已知函数⎪⎩⎪⎨⎧≥<≤=1,4sin 10,2)(x x x x f x π,则=-+)7log 3()2(2f fA .87 B . 227 C .158 D . 1579.我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架“歼— 15”飞机准备着舰,如果乙机不能最先着舰,而丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为( ) A. 24 B. 36 C.48 D. 9610.已知抛物线C :24y x =的焦点为F ,直线24y x =-与C 交于A ,B 两点.则cos AFB ∠=( )A .45B .35C .35-D .45-11. 中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖b i e.如图为一个阳马与一个鳖臑的组合体,已知三棱锥P ADE -为鳖臑,且PA ⊥平面ABCE ,2AB AD ==,1ED =,该鳖臑..的外接球的表面积为9π,则阳马..的外接球的体积为A. B. C. D.12.已知函数()(1)(2)e e xf x m x x =----,若关于x 的不等式0)(>x f 有且只有一个正整数解,则实数m 的最大值为A .3e e 2+B .2e e 2+C .3e e 2-D .2e e2-第Ⅱ卷(非选择题,共90分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用2B 铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚,在试题卷上作答无效. 二、填空题:本大题共4个小题,每小题5分,共20分.13. 已知平面向量(==m ,n ,则m 在n 上的投影=_______.14. 已知6260126(2)(1)(1)...(1)x a a x a x a x +=+++++++,则3a = .(结果用数值表示).15.在ABC △中,AB BC =,7cos 18B =-.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .16.对1x R ∀∈,[]23,4x ∃∈,使得不等式2211221223x x x x x mx ++≥++成立,则实数m 的取值范围是 .三、解答题:共70分.解答应写出文字说明、证明过程和演算步骤.第17~21题为必考题,每个试题考生都必须做答.第22、23题为选考题,考生根据要求做答. 17. (本小题满分12分)已知数列{a n }满足a l =﹣2,a n+1=2a n +4. (I )证明数列{a n +4}是等比数列;(Ⅱ)求数列{|a n |}的前n 项和S n .18. (本小题满分12分)如图,已知长方形ABCD 中,22AB =,2AD =,M 为DC 的中点.将∆ADM 沿AM 折起,使得平面ADM ⊥平面ABCM.(1)求证:AD BM ⊥;(2若点E 是线段DB 上的一动点,问点E 在何位置时,二面角E AM D --的余弦值为519. (本小题满分12分)四川省阆中中学某部根据运动场地的影响,但为尽大可能让学生都参与到运动会中来,在2018春季运动会中设置了五个项目,其中属于跑步类的两项,分别是200米和400米,另外三项分别为跳绳、跳远、跳高.学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:其中参加跑步类的人数所占频率为713,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取..13..人进行分析.......(Ⅰ)求条形图中m 和n 的值以及抽取的13人中参加200米的学生人数;(Ⅱ)现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X ,求离散型随机变量X 的分布列与数学期望.20.(本小题满分12分)已知椭圆C :22221x y a b+=(0a b >>)的左右焦点分别为1F ,2F ,离心率为12,点A 在椭圆C 上,1||2AF =,1260F AF ∠=︒,过2F 与坐标轴不垂直的直线l 与椭圆C 交于P ,Q 两点.(Ⅰ)求椭圆C 的方程;(Ⅱ)若P ,Q 的中点为N ,在线段2OF 上是否存在点(,0)M m ,使得MN PQ ⊥?若存在,求实数m 的取值范围;若不存在,说明理由. 21.(本小题满分12分)已知函数()()R a a x x a x x x f ∈+--=22ln 在其定义域内有两个不同的极值点. (1)求a 的取值范围;(2)记两极值点分别为.,,2121x x x x <且已知0>λ,若不等式112e x x λλ+<⋅恒成立,求λ的范围.请考生在第22,23,三题中任选一题作答,如果多做,则按所做的第一题给分.作答时请写清题号22. (本小题满分10分)已知曲线C : 21sin ρθ=-,直线cos :sin x t l y t αα=⎧⎨=⎩(t 为参数,0απ≤<). (Ⅰ)求曲线C 的直角坐标方程;(Ⅱ)设直线 与曲线C 交于A 、B 两点(A 在第一象限),当30OA OB +=时,求α的值. 23. (本小题满分10分)已知函数f (x )=﹣x 2+ax+4,g (x )=|x+1|+|x ﹣1|. (1)当a=1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[﹣1,1],求a 的取值范围.理科数学答案一、选择题(每小题5分,共计60分)二.填空题(每小题5分,共计20分)13. -1 14. 20 15. 3816.(],3-∞ 三、解答题17.(I )证明:∵数列{a n }满足a l =﹣2,a n+1=2a n +4,∴a n+1+4=2(a n +4)..................3分 ∴数列{a n +4}是等比数列,公比与首项为2................................................................6分 (II )解:由(I )可得:a n +4=2n , ∴a n =2n ﹣4,...............................................8分∴当n=1时,a 1=﹣2;n≥2时,a n ≥0,..........................................................................9分 ∴n≥2时,S n =﹣a 1+a 2+a 3+…+a n =2+(22﹣4)+(23﹣4)+…+(2n ﹣4) =﹣4(n ﹣1)=2n+1﹣4n+2.n=1时也成立.............................................11分∴S n =2n+1﹣4n+2.n ∈N * ..............................................................................................12分 18. 【答案】(1)解:证明:∵长方形ABCD 中,AB=,AD=,M 为DC 的中点,∴AM=BM=2,∴BM ⊥AM.....................................3分∵平面ADM ⊥平面ABCM ,平面ADM∩平面ABCM=AM ,BM ⊂平面ABCM ∴BM ⊥平面ADM ∵AD ⊂平面ADM∴AD ⊥BM.......................................................5分 (2)解:建立如图所示的直角坐标系设,则平面AMD 的一个法向量 ,...................................7分,设平面AME 的一个法向量 则 取y=1,得所以,............................................10分因为 ,求得 ,所以E 为BD 的中点 .......................11分19..(Ⅱ)由题意,得抽取的13人中参加400米的学生人数有240134780⨯=,参加跳绳的学生人数有3人,所以X 的所有可能取值为1、2、3、4,………………6分()134347C C 41C 35P X ===,()224347C C 182C 35P X ===,()314347C C 123C 35P X ===,()4447C 14C 35P X ===,………………9分所以离散型随机变量X 的分布列为:……………………………………………………………………………11分 所以41812116()1234353535357E X =⨯+⨯+⨯+⨯=.………………12分 20.解:(Ⅰ)由12e =得2a c =,1||2AF =,2||22AF a =-, 由余弦定理得,222121212||||2||||cos ||AF AF AF AF A F F +-⋅=,解得1c =,2a =,2223b a c =-=,所以椭圆C 的方程为22143x y +=. (5)分(Ⅱ)存在这样的点M 符合题意. 设11(,)P x y ,22(,)Q x y ,00(,)N x y , 由2(1,0)F ,设直线PQ 的方程为(1)y k x =-,由221,43(1),x y y k x ⎧+=⎪⎨⎪=-⎩得2222(43)84120k x k x k +-+-=,…………………7分 由韦达定理得2122843k x x k +=+,故212024243x x k x k +==+, 又点N 在直线PQ 上,02343k y k -=+,所以22243(,)4343k kN k k -++. …………………9分 因为MN PQ ⊥,所以22230143443MNk k k k k m k --+==--+,整理得22211(0,)34344k m k k==∈++, 所以存在实数m ,且m 的取值范围为1(0,)4....12分21.I 依题意得函数)(x f 得定义域为(0,+∞),所以方程0)('=x f 在(0,+∞)有两个不同的根, 即方程0ln =-ax x 在(0,+∞)有两个不同的根. 问题转化为函数xx x g ln )(=与ay =的图象(0,+∞)有两个不同的交点. 又,ln 1)('2xxx g -=即当e x <<0时,0)('>x g ;当e x >时,0)('<x g , 所以)(x g 在),0(e 上单调递增,在),(+∞e 上单调递减.从而ee g x g 1)()(==极大值 ………………3分 又)(x g 有且只有一个零点是1,且当0→x 时,-∞→)(x g ;当+∞→x 时,0)(→x g . 所以,要想函数xxx g ln )(=与函数a y =的图象(0,+∞)有两个不同的交点, 只需e a 10<<.…6分 (II )因为λλ+⋅<211x x e 等价于21ln ln 1x x λ+<λ+,由(I )知21,x x 是方程0ln =-ax x 的两个根,即2211ln ,ln ax x ax x ==,所以原式等价于)(ln ln 12121x x a x x λ+=λ+<λ+,因为2100x x <<>λ,,所以原式等价于211x x a λ+λ+>. …………8分又由2211ln ,ln ax x ax x ==作差得)(ln2121x x a x x -=,即2121ln x x x x a -=.所以原式等价于2121211lnx x x x x x λ+λ+>-,因为210x x <<时,原式恒成立,即212121)()1(ln x x x x x x λλ+-+〈恒成立. 令)1,0(,21∈=t x x t ,则不等式)1()1(ln -++<t t t λλ在)1,0(∈t 上恒成立. 令λλ+-+-=t t t t h )1()(1ln )(,又2222)()()1()()(11)('λ+λ--=λ+λ+-=t t t t t t t h ,当12≥λ时,可见)(0,1∈t 时,0)('>t h ,所以)(0,1)(∈t t h 在上单调递增, 又)(0,10)(,0)(1∈<=t t h h 在上恒成立,符合题意. …………10分当12<λ时,可见当)(0,2λ∈t 时,0)('>t h ,当)1(2,λ∈t 时,0)('<t h 所以)(0,)(2λ∈t t h 在上单调递增, 在),1(2λ∈t 上单调递减,又)(0,10)(,0)(1∈<=t t h h 在上不恒成立,不符合题意,舍去.综上所述,若不等式λλ+⋅<211x x e 恒成立,只需12≥λ,又0>λ,所以1≥λ…………12分22解:(Ⅰ)由 ,得 ,................................................................2分 所以曲线C 的直角坐标方程为 ................................................................................5分(Ⅱ)将直线l 的参数方程代入,得 ,.......7分设A ,B 两点对应的参数分别为 ,由韦达定理及 得 ,故 (10)分23.(1)解:(1)当a=1时,f (x )=﹣x 2+x+4,是开口向下,对称轴为x=的二次函数,g (x )=|x+1|+|x ﹣1|= ,................................................................................2分当x ∈(1,+∞)时,令﹣x 2+x+4=2x ,解得x=,g (x )在(1,+∞)上单调递增,f (x )在(1,+∞)上单调递减,∴此时f (x )≥g (x )的解集为(1,]; (3)分当x ∈[﹣1,1]时,g (x )=2,f (x )≥f (﹣1)=2.当x ∈(﹣∞,﹣1)时,g (x )单调递减,f (x )单调递增,且g (﹣1)=f (﹣1)=2. 综上所述,f (x )≥g (x )的解集为[﹣1,];...........................................................5分(2)依题意得:﹣x 2+ax+4≥2在[﹣1,1]恒成立,即x 2﹣ax ﹣2≤0在[﹣1,1]恒成立,则只需,解得﹣1≤a≤1,故a 的取值范围是[﹣1,1]. ...............................................................................................10分。
浙江省宁波市五校联盟2023-2024学年高一下学期4月期中联考数学试题(含答案)

第二学期宁波五校联盟期中联考高一年级数学学科 试题考生须知:1.本卷共4页满分150分,考试时间120分钟。
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。
3.所有答案必须写在答题纸上,写在试卷上无效。
4.考试结束后,只需上交答题纸。
选择题部分一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数()i 1i z =-,则z =( )A .2B .3C D2.如图,用斜二测画法得到ABC △的直观图为等腰直角三角形A B C ''',其中A B ''=,则ABC △的面积为()A .B .C .2D .13.设{}12,e e是平面内的一个基底,则下面的四组向量不能构成基底的是( )A .122e e + 和12e e -B .123e e - 和2126e e -C .123e e + 和213e e + D .1e 和12e e + 4.在ABC △中,a x =,2b =,60B =︒,若三角形有两解,则x 的取值范围是( )A .2x <<B .2x <<C 2x <<D .2x <<5.,a b 为不重合的直线,,αβ为互不相同的平面,下列说法正确的是( )A .若αβ∥,a α⊂,b β⊂,则a b ∥B .若a b ∥,a α∥,b β∥,则αβ∥C .若a b ∥,b α∥,则a α∥D .若a α∥,b α⊂,则a b ∥或a 与b 异面6.已知向量(1,a = ,1b = ,且()()223a b a b -⋅+=.则2a b + 在a 方向上的投影向量的坐标是( )A.32⎛⎝B.12⎛⎝C.12⎛- ⎝D.32⎛ ⎝.7.点O 在ABC △的内部,且满足:1255AO AB AC =+,则ABC △的面积与AOB △的面积之比是( )A .72B .3C .52D .28.已知,,a b e是平面向量,e 是单位向量,若非零向量a 与e 的夹角为π4,向量b 满足2680b b e -⋅+= ,则a b -的最小值是( )A1-B1+C1+D.2二、多选题:本题共3小题,共18分。
浙江省届高三下学期五校联考试题数学Word版含

2018学年浙江省高三“五校联考”考试数学试题卷命题学校:绍兴一中说明:本试题卷分选择题和非选择题两部分.全卷共4页,满分150分,考试时间 120分钟.请考生按规定用笔将全部试题的答案涂、写在答题纸上.参照公式柱体的体公式:V=Sh ,此中S 表示柱体的底面,h 表示柱体的高;体的体公式:V=1Sh ,此中S 表示体的底面,h 表示体的高;3台体的体公式:V1 (S 1 S1S2S2)h ,此中S 1,S2分表示台体的上、下底面,h 表示台体的高;3球的表面公式: 2 ,球的体公式:V=4 3S=4πR πR ,此中R 表示球的半径;3若事件A,B 互斥, P(A+B)=P(A)+P(B);若事件A,B 互相独立, P(A·B)=P(A)·P (B);k若事件A 在一次中生的概率是p,n 次独立重复中事件A 恰巧生k 次的概率Pn(k)=Cn kpn-kn)⋯., (1-p)(k=0,1,2,选择题部分(共一、选择题:本大题共 10目要求的.40分)小题,每题4分,共40分,在每题给出的四个选项中,只有一项为哪一项切合题1.已知会合U 1,1,3,5,7,9,A{1,5},B1,5,7,则C U (AB) (▲)A.3,9B.1,5,7C.1,1,3,9D. 1,1,3,7,9 2.如图,网格纸上的小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为(▲ )A.426B.46C.422D.423.已知数列{a },知足 an 1 3an,且aa a69,则n2 4log 3a 5log 3a 7log 3a 9 (▲)(第2)A.5B.6C.8D.114.已知xy0 ,则“x”是“2|x|x 22|y|y 2”的(▲)A.充足不用要条件B. 必需不充足条件C.充足必需条件D. 既不充足也不用要条件5.函数y1x e x的大概图象为(▲)1 xCy1,6.已知实数x,y知足y2x10,假如目标函数z x y的最小值为-1,则实数m等于(▲)x y m0,A.7B.5C.4D.37.已知M tan sin cos,N tan(tan82),则M和N的关系是(▲)28A.M NB.M NC.M ND.M和N没关8.已知函数f(x)|log2x|,x0,|2f(x)m|1,且mZ,若函数g(x)存在5个零1x,x,函数g(x)0.点,则m的值为(▲)9.设a,b,c为平面向量,|a||b|2,若(2c a)(c b)0,则cb的最大值为(▲)A.2B.9C.17D.5 4410.如图,在三棱锥S ABC中,SC AC,SCB,ACB,二面角S BC A的平面角为,则(▲)A. B.SCA C.SBA D.SBA非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.已知复数z知足1+2iz2i,则z=▲,|z|=▲.12.f(x)(x2x1)(2x1)5的睁开式中各项系数的和为▲,该睁开式中的常数项为▲. x13.已知函数f(x)cos(x)(0,||)象中两相的最高点和最低点分(,1),72121),函数f(x)的增区▲,将函数f(x)的象起码平移▲个位度后对于直(,12x称.414.一个正四周体的四个面上分有1,2,3,4,将正四周体抛两次,向下一面的数字和偶数的概率▲,两个数字和的数学希望▲.15.已知双曲x2y21(a0,b0)中,A1,A2是左、右点,F是右焦点,B是虚的上端点.若在a2b2段BF上(不含端点)存在不一样的两点P i(i1,2),使得PA i1PA i20,双曲离心率的取范是▲.16.从0,1,2,⋯,8九个数字中取五个不一样的数成五位偶数,且奇数数字不可以放在偶数位(从万位到个位分是第一位,第二位⋯⋯),有▲个不一样的数.(用数字作答)17.已知数x,y[1,1]a,a b,,max{a,b}b.b,amax{x2y21,|x2y|}的最小▲.三、解答:本大共5小,共74分,解答写出文字明、明程或演算步. 18.(安分14分)已知ABC中,角A,B,C所的分a,b,c,且cos AsinA2.222(Ⅰ)求角A的大小;(Ⅱ)当a7,sin(A C)21,求c的. 1419.(安分15分)如,已知ABC中,ABBC7,AC1,点A平面,点B,C在平面的同,且B,C在平面上的射影分E,D,BE2CD2.(Ⅰ)求:平面ABE平面BCDE;(Ⅱ)若M是AD中点,求平面BMC与平面所成二面角的余弦.20.(此题满分15分)已知正项数列a n的前n项和为S n,知足2S n12a n2a n(nN).(Ⅰ)(i)求数列a n的通项公式;(ii)已知对于n 1111M的最小值;N,不等式S2S3M恒建立,务实数S1S n(Ⅱ)数列b n的前n项和为T n,知足42a n1T n2(n N),能否存在非零实数,使得数列b n为等比数列?并说明原因.21.(此题满分15分)x2y21,抛物线x22y的准线与椭圆交于A,B两点,过线段AB上的动点P作斜率已知椭圆4为正的直线l与抛物线相切,且交椭圆于M,N两点.(Ⅰ)求线段AB的长及直线l斜率的取值范围;1MNQ面积的最大值.(Ⅱ)若Q(0,),求422.(此题满分15分)已知函数f(x) e x ax (Ⅰ)若f(x)0恒建立,求b.(此中e为自然对数的底数ab的最大值;)(Ⅱ)设g(x)lnx1,若F(x)g(x)f(x)存在独一的零点,且对知足条件的a,b不等式m(ae1)b恒建立,务实数m的取值会合.。
浙江省宁波市五校联盟2023-2024学年高一上学期期中联考数学试题含解析

2023学年第一学期宁波五校联盟期中联考高一年级数学学科试题(答案在最后)考生须知:1.本卷共5页满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、单项选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}{}{}1,2,3,4,5,6,1,3,5,3,4,5U A B ===,则()U A B ⋃=ð()A.{}2,6 B.{}3,5 C.{}1,3,4,5 D.{}1,2,4,6【答案】A 【解析】【分析】先求A B ⋃,再求补集可得答案.【详解】集合{}{}{}1,3,53,4,51,3,4,5== A B ,则(){}2,6U A B ⋃=ð.故选:A.2.=是“22=”的()A .充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】利用充分必要条件的判断方法判断即可.=1,1a b =-=-,22=不成立,则充分性不成立;当22=时,0a b =≥,则220a b =≥,=综上:=是“22=”的必要不充分条件.故选:B.3.已知命题p :“R x ∃∈,210x ax -+<”为假命题,则实数a 的取值范围为().A.(],2-∞ B.()2,2-C.()(),22,∞∞--⋃+ D.[]22-,【答案】D 【解析】【分析】由命题p ⌝为真命题,则0∆≤,解不等式得出实数a 的取值范围即可.【详解】命题2:,10p x R x ax ∃∈++<为假命题,所以2:,10p x R x ax ⌝∀∈++≥为真命题,则240a ∆=-≤,解得[]2,2a ∈-故选:D4.已知0x >,0y >,且21x y +=,下列结论中错误的是()A.xy 的最大值是18B.24x y +的最小值是2C.12x y+的最小值是9 D.224x y +的最小值是12【答案】B 【解析】【分析】根据基本不等式判断各选项即可.【详解】对于A ,由0x >,0y >,且21x y +=,由2x y +≥,当且仅当122x y ==时,等号成立,所以1≤,解得18xy ≤,即xy 的最大值为18,故A 正确;对于B ,由22224x y x y =+≥=+=当且仅当122x y ==时,等号成立,所以24x y +最小值为B 错误;对于C ,()1212222559y x x y x y x y x y ⎛⎫+=++=++≥+= ⎪⎝⎭,当且仅当22y x x y =,即13x y ==时,等号成立,所以12x y +的最小值是9,故C 正确;对于D ,由()2222224212224x y x yx y +++⎛⎫=≥= ⎪⎝⎭,当且仅当122x y ==时,等号成立,所以224x y +的最小值是12,故D 正确.故选:B.5.设(,)a -∞是函数245y x x =-+的一个减区间,则实数a 的取值范围为()A.2a ≤- B.2a ≥- C.2a ≥ D.2a ≤【答案】A 【解析】【分析】根据图象的翻折变换作出函数图象,观察图象可得.【详解】函数224545y x x x x =-+=-+,先作函数245y x x =-+的图象,如图:根据函数图象的翻折变换可得245y x x =-+的图象如图:由图可知,当2a ≤-时,(,)a -∞是函数245y x x =-+的一个减区间,所以,实数a 的取值范围为(,)a -∞.故选:A6.已知函数()f x 是偶函数,()g x 是奇函数,满足2()()2f x g x x x +=+-,则(2)f =()A.1B.2C.3D.4【答案】B 【解析】【分析】根据奇偶性求得函数()f x ,然后再代入计算函数值.【详解】2()()2f x g x x x +=+-,则2()()2f x g x x x +-=---,又函数()f x 是偶函数,()g x 是奇函数,则2()()2f x g x x x =---,所以()()()()()()22222222x x x x f x g x f x g x f x x +-+--⎡⎤⎡⎤++-⎣⎦⎣⎦===-,2(2)222f =-=,故选:B .7.已知2535a ⎛⎫= ⎪⎝⎭,3525b ⎛⎫= ⎪⎝⎭,2525c ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系为()A.a b c <<B.c b a <<C.b<c<aD.c<a<b【答案】C 【解析】【分析】根据指数函数和幂函数的单调性即可比较.【详解】25y x= 在()0,+¥为增函数,22553255⎛⎫⎛⎫∴> ⎪ ⎪⎝⎭⎝⎭,即a c >,25xy ⎛⎫= ⎪⎝⎭为减函数,32552255⎛⎫⎛⎫∴< ⎪ ⎪⎝⎭⎝⎭,即b c <,a c b ∴>>,故选:C.【点睛】本题考查了指数函数和幂函数的单调性,属于基础题.8.已知幂函数f (x )=x a 的图象经过点(2),则函数f (x )为()A.奇函数且在()0,+∞上单调递增B.偶函数且在()0,+∞上单调递减C.非奇非偶函数且在()0,+∞上单调递增D.非奇非偶函数且在()0,+∞上单调递减【答案】C 【解析】【分析】根据已知求出a=12,从而函数f(x)=12x ,由此得到函数f(x)是非奇非偶函数且在(0,+∞)上单调递增.【详解】∵幂函数f(x)=x a),∴2a,解得a=12,∴函数f(x)=12x ,∴函数f(x)是非奇非偶函数且在(0,+∞)上单调递增.故选C.【点睛】本题考查命题真假的判断,考查幂函数的性质等基础知识,考查运算求解能力,是基础题.二、多项选择题(本大题共4个小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求全部选对得5分,选对但不全的得3分,有选错的得0分)9.下列各组函数中是同一函数的是()A.()f x =()g x =B.()f x =,()g x =C.()||f x x =,()g t =D.()1f x x =+,()1g t t =-【答案】BC 【解析】【分析】逐一判断定义域和对应关系即可.【详解】A 选项:由1010x x +≥⎧⎨-≥⎩得()f x 的定义域为[)1,+∞,由()()110x x +-≥解得()g x 的定义域为(][),11,-∞-⋃+∞,A 错误;B 选项:由1010x x +≥⎧⎨-≥⎩得()f x 的定义域为[]1,1-,由()()110x x +-≥解得()g x 的定义域为[]1,1-,且()f x ==,故B 正确;C 选项:()f x 和()g x 的定义域都是R ,()g t t ==,对应关系相同,故C 正确;D 选项:对应关系不同,故D 错误.故选:BC10.已知关于x 的不等式20ax bx c ++>的解集为{|2x x <-或}3x >,则下列说法正确的是()A.0a >B.不等式0bx c +>的解集是{}6x x <C.0a b c ++<D.不等式20cx bx a -+<的解集是{1|3x x <-或12x ⎫>⎬⎭【答案】ACD 【解析】【分析】由不等式20ax bx c ++>与方程20ax bx c ++=之间的关系及题设条件得到,,a b c 之间的关系,然后逐项分析即可得出正确选项.【详解】由题意不等式20ax bx c ++>的解集为{|2x x <-或}3x >,则可知0a >,即A 正确;易知,2-和3是方程20ax bx c ++=的两个实数根,由韦达定理可得2323b ac a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩,则,6b a c a =-=-;所以不等式0bx c +>即为60ax a -->,解得6x <-,所以B 错误;易知60a b c a ++=-<,所以C 正确;不等式20cx bx a -+<即为260ax ax a -++<,也即2610x x -->,解得{1|3x x <-或12x ⎫>⎬⎭,所以D 正确.故选:ACD11.如果函数()f x 在[],a b 上是增函数,对于任意的[]()1212,,x x a b x x ∈≠,则下列结论中正确的是()A.()()1212f x f x x x ->- B.()()()12120x x f x f x -->⎡⎤⎣⎦C.()()()()12f a f x f x f b ≤<≤ D.()()12f x f x >【答案】AB 【解析】【分析】根据函数单调性的等价条件进行判断即可.【详解】由函数单调性的定义可知,若函数()f x 在给定的区间上是增函数,则12x x -与()()12f x f x -同号,由此可知,选项A ,B 正确;对于选项C ,D ,因为12,x x 的大小关系无法判断,则()()12,f x f x 的大小关系确定也无法判断,故C ,D 不正确.故选:AB【点睛】结论点睛:若函数()f x 在[],a b 上是增函数,对于任意的[]()1212,,x x a b x x ∈≠,则有()()12120f x f x x x ->-(或者()()()12120x x f x f x -->⎡⎤⎣⎦);若函数()f x 在[],a b 上是减函数,对于任意的[]()1212,,x x a b x x ∈≠,则有()()12120f x f x x x -<-(或者()()()12120x x f x f x --<⎡⎤⎣⎦);12.形如()()0af x x a x=+>的函数,我们称之为“对勾函数”.“对勾函数”具有如下性质:该函数在(上单调递减,在)+∞上单调递增.已知函数()()0af x x a x=+>在[]2,4上的最大值比最小值大1,则a 的值可以是()A.4B.12C.6-D.6+【答案】AD 【解析】2≤、4≥、24<<三种情况讨论,分别求出函数的最值,即可得到方程,解得即可.【详解】依题意可得()()0af x x a x=+>在(上单调递减,在)+∞上单调递增,2≤,即04a <≤时()f x 在[]2,4上单调递增,所以()()max 444a f x f ==+,()()min 222a f x f ==+,所以()()max min 4221424a a af x f x ⎛⎫-=+-+=-= ⎪⎝⎭,解得4a =;4≥,即16a ≥时()f x 在[]2,4上单调递减,所以()()min 444af x f ==+,()()max 222a f x f ==+,所以()()max min 2421244a a af x f x ⎛⎫-=+-+=-= ⎪⎝⎭,解得12a =(舍去);当24<<,即416a <<时()f x 在⎡⎣上单调递减,在4⎤⎦上单调递增,所以()min f x f ==,()()(){}max max 2,4f x f f =,若4242a a +>+且416a <<,即48a <<,()()max 444af x f ==+,所以()()max min 414af x f x -=+-=,解得4a =或36a =(舍去);若4242a a +≤+且416a <<,即816a ≤<,()()max 222a f x f ==+,所以()()max min 212af x f x -=+-=,解得6a =+或6a =-(舍去);综上可得6a =+或4a =.故选:AD非选择题部分三、填空题(本大题共4个小题,每小题5分,共20分)13.221302182********--⎛⎫⎛⎫+--= ⎪ ⎪⎝⎭⎝⎭______.【答案】54-【解析】【分析】根据幂的运算法则计算.【详解】222133()03218295202316144()1227344--⨯-⎛⎫⎛⎫+--=+--=-=- ⎪ ⎪⎝⎭⎝⎭,故答案为:54-.14.集合{}Z |23A x x =∈-≤<的子集个数是______.【答案】32【解析】【分析】确定出集合A 中元素个数,由子集的概念可得.【详解】由已知{2,1,0,1,2}A =--,A 有5个元素,它的子集个数为5232=.故答案为:32.15.若函数()f x x x a =-在区间(0,2]上既有最小值又有最大值,那么实数a 的取值范围是______.【答案】(0,2]【解析】【分析】当a<0,0a =讨论函数单调性,当0a >时,利用函数图象分析可得.【详解】当a<0时,在(0,2]上2()f x x ax =-,对称轴为2ax =,所以,函数()f x 在(0,2]上单调递增,所以()f x 有最大值,无最小值;当0a =时,在(0,2]上2()f x x =,在(0,2]上单调递增,所以()f x 有最大值,无最小值;当0a >时,22,(),x ax x af x ax x x a ⎧-≥=⎨-<⎩,函数图象如图所示,()f x 在0,2a ⎛⎫ ⎪⎝⎭和(),a +∞上单调递增,在,2a a ⎛⎫⎪⎝⎭上单调递减,要使()f x 在(0,2]上既有最小值又有最大值,则02a <≤,即实数a 的取值范围为(0,2].故答案为:(0,2]16.设()f x 是定义在R 上的奇函数,且当0x ≥时,2()f x x =,若对任意的[,1]x t t ∈+,不等式()2()f x t f x +≥恒成立,则实数t 的最小值是______.【答案】2【解析】【分析】由奇偶性求得()f x 的解析式,从而可得2())f x f =,然后由函数的单调性求解不等式.【详解】由已知0x <时,22()()()f x f x x x =--=--=-,即22,0(),0x x f x x x ⎧≥=⎨-<⎩,所以()f x 在R 上是增函数,且2())f x f =,不等式()2()f x t f x +≥化为())f x t f +≥,所以x t +≥,1)x t -≤,所以1)x t ≤,在[,1]x t t ∈+时恒成立,1)(1)t t -+≤,2t ≥,所以t 的最小值是2,故答案为:2.四、解答题(共6小题,共70分.解答题应写出文字说明,证明过程或演算步骤)17.已知集合A x y ⎧⎫⎪==⎨⎪⎩,{|123}B x m x m =-≤≤+.(1)当0m =时,求A B ⋂,A B ⋃;(2)若B A ⊆时,求实数m 的取值范围.【答案】(1)[1,2)A B ⋂=,(1,3]A B =- .(2)1,2⎛⎫-∞-⎪⎝⎭.【解析】【分析】(1)先解一元二次不等式得集合A ,然后由集合的运算可得;(2)根据集合的包含关系可解.【小问1详解】由220-++>x x 解得(1,2)A =-,当0m =时,[1,3]B =,故[1,2)A B ⋂=,(1,3]A B =- .【小问2详解】由题知B A ⊆,(ⅰ)当123m m ->+,即23m <-时,B =∅符合题意;(ⅱ)当123m m -≤+,即23m ≥-时,B ≠∅,因为B A ⊆,所以11232m m -<-⎧⎨+<⎩,解得12m <-,所以2132m -≤<-.综上所述,实数m 的取值范围为12∞⎛⎫--⎪⎝⎭.18.已知命题2:23,0p x x a ∀≤≤-≥,命题2:R,220q x x ax a ∃∈++=.(1)若命题p ⌝为假命题,求实数a 的取值范围;(2)若命题p 和q ⌝均为真命题,求实数a 的取值范围.【答案】(1)(],4∞-(2)()0,2【解析】【分析】(1)根据题意,由条件可得命题p 为真命题,列出不等式,即可得到结果;(2)根据题意,先求得当命题q 为真命题时a 的范围,即可得到q ⌝为真命题时a 的范围,再结合(1)中的结论,即可得到结果.【小问1详解】若命题p ⌝为假命题,则命题p 为真命题,即2a x ≤在[]2,3x ∈恒成立,所以()2min 4a x≤=,即实数a 的取值范围是(],4∞-.【小问2详解】当命题q 为真命题时,因为2R,220x x ax a ∃∈++=,所以2480a a ∆=-≥,解得0a ≤或2a ≥,因为q ⌝为真命题,则02a <<,又由(1)可知,命题p 为真命题时4a ≤,所以4a ≤且02a <<,即实数a 的取值范围是()0,2.19.已知二次函数2()(24)3(15)f x x a x a x =--++≤≤.(1)记()f x 的最小值为()g a ,求()g a 的解析式;(2)记()f x 的最大值为()h a ,求()h a 的解析式.【答案】(1)28,3()51,37489,7a a g a a a a a a -<⎧⎪=-+-≤≤⎨⎪->⎩(2)489,5()8,5a a h a a a -<⎧=⎨-≥⎩【解析】【分析】(1)结合二次函数()f x 的图像和性质,分类讨论单调性和最小值,求出()g a ,最后写成分段函数的形式即可;(2)结合二次函数()f x 的图像和性质,分类讨论函数最大值,求出()h a ,最后写成分段函数的形式即可.【小问1详解】二次函数()f x 的图像抛物线开口向上,对称轴为直线2=-x a ,(ⅰ)当21a -≤,即3a ≤时,此时()f x 在区间[1,5]上单调递增,所以()f x 的最小值()(1)8g a f a ==-;(ⅱ)当25a -≥,即7a ≥时,此时()f x 在区间[1,5]上单调递减,所以()f x 的最小值()(5)489g a f a ==-;(ⅲ)当125a <-<,即37a <<时,函数()f x 在[]1,2a -上单调递减,在(]25a -,上单调递增,此时()f x 的最小值2()(2)51g a f a a a =-=-+-;综上所述,()28,351,37489,7a a g a a a a a a -≤⎧⎪=-+-<<⎨⎪-≥⎩.【小问2详解】二次函数()f x 的图像抛物线开口向上,对称轴为直线2=-x a ,(ⅰ)当23a -<,即5a <时,右端点5x =距离对称性较远,此时()f x 的最大值()(5)489h a f a ==-;(ⅱ)当23a -≥,即5a ≥时,左端点1x =距离对称轴较远,此时()f x 的最大值()(1)8h a f a ==-;综上所述,489,5()8,5a a h a a a -<⎧=⎨-≥⎩.20.(1)已知正数,a b 满足121a b+=,求8a b +的最小值;(2)已知正数,a b 满足21a b +=,求11a ab+的最小值.【答案】(1)25;(2)5+.【解析】【分析】(1)(2)妙用“1”求解即可.【详解】(1)因为121a b+=,所以128(8)a b a b a b ⎛⎫+=++⎪⎝⎭281161717825a b b a =+++≥+=+=,当且仅当28121a b b a a b⎧=⎪⎪⎨⎪+=⎪⎩,即552a b =⎧⎪⎨=⎪⎩时,取得最小值,最小值为25.(2)因为21a b +=,所以111231a b a ab a ab a b++=+=+316(2)32552b a a b a b a b ⎛⎫=++=+++≥++ ⎪⎝⎭,当且仅当621b a a b a b ⎧=⎪⎨⎪+=⎩,即312a b ⎧=-⎪⎨=-⎪⎩时,取得最小值,最小值为5+.21.“绿色低碳、节能减排”是习近平总书记指示下的新时代发展方针.某市一企业积极响应习总书记的号召,采用某项新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品,以达到减排效果.已知该企业每月的二氧化碳处理量最少为300吨,最多为600吨,月处理成本y (元)与月处理量x (吨)之间的函数关系式可近似地表示为213001250002y x x =-+,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.(1)该企业每月处理量为多少吨时,才能使其每吨的平均处理成本最低?(2)该市政府也积极支持该企业的减排措施,试问该企业在该减排措施下每月能否获利?如果获利,请求出最大利润;如果不获利,则该市政府至少需要补贴多少元才能使该企业在该措施下不亏损?【答案】(1)500(2)不能获利,该市政府需要补贴45000元【解析】【分析】(1)由题意列出每吨二氧化碳的平均处理成本的表达式,进而结合基本不等式求解即可;(2)由题意列出该企业每月的利润的函数表达式,进而结合二次函数的性质求解即可.【小问1详解】由题意,()213001250003006002y x x x =-+≤≤,所以每吨二氧化碳的平均处理成本为11250003003002002y x x x =-+≥=元,当且仅当11250002x x=,即500x =时,等号成立,所以该企业每月处理量为500吨时,才能使其每吨的平均处理成本最低.【小问2详解】设该企业每月的利润为()P x ,则()()22211130012500040012500040045000022210x P x x x x x x -++-=⎛⎫=-=- -⎪⎝⎭--,因为300600x ≤≤,所以当400x =时,函数()P x 取得最大值,即()()max 40045000P x P ==-,所以该企业每月不能获利,该市政府至少需要补贴45000元才能使该企业在该措施下不亏损.22.已知函数21()x f x ax b+=+是定义域上的奇函数,且(1)2f -=-.(1)判断并用定义证明函数()f x 在(0,)+∞上的单调性;(2)设函数()()g x f x m =-,若()g x 在(0,)+∞上有两个零点,求实数m 的取值范围;(3)设函数221()2()(0)h x x t f x t x =+-⋅<,若对121,,22x x ⎡⎤∀∈⎢⎥⎣⎦,都有()()12154h x h x -≤,求实数t 的取值范围.【答案】(1)()f x 在(0,1)上单调递减,在(1,)+∞上单调递增,证明见解析(2)m>2(3)3,02⎡⎫-⎪⎢⎣⎭【解析】【分析】(1)根据奇函数性质和已知列方程求出a ,b ,然后按照定义法证明单调性的步骤取值、作差、化简、定号、下结论即可;(2)利用一元二次方程根的分布列不等式组求解可得;(3)令1z x x =+换元得222y z tz =--,将问题转化为求最值问题,然后由()()max min 154h z h z -≤求解可得.【小问1详解】由(1)2f -=-,且()f x 是奇函数,得(1)2f =,于是2222a b a b ⎧=-⎪⎪-+⎨⎪=⎪+⎩,解得10a b =⎧⎨=⎩,即1()f x x x =+.经检验,()f x 是奇函数,满足题意.函数()f x 在(0,1)上单调递减,在(1,)+∞上单调递增,证明如下:任取12,(0,)x x ∈+∞,且12x x <,则()()()()121212121212121211111x x f x f x x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫--=+-+=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,当12,(0,1)x x ∈,且12x x <,则120x x -<,1201x x <<,∴1210x x -<,∴12())0(f x f x ->,即()()12f x f x >,所以,函数()f x 在(0,1)上单调递减.当()12,1,x x ∈+∞,且12x x <,则120x x -<,121x x >,∴1210x x ->,∴12())0(f x f x -<,即()()12f x f x <所以,函数()f x 在(1,)+∞上单调递增.【小问2详解】函数()g x 在(0,)+∞上有两个零点,即方程10x m x+-=在(0,)+∞上有两个不相等的实数根,所以210x mx -+=在(0,)+∞上有两个不相等的实数根,则21212Δ400210m m x x x x ⎧=->⎪⎪+=>⎨⎪=>⎪⎩,解得m>2.【小问3详解】由题意知2221111()222h x x t x x t x x x x x ⎛⎫⎛⎫⎛⎫=+-+=+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,令1z x x=+,则222y z tz =--,由(1)可知函数1z x x =+在1,12⎡⎤⎢⎥⎣⎦上单调递减,在[1,2]上单调递增,∴52,2z ⎡⎤∈⎢⎥⎣⎦,因为函数222y z tz =--的对称轴方程为0z t =<,∴函数222y z tz =--在52,2⎡⎤⎢⎥⎣⎦上单调递增,当2z =时,222y z tz =--取得最小值,min 42y t =-+;当52z =时,222y z tz =--取得最大值,max 1754y t =-+.所以min ()42h x t =-+,max 17()54h x t =-+,又因为对任意的1x ∀,21,22x ⎡⎤∈⎢⎥⎣⎦都有()()12154h x h x -≤恒成立,∴max min 15()()4h x h x -≤,即17155(42)44t t -+--+≤,解得32t ≥-,。
2018~2019学年浙江省5月高三模拟考五校联考数学试卷 word版 含参考答案

2018学年浙江省高三“五校联考”考试数学试题卷命题学校:绍兴一中说明:本试题卷分选择题和非选择题两部分.全卷共4页,满分150分,考试时间120分钟.请考生按规定用笔将所有试题的答案涂、写在答题纸上. 参考公式选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}1,1,3,5,7,9U =-,{1,5}A =,{}7,5,1-=B ,则()U C A B =( ▲ )A.{}3,9B.{}1,5,7C.{}9,3,1,1-D.{}1,1,3,7,9-2. 如图,网格纸上的小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( ▲ ) A. 624+ B. 64+C. 224+D. 24+3. 已知数列}{n a ,满足n n a a 31=+,且9642=a a a ,则 =++937353log log log a a a ( ▲ ) A.5 B. 6 C. 8 D. 114. 已知0>+y x ,则“0>x ”是“2||2||22y x y x +>+”的 ( ▲ ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件(第2题图)5. 函数1e 1xx y x--=+的大致图象为( ▲ )6. 已知实数y x ,满足1,210,0,y y x x y m ≥⎧⎪-+≤⎨⎪+-≤⎩如果目标函数y x z -=的最小值为-1,则实数m 等于( ▲ )A .7B .5C .4D .3 7. 已知αααcos sin 2tan+=M ,)28(tan8tan+=ππN ,则M 和N 的关系是( ▲ )A.N M >B.N M <C.N M =D. M 和N 无关 8. 已知函数2|log |,0,()1,0.x x f x x x >⎧=⎨-≤⎩,函数1|)(2|)(--=m x f x g ,且Z m ∈,若函数)(x g 存在5个零点,则m 的值为( ▲ )A. 5B. 3C. 2D. 19. 设,,为平面向量,2||||==,若0)()2(=-⋅-,则⋅的最大值为( ▲ ) A. 2 B.49C. 174D. 5 10. 如图,在三棱锥ABC S -中,AC SC =,θ=∠SCB ,θπ-=∠ACB ,二面角A BC S --的平面角为α,则 ( ▲ )A.θα≥B.α≥∠SCAC.α≤∠SBAD.SBA α∠≥非选择题部分(共110分)二、填空题:本大题共7小题,多空题每小题6分,单空题每小题4分,共36分. 11.已知复数z 满足()1+22i z i =+,则z = ▲ ,|z |= ▲ .12. 251()(1)(2)f x x x x x=++-的展开式中各项系数的和为 ▲ ,该展开式中的常数项为 ▲ .B (第 10题图)SACB13.已知函数()cos()(0,||)2f x x πωϕωϕ=+><图象中两相邻的最高点和最低点分别为(,1),12π7(,1)12π-,则函数()f x 的单调递增区间为 ▲ ,将函数()f x 的图象至少平移 ▲ 个单位长度后关于直线4x π=-对称.14.一个正四面体的四个面上分别标有1,2,3,4,将该正四面体抛掷两次,则向下一面的数字和为偶数的概率为 ▲ ,这两个数字和的数学期望为 ▲ .15.已知双曲线22221(0,0)x y a b a b-=>>中,12,A A 是左、右顶点,F 是右焦点,B 是虚轴的上端点.若在线段BF 上(不含端点)存在不同的两点(1,2)i P i =,使得120i i PA PA ⋅=,则双曲线离心率的取值范围是 ▲ .16.从0,1,2,…,8这九个数字中取五个不同的数组成五位偶数,且奇数数字不能放在偶数位(从万位到个位分别是第一位,第二 位……),有 ▲ 个不同的数.(用数字作答) 17.已知实数,[1,1]x y ∈-,,,max{,},.a a b a b b a b ≥⎧=⎨<⎩则22max{1,|2|}x y x y -+-的最小值为 ▲ .三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.18.(本题满分14分) 已知ABC ∆中,角,,A B C 所对的边分别为,,a b c,且cos sin 22A A -= (Ⅰ)求角A 的大小; (Ⅱ)当)14a A C =+=,求c 的值.19.(本题满分15分)如图,已知ABC ∆中,AB BC AC ===,点A ∈平面α,点,B C 在平面α的同侧,且,B C 在平面α上的射影分别为,E D ,22BE CD ==. (Ⅰ)求证:平面ABE ⊥平面BCDE ;(Ⅱ)若M 是AD 中点,求平面BMC 与平面α所成锐二面角的余弦值.AE.BCDMα(第19题图)20.(本题满分15分)已知正项数列{}n a 的前n 项和为n S ,满足2212(N )n n n S a a n *+=+∈.(Ⅰ)(i )求数列{}n a 的通项公式; (ii )已知对于N n *∈,不等式1231111nM S S S S ++++<恒成立,求实数M 的最小值; (Ⅱ) 数列{}n b 的前n 项和为n T ,满足2142(N )n a n T n λ-*=-∈,是否存在非零实数λ,使得数列{}n b为等比数列? 并说明理由. 21.(本题满分15分)已知椭圆2214x y +=,抛物线22x y =的准线与椭圆交于,A B 两点,过线段AB 上的动点P 作斜率 为正的直线l 与抛物线相切,且交椭圆于,M N 两点. (Ⅰ)求线段AB 的长及直线l 斜率的取值范围; (Ⅱ)若104Q (,),求MNQ ∆面积的最大值.22.(本题满分15分)已知函数()e xf x ax b =--.(其中e 为自然对数的底数)(Ⅰ)若()0f x ≥恒成立,求ab 的最大值;(Ⅱ)设()ln 1g x x =+,若()()()F x g x f x =-存在唯一的零点,且对满足条件的,a b 不等式e 1)-+≥(m a b 恒成立,求实数m的取值集合.2019 五校联考参考答案一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题11.4355i-,1; 12. 3,-40 ; 13.5[,]()1212k k k Zππππ-+∈,6π; 14.12,5;15e<<; 16.1680; 17.32.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18. 解:(Ⅰ)由得21)2sin2(cos2=-AA,即212cos2sin21=-AA21sin=A,-------------------3分又π<<A0,02sin2cos>-AA,2sin)22sin(2cosAAA>-=π,2,222ππ<>-AAA所以6π=A-------------------7分(Ⅱ)由1421)sin(=+AC,得1421sin=B由正弦定理:BbAasinsin=,得3=b-------------------10分由余弦定理:Abccba cos2222-+=,得cc3372-+=,4=c或1-=c(舍去)所以4=c-------------------14分19. (Ⅰ)证明:由条件,ADEBE平面⊥,AEBE⊥∴,由计算得3,6,3===ADEDAE,222ADEDAE=+∴,AEED⊥又EBEED=⋂,BCDEAE平面⊥∴,而ABEAE平面⊂∴BCDEABE平面平面⊥------------------6分(Ⅱ)以E为坐标原点,直线EA,ED,EB为x,y,z轴建立空间直角坐标系,)1,6,0(),0,6,0(),2,0,0(),,0,3(CDBA,则)0,26,23(M,3(,2)22BM=-, 1)BC=-,平面α的法向量为(0,0,1)m=-------------------8分设平面MBC的法向量),,(zyxn=,由{n BCn BM⋅=⋅=20zz-=-=⇒取1,(32,1,y n==------------------11分设平面BMC 与平面α所成锐二面角为θ,则6cos ||5||||m n m n θ⋅==⋅所以平面BMC 与平面α所成锐二面角的余弦值为5. -------------------15分20. 解:(Ⅰ) (i )1,所以0又,212,时111211=>+=+=a a a a a n n ,…………………….1分 当,时2≥n )(2122∙∈+=+N n a a S n n n )(2121-21-1-∙∈+=+N n a a S n n n作差整理得: ,因为 ,所以,故数列{}n a 为等差数列,. ……………………………………………………..4分 (ii )由(i )知,4)3(+=n n S n ,所以)311(34)3(41+-=+=n n n n S n,从而=++++nS S S S 1111321)311()2111()1121()6131()5121()411((34+-++--++--++-+-+-n n n n n n )31211131211(34+-+-+-+++=n n n 922)312111611(34<+-+-+-+=n n n , 所以922≥M ,故实数的最小值为922…………………………………….8分 (Ⅱ)由)(2412∙-∈-=N n T n a n λ知λλλ241,24+=-=n n n n T T …………………………..9分当λ6,时11==b n ,……………………………………………………10分当λλλλ241241,时211--+=-=≥--n n n n n T T b n143-=n λ所以)2(4431≥==+n b b n n n λ,…………………………………………………….12分若数列{}n b 是等比数列,则有124b b =而λ122=b ,所以212=b b 与b 2=4b 1矛盾。
2018年浙江省“五校联考”高考数学二模试卷(解析版)

2018年浙江省“五校联考”高考数学二模试卷一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4分)设集合A={x||x﹣1|≤1},B={x|log2x≤2},则B∩∁R A=()A.[2,4]B.(2,4]C.[0,4]D.(2,4]∪(﹣∞,0)2.(4分)若复数z满足z(1+i)=|1﹣i|+i(其中i为虚数单位),则z的虚部为()A.B.C.D.3.(4分)已知随机变量X~B(4,p),若,则P(X=2)=()A.B.C.D.4.(4分)设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是()A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β5.(4分)如图,设A、B是半径为2的圆O上的两个动点,点C为AO中点,则的取值范围是()A.[﹣1,3]B.[1,3]C.[﹣3,﹣1]D.[﹣3,1]6.(4分)(1﹣)6(1+)4的展开式中x的系数是()A.﹣4B.﹣3C.3D.47.(4分)点D是△ABC的边AB的中点,∠ABC=120°,,若以A、B为焦点的双曲线恰好经过点C,则该双曲线的离心率为()A.B.C.D.8.(4分)若,则α∈()A.B.C.D.9.(4分)已知△ABC的三边长分别为a、b、c,有以下四个命题:(1)以,,为边长的三角形一定存在;(2)以2a,2b,2c为边长的三角形一定存在;(3)以a3,b3,c3为边长的三角形一定存在;(4)以|a﹣b|+c,|b﹣c|+a,|c﹣a|+b为边长的三角形一定存在,其中正确命题的个数为()A.1个B.2个C.3个D.4个10.(4分)已知函数的最小值为2a﹣1,则实数a的取值范围是()A.a=±1B.0≤a≤1C.a≤0或a=1D.a≤0或a≥1二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.(4分)已知2log6x=1﹣log63,则x的值是.12.(6分)若实数x,y满足,则x+y的最大值为,x2+y2的取值范围为.13.(6分)一个三棱锥的三视图如图所示,则其表面积为,其外接球的体积是.14.(6分)点G是△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且,.若,则y=,若,则x+y=.15.(6分)已知正项等比数列{a n}的前n项和为S n,若﹣1,S5,S10成等差数列,则S10﹣2S5=,S15﹣S10的最小值为.16.(4分)将一个4×4正方形棋盘中的8个小正方形方格染成红色,使得每行、每列都恰有两个红色方格,则有种不同的染色方法.17.(4分)棱长为36的正四面体A﹣BCD的内切球球面上有一动点M,则的最小值为.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.(14分)在△ABC中,角A、B、C的对边分别为a、b、c,且,.(Ⅰ)求角A和角B的大小;(Ⅱ)已知当x∈R时,函数f(x)=sin x(cos x+a sin x)的最大值为,求a的值.19.(15分)如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,,(Ⅰ)证明;AC⊥BP;(Ⅱ)求直线AD与平面APC所成角的正弦值.20.(15分)(Ⅰ)求证:;(Ⅱ)设函数(ⅰ)求证:f(x)是减函数;(ⅱ)若不等式对任意n∈N*恒成立(e是自然对数的底数),求实数a的取值范围.21.(15分)如图,已知椭圆离心率为,焦距为2.(Ⅰ)求椭圆C的方程;(Ⅱ)直线l与椭圆切于点P,OQ⊥l,垂足为Q,其中O为坐标原点.求△OPQ面积的最大值.22.(15分)已知正项数列{a n}满足a1=4,,n∈N*.(Ⅰ)求证:a n≥4n;(Ⅱ)求证:2018年浙江省“五校联考”高考数学二模试卷参考答案与试题解析一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4分)设集合A={x||x﹣1|≤1},B={x|log2x≤2},则B∩∁R A=()A.[2,4]B.(2,4]C.[0,4]D.(2,4]∪(﹣∞,0)【解答】解:集合A={x||x﹣1|≤1}={x|﹣1≤x﹣1≤1}={x|0≤x≤2}=[0,2],B={x|log2x≤2}={x|0<x≤4}=(0,4],∴∁R A=(﹣∞,0)∪(2,+∞),∴B∩∁R A=(2,4].故选:B.2.(4分)若复数z满足z(1+i)=|1﹣i|+i(其中i为虚数单位),则z的虚部为()A.B.C.D.【解答】解:设z=a+bi,∵复数z满足z(1+i)=|1﹣i|+i(其中i为虚数单位),∴(a+bi)(1+i)=+i,∴a+bi+ai+bi2=a﹣b+(b+a)i=+i,∴,解得a=,b=.∴z的虚部为.故选:A.3.(4分)已知随机变量X~B(4,p),若,则P(X=2)=()A.B.C.D.【解答】解:由随机变量X~B(4,p),且,即np=4p=,解得p=;∴P(X=2)=••=.故选:B.4.(4分)设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是()A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β【解答】解:A、B、D的反例如图.故选:C.5.(4分)如图,设A、B是半径为2的圆O上的两个动点,点C为AO中点,则的取值范围是()A.[﹣1,3]B.[1,3]C.[﹣3,﹣1]D.[﹣3,1]【解答】解:如图所示,可得O(0,0),A(﹣2,0),C(﹣1,0),设B(2cosθ,2sinθ).θ∈[0,2π).=(1,0)•(2cosθ+1,2sinθ)=2cosθ+1∈[﹣1,3].故选:A.6.(4分)(1﹣)6(1+)4的展开式中x的系数是()A.﹣4B.﹣3C.3D.4【解答】解:的展开式的通项为∴展开式中常数项为C60,含x的项的系数为C62,含的项的系数为﹣C61的展开式的通项为∴的展开式中的x的系数为C42,常数项为C40,含的项的系数为C41故的展开式中x的系数是C60C42+C62C40﹣C61C41=6+15﹣24=﹣3故选:B.7.(4分)点D是△ABC的边AB的中点,∠ABC=120°,,若以A、B为焦点的双曲线恰好经过点C,则该双曲线的离心率为()A.B.C.D.【解答】解:不妨设AB=2,则CD=,BD=AB=1,在△BCD中,由余弦定理可得:cos∠ABC==﹣,解得BC=1,在△ABC中,由余弦定理得AC==,不妨设以AB为焦点的双曲线方程为=1,则2a=AC﹣BC=﹣1,2c=AB=2,∴离心率e===.故选:A.8.(4分)若,则α∈()A.B.C.D.【解答】解:cosα+sinα=,当0<α<时,<<,则∈(1,]⊂(1,),∴tanα∈(1,).得α∈().故选:C.9.(4分)已知△ABC的三边长分别为a、b、c,有以下四个命题:(1)以,,为边长的三角形一定存在;(2)以2a,2b,2c为边长的三角形一定存在;(3)以a3,b3,c3为边长的三角形一定存在;(4)以|a﹣b|+c,|b﹣c|+a,|c﹣a|+b为边长的三角形一定存在,其中正确命题的个数为()A.1个B.2个C.3个D.4个【解答】解:三角形ABC的三边长分别为a,b,c,不妨设a≥b≥c,则b+c>a.(1)∵()2﹣()2=b+c﹣a+2>0,∴+>,∴以,,为边长的三角形一定存在;(2)当b=3,c=2,a=4时,22+23>24不成立,因此以2a,2b,2c为边长的三角形不一定存在;(3)当b=3,c=2,a=4时,a3>b3+c3不成立,因此以a3,b3,c3为边长的三角形不一定存在;(4)∵|a﹣b|+c+|b﹣c|+a≥|a﹣c|+c+a>|c﹣a|+b,∴以|a﹣b|+c,|b﹣c|+a,|c﹣a|+b为边长的三角形一定存在;其中正确命题的个数为2个.故选:B.10.(4分)已知函数的最小值为2a﹣1,则实数a的取值范围是()A.a=±1B.0≤a≤1C.a≤0或a=1D.a≤0或a≥1【解答】解:若a=0,则f(x)=,可得x<0时,f(x)>﹣1;x≥0时,f(x)≥0,可得f(x)的值域为(﹣1,+∞),无最小值;当a=1时,f(x)=,当x<0时,f(x)=|x﹣1|+1>2,当x≥0时,f(x)=|(x﹣1)2﹣1|+1≥1,当x=0时,取得最小值1,则f(x)的最小值为1,满足题意,当a=﹣1时,f(x)=,当x<0时,f(x)≥﹣3;当x≥0时,f(x)=x2+2x﹣1的值域为[﹣1,+∞),可得f(x)的最小值为﹣1.故排除B,C,D,故选:A.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.(4分)已知2log6x=1﹣log63,则x的值是.【解答】解:原式等价于log6x2=log66﹣log63=log62,所以x2=2,又x>0,∴x=,故答案为:.12.(6分)若实数x,y满足,则x+y的最大值为5,x2+y2的取值范围为[,13].【解答】解:不等式组可化为或,在同一坐标系中画出两个不等式组表示的平面区域,如图所示;则由图形知,目标函数z=x+y过点C时,z取得最大值,由,解得C(2,3),∴x+y的最大值为5;又z=x2+y2表示区域内的点到原点的距离的平方,由图形知,x2+y2的最小值为,最大值为22+32=13,∴x2+y2的取值范围是[,13].故答案为:5,[,13].13.(6分)一个三棱锥的三视图如图所示,则其表面积为26+2,其外接球的体积是.【解答】解:如图:P A⊥平面ABC,AB⊥BC,P A=5,AB=3,BC=4,三棱锥的表面积为:=26+2三棱锥的外接球就是长方体三度为:5,4,3的外接球,所以外接球的半径为:=.外接球的体积为:=.故答案为:26+2;.14.(6分)点G是△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且,.若,则y=1,若,则x+y=2.【解答】解:根据条件:=,=;又=+;∴=+;又M,G,N三点共线;∴+=1;∵x=,∴y=1;∵,∴==xy=,又=3,即=3,∴x+y=2.故答案为:1,2.15.(6分)已知正项等比数列{a n}的前n项和为S n,若﹣1,S5,S10成等差数列,则S10﹣2S5=1,S15﹣S10的最小值为4.【解答】解:∵﹣1,S5,S10成等差数列,∴2S5=S10﹣1,∴S10﹣2S5=1,又由等比数列的性质可得S5,S10﹣S5,S15﹣S10为等比数列,∴S5(S15﹣S10)=(S10﹣S5)2,∴S15﹣S10===S5++2≥2+2=4,当且仅当S5=即S5=1时取等号,∴S15﹣S10的最小值为4,故答案为:1;4.16.(4分)将一个4×4正方形棋盘中的8个小正方形方格染成红色,使得每行、每列都恰有两个红色方格,则有90种不同的染色方法.【解答】解:第一行染2个红色方格有C42种染法;第一行染好后,有如下三种情况:①第二行的红色方格均与第一行的红色方格同列,这时其余行都只有1种染法;②第二行染的红色方格与第一行的红色方格均不同列,这时第三行有C42种染法,第四行的染法随之确定;③第二行染的红色方格恰有一个与第一行的红色方格同列,而第一、第二这两行染好后,第三行的红色方格必然有一个与上面的红色方格均不同列,这时第三行的染法有2种,第四行染法随之确定.因此,共有染法为:6×(1+6+4×2)=90(种).故答案为:9017.(4分)棱长为36的正四面体A﹣BCD的内切球球面上有一动点M,则的最小值为4.【解答】解:由阿波罗尼斯球得内切球球心O是线段CH上以C,E为定点,空间中满足=λ(λ≠1)的点P的集合,连结CO并延长交平面ABD于H,交内切球上方的点设为K,过M作ME⊥CH,交CH于E,连结BM,CM,设OE=x,由已知得CO=9,OH=3,=,∴=,解得x=,∴λ===3,∴,∴,∴MB+=MB+ME≥BE,在△BOE中,BO=CO=9,OE=,cos∠BOE=﹣cos∠BOH=﹣,∴BE==4.∴的最小值为4.故答案为:4.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.(14分)在△ABC中,角A、B、C的对边分别为a、b、c,且,.(Ⅰ)求角A和角B的大小;(Ⅱ)已知当x∈R时,函数f(x)=sin x(cos x+a sin x)的最大值为,求a的值.【解答】解:(Ⅰ)由,可得:b2+c2﹣a2=bc,所以cos A===,又0<A<π,可得:A=,由sin A sin B=cos2,可得:sin B=,sin B=1+cos C,∴B+C=,则sin(﹣C)=1+cos C,∴可得:sin C=1,解得C=,∴B=.…(6分)(Ⅱ)f(x)=sin x(cos x+a sin x)=sin2x+(1﹣cos2x)=+sin(2x﹣θ),tanθ=a,∵函数f(x)=sin x(cos x+a sin x)的最大值为,∴+=,∴解得a=..…(6分)19.(15分)如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,,(Ⅰ)证明;AC⊥BP;(Ⅱ)求直线AD与平面APC所成角的正弦值.【解答】(I)证明:取AC的中点M,连接PM,BM,∵AB=BC,P A=PC,∴AC⊥BM,AC⊥PM,又BM∩PM=M,∴AC⊥平面PBM,∵BP⊂平面PBM,∴AC⊥BP.(II)解:∵底面ABCD是梯形.BC∥AD,AB=BC=CD=1,AD=2,∴∠ABC=120°,∵AB=BC=1,∴AC=,BM=,∴AC⊥CD,又AC⊥BM,∴BM∥CD.∵P A=PC=,CM==,∴PM=,∵PB=,∴cos∠BMP==﹣,∴∠PMB=120°,以M为原点,以MB,MC的方向为x轴,y轴的正方向,以平面ABCD在M处的垂线为z轴建立坐标系M﹣xyz,如图所示:则A(0,﹣,0),C(0,,0),P(﹣,0,),D(﹣1,,0),∴=(﹣1,,0),=(0,,0),=(﹣,,),设平面ACP的法向量为=(x,y,z),则,即,令x=得=(,0,1),∴cos<,>==﹣,∴直线AD与平面APC所成角的正弦值为|cos<,>|=.20.(15分)(Ⅰ)求证:;(Ⅱ)设函数(ⅰ)求证:f(x)是减函数;(ⅱ)若不等式对任意n∈N*恒成立(e是自然对数的底数),求实数a的取值范围.【解答】(I)证明:令g(x)=lnx﹣(x>1),则g′(x)=﹣===﹣<0,∴g(x)在(1,+∞)上单调递减,∴g(x)<g(1)=0,即lnx﹣<0.∴lnx<(x>1).(II)证明:(i)f′(x)=﹣+=,由(I)可知lnx<,∴(lnx)2<,∴x(lnx)2<(x﹣1)2,∴f′(x)<0,∴f(x)=﹣(x>1)是减函数.(ii)由得(n+a)ln(1+)<1,∵ln(1+)>ln1=0,∴n+a<,即a<﹣n,令1+=t,则n=(1<t≤2).∴a<﹣=f(t),由(i)可知f(t)在(1,2]上单调递减,∴f(t)的最小值为f(2)=.∴a<.21.(15分)如图,已知椭圆离心率为,焦距为2.(Ⅰ)求椭圆C的方程;(Ⅱ)直线l与椭圆切于点P,OQ⊥l,垂足为Q,其中O为坐标原点.求△OPQ面积的最大值.【解答】解:(Ⅰ)由椭圆的离心率e==,则2c=2,c=1,则a=2,b==3,∴椭圆C的方程:;(Ⅱ)方法一:设P(x0,y0),(x0≠0,y0≠0)由椭圆在P的切线方程:,即3x0x+4y0y﹣12=0,则直线OQ的方程:y=x,即3x0y﹣4y0x=0,则|OQ|=,|PQ|==,则△OPQ面积S△OPQ=×|OQ|×|PQ|=××=≤=,当且仅当9x02=16y02,即x02=,y02=时取等号,△OPQ面积的最大值.方法二:设切线方程:y=kx+m,(k≠0)切点P(x0,y0),(x0≠0,y0≠0),O到切线的距离:|OQ|=,联立,整理得:(3+4k2)x2+8kmx+4m2﹣12=0,△=(8km)2﹣4×(3+4k2)(4m2﹣12)=0,整理得:m2=3+4k2,代入解得:x0=﹣,y0=k0x+m=,直线OQ的方程:y=﹣x,即ky+x=0,则|PQ|==,则则△OPQ面积S△OPQ=×|OQ|×|PQ|=×|PQ|•|OQ|=ו=×≤×=,当且仅当k2=1时,即x02=,y02=时取等号,△OPQ面积的最大值.22.(15分)已知正项数列{a n}满足a1=4,,n∈N*.(Ⅰ)求证:a n≥4n;(Ⅱ)求证:【解答】证明:(Ⅰ)首先利用lnx≤x﹣1,可得,即,以下用数学归纳法证明a n≥4n,①当n=1时显然成立;②假设当n=k时,不等式成立,即a k≥4k,则当n=k+1时,由函数的单调性可得,,也就是说,当n=k+1时,不等式也成立;由①②可知,a n≥4n对任意的n∈N*成立;(Ⅱ)易知,由≥3a n+4,则a n+1+2≥3(a n+2),所以,,则,因此,=,所以,.。
浙江省宁波市五校2017-2018学年高三下学期适应性联考数学(文)试卷 Word版含解析

浙江省宁波市五校联考2017-2018学年高考数学适应性试卷(文科)一、选择题(本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中只有一项是符合题目要求的)1.已知p:∀x∈R,x2﹣2x﹣4≤0,则¬p为( )A.∀x∈R,x2﹣2x﹣4≥0 B.∃x0∈R,x02﹣2x0﹣4>0C.∀x∉R,x2﹣2x+4≤0 D.∃x0∈R,x02﹣2x0﹣4>02.已知x,y∈R,则“x>y”是“|x|>|y|”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.已知α∈(π,2π),且cosα+sinα=,则tanα=( )A.B.﹣C.D.﹣4.已知直线m,n及平面α,β,下列中正确的是( )A.若m⊥α,n∥β,且m∥n,则α∥βB.若m∥α,n∥β,且m∥n,则α∥βC.若m⊥α,n∥β,且m⊥n,则α⊥βD.若m⊥α,n⊥β,且m⊥n,则α⊥β5.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是( )A.B.C.D.6.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递增.若实数a满足f (log2a)+f(log a)≤2f(1),则a的取值范围是( )A.[1,2]B.C.D.(0,2]7.已知数列{a n}中满足a1=15,=2,则的最小值为( )A.10 B.2﹣1 C.9 D.8.设双曲线=1(a>0,b>0)的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若(λ,μ∈R),λ•μ=,则双曲线的离心率为( )A.B.C.D.二、填空题(本大题共7小题,9~12小题每题6分,其它小题每题4分,共36分)9.已知全集U=R,集合A={x||x|<1},B={x|x>﹣},则A∪B=__________,A∩B=__________,(∁U B)∩A=__________.10.已知直线l1:ax+y﹣1=0,直线l2:x﹣y﹣3=0,若直线l1的倾斜角为,则a=__________;若l1⊥l2,则a=__________;若l1∥l2,则两平行直线间的距离为__________.11.函数y=3sin(4x+)﹣3的最小正周期为__________,单调递减区间为__________.12.设x、y满足约束条件目标函数z=2x+y的最大值是__________,若目标函数z=ax+by(a>0,b>0)的最大值为10,则+的最小值为__________.13.已知两圆C1:(x+1)2+y2=1与C2:(x﹣1)2+y2=25,动圆M与这两个圆都内切,则动圆的圆心M的轨迹方程为__________.14.若直线l:xcosθ+ysinθ﹣1=0与圆(x﹣cosθ)2+(y﹣1)2=相切,且θ为锐角,则直线l的斜率是__________.15.设非零向量与的夹角是,且||=|+|,则的最小值是__________.三、解答题(共5小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)16.设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=(Ⅰ)求△ABC的周长;(Ⅱ)求cos(A﹣C)的值.17.已知公差不为0的等差数列{a n}的前n项和为S n,满足a2,a3,a5成等比数列,S6=45.(Ⅰ)求数列{a n}的通项公式及前n项和S n;(Ⅱ)令p n=+,是否存在正整数M,使不等式p1+p2+…+p n﹣2n≤M 恒成立,若存在,求出M的最小值;若不存在,说明理由.18.如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.(Ⅰ)求证:EF∥平面BCC1;(Ⅱ)若异面直线EF,BC1所成的角为30°,求直线C1D与平面ABCD所成角的正弦值.19.如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.(1)求证:KF平分∠MKN;(2)O为坐标原点,直线MO、NO分别交准线于点P、Q,求|PQ|+|MN|的最小值.20.已知二次函数f(x)=x2+bx+c,其中常数b,c∈R.(Ⅰ)若任意的x∈[﹣1,1],f(x)≥0,f(2+x)≤0,试求实数c的取值范围;(Ⅱ)若对任意的x1,x2∈[﹣1,1],有|f(x1)﹣f(x2)|≤4,试求实数b的取值范围.浙江省宁波市五校联考2015届高考数学适应性试卷(文科)一、选择题(本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中只有一项是符合题目要求的)1.已知p:∀x∈R,x2﹣2x﹣4≤0,则¬p为( )A.∀x∈R,x2﹣2x﹣4≥0 B.∃x0∈R,x02﹣2x0﹣4>0C.∀x∉R,x2﹣2x+4≤0 D.∃x0∈R,x02﹣2x0﹣4>0考点:的否定;特称.专题:简易逻辑.分析:直接利用全称的否定是特称写出结果即可.解答:解:因为全称的否定是特称,所以,p:∀x∈R,x2﹣2x﹣4≤0,则¬p为:∃x0∈R,x02﹣2x0﹣4>0.故选:B.点评:本题考查的否定,特称与全称的否定关系,基本知识的考查.2.已知x,y∈R,则“x>y”是“|x|>|y|”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件考点:充要条件.专题:简易逻辑.分析:举例,结合结合充分条件和必要条件的定义即可得到结论.解答:解:若x>y,如x=1,y=﹣1,则|x|>|y|不成立,故:“x>y”⇒“|x|>|y|”为假;若|x|>|y|成立,如x=﹣2,y=1则x>y不成立,故:“|x|>|y|”⇒“x>y”为假;故x>y”是“|x|>|y|”的既不充分也不必要条件.故选:D.点评:本题考查的知识点是充要条件的定义,我们先判断p⇒q与q⇒p的真假,再根据充要条件的定义给出结论是解答本题的关键.3.已知α∈(π,2π),且cosα+sinα=,则tanα=( )A.B.﹣C.D.﹣考点:同角三角函数基本关系的运用.专题:三角函数的求值.分析:已知等式两边平方,利用完全平方公式及同角三角函数间基本关系化简,整理求出cosα﹣sinα的值,与已知等式联立求出cosα与sinα的值,即可求出tanα的值.解答:解:∵α∈(π,2π),且cosα+sinα=①,∴两边平方得:1+2sinαcosα=,即2sinαcosα=﹣,∴α∈(,2π),即sinα<0,cosα>0,∴cosα﹣sinα>0,∴(cosα﹣sinα)2=1﹣2sinαcosα=,即cosα﹣sinα=②,联立①②解得:sinα=﹣,cosα=,则tanα=﹣,故选:B.点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.4.已知直线m,n及平面α,β,下列中正确的是( )A.若m⊥α,n∥β,且m∥n,则α∥βB.若m∥α,n∥β,且m∥n,则α∥βC.若m⊥α,n∥β,且m⊥n,则α⊥βD.若m⊥α,n⊥β,且m⊥n,则α⊥β考点:平面与平面之间的位置关系.专题:空间位置关系与距离.分析:根据直线与平面平行,垂直的性质定理,判断定理,灵活判断,可以正确推导,也可以举反例说明.解答:解:(1)∵若m⊥α,n∥β,且m∥n,∴n⊥α,n∥β,∴α⊥β故A不正确;(2)若m∥α,n∥β,且m∥n,则α∥β.不正确,如两个面相交,两个相交的墙面,直线m,n都平行于交线,也满足,m∥α,n∥β,所以B不正确;(3)若m⊥α,n∥β,且m⊥n,则有可能α∥β,不一定α⊥β,所以C不正确;(4)若m⊥α,n⊥β,且m⊥n可以判断α⊥β是正确的,因为可以设两个平面的,,可得数量积为零,⊥,所以可判断α⊥β是正确的,故D 正确,故选:D点评:本题考察了直线与平面的位置关系,熟练掌握好平行,垂直的定理即可判断.5.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是( )A.B.C.D.考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,求出底面面积,代入锥体体积公式,可得答案.解答:解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,其底面面积S=×1×(1+1)=1,高h=,故体积V==,故选:A点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.6.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递增.若实数a满足f (log2a)+f(log a)≤2f(1),则a的取值范围是( )A.[1,2]B.C.D.(0,2]考点:奇偶性与单调性的综合.专题:函数的性质及应用.分析:根据偶函数的定义将所给的式子化为:f(|log2a|)≤f(1),再利用偶函数的单调性列出关于a的不等式求解.解答:解:∵f(x)是定义在R上的偶函数,∴,∴可变为f(log2a)≤f(1),即f(|log2a|)≤f(1),又∵在区间[0,+∞)上单调递增,且f(x)是定义在R上的偶函数,∴,即,解得≤a≤2,故选:C.点评:本题考查了函数的奇偶性和单调性的综合应用,易错处是忽略定义域内的单调性不同,即对称区间单调性相反,注意自变量的取值范围,考查了学生的转化能力.7.已知数列{a n}中满足a1=15,=2,则的最小值为( )A.10 B.2﹣1 C.9 D.考点:数列递推式.专题:等差数列与等比数列.分析:由已知得a n+1﹣a n=2n,从而a n=a1+(a2﹣a1)+(a3﹣a2)+…+(a n﹣a n﹣1)=n2﹣n+15,进而=n+﹣1,由此能求出当且仅当n=,即n=4时,取最小值4+=.解答:解:∵数列{a n}中满足a1=15,=2,∴a n+1﹣a n=2n,∴a n=a1+(a2﹣a1)+(a3﹣a2)+…+(a n﹣a n﹣1)=15+2+4+6+8+…+2(n﹣1)=15+=n2﹣n+15,∴=n+﹣1≥2﹣1,∴当且仅当n=,即n=4时,取最小值4+=.故选:D.点评:本题考查的最小值的求法,是中档题,解题时要注意累加法和均值定理的合理运用.8.设双曲线=1(a>0,b>0)的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若(λ,μ∈R),λ•μ=,则双曲线的离心率为( )A.B.C.D.考点:双曲线的简单性质.专题:平面向量及应用;直线与圆;圆锥曲线的定义、性质与方程.分析:由方程可得渐近线,可得A,B,P的坐标,由共线向量式可得λ+μ=1,λ﹣μ=,解之可得λμ的值,由λ•μ=可得a,c的关系,由离心率的定义可得.解答:解:双曲线的渐近线为:y=±x,设焦点F(c,0),则A(c,),B(c,﹣),P(c,),因为=λ+μ,所以(c,)=((λ+μ)c,(λ﹣μ)),所以λ+μ=1,λ﹣μ=,解得:λ=,μ=,又由λμ=,得:=,解得:=,所以,e==.故选:A.点评:本题考查双曲线的简单性质,涉及双曲线的离心率的求解,属于中档题.二、填空题(本大题共7小题,9~12小题每题6分,其它小题每题4分,共36分)9.已知全集U=R,集合A={x||x|<1},B={x|x>﹣},则A∪B={x|x>﹣1},A∩B={x|﹣<x<1},(∁U B)∩A={x|x|﹣1<x≤﹣}.考点:交、并、补集的混合运算.专题:集合.分析:根据集合的基本运算进行计算即可.解答:解:A={x||x|<1}={x|﹣1<x<1},∁U B={x|x≤﹣},则A∪B={x|x>﹣1},A∩B={x|﹣<x<1},(∁U B)∩A={x|﹣1<x≤﹣};故答案为:{x|x>1},{x|﹣<x<1},{x|x|﹣1<x≤﹣};点评:本题主要考查集合的基本运算,比较基础.10.已知直线l1:ax+y﹣1=0,直线l2:x﹣y﹣3=0,若直线l1的倾斜角为,则a=﹣1;若l1⊥l2,则a=1;若l1∥l2,则两平行直线间的距离为2.考点:两条平行直线间的距离;直线的倾斜角.专题:直线与圆.分析:求出直线的斜率即可求解a,利用直线的垂直,斜率乘积为﹣1,求解a;通过直线的平行求解a,然后求解平行线之间的距离.解答:解:直线l1:ax+y﹣1=0,直线l2:x﹣y﹣3=0,若直线l1的倾斜角为,k=1,即﹣a=1,则a=﹣1:若l1⊥l2,则﹣a×1=﹣1,解得a=1;若l1∥l2,所以a=﹣1,则两平行直线间的距离为:=.故答案为:﹣1;1;.点评:本题考查直线的垂直,平行,平行线之间的距离求法,考查计算能力.11.函数y=3sin(4x+)﹣3的最小正周期为,单调递减区间为[+,+],k∈z.考点:正弦函数的图象.专题:三角函数的图像与性质.分析:由题意根据正弦函数的周期性求得它的最小正周期,再根据正弦函数的单调性求得它的减区间.解答:解:对于函数y=3sin(4x+)﹣3,它的最小正周期为=,令2kπ+≤4x+≤2kπ+,求得+≤x≤+,k∈z,故函数的减区间为[+,+],k∈z,故答案为:;[+,+],k∈z.点评:本题主要考查正弦函数的周期性和单调性,属于基础题.12.设x、y满足约束条件目标函数z=2x+y的最大值是14,若目标函数z=ax+by(a>0,b>0)的最大值为10,则+的最小值为5.考点:简单线性规划.专题:不等式的解法及应用.分析:①作出不等式对应的平面区域,①由z=2x+y得:y=﹣2x+z,显然y=﹣2x+z过A 点时,z最大,将A(4,6)代入求出即可;②利用线性规划的知识先求出a,b的关系,然后利用基本不等式的性质求出+的最小值即可.解答:解:由z=ax+by(a>0,b>0)得y=﹣x+,作出可行域如图:①由z=2x+y得:y=﹣2x+z,显然y=﹣2x+z过A点时,z最大,由,解得,即A(4,6),∴z最大值=2×4+6=14,②∵a>0,b>0,∴直线y=﹣x+的斜率为负,且截距最大时,z也最大.平移直线y=﹣x+,由图象可知当y=﹣x+经过点A时,直线的截距最大,此时z也最大.此时z=4a+6b=10,即2a+3b﹣5=0,即+=1,则+=(+)(+)=+++≥+2=+=5,当且仅当=,即a=b=1时,取等号,故+的最小值为5,故答案为:14,5.点评:本题主要考查线性规划的应用以及基本不等式的应用,利用数形结合是解决线性规划题目的常用方法.13.已知两圆C1:(x+1)2+y2=1与C2:(x﹣1)2+y2=25,动圆M与这两个圆都内切,则动圆的圆心M的轨迹方程为.考点:轨迹方程.专题:计算题;直线与圆;圆锥曲线的定义、性质与方程.分析:设圆(x+1)2+y2=1的圆心O1(﹣1,0),半径r1=1;圆(x﹣1)2+y2=25的圆心O2(1,0),半径r2=5.设动圆C的圆心C(x,y),半径R.由于动圆C与圆(x+1)2+y2=1及圆(x﹣1)2+y2=25都内切,可得|O1C|=R﹣1,|O2C|=5﹣R.于是|O1C|+|O2C|=5﹣1=4>|O1O2|=2,利用椭圆的定义可知:动点C的轨迹是椭圆.求出即可.解答:解:设圆(x+1)2+y2=1的圆心O1(﹣1,0),半径r1=1;圆(x﹣1)2+y2=25的圆心O2(1,0),半径r2=5.设动圆C的圆心C(x,y),半径R.∵动圆C与圆(x+1)2+y2=1及圆(x﹣1)2+y2=25都内切,∴|O1C|=R﹣1,|O2C|=5﹣R.∴|O1C|+|O2C|=5﹣1=4>|O1O2|=2,因此动点C的轨迹是椭圆,2a=4,2c=2,解得a=2,c=1,∴b2=a2﹣c2=3.因此动圆圆心C的轨迹方程是.故答案为:.点评:本题考查了两圆相内切的性质、椭圆的定义,属于中档题.14.若直线l:xcosθ+ysinθ﹣1=0与圆(x﹣cosθ)2+(y﹣1)2=相切,且θ为锐角,则直线l的斜率是﹣.考点:直线与圆相交的性质.专题:计算题;直线与圆.分析:由条件利用直线和圆相切的性质,点到直线的距离公式求得sinθ=.再结合θ为锐角,可得θ=,从而求得直线xcosθ+ysinθ﹣1=0的斜率的值.解答:解:由题意可得圆心(cosθ,1)到直线xcosθ+ysinθ﹣1=0的距离等于半径,即=,化简可得|sinθ﹣sin2θ|=,即sinθ﹣sin2θ=,求得sinθ=.再结合θ为锐角,可得θ=,故直线xcosθ+ysinθ﹣1=0的斜率为﹣,故答案为:﹣.点评:本题主要考查直线和圆相切的性质,点到直线的距离公式的应用,体现了转化的数学思想,属于基础题.15.设非零向量与的夹角是,且||=|+|,则的最小值是.考点:平面向量数量积的运算.专题:平面向量及应用.分析:由已知利用模的等式两边平方得到||=||,将所求平方利用此关系得到关于t的二次函数解析式,然后求最小值.解答:解:因为非零向量与的夹角是,且||=|+|,所以||2=|+|2=||2+2+||2,所以||=||,则()2==t2+2t+=(t+1)2+,所以当t=﹣1时,的最小值是;故答案为:.点评:本题考查了向量的数量积以及向量的平方与模的平方相等的运用.三、解答题(共5小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)16.设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=(Ⅰ)求△ABC的周长;(Ⅱ)求cos(A﹣C)的值.考点:余弦定理;两角和与差的余弦函数.专题:计算题.分析:(I)利用余弦定理表示出c的平方,把a,b及cosC的值代入求出c的值,从而求出三角形ABC的周长;(II)根据cosC的值,利用同角三角函数间的基本关系求出sinC的值,然后由a,c及sinC 的值,利用正弦定理即可求出sinA的值,根据大边对大角,由a小于c得到A小于C,即A为锐角,则根据sinA的值利用同角三角函数间的基本关系求出cosA的值,然后利用两角差的余弦函数公式化简所求的式子,把各自的值代入即可求出值.解答:解:(I)∵c2=a2+b2﹣2abcosC=1+4﹣4×=4,∴c=2,∴△ABC的周长为a+b+c=1+2+2=5.(II)∵cosC=,∴sinC===.∴sinA===.∵a<c,∴A<C,故A为锐角.则cosA==,∴cos(A﹣C)=cosAcosC+sinAsinC=×+×=.点评:本题主要考查三角函数的基本公式和解斜三角形的基础知识,同时考查学生的基本运算能力,是一道基础题.17.已知公差不为0的等差数列{a n}的前n项和为S n,满足a2,a3,a5成等比数列,S6=45.(Ⅰ)求数列{a n}的通项公式及前n项和S n;(Ⅱ)令p n=+,是否存在正整数M,使不等式p1+p2+…+p n﹣2n≤M 恒成立,若存在,求出M的最小值;若不存在,说明理由.考点:数列的求和;等差数列的性质.专题:等差数列与等比数列.分析:(1)通过设公差为d,利用=a2a5、S6=45得a2=d=3,进而可得结论;(2)由(1)计算可得p n=2+﹣,并项相加可得p1+p2+…+p n﹣2n=2﹣,进而可得结论.解答:解:(1)设公差为d,由已知,得=a2a5,即=a2(a2+3d),解得a2=d,由S6=45得2a2+3d=15,∴a2=d=3,∴数列{a n}的通项a n=3n﹣3,前n项和S n=;(2)结论:存在最小的正整数M=2,使不等式p1+p2+…+p n﹣2n≤M恒成立.理由如下:p n=+=+=2+﹣,∴p1+p2+…+p n﹣2n=2(1﹣+﹣+﹣+…+﹣)=2﹣.由n为整数,可得p1+p2+…+p n﹣2n<2,故存在最小的正整数M=2,使不等式p1+p2+…+p n﹣2n≤M恒成立.点评:本题考查求数列的通项及前n项和,判定和的取值范围,注意解题方法的积累,属于中档题.18.如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.(Ⅰ)求证:EF∥平面BCC1;(Ⅱ)若异面直线EF,BC1所成的角为30°,求直线C1D与平面ABCD所成角的正弦值.考点:直线与平面所成的角;直线与平面平行的判定.专题:空间位置关系与距离;空间角.分析:(Ⅰ)先连接CC1,取CC1的中点G,并连接FG,BG,从而可说明四边形FGBE为平行四边形,从而得到EF∥BG,根据线面平行的判定定理即可得到EF∥平面BCC1;(Ⅱ)容易说明∠C1BG=30°,从而得到∠C1BC=60°,从而△BCC1为等边三角形,能够说明直线AB⊥平面BCC1,从而得到平面ABCD⊥平面BCC1.取BC中点H,连接C1H,从而有C1H⊥BC,根据面面垂直的性质定理即知C1H⊥平面ABCD,连接DH,∠C1DH便是直线C1D和平面ABCD所成的角,根据已知边的长度即可求C1D,C1H,从而能求出sin∠C1DH.解答:解:(Ⅰ)证明:连接CC1,取CC1的中点G,连接FG,BG,则:∵四边形ABCD是平行四边形,E,F分别为AB,C1D的中点;∴FG∥BE,且FG=BE;∴四边形BEFG是平行四边形;∴EF∥BG,BG⊂平面BCC1,EF⊄平面BCC1;∴EF∥平面BCC1;(Ⅱ)由(Ⅰ)可知,∠C1BG为异面直线EF,BC1所成的角,∴∠C1BG=30°,∠C1BC=60°;又BC=BC1,∴△C1BC为等边三角形;AB=5,AD=4,BD=3,∴∠ADB=∠CBD=∠C1BD=90°;∴BD⊥BC,BD⊥BC1,且BC∩BC1=B;∴BD⊥平面BCC1;∴平面ABCD⊥平面BCC1,平面ABCD∩平面BCC1=BC;取BC中点H,连接C1H,则C1H⊥平面ABCD;连接DH,则∠C1DH即为直线C1D和平面ABCD所成的角;∴;∴直线C1D与平面ABCD所成角的正弦值为.点评:考查三角形中位线的性质,平行四边形的定义,线面平行的判定定理,异面直线所成角的定义,线面垂直、面面垂直的判定定理,以及面面垂直的性质定理,线面角的定义及求法.19.如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.(1)求证:KF平分∠MKN;(2)O为坐标原点,直线MO、NO分别交准线于点P、Q,求|PQ|+|MN|的最小值.考点:直线与圆锥曲线的关系.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)设KM和KN的斜率分别为k1,k2,证明KF平分∠MKN,只需证k1+k2=0即可;(2)设M、N的坐标分别为,利用三点共线可得P、Q点的坐标.设直线MN的方程为x=my+1,代入抛物线方程,结合韦达定理,求出|PQ|,|MN|,从而可求|PQ|+|MN|的最小值.解答:(1)证明:抛物线焦点坐标为F(1,0),准线方程为x=﹣1….设直线MN的方程为x=my+1,M、N的坐标分别为由,∴y1+y2=4m,y1y2=﹣4…..设KM和KN的斜率分别为k1,k2,显然只需证k1+k2=0即可.∵K(﹣1,0)∴k1+k2==0…(2)解:设M、N的坐标分别为,由M,O,P三点共线可得P点的坐标为,同理可由N,O,Q三点共线可求出Q点坐标为,…设直线MN的方程为x=my+1.由∴y1+y2=4m,y1y2=﹣4,则=…又直线MN的倾斜角为θ,则∴….同理可得…..∴(时取到等号)…..点评:本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,考查学生的计算能力,综合性强.20.已知二次函数f(x)=x2+bx+c,其中常数b,c∈R.(Ⅰ)若任意的x∈[﹣1,1],f(x)≥0,f(2+x)≤0,试求实数c的取值范围;(Ⅱ)若对任意的x1,x2∈[﹣1,1],有|f(x1)﹣f(x2)|≤4,试求实数b的取值范围.考点:二次函数的性质.专题:函数的性质及应用.分析:(Ⅰ)若任意的x∈[﹣1,1],f(x)≥0,f(2+x)≤0,可得是f(1)=0,即1为函数函数f(x)的一个零点.由韦达定理,可得函数f(x)的另一个零点,进而可得实数c的取值范围;(Ⅱ)若对任意的x1,x2∈[﹣1,1],有|f(x1)﹣f(x2)|≤4,f(x)max﹣f(x)min≤4,结合二次函数的图象和性质分类讨论,可得实数b的取值范围.解答:解:(Ⅰ)因为x∈[﹣1,1],则2+x∈[1,3],由已知,有对任意的x∈[﹣1,1],f(x)≥0恒成立,任意的x∈[1,3],f(x)≤0恒成立,故f(1)=0,即1为函数函数f(x)的一个零点.由韦达定理,可得函数f(x)的另一个零点,又由任意的x∈[1,3],f(x)≤0恒成立,∴[1,3]⊆[1,c],即c≥3(Ⅱ)函数f(x)=x2+bx+c对任意的x1,x2∈[﹣1,1],有|f(x1)﹣f(x2)|≤4恒成立,即f(x)max﹣f(x)min≤4,记f(x)max﹣f(x)min=M,则M≤4.当||>1,即|b|>2时,M=|f(1)﹣f(﹣1)|=|2b|>4,与M≤4矛盾;当||≤1,即|b|≤2时,M=max{f(1),f(﹣1)}﹣f()=﹣f()=(1+)2≤4,解得:|b|≤2,即﹣2≤b≤2,综上,c的取值范围为﹣2≤b≤2.点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.。
浙江省2018届高三“五校联考”第二次考试数学试题(含答案)(2018.05)

A. a 1
第Ⅱ卷(非选择题部分,共 110 分)
二、填空题:本大题共 7 小题,多空题每题 6 分,单空题每题 4 分,共 36 分.
11.已知 2 log 6 x 1 log 6 3 ,则 x 的值是 12.若实数 x , y 满足 为 ▲ .
▲
. ,x
2
x y 1 ,则 x y 的最大值为 y | 2 x 1|
D.
3 1
8. 若 cos sin tan 0 A. (0,
,则 ( ▲ ) 2
C. (
) 6
B. (
, ) 6 4
, ) 4 3
D. (
, ) 3 2
9.已知 ABC 的三边长分别为 a、b、c,有以下四个命题: (1)以 (2)以 2 (3)以 a (4)以
1 MC 的最小值 3
三、解答题:本大题共 5 小题,共 74 分.解答应写出文字说明、证明过程或演算步骤. 18. (本题满分 14 分)在 ABC 中,角 A 、 B 、 C 的对边分别为 a 、 b 、 c , 且 (b c) a (2
8 ,则 P ( X 2) 3
C.
8 3
B.
8 27
2 3
D.
4 9
4.设 a , b 是两条直线, , 是两个平面,则“ a b ”的一个充分条件是 ( ▲ )
A. a , b ∥ , C. a , b , ∥
B. a , b , ∥ D. a , b ∥ ,
2 ( x a ) 1 a, x 0 10.已知函数 f ( x ) 的最小值为 2a 1 ,则实数 a 的取值范围是 x a 2 a 1, x 0
浙江省五校联考2018年高考模拟数学理科试卷及答案解析

浙江省五校联考2018年高考模拟数学理科试卷(总分:150分 时间:120分钟)一、选择题:本题共12小题,每小题5分,共60分. 1. 已知集合(){},|1A x y y x ==-,(){},|1B x y y x ==-+,则A B =I( )A.∅B.{}1C.{}0,1D.(){}1,02.已知复数z= 201821i i++(i 为虚数单位),则复数z 的共轭复数....在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x 、y 的 值分别为( )A. 7、8B. 5、7C. 8、5D. 7、74. 设向量a ,b 满足,()3-=g a a b ,则a 与b 的夹角为5若123)(23++-=x x a x x f 在区间⎪⎭⎫⎝⎛3,21上有极值点,则实数的取值范围是( )A. B. C. D.6. 执行如图所示的程序框图,若输出的57S =,则判断框内应填入的条件是( ) A .4k > B .5k > C.6k > D .7k >7. 已知ABCD 为正方形,其内切圆I 与各边分别切于E ,F ,G ,H ,连接EF ,FG ,GH ,HE .现向正方形ABCD 内随机抛掷一枚豆子,记事件A :豆子落在圆I 内,事件B :豆子落在四边形EFGH 外,则(|)P B A =( )A .14π-B .4π C .21π-D .2π8. 已知函数⎪⎩⎪⎨⎧≥<≤=1,4sin 10,2)(x x x x f x π,则=-+)7log 3()2(2f fA .87 B . 227 C .158 D . 1579.我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架“歼— 15”飞机准备着舰,如果乙机不能最先着舰,而丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为( ) A. 24 B. 36 C.48 D. 9610.已知抛物线C :24y x =的焦点为F ,直线24y x =-与C 交于A ,B 两点.则cos AFB ∠=( )A .45B .35C .35-D .45-11. 中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖b i e.如图为一个阳马与一个鳖臑的组合体,已知三棱锥P ADE -为鳖臑,且PA ⊥平面ABCE ,2AB AD ==,1ED =,该鳖臑..的外接球的表面积为9π,则阳马..的外接球的体积为A. B. C. D.12.已知函数()(1)(2)e e xf x m x x =----,若关于x 的不等式0)(>x f 有且只有一个正整数解,则实数m 的最大值为A .3e e 2+B .2e e 2+C .3e e 2-D .2e e2-第Ⅱ卷(非选择题,共90分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用2B 铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚,在试题卷上作答无效. 二、填空题:本大题共4个小题,每小题5分,共20分.13. 已知平面向量(==m ,n ,则m 在n 上的投影=_______.14. 已知6260126(2)(1)(1)...(1)x a a x a x a x +=+++++++,则3a = .(结果用数值表示).15.在ABC △中,AB BC =,7cos 18B =-.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .16.对1x R ∀∈,[]23,4x ∃∈,使得不等式2211221223x x x x x mx ++≥++成立,则实数m 的取值范围是 .三、解答题:共70分.解答应写出文字说明、证明过程和演算步骤.第17~21题为必考题,每个试题考生都必须做答.第22、23题为选考题,考生根据要求做答. 17. (本小题满分12分)已知数列{a n }满足a l =﹣2,a n+1=2a n +4. (I )证明数列{a n +4}是等比数列;(Ⅱ)求数列{|a n |}的前n 项和S n .18. (本小题满分12分)如图,已知长方形ABCD 中,22AB =,2AD =,M 为DC 的中点.将∆ADM 沿AM 折起,使得平面ADM ⊥平面ABCM.(1)求证:AD BM ⊥;(2若点E 是线段DB 上的一动点,问点E 在何位置时,二面角E AM D --的余弦值为519. (本小题满分12分)四川省阆中中学某部根据运动场地的影响,但为尽大可能让学生都参与到运动会中来,在2018春季运动会中设置了五个项目,其中属于跑步类的两项,分别是200米和400米,另外三项分别为跳绳、跳远、跳高.学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:其中参加跑步类的人数所占频率为713,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取..13..人进行分析.......(Ⅰ)求条形图中m 和n 的值以及抽取的13人中参加200米的学生人数;(Ⅱ)现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X ,求离散型随机变量X 的分布列与数学期望.20.(本小题满分12分)已知椭圆C :22221x y a b+=(0a b >>)的左右焦点分别为1F ,2F ,离心率为12,点A 在椭圆C 上,1||2AF =,1260F AF ∠=︒,过2F 与坐标轴不垂直的直线l 与椭圆C 交于P ,Q 两点.(Ⅰ)求椭圆C 的方程;(Ⅱ)若P ,Q 的中点为N ,在线段2OF 上是否存在点(,0)M m ,使得MN PQ ⊥?若存在,求实数m 的取值范围;若不存在,说明理由. 21.(本小题满分12分)已知函数()()R a a x x a x x x f ∈+--=22ln 在其定义域内有两个不同的极值点. (1)求a 的取值范围;(2)记两极值点分别为.,,2121x x x x <且已知0>λ,若不等式112e x x λλ+<⋅恒成立,求λ的范围.请考生在第22,23,三题中任选一题作答,如果多做,则按所做的第一题给分.作答时请写清题号22. (本小题满分10分)已知曲线C : 21sin ρθ=-,直线cos :sin x t l y t αα=⎧⎨=⎩(t 为参数,0απ≤<). (Ⅰ)求曲线C 的直角坐标方程;(Ⅱ)设直线 与曲线C 交于A 、B 两点(A 在第一象限),当30OA OB +=时,求α的值. 23. (本小题满分10分)已知函数f (x )=﹣x 2+ax+4,g (x )=|x+1|+|x ﹣1|. (1)当a=1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[﹣1,1],求a 的取值范围.理科数学答案一、选择题(每小题5分,共计60分)二.填空题(每小题5分,共计20分)13. -1 14. 20 15. 3816.(],3-∞ 三、解答题17.(I )证明:∵数列{a n }满足a l =﹣2,a n+1=2a n +4,∴a n+1+4=2(a n +4)..................3分 ∴数列{a n +4}是等比数列,公比与首项为2................................................................6分 (II )解:由(I )可得:a n +4=2n , ∴a n =2n ﹣4,...............................................8分∴当n=1时,a 1=﹣2;n≥2时,a n ≥0,..........................................................................9分 ∴n≥2时,S n =﹣a 1+a 2+a 3+…+a n =2+(22﹣4)+(23﹣4)+…+(2n ﹣4) =﹣4(n ﹣1)=2n+1﹣4n+2.n=1时也成立.............................................11分∴S n =2n+1﹣4n+2.n ∈N * ..............................................................................................12分 18. 【答案】(1)解:证明:∵长方形ABCD 中,AB=,AD=,M 为DC 的中点,∴AM=BM=2,∴BM ⊥AM.....................................3分∵平面ADM ⊥平面ABCM ,平面ADM∩平面ABCM=AM ,BM ⊂平面ABCM ∴BM ⊥平面ADM ∵AD ⊂平面ADM∴AD ⊥BM.......................................................5分 (2)解:建立如图所示的直角坐标系设,则平面AMD 的一个法向量 ,...................................7分,设平面AME 的一个法向量 则 取y=1,得所以,............................................10分因为 ,求得 ,所以E 为BD 的中点 .......................11分19..(Ⅱ)由题意,得抽取的13人中参加400米的学生人数有240134780⨯=,参加跳绳的学生人数有3人,所以X 的所有可能取值为1、2、3、4,………………6分()134347C C 41C 35P X ===,()224347C C 182C 35P X ===,()314347C C 123C 35P X ===,()4447C 14C 35P X ===,………………9分所以离散型随机变量X 的分布列为:……………………………………………………………………………11分 所以41812116()1234353535357E X =⨯+⨯+⨯+⨯=.………………12分 20.解:(Ⅰ)由12e =得2a c =,1||2AF =,2||22AF a =-, 由余弦定理得,222121212||||2||||cos ||AF AF AF AF A F F +-⋅=,解得1c =,2a =,2223b a c =-=,所以椭圆C 的方程为22143x y +=. (5)分(Ⅱ)存在这样的点M 符合题意. 设11(,)P x y ,22(,)Q x y ,00(,)N x y , 由2(1,0)F ,设直线PQ 的方程为(1)y k x =-,由221,43(1),x y y k x ⎧+=⎪⎨⎪=-⎩得2222(43)84120k x k x k +-+-=,…………………7分 由韦达定理得2122843k x x k +=+,故212024243x x k x k +==+, 又点N 在直线PQ 上,02343k y k -=+,所以22243(,)4343k kN k k -++. …………………9分 因为MN PQ ⊥,所以22230143443MNk k k k k m k --+==--+,整理得22211(0,)34344k m k k==∈++, 所以存在实数m ,且m 的取值范围为1(0,)4....12分21.I 依题意得函数)(x f 得定义域为(0,+∞),所以方程0)('=x f 在(0,+∞)有两个不同的根, 即方程0ln =-ax x 在(0,+∞)有两个不同的根. 问题转化为函数xx x g ln )(=与ay =的图象(0,+∞)有两个不同的交点. 又,ln 1)('2xxx g -=即当e x <<0时,0)('>x g ;当e x >时,0)('<x g , 所以)(x g 在),0(e 上单调递增,在),(+∞e 上单调递减.从而ee g x g 1)()(==极大值 ………………3分 又)(x g 有且只有一个零点是1,且当0→x 时,-∞→)(x g ;当+∞→x 时,0)(→x g . 所以,要想函数xxx g ln )(=与函数a y =的图象(0,+∞)有两个不同的交点, 只需e a 10<<.…6分 (II )因为λλ+⋅<211x x e 等价于21ln ln 1x x λ+<λ+,由(I )知21,x x 是方程0ln =-ax x 的两个根,即2211ln ,ln ax x ax x ==,所以原式等价于)(ln ln 12121x x a x x λ+=λ+<λ+,因为2100x x <<>λ,,所以原式等价于211x x a λ+λ+>. …………8分又由2211ln ,ln ax x ax x ==作差得)(ln2121x x a x x -=,即2121ln x x x x a -=.所以原式等价于2121211lnx x x x x x λ+λ+>-,因为210x x <<时,原式恒成立,即212121)()1(ln x x x x x x λλ+-+〈恒成立. 令)1,0(,21∈=t x x t ,则不等式)1()1(ln -++<t t t λλ在)1,0(∈t 上恒成立. 令λλ+-+-=t t t t h )1()(1ln )(,又2222)()()1()()(11)('λ+λ--=λ+λ+-=t t t t t t t h ,当12≥λ时,可见)(0,1∈t 时,0)('>t h ,所以)(0,1)(∈t t h 在上单调递增, 又)(0,10)(,0)(1∈<=t t h h 在上恒成立,符合题意. …………10分当12<λ时,可见当)(0,2λ∈t 时,0)('>t h ,当)1(2,λ∈t 时,0)('<t h 所以)(0,)(2λ∈t t h 在上单调递增, 在),1(2λ∈t 上单调递减,又)(0,10)(,0)(1∈<=t t h h 在上不恒成立,不符合题意,舍去.综上所述,若不等式λλ+⋅<211x x e 恒成立,只需12≥λ,又0>λ,所以1≥λ…………12分22解:(Ⅰ)由 ,得 ,................................................................2分 所以曲线C 的直角坐标方程为 ................................................................................5分(Ⅱ)将直线l 的参数方程代入,得 ,.......7分设A ,B 两点对应的参数分别为 ,由韦达定理及 得 ,故 (10)分23.(1)解:(1)当a=1时,f (x )=﹣x 2+x+4,是开口向下,对称轴为x=的二次函数,g (x )=|x+1|+|x ﹣1|= ,................................................................................2分当x ∈(1,+∞)时,令﹣x 2+x+4=2x ,解得x=,g (x )在(1,+∞)上单调递增,f (x )在(1,+∞)上单调递减,∴此时f (x )≥g (x )的解集为(1,]; (3)分当x ∈[﹣1,1]时,g (x )=2,f (x )≥f (﹣1)=2.当x ∈(﹣∞,﹣1)时,g (x )单调递减,f (x )单调递增,且g (﹣1)=f (﹣1)=2. 综上所述,f (x )≥g (x )的解集为[﹣1,];...........................................................5分(2)依题意得:﹣x 2+ax+4≥2在[﹣1,1]恒成立,即x 2﹣ax ﹣2≤0在[﹣1,1]恒成立,则只需,解得﹣1≤a≤1,故a 的取值范围是[﹣1,1]. ...............................................................................................10分。
2018届浙江省五校高三第二次联考文科数学试题及答案

2018学年浙江省第二次五校联考数学(文科)试题卷第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}1A x x =>,{}B x x m =<,且A B =R ,那么m 的值可以是( )A .1-B .0C .1D .2 2.已知,a b R ∈,则“222a b +<”是 “1ab <”的( ) A .必要而不充分条件 B .充要条件C .充分而不必要条件D .既不充分也不必要条件3.如图是某班50位学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是:[)4050,,[)5060,,[)6070,,[)7080,,[)8090,,[]90100,,则图中x 的值等于A .0.12B .0.18C .0.012D .0.0184.已知()cos()3f x x πω=+的图像与1=y 的图象的两相邻交点间的距离为,π要得到()y f x =的图像,只需把sin y x ω=的图像 ( )A .向右平移127π个单位 B .向左平移127π个单位 C .向右平移56π个单位 D . 向左平移56π个单位5.下列命题正确的是( )A .若平面α不平行于平面β,则β内不存在直线平行于平面αB .若平面α不垂直于平面β,则β内不存在直线垂直于平面αC .若直线l 不平行于平面α,则α内不存在直线平行于直线lD .若直线l 不垂直于甲面α,则α内不存在直线垂直于直线l6.执行如图所示的程序框图,输出的S 值为( )A .126B .105C .91D .667.若(,),4παπ∈且3cos 24sin(),4παα=-则α2sin 的值为 ( )A .79B .79- C .19- D .198.已知双曲线2222:1x y C a b-=的左、右焦点分别是12,F F ,正三角形12AF F 的一边1AF 与双曲线左支交于点B ,且114AF BF =,则双曲线C 的离心率的值是( ) A .123+ B. C .1313+ D9.已知函数32()69f x x x x abc =-+-, 其中a b c <<,且0)()()(===c f b f a f ,现给出如下结论:①0)1()0(>f f ;②0)1()0(<f f ;③(0)(3)0f f >;④0)3()0(<f f . 其中正确结论的个数是( )A .1B .2C .3D .410.用()n A 表示非空集合A 中的元素个数,定义()(),()(),()(),()()n A n B n A n B A B n B n A n A n B -≥⎧*=⎨-<⎩当当若22{|140,},{||2014|2013,}A x x ax a RB x x bx b R =--=∈=++=∈,设{|1}S b A B =*=,则()n S 等于( ) A .4B .3C .2D .1第Ⅱ卷二、填空题(本大题共7小题,每小题4分,共28分)11.分别在集合{1,2,4}A =和{3,5,6}B =中随机的各取一个数,则这两个数的乘积为偶数的概率为 ;12.一个几何体的三视图如图所示,侧视图是一个等边三角形,俯视图是半圆和正方形,则这个几何体的体积为 .13.过点(11,2)A 作圆22241640x y x y ++--=的弦,其中弦长为整数的共有 条。
2018年浙江省“五校联考”高考数学二模试卷

2018年浙江省“五校联考”高考数学二模试卷一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合A={x||x−1|≤1},B={x|log2x≤2},则B∩∁R A=()A.[2, 4]B.(2, 4]C.[0, 4]D.(2, 4]∪(−∞, 0)2. 若复数z满足z(1+i)=|1−i|+i(其中i为虚数单位),则z的虚部为()A.1−√22B.√2−12C.−√2+12i D.√2−12i3. 已知随机变量X∼B(4, p),若EX=83,则P(X=2)=()A.8 3B.827C.23D.494. 设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是()A.a⊥α,b // β,α⊥βB.a⊥α,b⊥β,α // βC.a⊂α,b⊥β,α // βD.a⊂α,b // β,α⊥β5. 如图,设A、B是半径为2的圆O上的两个动点,点C为AO中点,则CO→∗CB→的取值范围是()A.[−1, 3]B.[1, 3]C.[−3, −1]D.[−3, 1]6. (1−√x)6(1+√x)4的展开式中x的系数是()A.−4B.−3C.3D.47. 点D是△ABC的边AB的中点,∠ABC=120∘,|CD||AB|=√32,若以A、B为焦点的双曲线恰好经过点C,则该双曲线的离心率为()A.√7+13B.√5+12C.√2+1D.√3+18. 若cosα+sinα=tanα(0<α<π2),则α∈()A.(0,π6) B.(π6,π4) C.(π4,π3) D.(π3,π2)9. 已知△ABC的三边长分别为a、b、c,有以下四个命题:(1)以√a,√b,√c为边长的三角形一定存在;(2)以2a ,2b ,2c 为边长的三角形一定存在;(3)以a 3,b 3,c 3为边长的三角形一定存在;(4)以|a −b|+c ,|b −c|+a ,|c −a|+b 为边长的三角形一定存在,其中正确命题的个数为( ) A.1个 B.2个 C.3个 D.4个10. 已知函数f(x)={|(x −a)2−1|+a,x ≥0|x −a|+2a −1,x <0 的最小值为2a −1,则实数a 的取值范围是( ) A.a =±1 B.0≤a ≤1 C.a ≤0或a =1 D.a ≤0或a ≥1二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.已知2log 6x =1−log 63,则x 的值是________.若实数x ,y 满足{−x +y ≤1y ≥|2x −1| ,则x +y 的最大值为________,x 2+y 2的取值范围为________.一个三棱锥的三视图如图所示,则其表面积为________.点G 是△ABC 的重心,过G 作直线与AB 、AC 两边分别交于M 、N 两点,且AM →=xAB →,AN →=yAC →.若x =12,则y =________,若S △AMN =23S △ABC ,则x +y =________.已知正项等比数列{a n }的前n 项和为S n ,若−1,S 5,S 10成等差数列,则S 10−2S 5=________,S 15−S 10的最小值为________.将一个4×4正方形棋盘中的8个小正方形方格染成红色,使得每行、每列都恰有两个红色方格,则有________种不同的染色方法.棱长为36的正四面体A−BCD的内切球球面上有一动点M,则MB+13MC的最小值为________.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.在△ABC中,角A、B、C的对边分别为a、b、c,且(b+c)2−a2=(2+√2)bc,sinAsinB=cos2C2.(Ⅰ)求角A和角B的大小;(Ⅱ)已知当x∈R时,函数f(x)=sinx(cosx+asinx)的最大值为32,求a的值.如图,四棱锥P−ABCD的底面是梯形.BC // AD,AB=BC=CD=1,AD=2,PB=√132,PA=PC=√3(Ⅰ)证明;AC⊥BP;(Ⅱ)求直线AD与平面APC所成角的正弦值.(Ⅰ)求证:lnx<√x>1);(Ⅱ)设函数f(x)=1lnx −1x−1(x>1)(ⅰ)求证:f(x)是减函数;(ⅱ)若不等式(1+1n)n+a<e对任意n∈N∗恒成立(e是自然对数的底数),求实数a的取值范围.如图,已知椭圆C:x2a2+y2b2=1(a>b>0)离心率为12,焦距为2.(Ⅰ)求椭圆C的方程;(Ⅱ)直线l与椭圆切于点P,OQ⊥l,垂足为Q,其中O为坐标原点.求△OPQ面积的最大值.已知正项数列{a n}满足a1=4,lna n+1=1na n2−a n+3,n∈N∗.(Ⅰ)求证:a n≥4n;(Ⅱ)求证:16≤12+a1+12+a2+..+12+a n≤14参考答案与试题解析2018年浙江省“五校联考”高考数学二模试卷一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】 B【考点】交、并、补集的混合运算 【解析】解不等式求得集合A 、B ,根据交集与补集的定义计算即可. 【解答】集合A ={x||x −1|≤1}={x|−1≤x −1≤1}={x|0≤x ≤2}=[0, 2], B ={x|log 2x ≤2}={x|0<x ≤4}=(0, 4], ∴ ∁R A =(−∞, 0)∪(2, +∞), ∴ B ∩∁R A =(2, 4]. 2.【答案】 A【考点】 复数的运算 【解析】复数z 满足z(1+i)=|1−i|+i ,则(a +bi)(1+i)=a −b +(b +a)i =√2+i ,列方程组能求出z 的虚部. 【解答】设z =a +bi ,∵ 复数z 满足z(1+i)=|1−i|+i (其中i 为虚数单位), ∴ (a +bi)(1+i)=√2+i ,∴ a +bi +ai +bi 2=a −b +(b +a)i =√2+i , ∴ {a −b =√2a +b =1 ,解得a =√2+12,b =1−√22.∴ z 的虚部为1−√22.3.【答案】 B【考点】离散型随机变量的期望与方差 【解析】根据数学期望值求出p ,再利用公式计算概率P(X =2)的值. 【解答】由随机变量X ∼B(4, p), 且EX =83,即np =4p =83,解得p =23;∴ P(X =2)=C 42⋅(23)2⋅(1−23)2=827. 4.【答案】 C【考点】空间中直线与直线之间的位置关系 充分条件、必要条件、充要条件 【解析】根据题意分别画出错误选项的反例图形即可. 【解答】A 、B 、D 的反例如图.5.【答案】 A【考点】平面向量数量积的性质及其运算律 【解析】如图所示,可得O(0, 0),A(−2, 0),C(−1, 0),设B(2cosθ, 2sinθ).θ∈[0, 2π).利用数量积运算性质与三角函数的单调性可得CO →∗CB →范围.【解答】 如图所示,可得O(0, 0),A(−2, 0),C(−1, 0),设B(2cosθ, 2sinθ).θ∈[0, 2π). CO →∗CB →=(1, 0)⋅(2cosθ+1, 2sinθ)=2cosθ+1∈[−1, 3]. 6.【答案】 B【考点】二项式定理的应用 【解析】展开式中x 的系数由三部分和组成:(1−√x)6的常数项与(1+√x)4展开式的x 的系数积;(1−√x)6的展开式的x 的系数与(1+√x)4的常数项的积;(1−√x)6的√x 的系数与(1+√x)4的√x 的系数积.利用二项展开式的通项求得各项系数. 【解答】(1−√x)6的展开式的通项为T r+1=C 6r (−√x)r =(−1)rC 6rx r2∴ (1−√x)6展开式中常数项为C 60,含x 的项的系数为C 62,含√x 的项的系数为−C 61 (1+√x)4的展开式的通项为T r+1=C 4r(√x)r∴(1+√x)4的展开式中的x的系数为C42,常数项为C40,含√x的项的系数为C41故(1−√x)6(1+√x)4的展开式中x的系数是C60C42+C62C40−C61C41=6+15−24=−37.【答案】A【考点】双曲线的特性【解析】设AB=2,根据余弦定理计算BC,AC,从而得出离心率.【解答】不妨设AB=2,则CD=√3,BD=12AB=1,在△BCD中,由余弦定理可得:cos∠ABC=BC2+1−32BC =−12,解得BC=1,在△ABC中,由余弦定理得AC=√4+1−2∗2∗1∗cos120∘=√7,不妨设以AB为焦点的双曲线方程为x2a2−y2b2=1,则2a=AC−BC=√7−1,2c=AB=2,∴离心率e=ca =√7−1=√7+13.8.【答案】C【考点】三角函数的恒等变换及化简求值【解析】把等式左边利用辅助角公式化积,结合α的范围求出cosα+sinα的范围进一步得到tanα的范围,则答案可求.【解答】cosα+sinα=√2sin(α+π4),当0<α<π2时,π4<α+π4<3π4,则√2sin(α+π4)∈(1, √2]⊂(1, √3),∴tanα∈(1, √3).得α∈(π4,π3 ).9.【答案】∵(√b+√c)2−(√a)2=b+c−a+2√bc>0,∴√b+√c>√a,∴以√a,√b,√c为边长的三角形一定存在;当b=3,c=2,a=4时,22+23>24不成立,因此以2a,2b,2c为边长的三角形不一定存在;当b=3,c=2,a=4时,a3>b3+c3不成立,因此以a3,b3,c3为边长的三角形不一定存在; B【考点】 三角形求面积 【解析】三角形ABC 的三边长分别为a ,b ,c ,不妨设a ≥b ≥c ,则b +c >a .通过作差或平方作差,利用绝对值不等式的性质及其三角形三边大小关系即可判断出结论. 【解答】∵ (√b +√c)2−(√a)2=b +c −a +2√bc >0,∴ √b +√c >√a ,∴ 以√a ,√b ,√c 为边长的三角形一定存在;当b =3,c =2,a =4时,22+23>24不成立,因此以2a ,2b ,2c 为边长的三角形不一定存在;当b =3,c =2,a =4时,a 3>b 3+c 3不成立,因此以a 3,b 3,c 3为边长的三角形不一定存在;∵ |a −b|+c +|b −c|+a ≥|a −c|+c +a >|c −a|+b ,∴ 以|a −b|+c ,|b −c|+a ,|c −a|+b 为边长的三角形一定存在; 其中正确命题的个数为2个. 故选:B . 10.【答案】 A【考点】分段函数的应用函数的最值及其几何意义 【解析】讨论a =0,a =1,求得f(x)的解析式,运用二次函数、绝对值函数的值域,可得最值,即可得到结论. 【解答】解:若a =0,则f(x)={|x 2−1|,x ≥0|x|−1,x <0 , 可得x <0时,f(x)>−1; x ≥0时,f(x)≥0,可得f(x)的值域为(−1, +∞),无最小值; 当a =1时,f(x)={|(x −1)2−1|+1,x ≥0|x −1|+1,x <0 , 当x <0时,f(x)=|x −1|+1>2,当x ≥0时,f(x)=|(x −1)2−1|+1≥1, 当x =0时,取得最小值1,则f(x)的最小值为1,满足题意,当a =−1时,f(x)={|(x +1)2−1|−1,x ≥0|x +1|−3,x <0, 当x <0时,f(x)≥−3;当x ≥0时,f(x)=x 2+2x −1的值域为[−1, +∞), 可得f(x)的最小值为−1. 故排除B ,C,D. 故选A .二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 【答案】 √2【考点】对数的运算性质 【解析】由对数的性质分别化简等号两边,再根据对数函数的定义域和单调性求值. 【解答】原式等价于log 6x 2=log 66−log 63=log 62, 所以x 2=2, 又x >0, ∴ x =√2, 【答案】 5,[0, 13] 【考点】 简单线性规划 【解析】画出不等式组表示的平面区域,由图形求出目标函数z =x +y 的最大值,再根据z =x 2+y 2表示区域内的点到原点的距离的平方,求出x 2+y 2的取值范围. 【解答】不等式组{−x +y ≤1y ≥|2x −1| 可化为 {x −y ≥−1y ≥2x −1y ≥0 或{x −y ≥−1y ≥−2x +1y ≥0, 在同一坐标系中画出两个不等式组表示的平面区域,如图所示;则由图形知,目标函数z =x +y 过点C 时,z 取得最大值, 由{x −y =−1y =2x −1 ,解得C(2, 3), ∴ x +y 的最大值为5;又z =x 2+y 2表示区域内的点到原点的距离的平方, 由图形知,x 2+y 2的最小值为0, 最大值为22+32=13,∴ x 2+y 2的取值范围是[0, 13]. 【答案】26+2√34,其外接球的体积是125√23π【考点】由三视图求体积 【解析】判断几何体的形状,利用所使用的数据求解三棱锥的表面积以及外接球体积即可. 【解答】如图:PA ⊥平面ABC ,AB ⊥BC ,PA =5,AB =3,BC =4,三棱锥的表面积为:12×3×5+12×3×4+12×4×√25+9+12×5×√9+16=26+2√34 三棱锥的外接球就是长方体三度为:5,4,3的外接球,所以外接球的半径为:12√32+42+52=5√22.外接球的体积为:4π3×(5√22)3=125√23π. 【答案】 1,2【考点】平面向量的基本定理 【解析】用AM →,AN →表示出AG →,根据三点共线求出x ,y 的关系,根据三角形的面积比得出xy =23,从而可求出x +y 的值. 【解答】根据条件:AC →=1y AN →,AB →=1x AM →;又AG →=13AB →+13AC →;∴ AG →=13x AM →+13y AN →; 又M ,G ,N 三点共线; ∴ 13x +13y =1; ∵ x =12,∴ y =1; ∵ S △AMN =23S △ABC , ∴12AM∗AN∗sin∠MAN 12AB∗AC∗sin∠BAC =AM AB∗AN AC =xy =23,又1x +1y =3,即x+yxy =3, ∴ x +y =2.【答案】1,4【考点】等比数列的前n项和【解析】由题意和等差数列易得第一问;再根据S5,S10−S5,S15−S10为等比数列,可得S15−S10为S5的式子,由基本不等式可得第二问.【解答】∵−1,S5,S10成等差数列,∴2S5=S10−1,∴S10−2S5=1,又由等比数列的性质可得S5,S10−S5,S15−S10为等比数列,∴S5(S15−S10)=(S10−S5)2,∴S15−S10=(S10−S5)2S5=(1+2S5−S5)2S5=S5+1S5+2≥2√S5∗1S5+2=4,当且仅当S5=1S5即S5=1时取等号,∴S15−S10的最小值为4,【答案】90【考点】排列、组合及简单计数问题【解析】根据题意,先分析第一行的染法数目,进而分类讨论第一行染好后的3种情况,①第二行的红色方格均与第一行的红色方格同列,②第二行染的红色方格与第一行的红色方格均不同列,③第二行染的红色方格恰有一个与第一行的红色方格同列,依次分析第三、四行的染法数目,综合可得第二、三、行的染法数目,由分步计数原理可得答案.【解答】第一行染2个红色方格有C42种染法;第一行染好后,有如下三种情况:①第二行的红色方格均与第一行的红色方格同列,这时其余行都只有1种染法;②第二行染的红色方格与第一行的红色方格均不同列,这时第三行有C42种染法,第四行的染法随之确定;③第二行染的红色方格恰有一个与第一行的红色方格同列,而第一、第二这两行染好后,第三行的红色方格必然有一个与上面的红色方格均不同列,这时第三行的染法有2种,第四行染法随之确定.因此,共有染法为:6×(1+6+4×2)=90(种).【答案】4√33【考点】球内接多面体【解析】由阿波罗尼斯球得内切球球心O是线段CH上以C,E为定点空间中满足PCPE=λ(λ≠1)的点P的集合,连结CO并延长交平面ABD于H,交内切球上方的点设为K,过M作ME⊥CH,交CH于E,连结BM,CM,设OE=x,由已知得CO=9√6,OH=3√6,KCKE=HC HE ,推导出x=√6,λ=3,从而13MC=ME,进而MB+13MC=MB+ME≥BE,由此能求出MB+13MC的最小值.【解答】由阿波罗尼斯球得内切球球心O是线段CH上以C,E为定点,空间中满足PCPE=λ(λ≠1)的点P的集合,连结CO并延长交平面ABD于H,交内切球上方的点设为K,过M作ME⊥CH,交CH于E,连结BM,CM,设OE=x,由已知得CO=9√6,OH=3√6,KC KE =HCHE,∴√63√6−x=√63√6+x,解得x=√6,∴λ=KCKE =√62√6=3,∴MCME =3,∴13MC=ME,∴MB+13MC=MB+ME≥BE,在△BOE中,BO=CO=9√6,OE=√6,cos∠BOE=−cos∠BOH=−13,∴BE=√(9√6)2+(√6)2−2×9√6×√6×(−13)=4√33.∴MB+13MC的最小值为4√33.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.【答案】(Ⅰ)由(b+c)2−a2=(2+√2)bc,可得:b2+c2−a2=√2bc,所以cosA=b2+c2−a22bc =√2bc2bc=√22,又0<A<π,可得:A=π4,由sinAsinB=cos2C2,可得:√22sinB=1+cosC2,√2sinB=1+cosC,∴B+C=3π4,则√2sin(3π4−C)=1+cosC,∴可得:sinC=1,解得C=π2,∴B=π4.(Ⅱ)f(x)=sinx(cosx+asinx)=12sin2x+a2(1−cos2x)=a2+√1+a22sin(2x−θ),tanθ=a,∵函数f(x)=sinx(cosx+asinx)的最大值为32,∴a2+√1+a22=32,∴解得a=43..【考点】余弦定理【解析】(Ⅰ)由已知可得:b2+c2−a2=√2bc,利用余弦定理可求cosA,结合范围0<A<π,可求A=π4,由已知可得sinB=1+cosC,由B+C=3π4,则利用三角函数恒等变换的应用可求sinC=1,解得C=π2,利用三角形内角和定理解得B=π4.(Ⅱ)利用恒等变换公式对f(x)=sinx(cosx+asinx)化简得到f(x)=a2+√1+a22sin(2x−θ),再由最大值,建立方程即可求出a的值.【解答】(Ⅰ)由(b+c)2−a2=(2+√2)bc,可得:b2+c2−a2=√2bc,所以cosA=b2+c2−a22bc =√2bc2bc=√22,又0<A<π,可得:A=π4,由sinAsinB=cos2C2,可得:√22sinB=1+cosC2,√2sinB=1+cosC,∴B+C=3π4,则√2sin(3π4−C)=1+cosC,∴可得:sinC=1,解得C=π2,∴B=π4.(Ⅱ)f(x)=sinx(cosx+asinx)=12sin2x+a2(1−cos2x)=a2+√1+a22sin(2x−θ),tanθ=a,∵函数f(x)=sinx(cosx+asinx)的最大值为32,∴a2+√1+a22=32,∴解得a=43..【答案】则A(0, −√32, 0),C(0, √32, 0),P(−34, 0, 3√34),D(−1, √32, 0),∴AD→=(−1, √3, 0),AC→=(0, √3, 0),AP→=(−34, √32, 3√34),设平面ACP 的法向量为n →=(x, y, z),则{n →∗AC →=0n →∗AP →=0 ,即{√3y =0−34x +√32y +3√34z =0 , 令x =√3得n →=(√3, 0, 1), ∴ cos <n →,AD →>=n →∗AD →|n →||AD →|=−√34, ∴ 直线AD 与平面APC 所成角的正弦值为|cos <n →,AD →>|=√34.【考点】直线与平面垂直 直线与平面所成的角 【解析】(I )取AC 的中点M ,连接PM ,BM ,通过证明AC ⊥平面PBM 得出AC ⊥BP ; (II)以M 为原点建立坐标系,求出平面APC 的法向量n →,通过计算n →与AD →的夹角得出AD 与平面APC 所成角. 【解答】(I )证明:取AC 的中点M ,连接PM ,BM , ∵ AB =BC ,PA =PC ,∴ AC ⊥BM ,AC ⊥PM ,又BM ∩PM =M , ∴ AC ⊥平面PBM , ∵ BP ⊂平面PBM , ∴ AC ⊥BP .(II)∵ 底面ABCD 是梯形.BC // AD ,AB =BC =CD =1,AD =2, ∴ ∠ABC =120∘,∵ AB =BC =1,∴ AC =√3,BM =12,∴ AC ⊥CD , 又AC ⊥BM ,∴ BM // CD .∵ PA =PC =√3,CM =12AC =√32,∴ PM =32,∵ PB =√132,∴ cos∠BMP =PM 2+BM 2−BP 22PM∗BM=−12,∴ ∠PMB =120∘,以M 为原点,以MB ,MC 的方向为x 轴,y 轴的正方向,以平面ABCD 在M 处的垂线为z 轴建立坐标系M −xyz , 【答案】(1)证明:令g(x)=lnx −√x>1),则g′(x)=1x −√x−(x−1)⋅12√xx=1−√x+x−12√xx=(√x−1)⋅1−√x 2√xx=√x−1)22x √x<0,∴ g(x)在(1, +∞)上单调递减, ∴ g(x)<g(1)=0,即lnx √x<0.∴ lnx <x>1).(2)证明:(i)f′(x)=−1x(lnx)2+1(x−1)2=x(lnx)2−(x−1)2(x−1)2(lnx)2,由(I)可知lnx <√x,∴ (lnx)2<(x−1)2x,∴ x(lnx)2<(x −1)2,∴ f′(x)<0,∴ f(x)=1lnx −1x−1(x >1)是减函数. (ii)由(1+1n )n+a <e 得(n +a)ln(1+1n )<1, ∵ ln(1+1n )>ln1=0,∴ n +a <1ln(1+1n),即a <1ln(1+1n)−n ,令1+1n =t ,则n =1t−1(1<t ≤2). ∴ a <1lnt −1t−1=f(t),由(i)可知f(t)在(1, 2]上单调递减, ∴ f(t)的最小值为f(2)=1ln2−1. ∴ a <1ln2−1.【考点】不等式的证明 【解析】(I )作差求导,根据单调性和最值得出结论;(II)(i)根据(I)的结论判断f′(x)<0,从而结论得证;(ii)分离参数可得a <1ln(1+1n)−n ,使用换元法和(i)的单调性求出函数的最小值即可得出a 的范围. 【解答】(1)证明:令g(x)=lnx −√x>1),则g′(x)=1x−√x−(x−1)⋅12√xx=1−√x+x−12√xx=(√x−1)⋅1−√x 2√xx=√x−1)22x √x<0,∴ g(x)在(1, +∞)上单调递减, ∴ g(x)<g(1)=0,即lnx √x<0.∴ lnx <x>1).(2)证明:(i)f′(x)=−1x(lnx)2+1(x−1)2=x(lnx)2−(x−1)2(x−1)2(lnx)2,由(I)可知lnx <√x,∴ (lnx)2<(x−1)2x,∴ x(lnx)2<(x −1)2,∴ f′(x)<0,∴ f(x)=1lnx −1x−1(x >1)是减函数. (ii)由(1+1n )n+a <e 得(n +a)ln(1+1n )<1, ∵ ln(1+1n )>ln1=0,∴ n +a <1ln(1+1n),即a <1ln(1+1n)−n ,令1+1n =t ,则n =1t−1(1<t ≤2). ∴ a <1lnt −1t−1=f(t),由(i)可知f(t)在(1, 2]上单调递减, ∴ f(t)的最小值为f(2)=1ln2−1. ∴ a <1ln2−1. 【答案】(1)由椭圆的离心率e =ca =12,则2c =2,c =1, 则a =2,b =√a 2−b 2=3, ∴ 椭圆C 的方程:x 24+y 23=1;(2)方法一:设P(x 0, y 0),(x 0≠0, y 0≠0)由椭圆在P 的切线方程:x 0x 4+y 0y 3=1,即3x 0x +4y 0y −12=0,则直线OQ 的方程:y =4y3x 0x ,即3x 0y −4y 0x =0,则|OQ|=√9x 0+16y 0,|PQ|=0000√9x 0+16y 0=00√9x 0+16y 0,则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12√9x 0+16y 0×00√9x 0+16y 0=6|x 0y 0|9x 02+16y 02≤6|x 0y 0|2×3×4|x 0y 0|=14,当且仅当9x 02=16y 02,即x 02=167,y 02=97时取等号, △OPQ 面积的最大值14.方法二:设切线方程:y =kx +m ,(k ≠0)切点P(x 0, y 0),(x 0≠0, y 0≠0), O 到切线的距离:|OQ|=√1+k 2,联立{y =kx +m x 24+y 23=1,整理得:(3+4k 2)x 2+8kmx +4m 2−12=0,△=(8km)2−4×(3+4k 2)(4m 2−12)=0,整理得:m 2=3+4k 2, 代入解得:x 0=√3+4k 2,y 0=k 0x +m =√3+4k 2, 直线OQ 的方程:y =−1k x ,即ky +x =0,则|PQ|=|√3+4k 2−√3+4k 2|√1+k 2=√3+4k 2√1+k 2,则则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12×|PQ|⋅|OQ|=12√3+4k 2√1+k 2⋅√1+k 2=12×|k|1+k 2≤12×|k|2|k|=14, 当且仅当k 2=1时,即x 02=167,y 02=97时取等号, △OPQ 面积的最大值14.【考点】椭圆的标准方程 椭圆的应用直线与椭圆的位置关系 【解析】(Ⅰ)根据椭圆的离心率公式及c =1,即可求得a 和c 的值,即可求得椭圆方程;(Ⅱ)方法一:根据椭圆的切线方程,求得直线OQ 的方程,根据点到直线的距离公式即可求得|OQ|及|PQ|,利用三角形的面积公式和基本不等式即可求得△OPQ 面积的最大值;方法二:设切线方程y =kx +m ,求得直线OQ 方程,将切线方程代入椭圆方程,由△=0,即可求得m 2=3+4k 2,利用点到直线的距离公式分别求得|OQ|及|PQ|,根据三角形的面积公式及基本不等式的性质,即可求得△OPQ 面积的最大值. 【解答】(1)由椭圆的离心率e =ca =12,则2c =2,c =1, 则a =2,b =√a 2−b 2=3, ∴ 椭圆C 的方程:x 24+y 23=1;(2)方法一:设P(x 0, y 0),(x 0≠0, y 0≠0)由椭圆在P 的切线方程:x 0x 4+y 0y 3=1,即3x 0x +4y 0y −12=0,则直线OQ 的方程:y =4y3x 0x ,即3x 0y −4y 0x =0,则|OQ|=√9x 0+16y 0,|PQ|=0000√9x 0+16y 0=00√9x 0+16y 0,则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12√9x 0+16y 0×00√9x 0+16y 0=6|x 0y 0|9x 02+16y 02≤6|x 0y 0|2×3×4|x 0y 0|=14, 当且仅当9x 02=16y 02,即x 02=167,y 02=97时取等号,△OPQ 面积的最大值14.方法二:设切线方程:y =kx +m ,(k ≠0)切点P(x 0, y 0),(x 0≠0, y 0≠0), O 到切线的距离:|OQ|=√1+k 2,联立{y =kx +mx 24+y 23=1,整理得:(3+4k 2)x 2+8kmx +4m 2−12=0,△=(8km)2−4×(3+4k 2)(4m 2−12)=0,整理得:m 2=3+4k 2, 代入解得:x 0=√3+4k 2,y 0=k 0x +m =√3+4k 2, 直线OQ 的方程:y =−1k x ,即ky +x =0,则|PQ|=|√3+4k 2−√3+4k 2|√1+k 2=√3+4k 2√1+k 2,则则△OPQ 面积S △OPQ =12×|OQ|×|PQ|=12×|PQ|⋅|OQ|=12√3+4k 2√1+k 2⋅√1+k 2=12×|k|1+k 2≤12×|k|2|k|=14, 当且仅当k 2=1时,即x 02=167,y 02=97时取等号, △OPQ 面积的最大值14. 【答案】证明:(Ⅰ)首先利用lnx ≤x −1,可得1n a n 2+a n −3=lna n+1≤a n+1−1,即a n+1≥1na n 2+a n −4,以下用数学归纳法证明a n ≥4n , ①当n =1时显然成立;②假设当n =k 时,不等式成立,即a k ≥4k ,则当n =k +1时,由函数f(x)=1k x 2−x +4的单调性可得,a k+1≥1k ⋅a k 2−a k +4≥1k(4k)2−4k +4=12k +4>4(k +1),也就是说,当n =k +1时,不等式也成立;由①②可知,a n ≥4n 对任意的n ∈N ∗成立; (2)易知12+a 1+12+a 2+⋯+12+a n>12+a 1=16,由a n+1≥1n a n2−a n +4=a n (an n−1)+4≥3a n +4,则a n+1+2≥3(a n +2), 所以,a n +2≥3(a n−1+2)≥32(a n−2+2)≥⋯≥3n−1(a 1+2)=3n−1⋅6=2⋅3n ,则12+a n≤12⋅13,因此,12+a 1+12+a 2+⋯+12+a n≤12(13+132+⋯+13n )=12⋅13(1−13n )1−13=14(1−13n )=14,所以,16≤12+a 1+12+a 2+⋯+12+a n≤14.【考点】数列与不等式的综合 【解析】(Ⅰ)由lnx ≤x −1,得a n+1≥1n a n2−a n +4,然后利用数学归纳法证明不等式a n ≥4n 成立;(Ⅱ)先由12+a 1+12+a 2+⋯+12+a n>12+a 1=16成立,再由a n+1≥1n a n2−a n +4≥3a n +4成立,于是得到a n+1+2≥3(a n +2)成立,进而得到a n +2≥2⋅3n ,于是得到12+a n≤12⋅13n,然后利用不等式的可加性与等比数列求和公式可证明12+a 1+12+a 2+⋯+12+a n≤14成立.【解答】证明:(Ⅰ)首先利用lnx ≤x −1,可得1n a n 2+a n −3=lna n+1≤a n+1−1,即a n+1≥1na n 2+a n −4,以下用数学归纳法证明a n ≥4n , ①当n =1时显然成立;②假设当n =k 时,不等式成立,即a k ≥4k ,则当n =k +1时,由函数f(x)=1k x 2−x +4的单调性可得,a k+1≥1k ⋅a k 2−a k +4≥1k(4k)2−4k +4=12k +4>4(k +1),也就是说,当n =k +1时,不等式也成立;由①②可知,a n ≥4n 对任意的n ∈N ∗成立; (2)易知12+a 1+12+a 2+⋯+12+a n>12+a 1=16,由a n+1≥1n a n2−a n +4=a n (an n −1)+4≥3a n +4,则a n+1+2≥3(a n +2), 所以,a n +2≥3(a n−1+2)≥32(a n−2+2)≥⋯≥3n−1(a 1+2)=3n−1⋅6=2⋅3n ,则12+a n≤12⋅13n ,因此,12+a 1+12+a 2+⋯+12+a n≤12(13+13+⋯+13)=12⋅13(1−13n )1−13=14(1−13)=14,所以,16≤12+a 1+12+a 2+⋯+12+a n≤14.。
2018届浙江省高三第二次五校联考文科数学试题及答案 精品

2018学年浙江省五校联考第二次考试数学(文科)试题卷本试题卷分选择题和非选择题两部分.全卷共4页, 选择题部分1至2页, 非选择题部分3至4页.满分150分, 考试时间120分钟.请考生按规定用笔将所有试题的答案涂、写在答题纸上.参考公式:柱体的体积公式V =Sh 其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式 V =13Sh 其中S 表示锥体的底面积,h 表示锥体的高台体的体积公式1()123V h S S =++ 其中S 1,S 2分别表示台体的上,下底面积球的表面积公式S =4πR 2其中R 表示球的半径,h 表示台体的高球的体积公式V =43πR3其中R 表示球的半径第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 在C ∆AB 中,“C 0AB⋅A =”是“C ∆AB 为直角三角形”的( ▲ ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件2. 已知数列{}n a 满足:21n a n n =+,且910n S =,则n 的值为( ▲ ) A .7 B .8 C .9 D .103.要得到函数sin 2y x =的图象,只需将函数πcos(2)3y x =-的图象( ▲ )A .向右平移π6个单位长度B .向左平移π6个单位长度C .向右平移π12个单位长度D .向左平移π12个单位长度4.若αβ、是两个相交平面,则在下列命题中,真命题的序号为( ▲ )①若直线m α⊥,则在平面β内,一定不存在与直线m 平行的直线. ②若直线m α⊥,则在平面β内,一定存在无数条直线与直线m 垂直. ③若直线m α⊂,则在平面β内,不一定存在与直线m 垂直的直线. ④若直线m α⊂,则在平面β内,一定存在与直线m 垂直的直线. A .①③ B.②③ C.②④ D.①④ 5.已知菱形ABCD 的对角线AC 长为1,则ADAC =( ▲ )A .4B .2C .1D .216.设x R ∈, 对于使22x x M -+≤成立的所有常数M 中,我们把M 的最小值1叫做22x x -+ 的上确界. 若,a b R +∈,且1a b +=,则122a b--的上确界为( ▲ ) A .5-B .4-C .92D .92-7.如图,已知椭圆C 1:112x +y 2=1,双曲线C 2:22a x —22by =1(a >0,b >0),若以C 1的长轴为直径的圆与C 2的一条渐近线交于A 、B 两点,且C 1与该渐近线的两交点将线段AB 三等分,则C 2的离心率为( ▲ ) A .5 B .5 C .17 D .71428. 如图,正ABC ∆的中心位于点G (0,1),A (0,2),动点P 从A 点出发沿ABC ∆的边界按逆时针方向运动,设旋转的角度(02)AGP x x π∠=≤≤,向量OP 在(1,0)a =方向的投影为y (O 为坐标原点),则y 关于x 的函数()y f x =的图像是( ▲ )非选择题部分(共110分)二、填空题(本大题共7小题,前4题每题6分,后3题每空4分,共36分.)9.设全集U R =,集合2{|340}A x x x =--<,2{|log (1)2}B x x =-<,则A B =▲ ,AB = ▲ ,RC A = ▲ .10.若变量,x y 满足202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩,则2x y+的最大值为 ▲ ,_____21的取值范围-+x y ▲ . 11. 已知命题p :R x ∈∃,x-1>lnx .命题q :R x ∈∀,0>x ,则⌝p : ▲ ,命题p∧(⌝q )是 ▲ (填真命题或假命题)。
浙江省五校联盟2023-2024学年高三下学期3月联考试题 数学含答案

浙江省五校联盟2023-2024学年高三下学期3月联考数学试卷(答案在最后)命题:一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.若全集U ,集合A,B 及其关系如图所示,则图中阴影部分表示的集合是()A.()U A B ⋂ðB.()U A B ⋃ðC.()U A B⋂ð D.()U A B⋂ð2.已知(1,2),||2a b == ,且a b ⊥ ,则a b - 与a的夹角的余弦值为()A.5B.3C.4D.63.设b ,c 表示两条直线,,αβ表示两个平面,则下列说法中正确的是()A.若//,b c αα⊂,则//b cB.若//,b c b α⊂,则//c αC.若,//c αβα⊥,则c β⊥ D.若//,c c αβ⊥,则αβ⊥4.已知角α的终边过点(3,2cos )P α-,则cos α=()A.2B.2-C.2±D.12-5.设等比数列{}n a 的公比为q ,前n 项和为n S ,则“2q =”是“{}1n S a +为等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知实数x ,y 满足3x >,且2312xy x y +-=,则x y +的最小值为()A.1+B.8C. D.1+7.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,点A 为双曲线的左顶点,以12F F 为直径的圆交双曲线的一条渐近线于P ,Q 两点,且23PAQ π∠=,则该双曲线的离心率为()C.2138.在等边三角形ABC 的三边上各取一点D ,E ,F ,满足3,90DE DF DEF ︒==∠=,则三角形ABC 的面积的最大值是()A. B.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.在学校组织的《青春如火,初心如炬》主题演讲比赛中,有8位评委对每位选手进行评分(评分互不相同),将选手的得分去掉一个最低评分和一个最高评分,则下列说法中正确的是()A.剩下评分的平均值变大B.剩下评分的极差变小C.剩下评分的方差变小D.剩下评分的中位数变大10.在三棱锥A BCD -中,已知3,2AB AC BD CD AD BC ======,点M ,N 分别是AD ,BC 的中点,则()A.MN ⊥ADB.异面直线AN ,CM 所成的角的余弦值是78C.三棱锥A BCD -的体积为3D.三棱锥A BCD -的外接球的表面积为11π11.已知函数()(sin cos )xf x e x x =⋅+,则()A.()f x 的零点为,4x k k Z ππ=-∈B.()f x 的单调递增区间为32,2,22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C.当0,2x π⎡⎤∈⎢⎣⎦时,若()f x kx ≥恒成立,则22k e ππ≤⋅D.当10031005,22x ππ⎡⎤∈-⎢⎥⎣⎦时,过点1,02π-⎛⎫⎪⎝⎭作()f x 的图象的所有切线,则所有切点的横坐标之和为502π三、填空题:本题共3小题,每小题5分,共15分.12.直线3430x y -+=的一个方向向量是.13.甲、乙两人争夺一场羽毛球比赛的冠军,比赛为“三局两胜”制.如果每局比赛中甲获胜的概率为23,乙获胜的概率为13,则在甲获得冠军的情况下,比赛进行了三局的概率为.14.已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=,若(21),(2)f x g x --均为偶函数,且当[1,2]x ∈时,3()2f x mx x =-,则(2024)g =.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,斜三棱柱111ABC A B C -的底面是直角三角形,90ACB ︒∠=,点1B 在底面ABC 内的射影恰好是BC 的中点,且2BC CA ==.(I)求证:平面11ACC A ⊥平面11B C CB ;(II),求平面1ABB 与平面11AB C 夹角的余弦值.16.(本小题满分15分)己知函数()ln f x x ax =-,其中a R ∈.(I)若曲线()y f x =在1x =处的切线在两坐标轴上的截距相等,求a 的值;(II)是否存在实数a ,使得()f x 在(0,]x e ∈上的最大值是-3?若存在,求出a 的值;若不存在,说明理由.17.(本小题满分15分)记复数的一个构造:从数集中随机取出2个不同的数作为复数的实部和虚部.重复n 次这样的构造,可得到n 个复数,将它们的乘积记为n z .已知复数具有运算性质:|()()||()||()|a bi c di a bi c di +⋅+=+⋅+,其中,,,a b c d R ∈.(I)当2n =时,记2z 的取值为X ,求X 的分布列;(II)当3n =时,求满足32z ≤的概率;(III)求5n z <的概率n P .18.(本小题满分17分)在平面直角坐标系xOy 中,我们把点*(,),,x y x y N ∈称为自然点.按如图所示的规则,将每个自然点(,)x y 进行赋值记为(,)P x y ,例如(2,3)8P =,(4,2)14,(2,5)17P P ==.(I)求(,1)P x ;(II)求证:2(,)(1,)(,1)P x y P x y P x y =-++;(III)如果(,)P x y 满足方程(1,1)(,1)(1,)(1,1)2024P x y P x y P x y P x y +-+++++++=,求(,)P x y 的值.19.(本小题满分17分)在平面直角坐标系xOy 中,过点(1,0)F 的直线l 与抛物线2:4C y x =交于M ,N 两点(M在第一象限).(I)当||3||MF NF =时,求直线l 的方程;(II)若三角形OMN 的外接圆与曲线C 交于点D (异于点O ,M ,N ),(i)证明:△MND 的重心的纵坐标为定值,并求出此定值;(ii)求凸四边形OMDN 的面积的取值范围.参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.题号12345678答案CBDBCACA二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.题号91011答案BCABDACD三、填空题:本题共3小题,每小题5分,共15分.12.31,4⎛⎫⎪⎝⎭(答案不唯一)13.2514.-6四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)(第I 问,6分;第II 问,7分)解:(I)取BC 中点为M ,连接11,B M B 在底面内的射影恰好是BC 中点,1B M ∴⊥平面ABC ,又AC ⊂ 平面1,ABC B M AC ∴⊥,又90,ACB AC BC ︒∠=∴⊥ ,1,B M BC ⊂ 平面111,,B C CB B M BC M AC ⋂=∴⊥平面11B C CB ,又AC ⊂ 平面11,ACC A ∴平面11ACC A ⊥平面11B C CB .(II)以C 为坐标原点,建立如图所示空间直角坐标系,2BC CA == ,11(2,0,0),(0,2,0),(0,1,0),(0,A B M B C ∴-,111((2,2,0),(0,2,0)AB AB B C =-=-=-,设平面1BAB 的法向量为(,,)n x y z =,100n AB n AB ⎧⋅=⎪∴⎨⋅=⎪⎩则有20220x y x y ⎧-++=⎪⎨-+=⎪⎩,令z =,则3,x y n ==∴= ,设平面1BAB 的法向量为(,,)m a b c =,11100m AB m B C ⎧⋅=⎪∴⎨⋅=⎪⎩则有2020a b b ⎧-++=⎪⎨-=⎪⎩,令a =则0,2,b c n ==∴=,||5|cos ,||||7| n m n m n m ⋅∴<〉==,平面1ABB 与平面11AB C 夹角的余弦值为57.16.(本小题满分15分)(第I 问,6分;第II 问,9分)(I)1()f x a x'=-,则(1)1,(1)f a f a '=-=-,故曲线()y f x =在1x =处的切线为(1)(1)y a a x +=--,即(1)1y a x =--,当1a =时,此时切线为1y =-,不符合要求当1a ≠时,令0x =,有1y =-,令0y =,有11x a =-,故111a=--,即2a =,故2a =(II)11()ln ,()axf x x ax f x a x x-=-∴=-= ,①当0a ≤时,()f x 在(0,e]上单调递增,()f x ∴的最大值是(e)1e 3f a =-=-,解得40ea =>,舍去;②当0a >时,由11()0ax f x a x x -=-==,得1x a=,当10e a <<,即1a e >时,10,a x ⎛⎫∴∈ ⎪⎝⎭时,1()0;,e f x x a ⎛⎫>∈ ⎪⎝⎭时,()0f x <,()f x ∴的单调递增区间是10,a ⎛⎫ ⎪⎝⎭,单调递减区间是1,e a ⎛⎫ ⎪⎝⎭,又()f x 在(0,e]上的最大值为2max 13,()1ln 3,e f x f a a a ⎛⎫-∴==--=-∴= ⎪⎝⎭;当1e a ≤,即10ea <≤时,()f x 在(0,e]上单调递增,max ()(e)1e 3f x f a ∴==-=-,解得41e ea =,舍去.综上,存在a 符合题意,此时2e a =17.(本小题满分15分)(第I 问,6分;第II 问,4分;第III 问,5分)(I)由题意可知,可构成的复数为{1,,1}i i +,|1|||1,||||||| 2.i i =====+=且X的可能取值为,111111224242111111666666122(1),(,(2)999C C C C C C P X P X P X C C C C C C ⋅⋅⋅=========⋅⋅⋅,112211661(3)9C C P X C C ⋅===⋅111142221111666621(,(4)99C C C C P X P X C C C C ⋅⋅======⋅⋅,所以分布列为:(II)共有111666216CC C ⋅⋅=种,满足32z ≤的情况有:①3个复数的模长均为1,共有1112228C C C ⋅⋅=种;②3个复数中,2个模长均为1,1或者2,共有2111322448C C C C ⋅⋅⋅=种;所以()38487221627P z +≤==.(III)当1n =或2时,显然都满足,此时1n P =;当3n ≥时,满足5n z <共有三种情况:①n 个复数的模长均为1,则共有()122nn C =;②1n -个复数的模长为1,剩余1或者2,则共有()11111242n n n n C C C n --+⋅⋅=⋅;③2n -个复数的模长为1,剩余2个模长为2,则共有()221111244(1)2n n n nCCC C n n --+⋅⋅⋅=-⋅.故()()()2112621222(1)212563n n n n n nn nn n n n n P z C ++++⋅+-⋅+<===,此时当1,2n =均成立.所以()21253n nn P z +<=.18.(本小题满分17分)(第I 问,4分;第II 问,7分;第III 问,6分)解:(I)根据图形可知(1)(,1)1232x x P x x +=++++=,(II)固定x ,则(,)P x y 为一个高阶等差数列,且满足(,1)(,)1,(1,)(,),P x y P x y x y P x y P x y x y +-=+-+-=+所以(1)(,1)(,1)12(1)(1)2y y P x y P x y y x y x ++-=++++-=+- (1)(1)(,1)(1)22y y x x P x y y x +++=+-+所以(1)(1)(,)(1)(1)22x x y y P x y x y +-=++--,(1)(1)(1,)(2)(1)22x x y y P x y x y ---=++--,所以(1)(1)(1)(1)(,1)(1,)(2)(1)(1)2222x x y y y y x x P x y P x y x y y x --++++-=++--++-+222322(,)x y xy y x P x y =++--+=(III)P(x +1,y -1)+P(x ,y +1)+P(x +1,y )+P(x +1,y +1)=2024等价于(,)(,1)(1,)(1,1)2023P x y P x y P x y P x y +++++++=,等价于(,1)3(1,)2023P x y P x y +++=即13[(1)(21)][(1)(2)(1)(2)]202322x x y y x x x y y x +++-++++-+=,化简得2221010(1)()21010y xy x y x x y x y x ++-+=⇔+-++=,由于x y +增大,(1)()x y x y +-+也增大,当31x y +=时,(1)()29921010x y x y x +-++<<,当33x y +=时,(1)()210561010x y x y x +-++>>,故当32x y +=时,(1)()210109,23x y x y x x y +-++=⇒==,即9102322(9,23)82247422P ⨯⨯=++⨯=19.(本小题满分17分)(第I 问,4分;第II 问,5分;第III 问,8分)解:(I)设直线()()1122:1,,,,MN X my M x y N x y =+联立214x my y x=+⎧⎨=⎩,消去x ,得2440y my --=,所以12124,4y y m y y +=⋅=-,||3||MF NF =,则123y y =-122212224,34y y y m y y y +=-=∴⋅=-=-,则213m =,又由题意0,3m m >∴=,直线的方程是y =;(II)(i)方法1:设()()()112233,,,,,M x y N x y D x y 因为O ,M ,D ,N 四点共圆,设该圆的方程为220x y dx ey +++=,联立22204x y dx ey y x⎧+++=⎨=⎩,消去x ,得42(416)160y d y ey +++=,即()3(416)160y y d y e +++=,所以123,,y y y 即为关于y 的方程3(416)160y d y e +++=的3个根,则()()()3123(416)16y d y e y y y y y y +++=---,因为()()()()()32123123122313123y y y y y y y y y y y y y y y y y y y y y ---=-+++++-,由2y 的系数对应相等得,1230y y y ++=,所以MND 的重心的纵坐标为0.方法2:设()()()112233,,,,,M x y N x y D x y ,则1213234444,,,OM ON MD ND k k k k y y y y y y ====++,因为O,M,C,N 四点共圆,所以MON MDN π∠+∠=,即tan tan 0MON MDN ∠+∠=,()21124tan 116OM ONOM ON y y k k MON k k y y --∠==+⋅+()()()1213234tan ,116ND MDND MD y y k k MDN k k y y y y --∠==+⋅+++化简可得:312y y y =--,所以MND 的重心的纵坐标为0.(ii)记,OMN MND 的面积分别为12,S S ,由已知得直线MN 的斜率不为0设直线:1MN x my =+,联立214x my y x=+⎧⎨=⎩,消去x ,得2440y my --=,所以12124,4y y m y y +=⋅=-,所以11211||22S OF y y =⋅⋅-==由(i)得,()3124y y y m =-+=-,所以2223311(4)444x y m m ==⨯-=,即()24,4D m m -,因为()21212||2444MN x x m y y m =++=++=+,点D 到直线MN的距离d =所以()22211||448122S MN d m m =⋅⋅=⋅+⋅-,所以)221281181S S S m m =+=+-=+-M 在第一象限,即1230,0,40y y y m ><=-<,依次连接O,M,D,N 构成凸四边形OMDN ,所以()3122y y y y =-+<,即122y y -<,又因为122244,2y y y y ⋅=-<,即222y <,即20y <<,所以122244m y y y y =+=->+=,即24m >,即218m >,所以)218116S m m =+-=,设t =,则4t >,令()2()161f t t t =-,则()()222()1611614816f t t t t t ''=-+-=-,因为4t >,所以2()48160f t t '=->,所以()f t在区间4⎛⎫+∞⎪⎝⎭上单调递增,所以()42f t f ⎛⎫>=⎪⎝⎭,所以S的取值范围为,2⎛⎫+∞ ⎪⎝⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省2018年五校联考试题
数学(文史类)答案
11.
()⎪⎪⎩
⎪⎪⎨
⎧⎪
⎭⎫ ⎝⎛
<-⎪⎭⎫ ⎝⎛≥-21121122x x x 12.(]4,∞- 13.1- 14.()2,0 三、解答题:本大题共6小题,每小题14分,共84分。
解答应写出文字说明,证明过程或演算步骤。
15.解:设()11,y x =,()22,y x =………………………………………………(2分) 则023211=+-=⋅y x c a ;
423222-=+-=⋅y x c b ;………………………………………………(
6分) 82
121=+=y x ;
42
22
2=+=y x .………………………………………………(10分)
解得⎩⎨⎧==6211y x ,或⎩⎨⎧-=-=6211y x ,对应的b 分别为⎩⎨⎧-==2022y x ,或⎩⎨⎧==1
322y x ,
分别代入()
2,32-=+=n m ,解得6,4±=-=m n ……………(14分)
16.解:()(
)cos 1sin sin 4f x a x x b x a b π⎛
⎫=+++=+++ ⎪⎝
⎭……………(2分)
(Ⅰ)当1a =时,()14f x x b π⎛
⎫==+++ ⎪⎝
⎭
∴当()222
4
2
k x k k Z π
π
π
ππ-
≤+
≤+
∈时,()f x 是增函数,
∴函数()f x 的单调增区间为()32,244k k k Z ππππ⎡
⎤-+∈⎢⎥⎣
⎦……………(8分) (Ⅱ)由0x π≤≤得5444
x πππ
≤+≤
∴sin 14x π⎛
⎫≤+≤ ⎪⎝
⎭………………………………………………(10分)
∵0a <
∴当sin 14x π⎛
⎫+= ⎪⎝
⎭时,()f x 取最小值33a b ++=……………(※)
当sin 4x π⎛
⎫+= ⎪⎝⎭
时, ()f x 取最大值4,即4b =
将4b =代入(※)式得1a =5a b +=(14分) 17.解:(Ⅰ)3P =
3
1
………………………………………………(4分) (Ⅱ)由于第n 次到顶点A 是从D C B ,,三个顶点爬行而来,从其中任何一个顶点
到达A 的概率都是3
1
,而第1-n 次在顶点A 与小虫在D C B ,,是对立事件. 因此,第n 次到顶点A 的概率为()113
1
--=n n P P ………………(8分)
即⎪⎭⎫
⎝⎛--=-
-4131411n n P P ………………………………………(11分) ⎭
⎬⎫⎩
⎨⎧-∴=41,11n P P 是以43411=-P
为首项,公比为3
1
-的等比数列, ()N n n P n n ∈≥+⎪
⎭
⎫
⎝⎛-=∴-,2 4
1
31431
………………………………(14分) 18.
(Ⅰ)取1CC 的中点G ,则DG 为AE 在面1DC 内的射影,11D F DG AE D F ⊥∴⊥ 又1AD AE A D F ⋂=∴⊥面ADE ………………………………(5分) (Ⅱ)不成立………………………………(7分) 设1CC 、F D 1与平面ADE 的交点分别为G 、H, 在菱形11C CDD 中,可得DG DD ⊥1 又 平面⊥ABCD 平面11C CDD ,
且平面⋂ABCD 平面11C CDD =CD ,CD AD ⊥
1DD AD ⊥∴,因此AED DD 平面⊥1
所以1DHD ∠为直线ADE F D 与平面1所成的角………………………………(10分) 在菱形11C CDD 内,因为CD C 1∠=0
60,所以0
1120=∠DE D
可求得a F D 271=
,所以14
7
5arccos
1=∠F D D , 在H DD Rt 1∆中,2
11π
=
∠+∠HD D H DD ,∴1DHD ∠=14
7
5arcsin
所以直线ADE F D 与平面1所成的角为14
7
5arcsin
.………………………(14分) 19.解:
(Ⅰ)88a b +=⇒
设12(0,2),(0,2)F F -,则128MF MF +=
因此,点M 的轨迹是以12F F 、为焦点,长轴长为8的椭圆,其方程为:22
11216
x y +=
…………………………………………………(6分) (Ⅱ)假设存在这样的直线,使得OAPB 为矩形,并设:3l y kx =+
与椭圆方程联立得:2(324)18210(*)k x kx ++-= 设1122(,),(,)A x y B x y ,则12x x 、是(*)的两根,
且121222
1821
,3434
k x x x x k k +=-
=-++………………………………(8分) 因为OAPB 为矩形,故OB OA ⊥ 则02121=+y y x x ,()()0332121=+++kx kx x x
()
()093121212
=++++x x k x x k
……………………(11分)
由此可得:()
094
31834312122
22=++
⨯-++-
k k k k 解得:25
16
k k =
∴=因此,当直线的斜率为时,可使OAPB 为矩形. ………………………………(14分)
20.解:(Ⅰ)()x f 为非奇非偶函数.
()()3
32x m x x f ++-=- ,而33)(2)(x m x x f -+=
()()x f x f --∴()3
32x m x ++-=33)(2x m x ---=x m x 2362+-不恒为零,
同样,()()x f x f +-也不恒为零.………………………………(6分)
y
x
l
B
A
O
P
Ⅱ) 33)(2)(x m x x f -+= ()22'363m mx x x f -+=∴
又 )(x f 在),5[+∞上单调递增,()036322'≥-+=∴m mx x x f 在),5[+∞上恒成立.
因此⎩⎨
⎧
≥-+≤-0
3307552
m m m ,得255255+≤≤-m ,又因为0>m , 所以2550+≤<m .………………………………(14分)。
