最新异面直线夹角求法
异面直线所成角的几种求法资料讲解

异面直线所成角的几种求法仅供学习与交流,如有侵权请联系网站删除 谢谢2异面直线所成角的几种求法异面直线所成角的大小,是由空间一点分别引它们的平行线所成的锐角(或直角)来定义的。
因此,通常我们要求异面直线所成的角会要求学生通过平移直线,形成角,然后在某个三角形中求出角的方法来得到异面直线所成角的大小。
在这一方法中,平移直线是求异面直线所成角的关键,而如何平移直线要求学生有良好的空间观和作图能力。
一、向量法求异面直线所成的角例1:如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是相邻两侧面BCC 1B 1及CDD 1C 1的中心。
求A 1E 和B 1F 所成的角的大小。
解法一:(作图法)作图关键是平移直线,可平移其中一条直线,也可平移两条直线到某个点上。
作法:连结B 1E ,取B 1E 中点G 及A 1B 1中点H , 连结GH ,有GH//A 1E 。
过F 作CD 的平行线RS , 分别交CC 1、DD 1于点R 、S ,连结SH ,连结GS 。
由B 1H//C 1D 1//FS ,B 1H=FS ,可得B 1F//SH 。
在△GHS 中,设正方体边长为a 。
GH=46a (作直线GQ//BC 交BB 1于点Q , B A CD FEB 1 A 1 D 1C 1G HSRPQ仅供学习与交流,如有侵权请联系网站删除 谢谢3连QH ,可知△GQH 为直角三角形),HS=26a (连A 1S ,可知△HA 1S 为直角三角形), GS=426a (作直线GP 交BC 于点P ,连PD ,可知四边形GPDS 为直角梯形)。
∴Cos ∠GHS=61。
所以直线A 1E 与直线B 1F解法二:(向量法)分析:因为给出的立体图形是一个正方体, 所以可以在空间建立直角坐标系,从而可以利用 点的坐标表示出空间中每一个向量,从而可以用 向量的方法来求出两条直线间的夹角。
以B 为原点,BC 为x 轴,BA 为y 轴,BB 1为z 轴,设BC 长度为2。
异面直线夹角公式

异面直线夹角公式有几种基本的几何形体,例如圆形、矩形、三角形等,其中,直角夹角是比较重要的一个概念,也是学习几何的基础。
角夹角的基本概念是指夹角的两个边同时垂直于一条垂直线,比如,在一个矩形中,所有的角都是直角夹角。
在几何中,夹角是一个关于角度、边长、斜率之间关系的重要概念。
角的值有三种:直角夹角、锐角夹角和钝角夹角。
夹角的两边都垂直于一条垂直线时,夹角就是直角夹角,其值为90°。
直角夹角有两种计算方法,一种是直接计算,另一种是用公式法计算。
几何中,最常用的直角夹角公式是勾股定理,该定理指出:在一个三角形中,如果三边的长度等于两边的平方和,则该三角形肯定是直角三角形。
此,可以用勾股定理来计算一个三角形的直角夹角,即:c2=a2+b2,其中c是斜边,a和b分别是两个直角边的长度。
另外,还有一种计算直角夹角的方法,即直接测量角度。
例如,如果要计算一个三角形的垂直角,可以用一个尺子将三角形的底边分为两块,然后用一个角规测量它们之间的夹角,从而得到三角形的直角夹角。
此外,在空间几何中,也有一些复杂的夹角,它们也可以用公式法或直接测量法来计算。
例如,异面直角夹角是一种复杂的夹角,它指的是在一组平面之间存在直角夹角,这个夹角可以用公式法计算,即:cosα=ABAC,其中α是两条直线之间的夹角,AB和AC分别是这两条直线的单位向量。
总之,几何中的直角夹角是一个重要的概念,它可以用公式法或直接测量法来计算,也可以用勾股定理来计算三角形的直角夹角,而在空间几何中,还有一些比较复杂的夹角,比如异面直角夹角。
在几何学中,直角夹角是一种重要的概念,有助于对几何空间的理解,学习直角夹角的重要性不容忽视。
计算机可视化中,夹角的计算也很重要,比如用于三维模型的渲染,这些都需要通过计算直角夹角来实现。
综上所述,直角夹角是几何的重要概念,也是很多科学技术领域的基础,其计算也是几何学的重要课题,可以用公式法、直接测量法以及勾股定理来计算夹角,异面直角夹角也可以用公式来计算。
高中数学异面直线夹角自编

浅谈异面直线所成的角异面直线所成角的求法求异面直线夹角主要有三种主要方法,一是几何法,二是矢量法,三是公式法。
一、几何法:几何法求异面直线所成角的思路是:通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几何知识求解。
基本思路是选择合适的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊位置的点。
常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
例:长方体ABCD—A1B1C1D1中,若AB=BC=3,AA1=4,求异面直线B1D与BC1所成角的大小。
直接平移:常见的利用其中一个直线a和另一个直线b上的一个已知点,构成一个平面,在此平面内做直线a的平行线。
解法一:如图④,过B1点作BE∥BC1交CB的延长线于E点。
则∠DB1E就是异面直线DB1与BC1所成角,连结DE交AB于M,cos∠DB1∴∠DB1E=cosarc解法二:如图⑤,在平面D1DBB1中过B点作BE∥DB1交D1B1的延长线于E,则∠C1BE就是异面直线DB1与BC1所成的角,连结C1E,在△B1C1E中,∠C1B1E=135°,C1cos∠C1,∴∠C1BE=cosarc课堂思考:1.如图,PA 矩形ABCD,已知PA=AB=8,BC=10,求AD与PC所成角的余切值为。
2.在长方体ABCD- A1B1C1D1中,若棱B B1=BC=1,AB=3,求D B和AC所成角的余弦值.【例2】如图所示,长方体A1B1C1D1-ABCD中,∠ABA1=45°,∠A1AD1=60°,求异面直线A1B与AD1所成的角的度数.中位线平移法分析:构造三角形找中位线,然后利用中位线的性质,将异面直线所成的角转化为平面问题,解三角形求之。
异面直线所成的角与求法

C1
D1
A1
B
1
例1:如图正方体AC1, ①求异面直线AB1和CC1所成角的
大小
②求异面直线AB1和A1D所成角的 大小
〖分析〗 1、做异面直线的平行线 2、说明哪个角就是所求角 3、把角放到平面图形中求解
解: ①∵ CC1//BB1 ∴ AB1和BB1所成的锐角是异面直线AB1和CC1所成的角 ∵ 在△ABB1中,AB1和BB1所成的角是450 ∴ 异面直线AB1和CC1所成的角是450 。
(2)异面直线所成的角的范围是: (0°<θ≤90°)
这个很 重要哦
(3)如果两条异面直线所成的角是直角,那么我们就说 这两条直线互相垂直,两条互相垂直的异面直线a,b,
记作a⊥b
说明空间的垂直有相交垂直和异面垂直,区别在于一个是相交,一个是异面.
异面直线所成的角的求法:
典例剖析
D
C
A
B
D D1
1
正方体ABCD- A1B1C1D1中,P为 BB1的中点,
如图画出下面各题中指定的异面直线
D1 A1
D A
C1
D1
C1
D1
A1 B1
B1
A1
C
B
P●
D
C
A
B
D A
C1 B1
C
B
异面直线所成的角是锐角或直角,当三角形内角是钝角时, 表示异面直线所成的角是它的补角.
以第三幅图为例,设正方体的棱长为1, 求异面直线的夹角
异面直线所成的角的求法:
典例剖析
D
C
A
B
D D1
1
C1
D1
பைடு நூலகம்A1
B
异面直线夹角的求法

一、 等角定理:一个角的二边分别取另一个角的二边仄止,
则二个角相等或者互补.之阳早格格创做
二:同里曲线夹角
(1)意思:(2)0,]
注:二同里曲线夹角为
时,也喊干二曲线互相笔曲. 三、同里曲线夹角的供法:
1、仄移没有改变线段少度[主要适用于柱体]{曲交法}
2 .A1B1C1—ABC 是曲三棱柱,∠BCA=90°,面D1、F1分别是A1B1、A1C1的中面
若BC=CA=CC1,供BD1取AF1所成角的余弦值. 3.正在棱少为1的正圆体ABCD —A1B1C1D1中,M 战N 分别为A1B1
战BB1的中面,
供曲线A 取CN 所成角的余弦值
二、仄移改变线段少度[主要适用于锥体] 注:采用仄移目标的规则:正在二条同里曲线上,各采用一个面产死线段,则该线段的中面便是仄移的目标位子.
注:正三棱锥对于棱笔曲.[本量]
三、补形[主要适用于线段的位子没有简单爆收移动,如体对于角线,共时央供正在准则的柱体中如正圆体、少圆体中战一些正棱柱中] 例:正圆体ABCD -中,供同里曲线所成的角. B 1 (第6题) A 1 A B C 1 D 1
C
D M
N (第5题) F 1
A B C D 1
C 1
A 1
B 1。
异面直线所成角的几种求法(最新编写)

异面直线所成角的几种求法异面直线所成角的大小,是由空间一点分别引它们的平行线所成的锐角(或直角)来定义的。
因此,通常我们要求异面直线所成的角会要求学生通过平移直线,形成角,然后在某个三角形中求出角的方法来得到异面直线所成角的大小。
在这一方法中,平移直线是求异面直线所成角的关键,而如何平移直线要求学生有良好的空间观和作图能力。
一、向量法求异面直线所成的角例1:如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是相邻两侧面BCC 1B 1及CDD 1C 1的中心。
求A 1E 和B 1F 所成的角的大小。
解法一:(作图法)作图关键是平移直线,可平移其中一条直线,也可平移两条直线到某个点上。
作法:连结B 1E ,取B 1E 中点G 及A 1B 1中点H ,连结GH ,有GH//A 1E 。
过F 作CD 的平行线RS ,分别交CC 1、DD 1于点R 、S ,连结SH ,连结GS 。
由B 1H//C 1D 1//FS ,B 1H=FS ,可得B 1F//SH 。
在△GHS 中,设正方体边长为a 。
GH=a (作直线GQ//BC 交BB 1于点Q ,46连QH ,可知△GQH 为直角三角形),HS=a (连A 1S ,可知△HA 1S 为直角三角形),26GS=a (作直线GP 交BC 于点P ,连PD ,可知四边形GPDS 为直角梯形)。
426∴Cos ∠GHS=。
61所以直线A 1E 与直线B 1F 所成的角的余弦值为。
61解法二:(向量法)分析:因为给出的立体图形是一个正方体,所以可以在空间建立直角坐标系,从而可以利用点的坐标表示出空间中每一个向量,从而可以用向量的方法来求出两条直线间的夹角。
以B 为原点,BC 为x 轴,BA 为y 轴,BB 1为z 轴,设BC 长度为2。
B A CDF E B 1A 1D 1C 1GH S R PQ 1则点A 1的坐标为(0,2,2),点E 的坐标为(1,0,1),点B 1的坐标为(0,0,2),点F 的坐标为(2,1,1);所以向量的坐标为(-1,2,1),向量的坐标为(2,1,-1),1EA F B 1所以这两个向量的夹角θ满足cos θ==-。
异面直线夹角求法

在解决实际问题中的应用
建筑设计
在建筑设计领域,异面直线夹角可以用于确定建筑物的外观、结构等,以确保建筑物的稳定性和美观 性。
机械设计
在机械设计领域,异面直线夹角可以用于确定机械零件的形状、尺寸等,以确保机械零件的准确性和 可靠性。
04
异面直线夹角的特殊情况
异面直线夹角为直角的情况
总结词
当两条异面直线之间的夹角为直角时,它们之间的夹角是确定的,即90度。
利用向量的数量积求异面直线夹角
总结词
通过向量的数量积,可以计算出异面直线之间的夹角的余弦 值。
详细描述
首先分别求出两条异面直线的方向向量,然后计算这两个方 向向量的数量积。数量积的绝对值等于两向量的模的乘积与 两向量夹角的余弦值的乘积,由此可以求出夹角的余弦值。
利用空间几何的性质求异面直线夹角
总结词
利用空间几何的性质,通过观察空间几何图形,可以直观地求出异面直线之间的 夹角。
详细描述
首先根据异面直线的位置关系,构建一个空间几何图形。然后利用空间几何图形 的性质,如平行线之间的夹角、三角形中的角度关系等,可以求出异面直线之间 的夹角。
03
异面直线夹角的应用
在几何图形中的应用
确定几何形状
异面直线夹角可以用于确定几何图形 的形状和大小,例如在三维建模、建 筑设计等领域。
异面直线夹角的性质
异面直线夹角是两条异面直线在同一 平面内投影所形成的角度,因此不会 超过$90^circ$。
异面直线夹角的大小与两条异面直线 的方向向量有关,方向向量之间的夹 角等于异面直线夹角的补角。
异面直线夹角的取值范围
1
异面直线夹角的取值范围是$0^circ$到 $90^circ$,不包括$0^circ$和$90^circ$。
高中数学:异面直线所成的角求法(汇总大全)

异面直线所成的角一、平移法:常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
直角平移法:1.在空间四边形ABCD 中,AD =BC =2,E ,F 分别为AB 、CD 的中点,EF =3,求AD 、BC 所成角的大小.解:设BD 的中点G ,连接FG ,EG 。
在△EFG 中 EF =3FG =EG =1∴∠EGF =120° ∴AD 与BC 成60°的角。
2.正∆ABC 的边长为a ,S 为∆ABC 所在平面外的一点,SA =SB =SC =a ,E ,F 分别是SC和AB 的中点.求异面直线SA 和EF 所成角. 正确答案:45°3.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA=2π,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值. 证明:连结CM ,设Q 为CM 的中点,连结QN ,则QN ∥SM∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ,设SC =a ,在△BQN 中 BN =a 25 NQ =21SM =42a BQ =a 414∴COS ∠QNB =5102222=⋅-+NQ BN BQ NQ BN4.如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M 、N 分别是A 1B 1和A 1C 1的中点,若BC =CA =CC 1,求BM 与AN 所成的角.解:连接MN ,作NG ∥BM 交BC 于G ,连接AG , 易证∠GNA 是BM 与AN 所成的角.设:BC =CA =CC 1=2,则AG =AN =5,GN =BM =6, cos ∠GNA =1030562556=⨯⨯-+。
两异面直线夹角公式cos

两异面直线夹角公式为cosa=|m1m2+n1n2+p1p2|/[√(m1^2+n1^2+p1^2)√(m2^2+n2^2+p2^2)],计算时代入具体的数据即可。
异面直线是不在同一平面上的两条直线,异面直线是既不相交,又不平行的直线,因为两条直线如果相交或平行,则它们必在同一平面上。
两条直线的夹角公式cos:k=(y2-y1)/(x2-x1)。
夹角公式是基本数学公式,分为正切公式和余角公式,正切公式用tan表示,余角公式用cos表示。
正切公式(直线的斜率公式):k=(y2-y1)/(x2-x1);
余弦公式(直线的斜率公式):k=(y2-y1)/(x2-x1)。
两条直线的夹角公式cos公式推导:
1、A1X+B1Y+C1=0。
2、A2X+B2Y+C2=0。
则1的方向向量为u=(-B1,A1),2的方向向量为v=(-B2,A2)。
由向量数量积可知,cosφ=u·v/|u||v|,即两直线夹角公式:cosφ=A1A2+B1B2/[√(A1^2+B1^2)√(A2^2+B2^2)]。
注:k1,k2分别L1,L2的斜率,即tan(α-β)=(tanα-tanβ)/(1+tan αtanβ)。
异面直线夹角求法

练习:
练习册3.2.1作业1、作业2每个大题的最后一问。
C
B
平移法:
D
1
C
O
1
A 1 B 1
D A
E
C
B
平移法小结:
平移原则: 选择适当的点,平移异面直线中的一条或两条 使其成为相交直线。这里的点通常选择特殊位 置上的点,平移异面直线时尽量做到定一动一。
平移方法: 常见的有——中位线平移、直接平移。
补形法:
D 1
A1
D A
C1 B
1
C B
F1 E1
空间两条直线的位置关系: 平行 相交 异面
异面直线的概念: 异面直线夹角概念:
不同在任何一个平面内的两条直线叫做异面直线 b
a' a
异面直线夹角求解的思想方法
例:长方体ABCD-A1B1C1D1,AB=AA1=2,
AD=1,
求异面直线A1C1与BD1所成角的余弦值.
D
1
C
1
A
1
B
1
D A
F E
补形法小结:
补形原则: “补形法”属于平移法,它是立体几何中一种 常见的方法。通过补形,可将问题转化为易于 研究的几何体来处理,利用“补形法”找两异 面直线所成的角也是常用的方法之一。
补形方法: 常见的有——把空间图形补成熟悉的或完整 的几何体,如正方体、长方体等。
A 1 B 1
解题原则: 选择适当的点作为坐标原点,建立空间直角坐 标系,把异面直线转化为向量坐标表示,然后 套用公式求解。
解题公式:
ca o , b = s
a 1 b 1 a 2 b 2 a 3 b 3
异面直线所成的角的两种求法

异面直线所成的角的两种求法,求异面直线所成的角是初学立几的同学遇到的第一个难点。
难在何处? 下面介绍两种求法,与大家共磋商。
一.传统求法--------找、作、证、求解。
求异面直线所成的角,关键是平移点的选择及平移面的确定。
平移点的选择:一般在其中一条直线上的特殊位置,但有时选在空间适当位置会更简便。
平移面的确定:一般是过两异面直线中某一条直线的一个平面,有时还要根据平面基本性质将直观图中的部分平面进行必要的伸展,有时还用“补形”的办法寻找平移面。
例1 设空间四边形ABCD ,E 、F 、G 、H 分别是AC 、BC 、DB 、DA 的中点,若AB =122,CD =4 2,且四边形EFGH 的面积为12 3,求AB 和CD 所成的角.解 由三角形中位线的性质知,HG∥AB,HE∥CD,∴ ∠EHG 就是异面直线AB 和CD 所成的角.∵ EFGH 是平行四边形,HG =21AB =62, HE =21,CD =23, ∴ S EFGH =HG·HE·sin∠EHG=126 sin∠EHG,∴ 12 6sin∠EHG=123.∴ sin∠EHG=22,故∠EHG=45°. ∴ AB 和CD 所成的角为45°注:本例两异面直线所成角在图中已给,只需指出即可。
例2.点A 是BCD 所在平面外一点,AD=BC ,E 、F 分别是AB 、CD 的中点,且EF=22AD ,求异面直线AD 和BC 所成的角。
(如图) 解:设G 是AC 中点,连接DG 、FG 。
因D 、F 分别是AB 、CD 中点,故EG∥BC 且EG=21 BC ,FG∥AD,且FG=21AD ,由异面直线所成角定义可知EG 与FG 所成锐角或直角为异面直线AD 、BC 所成角,即∠EGF 为所求。
由BC=AD 知EG=GF=21AD ,又EF=AD ,由余弦定理可得cos∠EGF=0,即∠EGF=90°。
求异面直线所成角的步骤

求异面直线所成角的步骤
1. 确定直线的方向向量:首先找到直线上的两个点,计算这两个点的坐标差值,得到直线的方向向量。
2. 求两个面的法向量:找到两个平面的方程,然后将方程转化为法向量的形式。
3. 计算直线与两个平面的法向量的夹角:使用向量的点乘公式,计算直线的方向向量与两个平面的法向量的点乘,得到两个夹角的余弦值。
4. 通过余弦值得到角度:使用反余弦函数,计算出两个夹角的角度值。
注意:根据夹角的符号可判断当异面直线存在时,夹角的位置关系。
夹角最新版

B1 M
C Y
2
A
B
X
所以AC1与侧面ABB1A1所成的角为300。
方法二、因为直角三角形AC1M中,
AC1=
3a
,1、一条直线与平面所成的角为π/3,则此直线与 这平面内所有直线所成角中最大的角是————
2、正方体ABCD-A1B1C1D1中AE与CF所成的角 的余弦值是————
的毅力。所以我们既然选择了,就一定要走下去,不要在有限的时间里,蹉跎无限的光阴。只有如此,到暮年之时,细细回想起来,才不会有年华虚度、韶华易逝的感慨。
Z C1
作CYCX,如图建立坐标系C-XYZ, 设CA=a,则
A1
c A o 1sA C (1 ,C A a,0 ,M 2 |a A A )A |C C ,|A A M M |M ( 1 41 a 4 2a 3 a ,0 4 3 3 a2a a,22 a 23 )
Y
所直以线A1EA、1EC,C F所F成的a角r为cac11rcoc76oss
16 17
A X
E
B
2、正三棱柱ABC-A1B1C1的底面边长为a,
解:侧作棱A1长B1的为中点2Ma,,求连ACC1M1与,A侧M。面ABB1A1所成的角。
C1M A1B1,C1M 平面AB1,所以AC1 与AM所成的角是AC1与侧面AB1所成的角。
ι
α
β
p
A
B
B
ι
pβ
α
A
β
B
p
O
α
ι
A
二面角的计算:
1、找到或作出二面角的平面角 2、证明 1中的角就是所求的角 3、计算出此角的大小
一“作”二“证”三“计算”
异面直线夹角与线面角的求法
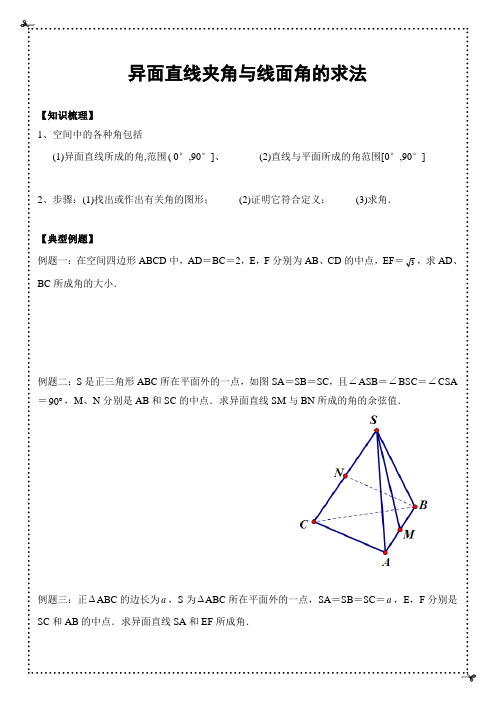
(B)不相交的直线
(C)相交直线或平行直线
(D)既不相交又不平行直线
()
2.设 a, b, c 是空间的三条直线,下面给出三个命题:① 如果 a, b 是异面直线,b, c 是异面直线,
则 a, c 是异面直线;② 如果 a, b 相交,b, c 也相交,则 如图,五面体 ABCDE 中,四边形 ABDE 是菱形, ABC 是边长为 2 的正三角形, DBA 60 , CD 3 . (1)证明: DC AB ; (2)若点 C 在平面 ABDE 内的射影 H ,求 CH 与平面 BCD 所成的角的正弦值.
12、在单位正方体 ABCD A1B1C1D1 中,求直线 A1C1 与截面 ABC1D1 所成的角.
【跟踪训练 2】如图,四边形 ABCD 与 BDEF 均为菱形, DAB DBF 60,且 FA FC . (1)求证: AC 平面 BDEF ; (2)求直线 AF 与平面 BCF 所成角的正弦值.
【课堂巩固】
一:选择题
1.分别和两条异面直线都相交的两条直线一定是
(A)不平行的直线
(C) 3
5
(D) 4
5
6.右图是正方体的平面展开图,在这个正方体中,①BM 与 ED 平行; ②CN 与 BE 是异面直线;
③CN 与 BM 成 60 角; ④DM 与 BN 垂直.以上四个命题中,正确命题的序号是( )
(A)① ② ③
(B)② ④
(C)③ ④
(D)② ③ ④
S
7、在三棱锥 S—ABC 中, SAB SAC ACB 90 , AC 2, BC 13 , SB 29 ,求异面直线 SC 与 AB 所成角的余弦值。
BC 3, CD 4 , PD 2.
异面直线夹角的求法

一、等角定理:一个角的两边分别与另一个角的两边平行,则两个角相等或互补。
二:异面直线夹角
(1)意义:(2)θ∈(0,π
2
]
注:两异面直线夹角为90。
时,也叫做两直线互相垂直。
三、异面直线夹角的求法:
1、平移不改变线段长度[主要适用于柱体]{直接法}
2 .A1B1C1—ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点
若BC=CA=CC1,求BD1与AF1所成角的余弦值.
3.在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,
求直线A D
1
与CN所成角的余弦值
二、平移改变线段长度[主要适用于锥体]
注:选择平移方向的法则:在两条异面直线上,各选择一个点形成线段,则该线段的中点就是平移的目标位置。
B1
(第6题)
A1
A B
C1
D1
C
D
M
N (第5题)
F1
A
B
C
D1
C1
A1
B1
注:正三棱锥对棱垂直。
[性质]
三、补形[主要适用于线段的位置不易发生移动,如体对角线,同时要求在规则的柱体中如正方体、长方体中和一些正棱柱中]
例:正方体ABCD-A
B1C1D1中,求异面直线A1C与BD所成的角.
1。
高考数学-异面直线夹角专题

异面直线夹角【考点例题解析】一、平移法:常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
直接平移法1.在空间四边形ABCD 中,AD =BC =2,E ,F 分别为AB 、CD 的中点,EF =3,求AD 、BC 所成角的大小.2.正∆ABC 的边长为a ,S 为∆ABC 所在平面外的一点,SA =SB =SC =a ,E ,F 分别是SC 和AB 的中点.求异面直线SA 和EF 所成角.3.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2π,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.BM AN CSABCD A 1B 1C 1D 1EF4.如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M 、N 分别是A 1B 1和A 1C 1的中点,若BC =CA =CC 1,求BM与AN 所成的角.5.如图,在正方体1111D C B A ABCD -中,E 、F 分别是1BB 、CD 的中点.求AE 与F D 1所成的角。
6.如图1—28的正方体中,E 是A ′D ′的中点(1)图中哪些棱所在的直线与直线BA ′成异面直线? (2)求直线BA ′和CC ′所成的角的大小; (3)求直线AE 和CC ′所成的角的正切值; (4)求直线AE 和BA ′所成的角的余弦值7. 长方体ABCD —A 1B 1C 1D 1中,若AB=BC=3,AA 1=4,求异面直线B 1D 与BC 1所成角的大小。
B '(图1-28)A 'ABC 'D 'CD FE2.中位线平移法:构造三角形找中位线,然后利用中位线的性质,将异面直线所成的角转化为平面问题,解三角形求之。
异面直线的夹角-线面角(含答案)

异面直线的夹角-线面角(含答案)空间角1、异面直线所成角的求法一是几何法,二是向量法。
异面直线所成的角的范围:]2,0(π几何法求异面直线所成角的思路是:通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几何知识求解。
基本思路是选择合适的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊位置的点。
常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
例1在正方体ABCD A B C D ''''-中,E 是AB 的中点,(1)求BA /与CC /夹角的度数. (2)求BA /与CB /夹角的度数.(3)求A /E 与CB /夹角的余弦值.例2:长方体ABCD —A 1B 1C 1D 1中,若AB=BC=3,AA 1=4,求异面直线B 1D 与BC 1所成角的余弦值。
直接平移:常见的利用其中一个直线a 和另一个直线b 上的一个已知点,构成一个平面,在此平面内做直线a 的平行线。
解法一:如图④,过B 1点作BE ∥BC 1交CB 的延长线于E 点。
则∠DB 1E 就是异面直线DB 1与BC 1所成角,连结DE 交AB 于M ,DE=2DM=35,cos∠DB1E=734解法二:如图⑤,在平面D1DBB1中过B点作BE∥DB1交D1B1的延长线于E,则∠C1BE就是异面直线DB1与BC1所成的角,连结C1E,在△B1C1E中,∠C1B1E=135°,C1E=35,cos∠C1BE=734170课堂思考:1.如图,PA 矩形ABCD,已知PA=AB=8,BC=10,求AD与PC所成角的余切值为。
DC1B1A1CD2.在长方体ABCD- A1B1C1D1中,若棱B B1=BC=1,AB=3,求D B和AC所成角的余弦值.例3 如图所示,长方体A1B1C1D1-ABCD中,∠ABA1=45°,∠A1AD1=60°,求异面直线A1B与AD1所成的角的度数.课堂练习如图空间四边形ABCD中,四条棱AB,BC,CD,DA及对角线AC,BD均相等,E为AD的中点,F为BC中,(1)求直线AB和CE 所成的角的余弦值。
2020年异面直线夹角的求法

作者:空青山
作品编号:89964445889663Gd53022257782215002 时间:2020.12.13
一、
等角定理:一个角的两边分别与另一个角的两边平行,则两个角相等或互补。
二:异面直线夹角 (1)意义:(2
)0,]
注:两异面直线夹角为
时,也叫做两直线互相垂直。
三、异面直线夹角的求法:
1、平移不改变线段长度[主要适用于柱体]{直接法}
2 .A 1B 1C 1—ABC 是直三棱柱,∠BCA=90°,点D 1、F 1 分别是A 1B 1、A 1C 1的中点 若BC=CA=CC 1,求BD 1与AF 1所成角的余弦值.
3.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,
求直线A
与CN 所成角的余弦值
二、平移改变线段长度[主要适用于锥体]
注:选择平移方向的法则:在两条异面直线上,各选择一个点形成线段,则该线段的中点就是平移的目标位置。
B 1
(第6题)
A 1
A
B C 1
D 1
C
D M N (第5题)
F 1
A B C D 1 C 1 A 1
B 1
注:正三棱锥对棱垂直。
[性质]
三、补形[主要适用于线段的位置不易发生移动,如体对角线,同时要求在规则的柱体中如正方体、长方体中和一些正棱柱中]
例:正方体ABCD-中,求异面直线所成的角.
作者:空青山
作品编号:89964445889663Gd53022257782215002 时间:2020.12.13。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间两条直线的位置关系: 平行 相交 异面
异面直线的概念: 异面直线夹角概念:
不同在任何一个平面内的两条直线叫做异面直线 b
a' a
异面直线夹角求解的思想方法
例:长方体ABCD-A1B1C1D1,AB=AA1=2,
AD=1,
求异面直线A1C1与BD1所成角的余弦值.
D
1
方法的选择: 求异面直线的夹角还有其它方法,经过本节课 的探讨,建议同学们选择——纯几何的平移法 和向量中的代数法(坐标法)。
注意的问题: 异面直线夹角的范围及其余弦值的正负关系。
练习:练习ຫໍສະໝຸດ 3.2.1作业1、作业2每个大题的最后一问。
1
C B
F1 E1
F E
补形法小结:
补形原则: “补形法”属于平移法,它是立体几何中一种 常见的方法。通过补形,可将问题转化为易于 研究的几何体来处理,利用“补形法”找两异 面直线所成的角也是常用的方法之一。
补形方法: 常见的有——把空间图形补成熟悉的或完整 的几何体,如正方体、长方体等。
向量几何法:
C
1
A
1
B
1
D A
C
B
平移法:
D
1
C
O
1
A 1 B 1
D A
E
C
B
平移法小结:
平移原则: 选择适当的点,平移异面直线中的一条或两条 使其成为相交直线。这里的点通常选择特殊位 置上的点,平移异面直线时尽量做到定一动一。
平移方法: 常见的有——中位线平移、直接平移。
补形法:
D 1
A1
D A
C1 B
向量代数(坐标)法小结:
解题原则: 选择适当的点作为坐标原点,建立空间直角坐 标系,把异面直线转化为向量坐标表示,然后 套用公式求解。
解题公式:
co a ,b s=
a 1 b 1 a 2 b 2 a 3 b 3
a 1 2 a 2 2 a 3 2 b 1 2 b 2 2 b 3 2
课堂小结:
D
1
C
1
A 1 B 1
D A
C
B
向量几何法小结:
解题原则: 选择适当空间基底,建立空间直角坐标系,把 异面直线转化为向量,并用空间基底表示,然 后套用公式求解。
解题公式:
c o sa,b
= ab
ab
向量代数(坐标)法:
z
1,0,2A 1
D 10,0,2
B 1
C 0,2,2 1
D
A
x
C
y
B1,2,0
