大学物理第9章静电场中的导体
大学物理学 大作业参考解答

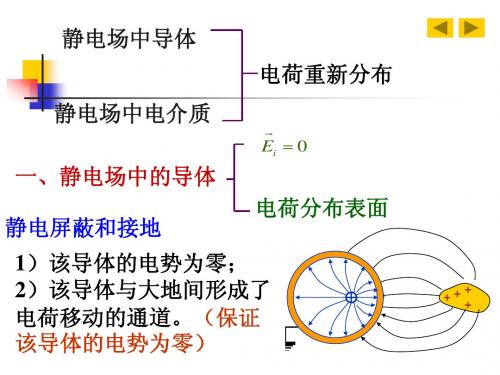
静电场中的导体和电介质
大作业参考解答
选择题1:当一个带电导体达到静电平衡时, (A)导体表面上电荷密度较大处电势较高; (B)导体表面曲率较大处电势较高; (C)导体内部的电势比导体表面的电势高; (D)导体内任一点与表面上任一点的电势差等于零。
NIZQ 第1页
大学物理学
静电场中的导体和电介质
d a
a
E dx
x
d a d ln ln 0 a 0 a
0 q 1 C U U A U B ln d a
NIZQ 第18页
大学物理学
静电场中的导体和电介质
计算题3:如图所示,在一不带电的金属球旁,有一点电荷 +q,金属球半径为R,点电荷+q与金属球球心的间距为d, 试求: (1)金属球上感应电荷在球心处产生的电场强度。 (2)若取无穷远处为电势零点,金属球的电势为多少?
-σ1 σ1 σ2 -σ2
d1 (A) d2 (C) 1
d2 (B) d1 d2 (D) 2 d1
2
d1
d2
1 2 d1 d2 0 0
NIZQ 第8页
大学物理学
静电场中的导体和电介质
填空题1:如图所示,两同心导体球壳,内球壳带 电量+q,外球壳带电量 -2q . 静电平衡时,外球壳 的内表面带电量为 ;外表面带电量 -q 为 。 -q
q CU r C 0U r q 0
U E E0 d
1 1 1q 2 W qU CU r E0 2 2 2C
NIZQ 第16页
2
计算题1:两块相互平行的导体板a和b ,板面积均为S,
大学物理学
静电场中的导体和电介质
张三慧《大学物理学:力学、电磁学》(第3版)(B版)(课后习题 静电场中的导体)【圣才出品】

第9章 静电场中的导体9.1 求导体外表面紧邻处场强的另一方法。
设导体面上某处面电荷密度为σ,在此处取一小面积ΔS,将ΔS 面两侧的电场看成是ΔS 面上的电荷的电场(用无限大平面算)和导体上其他地方以及导体外的电荷的电场(这电场在ΔS 附近可以认为是均匀的)的叠加,并利用导体内合电场应为零求出导体表面紧邻处的场强为σ/ε0(即教材式(8.2))。
解:如图8-1所示,导体表面小面积ΔS 上所带电荷在它的两侧分别产生场强为σ/2ε的电场E'1和E'2,ΔS以外的电荷在ΔS 附近产生的电场为E",可视为均匀的。
由电场叠加原理,在ΔS 的导体内一侧应有于是在ΔS的导体外一侧,则合电场应为这说明E ex 的大小为2σ/(2ε0)=σ/ε0,而其方向垂直于导体表面。
图8-19.2 一导体球半径为R1,其外同心地罩以内、外半径分别为R2和R3的厚导体壳,此系统带电后内球电势为φ1,外球所带总电量为Q 。
求此系统各处的电势和电场分布。
解:设内球带电为q 1,则球壳内表面带电将为-q1,而球壳外表面带电为q 1+Q ,这样就有由此式可解得于是,可进一步求得9.3 在一半径为R1=6.0 cm 的金属球A 外面套有一个同心的金属球壳B 。
已知球壳B 的内、外半径分别为R2=8.0 cm ,R3=10.0 cm 。
设A 球带有总电量QA =3×10-8 C ,球壳B 带有总电量QB =2×10-8C 。
(1)求球壳B 内、外表面上各带有的电量以及球A 和球壳B 的电势;(2)将球壳B 接地然后断开,再把金属球A 接地。
求金属球A 和球壳B内、外表面上各带有的电量以及球A 和球壳B 的电势。
解:(1)由高斯定律和电荷守恒可得球壳内表面带的电量为球壳外表面所带电量为于是(2)B 接地后断开,则它带的总电量变为然后球A 接地,则φ'a=0。
设此时球A 带电量为q'A ,则由此解得9.4 一个接地的导体球,半径为R ,原来不带电。
大学物理下 第九章 静电场中的导体和电介质5
2
ε0S C= d
四,静电场的能量 (1)电容器的能量 )
1 Q2 W = CU 2 = 2 2C
(2)静电场的能量 有电场的地方就有能量 )
1 ωe = D E 2
W = ∫ ωe dV
(3)静电场的能量与功的关系 )
A 静 = W
已知 ε r1 : ε r 2 = 1 : 2 ,问 W1 : W2 = ?
λ o d a
λ λ U = ∫ + dr 2πε0r 2πε0 (d r ) a -λ λ λ d a λ d = Ln ≈ Ln πε0 a πε0 a
λ λ πε 0 ∴ C0 = = = d d λ U Ln Ln a a πε 0
r
d a
P79 99 讨论
1)通电后维持电压不变插入电介质 ) 2)通电后断开再插入电介质 ) 讨论插入前后的 E,D,U,Q. , , , 令插入前为E , , , (令插入前为 0,D0,U0,Q0) 2) Q = Q 0
4a
UBA = UB∞
场具有球对称性
a
3a
解(1)a < r < 3a
∫∫ D dS = ∫∫ DdS = D4πr = QA
2 S S
Q
4a
a
QA D= 2 4πr
D QA E= = 2 ε0εr 4πε0εr r
3a
r > 4a ∫∫ D dS = D 4 πr = Q + Q A
2 S
Q + QA D= 2 4 πr
∫∫ D dS = Q0
S
E = E0 + E'
9-6,8 ,
E0
讨论 p79
大学物理习题答案 19 静电场中的导体(1)

与球外点电荷 + q 的作用力: F1
=
1 4πε 0
− q′ ⋅ q (r − b)2
,
由于 1 (r − b)2
>
1 r2
⇒
F1
=
1 4πε 0
− q′⋅ q (r − b)2
<
1 4πε 0
− q′⋅q r2
;
左侧电荷 Q
+
q′ 与点电荷 +
q 的作用力: F2
=
1 4πε 0
(Q + q′)⋅ q (r + a)2
50
大学物理习题解答
σ′ =
Q+q 4π R22
= 1.274 ×10−5 C
m2
,金属球外表面场强大小: E
σ′ =
ε0
= 1.44 ×106 V
m.
6. 题目有误!
7. 点电荷 − Q 位于空腔导体内,静电平衡后,空腔导体内表面感应电荷的电量为 + Q ,空腔导体原来电中性,
不带电,则空腔导体外表面感应电荷的电量为 − Q ;所以空腔导体外表面的净余电荷总量是 − Q ,空腔导体内表
− VC
=
E2
⋅d
=
σ2 ε0
d2 ;
B
A
C
σ1 σ2
−σ1 −σ2
由于 B 和 C 板用导线相连,电势相等,即VB = VC ⇒ VA −VB = VA −VC
即
σ1 ε0
d1
=
σ2 ε0
d2
⇒ σ1 = d2 . σ 2 d1
(第 10 题图)
11. (1)金属平板静电平衡后,金属平板 A 和 B 相邻两表面电荷电量等量异号,设电荷面密度分别为 σ 和 − σ ;
静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0
i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi
大学物理——静电场中的导体和电介质

v E
二、导体上电荷的分布 由导体的静电平衡条件和静电场的基本性 dV 质,可以得出导体上的电荷分布。 1.导体内部无静电荷 证明:在导体内任取体积元 dV
E内 = 0
r r 由高斯定理 E dS ⋅ = 0 ∫
S
∑q = ∫ ρ dV = 0
i i V
Q体积元任取 导体带电只能在表面!
ρ =0
证毕
A B σ1 σ 2σ 3
场 两板之间 强 分 布 两板之外
Q E = ε0S
r E
E=0
练习
已知: 两金属板带电分别为q1、q2 求:σ1 、σ2 、σ3 、σ4
q1
q2
q1 + q2 σ1 = σ 4 = 2S
σ1
σ2
σ3
σ4
q1 − q2 σ 2 = −σ 3 = 2S
2.导体表面电荷 表面附近作圆柱形高斯面
r r σΔS 0 ∫ E • dS = E ⋅ ΔS ⋅ cos 0 =
σ
r E
ΔS
ε0
σ ∴E = ε0
r σ ^ ^ E表 = n n :外法线方向
ε0
3.孤立带电导体表面电荷分布 一般情况较复杂;孤立的带电导体,电荷 分布的实验的定性的分布: 曲率较大,表面尖而凸出部分,电荷面密度较大 曲率较小,表面比较平坦部分,电荷面密度较小 曲率为负,表面凹进去的部分,电荷面密度最小
例3.已知:导体板A,面积为S、带电量Q,在其旁边 放入导体板B。 求:(1)A、B上的电荷分布及空间的电场分布 (2)将B板接地,求电荷分布
σ1 σ 2 σ 3 σ4 − − − =0 a点 2ε 0 2ε 0 2ε 0 2ε 0
A B σ1 σ 2σ 3 σ 4
大学物理9-2空腔导体内外的静电场

q
q
a. 腔内无带电体:
腔外电场不能穿入腔内, 腔内电场恒为零。
b. 腔内有带电体:
导体接地,可屏蔽内 电场。
空腔导体内外的静电场
例9-2 在内外半径分别为R1和R2的导体球壳内,有一个半 径为r 的导体小球,小球与球壳同心,让小球与球壳分别 带上电荷量q和Q。试求:
(1)小球的电势Vr,球壳内、外表面的电势; (2)小球与球壳的电势差; (3)若球壳接地,再求小球与球壳的电势差。
空腔导体内外的静电场
(2)腔内有带电体:
腔体内表面所带的电量和腔内带电体所带的电量等量异号, 腔体外表面所带的电量由电荷守恒定律决定,腔外的导体和电场 不影响腔内电场,腔内电场由腔内电荷决定。
q+Q
q q
q q
腔内电荷的位置不影响 导体外电场。
外表面接地,腔外电场 消失。
静电屏蔽
2. 静电屏蔽
失。两球的电势分别为
Vr
q
40
1 r
1 R1
VR1 VR2 0
空腔导体内外的静电场
两球的电势差仍为
Vr
VR
q
40
1 r
1 R1
由结果可以看出,不管外球壳接地与否,两
球的电势差恒保持不变。当q为正值时,小球的电
势高于球壳;当q为负值时,小球的电势低于球壳 。
如果两球用导线相连或小球与球壳相接触,电荷q
Vr
1
4 0
q r
q R1
q Q R2
VR1
1
4 0
q R1
q R1
q Q R2
4 0 R2
空腔导体内外的静电场
VR2
1
40
《大学物理学》第二版下册习题解答

第九章 静电场中的导体9.1 选无穷远处为电势零点,半径为R 的导体球带电后,其电势为U 0,则球外离球心距离为r 处的电场强度的大小为(A) 302rU R . (B) R U 0. (C) 20rRU . (D) r U 0. [ C ] 9.2如图所示,一厚度为d 的“无限大”均匀带电导体板,电荷面密度为σ ,则板的两侧离板面距离均为h 的两点a 、b 之间的电势差为:(A) 0. (B)2εσ. (C) 0εσh . (D) 02εσh. [ A ]9.3 一个未带电的空腔导体球壳,内半径为R .在腔内离球心的距离为d 处( d < R ),固定一点电荷+q ,如图所示. 用导线把球壳接地后,再把地线撤去.选无穷远处为电势零点,则球心O 处的电势为 (A) 0 . (B)dq04επ.(C)R q 04επ-. (D) )11(4Rd q -πε. [ D ]9.4 在一不带电荷的导体球壳的球心处放一点电荷,并测量球壳内外的场强分布.如果将此点电荷从球心移到球壳内其它位置,重新测量球壳内外的场强分布,则将发现: (A) 球壳内、外场强分布均无变化. (B) 球壳内场强分布改变,球壳外不变. (C) 球壳外场强分布改变,球壳内不变.(D) 球壳内、外场强分布均改变. [ B ]9.5在一个孤立的导体球壳内,若在偏离球中心处放一个点电荷,则在球壳内、外表面上将出现感应电荷,其分布将是:(A) 内表面均匀,外表面也均匀. (B) 内表面不均匀,外表面均匀. (C) 内表面均匀,外表面不均匀.(D) 内表面不均匀,外表面也不均匀. [ B ]9.6当一个带电导体达到静电平衡时: (A) 表面上电荷密度较大处电势较高. (B) 表面曲率较大处电势较高. (C) 导体内部的电势比导体表面的电势高.(D) 导体内任一点与其表面上任一点的电势差等于零. [ D ]9.7如图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q .设无限远处为电势零点,试求: (1) 球壳内外表面上的电荷. (2) 球心O 点处,由球壳内表面上电荷产生的电势. (3) 球心O 点处的总电势.解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q .(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为adqU q 04επ=⎰-aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+9.8有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷.如图所示,试求: (1) 导体板面上各点的感生电荷面密度分布.(2) 面上感生电荷的总电荷.解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为σ.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()024cos 0220=++=⊥εσεθb r q E P π 2分 ∴ ()2/3222/b r qb +-=πσ 1分(2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()2/322/d d b r qbrdr S Q +-==σ总电荷为 ()q brrdrqb dS Q S-=+-==⎰⎰∞2/322σ 2分O9.9 如图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为q A 和q B 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净带电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为σ. ()()0004///4/d εεσπ++π⋅==⎰⎰a q a q R S U U B A S P A∵0d =⋅⎰⎰AS S σ∴ ()()04///επ+=a q a q U B A P9.10三个电容器如图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C第十章 静电场中的电介质10.1 关于D的高斯定理,下列说法中哪一个是正确的? (A) 高斯面内不包围自由电荷,则面上各点电位移矢量D为零.(B) 高斯面上处处D为零,则面内必不存在自由电荷.(C) 高斯面的D通量仅与面内自由电荷有关.(D) 以上说法都不正确. [ C ]10.2一导体球外充满相对介电常量为εr 的均匀电介质,若测得导体表面附近场强为E ,则导体球面上的自由电荷面密度σ为(A) ε 0 E . (B) ε 0 ε r E .(C) ε r E . (D) (ε 0 ε r - ε 0)E . [ B ]10.3 一平行板电容器中充满相对介电常量为εr 的各向同性均匀电介质.已知介质表面极化电荷面密度为±σ′,则极化电荷在电容器中产生的电场强度的大小为:(A) 0εσ'. (B) r εεσ0'. (C) 02εσ'. (D)rεσ'. [ A ]10.4一平行板电容器始终与端电压一定的电源相联.当电容器两极板间为真空时,电场强度为0E ,电位移为0D,而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时,电场强度为E ,电位移为D,则(A) r E E ε/0 =,0D D =. (B) 0E E =,0D D rε=.(C) r E E ε/0 =,r D D ε/0 =. (D) 0E E =,0D D=. [ B ]10.5如图所示, 一球形导体,带有电荷q ,置于一任意形状的空腔导体中.当用导线将两者连接后,则与未连接前相比系统静电场能量将 (A) 增大. (B) 减小.(C) 不变. (D) 如何变化无法确定. [ B ]q10.6将一空气平行板电容器接到电源上充电到一定电压后,断开电源.再将一块与极板面积相同的各向同性均匀电介质板平行地插入两极板之间,如图所示. 则由于介质板的插入及其所放位置的不同,对电容器储能的影响为:(A) 储能减少,但与介质板相对极板的位置无关. (B) 储能减少,且与介质板相对极板的位置有关. (C) 储能增加,但与介质板相对极板的位置无关.(D) 储能增加,且与介质板相对极板的位置有关. [ A ]介质板10.7静电场中,关系式 P E D+=0ε(A) 只适用于各向同性线性电介质. (B) 只适用于均匀电介质. (C) 适用于线性电介质.(D) 适用于任何电介质. [ D ]10.8一半径为R 的带电介质球体,相对介电常量为εr ,电荷体密度分布ρ = k / r 。
静电场中的导体

一、静电感应
1.静电感应 静电感应
r E0
r E 0 r ′ r Er
=0
r E′
r E = E0 + E′ 内
无外场时自由电 子无规运动: 子无规运动: 电子气” “电子气”
r 在外场 E 0 中 无规运动; 1. 无规运动; 2. 宏观定向运动
导体内电荷重新分布 r' 出现附加电场 E 直至静电平衡
∴U R3
−q Q+q Q+q = + + = 4πε 0 R3 4πε 0 R3 4πε 0 R3 4πε 0 R3 q
1 q q q +Q UR1 = − + 4πε0 R R2 R 1 3
q +Q UR3 = 4πε0R 3
(2)两球的电势差为 )
R3
R R 1 2
q 1 1 UR1 −UR3 = − 4 0 R R πε 1 2
1 1
−q Q+q ∴U R1 = U 0 = + + 4πε 0 R1 4πε 0 R2 4πε 0 R3 q
同理球壳内外表面的电势分别为: 同理球壳内外表面的电势分别为: q −q Q+q Q+q ∴U R2 = + + = 4πε 0 R2 4πε 0 R2 4πε 0 R3 4πε 0 R3
01
=
1 4 πε
0
q L
感应电荷Q在O点电势:
q L
O R
U 02 =
=
∫∫
S
1
1 σ ′dS = 4πε 0 R 4πε 0 R
∫∫
S
σ ′dS
4πε 0
Q ⋅ R
大学物理下 静电场中的导体和电介质习题解答

q
q q
2.如图所示,一带负电荷的金属球,外面同 心地罩一不带电的金属球壳,则在球壳中一点 P处的场强大小与电势(设无穷远处为电势零 点)分别为:
(A) E = 0,U > 0. (B) E = 0,U < 0. B
(C) E = 0,U = 0. (D) E > 0,U < 0.
P
球壳内表面带正电荷,外表面带负电荷 金属球壳是一个等势体
ε1 ε2
5. 一导体球外充满相对介电常量为εr的均匀电介质,若测得导 体表面附近场强为 E ,则导体球面上的自由电荷面密度ε0 εr E 。
D ds Dds ds D
s
D
0
r
E
6. 一电荷为q的点电荷,处在半径为R、介电常量为ε1的各向同性、
均匀电介质球体的中心处,球外空间充满介电常量为ε2的各向同
性、均匀电介质,则在距离点电荷r (r<R) 处的场强为
,
电势 (选U∞=0)为
。
D ds qi
s
i
4r 2 Dr q
Er Dr
U
E
4Rrq1rR2
Er d r , U
q 4π1
1 r
1 R
q 4 2 R
2 1 qr R
7. 两金属球的半径之比为1:4,带等量的同号电荷。当两者的距 离远大于两球半径时,系统具有电势能W04 r
q 4 r
0
0
球心O点处总电势为分布在球壳内、外表面上的电荷和点电荷
q在O点产生的电势的代数和,
U 0
Uq
Uq
UQq
q 4 r
0
q 40R1
q Q 4 R
02
大学物理---静电场中的导体和电介质

, E ; E
+
+ + + +
++ ++
E 0
注意 导体表面电荷分布与导体形状以及周围环境有关. 导体凸出部分的表面曲率越大处, 电荷面密度越大, 附近 电场也越强。孤立导体表面的电荷密度与曲率之间不存 在单一的函数关系。
尖端放电现象
E
带电导体尖端附近电场最强
B A
Q RB (4)电容 C 2 π 0 r l ln U RA
2 π 0 r lRA 0 r S d RB RA RA , C d d 2
en
+
+
E
d+ l
+
eτ
导体内部电势相等
U AB
AB
E dl 0
A
B
二
静电平衡时导体上电荷的分布
1 实心导体
E 0
2
q E dS 0
S
+
+ + + +
+
S
+
q 0
有空腔导体
空腔内无电荷
0
+
+ +
结论 导体内部无电荷
结论 电荷分布在外表面上(内表面无电荷)
空腔内有电荷
E dS 0, qi 0
S1
电荷分布在表面上
E d S 0 , q 0 i
S2
内表面上有电荷吗?
S2
q
q
S1
q内 q
结论 当空腔内有电荷 q 时,内表面因静电感应出 现等值异号的电荷 q ,外表面有感应电荷 q (电荷 守恒)
大学物理静电场中的导体和电介质

03
在静电场中,导体和电介质的 性质和行为表现出显著的差异 ,因此了解它们的特性是学习 大学物理静电场的重要基础。
学习目标
01
掌握导体和电介质的定义、性质和分类。
02
理解静电场中导体和电介质的电场分布和电荷分布。
03
掌握导体和电介质在静电场中的行为和相互作用, 以及它们在电路中的作用。
02
导体
导体的定义与性质
感应电荷的产生是由于导体内 部自由电荷受到电场力的作用 而重新分布,这种效应称为静 电感应现象。
静电感应现象在生产和生活中 的应用十分广泛,如静电除尘、 静电喷涂等。
导体的静电平衡状态
当导体放入静电场中并达到稳定状态时,导体内部的自由电荷不再发生定向移动, 此时导体的状态称为静电平衡状态。
在静电平衡状态下,感应电荷在导体内、外表面产生附加电场,该电场与外界电场 相抵消,使得导体内部的总电场为零。
应用
了解电场强度在电介质中 的分布和变化规律,有助 于理解电子设备和器件的 工作原理。
电介质的电位移矢量
01
02
03
04
定义
电位移矢量是指描述电场中电 荷分布情况的物理量。
特点
在静电场中,电位移矢量与电 场强度之间存在线性关系,可
以用介电常数表示。
计算
根据电位移矢量的定义和电场 强度的计算公式,可以计算出
定义
导体是指能够让电流通过的物质。在 静电场中,导体内部自由电荷会受到 电场力的作用而发生移动,从而形成 电流。
性质
导体具有导电性,其导电能力与温度 、光照、化学状态等因素有关。金属 导体是电导率最高的物质之一,而绝 缘体则几乎不导电。
导体的静电感应现象
当导体放入静电场中时,导体 表面会产生感应电荷,感应电 荷的分布与外界电场有关。
大学物理第九章导体和介质中的静电场

第九章导体与介质中的静电场Electrostatic field in conductor and dielectric §9-1,2静电场中的导体§9-3电容器的电容§9-6电介质中的高斯定理§9-8 静电场的能量§9-1,2静电场中的导体一、导体的静电平衡( electrostatic equilibrium )1.导体绝缘体半导体1)导体(conductor)导电能力极强的物体(存在大量可自由移动的电荷)2)绝缘体(电介质,dielectric)导电能力极弱或不能导电的物体3)半导体(semiconductor)导电能力介于上述两者之间的物体EE E E iii E e E q F 导体静电平衡条件:导体内任一点的电场强度都等于零Ei E E2. 导体的静电平衡条件导体的内部和表面都没有电荷作任何宏观定向运动的状态.导体的静电平衡状态:静电感应E* 推论(静电平衡状态)证:在导体上任取两点p , ql d E V V i qpq pqp V V 0i Epq导体静电平衡条件:2)导体表面任一点场强方向垂直于表面1)导体为等势体,导体表面为等势面否则其切向分量将引起导体表面自由电子的运动,与静电平衡相矛盾。
3.导体上电荷的分布1)当带电导体处于静电平衡状态时,导体内部处处没有净电荷存在, 电荷只能分布于导体的表面上.qdV iiV证明:在导体内任取体积元dV由高斯定理体积元d v 任取导体带电只能在表面!iiqS d E 01 ,0 i E dVn e En e E E S d e E S d E nS E 0S2).导体表面附近的场强方向与表面垂直,大小与该处电荷的面密度成正比.ne ES结论:孤立的带电导体,外表面各处的电荷面密度与该处曲率半径成反比,410R Q V RRrr R ,44,22rRr R rR q Q r R R rQq1)导体表面凸出而尖锐的地方(曲率较大)电荷面密度较大2)导体表面平坦的地方(曲率较小)电荷面密度较小3)导体表面凹进去的地方(曲率为负)电荷面密度更小rq V r 041rq R Q V V R r 004141l d E 导体内,0l d E 腔沿电场线l d E (违反环路定理)在静电平衡状态下,导体空腔内各点的场强等于零,空腔的内表面上处处没有电荷分布.ld E l d E l d E导体内腔沿电场线二、空腔导体(带电荷Q )1 腔内无电荷,导体的电荷只能分布在外表面。
大学物理课件第九章

R2
34
仿以上两种方法,同学们可自行计
算得如下结果
q
q qQ
Ur 2 40r2 40R2 40R3
静电场中的导体
U r3 40R3
(3)接地后
q
ε E1=4π
r2
0
E2 = 0
E3 = 0
静电场中的导体
U r4 40r4
R2 R1
q q R0
7 静电屏蔽
静电场中的导体
球体的电势
方法一:
U r1 E dl
r1
R1
E1
dr
R2
E2
dr
r1
R1
R3
E3
dr
E4
dr
R2
R3
R2 R1
q
4 0r22
dr
R3
4 0r42
dr
q q qQ
F
F
电偶极矩趋于外电场的方向
有极分子的无序排列
注意
介质表面出现极化电荷,介质内产生极化电场
1)极化作用将在电介质表面产生束缚电荷;
2)束缚电荷产生附加电场 E.
二、电极化强度
1. 电极化强度: 在电介质中任取一宏观小体积V :
无外场 介质不极化
p0
有外场 介质被极化 p 0
定义: P p
l
VP VQ
与导体是一等势体矛盾.
P+
(2) 腔内有带电体+q :
腔体内表面所带的电量和腔内带电体所带的电量等量异
大学物理第章静电场中导体和电介质小结

1 Q2 Q2
4 0R1 2 8 0R1
本章小结
一、导体的静电感应
1、自由电子 2、静电平衡:导体上没有电荷作定向运动的状态 3、静电平衡条件: 4、导体表面的电荷分布
二、电介质的极化
1、极化电荷
2、介质内场强的变化: 3、极化强度矢量:
4、电位移矢量:
E E0 E P e0 E
0
E0
0
(1 x
l
1) x
A
B
两导线间的电势差:
U
l
a E
dx
la
(1 1 )dx ln l a
a
a 2 0 x l x
0 a
单位长度的电容:
C
Q0 U
U
0
ln l a
a
说明:任何导体之间,实际上都存在着电容,导线 之间,导线与电器元件之间,与金属外壳之间等, 称为“分布电容”,通常分布电容很小,可不计。 但对于高频电路就必须考虑分布电容的影响。
二、带电体系所储藏的静电能(电场能)
electrostatic energy of charged system
一带电系统,带电 qi 电势 Vi ,再从∞处将 qi
移到该系统,外力作功:
Ai Viqi Wi
分成 N 步,外力作的总功:(系统所储藏的静电能)
A Ai Viqi W
若带电体连续分布
例题3 有A、B、C是三块平行金属板,面积均为 200cm2, A、B相距4.0mm,A、C相距2.0mm,B、C两 板接地,设A板带电荷q=+3.0×10-7C,不计边缘效应, 求(1)B板和C板上的感应电荷。(2)A板的电势。
CA B
-q2 +q2 +q1 -q1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SEdS0 qi0 i
电荷分布在表面
内表面? 外表面?
高斯 面
S
空腔带电导体
若内表面带电,必等量异号
EdS
qi 0
S
ε0
AB AB E d l 0
与导体是等势体矛盾
高斯
面
++
+
+
+
A
+
+
+
-
B
+
S+
+
空腔带电导体
结论:空腔内无电荷时,电荷分布在外表面, 内表面无电荷.
空腔内有电荷时
SEdS0
应用:同轴电缆,抗干扰罩/网等
§9.3 有导体存在时静电场 分布的分析与计算
在涉及导体的静电场问题中,静电平衡导体表面电荷和其 外部空间的电场分布是唯一的、确定的。求解这种问题需要考 虑以下规律:
静电场的基本性质(如场强叠加原理,Gauss 定理等); 电荷守恒定律; 静电平衡条件。
例:设有两个相距很远的导体球,半径分别为R和r(R>r),用
导体——导电能力极强的物体。金属是最常见的导体。 金属导体的导电特征:金属内部存在自由电子,当导体
处于静电场中时,自由电子受到电场力作用而产生定向运动, 使导体上的宏观电荷重新分布。
本章主要是应用静电场的性质,讨论导体上电荷分布规律, 及其与周围的电场的关系。
§9.1 导体的静电平 衡条件
1 静电感应
qi 0
高斯 q面
+q -q
S
空腔导体
结论: 空腔内有电荷+q时,空腔内表面有感 应电荷-q,外表面有感应电荷+q.
3 导体表面附近场强与电荷面密度的关系
作扁圆柱形高斯面
SEdSES
σS/ε0
σ E
ε0
S
+ + ++
+ + E0
+
4 导体表面电荷分布规律
E σ ε0
σE;σ,E
++ + ++
+++++
1 2
1
导体体内任一点P场强为零
P 2 0
2
1
2 0
2 0
x
1
1
2
1 2 0 2
20 20 20
2
1
2
[例2] 两块面积均为 S 的大金属平板 A 和 B,各带电量 QA 和 QB,求: (1)两导体板之间及左右两侧的电场强度;(2)如将 B 板接地,电场如 何分布?假设金属板可看作无限大。
210220230 EinB t,0
2 3 0
12QA S
解得 10, 23Q SA
EI EIII0, EIIQ0SA
QA QB 1 2
34 I II III
AB
讨论:
如果两导体板带等量异号电荷,即 QB = QA ,则
1 4 0 , 2 Q A S , 3 Q B S
EI EIII0, EIIQ0SA
解:设四个导体平面上面电荷密度分别为 1,2,3 和 4 。
(1)每一面电荷单独存在时产生的场强为 i/20 ( i = 1, 2, 3, 4) ,取导体
板 B 中任一点,利用静电平衡条件,有
2 102 202 302 40EinBt , 0
取如图所示的高斯面 S’ ,有 E dS S2300 S
++
++++ + + + +
感应电荷
2 静电平衡
——导体内部和表面的宏观电荷无定向移动。
+
E0
+
+
E'
+ + +
E0
E0 +
+
静电平衡条件:
(1)导体内部任何一点处的电场强度为零; (2)导体表面处电场强度的方向,都与导 体表面垂直.
推论:导体为等势体
导体内各点电势相等
E0
A BAB E d l 0
第9章 静电场中的导体
本章主要内容
§9.1 导体的静电平衡条件 §9.2 静电平衡导体上的电荷分布 §9.3 静电平衡导体的应用 §9.4 有导体时静电场分布的计算 §9.5 静电屏蔽
第9章 静电场中的导体
实际中,电荷总是分布在实物物体上的,电场中也往往 存在物体。通常按导电能力将物体分为导体和绝缘体。
尖端放电现象
带电导体尖端附 近的电场特别大,可 使尖端附近的空气发 生电离而成为导体产 生放电现象.
σE
避雷针的工作原理
+ +
+ +带+电云+ +
- -- - - -
避雷针必须可靠接地
§9.4 静电屏蔽
静电屏蔽 带空腔导体的空腔中的电场不受外面 静电场的影响,这种现象称为静电屏蔽。 空腔内电场与空腔中带电体分布和空 腔几何形状有关;内壁上电荷分布是静电 平衡条件所要求的分布(内壁上电荷的场 与空腔中带电体的场在内壁以外区域叠加 相互抵消)。
此时,如果 B 板再接地,结果不变。
[例3] 一半径为 R1 的导体球,带电荷 QA,在它外面同心地放置一内、 外径分别为 R2 和 R3 的导体球壳,带电荷 QB。求各处的场强和电势分布。
解:中央球体电荷只分布在表面;球壳是一个
带空腔导体,内壁带电为 QA,再由电荷守恒知, 外表面带电为 QA + QB。所有导体表面电荷均为均 匀分布。
一导线将两球相连,求两个导体球的面电荷密度之间的关系
R
1
40
Q R
4R 2 R 0
r
1
40
q r
4 r 2 r 4 0 r
r r 0
r q
r
r R R r
例1.
1 2
无限大的带电平面的场中平行 放置一无限大金属平板。
求:金属板两面电荷面密度
解:设金属板面电荷密度 、
由对称性和电量守恒
利用 Gauss 定理可求出各区域的场强
R2 R3 R 1 I IIIIIIV
利E 用I E II IE0 , dE rI求I 得4Q A 0 r2,E IV Q 4 A 0 Q r2 B
P
IVQ 4A 0 Q rB,IIIQ 4A0Q R3B,II4Q A01 rR 12Q 4A0Q R3B,
QA QB
1 2 34
14 0 2 3 0
1 3 2 4 Q QA B S S
(电荷守恒)
1
4
QAQB 2S
2
3QA2SQB
S AB
于是
EI EIIIQ2A0SQB
EII
QA QB
20S
(2)如果导体板 B 接地, EIII = 0(B = = 0 ),故有
4 = 0,但 3 = 3 +4 QB/S,仍有
导体表面为等势面
en
+
E dl
+A+
+
B
eτ
+
Edl +
A BAB E d l 0
§9.2 静电平衡导体 上的电荷分布
1 实心导体
E0
q
EdS 0
S
ε0
q 0
高斯
面
++ + +
+ +
S+
+
++
实心带电导体
结论:导体内部无净电荷,
电荷只分布在导体表面.
2 空腔导体 空腔内无电荷时
I 4Q A0R 11R 12Q 4A0Q R3B
[例4]半径为R的不带电导体球附近有一点 电荷q,它与球心O相距d,求(1)导体球上 感应电荷在球心处产生的电场强度及此时 球心处的电势;(2)若将导体球接地,球上 的净电荷为多少?
