北京丰台0809学年九年级上期末练习试卷数学
北京市丰台区2019-2020学年九年级上数学期末试题含答案

北京市丰台区2019-2020学年九年级上数学期末试题含答案-学年度第一学期期末练习初三数学学校姓名考号一、选择题(本题共30分,每小题3分,)下列各题均有四个选项,其中只有一个..是符合题意的. 1.如图,在Rt △ABC 中,∠C =90°,BC =3,AB =4,则cos B 的值是A .37B .47C .43D .342.如图,在△ABC 中,点D 、E 分别在AB 、AC 边上,且DE ∥BC ,如果AD ∶DB =3∶2,那么AE ∶AC 等于A .3∶2B .3∶1C .2∶3D .3∶53.⊙O 的半径为3cm ,如果圆心O 到直线l 的距离为d ,且d =5cm ,那么⊙O 和直线l 的位置关系是A .相交B .相切C .相离D .不确定 4.抛物线3)2(2+-=x y 的顶点坐标是()A .(2,3)B .(-2,3)C .(2,-3)D .(-2,-3)E D CBA5.如果ABC DEF △∽△,相似比为2∶1,且△DEF 的面积为4,那么△ABC 的面积为A .1B .4C .8D .166.如图,四边形ABCD 内接于⊙O ,∠BCD =120°,则∠BAD 的度数是A .30°B .60°C .80°D .120°7.对于反比例函数2y x,下列说法正确的是 A .图象经过点(2,-1) B .图象位于第二、四象限C .当x <0时,y 随x 的增大而减小D .当x >0时,y 随x 的增大而增大8.如图,为了测量某棵树的高度,小明用长为2m 的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m ,与树相距10m ,则树的高度为A. 5mB. 6mC. 7mD.8m9圆的是AB CD二、填空题(本题共22分,第11题3分,第12题3分,第13-16题,每小题4分) 11.如果A ∠是锐角,且sin A =21,那么=∠A __________゜. 12.已知y x 5=2,则=yx__________. 13.圆心角是60°的扇形的半径为6,则这个扇形的面积是.14.排水管的截面为如图所示的⊙O ,半径为5m ,如果圆心O 到水面的距离是3m ,那么水面宽AB =__________m .15.请写出一个符合以下三个条件的二次函数的解析式:. ①过点(1,1);②当0x 时,y 随x 的增大而减小; ③当自变量的值为3时,函数值小于0. 16.阅读下面材料:在数学课上,老师请同学思考如下问题:老师说请你回答:小亮的作图依据是_________________________.三、解答题(本题共24分,每小题6分) 17.计算:2cos30°-tan 45°+sin 60°.18.函数5-4+=1-3x mxy m 是二次函数. (1)求m 的值;(2)写出这个二次函数图象的对称轴:;将解析式化成y=a (x -h )2+k 的形式为:.19.如图,在ABC △中,D 是AB 上一点,连接CD ,且∠ACD =∠ABC .(1)求证:△ACD ∽△ABC ;(2)若AD =6,AB =10,求AC 的长.20.如图,直线2+=1x y 与双曲线xky =2相交于A ,B 两点 其中点A 的纵坐标为3,点B 的纵坐标为-1. (1)求k 的值;(2)若21<y y ,请你根据图象确定x 的取值范围.四、解答题(本题共28分,每小题7分)21.如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB ,已知距电线杆AB 水平距离14米处是观景台,即BD =14米,该观景台的坡面CD 的坡角∠CDF 的正切值为2,观景台的高CF 为2米,在坡顶C 处测得电线杆顶端A 的仰角为30°,D 、E 之间是宽2米的人行道,如果以点B 为圆心,以AB 长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB 时,人行道是否在危险区域内?(73.13,41.12≈≈)22.如图,D 为O ⊙上一点,点C 在直径BA 的延长线上,CDA CBD ∠=∠. (1)求证:CD 是O ⊙的切线;(2)过点B 作O ⊙的切线交CD 的延长线于点E ,若AB =6,tan 23CDA ∠=, 依题意补全图形并求DE 的长A23.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A 处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A 的水平距离为x (米),距桌面的高度为y (米),运行时间为t (秒),经多次测试后,得到如下部分数据:(1① 如下图,在平面直角坐标系tOy 中,描出了上表中y 与t 各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;②当t 为何值时,乒乓球达到最大高度?(2)如果y 是关于x 的二次函数,那么乒乓球第一次落在桌面时,与端点A 的水平距离是多少?24.如图,⊙O 为△ABC 的外接圆,直线l 与⊙O 相切与点P ,且l ∥B C .(1)请仅用无刻度的直尺........,在⊙O 中画出一条弦.,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法);(2)请写出证明△ABC 被所作弦分成的两部分面积相等的思路.lP五、解答题(本题共16分,每小题8分)25.已知抛物线G 1:y =ax 2+b x +c 的顶点为(2,-3),且经过点(4,1). (1)求抛物线G 1的解析式;(2)将抛物线G 1先向左平移3个单位,再向下平移1个单位后得到抛物线G 2,且抛物线G 2与x 轴的负半轴相交于A 点,求A 点的坐标;(3)如果直线m 的解析式为3+21=x y ,点B 是(2)中抛物线G 2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n 过点A 和点B .问:是否存在点B ,使直线m 、n 、x 轴围成的三角形和直线m 、n 、y 轴围成的三角形相似?若存在,求出点B 的坐标;若不存在,请说明理由.26.在平面直角坐标系xOy 中,定义点P (x ,y )的变换点为P ′(x +y , x -y ).备用图1备用图2(1)如图1,如果⊙O的半径为①请你判断M(2,0),N(-2,-1)两个点的变换点与⊙O的位置关系;②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.(2)如图2,如果⊙O的半径为1,且P的变换点P’在直线y=-2x+6上,求点P与⊙O上任意一点距离的最小值.图2。
2019年北京市丰台区九年级上册期末数学试题有答案【优质版】

丰台区第一学期期末练习初三数学考生须知1. 本试卷共6页,共三道大题,28道小题,满分100分。
考试时间120分钟。
2. 在试卷和答题卡上认真填写学校名称、姓名和考号。
3. 试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4. 在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
5. 考试结束,将本试卷和答题卡一并交回。
一、选择题(本题共16分,每小题2分)下列各题均有四个选项,其中只有一个..是符合题意的.1.如果32a b(0ab),那么下列比例式中正确的是A.32abB.23baC.23a bD.32a b2.将抛物线y =2向上平移2个单位后得到新的抛物线的表达式为A.22y x B.22y xC.22y x D.22y x3.如图,在Rt△ABC中,∠C = 90°,AB = 5,BC = 3,则tanA的值为A.35B.34C.45D.434.“黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置A.①B.②C.③D.④5.如图,点A为函数kyx(> 0)图象上的一点,过点A作轴的平行线交y轴于点B,连接OA,如果△AOB的面积为2,那么的值为CBA②①③④ABx OyA .1B .2C .3D .46.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC 相似的是AB C D7.如图,A ,B 是⊙O 上的两点,C 是⊙O 上不与A ,B 重合的任意一点. 如果∠AOB=140°,那么∠ACB 的度数为A .70°B .110°C .140°D .70°或110°8.已知抛物线2y axbx c 上部分点的横坐标与纵坐标y 的对应值如下表:…10 1 2 3 …y…31m3…有以下几个结论:①抛物线2y ax bx c 的开口向下;②抛物线2y ax bx c 的对称轴为直线1x;③方程20ax bxc的根为0和2;④当y >0时,的取值范围是<0或>2.其中正确的是A .①④B .②④C .②③D .③④二、填空题(本题共16分,每小题2分)9.如果sin α=12,那么锐角α=.10.半径为2的圆中,60°的圆心角所对的弧的弧长为.11.如图1,物理课上学习过利用小孔成像说明光的直线传播.现将图1抽象为图2,其中线段AB 为蜡烛的火焰,线段A 'B '为其倒立的像. 如果蜡烛火焰AB 的高度为2cm ,倒立的像A 'B '的高度为5cm ,点O到AB 的距离为4cm ,那么点O 到A 'B '的距离为cm. 12.如图,等边三角形ABC 的外接圆⊙O 的半径OA 的长为2,则其内切圆半径的长为.13.已知函数的图象经过点(2,1),且与轴没有交点,写出一个满足题意的函数的表达式.14.在平面直角坐标系中,过三点A (0,0),B (2,2),C (4,0)的圆的圆心坐标为.15.在北京市治理违建的过程中,某小区拆除了自建房,改建绿地. 如图,自图1图2 ABCE DGFHACBA B'A'BOOAC BOAB建房占地是边长为8m 的正方形ABCD ,改建的绿地是矩形AEFG ,其中点E 在AB 上,点G 在AD的延长线上,且DG = 2BE. 如果设BE 的长为(单位:m ),绿地AEFG 的面积为y (单位:m 2),那么y 与的函数的表达式为;当BE =m 时,绿地AEFG 的面积最大.16.下面是“过圆外一点作圆的切线”的尺规作图过程.请回答以下问题:(1)连接OA ,OB ,可证∠OAP =∠OBP = 90°,理由是;(2)直线P A ,PB 是⊙O 的切线,依据是.三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26,27题,每小题7分,第28题8分)17.计算:2cos30sin 45tan60.18.如图,△ABC 中,DE ∥BC ,如果AD = 2,DB = 3,AE = 4,求AC 的长.19.已知二次函数y = 2- 4+ 3.(1)用配方法将y = 2- 4+ 3化成y = a(-h)2+ 的形式;(2)在平面直角坐标系xOy 中画出该函数的图象;(3)当0≤≤3时,y 的取值范围是.20.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB 为⊙O 的直径,弦CD ⊥AB554444123123321213xOyD CBAE已知:⊙O 和⊙O 外一点P .求作:过点P 的⊙O 的切线.作法:如图,(1)连接OP ;(2)分别以点O 和点P 为圆心,大于12OP 的长为半径作弧,两弧相交于M ,N 两点;(3)作直线MN ,交OP 于点C ;(4)以点C 为圆心,CO 的长为半径作圆,交⊙O 于A ,B 两点;(5)作直线PA ,PB .直线P A ,PB 即为所求作⊙O 的切线.O EA BCDOPCNPOAMB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.21.在平面直角坐标系xOy中,直线1y x与双曲线kyx的一个交点为P(m,2).(1)求的值;(2)M(2,a),N(n,b)是双曲线上的两点,直接写出当 a > b时,n的取值范围.22.在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为 1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN 顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)23.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线. 如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离.24.如图,AB是⊙O的直径,点C是?AB的中点,连接AC并延长至点D,使CD AC,点E是OB上一点,且23OEEB,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.(1)求证:BD是⊙O的切线;(2)当2OB时,求BH的长.OABCD HFECDABNMEPCBA25.如图,点E 是矩形ABCD 边AB 上一动点(不与点B 重合),过点E 作EF ⊥DE 交BC 于点F ,连接DF .已知AB = 4cm ,AD = 2cm ,设A ,E 两点间的距离为cm ,△DEF 面积为ycm 2.小明根据学习函数的经验,对函数y 随自变量的变化而变化的规律进行了探究.DC BAEF下面是小明的探究过程,请补充完整:(1)确定自变量的取值范围是;(2)通过取点、画图、测量、分析,得到了与y 的几组值,如下表:/cm 0 0.5 1 1.5 22.5 33.5 …y/c m24.03.73.93.83.32.0…(说明:补全表格时相关数值保留一位小数)(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(4)结合画出的函数图象,解决问题:当△DEF 面积最大时,AE 的长度为cm .26.在平面直角坐标系Oy 中,抛物线2yxbx c 经过点(2,3),对称轴为直线=1.(1)求抛物线的表达式;(2)如果垂直于y 轴的直线l 与抛物线交于两点A (1x ,1y ),B (2x ,2y ),其中01x ,02x ,与y 轴交于点C ,求BCAC 的值;(3)将抛物线向上或向下平移,使新抛物线的顶点落在轴上,原抛物线上一点P 平移后对应点为点Q ,如果OP=OQ ,直接写出点Q 的坐标.27.如图,∠BAD=90°,AB=AD ,CB=CD ,一个以点C 为顶点的45°角绕点C 旋转,角的两边与BA ,DA 交于点M ,N ,与BA ,DA 的延长线交于点E ,F ,连接AC.(1)在∠FCE 旋转的过程中,当∠FCA =∠ECA 时,如图1,求证:AE=AF ;(2)在∠FCE 旋转的过程中,当∠FCA ≠∠ECA 时,如图2,如果∠B=30°,CB=2,用等式表示线段AE ,AF 之间的数量关系,并证明.28.对于平面直角坐标系Oy 中的点P 和⊙C ,给出如下定义:如果⊙C 的半径为r ,⊙C 外一点P 到⊙C的切线长小于或等于2r ,那么点P 叫做⊙C 的“离心点”.(1)当⊙O 的半径为1时,①在点P 1(12,32),P 2(0,-2),P 3(5,0)中,⊙O 的“离心点”是;②点P (m ,n )在直线3y x 上,且点P 是⊙O 的“离心点”,求点P 横坐标m 的取值范围;(2)⊙C 的圆心C 在y 轴上,半径为2,直线121x y与轴、y 轴分别交于点A ,B. 如果线段AB 上的所有点都是⊙C 的“离心点”,请直接写出圆心C 纵坐标的取值范围.EMNFBA DCEMN FBADC图1图2丰台区第一学期期末练习初三数学参考答案一、选择题(本题共16分,每小题2分)题号 12345678答案CABBDADD二、填空题(本题共16分,每小题2分)9. 30°;10. 2π3;11. 10;12. 1;13.2yx或245y xx 等,答案不唯一;14.(2,0);15.22864(08)y xx x (可不化为一般式),2;16.直径所对的圆周角是直角;经过半径的外端,并且垂直于这条半径的直线是圆的切线.三、解答题(本题共68分,第17-24题每小题5分,第25题6分,第26,27题每小题7分,第28题8分)17. 解:2cos30sin 45tan60=322322,……3分=2332……4分=22.……5分18. 解:∵DE ∥BC ,∴ADAE DBEC.……2分即243EC.∴EC =6.……4分∴AC =AE + EC =10.……5分其他证法相应给分.19.解:(1)2444+3y x x 221x.……2分(2)如图:….3分(3)13y ….5分20.解:连接OC ,∵AB 为⊙O 的直径,弦CD ⊥AB 于点E ,且CD =10,∴∠BEC =90°,152CECD.……2分设OC =r ,则OA=r ,∴OE=1r .在Rt OCE 中,∵222OE CEOC ,∴22125rr .∴=13r . …4分∴AB = 2r = 26(寸). 答:直径AB 的长26寸.…5分21. 解:(1)一次函数1y x 的图象经过点(,2)P m ,1m .……… 1分点P 的坐标为(1,2). ……… 2分∵反比例函数k yx的图象经过点P(1,2),2k ………3分(2)0n 或2n …………5分22.解:由题意得,四边形ACDB ,ACEN 为矩形,∴EN=AC=1.5. AB=CD=15.在Rt MED 中,∠MED =90°,∠MDE =45°,∴∠EMD =∠MDE =45°. ∴ME =DE .…2分设ME =DE =,则EC =+15. 在Rt MEC 中,∠MEC =90°,∠MCE =35°,∵tan ME EC MCE ,∴0.715x x .∴35x .∴35ME .…4分∴36.5MNMEEN.∴人民英雄纪念碑MN.的高度约为36.5米.…5分23.解:建立平面直角坐标系,如图.于是抛物线的表达式可以设为2y a x hk根据题意,得出A ,P 两点的坐标分别为A (0,2),P (1,3.6).……2分∵点P 为抛物线顶点,∴1 3.6h k , .∵点A 在抛物线上,∴3.62a , 1.6a.…3分∴它的表达式为21.613.6y x . ……4分当点C 的纵坐标y=0时,有OE ABC DC D ABN MED CBA Ex=2y=x 2-4x+354411231213xOyOyxPCA21.61 3.6=0x.10.5x(舍去),2 2.5x.∴BC=2.5.∴水流的落地点C到水枪底部B的距离为2.5m. ……5分24.(1)证明:连接OC ,∵AB 为⊙O 的直径,点C 是?AB 的中点,∴∠AOC =90°. ……1分∵OAOB ,CDAC ,∴OC 是ABD 的中位线.∴OC ∥BD.∴∠ABD =∠AOC =90°. ……2分∴ABBD .∴BD 是⊙O 的切线.……3分其他方法相应给分.(2)解:由(1)知OC ∥BD ,∴△OCE∽△BFE.∴OC OE BFEB.∵OB = 2,∴OC = OB = 2,AB = 4,∵23OE EB,∴223BF,∴BF =3. ……4分在Rt ABF 中,∠ABF =90°,225AFABBF.∵1122ABFSAB BFAF BH ,∴AB BF AF BH .即435BH .∴BH =125..……5分其他方法相应给分.25.(1)04x ;.……1分(2)3.8,4.0;……3分(3)如图……4分(4)0或2.……6分26. 解:(1)1,242 3.bb c……1分解得2,3.b c.……2分∴322x xy.……3分(2)如图,设l 与对称轴交于点M ,由抛物线的对称性可得,BM= AM. …… 3分∴BC -AC = BM+MC-AC = AM+MC-AC= AC+CM+MC -AC =2 CM=2. ……5分其他方法相应给分.(3)点Q 的坐标为(12,2)或(12,2).……7分27.解:(1)证明:∵AB=AD ,BC=CD ,AC=AC ,∴△ABC ≌△ADC .…1分∴∠BAC =∠DAC =45°,可证∠FAC =∠EAC =135°. ……2分又∵∠FCA =∠ECA ,∴△ACF ≌△ACE .∴AE =AF . ……3分其他方法相应给分.(2)过点C 作CG ⊥AB 于点G ,求得AC =2.……4分∵∠FAC =∠EAC =135°,∴∠ACF +∠F=45°.又∵∠ACF +∠ACE =45°,∴∠F=∠ACE .∴△ACF ∽△AEC. ……5分∴ACAF AEAC ,即AF AE AC 2. ……6分∴2AF AE .……7分28.解:(1)①2P ,3P ;……2分②设P (m ,-m +3),则5322m m .…3分解得11m ,22m .……4分故1≤m ≤2.……6分(2)圆心C 纵坐标C y 的取值范围为:521≤C y <51或3<C y ≤4.……8分xylBCA–3–2–11234–3–2–112345OO ABCDHFE Oyx43211234GEMNFBADC。
213.丰台答案

丰台区2018—2019学年度第一学期期末练习初三数学参考答案一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题2分)9.56; 10. 3︰2; 11. 2m >即可; 12. 70; 13.4; 14. (1,4)-; 15. 3.12; 16.不正确; EF GH 、平分的不是弧AM 、弧BM 所对的弦.三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)17. 解: 1=1222-+⨯原式. ...............…........3分11-+ ...…….................4分. ……......................5分 18. 解:(1)-1; ...............…..........2分(2)略. .................…..........5分 19. 解:(1)证明:∵∠ADE =∠ACB , ∠A =∠A ,∴△ADE ∽△ACB . .................…..........2分(2)由(1)知△ADE ∽△ACB ,∴AD AE AC AB=. ∵点E 是AC 的中点,设AE =x , ∴22AC AE x ==. ∵AD =8,AB =10, ∴8210x x =.解得x =.∴AE = .................…..........5分20.解:(1)由题意,得A (2,2) . ∵反比例函数xky =的图象经过点A , ∴4k =.∴反比例函数的表达式4y x=. .................…..........2分 (2)040k k <≤≤<或-4. .................…..........5分21. 解:(1)54;.................…..........4分 (2)略. .................….......... 5分 22. 解:(1)略; ........................... 2分(2)略.....................................5分 23. 解:作图正确. ........…....... ........... 1分(1)证明:连接AF .∵AB 是⊙O 的直径, ∴∠AFB =90°.∵AB = AE , ∴∠BAE =2∠BAF .∵BD 是⊙O 的切线, ∴∠ABD =90°.∵∠BAF +∠ABF =90°,∠EBD +∠ABF =90°, ∴∠BAF =∠EBD .∴∠BAE =2∠EBD . .....................….......... 3分(2)过点E 作EH ⊥BD 于H .∵∠BAF =∠EBD .∴sin sin BAF EBD ∠=∠.在Rt △ABF 中, ∵AB = 5,∴BF =∴2BE BF ==在Rt △EBH 中,∴sin 2EH BE EBH =⋅∠=.∴BH=4. ∵EH ∥AB , ∴EH DH AB DB=. ∴254DH DH =+,解得83DH =.∴203BD BH HD =+=. .....................….........6分 H24. 解:(1)1;....................................2分 (2)设直线的表达式为1(0)y kx b k =+≠. ∵点(3,5)和(6,3)在直线上,∴直线的表达式为1273y x =-+.设抛物线的表达式为22()y a x h k =-+.∵顶点(6,1),点(3,4)在抛物线上,∴抛物线的表达式为221(6)13y x =-+.∴212217[(6)1]33y y x x -=-+--+217(5)33x =--+.∴在5月销售这种多肉植物,单株获利最大. .............................6分25.解:(1)2.8;.........................2分(2)略. .........................4分 (3)3.3. ........................6分26.解:(1)∵抛物线23y ax bx a =++过点A (-1,0), ∴30a b a -+=. ∴4b a =.∴抛物线解析式可化为243y ax ax a =++.∴抛物线的对称轴为422ax a=-=-. .........................2分 (2)由题意,得B (0,4),C (-2,2)∵抛物线243y ax ax a =++过点A (-1,0)且抛物线的对称轴为2x =-,由抛物线的对称性可知,抛物线也一定经过A 的对称点(-3,0).①0a >时,如图1,将0x =代入抛物线得3y a =, ∵抛物线与线段BC 有交点,∴34a ≥,解得43a ≥.②0a <时,如图2, 将2x =-代入抛物线 得y a =-,∵抛物线与线段BC 有交点, ∴2a -≥,解得2a ≤-.综上所述,423a a ≥≤-或..........................6分图1 图227. 解:(1)60°; .........................1分(2)1; .........................2分(3)11AF BF n =-. .........................3分 证明:延长FE 至G ,使FG =FB . 连接GB ,GC .由(1)知,∠BFG=60°.∴△BFG 为等边三角形.∴BF =BG ,∠FBG=∠FGB=60°. ∵△ABC 是等边三角形, ∴AB=BC ,∠ABC=60°.∴∠ABF=∠CBG .∴△ABF ≌△CBG .∴∠BF A=∠BGC=120°. ∴∠FGC=60°. ∴∠FGC=∠BFG . ∴FB ∥CG . ∴AF AD FG DC =. ∵1AD AC n =, ∴11AF FG n =-. ∴11AF BF n =-. .........................7分 28. 解:(1) ①D 、F ; .........................2分②若直线EF 上存在点T (m ,n )是⊙O 的“等径点”, 则点T 满足02OT ≤≤.如图,以O 为圆心,OF 为半径作圆, 设该圆与直线EF 的另一个交点为A . 在Rt △EOF中,2OE OF ==, ∴∠EFO =60°. ∵OA=OF ,∴△AFO 为等边三角形. ∴过A 作AB ⊥x 轴于B . ∴FB=OB=1.∴21m -≤≤-. .........................5分(2)2r ≥. .........................7分CA EB D F初中数学公式大全1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180 °18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形21 平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形22 平行四边形判定定理 3 对角线互相平分的四边形是平行四边形23 平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形24 矩形性质定理 1 矩形的四个角都是直角25 矩形性质定理 2 矩形的对角线相等26 矩形判定定理 1 有三个角是直角的四边形是矩形27 矩形判定定理 2 对角线相等的平行四边形是矩形28 菱形性质定理 1 菱形的四条边都相等29 菱形性质定理 2 菱形的对角线互相垂直,并且每一条对角线平分一组对角30 菱形面积= 对角线乘积的一半,即S= (a×b )÷231 菱形判定定理1 四边都相等的四边形是菱形32 菱形判定定理2 对角线互相垂直的平行四边形是菱形33 正方形性质定理1 正方形的四个角都是直角,四条边都相等34 正方形性质定理 2 正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角35 定理1 关于中心对称的两个图形是全等的36 定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分37 逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称38 等腰梯形性质定理等腰梯形在同一底上的两个角相等。
北京市丰台区2019—2020学年初三上学期期末试题(数学)doc初中数学

北京市丰台区2019—2020 学年初三上学期期末试题(数学)doc 初中数学初三数学期末练习第2页(共6页)7.如图f A»A!iOO 的弦,OD 丄AB F 点D •交€>o 于点E •则尸列说法怖瑙的见A. AD=BDB. 乙 ACB 二乙 AOEC. .AE =品D. OD = I>E8.如图.点A 、B 、C 、D 为<30的四等分点•动点P 从恻心0出发.沿线段0C ・&)-线段DO 的路线作匀連迖动•设运动时间为Q 秒.Z APB 的度数为y 厘•则卜列图彖中农示y 与< 的用数关系姐恰卅的址二、填空題(本《!共4个小題•毎小& 4分•共16分)9. 若反比例换数y = -j 的圏編经过点(2.3>.则k = _________________ ・10. 若圍形的半忆为6 5,囲心角的度數为90。
・则闻形的面积为 _______________ _ ____ cm 2.II •如图.—E 两点分别在ZSABC 的边AB.AC 上与RC 不平行•若便△ ADE S AACB •需滾海加的条件是 ____________________________________ ■(写出一个即町)12•如图所示•边氏为I 的小正方形构成的网恪屮,半轻为1的GX )的圆心()住格点上■则Z AEI )的止切值竽F _____________ •三、解答题(本題共6个小题,共29分)13.(本小唸讚分S 分)i| V :lan45° -2^o309 *sir>60o .初三數学期末垛习第3页(共6页)14 .〈本小勒橫分5分)匕血:二次西数的解析式为y = -4x 2 *8x.(I )求这个二次噸效图彖的对称轴和汝点唯标;(2 )求这个二次换数图彖与x 轴的交点坐标;(3)若点A (」・yj 、点郝住废臥数囹欧上.试比较y 「与力的大小・ 15.(*小越满分4分〉已知:如1刃,住△")(:中.DE^BC.EF//Aft.试判期館二览戍立吗。
【推荐】2019秋北京市丰台区九年级上册期末数学试题有答案.doc

丰台区第一学期期末练习初 三 数 学一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个..是符合题意的. 1. 如图,点D ,E 分别在△ABC 的AB ,AC 边上,且DE ∥BC , 如果AD ∶AB =2∶3,那么DE ∶BC 等于 A. 3∶2B. 2∶5C. 2∶3D. 3∶52. 如果⊙O 的半径为7cm ,圆心O 到直线l 的距离为d ,且d =5cm ,那么⊙O 和直线l的位置关系是 A. 相交B. 相切C. 相离D. 不确定3. 如果两个相似多边形的面积比为4∶9,那么它们的周长比为 A. 4∶9B. 2∶3C.2∶3D. 16∶814. 把二次函数422+-=x x y 化为()k h x a y +-=2的形式,下列变形正确的是A. ()312++=x yB. ()322+-=x yC. ()512+-=x yD. ()312+-=x y5. 如果某个斜坡的坡度是1:3,那么这个斜坡的坡角为 A. 30° B. 45° C. 60°D. 90°6. 如图,AB 是⊙O 的直径,C ,D 两点在⊙O 上, 如果∠C =40°,那么∠ABD 的度数为 A. 40° B. 50°C. 70°D. 80°7. 如果A (2,1y ),B (3,2y )两点都在反比例函数xy 1=的图象上,那么1y 与2y 的大小关系是A. 21y y <B. 21y y >C. 21y y =D. 21y y ≥8. 如图,AB 为半圆O 的直径,弦AD ,BC 相交于点P ,如果CD = 3,AB = 4, 那么S △PDC ∶S △PBA 等于 A. 16∶9B. 3∶4C. 4∶3D. 9∶169. 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF 测量操场旗杆AB 的高度,他们通过调整测量位置,使斜边DF 与地面保持平行,并使边DE 与旗杆顶点A 在同一直线上,已知DE =0.5米,EF =0.25米,目测点D 到地面的距离DG =1.5米,到旗杆的水平距离GFABCD E ABADECDC =20米,则旗杆的高度为 A. 105米 B.(105+1.5)米 C. 11.5米D. 10米10. 如图,在菱形ABCD 中,AB =3,∠BAD =120°,点E从点B 出发,沿BC 和CD 边移动,作EF ⊥直线AB 于点F ,设点E 移动的路程为,△DEF 的面积为y ,则y 关于的函数图象为A. B. C. D.二、填空题(本题共18分,每小题3分)11. 二次函数()5122--=x y 的最小值是__________.12. 已知34=y x ,则=-yyx __________. 13. 已知一扇形的面积是24π,圆心角是60°,则这个扇形的半径是 .14. 请写出一个符合以下两个条件的反比例函数的表达式: .①图象位于第二、四象限;②如果过图象上任意一点A 作AB ⊥轴于点B ,作AC ⊥y 轴于点C ,那么得到的矩形ABOC 的面积小于6.15. 如图,将半径为3cm 的圆形纸片折叠后,劣弧中点C 恰好与圆心O 距离1cm ,则折痕AB 的长为 cm .16. 太阳能光伏发电是一种清洁、安全、便利、高效的新兴能,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB 的长度相同,支撑角钢EF 长为33290cm ,AB 的倾斜角为30°,BE =CA =50 cm ,支撑角钢CD ,EF 与底座地基台面接触点分别为D ,F ,CD 垂直于地面,FE ⊥AB 于点E .两个底座地基高度相同(即点D ,F 到地面的垂直距离相同),均为 30 cm ,点A 到地面的垂直距离为50 cm ,则支撑角钢CD 的长度是 cm ,AB 的长度是 cm .三、解答题(本题共35分,每小题5分)17. 计算:6tan 30°+cos 245°-sin 60°.18. 如图,在Rt △ABC 中,∠C =90°,43=A tan ,BC =12, 求AB 的长.A BC19. 已知二次函数c x x y ++-=2(1(2)当取何值时,y 随的增大而减小.20. 如图,已知AE 平分∠BAC ,ACADAE AB =.(1)求证:∠E =∠C ;(2)若AB =9,AD =5,DC =3,求BE21. 如图,在平面直角坐标系Oy 图象的一个交点为A (-1,m ). (1)求这个反比例函数的表达式;(2)如果一次函数1+-=x y 点B (n ,0),请确定当<n 比例函数xky =的值的范围.22. 如图,已知AB 为⊙O 的直径,P A ,PC 是(1)求∠P 的度数; (2)若AB =6,求P A 的长.已知:△ABC .(1)求作:△ABC 的外接圆,请保留作图痕迹;(2)至少写出两条作图的依据. 22分,第24至25题,每小题5分,第26至27题,每小题6青青书店购进了一批单价为20元的中华传统文化丛书.在销售的过程中发现,这种图书每天的销售数量y (本)与销售单价(元)满足一次函数关系:1083+-=x y ()3620<<x .如果销售这种图书每天的利润为p (元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少? 如图,将一个Rt △BPE 与正方形ABCD 叠放在一起,并使其直角顶点P 落在线段CD上(不与C ,D 两点重合),斜边的一部分与线段AB 重合.1)图中与Rt △BCP 相似的三角形共有________个,分别是______________;AB C(2)请选择第(1)问答案中的任意一个三角形,完成该三角形与△BCP 相似的证明.26. 有这样一个问题:探究函数xx y 2+=的图象与性质.小美根据学习函数的经验,对函数xx y 2+=的图象与性质进行了探究.下面是小美的探究过程,请补充完整: (1)函数xx y 2+=的自变量的取值范围是___________; (2)下表是y 与的几组对应值.(3)如下图,在平面直角坐标系Oy 中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象;(4)结合函数的图象,写出该函数的一条性质:.D EFACB POyx-1-2-4-3-5-1-2-4-5-3124351243527. 如图,以△ABC 的边AB 为直径作⊙O ,与BC 交于点D ,点E 是BD的中点,连接AE 交BC 于点F ,2ACB BAE ∠=∠. (1)求证:AC 是⊙O 的切线; (2)若32=B sin ,BD=5,求BF 的长.五、解答题(本题共15分,第28题7分,第29题8分)28. 已知抛物线G 1:()22+-=h x a y 的对称轴为 = -1,且经过原点. (1)求抛物线G 1的表达式;(2)将抛物线G 1先沿轴翻折,再向左平移1个单位后,与轴分别交于A ,B 两点(点A在点B 的左侧),与y 轴交于C 点,求A 点的坐标;(3)记抛物线在点A ,C 之间的部分为图象G 2(包含A ,C 两点),如果直线 m :2-=kx y 与图象G 2只有一个公共点,请结合函数图象,求直线m 与抛物线G 2的对称轴交点的纵坐标t 的值或范围.29. 如图,对于平面直角坐标系Oy 中的点P 和线段AB ,给出如下定义:如果线段AB上存在两个点M ,N ,使得∠MPN =30°,那么称点P 为线段AB 的伴随点.⌒(1)已知点A (-1,0),B (1,0)及D (1,-1),E ⎪⎭⎫ ⎝⎛-325 , ,F (0,32+), ①在点D ,E ,F 中,线段AB 的伴随点是_________;②作直线AF ,若直线AF 上的点P (m ,n )是线段AB 的伴随点,求m 的取值范围; (2)平面内有一个腰长为1的等腰直角三角形,若该三角形边上的任意一点都是某条线段a 的伴随点,请直接写出这条线段a 的长度的范围.丰台区第一学期期末练习初 三 数 学 参 考 答 案一、选择题(本题共30分,每小题3分)11. -5; 12.31; 13. 12; 14. 答案不唯一,如:xy 5-=; 15.52; 16. 45,300. 三、解答题(本题共35分,每小题5分)17.解:原式=23223362-⎪⎪⎭⎫ ⎝⎛+⨯-----3分 =232132-+=2133+ -----5分18.解: ∵∠C =90°,BC =12,43==AC BC A tan ,∴AC =16. -----3分 ∵AB 2= AC 2 +BC 2,∴AB 2= 162 +122=400, AB=20. -----5分 19.解:(1)由题意得△=1+4c =0,∴41-=c . ∴412-+-=x x y . -----2分 ∵当212=-=a b x 时,0=y ,∴顶点坐标为⎪⎭⎫⎝⎛0,21. -----3分(2)∵01<-=a ,开口向下,∴当21>x 时,y 随的增大而减小.20.(1)证明:∵AE 平分∠BAC , ∴∠BAE =∠EAC 又∵AC AD AE AB =, 得到ACAEAD AB =∴△ABE ∽△ADC ∴∠E =∠C . (2)解:∵△ABE ∽△ADC , ∴DCBEAD AB =设BE =, ∵359x=, ∴527=x ,即BE21.解:(1)∵点A 在一次函数1+-=x y ∴m =2. ∴A (-1,2). ∵点A 在反比例函数xky =的图象上, ∴ = -2.∴xy 2-=. (2) 令y = -+1=0,=1,∴B (1,0). ∴当= 1时,xy 2-== -2.由图象可知,当<1时,y >0或y <-2. 22. 解:(1)∵PA 、PC 是⊙O 的切线,∴PA =PC ,∠∵∠BAC =30°, ∴∠PAC =60°.∴△ACP 为等边三角形. ∴∠P =60°. -----3分 (2)连接BC ,∵AB 为⊙O 的直径,∴∠ACB =90°. -----4分∵∠BAC =30°, AB =6,23==∠AB AC CAB cos . ∴AC =33.∴PA = AC =33. -----5分解:作图正确 -----3分 作图依据:)两点确定一条直线;)垂直平分线上一点到线段的两个端点距离相等;)在平面内,圆是到定点的距离等于定长的点的集合22分,第24至25题,每小题5分,第26至27题,每小题6分)解:p =(-20)(-3+108)= -32+168-2160 -----2分 ∵20<<36,且a =-3<0,∴当= 28时, y 最大= 192. -----4分答:销售单价定为28元时,每天获得的利润最大,最大利润是192元. -----5分 解:(1)3;Rt △EPB ,Rt △PDF ,Rt △EAF . -----2分 (2)答案不唯一,如:∵四边形ABCD 是正方形,∴∠ABP +∠PBC =∠C =90°. ∵∠PBC +∠BPC =90°, ∴∠ABP =∠BPC .又∵∠BPE =∠C = 90°,∴Rt △BCP ∽Rt △EPB . -----5分26. 解:(1)≥-2且≠0. -----2分 (2)当=2时,1222=+=m . -----3分 (3-----5分 (4)当-2≤<0或分27.(1)证明:连接AD .∵ E 是弧BD 的中点,∴弧BE = 弧ED ,∴∠BAD =2∠BAE . ∵2ACB BAE ∠=∠,∴∠ACB=∠BAD . -----1分 ∵AB 为⊙O 直径, ∴∠ADB =90°,∴∠DAC +∠ACB =90°.∴∠BAC =∠DAC +∠BAD =90°. -----2分 ∴AC 是⊙O 的切线. -----3分(2)解:过点F 作FG ⊥AB 于点G .∵∠BAE =∠DAE ,∠ADB =90°,∴GF =DF . -----4分在Rt △BGF 中,∠BGF =90°,32==BF GF sinB , 设BF =,则GF =5-,∴325=x x -,=3,即BF =3. -----6分五、解答题(本题共15分,第28题7分,第29题8分)28. 解:(1)∵抛物线G 1:()22+-=h x a y 的对称轴为= -1,∴y =a (+1)2+2.∵抛物线y =a (+1)2+2经过原点, ∴a (0+1)2+2=0.解得 a =-2.∴抛物线G 1的表达式为y = -2(+1)2+2= -22-4. -----2分(2)由题意得,抛物线G 2的表达式为y =2(+1+1)2﹣2=22+8+6.∴当y =0时,= -1或-3.∴A (﹣3,0) -----4分 (3)由题意得,直线m 2-=kx y 交y 轴于点D (0,-2). 由抛物线G 2的解析式y =22+8+6,得到顶点E (-2,-2).当直线2-=kx y 过E (-2,-2)时与图象G 2只有一个公共点,此时t = -2. 当直线2-=kx y 过A (-3,0)时,把= -3代入2-=kx y , =32-,∴232--=x y . 把= -2代入232--=x y ,∴y =32-,即t =32-.∴结合图象可知2-=t 或32->t . -----7分29. 解:(1)○1D 、F ; -----2分 ○2以AB 为一边,在轴上方、下方分别构造等边△ABO 1和等边△ABO 2, 分别以点O 1,点O 2为圆心,线段AB∵线段AB 关于y 轴对称,∴点O 1,点O 2都在y 轴上. ∵AB =AO 1=2,AO =1,∴OO 1∴O 1(0. 同理O 2(0,.∵F (2,0)+,∴O 1F =22AB +-==. ∴点F 在⊙1O 上.设直线AF 交⊙2O 于点C ,∴线段FC 上除点A 以外的点都是线段AB ∴点P (m ,n )是线段FC 上除点A 以外的任意一点. 连接O 2C ,作CG ⊥y 轴于点G ,∵等边△O 1AB 和等边△O 2AB ,且y 轴垂直AB ,∴∠AO 1B =∠AO 2B =∠O 1AB =∠O 2AB = 60°, ∠AO 1O =∠AO 2O =30°. ∵O 1A =O 1F ,∴∠AFO 1=∠FAO 1=15°.∴∠CAO 2=∠AFO 2+∠AO 2F =15°+30°=45°. ∵O 2A =O 2C ,∴∠CAO 2=∠ACO 2=45°. ∴∠O 2CG =180°-∠CFG -∠FGC -∠ACO 2=30°. ∴CG =O 2C ·cos30°=3232=⨯. 0m ∴≤≤ 且1m ≠-. -----6分(2)22≥a . -----8分。
北京丰台区2019年初三上学期年末考试数学试题

北京丰台区2019年初三上学期年末考试数学试题初三数学学校姓名考号【一】选择题〔共8个小题,每题4分,共32分〕以下各题均有四个选项,其中只有一个是符合题意的、 1、23(0)x y xy =≠,那么以下比例式成立的是 A 、32x y= B 、32xy = C 、23x y = D 、23=x y2、二次函数2)1(2-+=x y 的最小值是A 、1B 、-1C 、2D 、-23、⊙O 1和⊙O 2的半径分别为3cm 和5cm ,假设O 1O 2=8cm ,那么⊙O 1和⊙O2A 、外切B 、相交C 、内切D、内含4、假设ABC DEF △∽△,相似比为1∶2,且△ABC 的面积为4,那么△DEF 的面积为 A 、16 B 、8 C 、4 D 、25、将∠α放置在正方形网格纸中,位置如下图,那么tan α的值是 A 、21B 、2C 、25D 、552 6、如图,⊙O 的半径为5,AB 为弦,半径OC ⊥AB ,垂足为点E ,假设CE =2,那么AB 的长是A 、4B 、6C 、8D 、107、如图,假设点P 在反比例函数(0)ky k x=≠的图象上,过点P 作PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,假设矩形PMON 的面积为6,那么k 的值是A 、-3B 、3C 、-6D 、6 8、如图,在矩形ABCD 中,AB =4cm ,AD =2cm ,动点M 自点A 出发沿A →B 的方向,以每秒1cm的速度运动,同时动点N 自点A 出发沿A →D →C 的方向以每秒2cm 的速度运动,当点N 到达点C 时,两点同时停止运动,设运动时间为x 〔秒〕,△AMN 的面积为y 〔cm 2〕,那么以下图象中能反映y 与x 之间的函数关系的是考生须知1、本试卷共6页,共五道大题,25道小题,总分值120分。
考试时间120分钟。
2、在试卷和答题卡上认真填写学校名称、姓名和考号。
3、试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
丰台九上初三期末数学试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共30分)1. 若一个数的平方根是-2,则这个数是()A. 4B. -4C. 2D. -22. 下列各组数中,互为相反数的是()A. 3和-3B. 0和0C. 1和-1D. 2和33. 已知x² + 4x + 4 = 0,则x的值为()A. 2B. -2C. 1D. -14. 下列函数中,y是x的一次函数的是()A. y = 2x + 3B. y = 3x² + 2C. y = 2x + 3xD. y = 2x³ + 15. 已知直角三角形的一条直角边长为3,斜边长为5,则另一条直角边长为()A. 4B. 2C. 5D. 8二、填空题(每题5分,共20分)6. 若a > b,则a - b的值是()7. 已知x + y = 5,x - y = 1,则x的值为(),y的值为()8. 若函数y = 2x - 3的图象与x轴的交点坐标为(2,0),则该函数的k值为(),b值为()9. 在直角坐标系中,点P(-3,4)关于y轴的对称点坐标为()三、解答题(共50分)10. (10分)解下列方程:(1) 2(x - 1) - 3(x + 2) = 0(2) 5x² - 10x + 5 = 011. (15分)已知函数y = kx + b(k ≠ 0),当x = 1时,y = 2;当x = 2时,y = 4,求函数的解析式。
12. (15分)在直角坐标系中,点A(2,3),点B(-1,-2),求线段AB的中点坐标。
13. (10分)已知正方形的边长为4,求该正方形的面积和周长。
四、综合题(15分)14. (15分)某班级共有50名学生,其中有30名学生参加了数学竞赛,其中有20名学生参加了物理竞赛,已知有5名学生同时参加了数学和物理竞赛,求:(1) 只参加数学竞赛的学生人数;(2) 只参加物理竞赛的学生人数;(3) 既没有参加数学竞赛也没有参加物理竞赛的学生人数。
2008-2009学年北京市丰台区九年级(上)期末数学试卷

2008-2009 学年北京市丰台区九年级(上)期末数学试卷一、选择题(共8 小题,每小题4 分,满分32 分)1.(4 分)若,则的值是()A.B.C.D.32.(4 分)已知⊙O 的半径为5cm,若OP=3cm,则点P 与⊙O 的位置关系是()A.点P 在⊙O 外B.点P 在⊙O 上C.点P 在⊙O 内D.不能确定3.(4分)随机掷两枚硬币,落地后全部正面朝上的概率是()A.B.C.D.4.(4 分)若反比例函数,当x<0 时,y 随x 的增大而增大,则k 的取值范围是()A.k<0 B.k>0 C.k≤0 D.k≥05.(4分)正方形网格中,∠AOB 如图放置,则cos∠AOB 的值为()A.B.C.D.26.(4 分)圆心角为120°的扇形的半径是3cm,则这个扇形的面积是()A.6πcm2 B.3πcm2 C.9πcm2 D.πcm27.(4 分)如图,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC,DE∥BC,那么在图中与△ABC 相似的三角形的个数有()A.1 个B.2 个C.3 个D.4 个8.(4 分)如图,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x,且0<x≤10,阴影部分的面积为y,则能反映y 与x 之间函数关系的大致图象是()A.B.C.D.二、填空题(共4 小题,每小题4 分,满分16 分)9.(4 分)两个相似三角形对应边的比是3:2,那么这两个相似三角形面积的比是.10.(4 分)如图,有一圆形展厅,在其圆形边缘上的点 A 处安装了一台监视器,它的监控角度是65 度.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器台.11.(4 分)将抛物线y=x2+3 向右平移2 个单位后,所得抛物线的顶点坐标是.12.(4 分)如图,抛物线y=ax2+bx+c 的对称轴是x=﹣1.若点(﹣,y1)、(2,y2)是抛物线上两点,试比较y1 与y2 的大小:y1y2.三、解答题(共13 小题,满分72 分)13.(5 分)计算:3tan30°﹣sin60°+2cos45°14.(5 分)已知:反比例函数y=的图象经过点(2,3),求当x=4 时,y 的值.15.(5 分)已知:抛物线经过点A(﹣1,7)、B(2,1)和点C(0,1).(1)求这条抛物线的解析式;(2)求该抛物线的顶点坐标.16.(5 分)如图,梯形ABCD 中,AB∥CD,F 是DC 的中点,BF 的延长线交射线AD 于点G,BG 交AC 于点E.求证:.17.(5 分)已知:如图,在△ABC 中,∠A=120°,AB=AC=6,求BC 的长.18.(5 分)已知:如图,在⊙O 中,直径AB 的长为10,弦AC 的长为6,∠ACB 的平分线交⊙O 于点D,求BC 和BD 的长.19.(5 分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A 看大树顶端C 的仰角为35°;(2)在点A 和大树之间选择一点B(A,B,D 在同一直线上),测得由点B 看大树顶端C 的仰角恰好为45°;(3)量出A,B 两点间的距离为4.5 米.请你根据以上数据求出大树CD 的高度.(精确到0.1 米)(可能用到的参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)20.(5 分)A 口袋中装有2 个小球,它们分别标有数字1 和2;B 口袋中装有3 个小球,它们分别标有数字3,4 和5.每个小球除数字外都相同.甲、乙两人玩游戏,从A,B 两个口袋中随机地各取出1 个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.这个游戏对甲、乙双方公平吗?请说明理由.21.(5 分)如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的坐标为(8,0),点C、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,求点C 的坐标.22.(6 分)如图,△ABC 内接于⊙O,过点A 的直线交⊙O 于点P,交BC 的延长线于点D,AB2=AP•AD.(1)求证:AB=AC;(2)如果∠ABC=60°,⊙O 的半径为1,且P 为的中点,求AD 的长.23.(6 分)如图,二次函数(m<4)的图象与x 轴相交于点A、B 两点.(1)求点A、B 的坐标(可用含字母m 的代数式表示);(2)如果这个二次函数的图象与反比例函数的图象相交于点C,且∠BAC 的余弦值为,求这个二次函数的解析式.24.(7 分)如图,已知点P 是边长为4 的正方形ABCD 内一点,且PB=3,BF⊥ BP,垂足是B.请在射线BF 上找一点M,使以点B、M、C 为顶点的三角形与△ABP 相似.(请注意:全等图形是相似图形的特例)25.(8 分)已知抛物线y=ax2+bx+c 与x 轴交于A、B 两点,与y 轴交于点C,其中点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB、OC 的长(OB<OC)是方程x2﹣10x+16=0 的两个根,且抛物线的对称轴是直线x=﹣2.(1)求A、B、C 三点的坐标;(2)求此抛物线的表达式;(3)连接AC、BC,若点E 是线段AB 上的一个动点(与点A、点B 不重合),过点E 作EF∥AC 交BC 于点F,连接CE,设AE 的长为m,△CEF 的面积为S,求S 与m 之间的函数关系式,并写出自变量m 的取值范围;(4)在(3)的基础上试说明S 是否存在最大值?若存在,请求出S 的最大值,并求出此时点E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由.2008-2009 学年北京市丰台区九年级(上)期末数学试卷参考答案与试题解析一、选择题(共8 小题,每小题4 分,满分32 分)1.(4 分)若,则的值是()A.B.C.D.3【分析】根据比例的合比性质即可得出答案;亦可把变化为b=3a,代入可求出式子的值.【解答】解:原式===.故选:C.【点评】主要考查的是对比例式合比性质的掌握和灵活运用.2.(4 分)已知⊙O 的半径为5cm,若OP=3cm,则点P 与⊙O 的位置关系是()A.点P 在⊙O 外B.点P 在⊙O 上C.点P 在⊙O 内D.不能确定【分析】根据点到圆心的距离和圆的半径之间的数量关系,即可判断点和圆的位置关系.点到圆心的距离小于圆的半径,则点在圆内;点到圆心的距离等于圆的半径,则点在圆上;点到圆心的距离大于圆的半径,则点在圆外.【解答】解:∵点到圆心的距离d=3<5=r,∴该点P 在⊙O内.故选:C.【点评】考查了点和圆的位置关系与数量之间的联系:当点到圆心的距离小于圆的半径时,则点在圆内.3.(4 分)随机掷两枚硬币,落地后全部正面朝上的概率是()A.B.C.D.【分析】本题是由两步完成的实验,会有:正正,正反,反正,反反四种结果.并且出现每种结果的机会相同,可以用列举法求概率.【解答】解:有正正,正反,反正,反反四种结果,出现正正只有一种.所以P(全部正面朝上)=.故选B.【点评】如果一个事件有n 种可能,而且这些事件的可能性相同,其中事件A 出现m 种结果,那么事件A 的概率P(A)=.4.(4 分)若反比例函数,当x<0 时,y 随x 的增大而增大,则k 的取值范围是()A.k<0 B.k>0 C.k≤0 D.k≥0【分析】根据x<0 时,y 随x 的增大而增大得反比例函数比例系数k<0.【解答】解:根据反比例函数的性质,∵当x<0 时,y 随x 的增大而增大,∴k<0.故选:A.【点评】本题考查了反比例函数的性质,当k<0 时,在每个象限内,y 随x 的增大而增大.5.(4 分)正方形网格中,∠AOB 如图放置,则cos∠AOB 的值为()A.B.C.D.2【分析】作EF⊥OB,则求cos∠AOB 的值的问题就可以转化为直角三角形边的比的问题.【解答】解:如图,作EF⊥OB,则EF=2,OF=1,由勾股定理得,OE=.∴cos∠AOB= ==.故选:A.【点评】本题通过构造直角三角形,利用勾股定理和锐角三角函数的定义求解.6.(4 分)圆心角为120°的扇形的半径是3cm,则这个扇形的面积是()A.6πcm2 B.3πcm2 C.9πcm2 D.πcm2【分析】根据扇形的面积公式S= 计算可得答案.【解答】解:扇形的面积公式= =3πcm2,故选:B.【点评】本题考查扇形的面积公式.7.(4 分)如图,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC,DE∥BC,那么在图中与△ABC 相似的三角形的个数有()A.1 个B.2 个C.3 个D.4 个【分析】平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似,可判断△AED∽△ABC,再由两角对应相等的两个三角形相似可判断△BCD∽△ABC.【解答】解:∵DE∥BC,∴△AED∽△ABC,∵AB=AC,∠A=36°,BD 平分∠ABC,∴∠DBC=36°=∠A,∠C=72°,∴△BDC∽△ABC,∴有两个与△ABC 相似的三角形.故选:B.【点评】考查相似三角形的判定定理:(1)两角对应相等的两个三角形相似.(2)两边对应成比例且夹角相等的两个三角形相似.(3)三边对应成比例的两个三角形相似.8.(4 分)如图,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x,且0<x≤10,阴影部分的面积为y,则能反映y 与x 之间函数关系的大致图象是()A.B.C.D.【分析】主要考查了能通过分析题中的实际意义找出变量之间的关系和函数图象的读图能力.【解答】解:根据题意和图形可知:y=x2,0<x≤10,所以y 与x 之间函数关系的大致图象是.故选:D.【点评】要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.二、填空题(共4 小题,每小题4 分,满分16 分)9.(4 分)两个相似三角形对应边的比是3:2,那么这两个相似三角形面积的比是 9:4 .【分析】已知了相似三角形的对应边的比即可得出相似三角形的相似比,而相似三角形的面积比等于相似比的平方,由此得解.【解答】解:∵两个相似三角形对应边的比是3:2,∴它们的相似比为3:2;故它们的面积比为9:4.【点评】此题考查了相似三角形的性质:相似三角形的一切对应线段(包括对应边、对应高、对应中线、对应角平分线等)的比等于相似比,面积比等于相似比的平方.10.(4 分)如图,有一圆形展厅,在其圆形边缘上的点 A 处安装了一台监视器,它的监控角度是65 度.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器 3 台.【分析】根据一条弧所对的圆周角等于它所对的圆心角的一半,得该圆周角所对的弧所对的圆心角是130°,则共需安装360°÷130°≈3.【解答】解:∵∠A=65°,∴该圆周角所对的弧所对的圆心角是130°,∴共需安装360°÷130°≈3.【点评】此题考查了要圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.注意把实际问题转化为数学问题,能够把数学和生活联系起来.11.(4 分)将抛物线y=x2+3 向右平移2 个单位后,所得抛物线的顶点坐标是(2,3).【分析】利用抛物线的性质,结合草图可以解答.【解答】解:原抛物线的顶点为(0,3),向右平移2 个单位,那么新抛物线的顶点为(2,3).【点评】左右平移只改变顶点的横坐标,左减右加即可..(5 分)12.(4 分)如图,抛物线 y=ax 2+bx +c 的对称轴是 x=﹣1.若点(﹣,y 1)、(2,y 2)是抛物线上两点,试比较 y 1 与 y 2 的大小:y 1 < y 2.【分析】根据抛物开口向上及对称轴为 x=﹣1,点(﹣,y 1)、(2,y 2)是抛物线上两点,且在右半边.【解答】解:∵抛物线 y=ax 2+bx +c 的对称轴是 x=﹣1,而点(﹣,y 1)、(2,y 2)是抛物线上两点,∴点(﹣,y 1)、(2,y 2)都在抛物线的右半边.∵抛物线 y=ax 2+bx +c 的开口向上,而﹣ <2,∴y 1<y 2.故答案为:<.【点评】本题考查了二次函数图象上的点的坐标特征,理清二次函数图象的增减性是解题的关键.三、解答题(共 13 小题,满分 72 分)13.(5 分)计算:3tan30°﹣sin60°+2cos45°【分析】分别把 tan30°=,sin60°= ,cos45°= 代入代数式计算即可.【解答】解:3tan30°﹣sin60°+2cos45°,= ,(3 分)=【点评】此题比较简单,只要熟记特殊角的三角函数值即可. 得解得 .14.(5 分)已知:反比例函数 y=的图象经过点(2,3),求当 x=4 时,y 的值.【分析】先用待定系数法求出 k 的值,得到反比例函数的解析式,再把 x=4 代入解析式得到 y 的值.【解答】解:∵反比例函数 y=的图象经过点(2,3),∴=3,(2 分)∴k=6,(3 分)∴反比例函数解析式为:y=,(4 分)当 x=4 时,y=.(5 分)【点评】本题考查用待定系数法求函数解析式和用代入法求函数的值,侧重于对方法的考查,是以一道好题.15.(5 分)已知:抛物线经过点 A (﹣1,7)、B (2,1)和点 C (0,1).(1)求这条抛物线的解析式;(2)求该抛物线的顶点坐标.【分析】(1)设所求抛物线解析式为 y=ax 2+bx +c ,将 A (﹣1,7)、B (2,1)和点 C (0,1)代入,用待定系数法求得二次函数的解析式.(2)利用顶点公式求出顶点坐标.【解答】解:(1)设所求抛物线解析式为 y=ax 2+bx +c .根据题意,,故所求抛物线的解析式为 y=2x 2﹣4x +1.(2)∵ ,∴该抛物线的顶点坐标是(1,﹣1).【点评】在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.16.(5 分)如图,梯形ABCD 中,AB∥CD,F 是DC 的中点,BF 的延长线交射线AD 于点G,BG 交AC 于点E.求证:.【分析】欲证,可证△GDF∽△GAB,△FCE∽△BAE,得到,,又已知DF=CF,即证结论.【解答】证明:∵AB∥CD,∴△GDF∽△GAB,△FCE∽△BAE,(2 分)∴,,(4 分)∵DF=CF,∴.(5 分)【点评】本题主要考查了相似三角形的判定和性质,相似三角形中对应线段成比例.17.(5 分)已知:如图,在△ABC 中,∠A=120°,AB=AC=6,求BC 的长.【分析】过点A 作AD⊥BC 于D.根据等腰三角形的三线合一,发现30°的直角三角形,再根据锐角三角函数值进行求解.【解答】解:过点A 作AD⊥BC 于D.∵AB=AC,∠BAC=120°,∴∠B=30°,BC=2BD.在Rt△ABD 中,∠ADB=90°,∠B=30°,AB=6,,∴,∴.【点评】此题综合运用了等腰三角形的三线合一的性质和特殊角的锐角三角函数值.18.(5 分)已知:如图,在⊙O 中,直径AB 的长为10,弦AC 的长为6,∠ACB 的平分线交⊙O 于点D,求BC 和BD 的长.【分析】根据直径所对的圆周角是直角可得∠ACB=∠ADB=90°,在Rt△ABC 中,利用勾股定理列式即可求出BC 的长度,再根据CD 是∠ACB 的平分线可得AD=BD,然后再等腰直角三角形中求解即可得到BD 的长度.【解答】解:∵⊙O 直径AB 为10,∴∠ACB=∠ADB=90°,∵弦AC 为6,∴BC= ==8,∵∠ACB 的平分线交⊙O 于D,∴=,∴AD=BD,∴AD=BD=5 .故BC=8,BD=5.【点评】熟练运用圆周角定理的推论及其勾股定理进行计算.19.(5 分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A 看大树顶端C 的仰角为35°;(2)在点A 和大树之间选择一点B(A,B,D 在同一直线上),测得由点B 看大树顶端C 的仰角恰好为45°;(3)量出A,B 两点间的距离为4.5 米.请你根据以上数据求出大树CD 的高度.(精确到0.1 米)(可能用到的参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)【分析】首先分析图形:本题涉及到两个直角三角形△DBC、△ADC,应利用其公共边CD 构造等量关系,借助AB=AD﹣DB=4.5 构造方程关系式,进而可求出答案.【解答】解:设CD=x 米;∵∠DBC=45°,∴DB=CD=x,AD=x+4.5;在Rt△ACD 中,tan∠A=,∴tan35°= ;解得:x=10.5;所以大树的高为10.5 米.解法2:在Rt△ACD 中,tan∠A=,∴AD= ;在Rt△BCD 中,tan∠CBD= ,∴BD= ;而AD﹣BD=4.5,即=4.5,﹣解得:CD=10.5;所以大树的高为10.5 米.【点评】本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.20.(5 分)A 口袋中装有2 个小球,它们分别标有数字1 和2;B 口袋中装有3 个小球,它们分别标有数字3,4 和5.每个小球除数字外都相同.甲、乙两人玩游戏,从A,B 两个口袋中随机地各取出1 个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.这个游戏对甲、乙双方公平吗?请说明理由.【分析】游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.【解答】解:画树状图:或列表:B 袋3 4 5A 袋1 (1,3)和为4 (1,4)和为5 (1,5)和为62 (2,3)和为5 (2,4)和为6 (2,5)和为7数字之和共有6 种可能情况,其中和为偶数的情况有3 种,和为奇数的情况有3 种.∴P(和为偶数)= ,P(和为奇数)= ,(6 分)∴符合甲赢条件的有3 种,符合乙赢条件的有3 种,游戏对甲、乙双方是公平的.(8分)【点评】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.21.(5 分)如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的坐标为(8,0),点C、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,求点C 的坐标.【分析】过点M 作MF⊥CD 于F,过C 作CE⊥OA 于E,在Rt△CMF 中,根据勾股定理即可求得MF 与EM,进而就可求得OE,CE 的长,从而求得C 的坐标.【解答】解:∵四边形OCDB 是平行四边形,点B 的坐标为(8,0),CD∥OA,CD=OB=8,过点M 作MF⊥CD 于F,则CF=CD=4,过C 作CE⊥OA 于E,∵A(10,0),∴OA=10,OM=5∴OE=OM﹣ME=OM﹣CF=5﹣4=1连接MC,MC=OA=5∴在Rt△CMF 中,MF=,∴点C 的坐标为(1,3).【点评】此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.22.(6 分)如图,△ABC 内接于⊙O,过点A 的直线交⊙O 于点P,交BC 的延长线于点D,AB2=AP•AD.(1)求证:AB=AC;(2)如果∠ABC=60°,⊙O 的半径为1,且P 为的中点,求AD 的长.【分析】(1)根据AB2=AP•AD,可以连接BP,构造相似三角形.根据相似三角形的性质得到∠APB=∠ABD,再根据圆周角定理得到∠APB=∠ACB,即∠ABC=∠ACB,再根据等角对等边证明结论;(2)根据有一个角是60°的等腰三角形是等边三角形,发现等边三角形ABC,再根据点P 为弧的中点,连接BP,发现30°的直角三角形,且BP 是直径,从而求得AP 的长,AB 的长.再根据已知中的条件求得AD 的长.【解答】(1)证明:连接BP,∵AB2=AP•AD,∴,又∵∠BAD=∠PAB,∴△ABD∽△APB,∵∠ABC=∠APB,∠APB=∠ACB,∴∠ABC=∠ACB,∴AB=AC;(2)解:由(1)知AB=AC,∵∠ABC=60°,∴△ABC 为等边三角形,∴∠BAC=60°,∵P 为的中点,∴∠ABP=∠PAC= ∠ABC=30°,∴∠BAP=∠BAC+∠PAC=90°,∴BP 为直径,∴BP 过圆心O,∴BP=2,∴AP= BP=1,∴AB2=BP2﹣AP2=3,∵AB2=AP•AD,∴AD= =3.【点评】掌握相似三角形的性质和判定,能够结合已知条件发现等边三角形和30°的直角三角形,根据它们的性质分析求解,属中等难度.23.(6 分)如图,二次函数(m<4)的图象与x 轴相交于点A、B 两点.(1)求点A、B 的坐标(可用含字母m 的代数式表示);(2)如果这个二次函数的图象与反比例函数的图象相交于点C,且∠BAC 的余弦值为,求这个二次函数的解析式.【分析】(1)求点A、B 的坐标,由图形知A、B 的纵坐标=0,代入二次函数(m<4),得到关于x 的方程,求出点A、B 的横坐标,从而解决问题;(2)求二次函数(m<4)的解析式,要解决m 的值,需求出一点的坐标,可以根据∠BAC 的余弦值为,设AD=4k,AC=5k,则CD=3k,得到点C(4k﹣4,3k),又二次函数的图象与反比例函数的图象相交于点C,通过反比例函数求出点C 的坐标,代入(m<4),得到二次函数的解析式.【解答】解:(1)当y=0 时,,(1 分)x2+(m+4)x+4m=0,x1=﹣4,x2=﹣m.(2 分)∵m<4,∴A(﹣4,0),B(﹣m,0)(5 分)(2)过点C 作CD⊥x 轴,垂足为D,cos∠BAC=,设AD=4k,AC=5k,则CD=3k.(6 分)∵OA=4,∴OD=4k﹣4,点C(4k﹣4,3k).(7 分)∵点C 在反比例函数的图象上,∴.(8 分)4k2﹣4k﹣3=0,(舍去),.(9 分)∴C(2,).∵点C 在二次函数的图象上,∴,∴m=1,(11 分)∴二次函数的解析式为.(12 分)【点评】本题考查了反比例函数,代入法求二次函数的坐标及函数解析式,同时考查了解一元二次方程.24.(7 分)如图,已知点P 是边长为4 的正方形ABCD 内一点,且PB=3,BF⊥ BP,垂足是B.请在射线BF 上找一点M,使以点B、M、C 为顶点的三角形与△ABP 相似.(请注意:全等图形是相似图形的特例)【分析】此题有两种情况,(1)当△CBM≌△ABP 时,全等图形是相似图形的特例,此时BP 和BM 为一组对应边且相等,BM=BP=3;(2)当△MBC∽△ABP 时,有MB:AB=BC:BP,从而求出BM 的值.【解答】解:在射线BF 上截取线段,连接M1C,⇒,⇒∠ABP=∠CBM1,∴△M1BC∽△ABP.在射线BF 上截取线段BM2=BP=3,连接M2C,⇒△CBM2≌△ABP.(全等必相似)∴在射线BF 上取或BM2=3 时,M1,M2 都为符合条件的M.(说明:其他解法请参照给分)【点评】此题主要是考查三角形相似的判定,属中等难度.25.(8 分)已知抛物线y=ax2+bx+c 与x 轴交于A、B 两点,与y 轴交于点C,其中点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB、OC 的长(OB<OC)是方程x2﹣10x+16=0 的两个根,且抛物线的对称轴是直线x=﹣2.(1)求A、B、C 三点的坐标;(2)求此抛物线的表达式;(3)连接AC、BC,若点E 是线段AB 上的一个动点(与点A、点B 不重合),过点E 作EF∥AC 交BC 于点F,连接CE,设AE 的长为m,△CEF 的面积为S,求S 与m 之间的函数关系式,并写出自变量m 的取值范围;(4)在(3)的基础上试说明S 是否存在最大值?若存在,请求出S 的最大值,并求出此时点E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由.【分析】(1)先解一元二次方程,得到线段OB、OC 的长,也就得到了点B、C两点坐标,根据抛物线的对称性可得点A 坐标;(2)把A、B、C 三点代入二次函数解析式就能求得二次函数解析式;(3)易得S△EFF=S△BCE﹣S△BFE,只需利用平行得到三角形相似,求得EF 长,进而利用相等角的正弦值求得△BEF 中BE 边上的高;(4)利用二次函数求出最值,进而求得点 E 坐标.OC 垂直平分BE,那么EC=BC,所求的三角形是等腰三角形.【解答】解:(1)解方程x2﹣10x+16=0 得x1=2,x2=8 (1 分)∵点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,且OB<OC∴点B 的坐标为(2,0),点C 的坐标为(0,8)又∵抛物线y=ax2+bx+c 的对称轴是直线x=﹣2∴由抛物线的对称性可得点A 的坐标为(﹣6,0)(2 分)(2)∵点C(0,8)在抛物线y=ax2+bx+c 的图象上∴c=8,将A(﹣6,0)、B(2,0)代入表达式,得:解得∴所求抛物线的表达式为y=﹣x2﹣x+8(5 分)(3)依题意,AE=m,则BE=8﹣m,∵OA=6,OC=8,∴AC=10∵EF∥AC∴△BEF∽△BAC∴= ,即=∴EF= (6 分)过点F 作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=∴=∴FG= •=8﹣m∴S=S△BCE﹣S△BFE=(8﹣m)×8﹣(8﹣m)(8﹣m)=(8﹣m)(8﹣8+m)=(8﹣m)m=﹣m2+4m(8 分)自变量m 的取值范围是0<m<8 (9 分)(4)存在.理由:∵S=﹣m2+4m=﹣(m﹣4)2+8 且﹣<0,∴当m=4 时,S 有最大值,S 最大值=8 (10 分)∵m=4,∴点E 的坐标为(﹣2,0)∴△BCE 为等腰三角形.【点评】本题综合考查一元二次方程的解法;用待定系数法求二次函数解析式;以及求二次函数的最值等知识点.。
北京市丰台区2019届九年级(上)期末数学试题-5997394f8a7c4a539963687221fcfb5b

试卷第1页,总9页 ……外………装…………○姓名:___________班级……内………装…………○绝密★启用前 北京市丰台区2019届九年级(上)期末数学试题 试卷副标题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 第I 卷(选择题) 请点击修改第I 卷的文字说明 一、单选题 1.如果∠A 是锐角,且sin A =12,那么∠A 的度数是( ) A .90° B .60° C .45° D .30° 2.如图,A ,B ,C 是⊙O 上的点,如果∠BOC=120°,那么∠BAC 的度数是( ) A .90° B .60° C .45° D .30° 3.将二次函数y =x 2﹣4x+1化成y =a (x ﹣h )2+k 的形式为( ) A .y =(x ﹣4)2+1 B .y =(x ﹣4)2﹣3 C .y =(x ﹣2)2﹣3 D .y =(x+2)2﹣3 4.如图,在▱ABCD 中,E 是AB 的中点,EC 交BD 于点F ,那么EF 与CF 的比是( ) A .1:2 B .1:3 C .2:1 D .3:1 5.如图,在平面直角坐标系xOy 中,点A ,B 在反比例函数y =2x (x >0)的图象上,如果将矩形OCAD 的面积记为S 1,矩形OEBF 的面积记为S 2,那么S 1,S 2的关系是( )试卷第2页,总9页 ……外…………………○…………………○………………○……※※在※※装※※订※※线※※答※※题※※ ……内…………………○…………………○………………○…… A .S 1>S 2 B .S 1=S 2 C .S 1<S 2 D .不能确定 6.如图,将一把折扇打开后,小东测量出∠AOC=160°,OA =25cm ,OB =10cm ,那么由弧AC ,弧BD 及线段AB ,线段CD 所围成的扇面的面积约是( )A .157cm 2B .314cm 2C .628cm 2D .733cm 2 7.二次函数y =ax 2+bx+c (a≠0)的图象如图所示,那么下列说法正确的是( )A .a >0,b >0,c >0B .a <0,b >0,c >0C .a <0,b >0,c <0D .a <0,b <0,c >08.对于不为零的两个实数a ,b ,如果规定:a★b=()()a b ab aa b b +<⎧⎪⎨-≥⎪⎩,那么函数y =2★x的图象大致是( )A .B .C .试卷第3页,总9页 …………外……○…………装…订……………………○……学校:___________姓名____考号:_______…………内……○…………装…订……………………○…… D . 第II 卷(非选择题) 请点击修改第II 卷的文字说明 二、填空题 9.如图,在Rt△ABC 中,∠C=90°,BC =5,AB =6,那么cosB =_____. 10..若2m = 3n ,那么m ︰n = . 11.已知反比例函数y=2m x ,当x >0时,y 随x 增大而减小,则m 的取值范围是_____.12.永定塔是北京园博园的标志性建筑,其外观为辽金风格的八角九层木塔,游客可登至塔顶,俯瞰园博园全貌.如图,在A 处测得∠CAD=30°,在B 处测得∠CBD=45°,并测得AB =52米,那么永定塔的高CD 约是_____米.留整数) 13.如图,⊙O 的直径AB 垂直于弦CD ,垂足为E .如果∠B=60°,AC =4,那么CD 的长为_____. 14.已知某抛物线上部分点的橫坐标x ,纵坐标y 的对应值如下表:那么该抛物线的顶试卷第4页,总9页装…………○……要※※在※※装※※订※※装…………○……点坐标是_____.15.刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)三、解答题16.阅读下面材料:在数学课上,老师请同学们思考如下问题:请利用直尺和圆规四等分AB.小亮的作法如下:如图,(1)连接AB;(2)作AB的垂直平分线CD交AB于点M.交AB于点T;(3)分别作线段AT,线段BT的垂直平分线EF,GH,交AB于N,P两点;试卷第5页,总9页 ………外………………装…………○……………○…………线……__________姓名:___________班级:____________………内………………装…………○……………○…………线……那么N ,M ,P 三点把AB 四等分. 老师问:“小亮的作法正确吗?” 请回备:小亮的作法 _____(“正确”或“不正确”)理由是 _____. 17.计算:sin60°﹣tan45°+2cos60° 18.函数y =mx 2﹣2mx ﹣3m 是二次函数. (1)如果该二次函数的图象与y 轴的交点为(0,3),求m 的值; (2)在给定的坐标系中画出(1)中二次函数的图象. 19.如图,在△ABC 中,D ,E 分别是边AB ,AC 上的点,连接DE ,且∠ADE =∠ACB .(1)求证:△ADE ∽△ACB ; (2)如果E 是AC 的中点,AD =8,AB =10,求AE 的长. 20.如图,在平面直角坐标系xOy 中,点O 为正方形ABCD 对角线的交点,且正方形ABCD 的边均与某条坐标轴平行或垂直,AB =4.试卷第6页,总9页 …………装…………○……○…………线………※※请※※不※※要※※在※※装※※订※※…………装…………○……○…………线………(1)如果反比例函数y =k x 的图象经过点A ,求这个反比例函数的表达式; (2)如果反比例函数y =k x 的图象与正方形ABCD 有公共点,请直接写出k 的取值范围. 21.如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形. 请你帮助小刚的学习小组解决下面的问题: (1)盲区1的面积约是多少m 2;盲区2的面积约是多少m 2; sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数) (2)如果以大货车的中心A 点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域. 22.如图是边长为1的正方形网格,△A 1B 1C 1的顶点均在格点上. (1)在该网格中画出△A 2B 2C 2(顶点均在格点上),使△A 2B 2C 2∽△A 1B 1C 1; (2)请写出(1)中作图的主要步骤,并说明△A 2B 2C 2和△A 1B 1C 1相似的依据.试卷第7页,总9页 外…………○…………………订…………………○……学校:______级:___________考号:______内…………○…………………订…………………○…… 23.如图,AB 是⊙O 的直径,C 是⊙O 上一点,连接AC .过点B 作⊙O 的切线,交AC 的延长线于点D ,在AD 上取一点E ,使AE =AB ,连接BE ,交⊙O 于点F . 请补全图形并解决下面的问题:(1)求证:∠BAE=2∠EBD; (2)如果AB =5.求BD 的长. 24.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”.小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表: (1)如果在三月份出售这种植物,单株获利多少元; (2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大?(提示:单株获利=单株售价﹣单株成本) 25.如图,P 是弧AB 所对弦AB 上一动点,过点P 作PC⊥AB 交弧AB 于点C ,取AP 中点D ,连接CD .已知AB =6cm ,设A ,P 两点间的距离为xcm ,C .D 两点间的距离为ycm .(当点P 与点A 重合时,y 的值为0;当点P 与点B 重合时,y 的值为3) 小凡根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小凡的探究过程,请补充完整:试卷第8页,总9页…………装…………○…………订……※请※※不※※要※※在※※装※※订※※线※※内※※答※※…………装…………○…………订……(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为多少cm.26.在平面直角坐标系xOy中,抛物线y=ax2+bx+3a过点A(﹣1,0).(1)求抛物线的对称轴;(2)直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C.如果该抛物线与线段BC有交点,结合函数的图象,求a的取值范围.27.如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.(1)∠BFE的度数是多少;(2)如果12ADAC=,那么AFBF等于多少;(3)如果1ADAC n=时,请用含n的式子表示AF,BF的数量关系,并证明.试卷第9页,总9页 …………○………………○…… 28.对于平面直角坐标系xOy 中的点P 和⊙C,给出如下定义:若⊙C 上存在一个点M ,使得MP =MC ,则称点P 为⊙C 的“等径点”,已知点D (12,13),E (0,,F (﹣2,0). (1)当⊙O 的半径为1时, ①在点D ,E ,F 中,⊙O 的“等径点”是哪几个点; ②作直线EF ,若直线EF 上的点T (m ,n )是⊙O 的“等径点”,求m 的取值范围. (2)过点E 作EG⊥EF 交x 轴于点G ,若△EFG 各边上所有的点都是某个圆的“等径点”,求这个圆的半径r 的取值范围.参考答案1.D【解析】【分析】利用特殊角的三角函数值解答即可.【详解】A∠是锐角,且1 sin2A=,∴A∠的度数是30°.故选:D.【点睛】此题考查特殊角的三角函数值,关键是利用特殊角的三角函数值解答. 2.B【解析】【分析】直接根据圆周角定理即可得出结论.【详解】∵∠BOC与∠BAC是同弧所对的圆心角与圆周角,∠BOC=120°,∴∠BAC=12∠BOC=60°.故选:B.【点睛】本题考查了圆周角定理,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.3.C【解析】【分析】先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.【详解】y=x2﹣4x+1=(x2﹣4x+4)+1﹣4=(x﹣2)2﹣3.所以把二次函数y=x2﹣4x+1化成y=a(x﹣h)2+k的形式为:y=(x﹣2)2﹣3.故选:C.【点睛】本题考查了二次函数的三种形式.二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c (a≠0,a、b、c为常数);(2)顶点式:y=a(x﹣h)2+k;(3)交点式(与x轴):y=a (x﹣x1)(x﹣x2).4.A【解析】【分析】根据平行四边形的性质可以证明△BEF∽△DCF,然后利用相似三角形的性质即可求出答案.【详解】解:由平行四边形的性质可知:AB∥CD,∴△BEF∽△DCF,∵点E是AB的中点,∴12 BE BEAB CD==∴12 EF BECF CD==,故选:A.【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.5.B【解析】【分析】因为过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值,即S=|k|.从而证得S1=S2.【详解】∵点A,B在反比例函数y=(x>0)的图象上,∴矩形OCAD 的面积S 1=|k |=2,矩形OEBF 的面积S 2=|k |=2, ∴S 1=S 2 故选:B . 【点睛】本题考查了反比例函数y =kx中k 的几何意义,即过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积为|k |. 6.D 【解析】 【分析】根据扇形面积公式计算即可. 【详解】由,AC BD 及线段AB ,线段CD 所围成的扇面的面积=221602516010360360ππ⨯⨯-≈733(cm 2), 故选:D . 【点睛】本题考查的是扇形面积计算,掌握扇形面积公式:S 扇形=360nπR 2是解题的关键. 7.B 【解析】 【分析】利用抛物线开口方向确定a 的符号,利用对称轴方程可确定b 的符号,利用抛物线与y 轴的交点位置可确定c 的符号. 【详解】∵抛物线开口向下, ∴a <0,∵抛物线的对称轴在y 轴的右侧, ∴x =﹣2ba>0,∵抛物线与y轴的交点在x轴上方,∴c>0,故选:B.【点睛】本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a 决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac <0时,抛物线与x轴没有交点.8.C【解析】【分析】先根据规定得出函数y=2★x的解析式,再利用一次函数与反比例函数的图象性质即可求解.【详解】由题意,可得当2<x,即x>2时,y=2+x,y是x的一次函数,图象是一条射线除去端点,故A、D错误;当2≥x,即x≤2时,y=﹣2x,y是x的反比例函数,图象是双曲线,分布在第二、四象限,其中在第四象限时,0<x≤2,故B错误.故选:C.【点睛】本题考查了新定义,函数的图象,一次函数与反比例函数的图象性质,根据新定义得出函数y=2★x的解析式是解题的关键.9.5 6【解析】【分析】直接利用锐角三角函数的定义分析得出答案.∵∠C=90°,BC=5,AB=6,∴cos B=56 BCAB=.故答案为:56.【点睛】本题考查了锐角三角函数的定义,正确把握定义是解题的关键.10.3︰2【解析】此题考查比例的知识23m n=,32 m n∴=,3::3:22m n n n∴==答案3︰211.m>2.【解析】分析:根据反比例函数y=2mx-,当x>0时,y随x增大而减小,可得出m﹣2>0,解之即可得出m的取值范围.详解:∵反比例函数y=2mx-,当x>0时,y随x增大而减小,∴m﹣2>0,解得:m>2.故答案为:m>2.点睛:本题考查了反比例函数的性质,根据反比例函数的性质找出m﹣2>0是解题的关键.12.74【解析】【分析】首先证明BD=CD,设BD=CD=x,在Rt△ACD中,由∠A=30°,推出AD=CD,由此构建方程即可解决问题.【详解】如图,∵CD⊥AD,∠CBD=45°,∴∠CDB=90°,∠CBD=∠DCB=45°,∴BD=CD,设BD=CD=x,在Rt△ACD 中,∵∠A =30°,∴AD CD ,∴52+x ,∴xm ),故答案为74, 【点睛】本题考查了解直角三角形的应用,解题的关键是学会利用参数构建方程解决问题. 13.4 【解析】 【分析】由AB 是⊙O 的直径,根据直径所对的圆周角是直角,可求得∠ACB =90°,又由∠B =60°,AC =4,即可求得BC 的长,然后由AB ⊥CD ,可求得CE 的长,又由垂径定理,求得答案.【详解】∵AB 是⊙O 的直径, ∴∠ACB =90°, ∵∠B =60°,AC =4,∴BC =tan 60AC =︒, ∵AB ⊥CD ,∴CE =BC •sin60°=32=2, ∴CD =2CE =4. 故答案为:4. 【点睛】本题考查了圆周角定理、垂径定理以及三角函数的性质.注意直径所对的圆周角是直角,得到∠ACD =90°是关键 14.(1,﹣4) 【解析】【分析】根据二次函数的对称性求得对称轴,进而根据表格的数据即可得到抛物线的顶点坐标. 【详解】∵抛物线过点(0,﹣3)和(2,﹣3), ∴抛物线的对称轴方程为直线x =022=1, ∵当x =1时,y =﹣4,∴抛物线的顶点坐标为(1,﹣4); 故答案为:(1,﹣4). 【点睛】本题考查了二次函数的性质,掌握二次函数的对称性是解题的关键. 15.3.12 【解析】 【分析】连接OA 1、OA 2,根据正十二边形的性质得到∠A 1OA 2=30°,△A 1OA 2是等腰三角形,作OM ⊥A 1A 2于M ,根据等腰三角形三线合一的性质得出∠A 1OM =15°,A 1A 2=2A 1M .设圆的半径R ,解直角△A 1OM ,求出A 1M ,进而得到正十二边形的周长L ,那么圆周率π≈2L R. 【详解】如图,设半径为R 的圆内接正十二边形的周长为L . 连接OA 1、OA 2,∵十二边形A 1A 2…A 12是正十二边形, ∴∠A 1OA 2=30°.作OM ⊥A 1A 2于M ,又OA 1=OA 2, ∴∠A 1OM =15°,A 1A 2=2A 1M .在直角△A 1OM 中,A 1M =OA 1•sin∠A 1OM =0.26R , ∴A 1A 2=2A 1M =0.52R , ∴L =12A 1A 2=6.24R , ∴圆周率π≈2L R =6.242R=3.12. 故答案为3.12.【点睛】本题考查了解直角三角形的应用,正多边形和圆,等腰三角形的性质,求出正十二边形的周长L是解题的关键.16.不正确EF,GH平分的不是弧AM,BM所对的弦【解析】【分析】由作法可知,弦AN与MN不相等,根据圆心角、弧、弦的关系定理得到AN≠NM,即EF 平分的不是弧AM所对的弦.同理可得GH平分的不是弧BM所对的弦.由此得出小亮的作法不正确.【详解】小亮的作法不正确.理由是:如图,连结AN并延长,交CD于J,连结MN,设EF与AB交于I.由作法可知,EF∥CD,AI=IT,∴AN=NJ,∵∠NMJ>∠NJM,∴NJ>MN,∴AN>MN,∴弦AN与MN不相等,则AN≠NM,即EF平分的不是弧AM所对的弦.同理可得GH平分的不是弧BM所对的弦.故答案为不正确;EF,GH平分的不是弧AM,BM所对的弦.【点睛】本题考查了作图﹣复杂作图,线段垂直平分线的性质,圆心角、弧、弦的关系定理.根据作法得出弦AN与MN不相等或弦BP与PM不相等是解题的关键.17.2【解析】【分析】利用特殊角的三角函数值计算即可.【详解】1-+⨯122=.2【点睛】本题考查了特殊角的三角函数值,关键是利用特殊角的三角函数值计算.18.(1)m=﹣1;(2)画图见解析.【解析】【分析】(1)由抛物线与y轴交于(0,3),将x=0,y=3代入抛物线解析式,即可求出m的值;(2)由(1)求得解析式,配方后找出顶点坐标,根据确定出的解析式列出相应的表格,由表格得出7个点的坐标,在平面直角坐标系中描出7个点,然后用平滑的曲线作出抛物线的图象.【详解】(1)∵该函数的图象与y轴交于点(0,3),∴把x=0,y=3代入解析式得:﹣3m=3,解得m=﹣1;(2)由(1)可知函数的解析式为y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点坐标为(1,4);列表如下:描点;画图如下:【点睛】本题考查了待定系数法确定函数解析式,函数图象的画法,以及二次函数的图象上点的坐标特征.19.(1)证明见解析;(2)【解析】【分析】(1)根据相似三角形的判定即可求出证.(2)由于点E是AC的中点,设AE=x,根据相似三角形的性质可知AD AEAC AB,从而列出方程解出x的值.【详解】解:(1)∵∠ADE=∠ACB,∠A=∠A,∴△ADE∽△ACB;(2)由(1)可知::△ADE∽△ACB,∴AD AE AC AB=,∵点E是AC的中点,设AE=x,∴AC=2AE=2x,∵AD=8,AB=10,∴8210xx=,解得:x=,∴AE=.【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.20.(1)y=4x;(2)k的取值范围是0<k≤4或﹣4≤k<0.【解析】【分析】(1)根据题意得出A的坐标,然后根据待定系数法即可求得;(2)根据A、B、C、D的坐标,结合图象即可求得.【详解】(1)由题意得,A(2,2),∵反比例函数y=kx的图象经过点A,∴k=2×2=4,∴反比例函数的表达式为:y=4x;(2)由图象可知:如果反比例函数y=kx的图象与正方形ABCD有公共点,k的取值范围是0<k≤4或﹣4≤k<0.【点睛】本题考查了待定系数法求反比例函数的解析式,正方形的性质以及反比例函数的图象,根据图象得出正方形各点的坐标是解题的关键.21.(1)盲区1的面积约是5m 2;盲区2的面积约是4m 2;(2)以A 为圆心,AC 长为半径所画的圆为大货车的危险区域.如图所示见解析.【解析】【分析】(1)作OP ⊥CD 于P .根据等腰梯形的性质求出DP =(CD ﹣OB )=1.解直角△ODP ,得出OP =DP •tan∠D =,再利用梯形的面积公式即可求出盲区1的面积;解直角△BEN ,求出BE =≈4,那么S △BEN =BE •EN ≈4m 2,即为盲区2的面积;(2)利用勾股定理求出AC =AD ==,AH =AG ==,AM =AN ==,得到AC 最大,那么以A 为圆心,AC 长为半径所画的圆为大货车的危险区域.【详解】(1)如图,作OP⊥CD 于P .∵OBCD 是等腰梯形,OB =2,CD =4, ∴DP=12(CD ﹣OB )=1. 在直角△ODP 中,∵∠D=60°,,∴S 梯形OBCD =12(OB+CD )•OP=12(2+4≈3×1.7≈5(m 2), 即盲区1的面积约是5m 2;在直角△BEN 中,∵∠EBN=25°,EN =2,∴BE=2tan0.5ENEBN=∠=4,∴S△BEN=12BE•EN≈12×4×2=4(m2),即盲区2的面积约是4m2.故答案为5,4;(2)∵AC=AD=AH=AG=AM=AN=∴AC=AD>AH=AG>AM=AN,∴以A为圆心,AC长为半径所画的圆为大货车的危险区域.如图所示.【点睛】本题考查了作图﹣应用与设计作图,解直角三角形的应用,视点、视角和盲区,等腰梯形、矩形、正方形的性质以及勾股定理.准确作出辅助线构造直角三角形是解题的关键.22.(1)如图所示,△A2B2C2即为所求见解析;(2)见解析.【解析】【分析】(1)根据相似三角形的判定,结合网格特点作图即可;(2)利用勾股定理得出线段的长,并根据网格特点得出角的度数,再依据相似三角形的判定求解可得.【详解】(1)如图所示,△A2B2C2即为所求;(2)先取一格点A 2,在水平方向上取A 2C 2=2,再在网格中取一格点B 2,使∠C 2A 2B 2=135°,且A 2B 2则△A 2B 2C 2∽△A 1B 1C 1;∵A 1C 1=4,∠C 1A 1B 1=135°,A 1B 1=∴2222111112A C AB AC A B ==,∠C 2A 2B 2=∠C 1A 1B 1, ∴△A 2B 2C 2∽△A 1B 1C 1.【点睛】本题考查了作图﹣相似变换,解题的关键是掌握相似三角形的判定和性质,并根据相似三角形的判定和性质得出变换后的对应点位置及勾股定理.23.(1)证明见解析;(2)BD =203. 【解析】【分析】(1)利用等腰三角形的性质证明∠BAE =2∠BAF ,再证明∠EBD =∠BAF 即可解决问题;(2)作EH ⊥BD 于H .由sin∠BAF =sin∠EBD =,AB =5,推出BF =,推出BE =2BF =2,在Rt△ABF 中,EH =BE •sin∠EBH =2,推出BH ==4,由EH ∥AB ,推出=,由此即可求出DH 解决问题;【详解】(1)证明:连接AF .∵AB是直径,∴∠AFB=90°,∴AF⊥BE,∵AB=AE,∴∠BAE=2∠BAF,∵BD是⊙O的切线,∴∠ABD=90°,∵∠BAF+∠ABE=90°,∠ABF+∠EBD=90°,∴∠EBD=∠BAF,∴∠BAE=2∠EBD.(2)解:作EH⊥BD于H.∵∠BAF=∠EBD,,∵AB=5,∴BE=2BF=在Rt△ABF中,EH=BE•sin∠EBH=2,4,∵EH∥AB,∴EH DH AB DB=,∴254DHDH=+,∴DH=83,∴BD=BH+HD =203. 【点睛】 本题属于圆综合题,考查了切线的性质,解直角三角形,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直径三角形解决问题.24.(1)每株获利为1元;(2)5月销售这种多肉植物,单株获利最大.【解析】【分析】(1)从左图看,3月份售价为5元,从右图看,3月份的成本为4元,则每株获利为5﹣4=1(元),即可求解;(2)点(3,5)、(6,3)为一次函数上的点,求得直线的表达式为:y 1=﹣x +7;同理,抛物线的表达式为:y 2=(x ﹣6)2+1,故:y 1﹣y 2=﹣x +7-(x ﹣6)2﹣1=﹣(x ﹣5)2+,即可求解.【详解】(1)从左图看,3月份售价为5元,从右图看,3月份的成本为4元,则每株获利为5﹣4=1(元),(2)设直线的表达式为:y 1=kx+b (k≠0),把点(3,5)、(6,3)代入上式得:5=3{36k b k b +=+,解得:2{37k b =-=, ∴直线的表达式为:y 1=﹣23x+7; 设:抛物线的表达式为:y 2=a (x ﹣m )2+n , ∵顶点为(6,1),则函数表达式为:y 2=a (x ﹣6)2+1,把点(3,4)代入上式得:4=a (3﹣6)2+1,解得:a =13, 则抛物线的表达式为:y 2=13(x ﹣6)2+1, ∴y 1﹣y 2=﹣23x+7-13(x ﹣6)2﹣1=﹣13(x ﹣5)2+73,∵a=﹣13<0,∴x=5时,函数取得最大值,故:5月销售这种多肉植物,单株获利最大.【点睛】本题考查了二次函数的性质在实际生活中的应用.最大利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.25.(1)CD≈2.9.(2)利用描点法画出图象如图所示见解析;(3)AP的长度为3.3.【解析】【分析】(1)根据对称性可知:当x=2和x=4时,PA=BP′=2,因为PC⊥AB,P′C′⊥AB,即可推出PC=P′C(2)利用描点法即可解决问题;(3)函数图象与直线y=x的交点的横坐标即为PA的长,利用图象法即可解决问题;【详解】(1)如图,根据对称性可知:根据对称性可知:当x=2和x=4时,PA=BP′=2,∵PC⊥AB,P′C′⊥AB,,≈2.9.(2)利用描点法画出图象如图所示:(3)当∠DCP=30°时,CD=2PD,即y=x,观察图象可知:与函数图象与直线y=x的交点为(3.3,3.3),∴AP的长度为3.3.【点睛】本题属于圆综合题,考查了勾股定理,函数图象,直角三角形30度角的性质等知识,解题的关键是理解题意,学会利用对称性解决问题,学会利用图象法解决问题.26.(1)抛物线的对称轴为x=﹣2;(2)a≥43或a≤﹣2.【解析】【分析】(1)根据坐标轴上点的坐标特征代入点A的坐标,得出b=4a,则解析式为y=ax2+4ax+3a,进一步求得抛物线的对称轴;(2)结合图形,分两种情况:①a>0;②a<0;进行讨论即可求解.【详解】解:(1)∵抛物线y=ax2+bx+3a过点A(﹣1,0),∴a﹣b+3a=0,∴b=4a,∴抛物线的解析式为y=ax2+4ax+3a,∴抛物线的对称轴为x=﹣42aa=﹣2;(2)∵直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C,∴B(0,4),C(﹣2,2),∵抛物线y=ax2+bx+3a经过点A(﹣1,0)且对称轴x=﹣2,由抛物线的对称性可知抛物线也一定过A的对称点(﹣3,0),①a>0时,如图1,将x=0代入抛物线得y=3a,∵抛物线与线段BC恰有一个公共点,∴3a≥4,解得a≥43,②a<0时,如图2,将x=﹣2代入抛物线得y=﹣a,∵抛物线与线段BC恰有一个公共点,∴﹣a≥2,解得a≤﹣2;综上所述,a≥43或a≤﹣2.【点睛】本题考查了二次函数的性质以及解一元一次不等式,解题的关键是熟练掌握解一元一次不等式,待定系数法求抛物线解析式.本题属于中档题,难度不大,但涉及知识点较多,需要对二次函数足够了解才能快捷的解决问题.27.(1)∠BFE=60°;(2)AFBF=1;(3)1=1AFBF n-.证明见解析.【解析】【分析】(1)易证△ABD≌△ACE,可得∠DAF=∠ABF,根据外角等于不相邻两个内角的和即可解题.(2)如图1中,当=时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,由△ABD≌△CAE,推出BD=AE,设BD=AE=m,利用相似三角形的性质,列出关系式即可解决问题;【详解】(1)∵△ABC是等边三角形,∴AB=AC,∠BAD=∠C=60°,在△ABD和△ACE中,{AB AC BAD C AD CE=∠=∠=,∴△ABD≌△ACE(SAS)∴∠DAF=∠ABD,∴∠BFE=∠ABD+∠BAF=∠DAF+∠BAF=∠BAD=60°,(2)如图1中,当ADAC=12时,由题意可知:AD=CD,BE=CE.∵△ABC是等边三角形,BE=EC,AD=CD,∴∠BAE=12∠BAC=12×60°=30°,∠ABD=12∠ABC=30°,∴∠FAB=∠FBA,∴FA=FB,∴AFBF=1.(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,∵△ABD≌△CAE,∴BD=AE,∠DAF=∠ABD,设BD=AE=m,∵∠ADF=∠BDA,∴△ADF∽△BDA,∴AF AD AB BD=,∴1xn m=①,∵∠FBE=∠CBD,∠BFE=∠C=60°,∴△BFE∽△BCD,∴BF BE BC BD=,∴1y nn m-=②,①÷②得到:11 xy n=-,∴11 AFBF n=-.【点睛】本题属于三角形综合题,考查了等边三角形的性质,相似三角形的判定和性质的等知识,解题的关键是正确寻找相似三角形解决问题,学会利用参数解决问题.28.(1)①⊙O的“等径点”是D,E;②﹣2≤m≤﹣1;(2)这个圆的半径r的取值范围为r≥2.【解析】【分析】(1)①根据“等径点”的定义可知,“等径点”到圆心的距离小于等于圆的半径的2倍,由此即可判定;②如图2中,设直线EF 交半径为2的⊙O 于点K ,连接OK ,作KM ⊥OF 于M .当点T 在线段FK 上时,点T 是“等径点”,求出点K 的坐标即可解决问题;(2)因为△EFG 各边上所有的点都是某个圆的“等径点”,所以这个圆的圆心Q 是线段FG 的中点,易知Q (2,0),设这个圆的半径为r .根据QG ≤2r ,构建不等式即可解决问题.【详解】(1)根据“等径点”的定义可知,“等径点”到圆心的距离小于等于圆的半径的2倍.即半径为1的⊙O 的“等径点”在以O 为圆心2为半径的圆内或圆上.如图1中,观察图象可知:在点D ,E ,F 中,⊙O 的“等径点”是D ,E .②如图2中,设直线EF 交半径为2的⊙O 于点K ,连接OK ,作KM⊥OF 于M .∵OF=2,OE =,∴tan∠EFO=EO OF ,∴∠OFK=60°,∵OF=OK,∴△OFK是等边三角形,∴OF=OK=FK=2,∵KM⊥OF,∴FM=OM=1,KM∴K(﹣1),∵当点T在线段FK上时,点T是“等径点”,∴﹣2≤m≤﹣1.(2)如图3中,∵△EFG是直角三角形,∠FEG=90°,∠EFG=60°,∴EF=2OF=4,FG=2EF=8,∴OG=6,由题意△EFG各边上所有的点都是某个圆的“等径点”,这个圆的圆心Q是线段FG的中点,Q(2,0),设这个圆的半径为r.由题意:QG≤2r∴4≤2r,∴r≥2,即这个圆的半径r的取值范围为r≥2.【点睛】本题属于圆综合题,考查了“等径点”的定义,解直角三角形,勾股定理,锐角三角函数等知识,解题的关键是理解题意,学会添加常用辅助线,构造直角三角形解决问题.。
2019年北京市丰台区届九年级上期末练习数学试题及答案
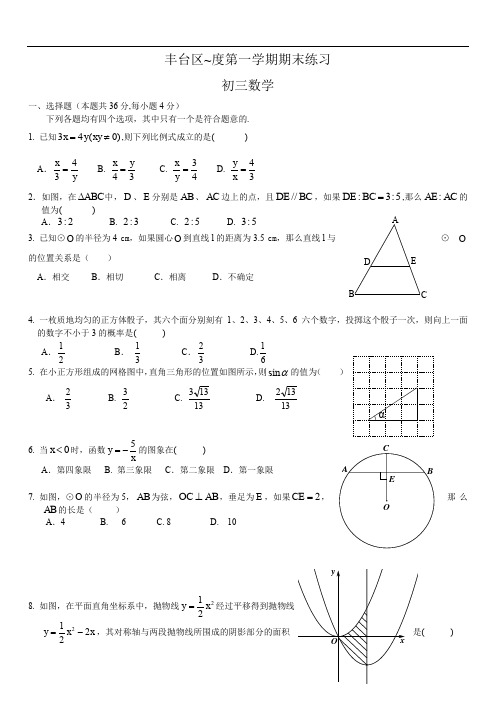
丰台区~度第一学期期末练习初三数学一、选择题(本题共36分,每小题4分)下列各题均有四个选项,其中只有一个是符合题意的. 1. 已知)0(43≠=xy y x ,则下列比例式成立的是( )A .y x 43= B. 34y x = C. 43=y x D. 43y x =2.如图,在ABC ∆中,D 、E 分别是AB 、AC 边上的点,且BC DE //,如果5:3:=BC DE ,那么AC AE :的值为( )A .2:3 B. 3:2 C. 5:2 D. 5:3 3. 已知⊙O 的半径为4 cm ,如果圆心O 到直线l 的距离为3.5 cm ,那么直线l 与⊙O的位置关系是( )A .相交B .相切C .相离D .不确定4. 一枚质地均匀的正方体骰子,其六个面分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字不小于3的概率是( )A .21B . 31C .32 D.61 5. 在小正方形组成的网格图中,直角三角形的位置如图所示,则sin α的值为( )A .32 B. 23C. 13133D. 131326. 当0<x 时,函数xy 5-=的图象在( ) A .第四象限 B. 第三象限 C .第二象限 D7. 如图,⊙O 的半径为5,AB 为弦,AB OC ⊥,垂足为E 那么AB 的长是( )A .4 B. 6 C. 8 D. 108. 如图,在平面直角坐标系中,抛物线221x y =x x y 2212-=)ED C B A α图(2)A .2 B. 4 C. 8 D. 169. 如图(1),E 为矩形ABCD 边AD 上一点,点P 从点B 沿折线DC ED BE --运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止,它们运动的速度都是s cm /1.如果点P 、Q 同时开始运动,设运动时间为)(s t ,BPQ ∆的面积为)(2cm y ,已知y 与t 的函数关系的图象如图(2)所示,那么下列结论正确的是( )图(1)A. 8AE =B. 100≤≤t 当时,254t y = C. 4sin 5EBC ∠=D. 当s t 12=时,BPQ ∆是等腰三角形二.填空题(本题共20分,每小题4分)10. 两个相似三角形的面积比是9:5,则它们的周长比是_______. 11. 在ABC Rt ∆中,090=∠C ,如果3tan =A ,那么=∠A _______°.12. 如果扇形的圆心角为120°,半径为3cm ,那么扇形的面积是__________________2cm .13. 一个口袋里放有三枚除颜色外都相同的棋子,其中有两枚是白色的,一枚是红色的.从中随机摸出一枚记下颜色,放回口袋搅匀,再从中随机摸出一枚记下颜色,两次摸出棋子颜色不同的概率是_______.14. 如图,点A 1、A 2 、A 3 、…,点B 1、B 2 、B 3 、…,分别在射线OM 、ON 上,A 1B 1∥A 2B 2∥A 3B 3∥A 4B 4∥….如果A 1B 1=2,A 1A 2=2OA 1,A 2A 3=3OA 1,A 3A 4=4OA 1,…. 那么A 2B 2= ,A nB n = .(n 为正整数)三、解答题(本题共19分,第15题4分,第16题5分,第17题 5分,第18题5分)15. 计算:00060sin 245cos 30tan 3+- .4N M A 1A 2A3A 432116. 已知二次函数221y x x =+-.(1)写出它的顶点坐标;(2)当x 取何值时,y 随x 的增大而增大; (3)求出图象与x 轴的交点坐标.17.如图,在⊙O 中,C ﹑D 为⊙O 上两点,AB 是⊙O 的直径,已知0130=∠AOC ,2=AB .求(1)⌒AC 的长; (2)的度数D ∠.18.如图,在ABC ∆中,090=∠C ,52sin =A ,D 为AC 上一点,045=∠BDC ,6=DC ,求AD 的长.四、解答题(本题共17分,第19题5分,第20题6分,第21题6分)19. 如图,PA ﹑PB 是⊙O 的切线,A ﹑B 是切点,AC 是⊙O 的直径,070=∠ACB .求P ∠的度数.20. 如图,一次函数11+=x y 的图象与反比例函数xky =2(k 为常数,且0≠k )的图象都经过点)2,(m A . (1)求点A 的坐标及反比例函数的解析式; (2)观察图象,当0>x 时,直接写出1y 与2y 的大小关系.D CBA21. 如图,BC A ∆是⊙O 的内接三角形,⊙O 的直径BD 交AC 于点E ,BD AF ⊥与点F ,延长AF 交BC 于点G . 求证:2AB BG BC =.五.解答题(本题共28分,第22题6分,第23题7分,第24题7分,第25题8分)22.如图,一艘海轮位于灯塔P 的南偏东060方向,距离灯塔100海里的A 处,它计划沿正北方向航行,去往位于灯塔P 的北偏东045方向上的B 处.2.449≈≈≈)(1)问B 处距离灯塔P 有多远?(结果精确到0.1海里)(2)假设有一圆形暗礁区域,它的圆心位于射线PB 上,距离灯塔190海里的点O 处.圆形暗礁区域的半径为50海里,进入这个区域,就有触礁的危险.请判断海轮到达B 处是否有触礁的危险,并说明理由.23.如图(11m ,拱桥的跨度为10m ,桥洞与水面的最大距离是5m ,桥洞两侧壁上各有一盏距离水面4m 的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2). 求(1)抛物线的解析式;(2)两盏景观灯1P 、2P 之间的水平距离.B24. 已知直线y=kx3与x 轴交于点A (4,0),与y 轴交于点C ,抛物线234y x mx n =-++经过点A 和点C,动点P 在x 轴上以每秒1个长度单位的速度由抛物线与x 轴的另一个交点B 向点A 运动,点Q 由点C 沿线段CA 向点A 运动且速度是点P 运动速度的2倍.(1)求此抛物线的解析式和直线的解析式;(2)如果点P 和点Q 同时出发,运动时间为t (秒),试问当t 为何值时,以A 、P 、Q 为顶点的三角形与△AOC相似;(3)在直线CA 上方的抛物线上是否存在一点D ,使得△ACD 的面积最大.若存在,求出点D 的坐标;若不存在,请说明理由.25. 已知ABD ∆和CBD ∆关于直线BD 对称(点A的对称点是点C),点E 、F 分别是线段BC 和线段BD上的点,且点F 在线段EC 的垂直平分线上,联结AF 、AE ,AE 交BD 于点G . (1)如图(1),求证:ABD EAF ∠=∠;(2)如图(2),当AD AB =时,M 是线段AG 上一点,联结BM 、ED 、MF ,MF 的延长线交ED 于点N ,BAF MBF ∠=∠21,AD AF 32=,试探究线段FM 和FN 之间的数量关系,并证明你的结论.图(1) 图(2)备用图G FEDCBA NMGF EDBAP丰台区~度第一学期初三数学练习期末参考答案二.填空题(本题共20分,每小题4分) 10.3:511. 06012. 3π13.4914. (1)11A B = 6 ,(2)n n A B =(1)n n + 三.解答题(本题共19分,第15题4分,第16题5分,第17题 5分,第18题5分)15.解:原式32322=⨯-+⨯………3分 16.解:(1)(1,2) ……………………1分 2= (2)x>1-, ……………………3分2= ……………4分 (3)坐标为()()1--,…5分 17.解(1)130AOC ∠=∴⌒AC=130180R π………………………………1分1301318018ππ==(或1318π) ……………2分(2)由130AOC ∠=得50BOC ∠=…………………………………3分又12D BOC ∠=∠ ……………………………4分150252D ∴∠=⨯= …………………………5分 18. 解:在BDC ∆中,090=∠C , 045=∠BDC ,6=DC∴tan 451BCDC︒==∴6BC = …………………………………1分在ABC ∆中,52sin =A ,∴25BC AB =,……2分 ∴15AB =……………………………………3分∴AC =4分 ∴6AD =……………………………5分 19.解:∵PA 、PB 是⊙O 的切线,A 、B 是切点,∴PA=PB ,∠PAC=900…………………2分 ∴∠PAB=∠PBA …………………………3分∠P=18002∠PAB 又∵AC 是⊙O 的直径∴∠ABC=900 ,……………………………4分∴∠BAC=900∠ACB=200∠PAB=900200=700∴18027040P ∠=-⨯= ……………5分CDB四、解答题(本题共17分,第19题5分,第20题6分,第21题6分) 20.解:(1)∵ 一次函数11y x =+的图象经过点(A m ,2),∴ 21m =+. 解得 1m =. ………………………………………………………1分 ∴ 点A 的坐标为(1A ,2).………………………………………2分∵ 反比例函数2ky x=的图象经过点(1A ,2), ∴ 21k=.解得 2k =. …………………………………………3分 ∴ 反比例函数的表达式为22y x=.………………………………4分(2)观察图象,得①当01x <<时,12y y <; ………………………5分②当1x >时,12y y >;………………………………6分③当1x =时,12y y =.注:若①+③或②+③,只给1分。
2019届北京市丰台区九年级上学期期末数学试卷【含答案及解析】

2019届北京市丰台区九年级上学期期末数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是()A. B. C. D.2. 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于()A.3:2 B.3:1 C.2:3 D.3:53. ⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是()A.相交 B.相切 C.相离 D.不确定4. 抛物线y=(x﹣2)2+3的顶点坐标是()A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)5. 如果△ABC∽△DEF,相似比为2:1,且△DEF的面积为4,那么△ABC的面积为()A.1 B.4 C.8 D.166. 如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是()A.30° B.60° C.80° D.120°7. 对于反比例函数,下列说法正确的是()A.图象经过点(2,﹣1)B.图象位于第二、四象限C.当x<0时,y随x的增大而减小D.当x>0时,y随x的增大而增大8. 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为()A.5m B.6m C.7m D.8m9. 小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半圆的是()A. B.C. D.10. 如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO 的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是()A. B. C. D.二、填空题11. 如果∠A是锐角,且sinA=,那么∠A= ゜.12. 若2x=5y,则= .13. 圆心角是60°的扇形的半径为6,则这个扇形的面积是.14. 排水管的截面为如图所示的⊙O,半径为5m,如果圆心O到水面的距离是3m,那么水面宽AB= m.15. 请写出一个符合以下三个条件的二次函数的解析式:.①过点(1,1);②当x>0时,y随x的增大而减小;③当自变量的值为3时,函数值小于0.三、解答题16. 阅读下面材料:在数学课上,老师请同学思考如下问题:小亮的作法如下:老师说:“小亮的作法正确.”请你回答:小亮的作图依据是.四、计算题17. 计算:2cos30°﹣tan45°+sin60°.五、解答题18. 函数y=mx3m﹣1+4x﹣5是二次函数.(1)求m的值;(2)写出这个二次函数图象的对称轴:;将解析式化成y=a(x﹣h)2+k的形式为:.19. 如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.(1)求证:△ACD∽△ABC;(2)若AD=6,AB=10,求AC的长.20. 如图,直线y1=x+2与双曲线相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.(1)求k的值;(2)若y1<y2,请你根据图象确定x的取值范围.21. 如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?(≈1.73)22. 如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.(1)求证:CD是⊙O的切线;(2)过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA=,依题意补全图形并求DE的长.23. 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:24. t(秒)00.160.20.40.60.640.8…x(米)00.40.511.51.62…y(米)0.250.3780.40.450.40.3780.25…td25. 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.26. 已知抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1).(1)求抛物线G1的解析式;(2)将抛物线G1先向左平移3个单位,再向下平移1个单位后得到抛物线G2,且抛物线G2与x轴的负半轴相交于A点,求A点的坐标;(3)如果直线m的解析式为,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x 轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.27. 在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).(1)如图1,如果⊙O的半径为,①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O 上任意一点距离的最小值.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】第26题【答案】。
北京市丰台区九年级上学期期末考试数学试题有答案

丰台区度第一学期期末练习初 三 数 学学校 姓名 考号一、选择题(本题共30分,每小题3分,)下列各题均有四个选项,其中只有一个..是符合题意的. 1.如图,在Rt △ABC 中,∠C =90°,BC =3,AB =4, 则cos B 的值是A .37B .47 C .43D .342.如图,在△ABC 中,点D 、E 分别在AB 、AC 边上,且 DE ∥BC ,如果AD ∶DB =3∶2, 那么AE ∶AC 等于A .3∶2B .3∶1C .2∶3D .3∶5 3.⊙O 的半径为3cm ,如果圆心O 到直线l 的距离为d , 且d =5cm ,那么⊙O 和直线l 的位置关系是A .相交B .相切C .相离D .不确定 4.抛物线3)2(2+-=x y 的顶点坐标是( )A .(2,3)B .(-2,3)C .(2,-3)D .(-2,-3)5.如果ABC DEF △∽△,相似比为2∶1,且△DEF 的面积为4,那么△ABC 的面积为A .1B .4C .8D .16E D CBA6. 如图,四边形ABCD 内接于⊙O ,∠BCD =120°,则∠BAD 的度数是A .30°B .60°C .80°D .120°7.对于反比例函数2y x,下列说法正确的是 A .图象经过点(2,-1) B .图象位于第二、四象限C .当x < 0时,y 随x 的增大而减小D .当x > 0时,y 随x 的增大而增大8.如图,为了测量某棵树的高度,小明用长为2m 的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m ,与树相距10m ,则树的高度为A. 5mB. 6mC. 7mD. 8m9.小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半ABC D 10.如图,点A 、B 、C 、D 、E 、F 为⊙O 的六等分点,动点P 从圆心O 出发,沿OE 弧EF FO 的路线做匀速运动,设运动的时间为t ,∠BPD 的度数为y ,则下列图象中表示y 与t 之间函数关系最恰当的是EBFCDAOABC D二、填空题(本题共22分,第11题3分,第12题3分,第13-16题,每小题4分) 11.如果A ∠是锐角,且sin A =21,那么=∠A __________゜.12.已知y x 5=2,则 =yx__________.13.圆心角是60°的扇形的半径为6,则这个扇形的面积是 .14.排水管的截面为如图所示的⊙O ,半径为5m , 如果圆心O 到水面 的距离是3m ,那么水面宽AB =__________ m .15.请写出一个符合以下三个条件的二次函数的解析式: .①过点(1,1);②当0x 时,y 随x 的增大而减小; ③当自变量的值为3时,函数值小于0.16.阅读下面材料:在数学课上,老师请同学思考如下问题:小亮的作法如下:老师说:“小亮的作法正确.”请你回答:小亮的作图依据是_________________________.三、解答题(本题共24分,每小题6分) 17.计算:2cos30°-tan 45°+sin 60°. 18.函数5-4+=1-3x mx y m 是二次函数.(1)求m 的值;(2)写出这个二次函数图象的对称轴: ;将解析式化成y=a (x -h )2+k 的形式为: .19.如图,在ABC △中,D 是AB 上一点,连接 CD ,且∠ACD =∠ABC . (1)求证:△ACD ∽△ABC ; (2)若AD =6,AB =10,求AC 的长.20.如图,直线2+=1x y 与双曲线xk y =2相交于A ,B 两点 其中点A 的纵坐标为3,点B 的纵坐标为-1. (1)求k 的值;(2)若21<y y ,请你根据图象确定x 的取值范围.四、解答题(本题共28分,每小题7分)21.如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB ,已知距电线杆AB 水平距离14米处是观景台,即BD =14米,该观景台的坡面CD 的坡角∠CDF 的正切值为2,观景台的高CF 为2米,在坡顶C 处测得电线杆顶端A 的仰角为30°,D 、E 之间是宽2米的人行道,如果以点B 为圆心,以AB 长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB 时,人行道是否在危险区域内?(73.13,41.12≈≈)ABCDA22.如图,D 为O ⊙上一点,点C 在直径BA 的延长线上,CDA CBD ∠=∠. (1)求证:CD 是O ⊙的切线;(2)过点B 作O ⊙的切线交CD 的延长线于点E ,若AB =6,tan23CDA ∠=,依题意补全图形并求DE 的长23.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A 处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A 的水平距离为x (米),距桌面的高度为y (米),运行时间为t (秒),经多次测试后,得到如下部分数据:(1)如果y ① 如下图,在平面直角坐标系tOy 中,描出了上表中y 与t 各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;②当t 为何值时,乒乓球达到最大高度?(2)如果y 是关于x 的二次函数,那么乒乓球第一次落在桌面时,与端点A 的水平距离是多少?24.如图,⊙O 为△ABC 的外接圆,直线l 与⊙O 相切与点P ,且l ∥B C .(1) 请仅用无刻度的直尺........,在⊙O 中画出一条弦.,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法);(2) 请写出证明△ABC 被所作弦分成的两部分面积相等的思路.五、解答题(本题共16分,每小题8分)25.已知抛物线G 1:y =ax 2+b x +c 的顶点为(2,-3),且经过点(4, 1). (1)求抛物线G 1的解析式;(2)将抛物线G 1先向左平移3个单位,再向下平移1个单位后得到抛物线G 2,且抛物线G 2与x 轴的负半轴相交于A 点,求A 点的坐标; (3)如果直线m 的解析式为3+21=x y ,点B 是(2)中抛物线G 2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n 过点A 和点B .问:是否存在点B ,使直线m 、n 、x 轴围成的三角形和直线m 、n 、y 轴围成的三角形相似?若存在,求出点B 的坐标;若不存在,请说明理由.l备用图1备用图226.在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x-y) .(1) 如图1,如果⊙O的半径为,①请你判断M(2,0),N(-2,-1)两个点的变换点与⊙O的位置关系;②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.(2) 如图2,如果⊙O的半径为1,且P的变换点P’在直线y=-2x+6上,求点P与⊙O上任意一点距离的最小值.丰台区度第一学期期末练习 初 三 数 学 参 考 答 案一、选择题(本题共30分,每小题3分)11. 30; 12.52; 13.π6; 14. 8; 15.如:y = -x 2+2;16.不在同一条直线上的三个点确定一个圆;线段垂直平分线上的点到线段两个端点距离相等;两条直线交于一点.三、解答题(本题共24分,每小题6分) 17.解:原式=21-----3分1-----4分1-----6分18.解:(1)由题意得:312m -=,解得1m =. -----2分(2)二次函数的对称轴为 2x =-; -----4分 顶点式为:2(2)9y x =+-. -----6分19.(1)证明:∵∠A =∠A , ∠ACD =∠ABC , ∴ΔACD ∽ΔABC . -----2分 (2)解:∵ΔACD ∽ΔABC , .AC ADAB AC∴= -----4分 2AC AD AB ∴=⋅, AC ∴= -----6分20.解:(1)∵点A 的纵坐标为3, ∴x +2=3. ∴x =1.∴点A 坐标是(1,3). -----1分 ∵点A 在反比例函数2k y x=的图象上, ∴ k =xy =3. -----3分 (2) ∵点B 的纵坐标为-1,∴x +2= -1. ∴x = -3. ∴点B 坐标是(-3,-1). -----4分由图象知:当-3<x 或当1<<0x 时,y 1< y 2 . -----6分 四、解答题(本题共28分,每小题7分)21.解:由题意可知,∠CGB =∠B =∠CFD = 90°. 在Rt △CDF 中,tan ∠CDF =CF DF=2,CF =2.∴DF =1,BG =2. -----2分 ∵BD =14,∴BF =GC =15.在Rt △AGC 中,由tan30°,∴AG ==-----4分∴AB = 2 ≈ 10.65 . -----5分 ∵BE =BD -ED =12 , -----6分 ∴AB < BE ,∴人行道不在危险区域内. -----7分22.(1)证明:连接OD .∵OB=OD ,∴∠OBD=∠ODB . -----1分 ∵∠CDA =∠CBD ,∴∠CDA =∠ODB .∵AB 是⊙O 的直径,∴∠ADO +∠ODB =90°. -----2分 ∴∠ADO +∠CDA=90°, 即CD ⊥OD .又∵D 为O ⊙上一点,∴CD 是⊙O 的切线. -----3分 (2)解:如图补全图形并连接OE . ∵CE 、BE 是⊙O 的切线,∴BE =DE ,∠DEO =∠BEO ,BE ⊥BC . -----5分 ∴OE ⊥BD .可得∠BEO =∠CBD =∠CDA . -----6分 ∴tan ∠BEO = tan ∠CDA . ∴32=BE OB.∵AB =6,∴OB =3. ∴BE =92.∴DE =92.-----7分23.(1)①如图所示:-----2分②答:当t =0.4秒时,乒乓球达到最大高度. -----3分(2)设二次函数的解析式为y =a (x -1)2+0.45且经过点(0,0.25),∴a (0-1)2+0.45=0.25,解得 a =15-.∴解析式为y =15-(x -1)2+0.45. -----5分当0y =时,15-(x -1)2+0.45=0,解得10.5x =-(舍),22.5x =.∴乒乓球第一次落在桌面时与端点A 的水平距离是2.5米. -----7分 24.(1)解:如图所示.-----3分(2)思路:a .由切线性质可得PO ⊥l ;b .由l ∥BC 可得PD ⊥BC ;c .由垂径定理知,点E 是BC 的中点;d .由三角形面积公式可证S △ABE = S △AEC . -----7分 五、解答题(本题共16分,每题8分)25. 解:(1)∵抛物线G 1:y =ax 2+b x +c 的顶点为(2,-3),∴y =a (x -2)2﹣3.∵抛物线y =a (x -2)2﹣3且经过点(4,1), ∴a (4-2)2﹣3=1.解得 a =1.∴抛物线G 1的解析式为y=(x -2)2﹣3=x 2-4x +1. -----2分lF(2)由题意得,抛物线G 2的解析式为y =(x -2+3)2﹣3﹣1=(x +1)2﹣4.∴当y =0时,x = -3或1.∴A (﹣3,0) -----5分(3)由题意得,直线m 交x 轴于点C (-6,0),交y 轴于点D (0,3).设直线n 交y 轴于点E (0,t ),与直线m 交于点F . 当m ∥n 时,t =32,不能构成三角形.∵t =0时,直线n 与x 轴重合, ∴直线n ,m 与x 轴不能构成三角形. ∴0t ≠且t32≠. ① 当t <0时,如图所示,当∠CF A =∠EFD =90°时,∵∠COE =90°, ∴∠FCA =∠FED . ∴△FCA ∽△FED .∵tan ∠FCA =tan ∠FED ,∴OE =6. ∴点E 的坐标为(0,﹣6). ∴直线n 的解析式为y =﹣2x ﹣6.此时符合条件的B 点坐标为(-1,-4). ② 当0< t<32时,符合条件的点B 不存在.③ 当t >32时,如图所示,∵∠EFD =∠CF A ,∴当∠FED =∠FCA 时,△EFD ∽△CF A . 解得OE =6. ∴点E 的坐标为(0,6). ∴直线n 的解析式为y =2x +6. 此时符合条件的B 点坐标为(3,12). 综上所述:存在满足条件的B 点坐标为(-1,-4),(3,12). -----8分 26.解:(1)①由题意得,'(2,2),'(3,1).M N -- ∴''OM ON ==>∴'M 在⊙O 上,'N 在⊙O 外. ----2分 ②设点(,2)P x x +,则'(22,2)P x +-. ∵点'P 在⊙O 内,∴2<2+2<2-x ,解得0<<2-x .∴点P 横坐标的取值范围是0<<2-x. (2)设点(,)P a b ,则'(,)P a b a b +-. 由题意,得2()6.a b a b -++=- 整理,得3 6.b a =-+ ∴36P y x =-+点在直线上. ∴点O 到直线y = -3x +6的距离是1053∴点P 与⊙O 上任意一点的最短距离是1-1053. -----8分。
北京丰台区2019届初三第一学期期末数学试题及答案

丰台区2018—2019学年度第一学期期末练习初三数学一、选择题(本题共16分,每小题2分)下列各题均有四个选项,其中只有一个..是符合题意的. 1.如果A ∠是锐角,且21sin =A ,那么A ∠的度数是 (A )90°(B )60°(C )45°(D )30°2.如图,A ,B ,C 是⊙O 上的点,如果∠BOC = 120°, 那么∠BAC 的度数是 (A )90° (B )60°(C )45°(D )30°3.将二次函数142+-=x x y 化成k h x a y +-=2)(的形式为 (A )1)4(2+-=x y (B )3)4(2--=x y (C )3)2(2--=x y(D )3)2(2-+=x y4.如图,在□ABCD 那么EF 与CF (A )1∶2 (C )2∶15)0(2>=x x y 矩形OEBF (A )S 1 > S 2 (C )S 1 < S 2 6OA = 25 cm ,OB 线段CD (A )157 cm 2(C )628 cm 2BAO CD7.二次函数)(02≠++=a c bx ax y 的图象如图所示, 那么下列说法正确的是(A )000>>>c b a ,, (B )000>><c b a ,, (C )000<><c b a ,, (D )000><<c b a ,,8.对于不为零的两个实数a ,b ,如果规定:a ★b =⎪⎩⎪⎨⎧≥-<+,)((b a baa ba那么函数y = 2★x的图象大致是二、填空题(本题共16分,每小题2分)9.如图,在Rt △ABC 中,∠C = 90°,BC = 5,AB = 6,那么=B cos _____. 10.如果n m 32=,那么=n m :_____. 11.如果反比例函数xm y 2-=,当0>x 时,y 随x 的 增大而减小,那么m 的值可能是____(写出一个即可). 12.永定塔是北京园博园的标志性建筑,其外观为辽金风格的八角九层木塔,游客可登 至塔顶,俯瞰园博园全貌. 如图,在A 处 测得∠CAD = 30°,在B 处测得∠CBD = 45°,并测得AB = 52米,那么永定塔的高CD 约 是 米.(4.12≈,7.13≈,结果保留整数) 13.14那么该抛物线的顶点坐标是 .15.刘徽是我国古代最杰出的数学家之一,他在《九章算术圆田术》中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法. (注:圆周率=圆的周长与该圆直径的比值.)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”. 刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.(A) (B ) (C ) (D )刘徽(约225年—约295年)刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R ,此时圆内接正六边形的周长为6R ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3. 当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为 .(参考数据:sin15° ≈ 0.26)16.阅读下面材料:在数学课上,老师请同学们思考如下问题:小亮的作法如下:老师问:“小亮的作法正确吗?”请回答:小亮的作法______(“正确”或“不正确”),理由是_________.三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)解答应写出文字说明、演算步骤或证明过程. 17.计算:︒+︒-︒60cos 245tan 60sin .18.函数m mx mx y 322--=是二次函数.(1)如果该二次函数的图象与y 轴的交点为(0,3),那么m = ;(2)在给定的坐标系中画出(1)中二次函数的图象.19.如图,在ABC △中,D ,E 分别是边AB ,AC 上的点,连接DE ,且∠ADE =∠ACB . (1)求证:△ADE ∽△ACB ;(2)如果E 是AC 的中点,AD =8,AB =10,求AE 的长.20.如图,在平面直角坐标系xOy 中,点O 为正方形ABCD 对角线的交点,且正方形ABCD 的边均与某条坐标轴平行或垂直,AB =4.(1)如果反比例函数x ky =的图象经过点A ,求这个反比例函数的表达式; (2)如果反比例函数xky =的图象与正方形ABCD 有公共点,请直接写出k 的取值范围.21.如图1,某学校开展“交通安全日”活动. 在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全. 小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2. 在图2中大货车的形状为矩形,盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.图1 图2 请你帮助小刚的学习小组解决下面的问题:(1)盲区1的面积约是 m 2;盲区2的面积约是 m 2;(4.12≈,7.13≈,4.025sin ≈︒,9.025cos ≈︒,5.025tan ≈︒,结果保留整数) (2)如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险EABCD区域,请在图2中画出大货车的危险区域.22.如图是边长为1的正方形网格,△111A B C 的顶点均在格点上. (1)在该网格中画出△222A B C (△222A B C 的顶点均在格点上),使△222A B C ∽△111A B C ;(2)请写出(1)中作图的主要步骤,并说明△222A B C 和△111A B C 相似的依据.23.如图,AB 是⊙O 的直径,C 是⊙O 上一点,连接AC . 过点B 作⊙O 的切线,交AC 的延长线于点D ,在AD 上取一点E ,使AE = AB ,连接BE ,交⊙O 于点F . 请补全图形并解决下面的问题: (1)求证:∠BAE =2∠EBD ; (2)如果AB = 5,55sin =∠EBD ,求BD 的长.24.小哲的姑妈经营一家花店.随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”.小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:(1)如果在三月份出售这种植物,单株获利 元;(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大? (提示:单株获利 = 单株售价-单株成本)25.如图,P 是AB⌒所对弦AB 上一动点,过点P 作PC ⊥AB 交AB ⌒于点C ,取AP 中点D ,连接CD . 已知AB = 6cm ,设A ,P 两点间的距离为x cm ,C ,D 两点间的距离为y cm .(当点P 与点A 重合时,y 的值为0;当点P 与点B 重合时,y 的值为3)小凡根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小凡的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合所画出的函数图象,解决问题:当∠C =30°时,AP 的长度约为 cm .26.在平面直角坐标系xOy 中,抛物线2+3y ax bx a =+过点A (-1,0).(1)求抛物线的对称轴;(2)直线4y x =+与y 轴交于点B ,与该抛物线对称轴交于点C ,如果该抛物线与线段BC 有交点,结合函数的图象,求a 的取值范围.27.如图,△ABC 是等边三角形,D ,E 分别是AC ,BC 边上的点,且AD = CE ,连接BD ,AE 相交于点F .(1)∠BFE 的度数是 ;(2)如果21=AC AD ,那么=BF AF ; (3)如果nAC AD 1=时,请用含n 的式子表示AF ,BF 的数量关系,并证明.28.对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:若⊙C 上存在一个点M ,使得PM = MC ,则称点P 为⊙C 的“等径点”.已知点D )3121(,,E )320(,,F )02(,-. (1)当⊙O 的半径为1时,①在点D ,E ,F 中,⊙O 的“等径点”是 ;②作直线EF ,若直线EF 上的点T (m ,n )是⊙O 的“等径点”,求m 的取值范围.(2)过点E 作EG ⊥EF 交x 轴于点G ,若△EFG 上的所有点都是某个圆的“等径点”,求这个圆的半径r 的取值范围.丰台区2018—2019学年度第一学期期末练习ADBFE初三数学参考答案一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题2分)9. 56;10. 3︰2;11. 2m>即可;12. 70;13.4;14. (1,4)-;15. 3.12;16.不正确;EF GH、平分的不是弧AM、弧BM所对的弦.三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)17. 解: 1122+⨯原式. ...............…........3分11+ ...…….................4分……......................5分 18. 解:(1)-1; ...............…..........2分(2)略. .................…..........5分 19. 解:(1)证明:∵∠ADE =∠ACB , ∠A =∠A ,∴△ADE ∽△ACB . .................…..........2分(2)由(1)知△ADE ∽△ACB ,∴AD AE AC AB=. ∵点E 是AC 的中点,设AE =x , ∴22AC AE x ==. ∵AD =8,AB =10, ∴8210x x =.解得x =(负值舍去).∴AE = .................…..........5分20.解:(1)由题意,得A (2,2) . ∵反比例函数xky =的图象经过点A , ∴4k =.∴反比例函数的表达式4y x=. .................…..........2分 (2)040k k <≤≤<或-4. .................…..........5分21. 解:(1)54;.................…..........4分 (2)略. .................….......... 5分 22. 解:(1)略; ........................... 2分(2)略.....................................5分 23. 解:作图正确. ........…....... ........... 1分(1)证明:连接AF .∵AB 是⊙O 的直径,∴∠AFB =90°. ∵AB = AE , ∴∠BAE =2∠BAF . ∵BD 是⊙O 的切线, ∴∠ABD =90°.∵∠BAF +∠ABF =90°,∠EBD +∠ABF =90°, ∴∠BAF =∠EBD .∴∠BAE =2∠EBD . .....................….......... 3分(2)过点E 作EH ⊥BD 于H .∵∠BAF =∠EBD .∴sin sin BAF EBD ∠=∠.在Rt △ABF 中, ∵AB = 5,∴BF =.∴2BE BF ==在Rt △EBH 中,sin 2EH BE EBH =⋅∠=.∴∴BH=4. ∵EH ∥AB , ∴EH DHAB DB=. ∴254DH DH =+,解得83DH =.∴203BD BH HD =+=. .....................….........6分 24. 解:(1)1;....................................2分 (2)设直线的表达式为1(0)y kx b k =+≠. ∵点(3,5)和(6,3)在直线上,∴直线的表达式为1273y x =-+.设抛物线的表达式为22()y a x h k =-+.∵顶点(6,1),点(3,4)在抛物线上, ∴抛物线的表达式为221(6)13y x =-+. ∴212217[(6)1]33y y x x -=-+--+217(5)33x =--+. ∴在5月销售这种多肉植物,单株获利最大. .............................6分 25.解:(1)2.8;.........................2分(2)略. .........................4分(3)3.3. ........................6分 26.解:(1)∵抛物线23y ax bx a =++过点A (-1,0), ∴30a b a -+=.∴4b a =.∴抛物线解析式可化为243y ax ax a =++. ∴抛物线的对称轴为422ax a =-=-. .........................2分(2)由题意,得B (0,4),C (-2,2)∵抛物线243y ax ax a =++过点A (-1,0)且抛物线的对称轴为2x =-,由抛物线的对称性可知,抛物线也一定经过A 的对称点(-3,0). ①0a >时,如图1,将0x =代入抛物线得3y a =,∵抛物线与线段BC 有交点,∴34a ≥,解得43a ≥.②0a <时,如图2,将2x =-代入抛物线得y a =-,∵抛物线与线段BC 有交点, ∴2a -≥,解得2a ≤-. 综上所述,423a a ≥≤-或. .........................6分27. 解:(1)60°; .........................1分 (2)1; .........................2分(3)CAE B DF11AF BF n =-. .........................3分证明:延长FE 至G ,使FG =FB .连接GB ,GC .由(1)知,∠BFG=60°.∴△BFG 为等边三角形.∴BF =BG ,∠FBG=∠FGB=60°.∵△ABC 是等边三角形,∴AB=BC ,∠ABC=60°.∴∠ABF=∠CBG .∴△ABF ≌△CBG .∴∠BFA=∠BGC=120°.∴∠FGC=60°.∴∠FGC=∠BFG .∴FB ∥CG . ∴AF ADFG DC =. ∵1AD AC n =, ∴11AF FG n =-. ∴11AF BF n =-. .........................7分28. 解:(1) ①D 、F ; .........................2分②若直线EF 上存在点T (m ,n )是⊙O 的“等径点”, 则点T 满足02OT ≤≤.如图,以O 为圆心,OF 为半径作圆,设该圆与直线EF 的另一个交点为A .在Rt △EOF中,2OE OF ==, ∴∠EFO =60°. ∵OA=OF , ∴△AFO 为等边三角形.∴过A 作AB ⊥x 轴于B . ∴FB=OB=1.∴21m -≤≤-. (5)分 (2)2r ≥. .........................7分初三数学第27页(共8页)初三数学第28页(共8页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京丰台0809学年九年级上期末练习试卷数学初三数学2009.l第Ⅰ卷 (机读卷 共32分)一、选择题(共8道小题,每小题4分,共32分)下列各题均有四个选项,其中只有一个是符合题意的.请用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑. 1.若31=b a ,则b ba +的值是( ) A .32B .43 C .34 D .32.假如⊙O 的半径为6cm ,OP =5cm ,则点P 与⊙O 的位置关系是( ) A.点P 在⊙O 内 B .点P 在⊙O 上 C .点P 在⊙O 外D .不能确定3.同时抛掷两枚质地相同的硬币,落地后正面都朝上的概率是( ) A .1B .21 C .31 D .41 4.若反比例函数y =xk,当x >0时,y 随x 的增大而增大,则k 的取值范畴是( ) A. k <0B. k >0C .k ≤0D .k ≥05.在正方形网格中,∠AOB 的放置如图所示,则tan ∠AOB 的值是( ) A .55B .552 C .21 D .26.圆心角为120º的扇形的半径是3cm ,则那个扇形的面积是( ) A. 6πcm 2B 3πcm 2C .9πcm 2D .πcm27.如图,在ΔABC 中,AB =AC ,∠A =36ºBD 平分∠ABC ,DE ∥BC ,则图中与ΔABC 相似的三角形(不包括ΔABC )的个数有( ) A. 0个 B .1个C .2个D .3个8.如图,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x ,且0<x 10,阴影部分的面积为y ,则能反映y 与x 之间函数关系的大致图象是( )第Ⅱ卷 (非机读卷 共88分)二、填空题(共4道小题,每小题4分,共16分)9.两个相似三角形对应边的比是3:2,那么这两个相似三角形面积的比是__________________.10.如图,有一圆形展厅,在其圆形边缘上的点A 处安装了一台监视器,它的监控角度是65º.为了监控整个展厅,最少需在圆形边缘上安装如此的监视器共______________台.11.将抛物线y =x 2+3向右平移2个单位后,所得抛物线的顶点坐标是________________.12.如图,抛物线y =ax 2+bx +c 的对称轴是x =-1.若点(-21,y 1)、(2,y 2)是抛物线上两点,试比较y 1与y 2的大小:y 1_________y 2(填“>”,“<”或“=”号).三、解答题(共3道小题,共15分) 13.(本小题满分5分)运算:3tan30º-sin60º+2cos45º. 解:14.(本小题满分5分) 已知:反比例函数y =xk的图象通过点(2,3),求当x =4时,y 的值. 解:15.(本小题满分5分)已知:抛物线通过点A (-1,7)、B (2,1)和点C (0,1).(1)求这条抛物线的解析式; (2)求该抛物线的顶点坐标.解:四、解答题(共3道小题,共15分) 16.(本小题满分5分)如图,梯形ABCD 中,AB ∥CD ,F 是DC 的中点,BF 的延长线交射线AD 于点G ,BG 交AC 于点E . 求证:BEFEGB GF证明:17.(本小题满分5分)已知:如图,在△ABC 中,∠A =120º,AB =AC =6,求BC 的长.解:18.(本小题满分5分)已知:如图,在⊙O 中,直径AB 的长为10,弦AC 的长为6,∠ACB 的平分线交⊙O 于点D ,求BC 和BD 的长.解:五、解答题(共2道小题,共10分) 19.(本小题满分5分)在数学活动课上,九年级(1)班数学爱好小组的同学们测量校园内一棵大树的高度, 设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35º;(2)在点A和大树之间选择一点B(A、B、D在同一直线上),测得由点B看大树顶端C的仰角为45º;(3)量得A、B两点间的距离为4.5米.请你依照以上数据求出大树CD的高度.(可能用到的参考数据:sin35º≈0.57,cos35º≈0.82,tan35º≈0.70)解:20.(本小题满分5分)A口袋中装有2个小球,它们分别标有数字1和2;B口袋中装有3个小球,它们分别标有数字3、4和5.每个小球除数字外都相同.甲、乙两人玩游戏,从A、B两个口袋中随机各取出1个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.那个游戏对甲、乙双方公平吗?请说明理由.解:六、解答题(共2道小题,共11分)21.(本小题满分5分)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.解:22.(本小题满分6分)如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且AB2=AP·AD.(1)求证:AB=AC;(2)假如∠ABC=60º,⊙O的半径为1,且P为弧AC的中点,求AD的长.解:七、解答题(本题满分6分) 23.如图,二次函数y =41x 2+(4m+l )x +m (m <4)的图象与x 轴相交于A 、B 两点. (1)求A 、B 两点的坐标(可用含字母m 的代数式表示); (2)假如那个二次函数的图象与反比例函数y =x9的图象相交于点C ,且∠BAC 的正弦值为53,求那个二次函数的解析式. 解:八、解答题(本题满分7分)24.如图,点P 是边长为3的正方形ABCD 内一点,且PB =2,BF ⊥BP ,垂足为B .请在射线BF 上确定点M ,使以点B 、M 、C 为顶点的三角形与△ABP 相似,并证明你的结论. 解:九、解答题(本题满分8分)25.已知抛物线y =ax 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB 、OC 的长(OB <OC )是方程x 2-10x +16=0的两个根,且抛物线的对称轴是直线x =-2. (1)求此抛物线的解析式;(2)联结AC 、BC .若点E 是线段AB 上的一个动点(与点A 、点B 不重合),过点E 作EF ∥AC 交BC 于点F ,联结CE ,设AE 的长为m ,△CEF 的面积为s ,求s 与m 之间 的函数关系式,并写出自变量m 的取值范畴;(3)在(2)的基础上试说明s 是否存在最大值,若存在,要求出s 的最大值,并求出现在点E 的坐标,判定现在△BCE 的形状;若不存在.请说明理由. 解:北京市丰台区2008—2009学年度第一学期初三数学期末试卷参考答案及评分标准一、选择题(共8道小题,每小题4分,共32分) 1.C2.A3.D4.A5. D6.B7.C8.B二、填空题(共4道小题,每小题4分,共16分) 9.9:4, 10.311.(2;3) 12.<.三、解答题(共3道小题,共15分) 13.(本小题满分5分) 解:3tan30º-sin60º+2cos45º=22223333⨯+-⨯……………………………………………………3分 =223+……………………………………………………………………5分 14.(本小题满分5分) 解:∵ 反比例函数y =xk的图象通过点(2,3), ∴2k=3,……………………………………………………2分 ∴ k =6. ………………………………………………………3分 ∴反比例函数解析式为:y =x6,……………………………………4分 当x=4时,y =23………………………………………………………5分 15.(本小题满分5分)解:(1)设所求抛物线解析式为y =ax 2+bx+c .依照题意,得⎪⎩⎪⎨⎧==++=+=11247c c b a c b a ……………………………………………………………1分解得,⎪⎩⎪⎨⎧=-==142c b a ……………………………………………………………2分所求抛物线解析式为1422+-=x x y ………………………………3分(2)12242=⨯--=-a b ,()12441244422-=⨯--⨯⨯=-a b ac因此该抛物线的顶点坐标是(1,-1)………………………………5分 四、解答题(共3道小题,共15分) 16.(本小题满分5分)证明:∵ AB ∥CD, ∴△GDF ∽△GAB ,△FCE ∽△BAE ,…………………2分∴AB DF GB GF =,ABCFBE FE =…………………………4分 ∵CF DF =,∴BEFEGB GF =………………………5分17.(本小题满分5分) 解:过点A 作AD ⊥BC 于D ;∵AB=AC ;∠BAC=120º ∴∠B=30º,…………………………………1分 ∴BC =2BD ,…………………………………………………………2分在Rt △ABD 中,∠ADB=90º,∠B=30º,AB =6,ABBDB =cos ,…………………………………………………………3分 ∴3323630cos =⨯=︒=AB BD ,……………………4分 36=BC ………………………………………………5分18.(本小题满分5分)解:∵AB 为直径,∴∠ACB=∠ADB=9O º,……………………2分在Rt △ACB 中,86102222=-=-=AC AB BC ……………………3分∵CD 平分∠ACB ,∴⋂AD =⋂BD ,∴AD=BD …………………4分 在等腰直角三角形ADB 中,25221045sin =⨯=︒⨯=AB BD ……………………5分 五、解答题(共2道小题,共10分) 19,(本小题满分5分〕解:在Rt △BCD 中,∵∠CBD =45º,∴∠BCD=45º, ∴CD=BD ………………………l 分设CD=BD =x ,∴AD =x+4.5………………2分在Rt △ACD 中,tan ∠CAD=ADCD, ∴tan35º=5.4+x x……………………………………4分解得:x ≈10.5因此大树的高约为10.5米…………………………………5分 20.(本小题满分5分)解:从A ,B 两个口袋中随机地各取出1个小球,两个小球上的数字之和的所有可能显现的 结果有6个:4,5,6,5,6, 7,……………………………………… 2分每个结果发生的可能性都相等,显现和为偶数的结果有3个;和为奇数的结果也有3个∴P (数字之和为偶数)=63=21,……………………………………… 3分 P(数字之和为奇数)=63=21……………………… 4分 因此那个游戏对甲、乙双方公平………………………………………5分 六、解答题(共2道小题,共11分) 21.(本小题满分5分)解:∵四边形OCDB 是平行四边形,点B 的坐标为(8,0),CD ∥OA ,CD=OB=8…………………………………………1分 过点M 作MF ⊥CD 于F ,则CF =21CD =4………………………………3分 过C 作CE ⊥OA 于E ,∵A (10,0),∴OA=10,OM =5∴OE=OM -ME=OM -CF=5-4=1 联结MC ,MC=21OA=5 ∴在R T △CMF 中,MF=3452222=-=-CF MC …………………………4分∴点C 的坐标为(1,3)…………………………………………………5分 22.(本小题满分6分) 解:(1)证明:联结BP∵AB 2=AP -AD ,∴ABADAP AB =∵∠BAD=∠PAB, ∴△ABD ∽△APB ………………2分 ∴∠ABC=∠APB, ∵∠ACB=∠APB,∴∠ABC=∠ACB, ∴AB-AC …………………………3分(2)由(1)知AB=AC, ∵∠ABC=60º, ∴△ABC 是等边三角形 ∴∠BAC=60º, ∵P 为弧AC 的中点, ∴∠ABP=∠PAC=21∠ABC=30º………………………………4分 ∴∠BAP=90º, ∴BP 是⊙0的直径,………………………………5分 ∴BP=2, ∴AP=21BP=1, 在RT △PAB 中,由勾股定理得 AB 2=BP 2-AP 2=3∴32==APAB AD …………………………………………………………6分 七、解答题(本题满分6分) 23.解:(1)解方程0)14(412=+++m x mx 得,,41-=x m x -=2 ∵m<4,∴A (-4,0),B (-m ,0)……………………………………2分 (2)过点C 作CD ⊥x 轴,垂足为D , ∵sin ∠BAC=53=AC CD , ∴ tan ∠BAC=43=AD CD 设CD =3k ,则AD =4k ,∵OA =4, ∴OD =4k -4, ∴C (4k -4,3k )∵点C 在反比例函数x y 9=的图象上,∴k k 3449=-解得,211=k (不合题意,舍去),232=k ,∴C (2,29)……………4分∵点C 在二次函数m x mx y +++=)14(412的图象上∴292)14(2412=+⨯++⨯m m ,∴m =1∴二次函数的解析式为145412++=x x y …………………………………………6分 八、解答题(本题满分7分)24.解法一:作∠BCM 1=∠BAP,CM 1交BF 于点M 1,作∠BC M 2=∠BPA, C M 2交BF 于点M 2,…………4分则△CB M 1∽△ABP, △M 2BC ∽△ABP ∵四边形ABCD 是正方形,∴∠ABC=90º, ∵BF ⊥BP, ∴∠PBF=90º,∴∠ABP=∠CB M 1,……………………………………5分 又∵∠BC M 1=∠BAP, ∴△CB M 1∽△ABP …………6分同理可证△M 2BC ∽△ABP ………………………………7分解法二:在射线BF 上截取线段B M 1=2,联结M 1C …………2分 在射线BF 上截取线段B M 2=29,联结M 2C …………4分 则△CB M 1∽△ABP ,△M 2BC ∽△ABP同解法一可证∠ABP=∠CB M 1 …………………………5分 ∵AB=BC=3, PB=B M 1=2, ∴△CB M 1≌△ABP∴△CB M 1∽△ABP …………………………………………6分∵AB=BC=3, PB=2, BM 2=29 ∴232=AB BM , 23=BP BC ∴BPBCAB BM =2,∴△M 2BC ∽△ABP ……………………7分 九、解答题(本题满分8分)25.解(1)解放程016102=+-x x 得,21=x ,82=x ∵点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,且OB<OC ∴点B 的坐标为(2,0),点C 的坐标为(0,8) 又∵抛物线c bx ax y ++=2的对称轴是直线2-=x∴由抛物线的对称性可得点A 的坐标为(-6,0)⎪⎪⎩⎪⎪⎨⎧-=-==++228024a bc c b a 解得, ⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=83832c b a ∴所求抛物线的解析式为:838322+--=x x y ………………………2分 (2)依题意,AE =m ,则BE =8-m∵OA=6, OC=8,∴AC=10∵EF ∥AC ∴△BEF ∽△BAC ∴AB BE AC EF = 即 8810m EF -=, ∴4540m EF -= 过点F 作FG ⊥AB ,垂足为G ,则sin ∠FEG=sin ∠CAB=54 ∴54=EF FG ∴m m FG --⨯=8454054 ∴)8)(8(218)8(21m m m S S S BFE BCE ---⨯-=-=∆∆∴m m S 4212+-=…………………………………………………………5分 自变量m 的取值范畴是0<m<8………………………………………………6分(3)存在。
