电路原理邱关源第九章详解
合集下载
电路原理经典版课件第九章.ppt
300I1
60
300
U 0 j300
60
U o
60 1 j
30
2450
求短路电流： ISC 60 100 0.600
Z eq
U 0 ISC
30
2450 50 0.6
2450
例3
用叠加定理计算电流
I2
已知 : U S 10045o V,
IS
Z1
Z2
III222"'
+
IS 40o A, Z1 Z3 5030o Ω,
Z3
- US
Z2 50 30o Ω .
(2) U S 单独作用(I S 开路) :
解
(1) I S 单独作用(U S 短路) :
I
''
2
US Z2 Z3
I
'
2
(R
jX ) I
Z
U I
R
jL
j1
C
R
jX
Z
Z— 复阻抗；R—电阻(阻抗的实部)；X—电抗(阻抗的虚部)；
|Z|—复阻抗的模； —阻抗角。
关系： 或
|Z
|
R2 X 2
X
φ arctg R
R=|Z|cos X=|Z|sin
Z U I
第9章 正弦稳态电路的分析
(Sinusoidal Steady-state Analysis )
邱关源电路教材重点分析兼复习纲要-武汉大学电路
第一章电路模型和电路定律，第二章电阻电路的等效变换，第三章电阻电路的一般分析，第四章电路定理。
这四章是电路理论的基础，全部都考，都要认真看，打好电路基础。
第一章1-2电流和电压的参考方向要注意哈，个人认为搞清楚方向是解电路最重要的一步了，老师出题，喜欢把教材上常规的一些方向标号给标反，这样子，很多式子就得自己重推，这也是考验你学习能力的方式，不是死学，比如变压器那章，方向如果标反，式子是怎样，需要自己推导一遍。
第二章都要认真看。
第三章3-1 电路的图。
图论是一门很重要的学科，电路的图要好好理解，因为写电路的矩阵方程是考试重点，也是送分题，而矩阵方程是以电路图论为基础的。
第四章4-7对偶原理。
自己看一下，懂得什么意思就行了。
其他小节都是重点，特别是特勒跟和互易。
这几年真题第一题都考这个知识点。
第五章含有运算放大器的电阻电路。
这个知识点是武大电路考试内容，一定要懂，虚短和虚断在题目中是怎么用的，多做几个这章的题就很清楚了。
5-2 比例电路的分析。
这一节真题其实不怎么常见，跟第三节应该是一个内容，还是好好看一下吧。
第六章储能元件。
亲，这是电路基础知识，老老实实认真看吧。
清楚C和L的能量计算哦。
第七章一阶电路和二阶电路的时域分析。
一阶电路的都是重点，二阶电路的时域分析，其实不怎么重要，建议前期看一下，从来没有出现过真性二阶电路让考生用时域法解的，当然不是不可以解，只是解微分方程有点坑爹，而且基本上大家都是要背下来那么多种情况的解。
所以，这章的课后习题中，二阶的题用时域解的就不用做了，一般后面考试都是用运算法解。
7-1 7-2 7-3 7-4 都是重点，每年都考。
好好看。
7-5,7-6，两节，看一下即可，其实也不难懂，只是很难记。
7-7，7-8很重要，主要就是涉及到阶跃和冲激两个函数的定义和应用，是重点。
7-9，卷积积分，这个方法很有用，也不难懂，不过我没看过也不会用也不会做，每次遇到题目都是死算，建议好好研究下卷积。
电路 第五版 课件 邱关源 罗先觉第九章-4
+
定义：
U _
S UI(Ψ u Ψ i ) UIφ Sφ UIcosφ jUIsin φ P jQ
也可表示为：
I* Z I I* ZI 2 (R jX)I 2 RI 2 jXI 2 S U
or
* * * * 2 * S UI U (UY ) U U Y U Y
3
co s φ1 0 . 9 φ1 25 . 84 o co s φ 2 0 . 95 φ 2 18 . 19
o
返 回
上 页
下 页
9.5
1. 复功率
I
负 载
复功率
* S U I 单 位 VA
和 I 来 计 算 功 率 ， 引 入 “ 复 功 率 ” 为 了 用 相 量U
（3）并联电容，提高功率因数 。
返 回 上 页 下 页
分析 +
I
R
C I
L I
C
1 2
U
_
特点：
I
U
IC
L
L I
并联电容后，原负载的电压和电流不变， 吸收的有功功率和无功功率不变，即：负载的 工作状态不变。但电路的功率因数提高了。
返 回 上 页 下 页
并联电容的确定：
第九章 正弦稳态电路IV 主讲：鲁俊超
作业：9-19、9-21
7. 功率因数的提高
功率因数低带来的问题：
①设备不能充分利用，电流到了额定值，但功率容 量还有；
P=UIcos=Scos
S 75kVA
负载
cos =1,
P=S=75kW
cos =0.7, P=0.7S=52.5kW
定义：
U _
S UI(Ψ u Ψ i ) UIφ Sφ UIcosφ jUIsin φ P jQ
也可表示为：
I* Z I I* ZI 2 (R jX)I 2 RI 2 jXI 2 S U
or
* * * * 2 * S UI U (UY ) U U Y U Y
3
co s φ1 0 . 9 φ1 25 . 84 o co s φ 2 0 . 95 φ 2 18 . 19
o
返 回
上 页
下 页
9.5
1. 复功率
I
负 载
复功率
* S U I 单 位 VA
和 I 来 计 算 功 率 ， 引 入 “ 复 功 率 ” 为 了 用 相 量U
（3）并联电容，提高功率因数 。
返 回 上 页 下 页
分析 +
I
R
C I
L I
C
1 2
U
_
特点：
I
U
IC
L
L I
并联电容后，原负载的电压和电流不变， 吸收的有功功率和无功功率不变，即：负载的 工作状态不变。但电路的功率因数提高了。
返 回 上 页 下 页
并联电容的确定：
第九章 正弦稳态电路IV 主讲：鲁俊超
作业：9-19、9-21
7. 功率因数的提高
功率因数低带来的问题：
①设备不能充分利用，电流到了额定值，但功率容 量还有；
P=UIcos=Scos
S 75kVA
负载
cos =1,
P=S=75kW
cos =0.7, P=0.7S=52.5kW
邱关源《电路》第五版 第九章 正弦稳态电路的分析
U Z R jX I
1 1 ( R jX ) Y Z R jX ( R jX )(R jX )
R X R jX 2 j 2 2 Geq jBeq 2 R X2 R X2 R X
§9-1 阻抗和导纳
例：设图示电路的阻抗为 1- j2，试求串联等效参 数和并联等效参数，并判断电路性质。
§9-2 相量图
【例2 】已知图中电压表V 、 V1 、 V2的读数分别为 100V、171V、240V，Z2=j60，求Z1。
V1
+
U
I
Z1
V V2
解： U 2 U12 U 22 2U1U 2 cos
20.58
Z2
90 69.42
U1 171 69.42 V
§9-1 阻抗和导纳
四、阻抗与导纳间的关系
I
U
N
I U Y Y y Z Z Z U I 1 1 Z Y 阻抗与导纳互为倒数 Y Z
Z
Geq jBeq
I
R
U
U
I
1 Y
Y
1 Z
模互为倒数
jX
Z y
阻抗角与导纳角差一负号
L
L
1 0 Z 0 u i同相，Z呈阻性。 C
§9-1 阻抗和导纳
2、 RLC并联电路的导纳
I
IR
U
R
jL
IL
IC
1 j C
1 1 I 1 j( BC BL ) Y j jC R L R U
G jB Y y
b
邱关源—电路—教学大纲—第九章-2
并联电容的作用：减小电流，提高功率因数 *感性负载吸收的无功功率一部分由电源提供，一部分由电容提供。
g g g
g
g
I1 cos ϕ1 I sin ϕ
g
I 1 的有功分量 I cos ϕ = I1 cos ϕ1 I 的有功分量
g
g
I 的无功分量
IC
ϕ ϕ1
IC I IC
g g
U
I 1 的无功分量
给定 P 1 、 cos ϕ1 ，要求将 cos ϕ1 提高 cos ϕ ，求 C＝？
: g ∗ g g g ∗ g
则 S = U I = U ∠ψ u ⋅ I ∠ − ψ i = UI ∠(ψ u − ψ i ) = S ∠ϕ Z
= S ⋅ cos ϕ Z + jS ⋅ sin ϕ Z = P + jQ (VA) S = U I = Z I I = ZI 2 = ( R + jX ) I 2 ∴ P = RI 2 = Re [ Z ] ⋅ I 2 Q = XI 2 = Im [ Z ] ⋅ I 2 S = U I = U (U Y ) = Y U U = (G − jB)U 2 P = GU 2 , Q = − BU 2
2. QR = 0, QL = UI , QC = −UI
0o < ϕ < 90o Q > 0 −90o < ϕ < 0o Q < 0
四．视在功率
吸收无功功率 发出无功功率
S @ UI ，反映电源设备的容量（可能输出的最大平均功率） ，量纲：伏安（VA） 。
P、Q 和 S 之间满足下列关系 即有
S 2＝P 2+Q 2
g
I1 sin ϕ1
I1
g g g
g
g
I1 cos ϕ1 I sin ϕ
g
I 1 的有功分量 I cos ϕ = I1 cos ϕ1 I 的有功分量
g
g
I 的无功分量
IC
ϕ ϕ1
IC I IC
g g
U
I 1 的无功分量
给定 P 1 、 cos ϕ1 ，要求将 cos ϕ1 提高 cos ϕ ，求 C＝？
: g ∗ g g g ∗ g
则 S = U I = U ∠ψ u ⋅ I ∠ − ψ i = UI ∠(ψ u − ψ i ) = S ∠ϕ Z
= S ⋅ cos ϕ Z + jS ⋅ sin ϕ Z = P + jQ (VA) S = U I = Z I I = ZI 2 = ( R + jX ) I 2 ∴ P = RI 2 = Re [ Z ] ⋅ I 2 Q = XI 2 = Im [ Z ] ⋅ I 2 S = U I = U (U Y ) = Y U U = (G − jB)U 2 P = GU 2 , Q = − BU 2
2. QR = 0, QL = UI , QC = −UI
0o < ϕ < 90o Q > 0 −90o < ϕ < 0o Q < 0
四．视在功率
吸收无功功率 发出无功功率
S @ UI ，反映电源设备的容量（可能输出的最大平均功率） ，量纲：伏安（VA） 。
P、Q 和 S 之间满足下列关系 即有
S 2＝P 2+Q 2
g
I1 sin ϕ1
I1
电路邱关源第三版第九章
+ +
U1
1 jω C
Us U S U1 U 2 200 V U S、U1、U 2 三个相量构成一个等边三角形。 U S 200 60 V U 2 200 0 V， 1 200 120 V U
+
U2
-
(U 2 ) U1
作出相量模型电路图后，仿照直流电路进行分析。 2. 仿直分析：
二、相量图解法：
1. 参考相量的选取原则： 串联： 选电流相量； 并联： 选电压相量。 2. 应非常熟悉单个元件上或一条支路上电压、电流在相位和 幅度上的关系。 直角三角形； 3. 数学工具： 一般三角形：余弦、正弦定理等。
8
例 列图示电路的结点电压方程。
Z3
I3
解： 以结点2为参考结点。
U 结点1： n1 U S 2
1
+
2
U S 3_
3 Z4
+
Z1
_
US2
I 3
4
Z5
结点3： Y3U n1 (Y3 Y4 Y5 )U n3 Y5U n 4 Y3U S 3 结点4： Y1U n1 Y5U n 3 (Y1 Y5 )U n 4 I 3 另有： 3 Y3 (U n1 U S 3 U n 3 ) I
即虚部为零，故 I 与 U S 同相。
+ I
1 j C
I1
j L
IC
令 U S 380 0 V 则 I 2.590 A， I C jCU S j9.66 A
设 I1 I1 1A， 则由KCL有： .590 j9.66 I1 1， 2 9.66 2 2 10 A I1 1 2.590 j9.66 2.59 9.66 arctan 2.59 ∴A1读数为10A。 12
《电路原理》第五版_邱关源_9.8串联电路的谐振、9.9
R,L,C 电路
U Z R I
发生 谐振
2.
串联谐振的条件
+
I
R j L
1 j C
Z R j(ωL 1 ) R j( X L X C ) ωC R jX
U _
当 X 0
ω0
f0
ω 0L 1 0C
时，电路发生谐振。
谐振条件
1 LC
L (b) 电流一定时，总电压达最大值： U 0 I 0 Z I 0 RC
(c) 支路电流是总电流的Q倍，设R<<L
R (ω0 L) (ω0 L) Z (ω0 ) R0 L R RC R
2 2 2
U I L IC U 0C 0 L U / 0 L 0 L I L IC 1 Q I 0 I 0 U /( RC / L) 0 RC R
9.8
串联电路的谐振
谐振(resonance)是正弦电路在特定条件下所产生的一种 特殊物理现象，谐振现象在无线电和电工技术中得到广泛应 用，对电路中谐振现象的研究有重要的实际意义。
1. 谐振的定义
含有R、L、C的一端口电路，在特定条件下出现端口 电压、电流同相位的现象时，称电路发生了谐振。
I
U
1 1 L Q R 0CR R C
0 L
品质因数 quality factor
当 Q>1时， UL= UC >U; 当Q>>1 时，UL= UC >>U 。
(3) 谐振时的功率 P=UIcos＝UI＝RI02=U2/R，
电源向电路输送电阻消耗的功率，电阻功率达最大。
U Z R I
发生 谐振
2.
串联谐振的条件
+
I
R j L
1 j C
Z R j(ωL 1 ) R j( X L X C ) ωC R jX
U _
当 X 0
ω0
f0
ω 0L 1 0C
时，电路发生谐振。
谐振条件
1 LC
L (b) 电流一定时，总电压达最大值： U 0 I 0 Z I 0 RC
(c) 支路电流是总电流的Q倍，设R<<L
R (ω0 L) (ω0 L) Z (ω0 ) R0 L R RC R
2 2 2
U I L IC U 0C 0 L U / 0 L 0 L I L IC 1 Q I 0 I 0 U /( RC / L) 0 RC R
9.8
串联电路的谐振
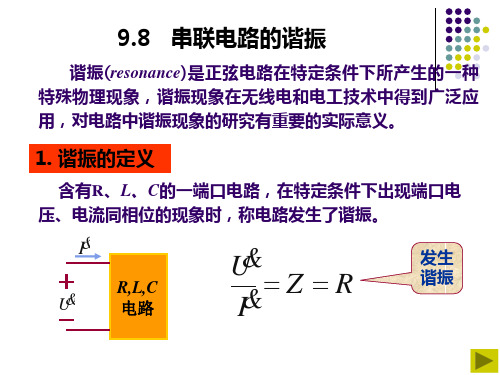
谐振(resonance)是正弦电路在特定条件下所产生的一种 特殊物理现象，谐振现象在无线电和电工技术中得到广泛应 用，对电路中谐振现象的研究有重要的实际意义。
1. 谐振的定义
含有R、L、C的一端口电路，在特定条件下出现端口 电压、电流同相位的现象时，称电路发生了谐振。
I
U
1 1 L Q R 0CR R C
0 L
品质因数 quality factor
当 Q>1时， UL= UC >U; 当Q>>1 时，UL= UC >>U 。
(3) 谐振时的功率 P=UIcos＝UI＝RI02=U2/R，
电源向电路输送电阻消耗的功率，电阻功率达最大。
邱关源《电路》第九章正弦稳态电路的分析1
BUCT
设备额定容量SN向负载送多少有功功率要由负载的阻抗角决定。
cosj = P/S
SN
负载 cosj = 1, P =S=75kW
75kVA
cosj = 0.7, P=0.7S=52.5kW
功率因数低带来的问题：
S
j2
Q2
(1) 设备不能充分利用，效率低； P2
S
j1
Q1
P1
(2) 当输出相同的有功功率时，线路上电流大 I=P/(Ucosj )，线路压降损耗大。
反映电气设备（如：发电机、变压器等）的容量。
BUCT
功率、电压、阻抗三角形
S
•
U
•
Q
Z
j
UX X
阻抗三角形 R
•
UR
电压三角形
P
功率三角形
S = P2 + Q2
+
U
R
_
º+ R +
U_
U_X
jX
º
9
交流电路功率的测量
i
*
W
*
+ u
Z
i1
-
i2 电压线圈
R 电流线圈
W1
A1
V1
*
* * 0.75A 3A 125V 500V 1.5A自动 250V U V W N
第九章 正弦稳态电路的分析
BUCT
9. 1 阻抗和导纳 9. 2 阻抗（导纳）的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
邱关源《电路》(第5版)笔记和课后习题(含考研真题)详解
1-5 试求图1-14中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
解： （1）图1-14(a)所示 电压源u、i参考方向非关联，发出功率：
电阻元件吸收功率：
电流源u、i参考方向关联，吸收功率：
图1-14
（2）图1-14(b)所示
电阻元件吸收功率：
电流源u、i参考方向非关联，发出功率： 电压源u、i参考方向非关联，发出功率：
目 录
8.2 课后习题详解 8.3 名校考研真题详解 第9章 正弦稳态电路的分析 9.1 复习笔记 9.2 课后习题详解 9.3 名校考研真题详解 第10章 含有耦合电感的电路 10.1 复习笔记 10.2 课后习题详解 10.3 名校考研真题详解 第11章 电路的频率响应 11.1 复习笔记 11.2 课后习题详解 11.3 名校考研真题详解 第12章 三相电路 12.1 复习笔记 12.2 课后习题详解 12.3 名校考研真题详解 第13章 非正弦周期电流电路和信号的频谱 13.1 复习笔记 13.2 课后习题详解 13.3 名校考研真题详解 第14章 线性动态电路的复频域分析 14.1 复习笔记 14.2 课后习题详解 14.3 名校考研真题详解 第15章 电路方程的矩阵形式 15.1 复习笔记 15.2 课后习题详解 15.3 名校考研真题详解 第16章 二端口网络 16.1 复习笔记
图1-11
解： 根据关联参考方向、功率吸收和发出的相关概念可得：
图1-11(a)，对于NA ，u、i的参考方向非关联，乘积ui对NA 意味着发出功率；对于NB ，u，i的参考方向关 联，乘积ui对NB 意味着吸收功率。
图1-11(b)，对于NA ，u、i的参考方向关联，乘积ui对NA 意味着吸收功率；对于NB ，u，i的参考方向关 联，乘积ui对NB 意味着发出功率。
解： （1）图1-14(a)所示 电压源u、i参考方向非关联，发出功率：
电阻元件吸收功率：
电流源u、i参考方向关联，吸收功率：
图1-14
（2）图1-14(b)所示
电阻元件吸收功率：
电流源u、i参考方向非关联，发出功率： 电压源u、i参考方向非关联，发出功率：
目 录
8.2 课后习题详解 8.3 名校考研真题详解 第9章 正弦稳态电路的分析 9.1 复习笔记 9.2 课后习题详解 9.3 名校考研真题详解 第10章 含有耦合电感的电路 10.1 复习笔记 10.2 课后习题详解 10.3 名校考研真题详解 第11章 电路的频率响应 11.1 复习笔记 11.2 课后习题详解 11.3 名校考研真题详解 第12章 三相电路 12.1 复习笔记 12.2 课后习题详解 12.3 名校考研真题详解 第13章 非正弦周期电流电路和信号的频谱 13.1 复习笔记 13.2 课后习题详解 13.3 名校考研真题详解 第14章 线性动态电路的复频域分析 14.1 复习笔记 14.2 课后习题详解 14.3 名校考研真题详解 第15章 电路方程的矩阵形式 15.1 复习笔记 15.2 课后习题详解 15.3 名校考研真题详解 第16章 二端口网络 16.1 复习笔记
图1-11
解： 根据关联参考方向、功率吸收和发出的相关概念可得：
图1-11(a)，对于NA ，u、i的参考方向非关联，乘积ui对NA 意味着发出功率；对于NB ，u，i的参考方向关 联，乘积ui对NB 意味着吸收功率。
图1-11(b)，对于NA ，u、i的参考方向关联，乘积ui对NA 意味着吸收功率；对于NB ，u，i的参考方向关 联，乘积ui对NB 意味着发出功率。
《电路》课件 第五版 原著：邱关源 修订：罗先觉 (内蒙古工业大学用) 第九章
39.45∠ − 40.5 = 10.89 + j 2.86
∴ Z ab = Z 3 + Z = 15 + j15.7 + 10.89 + j 2.86 = 25.89 + j18.56 = 31.9∠ 35.6 o Ω
§９－２电路相量图 1. 同频率的正弦量才能表示在同一个相量图中； 同频率的正弦量才能表示在同一个相量图中； 2. 以ω 角速度反时针方向旋转； 角速度反时针方向旋转； 3. 选定一个参考相量 设初相位为零。) 选定一个参考相量(设初相位为零。 设初相位为零 • 例 ： 选 ÙR为参考相量 IC • • UL jω L I
• I 1 = 0.570 ∠70.1 ° A
• I3 =
R1 R1 − j 1 ωC
i1 = 0.598 2 sin( 314 t + 52.3° ) A i2 = 0.182 2 sin( 314t − 20°) A i 3 = 0.57 2 sin( 314 t + 70°) A
例题2:电路如图所示， 例题 电路如图所示，求 Zab 。 电路如图所示 10Ω aº Zab bº 4Ω · I1 + • 12I1 • I aº + • U 10Ω 4Ω · I1 + • 12I1
电导 电纳
设： = G − jB =| Y |∠-ϕ Y
I 导纳的模 单位：S 单位： Y = U ϕ ′ = ψ i −ψ u 导纳角
|Y| ϕ G
导纳三角形
B
R-L-C 并联电路稳态分析：（根据对偶性） 并联电路稳态分析：（根据对偶性） ：（根据对偶性 Y=G-j(ΒL-BC)=|Y|∠- ϕ 90°） （- 90º < ϕ < 90°）
∴ Z ab = Z 3 + Z = 15 + j15.7 + 10.89 + j 2.86 = 25.89 + j18.56 = 31.9∠ 35.6 o Ω
§９－２电路相量图 1. 同频率的正弦量才能表示在同一个相量图中； 同频率的正弦量才能表示在同一个相量图中； 2. 以ω 角速度反时针方向旋转； 角速度反时针方向旋转； 3. 选定一个参考相量 设初相位为零。) 选定一个参考相量(设初相位为零。 设初相位为零 • 例 ： 选 ÙR为参考相量 IC • • UL jω L I
• I 1 = 0.570 ∠70.1 ° A
• I3 =
R1 R1 − j 1 ωC
i1 = 0.598 2 sin( 314 t + 52.3° ) A i2 = 0.182 2 sin( 314t − 20°) A i 3 = 0.57 2 sin( 314 t + 70°) A
例题2:电路如图所示， 例题 电路如图所示，求 Zab 。 电路如图所示 10Ω aº Zab bº 4Ω · I1 + • 12I1 • I aº + • U 10Ω 4Ω · I1 + • 12I1
电导 电纳
设： = G − jB =| Y |∠-ϕ Y
I 导纳的模 单位：S 单位： Y = U ϕ ′ = ψ i −ψ u 导纳角
|Y| ϕ G
导纳三角形
B
R-L-C 并联电路稳态分析：（根据对偶性） 并联电路稳态分析：（根据对偶性） ：（根据对偶性 Y=G-j(ΒL-BC)=|Y|∠- ϕ 90°） （- 90º < ϕ < 90°）
《电路》邱关源g(第五版)第9章解读
w L<1/w C ，X<0， j <0，电压落后电流j角，电路呈容性； w L=1/w C ，X=0， j =0，电压与电流同相，电路呈纯阻性；
画相量图：选电流为参考向量
阻抗三角形各边乘以电流 I = 电压三角形
U |Z| X UX j
R UR
则 U=
U
2 R
U
2 X
= UR2 （U L-UC）2
设参考相量。 串联电路设电流； 并联电路设电压； 混联电路设已知条件。
与电阻电路的分析方法、思路相同。 列相量等效电路的复数形式的代数方程。
需要时，将相量还原为正弦量。
例题1: 已知:R1 = 1000 , R2 = 10 , L = 500mH , C = 10mF ,
i1
i2 i3
= G jB
电导
电纳
Y = I 导纳的模 单位：S U
j = i u 导纳角
|Y| B
j
G
导纳三角形
R-L-C 并联电路稳态分析：（根据对偶性）
Y=G-j(BL-BC)=|Y|∠- j
（- 90º
）
BL > BC ，B>0， j >0，电压领先电流，电路呈感性；
BL < BC ，B<0， j <0，电压落后电流，电路呈容性； BL = BC ， B=0， j =0，电压与电流同相，电路呈纯阻性；
第九 章
《正弦交流电路的稳态分析》 重点
复阻抗、复导纳 电路的相量图 简单正弦交流电路的分析 复杂正弦交流电路的分析 正弦交流电路的功率及复功率
Heinrich Rudorf Hertz (1857-1894)： 赫兹
邱关源《电路》第五版第9章-正弦稳态电路分析
第9章 正弦稳态电路分析9-1 阻抗和导纳一．阻抗1． 定义：在正弦稳态无源二端网络端钮处的电压相量与电流相量之比定义为该二端网络的阻抗，记为Z ，注意：此时电压相量U 与电流相量I 的参考方向向内部关联。
uiU U ZI Iψψ∠=∠ （复数）阻抗()Ωz j Z R X ψ=∠=+其中 ()UZ I=Ω —阻抗Z 的模，即阻抗的值。
Z u i ϕψψ=- —阻抗Z 的阻抗角 z cos ()R Z ϕ=Ω —阻抗Z 的电阻分量 z sin ()X Z ϕ=Ω —阻抗Z 的电抗分量电阻元件的阻抗： 在电压和电流关联参考方向下电阻的伏安关系的相量形式为U U Z I=-RX|Z |Zϕ R UR IR I 与R U 共线阻抗三角形R R U R I =则 R R RU Z R I ==电感元件的阻抗： 在电压和电流关联参考方向下电感的伏安关系的相量形式为L L j U L I ω=则 L L L Lj j U Z L X I ω==电容的阻抗： 在电压和电流关联参考方向下电容的伏安关系的相量形式为jU1j- C UCC CC CC j 11j j I C U U I I C Cωωω===- 则 C C C C1jj U Z X C I ω=-= C 1X Cω=-—容抗 2. 欧姆定律的相量形式 U Z I = 电阻、电感、电容的串联阻抗：在电压和电流关联参考方向下，电阻、电感、电容的串联，得到等效阻抗eq ZR L C eq R L C1LC ZZ I Z I Z IU Z Z Z Z II R j L R jX jX R jX j C Z ωωϕ++===++=++=++=+=∠其中：阻抗Z 的模为 ||Z =阻抗角分别为 1/LCZX L C arctg arctgarctgRRRXXωωϕ+-===。
可见，电抗X 是角频率ω的函数。
当电抗X ＞0(ωL ＞1/ωC )时，阻抗角φZ ＞0，阻抗Z 呈感性； 当电抗X ＜0(ωL ＜1/ωC ＝时，阻抗角φZ ＜0，阻抗Z 呈容性； 当电抗X ＝0(ωL ＝1/ωC )时，阻抗角φZ ＝0，阻抗Z 呈阻性。
《电路》第五版 邱关源罗先觉第九章(谐振)
R 2 (ω0 L) 2 Z (ω0 ) R0 L R RC
谐振(resonance)是正弦电路在特定条件下所产生的一种 特殊物理现象，作为电路计算没有新内容，主要分析谐振电 路的特点。
9. 7 串联电路的谐振
一、 谐振的定义 I R +
j L
1 jω C
U _
Z R j(ωL 1 ) R jX Z| φ | ωC 1 当ωL , 即 X 0 感性 ωC
1 当ωL , ωC 即 X0 容性
谐振： 当满足一定条件(对RLC串联电路，使 L=1/ C)， 电路 中电压、电流同相，电路的这种状态称为谐振。
串联谐振：ω 0 L 1 0C
ω0 f0 1 LC 1 2π LC
谐振角频率 (resonant angular frequency) 谐振频率 (resonant frequency)
通常收音机选台，即选择不同频率的信号，就采用改变C 使电路达到谐振。
三、RLC串联电路谐振时的特点
1. U 与 I 同相 .
2. 入端阻抗Z为纯电阻，即Z=R。电路中阻抗值|Z|最小。
3. 电流I达到最大值I0=U/R (U一定)。 根据这个特征来判断电路 是否发生了串联谐振。 + I
O
0
T0 1 / f 0 2π LC 谐振周期 (resonant period)
二、使RLC串联电路发生谐振的条件 1. L C 不变，改变 。 0由电路本身的参数决定，一个 R L C 串联电路只能有一 个对应的0 , 当外加频率等于谐振频率时，电路发生谐振。
2. 电源频率不变，改变 L 或 C ( 常改变C )。
电路原理邱关源第九章详解
Z2 R2 jL 10 j157
Z Z1 Z2 92.11 j289.13 10 j157 102.11 j132.13 166.99 52.3
I1
+
I2 R1
I3
j1
C
R2
U Z1 _
Z2
jL
返回 上页 下页
I1
U Z
1000 166.99 52.3
0.652.3
A
U1 U o
Z1 Z2 Z2
1
Z1 Z2
jXC
－
＋
R
uo
－
Z1
R jX C
(R jX C )2
Z2 jRXC (R jX C )
jRXC
R2
X2 C
j2RXC
2
R2 j
X2 C
实数
jRXC
RXC
R XC
U1 U o
1 2 3
返回 上页 下页
9.3 正弦稳态电路的分析
电阻电路与正弦电流电路的分析比较：
,
φy φz
注意 一般情况G1/R ，B1/X。若Z为感
性，X>0，则 B<0，即仍为感性。
返回 上页 下页
同样，若由Y变为Z，则有：
Y G jB
R
Z
jX
Y G jB | Y | φy , Z R jX | Z | φz
Z
1 Y
1 G jB
G jB G2 B2
R
jX
R
G G2B2
,
X
B G2B2
正弦稳态电路的分析首页本章重点正弦稳态电路的分析93正弦稳态电路的功率94复功率95最大功率传输96阻抗和导纳9191阻抗和导纳阻抗正弦稳态情况下线性网络阻抗模阻抗角欧姆定律的相量形式rlc串联电路kvl
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
转换关系：
| Z | R2 X 2
φz
arctan
X R
或 R=|Z|cosz X=|Z|sinz
Z U I
z u i
阻抗三角形
|Z| X
z
R
返回 上页 下页
分析 R、L、C 串联电路得出：
（1）Z=R+j(L-1/C)=|Z|∠z 为复数，称复阻抗 （2）L > 1/C ，X>0， z>0，电路为感性，
分析 R、L、C 并联电路得出：
（1）Y=G+j(C-1/L)=|Y|∠y为复数，称复导纳； （2）C >1/L，B>0，y>0，电路为容性，
电流超前电压。
相量图：选电压为参考向量， u 0
..
I
y
IL IC
I
I2 G
I2 B
I2 G
(IC
IL )2
IBU
.
注意
IG
RLC并联电路会出现分电流大于总电流的现象
33.5463.4o Ω
返回 上页 下页
I U 560o 0.149 3.4o A Z 33.5463.4o
U R R I 15 0.149 3.4o 2.235 3.4o V
U L jLI 56.590o 0.149 3.4o 8.4286.4o V
U C j 1 I 26.5 90o 0.149 3.4o 3.95 93.4o V
1
j L
j BL
Y
I U
j C
jBC
表明 Y 可以是实数，也可以是虚数。
返回 上页 下页
4. RLC并联电路
i
+
iR iL iC
uR L C
-
I
+
U R -
IR IL IC
jL 1 jC
由KCL：I
IR
IL
IC
GU
j 1 U
L
jCU
(G
j1
L
jC)U [G
j( BL
BC )U
(G
jB)U
C 则 i 0.149 2cos(ωt 3.4o ) A
uR 2.235 2cos(ω t 3.4o ) V uL 8.42 2cos(ω t 86.6o ) V uC 3.95 2cos(ω t 93.4o ) V
返回 上页 下页
相量图
注意
UC U L
U
-3.4°
U R I
UL=8.42>U=5，分电压大于总电压。
电路原理邱关源第九章ppt课件
重点： 1. 阻抗和导纳； 2. 正弦稳态电路的分析； 3. 正弦稳态电路的功率分析；
返回
9.1 阻抗和导纳
1. 阻抗 正弦稳态情况下
I
+
U I
无源 线性
-
网络
+
U
Z
-
Z
def
U I
| Z
| φz
欧姆定律的相 量形式
Z U
阻抗模
I
z u i 阻抗角
返回 上页 下页
Y
I U
G
jC
j1
L
G
jB
Y
y
返回 上页 下页
Y—复导纳；|Y| —复导纳的模；y—导纳角；
G —电导(导纳的实部)；B —电纳(导纳的虚部)；
转换关系：
|Y |
G2 B2
φy
arctan
B G
或 G=|Y|cos y B=|Y|sin y
YI U
y i uຫໍສະໝຸດ 导纳三角形|Y| B
y
G
返回 上页 下页
U2 R
U
2 X
U2 R
(UC
U L )2
I + U R -
U
UC
L
等效电路
+
.
U
-
R
+
1 U X
jCeq -
（UU4CL）电L压=U1与/R电C流，同XI=相0等。，效电z=路0，电+-路U为电I阻R 性-U+， R
返回 上页 下页
例 已知：R=15, L=0.3mH, C=0.2F,
u 5 2cos(t 60 ), f 3104 Hz .
电压超前电流。
相量图：一般选电流为参考向量， i 0
电压
三角 形
U
z
U L U
U C
U2 R
U
2 X
U2 R
(UL
UC
)2
+ U R -
UX 等效电路 +
UR I
-
R
+ U-X
j Leq
返回 上页 下页
（3）L<1/C， X<0， z <0，电路为容性，
电压落后电流。 U
z
U
U R UX I
,
φy φz
注意 一般情况G1/R ，B1/X。若Z为感
性，X>0，则 B<0，即仍为感性。
返回 上页 下页
同样，若由Y变为Z，则有：
Y G jB
R
Z
jX
返回 上页 下页
等效电路
+ I
U R -
IR
1
IB
jCeq
（3）C<1/L，B<0，y<0，电路为感性，
电流落后电压；
y
.
IG
U
I .
I
I2 G
I2 B
I2 G
(IL
IC )2
IC
.
IL
返回 上页 下页
等效电路
I
+ U R -
IR
IB
j Leg
（4）C=1/L，B=0， y =0，电路为电阻性，
返回 上页 下页
3.导纳 正弦稳态情况下
I
+
U I
无源 线性
-
网络
+
U
Y
-
定义导纳
I Y U | Y | φy S
YI U
导纳模
y i u 导纳角
返回 上页 下页
对同一二端网络:
Z 1 ,Y 1
Y
Z
当无源网络内为单个元件时有：
I
I
I
+
+
U -
R U
-
L
+ U
-
C
Y
I U
1 R
G
Y
I U
1
-
I jC
+.
-U C
KVL：
.
U
.
UR
[R j(L 1 C
.
U
)] I
.
.
.
L UC R I jL I j
[R j( X L XC )]I
1
.
I
C
(R
jX
)
I
Z
U I
R
jL
j1
C
R
jX
Z
z
返回 上页 下页
Z — 复阻抗；|Z| —复阻抗的模；z —阻抗角； R —
电阻(阻抗的实部)；X—电抗(阻抗的虚部)。
求 i, uR , uL , uC .
解 画出相量模型
U 560 V
jL j2π 3104 0.3103
RR jLL
++ Uu--
++UuRR --
i.
I
++ UuLL --
1C jC
--U++u. CC
j56.5Ω
j 1 j
1
j26.5Ω
C 2π 3104 0.2 106
Z R jL j 1 15 j56.5 j26.5 C
电流与电压同相。
IC
IL
I IG U 等效电路 +-U
I
R
U+
-
R
返回 上页 下页
5. 复阻抗和复导纳的等效互换
R
Z
jX
Y G jB
Z R jX | Z | φz Y G jB | Y | φy
Y
1 Z
1 R jX
R jX R2X 2
G
jB
G
R R2 X
2
,
B
X R2 X
2
1
| Y | |Z|
当无源网络内为单个元件时有：
I
I
I
+ U -
+ R U
-
+
C U
-
L
Z
U I
R
Z
U I
j 1
C
jX C
Z
U I
j
L
jX L
表明 Z 可以是实数，也可以是虚数。
返回 上页 下页
2. RLC串联电路
R
L
+ + uR - + uL - +
u -
i
C uC -
R j L
+ U
+U R -
.
+ U L -