差微分方程 数学建模经典案例
微分方程中的数学建模实例分析

微分方程中的数学建模实例分析作者:邹佩来源:《科技风》2024年第05期摘要:传统高等数学教学有较好的基础,但是由于教学手段单一,教学内容单调枯燥,学生很难将所学知识应用于实践。
数学建模将实际问题经过分析、抽象、通过合理假设、化简,变化成一个数学问题,再通过数值分析方法求解问题,最后将结果应用于实践。
本文旨在通过多个微分方程模型实例,探讨将数学建模思想和建模方法渗透和融入高等数学课程的教学中,培养和提高学生应用随机数学的思想方法建模、解决实际问题的实践、应用能力。
关键词:数学建模;微分方程;分離变量法;齐次方程微积分是高等数学教学内容中非常重要的一部分,它以极限思想为基础来研究实数函数。
微分方程模型描述的是动态系统,需要通过随时间或空间的演变过程,分析动态对象的变化规律、研究变化特性、预测其未来发展性。
这个过程就需要确定函数和其导数之间的关系,根据建模目的和问题分析作出简化假设,按照内在规律建立微分方程,最终通过对微分方程的求解来指导实践。
一、数学建模实例选择标准高等数学中很多问题和数学建模思想相关,而渗透建模思想的主要途径就是联系实际。
于是选择教学案例时要注意以下几点。
首先,数学建模的实例要简单易懂,学生要能直观感受其中的数学关系,否则会过多占用学生思考时间,影响后续教学进度;其次,案例密切联系实际,既有助于教学内容的理解,又通过对问题的分析,抽象能用学过的知识解决问题;再次,案例要与高等数学的知识范围相关,如果案例中数学知识超出课程大纲范畴,学生难以理解,教学效果得不到保证,而所用知识太简单,又不足以帮助学生深入理解数学建模过程,达不到教学目的;最后,建模案例应具备一定科学性,所选的案例要符合客观事件发展规律,有较严谨的逻辑关系。
二、微分模型实例分析建立微分模型的关键词是“瞬时变化率”,而在实际中应用的表述变化的词有物理学中的速度、经济学中增长率、边际利润等,并且注意对象描述中的绝对增加率和相对增加率的计算。
数学建模差分方程PPT课件

的方程都是差分方程。 方程中所含未知函数角标的最大值与最小值的差数称为差分
方程的阶。 若一个函数代入差分方程后,方程两端恒等,则称此函数为
差分方程的解。如果解中所含相互独立的任意常数的个数等于方 程的阶数,则称该解为差分方程的通解。满足初始条件的解称为 特解。
• 第一阶段: w(k)每周减1千克, c(k)减至下限10000千卡
w (k)w (k1)1 w ( k 1 ) w ( k ) c ( k 1 ) w ( k )
c(k1) 1[w(k)1] w (k)w (0)k
c(k1) w (0) 1(1k)
1 8000
0.025
120 200 k 00Cm 10000 k 10
2 x k 2 x k 1 x k 2 ( 1 ) x 0 , k 1 , 2 ,
二阶线性常系数差分方程
x0为平衡点 研究平衡点稳定,即k, xkx0的条件
模型的推广 2 x k 2 x k 1 x k 2 ( 1 ) x 0
方程通解
xk
c1
k 1
c2
k 2
(c1, c2由初始条件确定)
相当于70千克的人每天消耗2000千卡 ~ 3200千卡;
3)运动引起的体重减少正比于体重,且与运动 形式有关;
4)为了安全与健康,每周体重减少不宜超过1.5 千克,每周吸收热量不要小于10000千卡。
减肥计划
某甲体重100千克,目前每周吸收20000千卡热量, 体重维持不变。现欲减肥至75千克。
1 2 k 是(3)的 k 重根,则只要将 Y1 (i),Y2 (i),,Yk (i) 换为
数学建模实验二:微分方程与差分方程模型Matlab求解
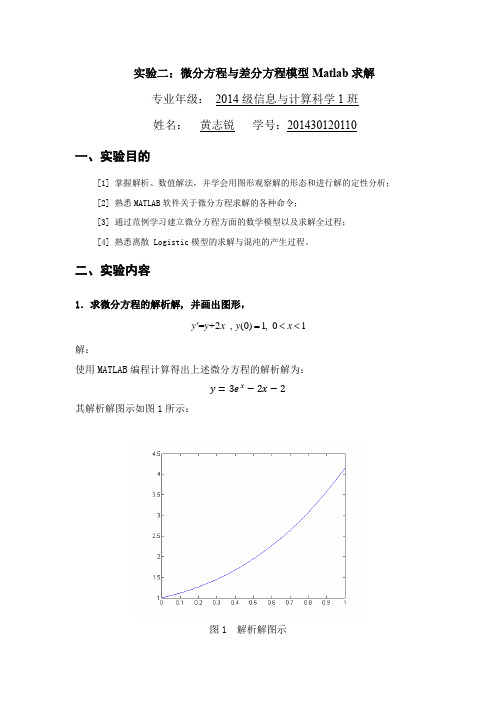
实验二:微分方程与差分方程模型Matlab 求解专业年级: 2014级信息与计算科学1班 姓名: 黄志锐 学号:201430120110一、实验目的[1] 掌握解析、数值解法,并学会用图形观察解的形态和进行解的定性分析; [2] 熟悉MATLAB 软件关于微分方程求解的各种命令;[3] 通过范例学习建立微分方程方面的数学模型以及求解全过程; [4] 熟悉离散 Logistic 模型的求解与混沌的产生过程。
二、实验内容1.求微分方程的解析解, 并画出图形,解:使用MATLAB 编程计算得出上述微分方程的解析解为:y =3e x −2x −2其解析解图示如图1所示:图1 解析解图示=+2,(0)1,01y y x y x '=<<MATLAB代码运行结果截图如下所示:2.求微分方程的数值解, 并画出图形,解:使用MATLAB编程计算上述微分方程的数值解,并作出其数值解的图示如图2所示:图2 数值解图示cos0,(0)1,(0)0y y x y y'''+===3.两种相似的群体之间为了争夺有限的同一种食物来源和生活空间而进行生存竞争时,往往是竞争力较弱的种群灭亡,而竞争力较强的种群达到环境容许的最大数量。
假设有甲、乙两个生物种群,当它们各自生存于一个自然环境中,均服从 Logistic 规律。
(1)是两个种群的数量; (2)是它们的固有增长率; (3)是它们的最大容量;(4)为种群乙(甲)占据甲(乙)的位置的数量,并且建立模型如下:)(),(21t x t x 21,r r 21,n n )(12m m .1122;x m x m βα==计算, 画出图形及相轨线图。
解释其解变化过程。
2)121,r r ==设12100,n n ==102010x x ==,=1.5,=0.7,计算, 画出图形及相轨线图。
解释其解变化过程。
解:(1)使用MATLAB 编程实现上述模型,并输入相关参数后,计算得出, 并画出图形及相轨线图如下所示:图3 数值解图示)(),(21t x t x αβ)(),(21t x t x )(),(21t x tx图4 相轨线图详细MATLAB代码如下:由图3、图4可以看出,甲、乙两个生物种群以几乎一致的趋势不断增长,直到达到一个相对稳定的数量。
微分方程模型-伪造名画案

知识回顾 Knowledge Review
祝您成功!
设 t 时刻的原子数为N (t) ,则有
dN N
dt
为物质的衰变常数。
初始条件
N t t0
N0
N (t)
N e (tt0 ) 0
t
t0
1
ln
N0 N
t
t0
1
ln
N0 N
半衰期 T 1 ln 2
碳-14 T 5568 年
镭-226
T 1600 年
铀-238 T 45亿年 铅-210 T 22年
微分方程建模案例—— 范. 梅格伦伪造名画案
第二次世界大战比利时解放后,荷兰保安机关开始搜 捕纳粹分子的合作者,发现一名三流画家H.A.Vanmeegren 曾将17世纪荷兰著名画家Jan.Vermeer的一批名贵油画盗卖 给德寇,于1945年5月29日通敌罪逮捕了此人。
Vanmeegren被捕后宣称他从未出卖过荷兰的利益,所 有的油画都是自己伪造的,为了证实这一切,在狱中开始 伪造Vermeer的画《耶稣在学者中间》。当他的工作快完成 时,又获悉他可能以伪造罪被判刑,于是拒绝将画老化, 以免留下罪证。
但是,许多人还是不相信其余的名画是伪造的,因为, Vanmeegren在狱中作的画实在是质量太差,所找理由都 不能使怀疑者满意。直到20年后,1967年,卡内基梅隆 大学的科学家们用微分方程模型解决了这一问题。
原理 著名物理学家卢瑟夫(Rutherford)指出:
物质的放射性正比于现存物质的原子数。
(2)钋的半衰期为138天容易测定,铅210的半 衰期为22年,对要鉴别的300多年的颜料来说, 每克白铅中每分钟钋的衰变数与铅210的衰变数 可视为相等。
微分方程建模案例

微分方程建模案例微分方程是数学中的一种重要工具,它被广泛应用于各个领域的建模和问题求解中。
下面将以一个具体的案例来介绍微分方程建模的过程,并通过求解微分方程来解决实际问题。
案例:生物种群的增长模型在生态学中,研究生物种群的增长是一个重要的课题。
种群的增长速度与种群中的个体数量有关。
如果种群中个体数量增加的速度与当前个体数量成正比,可以建立如下的微分方程模型:$$\frac{dN}{dt} = rN$$其中,$N$表示种群的个体数量,$t$表示时间,$r$表示增长的速率。
这个微分方程描述了种群个体数量随时间变化的规律。
解:首先,我们需要求解上述微分方程,得到种群个体数量随时间的函数关系。
这是一个一阶线性常微分方程,我们可以使用分离变量的方法求解。
将微分方程变形为:$$\frac{dN}{N} = rdt$$将方程两边同时积分,得到:$$\int \frac{dN}{N} = \int rdt$$经过积分运算,得到:$$\ln N = rt + C$$其中,$C$为积分常数。
进一步求解,得到:$$N = e^{rt + C}$$根据初始条件,当$t=0$时,$N=N_0$,其中$N_0$为初始种群个体数量。
代入初始条件,解得$C=\ln N_0$,将其代入上述方程,得到最终的解:$$N = N_0e^{rt}$$这个解描述了种群个体数量随时间的增长情况。
接下来,我们来解决一个具体的问题,一个兔子种群的增长情况。
假设初始时刻兔子种群中有100只兔子,增长速率$r=0.02$,那么该种群在未来的10个月内,兔子的数量会如何变化?根据上面的微分方程解,代入初始条件$N_0=100$,$r=0.02$,$t=10$,得到:$$N=100e^{0.02t}$$将$t=10$代入上述方程,可以得到10个月后兔子种群的个体数量:所以,10个月后的兔子种群中大约有122只兔子。
通过这个模型,我们可以预测种群在未来的增长情况,并在实践中应用于生态学、环境保护等领域,为实际问题的决策提供参考。
微分方程建模 个例

A1
C
C1
分析:1.追击开始后,大家将进入正方 A 形里面,距离将变小,由于追击的规则 及四个人速度和方向的假定,四人还是 在某个正方形的顶点上。 2.会不会出现四个人绕一个圆循环追? 不会!距离会不断缩小最后到一点,就 是正方形的中心。追击曲线是四条指向 D1 中心的螺旋线(可能绕中心几周) 3.坐标架怎么建? D O点在中心,直角坐标架。
2H g
2.二氧化碳的吸收
空气通过盛有CO2的吸收剂的圆柱形器皿,已知它吸收CO2的量与 CO2的浓度及吸收层的厚度成正比,今有含CO28%的空气通过厚度 为10cm的吸收层后浓度为2%,求: (1)若吸收层变为30cm厚,出口浓度是多少? (2)要使出口浓度为1%,应该设多厚的吸收层? 解: 记吸收层厚度为d,等分n份,每小层d/n厘米。入口浓 度为8%,在每小层看吸收量,第一层后被吸收量为: kd k8%d/n,含量变为: 8%(1)
v0t y x(0) 0 y , 就是曲线的切向量, 1 x y (0) 0
Q(1,v0t) 模型里y(t),x(t)都是t的函数,但是三个 变量不好处理,注意我们要求的是y(x)。 P(x,y) O 1 x
(1 x) y y v0t实现了变量t的分离
再建立一个y(t),x(t),t的关系:t时间里导弹已 飞行的距离是可求的。 x 1 y2 dx 5v0t (1 x) y y v0t , x0 0, y0 0
v r (0) 2 2 , (2r cos dx cos dr r sin d dx r sin cos d , , y r sin dy sin dr r cos d dy r cos sin dr d 1 sin cos dx dr r r cos r sin dy
数学建模中的微分方程与差分方程

微分方程和差分方程是数学建模中两个重要的工具,它们在描述和解决现实问题中起到了关键作用。
微分方程描述了变量之间的变化率关系,而差分方程描述了变量在不同时间点之间的差异。
本文将讨论微分方程和差分方程在数学建模中的应用以及它们之间的联系。
首先,微分方程在数学建模中的应用非常广泛。
以生态系统建模为例,人们关心物种之间的相互作用,而微分方程提供了描述这些相互作用的数学工具。
例如,Lotka-Volterra模型是描述捕食者与被捕食者之间的关系,其中包含一组微分方程,描述了捕食者和被捕食者的数量随时间的变化。
另外,微分方程还可以用于描述传染病模型、金融模型等各种实际问题。
其次,差分方程也在数学建模中发挥着重要的作用。
差分方程适用于离散时间点的模型建立。
这种模型可以用于描述各类实际问题,比如金融市场波动、天气预测等。
例如,差分方程可以用来模拟股票价格的变化。
我们可以将股价视作一个时间序列,每个时间点的股价与前一时间点的股价之间存在差异。
通过建立差分方程模型,我们可以预测未来股价的变化趋势。
微分方程和差分方程之间存在紧密的联系。
在某些情况下,当离散时间趋于无穷小时,差分方程可以无限地逼近相应的微分方程。
这个过程被称为“微分方程与差分方程的近似”。
通过这个近似,我们可以将微分方程转化为差分方程进行数值计算,从而得到问题的解决办法。
另外,差分方程也可以通过细化时间步长,将离散的解逼近到连续解,并逼近相应的微分方程解。
在数学建模中,我们需要考虑实际问题的特点,来决定使用微分方程还是差分方程。
一般来说,微分方程适用于描述连续变量之间的关系,而差分方程适用于描述离散变量之间的关系。
根据问题的特点,我们可以选择合适的数学工具,并进行模型建立和求解。
综上所述,微分方程和差分方程在数学建模中是不可分割的。
微分方程用于描述连续变量之间的关系,差分方程用于描述离散变量之间的关系。
虽然它们有着不同的应用场景和数学表达方式,但通过近似和转化,它们可以相互联系,并共同为解决实际问题提供了强有力的工具。
数学建模中的差分方程与微分方程

数学建模是一门研究如何用数学方法解决实际问题的学科,它在现代科学、工程技术以及社会经济领域中扮演着重要的角色。
在数学建模的过程中,我们经常会遇到需要描述连续或离散变化的问题,而差分方程与微分方程则成为了解决这类问题的有力工具。
差分方程是描述离散变化的方程,它将一个变量与它在前一时刻或前几个时刻的取值联系起来。
在数学建模中,差分方程常常被用来描述离散的时间或空间变化,比如物种数量的变化、金融市场的波动等。
差分方程最简单的形式是递推式,它用一个前一时刻的变量的值来表示当前时刻的变量的值。
例如,一个典型的一阶差分方程可以写作:$x_{n+1}=f(x_n)$,其中$x_n$表示第$n$个时刻的变量的值,$f(x_n)$表示根据$x_n$计算出的$x_{n+1}$的函数。
通过递推式,我们可以得到变量在不同时刻的取值,进而研究它的变化规律。
微分方程是描述连续变化的方程,它涉及到变量对时间的导数或各个变量之间的关系。
微分方程在数学建模中的应用非常广泛,尤其在物理学、生物学等自然科学领域中经常被用来描述变化的物理现象。
微分方程的形式多种多样,比如一阶线性微分方程、二阶非线性微分方程等等。
一阶微分方程的一般形式可以写作:$\frac{dx}{dt}=f(x,t)$,其中$x$表示一个或多个变量,$t$表示时间,$f(x,t)$表示$x$和$t$的关系。
通过求解微分方程,我们可以得到变量随时间的变化规律,并进一步分析问题。
在实际问题中,差分方程与微分方程往往会相互呼应和融合,一些问题既可以用差分方程描述离散变化,也可以用微分方程描述连续变化。
这时,我们可以通过将差分方程转化为微分方程或将微分方程离散化为差分方程来求解问题。
例如,在人口增长的问题中,我们可以通过建立一个差分方程来描述每一年的人口数量,而利用微分方程的分析方法可以得到人口增长的长期行为。
又例如,在物理学中,连续介质的运动可以用微分方程描述,而粒子的运动可以用差分方程描述。
数学建模案例分析2生态系统--差分方程方法建模

§2 生态系统一、一阶常系数线性差分方程),2,1,0()(1 ==++n n f ay y n n其通解是对应齐次方程),2,1,0(01 ==++n ay y n n的通解n n a C y )(-=加上原方程的一个特解*y 。
*y 的算法是待定系数法。
(1)m n P n f m -=)()(次多项式⎩⎨⎧-=-≠==1,11,0,)(*a a k n Q n y m k(2)-=n bd n f )(指数函数⎩⎨⎧-=-≠==d a d a k d An y nk ,1,0,* 二、应用举例设想在一个长满了青草的小荒岛上栖息繁衍着一群野兔。
开始时共有野兔0y 只,我们来研究其数目随时间变化的规律。
假设第n 年野兔的数目用n y 表示。
记第0年的野兔数为0y 。
(1)先作如下的假设:下一年野兔的净增加数目和上一年的数目成正比,且比例系数是一个常数,记为)1(>K K 。
这种假设是很合理的,因为在野兔的食物——青草非常充足的条件下,一年内新出生的野兔数和成年母兔数成正比,而成年母兔数又和野兔总数成正比,因而一年内新出生的野兔数和野兔总数成正比。
另一方面,一年内死亡的野兔数大体也和野兔总数成正比。
这样,第n 年野兔的净增加数(出生数减去死亡数)1--n n y y 和上一年野兔的数目1-n y 成正比,即可以列出方程:11--'=-n n n y K y y移项整理后得到方程1-=n n y K y (1) 这里1+'=K K 。
这是一阶常系数齐次线性差分方程。
可以计算出第n 年的野兔总数为n n K y y 0=。
这个描述野兔数目的模型是否合理呢?假设4.1=K ,1000=y ,计算对应的n y 值列表如下: n 01 2 3 4 8 10 15 20 50 n y 100 140 196 274 384 1 475 2 893 15 57683 668 20(亿) 这是一个按指数增长的量,由表中数据我们发现,50年后野兔的总数为20亿!也许有人会认为4.1=K 太大,但是对于一年可以生育2~3次的兔子来说4.1=K 不应该算太大。
微分方程与差分方程_详解与例题

第七章 常微分方程与差分方程常微分方程是高等数学中理论性和应用性都较强的一部分,是描述客观规律的一种重要方法,是处理物理、力学、几何等应用问题的一个重要工具,微分和积分的知识是研究微分方程的基础。
微分方程作为考试的重点内容,每年研究生考试均会考到。
特别是微分方程的应用问题,既是重点,也是难点,在复习时必须有所突破。
【数学一大纲内容】常微分方程的基本概念;变量可分离的方程;齐次方程;一阶线性方程;伯努利(Bernoulli )方程;全微分方程;可用简单的变量代换求解的某些微分方程;可降阶的高阶微分方程;线性微分方程解的性质及解的结构定理;二阶常系数齐次线性微分方程;高于二阶的某些常系数齐次线性微分方程;简单的二阶常系数非齐次线性微分方程;欧拉(Euler )方程;微分方程的简单应用。
【数学二大纲内容】常微分方程的基本概念;变量可分离的方程;齐次方程;一阶线性微分方程;可降阶的高阶微分方程;线性微分方程解的性质及解的结构定理;二阶常数齐次线性微分方程;高于二阶的某些常系数齐次线性微分方程;简单的二阶常系数非齐次线性微分方程;微分方程的一些简单应用。
【大纲要求】要理解微分方程的有关概念,如阶、解、通解、特解、定解条件等,掌握几类方程的解法:如变量可分离方程,齐次方程,一阶线性微分方程,伯努利方程,可降阶方程等。
理解线性微分方程解的性质和解的结构,掌握求解常系数齐次线性方程的方法,掌握求解某些自由项的常系数非齐次线性方程的待定系数法。
了解欧拉方程的概念,会求简单的欧拉方程。
会用微分方程处理物理、力学、几何中的简单问题。
【考点分析】本章包括三个重点内容:1.常见的一阶、二阶微分方程求通解或特解。
求解常微分方程重要的是判断方程为哪种类型,并记住解法的推导过程。
2.微分方程的应用问题,这是一个难点,也是重点。
利用微分方程解决实际问题时,若是几何问题,要根据问题的几何特性建立微分方程。
若是物理问题,要根据某些物理定律建立微分方程,也有些问题要利用微元法建立微分方程。
微分方程在数学建模中的应用

常微分方程在数学建模中的应用这里介绍几个典型的用微分方程建立数学模型的例子. 一、人口预测模型由于资源的有限性,当今世界各国都注意有计划地控制人口的增长,为了得到人口预测模型,必须首先搞清影响人口增长的因素,而影响人口增长的因素很多,如人口的自然出生率、人口的自然死亡率、人口的迁移、自然灾害、战争等诸多因素,如果一开始就把所有因素都考虑进去,则无从下手.因此,先把问题简化,建立比较粗糙的模型,再逐步修改,得到较完善的模型.例1( 马尔萨斯 (Malthus ) 模型) 英国人口统计学家马尔萨斯(1766—1834)在担任牧师期间,查看了教堂100多年人口出生统计资料,发现人口出生率是一个常数,于1789年在《人口原理》一书中提出了闻名于世的马尔萨斯人口模型,他的基本假设是:在人口自然增长过程中,净相对增长(出生率与死亡率之差)是常数,即单位时间内人口的增长量与人口成正比,比例系数设为r ,在此假设下,推导并求解人口随时间变化的数学模型.解 设时刻t 的人口为)(t N ,把)(t N 当作连续、可微函数处理(因人口总数很大,可近似地这样处理,此乃离散变量连续化处理),据马尔萨斯的假设,在t 到t t ∆+时间段内,人口的增长量为t t rN t N t t N ∆=-∆+)()()(,并设0t t =时刻的人口为0N ,于是⎪⎩⎪⎨⎧==.,00)(d d N t N rN t N这就是马尔萨斯人口模型,用分离变量法易求出其解为)(00e )(t t r N t N -=,此式表明人口以指数规律随时间无限增长.模型检验:据估计1961年地球上的人口总数为91006.3⨯,而在以后7年中,人口总数以每年2%的速度增长,这样19610=t ,901006.3⨯=N ,02.0=r ,于是)1961(02.09e1006.3)(-⨯=t t N .这个公式非常准确地反映了在1700—1961年间世界人口总数.因为,这期间地球上的人口大约每35年翻一番,而上式断定34.6年增加一倍(请读者证明这一点).但是,后来人们以美国人口为例,用马尔萨斯模型计算结果与人口资料比较,却发现有很大的差异,尤其是在用此模型预测较遥远的未来地球人口总数时,发现更令人不可思议的问题,如按此模型计算,到2670年,地球上将有36 000亿人口.如果地球表面全是陆地(事实上,地球表面还有80%被水覆盖),我们也只得互相踩着肩膀站成两层了,这是非常荒谬的,因此,这一模型应该修改.例2(逻辑Logistic 模型) 马尔萨斯模型为什么不能预测未来的人口呢?这主要是地球上的各种资源只能供一定数量的人生活,随着人口的增加,自然资源环境条件等因素对人口增长的限制作用越来越显著,如果当人口较少时,人口的自然增长率可以看作常数的话,那么当人口增加到一定数量以后,这个增长率就要随人口的增加而减小.因此,应对马尔萨斯模型中关于净增长率为常数的假设进行修改.1838年,荷兰生物数学家韦尔侯斯特(Verhulst)引入常数m N ,用来表示自然环境条件所能容许的最大人口数(一般说来,一个国家工业化程度越高,它的生活空间就越大,食物就越多,从而m N 就越大),并假设将增长率等于⎪⎪⎭⎫⎝⎛-m N t N r )(1,即净增长率随着)(t N 的增加而减小,当m N t N →)(时,净增长率趋于零,按此假定建立人口预测模型.解 由韦尔侯斯特假定,马尔萨斯模型应改为⎪⎩⎪⎨⎧=⎪⎪⎭⎫⎝⎛-=,,000)(1d d N t N N N N r t N 上式就是逻辑模型,该方程可分离变量,其解为,)(00e11)(t t r m mN N N t N --⎪⎪⎭⎫ ⎝⎛-+=.下面,我们对模型作一简要分析.zzzaazz(1)当∞→t ,m N t N →)(,即无论人口的初值如何,人口总数趋向于极限值m N ; (2)当m N N <<0时,01d d >⎪⎪⎭⎫⎝⎛-=N N N r t N m ,这说明)(t N 是时间t 的单调递增函数;(3)由于N N N N N r t N m m ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=211d d 222,所以当2m N N <时,0d d 22>t N ,t N d d 单增;当2m N N >时,0d d 22<tN ,t N d d 单减,即人口增长率t Nd d 由增变减,在2m N 处最大,也就是说在人口总数达到极限值一半以前是加速生长期,过这一点后,生长的速率逐渐变小,并且迟早会达到零,这是减速生长期;(4)用该模型检验美国从1790年到1950年的人口,发现模型计算的结果与实际人口在1930年以前都非常吻合,自从1930年以后,误差愈来愈大,一个明显的原因是在20世纪60年代美国的实际人口数已经突破了20世纪初所设的极限人口.由此可见该模型的缺点之一是m N 不易确定,事实上,随着一个国家经济的腾飞,它所拥有的食物就越丰富, m N 的值也就越大;(5)用逻辑模型来预测世界未来人口总数.某生物学家估计,029.0=r ,又当人口总数为91006.3⨯时,人口每年以2%的速率增长,由逻辑模型得⎪⎪⎭⎫⎝⎛-=m N N r t N N 1d d 1, 即 ⎪⎪⎭⎫ ⎝⎛⨯-=m N 91006.31029.002.0, 从而得 91086.9⨯=m N ,即世界人口总数极限值近100亿.值得说明的是:人也是一种生物,因此,上面关于人口模型的讨论,原则上也可以用于在自然环境下单一物种生存着的其他生物,如森林中的树木、池塘中的鱼等,逻辑模型有着广泛的应用.二、市场价格模型对于纯粹的市场经济来说,商品市场价格取决于市场供需之间的关系,市场价格能促使商品的供给与需求相等(这样的价格称为(静态)均衡价格).也就是说,如果不考虑商品价格形成的动态过程,那么商品的市场价格应能保证市场的供需平衡,但是,实际的市场价格不会恰好等于均衡价格,而且价格也不会是静态的,应是随时间不断变化的动态过程.例3 试建立描述市场价格形成的动态过程的数学模型解 假设在某一时刻t ,商品的价格为)(t p ,它与该商品的均衡价格间有差别,此时,存在供需差,此供需差促使价格变动.对新的价格,又有新的供需差,如此不断调节,就构成市场价格形成的动态过程,假设价格)(t p 的变化率tpd d 与需求和供给之差成正比,并记),(r p f 为需求函数,)(p g 为供给函数(r 为参数),于是()()[]⎪⎩⎪⎨⎧=-=,,0)0(,d d p p p g r p f tpα 其中0p 为商品在0=t 时刻的价格,α为正常数.若设b ap r p f +-=),(,d cp p g +=)(,则上式变为⎪⎩⎪⎨⎧=-++-=,,0)0()()(d d p p d b p c a t pαα ① 其中d c b a ,,,均为正常数,其解为ca db c a d b p t p t c a +-+⎪⎭⎫ ⎝⎛+--=+-)(0e)(α.下面对所得结果进行讨论:(1)设p 为静态均衡价格 ,则其应满足0)(),(=-p g r p f ,即d p c b p a +=+-,于是得ca db p +-=,从而价格函数)(t p 可写为 p p p t p tc a +-=+-)(0e )()(α ,令+∞→t ,取极限得p t p t =+∞→)(lim这说明,市场价格逐步趋于均衡价格.又若初始价格p p =0,则动态价格就维持在均衡价格p 上,整个动态过程就化为静态过程;(2)由于t c a c a p p tp)(0e )()(d d +-+-=αα , 所以,当p p >0时,0d d <t p ,)(t p 单调下降向p 靠拢;当p p <0时, 0d d >tp ,)(t p 单调增加向p 靠拢.这说明:初始价格高于均衡价格时,动态价格就要逐步降低,且逐步靠近均衡价格;否则,动态价格就要逐步升高.因此,式①在一定程度上反映了价格影响需求与供给,而需求与供给反过来又影响价格的动态过程,并指出了动态价格逐步向均衡价格靠拢的变化趋势.三、混合溶液的数学模型例 4 设一容器内原有100L 盐,内含有盐10kg,现以3L/min 的速度注入质量浓度为0.01kg/L 的淡盐水,同时以2L/min 的速度抽出混合均匀的盐水,求容器内盐量变化的数学模型.解 设t 时刻容器内的盐量为)(t x kg,考虑t 到t t d +时间内容器中盐的变化情况,在dt 时间内容器中盐的改变量=注入的盐水中所含盐量-抽出的盐水中所含盐量容器内盐的改变量为x d ,注入的盐水中所含盐量为t d 301.0⨯,t 时刻容器内溶液的质量浓度为tt x )23(100)(-+,假设t 到t t d +时间内容器内溶液的质量浓度不变(事实上,容器内的溶液质量浓度时刻在变,由于t d 时间很短,可以这样看).于是抽出的盐水中所含盐量为t tt x d 2)23(100)(-+,这样即可列出方程t txt x d 1002d 03.0d +-=,即tx t x +-=100203.0d d . 又因为0=t 时,容器内有盐10kg,于是得该问题的数学模型为d 20.03d 100(0)10xx t tx ⎧+=⎪+⎪⎨⎪⎪=⎩,, 这是一阶非齐次线性方程的初值问题,其解为24)100(109)100(01.0)(t t t x +⨯++=.下面对该问题进行一下简单的讨论,由上式不难发现:t 时刻容器内溶液的质量浓度为34)100(10901.0100)()(t t t x t p +⨯+=+=, 且当+∞→t 时,01.0)(→t p ,即长时间地进行上述稀释过程,容器内盐水的质量浓度将趋于注入溶液的质量浓度.溶液混合问题的更一般的提法是:设有一容器装有某种质量浓度的溶液,以流量1V 注入质量浓度为1C 的溶液 (指同一种类溶液,只是质量浓度不同),假定溶液立即被搅匀,并以2V 的流量流出这种混合溶液,试建立容器中质量浓度与时间的数学模型.首先设容器中溶质的质量为)(t x ,原来的初始质量为0x ,t =0时溶液的体积为2V ,在d t 时间内,容器内溶质的改变量等于流入溶质的数量减去流出溶质的数量,即t V C t V C x d d d 2211-=,其中1C 是流入溶液的质量浓度, 2C 为t 时刻容器中溶液的质量浓度,,tV V V xC )(2102-+=于是,有混合溶液的数学模型 11220d d (0)xC V C V tx x ⎧=-⎪⎨⎪=⎩,. 该模型不仅适用于液体的混合,而且还适用于讨论气体的混合.四、振动模型振动是生活与工程中的常见现象.研究振动规律有着极其重要的意义.在自然界中,许多振动现象都可以抽象为下述振动问题.例5 设有一个弹簧,它的上端固定,下端挂一个质量为m 的物体,试研究其振动规律. 解 假设(1)物体的平衡位置位于坐标原点,并取x 轴的正向铅直向下(见图4).物体的平衡位置指物体处于静止状态时的位置.此时,作用在物体上的重力与弹性力大小相等,方向相反;(2)在一定的初始位移0x 及初始速度0v 下,物体离开平衡位置,并在平衡位置附近作没有摇摆的上下振动;(3)物体在t 时刻的位置坐标为)(t x x =,即t 时刻物体偏离平衡位置的位移;(4)在振动过程中,受阻力作用.阻力的大小与物体速度成正比,阻力的方向总是与速度方向相反,因此阻力为txhd d -,h 为阻尼系数;(5)当质点有位移)(t x 时,假设所受的弹簧恢复力是与位移成正比的,而恢复力的方向总是指向平衡位置,也就是总与偏离平衡位置的位移方向相反,因此所受弹簧恢复力为kx -,其中k 为劲度系数;(6)在振动过程中受外力)(t f 的作用.在上述假设下,根据牛顿第二定律得)(d d d d 22x f kx t xh tx m +--= , ①这就是该物体的强迫振动方程.由于方程①中, )(t f 的具体形式没有给出,所以,不能对式 ①直接求解.下面我们分四种情形对其进行讨论.1. 无阻尼自由振动在这种情况下,假定物体在振动过程中,既无阻力、又不受外力 作用.此时方程①变为0d d 22=+kx txm ,令2ω=mk,方程变为 0d d 222=+x tx ω,特征方程为 022=+ωλ,特征根为 ωλi 2,1±=,通解为 t C t C x ωωcos sin 21+=,或将其写为⎪⎪⎭⎫ ⎝⎛++++=t C C C t C C C C C x ωωcos sin 22212222112221图4()t t A ωϕωϕcos sin sin cos +=,)sin(ϕω+=t A 其中 2221C C A +=,22212sin CC C +=ϕ,22211cos CC C +=ϕ.这就是说,无阻尼自由振动的振幅2221C C A +=,频率mk=ω均为常数. 2.有阻尼自由振动在该种情况下,考虑物体所受到的阻力,不考虑物体所受的外力.此时,方程①变为0d d d d 22=++kx t xh tx m ,令2ω=m k ,δ2=mh,方程变为 0d d 2d d 222=++x t xtx ωδ, 特征方程为0222=++ωδλλ,特征根 222,1ωδδλ-±-=.根据δ与ω的关系,又分为如下三种情形:(1)大阻尼情形, δ>ω.特征根为二不等实根,通解为ttC C x )(2)(12222e e ωδδωδδ-+--+-+=(2)临界阻尼情形,ωδ=.特征根为重根,通解为tt C C x δ-+=e)(21这两种情形,由于阻尼比较大,都不发生振动.当有一初始扰动以后,质点慢慢回到平衡位置,位移随时间t 的变化规律分别如图5和图6所示.图5 图6(3)小阻尼情形,δ<ω.特征根为共轭复根,通解为)sin C sinC (e 222221t t x t δωδωδ-+-=- 将其简化为)sin(e 22ϕδωδ+-=-t A x t其中,cos ,sin ,22211222122221C C C C C C C C A ++=+=ϕϕ振幅A tδ-e 随时间t 的增加而减小.因此,这是一种衰减振动.位移随时间t 的变化规律见图7.3.无阻尼强迫振动在这种情形下,设物体不受阻力作用,其所受外力为简 谐力pt m t f sin )(=,此时,方程①化为pt m kx t xm sin d d 22=+,pt x tx sin d d 222=+ω, 根据p i 是否等于特征根ωi ,其通解分为如下两种情形:(1)当ω≠p 时,其通解为 图7t C t C pt p x ωωωcos sin sin 12122++-=,此时,特解的振幅221p-ω为常数,但当p 接近于ω时,将会导致振幅增大,发生类似共振的现象;(2)当ω=p 时,其通解为t C t C pt t px ωωcos sin cos 2121++-=, 此时,特解的振幅t p21随时间t 的增加而增大,这种现象称为共振,即当外力的频率p 等于物体的固有频率ω时,将发生共振.4.阻尼强迫振动在这种情形下,假定振动物体既受阻力作用,又受外力pt m x f sin )(=的作用,并设ωδ<,方程①变为pt x t xtx sin d d 2d d 222=++ωδ , 特征根0,i22≠-±-=δδωδλ,则p i 不可能为特征根,特解为pt B pt A x cos sin *+=,其中22222224)(p p p A δωω+--=,222224)(2p p pB δωδ+--=,还可将其化为*22222221[()sin 2cos ]()4x w p pt p pt w p pδδ=---+, 由此可见,在有阻尼的情况下,将不会发生共振现象,不过,当ω=p 时,pt px cos 21*δ-=, 若δ很小,则仍会有较大的振幅;若δ比较大,则不会有较大的振幅.。
微分方程建模案例1

微分方程建模案例1微分方程建模案例1微分方程是数学中的一个重要分支,它可以用来描述自然界中很多现象和问题的变化规律。
在实际问题的建模中,微分方程起到了至关重要的作用。
本文将介绍一个微分方程建模的案例,以帮助读者更好地理解微分方程的应用。
案例1:放烟花问题描述:小明在庆祝活动中放了一颗烟花。
烟花在起飞后爆炸,产生鲜艳的火花,并逐渐消散。
请问如何用微分方程来描述烟花燃烧和消散的过程?解决思路:我们可以用烟花高度和火花数量来描述烟花的燃烧和消散过程。
假设烟花的高度为h(t),火花的数量为n(t),其中t表示时间。
高度的变化:根据物理知识,烟花往上升的时候速度越来越慢,最后停止在一些高度。
因此,我们可以通过速度来描述高度的变化。
根据牛顿第二定律,物体的加速度等于物体所受到的合力除以物体的质量。
考虑到重力和空气阻力的存在,烟花受到的合力可以表示为:mg - kv,其中m是烟花的质量,g是重力加速度,k是阻力系数,v是烟花的下降速度。
根据牛顿第二定律可得:m・h''(t) = mg - kv(t)火花数量的变化:一颗烟花燃烧后会产生一定数量的火花,这些火花在空气中逐渐消散。
假设火花的数量随时间的变化满足指数衰减规律,即火花数量每过一段时间t0会减少到原来的1/2、因此,火花数量的变化可以用指数衰减方程来描述:n'(t)=-k1n(t)整理得到微分方程组:m・h''(t) = mg - kv(t)n'(t)=-k1n(t)其中m、g、k、k1为常数。
求解微分方程:对于高度的微分方程,我们可以使用常系数线性微分方程的求解方法来求解。
我们可以根据初始条件来确定h(t)的具体形式。
对于火花数量的微分方程,它是一个一阶线性微分方程,可以使用变量分离法来求解。
我们可以根据初始条件来确定n(t)的具体形式。
讨论和应用:通过以上微分方程组的求解,我们可以得到小明放的烟花的高度和火花数量随时间变化的具体函数形式。
微分方程建模案例

微分方程建模案例微分方程是一种描述自然现象和数学模型中变化规律的数学工具。
它广泛应用于物理学、生物学、经济学等领域,能够帮助研究者解释和预测系统的行为。
接下来,我们将介绍一个微分方程建模的案例,以帮助读者更好地理解和应用微分方程。
案例背景:假设我们要研究一个自然保护区中的狼和兔子的数量变化。
该自然保护区面积有限,为了研究物种的动态平衡以及影响因素对其数量的影响,我们需要建立一个微分方程模型。
问题分析:在自然保护区中,狼以兔子为食物,而兔子则面临被捕食的风险。
因此,我们可以推测狼的数量对于兔子的数量产生压力,并且预测狼的数量与兔子的数量之间存在其中一种关系。
模型建立:假设R(t)表示时间t时刻的兔子的数量,W(t)表示时间t时刻的狼的数量。
为了建立一个微分方程模型,我们需要引入一些假设。
1.兔子的繁殖速率与兔子当前的数量成正比,同时也会受到狼的捕食速率的影响。
我们假设兔子繁殖率为α,捕食速率为β,兔子数量的增长速率与当前兔子的数量和受捕食的比例有关。
因此,兔子数量的增长速率可以表示为αR(t)-βW(t)R(t)。
2.狼的数量的变化与狼的死亡率和捕食率有关。
我们假设狼的死亡率为δ,捕食率为γ,狼的数量的变化率可以表示为-δW(t)+γW(t)R(t)。
综上所述,我们可以得到一个微分方程模型:dR(t)/dt = αR(t) - βW(t)R(t)dW(t)/dt = -δW(t) + γW(t)R(t)模型求解与分析:通过求解该微分方程模型,我们可以得到兔子和狼数量随时间变化的解析解。
对于一个给定的初值条件,我们可以通过数值方法(如欧拉法、龙格-库塔法等)求解微分方程模型,并绘制兔子和狼的数量随时间变化的图像。
在模型的分析过程中,我们可以通过改变模型中的参数(如α、β、δ和γ)来分析它们对系统行为的影响。
通过研究模型的稳定点、极限环等特征,我们可以得出关于狼和兔子数量变化的结论。
总结:这个案例展示了微分方程建模的过程,通过建立微分方程模型,我们可以研究和预测自然保护区中狼和兔子数量的变化规律。
数学建模微分方程的应用举例

数学建模——微分方程的应用举例分布图示★衰变问题 ★逻辑斯谛方程 ★价格调整问题 ★人才分配问题模型 ★追迹问题内容要点一、衰变问题例1 镭、铀等放射性元素因不断放射出各种射线而逐渐减少其质量, 这种现象称为放射性物质的衰变. 根据实验得知, 衰变速度与现存物质的质量成正比, 求放射性元素在时刻t 的质量.解 用x 表示该放射性物质在时刻t 的质量, 则dtdx表示x 在时刻t 的衰变速度, 于是“衰变速度与现存的质量成正比”可表示为.kx dtdx-= (8.1) 这是一个以x 为未知函数的一阶方程, 它就是放射性元素衰变的数学模型, 其中0>k 是比例常数, 称为衰变常数, 因元素的不同而异. 方程右端的负号表示当时间t 增加时, 质量x 减少.解方程(8.1)得通解.ktCex -=若已知当0t t =时, ,0x x =代入通解kt Ce x -=中可得,00kt e x C -= 则可得到方程(8.1)特解,)(00t t k e x x --=它反映了某种放射性元素衰变的规律.注: 物理学中, 我们称放射性物质从最初的质量到衰变为该质量自身的一半所花费的时间为半衰期, 不同物质的半衰期差别极大. 如铀的普通同位素(U 238)的半衰期约为50亿年;通常的镭(Ra 226)的半衰期是上述放射性物质的特征, 然而半衰期却不依赖于该物质的初始量, 一克Ra 226衰变成半克所需要的时间与一吨Ra 226衰变成半吨所需要的时间同样都是1600年, 正是这种事实才构成了确定考古发现日期时使用的著名的碳-14测验的基础.二、 逻辑斯谛方程:逻辑斯谛方程是一种在许多领域有着广泛应用的数学模型, 下面我们借助树的增长来建立该模型.一棵小树刚栽下去的时候长得比较慢, 渐渐地, 小树长高了而且长得越来越快, 几年不见, 绿荫底下已经可乘凉了; 但长到某一高度后, 它的生长速度趋于稳定, 然后再慢慢降下来. 这一现象很具有普遍性. 现在我们来建立这种现象的数学模型.如果假设树的生长速度与它目前的高度成正比, 则显然不符合两头尤其是后期的生长情形, 因为树不可能越长越快; 但如果假设树的生长速度正比于最大高度与目前高度的差, 则又明显不符合中间一段的生长过程. 折衷一下, 我们假定它的生长速度既与目前的高度,又与最大高度与目前高度之差成正比.设树生长的最大高度为H (m), 在t (年)时的高度为h (t ), 则有)]()[()(t h H t kh dtt dh -= (8.2) 其中0>k 是比例常数. 这个方程为Logistic 方程. 它是可分离变量的一阶常数微分方程.下面来求解方程(8.2). 分离变量得,)(kdt h H h dh=-两边积分,)(⎰⎰=-kdt h H h dh得 ,)]ln([ln 11C kt h H h H+=-- 或,21kHt H C kHt e C e hH h ==-+故所求通解为,11)(22kHtkHt kHt CeH e C He C t h -+=+= 其中的⎪⎪⎭⎫ ⎝⎛>==-0112H C e C C C 是正常数. 函数)(t h 的图象称为Logistic 曲线. 图8-8-1所示的是一条典型的Logistic 曲线, 由于它的形状, 一般也称为S 曲线. 可以看到, 它基本符合我们描述的树的生长情形. 另外还可以算得.)(lim H t h t =+∞→这说明树的生长有一个限制, 因此也称为限制性增长模式.注: Logistic 的中文音译名是“逻辑斯谛”. “逻辑”在字典中的解释是“客观事物发展的规律性”, 因此许多现象本质上都符合这种S 规律. 除了生物种群的繁殖外, 还有信息的传播、新技术的推广、传染病的扩散以及某些商品的销售等. 例如流感的传染、在任其自然发展(例如初期未引起人们注意)的阶段, 可以设想它的速度既正比于得病的人数又正比于未传染到的人数. 开始时患病的人不多因而传染速度较慢; 但随着健康人与患者接触, 受传染的人越来越多, 传染的速度也越来越快; 最后, 传染速度自然而然地渐渐降低, 因为已经没有多少人可被传染了.下面举两个例子说明逻辑斯谛的应用.人口阻滞增长模型 1837年, 荷兰生物学家V erhulst 提出一个人口模型00)(),(y t y by k y dtdy=-= (8.3)其中b k ,的称为生命系数.我们不详细讨论这个模型, 只提应用它预测世界人口数的两个有趣的结果.有生态学家估计k 的自然值是0.029. 利用本世纪60年代世界人口年平均增长率为2%以及1965年人口总数33.4亿这两个数据, 计算得,2=b 从而估计得:(1)世界人口总数将趋于极限107.6亿. (2)到2000年时世界人口总数为59.6亿.后一个数字很接近2000年时的实际人口数, 世界人口在1999年刚进入60亿. 新产品的推广模型 设有某种新产品要推向市场, t 时刻的销量为),(t x 由于产品性能良好, 每个产品都是一个宣传品, 因此, t 时刻产品销售的增长率,dtdx与)(t x 成正比, 同时, 考虑到产品销售存在一定的市场容量N , 统计表明dtdx与尚未购买该产品的潜在顾客的数量)(t x N -也成正比, 于是有)(x N kx dtdx-= (8.4)其中k 为比例系数. 分离变量积分, 可以解得kNtCeNt x -+=1)( (8.5)由,)1()1(,)1(2322222kNt kNt kNt kNt kNt Ce Ce e N Ck dt x d Ce ke CN dt dx -----+-=+= 当N t x <)(*时, 则有,0>dt dx 即销量)(t x 单调增加. 当2)(*N t x =时, ;022=dt x d 当2)(*N t x >时, ;022<dt x d 当2)(*Nt x <时, 即当销量达到最大需求量N 的一半时, 产品最为畅销, 当销量不足N 一半时, 销售速度不断增大, 当销量超过一半时, 销售速度逐渐减少.国内外许多经济学家调查表明. 许多产品的销售曲线与公式(8.5)的曲线(逻辑斯谛曲线)十分接近. 根据对曲线性状的分析, 许多分析家认为, 在新产品推出的初期, 应采用小批量生产并加强广告宣传, 而在产品用户达到20%到80%期间, 产品应大批量生产; 在产品用户超过80%时, 应适时转产, 可以达到最大的经济效益.三、价格调整模型在本章第一节例3已经假设, 某种商品的价格变化主要服从市场供求关系. 一般情况下,商品供给量S 是价格P 的单调递增函数, 商品需求量Q 是价格P 的单调递减函数, 为简单起见, 分别设该商品的供给函数与需求函数分别为P P Q bP a P S βα-=+=)(,)( (8.6)其中βα,,,b a 均为常数, 且.0,0>>βb当供给量与需求量相等时, 由(8.6)可得供求平衡时的价格baP e +-=βα 并称e P 为均衡价格.一般地说, 当某种商品供不应求, 即Q S <时, 该商品价格要涨, 当供大于求, 即Q S >时, 该商品价格要落. 因此, 假设t 时刻的价格)(t P 的变化率与超额需求量S Q -成正比, 于是有方程)]()([P S P Q k dtdP-= 其中,0>k 用来反映价格的调整速度.将(8.6)代入方程, 可得)(P P dtdPe -=λ (8.7) 其中常数,0)(>+=k b βλ方程(8.7)的通解为t e Ce P t P λ-+=)(假设初始价格,)0(0P P =代入上式, 得,0e P P C -=于是上述价格调整模型的解为t e e e P P P t P λ--+=)()(0由于0>λ知, +∞→t 时, .)(e P t P →说明随着时间不断推延, 实际价格)(t P 将逐渐趋近均衡价格e P .四、人才分配问题模型每年大学毕业生中都要有一定比例的人员留在学校充实教师队伍, 其余人员将分配到国民经济其他部门从事经济和管理工作. 设t 年教师人数为),(1t x 科学技术和管理人员数目为),(2t x 又设1外教员每年平均培养α个毕业生, 每年人教育、科技和经济管理岗位退休、死亡或调出人员的比率为βδδ),10(<<表示每年大学生毕业生中从事教师职业所占比率),10(<<δ于是有方程111x x dt dx δαβ-= (8.8) 212)1(x x dtdx δβα--= (8.9) 方程(8.8)有通解t e C x )(11δαβ-=(8.10)若设,)0(101x x =则,101x C =于是得特解te x x )(101δαβ-= (8.11)将(8.11)代入(8.9)方程变为tex x dtdx )(1022)1(δαββαδ--=+ (8.12) 求解方程(8.12)得通解t te x eC x )(122)1(δαβδββ---+= (8.13)若设,)0(202x x =则,110202x x C ⎪⎪⎭⎫⎝⎛--=ββ于是得特解 tt ex e x x x )(101020211δαβδββββ--⎪⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--= (8.14) (8.11)式和(8.14)式分别表示在初始人数分别为)0(),0(21x x 情况, 对应于β的取值, 在t 年教师队伍的人数和科技经济管理人员人数. 从结果看出, 如果取,1=β即毕业生全部留在教育界, 则当∞→t 时, 由于,δα>必有+∞→)(1t x 而,0)(2→t x 说明教师队伍将迅速增加. 而科技和经济管理队伍不断萎缩, 势必要影响经济发展, 反过来也会影响教育的发展. 如果将β接近于零. 则,0)(1→t x 同时也导致,0)(2→t x 说明如果不保证适当比例的毕业生充实教师选择好比率β, 将关系到两支队伍的建设, 以及整个国民经济建设的大局.五、追迹问题设开始时甲、乙水平距离为1单位, 乙从A 点沿垂直于OA 的直线以等速0v 向正北行走; 甲从乙的左侧O 点出发, 始终对准乙以)1(0>n mv 的速度追赶. 求追迹曲线方程, 并问乙行多远时, 被甲追到.解 设所求追迹曲线方程为).(x y y =经过时刻t , 甲在追迹曲线上的点为),,(y x P 乙在点).,1(0t v B 于是有,1tan 0xyt v y --='=θ (8.15) 由题设, 曲线的弧长OP 为,1002t nv dx y x='+⎰解出t v 0代入(8.15), 得.11)1(02⎰'+=+'-x dx y ny y x 两边对x 求导, 整理得.11)1(2y ny x '+=''- 这就是追迹问题的数学模型.这是一个不显含y 的可降阶的方程, 设p y x p y ''=''='),(, 代入方程得211)1(p np x +='- 或 ,)1(12x n dxp dp -=+两边积分, 得|,|ln |1|ln 1)1ln(12C x np p +--=++即 .1112nxC p p -=++ 将初始条件00||==='x x p y 代入上式, 得.11=C 于是,1112nxy y -='++' (8.16) 两边同乘,12y y '+-'并化简得,112n x y y --='+-' (8.17)(8.16)与(8.17)式相加, 得,11121⎪⎭⎫ ⎝⎛---='n n x x y两边积分, 得.)1(1)1(121211C x n n x n ny nn nn +⎥⎦⎤⎢⎣⎡-++---=+-代入初始条件0|0==x y 得,122-=n nC 故所求追迹曲线方程为 ),1(11)1(1)1(2211>-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-=-+n n n n x n x n y n n n n甲追到乙时, 即曲线上点P 的横坐标,1=x 此时.12-=n n y 即乙行走至离A 点12-n n个单位距离时被甲追到.。
数学建模-常微分方程模型及差分模型

i0
>1
1
1-1/
i0 di/dt < 0
0
1-1/ 1 i
i0
0
i() 11 , 1
0,
1
t
0
t
接触数 =1 ~ 阈值
1i(t)
i0小
1
i(t)按S形曲线增长感染期内有效接触感染的 健康者人数不超过病人数
模型2(SI模型)如何看作模型3(SIS模型)的特例
2013-3-17
Anna
19
模型4
传染病有免疫性——病人治愈 后即移出感染系统,称移出者
SIR模型
假设 1)总人数N不变,病人、健康人和移
出者的比例分别为 i(t)s ,(t)r ,(t)
2)病人的日接触率 , 日治愈率, 接触数 = /
建模 s(t) i(t) r(t) 1
di dt
i(1 i)
i
i(0) i0
~ 日接触率 1/ ~平均感染期
/ ~ 一个感染期内每个病人的
有效接触人数,称为接触数。
2013-3-17
Anna
18
模型3
di/dt
dii(1i)i /
dt
i
dii[i(11)]
dt
i
>1
假设 r(x)r s(x r,s0 )r~固有增长率(x很小时)
xm~人口容量(资源、环境能容纳的最大数量)
r(xm)0
2013-3-17
s r xm
Anna
r(x) r(1 x ) xm
9
阻滞增长模型(Logistic模型)
dx rx dt
微分方程建模实例二市公开课金奖市赛课一等奖课件

dx/dt
此方程即Logistic模 型,解为:
x(t)
1
K Ce Kkt
.
0
K/2
Kx
在销出量小于最大需求量二 分之一时,销售速度是不断 增大,销出量达到最大需求 量二分之一时,该产品最为 畅销,接着销售速度将开始
下降.
第30页
dx kx(K x)
第17页
然而,事情到此并未结束,许多人还是不愿相信著名《在埃牟斯门徒》是米 格伦伪造. 事实上,在此之前这幅画已经被文物鉴定家认定为真迹,并以17万 美元高价被伦布兰特学会买下. 专家小组对于怀疑者回答是:由于米格伦曾因他在艺术界中没有地位而十分 懊恼,他下决心绘制《在埃牟斯门徒》,来证实他高于三流画家. 当创造出这 样杰作后,他志气消退了. 并且,当他看到这幅《在埃牟斯门徒》那么容易卖 掉以后,他在炮制以后伪制品时就不太专心了. 这种解释不能使怀疑者感到满意,他们要求完全科学拟定地证实《在埃牟斯 门徒》确实是一个伪造品. 这一问题拖了,直到1967年,才被卡内基·梅伦大学科学家们基本处理.
第20页
与本问题相关其它知识:
(1) 艺术家们应用白铅作为颜料之一,已有两千多 年历史. 白铅中含有微量放射铅210,白铅是从铅 矿中提炼出来,而铅又属于铀系.
(2) 衡量物质衰变一个惯用参数是它半衰期,即给 定数目的放射性原子衰变二分之一所需时间.
利用 N (t) N0e (tt0 ) ,
令 N 1 N0 2
第27页
4.2.3 耐用新产品销售速度问题
• 一个耐用新产品进入市场后,普通会都通过一 个销售量先不断增长,然后下降过程. 研究新 产品销售量改变规律,对于制定生产计划以及 制定促销策略都很故意义.
• 如何建立数学模型描述产品销售速度,并由此 给出一些有用结果以指导生产?
差微分方程 数学建模经典案例

差分方程作业题黄冈职业技术学院宋进健 胡敏 熊梦颖1.一对年轻夫妇准备购买一套住房,但缺少资金近6万元。
假设它们每月可有节余900元,且有如下的两种选择:(1)使用银行贷款60000元。
月利率0.01,贷款期25年=300个月; (2) 到某借贷公司借贷60000元,月利率0.01,22年还清。
只要(i )每半个月还316元,(ii) 预付三个月的款。
你能帮他们做出明智的选择吗? 模型假设:(1)银行及借贷公司在贷款期限内利率不变; (2)不考虑物价变化和经济等因素从而影响利率;(3)银行利息按复利计算且单位时间可任意缩短至时间变量连续性变化 建立模型:对第一种情况有: 设n 年期贷款月利率为r ,共贷款 元,贷款后第k 个月时欠款余额为 元,月还款m 元。
模型求解:由MATLAB 得出结果m=631.9345 建立模型:对第二种情况有: 设n 年期贷款半月利率为r ,共贷款A 0元,贷款后第k 个月时欠款余额为A k 元,半月还款m 元。
模型求解:()()0111,kkk r A A r m k Nr+-=+-∈10)1()1(300300300-=⇒=++r r A Ar m Nk m r AAkK ∈-+=+,)1(1Nk m r AAkK ∈-+=+,)1(1()()0111,kkk r A A r mk Nr+-=+-∈10)1()1(528528528-=⇒=++r r A Arm A k A 0由MATLAB 得出结果m= 313.0038模型分析:由第一种方式计算m=631.9345小于月节余额900元,能够承受月还款;由第二种方式计算m= 313.0038小于借贷公司要求没半个月还款316元,如果按照借贷公司要求则每月还款为632元大于第一种还款方式631.9345元,故选择第一种还款方式。
2. 在一城市的某商业区内,有两家有名的快餐店“肯德基”分店和“麦当劳”分店。
据统计每年“肯德基”保有其上一年老顾客的1/3,而另外的2/3顾客转移到“麦当劳”;每年“麦当劳”保有其上一年的老顾客的1/2,而另外的1/2顾客转移到“肯德基”。
实验二微分方程与差分方程模型Matlab求解

实验二: 微分方程与差分方程模型Matlab 求解一、实验目的[1]掌握解析、数值解法,并学会用图形观察解的形态和进行解的定性分析; [2] 熟悉MATLAB 软件关于微分方程求解的各种命令;[3]通过范例学习建立微分方程方面的数学模型以及求解全过程; [4] 熟悉离散 Logistic 模型的求解与混沌的产生过程。
二、实验原理1. 微分方程模型与MATLAB 求解解析解用MATLAB 命令dsolve(‘eqn1’,’eqn2’, ...) 求常微分方程(组)的解析解。
其中‘eqni'表示第i 个微分方程,Dny 表示y 的n 阶导数,默认的自变量为t 。
(1) 微分方程 例1 求解一阶微分方程 21y dxdy+= (1) 求通解 输入:dsolve('Dy=1+y^2')输出:ans =tan(t+C1)(2)求特解 输入:dsolve('Dy=1+y^2','y(0)=1','x')指定初值为1,自变量为x 输出:ans =tan(x+1/4*pi)例2求解二阶微分方程221()04(/2)2(/2)2/x y xy x y y y πππ'''++-=='=-原方程两边都除以2x ,得211(1)04y y y x x'''++-= 输入:dsolve('D2y+(1/x)*Dy+(1-1/4/x^2)*y=0','y(pi/2)=2,Dy(pi/2)=-2/pi','x') ans =- (exp(x*i)*(pi/2)^(1/2)*i)/x^(1/2) +(exp(x*i)*exp(-x*2*i)*(pi/2)^(3/2)*2*i)/(pi*x^(1/2))试试能不用用simplify 函数化简 输入: simplify(ans)ans =2^(1/2)*pi^(1/2)/x^(1/2)*sin(x) (2)微分方程组例3 求解 d f /d x =3f +4g ; d g /d x =-4f +3g 。
微分方程建模案例2

(3.6)
其中N0=N(t0)为初始时刻t0时的种群数。 马尔萨斯模型的一个显著特点:种群数量翻一番所需 的时间是固定的。 令种群数量翻一番所需的时间为T,则有: 故
T ln 2 r
2 N0 N0erT
模型检验 模型预测 假如人口数真能保持每34.6年增加一倍,那么人口数将 比较历年的人口统计资料,可发现人口增长的实际情况 与马尔萨斯模型的预报结果基本相符,例如, 以几何级数的方式增长。例如,到 251பைடு நூலகம்年,人口达 19612 年世界人 ×1014个, 口数为30.6 (即3.06×109),人口增长率约为 即使海洋全部变成陆地,每人也只有 9.3平方英尺的活动范围, 2%,人口数 Malthus模型实际上只有在群体总 大约每 而到 2670 35年,人口达 年增加一倍。检查 36×1015 1700 个,只好一个人站在另一人的 年至1961的260年人口实际 数不太大时才合理,到总数增大时, 肩上排成二层了。 故马尔萨斯模型是不完善的。 数量,发现两者几乎完全一致,且按马氏模型计算,人口数 所以Malthus 模型假设的人口 生物群体的各成员之间由于有限的 量每34.6年增加一倍,两者也几乎相同。 净增长率不可能始终保持常数, 生存空间,有限的自然资源及食物 它应当与人口数量有关。 等原因,就可能发生生存竞争等现 象。
钋210
T=138天
铅206
若画为真品,颜料应有300年左右或300年以上的历史,容易证 明:每克白铅中钋210的分解数等于铅210的分解数(相差极微, 已无法区别)。可用前者代替后者,因钋的半衰期较短,易于 测量 。
建模: (1)记提炼白铅的时刻为t=0,当时每克白铅中铅210的分子 数为y0,由于提炼前岩石中的铀系是处于放射性平衡的,故铀 与铅的单位时间分解数相同。可以推算出当时每克白铅中铅 210每分钟分解数不能大于30000个。 若 uU0 y0 30000
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
差分方程作业题
黄冈职业技术学院
宋进健 胡敏 熊梦颖
1.一对年轻夫妇准备购买一套住房,但缺少资金近6万元。
假设它们每月可有节余900元,且有如下的两种选择:
(1)使用银行贷款60000元。
月利率0.01,贷款期25年=300个月; (2) 到某借贷公司借贷60000元,月利率0.01,22年还清。
只要(i )每半个月还316元,(ii) 预付三个月的款。
你能帮他们做出明智的选择吗? 模型假设:
(1)银行及借贷公司在贷款期限内利率不变; (2)不考虑物价变化和经济等因素从而影响利率;
(3)银行利息按复利计算且单位时间可任意缩短至时间变量连续性变化 建立模型:
对第一种情况有: 设n 年期贷款月利率为r ,共贷款 元,贷款后第k 个月时欠款余额为 元,月还款m 元。
模型求解:
由MATLAB 得出结果m=631.9345 建立模型:
对第二种情况有: 设n 年期贷款半月利率为r ,共贷款A 0元,贷款后第k 个月时欠款余额为A k 元,半月还款m 元。
模型求解:
()()
011
1,k
k
k r A A r m k N
r
+-=+-∈1
0)1()1(300
300
300
-=
⇒=++r r A A
r m N
k m r A
A
k
K ∈-+=+,)
1(1
N
k m r A
A
k
K ∈-+=+,)
1(1
()()
011
1,k
k
k r A A r m
k N
r
+-=+-∈1
0)1()1(528
528
528
-=
⇒=++r r A A
r
m A k A 0
由MATLAB 得出结果m= 313.0038
模型分析:由第一种方式计算m=631.9345小于月节余额900元,能够承受月还款;由第二种方式计算m= 313.0038小于借贷公司要求没半个月还款316元,如果按照借贷公司要求则每月还款为632元大于第一种还款方式631.9345元,故选择第一种还款方式。
2. 在一城市的某商业区内,有两家有名的快餐店“肯德基”分店和“麦当劳”分
店。
据统计每年“肯德基”保有其上一年老顾客的1/3,而另外的2/3顾客转移到“麦当劳”;每年“麦当劳”保有其上一年的老顾客的1/2,而另外的1/2顾客转移到“肯德基”。
用二维向量X k =[x k y k ]T 表示两个快餐店市场分配的情况,初始的市场分配为X 0 = [200 200]T
如果有矩阵L 存在,使得 X k +1 = LX k ,则称 L 为状态转移矩阵。
(1) 写出X k =[x k y k ]T 和X k+1=[x k +1 y k +1]T 的递推关系式,以及状态转移矩阵L 。
(2) 根据递推关系计算近几年的市场分配情况;
模型假设:
(1) 当前的肯德基和麦当劳的市场份额继续不变。
(2) 肯德基和麦当劳不推出优惠活动和新的经营计划。
模型建立:
初始的市场分配数量为:200,2000
0==y x
以一年为一时间段,则某时刻两个快餐店的顾客数量可用向量]
,[1
1y x T
X =表
示。
用向量]
,[y x X k
k T
k =表示第K 年两个快餐店顾客数量分布。
⎪⎪⎩
⎪⎪⎨⎧+
=
+
=
++x
y
y
y x
x k
k
k k
k
k 3
22
121311
1
模型求解:
故X k =[x k y k ]T
和X k+1=[x k +1
y k +1]T 的递推关系式为⎪⎪⎩
⎪
⎪⎨
⎧
+
=+
=++x
y
y y x
x k
k
k k
k
k 3
221
21311
1,状
态转移矩阵⎥⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢
⎢⎣⎡=3221213
1
L
由初始数据计算近几年的市场分配情况,MATLAB 程序如下:
x0=[200;200];
L=[1/3,1/2; 1/2,2/3]; X=x0;
x(1)=X(1);y(1)=X(2); for k=2:6 X=L*X;
x(k)=X(1);y(k)=X(2); end t=0:5;
figure,bar(t,x), figure,bar(t,y) 运行结果如下:
1
2
3
4
5
20406080100120140160180
200
肯德基五年内市场分配情况
012345
50
100
150
200
250
300
麦当劳五年内市场分配情况。
