力学的算符表示和表象
第三章 力学量的算符汇总
其中Fn, ψn 分别称为算符 F的本征值和相应的本征态, 上式即是算符F的本征方程。求解时,ψ 作为力学量 的本征态或本征函数还要满足物理上对波函数的要求 即波函数的标准条件。
问题:本征值、本征态、本征方程
§3-3 算符的运算规则 线性厄米算符
(1)线性算符
满足如下运算规律的 算符 Ô 称为线性算符
第三章 力学量的算符
§3-1 算符的引入
代表对波函数进行某种运算或变换的符号
由于算符只是一种运算符号,所以它单独存 在是没有意义的,仅当它作用于波函数上,对波 函数做相应的运算才有意义,例如:
Ôu
换的算符。
1)du / dx = v , d / dx
n
综上所述,量子力学作如下假定:
就是算符,其作用 是对函数 u 微商, 故称为微商算符。
2)x u = v, x
也是算符。 它对 u 作用 是使 u 变成 v。
体系状态用坐标表象中的波函数 ψ(r) 描 写时,坐标 x 的算符就是其自身,即
xˆ x
说明力学量在自身表象中的算符形式最简单。
而动量 px 在坐标表象(非自身表象)中的形式 必须改造成动量算符形式:
(12) 厄米算符
满足如右关系的算符 称为厄密算符.
d *Oˆ d (Oˆ )*
或 Oˆ Oˆ
性质 I: 两个厄密算符之和 仍是厄密算符。
Ô + = Ô , Û+ = Û (Ô +Û)+ = Ô + + Û+ = (Ô +Û)
问题:厄米算符
性质 II: 两个厄密算符之积一般 不是厄密算符, 除非二算符对易。 因为
注意,算符运算没有相减,因为减可用加来代替。 Ô - Û = Ô + (-Û)。
第五章 力学量的算符表示

137第5章力学量的算符表示§5.1 算符及其运算规则在第二章中,已经引入了算符的概念,动量算符和哈密顿量算符分别为∇-= i ˆp(5.1.1) )(2ˆ22r V mH +∇-= (5.1.2) 在量子力学中,算符表示对它后面的波函数的一种运算或者操作,上述的动量算符与哈密顿算符皆表示对其后面的波函数的微商运算,本章的后面将引入的宇称算符πˆ则表示对其后面的波函数的一种操作,即把波函数中的坐标变量改变一个符号。
由算符化规则可知,物理上可观测的力学量(例如,坐标、动量、角动量和能量等)与相应的算符相对应,并要求相应的算符为线性厄米特算符,力学量的取值情况由相应算符满足的本征方程的解来决定。
§5.1.1 算符及其运算规则1、线性算符138满足下列运算规则22112211ˆˆ)(ˆψψψψA c A c c c A +=+ (5.1.3)的算符Aˆ,称之为线性算符,其中,21,c c 是两个任意复常数,21,ψψ是两个任意的波函数。
在量子力学中,可观测量对应的算符都是线性算符,这是状态叠加原理所要求的。
如无特殊声明,下面所涉及到的算符皆为线性算符。
2 、单位算符若对任意的波函数ψ,算符I ˆ满足ψψ=Iˆ (5.1.4)则称Iˆ为单位算符。
3、 算符之和若对任意的波函数ψ,下式ψψψB A B Aˆˆ)ˆˆ(+=+ (5.1.5) 总是成立,则称算符B Aˆˆ+为算符A ˆ与算符B ˆ之和。
算符的加法运算满足交换律和结合律,即A B B A ˆˆˆˆ+=+ (5.1.6) C B A C B Aˆ)ˆˆ()ˆˆ(ˆ++=++ (5.1.7) 4、 算符之积两个算符A ˆ和B ˆ之积记为)ˆˆ(B A ,对任意的波函数ψ,算符)ˆˆ(B A的作用定义为下列运算)ˆ(ˆ)ˆˆ(ψψB A B A= (5.1.8)139即算符之积)ˆˆ(B A 对任意波函数的运算过程是,先用算符B ˆ对ψ进行运算,得到一个新的波函数(ψB ˆ),然后,再用算符Aˆ对(ψB ˆ)进行运算。
第二讲 力学量算符

(2-20)
ˆ,a ˆ 1 ˆ 是方向的动量算符, a ˆ 与a ˆ 满足的对易关系 a 其中 p ˆ n =a ˆ n n 1 = na ˆ n 1 ˆ a ˆ n =a N
= n n n =n n
(2-21)
ˆ 的本征值为粒子数 n 0,1, 2.... ,故称 N ˆ =a ˆ a ˆ 为粒子数算符, n 为 n 粒子态 即N
(5)证明:论据同(4) :
2 2 [ p, pf p] p f p pf p p( pf f p) p
h pf p i
5
石家庄学院量子力学考研辅导习题讲解之二 力学量算符
主讲教师
吴海滨
(6)证明:论据同(4) :
2 2 2 2 2 h [ p, f p ] pf p f p ( pf f p) p f p i
qpfp pfpq hipf qpfp pqfp hipf ( qp pq ) fp hipf hi ( fp pf )
(3)证明:同前一题论据:
[ q, fp 2 ] qfpp fppq fqpp fppq fqpp fp ( qp hi ) fqpp fpqp hifp
f ( qp pq ) p hifp 2hifp
(4)证明:根据题给对易式外,另外应用对易式
[ p , f ( q )]
h f i
( f )
df dq
2 2 2 2 [ p, p f] p f p f p p ( pf f p)
2 h 2 p [ p, f ] p f i
h 2 p f i h pf p i h f p2 i
2.7力学量算符(18)好

1
c( px ) (2)1/ 2
( x) exp( ipx x / )dx
|
c(
px
)
|2
粒子动子动量的几率密度, x
则
px px
px | c( px ) |2 dpx
px px
px | c( px ) |2 dpx
c( px ) pxc( px )dpx
( x)(i d )( x)dx dx
( x) pˆ x( x)dx
过程繁琐,略
(3) 力学量平均值公式
当系统处于状态
(r )
时,力学量
Aˆ
的平均值:
A
*
(r )
Aˆ
(r )d
3)两个力学量同时有确定值的条件
1.两个力学量同时有确定值的条件是它们有共同的本征函数。
2.两个力学量同时有确定值的条件是它们可对易:
Aˆ
n
(r )
n
当体系处在任一态中时,测量体系的能量无确定值,而有一系列可能值,
这些可能值均为 的H本ˆ 征值。这表明 的H本ˆ征值是体系能量的可测值,
将该结论推广到一般力学量算符提出一个基本假设。该假设给出了表示力 学量的算符与该力学量的关系。
力学如量果F 算有符确F定ˆ 值表,示这力个学值量就F,是那么当属Fˆ体于系该处本于征态Fˆ 的的本本征征值态。中时,
量子力学中的算符
px
i
x
,
py
i
y
,
pz
i
z
或
p
i
二.算符的一般性质
1.算符
某一种运算把函数 u 变为 v ,表为 Aˆ u v 则 Aˆ 称为一个算符。
第四章-表象—态和力学量的表达方式

归一化条件
Ψ (t )Ψ (t ) = ∑ cn (t ) = 1
+ 2 n
* * Φ + (t ) = b1* (t ) b2 (t ) L bn (t ) L
+ * n *
∞ r r Ψ (r , t ) = ∑ c n (t )ψ n (r ) n= 0
编号有时是从零开始的, 注: 编号有时是从零开始的,例如谐振子情况 r 连续谱情况
r 有时需要重新编号, 有时需要重新编号,例如氢原子情况 Ψ (r , t ) = ∑ cnlm (t )ψ nlm (r )
n
∑ c (t )
n n
2
r 2 = ∫ Ψ (r , t ) dV
r Ψ (r , t )描述状态 ⇔ {cn (t ), n = 1,2, L}描述状态
* * * Ψ + (t ) = c1 (t ) c2 (t ) L cn (t ) L
状态可由矢量描述——态矢量 态矢量 状态可由矢量描述 列矢量
矩阵元
厄米共扼——转置+共扼(F 转置+ 厄米共扼 转置
+
)
nm
* = Fmn
r ˆ r r ˆ r * ˆ 是厄米算符时 F = φ * (r )Fφ (r )dV = φ (r ) Fφ (r ) dV = F * F nm m n mn ∫ n ∫ m
(
)
(F )
+
nm
= Fnm , 即,F + = F
描述状态 前面——波函数 波函数 前面 ——算符 算符 描述力学量 r r ˆ F (r ,− ih∇ )Ψ (r , t ) 这种描述方式(坐标表象 坐标表象)不是描述态和力学量的唯一方式 这种描述方式 坐标表象 不是描述态和力学量的唯一方式 态和力学量的具体表达(描述) 态和力学量的具体表达(描述) 方式称为表象 下面从坐标表象出发讨论其它表象——表象理论 坐标表象出发讨论其它表象 下面从坐标表象出发讨论其它表象 表象理论 第1节 态的表象
25 力学量的平均值、算符表示 平均值
§2.5 力学量的平均值、算符表示—算符表示
Cartesian coordinates
Spherical coordinates
( x, y, z )
(r , , )
x r sin cos y r sin sin z r cos
r x2 y 2 z 2 z arccos x2 y 2 z 2 y arctan x
i
p r
d
( p, t )
2
表示平面波
e
pr
的所占的比重,即粒子动量取为 p 的概率。
(p,符表示—平均值
所以,动量的平均值
p
p ( p, t ) dp * ( p, t ) p ( p, t )dp
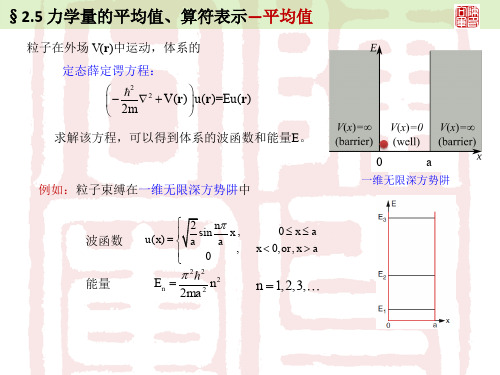
定态薛定谔方程:
2 2 V (r ) u (r )=Eu (r ) 2m
ˆ (r)=Eu(r) Hu
§2.5 力学量的平均值、算符表示—算符表示
量子力学中,描述微观粒子的力学量均有对应的算符
(1) 位矢 r r (2) 势能 V(r) V(r) (3) 动量 p
r x2 y 2 z 2 z arccos x2 y 2 z 2 y arctan x
§2.6 单电子(H)原子—中心力场薛定谔方程
From
求解中心力场中的薛定谔方程,球坐标系是自然的选择
ˆ ˆ z zp ˆ y i Lx yp ˆ ˆ x xp ˆ z i Ly zp ˆz xp ˆ y yp ˆ x i L
y z y z z x z x x y x y
第四章 表象理论1

(4.2-6)
因此算符 在Q表象中是一个矩阵, (4.2-6)式也可简写为:
称为矩阵元。
(4.2-7)
说明: 力学量算符 于表象基矢
在 表象中的矩阵元 依赖
2. 厄密矩阵 对其取复共轭得到 根据厄密算符的定义
故有:
(4.2-8)
(4.2-8)式表示算符在Q表象中的表示是一个厄密矩阵 。
补充: 1、转置矩阵:矩阵A的行列互换,所得的新矩阵称 为矩阵A的转置矩阵,用符号 表示。 即:如果,则由(43) 得到(4.1-5)
在动量表象中, 粒子具有确定动量p’ 的波函数是以动 量p为变量的函数: 同理可得: 在坐标表象中, 粒子具有确定坐标x’ 的波函数是以坐标x 为变量的函数: 坐标算符的本征值方程为:
(4.1-6)
2. 一般情况 在任意力学量Q 的表象中, 假设具有分立的本征值, 对应的本征函数是 :
体系的归一化条件 写成矩阵形式: 对表象的理解: (1) 状态ψ : 态矢量
(4.1-13)
(2) Q表象: 坐标系 (无限维希耳伯特空间)。
(3) 本征函数: (4) 基矢量的分量。
坐标系的基矢量。 是态矢量ψ 在表象中沿各
态矢 在 表象基矢上的分量
构成了 在 表象中的
表示 ,由于
构成的空间维数可以是无穷的,甚至是不
故有:
内容小节
1、表象:量子力学中状态和力学量的具体表示方式 2、ψ(x,t) 态在动量表象中的表示:
其中: 3、ψ(x,t) 态在Q表象中的波函数是:
4、力学量F在Q表象中的表示 力学量F在Q表象中的表示是一个矩阵:
其中矩阵元: 算符在自身表象中是一个对角矩阵。
§4.3 量子力学公式的矩阵表述
第四章矩阵力学基础——表象理论

第四章矩阵力学基础——表象理论部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑第四章矩阵力学基础(Ⅱ>——表象理论4.1态和算符的表象表示1.态的表象表示(1> 坐标表象以坐标算符的本征态为基底构成的表象称为坐标表象。
以一维的x 坐标为例。
算符本征方程是(4-1-1>本征函数是量子态总可按x的本征函数系展开,得<4.1.2)展开系数必就是该量子态在x表象的表示,即波函数。
(2> 动量表象以动量算符的本征态为基底构成的表象是动量表象。
选x为自变量,动量算符的本征函数是平面波。
以动量算符为例,其本征态为:b5E2RGbCAP(4 .1 .3>将量子态按展开(4 .1 .4>C(px>就是动量表象中的波函数。
这正是第二章中已熟知的结果。
动量表象也可以用动量为自变量表示。
在Px表象中,粒子具有确定动量分量Px的波函数是以Px为自变量的函数p1EanqFDPw<4.1.5)在动量表象中的波函数也可以用类似于(4. 1. 2>式的方式给出。
(3> 任意表象设有某一线性厄M算符。
为叙述方便起见,假定算符具有分立本征值谱。
它的本征方程为(4.1.6>将波函数按算符的正交归一本征函数系展开<4.1.7)展开系数{an(t>}就是波函数必在Q表象中的表示。
它可由的正交归一性推出。
将(4.1.7>式两边分别乘并对空间积分,得DXDiTa9E3d(4 .1 .8>an(t>的物理意义是:当体系处在以(r,t>所描述的状态时,力学量Q具有确定值Qn的概率是具有和波函数统计解释相同的概率解释。
因此我们可以用一组系数RTCrpUDGiT{(t>}代替户(,t>来描述该状态。
将数列 a 1(t>,a2(t>,…,an(t>,…写成一个列矩阵,则(r,t>在Q表象的表示为5PCzVD7HxA<4.1.9)它的共轭矩阵是<4.1.10)归一条件是<4.1.10)(4.1.9>式是波函数在Q表象中的表示。
量子力学导论习题答案(曾谨言)

第四章 力学量用算符表达与表象变换 4.1)设A 与B 为厄米算符,则()BA AB +21和()BA AB i-21也是厄米算符。
由此证明,任何一个算符F 均可分解为-++=iF F F ,+F 与-F 均为厄米算符,且()()+++-=+=F F iF F F F 21 ,21 证:ⅰ)()()()()BA AB AB BA B A A B BA AB +=+=+=⎥⎦⎤⎢⎣⎡++++++21212121()BA AB +∴21为厄米算符。
ⅱ)()()()()BA AB i AB BA i B A A B i BA AB i -=--=--=⎥⎦⎤⎢⎣⎡-+++++21212121()BA AB i-∴21也为厄米算符。
ⅲ)令AB F =,则()BA A B AB F ===++++,且定义 ()()+++-=+=F F iF F F F 21 ,21 (1) 由ⅰ),ⅱ)得-+-+++==F F F F ,,即+F 和-F 皆为厄米算符。
则由(1)式,不难解得 -++=iF F F4.2)设),(p x F 是p x ,的整函数,证明[][]F ,F,,pi F x x i F p ∂∂=∂∂-=整函数是指),(p x F 可以展开成∑∞==,),(n m n m mnp x Cp x F 。
证: (1)先证[][]11, ,,--=-=n n m mp ni p x xmi xp 。
[][][][][][][][]()()[]()111111331332312221111,1,3,,2,,,,,------------------=---=+--==+-=++-=++-=+=m m m m m m m m m m m m m m m m m mx m i x i x i m xxp x i m x x p x i x x p x x p x x i x x p x x p x x i xx p x p x x p同理,[][][][][][]1221222111,2,,,,,--------==+=++=+=n n n n n n n n np ni ppx pi p p x p p x p p i pp x p x p p x现在,[][]()∑∑∑∞=-∞=∞=-==⎥⎦⎤⎢⎣⎡=0,1,0,,,,n m nm mnn m n m mn n m n m mn px m i C p x p C p x C p F p而 ()∑∞=--=∂∂-0,1n m n m mn p x mi C x Fi 。
力学量与算符

令本征值 令本征值
′h2 上式可写为: λ = λ 上式可写为:
该微分方程被称为球谐方程。 该微分方程被称为球谐方程。在数学物理方法中 有专门的讲述
ˆ Aunj =anunj
j =12,3,⋅⋅⋅g ,
g 为简并度
ˆ = −ih d 的本征值及本征波函数。 的本征值及本征波函数。 例1:求解算符 Lz : dϕ
解:首先写出该算符的本征值方程为: 首先写出该算符的本征值方程为:
ˆ Φ(ϕ) =−ih d Φ(ϕ) = L Φ(ϕ) Lz z dϕ i 求解此方程: 求解此方程: dΦ i Lzϕ = Lzdϕ ⇒Φ(ϕ) =ceh Φ h
i Lz 2π eh
Φ(ϕ) =Φ(ϕ +2π)
=1
2 Lz π +isin 2πLz =1 cos h h 2πLz 2 Lz π =m2π m=0,±1±2,±3⋅⋅⋅ cos =1⇒ , h h
则本征值及本征波函数为: 则本征值及本征波函数为:
Lz = mh m=0,±1±2,±3⋅⋅⋅ , Φ(ϕ) =ceimϕ 积分常数c 利用归一化条件来确定积分常数 : 2π 1 2 2 ∫0 Φ(ϕ) dϕ = c 2π =1⇒c = 2π 最后结果: 最后结果: Lz = mh m=0,±1±2,±3⋅⋅⋅ , 1 imϕ Φ(ϕ) = e 2π
§2、力学量的测得值与平均值
问题: 问题 如何确定在一定的微观状态下, 如何确定在一定的微观状态下 微观粒子各力学量的取值呢? 微观粒子各力学量的取值呢
对微观粒子进行力学量的测量, 对微观粒子进行力学量的测量 每次测得的结果只能是该力学量算 符的所有本征值中的一个. 符的所有本征值中的一个
第三章 力学量与算符

H
U t , t0 e
力学量与算符
• • • • • 作业: 1、分析厄米算符 2、讨论幺正算符(投影算符、宇称算符) 3、算符运算的证明 4、讲课过程中的简单证明,一些概念、或 是各算符的特性
力学量与算符
定义
r r
性质 (1) 2 1 ,本征值为 1 ; (2)是厄米、幺正算符 (3)波函数和算符按宇称分类
A, 0
r r
偶宇称
奇宇称
A, 0 r r
力学量与算符
性质12完备性三宇称算符定义2是厄米幺正算符3波函数和算符按宇称分类力学量与算符4宇称算符的选择定律力学量与算符四时间演化算符不显含时间力学量与算符力学量与算符力学量与算符
力学量与算符
力学量与算符
算符的定义及运算 算符的定义 单位算符 算符的和 积 转置
ˆ F
I
ˆB ˆ B ˆ ˆ A A
d
d A B A B A B d
力学量与算符
3.2.2设算符 A、B 不可对易: A , B C ,但
A, C , B , C ,试证明Glauber公式:
e A B e A e B e
n n 1
C1 A C 0,则
A有 n 个本征值,且满足
Cnan Cn 1an 1 C1a C 0
。
力学量与算符
二、算符导数 1.定义
F F ,
为参量,
dF F F lim 0 d
2.基本性质 d A B A B
Aij
第三章-力学量的算符表示

p
'
x
(
x)
px (x)dx
CC
exp(i
px
px
x)dx
因为
1
exp(ikx)dx (k)
2
13
p'x
( x)
px
( x)dx
C
2
2 ( px
p'x
)
假如取 C
1
2
,
px (x) 的归一化为 函数
p'x
( x)
简并:一种本征值相应一种以上本征函数旳情况
简并度:相应于同一本征值旳本征函数旳数目
27
LˆzYlm mYlm
在Ylm态中,体系角动量在z方向上旳投影为m 前面几种球函数
1
Y00 4
Y1,1
3 sinei 8
Y1,0
3 cos 4
Y1,1
3 sinei 8
28
3.5 厄密算符本征函数旳性质
31
f重简并: 对一种本征值ln, 若同步有f个本征函数与之相应
属于同一种本征值ln旳简并波函数ψnk,,有
Lˆ nk ln nk , k 1, ..., f
一般来说,ψnk不正交, 但总能够找到正交函数。
例题 对下面两个氢原子旳未归一化旳1s和2s电子旳波函数
1s (r, , ) 1s (r) er /a ,
假如 Aˆ Bˆ BˆAˆ 0 则Aˆ 和Bˆ对易 记为 [ Aˆ, Bˆ] Aˆ Bˆ BˆAˆ 0
例 [xˆ, pˆ x ] ?
(xˆpˆ x
pˆ x xˆ)
ix
态和力学量的表象

.n n nc ψφ=∑第四章 态和力学量的表象量子力学中态和力学量的具体表示方式称为表象。
在前面,我们采用的表象是坐标表象,还可以用其它表象表示体系状态。
在选定了一定的表象后,力学量算符用矩阵表示,算符的运算归结为矩阵的运算。
因此,引入表象理论后的量子力学也称为矩阵力学。
本章首先给出态、算符和量子力学公式的表象表示,以及它们在不同表象间的变换关系,并证明量子力学在幺正变换下的不变性。
之后介绍文献中常见的狄拉克(Dirac )符号,最后在粒子数表象中重新讨论了线形谐振子问题。
§4.1态的表象表示由前两章讨论可知,任意波函数可按某力学量的本征函数做完全性展开例如,动量的本征函数表示组成完全系,任意波函数(,)x t ψ可以按 ()x p x ψ展开为(,)(,)()xx p x x t c p t x dp ψψ=⎰ ,展开系数(,)x c p t 由下式给出()(),(),x x p c p t x x t dx ψψ*=⎰. 设 (,)x t ψ已归一化,则容易证明(,)x c p t 也是归一化的,2(,)x t dx ψ代表体系处于(,)x t ψ所描写的态中,发现粒子位置在x x dx →+范围内的几率;2(,)x x c p t dp 代表在该态下发现粒子动量在 x x x p p dp →+范围内的几率。
(,)x c p t 和 (,)x t ψ描写同一状态。
我们称(,)x t ψ是这个状态在x -表象(坐标表象)中的波函数;(,)x c p t 是同一状态在p -表象(动量表象)中的波函数。
动量表象中的波函数(,)x c p t 以动量为自变量,它的获得是通过动量本征函数系的完全性展开取得展开系数得来的。
在量子力学中,选定一组本征函数系作为基失,就称为选定了一个表象。
这与三维空间中的坐标系类似。
表象中的基矢与坐标系中的单位矢量一样具有正交归一完全性。
所不同的是本征函数有多个,所以态矢量所在的空间是多维的函数空间。
7.2 力学量(算符)的矩阵表示

量子力学教程(第二版)
三、力学量的表象变换
ˆ L kj (y k , Ly j ) F表象(基矢yk)中,力学量L表示为矩阵(Lkj),矩阵 元 ˆ F′表象(基矢y)中,力学量L表示为矩阵(L'b),矩阵元 L b (y , Ly b )
y
y k (y k , y )
a
k
k
ˆ Ly
k
7.2 力学量(算符)的矩阵表示
量子力学教程(第二版)
两边左乘 y
bj
j
,取标积,得
ˆ (y j , Ly k )a k
k
L
k
jk
ak
(6 )
其中
ˆ L jk (y j , Ly k )
(7 )
式(6)表示成矩阵形式则为
b1 b2 L1 1 L21 L1 2 L22 ... a 1 ... a 2
sin q A1 co s q A 2
7.2 力学量(算符)的矩阵表示
量子力学教程(第二版)
把矢量逆时针方向旋转q角的操作可用R(q )刻画
co s q R (q ) sin q
sin q
co s q
(4)
它的矩阵元是描述基矢在旋转下如何变化的. 例如第一列元素
xy
n
1
n 2
y
n 1
n 1
y n 1 2
(9 )
d dx
y
n
n 2
y
n 1
n 1
y n 1 2
第3章 力学量用算符表达

证明如下:
设
Aˆn Ann,
Aˆ m Amm,
并设 m,n 存在, 对 Aˆm Amm, 取复共轭, 得到
* 定义一个量子体系的任意两个波函数(态) 与
的标积
, d *
d 是指对体系的全部空间坐标进行积分,
d 是坐标空间体积元.
则可以证明:
, 0
,* ,
,c11 c22 c1 ,1 c2 ,2
c11 c22, c1* 1, c2* 2,
式中 c1 与 c2 为任意常数.
第3章
力学量用算符表达
3.1 算符的运算规则
量子力学中的算符, 表示对波函数(量子态)的一 种运算.例如
d ,V (r) , ,2
dx
讨论 量子力学中算符的一般性质:
(a)线性算符
凡满足下列规则的算符 Aˆ , 称为线性算符,
Aˆ c11 c22 c1Aˆ1 c2 Aˆ2
其中 1 和 2是任意两个波函数,c1 与 c2 是
F x eax, 可定义
F
d dx
a
e
d dx
n0
an n!
dn dxn
.
ad
e dx
x
x
a
算符
a
e
d dx
的物理意义,
是与体系沿 x方向平移a
有关的算符.
两个(或多个)算符的函数也可类似定义.
令
F n,m
x,
y
n xn
m y m
F
x,
y,
则
F ˆ, Bˆ Fn,m 0, 0 ˆ nBˆ m. n,m0 n!m!
r
将(3)式两 边分别对 x y z 求偏导数得:
3.1表示力学量的算符

§3.1 表示力学量的算符一、算符的定义:算符是指作用一个函数上得出另一个函数的运算符号。
v u F =表示F 把函数u 变成 v ,F就是这种变换的算符。
为强调算符的特点,常常在算符的符号上方加一个“^”号。
但在不会引起误解的地方,也常把“^”略去。
算符的本征值和本征函数:λψψ=F本征值方程,ψ叫本征值λ的本征函数。
二、算符的一般特性 1、算符相等若两个算符Â、ˆB 对体系的任何波函数ψ的运算结果都相同,即ˆˆA B ψψ=,则算符Â和算符ˆB相等记为ˆˆA B =。
2、单位算符:对波函数运算后保持不变的算符称为单位算符。
ψψ=I (4-2)式中ψ为任意波函数,简记为I3、算符之和若两个算符Â、ˆB对体系的任何波函数ψ有:ˆˆˆˆˆ()A B A B C ψψψψ+=+=,则ˆˆˆAB C += (4-3)称为算符之和。
ˆˆˆˆA B B A +=+,ˆˆˆˆˆˆ()()A B C A B C ++=++4、算符之积算符Â与ˆB之积,记为ˆˆAB ,定义为 ˆˆˆˆ()()ABA B ψψ=ˆC ψ= (4-4) ψ是任意波函数。
一般来说算符之积不满足交换律,即ˆˆˆˆABBA ≠。
但算符之积的结合律仍然成立,即)()(C B A C B A =5、逆算符(1). 定义: 设Âψ=φ, 能够唯一的解出ψ, 则可定义算符Â之逆Â-1为: 1ˆAφψ-= 若算符Â之逆Â-1存在,则11ˆˆˆˆAAA A I --==, 1ˆˆ[,]0AA -= (4-8) 推论1: 若[]I B A=,(或[]I A B =,,则1-=A B推论2:若Â,ˆB均存在逆算符, 则)(B A的逆算符也存在,且 111ˆˆˆˆ()ABB A ---= (4-9) 证明:因为Â,ˆB均存在逆算符,则 I A A A I A A B B A A B B A====------111111)())((6、线性算符满足如下运算规律的算符Â,称为线性算符11221122ˆˆˆ()A c c c A c A ψψψψ+=+ (4-1) 其中c 1, c 2是任意复常数,ψ1, ψ2是任意两个波函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)
(二)再论(归一化的) r , t 和 C r , t 的物理意义
2 2
与波函数相联系的粒子,一般既不具有精确的位置,有不具有精确的动量。一般 地,对于 ψ 表示的单个粒子系统,要对该粒子的动力学变量中的这个或者那个做测量 时,我们不能对测量结果做确定的预言,但是对于 N 个大量数目、彼此独立的等价系统 (每个系统都由同一波函数 ψ 描述) ,如果我们对它们中的每一个做位置测量,则 给
i 3
e
dp
-2-
drdr * r , t r , t i 3 r r dr * r , t i dr r , t 3 r r dr * r , t i r , t
(15) (16) (17)
ˆ y r , t dr p y * r , t p ˆ z r , t dr pz * r , t p
不难证明,对于正整数 n,有
ˆ x n r , t dr px n * r , t p
(1)
等均代表对 的运算。概括起来讲,设某种运算将函数 变为函数 u,记作
ˆ u Fv
ˆ 称作算符。若算符 F ˆ 满足 则表示这种运算的符号 F
(2)
ˆ c v c v c F ˆ ˆ F 1 1 2 2 1 v1 c2 Fv2
(3)
ˆ 为线性算符。动量算符, 其中 v1 和 v2 是任意函数, c1 和 c2 是常数(一般为复数) ,则称 F
2
C p, t
1
2
2
3
2
r , t e
i
Et p r
dr
(7)
给出。因此,动量 p 的平均值可以表示为
p C p, t pdp C * p, t pC p, t dp
(8)
这里已经用了 若 r , t 归一,则 C p, t 也归一的条件。
2
-1-
出的就是这个量子统计系统成员数 N 趋于无穷大极限下,N 次测量结果的分布,则 C 给 出动量测量结果的分布。 (三)在坐标和动量表象中的力学量平均值 (1)首先讨论坐标表象的情况。对以波函数 r , t 描写的状态,按照波函数的统计 2 解释, r , t dr 表示在 t 时刻在 r r dr 中找到粒子的几率,因此坐标 r 的平均值显 然是
(24)
一般地,微观粒子的任何一个力学量 F 的平均值总可以表示为
ˆ dr o *o
ˆ 由经典表达式 o r , p 中将 p 换成算符 p 而得出,即 力学量的算符 o
ˆo ˆ r , p o ˆ r , i o
(25)
ˆ 是力学量 o 相应的算符。如果该力学量 o 在经典力学中有相对的力学量,则表示该 其中 o
(9) 这样我们就找到了一个用波函数 r , t 直接计算动量平均值的公式,即只需以微分算符 i 作用在 r , t 之上,然后乘以 * r , t ,再对全空间积分就可以了。记动量算符为
ˆ -i p
(10)
则 (9)式 可表为:
ˆ r , t dr p p * r , t p
1 dr * r , t dr r , t 2 1 dr * r , t dr r , t 2
pe
3
i
p r r
dp
i p r r
*
n ˆx r , t dr r , t Cn p n
ˆ x r , t dr r , t G p r , t G r , t dr i x
-3-
(20)
上面的结果立即可以推广到三维情形:
第四章 力学的算符表示和表象
§1 力学量的平均值
在量子力学中,微观粒子的运动状态用 波函数来描述。一般认为,一旦给出了波函 数 ψ,就确定了微观粒子的运动状态。但波函数本身不是直接的可观测量,当微观粒子处 于某一状态时,粒子的力学量一般不具有确定的值,而是具有一系列的可能值,每一可能 值以一定的几率出现。 当给定描述粒子运动状态的波函数 ψ 后力学量出现的各种可能值的 相应几率就完全确定。利用统计平均的方法,可以算出该力学量的平均值,进而和实验观 测值做比较。原则上,一切力学量的平均值都能由 ψ 给出,而且这些平均值就是在 ψ 所描 写的状态下相应的力学量的观测结果。在这种意义下,一般认为,波函数描写了粒子的运 动状态。
2
(6)
2 因为 r , t dr 只表示粒子在 r r dr 中的几率,而不代表在 p p dp 中找到粒子的
要计算 p ,就应该先找出在 t 时刻在 p p dp 中找到粒子的几率 C p, t dp 。而 C p, t 由公式
例如:
ˆx,B ˆ d A dx ˆ ˆ x x df xf ABf dx ˆ ˆ x d xf x df f xf f BAf dx dx
(8)
(9)
(3)算符之积 ˆ 与B ˆB ˆ ,定义为 ˆ 之积 A 算符 A
ˆ ˆ A ˆ B ˆ AB
且满足 但不满足交换律
ˆ ˆ BA ˆˆ AB
(乘法结合律) (分配率)
ˆ B ˆ AB ˆ ˆ ACs ˆˆ ˆ C A
(10)
ˆ 和B ˆ 在一般的情况下不能交换顺序。 即两个线性算符 A
(一)统计平均值的意义
如果通过一系列的实验测定系统的一个状态参量 ξ,得到相应的值为 A1,A2……AS,在 总的试验次数 N 中,得到这些值的次数分别是 N1,N2,……NS,则 ξ 的(算数)平均值为
AN
i 1
Ai
i 1
s
Ni N
(1)
i
当总的试验次数 N 时,量 ξ 的平均值的极限便是ξ的统计平均值
积分算符等都是线性算符。量子力学碰到的算符并不都是线性算符,例如取复共轭就不是 线性算符。但是刻画可观测量的算符都是线性的,这是态迭加原理的反应。 例:
i ˆ H t
(4)
若 1 是方程的解, 2 也是方程的解,则 C1 1 C2 2 也是体系的可能解。事实上,
i ˆ C H ˆ C1 1 C2 2 C1i 1 C2i 2 C1 H 1 2 2 t t t
(18)
对于 p y , p z 也有同样的等式。如果 G px 是 p x 的解析函数,且可展成 p x 的幂级数 G p x Cn p x n (19)
n
则有
n ˆx G px G px Cn * r , t p r , t dr n
(22)
角动量的平均值是:
L L r p * r i dr
(23)
(9)式表明:动量的平均值依赖于波函数的梯度 。按照德布罗意关系,波长越短, 动量越大。显然,若 越大,则 越短,因而动量平均值也越大。 综上所述,我们可以得出,在求平均值的意义下,力学量可以用算符来代替。当我们 用坐标表象波函数来计算动量平均值时,需要引进动量算符,除此之外,能量算符和角动 量算符也可依次引进:
(5)
ˆ 是线性算符时才有 仅当 H
ˆ C H ˆ ˆ C C1 H 1 2 2 H C1 1 2 2
ˆ 满足 若算符 I
ˆ v Iv
ˆ 为单位算符。显然 I ˆ 是线性算符。 其中 v 为任意函数,则称 I
(6)
(二)算符的运算法则
(1)算符的和 ˆB ˆ B ˆ 对任意函数 的运算结果与 A ˆ 相同。显然,算符之和 ˆ 与B ˆ 之和 A 算符 A
ˆ i p ˆ H
2
2m
2 V r
ˆ r i L ˆ yp zp i y z L x z y y z ˆ zp xp i z x L y x z z x ˆ xp yp i x y L z y x x y
G p * r , t G p r , t dr * r , t G r , t dr i
(21)
例如,动能的平均值是
T T
2 p2 * 2 dr 2m 2m
lim Ai
n i 1
s
s s Ni N Ai lim i Ai Pi N i 1 n N i 1
(2)
式中 Pi 为量 ξ 出现值 Ai 的几率。如果变量 ξ 是连续分布的,则上述统计平均值可以表示 成
A x dx
式中 x 为量 ξ 处于单位间隔内的几率,或称几率密度,或称量 ξ 的统计分布函数
-5-
满足
ˆB ˆ ˆB ˆA A
(加法交换律)
ˆ B ˆ A ˆB ˆ ˆ C ˆ C A
而且线性算符之和仍为线性算符。
(加法结合律)
(2)算符相等 ˆ 和B ˆ 对体系的任何波函数 的运算所得结果都相同 设算符 A
ˆ B ˆ A
则称两个算符相等,记作
ˆB ˆ A
(5)
其物理意义和我们对 r , t 所做的解释一样:它是 N 个大量数目的、等价的、彼此独
2
立的且由同一波函数 表示的体系做 F r 测量结果的平均值。 (2)现在讨论动量算符的平均值。显然, p 的平均值 p 不能简单的写成
