浙教版九年级数学(上)3.3_垂径定理(1) 课件
3.3 垂径定理 浙教版数学九年级上册课件

分析:要证圆是轴对称图形,只需要证明圆上任意一点关于直径
所在直线(对称轴)的对称点也在圆上.
证明:过点A作AA'⊥CD交⊙O于点B,垂足为E,连
C
接OA、OB.
在△OAAB中
∵OA=OB ∴△OAB是
__等__腰__三__角_形_
·O
又∵AB⊥CD
∴AE= ___E_B___ ( 三线合 一) ∴CD是AB的 ___垂__直__平__分__线__ .
AE
B
即对于圆上任意一点A,在圆上都有关于直线CD的对
D
称点B
∴⊙O关于直线CD对称
即圆是轴对称图形,任何一条直径所在的直
线都是它的对称轴.
垂直于弦AB的直径CD所在的直线是是⊙O的对
称轴,把圆沿着CD折叠时CD两侧的两个半圆重合,
点A与点B重合,AE与BE重合,因此, AE=BE C
弧: A⌒C=B⌒C, AD⌒=B⌒D
H,EF=10,HG=6,AH=4.求BE4.如4.如图,圆O 与矩形ABCD交于E、F、G、 H,EF=10,HG=6,AH=4.求BE的长.
• 图,圆O与矩形ABCD交于E、F、G、 H,EF=10,HG=6,AH=4.求BE的长.
• 的长.
如图,AB、AC都是圆O的 弦,OM⊥AB,ON⊥AC, 垂足分别为M、N,如果
(2)将直径AB向下或向上平移变成非直径的弦时,在圆纸片上
画出平移后的弦AB和直径CD ,交点记作点E,观察整个图形,它还
是轴对称图形吗?对称轴是什么? 图中有哪些相等的线段和弧?
为什么?
C
C
O
A
B
D
O
A
B
A
E
B
3.3垂径定理2

直径平分弦所对的弧
直径平分弦
辨一辨
(1)垂直于弦的直线平分弦,并且平分弦 所对的弧. (2)平分弦的直径垂直于弦,并且平分弦所对 的两条弧. (3)平分弦的直线,必定过圆心。
(4)弦所对的两弧中点的连线,垂直于弦,并且经过圆心.
例1、1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是 圆弧形,它的跨度(弧所对是弦的长)为 37.2 m,拱高(弧的中点 到弦的距离,也叫弓形高)为7.23m,求桥拱的半径(精确到0.01m).
第二课时
请用文字叙述垂径定理:
垂直弦的直径,平分这条弦,并且平分弦所对的弧
几何语言
直径垂直弦 如直图径∵C平CD分D⊥是弦A直B,径, 直径平分弦所对的弧
条件
∴AM=BM,
⌒A结C论=⌒BC,
⌒AD
⌒
=BD.
C
A
BM└●O逆命题?D直径垂直弦
直径平分弦 (不是直径!) 直径平分弦所对的弧
直径垂直弦
3,3垂径定理-九年级数学下册课件(北师大版)

总结
本题运用转化思想将实际问题转化为数学问题,先正确画 出图形,找出图中的已知量,然后构造直角三角形,最后利用 勾股定理求解.
1 1400年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的 跨度(即弧所 对的弦长)为37.4 m,拱高(即弧的中点到弦的距 离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1).
弦所对的弧,即:如图,在⊙O 中,
CD是直径 CD AB
CD平分AB
AD
BD
AB不是直径
AC
BC
即:如图,在⊙O 中,
CD是直径
CD AB
CD平分AB
AD
BD
AC BC
(3)平分弦所对的一条弧的直径垂直平分这条弦,并且平分弦所对的另
一条弧,即:如图,在⊙O 中,
CD是直径
1 如图,⊙O 的直径CD=10 cm,AB 是⊙O 的弦,AM=BM, OM∶OC=3∶5,则AB 的长为( A )
A.8 cm B. 91 cm C.6 cm D.2 cm
2 如图,△ABC 的三个顶点都在⊙O上,∠AOB=60°,AB=AC =2,则弦BC 的长为( C )
A. 3 B.3 C.2 3 D.4
CD AE
AB BE
AD BD
AC
BC
例3 下列说法正确的是( C ) A.经过弦的中点的直线平分弦所对的弧 B.过弦的中点的直线一定经过圆心 C.弦所对的两条弧的中点的连线垂直平分弦且经过圆心 D.弦的垂线平分弦所对的弧
例4 如图, —条公路的转弯处是一段圆弧(即图中 CD ,点O 是 CD 所在圆的圆心),其中CD= 600m, E 为CD 上一点,且OE 丄CD,垂足为F,EF =90m.求这段弯路的半径.
第十六讲 垂径定理-2021年新九年级数学(浙教版)(解析版)

第十六讲 垂径定理3.3垂径定理【学习目标】1.掌握垂径定理及其推论;2.利用垂径定理及其推论进行简单的计算和证明.【基础知识】一、垂径定理 1.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的弧.如图,几何语言为:CD 是直径 AC BC要点: 2.推论 定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.定理2:平分弧的直径垂直平分弧所对的弦. 要点:(1)分一条弧成相等的两条弧的点,叫做这条弧的中点.(2)这里的直径也可以是半径,也可以是过圆心的直线或线段. 二、垂径定理的拓展根据圆的对称性及垂径定理还有如下结论:(1)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. 要点:在垂径定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)【考点剖析】例1.如图,在⊙O 中,C 为弦AB 上一点,AC =2,BC =6,⊙O 的半径为5,则OC =( )A .13B .4C .3D .23【答案】A 【解析】过点O 作OD ⊥AB 于点D ,连接OA ,先根据垂径定理求出AD 的长,再由勾股定理求出OD 的长,在Rt △OCDCD ⊥ABAE=BE中根据勾股定理即可得出OC的长.解:过点O作OD⊥AB于点D,连接OA,∵AC=2,BC=6,∴AB=8,∴AD=12AB=4,在Rt△AOD中,OA=5,AD=4,∴OD=22OA AD=3,在Rt△COD中,OD=3,CD=AD-AC=4-2=2,∴OC=,故选:A..【点睛】此题考查圆的垂径定理,勾股定理,根据题意引出辅助线,利用垂径定理和勾股定理进行计算是解题的关键.例2.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有()A.1组B.2组C.3组D.4组【答案】D【解析】先根据OH⊥AB于点H可知,AH=BH,CH=DH,故可得出AC=BD,AD=BC,进而可得出结论.解:由垂径定理知,点H是AB的中点,也是CD的中点,则有CH=HD,AH=HB,所以AD=BC,AC =BD.所以共有4组相等的线段.故选:D.【点睛】本题考查的是垂径定理,熟知垂直于弦的直径平分弦是解答此题的关键.例3.下列说法错误的是()A.垂直于弦的直径平分弦B.垂直于弦的直径平分弦所对的弧C.平分弦的直径平分弦所对的弧D.平分弧的直径垂直平分弧所对的弦【答案】C【详解】根据垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧,故选项A、B正确;C中,当被平分的弦是直径时,平分弦的直径不一定平分弦所对的弧;D中,平分弧的直径垂直平分弧所对的弦正确.故选C.例4.如下图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB 交于点D,则AD的长为A .95B .C .185D .52【答案】C 【解析】如图,过C 作CM ⊥AB ,交AB 于点M ,由垂径定理可得M 为AD 的中点,∵ABC 11S AC BC AB CM 22∆=⋅=⋅,且AC=3,BC=4,AB=5, ∴12CM 5=.在Rt △ACM 中,根据勾股定理得:222AC AM CM =+,∴222128199AM AM AM 5255⎛⎫=+⇒=⇒= ⎪⎝⎭(舍去负值). ∴18AD 2AM 5==.故选C . 例5.如图,拱桥可以近似地看作直径为250m 的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB 长度为150m ,那么这些钢索中最长的一根的长度为( )A .50mB .40mC .30mD .25m 【答案】D 【解析】设圆弧的圆心为O ,过O 作OC ⊥AB 于C ,交AB 于D ,连接OA ,先由垂径定理得AC =BC =12AB =75m ,再由勾股定理求出OC =100m ,然后求出CD 的长即可. 【详解】解:设圆弧的圆心为O ,过O 作OC ⊥AB 于C ,交AB 于D ,连接OA , 则OA =OD =12×250=125(m ),AC =BC =12AB =12×150=75(m ), ∴OC =22OA AC -=2212575-=100(m ),∴CD =OD ﹣OC =125﹣100=25(m ),即这些钢索中最长的一根为25m , 故选:D .【点睛】本题考查了垂径定理和勾股定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.例6.如图,在圆O 中,弦AB=4,点C 在AB 上移动,连接OC ,过点C 作CD ⊥OC 交圆O 于点D ,则CD 的最大值为 ( )A .22B .2C .32D .【答案】B 【解析】连接OD ,利用勾股定理得到CD ,利用垂线段最短得到当OC ⊥AB 时,OC 最小,根据垂径定理计算即可.【详解】连接OD ,如图,设圆O 的半径为r , ∵CD ⊥OC , ∴∠DCO=90°, ∴CD=2222OD OC r OC -=-,∴当OC 的值最小时,CD 的值最大,而OC ⊥AB 时,OC 最小, 此时D 、B 重合,则由垂径定理可得:CD=CB=AC=12AB=2, ∴CD 的最大值为2. 故答案为:2.【点睛】本题考查垂径定理和勾股定理,作辅助线构造直角三角形应用勾股定理,并熟记垂径定理内容是解题的关键.例7.如图,在平面直角坐标系中,P 的圆心是,半径为3,函数y x =的图象被P 截得的弦AB的长为42a 的值是( ) A .23B .22+C .22D .32+【答案】D【解析】PC ⊥x 轴于C ,交AB 于D ,作PE ⊥AB 于E ,连结PB ,由于OC=3,PC=a ,易得D 点坐标为(3,3),则△OCD 为等腰直角三角形,△PED 也为等腰直角三角形.由PE ⊥AB ,根据垂径定理得AE=BE=122在Rt △PBE 中,利用勾股定理可计算出PE=1,则22所以2 【详解】过P 作PC x ⊥轴于点C ,交AB 于点D ,作于点E ,连接PB ,如图.的圆心坐标是(3,),3,a OC PC a ∴==, 把3x =代入y x =得3y =, D ∴点坐标为,OCD ∴为等腰直角三角形, PED ∴也为等腰直角三角形.,PE AB ⊥1222AE BE AB ∴===, 在Rt PBE △中,3,PB = ,32a ∴=+.故选D . 【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和等腰直角三角形的性质.例8.如图,⊙O 的半径OD 垂直于弦AB ,垂足为点C ,连接AO 并延长交⊙O 于点E ,连接BE ,CE .若AB =8,CD =2,则△BCE 的面积为( )A .12B .15C .16D .18【答案】A 【详解】∵⊙O 的半径OD 垂直于弦AB ,垂足为点C ,AB=8,∴AC=BC=12AB=4. 设OA=r ,则OC=r ﹣2, 在Rt △AOC 中,∵AC 2+OC 2=OA 2,即42+(r ﹣2)2=r 2,解得r=5, ∴AE=10,∴BE=22221086AE AB -=-= ,∴△BCE 的面积=12BC•BE=12×4×6=12. 故选A .例9.如图,点P 是等边三角形ABC 外接圆⊙O 上的点,在以下判断中,不正确的是A .当弦PB 最长时,ΔAPC 是等腰三角形 B .当ΔAPC 是等腰三角形时,PO ⊥AC C .当PO ⊥AC 时,∠ACP=30°D .当∠ACP=30°时,ΔPBC 是直角三角形 【答案】C 【解析】根据圆和等边三角形的性质逐一作出判断 【详解】当弦PB 最长时,PB 是⊙O 的直径,所以根据等边三角形的性质,BP 垂直平分AC ,从而根据线段垂直平分线上的点到线段两端距离相等的性质得PA=PC ,即ΔAPC 是等腰三角形,判断A 正确;当ΔAPC 是等腰三角形时,根据垂径定理,得PO ⊥AC ,判断B 正确;当PO ⊥AC 时,若点P 在劣弧AC 上,则∠ACP=30°,若点P 在优弧AC 上,则点P 与点B 重合,∠ACP=60°,则∠ACP=60°,判断C 错误; 当∠ACP=30°时,∠ABP=∠ACP=30°,又∠ABC=60°,从而∠PBC=30°;又∠BPC=∠BAC=60°,所以,∠BCP=90°,即ΔPBC 是直角三角形,判断D 正确. 故选C .例10.如图,AB 是O 的弦,OC AB ⊥交O 于点C ,点D 是O 上一点,,则BOC ∠的度数为( ).A .30°B .40°C .50°D .60°【答案】D 【解析】由垂径定理、等腰三角形的性质和平行线的性质证出∠OAC=∠OCA=∠AOC ,得出△OAC 是等腰三角形,得出∠BOC=∠AOC=60°即可. 【详解】解:如图,∵, ∴.∵AB 是O 的弦,OC AB ⊥交O 于点C , ∴AC BC =. ∴. 故选D .【点睛】本题考查垂径定理,解题关键证明AC BC =.例11.如图,在半径为3的O 中,B 是劣弧AC 的中点,连接AB 并延长到D .使BD AB =,连接AC 、BC 、CD ,如果2AB =,那么CD 等于( ) A .2 B .1C .23D .43【答案】D 【解析】BD AB =,BC AB =,得ACD 是直角三角形,以AB 为底1h 为高和以BO 为底2h 为高都等于2ABO S,12AB h BO h ⨯=⨯,221()222AB h AO =-=122224233AB h h BO ⨯⨯===28223AC h =⨯=,2243CD AD AC =- 【详解】解:∵BD AB =,BC AB =, ∴ACD 是直角三角形,设AOB 以AB 为底的高为1h ,BO 为底的高为2h , ∴221()2AB h AO =-, ∵3AO =,2AB =, ∴22123()222h =-=,∵以AB 为底1h 为高与AB 之积和以BO 为底2h 为高与BO 之积都等于2ABO S∴12AB h BO h ⨯=⨯, ∴122224233AB h h BO ⨯⨯===,∴28223AC h =⨯=,∴2243CD AD AC =-=.本题的答案是:D 【点睛】考查垂径定理和三角形中位线的性质的综合应用.例12.如图,在半圆O 中,直径4AB =,C 是半圆上一点,将弧AC 沿弦AC 折叠交AB 于D ,点E 是弧AD 的中点.连接OE ,则OE 的最小值为( )A 21B .42-C 21D .222【答案】D 【解析】把弧AEC 的圆补全为⊙F ,可知点F 与点O 关于AC 对称,求出∠F=90°,CE 长,OE 的最小值为EC-OC .【详解】解:把弧AEC 的圆补全为⊙F ,可知点F 与点O 关于AC 对称,半径为2, ∴∠FCA=∠ACO , ∵OA=OC ,∴∠ACO=∠CAO , ∴∠FCA=∠CAO ,∴CF ∥AB ,∵E 是弧AD 的中点, ∴FE ⊥AB ,∴∠F=∠BGE=90°, ∵FC=FE=2, ∴EC=22, ∵OE≥EC -OC 即OE≥22-2,OE 的最小值为222-,故选:D .【点睛】本题考查了轴对称、垂径定理、勾股定理和圆的有关知识,解题关键是通过作辅助线,根据三角形三边关系确定OE 的取值范围.【过关检测】一、单选题1.如图所示,如果AB 为⊙O 的直径,弦CD AB ⊥,垂足为E ,那么下列结论中,错误的是( )A .CE DE =B .BC BD =C .D .AC AD >【答案】D 【解析】根据垂径定理逐个判断即可. 【详解】解:AB 为⊙O 的直径,弦CD ⊥AB 垂足为E , 则AB 是垂直于弦CD 的直径,就满足垂径定理. 因而CE =DE ,BC BD =,∠BAC =∠BAD 都是正确的.根据条件可以得到AB 是CD 的垂直平分线,因而AC =AD .所以D 是错误的. 故选:D . 【点睛】本题主要考查的是对垂径定理的记忆与理解.2.如图,AB 是O 的直径,弦CD AB ⊥于点E ,,则AE 的长为( )A .2cmB .8cmC .16cmD .18cm 【答案】D 【详解】解:∵弦CD AB ⊥于点E ,12cm CD =,∴16(cm)2CE CD ==.在Rt OCE 中,,∴,∴. 3.往直径为52cm 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为( )A .8cmB .10cmC .14cmD .16cm 【答案】D 【解析】连接OB ,过点O 作OC ⊥AB 于点D ,交⊙O 于点C ,先由垂径定理求出BD 的长,再根据勾股定理求出OD 的长,进而可得出CD 的长. 【详解】解:连接OB ,过点O 作OC ⊥AB 于点D ,交⊙O 于点C ,如图所示:∵AB =48cm , ∴BD =12AB =12×48=24(cm ), ∵⊙O 的直径为52cm ,∴OB =OC =26cm ,在Rt △OBD 中,(cm ),∴CD =OC -OD =26-10=16(cm ), 故选:D . 【点睛】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键. 4.CD 是圆O 的直径,弦AB ⊥CD 于点E ,若OE =3,AE =4,则下列说法正确的是( )A .AC 的长为B .CE 的长为3C .CD 的长为12 D .AD 的长为10 【答案】A 【解析】连接AO ,分别在Rt △AOE 中,Rt △ACE 中,Rt △ADE 中,根据勾股定理即可求得相应线段的长度,依此判断即可. 【详解】解:连接AO ,∵AB ⊥CD 于点E ,OE =3,AE =4, ∴在Rt △AOE 中,根据勾股定理5AO ==,∵CD 为圆O 的直径, ∴OC=OD=OA=5,∴CD=10,CE=OC-OE=2,故B 选项和C 选项错误; 在Rt △ACE 中,根据勾股定理 ,故A 选项正确;在Rt △ADE 中,根据勾股定理AD ===D 选项错误;故选:A .【点睛】本题考查勾股定理,同圆半径相等.正确作出辅助线,构造直角三角形是解题关键.注意圆中半径相等这一隐含条件. 5.如图,在O 中,弦//AB CD ,OP CD ⊥,OM MN =,18AB =,12CD =,则O 的半径为( ) A .4B .42C .46D .43【答案】C 【解析】连接OA ,OC ,根据垂径定理得CN =6,AM =9,设O 的半径为x ,根据勾股定理列出方程,即可求解. 【详解】解:连接OA ,OC ,∵//AB CD ,OP CD ⊥, ∴OP AB ⊥,∵18AB =,12CD =, ∴CN =6,AM =9, 设O 的半径为x , ∵OM MN =, 2222629x x -=-46x =46-经检验是方程的根,且符合题意, ∴O 的半径为46故选C . 【点睛】本题主要考查垂径定理,勾股定理,添加辅助线,构造直角三角形,是解题的关键.6.如图,AB 为⊙O 的直径,弦CD AB ⊥于点F ,OE AC ⊥于点E ,若3OE =,5OB =,则CD 的长度是( ) A .9.6 B .45C .53D .19【答案】A 【解析】先利用垂径定理得出AE =EC ,CF =FD ,再利用勾股定理列方程即可【详解】 解:连接OC∵AB ⊥CD , OE ⊥AC ∴ AE =EC ,CF =FD ∵OE =3,OB =5 ∴OB =OC =OA =5 ∴在Rt △OAE 中∴AE =EC =4设OF =x ,则有2222AC AF OC OF -=-x =1.4在Rt △OFC 中, ∴29.6CD FC == 故选:A 【点睛】本题考查垂径定理、勾股定理、方程思想是解题关键 7.如图,已知O 的半径为5,弦8,AB P =为AB 上的动点(不与端点,A B 重合),若线段OP 的长为正整数,则满足条件的点P 的个数有( )A .1个B .2个C .3个D .5个【答案】C 【详解】当P 为AB 的中点时,由垂径定理可知此时OP 最短.O 的半径为5,弦8,AB =∴此时3OP =;当点P 与点A 或点B 重合时,此时OP 最长,5,35OP OP =∴≤<.3OP ∴=或4,根据圆的对称性可知,满足条件的点P 的个数有3个.8.如图,,,AB AC BC 都是O 的弦,,OM AB ON AC ⊥⊥,垂足分别为M ,N ,若2MN =,则BC 的值为( )A .3.5B .2C .3D .4【答案】D 【详解】根据垂径定理,得M ,N 分别是AB 与AC 的中点,故MN 是ABC 的中位线,由三角形的中位线定理得24BC MN ==. 9.如图,在半径为5的O 中,半径OD ⊥弦AB 于点C ,连接AO 并延长交O 于点E ,连接EC EB 、.若2CD =,则EC 的长为( )A .B .8C .D .【答案】D 【解析】由垂径定理和勾股定理得4AC BC ==,再证OC 是△ABE 的中位线,得26BE OC ==,然后由勾股定理求解即可. 【详解】解:∵⊙O 的半径为5, ∴OA =OD =5, ∵CD =2,∴3OC OD CD =-=, ∵OD ⊥AB , ∴,∵OA =OE ,∴OC 是△ABE 的中位线, ∴BE =2OC =6, ∴,故选:D . 【点睛】本题考查了垂径定理、勾股定理以及三角形中位线定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.10.如图,矩形ABCD 中,60AB =,45AD =,P ,Q 分别是AB ,AD 边上的动点,52PQ =,以PQ 为直径的O 与BD 交于点M ,N .则MN 的最大值为( ).A .48B .45C .42D .40 【答案】A 【解析】过A 点作AH ⊥BD 于H ,连接OM ,如图,先利用勾股定理计算出BD =75,则利用面积法可计算出AH =36,再证明点O 在AH 上时,OH 最短,此时HM 有最大值,最大值为24,然后根据垂径定理可判断MN 的最大值. 【详解】解:过A 点作AH ⊥BD 于H ,连接OM ,如图,在Rt △ABD 中,BD 75==,∵12×AH ×BD =12×AD ×AB , ∴AH ==36, ∵⊙O 的半径为522=26, ∴点O 在AH 上时,OH 最短,∵HM∴此时HM有最大值,最大值为:24,∵OH⊥MN,∴MN=2MH,∴MN的最大值为2×24=48.故选:A.【点睛】本题考查了垂径定理:直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了矩形的性质和勾股定理.11.如图,在⊙O中,∠AOB+∠COD=180°,弦CD=6,OE⊥AB于点E.则OE的长为()A.3 B.C.D.6【答案】A【解析】过O作OF⊥CD于F,由OC=OD,由三线合一可得CF=DF=132CD=,∠COF=∠DOF=12COD∠,由OE⊥AB,OA=OB,由三线合一AE=BE,∠AOE=∠BOE=12AOB∠,可得∠COF+∠AOE90=︒,由∠AOE+∠EAO=90°,可得∠EAO=∠COF,可证△AOE≌△OCF(AAS)可得OE=CF=3即可.【详解】解:过O作OF⊥CD于F,∵OC=OD,∴CF=DF=116322CD=⨯=,∠COF=∠DOF=12COD∠∵OE⊥AB,OA=OB,∴AE=BE,∠AOE=∠BOE=12AOB ∠,∴∠COF+∠AOE =12COD∠+12AOB∠=,又∵∠AOE+∠EAO=90°,∴∠EAO=∠COF,在△AOE和△OCF中,,∴△AOE≌△OCF(AAS),∴OE=CF=3.故选择:A.【点睛】本题考查等腰三角形性质,互余角性质,三角形全等判定与性质,圆的性质掌握等腰三角形性质,互余角性质,三角形全等判定与性质,圆的性质是解题关键.12.如图,在Rt△ABC中,∠ACB=90°,分别以AB,BC,CA为直径作半圆围成两月牙形,过点C作DF//AB 分别交三个半圆于点D,E,F.若,AC+BC=15,则阴影部分的面积为()A .16B .20C .25D .30【答案】C 【解析】连接AF ,BD ,先证明四边形ABDF 是矩形,然后由垂径定理,矩形的性质,勾股定理,表示出相应的线段长度,结合AC +BC =15,求出k 的值,得到各个扇形的半径,再利用间接法求出阴影部分的面积. 【详解】解:连接AF ,BD ,如图,∵AC 、BC 是直径, ∴∠AFC =90°,∠BDC =90°, ∵DF //AB ,∴四边形ABDF 是矩形, ∴AB =FD ;取AB 的中点O ,作OG ⊥FD , ∵,则设10DF k =,6CE k =,由垂径定理,则132CG CE k ==, ∴5OC OA OB k ===,∴4OG k =,,2CF DE k ==,由勾股定理,则AC ==,,∵AC +BC =15,∴15+=,∴k =;∴5AC =,10BC =,AB DF == ∴阴影部分的面积为 ∴; 故选:C . 【点睛】本题考查了垂径定理,矩形的判定和性质,勾股定理,以及求不规则图形的面积,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而求出线段的长度,进而求出面积.二、填空题13.如图,⊙O 的直径CD =20,AB 是⊙O 的弦,且AB ⊥CD ,垂足为M ,若CM =4,则AB 的长为_____.【答案】16【解析】连接OA,根据勾股定理求出AM,根据垂径定理求出AB=2AM.【详解】解:连接OA,∵⊙O的直径CD=20,∴OA=OC=10,∵CM=4,∴OM=10﹣4=6,在Rt OAM中,由勾股定理得:AM8,∴由垂径定理得:AB=2AM=16.故答案为:16.【点睛】本题考查了垂径定理和勾股定理的应用,关键是构造直角三角形.14.如图,在残破的圆形工件上量得一条弦BC=16,BC的中点D到BC的距离ED=4,则这个圆形工件的半径是_____.【答案】10.【解析】由DE⊥BC,DE平分弧BC,根据垂径定理的推论得到圆心在直线DE上,设圆心为O,连结OB,设圆的半径为R,根据垂径定理得BE=CE=12BC=8,然后根据勾股定理得到R2=82+(R﹣4)2,再解方程即可.【详解】∵DE⊥BC,DE平分弧BC,∴圆心在直线DE上,设圆心为O,如图,连结OB,设圆的半径为R,则OE=R﹣4,∵OE⊥BC,∴BE=CE=12BC=12×16=8,在Rt△OEB中,OB2=BE2+OE2,即R2=82+(R﹣4)2,解得R=10,即这个圆形工件的半径是10.故答案为10【点睛】本题考查了垂径定理的应用:垂径定理的应用很广泛,常见的有:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.15.过O内一点N的最长弦为6,最短的弦长为4,那么ON的长为=_________【解析】根据圆中的概念,首先应明确过一点圆中最长的弦是过这点的直径,最短的弦是垂直于这点和圆心的连线的弦,从而根据垂径定理和勾股定理进行计算.【详解】解:如图所示,直径AB是过点N的最长的弦,过点N作弦CD⊥AB,则CD是过点N的最短的弦,连接OC.∵ON⊥CD,∴CN=12CD=2,∵OC=3,∴ON=,【点睛】此题考查了垂径定理和勾股定理,难点在于弄清过圆内一点的最长的弦和最短的弦.16.如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为____.【答案】cm【解析】设OB=rcm,由于刻度尺的宽为2cm,所以OC=r-2,再根据另一边与圆两个交点处的读数恰好为“2”和“8”可求出BC的长,在Rt△OBC中利用勾股定理即可得出r的值.【详解】根据题意获得下图:设OB=r cm,∵刻度尺的宽为2cm,∴OC=r-2,∵另一边与圆两个交点处的读数恰好为“2”和“8”,∴BC=12×6=3,在Rt△OBC中,∵OB2=OC2+BC2,即r2=(r-2)2+32,解得r= cm.故答案为cm.【点睛】本题考查的是垂径定理的应用及勾股定理,根据题意得出BC=3是解答此题的关键.17.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=12∠BOD,则⊙O的半径为___.【答案】5 【解析】先根据∠BAC=12∠BOD可得出弧BC=弧BD,故可得出AB⊥CD,由垂径定理即可求出DE的长,再根据勾股定理即可得出结论.【详解】∵∠BAC=12∠BOD,∴弧BC=弧BD,∴AB⊥CD,∵AE=CD=8,∴DE=12CD=4,设OD=r,则OE=AE−r=8−r,在Rt△ODE中,OD=r,DE=4,OE=8−r,∵OD=DE+OE,即r=4+(8−r) ,解得r=5.故答案为5.【点睛】此题考查垂径定理,勾股定理,圆周角定理,解题关键在于得出AB⊥CD.18.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P P的坐标为_______.【答案】(3,2).【解析】过点P作PD⊥x轴于点D,连接OP,先由垂径定理求出OD的长,再根据勾股定理求出PD的长,故可得出答案.【详解】过点P作PD⊥x轴于点D,连接OP,∵A(6,0),PD⊥OA,∴OD=12OA=3,在Rt△OPD中∵OD=3,∴PD=2∴P(3,2) .故答案为(3,2).【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.19.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=2cm,则球的半径为____cm.【答案】5 4【解析】首先找到EF 的中点M ,作MN ⊥AD 于点M ,取MN 上的球心O ,连接OF ,设OF =x ,则OM 是2﹣x ,MF =1,然后在直角三角形MOF 中利用勾股定理求得OF 的长即可. 【详解】解:EF 的中点M ,作MN ⊥AD 于点M ,取MN 上的球心O ,连接OF ,∵四边形ABCD 是矩形, ∴∠C =∠D =90°,∴四边形CDMN 是矩形, ∴MN =CD =2设OF =x ,则ON =OF ,∴OM =MN ﹣ON =2﹣x ,MF =1,在直角三角形OMF 中,OM 2+MF 2=OF 2, 即:(2﹣x )2+12=x 2,解得:x =54, 故答案为:54.【点睛】本题考查了垂径定理及勾股定理的知识,解题的关键是正确的作出辅助线构造直角三角形.20.如图,AB 是⊙o 的直径,CD 是弦,若AB=10cm ,CD=8cm ,那么A 、B 两点到直线CD 的距离之和为__________.【答案】6cm. 【解析】试题分析:过O 作OG ⊥CD 于G ,连接OC ,如图所示,∵OG ⊥CD ,CD=8cm ,∴G 为CD 的中点,即CG=DG=4cm ,在Rt △OCG 中,OC=12AB=5cm ,CG=4cm ,根据勾股定理得:=3cm , 又AE ⊥EF ,OG ⊥EF ,BF ⊥EF ,∴AE ∥OG ∥BF ,又O 为AB 的中点,∴G 为EF 的中点,即OG 为梯形AEFB 的中位线,∴OG=12(AE+BF ),则AE+BF=2OG=6cm .故答案为6cm .考点:1.垂径定理;2.勾股定理;3.梯形中位线定理. 21.O 的半径为13cm ,AB 、CD 是O 的两条弦,.,10cm CD =,则AB 和CD 之间的距离为______ 【答案】7cm 或17cm 【解析】作OE ⊥AB 于E ,交CD 于F ,连结OA 、OC ,如图,根据平行线的性质得OF ⊥CD ,再利用垂径定理得到AE =12,CF =5,然后根据勾股定理,在Rt △OAE 中计算出OE =5,在Rt △OCF 中计算出OF =12,再分类讨论:当圆心O 在AB 与CD 之间时,EF =OF +OE ;当圆心O 不在AB 与CD 之间时,EF =OF−OE . 【详解】解:作OE ⊥AB 于E ,交CD 于F ,连结OA 、OC ,如图,∵AB ∥CD , ∴OF ⊥CD ,∴AE =BE =12AB =12,CF =DF =12CD =5, 在Rt △OAE 中,∵OA =13,AE =12,∴OE ,在Rt △OCF 中,∵OC =13,CF =5,∴OF ,当圆心O 在AB 与CD 之间时,EF =OF +OE =12+5=17; 当圆心O 不在AB 与CD 之间时,EF =OF−OE =12−5=7; 即AB 和CD 之间的距离为7cm 或17cm . 故答案为:7cm 或17cm . 【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和分类讨论的数学思想.22.如图,AB 、CD 是半径为5的O 的两条弦,8AB =,6CD =,MN 是直 径,AB MN ⊥于点E ,CD MN ⊥于点FPC ,P 为EF 上的任意一点,则PA PC +的最小值为____.【答案】【解析】A 、B 两点关于MN 对称,因而PA+PC=PB+PC ,即当B 、C 、P 在一条直线上时,PA+PC 的最小,即BC 的值就是PA+PC 的最小值 【详解】连接OA ,OB ,OC ,作CH 垂直于AB 于H .根据垂径定理,得到BE= 114,322BE AB CF CD ====4OF ===∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,在直角△BCH 中根据勾股定理得到则PA+PC 的最小值为【点睛】正确理解BC 的长是PA+PC 的最小值,是解决本题的关键.三、解答题23.如图,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长.【答案】8【解析】连接OB ,先根据垂径定理求出BM=12AB ,再根据勾股定理求出BM 的值,从而求出AB 的长度. 【详解】解:连接OB ,则OB =12×10=5, ∵OM ⊥AB ,OM 过O , ∴AB =2AM =2BM ,在Rt △OMB 中,由勾股定理得:BM 4, ∴AB =2BM =8. 【点睛】本题考查了垂径定理和勾股定理,通过连接OA 构造直角三角形进而利用勾股定理求解.24.已知:如图,在O 中,CD 是直径,AB 是弦,CD AB ⊥,垂足为E.求证:AE EB =,AC BC =,.【答案】详见解析 【解析】连接OA ,OB ,则OA OB =.然后根据轴对称的性质解答即可. 【详解】证明:如图,连接OA ,OB ,则OA OB =.又CD AB ⊥,直线CD 是等腰OAB 的对称轴,又是O 的对称轴.沿着直径CD 所在直线折叠时,CD 两侧的两个半圆重合,A 点和B 点重合,AE 和BE 重合,AC 和BC ,AD 和BD 分别重合.,AC BC =,【点睛】本题考查了垂径定理的应用,解此题的关键是能正确理解定理的内容,注意:垂直于弦的直径平分这条弦,并且平分弦所对的每一条弧. 25.如图,P 是⊙O 外一点,PA 交⊙O 于点B ,PD 交⊙O 于点C ,且∠APO=∠DPO. 弦AB 与CD 相等吗?为什么?【答案】AB=CD. 【解析】过O 点分别作AB 和CD 的垂线,交点分别为E 和F ,连接AO 和DO.由垂径定理可得OE 和OF 分别是AB 和CD 的垂直平分线;证明△PEO ≌△PFO 得OE=OF ,再证△AEO ≌△DFO 得AE=DF 即可. 【详解】 解:AB=CD.证明:过O 点分别作AB 和CD 的垂线,交点分别为E 和F ,连接AO 和DO ,∵∠OEP=∠OFP=90°,∠APO=∠DPO ,PO=PO,∴△PEO ≌△PFO ,∴OE=OF ,∵OE 为弦AB 的垂线,OF 为弦CD 的垂线,∴AE=EB ,DF=CF ,、∵AO=DO ,∴△AEO ≌△DFO ,∴AE=DF ,∴AB=2AE=2DF=CD ,即AB=CD.【点睛】本题结合三角形全等综合考察了垂径定理的知识.26.如图所示,AB 是直径,弦CD ⊥AB ,垂足为P ,AC =CD =OP 的长.【答案】1.【解析】试题分析:连接OC ,利用垂径定理构造直角三角形,求出圆的半径OC ,再求OP .试题解析:解:连接OC ,∵AB 是直径,CD ⊥AB ,∴CP =12CD Rt △ACP 中,AP =3,∴OP =AP -AO =3-AO =3-OC .在Rt △COP 中,OC 2=OP 2+CP 2,即OC 2=(3-OC )2+.解得OC =2.∴OP =3-2=1.27.在直径为10cm 的圆柱形油槽内装入一些油后,截面如图,油面宽AB 为6cm ,当油面宽AB 为8cm 时,油上升了多少厘米?王源的解题步骤如下:[解]连接AO ,过点O 作OC AB ⊥于点C .OC AB ⊥于点C ,且AB 为弦,12AC AB ∴=.当6cm AB =时,在Rt OAC △中,105cm,3cm,4cm 2OA AC OC ===∴==.当8cm AB =时,在Rt OAC 中,105cm,4cm,3cm 2OA AC OC ===∴==. 431(cm)∴-=.即油上升了1cm .请问王源的解题过程正确吗?如果不正确,请写出正确的解题步骤.【答案】王源的解题过程不正确.正确解题步骤见解析.油上升了1cm 或7cm .【解析】连接AO ,过点O 作OC ⊥AB 于点C ,根据垂径定理结合勾股定理求出当AB=6cm 和8cm 时OC 的长度,即可得出结论.【详解】王源的解题过程不正确.正确解题步骤如下:连接AO ,过点O 作OC AB ⊥于点C ,如图所示.∵OC AB ⊥于点C ,且AB 为弦,12AC AB ∴=.当6cm AB =时,在Rt OAC 中,5cm 3cm OA AC ==,,4cm OC ∴==;当8cm AB =时,在Rt OAC 中,5cm 4cm OA AC ==,,3cm OC ∴=.431(cm)∴-=或437(cm)+=.答:油上升了1cm 或7cm .【点睛】本题主要考查了垂径定理以及勾股定理,解题的关键是求出OC 的长,根据OC 的变化来得出结论. 28.如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度为7.2米,拱顶高出水面2.4米,现有一宽3米,船顶部为方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?【答案】能通过【解析】先求出弧形所在圆的半径;根据船宽,在Rt △OCH 中,利用勾股定理可以求出此拱桥可以通过的船的高度,与船的实际高度比较一下就可以知道能否通过.【详解】解:AB=7.2米,CD=2.4米,EF=3米.D 为AB 、EF 的中点,且CD,ME,NF 均垂直于AB,MN 交CD 于H .弧AB 所在的圆心为O,连接OA,ON .设OA=r,则OD=OC-DC=r-2.4,AD=12AB=3.6 有OA 2=AD 2+OD 2即在Rt △OAD 中,r 2=3.62+(r-2.4)2∴r=3.9(米)在Rt △ONH 中,有 3.6=(米).所以FN=DH=OH-OD=3.6-(3.9-2.4)=2.1(米)这里2米<2.1米,故可以通过该桥.但是余量较小,要非常小心才好.故答案为能通过.【点睛】本题考查垂径定理的应用, 勾股定理,解本题的关键是求出此拱桥可以通过的船的高度,再与船的实际高度比较一下就可以知道能否通过.29.如图,AC 是O 的直径,弦BD AO ⊥于E ,连接BC ,过点O 作OF BC ⊥于F ,若8BD cm =,2AE cm =,(1)求O 的半径;(2)求O 到弦BC 的距离.【答案】(1)O 的半径为5cm ;(2)O 到BC 【解析】(1)连接,设半径为r ,则2OE r =-,构建方程即可解决问题.(2)根据1122BCO S BC OF OC BE ∆=⋅=⋅,求解即可. 【详解】解:(1)连接,设半径为r ,则2OE r =-,AC 是O 的直径,弦BD AO ⊥于E ,8BD cm =,,在Rt OBE ∆中,222OE BE OB +=,222(2)4r r ∴-+=5r ∴=.(2)5r =, 10AC ∴=,8EC =,,OF BC ⊥,1122BCO S BC OF OC BE ∆∴=⋅=⋅54OF ∴=⨯,OF ∴=.【点睛】本题考查圆周角定理,垂径定理,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.30.已知:△AC 内接于⊙O ,D 是弧BC 上一点,OD ⊥BC ,垂足为 H.(1)如图 1,当圆心 O 在 AB 边上时,求证:AC=2OH ;(2)如图 2,当圆心 O 在△ABC 外部时,连接 AD 、CD ,AD 与 BC 交于点 P .求证:∠ACD=∠APB .【答案】(1)见解析;(2)见解析.【解析】(1)由OD ⊥BC 可知H 是BC 的中点,根据中位线的性质即可证明.(2)根据垂径定理可知BD =CD ,得∠BAD=∠DAC ,∠B=∠ADC ,根据三角形的内角和即可证明.【详解】(1)证明:∵OD ⊥BC ,∴BH=HC ,∴AC=2OH .(1)证明:∵OD ⊥BC ,∴BD =CD ,∴∠BAD=∠DAC ,∵∠B=∠ADC ,∠APB+∠BAD+∠B=180°,∠DAC+∠ACD+∠ADC=180°,∴∠APB=∠ACD .【点睛】考查圆周角定理,三角形中位线性质,三角形内角和定理等,比较基础,难度不大.31.如图,,,,A B C D 在O 上,//AB CD 经过圆心O 的线段EF AB ⊥于点F ,与CD 交于点E .(1)如图1,当O 半径为5,CD =若EF BF =,求弦AB 的长;(2)如图2,当O ,CD =若OB OC ⊥,求弦AC 的长.【答案】(1)8 (2)【解析】(1)连接OB OC 、,根据垂径定理求出OE 的长,因为EF BF =,进而在Rt BOF ∆中根据勾股定理求出BF 长,所以求出AB 的长即可;(2) 连接AB ,过点D 作DM AC ⊥于点M ,根据勾股定理和垂径定理求出OE ,可以证明BFO OEC ∆∆≌,进而求出EF 的长,根据所做的辅助线DM AC ⊥,可得DMC ∆为等腰直角三角形,所以可以求出DM 的长,然后根据1122ADC S DC EF AC DM ∆=⨯⨯=⨯⨯,进而求出AC 的长; 【详解】解:(1) 连接OB OC 、,根据垂径定理求出OE 的长,即:,EF BF =,设BF x =,则1OF x =-,由勾股定理得:222BF OB OF =-,即:2225(1)x x =--,解得:4x =,;(2)连接AB ,过点D 作DM AC ⊥于点M ,如图所示:。
3.3垂径定理(2)
思考题:
已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm ⊙O的半径为5cm, (1)请根据题意画出符合条件的图形(画草图) (2)求出AB、与CD间的距离。
A B A B
C O C D O
D
(1)
(2)
挑战自我试一试
如图,圆O与矩形ABCD交于E、F、G、 H,EF=10,HG=6,AH=4.求BE的长.
A H G D
B
E
· 0
F
C
课堂小结
1、圆是轴对称图形,其对称轴是每一条直径所在的直线或 经过圆心的每一条直线。
2、垂直于弦的直径平分这条弦,并且平分弦弦所对的两条弧。 C
CD过圆心 CD⊥AB CD平分弦AB
CD平分弧ACB
O
CD平分弧ADB
A B
D
推论(1)
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧 (2)弦的垂直平分线经过圆心,并且平分弦所 对的两条弧 (3)平分弦所对的一条弧的直径,垂直平分 弦,并且平分弦所对和的另一条弧
新浙教版九年级上第三章
3.3垂径定理 (2)
知识回顾
垂径定理: 垂直于弦的直径平分弦,
并且平分弦所对的弧.
C
题设
B O
结论
可推得
A
M└
●
① CD是直径 ② CD⊥AB
③AM=BM, ⌒ ⌒ ④AC=BC,
⌒ ⌒ ⑤AD=BD.
D
如果交换垂径定理的题设和结论的 部分语句,会有一些什么样的结论呢?
探索一:
O
设弯路的半径为Rm, 则OF ( R 90)m. OE CD, 1 1 D CF CD 600 300(m). 2 2 2 2 2 OC CF OF ,即 根据勾股定理, 得
浙教数学九上垂径定理课件(浙教版)

应用1:利用垂径定理作已知弧的中点
例1 已知 A⌒B ,用直尺和圆规求作这条弧的中点. 作法:
⒈ 连结AB.
C
⒉ 作AB的垂直平分线
CD,交弧AB于点E.
E
点E就是所求弧AB的中点. A 变式: 求弧AB的四等分点.
B D
错误
正确
强调:
等分弧时一定要作弧所对的弦的垂直平分线.
应用2:垂径定理的有关计算
① 平分弦
② 垂直于弦 条件
3.解题的主要方法:
② 平分弦所对的劣(优)弧 结论
(1)在圆有关的问题时,常常构造直角三角形, 利用垂径定理和勾股定理相结合的方法来解决。
(2)画弦心距和半径是圆中常见的辅助线;
(3)方程思想;
作业布置:(课本P78作业题) 1.必做题:1,2,3,4题 2.选做题:5,6题 课后思考题:第7题
例2 一条排水管的截面如图所示.排水管的半径 OB=10,水面宽AB=16,求截面圆心O到水面的距离 .
题后小结
1.圆心到圆的一条弦的距离叫 做弦心距.
2.作弦心距和半径是圆中常见的辅助线.
3 .半径(r)、半弦、弦心距(d)组成的直角
三角形是研究与圆有关问题的主要思路,它 A
们之间的关系:
O.
r d
叫做这条弧的中点.
A
⌒ 例如,点C是⌒AB的中点,点D是ADB的中点C. E O
D
B
辩一辩 在下列图形中,能使用垂径定理的图形有哪些?
C
C
C
O
AE B
A
D 不能
O
A EB
A
D
一条能直线具有:
① 经过圆心
② 垂直于弦 条件
O
垂径定理课件(26张PPT)冀教版数学九年级上册

知识点 2 垂径定理的推论
如图所示,在☉O中,直径CD与弦AB(非直径)相交于点E. C
【思考】
(1)若AE=BE,能判断CD与AB垂直吗?
O
AD 与 BD (或 AC 与 BC )相等吗?说明你的理由. A
EB
D
(2)若 AD = BD (或 AC =BC ),能判断CD与AB垂直吗?
AE与BE相等吗?说明你的理由.
C
O EB D
结论 垂直于弦的直径平分这条弦,并且平 分这条弦所对的两条弧.
能不能用所学过的知识证明你的结论?
C
O
A
EB
D
已知:如图,在⊙O中,CD为直径,AB为弦,且
CD⊥AB,垂足为E.
求证:AE=BE,AD BD,AC BC.
证明:如图,连接OA,OB.
C
在△OAB中,∵OA=OB,OE⊥AB, ∴AE=BE,∠AOE=∠BOE. ∴ AD BD . ∵∠AOC=180°-∠AOE,∠BOC=180°-∠BOE,
解:(1)CD⊥AB,AD BD (或 AC BC ). C
理由:连接OA,OB,如图所示,则△OAB是等 腰三角形,
∵AE得 AD BD, AC BC .
A
EB
(2)CD⊥AB,AE=BE. 理由: ∵ AD BD,∴∠AOD=∠BOD, 又∵OA=OB,OE=OE, ∴△AEO≌△BEO,
A
E C
O
D
B
拓宽视野: 对于圆中的一条直线,如果具备下列五个条件中的任意两个, 那么一定具备其他三个: (1)过圆心;(2)垂直于弦;(3)平分弦(非直径);(4) 平分弦所对的劣弧;(5)平分弦所对的优弧. 简记为“知二推三”.
3.3 垂径定理(选学)(课件)九年级数学上册(浙教版)
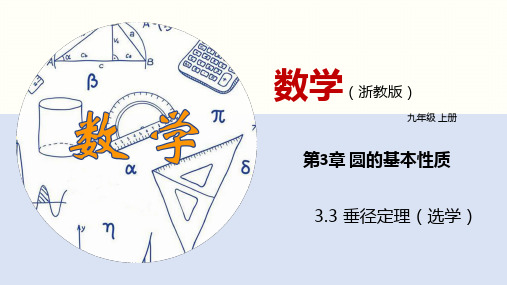
的半径为_________.
解:设弧CED所在圆的半径为r,
∵M是CD的中点,EM⊥CD,
1
∴EM过圆心O,CM= CD=2,
2
如图,连接OC,
∵EM=6,∴OM=6-r,
10
2
2
2
2
2
2
在Rt△OCM中,OC =CM +OM ,即r =2 +(6-r) ,解得:r= .
3
当堂检测
5.如图所示,⊙O的直径CD=10cm,AB是⊙O的弦, AM=BM,
由题意可知:OD=3,
∵OD⊥AB,
∴BD= AB= (AC+BC)=4(垂径定理),
∴CD=BD-BC=2,
在Rt△OCD中,OC2=CD2+OD2=22+32=13,
∴OC= .
D
当堂检测
3、如图,AB是⨀O的直径,弦CD⊥AB于点E,若CD=6,AB=10,
则AE的长为( A )
C
推导格式:
∵ CD是直径,CD⊥AB,(条件)
⌒ ⌒
⌒ =BC,
⌒ AD
∴ AP=BP, AC
=BD.(结论)
O
·
A
P
D
B
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,
形成整体,才能运用自如.
讲授新课
思考:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为
没有垂直
典例精析
例1、如图,⨀O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6
,则⨀O的半径长为_________.
第3章3.3垂径定理(教案)2023-2024学年九年级下册数学(教案)(北师大版)

(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与垂径定理相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。这个操作将演示垂径定理的基本原理。
5.培养学生养成良好的学习习惯,提高自主学习、探究学习的能力,形成终身学习的观念。
三、教学难点与重点
1.教学重点
-理解垂径定理的概念:垂径定理是圆的基本性质之一,对于圆的认识具有重要意义。教学过程中应重点讲解垂径定理的定义,使学生明确垂直于弦的直径平分弦,并且平分弦所对的两条弧。
-掌握垂径定理的证明方法:通过运用勾股定理和圆周角定理,引导学生理解并掌握垂径定理的证明过程,培养学生严谨的逻辑推理能力。
此外,在总结回顾环节,学生们能够较好地掌握垂径定理的基本概念和应用。但我也注意到,部分学生在提问环节显得较为拘况,我将在课堂上鼓励学生大胆提问,充分表达自己的观点,同时给予他们更多的肯定和鼓励。
最后,针对本节课的教学,我认为以下方面需要改进:
a.引导学生观察图形,发现垂径定理的规律。
b.分步骤解释证明过程,强调勾股定理和圆周角定理的应用。
c.通过提问和互动,了解学生在证明过程中遇到的难点,并针对性地进行解答。
d.组织学生进行小组讨论,共同解决证明过程中的问题,培养学生的团队合作能力。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《垂径定理》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要找到圆中某个点,使得从这个点到圆周上某点的距离最短的情况?”(例如:如何在一张纸上剪出一个最大的圆)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索垂径定理的奥秘。
浙教版初中数学九年级上册-3.3《垂径定理》教案

浙教版初中数学重点知识精选掌握知识点,多做练习题,基础知识很重要!浙教版初中数学和你一起共同进步学业有成!《垂径定理》教案教学目标:1、知识目标:通过实验观察,让学生理解圆的轴对称性;掌握垂径定理,理解其探索和证明过程;能初步运用垂径定理解决有关的计算和证明问题.2、能力目标:在研究过程中,进一步体验“实验—归纳—猜想—证明”的方法;在解题过程中,注重发散思维的培养,同一个问题会从不同的角度去分析解决.3、情感目标:通过圆的对称性,培养学生对数学的审美观,并激发学生对数学的热爱.教学重点:使学生掌握垂径定理、记住垂径定理的题设和结论.教学难点:对垂径定理的探索和证明,在解决问题时想到用垂径定理.教学用具:圆规,三角尺,PPT课件教学过程:一、复习引入1、我们已经学习了圆怎样的对称性质?(中心对称)B2、实验:探究圆的轴对称性.如图(1),若将⊙O沿直径AB对折,观察两部分是否重合?让学生用自己准备好的圆形纸片亲自实验,教师引导学生努力发现:圆是轴对称图形,过圆心的任意一条直线(或直径所在的直线)都是它的对称轴.3、引入新知:如图(2),左图中AB 是⊙O 的弦,直径CD 与弦AB 相交,那么沿直径CD 所在的直线折叠之后,图形可以重合吗?右图中,AB 是⊙O 的弦,直径CD ⊥AB ,垂足为E .此时再沿直径CD 所在直线折叠,图形可以重合吗?(重合,说明此图也是轴对称图形,称这种处于特殊位置的直径称为垂直于弦的直径),引出本节课研究的内容.二、新课(一)猜想,证明,形成垂径定理1、提问:继续观察图(2)的右图,根据圆的对称性,把圆沿直径CD 所在的直线折叠之后,圆中的线段和弧会出现怎样的位置关系?同时出现怎样的数量关系?2、猜想:可能出现的位置关系是:线段AE 和线段BE 重合,弧AC 和弧BC 重合,弧AD 和弧BD 重合.可能出现的数量关系是:,,AE BE AC BC AD BD=== 3、证明: 利用等腰三角形三线合一的性质或者三角形全等的知识来证明线段AE 与线段BD 相等,利用圆的对称性证明对应弧相等.板书:O CD AB,E AE BD CD AC BC AD BD=⎧⎫⎪⇒=⎬⎨⊥⎭⎪=⎩ 是圆的直径垂足为4、引导学生归纳总结垂径定理的文字表述,板书:垂直于弦的直径平分弦,并且平分弦所对的两条弧.(二)分析垂径定理的条件和结论1、再次明确垂径定理的条件和结论加深学生的印象.2、利用反例、变式图形对定理进一步引申,揭示定理的本质属性,以加深学生对定理本质的了解.练习:在下列图形中,能使用垂径定理的图形有哪些?3、引申定理:定理中垂直于弦的直径可以是直径、半径,也可以是过圆心的直线或线段.(三)例题例1 已知:如图(3),在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm.求:⊙O的半径.变式(1):如图(3),在⊙O中,圆心O到弦AB的距离为3cm,⊙O的半径为5cm.求:弦AB的长为多少?总结:在圆有关的问题时,常常构造直角三角形,利用垂径定理和勾股定理相结合的方法来解决.例2 已知:如图(4),在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C 、D 两点.求证:AC =BD .三、小结1、这节课我们学习了哪些主要内容?2、应用垂径定理要注意那些问题?相信自己,就能走向成功的第一步教师不光要传授知识,还要告诉学生学会生活。
浙教版数学九年级上册《3.3垂径定理》说课稿2

浙教版数学九年级上册《3.3 垂径定理》说课稿2一. 教材分析《垂径定理》是浙教版数学九年级上册第三章第三节的内容。
这一节主要介绍了圆中的一个重要定理——垂径定理。
垂径定理是指:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
这个定理在解决与圆相关的问题时非常有用,是圆的基本性质之一。
在教材中,垂径定理是通过探究活动来引导学生发现的。
首先,学生通过观察和动手操作,发现垂直于弦的直径能够平分弦。
然后,学生通过推理和证明,得出垂径定理的一般性结论。
这样的设计既有利于学生直观地理解垂径定理,又能培养学生的观察能力、动手能力和推理能力。
二. 学情分析九年级的学生已经学习了初中数学的大部分内容,对数学的基本概念、基本性质和基本定理有一定的了解。
他们在学习垂径定理之前,已经学习了圆的基本概念、圆的性质和圆的运算。
这些知识为基础,学生应该能够顺利地学习垂径定理。
然而,九年级的学生在学习过程中可能会遇到一些问题。
首先,垂径定理的概念比较抽象,学生可能难以理解和接受。
其次,证明过程需要一定的逻辑推理能力,学生可能在这方面遇到困难。
因此,在教学过程中,教师需要关注学生的学习情况,及时解答学生的疑问,帮助学生理解和掌握垂径定理。
三. 说教学目标1.知识与技能目标:学生能够理解垂径定理的内容,并能够运用垂径定理解决与圆相关的问题。
2.过程与方法目标:学生通过观察、动手操作、推理和证明等过程,培养观察能力、动手能力和推理能力。
3.情感态度与价值观目标:学生能够积极参与课堂活动,克服学习中的困难,增强对数学学科的兴趣和自信心。
四. 说教学重难点1.教学重点:学生能够理解并掌握垂径定理的内容。
2.教学难点:学生能够运用垂径定理解决与圆相关的问题,并能够进行推理和证明。
五. 说教学方法与手段在教学过程中,我将采用以下方法和手段:1.探究法:引导学生通过观察、动手操作、推理和证明等方法,自主发现和理解垂径定理。
2.讲解法:在学生自主探究的基础上,进行讲解和解释,帮助学生理解和掌握垂径定理。
浙教版九年级上册数学第3章 圆的基本性质 垂径定理的逆定理

又∵AD=AD,∴△ABD≌△ACD, ∴BD=DC,∴AD垂直平分BC. ∴OD=6cm, ∴AD=OA-OD=14-6=8(cm).
在Rt△OBD中,BD2=OB2-OD2=142-62=160.
在 Rt△ABD 中, AB= AD2+BD2= 82+160=4 14(cm). 综上可知,AB 的长为 4 35 cm 或 4 14 cm.
【答案】15°或75°
易错总结:在求两条弦的夹角时,容易忽略圆的轴对称性 而造成漏解.一般地,分类标准为圆心O在角的外部和圆 心O在角的内部.例如,本题分为圆心O在∠CAB的内部 和圆心O在∠CAB的外部两种情况.
︵ 12.如图,AB,AC是⊙O的两条弦,M,N分别为AB,
A︵C的中点,MN分别交AB,AC于点E,F.判断△AEF
6.如图,△ABC 的三个顶点都在⊙O 上,∠AOB=60°, AB=AC=2,则弦 BC 的长为( C ) A. 3 B.3 C.2 3 D.4
︵ 7.一种花边是由如图所示的弓形组成的,AB所在圆的半
径为5,弦AB=8,则弓形的高CD为( ) B
A.1B.2 C.3D.4
8.如图,一条公路弯道处是一段圆弧 AB,点 O 是这段弧所
ZJ版九年级上
第3章圆的基本性质
3.3 垂径定理 第2课时 垂径定理的逆定理
提示:点击 进入习题
1D
2A
3D
4C
5A
答案显示
6C 7B
8C
提示:点击 进入习题
9 25
答案显示
13 见习题
10 8
14 见习题
11 15°或75° 15 见习题 12 见习题
1.如图,CD是⊙O的直径,AB是弦,AB与CD相交于点
浙教版数学九年级上册圆全章分课时课件

圆上任意两点间的部分叫做圆弧, 简称弧. ⌒ ,读作“弧AB”. 以A,B两点为端点的弧.记作 AB
连接圆上任意两点间的线段叫做弦 (如弦AB).
经过圆心的弦叫做直径(如直径AC).
B
直径将圆分成两部分, 每一部分都叫做半圆 (如弧ABC).
●
A
O
C
⌒ 小于半圆的弧叫做劣弧,如记作 AB (用两个字母). ⌒ 大于半圆的弧叫做优弧, 如记作 ACB (用三个字母).
同一个方向,转动
同一个角度 ,这样的图形
改变叫做图形的旋转变换,简称旋转. 旋转中心 这个固定的点叫做___________. 旋转角 旋转的角度叫__________.
叙述一个旋转变换要注意旋转变换的三个要素: 1、旋转中心;
2、旋转的方向;
3、旋转的角度.
做一做
1.举出一些现实生活中旋转的实例.
当△ABC是钝角三角形时,外心O在△ABC的外部.
2.选择题: (1)三角形的外心具有的性质是( ) A.到三顶点的距离相等 B.到三边的距离相等 C.外心必在三角形的内部 D.到顶点的距离等于它到对边中点的距离 (2)等腰三角形的外心( ) A.在三角形内 B.在三角形外 C.在三角形的边上 D.在形外、形内或一边上都有可能
角度都是旋转的角度.
(4)图形上的每一点都绕旋转中心沿相同方向
转动了相同的角度.
当图形旋转的角度为180°时,所得的图形和原图 形关于旋转中心成中心对称.
例2 如图, 矩形A’B’C’D’是矩形ABCD以点A为旋转中心, 按逆时针方向旋转90°所得的图形. 求证:对角线BD与对角线B’D’所在的直线互相垂直.
知 点 能 作 无 数 个经 圆过 一 个 已
《垂径定理》PPT课件 (公开课获奖)2022年浙教版

•O D
C
A
(5)
C
•O A EB
D (6)
练一练
1、已知:如图,⊙O 中,弦AB∥CD,AB<CD,直径MN⊥AB,
垂足为E,交弦CD于点F.
图中相等的线段有 :
.
图中相等的劣弧有:
.
M
B
E
D
A
O
F
C
N
2、如图,圆O与矩形ABCD交于E、F、G、H,
EF=10,HG=6,AH=4.求BE的长.
2、物体在水下,水深每增加米承受的压力就会增加1个大气
压.当“蛟龙”号下潜至3500米时,它承受的压力约为340个
大气压.问当它承受压力增加到500个大气压时,它又继续下
潜了多少米?
340 1 x500
设它又继续下潜了x米 ,可列出方程 _______1_0__.3_3_________
3、小强、小杰、张明参加投篮比赛,每人投20次.小强投进10个
(7)平分弦的直线,必定过圆心。
(8)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。
A
C
C
C
OD
•O
(1) B
A
B
(2) D
•O
A
B
(3) D
(9)弦的垂直平分线一定是圆的直径。
(10)平分弧的直线,平分这条弧所对的弦。
(11)弦垂直于直径,这条直径就被弦平分。
•O ACB
(4)
B
2. 若 x 2 是关于 2x3mn0的方程的解,
则3m-n的值为
.
有的温度计有华氏、摄氏两种温标,华氏(℉)、摄氏(℃)
温标的转换公式是F=1.8C+32。请填下表:
九年级数学上册垂径定理课件(浙教版)

AEB O·
3. 如图,⊙O直径为10,弦AB的长为8,点P在AB
上运动. 则OP的取值范围是____3_≤_O__P_≤__5______.
O· AP B
•4. 如图,CD是⊙O的直径,弦AB⊥CD于E,CE=1,
AB=10,求直径CD的长.
A
解:连接OA.
∵ CD是直径,OE⊥AB, C E O·
D
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
∴A⌒A⌒CC和=B⌒BC⌒C重,合A⌒,D⌒ A=D和B⌒DB⌒.D重合.
归纳总结
定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
如图∵ CD是直径, 提示:
C
A M└
B
CD⊥AB, ∴AM = BM,
垂径定理是圆中一个 重要的结论,三种情 势要相互转化,形成
则下列结论中不成立的是( C )
A. ∠COE=∠DOE B. CE=DE
C. OE=AE
⌒⌒
D. BD=BC
A
C
D
E
O·
B
•2. 如图,OE⊥AB于E,若⊙O的半径为10cm, OE=6cm, 则AB= cm.
解:连接OA. ∵ OE⊥AB, ∴∠OEA=90°. ∴ AE OA2 OE2 102 62 8cm.
●O
条件
结论
D
由①CD是直径 ②CD⊥AB
可推得
③AM=BM, ④A⌒C=B⌒C,
⑤A⌒D=B⌒D.
垂径定理
如图,小明的理由是:
连接OA,OB, 则OA=OB.
在Rt△OAM和Rt△OBM中,
C
∵OA=OB,OM=OM, A M└
浙教版-数学-九年级上册-3.3 垂径定理(2) 教案

3.3 垂径定理(2)教学目标知识目标1.理解和掌握垂径定理的两个逆定理.2.会运用这两个逆定理解决有关弦、弧、弦心距及半径之间关系的证明和计算.能力目标:通过画图探索垂径定理的逆定理,培养学生探究能力和应用能力.情感目标:经历垂径定理逆定理的探索过程,培养学生大胆猜想、乐于探究的良好品质.教学重点难点重点:垂径定理的逆定理的探索及其应用.难点:利用垂径定理的逆定理解决有关实际问题.课堂教与学互动设计创设情境,引入新课1.垂径定理是指什么?你能用数学语言加以表达吗?2.若把上述已知条件CD⊥AB,改成CD平分AB,你能得到什么结论?3.若把上述已知条件CD⊥AB,改成CD平分弧AB,你又能得到什么结论?合作交流,探究新知一、自主探索1.垂直于弦的直径平分这条弦的逆命题是什么?它是真命题吗?为什么?2.平分弦的直径一定垂直于弧所对的弦吗?画图试一试.二、叙一叙定理1:_______弦(不是直径)的直径垂直于弦,并且平分_______.【答案】平分弦所对应的弧定理2:平分弦的直径________平分弦所对的________.【答案】垂直弦三、证一证已知:如图,⊙O的直径CD交弦AB(不是直径)于点P,AP=BP.求证:CD⊥AB,弧AC=弧BC.证明:连结OA,OB,则AO=BO∴△AOB是等腰三角形∵AP=BP∴CD⊥AB∴弧AC=弧BC例题解析,当堂练习例1如图,⊙O的弦AB,AC的夹角为50°,M,N分别是AB和AC的中点,求∠MON 的度数.w&ww.z*zste%^~hslx3y3h∵OC⊥AB,∴AB=2AD=2×56=112mm.。
【最新浙教版精选】浙教初中数学九上《3.3 垂径定理》word教案 (1).doc

3.3垂径定理 教学目标 1.使学生理解圆的轴对称性.2.掌握垂径定理.3.学会运用垂径定理解决有关弦、弧、弦心距以及半径之间的证明和计算问题. 教学重点垂径定理是圆的轴对称性的重要体现,是今后解决有关计算、证明和作图问题的重要依据,它有着广泛的应用,因此,本节课的教学重点是:垂径定理及其应用.教学难点 垂径定理的推导利用了圆的轴对称性,它是一种运动变换,这种证明方法学生不常用到,与严格的逻辑推理比较,在证明的表述上学生会发生困难,因此垂径定理的推导是本节课的难点.教学关键理解圆的轴对称性.教学环节的设计这节课我通过七个环节来完成本节课的教学目标,它们是:复习提问,创设情境;引入新课,揭示课题;讲解新课,探求新知;应用新知,体验成功; 目标训练,及时反馈;总结回顾,反思内化;布置作业,巩固新知.一、复习提问,创设情境1.教师演示:将一等腰三角形沿着底边上的高对折,启发学生共同回忆等腰三角形是轴对称图形,同时复习轴对称图形的概念;2.提出问题:如果以这个等腰三角形的顶点为圆心,腰长为半径作圆,得到的圆是否是轴对称图形呢?(教师用教具演示,学生自己操作) 二、引入新课,揭示课题1.在第一个环节的基础上,引导学生归纳得出结论:圆是轴对称图形,每一条直径所在的直线都是对称轴.强调:(1)对称轴是直线,不能说每一条直径都是它的对称轴; (2)圆的对称轴有无数条.判断:任意一条直径都是圆的对称轴( )设计意图:让学生更好的理解圆的轴对称轴新性,为下一环节探究新知作好准备.三、讲解新课,探求新知先按课本进行合作学习1.任意作一个圆和这个圆的任意一条直径CD ;2.作一条和直径CD 的垂线的弦,AB 与CD 相交于点E .提出问题:把圆沿着直径CD 所在的直线对折,你发现哪些点、线段、圆弧重合? 在学生探索的基础上,得出结论:(先介绍弧相等的概念) ①EA=EB ;② AC=BC ,AD=BD .理由如下:∵∠OEA=∠OEB=Rt ∠,根据圆的轴轴对称性,可得射线EA 与EB 重合, ∴点A 与点B 重合,弧AC 和弧BC 重合,弧AD 和弧BD 重合.∴ EA=EB , AC=BC,AD=BD . 思考:你能利用等腰三角形的性质,说明OA 平分CD 吗?(课内练习1) 注:老教材这个内容放在圆心角、圆周角之后,垂径定理完全可以不用圆的轴对称性来证,可用等腰三角形的性质来证明,现在只能证前面一个(略). AB C D O E ⌒ ⌒ ⌒ ⌒ A⌒ ⌒ ⌒ ⌒然后把此结论归纳成命题的形式:垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.垂径定理的几何语言∵CD 为直径,CD ⊥AB (OC ⊥AB ) ∴ EA=EB , AC=BC ,AD=BD . 四、应用新知,体验成功 例1 已知AB ,如图,用直尺和圆规求作这条弧的中点.(先介绍弧中点概念)作法:⒈连结AB.⒉作AB 的垂直平分线 CD , 交弧AB 于点E.点E 就是所求弧AB 的中点.变式一: 求弧AB 的四等分点.思路:先将弧AB 平分,再用同样方法将弧AE 、弧BE 平分.(图略)有一位同学这样画,错在哪里?1.作AB 的垂直平分线CD2.作AT 、BT 的垂直平分线EF 、GH (图略)教师强调:等分弧时一定要作弧所对的弦的垂直平分线.变式二:你能确定弧AB 的圆心吗? 方法:只要在圆弧上任意取三点,得到三条弦,画其中两条弦的垂直平分线,交点即为圆弧的圆心.例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求截面圆心O 到水面的距离OC .思路:先作出圆心O 到水面的距离OC ,即画 OC ⊥AB ,∴AC=BC=8,在Rt △OCB中,68102222=-=-=BC OB OC ∴圆心O 到水面的距离OC 为6.例3 已知:如图,线段AB 与⊙O 交于C 、D 两点,且OA=OB .求证:AC=BD .思路:作OM ⊥AB ,垂足为M , ∴CM=DM∵OA=OB , ∴AM=BM , ∴AC=BD .概念:圆心到圆的一条弦的距离叫做弦心距.小结:1.画弦心距是圆中常见的辅助线;2.半径(r )、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:弦长222d r AB -=.注:弦长、半径、弦心距三个量中已知两个,就可以求出第三个.五、目标训练,及时反馈1.已知⊙0的半径为13,一条弦的AB 的弦心距为5,则这条弦的弦长等于 .⌒ ⌒ ⌒ ⌒O A B C ⌒ ⌒ ⌒答案:242.如图,AB 是⊙0的中直径,CD 为弦,CD ⊥AB 于E ,则下列结论中不一定成立的是( )A .∠COE=∠DOEB .CE=DEC .OE=BED .BD=BC答案:C3.过⊙O 内一点M 的最长弦长为10cm ,最短弦长为8cm ,那么OM 长为( )A .3B .6cmC . cmD .9cm答案:A注:圆内过定点M 的弦中,最长的弦是过定点M 的直径,最短的弦是过定点M 与OM 垂直的弦,此结论最好让学生记住,课本作业题也有类似的题目.4.如图,⊙O 的直径为10,弦AB 长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( )A .3≤OM ≤5B .4≤OM ≤5C .3<OM<5D .4<OM<5答案:A5. 已知⊙O 的半径为10,弦AB ∥CD ,AB=12,CD=16,则AB 和CD 的距离为 . 答案:2或24 注:要分两种情况讨论:(1)弦AB 、CD 在圆心O 的两侧;(2)弦AB 、CD 在圆心O 的同侧.6.如图,已知AB 、AC 为弦,OM ⊥AB 于点M , ON ⊥AC 于点N ,BC=4,求MN 的长. 思路:由垂径定理可得M 、N 分别是AB 、AC 的中点,所以MN=21BC=2. 六、总结回顾,反思内化师生共同总结:1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.2.垂径定理的应用:(1)作图;(2)计算和证明.3.解题的主要方法:(1)画弦心距是圆中常见的辅助线;(2)半径(r )、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:弦长222d r AB -=.七、布置作业, 巩固新知P75作业题1~6,第7题选做.⌒ ⌒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
O
D
结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴。 强调:
(1)圆的对称轴是直线,不能说每一条直径都是圆的对称轴. (2)圆的对称轴有无数条.
判断:任意一条直径都是圆的对称轴(
X)
二
合作学习
1.在刚才操作的基础上,再作一条和直径CD垂直的弦 AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸 折叠,你发现哪些点、线互相重合?如果把能够重合的圆 弧叫做相等的圆弧(等弧),有哪些圆弧相等? 解:点A与点B重合,AE与BE重合, ⌒ ⌒ ⌒ ⌒ AC=BC,AD=BD.
A D E B C
1.如图,过已知⊙O内的一点A作弦,使A是该弦 的中点,然后作出弦所对的两条弧的中点. E
BC就是所要求的弦 点D,E就是所要求的弦 所对的两条弧的中点.
O
C
A
B
D
例2:一条排水管的截面如图所示。已知排水管的半
径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
想一想:排水管中水最深多少? 解:作OC⊥AB于C, 由垂径定理得: AC=BC=1/2AB=0.5×16=8. 由勾股定理得:
⌒ 解: 过O作OE⊥CD于点E,延长OE交CD于点F,
1 所以CE DE CD 8(厘米) 2
O
E 1 C D 又OD 20 10 厘米 2 F 2 2 在Rt ODE中,OE= OD DE (厘米) 6
所以油槽中油的最大深度EF=10-6=4(厘米)
3、已知:如图,⊙O 中, AB为 弦,OC ⊥AB OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径.
d A
O
.
C
r
B
弦长AB 2 r 2 d 2 .
想一想:
在同一个圆中,两条弦的长短与它们所对应的
弦心距之间有什么关系?
D C
.
B
答:在同一个圆中, 弦心距越长,所对应的弦就越短;
A
O
弦心距越短,所对应的弦就越长.
2.在直径为20厘米的球形油槽内装入一些油后,截面如 图所示,如果油面宽是16厘米,求油槽中油的最大深度. 连结OD. 因为OE⊥CD,
OC OB BC 10 8 6
2 2 2 2
8
C
10 8
答:截面圆心O到水面的距离为6.
D
圆心到圆的一条弦的距离叫做弦心距.
例如,上图中,OC的长就是弦AB的弦心见的辅助线; 2 .半径(r)、半弦、弦心 距(d)组成的直角三角形是研 究与圆有关问题的主要思路, 它们之间的关系:
C A
E
B
O
D
2.请你用命题的形式表述你的结论. 垂直于弦的直径平分这条弦, 并且平分弦所对的弧.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
3.请你对上述命题写出已知,求证,并给出证明. 解 已知:如图,CD是⊙O的直径,AB是⊙O的一 条弦,CD⊥AB,且交AB于点E. ⌒ ⌒ ⌒ ⌒ 求证: EA=EB, AC= BC, AD=BD. 证明:连结OA,OB. A 如果把⊙O沿着直径CD对折, 那么被CD分成的两个半圆互 C D 相重合. E O ∵∠OEA=∠OEB=Rt∠, B ∴线段EA与线段EB重合. 思考:你能利用等腰 ∴点A与点B重合,弧AC和弧BC重合,
O D C B
O
C
A
O C B
C D O
B
A
例1 已知弧AB,如图,用直尺和圆规求作这条弧 的中点.(先介绍弧中点的概念)
⌒
⌒ 分析:要平分AB,只要画垂直于弦AB的直径.而这
条直径应在弦AB的垂直平分线上.因此画AB的 ⌒平分. 垂直平分线就能把AB
作法: ⒈ 连结AB. ⒉ 作AB的垂直平分线 CD,交弧AB于点E. 点E就是所求弧AB的中点.
创设情境,引入新课
复习提问: (1)什么是轴对称图形
如果一个图形沿着一条直线对折,两侧的图形能 完全重合,这个图形就是轴对称图形。
(2)正三角形是轴对称性图形吗? 是 有几条对称轴? 3 (3)圆是否为轴对称图形?如果是,它的 对称轴是什么?你能找到多少条对称轴?
合作交流,探究新知
一自主探究 在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?
直径平分弦所对的弧 (结论)
垂径定理的几何语言叙述:
⌒ ⌒ ⌒ ⌒
∵CD为直径,CD⊥AB(或OC⊥AB)
∴ EA=EB, AC=BC, AD=BD. 2.分一条弧成相等的两条弧的点,
A C D
叫做这条弧的中点.
E B
O
例如,点C是AB的中点,点D是ADB的中点.
⌒
⌒
C
A D
O A D E B
B
A
A
C 1 3D O
3
B
1、已知⊙O的半径为10cm,点P是⊙O内一点,
且OP=8,则过点P的所有弦中,最短的弦是( D )
(A)6cm (B)8cm (C)10cm (D)12cm
O P
8
10 6
2.如图,⊙O的直径为10,弦AB长为8,M是 弦AB上的动点,则OM的长的取值范围是( ) A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
三角形的性质,说明 OC平分AB吗?
弧AD和弧BD重合. ⌒ ⌒ ⌒ ⌒ ∴ EA=EB, AC= BC, AD=BD.
4.圆的性质(垂径定理)
垂直于弦的直径平分这条弦, 并且平分弦所对的弧.
三 概括性质(垂径定理:垂直于弦的直 径平分这条弦,并且平分弦所对的弧.)
1.直径垂直于弦
(条件)
直径平分弦
A
O .
M
B
师生共同总结:
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法: (1)画弦心距和半径是圆中常见的辅助线; (2)半径(r)、半弦、弦心距(d)组成的直角三角形 是研究与圆有关问题的主要思路,它们之间的关系:
弦长AB 2 r 2 d 2 .
