八年级数学下册8认识概率83频率与概率1学案苏科版
新版苏科版江苏省徐州市新沂市八年级数学下册第八章认识概率8.3频率与概率1教案
教具:多媒体等
教
学
过
程
教
学
过
程
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
一、情境引入
飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此,保险公司必须精确计算出飞机失事的可能性有多大.类似这样的问题在我们的日常生活中也经常遇到.例如:
200
500
1000
2000
优等品频数m
46
93
194
472
953
1903
优等品频数
(1)计算并填写表中“抽到优等品”的频率;
(2)画出“抽到优等品”的频率的折线统计图;
(3)当抽到的足球数很大时,你测反馈
1、有大小、形状、颜色完全相同的5个乒乓球,每个球上分别标有数字1、2、3、4、5中的一个,将这5个球放入不透明的袋中搅匀,如果不放回的从中随机连续抽取两个,则这两个球上的数字之和为偶数的概率是_______.
2、一个口袋中有5粒糖,1粒红色,2色黄色,2粒白色,今从中任取一粒,是白色的概率为_________.
3、有5个零件,已知其中混入了一个不合格产品现取其中一个,是正品的概 率是_________.
4、投掷两枚硬币,都是反面的概 率为_________.
五、小结反思
有什么收获? 有什么疑惑和遗憾?
自学教材内容
完成检测题
交流问难
分组展示板演并讲解学生讲解
试试看。
小组讨论。
组内研讨后,汇报结论。
小结。
板
书
设
计
江苏省八年级数学下册第八章认识概率8.3频率与概率1教案新版苏科版

频 率与概率
主备人 课题 用案人 8.3 频率与概率 (1) 授课时间 __年__月__日 课型 总第 新授 课时
教学 目标
1、理解随机事件发生的可能性有大有小,概率的定义; 2.概率是随机事件自身的属性,它反映随机事件发生的可能性大小; 3.在多次重复试验中,体会频率的稳定性.
过 小组讨论。
程
组内研讨 后,汇报结 论。
第 4 页 共 5 页 伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。
成功的道路上,肯定会有失败;对于失败,我们要正确地看待和对待,不怕失败者,则必成功;怕失败者,则一 无是处,会更失败。
小结。
板
书
设
计
教学 札记
第 5 页 共 5 页 伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。
第 3 页 共 5 页 伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。
成功的道路上,肯定会有失败;对于失败,我们要正确地看待和对待,不怕失败者,则必成功;怕失败者,则一 无是处,会更失败。
中一个,是正品的概 率是_________. 学 4、投掷两枚硬币,都是反面的概 率为_________. 五、小结反思 有什么收获? 有什么疑惑和遗憾?
重点 教法教 具
频率稳定性的 理解.
难点
频率稳定性的理解.
自主先学 当堂检测 交流展示 检测反馈 小结反思 教具:多媒体等 教 学 内 容 学生主体活 教师主导活动 动 一、情境引入 飞机失事会给旅客造成意外伤害.一家保险公司要 为购买机票的旅客进行保险,应该向旅客收取多少保费 呢?为此,保险公司必须精确计算出飞机失事的可能性 有多大.类似这样的问题在我们的日常生活中也经常遇 个案调整
【苏科版八年级数学下册教案】8.3 频率与概率(第1课时)
学科数学年级八课题8.3 频率与概率第1课时主备人教学目标1.经历实验、统计等活动过程,在活动中进一步发展学生合作交流的意识和能力。
2.通过试验活动了解概率的意义,认识概率是对随机现象的一种数学描述,是刻画随机事件发生的可能性的大小。
3.通过实验,理解当实验次数较大时实验频率稳于理论概率.教学重难点实验中估计某一事件发生的概率。
教学准备教学过程个人二次备课一、分组实验、探索规律小组活动方法:准备两组相同的牌,每组两张,两张牌的牌面数字分别是1和2,从每组牌中各摸出一张,称为一次实验。
合作探究问题:(1)一次实验中两张牌的牌面数字和可能有哪些值?(2)每人做30次实验,根据实验结果填写下面表格:牌面数字积 2 3 4频数频率(3)根据上表,制作相应的频数分布直方图。
(4)你认为哪种情况的频率最大?(5)两张牌的牌面数字和等于3的频率是多少?(6)六个同学组成一个小组,分别汇总其中的两人、三人、四人、五人、六人的实验数据,相应得到实验60次、90次、120次、150次、180次时两张牌的牌的数字和等于3的频率,填写下表,并绘制相应的折线统计图。
实验次数60 90 120 150 180 两张牌的牌面数字和等于3的频数两张牌的牌面数字和等于3的频率学生合作探讨,小组实验,发现规律。
二、巩固深化、拓展思维议一议(1)在上面的实验中,你发现了什么?增加实验数据后频率渐趋于哪一个稳定值?(2)与其他小组交流所绘制的图表和发现的结论。
学生小组合作与全班性合作相结合,积极探究。
做一做(1)将各组的数据集中起来,求出两张牌的牌面数字和等于3的频率,它与你们的估计相近吗?(2)计算两张牌的牌面数字和等于3的概率。
学生小组合作实验,发现规律。
想一想两张牌的牌面数字和等于3的频率与两张牌的牌面数字和等于3的概率有什么关系?学生归纳、小结规律。
结论:当实验次数很大时,两张牌的牌面数字和等于3的频率稳定在相应的概率附近,因此可以通过多次实验,用一个事件发生的频率来估计这一事件发生的概率三、随堂练习P46课本随堂练习四、课堂总结学生自我小结。
配套K12八年级数学下册第八章认识概率8.3频率与概率1教案新版苏科版
2 、随机事件有概率,确定事件也有概率。
3、概率的求解方法。
(二)展示二(例题)
做“抛掷质地均匀的硬币试验”,每人10次.
1.分别汇总5人、10人、15人、…、50人……的试验结果,并将试验数据汇总填入下表:
(三)展示三(拓展)
某批足球产品质量检验获得 的数据.
抽取的足球数n
50
100
抛掷1枚均匀硬币,正面朝上.在装有彩球的袋子中,任意摸出的1个球恰好是红球.明天将会下雨.抛掷1枚均匀骰子,6点朝上.
二、自主先学
1、自学内容:P44--46
2、自学指导:
(1)随机事件的发生的可能性有大有小。
(2)概率:指一个事件发生可能性大小的数值。
(3)必然事件 发生的概率是1;不可能事件发生的概率是0;随机事件发生的概率是0和1之间的一个数。
2、一个口袋中有5粒糖,1粒红色,2色黄色,2粒白色,今从中任取一粒,是白色的概率为_________.
3、有5个零件,已知其中混入了一个不合格产品现取其中一个,是正品的概 率是_________.
4、投掷两枚硬币,都是反面的概 率为_________.
五、小结反思
有什么收获? 有什么疑惑和遗憾?
自学教材内容
完成检测题
交流问难
分组展示板演并讲解学生讲解
试试看。
小组讨论。组内研讨后,汇报结。小结。板书
设
计
教学
札记
自主先学当堂检测交流展示检测反馈小结反思
教具:多媒体等
教
学
过
程
教
学
过
程
教
学
过
程
教学内容
个案调整
教师主导活动
八年级数学下册第8章认识概率8.3频率与概率教案苏科版(new)

8.3 频率与概率
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of
this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
八年级数学下册第8章认识概率8.3频率与概率(1)教案苏科版(2021-2022学年)

课题:8.3 频率与概率 (1)教学目标:1.理解随机事件发生的可能性有大有小,概率的定义;2.概率是随机事件自身的属性,它反映随机事件发生的可能性大小;3.在多次重复试验中,体会频率的稳定性.教学重点:频率稳定性的理解教学难点:频率稳定性的理解.教学流程:一、情境创设飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此,保险公司必须精确计算出飞机失事的可能性有多大?类似这样的问题在我们的日常生活中也经常遇到.例如:抛掷1枚均匀硬币,正面朝上.在装有彩球的袋子中,任意摸出的1个球恰好是红球.明天将会下雨.抛掷1枚均匀骰子,6点朝上.……随机事件发生的可能性有大有小.一个事件发生可能性大小的数值,称为这个事件的概率.若用A 表示一个事件,则我们就用P(A )表示事件A 发生的概率.通常规定,必然事件发生的概率是1,记作P (A)=1;不可能事件发生的概率为0,记作P (A )=0;随机事件发生的概率是0和1之间的一个数,即0<P(A )<1.二、探索活动抛掷硬币试验:1.分别汇总5人,10人,15人,…,50人的试验结果,并将试验数据汇总填入下表:ﻬ2.根据上表,完成下面的折线统计图:3.观察上面的折线统计图,你发现了什么规律?请与同学交流。
下表是小明抛硬币试验获得的数据(折线图在课本P )45抛掷次数50100150200250300350400450500正面朝上的频数20537098115156169202219244正面朝上的频率0.40.530.470.490.460.520.480.510.490.49观察课本P 折线统计图,当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据。
观察此表,你发现了什么?从上表可以看出:“正面朝上”的频率总在附近波动,而且近似等于。
人们在抛掷硬币、骰子之类的游戏中发现:在充分多次试验中,一个随机事件的频率一般会在一个定值附近摆动,而且试验次数越多,摆动幅度越小.这个性质称为频率的稳定性。
苏科版八年级下册数学8.3.1频率与概率学案

8.3.1频率与概率1.学习目标:1)知识目标1.理解随机事件发生的可能性有大有小,概率的定义;2.概率是随机事件自身的属性,它反映随机事件发生的可能性大小;2)能力目标3.在多次重复试验中,体会频率的稳定性.2.学习重难点:理解随机事件发生的可能性有大有小,概率的定义;3.学习过程1)自主学习:阅读课本内容,找出重点概念并整理:附加:随机事件发生的可能性有大有小.一个事件发生可能性大小的数值,称为这个事件的概率.若用A表示一个事件,则我们就用P(A)表示事件A发生的概率.通常规定,必然事件发生的概率是1,记作P(A)=1;不可能事件发生的概率为0,记作P(A)=0;随机事件发生的概率是0和1之间的一个数,即0<P(A)<1.2)即时巩固:1.抛掷一枚均匀的骰子,它落地时,朝上的点数为1的概率为______。
朝上的点数为偶数的概率为_______ 。
朝上的点数不大于6的概率为______,朝上的点数大于4的概率为______。
2.从一副扑克牌(去掉大小王)中随意抽取一张,抽到红桃的概率为________,抽到10的概率为_______,抽到梅花4的概率为_____________.3.一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后均放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是.4.小华和父母一同从重庆乘火车到广安邓小平故居参观,火车车厢里每排有左、中、右三个座位,小华一家三口随意坐某排的三个座位,则小华坐在中间的概率是____________。
5.初三(1)班50名学生中有35名团员,他们都积极报名参加志愿者活动,根据要求,该班从团员中随机选取1名团员参加,则该班团员李明被选中的概率是_________。
3)要点理解:小组活动方法:准备两组相同的牌,每组两张,两张牌的牌面数字分别是1和2,从每组牌中各摸出一张,称为一次实验。
八年级数学下册第八章认识概率8.3频率与概率1教案苏科版.docx

苏科版 2018 届八年级数学下册教案频率与概率主备人用案人授课时间__年 __月 __日总第课时课题8.3频率与概率(1)课型新授教学1、理解随机事件发生的可能性有大有小,概率的定义;目标2.概率是随机事件自身的属性,它反映随机事件发生的可能性大小;3.在多次重复试验中,体会频率的稳定性.重点频率稳定性的理解.难点频率稳定性的理解.教法教自主先学当堂检测交流展示检测反馈小结反思具教具:多媒体等教学内容个案调整学生主体活教师主导活动动一、情境引入飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此,保险公司必须精确计算出飞机失事的可能性有多大.类似这样的问题在我们的日常生活中也经常遇教到.例如:抛掷 1 枚均匀硬币,正面朝上.在装有彩球的袋子中,任意摸出的 1 个球恰好是红球.明天将会下雨.抛掷 1 枚均匀骰子, 6 点朝上.学二、自主先学1 、自学内容: P44--462、自学指导:(1)随机事件的发生的可能性有大有小。
过( 2)概率:指一个事件发生可能性大小的数值。
(3)必然事件发生的概率是 1;不可能事件发生的概率是 0;随机事件生的概率是0 和 1 之的一个数。
自学教材内3、自学:容程( 1). 在一次抽活中,中概率是0.12 ,不中的概率是 _______.( 2)小明与父母从广州乘火回梅州参叶念,他到的火票是同一排相的三个座位,那么小明恰好坐在父母中的概率是_______.(3)疑,提出学中存在的。
三、交流展示(一)展示一完成分展示自主先学中的,所学知。
交流1概率的定。
2 、随机事件有概率,确定事件也有概率。
3、概率的求解方法。
(二)展示二(例)做“抛地均匀的硬”,每人 10 次.1.分 5 人、 10 人、 15 人、⋯、 50 人⋯⋯的果,并将数据填入下表:教分组展示板演并讲解学学生讲解过(三)展示三(拓展)试试看。
某批足球产品质量检验获得的数据.程抽取的足球数5010020050010002000n优等品频数m4693194 472 9531903优等品频数mn(1)计算并填写表中“抽到优等品”的频率;(2)画出“抽到优等品”的频率的折线统计图;(3)当抽到的足球数很大时,你认为“抽到优等品”的频率在哪个常数附近摆动?四、检测反馈1、有大小、形状、颜色完全相同的 5 个乒乓球,每个球上分别标有数字1、 2、 3、 4、 5 中的一个,将这 5 个球放入不透明的袋中搅匀,如果不放回的从中随机连续抽取两个,则这两个球上的数字之和为偶数的概率是_______.教2、一个口袋中有 5 粒糖, 1 粒红色, 2 色黄色, 2 粒白色,今从中任取一粒,是白色的概率为 _________.3、有 5 个零件,已知其中混入了一个不合格产品现取其中一个,是正品的概率是 _________.学4、投掷两枚硬币,都是反面的概率为_________.五、小结反思有什么收获?有什么疑惑和遗憾?过小组讨论。
【苏科版八年级数学下册教案】8.3频率与概率(第1课时)
学科课题教学目标教学重难点教学准备数学年级八8.3频次与概率主备人第 1课时1.经历实验、统计等活动过程,在活动中进一步发展学生合作沟通的意识和能力。
2.经过试验活动认识概率的意义,认识概率是对随机现象的一种数学描绘,是刻画随机事件发生的可能性的大小。
3.经过实验,理解当实验次数较大时实验频次稳于理论概率.实验中预计某一事件发生的概率。
教课过程个人二次备课一、分组实验、研究规律小组活动方法:准备两组同样的牌,每组两张,两张牌的牌面数字分别是 1 和 2,从每组牌中各摸出一张,称为一次实验。
合作研究问题:(1)一次实验中两张牌的牌面数字和可能有哪些值?(2)每人做 30 次实验,依据实验结果填写下边表格:牌面数字积234频数频次(3)依据上表,制作相应的频数散布直方图。
(4)你以为哪一种状况的频次最大?( 5)两张牌的牌面数字和等于 3 的频次是多少?( 6)六个同学构成一个小组,分别汇总此中的两人、三人、四人、五人、六人的实验数据,相应获得实验60 次、 90 次、 120 次、 150 次、180 次时两张牌的牌的数字和等于 3 的频次,填写下表,并绘制相应的折线统计图。
实验次数60 90 120 150180两张牌的牌面数字和等于 3 的频数两张牌的牌面数字和等于 3 的频次学生合作商讨,小组实验,发现规律。
二、稳固深入、拓展思想议一议(1)在上边的实验中,你发现了什么?增添实验数据后频次渐趋于哪一个稳固值?(2)与其余小组沟通所绘制的图表和发现的结论。
学生小组合作与全班性合作相联合,踊跃研究。
做一做( 1)将各组的数据集中起来,求出两张牌的牌面数字和等于 3 的频次,它与你们的预计邻近吗?( 2)计算两张牌的牌面数字和等于 3 的概率。
学生小组合作实验,发现规律。
想想两张牌的牌面数字和等于 3 的频次与两张牌的牌面数字和等于 3 的概率有什么关系?学生概括、小结规律。
结论:当实验次数很大时,两张牌的牌面数字和等于 3 的频次稳固在相应的概率邻近,所以能够经过多次实验,用一个事件发生的频次来预计这一事件发生的概率三、随堂练习P46 课本随堂练习四、讲堂总结学生自我小结。
八年级下册数学教学设计:频率与概率 (1)

《8.3 频率与概率 (1)》教学设计课题8.3频率与概率 (1)年级八年级适用类型新授讲解知识点来源苏科版初中数学八年级下册第八章第3节《频率与概率》教学目标1.理解随机事件发生的可能性有大有小,概率的定义.2.概率是随机事件自身的属性,它反映随机事件发生的可能性大小.3. 在多次重复试验中,体会频率的稳定性.教学重难点频率稳定性的理解.教学过程:一、情境创设我们的日常生活中经常会遇到类似这样的问题,例如:抛掷1枚均匀硬币,正面朝上.在装有彩球的袋子中,任意摸出的1个球恰好是红球.明天将会下雨.抛掷1枚均匀骰子,6点朝上.……【设计意图】由学生熟悉的知识点入手,给学生一个理解能力的机会,感受抽象的知识点与我们的生活戚戚相关.总结:随机事件发生的可能性有大有小.一个事件发生可能性大小的数值,称为这个事件的概率.若用A表示一个事件,则我们就用P(A)表示事件A发生的概率.通常规定,必然事件发生的概率是1,记作P(A)=1;不可能事件发生的概率为0,记作P(A)=0;随机事件发生的概率是0和1之间的一个数,即0<P(A)<1.【设计意图】归纳引出概念:一个随机事件发生的概率是由这个随机事件自身决定的,并且是客观存在的.概率是随机事件自身的属性,它反映这个随机事件发生的可能性大小.虽然此时学生理解不是那么透彻,但要学生戴着定义去学习每个随机事件的概率值是不一样的.二、活动操作(一)阅读1.阅读书P44的“尝试”——“抛掷质地均匀的硬币试验”,做实验之前不妨先思考2个问题。
2.问题1:你认为正面朝上与反面朝上哪个频率最大?问题2:预估一下正面朝上的频率是多少?【设计意图】让学生了解活动步骤并带着问题活动.(二)操作1.实验要求:抛掷一枚质地均匀的硬币,记录正面朝上的次数.2.填表。
3.将表格中数据,绘制频率折线统计图。
问题3:观察折线统计图,你发现了什么?【设计意图】通过学生主动参与到学习活动中来,亲身经历对随机现象的探索过程,使数学学习变得主动、有趣,培养学生合作交流精神和发散思维能力,在活动中思考,更好地体现数学的意义和价值.(三)阅读1.阅读书P45小明与同学做的实验数据及折线统计图.问题4:当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?2.阅读书P46的“18世纪以来一些统计学家进行抛硬币试验所得的数据”.。
八年级数学下册8.3 频率与概率导学案1(新版)苏科版

八年级数学下册8.3 频率与概率导学案1(新版)苏科版8、3 频率与概率1【学习目标】1、体会随机事件在每一次实验中是否发生是不可预言的,但在数多次的反复实验后,随机事件发生的频率(成功率)会逐渐稳定在某一数值上、2、通过试验,初步了解概率与频率的联系,会用频率估计概率、【学习重难点】知道随机事件随实验次数的增加而逐渐趋稳的事实、对实验结果的分析、【自主学习】(静下心来哦,开始明天数学的起航!)1、抛掷1枚均匀硬币,正面朝上、在装有彩球的袋子中,任意摸出的1个球恰好是红球、明天将会下雨、抛掷1枚均匀骰子,6点朝上、……随机事件发生的可能性有大有小、一个事件发生可能性大小的数值,称为这个事件的、若用A表示一个事件,则我们就用P(A)表示事件A发生的概率、通常规定,必然事件发生的概率是,记作P(A)=;不可能事件发生的概率为,记作P(A)=;随机事件发生的概率是0和1之间的一个数,即、2、根据10次掷硬币试验中,有6次正面朝上这一实验现象,填写表格频数频率正面朝上反面朝上和【课中交流】抛掷硬币试验:1、分别汇总5人,10人,15人,…,50人的试验结果,并将试验数据汇总填入下表:(1)根据上表,完成下面的折线统计图:(2)、观察上面的折线统计图,你发现了什么规律?请与同学交流、2、下表是某批足球产品质量检验获得的数据、抽取的足球数n50100xx0010002000优等品频数m46931944729531903优等品频数(1)计算并填写表中“抽到优等品”的频率;(2)画出“抽到优等品”的频率的折线统计图;(3)当抽到的足球数很大时,你认为“抽到优等品”的频率在哪个常数附近摆动?【目标检测】某射击运动员在同一条件下的射击成绩记录如下:射击次数20401002004001000射中9环以上次数153378158321801射中9环以上频率(1)计算表中相应的“射中9环以上”的频率(精确到0、01);(2)这些频率具有什么样的稳定性?(3)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0、1)、。
2016年春季新版苏科版八年级数学下学期8.3、频率与概率教案1

事件的概率。
教后感:
抛掷1枚均匀硬币,正面朝上。
在装有彩球的袋子中,任意摸出的1个球恰好是红球。
明天将会下雨。
抛掷1枚均匀骰子,6点朝上。
……
都是随机事件,你还能再举出一些随机事件吗?
新课讲解:
随机事件发生的可能性有大有小。一个事件发生可能性大小的数值,
称为这个事件的概率( )。若用 表示一个事件,则我们就
用 表示事件 发生的概率。
练一练:P46探索
课堂小结:
学生讨论、交流。若生说出规律有困难,师可引导学生完成
学生分别说出自己的观察结果。
学生观察、思考并说出自己的观察结果。若生说不好,师可引导学生说出。
学生自己总结,教师补充
板书设计:频率与概率(1)
一个事件发必然事件发生的概率是1,记作
生可能性大小的不可能事件发生的概率为0,记作
的频率是否比较稳定?
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据。
观察此表,你发现了什么?
从上表可以看出:“正面朝上”的频率总在 附近波动,而且近似等于 。
人们在抛掷硬币、骰子之类的游戏中发现:在充分多次试验中,一个随机事件的频率一般会在一个定值附近摆动,而且试验次数越多,摆动幅度越小。这个性质称为频率的稳定性。
1.分别汇总5人,10人,15人,…,50人的试验结果,并将
试验数据汇总填入下表:
2.根据上表,完成下面的折线统计图:
全班同学做抛掷硬币试验,每人10次。
学生在课本P44完成表和图。
3.观察上面的折线统计图,你发现了什么规律?请与同学交流。
下表是小明抛硬币试验获得的数据(折线图在课本P )
八年级数学下册8.3频率与概率教案1(新版)苏科版

频率与概率中国书法艺术说课教案今天我要说课的题目是中国书法艺术,下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。
一、教材分析:本节课讲的是中国书法艺术主要是为了提高学生对书法基础知识的掌握,让学生开始对书法的入门学习有一定了解。
书法作为中国特有的一门线条艺术,在书写中与笔、墨、纸、砚相得益彰,是中国人民勤劳智慧的结晶,是举世公认的艺术奇葩。
早在5000年以前的甲骨文就初露端倪,书法从文字产生到形成文字的书写体系,几经变革创造了多种体式的书写艺术。
1、教学目标:使学生了解书法的发展史概况和特点及书法的总体情况,通过分析代表作品,获得如何欣赏书法作品的知识,并能作简单的书法练习。
2、教学重点与难点:(一)教学重点了解中国书法的基础知识,掌握其基本特点,进行大量的书法练习。
(二)教学难点:如何感受、认识书法作品中的线条美、结构美、气韵美。
3、教具准备:粉笔,钢笔,书写纸等。
4、课时:一课时二、教学方法:要让学生在教学过程中有所收获,并达到一定的教学目标,在本节课的教学中,我将采用欣赏法、讲授法、练习法来设计本节课。
(1)欣赏法:通过幻灯片让学生欣赏大量优秀的书法作品,使学生对书法产生浓厚的兴趣。
(2)讲授法:讲解书法文字的发展简史,和形式特征,让学生对书法作进一步的了解和认识,通过对书法理论的了解,更深刻的认识书法,从而为以后的书法练习作重要铺垫!(3)练习法:为了使学生充分了解、认识书法名家名作的书法功底和技巧,请学生进行局部临摹练习。
三、教学过程:(一)组织教学让学生准备好上课用的工具,如钢笔,书与纸等;做好上课准备,以便在以下的教学过程中有一个良好的学习气氛。
(二)引入新课,通过对上节课所学知识的总结,让学生认识到学习书法的意义和重要性!(三)讲授新课1、在讲授新课之前,通过大量幻灯片让学生欣赏一些优秀的书法作品,使学生对书法产生浓厚的兴趣。
2、讲解书法文字的发展简史和形式特征,让学生对书法作品进一步的了解和认识通过对书法理论的了解,更深刻的认识书法,从而为以后的书法练习作重要铺垫!A书法文字发展简史:①古文字系统甲古文——钟鼎文——篆书早在5000年以前我们中华民族的祖先就在龟甲、兽骨上刻出了许多用于记载占卜、天文历法、医术的原始文字“甲骨文”;到了夏商周时期,由于生产力的发展,人们掌握了金属的治炼技术,便在金属器皿上铸上当时的一些天文,历法等情况,这就是“钟鼎文”(又名金文);秦统一全国以后为了方便政治、经济、文化的交流,便将各国纷杂的文字统一为“秦篆”,为了有别于以前的大篆又称小篆。
新苏科版八年级数学下册《8章认识概率8.3频率与概率》教案_6

第8章认识概率8.3频率与概率第1课时概率的概念与意义知识点概率的概念与意义1.必然事件的概率是()A.0.5 B.0C.1 D.小于 12.已知事件B为不可能事件,则下列关于概率P(B)的大小,说法正确的是()A.P(B)=1 B.0<P(B)<1C.P(B)=0 D.P(B)>13.“某市明天降水的概率是20%”,对此消息下列说法中正确的是()A.该市明天将有20%的地区降水B.该市明天将有20%的时间降水C.该市明天降水的可能性较小D.该市明天肯定不降水4.下列事件发生的概率为0的是()A.今年冬天南京会下雪B.任意买一张彩票会中奖C.测得某天南京的最低气温为-150 ℃D.掷一枚硬币,正面朝下5.商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”,下列说法正确的是() A.抽10次奖必有一次抽到一等奖B.抽一次不可能抽到一等奖C.抽10次也可能没有抽到一等奖D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖6.事件A:打开电视,它正在播广告;事件B:抛掷一个均匀的骰子,朝上的点数小于7;事件C:在标准大气压下,温度低于0 ℃时冰融化.3个事件的概率分别记为P(A),P(B),P(C),则P(A),P(B),P(C)的大小关系正确的是()A.P(C)<P(A)=P(B)B.P(C)<P(A)<P(B)C.P(C)<P(B)<P(A)D.P(A)<P(B)<P(C)7.一名篮球运动员罚球投中的概率是0.8.小明认为,这说明该运动员每10个罚球中,必有8个投中.你认为小明的判断正确吗?说说你的理由.8.下列各项中,两种事件发生的可能性大小相等的是()A.从一副扑克牌中随机抽出一张牌,是大王与是Q发生的概率B.掷一枚图钉,落地时钉尖“朝上”或“朝下”的概率C.小亮在沿着成直角三角形形状的小路上散步,他出现在各边上的概率D.小明用随机抽签的方式选择以上三种答案,A,B,C被选中的概率9.下列说法正确的是()A.概率很大的事件必然会发生B.如果一个事件不可能发生,那么它就是必然事件,即发生的概率为 1C.不太可能发生的事件的概率不为0D.一件事情肯定会发生,小明说“这件事200%会发生”10.有以下三个事件:事件A:投掷一枚均匀硬币时,正面朝上.事件B:在一个小时内,一只蜗牛爬行了80千米.事件C:若两数之和是负数,则其中必有一数是负数.(1)其中不可能事件是________,必然事件是________;(2)请你把相应事件的概率大小对应的字母A,B,C标在下面的数轴上.图8-3-1详解详析1.C 2.C 3.C 4.C 5.C6.B[解析] 事件A是随机事件,0<P(A)<1.事件B是必然事件,P(B)=1.事件C是不可能事件,P(C)=0.所以P(C)<P(A)<P(B).故选 B.7.解:小明的判断不正确.理由:一名篮球运动员罚球投中的概率是0.8,说明他投篮成功的可能性比较大,即他在10次一组的投篮中,平均会有8次投中,认为该运动员每10个罚球中,必有8个投中是不正确的.8.[全品导学号:85324029]D9.[全品导学号:85324030]C10.[全品导学号:85324031]解:(1)B C(2)。
八年级数学下册8.3 频率与概率学案1(新版)苏科版

八年级数学下册8.3 频率与概率学案1(新版)苏科版8、3 频率与概率(1)学习目标:1、经历试验、统计等活动过程,进一步发展学生合作意识和交流能力2、通过试验、理解当试验次数较大时试验的频率稳定于理论概率,据此一事件发生的概率学习过程:一:“学”自主学习1、情景引入飞机失事会给旅客造成意外伤害,一家保险公司要为购买飞机票的旅客进行保险,应该向旅客收取多少保险费呢?为此,保险公司必须计算飞机失事的可能性大小。
日常生活中类似例子也很多,比如:(1)明天下雨的可能性有多大?(2)买一张彩票中奖的可能性有多大?(3)抛掷1枚质地均匀的硬币,正面朝上的可能性有多大?(4)抛掷1枚质地均匀的骰子,向上一面的点数是6的可能性有多大?……2、概念学习⑴一个事件发生的,称为这个事件的概率。
如果用字母A表示一个事件,那么事件A发生的概率记作。
⑵必然事件A发生的可能性是,即必然事件A发生的概率是1,记作;不可能事件A发生的可能性是0,即不可能事件A发生的概率是0,记作;随机事件A发生的可能性介于事件和事件之间,所以随机事件A发生概率是0和1之间的一个数,记作<P(A)<,且可能性越大说明P(A)越接近,可能性越小说明P(A)越接近。
⑶概率是随机事件自身的属性,它反映这个随机事件发生的可能性的大小。
二:“思”乐学精思1、探索活动活动一做“抛掷质地均匀的硬币试验”,每人10次、(1)分别汇总5人、10人、15人、…、50人……的试验结果,并将试验数据汇总填入下表:(2)根据表格,画出折线统计图。
活动二下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据、观察此表,你发现了什么?2、例题讲解:一粒木质中国象棋“兵”,它的正面刻了一个“兵”字,反面是平的。
将它从一定的高度掷下,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下。
由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:实验次数204060801001xx0160“兵”字面朝上频数14384752667888相应频率0、70、450、630、590、520、560、55 ⑴请将数据表补充完整;⑵画出“兵”字面朝上的频率分布折线图;⑶如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?三:“练”巩固反馈当堂训练在一个不透明的盒子里装有除颜色不同其它相同的黑白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:摸球的次数n10020030050080010003000摸到白球的次数m651241783024815991803摸到白球的频率0、650、620、5930、6040、6010、5990、601 ⑴估计:当n很大时,摸到白球的频率将会接近(精确到0、1)⑵假如你摸一次,你摸到白球的概率P(白球)= 。
八年级数学苏科版下册 第八单元 《 8.3频率与概率》教学设计 教案

二、合作探究生长新知试验一“抛掷质地均匀的硬币试验”步骤1:试验规则:每小组分成两队,每队完成25次试验,每组共完成50次试验,做好记录:每小组的组长汇总50次试验的结果,并将正面朝上的频数输入到表格中.根据学生试验获得的数据,将正面朝上的频率用折线统计图表示出来.问题1观察数据、图表,能否体会出正面朝上的频率蕴含的规律?问题2数据虽然体现了一定的规律性,但还难以较为精确的估计出事件发生的概率,我们能否较为精确的估计出事件发生的概率呢?步骤2:将每小组获得的数据进行累加,填写表格.用类比学习法,你觉得我该如何研究了?将累加数据得到的正面朝上的频率用折线统计图表示出来.问题3 观察数据的频率是否体现出规律性?步骤3:以下是自18世纪以来一些统计学家进行抛硬币试验所得的数据.(预设:波动较大,频率最大值、最小值,在一个常数附近摆动.)类比(预设:稳定性)(预设:特别稳定)稳定在哪个数值呢?问题 4 随着抛掷次数的再一次的增多,也就是试验次数很大时,正面朝上的频率的变化趋势有什么规律?我们一起回顾一下硬币正面朝上的概率的得出过程…实验二(1)填写表中的空格;(2)画出优等品频率的折线统计图;(3)当抽取的足球数很大时,你认为优等品的频率会在哪个常数附近摆动?请模仿硬币正面朝上的概率的得出过程,总结出优等品的概率得出的过程.我们刚才研究的都是随机事件,你对概率定义中的“一个事件”有何想法呢?实验三(预设:0.5)这时能否用0.5作为正面朝上的概率呢?(在多次重复试验中,一个随机事件发生的频率会在一个常数附近摆动,随着试验次数增多,其频率会呈现出一定的稳定性,当试验次数很大时,人们常用这个事件发生的频率来估计概率.)我们再来研究课本上的某批足球质量检验获得的数据,进一步体会概率的得出过程.。
2019-2020年八年级数学下册 8.3 频率与概率教案1 (新版)苏科版

2019-2020年八年级数学下册 8.3 频率与概率教案1 (新版)苏科版【教学目标】体会随机事件在每一次实验中是否发生是不可预言的,但在数多次的反复实验后,随机事件发生的频率(成功率)会逐渐稳定在某一数值上.【重点难点】重点:知道随机事件随实验次数的增加而逐渐趋稳的事实.难点:对实验结果的分析.【预习导航】1.随机事件发生的可能性有大有小.一个事件发生可能性大小的数值,称为这个事件的概率.若用表示一个事件,则我们就用表示事件发生的概率.2.通常规定,必然事件发生的概率是1,记作;不可能事件发生的概率为0,记作;随机事件发生的概率是0和1之间的一个数,即0<<1.3.任一随机事件,它发生的概率是由它自身决定的,且是客观存在的,概率是随机事件自身的属性。
它反映这个随机事件发生的可能性大小.。
【课堂导学】2.例题教学试验一、抛掷硬币1、下表是小明抛硬币试验获得的数据:抛掷次数50100150200250300350400450500正面朝上的频数20537098115156169202219244正面朝上的频率0.40.530.470.490.460.520.480.510.490.49(1)根据上表,完成下面的折线统计图:(2)观察上面的折线统计图,你发现了什么规律?(3)观察折线统计图,当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?2、下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据。
观察此表,你发现了什么?总结:在多次重复试验中,一个随机事件的频率一般会在某一个___________附近摆动,而且随着试验次数增多,摆动的幅度减小。
这个性质称为频率的___________.【当堂训练】1.事件发生的可能性越大,则它的概率越接近;反之,事件发生的可能性越小,则它的概率越接近.2.在抛掷一枚硬币的实验中,出现正面的概率是,若小明连续抛掷9次都是正面朝上,则第10次抛掷,出现正面朝上的概率是.3.一个质量均匀的正方体骰子,每个面上分别有1~6个点,则随着所掷次数的增多,掷得的点数越来越接近 ( )A.奇数点比偶数点多 B.偶数点比奇数点多C.没有规律 D.奇、偶数点的次数相近4.下列说法正确吗?请说明理由(1)天气预报说,明天下雨的概率是90%,那么明天一定会下雨.(2)某医院说,该医院的某种疾病的治愈率为98.7%,因此,某患者去治疗该病一定能治好.(3)抛一枚普通的正方体骰子20次,掷得的点数是2的频数是6,所以掷得2的频率是,所以掷得2的概率是.(4)抛掷一枚质量分布均匀的硬币,因出现正、反面的概率均为,所以抛10次的话一定会有5次正面,5次反面.【课后巩固】1、可能发生的事件是指发生的概率介于和之间。
八年级数学下册第8章认识概率8.3频率与概率教案苏科版(1)(new)
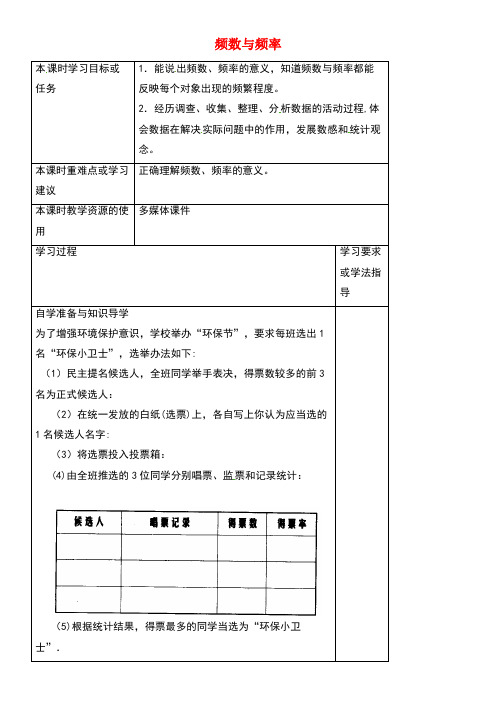
频数与频率本课时学习目标或任务1.能说出频数、频率的意义,知道频数与频率都能反映每个对象出现的频繁程度。
2.经历调查、收集、整理、分析数据的活动过程,体会数据在解决实际问题中的作用,发展数感和统计观念。
本课时重难点或学习建议正确理解频数、频率的意义。
本课时教学资源的使用多媒体课件学习过程学习要求或学法指导自学准备与知识导学为了增强环境保护意识,学校举办“环保节”,要求每班选出1名“环保小卫士”,选举办法如下:(1)民主提名候选人,全班同学举手表决,得票数较多的前3名为正式候选人:(2)在统一发放的白纸(选票)上,各自写上你认为应当选的1名候选人名字:(3)将选票投入投票箱:(4)由全班推选的3位同学分别唱票、监票和记录统计:(5)根据统计结果,得票最多的同学当选为“环保小卫士”.学习交流与问题研1. 频数:某个对象出现的次数;2.频率:频数与总次数的比值。
议一议:1.选举“环保小卫士”用的是哪种调查方法?2.每位候选人得票的频数指的是什么?3.每位候选人得票的频率指的是什么?4.你认为.通过选举产生“环保小卫士"与指定某同学为“环保小卫士”这两种方法,哪种更好?练习检测与拓展延伸(1)频数与频率是同一概念,且有时结果一样. ( )(2).判断下列说法是否正确.在数l 、2、3、2、1、2、3、2、2、1、2、3、2、1、2、1中“2”的频数是8,频率是.21 ( ) 2.在数字l241421235623412141中,“1”出现的频数是______,“2”出现的频数是________,“4”出现的频率是_______,“3”出现的频率是_______.3.下表是某班学生在一次身高测量中得到的统计结果:请回答:(1)这个班总人数是_______人;身高______、_____人数最多,分别是______人、_______人.(2)身高最高、最低的分别是______米、________米,他们分别是_______人、_______人.最高的与最低的相差_______米.4.历史上许多学者做过大量抛掷硬币的试验,请看下表:请你根据上表计算出正面的频率,根据计算你能发现什么规律吗?5.下表是对某班50名学生如何到校问题进行的~次调查结果,根据表中已知数据填表:反思或经验总结尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:8.3频率与概率(1)班级 姓名 备课组长【学习目标】3.在多次重复试验中,体会频率的稳定性. 【学习过程】 一、情境创设飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此,保险公司必须精确计算出飞机失事的可能性有多大。
类似这样的问题在我们的日常生活中也经常遇到.例如:抛掷1枚均匀硬币,正面朝上.在装有彩球的袋子中,任意摸出的1个球恰好是红球.明天将会下雨.抛掷1枚均匀骰子,6点朝上.……随机事件发生的可能性有大有小.一个事件发生可能性大小的数值,称为这个事件的概率.若用A 表示一个事件,则我们就用P (A )表示事件A 发生的概率.通常规定,必然事件发生的概率是1,记作P (A )=1;不可能事件发生的概率为0,记作P (A )=0;随机事件发生的概率是0和1之间的一个数,即0<P (A )<1. 二、探索活动活动一 做“抛掷质地均匀的硬币试验”,每人10次.1.分别汇总5人、10人、15人、…、50人……的试验结果,并将试验数据汇总填入下表:2.根据上表,完成下面的折线统计图:3.当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?4. 下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据.1.理解随机事件发生的可能性有大有小,概率的定义;2.概率是随机事件自身的属性,它反映随机事件发生的可能性大小;观察此表,你发现了什么?活动二下表是某批足球产品质量检验获得的数据.(1)计算并填写表中“抽到优等品”的频率;(2(3)当抽到的足球数很大时,你认为“抽到优等品”的频率在哪个常数附近摆动?活动三观察下面的表格你能发现什么?从上表可以看到,当实验的绿豆的粒数很多时,绿豆发芽的频率nm接近于某一个常数,并在它附近摆动。
三、归纳小结一般地,在一定条件下大量重复进行同一试验时,事件A发生的频率nm会稳定地在某一个常数附近摆动,这个常数就是事件A发生的概率P(A)。
事实上,事件A发生的概率P(A)的精确值还是未知的,但是在实际工作中,人们常把试验次数很大时事件发生的频率作为概率的近似值。
【课后提升】完成时间___________分钟1.抛掷一枚均匀的骰子,它落地时,朝上的点数为1的概率为______。
朝上的点数为偶数的概率为_______ 。
朝上的点数不大于6的概率为______,朝上的点数大于4的概率为______。
2.从一副扑克牌(去掉大小王)中随意抽取一张,抽到红桃的概率为________,抽到10的概率为_______,抽到梅花4的概率为_____________.3.一只不透明的布袋中有三种小球(除颜色以外没有任何区别),分别是2个红球,3个抽取的足球数n 50 100 200 500 1000 2000优等品频数m 46 93 194 472 953 1903优等品频率nm白球和5个黑球,每次只摸出一只小球,观察后均放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是 .4.小华和父母一同从重庆乘火车到广安邓小平故居参观,火车车厢里每排有左、中、右三个座位,小华一家三口随意坐某排的三个座位,则小华坐在中间的概率是____________。
5.初三(1)班50名学生中有35名团员,他们都积极报名参加志愿者活动,根据要求,该班从团员中随机选取1名团员参加,则该班团员李明被选中的概率是_________。
6.十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率是7.有一组卡片,制作的颜色,大小相同,分别标有1~20这20个数字,现在将它们背面向上任意颠倒次序,然后放好后任取一张,则: (1)P (抽到两位数)= ; (2)P (抽到一位数)= ;(3)P (抽到的数是3的倍数)= ; (4)P (抽到的数小于10)= 。
8.如图所示,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概率是 .9.一只小鸟自由自在地在空中飞行,然后随意落在图中所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在某个黑色方格中的概率是 ( ) A. B. C. D .10.如图,小明周末到外婆家,走到十字路口处,记不清前面哪条路通往外婆家,那么他能一次选对路的概率是 ( ) A. B. C. D .011.一箱灯泡有24个,合格率为80%,从中任意拿一个是次品的概率为 ( )A. B. 80% C. D.112.从A 地到达C 地必经过B 地,若从A 地到B 地有2条行走路线,从B 地到C 地有3条行走路线,那么从A 地到C 地的行走路线有 ( ) A.2条 B.3条 C.5条 D. 6条 13.从一副扑克牌中,任意抽一张。
问:(1)抽到小王的概率是 ; (2)抽到10的概率是 ; (3)抽到黑桃的概率是 ; (4)抽到红桃5的概率是 .5124202131412131151115414.阅读填空,再解答问题:(1)从0~9的数字中任取一个可得到一个一位数有9个(不含0)。
(2)从0~9的数字中任取两个(可重复取)组成两位数,我们先确定十位数,有9种可能(不含0);再确定个位数,有10种可能(含0),所以可组成两位数9×10=90(个)。
(3)从0~9的数字中任取三个(可重复取)组成三位数,我们先确定百位数,有种可能(不含0),再确定十位数,有种可能(含0);后确定个位数,有种可能(含0),所以可组成三位数 = (个)。
15.某鱼塘捕到100条鱼,称得总重为150千克,这些鱼大小差不多,做好标记后放回鱼塘,在它们混入鱼群后又捕到102条大小差不多的同种鱼,称得总重仍为150千克,其中有2条带有标记的鱼.(1)鱼塘中这种鱼大约有多少条;(2)估计这个鱼塘可产这种鱼多少千克.16. 自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:(1)该校本次调查中,共调查了多少名学生?(2)请将两个统计图补充完整;(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?2019-2020学年初二下学期期末数学模拟试卷一、选择题(每题只有一个答案正确)1.如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连结EF,若AB=6,BC=46,则FD的长为( )A.2 B.4 C.6D.232.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C 的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是()A.B.C.D.3.如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=()A.4cm B.6cm C.8cm D.10cm4.定义新运算:a⊙b=,则函数y=3⊙x的图象可能是()A.B.C.D.5.如图,菱形ABCD中,点E,F分别是AC,DC的中点,若EF=3,则菱形ABCD的周长是()A.12 B.16 C.20 D.246.如图,在▱ABCD中,对角线AC、BD相交于点O,下列哪个条件不能判定▱ABCD是矩形的是()A.AC=BD B.OA=OB C.∠ABC=90°D.AB=AD7.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN 在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为()A .4B .3C .2D .18.如图所示,在直角坐标系内,原点O 恰好是▱ABCD 对角线的交点,若A 点坐标为(2,3),则C 点坐标为()A .(-3,-2)B .(-2,3)C .(-2,-3)D .(2,-3)9.如图,四边形OABC 是矩形,(2,1)A ,(0,5)B ,点C 在第二象限,则点C 的坐标是()A .(1,3)-B .(1,2)-C .(2,3)-D .(2,4)-10.甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次、甲、乙两人的成绩如表所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数和方差两个因素分析,应选( ). 甲 乙 平均数98方差11A .甲B .乙C .丙D .丁二、填空题 11.如图,在等腰Rt △ABC 中,∠C =90°,AC =BC ,AD 平分∠BAC 交BC 于D ,DE ⊥AB 于D ,若AB =10,则△BDE 的周长等于_.12.为了解我市中学生的视力情况,从我市不同地域,不同年级中抽取1000名中学生进行视力测试,在这个问题中的样本是_____. 13.方程35x x -⋅-=0的解是___.14.已知12,12m n =+=-,则代数式223m n mn +-的值为_____.15.如图,在ABC 中,AC BC =,点D E ,分别是边AB AC ,的中点,延长DE 到点F ,使DE EF =,得四边形ADCF .若使四边形ADCF 是正方形,则应在ABC 中再添加一个条件为__________.16.一组数据3,2,4,5,2的众数是______.17.已知一组数据4,x ,6,9,12的众数为6,则这组数据的中位数为_________. 三、解答题18.为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:(1)本次抽测的男生人数为,图①中m的值为;(2)求本次抽测的这组数据的平均数、众数和中位数;(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.19.(6分)如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点(1)在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A′B′C′,请画出△A′B′C′;(2)B′C′的长度为___单位长度,△A′B′C′的面积为___平方单位。
20.(6分)计算(1271245(227×135353.21.(6分)在正方形ABCD中,BE平分CBD交边CD于E点.(1)尺规作图:过点E 作EF BD ⊥于F ;(保留作图痕迹,不写作法) (2)在(1)的条件下,连接FC ,求BCF ∠的度数.22.(8分)求知中学有一块四边形的空地ABCD ,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m ,BC=12m ,CD=13m ,DA=4m ,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?23.(8分)家乐商场销售某种衬衣,每件进价100元,售价160元,平均每天能售出30件为了尽快减少库存,商场采取了降价措施.调查发现,这种衬衣每降价1元,其销量就增加3件.商场想要使这种衬衣的销售利润平均每天达到3600元,每件衬衣应降价多少元?24.(10分)已知如图,反比例函数14y x=的图象与一次函数23y x =+的图象交于点(1,)A n ,点(,1)B m -.(1)求m ,n 的值; (2)求OAB 的面积;(3)直接写出12y y 时x 的取值范围.25.(10分)解不等式组:22112x x x x ≤+⎧⎪⎨-<+⎪⎩,并把不等式组的解集在数轴上表示出来.参考答案一、选择题(每题只有一个答案正确)1.B【解析】试题分析:∵E 是AD 的中点,∴AE=DE ,∵△ABE 沿BE 折叠后得到△GBE ,∴AE=EG ,AB=BG ,∴ED=EG ,∵在矩形ABCD 中,∴∠A=∠D=90°,∴∠EGF=90°,在Rt △EDF 和Rt △EGF 中,∵ED=EG ,EF=EF ,∴Rt △EDF ≌Rt △EGF (HL ),∴DF=FG ,设DF=x ,则BF=6+x ,CF=6﹣x ,在Rt △BCF 中,222(46)(6)(6)x x +-=+,解得x=3.故选B .考点:3.翻折变换(折叠问题);3.综合题.2.B【解析】【分析】△ADP 的面积可分为两部分讨论,由A 运动到B 时,面积逐渐增大,由B 运动到C 时,面积不变,从而得出函数关系的图象.【详解】解:当P 点由A 运动到B 点时,即0≤x≤2时,y =12×2x =x , 当P 点由B 运动到C 点时,即2<x <4时,y =12×2×2=2, 符合题意的函数关系的图象是B ;故选B.【点睛】本题考查了动点函数图象问题,用到的知识点是三角形的面积、一次函数,在图象中应注意自变量的取值范围.3.A【解析】由题意可知∠DFE=∠CDF=∠C=90°,DC=DF,∴四边形ECDF是正方形,∴DC=EC=BC-BE,∵四边形ABCD是矩形,∴BC=AD=10,∴DC=10-6=4(cm).故选A.4.C【解析】【分析】根据题意可得y=3⊕x=,再根据反比例函数的性质可得函数图象所在象限和形状,进而得到答案.【详解】由题意得y=3⊕x=,当x≥3时,y=2;当x<3且x≠0时,y=﹣,图象如图:故选:C.【点睛】此题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.5.D【解析】【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出AD,再根据菱形的周长公式列式计算即可得解.【详解】解:∵E、F分别是AC、DC的中点,∴EF是△ADC的中位线,∴AD=2EF=2×3=6,∴菱形ABCD的周长=4AD=4×6=1.故选:D.【点睛】本题主要考查了菱形的四条边都相等,三角形的中位线平行于第三边并且等于第三边的一半,求出菱形的边长是解题的关键.6.D【解析】【分析】根据平行四边形的性质,矩形的判定方法即可一一判断即可.【详解】解:∵四边形ABCD是平行四边形,∵AC=BD,∴ABCD是矩形,故A正确;∵四边形ABCD是平行四边形,∴AO=OC,BO=OD,∵OA=OB,∴AC=BD,∴ABCD是矩形,故B正确;∵四边形ABCD是平行四边形,∵∠ABC=90°,∴ABCD是矩形,故C正确;∵四边形ABCD 是平行四边形,∵AB=AD,∴ABCD是菱形,故D错误.故选:D.【点睛】本题考查了矩形的判定,平行四边形的性质,熟练掌握矩形的判定定理是解题的关键.7.B【解析】如图,过点P作PC垂直AO于点C,PD垂直BO于点D,根据角平分线的性质可得PC=PD,因∠AOB与∠MPN互补,可得∠MPN=∠CPD,即可得∠MPC=∠DPN,即可判定△CMP≌△NDP,所以PM=PN,(1)正确;由△CMP≌△NDP可得CM=CN,所以OM+ON=2OC,(2)正确;四边形PMON的面积等于四边形PCOD的面积,(3)正确;连结CD,因PC=PD,PM=PN,∠MPN=∠CPD,PM>PC,可得CD≠MN,所以(4)错误,故选B.8.C【解析】【分析】根据图像,利用中心对称即可解题.【详解】由题可知▱ABCD关于点O中心对称,∴点A和点C关于点O中心对称,∵A(2,3),∴C(-2,-3)故选C.【点睛】本题考查了中心对称,属于简单题,熟悉中心对称的点的坐标变换是解题关键.9.D【解析】【分析】过C 作CE ⊥y 轴于E ,过A 作AF ⊥y 轴于F ,得到∠CEO=∠AFB=90°,根据矩形的性质得到AB=OC ,AB ∥OC ,根据全等三角形的性质得到CE=AF ,OE=BF ,BE=OF ,于是得到结论.【详解】解:过C 作CE y ⊥轴于E ,过A 作AF y ⊥轴于F ,90CEO AFB ∴∠=∠=︒,四边形ABCO 是矩形,AB OC ∴=,//AB OC ,ABF COE ∴∠=∠,()OCE ABF AAS ∴∆≅∆,同理BCE OAF ∆≅∆,CE AF ∴=,OE BF =,BE OF =,(2,1)A ,(0,5)B ,2AF CE ∴==,1BE OF ==,5OB =,4OE ∴=,∴点C 的坐标是(2,4)-;故选:D .【点睛】本题考查了矩形的性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键. 10.C【解析】【详解】试题分析:丙的平均数=98910989109910+++++++++=9,丙的方差=110[1+1+1=1]=0.4,乙的平均数=8988798108710+++++++++=8.2,由题意可知,丙的成绩最好,故选C.考点:1、方差;2、折线统计图;3、加权平均数二、填空题11.1【解析】【分析】由题中条件可得Rt△ACD≌Rt△AED,进而得出AC=AE,然后把△BDE的边长通过等量转化即可得出结论.【详解】解:∵AD平分∠CAB,AC⊥BC于点C,DE⊥AB于E,∴CD=DE.又∵AD=AD,∴Rt△ACD≌Rt△AED,∴AC=AE.又∵AC=BC,∴BC=AE,∴△DBE的周长为:DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB=1.故答案为:1.【点睛】本题主要考查了角平分线的性质以及全等三角形的判定及性质,能够掌握并熟练运用.12.从中抽取的1000名中学生的视力情况【解析】【分析】根据从总体中取出的一部分个体叫做这个总体的一个样本解答即可.解:这个问题中的样本是从中抽取的1000名中学生的视力情况,故答案为从中抽取的1000名中学生的视力情况.【点睛】本题考查的是样本的概念,掌握从总体中取出的一部分个体叫做这个总体的一个样本是解题的关键.13.x =5.【解析】【分析】把两边都平方,化为整式方程求解,注意结果要检验.【详解】方程两边平方得:(x ﹣3)(x ﹣5)=0,解得:x 1=3,x 2=5,经检验,x 2=5是方程的解,所以方程的解为:x =5.【点睛】本题考查了无理方程的解法,解含未知数的二次根式只有一个的无理方程时,一般步骤是:①移项,使方程左边只保留含有根号的二次根式,其余各项均移到方程的右边;②两边同时平方,得到一个整式方程;③解整式方程;④验根.14.3【解析】【分析】把已知值代入,根据二次根式的性质计算化简,灵活运用完全平方公式.【详解】解:因为11m n =+=所以=3【点睛】二次根式的化简求值.15.答案不唯一,如∠ACB=90°或∠BAC=45°或∠B=45°【解析】【分析】先证明四边形ADCF是平行四边形,再证明AC=DF即可,再利用∠ACB=90°得出答案即可.【详解】∠ACB=90°时,四边形ADCF是正方形,理由:∵E是AC中点,∴AE=EC,∵DE=EF,∴四边形ADCF是平行四边形,∵AD=DB,AE=EC,∴DE=12 BC,∴DF=BC,∵CA=CB,∴AC=DF,∴四边形ADCF是矩形,点D. E分别是边AB、AC的中点,∴DE//BC,∵∠ACB=90°,∴∠AED=90°,∴矩形ADCF是正方形.故答案为∠ACB=90°.【点睛】此题考查正方形的判定,解题关键在于掌握判定法则16.1【解析】【分析】从一组数据中找出出现次数最多的数就是众数,发现1出现次数最多,因此1是众数.【详解】解:出现次数最多的是1,因此众数是1,故答案为:1.【点睛】本题考查了众数的意义,从一组数据中找到出现次数最多的数就是众数.17.1【解析】【分析】根据众数的定义求出x,然后根据中位数的概念求解.【详解】解:∵数据4,x,1,9,12的众数为1,∴x=1,则数据重新排列为4,1,1,9,12,所以中位数为1,故答案为:1.【点睛】本题考查了众数和中位数的概念,一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.三、解答题18.(1)50、1;(2)平均数为5.16次,众数为5次,中位数为5次;(3)估计该校350名九年级男生中有2人体能达标.【解析】分析:(Ⅰ)根据4次的人数及其百分比可得总人数,用6次的人数除以总人数求得m即可;(Ⅱ)根据平均数、众数、中位数的定义求解可得;(Ⅲ)总人数乘以样本中5、6、7次人数之和占被调查人数的比例可得.详解:(Ⅰ)本次抽测的男生人数为10÷20%=50,m%=1450×100%=1%,所以m=1.故答案为50、1;(Ⅱ)平均数为344105166147650⨯+⨯+⨯+⨯+⨯=5.16次,众数为5次,中位数为552+=5次;(Ⅲ)1614650++×350=2.答:估计该校350名九年级男生中有2人体能达标.点睛:本题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.19.(1)如图所示;见解析;(2)3,9;【解析】【分析】(1)利用位似图形的性质得出对应点坐标进而得出答案;(2)根据勾股定理和三角形的面积公式即可得到结论.【详解】(1)如图所示:△A′B′C′即为所求:(2)如图所示:B′C′的长度==3;∵A′C′=3,∴△A′B′C′的面积为=×3×6=9平方单位,故答案为:3,9.【点睛】此题考查作图-位似变换,勾股定理和三角形的面积公式,解题关键在于掌握作图法则20.(1)3+35(2)1【解析】试题分析:(1)先把二次根式化简再合并即可;(2)进行二次根式的乘法运算即可.试题解析:(1)原式=3323+35=3+35;(2)原式=3-5+3=1.21.(1)作图见解析;(2)67.5°.【解析】【分析】(1)利用基本作图作EF⊥BD于F;(2)利用正方形的性质得到∠DBC=45°,∠BCD=90°,再根据角平分线的性质得到EF=EC,则∠EFC=∠ECB,然后利用等角的余角相等和三角形等角和计算∠BCF的度数.【详解】(1)如图,EF为所作;(2)∵四边形ABCD为正方形,∴∠DBC=45°,∠BCD=90°,∵BE平分∠CBD,EF⊥BD,CE⊥BC,∴EF=EC,∴∠EFC=∠ECB,∴∠BFC=∠BCF=12(180°-45°)=67.5°.【点睛】本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了正方形的性质.22.学校需要投入9000元资金买草皮.【解析】【分析】仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.【详解】连接BD,在Rt△ABD中,BD2=AB2+AD2=32+42=52,在△CBD中,CD2=132,BC2=122,而122+52=132,即BC2+BD2=CD2,∴∠DBC=90°,S四边形ABCD=S△BAD+S△DBC=12•AD•AB+12DB•BC,=12×4×3+12×12×5=1.所以需费用1×250=9000(元),答:学校需要投入9000元资金买草皮.【点睛】本题考查了勾股定理的应用,通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.23.1元【解析】【分析】设每件衬衣降价x元,根据商场平均每天盈利数=每件的盈利×售出件数列出方程求解即可.【详解】解:设每件衬衣降价x元,依题意,得:(160﹣100﹣x)(1+3x)=3600,整理,得:x2﹣50x+600=0,解得:x1=20,x2=1,∵为了尽快减少库存,∴x=1.答:每件衬衣应降价1元.【点睛】本题考查一元二次方程的应用,商场平均每天盈利数=每件的盈利×售出件数;每件的盈利=原来每件的盈利-降价数.24.(1)m=-2,n=2;(2)152;(3)x的取值范围是x≤-2或0<x≤1.【解析】【分析】(1)将A,B两点分别代入一次函数解析式,即可求出两点坐标.(2)将△AOB分割为S△AOB=S△BOC+S△AOC,列式求出即可.(3)根据函数的图像和交点坐标即可求得.【详解】(1)把A点坐标(1,n)代入y2=x+3,得n=2;把B点坐标(m,-1)代入y2=x+3,得m=-2.∴m=-2,n=2.(2)如图,当y=0时,x+3=0,∴C(-3,0),∴S△AOB=S△BOC+S△AOC=12×3×1+12×3×2=152.(3)当12y y时x的取值范围是x≤-2或0<x≤1.【点睛】本题考查了一次函数和反比例函数的交点问题,涉及三角形的面积计算,一次函数的图像等知识点.25.3x2-<≤;数轴表示见解析.【解析】【分析】先把两个不等式分别求出来,然后根据不等式的解的口诀得到不等式的解集,然后把解集表示在数轴上即可.【详解】解:22112x xxx≤+⎧⎪⎨-<+⎪⎩①②,解不等式①,得:x2≤,解不等式②,得:x3>-,∴不等式的解集为:3x2-<≤,在数轴上表示为:【点睛】本题考查了解一元一次不等式组,解题的关键是正确解出每一个不等式,然后掌握求解集的口诀.2019-2020学年初二下学期期末数学模拟试卷一、选择题(每题只有一个答案正确)1.图中的两个三角形是位似图形,它们的位似中心是( )A .点PB .点DC .点MD .点N2.对于两组数据A ,B ,如果s A 2>s B 2,且A B x x ,则( ) A .这两组数据的波动相同 B .数据B 的波动小一些 C .它们的平均水平不相同 D .数据A 的波动小一些3.一次函数与图象如图:则下列结论①k<0;②a>0;③不等式x+a<kx+b 的解集是x<3;④a −b=3k −3中,正确的个数是( )A .1个B .2个C .3个D .4个4.莒南县欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表: 候选人甲 乙 丙 丁 测试成绩面试86919083笔试908383924的权.根据四人各自的平均成绩,你认为将录取( ) A .甲B .乙C .丙D .丁5.下列多项式中,不能运用公式进行分解因式的是( ) A .a 2+b 2B .x 2﹣9C .m 2﹣n 2D .x 2+2xy+y 26.等腰三角形的两边长分别为2、4,则它的周长为()A.8 B.10 C.8或10 D.以上都不对7.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于 ( )A.1B.1.5C.2D.2.58.如图,矩形ABOC的面积为2,反比例函数kyx=的图象过点A,则k的值为()A.2B.2-C.2D.2-9.某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是()A.1.95元B.2.15元C.2.25元D.2.75元10.如图是某射击选手5次设计成绩的折线图,根据图示信息,这5次成绩的众数、中位数分别是()A .7、8B .7、9C .8、9D .8、10二、填空题11.如图,ABCD 的对角线相交于点O ,且AD ≠CD ,过点O 作OM ⊥AC ,交AD 于点M .如果CDM 的周长为8,那么ABCD 的周长是__.12.已知菱形两条对角线的长分别为12和16,则这个菱形的周长为______.13.如图,在平面直角坐标系中,正方形OA 1B 1C 1,B 1A 2B 2C 2,B 2A 3B 3C 3,…的顶点B 1,B 2,B 3,…在x 轴上,顶点C 1,C 2,C 3,…在直线y=kx+b 上,若正方形OA 1B 1C 1,B 1A 2B 2C 2的对角线OB 1=2,B 1B 2=3,则点C 3的纵坐标是______________.14.如图,四边形纸片ABCD 中,90A C ︒∠=∠=,BC DC =.若8cm AB AD +=,则该纸片的面积为________ 2cm .15.将两块相同的含有30°角的三角尺按如图所示的方式摆放在一起,则四边形ABCD 为平行四边形,请你写出判断的依据_____.16.为了让居民有更多休闲和娱乐的地方,江宁区政府又新建了几处广场,工人师傅在铺设地面时,准备选用同一种正多边形地砖进行铺设.现有下面几种形状的正多边形地砖:正三角形、正方形、正五边形、正六边形,其中不能进行平面镶嵌的有______.17.分解因式:2a3﹣8a=________.三、解答题18.如图,平面直角坐标系内有一△ABC,且点A(2,4),B(1,1),C(4,2).(1)画出△ABC向下平移5个单位后的△A1B1C1;(2)画出△A1B1C1先向左平移5个单位再作关于x轴对称的△A2B2C2,并直接写出点A2,B2的坐标.19.(6分)如图,在正方形网格中,每个小正方形的边长都是1,点A、B、C、D都在格点上.(1)线段AB的长是______;(2)在图中画出一条线段EF,使EF13AB、CD、EF三条线段的长能否成为一个直角三角形三边的长?说明理由.20.(6分)在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.(1)如图1,证明平行四边形ECFG为菱形;(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.21.(6分)计算:(4+7)(4﹣7)22.(8分)如图,在矩形ABCD 中,对角线AC 、BD 相交于点O .若120AOD ∠=︒,3AB =,求AC 的长.23.(8分)解不等式组:233(2){132x x x x -≥--<,并把它的解集在数轴上表示出来。
