虚拟变量(中级计量经济学总结(四川大学,杨可扬)
自相关(中级计量经济学总结(四川大学,杨可扬)

自相关(wooldridge, Gujarati 12章)一,自相关的概念自相关:当误差项协方差不为零。
即,对某些观察值 i 和 m,cov(,)0 i m u u ¹ ,i m¹ 二,自相关的后果自相关不影响无偏性和一致性。
但是自相关使得 OLS 不再是 BLUE, 且 t,F 检验不再有效。
只要满足平稳性和弱相依性的条件则 Rsquared 仍然是一致的。
三,自相关的侦测1, 图表法用残差对时间做图,或者用残差对滞后一期的残差作图。
2, 直接对r 进行 t 检验假设自变量是严格外生的,且扰动项是 AR(1),即,1 u u e t t tr =+ - 那么我们只需要对 r 进行一个 t 检验就可以了。
备择假设既可以是 0 : 0 H r ¹ 也可以是, 0: 0 H r > 当然在这里还可以采用异方差稳健的统计量。
我们还可以放松严格外生的假定,并且可以考虑高阶的自回归:01111 ˆ ˆ ˆ t t k tk t k t ku x x u u b b b r r -- =+++++ …… ……+我们只需要对残差的K 个滞后值进行 F 检验就可以了。
注意: tk x 中可以包括因变量的滞后 值。
其实利用上面回归所得 Rsquared 我们还可以进行 BG 检验:2ˆ() u LM n q R =- 2q LM c : 对于 LM 统计量的计算各种书上略有差异。
上面的公式来自 Wooldridge ,其中 q 表示残差滞后的期数。
在 EVIEWS5 中所用的 LM 统计量的计算是 2 ˆ uLM nR = 。
3,DW 检验有上面的检验之后,已经不用再搞什么 DW 检验了。
但是它仍然被广泛使用,所以有必要 了解。
重点要注意它的局限性。
(1) 1ˆ ˆ 2(1)1 2d d r r »-» 也即, - r ££££ 既然-11,那么0d 4。
计量经济学虚拟变量

在实际分析当中,根据T检验的结 果,将不显著的季度虚拟变量从模型 中消除,用剩下的显著的虚拟变量对 模型进行估算就足够。
(2), 没有常数项的时候,可以设第4季 度的季度虚拟。
Yi 1D1 2D2 3D3 4D4 ui
(3),虚拟变量的陷阱
Yi a 1D1 2D2 3D3 4D4 ui
2,存在结果性变化。 3,需要对难以量化的数据进行处理。
• 计量经济中的虚拟变量,在明确其引入理 由基础上,被用于很多的多元回归模型。
二,虚拟变量的类型
1,临时虚拟
临时虚拟,也称为突发性虚拟。为了更好的对模型进行估算,经常需 要在回归模型中排除一些由突发性事件产生的异常值(outlier),及其对 模型的影响,例如战争,地震,内乱,罢工等。
• 第一季度到第四季度的常数项为:
第一季度:a 1
Yi (a 1) X i ui
第三季度:a 3
Yi (a 3 ) X i ui
第四季度: a
Yi a X i ui
• 现在第四季度是基准,分别表示第 四季度与各季度之差。
数虚拟变量和常数虚拟变量。
Yi a 1X i 2D ui
1 异常时期 D=
0 平时
Yi a 1Xi 2D1 3D2 ui
1
D1= 0
发生地震的年份 其他年份
1
D2= 0
发生水灾的年份 其他年份
2,定性数据的虚拟处理
学历,性别,人种等定性的差异
3,季度虚拟
(1),定义:季度虚拟是通过回归模型的常 数项的变化(斜率回归系数一定)来掌握 季度和月度等季节变化,因此,从技术角 度成为“常数项虚拟”。
这种“量化”通常是通过引入“虚拟变量” 来完成。根据这些因素的属性类型,构造只取 “0”或“1”的人工变量,通常称为虚拟变量 (dummy variables),记为D。
计量经济学课件虚拟变量

通过引入虚拟变量,可以更准确地刻画经济现象的非线性特征,从而提高计量经济学模型 的精度和预测能力。
拓展应用领域
虚拟变量的引入使得计量经济学模型能够应用于更多的领域,如金融、环境、社会等,进 一步拓展了计量经济学的应用范围。
未来研究方向和趋势
深入研究虚拟变量的理论 和方法
未来研究将进一步深入探讨虚 拟变量的理论和方法,包括虚 拟变量的选择、设定和估计方 法等,以更准确地刻画经济现 象。
https://
未来研究将积极推动虚拟变量 在交叉学科领域的应用,如环 境经济学、金融经济学等,以 促进不同学科之间的交流和合 作。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
要点二
虚拟变量的设置原则
在设置虚拟变量时,需要遵循完备性 和互斥性的原则。完备性要求虚拟变 量的取值能够覆盖所有可能的情况, 而互斥性则要求不同虚拟变量之间不 能存在重叠或交叉的情况。
要点三
虚拟变量的回归系数 解释
在线性回归模型中,虚拟变量的回归 系数表示该定性因素对因变量的影响 程度。当虚拟变量取值为1时,其对 应的回归系数表示该水平与参照水平 相比对因变量的影响;当虚拟变量取 值为0时,则表示该水平对因变量没 有影响。
参数估计与假设检验
参数估计
采用最小二乘法等估计方法,对引入虚拟变量后的模型进行参数估计,得到各 解释变量的系数估计值。
假设检验
根据研究问题和假设,构建相应的原假设和备择假设,通过t检验、F检验等方 法对参数进行假设检验,判断虚拟变量对模型的影响是否显著。
计量经济学-中-4-虚拟应变量

虚拟自变量的回归
(例题分析)
【例】为研究 考试成绩与性 别之间的关系 ,从某大学商 学院随机抽取 男女学生各8 名,得到他们 的市场营销学 课程的考试成 绩如下表
虚拟自变量的回归
(例题分析)
100
散点图
¼ Ô É ¨ ¿ Ê ³ ¼
75
50
25
男
女 Ð ± Ô ð
y与x的回归
¼ Ô É ¨ë Ô ð Ä ¢ ã ¼ ¿ Ê ³ ¼ Ó Ð ±µ É µ Í
3.5)中的干扰必定是同方差性的了。 真 E (Yi / X i ) 是不知道的,从而权wi 是不知 道的,为了估计 wi ,可采用如下两步法: 1.对(11.2.1)作最小二乘回归,暂且撇 ˆ 开异方差性问题。于是得到 Yi =真 E (Yi / X i ) 的OLS估计值。再由此求wi 的估计值
7
对数单位模型
我们用住房所有权的例子说明对数单位模型的基本概念。解 释住房所有权对收入的线性关系时的 线性概率模型曾是:
其中X为收入,而Y=1表示家庭拥有住房,但现
在考虑如下住房所有权的表达式:
Pi E (Y 1/ X i ) 1 2 X i
(11.7.1)
Pi E (Y 1/ X i )
显然,我们不再可能假定干扰项是正态分布的:实际 上,它遵循二项分布。 干扰项的异方差性 由(11.3.2)中可以得到 的概率分布: 当 ui 1 2 X i 概率为 1 Pi ; 当 ui 1 1 2 X i 概率为 Pi ,进而可得到:
var(ui ) Pi (1 Pi ) Pi (1 Pi )
ˆ (Yi / X 12) 0.9457 12(0.1021) =0.2795 就是说,收入为12000 美元的家庭拥有住宅的 概率为28%。 对于上面的估计受异方差的影响,因此我们可 ˆ Yi 是 以用WLS来获得更有效的估计值。由于某些 ˆ 负的,和某些 Yˆi 大于1,对于这些 Yˆi 来说,wi 将 是负的,因此删去这些值 。得到的WLS回归为:
面板(中级计量经济学总结(四川大学,杨可扬)

面板数据(主要参考 伍德里奇 第 13 章 第 14 章) 一, 一阶差分,FD(1)模型:两期时情形:001 *2*,1,2it t it i it y d x a u t b d b =++++= 200122 10111 ()*,2*,1i i i i i i i i y x a u t y x a u t b d b b b =++++= =+++= 01 i i iy x u d b D =+D +D三期及其以上时情形:在这里需要注意:u 在两期时,回归方程中没有明显包括年变量。
在三期及其以上时 候,年变量从第三期开始出现。
当然以上都是包括截距的。
关键 是:T=1 期的数据是缺失的。
例如在例 13.8 当中,我们不能直接 在差分方程中包括 d(luclms)。
这样做的结果是第一期, 也即 1980 的数据还存在,但显然是没有意义的。
解决方法两个:要么就把 数据结果首先转变成为面板,再像刚才那样做;要么就直接在样本设定中排除 1980 年的数据。
u 没有时间变异的数据不能被包括,时间变异为常值的变量也不能 被包括。
前者比较显然的例子是性别,比较隐蔽的是,如果我们 研究的对象是大学生,那么 SAT 成绩就没有时间变异。
后者的例 子是工作经历,该变量每年的增量都为 1,也即它的差分没有变 异。
(2)自相关和异方差如果没有自相关,BP 和 White 检验都可以直接用,或者直接使用异 方差稳健的标准误。
差分方程的残差对其滞后一期回归,以此来检验自相关。
在纠正自相 关的时候,不能直接使用软件,需要手算 FGLS,并且尽量使用 PW。
二, 固定效应,FE(1)模型其中也即需要注意:u 回归没有截距项。
EVIEWS 报告的截距不用理会。
u i y 是对所有时期的第 i 个横截面的 y 求平均, 因而不能直接在 EVIEWS 当中看 y 的均值,那是对所有时期、所有横截面的均值。
u 没有时间变异的变量不能被包括。
计量经济学虚拟变量

D=0 正常时期
• 设定模型 Y= b0 + b1 x +b2 D x +e • 异常时期模型:(截距相同斜率不同)
• Y= b0 + (b1 +b2 ) x +e • 正常时期模型:(截距相同斜率不同)
• Y= b0 + b1 x +e
17
加法与乘法组合引入——— 截距与斜率均不同
• D=1 异常时期 D=0 正常时期 • 设定模型 Y=b0+ b1x+ b2D + b3Dx +e • 异常时期模型:(截距与斜率均不同) • Y= (b0 + b2) + (b1 +b3) x +e • 反常时期模型:(截距与斜率均不同) • Y= b0 + b1 x +e
forecast xshe982 '显示预测结果
show xshe982
35
load c:\lx4\jjtzh.wf1 genr q2=(cos(t*2*3.14159/4)<-0.999999) genr q3=(sin(t*2*3.14159/4)<-0.999999) genr q4=(cos(t*2*3.14159/4)>0.999999) equation jjtzheq.ls xshe c t q2 q3 q4 forecast xshef1 equation wjjtzheq.ls xshe c t forecast xshef2 group xsh xshe xshef1 xshef2 show xsh.line
18
3。临界指标的虚拟变量的引入
• 在经济转折时期,可以建立临界值指标 的虚拟变量模型来反映
虚拟变量(中级计量经济学总结(四川大学,杨可扬)

虚拟变量(Wooldridge chapter 7 ,13and Gujarati chapter 9)本章所有内容都赋予一个统一的例题来总结:0121234 *** wage female married educ female married female educ married educ ub d d b b b b =+++ ++++ 显然本例是在研究性别、婚姻状况、教育状况同收入之间的 关系问题。
一,单个虚拟变量01 wage female ub d =++ 0 01(|0) (|1) E wage female E wage female b b d == ==+ 也就是说,男性的平均工资为 0 b ,而女性的平均工资为 01 b d + 。
检验 这两组平均工资是否显著不同只需检验 female 是否显著。
如果female 显著且 1ˆ d <0 则说明存在性别歧视。
这也是典型的用虚拟变量 来标志截距的不同。
换成对数——水平形式: 01 log() wage female u b d =++ 则男女之间工资 的百分比差异为: 1 100*[exp()1]d - 以下作一个简单的证明,表明以上公式不仅适用于虚拟变量:111011 101 101 10 1010log() log()log() log(/) / 1 %*100(1)*100 y x u y y y y y y e y y e y y y y e y bb b b b b b =++ -= = = - =- - D ==- 二,双个虚拟变量及其交互012 wage female married ub d d =+++ 02 012 (|0,) (|1,) E wage female married married E wage female married marriedb d b d d ==+ ==++ 因此 1 d 表示在给定婚姻状况条件下, 男女的工资差异。
双变量模型(中级计量经济学总结(四川大学,杨可扬)_图文(精)

——估计世界经济 06级杨可扬本章大纲 n普通最小二乘法的推导nOLS 估计量的性质 n拟和优度复习 1中级计量经济学杨可扬 6复习 2——OLS 估计量的推导nOLS 法是要找到一条直线,使残差平方和最小 n 也即是: (01 220 11ˆˆ 11 , ˆˆˆ n ni i i tMin u y x Minbb bb == =-- åå中级计量经济学杨可扬15OLS 的代数性质n 回归元(解释变量和 OLS 残差之间的样本协方差为零0 ˆ 1= å = ni ii u x复习 3——十大经典假设1. 线性回归模型2. 在重复抽样中 X 的值是固定的3. 零条件均值4. 同方差性5. 无自相关6. 扰动项和自变量简的协方差为零7. 观测次数大于待估参数8. X 又有变异9. 正确设定模型10. 没有完全的多重共线性OLS 估计量的统计性质n 高斯—马尔可夫定理 (Gauss- Markov theorem在给定经典线性回归的假定下,最小二乘估计量是具有最小方差的线性无偏估计量。
best liner unbiased estimator, BLUE2,无偏性ˆ ( E bb= 参数估计量的数学期望值等于真实值。
3,最小方差性n 最小方差性是在所有线形无偏估计量中,最小二乘法估计量的方差最小。
最小方差这一性质又称为有效性或最佳性。
中级计量经济学杨可扬313,最小方差性的证明1 11 1222122122 11 ˆ cov(, cov(, 0, ˆ var( var( var( ( ( ˆ var( var( i ii i i ii j i j iiiiiiiiw y w b y b y y u u i jw y ww b w b wb bb b bs bs bb ==¹ \== =+ +³ \³ å ååå å åå % % Q % Q % 由“ 线性性” 的证明中可知 : = 设是其它估计方法得到的的线性无偏估计量 = ( + ,其中是不全为零的常数估计误差方差(1n我们不知道误差方差 s2 是多少, 因为我们不能观察到误差 uin我们观测到的是残差 û in我们可以用残差构成误差方差的估计中级计量经济学杨可扬 33中级计量经济学杨可扬 34估计误差方差 (2n 首先,我们注意到 s 2 =E(u 2 , 所以 s2 的无偏估计量是 n u i 是不可观测的,但我们找到一个 u i 的无偏估计量å = ni iu n 1 2/ 1 (拟合优度(续拟合优度(续我们怎样衡量我们的样本回归线拟合样本数据有多好呢?w可以计算总平方和(SST 中被模型解释的部分,称此为回归 R 2w R 2 = SSE/SST = 1 – SSR/SST拟合优度(续1.R2 越大,表明回归直线与样本观察值拟合得越好,反之,拟合得就越差。
计量经济学第八章 虚拟变量

Yi X i Di X i i
如果该模型设定正确,此时有:
E(Yi
)
(
X
)
i
X
i
D 1 D0
可见,城镇ቤተ መጻሕፍቲ ባይዱ民的边际消费倾向为 ( ) ,农
村居民的边际消费倾向为 。
如果不同属性类别对应的截距项和斜率项都 是有差异的,可在回归模型中同时引入虚拟 变量的加法方式和乘法方式,结果如下:
1 东部 D1 0 其他
1 中部 D2 0 其他
若考虑不同区域居民对应回归模型截距的不同 ,可构建模型如下:
Yi 1D1i 2 D2i X i i
则有:
E (Yi
)
( (
2) 1)
X i X i
Xi
Yi Di X i Di X i i
对于城镇居民和农村居民这两个类别,有总 体回归函数如下:
E(Yi
)
(
)
( X i
)X
i
D 1 D0
可见, 和 分别表示城镇居民与农村居民
的消费函数在截距和斜率上的差异。
注:
对于包含多个类别(M个)的属性变量,构 建M-1个虚拟变量,如在消费模型中,考虑 区域因素(东部,中部,西部)影响,可构 建2个虚拟变量:
Yi 1D1i 2 D2i (D1i D2i ) X i i
• 则有: ( 1 2 ) Xi
E
(Yi
)
( 1) Xi ( 2 ) Xi
计量经济学之虚拟变量

四、虚拟变量的设置原则
每一定性变量所需的虚拟变量个数要比该定性变量的类别数少1,
即如果定性变量有m个类别,则只在模型中引入m-1个虚拟变量。
Y t 0 1 X 1 t … k X k t 1 D 1 t 2 D 2 t 3 D 3 t 4 D 4 t t
Y (X
D)
冷饮的销售额与季节因素的关系
计量经济学之虚拟 变量
为了能够在模型中反映这些因素的影响,并提高模型的精度,需要将 它们人为地“量化”,这种“量化”通常是通过引入“虚拟变量”来完成的。
这种用两个相异数字来表示对被解释变量有重要影响而自身又没有观测数值的一 类变量,称为虚拟变量。
虚拟变量的特点是:
1.虚拟变量是对经济变化有重要影响的不可测变量。 2.虚拟变量是赋值变量,一般根据这些因素的属性类型,构造只取 “0”或“1” 的人工变量,通常称为虚拟变量,记为D。这是为了便于计算而把定性因素这样数量 化的,所以虚拟变量的数值只表示变量的性质而不表示变量的数值。
一般的,基础类型和肯定类型取值为1;比较类型和否定类型 取值为0。
例如:
1)表示性别的虚拟变量可取为 D1=
1 男性 0 女性
2)表示文化程度的虚拟变量可取为 D2=
1 本科及以上学历 0 本科以下学历
3)表示地区的虚拟变量可取为
D3=
1 城市 0 农村
计量经济学课件虚拟变量

2. 检验模型结构的稳定性
定义: 如果模型中参数的估计值与样本的选取无关, 则称该模型结构是稳定的。 用途: (1)检验多重共线性; (2)比较两个回归模型是否存在显著差异。 例:不同时期、不同地区、不同行业
模型:
样本1
样本2
y a1 b1 x
y a2 b2 x
组合:y a bx D XD
1 D 0 1 D 0
1 D 0 1 D 0
宽松政策 紧缩政策 发达地区 不发达地区
销售旺季 销售淡季
高收入家庭 低收入家庭
作用:
⑴描述和测量定性因素的影响; ⑵正确反映经济变量之间的关系,提高模型的精度 ⑶便于处理异常数据。
本节学习要求: 1958 年 1 D 其他年份 ⑴如何设置虚拟变量; 0 ⑵如何描述和测量定性因素的影响。
东 中 西
中部地区 其他地区
α2 -α1
(a 1 ) bX
东部地区 其他地区
α1
a bX
方式3:设置3个虚拟变量
1 D1 0
1 D3 0
中部地区 其他地区
西部地区 其他地区
1 D2 0
东部地区 其他地区
D1 D2 D3 1
虚拟变量的设置原则 1:
第四节
虚拟变量
一、虚拟变量及其作用
问题: 在计量经济模型中如何反映定性因素影响?例如:
金融计量分析中的政策因素、心理因素 经济增长分析中的地区差异因素 产品销售分析中的季节因素、消费习惯等因素
定义: 用以描述定性因素影响、只取数值0和1的人工变 量为“虚拟变量”,一般用符号D表示。 (Dummy variable—哑变量)
计量经济学实验报告虚拟变量
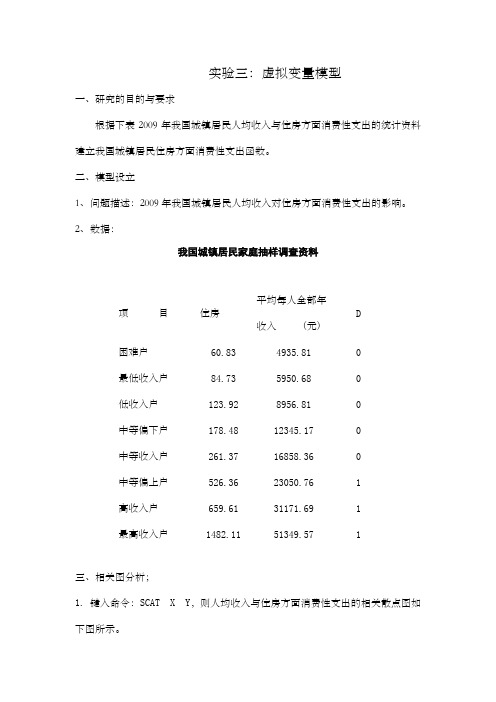
实验三:虚拟变量模型一、研究的目的与要求根据下表2009年我国城镇居民人均收入与住房方面消费性支出的统计资料建立我国城镇居民住房方面消费性支出函数。
二、模型设立1、问题描述:2009年我国城镇居民人均收入对住房方面消费性支出的影响。
2、数据:我国城镇居民家庭抽样调查资料平均每人全部年项目住房D收入 (元)困难户60.83 4935.81 0最低收入户84.73 5950.68 0低收入户123.92 8956.81 0中等偏下户178.48 12345.17 0中等收入户261.37 16858.36 0中等偏上户526.36 23050.76 1高收入户659.61 31171.69 1最高收入户1482.11 51349.57 1三、相关图分析;1. 键入命令:SCAT X Y,则人均收入与住房方面消费性支出的相关散点图如下图所示。
从相关图可以看出,前5个样本点(即中低收入家庭)与后3个样本点(中、高收入)的消费性支出存在较大差异,因此,为了反映“收入层次”这一定性因素的影响,设置虚拟变量如下:10D ⎧=⎨⎩中等偏高及高收入家庭中、低收入家庭2. 构造虚拟变量。
使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 3. 估计虚拟变量模型:再由t 检验值判断虚拟变量的引入方式,并写出各类家庭的消费性支出函数。
虚拟变量模型的估计结果如下:Dependent Variable: Y Method: Least Squares Date: 01/03/12 Time: 15:25 Sample: 2001 2008 Included observations: 8VariableCoefficient Std. Error t-Statistic Prob.X0.0164000.0057432.8556760.0461D1 -327.1185 118.4766 -2.777039 0.0498 XD 0.018709 0.006356 2.943588 0.0422 C-19.0028861.67034-0.3081360.7734R-squared0.992173 Mean dependent var 422.1763 Adjusted R-squared 0.986303 S.D. dependent var 479.4838 S.E. of regression 56.11683 Akaike info criterion 11.19960 Sum squared resid 12596.40 Schwarz criterion 11.23932 Log likelihood -40.79841 F-statistic 169.0152 Durbin-Watson stat3.162055 Prob(F-statistic)0.000115我国城镇居民住房方面消费性支出函数的估计结果为:ˆ19.002880.016400327.11850.018709i i i i yx D XD =-+-+ =t (-0.308136) ( 2.855676) (-2.777039) (2.943588)2R =0.992173 2R =0.986303 F =169.0152 S.E =56.11683 虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明我国城镇居民中低收入家庭与中等偏高及高收入家庭对住房的消费性支出,在截距和斜率上都存在着明显差异,所以以加法和乘法方式引入虚拟变量是合理的。
计量经济学实验报告(虚拟变量)

计量经济学实验报告实验三:虚拟变量模型姓名:上善若水班级:序号:学号:中国人均消费影响因素一、理论基础及数据1. 研究目的本文在现代消费理论的基础,分析建立计量模型,通过对1979——2008 年全国城镇居民的人均消费支出做时间序列分析和对2004—2008年各地区(31个省市)城镇居民的人均消费支出做面板数据分析,比较分析了人均可支配收入、消费者物价指数和银行一年期存款利率等变量对居民消费的不同影响。
2. 模型理论西方消费经济学者们认为,收入是影响消费者消费的主要因素,消费是需求的函数。
消费经济学有关收入与消费的关系,即消费函数理论有:(1)凯恩斯的绝对收入理论。
他认为消费主要取决于消费者的净收入,边际消费倾向小于平均消费倾向。
他假定,人们的现期消费,取决于他们现期收入的绝对量。
(2)杜森贝利的相对收入消费理论。
他认为消费者会受自己过去的消费习惯以及周围消费水准来决定消费,从而消费是相对的决定的。
当期消费主要决定于当期收入和过去的消费支出水平。
(3)弗朗科•莫迪利安的生命周期的消费理论。
这种理论把人生分为三个阶段:少年、壮年和老年;在少年与老年阶段,消费大于收入;在壮年阶段,收入大于消费,壮年阶段多余的收入用于偿还少年时期的债务或储蓄起来用来防老。
(4)弗里德曼的永久收入消费理论。
他认为消费者的消费支出主要不是由他的现期收入来决定,而是由他的永久收入来决定的。
这些理论都强调了收入对消费的影响。
除此之外,还有其他一些因素也会对消费行为产生影响。
(1)利率。
传统的看法认为,提高利率会刺激储蓄,从而减少消费。
当然现代经济学家也有不同意见,他们认为利率对储蓄的影响要视其对储蓄的替代效应和收入效应而定,具体问题具体分析。
(2)价格指数。
价格的变动可以使得实际收入发生变化,从而改变消费。
基于上述这些经济理论,我找到中国1979-2008年全国城镇居民人均消费以及城镇居民人均可支配收入、城镇居民消费者物价指数和2004—2008年各地区城镇居民人均消费以及城镇居民人均可支配收入、城镇居民消费者物价指数、以及银行一年期存款利率的官方数据。
自相关(中级计量经济学总结(四川大学,杨可扬)

自相关(wooldridge, Gujarati 12章)一,自相关的概念自相关:当误差项协方差不为零。
即,对某些观察值 i 和 m,cov(,)0 i m u u ¹ ,i m¹ 二,自相关的后果自相关不影响无偏性和一致性。
但是自相关使得 OLS 不再是 BLUE, 且 t,F 检验不再有效。
只要满足平稳性和弱相依性的条件则 Rsquared 仍然是一致的。
三,自相关的侦测1, 图表法用残差对时间做图,或者用残差对滞后一期的残差作图。
2, 直接对r 进行 t 检验假设自变量是严格外生的,且扰动项是 AR(1),即,1 u u e t t tr =+ - 那么我们只需要对 r 进行一个 t 检验就可以了。
备择假设既可以是 0 : 0 H r ¹ 也可以是, 0: 0 H r > 当然在这里还可以采用异方差稳健的统计量。
我们还可以放松严格外生的假定,并且可以考虑高阶的自回归:01111 ˆ ˆ ˆ t t k tk t k t ku x x u u b b b r r -- =+++++ …… ……+我们只需要对残差的K 个滞后值进行 F 检验就可以了。
注意: tk x 中可以包括因变量的滞后 值。
其实利用上面回归所得 Rsquared 我们还可以进行 BG 检验:2ˆ() u LM n q R =- 2q LM c : 对于 LM 统计量的计算各种书上略有差异。
上面的公式来自 Wooldridge ,其中 q 表示残差滞后的期数。
在 EVIEWS5 中所用的 LM 统计量的计算是 2 ˆ uLM nR = 。
3,DW 检验有上面的检验之后,已经不用再搞什么 DW 检验了。
但是它仍然被广泛使用,所以有必要 了解。
重点要注意它的局限性。
(1) 1ˆ ˆ 2(1)1 2d d r r »-» 也即, - r ££££ 既然-11,那么0d 4。
时间序列(中级计量经济学总结(四川大学,杨可扬)
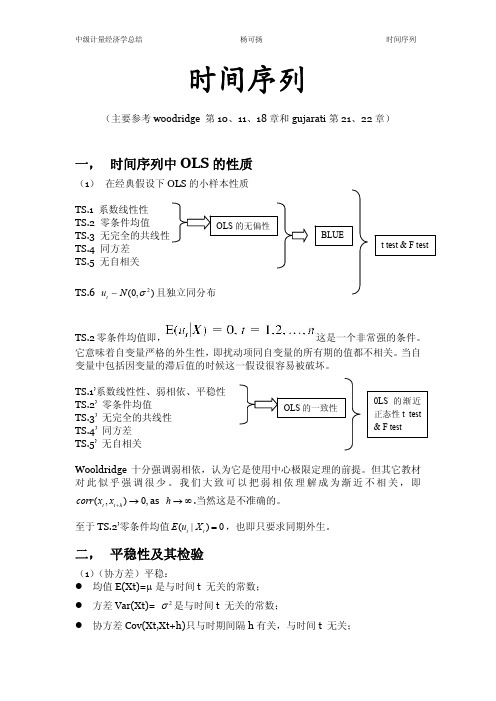
我们要去时间趋势,只需用上述方程的残差对 x 回归就可以了。要计算
y = b0 + b1x + b2t 的 R2 ,应该用该回归的残差对 x 和 t 回归之后得到的
R2 。如果原序列在去时间趋势之后是平稳的,我们就说该序列是趋势平
择。EVIEWS 的默认值都是整个样本。我们在习题中犯了好几处这样的错误。
六、VAR & Granger causality
(18.50)
中级计量经济学总结
杨可扬
时间序列
如果 zt-1, zt-2...... 是联合显著的,则认为 z Grangers causes y。
对于 Granger causality 需要注意两点: (1) 它不能代表 y 与 z 之间的当期关系。
Zt = XT ~ I(db)
其中,b>0, X=(X1t ,X2t ,....,Xkt )T ,则认为序列 (X1t ,X2t ,....,Xkt ) 是(d,b)阶协整,
记为 Xt~CI(d,b),a 为协整向量(cointegrated vector)。(d,d)阶协整是一类非 常重要的协整关系,它的经济意义在于:两个变量,虽然它们具有各自的长期波 动规律,但是如果它们是(d,d)阶协整的,则它们之间存在着一个长期稳定的 比例关系。Wooldridge 所举的六月期债券利息和三月期债权利息的例子十分恰 当:由于套利的存在两者差距不可能无限扩大,两者之间必存在长期的均衡关系。
å ( ) rk = t=1
n
Xt - X 2
l 样本自相关函数:
t =1
计量经济学-第5章虚拟变量

R2=0.88,
16
(-3.5)(11.6)
DW=1.85
可决系数小了很多,仅为0.88,这说明引 入虚拟变量非常必要
2.
乘法方式(用虚拟变量测量斜率变化)
• 加法方式引入虚拟变量,考察:截距的不同。 • 许多情况下:往往是斜率就有变化(即回归系数发生 变化) ,或斜率、截距同时发生变化。 • 斜率的变化可通过以乘法的方式引入虚拟变量来测度。
21
以Y为储蓄,X为收入,可令:
• 1990年前: Yi=1+2Xi+1i i=1,2…,n1
• 1990年后: Yi=1+2Xi+2i
i=1,2…,n2
则有可能出现下述四种情况中的一种:
(1) 1=1 ,且2=2 ,即两个回归相同,称为重 合回归(Coincident Regressions);
23
这一问题可通过引入加法与乘法形式的虚拟变量来解决。 将n1与n2次观察值合并,并用以估计以下回归:
Yi 0 1 X
i
3Di 4 (Di X i ) i
1 Di 0
Di为引入的虚拟变量: 于是有:
90 年前 90 年后
E (Y i | D i 0 , X i )
1 ( 有房户 ) D 0 (租房户)
14
• 建立回归模型
Yt 0 1 X t 2 D ut
利用表中数据得回归方程如下:
Yˆt 0 . 3204 0 . 0675 X t 0 . 8273 D (-5.2) (16.9) (11.0)
R2=0.9854,
Xt 20 24 12 16 11 32 10 40 32 7
《计量经济学》第八章 虚拟变量回归

收入;
Dt
1 0
反常年份 正常年份
反常年份 EYt | Xt , Dt 1 (1 2)Xt
正常年份 EYt | Xt , Dt 0 1Xt
在正常年份的基础上进行比较,(只有斜率系数发生改变)。
31
(2)截距和斜率均发生变化
模型形式:
Yi f Xt , Dt , Dt Xt 0 1D, 1 2D
在正常年份基础上比较,截距和斜率系数都改变,为什么?
32
不同截距、斜率的组合图形
重合回归:截距斜率均相同
平行回归:截距不同斜率相同
共点回归:截距相同斜率不同
交叉(不同)回归:截距斜率均不同
33
三、虚拟解释变量综合应用
所谓综合应用是指将引入虚拟解释变量的加法方 式、乘法方式进行综合使用。 基本分析方式仍然是条件期望分析。 本课主要讨论
38
(2)交互效应分析
交互作用: 一个解释变量的边际效应有时可能要依赖于另一 个解释变量。为此,Klein和Morgen(1951)提出了 有关收入和财产在决定消费模式上相互作用的假 设。他们认为消费的边际倾向不仅依赖于收入, 而且也依赖于财产的多少 ——较富有的人可能会 有不同的消费倾向。
冬季、农村居民
EYi | Xi , D1 0, D2 0 0 Xi
26
Y
上述图形的前提条件是什么?
X
27
运用OLS得到回归结果,再用t检验讨论因素 是否对模型有影响。 加法方式引入虚拟变量的一般表达式:
Yt 0 1D1t 2D2t ... k Dkt Xt ut
基本分析方法: 条件期望。
计量经济学
2023最新整理收集 do
something
第八章 虚拟变量回归
计量经济学讲义04虚拟变量

虚拟变量(dummy variable)在实际建模过程中,被解释变量不但受定量变量影响,同时还受定性变量影响。
例如需要考虑性别、民族、不同历史时期、季节差异、企业所有制性质不同等因素的影响。
这些因素也应该包括在模型中。
由于定性变量通常表示的是某种特征的有和无,所以量化方法可采用取值为1或0。
这种变量称作虚拟变量,用D表示。
虚拟变量应用于模型中,对其回归系数的估计与检验方法与定量变量相同。
1.截距移动设有模型,y= β0 + β1 x t + β2D + u t ,t其中y t,x t为定量变量;D为定性变量。
当D = 0 或1时,上述模型可表达为,β0 + β1x t + u t , (D = 0) y t D = 1 y t = β0+β2 D = 0(β0 + β2) + β1x t + u t , (D = 1) β0x t D = 1或0表示某种特征的有无。
反映在数学上是截距不同的两个函数。
若β显2著不为零,说明截距不同;若β2为零,说明这种分类无显著性差异。
例:中国成年人体重y(kg)与身高x(cm)的回归关系如下:–105 + x D = 1 (男)y = - 100 + x - 5D =– 100 + x D = 0 (女)注意:①若定性变量含有m个类别,应引入m-1个虚拟变量,否则会导致多重共线性,称作虚拟变量陷阱(dummy variable trap)。
②关于定性变量中的哪个类别取0,哪个类别取1,是任意的,不影响检验结果。
③定性变量中取值为0所对应的类别称作基础类别(base category)。
④对于多于两个类别的定性变量可采用设一个虚拟变量而对不同类别采取赋值不同的方法处理。
如:1 (大学)D = 0 (中学)-1 (小学)。
2.斜率变化以上只考虑定性变量影响截距,未考虑影响斜率,即回归系数的变化。
当需要考虑时,可建立如下模型:y= β0 + β1 x t + β2 D+ β3 x t D + u t ,t其中x t为定量变量;D为定性变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
虚拟变量(Wooldridge chapter 7 ,13and Gujarati chapter 9)本章所有内容都赋予一个统一的例题来总结:0121234 *** wage female married educ female married female educ married educ ub d d b b b b =+++ ++++ 显然本例是在研究性别、婚姻状况、教育状况同收入之间的 关系问题。
一,单个虚拟变量01 wage female ub d =++ 0 01(|0) (|1) E wage female E wage female b b d == ==+ 也就是说,男性的平均工资为 0 b ,而女性的平均工资为 01 b d + 。
检验 这两组平均工资是否显著不同只需检验 female 是否显著。
如果female 显著且 1ˆ d <0 则说明存在性别歧视。
这也是典型的用虚拟变量 来标志截距的不同。
换成对数——水平形式: 01 log() wage female u b d =++ 则男女之间工资 的百分比差异为: 1 100*[exp()1]d - 以下作一个简单的证明,表明以上公式不仅适用于虚拟变量:111011 101 101 10 1010log() log()log() log(/) / 1 %*100(1)*100 y x u y y y y y y e y y e y y y y e y bb b b b b b =++ -= = = - =- - D ==- 二,双个虚拟变量及其交互012 wage female married ub d d =+++ 02 012 (|0,) (|1,) E wage female married married E wage female married marriedb d b d d ==+ ==++ 因此 1 d 表示在给定婚姻状况条件下, 男女的工资差异。
区别于 gujarati example9.2 的解释,而同于 wooldridge 习题 7.12 的解释。
0122 *wage female married female married u b d d b =++++ 这里出现了 female 和 married 的交互项,于是研究对象其实就被分 成了 4 组:已婚男子、未婚男子、已婚女子、未婚女子。
其中未婚男 子作为基准组(base group )。
我们只能比较选定组于基准组之间是 否存在显著差异。
未婚男子的平均工资为 0 b 。
未婚女子比起未婚男子 的工资高出 1 d 。
已婚男子比未婚男子收入高出 2 d 。
已婚女子比未婚男 子工资高出 122 d d b ++ 。
当然上面的回归完全等价于:wage 对 female*married, female* single, male*married 回归。
在这里基准组仍然是未婚男子。
更广泛 地说,假设我们的模型包含了截距,如果我们分组为 m 组,那么模 型当中只能包括 m1 个虚拟变量。
我们还可以用虚拟变量来表示序数信息,比如 wooldridge 在 P229就举到了以虚拟变量来表示信用评级的例子。
信用评级一共 5 级,从 0 到 4。
于是我们可以设置 4 个虚拟变量:cr1,cr2,cr3,cr4 选定 0 级 为基准组。
当信用级别为 1 的时候 cr1=1,否则就为零。
当级别很多的 时候, 如 wooldridge example 7.8 则可以把 rank1_10 表示 1—10 级, 如此等等。
三,虚拟变量与定量变量之间的交互0113 *wage female educ female educ u b d b b =++++ 在这里首先需要注意的是,这里 0 b 代表的是 educ=0 时男子的平均工 资, 1 d 代表的是 educ=0 时男女的工资差异。
由于样本中的 educ 往 往没有等于 0 的,所以这两个系数的估计值可能都没有多大意义。
更 有意义的恐怕是在平均教育水平上对男女的工资情况进行对比, 只需 做回归:0113 *(12.5) wage female educ female educ ub d b b =+++-+ 其中 12.5 是样本中教育的平均年数。
这时, 1 d 代表的是 educ=12.5 时男女的工资差异。
还需要注意的是该方程允许了男女两组不同的斜率和截距。
男子组的 截距为 0 b ,而女子的截距为 01 b d + ,男子的斜率为 1 b ,而女子的斜率 为 1 b + 3 b 。
我们可以通过检验 female 和 female*educ 的联合显著性 来判断男女两组是否在回归模型上有着结构性差异。
这其实也就等同 于 chow test..四,Chow test如果需要检验结构差异的分组只有两组, 则直接如上所述使用虚拟变 量十分方便。
但是,如果分组较多,则一般需要使用 chow test 。
(1)对于方程 011 .... k ky x x b b b =+++ 。
如果我们需要检验它在 T 个时期上有无结构变化——既包括截距变化也包括斜率变化。
我们就 需要构筑:()/[(1)*(1)] /[(1)]r ur ur SSR SSR T k F SSR n T k --+ =-+ r SSR 是指对 011 .... k k y x x b b b =+++ 用所有样本点回归所得到的残差平方和。
12 .... ur T SSR SSR SSR SSR =+++ , 也即T 个时期每个时期回归所得残差平方和的加总。
关键要小心自由度的设置。
分子自由度的理解要 借助虚拟变量。
(1)*(1) T k -+ 其实是说的包含T1个虚拟变量,这些虚 拟变量与k 个斜率系数交互,并且被单独的包括进来(从而允许截距 不同)。
分母自由度很好理解。
(1) T k + 就是说的一共T 个时期,每个时 期k+1个系数。
这种形式的chow test 在EVIEWS 当中可以很方便地进 行:View/Stability Tests/Chow Breakpoint Test 。
可以参见Gujarati Page 274。
(2)比较麻烦的实际是我们只检验斜率是否发生了变化,同时在方 程中允许截距的变化。
这种类型 wooldridge 习题 7.19 最后一小题十 分典型。
还可以参见 wooldridge Page 432。
此时我们需要构筑:()/[(1)*] /[(1)]r ur ur SSR SSR T k F SSR n T k -- =-+ 首先需要注意的是这里的在求 r SSR 时的回归是包括了 T1 个时间变 量的,当然没有交互项。
而 12 .... urT SSR SSR SSR SSR =+++ 当中的任何 i SSR 都是没有包括时间变量的。
这里的 k 里边也不包括时间 变量。
(1)* T k - 表示的就是 T1 个时期乘以 k 个斜率。
(1) T k + 的含义 和原来一样。
当然这里的 T 既可以表示时期,也可以表示其它组数, 如 wooldridge 习题 7.19 当中表示家庭按规模分为 5 组。
这种检验不 能由 EVIEWS 直接完成。
最后需要注意的是 chow test 要求不同时期的扰动项方差相同。
另外 还需要考虑异方差问题。
五,独立混合横截面第四和第五都是 wooldridge 第 13 章的内容。
放到这里来主要是考虑 到其处理方法主要就是虚拟变量及其交互。
(1) 概念独立混合数据横截面是对一个大的总体在不同的时间点进行随机取 样得到的。
在自然试验中,我们把研究对象分为两组:control group and treatment group 。
Control group 就是不受政策影响的,treatment group 则反之。
如在焚烧场对房价影响的一例中,距离焚烧场远的房 子就是 control group,近的则属于 treatment group 。
我们把时间分为两个时期:政策实施前后,如,焚烧场修建前后。
(2)Differenceindifferences0011 *2**2*y d dB d dB u b d b d =++++ 这其实就是虚拟变量之间的交互。
d2 表示政策实施之后,dB 表示 treatment group 。
在上面我们已经知道 011 d b d ++ 的含义, 现在关键是 搞清 1 d 单独的含义。
12,2,1,1,ˆ ()() B A B A y y y y d =--- 这就是differenceindifferences 。
其实就是讲 B y 和 A y 之间的差距在第二阶段 比第一阶段所增大的部分。
在焚烧场一例(例 13.3)中就是表示因为 焚烧场的修建而造成的距离焚烧场近的房价下降。
以上公式的简单推导:01, ˆ A y b = , 02,1, ˆ A A y y d =- , 11,1, ˆ B A y y b =- , 2,0011ˆ ˆ ˆ ˆ B y b d b d =+++ 12,0012,1,2,1,1,1,2,2,1,1, ˆ ˆ ˆ ˆ ()()()() B B A A A B A B A B Ay y y y y y y y y y y d b d b =---=-----=--- 当然, 在焚烧场一例中更简单的办法是用房屋距离焚烧场的距离来替 换 dB , 此时 d2*log(dist)的系数就测度了因为焚烧场的修建造成距离 焚烧场近处的房屋价格的下降(见 wooldridge 习题 13.9)。
(3) 名义值和实际值之间的转换如果我们在方程中包括了年虚拟变量, 且对名义变量采取的是对数形 式, 且关心的是斜率, 那么我们就没有必要把名义值转变成为实际值。
如果要转换,如习题 13.8,就要注意每年的名义值所需除以的常数是 不同的。
