方腔环流的流场计算
流场的计算(流体力学)
SIMPLE算法
◆SIMPLE算法的流程图 算法的流程图
SIMPLE算法
◆SIMPLE算法的讨论 算法的讨论
①在速度修正方程中，略去邻点速度修正值的影响，这一个做法并 在速度修正方程中，略去邻点速度修正值的影响， 不影响最后收敛的值， 的负担。 不影响最后收敛的值，但加重了修正压力 p 的负担。
' ' ' '
(
)
任一点上速度修正由两部分组成： 任一点上速度修正由两部分组成：一部分是与该速 度在同一方向上的相邻两节点压力修正之差， 度在同一方向上的相邻两节点压力修正之差，这是 产生速度修正的直接动力； 产生速度修正的直接动力；另一部分由相邻点速度 修正所引起， 修正所引起，这又可以视为四周压力修正位置上对 速度修正的间接或隐含影响。
SIMPLE（Semi-Implicit Method for Pressure（ Linked Equations）算法是求解压力耦合方程的半隐 ） ' ∑ anb u nb 式法。在得到速度修正方程式的过程中， 式法。在得到速度修正方程式的过程中，略去了 去掉这一项就称为“半隐” 而保留这一部分时， 项，去掉这一项就称为“半隐”，而保留这一部分时u e' ， 方程就成为一个“全隐”的代数方程。 方程就成为一个“全隐”的代数方程。
SIMPLE算法
◆压力与速度的修正
a e u e = ∑ a nb u nb + S u + p P − p E Ae
' ' ' '
(
)
a n v n = ∑ a nb v nb + S v + p P − p N An
' ' ' '
方腔环流
sn1 0 ，在四边
n 1 s
2 sn sn ，在两侧和底边 h2 2 sn sn h ，在顶面 h2
sn1
3.计算步骤 求解过程，可按照下列步骤进行，
1) 给定 ， 的初值。可取 i,0j 0， i,0j 0
4h 2 4h 2 1 i 1, j 2 i , j i 1, j i , j 1 2 i , j i , j 1 2 2 Re h h
引进松弛因子 方程可化为下列的迭代格式
i 1, j i , j 1 i , j 1
3 n 1 1 n n 其中， R1 max in, ~ 10 4 j i , j ， R2 max i , j i , j ，C 为给定精度，可取 C r 10
7) 4.计算结果 随着雷诺数的增加， 减少，对于一个 25 25 的网格，当 Re 10 时，可取 1 ，而当
0 ，在腔体四边
v 0 ，在 AB 和 CD 上 x
u 0 ，在 AD 和 BC 上 y
其中，Re 为雷诺数
图 1 方腔环流
2.取正方形网格（如图所示） ，网格数视情况可取 25、50、100 等，一般不建议超过 200，雷诺 数 Re 一般不超过 5000，因为超过 5000 流场已经呈现出非线性，开始出现偏差，雷诺数超过 10000 甚至根本不能算出结果，这是因为强非线性情况下描述流场行为的方程已经不能做如上简化。
图 2 方腔 1, j
2 i , j i 1, j h2
i , j 1
方腔流动
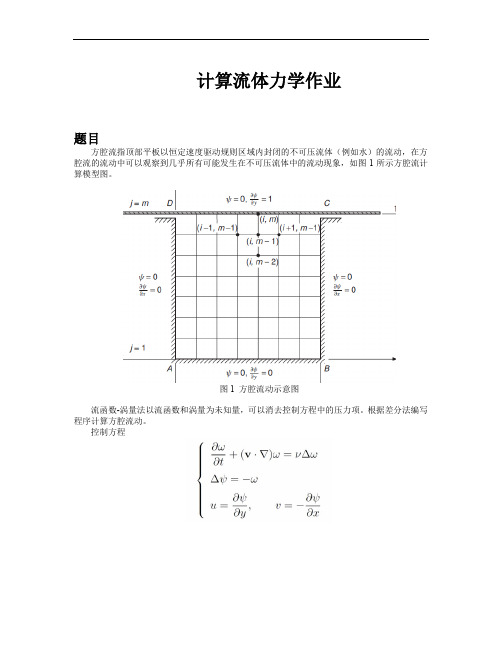
边界条件
流函数边界条件：根据已知条件，在四个壁上流函数均为 0，上边界平板速度 1，根据不可 滑移条件确定流函数偏导数条件。
涡量边界条件，采用（1）：
（1）可以用 Taylor 展开建立一般形式的 Thom 公式。假设某壁面切向速度 v ，沿其内法
向 n 有一节点，距离壁面距离为 h, 此点上的流函数为1 ，如果壁面上的流函数值为 0 ，那么
0
(1
0 2h2
v h)
时间导数采用向前 Euler 法，空间导数项可以用中心差分格式离散
计算步骤 1、计算 n + 1 时刻内点的涡量，需要考虑时间步长和空间步长和粘性项的关系。
2、计算 n + 1 时刻的流函数 n1 ，超松弛迭代法，松弛因子为-1.8。
3、计算 n + 1 时刻边界上的涡量
计算流体力学作业
题目
方腔流指顶部平板以恒定速度驱动规则区域内封闭的不可压流体（例如水）的流动，在方 腔流的流动中可以观察到几乎所有可能发生在不可压流体中的流动现象，如图 1 所示方腔流计 算模型图。
图 1 方腔流动示意图 流函数-涡量法以流函数和涡量为未知量，可以消去控制方程中的压力项。根据差分法编写 程序计算方腔流动。 控制方程
-0.5
0
0.5
1
1.5
3.995s 方腔速度矢量图
0
0.5
1
x0=0; x1=1; dx=(x1-x0)/(N-1); %空间步长 y0=0; y1=1; dy=(y1-y0)/(M-1); %空间步长
Thom 公式
1
0.8
0.6
0.4
0.2
0
-0.2
0
0.2
0.4
集水面积计算方法及隧道涌水量计算方法
集水面积计算方法及隧道涌水量计算方法（1）集水面积计算方法：
多平面积计算法是一种常用的计算集水面积的方法，它具体指用地形或水文断面图上的海拔高度点绘制平面，并由断面剖面和它们所确定的轮廓线的交点构成的边线，将区域划分成多个三角形片段，采用三角函数求和法来计算这些三角形片段的面积之和，以计算该区域的面积。
（2）隧道涌水量计算方法：
1）基本量计算法：该方法是根据现测获得的隧道方面粗糙度获取其其涌水量公式中最重要的参数--水力半径，然后通过计算水力半径来确定涌水量L（m3/s），其计算公式如下：L=1.456*R*R*V，其中，R为水力半径（m），V为流速（m/s）。
2）涡折尔定律：这种方法是根据涡折尔定律来确定排水量，这个定律是指在固定的圆形管道中，流体流量Q和流速V成反比，其公式为
Q=πR2V，其中R为管径，V为流速。
3）视比算法：该算法是利用粗糙度、流速和流量的比值来计算涌水量的，通过将当前的粗糙度和流速比值与预先确定的粗糙度和流速比值进行比较，就可以从而计算出涌水量。
不可压N-S方程的高效并行直接求解
不可压N-S方程的高效并行直接求解包芸;叶丰;张义招【摘要】对不可压N-S方程的数值计算,当计算规模增大时,不论是采用湍流模型计算还是直接数值模拟(Direct Numerical Simulation,DNS),大规模的并行计算都难以实现.该问题的关键是求解全场联立的压力泊松方程的并行计算技术.利用并行近似解求解方案,创建高效大规模并行计算的不可压N-S方程的直接求解方法.三维窄方腔热对流的DNS计算结果表明,该直接求解并行计算方法具有很好的并行效率,并且计算的三维湍流热对流的特性是合理的.【期刊名称】《计算机辅助工程》【年(卷),期】2016(025)003【总页数】5页(P19-23)【关键词】泊松方程;并行计算;不可压流动;湍流热对流;直接数值模拟【作者】包芸;叶丰;张义招【作者单位】中山大学力学系,广州 510275;中山大学力学系,广州 510275;中山大学力学系,广州 510275【正文语种】中文【中图分类】O357.5在航空航天等高科技工程的推动下，计算流体力学在可压缩流动的数值模拟计算技术领域进步非凡.不可压流动的数值模拟技术也在不断进步.超级计算机硬件技术的快速发展为计算流体力学数值模拟的进一步发展提供技术支持，高效并行计算技术的发展为进一步扩大不可压N-S方程的数值计算规模提供新的平台，并使计算结果数据能更好地反映流体的流动特性.热对流问题广泛存在于自然界和工业界中，研究其对全球气候变化、海洋环流、反应堆设计、工业冷却设计等问题的影响具有重要意义.[1-2]在Boussinesq假设下，湍流热对流的描述方程为不可压N-S方程联立温度对流扩散方程，因此热对流问题也是典型的不可压流动问题.高瑞利数Ra的湍流Rayleigh-Bénard(RB)热对流的直接数值模拟(Direct Numerical Simulation，DNS)面临重大挑战.[3]随着Ra的提高，热对流进入湍流状态，DNS模拟的规模不断增大导致计算所需要的成本巨大，数值计算难以实现.目前，湍流热对流的DNS只达到Ra=1012水平.[4]大规模可并行的高Ra湍流热对流DNS及其海量数据结果分析已成为热对流研究工作者们特别关注的问题.在不可压流动N-S方程的数值模拟计算中，不论采用何种计算模型或是DNS，其压力泊松方程的求解都是大规模并行计算的难题：直接求解方法不易于并行.迭代求解压力泊松方程通常采用局部算法从而较容易实现并行，但迭代计算过程占用大量的计算时间，所以很难实现高效率的大规模计算.这使得不可压流动的大规模数值模拟难以在有效时间内满足需求，因此妨碍大规模不可压流动N-S方程的湍流模型计算或DNS的进一步发展.一种新的泊松方程块三对角近似求解方案[5-6]可解决在超级计算机上的高效并行直接求解问题.这使得建立不可压流动N-S方程模拟的大规模高效并行计算方法成为可能，并可在超级计算机上实现三维高Ra湍流热对流特性研究的DNS.无量纲化后的三维不可压N-S方程为式中：V为速度矢量；p为压力；Re为雷诺数.计算边界条件为无滑移边界.投影法是数值求解不可压N-S方程组的有效方法之一.[7]实际上，不论采用何种湍流模型或DNS，以及采用何种思路求解不可压N-S方程的速度压力法，一般的动量方程都可以采用显式格式连续方程推导出压力泊松方程并进行迭代求解.大规模并行计算的主要困难为压力泊松方程必须全场联立求解.本文主要针对矩形计算域的特定情况，结合有效的泊松方程高效并行的直接求解方案，创建不可压流动DNS的可高效并行求解计算方法.2.1 网格布置和离散格式计算区域取矩形，见图1.网格数为nx×ny×nz.在设计大规模并行计算时，消息传递接口(Message Passing Interface，MPI)的计算区域沿xOy平面对z方向分割，即图中x方向较粗的线.在该面上并行计算需要数据通信；区域内部用OpenMP并行，无须数据通信.由于直接求解压力泊松方程要用到二维快速傅里叶离散余弦变换[8]，因此在x和y方向必须采用等距网格且最好网格数是2k,在z方向上可根据计算的需要采用非等距网格.本文采用不可压流动计算时常用的交错网格，时间方向采用一阶精度离散，空间采用二阶精度离散格式.2.2 不可压N-S方程的并行求解方案在不可压N-S方程的数值求解过程中，采用投影法将计算分步骤进行.动量方程中的速度计算采用显式格式，在求解中很容易实现并行.由连续方程推导出的压力泊松方程在求解时需要全场联立，是求解过程中计算工作量最大的部分.同时，联立求解也给并行造成困难，是大规模高效并行计算的难点.高效合理并可大规模并行计算的压力泊松方程求解方案，是解决不可压N-S方程大规模并行计算的关键技术.建立三维泊松方程的直接求解方法.计算方法只用于矩形计算区域，x方向采用等距网格.具体做法为在xOy平面上使用二维快速傅里叶变换将空间3个方向上都要求联立求解的压力泊松方程解耦，使泊松方程变换为只在z方向上的三对角方程.将三对角方程变换为块三角方程，设计高效且可并行计算求解方法，求解后再使用对应的反变换得到原来压力泊松方程的全场解.压力泊松方程为x和y方向使用等距网格，z方向使用变距网格.二阶精度中心差分的压力泊松方程的离散形式为使用二维离散余弦傅里叶变换将全场联立的泊松方程在x和y方向上解耦.余弦傅里叶变换能使压力泊松方程自动满足压力梯度为0的边界条件.变换通过FFTW软件包[8]实现.二维离散余弦傅里叶变换公式为将式(4)代入压力泊松方程，并令展开式两边对应系数相等，可以得到一组只沿z方向联立的三对角方程，使压力泊松方程在x和y方向上解耦，求解过程变简单. 在以往的二维热对流DNS中，利用追赶法求解三对角方程的泊松方程直接解法[9]，与采用迭代求解方法在计算机上单线程计算相比有效得多，但三对角方程的追赶法很难进行大规模并行计算.数学和计算机的研究者们尝试建立块三对角方程的大规模高效并行求解方案[5-6]，将变换得来的三对角方程写成块三对角的形式为式中为块三对角矩阵,和为M×N阶矩阵；和为M×N维列向量，T.为已知方程的右端项，通过式(4)求在计算得到块三对角方程的解后，通过对应的二维离散余弦傅里叶的反变换公式利用以上高效并行三维压力泊松方程直接求解方法，联合其他方便并行的动量方程等计算，创建三维不可压N-S方程高效并行直接求解计算方法，使得在一些特定情况下，大规模高效并行的不可压流动N-S方程湍流模型计算或者DNS成为可能.3.1 三维湍流热对流方程RB热对流是研究流体对流传热的典型物理模型.在封闭的盒子内，下底板加热而上底板冷却后形成对流传热的研究系统.在Boussinesq假设下，无量纲化后的三维热对流的描述方程为式中：Ra为瑞利数；Pr为普朗特数；θ为相对温度，下底板为加热，θ=0.5，上底板为冷却，θ=-0.5.通过热对流方程组可以看出，整个计算过程实际上就是数值求解不可压N-S方程组联立温度的对流扩散方程.本文对三维湍流热对流进行DNS.3.2 并行计算效率采用本文建立的三维不可压流动的直接求解并行计算方法，在超级计算机“天河二号”上进行加速比测试.每个计算节点包含24个计算物理核心.测试算例的计算网格数和物理计算核心数见表1.不同计算核数时直接求解并行计算方法的加速比见图2，其中加速比以计算节点24核心数为基数.计算中z方向上网格数1 536是24核心数的64倍.可知当使用32节点即32×24=768核心数时，具有约81.7%的计算效率，当使用64节点即64×24=1 536核心数时，具有约67%的计算效率.加速比随计算机核数的进一步增加仍有较好的可增长性.由于采用快速傅里叶变换解耦压力泊松方程的需要, 并行区域只在z方向上划分，由此本文创建的直接求解方法在大规模并行计算时z方向网格数与计算核心数之间有一定关联.总体上讲，本文的不可压流动直接求解方法在大规模并行计算上已得到较好的计算效率，可以进行较大规模的三维湍流热对流的DNS.新的直接求解计算方法与本课题组原有的迭代计算方法相比，节省1/2以上的总计算时间，计算技术的进步为系列三维热对流的DNS及物理特性的研究提供有力工具.3.3 三维湍流热对流计算结果选取窄方腔，宽高比Γ=1/4，Pr=4.3，对不同Ra的三维热对流进行计算.低Ra计算采用512×64×768网格，高Ra计算采用1 024×128×1 200网格.首先计算流动的初场，根据传热特性计算时平均场统计的需要，当热对流中出现较稳定的大尺度环流流动后，继续迭代计算至少100万时间步.根据不同的Ra及流动特性，计算时间的迭代至少达到300万时间步.RB热对流主要探讨由浮力产生的对流运动对流体传热特性的影响.Ra=1010的平均场温度等值面分布见图3，下底板加热为高温，上底板冷却为低温.温度作为热对流中的重要物理量，其平均场的分布反映传热过程中对流流动带动温度运动的情况.图3中方腔的中间部分没有温度的分布，表明中间没有流动也没有传热作用.图3显示由大尺度环流带动的温度分布形态，RB热对流中对流传热的热量主要沿着侧壁和棱边向上传输.RB热对流研究的核心问题之一是对流传热效率，表征传热的物理参数是努塞尔数Nu，表示流体对流传热与热传导传热的比值.Nu与Ra之间存在一定的标度关系[3]，因此需要一系列Ra数的不同数值模拟结果进行研究.一组三维方腔热对流的Nu/Ra0.3随Ra的变化见图4.图4中同时也给出计算得到的二维热对流Nu数的变化结果[10]，以及KACZOROWSKI等[11]的三维计算结果对比.由此可见，本文的三维湍流热对流的DNS模拟结果是合理的.图4中可以看到，二维和三维热对流的计算Nu随Ra的变化都存在很好的标度率.计算结果与理论预测和大量试验结果得到的结论一致.[3]Γ=1/4三维方腔的Nu总体偏大(向上平移).在试验和计算中也发现同样的Nu平移现象，并且不同的Γ变化会引起不同的Nu向上平移量.[12]在传热Nu对Ra的标度率中，三维和二维流动计算结果产生差异的物理原因，还有待更深入的研究.在三维不可压流动特性的研究过程中，尤其是到湍流阶段，超大规模的数值模拟计算十分必要.依靠超级计算机技术，探索高效并行的计算方法和计算技术，进行大规模的高自由度三维不可压N-S方程的数值计算，对更深入研究不可压流动的物理和流动特性具有很重要的意义.大规模并行数值模拟计算三维不可压N-S方程，最难的计算方法和计算技术问题是压力泊松方程的高效并行求解.利用块三对角方程的大规模高效并行近似解求解方案，创建大规模高效并行计算三维不可压N-S 方程的直接求解方法.DNS是研究高Ra湍流热对流的重要手段之一.热对流问题是典型的不可压流动问题.利用本文创建的高效并行不可压流动的直接求解方法，对高Ra三维湍流热对流进行DNS.通过并行效率的验证计算,证明本文建立的直接求解方法具有较好的并行效率.一系列不同Ra的三维窄方腔热对流计算得到的传热Nu具有合理的标度率. 本文创建的大规模高效并行计算的直接求解方法，为高Ra的湍流热对流大规模高效并行计算和数值模拟研究提供有价值的计算参考.ZHANG W, ZHANG H. Scalable parallel algorithm of block tridiagonal systems for initial boundary value problem[J]. Journal of Shanghai University(Natural Science), 2007, 13(5): 497-503.XU W, BAO Y. An efficient solution for 2D Rayleigh-Bénard convection using FFT[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 1-6. DOI: 10.6052/0459-1879-12-334.。
环流定理,涡度方程和散度方程
Ca C Ce C Ca Ce 绝对环流=相对环流+牵连环流：
故相对环流定理形如：
dCa dC dCa dCe ——（*） ，其中， dt 刚已讨论，那么 dt dt dt
Ce
？
○L A dr A d ，有： 由曲线-曲面积分转换（Stokes ）定理：
N区上升，L区下沉，近地面北风，高空南风。实际上引入地转效应后， 不应是单圈环流，而是三圈环流。这就是Hadley 等环流。 当然也可用其解释一些局地风，如海陆风，山谷风等。
RT p0
总之：斜压作用是大气运动中的一个重要因子。
6
§6.2 相对环流定理
已知，绝对速度为相对速度与牵连速度之矢量和：V V r a 两端对环线L积分： ○ LVa dr ○ LV dr ○ L ( r ) dr ，可见：
算子只对Ω运算，故 可互换，且省写下标
( r ) 2 ，代之入牵连环流的表达式（6.12），有：
Ce 2 d 2 d 2 ——（6.14）
~ 在赤道面上的投影，即其法线方向与 一致。 其中，
8
（6.14）代回到（*），有相对环流定理（Bjerknes环流定理）：
由于大中尺度运动是准水平的，故水平运动引起的垂直涡度较重要，
●
故有时又称
●
v u 为涡度 ， x y
v u ) 2 sin f x y
Ωsinφ Ω j Ω
φ
k
而绝对涡度～
a
(
——（6.27）
φ Ωcosφ
பைடு நூலகம்11
§6.4 绝对涡度矢量方程，Taylor-Proudman定理
方腔环流的流场计算
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
院系：工学院 姓名：刘广 学号：11309018 日期：2014 年 05 月 23 号
方腔环流示意图
我们取网格做如下说明，取正方形网格，网格数量由用户输入，但是建议不超过 200，因 为超过 200 计算量会急剧增大，雷诺数也是由用户输入，建议不超过 5000，因为超过 5000 流 场已经呈现出非线性，开始出现偏差，雷诺数超过 10000 甚至根本不能算出结果，这是因为强 非线性情况下描述流场行为的方程已经不能做如上简化， 同样的， 在计算过程中我们采用超松 弛迭代法，下面对离散形式做一下说明： 我们用二阶精度的差商代替微商做以下说明，得
姓名：刘广
学号：11309018
日期：2014 年 05 月 23 号
程序执行时，我输入的是10E-3作为计算精度，对于程序的说明程序注释已经说的很清楚， 这里不再赘述。最终会在目录下生成OUTPUT.txt 。 四：实验结果 最终会在目录下生成OUTPUT.txt 。然后我们可以用Matlab软件对计算出来的数据进一步整 理，画成云图和画出流线，我们做一下说明。
Re n n [( in, j 1 in, j 1 )( in in1, j in1, j )( in 1, j i 1, j ) ( , j 1 i , j 1 )]} 4 (1 ) in ,j
边界值的点需要特殊处理，然后由内点差分格式顺序扫描，一次次迭代直到满足用户输入的 精度为止。边界条件如下：
( i 1, j 2 i , j i 1, j ) / h 2 ( i , j 1 2 i , j i , j 1 ) / h 2 i , j ( i , j 1 i , j 1 )(
二维方腔环流计算
���������������,������+���+11
=
���������������������������,���������
−
������������∆������ 4ℎ2
(���������������,���������+1
−
���������������,���������−1)
(���������������+��� 1,������
cos(���⃗���,
���̂���)
4.用 fortran 编程（附件 1）进行计算，求出不同雷诺数（400，,1000,3200 等）下流场、
1
涡量场和压力场的数值解（调整ρ控制收敛速度）；再用 matlab 程序进行绘图（附件 3），进行分析和比较。 （三）使用 ADI 方法和亚松弛迭代法对非定常问题进行求解
+
���������������−���+11,������
+
���������������,������+���−11
+
������������ 4
[(���������������,���������+1
−
���������������,������+���−11)(���������������+��� 1,������
二维方腔环流计算
一、实验目的
二维方形腔体，腔体内部充满了流体。当顶板沿着水平方向被匀速（u=1）拉动时，腔体内 部的流体被带动而作环状运动。这种环流导致了腔体底边的二次涡。 方程与边界条件
用流函数涡量法求解方腔环流， 和 满足下列无量纲定常方程与边界条件
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 2 x 2 x 2 1 2 y x x y Re
（1）
（2）
0 ， 在腔体四边
v 0 ，在 AD 和 BC 上 x
u 0 ，在 AB 和 DC 上 y
其中，Re 为雷诺数。
Page 2 of 10
姓名：刘广
学号：11309018
日期：2014 年 05 月 23 号
Page 6 of 10
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
院系：工学院
E2=ABS(TEMPM1(I,1)-M1(I,1)) E1=ABS(TEMPM(I,1)-M(I,1)) IF(MAX(E1,E2)>E0)THEN E0=MAX(E1,E2) END IF END DO DO I=2,X M1(I,X+1)=-2*(TEMPM(I,X)-TEMPM(I,X+1)+H)/(H*H) E2=ABS(TEMPM1(I,X+1)-M1(I,X+1)) E1=ABS(TEMPM(I,X+1)-M(I,X+1)) IF(MAX(E1,E2)>E0)THEN E0=MAX(E1,E2) END IF END DO !层之间交换 TEMPM(:,:)=M(:,:) TEMPM1(:,:)=M1(:,:) END DO DO I=1,X+1,1 DO J=1,X+1,1 WRITE(8,*)I,',',J,',',M(I,J) END DO END DO DO I=1,X+1,1 DO J=1,X+1,1 WRITE(10,*)I,',',J,',',M1(I,J) END DO END DO END SUBROUTINE
i , j 1 )
Page 3 of 10
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
Байду номын сангаас院系：工学院
1 in ,j
姓名：刘广
学号：11309018
日期：2014 年 05 月 23 号
4
n n n { in 1, j i 1, j i , j 1 i , j 1
姓名：刘广
学号：11309018
日期：2014 年 05 月 23 号
程序执行时，我输入的是10E-3作为计算精度，对于程序的说明程序注释已经说的很清楚， 这里不再赘述。最终会在目录下生成OUTPUT.txt 。 四：实验结果 最终会在目录下生成OUTPUT.txt 。然后我们可以用Matlab软件对计算出来的数据进一步整 理，画成云图和画出流线，我们做一下说明。
中山大学工学院计算流体力学实验报告
实验名称：方腔环流的流场计算 姓 名： 刘广 刘广 11309018 詹杰民
参与组员： 学 号：
任课教师：
学科专业：工学院 理论与应用力学
中山大学 2014 年 05 月 23 日
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
院系：工学院 姓名：刘广 学号：11309018 日期：2014 年 05 月 23 号
方腔环流示意图
我们取网格做如下说明，取正方形网格，网格数量由用户输入，但是建议不超过 200，因 为超过 200 计算量会急剧增大，雷诺数也是由用户输入，建议不超过 5000，因为超过 5000 流 场已经呈现出非线性，开始出现偏差，雷诺数超过 10000 甚至根本不能算出结果，这是因为强 非线性情况下描述流场行为的方程已经不能做如上简化， 同样的， 在计算过程中我们采用超松 弛迭代法，下面对离散形式做一下说明： 我们用二阶精度的差商代替微商做以下说明，得
( i 1, j 2 i , j i 1, j ) / h 2 ( i , j 1 2 i , j i , j 1 ) / h 2 i , j ( i , j 1 i , j 1 )(
2 i 1, j
i 1, j )
4h 4h 2 1 i 1, j 2 i , j i 1, j i , j 1 2 i , j i , j 1 ( ) Re h2 h2
sn 1 0, 在四边
2( sn * sn ) , 在两侧和底边 h2 2( sn * sn h) n 1 s , 在顶边 h2
n 1 s
三：实验步骤: 学会对MS-FORTRAN的基本操作。 用Fortran编写程序计算方腔环流流场计算源代码，我们可 以写如下Fortran90程序： 主程序如下：
! Author : GUANG_LIU * owenyaa@ * ! Created Time : X+14-04-22 19:50 ! Last Revised : GUANG_LIU ,X+14-04-22 ! Remark : 以下实验结果中均为网格19×19，步长0.001，松弛因子0.5，迭代精度0.000001。 !Re=100 PROGRAM MAIN IMPLICIT NONE INTEGER::I WRITE(*,*)'请选择计算方法,流函数涡量法输入1,速度压力法输入2' READ(*,*)I IF (I==1)THEN CALL StreamFunctionVorticity() ELSE IF (I==2)THEN CALL PressureVelocity() Re=1000
院系：工学院 实验人姓名：刘广 日期：2014 年 05 月 23 号 专业：理论与应用力学 参加人姓名：刘广 温度：18° C 学号：11309018 年级：2011 级
实验六：方腔环流 一、 实验目的 1、在正方形水腔当中布满液体，水腔三方为墙壁，上方为盖板，盖板以速度 1 向右匀速 运动，当水腔内部液体达到平衡时，计算水箱内的流场。 2、计算全区域的流函数分布，并绘制流场图像。 二：实验仪器与设备: ① 装有 Fortran 的计算机 三、实验原理 1.方程与边界条件 用流函数涡量法， 和 满足下列无量纲定常方程与边界条件 1台
Re n n [( in, j 1 in, j 1 )( in in1, j in1, j )( in 1, j i 1, j ) ( , j 1 i , j 1 )]} 4 (1 ) in ,j
边界值的点需要特殊处理，然后由内点差分格式顺序扫描，一次次迭代直到满足用户输入的 精度为止。边界条件如下：
Page 4 of 10
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
院系：工学院
END IF WRITE(*,*)'请在目录下查看结果' PAUSE STOP END
姓名：刘广
学号：11309018
日期：2014 年 05 月 23 号
以下为流函数涡量法的子程序，
松弛因子 代入， i , j
n 1 2 n n n n ( in in, j , j h i 1, j i 1, j i , j 1 i , j 1 ) / 4 (1 )
( i 1, j i 1, j )(
i , j 1
Page 5 of 10
中山大学工学院、理论与应用力学刘广编制
实验编号及题目：实验六
方腔环流
《计算流体力学试验》课程实验报告纸
院系：工学院
E0=0 !循环中进行判断，但是这种方法不好，可以采用-1，0，1标记法，循环区间为大区间，计算之前判断，-1 为外点，CYCLE掉，1为内点，用迭代公式，0为边界点，值不变 DO I=2,X,1 DO J=2,X,1 M(I,J)=(1-W)*TEMPM(I,J)+(W/4)*(M(I-1,J)+TEMPM(I+1,J)+M(I,J1)+TEMPM(I,J+1)+H*H*TEMPM1(I,J)) M1(I,J)=(W/4)*(TEMPM1(I+1,J)+M1(I-1,J)+TEMPM1(I,J+1)+M1(I,J-1)+(RE/4)*((TEMPM(I,J+1)M(I,J-1))*(TEMPM1(I+1,J)-M1(I-1,J))-(TEMPM(I+1,J)-M(I-1,J))*(TEMPM1(I,J+1)-M1(I,J-1))))+(1W)*TEMPM1(I,J) E1=ABS(TEMPM(I,J)-M(I,J)) E2=ABS(TEMPM1(I,J)-M1(I,J)) IF(MAX(E1,E2)>E0)THEN E0=MAX(E1,E2) END IF END DO END DO DO J=1,X+1!左边 M1(1,J)=-2*(TEMPM(2,J)-TEMPM(1,J))/(H*H) E2=ABS(TEMPM1(1,J)-M1(1,J)) E1=ABS(TEMPM(1,J)-M(1,J)) IF(MAX(E1,E2)>E0)THEN E0=MAX(E1,E2) END IF END DO DO J=1,X+1!右边 M1(X+1,J)=-2*(TEMPM(X,J)-TEMPM(X+1,J))/(H*H) E2=ABS(TEMPM1(X+1,J)-M1(X+1,J)) E1=ABS(TEMPM(X+1,J)-M(X+1,J)) IF(MAX(E1,E2)>E0)THEN E0=MAX(E1,E2) END IF END DO DO I=2,X!底边 M1(I,1)=-2*(TEMPM(I,2)-TEMPM(I,1))/(H*H)