RBF神经网络设计
绝对经典RBF神经网络

平均值与目标值之平均值之间差异。
第6页
函数迫近问题(内插值)
普通函数都可表示成一组基函数线性组合,
RBF网络相当于用隐层单元输出组成一组基函数,
然后用输出层来进行线性组合,以完成迫近功效。
①给定样本数据
P {p1, p2 pi pQ},
②寻找函数,使其满足:ti F ( pi )
各隐节点扩展常数。因为RBF网隐节点数对其泛化能力有
极大影响,所以寻找能确定聚类数目标合理方法,是聚类
方法设计RBF网时需首先处理问题。除聚类算法外,还有
绝对经典RBF神经网络 梯度训练方法、资源分配网络(RAN)等
第16页
一. 自组织中心选取法
1989年,Moody和Darken提出了一个由两个阶段组成混合 学习过程思绪。
Cover定理能够定性地表述为:将复杂模式分类问题非线 性地投射到高维空间将比投射到低维空间更可能是线性可 分
空间转换
低维空间:线性不可分
高维空间:线性可分
绝对经典RBF神经网络
第12页
举例:逻辑运算异或分类
X1 X2
空间变换前
绝对经典RBF神经网络
Φ1(x)
w11
Φ2(x)
w11
Output y
j 1
设第j 个隐节点在第i个样本输出为: ij G( pi p j )
可矩阵表示:W T,若R可逆,则解为 W 1T 依据Micchelli定理可得,假如隐节点激活函数采取
径向基函数,且p1, p2 ,..., pQ 各不相同,则线性方程组
有唯一解。 Q RBF网络输出 F( pi ) wj( pi cj )
% 每一层神经元权值和阈值都与径向基函数位置和宽度相关系,输出层线性神经元将这些径 向基函数权值相加。假如隐含层神经元数目足够,每一层权值和阈值正确,那么径向基函 数网络就完全能够准确迫近任意函数。
实验四、RBF神经网络实验报告

如果对于输入空间的某个局部区域只有少数几个连接权值影响输出,则该网络称为局部逼近网络。常见的局部逼近网络有RBF网络、小脑模型(CMAC)网络、B样条网络等。
广义RBF网络
Cover定理指出:将复杂的模式分类问题非线性地映射到高维空间将比投影到低维空间更可能线性可分。
广义RBF网络:从输入层到隐藏层相当于是把低维空间的数据映射到高维空间,输入层细胞个数为样本的维度,所以隐藏层细胞个数一定要比输入层细胞个数多。从隐藏层到输出层是对高维空间的数据进行线性分类的过程,可以采用单层感知器常用的那些学习规则,参见神经网络基础和感知器。
寻找逼近函数F(x)通过最小化下面的目标函数来实现:
加式的第一项好理解,这是均方误差,寻找最优的逼近函数,自然要使均方误差最小。第二项是用来控制逼近函数光滑程度的,称为正则化项,λ是正则化参数,D是一个线性微分算子,代表了对F(x)的先验知识。曲率过大(光滑度过低)的F(x)通常具有较大的||DF||值,因此将受到较大的惩罚。
3)Inverse multiquadrics(拟多二次)函数
σ称为径向基函数的扩展常数,它反应了函数图像的宽度,σ越小,宽度越窄,函数越具有选择性。
完全内插存在一些问题:
1)插值曲面必须经过所有样本点,当样本中包含噪声时,神经网络将拟合出一个错误的曲面,从而使泛化能力下降。K,K<P,从样本中选取K个(假设不包含噪声)作为Φ函数的中心。
隐藏层的作用是把向量从低维m映射到高维P,低维线性不可分的情况到高维就线性可分了。
RBF神经网络算法研究及其在高维数据预处理中的应用

摘要当今人类社会已经进入了大数据时代,数据大多呈现出维数高、规模大、结构复杂等特性。
在大数据的研究当中,许多数据如媒体数据、遥感数据、生物医学数据、社交网络数据、金融数据等都是高维数据,尤其是在人类生产生活中,含高维数据的无解析模型或一次候选解的评价计算成本十分巨大的昂贵多目标问题,对其仿真求解势必面临维数灾难。
因此,寻找合适的降维方法处理高维数据已是迫切需求。
神经网络是模拟人脑的结构和功能而建立起来的分布式信息处理系统,面对高维多目标优化等非线性问题,与其他降维方法相比,神经网络具有巨大的优势,这得益于神经网络具有高度非线性、结构复杂、自学习、自适应等特点。
RBF神经网络是一种新颖有效的前馈式神经网络,它具有很强的非线性映射能力,能以任意精度全局逼近一个非线性函数,而且学习速度快。
利用RBF神经网络实现对高维数据的降维预处理,不仅有充分的理论依据,而且更具优越性。
本文在对RBF神经网络算法进行优化研究的基础上,研究了基于数据驱动的特征选择RBF 神经网络降维方法,并将其应用在高维多目标优化决策空间降维预处理及Pareto 优劣性预测中。
为了提高RBF神经网络的学习效率,本文首先对RBF神经网络进行改进研究。
通过自适应调节RBF神经网络的学习率和动量因子,加快了RBF神经网络的收敛速度;同时,利用遗传算法对RBF神经网络的三个参数初始值进行优化设计,提出了一种遗传自适应RBF神经网络算法。
将改进算法分别应用于故障诊断和UCI数据集的分类实验上,验证了改进RBF神经网络算法的有效性和优越性。
针对无解析模型的高维多目标优化问题,提出了一种最大信息系数与最大相关最小冗余相结合的特征选择方法,利用遗传自适应RBF神经网络算法在高维特征空间中选取出了一个低维的特征子集,从而实现对高维特征空间的降维。
通过在UCI数据集上的分类实验,证明了该降维算法在保证较好分类精度的前提下,大大减少了计算成本。
为了降低高维多目标优化的维数灾难,将本文提出的基于最大冗余最小相关的遗传自适应RBF神经网络特征选择算法用于多目标优化中的决策空间降维预处理,进行Pareto优劣性预测并将其嵌入MOEAs算法。
RBF神经网络在智能传感器模块设计中的应用

其 中 : . 网络 隐层 第 i 神经元的总输 入 ; . 第 i n为 个 b为 个 神经元的偏置值 ;0 9 为隐层权值矩 阵的第 i 个行 向量的 第j 个元素 ; ; 第 i P是 ; 个输入向量的 j 时刻输入值 。
R F神 经网络的输出层通常是纯线性神经 元 ,只是其 B
的特征输 入点 ,那 么其对 应的输 出应趋 于 1;2) ( 对于 非
样 本点输 入 ,输入与特征 输入 的点距离越远 ,则神经元 的 输 出越小 。 因此 , B R F神经网络 的输入权值是 由样本决定的 ,
而 与期望输 出并没有太大关系 。
R 神 经 网络Malb 程 序 BF t 源 a
O5 . 0
60 .
6O . 7O .
2 . 50
2 . 5O 2 . 5O
06 .
O6 . O7 .
56 .2
56 .2 65 .6
22 2 .3
28 9 .1 03 1 .2
8
9
01 .
02 .
70 .
70 .
2 . 50
2 . 5O
个) 传感 器系统 ; 若欲消 除 n 个干 扰量 的影响 ,则 需测量
n 1个参量的多 (+ 个 ) + n1 传感 器系统。 人工 神经网络具有较 强的非线性 映射 能力 、较好 的学 习和容错能 力 ,在 函数逼近 、预测 、信号处理 、控制系统 领域 中得到广泛 的应用 。径 向基 ( BF 神经 网络是 一种典 R ) 型 的性 能 良好的三层前馈 局部人工 神经网络 ,具有 较快 的 训练速 度和 非线性能 力 ,能以任意精 度全局逼迫 一个非线 性 函数 ,使 其在 很 多领 域得 到 广泛 应 用。本 文 采用 R F B 神 经网络 ,监测干扰 量温度 T的温度传感器的输 出电压为 U ,监测干扰量恒流源供 电电流 I 电流传感器的输 出电压 T 的 u ,改善压 阻式 压力 传感器 (C -0 ) . J Y 2 1 的温 度稳定 性与 恒
基于RBF神经网络整定的PID控制器设计及及认真设计

基于RBF神经网络整定的PID控制器设计及仿真摘要目前,因为PID控制具有简单的控制结构,可通过调节比例积分和微分取得基本满意的控制性能,在实际应用中又较易于整定,所以广泛应用于过程控制和运动控制中,尤其在可建立精确模型的确定性控制系统中应用比较多。
然而随着现代工业过程的日益复杂,对控制要求的逐步增高(如稳定性、准确性、快速性等),经典控制理论面临着严重的挑战。
对工业控制领域中非线性系统,采用传统PID 控制不能获得满意的控制效果。
采用基于梯度下降算法优化RBF神经网络,它将神经网络和PID控制技术融为一体,既具有常规PID控制器结构简单、物理意义明确的优点,同时又具有神经网络自学习、自适应的功能。
因此,本文通过对RBF神经网络的结构和计算方法的学习,设计一个基于RBF神经网络整定的PID控制器,构建其模型,进而编写M语言程序。
运用MATLAB软件对所设计的RBF神经网络整定的PID控制算法进行仿真研究。
然后再进一步通过仿真实验数据,研究本控制系统的稳定性,鲁棒性,抗干扰能力等。
关键词:PID;RBF神经网络;参数整定SETTING OF THE PID CONTROLLER BASED ON RBF NEURAL NETWORK DESIGN AND SIMULATIONAbstractAt present, because the PID control has a simple control structure, through adjusting the proportional integral and differential gain basic satisfactory control performance, and is relatively easy to setting in practical application, so widely used in process control and motion control, especially in the accurate model can be built more deterministic control system application. With the increasingly complex of the modern industrial process, however, increased step by step to control requirements (e.g., stability, accuracy and quickness, etc.), classical control theory is faced with severe challenges. Non-linear systems in industrial control field, using the traditional PID control can not obtain satisfactory control effect. Optimized RBF neural network based on gradient descent algorithm, it will be integrated neural network and PID control technology, with a conventional PID controller has simple structure, physical meaning is clear advantages, at the same time with neural network self-learning, adaptive function. Therefore, this article through to the RBF neural network structure and the calculation method of learning, to design a setting of the PID controller based on RBF neural network, constructs its model, and then write M language program. Using the MATLAB software to design the RBF neural network settingof PID control algorithm simulation research. Data and then further through simulation experiment, the control system stability, robustness, anti-interference ability, etc.Keywords: PID; RBF neural network; Parameter setting目录摘要 (Ⅰ)Abstract (Ⅱ)1 绪论 (1)1.1 课题研究背景及意义 (1)1.2神经网络的发展历史 (2)1.3本课题研究的主要内容 (5)2 神经网络 (6)2.1神经网络的基本概念和特点 (6)2.2人工神经网络构成的基本原理 (6)2.3神经网络的结构 (7)2.3.1前馈网络 (7)2.3.2 反馈网络 (7)2.4神经网络的学习方式 (8)2.4.1监督学习(有教师学习) (8)2.4.2非监督学习(无教师学习) (8)2.4.3再励学习(强化学习) (9)2.5 RBF神经网络 (9)2.5.1 RBF神经网络的发展简史 (9)2.5.2 RBF的数学模型 (9)2.5.3被控对象Jacobian信息的辨识算法 (10)2.5.4 RBF神经网络的学习算法 (11)2.6 本章小结 (13)3 PID控制器 (13)3.1 PID控制器简介 (13)3.2 经典PID控制原理 (13)3.3 现有PID控制器参数整定方法 (15)3.4 PID控制的局限 (15)3.5本章小结 (16)4 基于RBF神经网络整定的PID控制器设计 (17)4.1 RBF神经网络的PID整定原理 (17)4.2 神经网络PID控制器的设计 (17)4.3 本章小结 (18)5 仿真分析 (19)5.1 系统的稳定性分析 (19)5.2 系统抗干扰能力分析 (20)5.3 系统鲁棒性分析 (22)5.4 本章小结 (23)结论 (24)参考文献 (25)致谢 (26)附录仿真程序 (27)1 绪论1.1 课题研究背景及意义PID控制器(按比例、积分和微分进行控制的调节器)是最早发展起来的应用经典控制理论的控制策略之一,是工业过程控制中应用最广泛,历史最悠久,生命力最强的控制方式,在目前的工业生产中,90%以上的控制器为PID控制器。
RBF神经网络

的权向量为:W = [w , w
1
b j为节点的基宽度参数 , 且为大于零的数 。 网络 为节点的基宽度参数, 且为大于零的数。
2
⋯wj ⋯wm ]
k时刻网络的输出为: 时刻网络的输出为:
y m ( k )=wh = w1h1+w 2 h2+ ⋯⋯ +w m hm
设理想输出为y(k), 设理想输出为y(k),则性能指标函数为:
∂y (k ) ∂ym (k ) ≈ = ∂u (k ) ∂u (k )
m
∑w h
j =1
c1 j − x1 b2 j
j j
其中取 x1 = u(k) 。
6 RBF网络逼近仿真实例 RBF网络逼近仿真实例
使用RBF网络逼近下列对象:
y (k ) = u (k ) +
3
y ( k − 1) 1 + y ( k − 1)
Ii
wij
I
j
I1
. . .
R1
. . .
. .u .
u ..
R
j
. . .
1
1
.
V1
C1
. . .
j
j
.
Vj
.
u ..
Cj
i
i
.V
i
Ri
.
Ci
Hopfield网络模型 Hopfield网络模型
RBF神经网络 RBF神经网络
信息工程学院 Alen Fielding
1 RBF神经网络 RBF神经网络
径向基函数(RBF径向基函数(RBF-Radial Basis Function)神经网络 Function)神经网络 是由J Moody和 Darken在80年代末提出的一种神经 是由J.Moody和C.Darken在80年代末提出的一种神经 网络,它是具有单隐层的三层前馈网络。 网络,它是具有单隐层的三层前馈网络。由于它模拟 了人脑中局部调整、相互覆盖接收域(或称感受野了人脑中局部调整、相互覆盖接收域(或称感受野Receptive Field)的神经网络结构,因此,RBF网络 Field)的神经网络结构,因此,RBF网络 是一种局部逼近网络, 是一种局部逼近网络 , 它能够以任意精度逼近任意 连续函数,特别适合于解决分类问题。 连续函数,特别适合于解决分类问题。
基于遗传算法的RBF神经网络设计

1998年3月重庆大学学报 (自然科学版)V ol.21,№.2第21卷第2期J o urnal o f Ch ongqing U niv er sity(N atura l Science Editio n)M ar.1998基于遗传算法的RBF神经网络设计黄席樾 刘菡萏 石为人(重庆大学自动化系,重庆,400044;第一作者54岁,男,教授) 摘 要 采用了遗传算法自动构造RBF网络,把网络结构的形式作为一个子集选择问题来解决,并提出了新的遗传操作算子来改进遗传算法,加快了收敛速度,提高了算法的实用性。
文中介绍了遗传算法的结构与优化原理,并给出了RBF网络结构的生成方法,用仿真结果证明了本算法的可行性。
关键词 系统辩识/遗传算法;RBF网络;网络结构 中国图书资料分类法分类号 TP273.220 引 言非线性系统的控制是人们面临的一大难题。
神经网络以其逼近非线性函数的能力而被广泛用于解决非线性系统的控制问题。
对于连续系统,由于径向基函数(Radial basis Func-tion,简称RBF)神经网络的可调参数与网络的输出呈线性关系而用作非线性系统的模型,用于非线性连续系统的自动控制系统中。
然而,如何设计RBF神经网络结构,至今没有系统的规则可循。
目前训练RBF网络的方法大致分为两类:1)学习隐层的中心向量和宽度;2)学习隐层到输出层的连接权重。
在这些学习算法中,网络结构或隐层结点数目是基于先验知识预定的[1]。
但是,RBF网络结构是关于隐层结点数、中心向量和连接权的最小化问题。
由于隐层结点数是不连续和不可微的,而传统优化方法需要对象函数的导数信息,当对象函数是多模态时,存在很多局部极小,传统优化方法很可能陷入这些局部极小。
而且,当考虑网络结构和参数时,搜索空间实际上是无限的,对传统优化方法来说在计算上是不可能实现的。
由于这些原因,许多传统优化方法,例如随机法、梯度下降法、仿真退火法等,应用于完成搜索时都存在着很多问题。
Python实现的径向基(RBF)神经网络示例

Python实现的径向基(RBF)神经⽹络⽰例本⽂实例讲述了Python实现的径向基(RBF)神经⽹络。
分享给⼤家供⼤家参考,具体如下:from numpy import array, append, vstack, transpose, reshape, \dot, true_divide, mean, exp, sqrt, log, \loadtxt, savetxt, zeros, frombufferfrom numpy.linalg import norm, lstsqfrom multiprocessing import Process, Arrayfrom random import samplefrom time import timefrom sys import stdoutfrom ctypes import c_doublefrom h5py import Filedef metrics(a, b):return norm(a - b)def gaussian (x, mu, sigma):return exp(- metrics(mu, x)**2 / (2 * sigma**2))def multiQuadric (x, mu, sigma):return pow(metrics(mu,x)**2 + sigma**2, 0.5)def invMultiQuadric (x, mu, sigma):return pow(metrics(mu,x)**2 + sigma**2, -0.5)def plateSpine (x,mu):r = metrics(mu,x)return (r**2) * log(r)class Rbf:def __init__(self, prefix = 'rbf', workers = 4, extra_neurons = 0, from_files = None):self.prefix = prefixself.workers = workersself.extra_neurons = extra_neurons# Import partial modelif from_files is not None:w_handle = self.w_handle = File(from_files['w'], 'r')mu_handle = self.mu_handle = File(from_files['mu'], 'r')sigma_handle = self.sigma_handle = File(from_files['sigma'], 'r')self.w = w_handle['w']self.mu = mu_handle['mu']self.sigmas = sigma_handle['sigmas']self.neurons = self.sigmas.shape[0]def _calculate_error(self, y):self.error = mean(abs(self.os - y))self.relative_error = true_divide(self.error, mean(y))def _generate_mu(self, x):n = self.nextra_neurons = self.extra_neurons# TODO: Make reusablemu_clusters = loadtxt('clusters100.txt', delimiter='\t')mu_indices = sample(range(n), extra_neurons)mu_new = x[mu_indices, :]mu = vstack((mu_clusters, mu_new))return mudef _calculate_sigmas(self):neurons = self.neuronsmu = self.musigmas = zeros((neurons, ))for i in xrange(neurons):dists = [0 for _ in xrange(neurons)]for j in xrange(neurons):if i != j:dists[j] = metrics(mu[i], mu[j])sigmas[i] = mean(dists)* 2# max(dists) / sqrt(neurons * 2))return sigmasdef _calculate_phi(self, x):C = self.workersneurons = self.neuronsmu = self.musigmas = self.sigmasphi = self.phi = Nonen = self.ndef heavy_lifting(c, phi):s = jobs[c][1] - jobs[c][0]for k, i in enumerate(xrange(jobs[c][0], jobs[c][1])):for j in xrange(neurons):# phi[i, j] = metrics(x[i,:], mu[j])**3)# phi[i, j] = plateSpine(x[i,:], mu[j]))# phi[i, j] = invMultiQuadric(x[i,:], mu[j], sigmas[j]))phi[i, j] = multiQuadric(x[i,:], mu[j], sigmas[j])# phi[i, j] = gaussian(x[i,:], mu[j], sigmas[j]))if k % 1000 == 0:percent = true_divide(k, s)*100print(c, ': {:2.2f}%'.format(percent))print(c, ': Done')# distributing the work between 4 workersshared_array = Array(c_double, n * neurons)phi = frombuffer(shared_array.get_obj())phi = phi.reshape((n, neurons))jobs = []workers = []p = n / Cm = n % Cfor c in range(C):jobs.append((c*p, (c+1)*p + (m if c == C-1 else 0)))worker = Process(target = heavy_lifting, args = (c, phi))workers.append(worker)worker.start()for worker in workers:worker.join()return phidef _do_algebra(self, y):phi = self.phiw = lstsq(phi, y)[0]os = dot(w, transpose(phi))return w, os# Saving to HDF5os_h5 = os_handle.create_dataset('os', data = os)def train(self, x, y):self.n = x.shape[0]## Initialize HDF5 cachesprefix = self.prefixpostfix = str(self.n) + '-' + str(self.extra_neurons) + '.hdf5'name_template = prefix + '-{}-' + postfixphi_handle = self.phi_handle = File(name_template.format('phi'), 'w')os_handle = self.w_handle = File(name_template.format('os'), 'w')w_handle = self.w_handle = File(name_template.format('w'), 'w')mu_handle = self.mu_handle = File(name_template.format('mu'), 'w')sigma_handle = self.sigma_handle = File(name_template.format('sigma'), 'w') ## Mu generationmu = self.mu = self._generate_mu(x)self.neurons = mu.shape[0]print('({} neurons)'.format(self.neurons))# Save to HDF5mu_h5 = mu_handle.create_dataset('mu', data = mu)## Sigma calculationprint('Calculating Sigma...')sigmas = self.sigmas = self._calculate_sigmas()# Save to HDF5sigmas_h5 = sigma_handle.create_dataset('sigmas', data = sigmas)print('Done')## Phi calculationprint('Calculating Phi...')phi = self.phi = self._calculate_phi(x)print('Done')# Saving to HDF5print('Serializing...')phi_h5 = phi_handle.create_dataset('phi', data = phi)del phiself.phi = phi_h5print('Done')## Algebraprint('Doing final algebra...')w, os = self.w, _ = self._do_algebra(y)# Saving to HDF5w_h5 = w_handle.create_dataset('w', data = w)os_h5 = os_handle.create_dataset('os', data = os)## Calculate errorself._calculate_error(y)print('Done')def predict(self, test_data):mu = self.mu = self.mu.valuesigmas = self.sigmas = self.sigmas.valuew = self.w = self.w.valueprint('Calculating phi for test data...')phi = self._calculate_phi(test_data)os = dot(w, transpose(phi))savetxt('iok3834.txt', os, delimiter='\n')return os@propertydef summary(self):return '\n'.join( \['-----------------','Training set size: {}'.format(self.n),'Hidden layer size: {}'.format(self.neurons),'-----------------','Absolute error : {:02.2f}'.format(self.error),'Relative error : {:02.2f}%'.format(self.relative_error * 100)])def predict(test_data):mu = File('rbf-mu-212243-2400.hdf5', 'r')['mu'].valuesigmas = File('rbf-sigma-212243-2400.hdf5', 'r')['sigmas'].valuew = File('rbf-w-212243-2400.hdf5', 'r')['w'].valuen = test_data.shape[0]neur = mu.shape[0]mu = transpose(mu)mu.reshape((n, neur))phi = zeros((n, neur))for i in range(n):for j in range(neur):phi[i, j] = multiQuadric(test_data[i,:], mu[j], sigmas[j])os = dot(w, transpose(phi))savetxt('iok3834.txt', os, delimiter='\n')return os更多关于Python相关内容感兴趣的读者可查看本站专题:《》、《》、《》、《》及《》希望本⽂所述对⼤家Python程序设计有所帮助。
RBF(径向基)神经网络

RBF(径向基)神经⽹络 只要模型是⼀层⼀层的,并使⽤AD/BP算法,就能称作 BP神经⽹络。
RBF 神经⽹络是其中⼀个特例。
本⽂主要包括以下内容:什么是径向基函数RBF神经⽹络RBF神经⽹络的学习问题RBF神经⽹络与BP神经⽹络的区别RBF神经⽹络与SVM的区别为什么⾼斯核函数就是映射到⾼维区间前馈⽹络、递归⽹络和反馈⽹络完全内插法⼀、什么是径向基函数 1985年,Powell提出了多变量插值的径向基函数(RBF)⽅法。
径向基函数是⼀个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意⼀点c的距离,c点称为中⼼点,也就是Φ(x,c)=Φ(‖x-c‖)。
任意⼀个满⾜Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数,标准的⼀般使⽤欧⽒距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。
最常⽤的径向基函数是⾼斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中⼼,σ为函数的宽度参数 , 控制了函数的径向作⽤范围。
⼆、RBF神经⽹络 RBF神将⽹络是⼀种三层神经⽹络,其包括输⼊层、隐层、输出层。
从输⼊空间到隐层空间的变换是⾮线性的,⽽从隐层空间到输出层空间变换是线性的。
流图如下: RBF⽹络的基本思想是:⽤RBF作为隐单元的“基”构成隐含层空间,这样就可以将输⼊⽮量直接映射到隐空间,⽽不需要通过权连接。
当RBF的中⼼点确定以后,这种映射关系也就确定了。
⽽隐含层空间到输出空间的映射是线性的,即⽹络的输出是隐单元输出的线性加权和,此处的权即为⽹络可调参数。
其中,隐含层的作⽤是把向量从低维度的p映射到⾼维度的h,这样低维度线性不可分的情况到⾼维度就可以变得线性可分了,主要就是核函数的思想。
这样,⽹络由输⼊到输出的映射是⾮线性的,⽽⽹络输出对可调参数⽽⾔却⼜是线性的。
⽹络的权就可由线性⽅程组直接解出,从⽽⼤⼤加快学习速度并避免局部极⼩问题。
径向基神经网络学习算法(RBF)

Mezer chen 2018.5.9
RBF简介
1989年,Moody和Darken提出了一种由两个阶段组成的混 合学习过程的思路。
①无监督的自组织学习阶段 ②有监督学习阶段
其任务是用自组织聚类方法为隐 层节点的径向基函数确定合适的 数据中心,并根据各中心之间的 距离确定隐节点的扩展常数。 一般采用Duda和Hart1973年提 出的k-means聚类算法。
其任务是用有监督 学习算法训练输出 层权值,一般采用 梯度法进行训练。
RBF网络的工作原理
RBF网络特点
只有一个隐含层,且隐层神经元与输出层神经元的模型不同。 隐层节点激活函数为径向基函数,输出层节点激活函数为线 性函数。 隐层节点激活函数的净输入是输入向量与节点中心的距离 (范数)而非向量内积,且节点中心不可调。 隐层节点参数确定后,输出权值可通过解线性方程组得到。 隐层节点的非线性变换把线性不可分问题转化为线性可分问 题。 局部逼近网络(MLP是全局逼近网络),这意味着逼近一个输 入输出映射时,在相同逼近精度要求下,RBF所需的时间要 比MLP少。 具有唯一最佳逼近的特性,无局部极小。 合适的隐层节点数、节点中心和宽度不易确定。
RBF神经网络中心选取
① 从样本输入中选取中心
一般来说,样本密集的地方中心点可以适当多些,样本 稀疏的地方中心点可以少些;若数据本身是均匀分布的,
中心点也可以均匀分布。总之,选出的数据中心应具有代
表性。径向基函数的扩展常数是根据数据中心的散布而确 定的,为了避免每个径向基函数太尖或太平,一种选择方 法是将所有径向基函数的扩展常数设为
d max 2I
② 自组织选取中心法
常采用各种动态聚类算法对数据中心进行自组织选择,在
径向基(RBF)神经网络python实现

径向基(RBF)神经⽹络python实现 1from numpy import array, append, vstack, transpose, reshape, \2 dot, true_divide, mean, exp, sqrt, log, \3 loadtxt, savetxt, zeros, frombuffer4from numpy.linalg import norm, lstsq5from multiprocessing import Process, Array6from random import sample7from time import time8from sys import stdout9from ctypes import c_double10from h5py import File111213def metrics(a, b):14return norm(a - b)151617def gaussian (x, mu, sigma):18return exp(- metrics(mu, x)**2 / (2 * sigma**2))192021def multiQuadric (x, mu, sigma):22return pow(metrics(mu,x)**2 + sigma**2, 0.5)232425def invMultiQuadric (x, mu, sigma):26return pow(metrics(mu,x)**2 + sigma**2, -0.5)272829def plateSpine (x,mu):30 r = metrics(mu,x)31return (r**2) * log(r)323334class Rbf:35def__init__(self, prefix = 'rbf', workers = 4, extra_neurons = 0, from_files = None):36 self.prefix = prefix37 self.workers = workers38 self.extra_neurons = extra_neurons3940# Import partial model41if from_files is not None:42 w_handle = self.w_handle = File(from_files['w'], 'r')43 mu_handle = self.mu_handle = File(from_files['mu'], 'r')44 sigma_handle = self.sigma_handle = File(from_files['sigma'], 'r')4546 self.w = w_handle['w']47 self.mu = mu_handle['mu']48 self.sigmas = sigma_handle['sigmas']4950 self.neurons = self.sigmas.shape[0]5152def _calculate_error(self, y):53 self.error = mean(abs(self.os - y))54 self.relative_error = true_divide(self.error, mean(y))5556def _generate_mu(self, x):57 n = self.n58 extra_neurons = self.extra_neurons5960# TODO: Make reusable61 mu_clusters = loadtxt('clusters100.txt', delimiter='\t')6263 mu_indices = sample(range(n), extra_neurons)64 mu_new = x[mu_indices, :]65 mu = vstack((mu_clusters, mu_new))6667return mu6869def _calculate_sigmas(self):70 neurons = self.neurons71 mu = self.mu7273 sigmas = zeros((neurons, ))74for i in xrange(neurons):75 dists = [0 for _ in xrange(neurons)]76for j in xrange(neurons):77if i != j:78 dists[j] = metrics(mu[i], mu[j])79 sigmas[i] = mean(dists)* 280# max(dists) / sqrt(neurons * 2))81return sigmas8283def _calculate_phi(self, x):84 C = self.workers85 neurons = self.neurons86 mu = self.mu87 sigmas = self.sigmas88 phi = self.phi = None89 n = self.n909192def heavy_lifting(c, phi):93 s = jobs[c][1] - jobs[c][0]94for k, i in enumerate(xrange(jobs[c][0], jobs[c][1])):95for j in xrange(neurons):96# phi[i, j] = metrics(x[i,:], mu[j])**3)97# phi[i, j] = plateSpine(x[i,:], mu[j]))98# phi[i, j] = invMultiQuadric(x[i,:], mu[j], sigmas[j]))99 phi[i, j] = multiQuadric(x[i,:], mu[j], sigmas[j])100# phi[i, j] = gaussian(x[i,:], mu[j], sigmas[j]))101if k % 1000 == 0:102 percent = true_divide(k, s)*100103print(c, ': {:2.2f}%'.format(percent))104print(c, ': Done')105106# distributing the work between 4 workers107 shared_array = Array(c_double, n * neurons)108 phi = frombuffer(shared_array.get_obj())109 phi = phi.reshape((n, neurons))110111 jobs = []112 workers = []113114 p = n / C115 m = n % C116for c in range(C):117 jobs.append((c*p, (c+1)*p + (m if c == C-1 else 0)))118 worker = Process(target = heavy_lifting, args = (c, phi))119 workers.append(worker)120 worker.start()121122for worker in workers:123 worker.join()124125return phi126127def _do_algebra(self, y):128 phi = self.phi129130 w = lstsq(phi, y)[0]131 os = dot(w, transpose(phi))132return w, os133# Saving to HDF5134 os_h5 = os_handle.create_dataset('os', data = os)135136def train(self, x, y):137 self.n = x.shape[0]138139## Initialize HDF5 caches140 prefix = self.prefix141 postfix = str(self.n) + '-' + str(self.extra_neurons) + '.hdf5'142 name_template = prefix + '-{}-' + postfix143 phi_handle = self.phi_handle = File(name_template.format('phi'), 'w')144 os_handle = self.w_handle = File(name_template.format('os'), 'w')145 w_handle = self.w_handle = File(name_template.format('w'), 'w')146 mu_handle = self.mu_handle = File(name_template.format('mu'), 'w')147 sigma_handle = self.sigma_handle = File(name_template.format('sigma'), 'w') 148149## Mu generation150 mu = self.mu = self._generate_mu(x)151 self.neurons = mu.shape[0]152print('({} neurons)'.format(self.neurons))153# Save to HDF5154 mu_h5 = mu_handle.create_dataset('mu', data = mu)155156## Sigma calculation157print('Calculating Sigma...')158 sigmas = self.sigmas = self._calculate_sigmas()159# Save to HDF5160 sigmas_h5 = sigma_handle.create_dataset('sigmas', data = sigmas)161print('Done')162163## Phi calculation164print('Calculating Phi...')165 phi = self.phi = self._calculate_phi(x)166print('Done')167# Saving to HDF5168print('Serializing...')169 phi_h5 = phi_handle.create_dataset('phi', data = phi)170del phi171 self.phi = phi_h5172print('Done')173174## Algebra175print('Doing final algebra...')176 w, os = self.w, _ = self._do_algebra(y)177# Saving to HDF5178 w_h5 = w_handle.create_dataset('w', data = w)179 os_h5 = os_handle.create_dataset('os', data = os)180181## Calculate error182 self._calculate_error(y)183print('Done')184185def predict(self, test_data):186 mu = self.mu = self.mu.value187 sigmas = self.sigmas = self.sigmas.value188 w = self.w = self.w.value189190print('Calculating phi for test data...')191 phi = self._calculate_phi(test_data)192 os = dot(w, transpose(phi))193 savetxt('iok3834.txt', os, delimiter='\n')194return os195196 @property197def summary(self):198return'\n'.join( \199 ['-----------------',200'Training set size: {}'.format(self.n),201'Hidden layer size: {}'.format(self.neurons),202'-----------------',203'Absolute error : {:02.2f}'.format(self.error),204'Relative error : {:02.2f}%'.format(self.relative_error * 100)]) 205206207def predict(test_data):208 mu = File('rbf-mu-212243-2400.hdf5', 'r')['mu'].value209 sigmas = File('rbf-sigma-212243-2400.hdf5', 'r')['sigmas'].value 210 w = File('rbf-w-212243-2400.hdf5', 'r')['w'].value211212 n = test_data.shape[0]213 neur = mu.shape[0]214215 mu = transpose(mu)216 mu.reshape((n, neur))217218 phi = zeros((n, neur))219for i in range(n):220for j in range(neur):221 phi[i, j] = multiQuadric(test_data[i,:], mu[j], sigmas[j])222223 os = dot(w, transpose(phi))224 savetxt('iok3834.txt', os, delimiter='\n')225return os。
径向基神经网络的介绍及其案例实现

径向基神经网络的介绍及其案例实现径向基(RBF)神经网络是一种常用的人工神经网络模型,它以径向基函数作为激活函数来进行模式分类和回归任务。
该网络在模式识别、函数逼近、数据挖掘等领域都具有良好的性能,并且具有较好的泛化能力。
引言:径向基(RBF)神经网络最早是由Broomhead和Lowe于1988年引入的,它是一种前馈式神经网络。
RBF神经网络的主要思想是以输入向量与一组高斯函数的基函数作为输入层,然后再通过隐藏层进行特征映射,最后通过输出层进行模式分类或回归。
1.RBF神经网络的结构:RBF神经网络包括输入层、隐藏层和输出层三层。
输入层负责接收输入向量,隐藏层负责特征映射,输出层负责输出结果。
输入层:输入层接收具有所要分类或回归的特征的数据,通常使用欧几里德距离计算输入层的神经元与输入向量之间的距离。
隐藏层:隐藏层是RBF神经网络的核心部分,它通过一组径向基函数来进行特征映射。
隐藏层的神经元数量通常和训练样本数量相同,每个神经元负责响应一个数据样本。
输出层:输出层根据隐藏层的输出结果进行模式分类或回归预测,并输出网络的最终结果。
2.RBF神经网络的训练:RBF神经网络的训练主要包括两个步骤:聚类和权值调整。
聚类:首先通过K-means等聚类算法将训练样本划分为若干个类别,每个类别对应一个隐藏层神经元。
这样可以将输入空间划分为若干个区域,每个区域中只有一个样本。
权值调整:通过最小化残差误差或最小化目标函数来优化隐藏层和输出层的权值。
常用的优化算法有最小二乘法、梯度下降法等。
3.RBF神经网络的案例实现:案例1:手写数字识别案例2:股票市场预测RBF神经网络也可以应用于股票市场的预测。
该案例中,RBF神经网络接收一组与股票相关的指标作为输入,通过隐藏层的特征映射将指标转化为更有意义的特征表示,最后通过输出层进行未来股价的回归预测。
该系统的训练样本为历史股票数据以及与之对应的未来股价。
结论:径向基(RBF)神经网络是一种应用广泛且效果良好的人工神经网络模型。
神经网络控制RBF

神经网络控制RBF神经网络是一种模拟人脑处理信息的计算模型,可以通过学习数据来预测和控制各种系统。
在控制领域,神经网络已经被广泛应用,很多控制问题可以通过神经网络来实现优化控制。
而基于类RBF(径向基函数)神经网络的控制方法也得到广泛的研究和应用,该方法是一种自适应控制方法,可以处理非线性系统,具有一定的理论和实际应用价值。
1. RBF神经网络控制方法RBF神经网络是一种前馈神经网络,由输入层、隐层和输出层组成。
其中,输入层接受外界输入,隐层包含一组RBF神经元,其作用是将输入空间划分为若干子空间,并将每个子空间映射到一个神经元上。
输出层是线性层,负责将隐层输出进行线性组合,输出控制信号。
在控制系统中,RBF神经元用于计算控制信号,从而实现控制目标。
RBF神经网络的训练包括两个阶段:聚类和权重调整。
聚类过程将输入空间划分成若干个类别,并计算出每个类别的中心和半径。
聚类算法的目标是使得同一类别内的样本距离聚类中心最小,不同类别之间距离最大。
常用的聚类算法包括k-means算法和LVQ算法。
权重调整过程将隐层神经元的权重调整到最优状态,以便将隐层输出映射到目标输出。
在实际控制中,RBF神经网络控制方法应用较为广泛,可以替代PID控制器等传统控制方法,具有良好的鲁棒性、自适应能力和较好的控制性能。
2. 基于RBF神经网络的控制方法RBF神经网络控制方法广泛应用于各种领域的控制任务,特别是在非线性系统控制中具有重要的应用价值。
基于RBF神经网络的控制方法主要包括以下两种:(1)虚拟控制策略:将系统建模为线性结构和非线性结构两部分,其中线性结构可以采用传统的控制方法进行控制,而非线性结构则采用基于RBF神经网络的控制方法进行控制。
虚拟控制策略的优点是可以将传统控制和RBF神经网络控制各自的优势融合起来,减小系统的复杂度和计算量。
(2)基于反馈线性化的控制策略:利用反馈线性化的方法将非线性系统变为一个可控的线性系统,从而可以采用传统线性控制方法进行控制。
RBF神经网络概述

RBF 神经网络概述1 RBF 神经网络的基本原理2 RBF 神经网络的网络结构3 RBF 神经网络的优点1 RBF 神经网络的基本原理人工神经网络以其独特的信息处理能力在许多领域得到了成功的应用。
它不仅具有强大的非线性映射能力,而且具有自适应、自学习和容错性等,能够从大量的历史数据中进行聚类和学习,进而找到某些行为变化的规律。
径向基函数(RBF)神经网络是一种新颖有效的前馈式神经网络,它具有最佳逼近和全局最优的性能,同时训练方法快速易行,不存在局部最优问题,这些优点使得RBF 网络在非线性时间序列预测中得到了广泛的应用。
1985年,Powell 提出了多变量插值的径向基函数(Radial-Basis Function, RBF)方法。
1988年,Broomhead 和Lowe 首先将RBF 应用于神经网络设计,构成了径向基函数神经网络,即RBF 神经网络。
用径向基函数(RBF)作为隐单元的“基”构成隐含层空间,对输入矢量进行一次变换,将低维的模式输入数据变换到高维空间内,通过对隐单元输出的加权求和得到输出,这就是RBF 网络的基本思想。
2 RBF 神经网络的网络结构RBF 网络是一种三层前向网络:第一层为输入层,由信号源节点组成。
第二层为隐含层,隐单元的变换函数是一种局部分布的非负非线性函数,他对中心点径向对称且衰减。
隐含层的单元数由所描述问题的需要确定。
第三层为输出层,网络的输出是隐单元输出的线性加权。
RBF 网络的输入空间到隐含层空间的变换是非线性的,而从隐含层空间到输出层空间的变换是线性。
不失一般性,假定输出层只有一个隐单元,令网络的训练样本对为{,}(1,2,...,)n n X d n N =,其中12[,,...,],(1,2,...,)T n n n nM X x x x n N ==为训练样本的输入,(1,2,...,)n d n N =为训练样本的期望输出,对应的实际输出为(1,2,...,)n Y n N =;基函数(,)i X t ϕ为第i 个隐单元的输出12[,,...,,...,](1,2,...,)i i i im iM t t t t t i I ==为基函数的中心; (1,2,...,)i w i I =为第i 个隐单元与输出单元之间的权值。
神经网络控制(RBF)

17/20
1.3 基本概念 生物神经元的基本特征
神经元具有感知外界信息或其它神经元信息的输入端 神经元具有向外界或其它神经元输出信息的输出端 神经元之间的连接强度(连接权)决定信号传递的强 弱,而且联接强度是可以随训练改变的 信号可以是起刺激作用的,也可以是起抑制作用的, 即连接权的值(权值)可正、可负 每个神经元有一个阀值 神经元可以对接受的信号进行累积(加权) 神经元的兴奋程度(输出值的大小),取决于其传输 函数及其输入(输入信号的加权与阈值之和)
4/20
1.1 概述
神经细胞利用电-化学过程交换信号。输入信号来自另一些神 经细胞。这些神经细胞的轴突末梢(也就是终端)和本神经细胞的 树突相遇形成突触(synapse),信号就从树突上的突触进入本细胞。 信号在大脑中实际怎样传输是一个相当复杂的过程,但就我们而言, 重要的是把它看成和现代的计算机一样,利用一系列的0和1来进行 操作。就是说,大脑的神经细胞也只有两种状态:兴奋(fire)和不 兴奋(即抑制)。发射信号的强度不变,变化的仅仅是频率。神经 细胞利用一种我们还不知道的方法,把所有从树突上突触进来的信号 进行相加,如果全部信号的总和超过某个阀值,就会激发神经细胞 进入兴奋(fire)状态,这时就会有一个电信号通过轴突发送出去给 其他神经细胞。如果信号总和没有达到阀值,神经细胞就不会兴奋 起来。这样的解释有点过分简单化,但已能满足我们的目的。 。
绝对经典RBF神经网络

1
RBF学习算法
RBF学习的三个参数:①基函数的中心 t i ②方差(扩展常数) i ③隐含层与输出层间的权值 wij 当采用正归化RBF网络结构时,隐节点数即样本数,基函 数的数据中心即为样本本身,参数设计只需考虑扩展常数 和输出节点的权值。
当采用广义RBF网络结构时,RBF网络的学习算法应该解决 的问题包括:如何确定网络隐节点数,如何确定各径向基 函数的数据中心及扩展常数,以及如何修正输出权值。
2I
2.中心自组织选取
常采用各种动态聚类算法对数据中心进行自组织选择,在 学习过程中需对数据中心的位置进行动态调节。常用的方 法是K-means聚类,其优点是能根据各聚类中心之间的距 离确定各隐节点的扩展常数。由于RBF网的隐节点数对其 泛化能力有极大的影响,所以寻找能确定聚类数目的合理 方法,是聚类方法设计RBF网时需首先解决的问题。除聚 类算法外,还有梯度训练方法、资源分配网络(RAN)等
i i
G ( P C1
p1 p2
pQ
G( P C2
w2
w1
F P
wQ
G( P CQ )
1.网络隐层使用Q个隐节点。 2.把所有Q个样本输入分别作为Q个隐节点的中心。 3.各基函数取相同的扩展常数。 4.确定权值可解线性方程组:
w G(
j j 1
Q
pi p j ) t i 1 i Q
径向基函数(RBF)
1.
2 r Gauss(高斯)函数: r exp 2 2
2. 反演S型函数: r
1 r2 1 exp 2
1
3. 拟多二次函数:
r
神经网络及BP与RBF比较

机器学习第四章神经网络报告一、神经网络概述1.简介人工神经网络是模仿脑细胞结构和功能、脑神经结构以及思维处理问题等脑功能的信息处系统,它从模仿人脑智能的角度出发,探寻新的信息表示、存储和处理方式,这种神经网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的,它采用了与传统人工智能和信息处理技术完全不同的机理,克服了传统的基于逻辑符号的人工智能在处理直觉、非结有针对性化信息方面的缺陷,具有自适应、自组织和实时学习的特点,它通过预先提供的一批相互对应的输入和输出数据,分析掌握两者之间潜在的规律,最终根据这些规律,用新的输入数据来推算输出结果。
人工神经网络(ANN)学习对于训练数据中的错误健壮性很好,且已被成功地应用到很多领域,例如视觉场景分析、语音识别、机器人控制以及医学图像处理等。
人工神经网络2.人工神经网络的特点及功能2.1人工神经网络具有以下几个突出的优点:(1)能充分逼近复杂的非线性关系。
只有当神经元对所有输入信号的综合处理结果超过某一个限值后才能输出一个信号。
(2)所有定量或定性的信息都等势分布贮存于网络内的各神经元,每个神经元及其连线只能表示一部分信息,因此当有节点断裂时也不影响总体运行效果,具有很强的鲁棒性和容错能力。
(3)采用并行分布处理方法,使得快速进行大量运算成为可能。
(4)可学习和自适应不知道或不确定的系统。
2.2人工神经网络的特点和优越性,使其具有以下三个显著的功能:(1)具有自学习功能:这种功能在图像识别和处理以及未来预测方面表现得尤为明显。
自学习功能在未来预测方面也意义重大,随着人工神经网络的发展,未来它将在更多的领域,比如经济预测、市场预测、效益预测等等,发挥更好的作用。
(2)具有联想存储功能:人的大脑能够对一些相关的知识进行归类划分,进而具有联想的功能,当我们遇到一个人或者一件事情的时候,跟此人或者此事相关的一些信息会浮现在你的脑海,而人工神经网络则通过它的反馈网络,实现一些相关事物的联想。
RBF神经网络的结构动态优化设计

RBF神经网络的结构动态优化设计RBF神经网络的结构动态优化设计1. 前言随着人工智能技术的快速发展,神经网络在各个领域中得到了广泛应用。
RBF(Radial Basis Function)神经网络作为一种常见的神经网络模型,在模式识别、函数拟合等问题中具有广泛的应用前景。
然而,在实际应用中,如何优化RBF神经网络的结构是一个值得研究的问题。
本文旨在探讨RBF神经网络的结构动态优化设计,以提升其性能和应用效果。
2. RBF神经网络的基本原理RBF神经网络是一种三层前向神经网络,包含输入层、隐含层和输出层。
其基本原理如下:(1)输入层:接收外部输入的信号,并对其进行预处理和特征提取。
一般情况下,输入层的神经元节点数等于输入向量的维度。
(2)隐含层:由一系列径向基函数(Radial Basis Function)神经元构成,用于对输入信号进行非线性映射。
根据径向基函数的不同选择,可以得到不同的RBF神经网络模型。
(3)输出层:由线性输出神经元组成,负责将隐含层的输出映射到最终的输出空间,实现模式识别和函数拟合的功能。
3. RBF神经网络的结构优化方法为了进一步提升RBF神经网络的性能,需要对其结构进行优化设计。
以下是一些常用的RBF神经网络结构优化方法:(1)确定隐含层的神经元个数:隐含层的神经元个数决定了RBF神经网络的复杂度和拟合能力。
过多的神经元可能导致过拟合的问题,而过少的神经元可能无法充分表达数据的特征。
一种常用的方法是通过交叉验证等技术,综合考虑模型的复杂度和拟合效果,选择合适的隐含层神经元个数。
(2)确定径向基函数的类型和参数:径向基函数的类型和参数选择对RBF神经网络的性能影响较大。
常见的径向基函数包括高斯函数、多项式函数等。
通过试验和分析,选择合适的径向基函数类型和参数可以提升RBF神经网络的拟合能力和泛化性能。
(3)优化权重矩阵的学习算法:权重矩阵是RBF神经网络中非常重要的参数,直接关系到模型的拟合效果和泛化能力。
基于遗传算法的模糊RBF神经网络设计及应用

第31卷 第1期 吉首大学学报(自然科学版)Vol.31 No.1 2010年1月J ournal of J is ho u Uni ver s i t y (Nat ural Sci ence Editio n)J an.2010 文章编号:1007-2985(2010)01-0043-04基于遗传算法的模糊RB F 神经网络设计及应用3段明秀(吉首大学数学与计算机科学学院,湖南吉首 416000)摘 要:提出了一种基于遗传算法的模糊RB F 神经网络学习算法.采用遗传算法对模糊RB F 神经网络需要调整的参数进行优化,再将遗传算法优化的各参数结果作为模糊RB F 神经网络各个参数的初始值,并结合梯度下降法对网络的各参数进行动态调整.在对非线性函数逼近的仿真中,仿真结果验证了优化后的模糊RBF 神经网络具有更高的精度及强鲁棒性.关键词:遗传算法(G A );模糊RBF ;神经网络;函数逼近中图分类号:TP18 文献标识码:A神经网络具有并行计算、分布式信息存储、容错能力强以及具备自适应学习功能等优点,但不适合表达基于规则的知识,模糊控制比较适合于表达模糊或定性知识,其推理方式比较类似于人的思维模式,但缺乏学习和自适应能力.[1]模糊神经网络结合了模糊控制的推理能力强与神经网络学习能力强的特点,更适合非线性复杂系统.有效确定模糊RBF 神经网络的网络结构和参数,是当今的研究热点和难点.模糊RB F 神经网络需要确定的参数主要包括基函数的中心值和宽度、隐含层到输出层的连接权值.目前确定基函数的中心值最常用的方法是使用聚类方法,而隐藏层到输出层的权值采用伪逆法确定,但这种方法使得网络一旦训练完成便无法调整,往往达不到精度要求,而且网络的泛化能力很差;而采用梯度下降法的模糊RB F 神经网络学习算法又存在各层权值的初始值随机给定、网络的训练结果受初始值的影响极大的不利方面,导致网络的训练结果很不稳定[2-3].遗传算法[4]是模仿生物遗传学和自然选择机理,通过人工方式构造的一类优化搜索算法.遗传算法具有搜索范围广、搜索效率高、鲁棒性强的特点,运用遗传算法训练模糊RB F 神经网络无需先验知识,而且对初始参数不敏感,不会陷入局部极小点.笔者提出将模糊RB F 神经网络需要确定的参数看作染色体,利用遗传算法的强搜索能力,求出各参数的最优解或次优解,然后将经遗传算法优化的各参数结果作为模糊RB F 神经网络各个参数的初始值,再采用梯度下降法对网络的各参数进行动态调整,从而提高网络的泛化能力及稳定性.1 模糊RBF 神经网络的原理模糊RB F 神经网络由输入层、模糊化层、模糊推理层及输出层构成[5].(1)输入层.输入层的各个节点直接与输入量的各个分量连接,将输入量传到下一层.该层的每个节3收稿日期:2009-09-07基金项目:湖南省教育厅科学研究项目(09C795)作者简介段明秀(5),女,湖南茶陵人,吉首大学数学与计算机科学学院讲师,硕士,主要从事数据挖掘、神经网络、信息安全研究:197-.点i 表示一个输入变量:f 1(i)=X.X =(x 1,x 2,…,x n )T ,n 为输入向量的维数.(2)模糊化层.该层的作用是将输入划分为模糊集.该层的每个节点代表一个语言变量值,采用一种径向基函数如高斯函数为模糊隶属度函数求取各输入变量属于各语言变量的隶属度函数,c ij 和b ij 分别是第i 个输入变量第j 个模糊集合的隶属函数的均值(中心)和标准差(宽度).f 2(i ,j )=e xp {-(f 1(i )-c ij )2/(b ij )2}.(1)式中:i =1,2,…,n;j =1,2,…,N ;n 为网络第1层输入变量的个数;N 为网络第2层隐藏层节点的个数,即模糊集合的个数;f 2(i ,j)表示第i 个输入属于模糊集j 的隶属度,即概率密度.(3)模糊推理层.模糊推理层通过与模糊化层的连接来完成模糊规则的匹配,各个节点之间实现模糊运算,即通过各个节点的组合得到相应的点火强度.该层的每个节点表示一条模糊规则,完成模糊规则到输出空间的映射,每个节点的输出为该节点所有输入信号的乘积,即f 3(m)=∏N j =1∏ni =1f 2(i ,j),(2)式中m =1,2,…,M.M 为网络第3层的节点数.(4)输出层.f 4(l )=w 3f 3=∑M m =1w (l ,m )f 3(m ),(3)式中l =1,2,…,L.L 为输出层的节点数,w 为输出层节点与第3层各节点的连接权矩阵.2 遗传算法原理遗传算法(G enetic Al gorit hm s ,GA )的思想来源于生物遗传学和适者生存的自然规律,是一种群体操作,该操作以群体中的所有染色体为对象,通过选择、交叉和变异等操作产生新一代群体,直到获得满意的结果.(1)编码.将模糊RB F 神经网络需要进行优化的参数进行二进制编码,称此二进制串为染色体,每个参数用10位二进制表示.(2)选择操作.采用适应度比例方法,也称为赌轮法.该方法中染色体被选择的概率与其适应度成正比,即p i =f i /∑Nj =1f j ,其中f i 为第i 个染色体的适应度,N 为种群大小,p i 为第i 个染色体被选择的概率,具有较大适应值的染色体被选中的概率较大.为了保证搜索的全局最优,在进行交叉操作之前将本代染色体中的最优染色体直接保留到下一代中,其他染色体按照交叉概率和变异概率进行交叉操作和变异操作,以形成新的染色体[6].(3)交叉和变异操作.交叉操作可以提高遗传算法的搜索能力,一般采用2点交叉方式,保留一个最优染色体不进行交叉变异,确保了算法的收敛[7].根据交叉概率PC 选择染色体,交叉位随机选取.变异操作则可以增强遗传算法的局部搜索能力,同时使得遗传算法保持种群的多样性,确保种群能够继续进化.(4)适应度函数的选取.适应度函数应选取能够客观地反映染色体优劣的函数[8].对模糊RB F 神经网络的参数来说,网络输出的精度,即误差的大小可以充分反映染色体的优劣,定义模糊RB F 神经网络的性能指标为误差平方和,即E =12∑L i =1∑n j =1(d ij-o ij )2.(4)其中:d ij 和o ij 为第j 个样本的第i 个输出的期望输出和实际输出;n 为样本的个数;L 为输出层神经元的个数,即输出向量的维数.设计适应度函数为f i =1/E.44吉首大学学报(自然科学版)第31卷3 基于梯度下降法的模糊RB F 神经网络的参数调整模糊RB F 网络的可调参数包括隐层节点的中心、宽度和输出层权值.文中采用梯度下降法进行网络参数学习.隐层节点的中心的更新公式如下所示:c k (n +1)=c k (n )+Δc k (n +1)+η[c k (n )-c k (n -1)],Δc k (n +1)=-γ(d(n +1)-o (n +1))×w k (n +1)× f 3(k )×(x (1)-c (k ))×b (k )-2.(5)基函数宽度的更新公式如下所示:σk (n +1)=σk (n )+Δσk (n +1)+η[σk (n )-σk (n -1)],Δσk (n +1)=γ(d (n +1)-o (n +1))×w k (n +1)× f 3(k)×(x (1)-c(1,k))2×b (k)-3.(6)对输出层节点与上一层各节点的权值W 采用(6)式进行调整:w k (n +1)=w k (n)+Δw k (n +1)+η[w k (n)-w k (n -1)],Δw k (n +1)=-γ(d (n +1)-o (n +1))×f 3(k ).(7)其中:η为学习动量因子;n 为迭代步数;γ为学习速率;d 表示网络的期望输出;o 表示网络的实际输出.3.1算法描述基于遗传算法的模糊RB F 神经网络的学习算法描述如下:(a )依据模糊RB F 神经网络要优化的参数个数设置染色体的二进制串长度,并设置各参数的寻优范围;(b)随机初始化种群;(c )对种群中各个染色体进行译码,并根据网络的性能指标函数计算各个染色体的误差平方和;(d)依据适应度函数即(4)式计算种群中各个染色体的适应值,并对适应值排序,选择适应值最大的染色体作为最优染色体;(e )依据赌轮法计算每个染色体的选择概率.选择适应值较大的染色体来产生新的染色体;(f)设置交叉概率.产生1个随机数,若该数小于交叉概率,则将染色体相应的串进行交叉操作,保留1个最优染色体不进行交叉;(g )设置变异概率.产生1个随机数,若该数小于变异概率,则将染色体进行变异操作,保留1个最优染色体不进行变异;(h )若达到迭代次数则结束,否则转步骤(c );(i)将优化的模糊RB F 网络的各参数作为网络参数的初始值;(j )利用(1)至(3)式计算模糊RB F 神经网络各层节点的输出;(k )计算网络的实际输出与理想输出的差值;(l )利用(5)至(7)式调整模糊RB F 神经网络的各个参数;(m )重复步骤(j )至(l ),直到训练的模糊RB F 神经网络满足结束条件;(n )用测试数据对模糊RB F 神经网络进行验证.3.2仿真实验为了验证算法的有效性及准确性,对文中所设计的基于遗传算法优化的模糊RB F 神经网络用于函数逼近.函数y =si n c (x )的逼近效果如图1所示,图2是逼近过程的误差.从函数的逼近效果可以看出,文中所设计的基于遗传算法优化的模糊RB F 神经网络逼近所得结果基本与原函数一致,而且迭代过程中误差基本为0.4 结语利用遗传算法具有搜索范围广、搜索效率高、鲁棒性强的特点,运用遗传算法优化的模糊RB F 神经网络结构、参数,再采用梯度下降法对优化的网络参数进行动态调整,克服了遗传算法局部寻优能力的不足,54第1期 段明秀:基于遗传算法的模糊RB F 神经网络设计及应用图1 函数Y =si n c(x )的逼近效果 图2 函数Y=sin c(x )的逼近误差从而提高网络的泛化能力及稳定性.仿真结果表明了该算法的有效性.参考文献:[1] 高建英.基于遗传算法设计模糊RB F 神经网络控制器[D ].大连:大连理工大学,2000.[2] 李国勇.智能控制及其MA TLAB 实现[M ].北京:电子工业出版社,2005.[3] 何迎生,彭 华,段明秀.基于交叉验证的改进RB F 分类器设计[J ].微计算机信息,2009,25(6-3):248-250.[4] 王小平,曹立明.遗传算法———理论、应用与软件实现[M ].西安:西安交通大学出版社,2003.[5] 苗卓广,何秀然,魏永志.基于模糊RB F 神经网络整定的航空发动机多变量解耦控制[J ].空军工程大学学报,2009,10(2):10-13.[6] 高静巧,朱伟兴.基于遗传算法的RB F 神经模糊控制器[J ].计算机仿真,2003,20(11):53-54.[7] 陈小平,赵鹤鸣,杨新艳.遗传前馈神经网络在函数逼近中的应用[J ].计算机工程,2008,34(20):24-28.[8] 赵志刚,单晓虹.一种基于遗传算法的RB F 神经网络优化方法[J ].计算机工程,2007,33(6):13-15.Design of Fuzzy RBF N eural N et w or k B ased on G enetic Algor ithm an dits Applicat ionDU AN Mi ng 2xi u(College of Mathematics and Compute r Science ,Jishou Unive rsity ,Jishou 416000,Hunan China)Abstract :A fuzzy RB F ne ural net wor k learni ng algorit hm based on genetic al gori t hm i s propo sed.Thi s al 2gori t hm adopt s genet ic al gorit hm to opti mize t he fuzzy RB F neural network ’s st ruct ure parameter s ,a 2dapt s t he optimizat ion result as t he init ial value of t he f uzzy RB F neural net work ’s st ruct ure pa ramet ers ,and dynamicl y adj ust s t he parameter s using t he gradient decent met hods.Finall y t he al gorit hm is applied t o cl assif y t he dat a a nd function approximation.The sim ulation shows t hat t he f uzzy RB F neural net work has hi gher p reci sion and robust ness.K ey w or ds :genetic algori t hm (GA );f uzzy RB F ;neural net work ;f unct ion approximation(责任编辑 向阳洁)64吉首大学学报(自然科学版)第31卷。
RBF网络
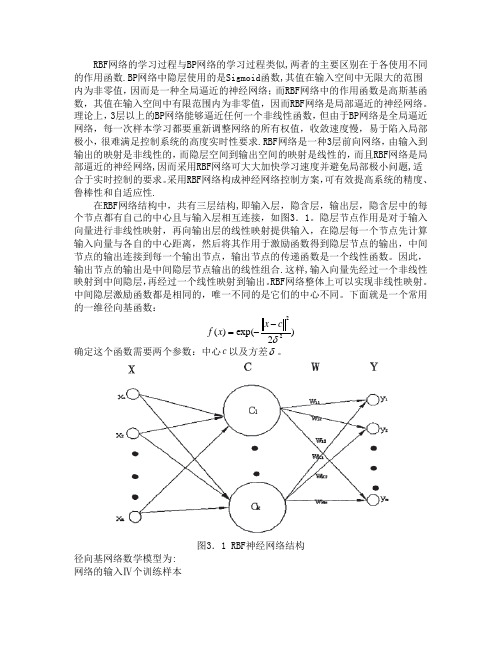
RBF 网络的学习过程与BP 网络的学习过程类似,两者的主要区别在于各使用不同的作用函数.BP 网络中隐层使用的是Sigmoid 函数,其值在输入空间中无限大的范围内为非零值,因而是一种全局逼近的神经网络;而RBF 网络中的作用函数是高斯基函数,其值在输入空间中有限范围内为非零值,因而RBF 网络是局部逼近的神经网络。
理论上,3层以上的BP 网络能够逼近任何一个非线性函数,但由于BP 网络是全局逼近网络,每一次样本学习都要重新调整网络的所有权值,收敛速度慢,易于陷入局部极小,很难满足控制系统的高度实时性要求.RBF 网络是一种3层前向网络,由输入到输出的映射是非线性的,而隐层空间到输出空间的映射是线性的,而且RBF 网络是局部逼近的神经网络,因而采用RBF 网络可大大加快学习速度并避免局部极小问题,适合于实时控制的要求。
采用RBF 网络构成神经网络控制方案,可有效提高系统的精度、鲁棒性和自适应性.在RBF 网络结构中,共有三层结构,即输入层,隐含层,输出层,隐含层中的每个节点都有自己的中心且与输入层相互连接,如图3.1。
隐层节点作用是对于输入向量进行非线性映射,再向输出层的线性映射提供输入,在隐层每一个节点先计算输入向量与各自的中心距离,然后将其作用于激励函数得到隐层节点的输出,中间节点的输出连接到每一个输出节点,输出节点的传递函数是一个线性函数。
因此,输出节点的输出是中间隐层节点输出的线性组合.这样,输入向量先经过一个非线性映射到中间隐层,再经过一个线性映射到输出。
RBF 网络整体上可以实现非线性映射。
中间隐层激励函数都是相同的,唯一不同的是它们的中心不同。
下面就是一个常用的一维径向基函数:)2exp()(22δc x x f --=确定这个函数需要两个参数:中心c 以及方差δ。
图3.1 RBF 神经网络结构径向基网络数学模型为:网络的输入Ⅳ个训练样本{}km k k k x x x X ,....,21=(N k ,...2,1=)网络对应的输出:{}km k k k y y y Y ,...,21= (N k ,...2,1=)网络输出连接权系数构成连接矩阵:}{,,..2,1,,...2,1,,J j I i j i W ===隐层节点个数I,中心点:{i C } I i ,...2,1= 方差i δ网络输入输出之间的关系:221)21exp()(i k i I i ij k kj C X w X y --=∑=δRBF 网络逼近的性能指标函数为:)(k E =2)]([21k kj k X y Y - 3.2 RBF 神经网络的性能改进3.2.1 RBF 神经网络训练数据的预处理1.进行数据预处理的原因对于使用有教师训练算法的前向神经网络,训练样本的质量对网络的性能非常重要.RBF 神经网络是一种局部网络,只有在隐含层节点中心的一定范围内的点才会使网络产生一定的输出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
rbf_simulate_data.dat文件 内容及格式
rbf_train_target_data.dat文件内容及格式
四、RBF网络应用于模式分类
(2)设置径向基函数的分布密度 Spread 为径向基层的分布密度,又称散布常数,默认值为 1 。散布常数是 RBF网络设计过程中一个非常重要的参数。一般情况下,散布常数应该足够大, 使得神经元响应区域覆盖所有输入区间。 (3)调用newrb构建并训练径向基函数神经网络; 在MATLAB中,构建径向基函数网络的函数文件有两个,分别为newrbe( )函数 和newrb()函数。应用newrbe( )函数可以快速设计一个径向基函数网络,并且 使得设计误差为0,调用方式如下: net=newrbe(p,t,spread); 其中,p为输入向量;t为期望输出向量(目标值),spread为径向基层的散布 常数,默认值为1。输出为一个径向基网络,其权值和阈值完全满足输入和期望 值关系要求。 由newrbe( )函数构建的径向基函数网络,其径向基层(第一层)神经元数 目等于输入向量的个数,那么在输入向量较多的情况下,则需要很多的神经元, 这就给网络设计带来一定的难度。函数 newrb( )则可自动增加网络的隐含层神 经元数目,直到均方差满足精度或神经元数目达到最大为止。
四、RBF网络应用于模式分类
基于MATLAB的RBF模式分类程序如下: clear; clc; %网络训练目标 pConvert=importdata('C:\Users\Administrator\Desktop\RBF\rbf_train_sample_dat a.dat'); p=pConvert'; t=importdata('C:\Users\Administrator\Desktop\RBF\rbf_train_target_data.dat'); plot3(p(1,:),p(2,:),p(3,:),'o'); grid;box; for i=1:29,text(p(1,i),p(2,i),p(3,i),sprintf(' %g',t(i))),end hold off f=t'; index1=find(f==1); index2=find(f==2); index3=find(f==3); index4=find(f==4);
基于RBF网络数据分类设计
主 单
讲:周润景 教授 位:电子信息工程学院
目 录
RBF神经网络简介 径向基函数的网络结构 径向基函数网络参数选择
RBF网络应用于模式分类 总结
一. RBF神经网络简介
从对函数的逼近功能而言,神经网络可分为全局逼近和局部逼近。
局部逼近网络具有学习速度快的优点。径向基函数( Radial Basis Function,RBF)就属于局部逼近神经网络。
四、RBF网络应用于模式分类
运行程序后,系统首先输出训练用样本及其类别分类图,如下图a所示。 接着输出RBF网络的训练结果图,如下图b所示。
图a 训练用样本及其类别分类图
图b RBF网络的训练结果图
RBF网络结果与原始数据对比
序 号
4
A
864.45
B
1647.31
C
2665.9
目标结果
1
RBF网络分类结果
输入层到隐含层为非线性映射,基函数是高斯函数:
|| x - ci ||2 Ri x exp 2 2 i
二.径向基函数的网络结构
RBF神经网络的拓扑结构是一种三层前向网络: 输入层由信号源结点构成,仅起到数据信息的传递作用,对输入信
息不进行任何变换;
第二层为隐含层,结点数视需要而定,隐含层神经元的核函数(作 用函数)为高斯函数,对输入信息进行空间映射变换;
径 向 基 函 数 RBF 神 经 网 络 ( 简 称 径 向 基 网 络 ) 是 由 J.Moody 和
C.Darken于20世纪80年代末提出的一种神经网络结构,RBF神经网 络是一种性能良好的前向网络,具有最佳逼近及克服局部极小值问
题的性能。
二.径向基函数的网络结构
径向基函数的网络结构
二.径向基函数的网络结构
1
6
16 25 8 14
877.88
1418.79 1449.58 2352.12 2297.28
2031.66
1775.89 1641.58 2557.04 3340.14
3071.18
2772.9 3405.12 1411.53 535.62
1
1 1 2 2
1
1 1 2 2
15
18 19 22 24 1
四、RBF网络应用于模式分类
24 1 3 7 11 17 20 21 26 2 5 9 10 12 13 23 27 28 29 2063.54 1739.94 1756.77 1803.58 1571.17 1845.59 1692.62 1680.67 1651.52 373.3 222.85 401.3 363.34 104.8 499.85 172.78 341.59 291.02 237.63 3199.76 1675.15 1652 1583.12 1731.04 1918.81 1867.5 1575.78 1713.28 3087.05 3059.54 3259.94 3477.95 3389.83 3305.75 3084.49 3076.62 3095.68 3077.78 1257.21 2395.96 1514.98 2163.05 1735.33 2226.49 2108.97 1725.1 1570.38 2429.47 2002.33 2150.98 2462.86 2421.83 2196.22 2328.65 2438.63 2088.95 2251.96 2 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4
2092.62
2205.36 2949.16 2802.88 2063.54 1739.94
3177.21
3243.74 3244.44 3017.11 3199.76 1675.15
Байду номын сангаас
584.32
1202.69 662.42 1984.98 1257.21 2395.96
2
2 2 2 2 3
2
2 2 2 2 3
四、RBF网络应用于模式分类
将排序后的数据及其类别绘制在三维图中直观地表示出来,作为 RBF网络训练时应达到的目标。排序后的数据及其类别的三维图如下图 所示。
四、RBF网络应用于模式分类
将样本数据及分类结果分别存放到“.dat”文件中。数据文件内容及格式如下图 所示。
rbf_train_sample_data.dat 文件内容及格式
四、RBF网络应用于模式分类
newrb定义为net= newrb(p,t,GOAL,SPREAD,MN,DF),各个参数的定义如下: P——Q个输入向量的R×Q维矩阵。这里Q=29,R=3 T——Q个目标类别向量的S×Q维矩阵。这里S=1 GOAL——期望的均方误差值,默认时为0.0。这里选择默认值 SPREAD——径向基函数的散布常数,默认时为1.0 MN——神经元的最大数目,默认时等于Q。这里设置为28 DF——每次显示时增加的神经元数目,默认时为25,并且返回一个新的径向基 函数网络。这里设置为2。 (4)调用sim,测试RBF网络的训练效果 (5)再次调用sim识别样本所属类别
第三层为输出层,它对输入模式做出响应,输出层神经元的作用函
数为线性函数,对隐含层神经元输出的信息进行线性加权后输出, 作为整个神经网络的输出结果。
三.径向基函数网络参数选择
四、RBF网络应用于模式分类
以酒瓶分类三元色数据为例,希望将数据按照颜色数据所表征的特 点,将数据按各自所属的类别归类。其中,前29组数据已确定类别, 后30组数据待确定类别。 (1)从样本数据库中获取训练数据 取前29组数据作为训练样本。为了编程方便,先对这29组数据按 类别进行升序排序。重新排序后的数据如下表所示。
四、RBF网络应用于模式分类
line(p(1,index1),p(2,index1),p(3,index1),'linestyle','none','marker','*','color','g'); line(p(1,index2),p(2,index2),p(3,index2),'linestyle','none','marker','*','color','r'); line(p(1,index3),p(2,index3),p(3,index3),'linestyle','none','marker','+','color','b'); line(p(1,index4),p(2,index4),p(3,index4),'linestyle','none','marker','+','color','y'); box;grid on;hold on; axis([0 3500 0 3500 0 3500]); title('训练用样本及其类别'); xlabel('A'); ylabel('B'); zlabel('C'); % RBF网络的创建和训练过程 net=newrb(p,t,0,410,28,2); A=sim(net,p) plot3(p(1,:),p(2,:),p(3,:),'r .'),grid;box; axis([0 3500 0 3500 0 3500]) for i=1:29,text(p(1,i),p(2,i),p(3,i),sprintf(' %g',A(i))),end hold off f=A';
