(精编)计数型(通止规)MSA测量系统分析
msa测量系统分析

msa测量系统分析MSA测量系统分析随着科技的不断发展和应用,测量系统在各个领域都起着至关重要的作用。
而为了确保测量结果的准确性和可靠性,我们需要对测量系统进行全面的分析和评估。
这就是测量系统分析(Measurement System Analysis,简称MSA)的目的所在。
本文将从理论、方法和实践等方面综述MSA的重要性和应用。
一、概述测量系统是实现测量目的的一套工具、设备和操作程序的集合,它可以对特定的量进行测量和分析。
测量系统分析是指对测量系统的各种因素进行评估和分析,以确保其满足预期的测量要求,并且可以提供准确可靠的测量结果。
二、MSA的重要性一个可靠的测量系统对于各个行业和领域都至关重要。
无论是在制造业、医疗保健、环境监测还是科学研究中,如果测量系统存在问题或者误差较大,将会导致错误的决策和不可靠的结果。
因此,MSA成为了保证测量系统准确性和可靠性的重要手段。
三、MSA的方法1. 重复性和再现性分析重复性是指在相同条件下,同一测量员对同一物体进行多次测量时得到的测量值的一致性。
再现性是指在不同条件下,不同测量员对同一物体进行测量时得到的测量值的一致性。
通过对重复性和再现性的分析,可以评估测量系统的稳定性和可靠性。
2. 偏倚分析偏倚是指测量结果与真实值之间的差异。
通过对偏倚进行分析,可以确定测量系统是否存在系统性误差,并对其进行校正和调整。
3. 线性度和稳定性分析线性度是指测量系统对于不同测量范围内的样本是否呈现线性关系。
稳定性是指测量系统的输出值是否随时间的推移而发生变化。
线性度和稳定性的分析可以帮助我们了解测量系统的工作状态,并进行相应的调整。
4. 分类和排序分析对于某些特定的测量系统,如视觉检测和图像识别系统,我们可以通过分类和排序分析来评估其性能和可靠性。
通过对样本的分类和排序,可以判断测量系统对于不同特征的判断准确程度。
四、MSA的实践MSA的实践需要依赖于科学的方法和工具,同时也需要结合具体的领域和应用情况。
(精品)计数型(通止规)MSA测量系统分析
A-1 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 0 1 0 1 1 0 1 1 0 1 1 0 1 0
A-2 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 0 1 1 0 1 0 1 1 0 0 1 0 1 1 0 1 0
B
总计
Po=
C与基准判断交叉表
C
总计
Po=
Kappa
来源 总受检数 符合的 错误地否定 错误地肯定 混合的 95%置信上限 计算得分 95%置信下限
总受检数 一致数 95%置信上限 计算得分 95%置信下限
注意: 1) 评价人自己在所有试验上都一致 2)评价人在所有试验上都与基准一致 3) 所有评价人自己保持一致,两两间一致 4)所有评价人自己和两两间一致并且于基 5) UCI和LCI分别是上、下置信区间边界线
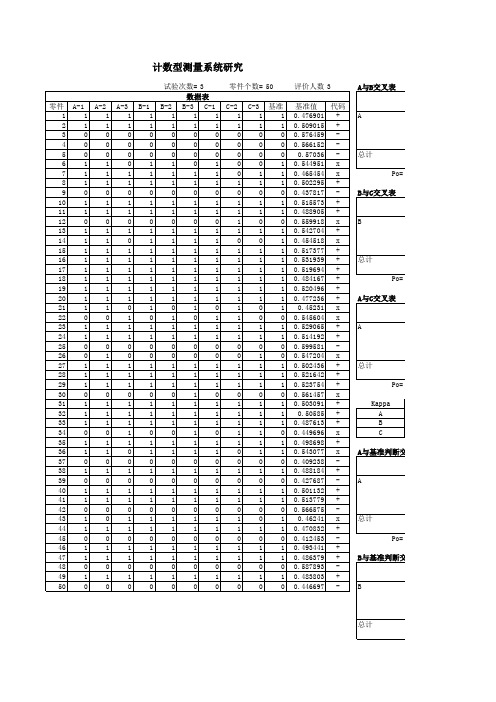
计数型测量系统研究
零件 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
零件个数= 50
C-2 C-3 基准 111 111 000 000 000 001 011 111 000 111 111 100 111 001 111 111 111 111 111 111 101 100 111 111 000 010 111 111 111 000 111 111 111 110 111 011 000 111 000 111 111 000 101 111 000 111 111 000 111 000
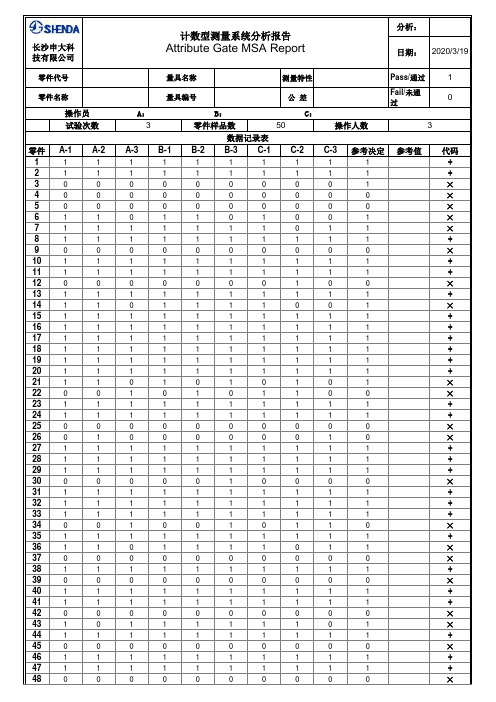
计数型MSA测量系统分析报告
D
D
A
C
D
D
D
D
D
B
C
A
A
A
D
D
D
A
A
A
D
D
D
D
D
D
A
A
A
D
C
B
D
D
D
A
A
A
D
D
D
D
D
D
A
A
A
D
D
D
D
D
D
D
D
D
A
A
A
A
A
A
A
A
A
1
0
3
0
1
分析用表格
A﹡参考
B﹡参考
1
2
3
1
2
3
D
DDDDD NhomakorabeaD
D
D
D
D
D
B
B
B
B
B
B
A
A
A
A
A
A
A
A
A
A
A
A
D
D
B
D
D
B
D
D
D
D
D
D
D
D
D
D
D
D
A
A
A
A
A
A
D
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
MSA量测系统分析

11
1
基准值
基准值
在测量范围全领域具有常数倍数的偏倚. / 虽有偏倚但是因为大小一定所以可以容易调整.
线性(Linearity)的分析
① 线性不好的情况 – 测量范围全领域偏倚(正确度)不一定的情况 无法矫正.
基准值 测定平均 偏倚
2
1
-1
4
3.5 -0.5
偏
倚
6
6
0
8
8.5
0.5
10
11
1
基准值
製程變異对比5~10%不到
製程變異对比10% 以上
措施 很适合 : 无改善的必要 适合 : 几乎不需要改善 一般 : 一部分需要改善 差 : 需要改善
③ 线性(Linearity)差时需要考虑的事项:
•调查量具测量范围中上部或下部的刻度是否合适 •检验基准值是否正确 •检验测量位置是否正确 •检验测量者是否正确的使用了仪器 •检验量具磨损与否 •检验量具校准与否 •调查量具本身内部设计问题
USL 真值
测定值
真值
☞ Gage通常是在操作范围的下限 (或者规格值)比上限它的正确度 差.
正确度偏差大
正确度偏差小
什么是精密度(Precision) ?
什么是重复性(Repeatability) ?
☞ 一名测量者对同样的部品用 同样的仪器对同样的特性在比较短的 时间内反复测量时所发生的测量值的 变異
Minitab 分析结果 Graph 解释
“在全体散布中 R&R 所占的比重是否充分小? ”
Gage R&R, Repeat,Reprod.的高度越接近 0 越好。
“作业者别重复量测值是否稳定?”
注意 !!! 要是超过R Chart的界限,就得调查其原因, 并重新量测。
MSA测量系统分析报告

MSA测量系统分析报告1. 引言测量系统分析(Measurement System Analysis,简称MSA)是指对用于测量和判断产品性能或特征的测量设备和方法进行评估和分析的过程。
MSA的目标是确认测量系统的可靠性和准确性,以确保其能提供可靠且准确的测量结果。
本报告将对某一特定的MSA测量系统进行分析,并评估其性能和准确性。
2. 测量系统描述2.1 测量系统的目的和背景该测量系统用于检测某一机械零件的尺寸。
此测量系统的目的在于确保机械零件的尺寸符合规定的标准要求,以确保零件的质量和性能。
2.2 测量设备描述该测量系统使用一台数字卡尺作为测量设备,该卡尺具有高精度和快速测量的特点。
卡尺具有显示屏和刻度尺,可以直接读取并显示测量结果。
3. 数据收集与分析为了评估测量系统的准确性和可靠性,我们采集了一组样本进行测量。
每个样本由同一机械零件的尺寸组成,共采集了50个样本。
我们使用卡尺对每个样本进行了三次重复测量,并记录下每次测量的结果。
下表是我们采集的样本数据:样本编号测量1 (mm) 测量2 (mm) 测量3 (mm)1 25.02 25.03 25.042 24.99 25.00 25.013 25.01 24.99 25.00…………50 24.98 24.97 24.993.1 重复性分析重复性是指在相同的测量条件下,重复测量的结果是否一致。
为了评估测量系统的重复性,我们计算了每个样本的测量值之间的标准偏差(Standard Deviation, SD)。
标准偏差越小,说明测量系统的重复性越好。
下图是测量值的标准偏差的概率分布图:Sample | Standard Deviation (mm)-------|-------------------1 | 0.012 | 0.023 | 0.01... | ...50 | 0.01从概率分布图中可以看出,大多数样本的标准偏差都在0.01mm左右,说明测量系统的重复性非常好。
测量系统分析(MSA)(DOC 4页)

测量系统分析(MSA)(DOC 4页)部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑测量系统分析(MSA)第一章通用测量系统指南第一节引言、目的和术语一.引言1.测量数据的作用:①测量数据和统计量与过程统计控制限值进行比较,确定过程是否调整。
②确定每个变量间是否存在函数关系。
2.测量数据的质量:①测量值与特性标准值“接近”——质量“高”。
测量值远离特性标准值——质量“低”。
②数据质量好坏的表现a.偏倚——指数据相对标准值的位置。
b.方差——指数据的分布。
二.目的:为评定测量系统提供可选择的方法三.术语1.量具——任何用来获得测量结果的装置:包括用来测量合格不合格的装置。
2.测量系统——用来对被测特性赋值的操作、程序、量具、设备、软件以及操作人员的集合。
3.测量过程——赋值的过程。
第二节测量系统的统计特性一.测量系统必须处于统计过程中。
二.测量系统变异小于制造过程变异。
三.变异应小于公差。
四.测量精度应高于过程变异和公差。
五.测量系统统计特性可能随被测项目改变而变形。
第三节标准一.分类最高标准——国家标准。
第一级标准——国家标准传递到下一级的标准。
第二级标准——第一级标准传递到下一级的标准。
工作标准——用来校准生产设备中建立的测量系统。
(也称生产标准)。
标准追溯性——通过一个不间断的比较链,可将单个测量结果与国家标准相联系。
二.使用:可追溯标准的使用有助于减少生产者和顾客间测量结果不一致时产生的矛盾。
第四节通用指南一.测量系统的评定步骤1.第一步:验证该测量系统在测量正确的变量。
2.第二步:确定该测量系统应具备什么样可接受的统计特性。
二.测量系统的评定1.第一阶段:了解测量过程,确定系统能否满足需要,有两个目的:①确定该系统是否具有所需要的统计特性。
应在实际使用该系统之前进行。
②确定对系统有显著影响的环境因素。
2.第二阶段:验证测量系统应持续具有恰当的统计特性。
常用“量具R和R平均值”形式。
MSA计数型测量系统分析指导书

5
10
93% 97% 90% 93% 97% 90%
84% 90% 80% 84% 90% 80%
71% 78% 66% 71% 78% 66%
来源 总受检数 符合的 错误的拒收(由于评价人偏移造成的拒收) 错误的接受(由于评价人偏移造成的接受) 不相配 95%上限 计算得分 95%下限
系统有效结果%
见表1
JT/C-7.6J-004
表1-计数型研究数据表
零 A- A-2 A-3 B-1 B-2 B-3 C-1 C-2 C-3 参 参考值 代
件1
考
码
1 1 1 1 1 1 1 1 1 1 1 0.476 901 2 1 1 1 1 1 1 1 1 1 1 0.509015 3 0 0 0 0 0 0 0 0 0 0 0.576459 - 4 0 0 0 0 0 0 0 0 0 0 0.566152 - 5 0 0 0 0 0 0 0 0 0 0 0.57036 - 6 1 1 0 1 1 0 1 0 0 1 0.544 951 7 1 1 1 1 1 1 1 1 1 1 0.465454 8 1 1 1 1 1 1 1 1 1 1 0.502295 9 0 0 0 0 0 0 0 0 0 0 0.437817 - 10 1 1 1 1 1 1 1 1 1 1 0.515573 11 1 1 1 1 1 1 1 1 1 1 0.488905 12 0 0 0 0 0 0 0 0 0 0 0.559918 13 1 1 1 1 1 1 1 1 1 1 0.542704 14 1 1 0 1 1 1 1 0 0 1 0.454518 15 1 1 1 1 1 1 1 1 1 1 0.517377 16 1 1 1 1 1 1 1 1 1 1 0.531939 17 1 1 1 1 1 1 1 1 1 1 0.519694 18 1 1 1 1 1 1 1 1 1 1 0.484167 19 1 1 1 1 1 1 1 1 1 1 0.520496 20 1 1 1 1 1 1 1 1 1 1 0.477236 21 1 1 0 1 0 1 0 1 0 1 0.452310 22 0 0 1 0 1 0 1 0 1 0 0.545604 23 1 1 1 1 1 1 1 1 1 1 0.529065 24 1 1 1 1 1 1 1 1 1 1 0.514192 25 0 0 0 0 0 0 0 0 0 0 0.599581 - 26 0 1 0 0 0 0 0 0 1 0 0.547204 27 1 1 1 1 1 1 1 1 1 1 0.502436 28 1 1 1 1 1 1 1 1 1 1 0.521642 29 1 1 1 1 1 1 1 1 1 1 0.523754
MSA测量系统分析(PPT116页)

24
3.1再现性不好的可能潜在原因
➢ 零件(样品)之间:使用同样的仪器、同样的操作者 和方法时,当测量零件的类型为A,B,C时的均值差。
➢ 仪器之间:同样的零件、操作者、和环境,使用仪 器A,B,C等的均值差
➢ 标准之间:测量过程中不同的设定标准的平均影响 ➢ 方法之间:改变点密度,手动与自动系统相比,零
■测量零件后: 1)确定零件是否可接受(在公差内)或不可接受 (在公差外)。 2)零件进行规定的分类
变异性。是指数据的分布。
位置 (Location )
宽度 (Width )
10
4.1低质量数据的原因和影响
■低质量数据的普遍原因之一是变差太大 ■一组数据中的变差多是由于测量系统及其环境的相
互作用造成的。 ■如果相互作用产生的变差过大,那么数据的质量会
太低,从而造成测量数据无法利用。如:具有较大 变差的测量系统可能不适合用于分析制造过程,因 为测量系统的变差可能掩盖制造过程的变差。
➢ 仪器设计或方法缺乏稳定
性;
➢ 应用了错误的量具;
➢ 不同的测量方法—设置、安装、夹紧、技术;
➢ 量具或零件随零件尺寸变化、变形;
➢ 环境影响—温度、湿度、震动、清洁度;
➢ 其它—零件尺寸、位置、操作者技能、疲劳、读错。
28
5.稳定性(Stability)
稳定性
是测量系统在某持续时间内测 量同一基准或零件的单一特性 时获得的测量值总变差。
➢ 违背研究中的假定 ➢ 仪器设计或方法缺乏稳健性 ➢ 操作者训练效果 ➢ 应用─零件尺寸、位置、观察误差(易读性、视差)
26
4.线性(Linearity)
在量具正常工作量程内的偏倚变化量 多个独立的偏倚误差在量具工作量程内的关系 是测量系统的系统误差构成
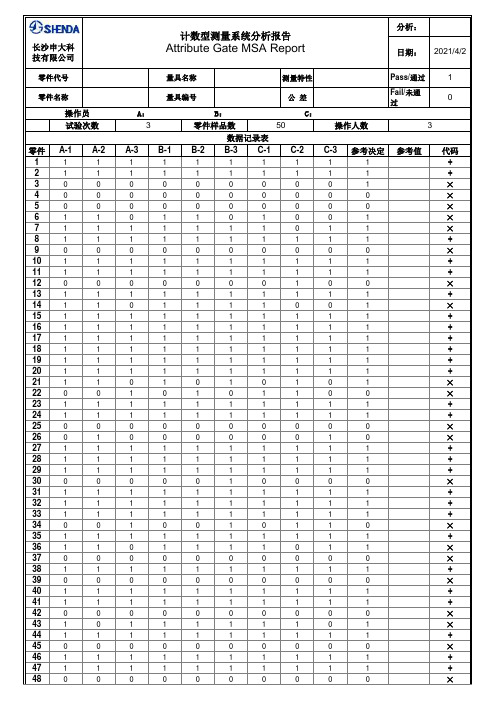
计数型MSA测量系统分析报告
D
B
D
D
D
C
D
A
A
D
D
A
A
D
D
D
D
A
A
D
C
D
D
A
A
D
D
D
D
A
A
0
I
0
II
0
II
0
III
0
III
A﹡C
1
2
3
D
D
D
D
D
D
A
A
A
A
A
A
A
A
A
D
B
A
D
B
D
D
D
D
A
A
A
D
D
D
D
D
D
A
C
A
D
D
D
D
B
A
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
B
D
A
C
C
B
D
D
D
D
D
D
A
A
A
A
B
C
D
D
D
D
D
D
D
D
D
A
A
A
D
D
D
D
D
D
D
计算结果
1
2
95%LCI
3
100.00% 90.00% 80.00% 70.00% 60.00% 50.00% 40.00% 30.00% 20.00% 10.00% 0.00%
测量系统分析MSA作业指导书

XXXX有限公司测量系统分析(MSA)指导书文件编号:版本:编制:审核:批准:XXX有限公司发布测量系统分析(MSA)作业指导书1目的:评价整个测量系统(即操作、程序、量具、设备、软件及操作人员的集合)是否具有可接受的测量水平,判定该测量系统是否适用。
2确定方法:2.1计量型量具(如游标卡尺)采用均值和极差法研究量具的重复性和再现性。
2.2计数型量具(如通止规),采用信号探测法或假设检验分析法研究。
2.3根据类型确定相应的计量型或计数型量具或设备,选择相应的研究方法3测量设备选购3.1测量系统必须有足够的灵敏性:3.1.1仪器要具有足够的分辨力:应至少保证仪器的分辨力能将公差分成十份或更多,即第一准则应至少是被测范围的十分之一,最好是保证为过程变差的十份之一。
3.1.2仪器要具有有效的分辨力:应保证仪器对所探测的产品或过程变差在一定的应用及环境下的变化具有足够的灵敏性。
3.2测量系统必须是稳定的:3.2.1在重复性的条件下,仪器变差只归因于普通原因而不是特殊原因。
3.2.2测量分析者必须经常考虑到仪器的稳定性对实际应用和统计的重要性。
3.3统计特性(误差)在预期的范围内一致,并足以满足测量的目的(产品或过程控制)。
4测量系统分析过程4.1采用均值和极差法研究量具的重复性和再现性指导:4.1.1准备工作:4.1.1.1确定评价人数量、被测零件、样品数量及重复读数次数。
4.1.1.1.1评价人:应从日常操作该仪器的人中选择,并且采用盲测(即选定评价人事先不知道本次研究事件),评价人数量至少为3人。
4.1.1.1.2被测零件:零件应从过程中选取并能代表整个工作范围。
对会直接影响测量结果的缺陷零件不应选用。
4.1.1.1.3样品数量和重复读数次数:零件样品数量至少应为5个,重复读数次数即试验次数至少为2次。
对每一个零件进行编号、定位。
注:对大或重的零件可选较少的样品和较多试验次数4.1.1.2制定操作程序和应用表格4.1.1.2.1确保每一位评价人都采用相同的方法,按规定的测量步骤测量特征尺寸。
测量系统分析(MSA)计数型测量系统研究

测量系统分析(MSA)计数型测量系统研究计数型测量系统研究计数型测量系统属于测量系统中的一类,是一种测量数值为有限的分类数量的测量系统,它与测量结果是连续值的计量型测量系统不同。
最常见的是通过/不通过量具,只可能有两个结果;其它的计数型测量系统,如目视标准,可能产生5~7个分级,如非常好、好、一般、差、非常差等。
MSA前面所介绍的分析方法不能被用来评价这样的系统。
计数型测量系统研究计数型量具的特点是,把每一个零件同一个特定的限定值进行比较。
如果满足限定值就接受这个零件,反之拒绝零件(如通过/不通过量具)。
多数这种类型的量具以一套标准零件为基础进行设定接受与拒绝。
与计量型量具不同的是,这个计数型量具不能指出一个零件有多好或多坏,只能指出零件可接受或拒绝。
计数型测量系统研究-范例计数型测量系统研究-范例表格中的“1”指定为可接受判断,“0”指定为不可接受判断。
表格中的基准判断和计量基准值不预先确定。
表格中的“代码”列还用“-”、“+”、“x”显示了零件是否在第Ⅲ,Ⅱ,Ⅰ,区域。
计数型测量系统研究-范例假设检验分析-交叉表方法由于研究人员不知道零件的基准判断值,他们开发了交叉表比较每个评价人之间的差异。
计数型测量系统研究-范例2016-11-24陈瑞泉8表中(期望的计算)值的计算过程如下:(44+3)(3+97)/150=31.3(6+97)(97+3)/150=68.7(3+44)(44+6)/150=15.7(97+6)(6+44)/150=34.3计数型测量系统研究-范例上述这些表格的目的是确定评价人之间意见一致的程度。
为了确定评价人一致的水平,研究人员用科恩的Kappa来测量两个评价人对同一目标评价值的一致程度。
1值表示完全一致,0值表示一致程度不比偶然的要好。
kappa只用于两个变量具有相同的分级值和相同的分级数的情况。
计数型测量系统研究-范例kappa是一个评价人之间一致性的测量值。
检验是否沿对角线格子中的计数(接收比率一样的零件)与那些仅是偶然的期望不同。
计数型测量系统分析(MSA)

计数型测量系统分析(MSA)计数型测量系统的最大特征是其测量值是一组有限的分类数,如合格、不合格、优、良、中、差、极差,等等。
当过程输出特性为计数型数据时,测量系统的分析方法会有所不同,一般可以从一致性比率和卡帕值两个方面着手考虑计数型测量系统分析。
➢计数型测量系统分析——一致性比率一致性比率是度量测量结果一致性最常用的一个统计量,计算公式可以统一地概括为:一致性比率=一致的次数/测量的总次数根据侧重点和比较对象的不同,又可以分为4大类。
1. 操作者对同一部件重复测量时应一致,这类似于计量型测量系统的重复性分析。
每个操作者内部的计数型测量系统都有各自的一致性比率。
2. 操作者不但对同一部件重复测量时应一致,而且应与该部件的标准值一致(若标准值已知),这类似于计量型系统的偏倚分析。
将每个操作者的计数型测量系统的结果与标准值相比较、分析,又有各自不同的一致性比率。
3. 所有操作者对同一部件重复测量时应一致,这类似计量型测量系统的再现性分析,操作者计数型测量系统分析之间有一个共同的一致性比率。
4. 各操作者不但对同一部件重复测量时应一致,而且应与该部件的标准值一致(若标准值已知)。
通常,使用这种一致性比率来衡量计数型测量系统的有效性。
一般说来,一致性比率至少要大于80%,最好达到90%以上。
当值小于80%,应采取纠正措施,以保证测量数据准确可靠。
➢计数型测量系统分析——卡帕值(k)K(希腊字母,读音kappa,中文为卡帕)是另一个度量测量结果一致程度的统计量,只用于两个变量具有相同的分级数和分级值的情况。
它的计算公式可以统一的概括为:以上公式中,P0为实际一致的比率;P e为期望一致的比率。
K在计算上有两种方法:Cohen 的k和Fleiss的k。
K的可能取值范围是从-1到1,当k为1时,表示两者完全一致;k为0时,表示一致程度不比偶然猜测好;当k为-1时,表示两者截然相反,判断完全不一致。
通常,k为负值的情况很少出现,下表归纳了常规情况下k的判断标准。
计数型测量系统分析报告MSA范本(带公式未加密)

5 5.15 5.02 5.05 4.98 5.07 5.05 5.16 5.15 5.13 5.12 5.17 5.08 5.08 5.06 5.07 5.01 4.99
5
代码
+ + + + + × + + + × + × + × + × + + + + × + + + × × + + × + + + × + + + × + × + + + + × +
核准:
基准
1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1 1 0 1
基准值
5.12 5.08 4.94 5.12 5.12 5.14
5 5.15 5.02 5.05 4.98 5.07 5.05 5.16 5.15 5.13 5.12 5.17 5.08 5.08 5.06 5.07 5.01 4.99
NO:
XXXXX
量具名称: 外形检
量具编号: MS13H
被测产品: CL-
被测参数下限:
5
零件
操作者A:
1
2
1
1
1
2
1
1
3
0
0
4
1
1
5
1
1
6
1
MSA测量系统分析课件(PPT 77页)

量步骤测量特征尺寸;
3.测量系统研究注意事项
1)测量必须按照随机顺序进行; 2)不应让评价人知道正在检查零件的编号; 3)测量读数应估计到可得到的最接近的数字; 4)研究工作应由知其重要性且仔细认真的人员进行; 5)每一位评价人在整个研究过程中应采用相同的测量
b) 指定1位操作人员在不知情的状况下使用校验合格的量具,共 测了5周(25个子组)以上个零件进行测量, 并重复3次,将操 作员所读数据进行记录, 研究其设备的稳定性。
c) 试验完后, 测试人员将量具测出数据计算均值、极差和控制限, 并作成均值极差控制图。
d) 计算结果均值、极差及控制限等。
计算出 相应的 数值。
方法;
测量系统分析方法分类
❖ 计量型MSA
1) 稳定性-均值极差法; 2) 偏倚-独立样本法; 3) 偏倚-均值极差法; 4) 线性-一元线性回归法; 5) GRR-均值极差法; 6) GRR-Crossed ANOVA; 7) GRR-Nested ANOVA;
❖ 计数型MSA
1) 解析法; 2) 交叉表法; 3) 信号探测法;
❖ 应首先的方法是 ? 其理由是?
方法 1 : 比起变差,解决平均的变化更为容易。
2.测量系统研究准备
1)计划要使用的方法; 2)确定评价人的数量、样品数量及重复读数次数; 3)从日常操作该仪器的人中挑选评价人; 4)样品必须从过程中选取并代表整个工作范围; 5)仪器的分辨力应允许至少读取特性的预期过程变差
第二个刻度的分辨率比两个部件之间的 差异要小,部件将产生不同的测量结果。
测量系统的有效分辨率( discrimination)
要求不低于过程变差或允许偏差( tolerance)的十分之一 零件之间的差异必须大于最小测量刻度 不同数据分级(ndc)的计算为
检具如何进行测量系统分析MSA

如何对检具进行测量系统分析?QS-9000是美国三大汽车公司为统一供应商质量管理体系而推行的采购要求。
出于美国汽车工业的影响和地位,QS-9000在世界范围内被广泛推广运用,尤其是为整车生产企业提供零部件、生产材料及加工的企业。
随着ISO9000标准被国内各行业广泛采用,近几年来,QS-9000作为体现汽车行业特点的质量体系标准,也逐渐得到了国内汽车行业的认同。
国内主要整车生产企业在以ISO9000质量体系作为对其供应商要求的基础上,增加了许多特殊要求,一些整车生产企业对其供应商提出了按QS-9000建立质量体系的要求,并以此作为决定供应商配套资格或其采购份额的条件。
本人在QS-9000认证审核中,发现以下问题较为普遍,在此提出,以供参考。
一、关于标准要求1、可行性评审可行性评审在什么阶段进行,应评审那些内容?标准中对可行性评审的要求是:“供方在签定生产某种产品合同之前,应研究并确定该产品的制造可行性。
……可行性评审应采用产品质量先期策划和控制计划(APQP)参考手册中…小组可行性承诺‟来形成文件”。
首先,从以上内容可知,可行性评审是在签定合同之前进行的。
APQP参考手册在产品开发所经历的五个阶段中第二阶段2.13条对…小组可行性承诺‟作出解释。
如果供应商承担设计责任,那么,所有的设计过程都可理解为为满足顾客要求所进行的合同评审过程。
由于产品设计和过程开发是同步进行的,在产品图样和/或规范输出后,过程开发也到了一定阶段,这时,横向协调小组通过对产品图样和/或规范以及过程阶段性开发输出结果的分析,对产品是否满足顾客的要求、设备和工装成本、材料、过程能力等内容进行评审,从而对产品制造可行性进行判定。
可行性评审可视为合同评审的一部分。
2、分承包方的零件批准(PAP)标准中规定供方应对其分承包方采用一种零件批准程序,批准的方法可按PPAP或其它零件批准(PAP)进行。
一个企业的分承包方可能会涉及到提供零部件和原材料的不同供方。
MSA计数型测量系统分析指导书

(MSA)计数型测量系统研究分析作业指导书批准:审核:编制:受控状态:分发号:XXXXXXXXXXXX发布XXXXXXXXX实施计数型测量系统研究分析作业指导书1目的为了配备并使用与要求的测量能力相一致的测量仪器,通过适当的统计技术,对计数型测量系统进行分析研究,使测量结果的不确定度已知,为准确评定产品提高质量保证。
2适用范围适用于公司使用的计数型测量仪器的测量系统的分析研究。
3职责3.1检验科负责确定过程所需要的计数型测量仪器,并定期校准和检定,对使用的测量系统进行研究分析,对存在的异常情况及时采取纠正预防措施。
3.2工会负责根据需要组织和安排计数型测量系统分析所需应用技术的培训。
3.3生产科配合对测量仪器进行测量系统分析。
4计数型测量系统简介计数型测量系统是一种测量数值为一有限的分类数量的测量系统,它与能获得一连串数值结果的计量型测量系统截然不同。
通/止规(go/no go gage )是最常用的量具,它只有两种可能的结果;其它的计数型测量系统,目标 如目视标准,可能产生五到七个分类,如非常好、好、 一般、差、非常差。
所以,针对计量性测量系统所描述的分析方法不能用于评价这样的系统。
当使用任何测量系统进行决策时,都存在一定程度的风险。
这些方法不能量化测量系统变异性,只有当顾客同意的情况下才能使用。
选择和应用于这些技术应以基于一个良好的统计实践,了解影响产品和测量过程变差源,以及错误决定最终顾客的影响。
计数型测量系统的变差来源,应该通过利用了人为因素和人机工程学的研究结果使之最小化。
5研究分析方法5.1某生产过程处于统计受控状态,其性能指数为Pp=PpK=0.5,这是不可接受的。
由于过程正在生产不合格的产品,于是被要求采取遏制措施,以便从生产过程中挑出不可接受的产品。
见图1:图1过程范例5.2具体的遏制行动是,过程小组采用了一个计数型量具,来对每一个零件与一个指定的限定值进行比较。
如果零件满足限定值就可接受该零件,不满足的零件则拒收(如通/止量具)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
零件 个数= 50
C-2 C-3 基准 111 111 000 000 000 001 011 111 000 111 111 100 111 001 111 111 111 111 111 111 101 100 111 111 000 010 111 111 111 000 111 111 111 110 111
0.45231 x 0.545604 x 0.529065 + 0.514192 + 0.599581 0.547204 x 0.502436 + 0.521642 + 0.523754 + 0.561457 x 0.503091 +
0.50585 + 0.487613 + 0.449696 x 0.498698 +
A-2 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 0 1
A-3 1 1 0 0 0 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 0 1 1 1 0 0 1 1 1 0 1 1 1 1 1
B-1 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1
注意: 1) 评价人自 己在所有试验 上都一致 2)评价人在 所有试验上都 与基准一致 3) 所有评价 人自己保持一 致,两两间一 致 4)所有评价 人自己和两两 间一致并且于 基准一致 5) UCI和LCI 分别是上、下 置信区间边界 线
A B C
0 1
0.94
计算 期望的计算 计算 期望的计算 计算 期望的计算
很好
评价人 A 50 42
% 评价人 1 评价人 B
50 45
92.83% 0.84
70.89%
96.67% 0.9
78.19%
评价人 C 50 40
89.97% 0.8
66.28%
显著性水平= 0.05 得分与计数 2
评价人 A 评价人 B 评价人 C
50
50
50
42
45
40
0
0
0
0
0
0
8
5
10
92.83%
96.67%
89.97%
0.84
0.9
0.8
70.89%
78.19%
66.28%
系统有效得分 3 50 39
0.884734154 0.78
0.640388012
系统有效得分与计数 4 50 39
0.884734154 0.78
0.640388012
有效性
漏发警报比例
误发警报比例
0.84 可接受边缘 0.9 可接受 0.8 可接受边缘
8
92
34
66
51
99
51
99
kappa= 0.776119403
总计
50 50 100 100 150 150
A 0.862944162 0.776119403
很好 很好
B 0.862944162
0.788007268
很好 -
很好
C 0.776119403 0.788007268
-
很好 很好
-
Pr(不合格 |
0.0625 0.0625
0.125
不可接受 不可接受 不可接受
0.049019608 可接受 0.019607843 可接受 0.088235294 可接受边缘
评价人数 3
基准值 代码 0.476901 + 0.509015 + 0.576459 0.566152 -
0.57036 0.544951 x 0.465454 x 0.502295 + 0.437817 0.515573 + 0.488905 + 0.559918 x 0.542704 + 0.454518 x 0.517377 + 0.531939 + 0.519694 + 0.484167 + 0.520496 + 0.477236 +
基准
0
1
总计
0
计算
45
2
47
期望的计算
15.04
31.96
47
1
计算
3
100
103
期望的计算
计算
期望的计算
0.966666667
Pe= 0.5672
32.96
70.04
103
48
102
150
48
102
150
kappa= 0.922982132
0 1
0.9
Pr(不合格 |
判不合格)= 0.026143618
基准
0
1
计算
42
9
期望的计算
16.32
34.68
计算
6
93
期望的计算
31.68
67.32
计算
48
102
期望的计算
48
102
Pe= 0.5576
kappa= 0.773960217
总计
51 51 99 99 150 150
A 0.878787879
很好
B 0.922982132
很好
C 0.773960217
Pe= 0.562222222
B
0
1
44
6
15.66666667 34.33333333
3
97
31.33333333 68.66666667
47
103
47
103
kappa= 0.862944162
总计
50 50 100 100 150 150
0
计算
期望的计算
1
计算
期望的计算
计算
期望的计算
0.906666667
47 1 1 1 1 1 1 1 1 1 1 0.486379 + 48 0 0 0 0 0 0 0 0 0 0 0.587893 49 1 1 1 1 1 1 1 1 1 1 0.483803 + 50 0 0 0 0 0 0 0 0 0 0 0.446697 -
A与B交叉表
A
总计 Po=
B与C交叉表
计数型测量系统研究
零件 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
A-1 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1
36 1 1 0 1 1 1 1 0 1 1 0.543077 x 37 0 0 0 0 0 0 0 0 0 0 0.409238 38 1 1 1 1 1 1 1 1 1 1 0.488184 + 39 0 0 0 0 0 0 0 0 0 0 0.427687 40 1 1 1 1 1 1 1 1 1 1 0.501132 + 41 1 1 1 1 1 1 1 1 1 1 0.513779 + 42 0 0 0 0 0 0 0 0 0 0 0.566575 43 1 0 1 1 1 1 1 1 0 1 0.46241 x 44 1 1 1 1 1 1 1 1 1 1 0.470832 + 45 0 0 0 0 0 0 0 0 0 0 0.412453 46 1 1 1 1 1 1 1 1 1 1 0.493441 +
判不合格)= 0.049224841
基准
0
1
0
计算
45
5
期望的计算
16
34
1
计算
3
97
期望的计算
32
68
计算
48
102
期望的计算
48
102
0.946666667
Pe= 0.56
kappa= 0.878787879
总计
50 50 100 100 150 150
Pr(不合格 |
判不合格)= 0.114600328
B
总计 Po=
Байду номын сангаасA与C交叉表
A
总计 Po=
Kappa A B C
A与基准判断 交叉表
A
总计 Po=
B与基准判断 交叉表
B
总计
Po=
C与基准判断 交叉表
C
总计
Po=
Kappa
来源 总受检数 符合的 错误地否定 错误地肯定 混合的 95%置信上限 计算得分 95%置信下限
总受检数 一致数 95%置信上限 计算得分 95%置信下限
Pe= 0.559733333
C
0
1
42
5
15.98
31.02
9
94
35.02
67.98
51
99
51
99
kappa= 0.788007268
总计
47 47 103 103 150 150
0 1
0.9
计算 期望的计算 计算 期望的计算 计算 期望的计算
Pe= 0.553333333
C
0
1
43
7
17
33
试验 次数= 3
数据表 B-2 B-3 C-1
111 111 000 000 000 101 111 111 000 111 111 000 111 111 111 111 111 111 111 111 010 101 111 111 000 000 111 111 111 010 111 111 111 010 111
