工程力学第06讲 第4章 刚体系的平衡 第五章 空间任意力系
工程力学课后习题标准答案静力学基本概念与物体受力分析标准答案
第一章静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。
1.1试画出下列各物体（不包括销钉与支座）的受力图。
解：如图1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。
解：如图1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题1.3图所示。
在定滑轮上吊有重为W的物体H。
试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。
解：如图1.4题1.4图示齿轮传动系统，O1为主动轮，旋转方向如图所示。
试分别画出两齿轮的受力图。
解：1.5结构如题1.5图所示，试画出各个部分的受力图。
解：第二章汇交力系2.1在刚体的A点作用有四个平面汇交力。
其中F1＝2kN，F2=3kN，F3=lkN，F4=2.5kN，方向如题2.1图所示。
用解读法求该力系的合成结果。
解2.2 题2.2图所示固定环受三条绳的作用，已知F1＝1kN，F2=2kN，F3=l.5kN。
求该力系的合成结果。
解：2.2图示可简化为如右图所示2.3 力系如题2.3图所示。
已知：F 1＝100N ，F 2=50N ，F 3=50N ，求力系的合力。
解：2.3图示可简化为如右图所示2.4 球重为W ＝100N ，悬挂于绳上，并与光滑墙相接触，如题2.4图所示。
已知，试求绳所受的拉力及墙所受的压力。
解：2.4图示可简化为如右图所示墙所受的压力F=57.74N2.5 均质杆AB 重为W 、长为 l ，两端置于相互垂直的两光滑斜面上，如题2.5图所示。
己知一斜面与水平成角，求平衡时杆与水平所成的角及距离OA 。
解：取 AB 杆为研究对象，受力如图所示由于杆件再三力作用下保持平衡，故三力应汇交于C 点。
AB 杆为均质杆，重力作用在杆的中点，则W 作用线为矩形ACBO 的对角线。
由几何关系得 所以 又因为 所以2.6 一重物重为20kN ，用不可伸长的柔索AB 及BC悬挂于题2.6图所示的平衡位置。
工程力学第4章 力系的平衡
2
即空间一般力系平衡的解析条件是力系中所有各力 在任一轴上投影的代数和为零，同时力系中各力对任一 轴力矩的代数和为零。式（4.2）称为空间一般力系的平 衡方程（equationsofequilibrium ofthreedimensionalforcesystem inspace）。 应当指出，由空间一般力系平衡的解析条件可知， 在实际应用平衡方程时，所选各投影轴不必一定正交， 且所选各力矩轴也不必一定与投影轴重合。此外，还可 用力矩方程取代投影方程，但独立平衡方程总数仍然是 6个。
30
4.3.1 有主次之分物体系统的平衡 有主次之分的物体系统，其荷载传递规律是：作用 在主要部分上的荷载，不传递给相应的次要部分，也不 传递给与它无关的其他主要部分；而作用在次要部分上 的荷载，一定要传递给与它相关的主要部分。
31
32
据此，先分析次要部分BD，其受力图如图4.11（b） 所示。建立图示参考系Oxy，列平衡方程并求解。由于 本题只要求出D处的约束反力，而不必要求出B处的约 束反力，故
12
13
建立参考系 Bxy，列平衡方程，求未知力。
14
15
例4.ቤተ መጻሕፍቲ ባይዱ 图4.5所示为一管道支架，其上搁有管道，设 每一支架所承受的管重G1=12kN，G2=7kN，且架重不计。 求支座A和C处的约束反力，尺寸如图所示。
16
17
解 取刚架AB为研究对象，其上所受力有：已知的 集中力F、集度为q的均布荷载，集中力偶；未知的3个 约束反力FAx，FAy，MA。刚架AB的受力图如图4.6（b） 所示。各力组成一平面一般力系。建立图示Oxy坐标系， 列平衡方程求解
9
2.平面一般力系平衡方程的其他形式 （1）二矩式平衡方程
河南理工大学《工程力学》课件5 空间任意力系
工程力学
第五章 空间任意力系
1) 空间任意力系简化为平衡的情形 当空间任意力系向一点简化时出现 主矢F'R＝0，主矩 MO ＝ 0 ，这是空间任意力系平衡的情形。 2) 空间任意力系简化为一合力偶的情形 F'R＝0，MO≠0 简化结果为一个与原力系等效的合力偶，其合力偶 矩矢等于对简化中心的主矩。此时力偶矩矢与简化 中心位置无关。
4R yC = 3π
河南理工大学土木工程学院
工程力学
第五章 空间任意力系
∑F
∑M
z
x
= 0， FA+FB+FC－F－W =0
( F ) = 0 ，1.5 m·FA－0.6m·F－0.5 m·W = 0 1.5 0.6m·F 0.5
∑M
y
( F ) = 0 ，－0.5 m·FA－1m·FB +0.4m·F+0.5 m·W = 0
从而求得 FA =5.667kN，FB =3.667kN，FC =5.666kN
y=
3 r 2
, z=h
M x ( F ) = yFz − zFy =
F ( h − 3r ) 4
M y ( F ) = zFx − xFz =
3 F (r + h) 4
1 M z ( F ) = xFy − yFx = − Fr 2
河南理工大学土木工程学院
工程力学
第五章 空间任意力系
§5-3 空间任意力系向一点简化
0 ∑ F =， F + F − ( F + F )cosθ = 0 0 ∑ M (F ) =， FBz (a + b + c) − ( F3 + F4 )(a + c)cosθ = 0
《工程力学(静力学)》全套精品课件第5章-空间任意力系
F2
A FAy
y
FAx
B
xW
C FC
谢传锋:工程力学(静力学)
7
静力学
§2 空间任意力系的平衡条件
方法二：六矩式方程
M Cy 0 FAz M x 0 F2 M z 0 FC M y 0 F1 M Dz 0 FAx
M Cz 0 FAy
谢传锋:工程力学(静力学)
z
n
n
•主矢 FR Fi Fi '
i1
i1
n
n
•主矩 MO Mi ri Fi
i1
i1
谢传锋:工（程与力简学(静化力点学无) 关）
（与简化点有关）
4
静力学
§2 空间任意力系的平衡条件
一、空间任意力系的平衡条件
空间任意力系简化 {F1, F2 ,, Fn} {FR , MO}
平衡
FR 0, MO 0
n
n
FR Fi ' Fi
i1
i1
n
n
MO Mi ri Fi
i1
i1
FR ( Fx )2 ( Fy )2 ( Fz )2 MO ( MOx )2 ( MOy )2 ( MOz )2
空间任意力系平衡的条件：
FR 0
Fx 0
Fy 0 MO 0
M Ox (F ) 0 M Oy (F ) 0
谢传锋:工程力学(静力学)
x
Fz M
0 x (F
)
0
M y (F ) 0
z
2
A
By
W
C
6
静力学
§2 空间任意力系的平衡条件
z
解：取板为研究对象 画受力图
清华大学本校用理论力学课件5-6 刚体系和变形体的平衡
刚体系和变形体的平衡
第5章
力 系 简 化 与 平 衡 问 题
平衡方程不是非刚体平衡 的充分条件，但却是非刚 体平衡的必要条件。
刚化原理（硬化原理）：已知非刚体处于平 衡状态，如果把它刚化（想象成刚体），则 平衡条件不变。
解决变形体的平衡还需要考虑变形条件。
例1
第5章
力 系 简 化 与 平 衡 问 题
(2) 再考虑连续梁整体AC
M A 0 mA 2( m qa 2 )
Rx 0 X A 0
B XB
q 2a
YC
(3) 校核
Ry 0 YA 2qa m YA m A a A XA
m
B
C
YC
M C m q 2a 2a mA YA 3a 0
第5章
各杆在端点用光滑铰链相连接，连接点称
力 系 简 化 与 平 衡 问 题
为节点
桁架的实际节点
理想节点
焊接或铆接，杆的端点不 能转动，可承受力矩。
光滑铰链，不能 承受力矩
杆的自重相对载荷可以忽略不计 载荷及支座反力均作用在节点上。
在以上假设下各杆均为二力杆
关于平面桁架的构成
第5章
简单桁架(三角形扩大法则)
北京首都国际机场航空港内钢结构飞机库 返回
塔架
第5章
力 系 简 化 与 平 衡 问 题
卫星发射塔。1983年 8月19日发射科学试 验卫星。
塔架
第5章
力 系 简 化 与 平 衡 问 题
返回
起重机
第5章
力 系 简 化 与 平 衡 问 题
ZT120型塔式起重机
返回
平面桁架的基本假设 (理想桁架)
工程力学(北航版)——第四章：平面任意力系
∑mA(F)=0
Q(6 − 2) − P ⋅ 2 + FB (2 + 2) = 0
限制条件为： 限制条件为： FB ≥ 0
解得： 解得：
Q≤350 kN
因此保证空、满载均不倒 应满足如下关系 应满足如下关系： 因此保证空、满载均不倒Q应满足如下关系
75 kN≤Q≤350 kN
当W=400KN时，Q的范围？ W=400KN时 的范围？
MO =
∑M
Oi
方向： 方向 方向规定 +
M A ≠ MO
7
简化中心： 简化中心 (与简化中心有关)
3. 平面一般力系的合成结果
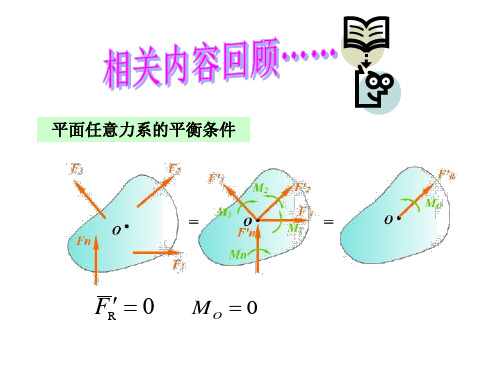
′ 初步简化结果： 初步简化结果：主矢 FR ，主矩 MO，下面分别讨论。
′ ， ① FR =0， MO =0，则力系平衡,下节专门讨论。 ，
′ ② FR = 0 , M O ≠ 0 即 简 化 结 果 为 一 力 偶 M = M O = ∑MOi， 此 时
刚体等效于只有一个力偶的作用（因为力偶可以在刚 体平面内任意移转，故这时，主矩与简化中心O无关。） ③ FR ≠0, O =0, ′ ≠0,M =0,即简化为一个作用于简化中心的合力。这时，
′ 简化结果就是合力（这个力系的合力）, FR = FR 。（此时 ,
与简化中心有关，换个简化中心，主矩不为零）
8
′ ≠0,M ≠0,为最一般的情况 此种情况还可以继续简 为最一般的情况。 ④ FR ≠0, O ≠0,为最一般的情况。此种情况还可以继续简
化为一个合力 FR 。
′ F R = F ′ R = − FR′ ′ M O = FR ⋅ d
F'R F'R F''R A FR FR
工程力学基础第4章空间任意力系
（3）只要保持力偶矩不变，力偶可在其作用面内 任意移转，且可以同时改变力偶中力的大小与力偶 臂的长短，对刚体的作用效果不变。
=
=
=
M
(
F1
,
F1)
rBA
F1
(4)只要保持力偶矩不变，力偶可从其所在平面 移至另一与此平面平行的任一平面，对刚体的 作用效果不变。
=
=
F1 F1 F2
(4-2)
称为空间汇交力系的平衡方程。
§4–2 力对点的矩和力对轴的矩
1、 力对点的矩以矢量表示 ——力矩矢 三要素：
(1）大小:力F与力臂的乘积
(2)方向:转动方向 (3)作用面：力矩作用面。
又 则
（4–3）
力对点O的矩
在
三个坐标轴上的投影为
（4–5）
（4–4）
动画
第5章 空间任意力系
力对点的矩
例题
空间任意力系
例题1
解：
由图示可以求出力F 在 各坐标轴上的投影和力F 作 用点C 的坐标分别为：
x= a = 4 m
y= b = 6 m z= c =－3 m
例题
空间任意力系
例题1
则可求得力F 对坐标轴之矩 以及对原点O之矩的大小和方向。
力F 对坐标轴之矩为：
力F 对原点O之矩大小：
称为力系的主矢 空间力偶系的合力偶矩
称为空间力偶系的主矩 由力对点的矩与力对轴的矩的关系，有
式中，各分别表示各
力
对 ， ， ,轴的矩。
动画
第5章 空间任意力系
空间力向任一点的简化
动画
第5章 空间任意力系
空间力系向任一点的简化
工程力学第五章习题答案
工程力学第五章习题答案工程力学第五章习题答案工程力学是一门研究物体受力和变形的学科，它在工程实践中起着重要的作用。
第五章是工程力学课程中的重要章节，主要讲述了刚体平衡和平面力系的平衡。
在这一章中，有许多习题需要我们进行解答和分析。
下面我将为大家提供一些工程力学第五章习题的答案，希望能对大家的学习有所帮助。
1. 习题：一个悬臂梁的长度为L，梁的质量为m，质心距离支点的距离为a。
求悬臂梁在支点处的支反力和力矩。
答案：根据平衡条件，悬臂梁在支点处的支反力应该等于悬臂梁的重力，即F= mg。
而力矩可以通过计算重力的力矩和质心的力矩来求解。
重力的力矩为0，因为支点处的支反力通过支点，所以力臂为0。
质心的力矩为Ma，即力矩M = mga。
2. 习题：一个平面力系由三个力组成，分别是F1 = 10N，F2 = 5N，F3 = 8N。
已知F1与F2夹角为60度，F2与F3夹角为120度，求力系合力的大小和方向。
答案：首先，我们需要将力系中的三个力进行分解。
根据三角函数的知识，可以得到F1在x轴和y轴上的分量分别为F1x = 10N * cos60°，F1y = 10N *sin60°；F2在x轴和y轴上的分量分别为F2x = 5N * cos120°，F2y = 5N *sin120°；F3在x轴和y轴上的分量分别为F3x = 8N * cos0°，F3y = 8N * sin0°。
然后，将各个力在x轴和y轴上的分量相加得到合力的分量Fx和Fy。
最后，利用勾股定理可以求得合力的大小F和方向θ。
3. 习题：一个物体质量为m，放在一个斜面上，斜面的倾角为θ。
已知斜面的摩擦系数为μ，求物体在斜面上的静摩擦力的大小和方向。
答案：物体在斜面上的重力可以分解为垂直于斜面的分力mgcosθ和平行于斜面的分力mgsinθ。
根据静摩擦力的定义，静摩擦力的大小不超过μmgcosθ。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§4 刚体系的平衡、静定与静不定
方法二： 解：1、研究整体（刚化），画受力图 B
FAy A
F
60
0
MA
FC C
F
x
0
FAx
F Ax
M
3、再研究整体
2、研究BC杆，画受力图
FBy
B
FBx
F
60
0
FC
F
y
0
0
FAy
a
B
C
FC
M
0
M
A
MA
§4 刚体系的平衡、静定与静不定
例：已知 F，求 AG 杆上的约束力。
平衡
FR Fi ' Fi
n n i 1 n i 1 n
FR 0 , M O 0
FR ( Fx ) 2 ( Fy ) 2 ( Fz ) 2 M O ( M Ox ) 2 ( M Oy ) 2 ( M Oz ) 2
M O M i ri Fi
A
a D a G
F
2a E a
B
a 解：1、研究AG杆， 画受力图.
C
H A
O
F
FDx
FDy
D
FGy
M M
D
(F ) 0 FGx
G
(F ) 0 FDx
FGx
G
§4 刚体系的平衡、静定与静不定
A C a D a G
F
2a E a
B a H
2、研究图示构件，画受力图
B C
FDx D
§4 刚体系的平衡、静定与静不定
一、刚化原理
变形体在某一力系作用下处于平衡，若将处于平衡态时的变 形体换成刚体（刚化），则平衡状态不变。
F
（a）
F
F
（b）
F
刚体的平衡条件是变形体平衡的必要条件
§4 刚体系的平衡、静定与静不定
二、刚体系的平衡问题
刚体系平衡 系统中每个刚体平衡 例：已知 F，M ，AB = BC = L ，F 作用在BC杆的中点， 求：A、C 处的约束力。 A B
0 FAx
Cz
0 FAy
§2 空间任意力系的平衡条件
思考题：下列方程中的投影轴和取矩轴不是同一根轴， 该方程组能否作为空间任意力系的平衡方程。
Fx 0 Fy 0 Fz 0
M x ' ( F ) 0 M y ' ( F ) 0 M z ' ( F ) 0
问题：上述方程中x,y,z 是否必须正交？x’,y’,z’轴是否必须正交？
i 1 i 1
空间任意力系平衡的条件：
M Ox ( F ) 0 M x ( F ) 0 Fx 0 FR 0 Fy 0 M O 0 M Oy ( F ) 0 M y ( F ) 0 M Oz ( F ) 0 M z ( F ) 0 Fz 0
FR 一个作用在O点上的力, MO 一个作用在刚体上的力偶
•主矢 FR Fi Fi '
i 1 i 1
n
n
•主矩 M O M i ri Fi
i 1 i 1
n
n
（与简化点无关）
（与简化点有关）
§2 空间任意力系的平衡条件
一、空间任意力系的平衡条件
空间任意力系简化 {F1 , F2 ,, Fn } {FR , M O }
F Ax
F2
C
y
FC
B
x
W
§2 空间任意力系的平衡条件
方法二：六矩式方程
z
M
Cy
0 FAz
F1
FAz A FAy
F Ax
F2
M x 0 F2 M z 0 FC
x
D
C
FC
y
B
W
M y 0 F1
M M
Dz
•在同一平面内 最多取两个平行的取矩轴 •在空间内 最多取三个平行的取矩轴
F
600
C
M
§4 刚体系的平衡、静定与静不定
A B
F
60
0
C
M
FAy A
方法一: 解：以每个物体 为研究对象, 画 其受力图。
Fx 0 Fy 0 M 0 A
M
B
FBx
MA
F Ax a
FBy FBy
B
FBx
F
60
0
FC
a
C
Fx 0 Fy 0 M 0 B
§2 空间任意力系的平衡条件 z
解：取板为研究对象 画受力图 方法一：基本方程
x
1 A
2
C
B y
W
z
Fx 0 Fy 0 Fz 0
M x ( F ) 0 M y ( F ) 0 M z ( F ) 0
F1
FAz A FAy
E
2a a a O
H
O
FCG
a
FDy
A
F
FDx
求出 FDy
FH
FDy
D
FGy G
M F
y
p
0 FDy
p
3、再研究AG 杆，求出 FGy
FGx
0 FGy
§4 刚体系的平衡、静定与静不定
思考题：人重W>板重P，若人有足够大的力量，能维持平衡的是
(a)
(b)
A：图(a)
B：图(b)
C:
F
C
M
问题1：对于静不定问题，能否求解出部分未知量 问题2：如何解除多余的约束，使其变为静定问题
§4 刚体系的平衡、静定与静不定
A
工程中的实例
B C D E
G
H
§4 刚体系的平衡、静定与静不定
05年9月8日下午2点06分，朝阳区某工地的塔吊在起吊一些预制板 构件时，第一根钢绳突然被绷断，紧接着吊臂开始变形，并向西南方向 倒下来，但无人员伤亡。
第五章 空间任意力系
•§1 空间任意力系简化 •§2 空间任意力系平衡条件
§1 空间任意力系简化
空间任意力系： 力的作用线在空间任意分布的力系
空间任意力系的实例
§1 空间任意力系简化
空间任意力系向一点简化
Fn
o
C
B AO称为简化点 NhomakorabeaFn'
Mn
FR
F2
M2
F
' 1
O
MO
O
F1
M1 F ' 2
{F1 , F2 , , Fn } {F1 ' , F2 ' , , Fn ' , M1 , M 2 , , M n } {F , M O } R
图(a)和(b)
§4 刚体系的平衡、静定与静不定
三、静定与静不定问题 A
F
B A
M
B
F
M
A
F
M
B
F
A
M
B
•上面图中存在多余的约束
•未知量的数目大于独立平衡方程的数目
§4 刚体系的平衡、静定与静不定
•静 定 问 题： 未知量的数目= 独立平衡方程的数目
•静不定问题： 未知量的数目> 独立平衡方程的数目 思考题：确定图示系统的静定性。 A B
§2 空间任意力系的平衡条件
二、空间平行力系平衡的条件：
z
空间问题
o
x
y
Fz 0 M x ( F ) 0 M y ( F ) 0
z
例：重为W 的均质正方形板
水平支承在铅垂墙壁上，求
绳1、2的拉力, BC杆的内力
1
2
A
x
C
B y
和球铰链A的约束力。
W