七年级数学几何证明题三角形

合集下载

初中数学几何题100条秘籍——三角形篇

个三角形外角的位置上，小角处在内角的位置上，再利用外角定理证题.
例：已知 D 为△ABC 内任一点，求证：∠BDC＞∠BAC
证法（一）：延长 BD 交 AC 于 E， ∵∠BDC 是△EDC 的外角， ∴∠BDC＞∠DEC
A
D
E
ቤተ መጻሕፍቲ ባይዱ
同理：∠DEC＞∠BAC ∴∠BDC＞∠BAC
B
CB
证法（二）：连结 AD，并延长交 BC 于 F
求证：∠EAD = 1 (∠C－∠B) 2
证明：∵AE 平分∠BAC
∴∠BAE =∠CAE = 1 ∠BAC 2
∵∠BAC =180°－(∠B＋∠C)
∴∠EAC = 1 [180°－(∠B＋∠C)] 2
∵AD⊥BC
∴∠DAC = 90° －∠C
∵∠EAD = ∠EAC－∠DAC
∴∠EAD = 1 [180°－(∠B＋∠C)]－(90°－∠C) 2
∵∠BDF 是△ABD 的外角， ∴∠BDF＞∠BAD 同理∠CDF＞∠CAD
A
D
E
A D
∴∠BDF＋∠CDF＞∠BAD＋∠BCAD 即：∠BDC＞∠BAC
CB
F
C
A
D
F
C
规律 21.有角平分线时常在角两边截取相等的线段，构造全等三角形.
例：已知，如图，AD 为△ABC 的中线且∠1 = ∠2，∠3 = ∠4，
①AB＋AF＞BD＋DG＋GF
②GF＋FC＞GE＋CE
③DG＋GE＞DE
∴①＋②＋③有
AB＋AF＋GF＋FC＋DG＋GE＞BD＋DG＋GF＋GE＋CE＋DE
∴AB＋AC＞BD＋DE＋CE
注意：利用三角形三边关系定理及推论证题时，常通过引辅助线，把求证的量（或与求

七年级数学典型几何证明50题

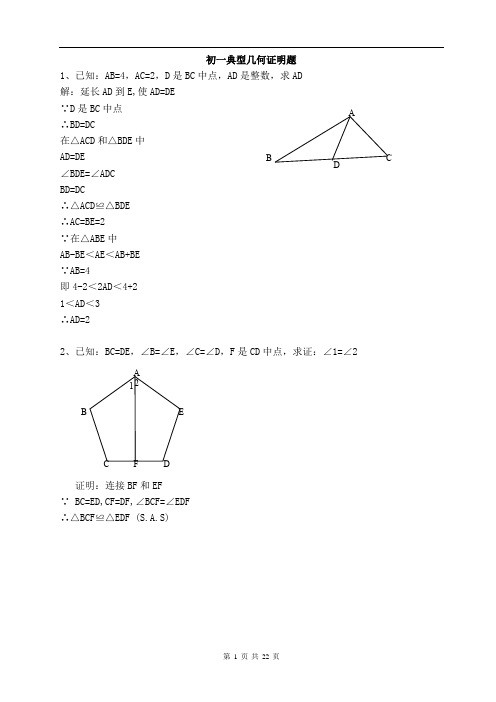
初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF，可得，∠EFD＝CGD DE ＝DC∠FDE＝∠GDC（对顶角） ∴△EFD≌△CGD EF ＝CG ∠CGD＝∠EFD 又，EF∥AB ∴，∠EFD＝∠1 ∠1=∠2 ∴∠CGD＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CBA CDF2 1 EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6、如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

初中数学：利用旋转证明三角形全等综合证明题专题

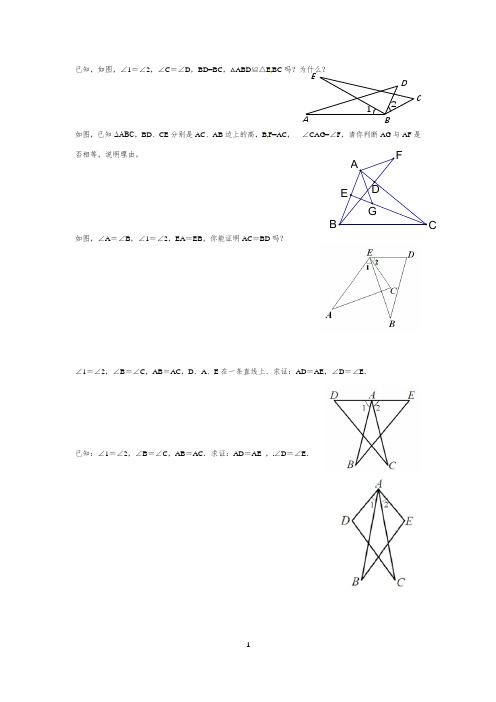
已知，如图，∠1＝∠2，∠C ＝∠D ，BD=BC ，△ABD ≌△E BC 吗？为什么？如图，已知ΔABC ，BD 、CE 分别是AC 、AB 边上的高，B F=AC ， ∠CAG=∠F ，请你判断AG 与AF 是否相等，说明理由。

如图，∠A ＝∠B ，∠1＝∠2，EA ＝EB ，你能证明AC ＝BD 吗？∠1＝∠2，∠B ＝∠C ，AB ＝AC ，D 、A 、E 在一条直线上．求证：AD ＝AE ，∠D ＝∠E ．已知：∠1＝∠2，∠B ＝∠C ，AB ＝AC ．求证：AD ＝AE ，∠D ＝∠E ．ABCDE1 2两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90∘，B，C，E在同一条直线上，连接DC.(1)请找出图2中与△ABE全等的三角形,并给予证明(2)证明：DC⊥BE.如图,在Rt△ABC中,∠ACB=90∘,点D. F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90∘后得CE，连接EF.(1)求证：△BCD≌△FCE；(2)若EF∥CD，求∠BDC的度数。

如图，在正方形ABCD中，△PBC、△QCD是两个等边三角形，PB与DQ交于M，BP与CQ交于E，CP与DQ交于F. 求证：PM=QM.如图,已知长方形ABCD,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB，MD. (1)求证：BE=DC；(2)求证：∠MBE=∠MDC如图所示，已知△ABC和△DCE均是等边三角形，点B，C，E在同一条直线上，AE与BD与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC，FG，其中正确结论的个数是（）①AE=BD；②AG=BF；③FG∥BE；④∠BOC=∠EOC．如图，△ABD与△ACE均为正三角形，且AB＜AC，则BE与CD之间的大小关系是（）如图，在▱ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF，EF，则以下四个结论一定正确的是（）①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边三角形；④CG⊥AE．已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=．下列结论：①△APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD+S△APB=1+；⑤S正方形ABCD=4+．其中正确结论的序号是（）如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF．求证：DE=BF．如图，△ABC中，AB=AC，延长BC至D，使CD=BC，点E在边AC上，以CE，CD为邻边做▱CDFE，过点C作CG∥AB交EF于点G，连接BG，DE．（1）∠ACB与∠GCD有怎样的数量关系？请说明理由；（2）求证：△BCG≌△DCE．如图所示、△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上．（1）求证：△AOC≌△BOD；（2）若AD=1，BD=2，求CD的长．如图，△ACD和△BCE都是等腰直角三角形，∠ACD=∠BCE=90°，AE交CD于点F，BD分别交CE、AE 于点G、H．试猜测线段AE和BD的数量和位置关系，并说明理由．已知：如图，点C是线段AB的中点，CE=CD，∠ACD=∠BCE，求证：AE=BD．已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过E点作AC的垂线，交CD的延长线于点F．求证：AB=FC．如图，分别以Rt△ABC的直角边AC，BC为边，在Rt△ABC外作两个等边三角形△ACE和△BCF，连接BE，AF．求证：BE=AF．如图，已知，等腰Rt△OAB中，∠AOB=90°，等腰Rt△EOF中，∠EOF=90°，连接AE、BF．求证：（1）AE=BF；（2）AE⊥BF．如图，在△ABD和△ACE中，有下列四个等式：（1）AB=AC；（2）AD=AE；（3）∠1=∠2；（4）BD=CE．请你以其中三个等式作为题设，余下的作为结论，写出一个真命题．（要求写出已知，求证及证明过程）如图，P是等边三角形ABC内的一点，连接PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连接CQ．（1）观察并猜想AP与CQ之间的大小关系，并证明你的结论；（2）若PA：PB：PC=3：4：5，连接PQ，试判断△PQC的形状，并说明理由．如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．（1）求证：△ACE≌△BCD；（2）若AD=5，BD=12，求DE的长．如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过E点作EF⊥AE交∠DCE 的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由．如图，△ABC是等腰直角三角形，其中CA=CB，四边形CDEF是正方形，连接AF、BD．（1）观察图形，猜想AF与BD之间有怎样的关系，并证明你的猜想；（2）若将正方形CDEF绕点C按顺时针方向旋转，使正方形CDEF的一边落在△ABC的内部，请你画出一个变换后的图形，并对照已知图形标记字母，题（1）中猜想的结论是否仍然成立？若成立，直接写出结论，不必证明；若不成立，请说明理由．正方形ABCD和正方形AEFG有一公共点A，点G．E分别在线段AD、AB上（如图（1）所示），连接DF、BF．（1）求证：DF=BF，（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG、BE（如图（2）所示），在旋转过程中，请猜想线段DG、BE始终有什么数量关系和位置关系并证明你的猜想．（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°，求证：①AC=BD；②∠APB=60度；（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为_______；∠APB的大小为_______；（3）如图③，在△AOB和△COD中，若OA=k•OB，OC=k•OD（k＞1），∠AOB=∠COD=α，则AC与BD 间的等量关系式为_______；∠APB的大小为_______．如图，四边形ABCD是边长为a的正方形，点G，E分别是边AB，BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F．（1）证明：∠BAE=∠FEC；（2）证明：△AGE≌△ECF；（3）求△AEF的面积．如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连结BE、EC．试猜想线段BE和EC的数量及位置关系，并证明你的猜想．△DAC, △EBC均是等边三角形，AE,BD分别与CD,CE交于点M,N,求证：（1）AE=BD (2)CM=CN (3) △CMN为等边三角形（4）MN∥BC已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2），其中结论正确的个数是（）如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．（1）求证：CE=CF；（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACD=∠DCE=90°，D为AB边上一点．求证：BD=AE．某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．（1）求证：△ADE≌△ABF；已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF（1）如图1，当点D在线段BC上时．求证CF+CD=BC；（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；①请直接写出CF，BC，CD三条线段之间的关系；②若正方形ADEF的边长为2，对角线AE，DF相交于点O，连接OC．求OC的长度．。

北师大版七年级下册数学第四章三角形含答案(综合题)

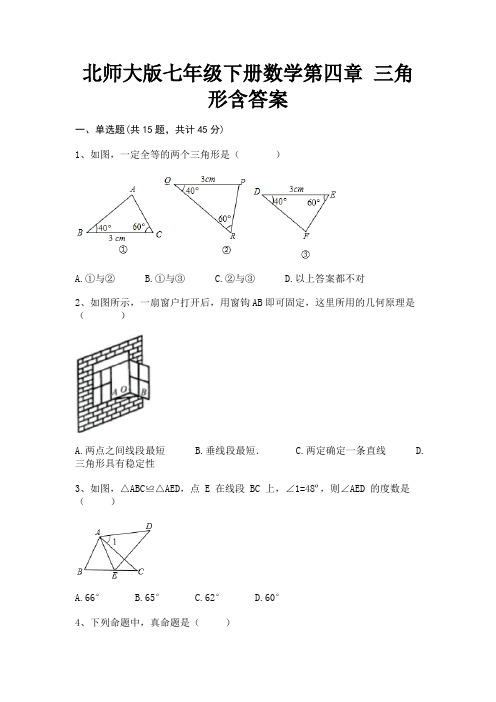
北师大版七年级下册数学第四章三角形含答案一、单选题(共15题，共计45分)1、如图，一定全等的两个三角形是（）A.①与②B.①与③C.②与③D.以上答案都不对2、如图所示，一扇窗户打开后，用窗钩AB即可固定，这里所用的几何原理是（）A.两点之间线段最短B.垂线段最短．C.两定确定一条直线D.三角形具有稳定性3、如图，△ABC≌△AED，点 E 在线段 BC 上，∠1=48º，则∠AED 的度数是（）A.66°B.65°C.62°D.60°4、下列命题中，真命题是（）A.周长相等的锐角三角形都全等B.周长相等的直角三角形都全等C.周长相等的钝角三角形都全等D.周长相等的等腰直角三角形都全等5、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②四边形CGMH是矩形；③△EGM≌△MHA；④S△ABC +S△CDE≥S△ACE；⑤图中的相似三角形有10对．正确结论是（）A.①②③④B.①②③⑤C.①③④D.①③⑤6、下列条件中，不能判定△ABC是直角三角形的是（）A.∠A：∠B：∠C=3：4：5B.∠A ∠B= ∠CC.∠B=50°，∠C=40°D.a=5，b=12，c=137、以下列各组线段长为边，能组成三角形的是( )A.1cm，2cm，3cmB.2cm，3cm，8cmC.5cm，12cm，6cm D.4cm，6cm，9cm8、如图，在等边中，，点在上，且，点是上一动点，连结，将线段绕点逆时针旋转得到线段．要使点恰好落在上，则的长是（）A. B. C. D.9、若△ABC∽△A'B'C'，∠A＝30°，∠C＝110°，则∠B'的度数为（）A.30°B.50°C.40°D.70°10、如图，中，于D，下列条件中：① ；②；③ ；④ ；⑤，⑥ ，一定能确定为直角三角形的条件的个数是（）A.1B.2C.3D.411、如图，，，，，则A.27°B.54°C.30°D.55°12、如图，在△ABC中，∠C=40 ° ，按图中虚线将∠C剪去后，∠1+∠2等于（）.A.140°B.210°C.220°D.320°13、已知m是整数，以4m＋5、2m－1、20－m这三个数作为同一个三角形三边的长，则满足条件的三角形个数有（）A.0个B.1个C.2个D.无数个14、如图，矩形ABCD中，AB＝3，AD＝9，点E在边AD上，AE＝1，过E、D两点的圆的圆心O在边AD的上方，直线BO交AD于点F，作DG⊥BO，垂足为G.当△ABF与△DFG全等时，⊙O的半径为（）A. B. C. D.15、如图所示，在中，，于，，则线段的长是（）A.3B.4C.8D.1二、填空题(共10题，共计30分)16、下列关于两个三角形全等的说法：①面积相等的两个三角形全等；②三条边对应相等的两个三角形全等；③有两角和其中一个角的对边对应相等的两个三角形全等；④有两边和一个角对应相等的两个三角形全等；⑤腰相等的两个等腰三角形一定全等．其中说法正确的是________．（填写序号）17、如图，△ABC中，∠ACB＝90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，则∠ADE＝________°．18、如图，AB＝AC，AD＝AE，∠BAC＝∠DAE，点D在线段BE上．若，∠2＝30°，∠3＝55°则∠1＝________.19、已知等腰三角形的周长为20，腰长为x，则x的取值范围是________ ．20、如图，中有6个条形方格图，图上由实线围成的图形是全等形的有哪几对________21、如图，△ABD与△AEC都是等边三角形，AB≠AC．下列结论中，正确的是________．①BE＝CD；②∠BOD＝60º；③△BOD∽△COE．22、已知，如图，AC=AE，∠1=∠2，AB=AD，若∠D=25°，则∠B的度数为________.23、若等腰三角形的两边长为3cm和7cm，则该等腰三角形的周长为________ cm.24、如图，在△ABC中，已知D，E，F分别为边BC，AD，CE的中点，且，则阴影部分的面积为________ cm2.25、三角形的一边是5，另一边是1，第三边如果是整数，则第三边是________.三、解答题(共5题，共计25分)26、如图，AB∥CD，AB=CD，CE=BF．请写出DF与AE的数量关系，并证明你的结论．27、如图，△ABC中，∠ACB=90°，AC=6，BC=8。

七年级下册数学期末考试几何大题证明必考题

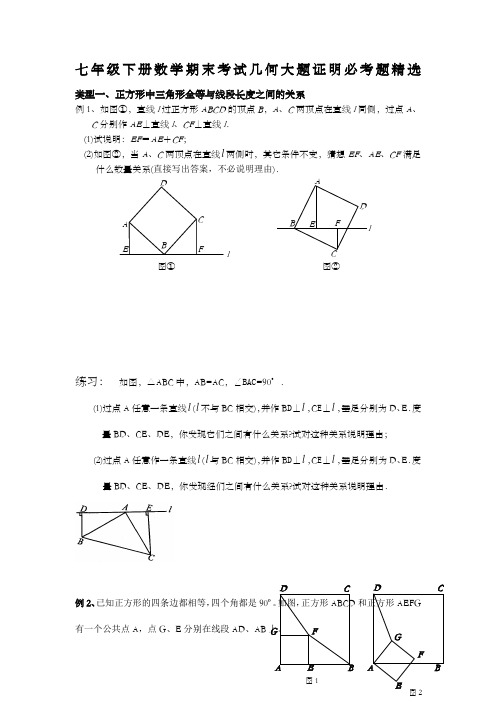
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①，直线l 过正方形ABCD 的顶点B ，A 、C 两顶点在直线l 同侧，过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l ． (1)试说明：EF ＝AE ＋CF ；(2)如图②，当A 、C 两顶点在直线l 两侧时，其它条件不变，猜想EF 、AE 、CF 满足什么数量关系(直接写出答案，不必说明理由)．练习：如图，△ABC 中，AB=AC ，∠BAC =90°．(1)过点A 任意一条直线l (l 不与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现它们之间有什么关系?试对这种关系说明理由； (2)过点A 任意作一条直线l (l 与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现经们之间有什么关系?试对这种关系说明理由．例2、已知正方形的四条边都相等，四个角都是90º。

如图，正方形ABCD 和正方形AEFG 有一个公共点A ，点G 、E 分别在线段AD 、AB 上。

A E B 图1D CG FA BD CG FE图2（1）如图1，连结DF 、BF ，说明：DF ＝BF ；（2）若将正方形AEFG 绕点A 按顺时针方向旋转，连结DG ，在旋转的过程中，你能否找到一条长度与线段DG 的长始终相等的线段？并以图2为例说明理由。

练习：如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，B 、C 、G 三点在一条直线上，且边长分别为2和3，在BG 上截取GP ＝2，连结AP 、PF. （1）观察猜想AP 与PF 之间的大小关系，并说明理由.（2）图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由.（3）若把这个图形沿着PA 、PF 剪成三块，请你把它们拼成一个大正方形，在原图上画出示意图，并请求出这个大正方形的面积.附加：如图，△ABC 与△ADE 都是等边三角形，连结BD 、CE（1）BD 与CE 相等吗？请说明理由．A BCFDE GP32B（2）你能求出BD与CE的夹角∠BFC的度数吗？（3）若将已知条件改为：四边形ABCD与四边形AEFG都是正方形，连结BE、DG交点记为点M（如图）．请直接写出线段BE和DGF例3、正方形四边条边都相等，四个角都是90o．如图，已知正方形ABCD在直线MN 的上方，BC在直线MN上，点E是直线MN上一点，以AE为边在直线MN的上方作正方形AEFG．（1）如图1，当点E在线段BC上（不与点B、C重合）时：①判断△ADG与△ABE是否全等，并说明理由；②过点F作FH⊥MN，垂足为点H，观察并猜测线段BE与线段CH的数量关系，并说明理由；（2）如图2，当点E在射线CN上（不与点C重合）时：①判断△ADG与△ABE是否全等，不需说明理由；②过点F 作FH ⊥MN ，垂足为点H ，已知GD ＝4，求△CFH 的面积．练习：如图1，四边形ABCD 是正方形，G 是CD 边上的一个点(点G 与C 、D 不重合)，以CG 为一边作正方形CEFG ，连结BG ，DE ．（1）如图1，说明BG= DE 的理由（2）将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度，得到如图2．请你猜想①BG= DE 是否仍然成立？②BG 与DE 位置关系？并选取图2验证你的猜想．图 2FG DA图 1FDA类型二、探究题例1、如图，已知等边△A B C 和点P ，设点P 到△A B C 三边A B 、A C 、B C （或其延长线）的距离分别为h 1、h 2、h 3，△A B C 的高为h ．在图（1）中，点P 是边B C 的中点，此时h 3=0，可得结论：h h h h =++321．在图（2）--（5）中，点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外．（1）请探究：图（2）--（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）（2）证明图（2）所得结论；（3）证明图（4）所得结论．（4）（附加题2分）在图（6）中，若四边形R B C S 是等腰梯形，∠B =∠C =60o ，R S =n ，B C =m ，点P 在梯形内，且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4，桥形的高为h ，则h 1、h 2、h 3、h 4、h 之间的关系为：；图（4）与图（6）中的等式有何关系？ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习：1、如图，在△ABC 中，AB=AC ，P 为底边上任意一点，PE ⊥AB ，PF ⊥AC ，BD ⊥AC.（1）求证：PE+PF=BD ；（2）若点P 是底边BC 的延长线上一点，其余条件不变，（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请画出图形，并探究它们的关系.CBAPDE2、如图，已知△ABC 三边长相等，和点P ，设点P 到△ABC 三边AB 、AC 、BC （或其延长线）的距离分别为h 1、h 2、h 3，△ABC 的高为h ．在图（1）中，点P 是边BC 的中点，由S △ABP+S △ACP=S △ABC 得，h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0，所以：h h h h =++321．图（2）~（5）中，点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外．（1）请探究：图（2）~（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）⑵ ⑶ ⑷ ⑸ （2）说明图（2）所得结论为什么是正确的；（3）说明图（5）所得结论为什么是正确的．ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形，将一块含30o 角的直角三角板DEF 如图1放置，当点E 与点B 重合时，点A 恰好落在三角板的斜边DF 上. （1）AC=CF 吗? 为什么?（2）让三角板在BC 上向右平行移动，在三角板平行移动的过程中，(如图2)是否存在与线段EB 始终相等的线段（设AB ，AC 与三角板斜边的交点分别为G ，H ）？如果存练习：1、如图1，一等腰直角三角尺GEF （∠EGF=90°,∠GEF=∠GFE=45°,GE=GF ）的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 相等吗？并说明理由；（2）若三角尺GEF 旋转到如图3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立C图1吗？请说明理由．2、已知：△ABC 为等边三角形，M 是BC 延长线上一点，直角三角尺的一条直角边经过点A ，且60º角的顶点E 在BC 上滑动，（点E 不与点B 、C 重合），斜边∠ACM 的平分线CF 交于点F（1）如图（1）当点B 在BC 边得中点位置时（6分） ○1猜想AE 与BF 满足的数量关系是。

几何证明练习题带答案

几何证明练习题带答案几何证明是数学中的一个重要部分，它要求学生运用逻辑推理和几何知识来证明几何命题的正确性。

以下是一些几何证明的练习题，以及相应的答案。

# 练习题1题目：证明在一个三角形中，大边对大角。

答案：设三角形ABC中，AB > AC。

我们需要证明∠B > ∠C。

证明：1. 延长BA和AC，使它们相交于点D。

2. 根据三角形的外角性质，我们知道∠BAC = ∠BAD + ∠DAC。

3. 由于AB > AC，根据三角形的边角关系，我们知道BD > CD。

4. 根据边角边(SAS)相似准则，三角形ABD ∽ 三角形ACD。

5. 相似三角形对应角相等，所以∠BAD = ∠CAD。

6. 因此，∠BAC = ∠BAD + ∠DAC > ∠DAC，即∠B > ∠C。

# 练习题2题目：证明在一个圆中，等弦所对的圆心角相等。

答案：设圆O中有两弦AB和CD，且AB = CD。

我们需要证明∠AOB = ∠COD。

证明：1. 根据圆的性质，我们知道OA = OB = OC = OD。

2. 由于AB = CD，根据SSS（边边边）相似准则，三角形OAB ∽ 三角形OCD。

3. 相似三角形对应角相等，所以∠AOB = ∠COD。

# 练习题3题目：证明直角三角形斜边上的中线等于斜边的一半。

答案：设直角三角形ABC中，∠C = 90°，D为斜边AB的中点。

我们需要证明CD = 1/2 AB。

证明：1. 连接CD。

2. 由于D为AB的中点，根据中点定理，我们知道CD = 1/2 AB。

3. 根据直角三角形斜边上的中线性质，我们知道CD垂直于AB，并且CD是AB的一半。

# 练习题4题目：证明平行四边形的对角线互相平分。

答案：设平行四边形ABCD，对角线AC和BD相交于点E。

我们需要证明E是AC和BD的中点。

证明：1. 由于ABCD是平行四边形，我们知道AB || CD且AB = CD。

七年级下册第三章三角形

第三章三角形3.1 认识三角形（1）【预习作业】 1、填空：（1）当0°＜α＜90°时，α是角；（2）当α＝ °时，α是直角；（3）当90°＜α＜180°时，α是角；（4）当α＝ °时，α是平角。

2、如图，∵AB ∥CE ，（已知） ∴∠A ＝，（） ∴∠B ＝，（）【合作探究1】1．一副三角板中，三角形的三个内角和等于 °那么是否对其他的三角形也有这样的结论呢？2．用自己剪好的一个三角形，把三个角撕下来，拼在一块。

你发现了什么？小组交流。

【探究归纳1】结论：三角形三个内角的和等于180° 几何表示： .【例题讲解1】证明三角形内角和定理：请设计一种证明三角形内角和是180°的方法，并写出推理过程。

【巩固练习1】 1、判断：（1）一个三角形的三个内角可以都小于60°；（）（2）一个三角形最多只能有一个内角是钝角或直角；（） 2、在△ABC 中，（1）∠C=70°，∠A=50°，则∠B= 度；（2）∠B=100°，∠A=∠C ，则∠C= 度；（3）2∠A=∠B+∠C ，则∠A= 度。

3、如图，在△ABC 中，∠A ＝x 3°∠＝x 2°∠＝x °求三个内角的度数。

解：∵∠A+∠B+∠C=180°，（） ∴=++x x x 23 ∴x 6=A B C D E 123x 2x 3x A BC∴x =从而，∠A= ，∠B= ，∠C= 【合作探究2】一个三角形中三个内角可以是什么角？（提醒：一个三角形中能否有两个直角？钝角呢？）小组讨论。

按三角形内角的大小把三角形分为三类： . 【探究归纳2】直角三角形表示为Rt △思考：直角三角形中的两个锐角有什么关系？结论：____________________ 【巩固练习2】1、观察下列的直角三角形，分别写出它们符号表示、直角边和斜边。

七年级数学下册第四章三角形4用尺规作三角形直角三角形全等的判定、尺规作图、测距离试题北师大版

直角三角形全等的判定、尺规作图、测距离知识点一：直角三角形的判定1.直角三角形全等的判定条件——HL如果两个直角三角形的斜边及一条直角边分别对应相等，那么这两个直角三角形全等.2.直角三角形全等的判定方法的综合运用.判定两个直角三角形全等的方法有五种，即SSS、SAS，ASA.AAS，HL.3.判定条件的选择技巧（1）上述五种方法是判定两直角三角形全等的方法，但有些方法不可能运用.如SSS，因为有两边对应相等就能够判定两个直角三角形全等.（2）判定两个直角三角形全等，必须有一组对应边相等.（3）证明两个直角三角形全等，可以从两个方面思考：①是有两边相等的，可以先考虑用HL，再考虑用SAS；②是有一锐角和一边的，可考虑用ASA或AAS.例1.如图所示，有两个长度相等的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯的水平方向的长度DF相等，则∠ABC＋∠DFE=________.分析：本题解决问题的关键是证明Rt△ABC≌Rt△DEF，由此，我们也知道三角形全等是解决问题的有力工具.解：由现实意义及图形提示可知CA⊥BF，ED⊥BF，即∠BAC=∠EDF=90°.又因为BC=EF，AC=DF，可知Rt△ABC≌Rt△DEF.得∠DFE=∠ACB.因为∠ACB＋∠ABC=90°，故∠ABC＋∠DFE=90°.例2.如图所示，△ABC中，AD是它的角平分线，BD=CD，DE.DF分别垂直于AB.AC，垂足为E.F.求证BE=CF.解：在△AED和△AFD中，∠ ∠ （垂直的定义）∠ ∠ （角平分线的定义）（公共边）所以△AED≌△AFD（AAS）.所以DE=DF（全等三角形的对应边相等）.在Rt△BDE和Rt△CDF中，（已知）（已证）所以Rt△BDE≌△Rt△CDF（HL）.所以BE= CF（全等三角形的对应边相等）.例3.如图所示，已知AB=AE，BC=ED，∠B=∠E，AF⊥CD，F为垂足，求证：CF=DF.分析：要证CF=DF，可连接AC.AD后，证△ACF≌△ADF即可.证明：连结AC.AD.在△ABC和△AED中，所以AC＝AD（全等三角形的对应边相等）.因为AF⊥CD（已知），所以∠AFC=∠AFD=90°（垂直定义）.在Rt△ACF和Rt△ADF中，（已证）（公共边）所以Rt△ACF≌Rt△ADF（HL）.所以CF=DF（全等三角形的对应边相等）.例4.已知在△ABC与△A′B′C′中，CD.C′D′分别是高，且AC=A′C′，AB=A′B′，CD=C′D′，试判断△ABC 与△A′B′C′是否全等，说说你的理由.分析：分析已知条件，涉及到三角形的高线，而三角形的高线有在三角形内、外或形上三种情形，故需分类讨论. 解：情形一，如果△ABC与△A′B′C′都为锐角三角形，如图所示.因为CD.C′D′分别是△ABC.△A′B′C′的高.所以∠ADC=∠A′D′C′=90°.在△ADC和△A′D′C′中∴Rt△ADC≌Rt△A′D′C′，则∠A=∠A′.在△ABC与△A′B′C′中，∴△ABC≌△A′B′C′（SAS）.情形二，当△ABC为锐角三角形，△A′B′C′为钝角三角形，如图.显然△ABC与△A′B′C′不全等.情形三，当△ABC与△A′B′C′都为钝角三角形时，如图.由CD.C′D′分别为△ABC和△A′B′C′的高，所以∠ADC=∠A′D′C′=90°，在Rt△ADC和Rt△A′D′C′中，CD=C′D′，AC=A′C′∴Rt△ACD≌Rt△A′C′D′，∴∠CAD=∠C′A′D′.∴∠CAB=∠C′A′B′，在△ABC与△A′B′C′中∴△ABC≌△A′B′C′.例5.阅读下题及证明过程：如图，已知D是△ABC中BC边上的一点，E是AD上一点，EB=EC，∠BAE=∠CAE，求证：∠ABE=∠ACE.证明：在△ABE和△ACE中∴△ABE≌△ACE 第一步∴∠ABE=∠ACE 第二步上面的证明过程是否正确？若正确，请写出每一步推理的根据，若不正确，请指出错在哪一步，并写出你认为正确的证明过程.分析：用三角形全等的判定条件去判断，易发现错在第一步，它不符合全等三角形的条件，因此需另辟途径.由题设知，当结论成立时，必有△ABE≌△ACE，而由已知条件不能求证这两个三角形全等，故需将这两个三角形中重新构造出全等三角形.解：上面的证明过程不正确，错在第一步，正确的证明过程如下：过E作EG⊥AB于G，EH⊥AC于H.如图所示则∠BGE=∠CHE=90°在△AGE与△AHE中∴△AGE≌△AHE∴EG=EH在Rt△BGE与Rt△CHE中，EG=EH，BE=CE.∴Rt△BGE≌Rt△CHE，∴∠ABE=∠ACE.例6.已知：如图所示，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD.（1）求证：BE⊥AC；（2）若把条件BF=AC和结论BE⊥AC互换，那么这个命题成立吗？（1）证明：因为AD⊥BC（已知），所以∠BDA=∠ADC=90°（垂直定义），∠1＋∠2=90°（直角三角形两锐角互余）.在Rt△BDF和Rt△ADC中，（已知）（已知）所以Rt△BDF≌Rt△ADC（HL）.所以∠2=∠C（全等三角形的对应角相等）.因为∠1＋∠2=90°（已证），所以∠1＋∠C=90°.因为∠1＋∠C＋∠BEC=180°（三角形内角和等于180°），所以∠BEC=90°.所以BE⊥AC（垂直定义）；（2）证明：命题成立，因为BE⊥AC，AD⊥BC，所以∠BDF=∠ADC=90°（垂直定义）.所以∠1＋∠C=90°，∠DAC＋∠C=90°.所以∠1=∠DAC（同角的余角相等）.在△BFD与△ACD中，∠ ∠ （已证）∠ ∠ °（已证）（已知）所以△BFD≌△ACD（AAS）.所以BF=AC（全等三角形的对应边相等）.知识二：利用三角形全等测距离通过探索三角形全等，得到了“边边边”，“边角边”，“角边角”，“角角边”定理，用这些定理能够判断两个三角形是否全等，掌握了这些知识，就具备了“利用三角形全等测距离”的理论基础．体会数学与生活的密切联系，能够利用三角形全等解决生活中的实际问题．在解决实际问题时确定方案使不能直接测量的物体间的距离转化为可以测量的距离（即把距离的测量转化为三角形全等的问题）．例1.如图，有一湖的湖岸在A.B之间呈一段圆弧状，A.B间的距离不能直接测得．•你能用已学过的知识或方法设计测量方案，求出A.B间的距离吗？答案：要测量A.B间的距离，可用如下方法：（1）过点B作AB的垂线BF，在BF上取两点C.D，使CD＝BC，再定出BF的垂线DE，使A.C.E在一条直线上，根据“角边角公理”可知△EDC≌△ABC．因此：DE＝BA．•即测出DE的长就是A.B之间的距离．（如图甲）（2）从点B出发沿湖岸画一条射线BF，在BF上截取BC＝CD，过点D作DE∥AB，使A.•C.E在同一直线上，这时△EDC≌△ABC，则DE＝BA．即DE的长就是A.B间的距离．（•如图乙）例2.如图、小红和小亮两家分别位于A.B两处隔河相望，要测得两家之间的距离，请你设计出测量方案．分析：本题的测量方案实际上是利用三角形全等的知识构造两个全等三角形，使一个三角形在河岸的同一边，通过测量这个三角形中与AB相等的线段的长，就可求出两家的距离．方案：如图，在点B所在的河岸上取点C，连接BC并延长到D，使CD＝CB，利用测角仪器使得∠B＝∠D，A.C.E三点在同一直线上．测量出DE的长，就是AB的长．因为∠B＝∠D，CD＝CB，∠ACB＝∠ECD，所以△ACB≌△ECD，所以AB＝DE．知识点三：尺规作图1.用尺规作三角形的根据是三角形全等的条件.2.尺规作图的几何语言①过点×、点×作直线××；或作直线××；或作射线××；②连接两点××；或连接××；③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交××于点×；④在××上截取××＝××；⑤以点×为圆心，××的长为半径作圆（或弧）；⑥以点×为圆心，××的长为半径作弧，交××于点×；⑦分别以点×、点×为圆心，以××、××的长为半径作弧，两弧相交于点×、×．3.用尺规作图具有以下三个步骤①已知：当题目是文字语言叙述时，要学会根据文字语言用数学语言写出题目中的条件；②求作：能根据题目写出要求作出的图形及此图形应满足的条件；③作法：能根据作图的过程写出每一步的操作过程.当不要求写作法时，一般要保留作图痕迹. 对于较复杂的作图，可先画出草图，使它同所要作的图大致相同，然后借助草图寻找作法.例1.已知三角形的两角及其夹边，求作这个三角形．已知：∠α，∠β，线段c(如图)．求作：△ABC，使∠A＝∠α，∠B＝∠β，AB＝c．请按照给出的作法作出相应的图形．例2.如图，已知线段a，b，c，满足a＋b>c，用尺规作图法作△ABC，使BC＝a，AC＝b，AB＝c.错误作法：(1)作线段AB＝c；（2）作线段BC＝a；（3）连接AC，则△ABC就是所求作的三角形(如图).分析：本题第2步作线段BC＝a，在哪个方向作，∠CBA的度数是多少是不确定，所以这步的作法不正确，不能保证AC的长一定等于b．错误的原因在于没有真正理解用尺规作三角形的方法．正确作法：（1）作射线CE；（2）在射线CE上截取CB＝a；（3）分别以C，B为圆心，b，c长为半径画弧，两弧交于点A．连接AC.AB，则△ABC为所求作的三角形(如图)．例3.已知两边和其中一边上的中线，求作三角形．已知线段A.b 和 m．求作△ABC，使BC＝a，AC＝b，BC边上的中线等于m.分析：如果BC已作出，则只要确定顶点A．由于AD是中线，则D为BC的中点，A在以D为圆心，m为半径的圆上，又AC＝b，点A也在以C为圆心b为半径的圆上，因此点A是这两个轨迹的交点．作法：1.作线段BC＝a．2.分别以B.C为圆心，大于长为半径画弧，在BC两侧各交于一点M、N，连接M、N交BC于点D．3.分别以D为圆心，m长为半径作弧，以C为圆心，b长为半径作弧，两弧交于点A．4.分别连接AB.AC．则△ABC就是所求作的三角形．思考：假定△ABC已经作出，其中 BC＝a，AC＝b，中线 AD＝m．显然，在△ADC中，AD＝m，DC＝，AC＝b，所以△ADC若先作出．然后由BD＝的关系，可求得顶点B的位置，同样可以作出△ABC．作法请同学们自己写出．1.如图，DB⊥AB，DC⊥AC，垂足分别为B.C，且BD=CD，求证：AD平分∠BAC.证明：∵DB⊥AB，DC⊥AC∴∠B=∠C=90°在Rt△ABD和Rt△ACD中∴Rt△ABD≌Rt△ACD（HL）∴∠1=∠2∴AD平分∠BAC.2.如图，已知AB=AC，AB⊥BD，AC⊥CD，AD和BC相交于点E，求证：（1）CE=BE；（2）CB⊥AD.证明：（1）∵AB⊥BD，AC⊥CD∴∠ABD=∠ACD=90°在Rt△ABD和Rt△ACD中∴Rt△ABD≌Rt△ACD (HL)∴∠1=∠2在△ABE和△ACE中∴△ABE≌△ACE（SAS）∴BE=CE（2）∵△ABE≌△ACE∴∠3=∠4又∵∠3＋∠4=180°∴∠3=90°∴CB⊥AD3.如图，已知一个角∠AOB，你能否只用一块三角板作出它的平分线吗？说明方法与理由.解：能.作法：（1）在OA，OB上分别截取OM=ON（2）过M作MC⊥OA，过N作ND⊥OB，MC交ND于P（3）作射线OP则OP为∠AOB的平分线证明：∵MC⊥OA.ND⊥OB∴∠1=∠2=90°在Rt△OMP和Rt△ONP中∴Rt△OMP≌Rt△ONP（HL）∴∠3=∠4∴OP平分∠AOB.4.如图，AB=AD，BC=DE，且BA⊥AC，DA⊥AE，你能证明AM=AN吗？解：能.理由如下：∵BA⊥AC，DA⊥AE，∴∠BAC=∠DAE=90° 在 Rt△ABC 和 Rt△ADE 中∴Rt△ABC≌Rt△ADE（HL） ∴∠C=∠E，AC=AE 在△AMC 和△ANE 中∴△AMC≌△ANE（ASA），∴AM=AN. 5.如图，CE⊥AB，DF⊥AB，垂足分别为 E.F，且 AE=BF，AD=BC，则（1）△ADF 和△BEC 全等吗？为什么？（2）CM 与 DN 相等吗？为什么？解：（1）△ADF≌△BCE，理由如下：∵CE⊥AB，DF⊥AB ∴∠1=∠2=∠3=∠4=90° 又∵AE=BF，∴AF=BE 在 Rt△ADF 和 Rt△BCE 中∴Rt△ADF≌Rt△BCE（HL）（2）CM=DN，理由如下： ∵△ADF≌△BCE ∴DF=CE，∠A=∠B 在△AME 和△BNF 中∴△AME≌△BNF（ASA） ∴ME=NF，又∵CE=DF ∴MC=ND. 6.如图所示，已知线段 a，b，∠α ，求作△ABC，使 BC＝a，AC＝b，∠ACB＝∠α ，•根据作图在下面空格中填上适当的文字或字母．（1）如图甲所示，作∠MCN＝________；（2）如图乙所示，在射线 CM 上截取 BC＝________，在射线 CN 上截取 AC＝________．（3）如图丙所示，连接 AB，△ABC 就是_________．答案：∠α ，a，b，所求作的三角形. 7.已知线段 a 及锐角α ，求作：三角形 ABC，使∠C＝90°，∠B＝∠α ，BC＝A．作法：（1）作∠MCN＝90°；（2）以 C 为圆心，a 为半径，在 CM 上截取 CB＝a；（3）以 B 为顶点，BC 为一边作∠ABC＝∠α ，交 CN 于点 A．连接 AB，则△ABC 即为所求作的三角形． 8.你一定玩过跷跷板吧！如图是贝贝和晶晶玩跷跷板的示意图，支柱 OC 与地面垂直，点 O 是横板 AB 的中点，AB 可以绕着点 O 上下转动，当 A 端落地时，∠OAC＝20°．（1）横板上下可转动的最大角度（即∠A′OA）是多少？（2）在上下转动横板的过程中，两人上升的最大高度 AA′，BB′有何数量关系？为什么？解：（1）∵OC⊥AB′，∠OAC＝20°， ∴∠AOC＝90°－20°＝70°，同理可求∠B′OC＝70°， ∴∠AOA′＝180°－2×70°＝40°；（2）AA′＝BB′，如图所示，连接 AA′、BB′， ∵AB＝A′B′，∠BAB′＝∠A′B′A，AB′＝B′A， ∴△A′AB′≌△BB′A，∴AA′＝BB′． 9.有一池塘，要测池塘两端 A.B 间的距离，可先在平地上取一个可以直接到达 A 和 B 的点 C，连接 AC 并延长到 D，使 CD＝CA，连接 BC 并延长到 E，使 CE＝CB，连接 DE，量出 DE 的长，这个长就是 A.B 之间的距离。

精品试卷：北师大版七年级数学下册第四章三角形必考点解析试题(含答案及详细解析)

北师大版七年级数学下册第四章三角形必考点解析考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，点E ，F 在线段BC 上，ABF ∆与DEC ∆全等，其中点A 与点D ，点B 与点C 是对应顶点，AF 与DE 交于点M ，则DEC ∠等于（）A ．B B ．A ∠C ．EMF ∠D ．AFB ∠2、下列条件中，能判定△ABC ≌△DEF 的是（）A ．∠A ＝∠D ，∠B ＝∠E ，AC ＝DFB ．∠A ＝∠E ，AB ＝EF ，∠B ＝∠DC ．∠A ＝∠D ，∠B ＝∠E ，∠C ＝∠F D ．AB ＝DE ，BC ＝EF ，∠A ＝∠E3、如图，ABC DEC ≌△△，A D ∠=∠，AC DC =，则下列结论：①BC CE =；②AB DE =；③ACE DCA ∠=∠；④DCA ECB ∠=∠．成立的是（）A ．①②③B ．①②④C ．②③④D ．①②③④4、如图，点O 在AD 上，∠A ＝∠C ，∠AOC ＝∠BOD ，AB ＝CD ，AD ＝8，OB ＝3，则OC 的长为（）A ．3B ．4C ．5D ．65、以下列各组线段为边，能组成三角形的是（）A ．2cm 、10cm 、13cmB ．3cm 、7cm 、4cmC ．4cm 、4cm 、4cmD ．5cm 、14cm 、6cm6、如图，AB ∥CD ，∠E +∠F ＝85°，则∠A +∠C ＝（）A ．85°B ．105°C ．115°D ．95°7、如图，在ABC ∆中，已知点D ，E ，F 分别为BC ，AD ，CE 的中点，且4ABC S ∆=，则∆BEF 的面积是（）A．1-B．1 C．5 D．5-8、以下列各组线段为边，能组成三角形的是（）A．3cm，4cm，5cm B．3cm，3cm，6cm C．5cm，10cm，4cm D．1cm，2cm，3cm9、如图，在ABC中，40∠=°，AD平分BACC=，则∠=︒，60B∠交BC于点D，在AB上截取AE AC∠的度数为（）EDBA．30°B．20°C．10°D．15°10、一个三角形的两边长分别为5和2，若该三角形的第三边的长为偶数，则该三角形的第三边的长为（）A．6 B．8 C．6或8 D．4或6第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，PA＝PB，请你添加一个适当的条件：___________，使得△PAD≌△PBC．2、如图，△ABE ≌△ACD ，∠A ＝60°，∠B ＝20°，则∠DOE 的度数为_____°．3、如图，∠1＝∠2，加上条件 _____，可以得到△ADB ≌△ADC （SAS ）．4、在平面直角坐标系中，点B （0，4），点A 为x 轴上一动点，连接AB ．以AB 为边作等腰Rt △ABE ，（B 、A 、E 按逆时针方向排列，且∠BAE 为直角），连接OE ．当OE 最小时，点E 的纵坐标为______．5、如图，方格纸中是9个完全相同的正方形，则∠1+∠2的值为 _____．三、解答题（5小题，每小题10分，共计50分）1、直线l 经过点A ，ABC 在直线l 上方，AB AC =．（1）如图1，90BAC ∠=︒，过点B ，C 作直线l 的垂线，垂足分别为D 、E ．求证：ABD CAE ≌（2）如图2，D ，A ，E 三点在直线l 上，若BAC BDA AEC α∠=∠=∠=（α为任意锐角或钝角），猜想线段DE 、BD 、CE 有何数量关系？并给出证明．（3）如图3，90BAC ∠=︒过点B 作直线l 上的垂线，垂足为F ，点D 是BF 延长线上的一个动点，连结AD ，作90DAE ∠=︒，使得AE AD =，连结DE ，CE ．直线l 与CE 交于点G ．求证：G 是CE 的中点．2、平行线是平面几何中最基本、也是非常重要的图形．在解决某些几何问题时，若能根据问题的需要，添加适当的平行线，往往能使证明顺畅、简洁．请根据上述思想解决问题：（1）如图（1），AB∥CD，试判断∠B，∠D与∠E的关系；（2）如图（2），已知AB∥CD，在∠ACD的角平分线上取两个点M、N，使得∠AMN=∠ANM，求证：∠CAM=∠BAN．3、如图，点B、E、F、D在同一直线上，AB CD∥，AB CD=，BE DF=．求证：ABF CDE△△．≅4、如图，AD是ABC的中线，分别过点C、B作AD及其延长线的垂线，垂足分别为F、E．（1）求证：CFD BED△△；≅（2）若ACF的面积为8，CFD△的面积．△的面积为6，求ABE5、如图，点B、F、C、E在同一条直线上，∠B＝∠E，AB＝DE，BF＝CE．求证：AC＝DF．-参考答案-一、单选题1、D【分析】根据点A与点D，点B与点C是对应顶点，得到ABF DCE∆≅∆，根据全等三角形的性质解答．【详解】解：ABF∆全等，点A与点D，点B与点C是对应顶点，∆与DEC∴∆≅∆，ABF DCE∴∠=∠．DEC AFB故选：D【点睛】本题主要考查了全等三角形的性质，熟练掌握全等三角形的对应边相等，对应角相等是解题的关键．2、A【分析】根据全等三角形的判定方法，对各选项分别判断即可得解．【详解】解：A 、∠A ＝∠D ，∠B ＝∠E ，AC ＝DF ，根据AAS 可以判定ABC DEF △≌△，故此选项符合题意；B 、∠A ＝∠E ，AB ＝EF ，∠B ＝∠D ，AB 与EF 不是对应边，不能判定ABC DEF △≌△，故此选项不符合题意；C 、∠A ＝∠D ，∠B ＝∠E ，∠C ＝∠F ，没有边对应相等，不可以判定ABC DEF △≌△，故此选项不符合题意；D 、AB ＝DE ，BC ＝EF ，∠A ＝∠E ，有两边对应相等，一对角不是对应角，不可以判定ABC DEF △≌△，故此选项不符合题意；故选A ．【点睛】本题考查了全等三角形的判定方法，一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．3、B【分析】根据全等三角形的性质直接判定①②，则有DCE ACB ∠=∠，然后根据角的和差关系可判定③④．【详解】解：∵ABC DEC ≌△△，∴,,BC EC AB DE ACB DCE ==∠=∠，故①②正确；∵,DCA DCE ACE BCE ACB ACE ∠=∠-∠∠=∠-∠，∴DCA ECB∠=∠，故③错误，④正确，综上所述：正确的有①②④；故选B．【点睛】本题主要考查全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．4、C【分析】证明△AOB≌△COD推出OB=OD，OA=OC，即可解决问题．【详解】解：∵∠AOC=∠BOD，∴∠AOC+∠COB=∠BOD+∠COB，即∠AOB=∠COD，∵∠A=∠C，CD=AB，∴△AOB≌△COD（AAS），∴OA=OC，OB=OD，∵AD=8，OB＝3，∴OC=AO=AD-OD=AD-OB=5．故选C．【点睛】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形解决问题．5、C【分析】由题意根据“三角形任意两边之和大于第三边，任意两边之差小于第三边”对各选项进行逐一分析即可．【详解】解：根据三角形的三边关系，A 、2+10＜13，不能组成三角形，不符合题意；B 、3+4＝7，不能够组成三角形，不符合题意；C 、4+4＞4，能组成三角形，符合题意；D 、5+6＜14，不能组成三角形，不符合题意．故选：C ．【点睛】本题主要考查三角形三边关系，注意掌握判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数．6、D【分析】设,AF CE 交于点G ，过点G 作GH AB ∥，根据平行线的性质可得A C AGC ∠+∠=∠，根据三角形的外角性质可得85F AGC E ∠+∠=∠=︒，进而即可求得A C ∠+∠【详解】解：设,AF CE 交于点G ，过点G 作GH AB ∥，如图，A AGH ∴∠=∠∵AB CD ∥∴HG CD ∥C CGH ∴∠=∠A C AGC ∴∠+∠=∠∠E +∠F ＝85°85E FGC F ∠+∠∴=∠=︒∴A C ∠+∠=180AGC FGC ∠=︒-∠=95︒故选D【点睛】本题考查了平行线的性质，三角形的外角性质，平角的定义，掌握三角形的外角性质是解题的关键．7、B【分析】根据三角形面积公式由点D 为BC 的中点得到122ABD ADC ABC S S S ∆∆∆===，同理得到112EBD EDC ABD S S S ∆∆∆===，则2BEC S ∆=，然后再由点F 为EC 的中点得到112BEF BEC S S ∆∆==．【详解】解：点D 为BC 的中点，122ABD ADC ABC S S S ∆∆∆∴===，点E 为AD 的中点，112EBD EDC ABD S S S ∆∆∆∴===， 2EBC EBD EDC S S S ∆∆∆∴=+=，点F 为EC 的中点，112BEF BEC S S ∆∆∴==．故选：B．【点睛】本题考查了三角形的中线与面积的关系，解题的关键是掌握是三角形的中线把三角形的面积平均分成两半．8、A【分析】三角形的任意两条之和大于第三边，任意两边之差小于第三边，根据原理再分别计算每组线段当中较短的两条线段之和，再与最长的线段进行比较，若和大于最长的线段的长度，则三条线段能构成三角形，否则，不能构成三角形，从而可得答案.【详解】解：345,所以以3cm，4cm，5cm为边能构成三角形，故A符合题意；3+3=6,所以以3cm，3cm，6cm为边不能构成三角形，故B不符合题意；4+510,所以以5cm，10cm，4cm为边不能构成三角形，故C不符合题意；1+2=3,所以以1cm，2cm，3cm为边不能构成三角形，故D不符合题意；故选A【点睛】本题考查的是三角形的三边之间的关系，掌握“利用三角形三边之间的关系判定三条线段能否组成三角形”是解本题的关键.9、B【分析】利用已知条件证明△ADE≌△ADC（SAS），得到∠DEA＝∠C，根据外角的性质可求EDB的度数．【详解】解：∵AD是∠BAC的平分线，∴∠EAD＝∠CAD在△ADE 和△ADC 中，AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩， ∴△ADE ≌△ADC （SAS ），∴∠DEA ＝∠C 60=︒，∵40B ∠=︒，∠DEA ＝∠B +EDB ∠，∴604020EDB ∠=︒-︒=︒；故选：B【点睛】本题考查了全等三角形的性质与判定，解决本题的关键是证明△ADE ≌△ADC ．10、D【分析】根据三角形两边之和大于第三边确定第三边的范围，根据题意计算即可．【详解】解：设三角形的第三边长为x ，则5﹣2＜x ＜5+2，即3＜x ＜7，∵三角形的第三边是偶数，∴x ＝4或6，故选：D ．【点睛】本题考查了三角形三边关系，在一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边．二、填空题1、∠D=∠C或∠PAD=∠PBC或∠DBC=∠CAD或PD=PC 或AC=BD．【分析】已有∠P是公共角和边PA=PB，根据全等三角全等的条件，利用AAS需要添加∠D=∠C，根据ASA需要添加∠PAD=∠PBC或∠DBC=∠CAD，根据边角边需要添加 PD=PC 或PC=PD．填入一个即可．【详解】解：∵PA=PB，∠P是公共角，∴根据AAS可以添加∠D=∠C，，在△PAD和△PBC中，∵PA=PB，∠P是公共角，∠D=∠C，∴△PAD≌△PBC（AAS）．根据ASA可以添加∠PAD=∠PBC，在△PAD和△PBC中，∵PA=PB，∠P是公共角，∠PAD=∠PBC，∴△PAD≌△PBC（ASA）．根据ASA可以添加∠DBC=∠CAD，∴180°-∠DBC=180°-∠CAD，即∠PAD=∠PBC，在△PAD和△PBC中，∵PA=PB，∠P是公共角，∠PAD=∠PBC，∴△PAD≌△PBC（ASA）．根据SAS可添加PD=PC在△PAD和△PBC中，∵PA=PB，∠P是公共角，PD=PC，∴△PAD≌△PBC（SAS）．根据SAS可添加BD=AC，∵PA=PB，BD=AC，∴PA+AC=PB+BD即PC=PD，在△PAD和△PBC中，∵PA=PB，∠P是公共角，PD=PC，∴△PAD≌△PBC（SAS）．故答案为：∠D=∠C或∠PAD=∠PBC或∠DBC=∠CAD或PD=PC 或AC=BD．【点睛】本题考查三角形全等添加条件，掌握三角形全等判定方法与定理是解题关键．2、100【分析】直接利用三角形的外角的性质得出∠CEO=80°，再利用全等三角形的性质得出答案．【详解】解：∵∠A=60°，∠B=20°，∴∠CEO=80°，∵△ABE≌△ACD，∴∠B=∠C=20°，∴∠DOE=∠C+∠CEO=100°．故答案为：100．【点睛】此题主要考查了全等三角形的性质以及三角形的外角的性质，求出∠CEO =80°是解题关键．3、AB =AC （答案不唯一）【分析】根据全等三角形的判定定理SAS 证得△ADB ≌△ADC ．【详解】解：加上条件，AB =AC ，可以得到△ADB ≌△ADC （SAS ）．在△ADB 与△ADC 中，12AB AC AD AD =⎧⎪∠=∠⎨⎪=⎩， ∴△ADB ≌△ADC （SAS ），故答案为：AB =AC （答案不唯一）．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．4、－2【分析】过E 作EF ⊥x 轴于F ，由三垂直模型，得EF ＝OA ，AF ＝OB ，设A （a ，0），可求得E （a ＋4，a ），点E 在直线y ＝x －4上，当OE ⊥CD 时，OE 最小，据此求出坐标即可．【详解】解：如图，过E 作EF ⊥x 轴于F ，∵∠AOB =∠EFA =∠BAE =90°，∴∠ABO +∠OAB =90°，∠EAF +∠OAB =90°，∴∠ABO=∠EAF，∵AB=AE，∴△ABO≌△EAF，∴EF＝OA，AF＝OB＝4，取点C（4，0），点D（0，-4），∴∠OCD=45°，∵CF＝4- OF，OA＝4- OF，∴CF＝OA ＝EF，∴∠ECF=45°，∴点E在直线CD上，当OE⊥CD时，OE最小，此时△EFO和△ECO为等腰Rt△，∴OF＝EF＝2，此时点E的坐标为：（2，－2）．故答案为：-2【点睛】本题考查了全等三角形的判定与性质，解题关键是确定点E运动的轨迹，确定点E的位置．5、90︒【分析】如图（见解析），先根据三角形全等的判定定理证出ABC ADE ≅，再根据全等三角形的性质可得23∠∠=，由此即可得出答案．【详解】解：如图，在ABC 和ADE 中，AC AE A A AB AD =⎧⎪∠=∠⎨⎪=⎩， ()ABC ADE SAS ∴≅，23∴∠=∠，121390∴∠+∠=∠+∠=︒，故答案为：90︒．【点睛】本题考查了三角形全等的判定定理与性质等知识点，正确找出两个全等三角形是解题关键．三、解答题1、（1）见解析；（2）猜想：DE BD CE =+，见解析；（3）见解析【分析】（1）先证明BDA AEC ∠=∠和ABD CAE ∠=∠，再根据AAS 证明ABD CAE ≌即可；（2）根据AAS 证明ABD CAE ≌得BD AE =，DA EC =，进一步可得出结论；（3）分别过点C 、E 作CM l ⊥，EN l ⊥，同（1）可证ABF CAM ≌，ADF EAN ≌，得出CM =EN ，证明CMG ENG ≌得CG EG =，从而可得结论．【详解】解：（1）证明：∵BD l ⊥，CE l ⊥，∴90BDA AEC ∠=∠=︒，∴90ABD DAB ∠+∠=︒∵90BAC ∠=︒，∴90CAE DAB ∠+∠=︒∴ABD CAE ∠=∠，在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()ABD CAE AAS ≌（2）猜想：DE BD CE =+，∵BDA BAC α∠=∠=∴180180ABD DAB BDA α∠+∠=︒-∠=︒-，180180CAE DAB BAC α∠+∠=︒-∠=︒-∴ABD CAE ∠=∠，在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABD CAE AAS ≌，∴BD AE =，DA EC =，∴DE AE DA BD CE =+=+（3）分别过点C 、E 作CM l ⊥，EN l ⊥，同（1）可证ABF CAM ≌，ADF EAN ≌，∴AF CM =，AF EN =∴CM EN =，∵CM l ⊥，EN l ⊥，∴90CMG ENG ∠=∠=︒在CMG 与ENG 中CMG ENG CGM EGN CM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMG ENG AAS ≌，∴CG EG =，∴G 为CE 的中点．【点睛】本题考查了全等三角形的判定与性质、垂线的定义、角的互余关系，证得△ABD≌△CAE是解决问题的关键．2、（1）∠BED=∠B＋∠D；（2）证明见详解．【分析】（1）作EF∥AB，证明AB∥EF∥CD，得到∠B=∠BEF，∠D=∠DEF，即可证明∠BED=∠B＋∠D；（2）根据（1）结论得到∠N=∠BAN＋∠DCN，进而得到∠AMN=∠BAN＋∠DCN，根据三角形外角定理得到∠AMN=∠ACM＋∠CAM，∠BAN＋∠DCN=∠ACM＋∠CAM，再根据∠DCN=∠CAN，即可证明∠CAM=∠BAN．【详解】解：如图1，作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠B=∠BEF，∠D=∠DEF，∵∠BED=∠BEF+∠DEF，∴∠BED=∠B＋∠D；（2）证明：∵AB∥CD，∴由（1）得∠N=∠BAN＋∠DCN，∵∠AMN=∠ANM，∴∠AMN=∠BAN＋∠DCN，∵∠AMN是△ACM外角，∴∠AMN =∠ACM ＋∠CAM ，∴∠BAN ＋∠DCN =∠ACM ＋∠CAM ，∵CN 平分∠ACD ，∴∠DCN =∠CAN ，∴∠CAM =∠BAN ．【点睛】本题考查了平行线的性质，角平分线的定义，三角形的外角定理等知识，熟知相关定理并根据题意添加辅助线进行角的转化是解题关键．3、见解析【分析】由“SAS ”可证△ABF ≌△CDE ，可得∠AFB =∠CED ，可得结论．【详解】解：∵BE DF =，∴BE EF DF EF +=+，即：BF DE =，∵AB CD ∥，∴B D ∠=∠，在ABF 和CDE △中，AB CD B D BF DE =⎧⎪∠=∠⎨⎪=⎩， ∴()ABF CDE SAS ≅△△.【点睛】本题考查了全等三角形的判定和性质，平行线的性质，证明三角形全等是解题的关键．4、（1）见解析（2）ABE △的面积为20．【分析】（1）根据已知条件得到E CFD ∠=∠、BD CD =，然后利用全等三角形的判定，进行证明即可．（2）分别根据ACF 和CFD △的面积，用CF 表示AF 、D F ，通过CFD BED ≅△△，得到BE CF =，DE DF =，用CF 表示出AE 的长，最后利用面积公式求解即可．（1）（1）解：由题意可知：90E CFD ∠=∠=︒AD 是ABC 的中线BD CD ∴=在CFD ∆与BED ∆中CDF BDE C CFD E D BD ∠=∠=∠=∠⎧⎪⎨⎪⎩∴∆∆()CFD BED AAS ≌．（2）解：ACF 的面积为8，CFD △的面积为6．182AF CF ∴⋅=，即16AF CF = 162DF CF ⋅=，即12DF CF= 由（1）可知：CFD BED ∆∆≌BE CF ∴=，12DE DF CF==40AE AF DF DE CF∴=++= 1202ABE S AE BE ∆∴=⋅=．【点睛】本题主要是考查了全等三角形的判定和性质，熟练根据条件证明三角形全等，利用其性质，证明对应边相等，这是解决本题的关键．5、见解析【分析】根据题意得出BC =EF ，即可利用SAS 证明△ABC 和△DEF ，再利用全等三角形的性质即可得解．【详解】证明：∵BF ＝CE ，∴B Ｆ＋FC ＝CE ＋FC ，即BC ＝EF ，在△ABC 和△DEF 中，AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF （SAS ），∴AC ＝DF ．【点睛】本题考查了全等三角形的判定与性质，利用SAS 证明△ABC ≌△DEF 是解题的关键．。

初一数学_几何_三角形基础知识和基本练习题讲解

第七章三角形（一）——三角形的基本概念学习目标：1、明确三角形的相关概念；能正确对三角形进行分类；2、能利用三角形三边关系进行有关计算。

学习过程：三角形的有关概念——阅读课本第63至64页，回答以下问题：（1）三角形概念：由不在同一直线上的条线段连接所组成的图形。

（2）三角形的表示法（如图1）三角形ABC可表示为：；（3）ΔABC的顶点分别为A、、；（3）ΔABC的内角分别为∠ABC，，；（4）ΔABC的三条边分别为AB，，；或a，、；（5）顶点A的对边是，顶点B的对边分别是，顶点C的对边分别是。

三角形的分类：（1）下图中，每个三角形的内角各有什么特点？（2）下图中，每个三角形的三边各有什么特点？（3）结合以上图形你认为三角形可以如何分类？试一试①按角分类：②按边分类：第1题3、三角形的三边关系问题1：如图，现有三块地，问从A 地到B 地有几种走法，哪一种走法的距离最近？请将你的设计方案填写在下表中：（3）阅读课本第64页，填写：三角形两边的和（4）用式子表示：BC + AC AB （填上“> ”或“ < ” ） ① BC + AB AC （填上“> ”或“ < ” ） ②AB + AC BC （填上“> ”或“ < ” ） ③4、三角形的稳定性问题2：盖房子时，在窗框未安装好前，木工师傅常先在窗框上斜钉一根木条，为什么？5、例题：用一条长为18cm 的细绳围成一个等腰三角形，如果腰长是底边的2倍，那么各边的长是多少？解：设底边长为xcm ，则腰长是 cm 因为三角形的周长为 cm所以：所以x= cm答：三角形的三边分别是、、课堂练习： A 组A 地(6)(5)(4)(3)(2)(1)1．①图中有个三角形，分别为 ②△ABC 的三个顶点是、、；三个内角是、、；三条边是、、；2、如图中有个三角形，用符号表示 3．判断下列线段能否组成三角形：①4，5，6 （）②1，2，3 （） ③2，2，6 （）④8，8，2 （） 4、下列的图形中具有稳定性的是（写编号）5、等腰三角形一腰长为6，底边长为7，则另一腰为，周长为。

初一上册几何证明题(精选多篇)

初一上册几何证明题(精选多篇)第一篇：初一上册几何证明题初一上册几何证明题1.在三角形abc中，∠acb=90°，ac=bc，e是bc边上的一点，连接ae，过c作cf ⊥ae于f，过b作bd⊥bc交cf的延长线于d，试说明：ae=cd。

满意回答因为ae⊥cf,bd⊥bc所以∠afc=90°,∠dbc=90°又∠acb=90°，所以∠ace=∠dbc因为∠cae+∠aec=90°∠ecf+∠aec=90°所以∠cae=∠ecf又ac=bc所以△ace全等于△cbd(asa)所以ae=cd像这类题目，一般用全等较好做些2.如图所示，已知ad、bc相交于o，∠a=∠d，试说明∠c=∠b.解：证1：∠a=∠d=====>ab∥cd=====>∠c=∠b(内错角相等)证2：△abo内角和180=△cdo内角和180∠a=∠d∠aob=∠d0c∴∠c=∠b证明：显然有:∠aob=∠cod(两直线相交,对顶角相等)又∠a=∠d,且三角形三个内角的和等于180º∴一定有∠c=∠b.3.(1)d是三角形abc的bc边上的点且cd=ab，角adb=角bad，ae是三角形abd的中线，求证ac=2ae。

(2)在直角三角形abc中，角c=90度，bd是角b的平分线，交ac于d，ce垂直ab于e，交bd于o，过o作fg平行ab，交bc于f，交ac于g。

求证cd=ga。

延长ae至f，使ae=ef。

be=ed，对顶角。

证明abe全等于def。

=》ab=df，角b=角edf角adb=角bad=》ab=bd，cd=ab=》cd=df。

角ade=bad+b=adb+edf。

ad=ad=》三角形adf全等于adc=》ac=af=2ae。

题干中可能有笔误地方：第一题右边的e点应为c点，第二题求证的cd不可能等于ga，是否是求证cd=fa或cd=co。

数学几何证明题

数学几何证明题一、在三角形ABC中，若AB = AC，且D为BC的中点，则AD与BC的关系是？A. AD垂直于BCB. AD平行于BCC. AD是BC的一半D. AD与BC相交于一点非中点（答案）A二、在平行四边形ABCD中，若AB = BC，则该平行四边形是？A. 矩形B. 菱形C. 正方形D. 梯形（答案）B三、在圆O中，弦AB与弦CD相交于点P，若AP = PB，且CP = PD，则OP与AB、CD的关系是？A. OP垂直于AB且垂直于CDB. OP平行于AB且平行于CDC. OP是AB、CD的角平分线D. OP与AB、CD无特定关系（答案）A四、在三角形ABC中，若角A = 60度，且角B的平分线与角C的外角平分线相交于点D，则角D的度数是？A. 30度B. 60度C. 90度D. 120度（答案）C五、在矩形ABCD中，对角线AC与BD相交于点O，若AC = 2AB，则角AOB的度数是？A. 30度B. 45度C. 60度D. 90度（答案）C六、在三角形ABC中，若D、E分别是AB、AC的中点，且DE = 1/3BC，则三角形ABC的形状是？A. 等边三角形B. 等腰三角形C. 直角三角形D. 一般三角形（答案）C七、在圆O中，若弦AB的长度等于半径OA，则角AOB的度数是？A. 30度B. 45度C. 60度D. 90度（答案）C（注：此题假设弦AB不是直径）八、在平行四边形ABCD中，若M、N分别是AB、CD的中点，且MN = 1/2AD，则平行四边形ABCD是？A. 矩形B. 菱形C. 正方形D. 梯形（但此选项不可能，因为已给出是平行四边形）（答案）A九、在三角形ABC中，若角A = 角B + 角C，则三角形ABC是？A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形（答案）C十、在圆O中，若弦AB与弦CD平行，且AB = 2CD，则弦AB与弦CD之间的距离与半径的关系是？A. 等于半径B. 小于半径C. 大于半径D. 与半径无关（答案）B（注：此题假设弦AB与弦CD不是同一个圆上的直径）。

烟台七年级数学第一章-三角形全等

第一章三角形1.1 认识三角形知识点1：三角形及其有关概念1、三角形：由不在同一条直线上的三个点首位顺次相接组成的图形叫做三角形。

例1：如图所示，图中共有多少个三角形？请写出这些三角形并指出所有以E 为顶点的三角形。

知识点2：三角形的内角和定理三角形三个内角的和等于180°。

几何语言：在△ABC 中，∠A+∠B+∠C=180° 题型一：利用三角形内角和求角度例1：在△ABC 中，若∠A=95°，∠B=40°，则∠C=_____________.例2：如图，在△ABC 中，∠ABC=∠ACB ，点P 为△ABC 内的一点，且∠PBC=∠PCA ，∠PBC=110°，则∠A 的大小为（）A 40°B 50°C 60°D 70°跟踪练习:1：在△ABC 中，∠B=∠A+10°，∠C=∠B+10°，求△ABC 各内角的度数。

2：如图，EF//BC ，AC 平分∠BAF ，∠B=80°，求∠C 的度数。

A3：如图，已知∠B=40°，则∠BEF+∠BFE+∠A+∠C= ______________.知识点3：三角形分类题型一：按角判断三角形形状例1：若一个三角形的三个内角度数比为2：3：4，则这个三角形是（）A 锐角三角形B 直角三角形C 钝角三角形D 等腰三角形跟踪练习:1：三角形三个内角满足∠A=21∠B=31∠C ，则这个三角形是（） A 锐角三角形 B 直角三角形 C 钝角三角形 D 等腰三角形2：在△ABC 中，∠A -∠B = ∠C ，则△ABC 是（）A 锐角三角形B 直角三角形C 钝角三角形D 无法确定知识点4：三角形按边分类及三边关系1、三角形按边分类2、三角形三边关系：任意两边之和小于第三边，任意两边之差大于第三边；注：判断技巧：两条最短边之和大于第三边；最长边与最短边之差小于第三边。

初中数学经典几何模型04-角平分线模型在三角形中的应用(含答案)

初中数学经典几何模型专题04 角平分线模型在三角形中的应用在初中几何证明中，常会遇到与角平分线有关的问题。

不少同学遇到这类问题时，不清楚应该怎样去作辅助线。

实际上这类问题是有章可循的，其策略是:明确辅助线作用，记清相应模型辅助线作法，理解作辅助线以后的目的。

能做到这三点，就能在解题时得心应手。

【知识总结】【模型】一、角平分线垂两边角平分线+外垂直当已知条件中出现OP 为OAB ∠的角平分线、PM OA ⊥于点M 时，辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等，利用相关结论解决问题.【模型】二、角平分线垂中间角平分线+内垂直当已知条件中出现OP 为AOB ∠的角平分线,PM OP ⊥于点P 时，辅助线的作法大都为延长MP 交OB 于点N 即可.即有OMN ∆是等腰三角形、OP 是三线等，利用相关结论解决问题.【模型】三、角平分线构造轴对称角平分线+截线段等当已知条件中出现OP 为AOB ∠的角平分线、PM 不具备特殊位置时，辅助线的作法大都为在OB 上截取ON OM =，连结PN 即可.即有OMP ∆≌ONP ∆，利用相关结论解决问题.【模型】四、角平分线加平行线等腰现角平分线+平行线当已知条件中出现OP 为AOB ∠的角平分线，点P 角平分线上任一点时，辅助线的作法大都为过点P 作PM //OB 或PM //OA 即可.即有OMP ∆是等腰三角形，利用相关结论解决问题.1、如图, ABN CBN ∠=∠, P 为BN 上的一点，并且PD BC ⊥于点D ,2AB BC BD +=,求证：180BAP BCP ∠+∠=︒.2、如图，在ABC ∆中，CD 是ACB ∠的平分线，AD CD ⊥于点D ,DE //BC 交AB 于点E ，求证:EA EB =.3、已知:如图7,2,,AB AC BAD CAD DA DB =∠=∠=，求证:DC AC ⊥.4、如图,AB //CD ,AE 、DE 分别平分BAD ∠和ADC ∠.探究:在线段AD 上是否存在点M ，使得2AD EM =.【基础训练】1、如图所示，在四边形ABCD中，DC//AB，∠DAB=90°，AC⊥BC，AC=BC，∠ABC的平分线交AD，AC于点E、F，则BFEF的值是___________.2、如图，D是△ABC的BC边的中点，AE平分∠BAC，AE⊥CE于点E，且AB =10，AC =16，则DE的长度为______3、如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ =13CE时，EP+BP =________.【巩固提升】1、如图，F，G是OA上两点，M，N是OB上两点，且FG =MN，S△PFG=S△PMN，试问点P是否在∠AOB 的平分线上？2、已知：在△ABC中，∠B的平分线和外角∠ACE的平分线相交于D，DG//BC，交AC于F，交AB于G，求证：GF =BG CF.3、在四边形ABCD中，∠ABC是钝角，∠ABC+∠ADC =180°，对角线AC平分∠BAD.（1）求证：BC =CD；（2）若AB +AD =AC，求∠BCD的度数；4、如图，在△ABC中，D、E、F分别为三边的中点，G点在边AB上，△BDG与四边形ACDG的周长相等，设BC =a、AC =b、AB =c.（1）求线段BG的长（2）求证：DG平分∠EDF.5、如图，BA⊥MN，垂足为A，BA=4，点P是射线AN上的一个动点（点P与点A不重合），∠B PC=∠BP A，BC⊥BP，过点C作CD⊥MN，垂足为D，设AP=x.CD的长度是否随着x的变化而变化？若变化，请用含x的代数式表示CD的长度；若不变化，请求出线段CD的长度.6、已知：平面直角坐标系中，四边形OABC的顶点分别为0（0，0）、A（5，0）、B（m，2）、C（m-5，2）.（1）问：是否存在这样的m，使得在边BC上总存在点P，使∠OP A=90°？若存在，求出m的取值范围；若不存在，请说明理由.（2）当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值.7、我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。

七年级证明题七年级上册数学证明题

七年级证明题七年级上册数学证明题ab//dc(同旁内角互补，两直线平行))在正方形abcd中，p(p靠近是d点)cd上的一点，be ap于e，df ap于f，说明△afd≌△bead--------c111111a--------bbae与 daf互余adf与 daf互余所以 bae= adf又待证明的两三角形都是rt三角形，且ab=da根据角角边定理，两三角形全等a=75第二题是不是有问题啊 gqd是30 吗应该是 gqh=30 吧还有不懂怎么算的你追问一下我们qq聊补充回答：∵ga//edebf= fhg=30 （两只线平行，同位角相等）fba= abd=（180 -30 ） 2=75∵ ahb= fhg=30 （对顶角）a=180 -75 -30 =75#formatimgid_0#还有一题等等啊补充回答：∵mn cdmhd=90∵ gqd=130gqh=180 -130 =50hgq=180 -90 -50 =40∵mn abagh=90ega=180 -90 -40 =50 您已经评价过!好:0您已经评价过!不好:0您已经评价过!原创:5您已经评价过!非原创:0第一题的答案：证明：因为这是等宽带所以ag平行de所以 ebf= gof=30 ( o 是我加上去的) 因为 ebf+ fbd=180所以 fbd=180 - ebf=150因为 fba由 abd折叠而成所以 fba= abd所以 fba=150 /2=75图为 aob和 gof为对顶角所以 aob= gof=30所以 gab=180 - abf- aob=75( gab是 a)第二题的答案：因为 dqe+ cqe=180所以 cqe=180 - dqe=50图为ab mn,cd mn所以ab平行cd所以 age= cqe=50因为mn垂直ab所以 agh=90所以 ngf=180 - ega- agh=40七年级下册证明题知识点中线定理1.三角形中，连接一个顶点和它所对边的中点的线段叫做三角形的中线。

平面几何：有关三角形五心的经典考题及证明-(中考提分助力)

平面几何：有关三角形五心的经典试题三角形的外心、重心、垂心、内心及旁心,统称为三角形的五心. 一、外心.三角形外接圆的圆心，简称外心。

与外心关系密切的有圆心角定理和圆周角定理。

例1．过等腰△ABC 底边BC 上一点P 引PM ∥CA 交AB 于M ；引PN ∥BA 交AC 于N 。

作点P 关于MN 的对称点P ′.试证：P ′点在△ABC 外接圆上。

(杭州大学《中学数学竞赛习题》）分析：由已知可得MP ′=MP =MB ,NP ′=NP=NC ，故点M 是△P ′BP 的外心,点N 是△P ′PC 的外心.有∠BP ′P =21∠BMP =21∠BAC , ∠PP ′C =21∠PNC =21∠BAC .∴∠BP ′C =∠BP ′P +∠P ′PC =∠BAC 。

从而,P ′点与A ,B ，C 共圆、即P ′在△ABC 外接圆上. 由于P ′P 平分∠BP ′C ，显然还有 P ′B ：P ′C =BP :PC .例2．在△ABC 的边AB ，BC ，CA 上分别取点P ，Q ,S .证明以△APS ，△BQP ，△CSQ 的外心为顶点的三角形与△ABC 相似。

(B ·波拉索洛夫《中学数学奥林匹克》）分析：设O 1，O 2,O 3是△APS ，△BQP ，△CSQ 的外心,作出六边形 O 1PO 2QO 3S 后再由外心性质可知 ∠PO 1S =2∠A , ∠QO 2P =2∠B ， ∠SO 3Q =2∠C 。

∴∠PO 1S +∠QO 2P +∠SO 3Q =360°.从而又知∠O 1PO 2+∠O 2QO 3+∠O 3SO 1=360°将△O 2QO 3绕着O 3点旋转到△KSO 3，易判断△KSO 1≌△O 2PO 1，同时可得△O 1O 2O 3≌△O 1KO 3。

∴∠O 2O 1O 3=∠KO 1O 3=21∠O 2O 1K=21（∠O 2O 1S +∠SO 1K )=21（∠O 2O 1S +∠PO 1O 2)=21∠PO 1S =∠A ;同理有∠O 1O 2O 3=∠B .故△O 1O 2O 3∽△ABC .A B C P P MN 'A B C K P O O O ....S 123二、重心三角形三条中线的交点，叫做三角形的重心.掌握重心将每条中线都分成定比2:1及中线长度公式，便于解题. 例3．AD ,BE ，CF 是△ABC 的三条中线，P 是任意一点.证明:在△PAD ，△PBE ,△PCF 中,其中一个面积等于另外两个面积的和. （第26届莫斯科数学奥林匹克）分析：设G 为△ABC 重心，直线PG 与AB，BC 相交.从A ,C ，D ，E ,F 分别作该直线的垂线，垂足为A ′，C ′， D ′,E ′，F ′。

七年级数学几何证明题三角形

最新版初中七年级数学题库 7.2.1 三角形的内角(含答案)

初中数学几何题100条秘籍——三角形篇

七年级数学典型几何证明50题

初中数学：利用旋转证明三角形全等综合证明题专题

北师大版七年级下册数学第四章三角形含答案(综合题)

七年级下册数学期末考试几何大题证明必考题

几何证明练习题带答案

七年级下册第三章三角形

七年级数学下册第四章三角形4用尺规作三角形直角三角形全等的判定、尺规作图、测距离试题北师大版

精品试卷：北师大版七年级数学下册第四章三角形必考点解析试题(含答案及详细解析)

初一数学_几何_三角形基础知识和基本练习题讲解

初一上册几何证明题(精选多篇)

数学几何证明题

烟台七年级数学第一章-三角形全等

最新北师大版七年级下册数学期末复习三角形全等证明练习试题以及答案

初中数学经典几何模型04-角平分线模型在三角形中的应用(含答案)

七年级证明题七年级上册数学证明题

平面几何：有关三角形五心的经典考题及证明-(中考提分助力)

七年级数学几何证明题三角形

最新版初中七年级数学题库 7.2.1 三角形的内角(含答案)

初中数学几何题100条秘籍——三角形篇

七年级数学典型几何证明50题

初中数学：利用旋转证明三角形全等综合证明题专题

北师大版七年级下册数学第四章 三角形含答案(综合题)

七年级下册数学期末考试几何大题证明必考题

几何证明练习题带答案

七年级下册第三章 三角形

七年级数学下册第四章三角形4用尺规作三角形直角三角形全等的判定、尺规作图、测距离试题北师大版

精品试卷：北师大版七年级数学下册第四章三角形必考点解析试题(含答案及详细解析)

初一数学_几何_三角形基础知识和基本练习题讲解

初一上册几何证明题(精选多篇)

数学几何证明题

烟台七年级数学第一章-三角形全等

最新北师大版七年级下册数学期末复习三角形全等证明练习试题以及答案

初中数学经典几何模型04-角平分线模型在三角形中的应用(含答案)

七年级证明题 七年级上册数学证明题

平面几何：有关三角形五心的经典考题及证明-(中考提分助力)

北师大版七年级下册数学第四章三角形含答案(综合题)

七年级下册第三章三角形

七年级证明题七年级上册数学证明题