沿程损失阻力系数的FLUENT数值模拟计算报告 李济然
管路沿程阻力测定实验报告

精心整理12101413实验一管路沿程阻力测定一实验目的1. 掌握流体流经管道时沿程阻力损失的测定方法。
2.测定流体流过直管时的摩擦阻力,确定摩擦系数λ与Re 的关系。
3.测定流体流过管件时的局部阻力,并求出阻力系数ξ。
4.学会压差计和流量计的使用。
二实验原理流体在管路中流动时,由于粘性剪应力和涡流的存在,不可避免地会引起压强损耗。
这种损耗包括流体流经直管的沿程阻力以及流体流动方向的改变或因管子大小、形状的改变所引起的局部阻力。
1.沿程阻力λ称为直管摩擦系数,滞留时,;湍流时,λ与e R 的关系受管壁粗糙度的影响,需由实验测得。
e 64R =λ根据伯努利方程可知,流体流过的沿程阻力损失,可直接得出所测得的液柱压差计度数R(m)算出:()g -R p 水指ρρ=∆2.局部阻力1)当量长度法2u d l l h 2e f ∙⎪⎪⎭⎫ ⎝⎛+=∑∑λ 2)阻力系数法2u h 2p ∙=ξ ξ-局部阻力系数,无因次;u-在小截面管中流体的平均流速(m/s )三实验装置与流程1.本实验装置及设备主要参数:被测元件:镀锌水管,管长2.0m ,管径(公称直径)0.021m ;闸阀D=3/4.1)测量仪表:U 型压差计(水银指示液);LW —15型涡轮流量计(精度0.5级,量程0.4~4.0m/h,仪器编号Ⅰ的仪表常数为599.41(次/升),仪器编号II 的仪表常数为605.30(次/升),MMD 智能流量仪)。
2)循环水泵。
3)循环水箱。
4)DZ15-40型自动开关。
5)数显温度表2.流程:3 4 5 68流体流动阻力损失实验流程图1)水箱6)放空阀11)取压孔2)控制阀7)排液阀12)U 形压差计3)放空阀8)数显温度表13)闸阀4)U 形压差计9)泵14)取压孔5)平衡阀10)涡轮流量计四实验操作步骤及注意事项1.水箱充水至80%2.仪表调整(涡轮流量计﹑MMD 智能流量计仪按说明书调节)3.打开压差计上平衡阀,关闭各放气阀。
沿程水头损失量测实验实验报告

沿程水头损失量测实验实验报告沿程水头损失实验沿程水头损失实验前言:确定沿程水头损失,首先得弄清沿程阻力系数的变化规律。
1933年尼古拉兹采用不同粒径的人工粗砂粘于管道内壁模拟粗糙的方法进行了一系列管道实验,得出了管道沿程阻力系数变化的一般规律。
(1)雷诺数Re2000 时,水流为层流,?与Re呈倒数关系,且?=64/Re. (2)2000Re4000 时,层流向紊流过渡,Re 为?的主要影响因素.(3)Re4000 时,水流处于紊流状态:(a)当Re较小时,由于粘性底层较厚,从而掩盖了圆管内壁粗糙度,流动处于紊流光滑区,?只与Re 有关,即λ=f(Re);(b)当Re 很大时,管壁糙面凸起完全深入管内紊流流核,沿程阻力主要受水流流经管壁糙面凸起时形成的小旋涡影响,流动处于紊流粗糙区,λ由相对粗糙度Δ/R(R为水力半径,下同)决定,λ=f(Δ/ d);(c)当Re 介于紊流光滑区与粗糙区之间时,λ由Re 和Δ/d 共同决定,流动处于紊流过渡粗糙区,λ=f(Δ/d,Re)。
1937 年泰科斯达在人工加糙明渠中进行了沿程阻力实验,得出了与尼古拉兹实验相似的论,说明管流和明渠流具有相同的变化规律.为满足工程实际应用的需要,人们通过实验总结出许多经验或半经验公式λ如适用于紊流光滑区的布拉修斯公式,适用于过渡粗糙区的柯—怀公式,适用于紊流光滑区的尼古拉兹经验公式,莫迪图经验公式,本实验采用莫迪图经验公式进行对比分析。
摘要:本次实验内容有,测量沿程阻力系数?,通过与莫迪图对比分析其合理性,提高实验成果分析能力;绘制lghf?lgV曲线,加深了解圆管层流和紊流的沿程损失随平均流速变化的规律。
实验原理 LV2hf??d2g 由达西公式2gdhf12gdhf?2hf2(d/Q)?K22L?L4Q得K??2gd5/8L其中hf为水头损失,?为沿程阻力系数,L为管道长度、d为管道内径,V为平均流速,另由能量方程对水平等直径圆管可得hf?(p1?p2)/h△h为测压管的液面高差实验装置实验方法与步骤准备Ⅰ对照装置图和说明,搞清各组成部件的名称、作用及其工作原理;记录有关实验常数:工作管内径d和实验管长L。
沿程损失阻力系数的FLUENT数值模拟计算报告 李济然

沿程损失阻力系数工程力学2007级李济然 20071210114 一概述:沿程损失水流流动过程中,由于固体壁面的阻滞作用而引起的摩擦阻力所造成的水头损失。
流体流动中为克服摩擦阻力而损耗的能量称为沿程损失。
沿程阻力损失与长度、粗糙度及流速的平方成正比,而与管径成反比,沿程能量损失的计算公式是:h r=λv2/(2dg)其中:l为管长,λ为沿程损失系数,d为管道内径,v2/(2g)为单位重力流体的动压头(速度水头),v为流体的运动粘度系数。
沿程损失能量损失的计算公式由带粘性的伯努利方程:v12/(2g)+p1/(ρg)+z1=v22/(2g)+p2/(ρg)+z2+h f推出:h f=(p1-p2)/ (ρg)其中:v22/(2g)——单位质量流体的动能(速度水头)。
流体静止时为0。
Z ——单位质量流体的势能(位置水头)。
p/(ρg)——单位质量流体的压力能(压强水头)。
又由量纲分析的π定理,得出Δp/(ρV2/2)=λL/d,计算出达西λ=f(Re)由于摩擦因子λ=2Δpd/(LρV2),则h f=λLV2/(2gD)d Re=Vd/v和v=μ/ρ,则λ=f(Re d)湍流光滑管的沿程损失系数按卡门一普朗特(Karmn-Prandtl)公式:1/λ1/2=2lg(Reλ1/2)-0.8当105<Re<3×106时,尼古拉兹的计算公式为:λ=0.0032+0.221Re-0.2371.湍流粗糙管过渡区 :26.98(d/ε)8/7<Re<2308(d/ε)0.85为湍流粗糙管过渡区。
该区域的沿程损失系数与按洛巴耶夫(Б.H.Лo6aeв)的公式进行计算,即λ=1.42[lg(dRe/ε)]-2=1.42[lg(1.273qv/vε)]-22.湍流粗糙管平方阻力区:2308(d/ε)0.85<Re为湍流粗糙管平方阻力区。
沿程损失系数与雷诺数无关,只与相对粗糙度有关。
平方阻力区的沿程能量损失可按尼占拉兹公式:1/λ1/2=2lg(d/2ε)+1.74关于沿程损失最著名的是尼古拉茨在1932~ 1933年问所做的实验(右图为实验装置图)。
山东大学沿程阻力实验
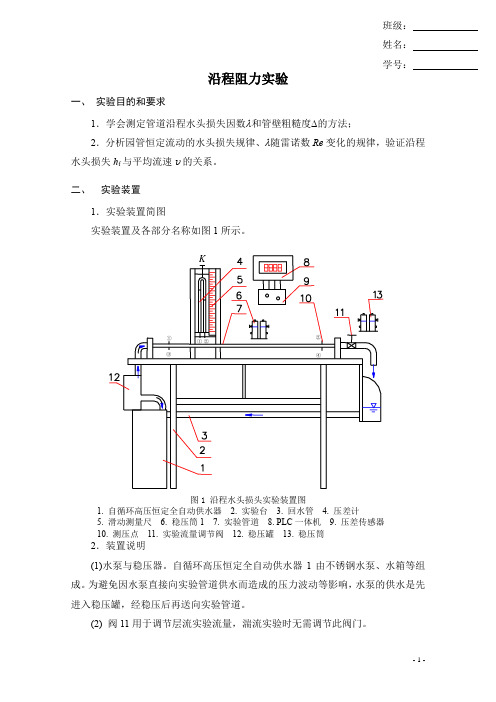
- 1 -沿程阻力实验一、 实验目的和要求1.学会测定管道沿程水头损失因数λ和管壁粗糙度∆的方法;2.分析园管恒定流动的水头损失规律、λ随雷诺数Re 变化的规律,验证沿程水头损失h f 与平均流速v 的关系。
二、 实验装置1.实验装置简图实验装置及各部分名称如图1所示。
图1 沿程水头损头实验装置图1. 自循环高压恒定全自动供水器2. 实验台3. 回水管4. 压差计5. 滑动测量尺6. 稳压筒17. 实验管道8. PLC 一体机9. 压差传感器 10. 测压点 11. 实验流量调节阀 12. 稳压罐 13. 稳压筒2.装置说明(1)水泵与稳压器。
自循环高压恒定全自动供水器1由不锈钢水泵、水箱等组成。
为避免因水泵直接向实验管道供水而造成的压力波动等影响,水泵的供水是先进入稳压罐,经稳压后再送向实验管道。
(2) 阀11用于调节层流实验流量,湍流实验时无需调节此阀门。
K① ②①②③④班级: 姓名: 学号:(3) 实验管道7为不锈钢管,其测压断面上沿十字型方向设有4个测压孔,经过均压环与测点管嘴相连通。
(4) 本实验仪配有压差计4(倒U型气-水压差计)和压差仪8,压差计测量范围为0~0.3 mH2O;压差电测仪测量范围为0~10 mH2O,视值单位为10-2 mH2O。
压差计4与压差电测仪8所测得的压差值均可等值转换为两测点的测压管水头差,单位以m表示。
在测压点与压差计之间的连接软管上设有小电磁阀,湍流实验时关闭,其他操作时均处于打开状态。
3.基本操作方法(1)实验准备:①打开测控型电测仪总电源,点击进入系统按钮,系统进入操作界面(界面提示:请按“系统启停”键启动);②点击“系统启停”按键,黄灯亮说明系统未开启,绿灯亮则说明系统已启动,实验过程中关闭可直接退出系统,退出后系统自动开阀、打气、排水保洁,然后进入待机(界面提示:请按“实验准备”键);③点击“实验准备”按键,系统自动完成下列操作:阀门开度调到约、打开小电磁阀、高低频率调节数次,使调压筒内加水到设定水位、U型测压计加水排气,最后全关出水阀门,实验准备完毕,可进入实验(约1分钟,界面提示:正在关阀中——调压筒第一次上水——调压筒第二次上水——正在关阀中——已完成实验准备,请选择层流或湍流进行实验)。
沿程阻力系数测定-实验报告

=KX h f / Q 2沿程水头损失实验实验人XXX 合作者XXXXX 年 XX 月 XX H一、实验目的1. 加深了解圆管层流和紊流的沿程损失随平均流速变化的规律,绘 制lghf 〜-lgy曲线;2. 掌握管道沿程阻力系数的量测技术和应用压差计的方法;3. 将测得的R 厂入关系值与莫迪图对比,分析其合理性,进一步提 高实验成果分析能力。
二、实验设备本装置有下水箱、自循环水泵、[供水阀、稳压筒、实验管道、流量 调节阀]三组,计量水箱、回水管、压差计等组成。
实验时接通电源水 泵启动,全开供水阀,逐次开大流量调节阀,每次调节流量时,均需稳 定2-3分钟,流量越小,稳定时间越长;测流量时间不小于8-10秒; 测流量的同时,需测记压差计、温度计[自备,应挂在水箱中]读数。
三 根实验管道管径不同,应分别作实验。
三、实验原理由达西公式h r = 2 • — •-—得2 =〃 2g另有能量方程对水平等直径圆管可得宀 对于多管式水银压差有下列关系hf= (Pi —P2) / Y .= ( Y « / V w — 1 ) (h 2—hi+hi —hs) =12. 6Ah a △ h ni - h?—hi+hi — h :<四、实验结果与分析实验中,我们测量了三根管的沿程阻力系数,三根管的直径分别为 10mm, 14mm,2gdh f _20mm o对每根管进行测量时,我们通过改变水的流速,在相距80cm的两点处分别测量对应的压强。
得到表1至表3中的实验结果。
相关数据说明:水温29.4°C,对应的动力学粘度系数为v = 0.0k7«2/5流量通过水从管中流入盛水箱的体积和时间确定。
水箱底面积为S = 20x20 cm2,记录水箱液面升高h = \2cm(从5cwi到17c/w或者从6cm 5*1 1 Scm)的时间从而计算出流量0二竺=削(期3/小f心)若管道直径为D,则水流速度为心腔;对三根管进行测量时,测量的两点之间距离均为L = S(km ;雷诺数Ry四;计算沿程阻力系数:层流人=里;紊流A,= 0.316 Re-0 25 v Re测量沿程阻力系数:A = Kh,/Q29其中K"g£>5/8厶,g=g.Sm/s2第一根管表一1 ( £)] = 10〃〃儿K[ =15.1 \ 3cnr / s2 )第二根管表一2 ( D2 = 14〃〃儿K2 =81 .280C/H52第三根管表一3 ( a = 20〃〃”, K3 = 483.610c/n‘ /s2通过对三根管的相关计算,我们发现实验测出的沿程阻力系数远远比层流情况下的计算值大,将近大一个数量级。
基于CFD的沿程阻力系数的计算

山西科技SHANXI SCIENCE AND TECHNOLOGY 2019年第34卷第2期长距离输水是实现水资源优化配置和水量合理调配的重要工程措施,输水管道水力计算的首要任务就是正确计算沿程水头损失,合理配置升压泵。
沿程水头损失的合理计算直接影响工程投资和运行费用[1],传统的确定沿程水头损失的方法是基于尼古拉兹方法的管壁贴砂试验[2],这种方法建立在反复实验的基础上,需要耗费大量的人力、财力和时间,而且研究范围有限,不能满足飞速发展的工程建设的需要。
近年来,随着计算机的发展与普及,数值模拟成为研究流体流动、开展流体力学实验的重要辅助手段[3-4]。
本文将采用基于C FD 原理的数值模拟方法,研究沿程水头损失变化规律。
1研究方法1.1沿程水头损失的定义沿程水头损失是指在固体边界平直的流体流动中,单位质量的流体自一断面流到另一断面所损失的机械能。
图1为有压管道流动示意图,其中沿程水头损失采用h f 表示。
依据重力场中不可压缩黏性流体恒定流的伯努利方程,写出图1中1-1到2-2断面的方程为:z 1+p 1ρg +v 122g =z 2+p 2ρg +v 222g+h f(1)式中:z 1和z 2为管轴线距离基准面的位置,如取基准面为管轴线位置,则z 1=z 2=0;p 1和p 2为管轴线处动水压强;v 1和v 2为断面平均流速,其中流速v 1=v 2=4Qπd 2,沿程不变;ρ为流体密度,g 为重力加速度。
将式(1)变形并简化得:h f =p 1-p 2ρg=Δpρg (2)另据达西—魏斯巴赫公式:h f =λl d v 22g(3)式中:l 为管长,λ为沿程阻力系数。
比较式(2)和(3)可得:λ=(Δpρg )/(l d v 22g)(4)────────────────*基金项目:山西大学第十六期本科生科研训练项目“沿程阻力系数的数值模拟”(项目编号:2018016506)。
**通信作者:张晓艳,1970生,山西大学动力工程系副教授,硕士,主要研究方向为水力学及河流动力学,邮箱:1015858702@ 。
基于fluent的阻力计算

湍流动能k方程:
(2.15)
湍流耗散率ε方程:
(2.16)
与标准k −ε模型相比较发现,RNG k−ε模型的主要变化:
通过修正湍动粘度,考虑了平均流动中的旋转流动情况;
在ε方程中增加了一项,从而反映了主流的时均应变率Eij,这样,RNG k−ε模型中产生项不仅与流动情况有关,而且在同一问题中也还是空间坐标的函数。
2.流动出口边界的位置选取
如果流动出口边界太靠近固体障碍物,流动可能尚未达到充分发展的状态(在流动方向上梯度为零),这将导致相当大的误差。一般来讲,为了得到准确的结果,出口边界必须位于最后一个障碍物后10倍于障碍高度或更远的位置。对于更高的精度要求,还要研究模拟结果对出口位于不同距离时的影响的敏感程度,以保证内部模拟不受出口位置选取的影响。
粘性不可压缩流体流动数学模型
连续方程
任何流动问题都必须满足质量守恒方程即:连续方程。根据连续介质假设,单位时间内流体微团的质量变化等于同时间间隔内进入微团的总净质量。按照这一定律,连续方程数学表达式写为:
(2.1)
以上是在笛卡尔直角坐标系下表示,上面给出的是瞬态可压流体连续方程。由于对于潜艇粘性流场介质的不可压缩,密度ρ为常数,引入散度算子,则方程(2.1)变成为:
(2.8)
将式(2.8)代入(2.1)和(2.7)再对时间积分就会得到下面的平均流方程。
(2.9)
(行业报告)沿程水头损失实验报告(报告范文)

沿程水头损失实验一、实验目的要求1、加深了解圆管层流和紊流的沿程水头损失随平均流速变化的规律,绘制v h f lg ~lg 曲线;2、掌握管道沿程阻力系数的量测技术和应用气—水压差计及电测仪测量压差的方法;3、将测得的 ~e R 关系值与莫迪图对比,分析其合理性,进一步提高实验成果分析能力。
二、实验装置本实验的装置如图7.1所示图7.1 自循环沿程水头损失实验装置图1.自循环高压恒定全自动供水器; 2.实验台; 3.回水管; 4.水压差计; 6.实验管道; 7.水银压差计;8.滑支测量尺; 9.测压点; 10.实验流量调节阀; 11.供水管与供水阀; 12.旁通管与旁通阀; 13.稳压筒。
根据压差测法不同,有两种方式测压差: 1、低压差时用水压差计量测;2、高压差时用电子量测仪(简称电测仪)量测(但本仪器暂时不能测定高压)。
本实验装置配备有:1、自动水泵与稳压器自循环高压恒定全自动供水器由离心泵、自动压力开关、气—水压力罐式稳压器等组成。
压力超高时能自动停机,过低时能自动开机。
为避免因水泵直接向实验管道供水而造成的压力波动等影响,离心泵的输水是先进入稳压器的压力罐,经稳压后再送向实验管道。
421.压力传感器;2.排气旋钮;3.连接管;4.主机2、旁通管与旁通阀由于本实验装置所采用水泵的特性,在供小流量时有可能时开时停,从而造成供水压力的较大波动,为了避免这种情况出现,供水器设有与蓄水箱直通的旁通管(图中未标出)。
通过分流可使水泵持续稳定运行。
旁通管中设有调节分流量至蓄水箱的阀门,即旁通阀,实验流量随旁通阀开度减小(分流量减小)而增大。
实际上旁通阀又是本装置用以调节流量的重要阀门之一。
3、稳压筒为了简化排气,并防止实验中再进气,在传感器前连接由2只充水(不满顶)之密封立筒构成。
4、电测仪由压力传感器和主机两部分组成,经由连通管将其接入测点(图7.2),压差读数(以厘米水柱为单位)通过主机显示。
三、实验原理由达西公式 (p 1-p 2)/ρ = Σhf =λLv 2/2d得 λ= △p*2d/ρL v 2 △p = ρgh则 λ= 2ghd / L v 2 (1)另由能量方程对水平等直径圆管可得γ/)(21p p h f -= (2) 流速计算公式 u = q / A = 4q / πd 2 雷诺数公式 Re = ρdv / μ压差可用压差计或电测。
沿程阻力数据处理
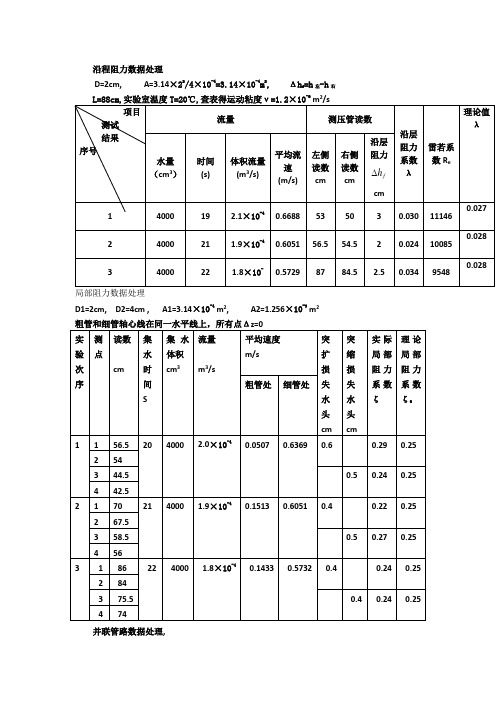
孔板前后测 压管液面差 ΔH cm
管路流量
分管路流量和 cm3/s
cm3/s
1
总管路 管路 3 管路 2 管路 1
140 105 85 94 114 80 78 70 90 57 54 44
75 58 65 64 62 46 60 48 49 29 39 26
65 47 20 30 52 34 18 22 41 28 15 18
-4
0.27
0.25
3
22
4000
0.1433
0.5732
0.4
0.24
0.25
0.4
0.24
0.25
并联管路数据处理,
孔 板 处 近 似 为 管 路 突 然 缩 小 模 型 , 取 ζ =0.5 ( 1-A2/A1 ) , 总 管 路 : A’/A=0.5, ζ =0.25,A’=2.27×10
56.5 54 44.5 42.5 70 67.5 58.5 56 1 2 3 4 86 84 75.5 74
20
4000
2.0×10
-4
0.0507
0.6369
0.6
0.5 1.9×10
-4
0.24
0.25
2
1 2 3 4
21
4000
0.1513
0.6051
0.4
0.22
0.25
0.5 1.8×10
810 215 223 373 718 183 212 320 643 166 194 289 649 715 811
2
总管路 管路 3 管路 2 管路 1
3
总管路 管路 3 管路 2 管路 1
结论:由表格数据可见,在误差允许的范围内,Q=Q1+Q2+Q3,即并联管路的干路流量 等于个支路流量之和。
沿程损失阻力系数的FLUENT数值模拟分析

沿程损失阻力系数的FLUENT数值模拟分析沿程损失阻力系数是计算流体力学中常用的一个参数,用来描述在流体输送管道中流体因于各种原因而失去动能所引起的压力损失。
在工程实际应用中,准确地预测沿程损失阻力系数对于设计和优化管道系统有着重要意义。
因此,针对沿程损失阻力系数的数值模拟研究具有一定的实际应用价值。
数值模拟方法是研究沿程损失阻力系数的一种有效手段,其中FLUENT是一种常用的计算流体力学软件。
通过数值模拟可以在计算机上对复杂的流体运动进行模拟和分析,从而获得各种流场参数,如速度、压力以及沿程损失阻力系数。
首先,进行沿程损失阻力系数的FLUENT数值模拟时,需要选择合适的计算模型。
一般来说,可以选择稳态或者非稳态模型。
对于稳态流动,可以根据计算区域的边界条件和物质输送的速度来设置相应的边界条件。
对于非稳态流动,需要分析和模拟输送过程中的时间变化。
其次,针对FLUENT数值模拟过程中的计算网格划分也需要进行合理的设计。
计算网格的划分要遵循准确性和计算效率的原则。
一般来说,对于复杂的流动问题,需要使用更为精细的网格划分方法来获得更为准确的结果。
同时,在计算网格的划分中还要考虑到流场中可能存在的不连续性和流动难以预测的因素。
此外,在进行FLUENT数值模拟时,还需要设置流体的物性,包括密度、动力粘度等。
这些物性参数的准确性对于模拟结果的精度和可靠性有着重要影响。
在设置物性时,可以参考相关的物性数据手册或者实验测试结果来获得尽可能准确的参数。
最后,在进行FLUENT数值模拟时,还需要设置相应的求解器和求解算法等。
在设置求解器时,可以根据具体问题的模拟对象和目标进行选择。
对于沿程损失阻力系数的模拟,可以选择合适的求解器来求解和分析压力和速度等流场参数。
在设置求解算法时,可以根据计算资源、时间要求和模拟准确性等因素进行选择和调整。
综上所述,FLUENT数值模拟可以有效地分析沿程损失阻力系数。
通过合适的计算模型、网格划分、物性设置和求解器选择等步骤,可以获得较为准确的模拟结果。
管路沿程水头损失试验

六、注意事项:
1、不要旋动电测仪主机上
旋钮
电测仪 主机
任何旋钮,电测仪已调好零点,可直接使用;
2、流量改变通过流量调节阀12,不要动阀10、11;
3、力求在实验设备整个流量范围内都均匀取到点, 实验数据记录可参考实验指导书上29页表3.12;
4、希望同学们在实验过程中爱护实验仪器。
秤 接水容器 秒表
秤 测量水重
QV t
式中V为t时间内水的体积;t为测量时间。 上图为测量流量的实验装置。
(3)流体运动粘度 的测量: 通过测定水温计算得到。
五、λ-Re曲线:
0.45
Hale Waihona Puke .0.4 0.35 0.3 0.25
...........
0.2
4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9
一、实验目的:
1.掌握管道沿程阻力系数λ的测量技术。 2.通过测定不同雷诺数Re时的沿程阻力
系数λ,从而掌握λ与Re的影响关系。
二、实验原理:
由达西公式
hf
l d
v2 2g
可得到
2gdhf
lv2
(1)
为沿程阻力系数;h f 管路沿程水头损失;v 断面平均流速;
l 实验管道长度;d 实验管道内径。
4
1
6-天平秤(测量水重) 7-秒表(测量时间) 8-实验段起点 9-实验段终点 10-实验段尾阀
11-实验供水阀 12-供水流量调节阀 13-调压筒
四、测量方法:
由
2 gdh f lv2
(1)、Re
vd
(2)、v
4Q
d2
(3)式可知实验
曲线隧道施工通风沿程阻力损失数值模拟

第16卷增刊2地下空间与工程学报Vol.16 2020年11月Chinese Journal of Underground Space and Engineering Nov.2020曲线隧道施工通风沿程阻力损失数值模拟*骆阳1,王英学1,宋相帅1,罗燕平2,文展3(1.西南交通大学土木工程学院,成都610031;2.四川川交路桥有限责任公司市政分公司,四川德阳618300;3.辽宁第一交通工程监理有限公司,沈阳110000)摘要:山岭地区修建隧道,受地形、地质等条件限制,时有采用曲线隧道方案。
相比于传统直线隧道,曲线隧道在施工通风方面存在差异。
本文依托某特长曲线隧道工程,采用三维数值模拟,建立“风机-风管-隧道”施工通风系统模型,对不同半径、不同风速条件下,曲线隧道及风管沿程阻力损失进行计算,并与直线隧道进行对比,得出下述结论:(1)曲线隧道沿程阻力损失系数随曲线半径减小而增大,受风速影响较小,与掌子面距离400m后发展稳定,并拟合出计算公式;(2)风管沿程阻力损失系数受隧道曲线半径和风速影响较小,与风机距离100m左右已发展稳定。
本文可为曲线隧道施工通风沿程阻力损失系数的选取提供参考,具有实际工程意义。
关键词:曲线隧道;施工通风;沿程阻力损失系数;数值模拟中图分类号:U453.5文献标识码:A文章编号:1673-0836(2020)增2-0897-07Numerical Simulation of Construction VentilationResistanceLoss along the Curved TunnelLuo Yang1,Wang Yingxue1,Song Xiangshuai1,Luo Yanping2,Wen Zhan3(1.School of Civil Engineering,Southwest Jiaotong University,Chengdu610031,P.R.China;2.Sichuan ChuanjiaoRoad&Bridge Co.,Ltd.,Deyang,Sichuan618300,P.R.China;3.Liaoning First Transportation Engineering Supervision Co.,Ltd.,Shenyang110000,P.R.China) Abstract:The construction of tunnels in the mountainous areas is restricted by terrain and geology,and the curve tunnel scheme is adopted.Compared with the traditional straight tunnel,the construction ventilation of curvedtunnel is different.Based on the extra long curved tunnel,this paper uses three-dimensional numerical method toestablish a“fan-wind pipe-tunnel”construction ventilation model,and calculates the resistance loss of curved tunnelsand wind pipe under different curve radius and the speeds of wind conditions.And the results are compared with thestraight tunnel.The following conclusions are drawn.(1)The resistance coefficient along curved tunnel increases withthe decrease of curve radius,and it is less affected by wind speed.It develops steadily after400m away from theworking face,and the calculation formula is fitted.(2)The resistance coefficient along the wind pipe is less affectedby the radius of the tunnel and the wind speed.It develops steadily after100m away from the fan.This paper canprovide a reference for the selection of resistance coefficient for tunnel construction ventilation,which has practicalengineering significance.Keywords:curved tunnel;tunnel construction ventilation;resistance coefficient;numerical simulation *收稿日期:2020-05-07(修改稿)作者简介:骆阳(1994—),男,重庆合川人,硕士生,主要从事隧道及地下工程等领域的科研工作,E-mail:2733498803@qq.com通讯作者:王英学(1972—),男,吉宁东辽人,博士,教授,主要从事高速铁路隧道空气动力学和隧道施工力学方面的科研工作,E-mail:wangyingxue@swjtu.edu.cn0引言随着我国交通事业的不断发展,隧道修建得越来越多,其中不乏曲线隧道,曲线半径从几百到几千米不等。
沿程水头损失实验报告

2.沿程水头损失实验一、实验目的1.通过实验了解圆管层流和紊流的沿程损失随平均流速变化的规律,绘制lgh f ~-lgv 曲线;2.掌握管流沿程阻力系数的量测技术和应用压差计的方法; 3.将测得的Re-λ关系值与莫迪图对比,提高实验成果分析能力。
二、实验原理对于圆管稳定流动,达西公式给出:gv d L h f 22⋅⋅=λ 对于给定管径、管长的圆管稳定流,由达西公式可得:22522228422Qh K Qh Lgd d Q L gdh Lvgdh f f f f ⨯=⨯=⎪⎭⎫ ⎝⎛==ππλ式中:Lgd K 852π=对水平安装的等直径圆管,由能量方程可得:γ21P P h f -=对于指示液,被测液体均为水的U 形管压差计,有:2121h h P P h f -=-=γ式中h f ——测定管段L 的沿程水头损失,cmH 2Oγ——实验水温和大气压力下的水容重三、实验装置1.沿程水头损失实验装置1套,结构示意如图1所示2.秒表1块3.温度计1支4.管径d=1.0cm 。
图1 沿程水头损失实验装置示意图1.水箱(内置潜水泵)2.供水管3.电器插座4.`流回水管5. 整流栅板6. 溢流板7.水箱8. 测压嘴9.实验管道10.差压计11.调节阀门12.调整及计量水箱13.回水管14.实验桌 15旁通管阀门 16 进水阀门本装置有下水箱、自循环水泵、供水阀、稳压水箱、实验管道、流量调节阀,计量水箱、回水管、压差计等组成。
实验时应将管道、胶管及压差计内的空气排出,接通电源水泵启动,开启供水阀,逐次开大流量调节阀,调整两个阀门开度。
每次调节流量时,均需稳定2-3分钟,流量愈小,稳定时间愈长;测流量时间不小于8-10秒;测流量的同时,需测记压差计、温度计[自备]应挂在水箱中读数。
四、实验步骤1.对照装置图和说明,搞清各组成部件的名称、作用及其工作原理,记录有关常数管道内径d ,测量管段长度L ,水箱长a 和宽b ;2.检查储水箱水位(不够高时冲水),旁通阀是否已关闭;3.接通电源,启动水泵,全开进水阀16,水泵自动开启供水,保持溢流板有稍许溢流。
沿程损失的简单分析

管道流动沿程损失的数值模拟及实验一、 背景流体在管道中流动时, 存在一定的能量损失,为克服摩擦阻力而损耗的能量称为沿程损失。
沿程损失与管道长度、管径、粗糙度及流体的流速都存在一定的关系。
二、原理如图所示,当流体从1点流至2点时,其流体的总能量(动能、压能和势能)将降低。
根据伯努利方程:2212112222l j V V p gz p gz E E ρρρρ++=++++(1.1)式中,111,,V p z 分别为1点处的流速、压强和高度;222,,V p z 分别为2点处的流速、压强和高度;ρ为流体的密度;g 为重力加速度;,l j E E 分别为沿程和局部能量损失。
沿程能量损失是指流体在直径不变的管道中流动,流动未发生急变时的能量损失。
用量纲分析的方法,沿程能量损失可用下面公式来计算:(Re)21),,,,(E 2λρμρd lV V d l f l ==,其中,l ,d 分别为管道的长度和直径;λ为沿程阻力系数,是雷诺数Re (Re Vd ν=,ν为流体的运动粘性系数)的函数。
三、 数值模拟用FLUENT 软件进行数值模拟,计算沿程阻力系数的方案:12(1)几何模型:建立三维管道模型,设置管径d=50mm , l=20d=1m 如下图(1):1 d 2图(1)(2)网格划分与计算:划分网格时,由于在边界上参量变化较大,边界层上网格应加密,设置相关系统参数后进行计算。
总体网格划分:边界层加密:·分析,直径d=0.5,根据边界 层与雷诺数和管道尺寸的关系2/1Re ~)(-d v d d δ,得出,边界层的厚度为0.01左右,如图 所示加密边界层。
lV(3)结果分析:对截面1、2进行分析,根据伯努利方程: 2212112222l j V V p gz p gz E E ρρρρ++=++++,由于从截面1到截面2没有截面突扩,没有高度差,管道尺寸也没有发生改变,则管道的局部损失0=j E ,两截面高度差021=-=∆z z z ,两截面处的速度V V V ==21,故沿程损失21p p E l -=,得沿程阻力系数221)(2lVdp p ρλ-=。
沿程阻力损失系数

沿程阻力损失系数沿程阻力损失系数是指在流体通过管道或管路时,由于管道摩擦和流体作用产生的阻力损失的程度。
阻力损失是流体力学中的一个重要概念,对于流体输送、压力损失和能量消耗有着重要的影响。
沿程阻力损失系数可以通过实验、经验公式或数值计算等方式进行求解。
在实际工程中,为了减小能量损失、提高流体传输效率,需要对沿程阻力损失进行研究和计算。
下面详细介绍一下沿程阻力损失系数的计算方法和影响因素。
计算方法:沿程阻力损失系数的计算方法有很多,常用的包括实验法、经验公式法和数值计算法。
实验法是通过在实验室或实际工程中进行流体流动实验,测量相应的压力差和流量,然后根据实验结果进行分析和计算,得到阻力损失系数。
经验公式法是通过总结大量实验数据,将实验结果归纳总结为简化的公式,以便工程应用。
例如,在圆形管道中流动的液体,可以使用达西公式进行计算:ΔP = λ(ρV^2/2)l/D,其中,ΔP为压力损失,λ为阻力损失系数,ρ为密度,V为平均流速,l为管道长度,D为管道直径。
数值计算法是利用数值计算方法,将流体流动过程划分为无数个小单元,通过迭代计算得到整个流程中的压力分布,进而计算出阻力损失系数。
数值计算方法通常使用计算流体力学(CFD)软件进行模拟。
影响因素:沿程阻力损失系数受到多个因素的影响,主要包括以下几个方面:1. 流体性质:流体的黏度、密度、流变性质和温度等都会影响阻力损失系数。
黏度越大,阻力损失系数越大;密度和温度增加会增大阻力损失系数。
2. 管道几何形状:管道的直径、长度和壁面粗糙度等几何形状参数对阻力损失系数有重要影响。
直径越小、长度越长、壁面越粗糙,阻力损失系数越大。
3. 流体流速:流速的大小对阻力损失系数有显著影响。
当流速较小时,阻力损失系数较小;而当流速较大时,阻力损失系数增大。
4. 流动条件:流动状态(层流或湍流)、流动方向和流体的入口和出口条件等都会影响阻力损失系数。
层流流动时,阻力损失系数较小;而湍流流动时,阻力损失系数增大。
自-实验5沿程阻力损失

《沿程阻力水头损失》实验报告
开课实验室: 2011年5月19日
学院
城环学院
年级、专业、班
环境09级01班
姓名
成绩
课程
名称
流体力学
实验项目
名称
0.298
2
266
120
2.22
5.936
30.7
7.914
517.5
17.10
16.85
0.25
0.113
0.124
3
394
90
4.38
11.71
31.2
7.850
1029.3
17.20
16.60
0.60
0.070
0.062
4
536
60
8.93
23.88
31.7
7.750
2126.1
17.80
15.75
沿程阻力水头损失
指导教师
江岸
教师评语
教师签名:
年月日
一、实验目的
1.加深了解圆管层流和紊流的沿程损失随平均流速变化的规律;
2.掌握管道沿程阻力系数的量测技术和应用气—水压差计及电测仪测量压差的方法;
3.将测得的 关系值与莫迪图对比,分析其合理性,进一步提高实验成果分析能力。
二、实验原理
由达西公式:
得:
c)改变流量3次,重复上述步骤。
d)层流~~稳流过渡区 测量
加大流量,测量2次过渡区实验数据并记录。
e)紊流实验1、关闭流Fra bibliotek调节阀,将电测仪读数(即管道两测点压差)调零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沿程损失阻力系数
工程力学2007级李济然 20071210114 一概述:
沿程损失水流流动过程中,由于固体壁面的阻滞作用而引起的摩擦阻力所造成的水头损失。
流体流动中为克服摩擦阻力而损耗的能量称为沿程损失。
沿程阻力损失与长度、粗糙度及流速的平方成正比,而与管径成反比,沿程能量损失的计算公式是:
h r=λv2/(2dg)
其中:l为管长,λ为沿程损失系数,d为管道内径,v2/(2g)为单位重力流体的动压头(速度水头),v为流体的运动粘度系数。
沿程损失能量损失的计算公式由带粘性的伯努利方程:
v12/(2g)+p1/(ρg)+z1=v22/(2g)+p2/(ρg)+z2+h f
推出:
h f=(p1-p2)/ (ρg)
其中:
v22/(2g)——单位质量流体的动能(速度水头)。
流体静止时为0。
Z ——单位质量流体的势能(位置水头)。
p/(ρg)——单位质量流体的压力能(压强水头)。
又由量纲分析的π定理,得出Δp/(ρV2/2)=λL/d,计算出达西
λ=f(Re)由于摩擦因子λ=2Δpd/(LρV2),则h f=λLV2/(2gD)
d Re=Vd/v和v=μ/ρ,则λ=f(R
e d)
湍流光滑管的沿程损失系数按卡门一普朗特(Karmn-Prandtl)公式:
1/λ1/2=2lg(Reλ1/2)-0.8
当105<Re<3×106时,尼古拉兹的计算公式为:
λ=0.0032+0.221Re-0.237
1.湍流粗糙管过渡区 :26.98(d/ε)8/7<Re<2308(d/ε)0.85为湍流粗糙管过渡区。
该区域的沿程损失系数与按洛巴耶夫(Б.H.Лo6aeв)的公式进行计算,即
λ=1.42[lg(dRe/ε)]-2=1.42[lg(1.273qv/vε)]-2
2.湍流粗糙管平方阻力区:2308(d/ε)0.85<Re为湍流粗糙管平方阻力区。
沿程损失系数与雷诺数无关,只与相对粗糙度有关。
平方阻力区的沿程能量损失可按尼占拉兹公式:
1/λ1/2=2lg(d/2ε)+1.74
关于沿程损失最著名的是尼古拉茨在1932~ 1933年问所做的实验(右图为实验装置图)。
其测得曲线,从此得出了几个重要结论:
1.层流区:Re<2320为层流
区。
在该区域内,管壁的相对粗
糙度对沿程损失系数没有影响。
2.过渡区:2320<Re<4000
为由层流向湍流的转换区,可能
是层流,也可能是湍流,实验数据分散,无一定规律,如图中的区域所示。
3.湍流光滑管区:4000<Re <26,98(d/ε)8/7,为湍流光滑管区。
勃拉修斯(p.Blasius )1911年用解析方法证明了该区沿程损失系数与相对粗糙度无关,只与雷诺数有关,并借助量纲分析得出了4×10e3<Re <10e5范围内的勃拉休斯的计算公式为
λ=0.3164/Re 0.25
二 实验目的:
1、测量管道两端压差ΔP
2、应用粘性的伯努利方程,求出管道的沿程能量损失hf
3、根椐hf=λlv2/(2gd),求出λ值,并绘出λ-f (Red)曲线。
三 实验原理:
由连通器原理,在管道上安装一根U 形管,U 形管两端与测压孔连通,U 形管中间有一阀门3与大气相通(见装置图),将要测量之溶液注入U 形管内,首先打开阀门3,用泵将管道中空气排出后,然后关闭阀门3。
U 形管内溶液的密度ρ为已知,当管道两端测压孔处存在压差时, U 形管中的二液面将有高差h ∆,由此,根据水静力学基本方程
p g h ρ∆=∆,由测出的高差h ∆,可求出管道两端测压孔处的压差p ∆。
四实验装置图
五实验过程
1、打开水伐,将水箱放满水,打开管路中的阀门一和阀门二,
然后再打开泵的电源开关,检查整个实验装置水路是否畅通。
2、当实验装置水路稳定后,再利用阀门三将U形管中的气体排
出,随后观察U形管中之液面的变化。
3、计录U形管中两端的水压差高度h 。
并记入记录表格。
测读
时应尽量减少误差。
4、记录表格
λ1为布拉休斯解
管径d=42mm管长L=3000mm μ=0.0012kg/m*s ρ=999kg/m3
六计算模型:
研究湍流水力光滑区的达西摩擦因子与Re的关系。
在FLUENT 中通过改变流速或者粘度系数控制Re,并进行数值模拟,从而计算出管中试验段两端的压力的差值,即可得到沿程损失阻力系数,再将所得的值与水力光滑区曲线对比,判断其是否正确。
模型:建立一个半径r=21mm,长l=5m的圆截面直管,其中前2m 是前置段,用来让湍流充分发展,后3m为实验段。
假设其材料是光
kg/m,粘度系数滑的,没有摩擦,内部流体为水。
设水的ρ为10003
μ为0.001kg/(m*s)。
左图就是试算的velocity inlet后端y v云图,说明在试验段之前设置前置段还是十分有必要的。
由于液体的粘性力作用,在壁面附近有比较大的速度梯度,而且在入口端是湍流发展段,所以需要端面使用边界层网格加密,轴向在
入口处加密。
具体步骤是:
1.做半径为0.22的圆。
2.做出x=0.022,y=0,z=5的点,并连接圆上与其对应的两点。
3.为该线line mesh,选择ratio 1.04,
让网格在圆附近加密。
在此同时将将端面的
圆分成60等分线网格。
4.使用sweep命令,选上with mesh
选项,让直线绕圆周旋转成圆柱面,并且将
网格自动画好。
5. 端面上创建边界层网格,first percentage在这里取了
14,rows取5层。
6. 为端面直接画面网格,由于之前端面的圆已经分好了网格和
边界层网格,不用设定参数gambit自动画网格,完成后如下图。
7.在生成体的选项中选择sweep,勾选with mesh选项,让圆端面沿管轴线方向扫过,即可完成体网格的绘制。
8.最后选择求解器(solver)Fluent 5/6,设置入口、壁面和出口。
注意:在画边界层网格时有个方向选择问题,打开edge的list里面,每个edge其实可以点多次,具体多少次看该edge属于多少个face,通过试验,就可以看到边界层具体会向哪个方向生成。
七数值模拟及数据处理
由于光滑圆管,则达西摩擦因子λ只是Re的函数。
Re<2000时,
圆管中的流动属于层流,在泊肃叶的实验中,经验公式为:
λ=64/Re d
Re d定义为dv/v,在这里V为距入口10m(即试验段的起始端)的截面平均流速,湍流时的Re也如此定义。
在圆管流动中雷诺数Re>2000时才进入湍流状态,并且在2000<Re<4000时,为层流向湍流过渡区。
为了更好的与尼古拉茨试验的比对,选择Re d=3*103~105内的10个值3500、4000、4500、5000、6000、7000、9000、12000、15000、20000作为入口的Re,具体的Re d需模拟后才能得出,再将这几个数值作出曲线和误差分析。
使用ANSYS12.0中的Fluent作为流场模拟的软件,在这里圆管属于细长结构中的流动用双精度模式模拟精确一些。
准备使用k-epsilon和S-A湍流模式分别计算。
Re in为入口雷诺数,v为入口速度,p1是试验段起始端的压力,p2是试验段结束端的压力。
Re d为实验段起始处雷诺数。
λ1和λ2分别为模拟算出的达西摩擦因子和用布拉休斯公式算出的达西摩擦因子。
标准k-epsilon在壁面区使用了不够精确的近壁函数的半经验公式,以及工况中流场为层流向湍流的过度区都有可能导致误差过大。
将FLUENT中对K-epsilon做修改(见附录二)。
再通过此表数据作出拟合曲线与布拉休斯公式的解对比,分析误差。
增强壁面函数的K-epsilon湍流模式计算结果
对比标准k-epsilon的精度高多了,但是仍然不够精确。
如果将网格划分得更精细些,将更好的控制误差。
S-A湍流模式计算
以上是两种湍流模式模拟的曲线图,很明显S-A模式模拟出的结果优于k-epslion模式的。
[参考文献]
[1] 周光垌,严宗毅,许世雄,章克本.流体力学[M].北京;高等教育出版社,2000.
[2] 周志军,林震,周俊虎,刘建忠,岑可法.不同湍流模型在管道流动阻力计算中的应用和比较[J].热力发电。
2007。
[3] 宁方飞,徐力平.Spalart—Allmaras湍流模型在内流流场数值模拟中的应用[J].工程热物理学报。
2001。
