系统辨识复习提纲(答案版)
云南-系统辨识基础(08243)复习资料

系统辨识基础(08243)复习资料选择题:1.描述线性连续系统的模型有?2.描述线性离散系统的模型有?3.辨识的准则是指?4.辨识中常用的误差是?5.如果系统的结构、组成和运动规律已知,则系统可以称为?6. 如果系统的结构、组成和运动规律部分已知称之?全部未知?7.下列哪种信号是辨识中常用的输入信号?8.频谱覆盖宽、能量均匀分布是哪种信号的特点?9. 系统辨识的基本内容?10下列哪种辨识方法需要输出量条件概率密度函数的先验知识?11.下列属于图表模型的是?12.下列属于物理模型的是?13.相关法在存在噪声时,效果较好14.在线辨识的缺点是?离线辨识的优点是?判断改错15.方程误差为白噪声是最小二乘法得到无偏估计的充分条件,非必要条件16.最小二乘法既能用于离线估计,又能用于在线估计17.当方程噪声为正态分布白噪声时,极大似然估计与最小二乘估计等价18.M序列是一种伪随机序列19.自衡对象不含有纯积分环节,无自衡对象至少含有一个纯积分环节名词解释20.物理模型21.图表模型22.脉冲响应23.阶跃响应24. 渐消记忆法25.限定记忆法26.在线辨识27.离线辨识28.最小二乘法29.极大似然法简答题30.辨识中合理的输入信号应满足什么条件?一般辨识中采用哪些输入信号?31.白噪声过程有什么特点?实际工程中一般采用什么信号?32. 什么是递推算法?与一次完成算法相比,有什么优缺点?33.什么是一次完成算法?与递推算法相比,有什么优缺点?34.一般如何评价一个估计方法的好坏?基本最小二乘法的统计性质如何?极大似然法的统计性质如何?35.一般如何评价一个估计方法的好坏?综合题36.试用最小二乘法拟合这些数据。
37.某系统的阶跃响应曲线如图所示,试用两点法写出其传递函数。
(注:要有详细的步骤)t。
系统辨识复习资料

1请叙述系统辨识的基本原理(方框图),步骤以及基本方法定义:系统辨识就是从对系统进行观察和测量所获得的信息重提取系统数学模型的一种理论和方法。
辨识定义:辨识有三个要素——数据、模型类和准则。
辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型辨识的三大要素:输入输出数据、模型类、等价准则基本原理:步骤:对一种给定的辨识方法,从实验设计到获得最终模型,一般要经历如下一些步骤:根据辨识的目的,利用先验知识,初步确定模型结构;采集数据;然后进行模型参数和结构辨识;最后经过验证获得最终模型。
基本方法:根据数学模型的形式:非参数辨识——经典辨识,脉冲响应、阶跃响应、频率响应、相关分析、谱分析法。
参数辨识——现代辨识方法(最小二乘法等)2随机语言的描述白噪声是最简单的随机过程,均值为零,谱密度为非零常数的平稳随机过程。
白噪声过程(一系列不相关的随机变量组成的理想化随机过程)相关函数: 谱密度: 白噪声序列,白噪声序列是白噪声过程的离散形式。
如果序列 满足: 相关函数: 则称为白噪声序列。
谱密度:M 序列是最长线性移位寄存器序列,是伪随机二位式序列的一种形式。
M 序列的循环周期 M 序列的可加性:所有M 序列都具有移位可加性辨识输入信号要求具有白噪声的统计特性 M 序列具有近似的白噪声性质,即 M 序列“净扰动”小,幅度、周期、易控制,实现简单。
3两种噪声模型的形式是什么 第一种含噪声的被辨识系统数学模型0011()()()()n ni i i i y k ay k i b u k i v k ===-+-+∑∑,式中,噪声序列v(k)通常假定为均值为零独立同分布的平稳随机序列,且与输入的序列u(k)彼此统计独立. 上式写成:0()()()T y k k v k ψθ=+。
其中,()()()()()()()=1212T k y k y k y k n u k u k u k n ψ------⎡⎤⎣⎦,,,,,,,)()(2τδστ=W R +∞<<∞-=ωσω2)(W S )}({kW ,2,1,0,)(2±±==l l R l W δσ2)()(σωω==∑∞-∞=-l l j W W e l R S ⎩⎨⎧≠=≈+=⎰0,00,Const )()(1)(0ττττT M dt t M t M T R bit )12(-=P P N第二种含噪声的被辨识系统数学模型:它与第一种的区别仅在于噪声的状况不同,第二种被辨识系统如下图所示:ξ(k)为噪声序列,假设为零均值独立同分布的平稳随即序列,且 ()()()y k x k k ξ=+ 由由以上两式可推导出0011()()()()n ni i i i y k a y k i b u k i v k ===-+-+∑∑,式中01()()()n i i v k k a k i ξξ==--∑4阐述最小二乘辨识方法的原理、数学模型以及推导数学模型:推导过程:含噪声的数学模型为:0011()()()()n ni i i i y k ay k i b u k i v k ===-+-+∑∑ 式中,噪声序列v(k)通常假定为均值为零独立同分布的平稳随机序列,且与输入的序列u(k)彼此统计独立. 上式写成:0()()()T y k k v k ψθ=+ 0θ是被辨识系统的真实参数向量(2n 维,n 为系统的阶数)。
山东XX工程大学《系统辨识基础》复习题

山东XX工程大学《系统辨识基础》复习题一、单项选择题1.如果对系统的客观规律一无所知,只能从系统的测试数据获取系统模型,则该问题为【】A 白箱B灰箱C黑箱 D 蓝箱2.下列哪种模型用来描述线性离散系统?【】A 描述函数B传递函数C微分方程D差分方程3.下列哪种信号是辨识中常用的输入信号?【】A伪随机序列B斜坡信号C阶跃信号D加速度信号4.下面哪些内容不属于系统辨识的基本内容?【】A观测数据B模型结构辨识C模型参数辨识D模型验证5.下面哪个不属于系统辨识过程中的3大要素之一?【】A输入输出数据 B AIC准则C模型类 D 等价准则6.下面哪个数学模型属于非参数型?【】A微分方程B状态方程C传递函数D脉冲响应模型7.下列哪个属于物理模型?【】A阶跃响应图B风洞C脉冲响应图 D 频率特性图8.下列哪种辨识方法需要输出量条件概率密度函数的先验知识?【】A最小二乘法B相关法C极大似然法D预报误差法9.以下哪种辨识算法对噪声最敏感【】A极大似然法B相关分析法C基本最小二乘D辅助变量法10.以下哪种方法可解决数据递推的饱和现象?【】5.下面哪个不属于系统辨识过程中的3大要素之一?【】A输入输出数据 B AIC准则C模型类 D 等价准则6.下面哪个数学模型属于参数型?【】A传递函数B频率响应C阶跃响应D脉冲响应模型7.下列哪个属于图表模型?【】A沙盘B风洞C频率特性图D汽车模型8.下列哪种辨识方法需要输出量条件概率密度函数的先验知识?【】A最小二乘法B相关法C预报误差法D极大似然法9.以下哪种辨识算法对噪声最敏感?【】A基本最小二乘B相关分析法C极大似然法D辅助变量法10.以下哪种方法可解决数据递推的饱和现象?【】A普通最小二乘法B随机逼近法C渐消记忆法D增广最小二乘法A限定记忆法B随机逼近法C普通最小二乘法D增广最小二乘法二、判断题11.极大似然法可以用于线性系统和非线性系统。
【】12.白噪声信号一定是均匀分布的。
系统分析与设计复习提纲答案

系统分析与设计复习提纲答案题型与分值:一、单项选择题:1分某10题(10%)二、多项选择题:2分某5题(10%)三、判断题:1分某10题(10%)四、填空题:1分某10空(10%)五、名词解释:3分某4题(12%)六、简答题:7分某3题(21%)七、应用设计题:3题(27%)1.数据流程图设计(7%)2.数据库设计(14%:E-R图设计8分;逻辑结构(数据表)设计6分)3.大作业自己所完成的工作简要描述(6分)第一章管理和信息系统1、什么是管理?P1(名词解释)管理是通过对企业资源进行有效的计划、组织、领导和控制来合理调配人力、物力、财力等资源,以实现企业目标的全部过程。
管理的职能:P2(填空或单选多选题)计划、组织、领导、控制2、信息与信息内容:P6信息:是客观存在的一切事物通过物质载体所发生的消息、情报、指令、数据和信号等所包含的可传递、可交换的有用知识。
信息的内容:信息是客观世界各种事物特征的反映,它是“经过加工的”,因而凝聚着人类的劳动。
信息是可记录、可通信的。
信息可以形成知识、因而有着“实现或潜在的价值”,可以被看做一种产品,一种人类生产活动的结晶。
3.信息系统与管理信息系统:P16信息系统:指对信息进行收集、处理、存储、管理、检索和传输并向人们提供有用信息的系统。
管理信息系统:是以现代管理理论为指导,以计算机和网络通信设施等现代信息技术为基础、以系统思想为主导,建立起来能进行信息的收集、传输、加工、储存并为管理人员提供决策信息的人机信息系统。
4、管理信息系统的概念结构:P19管理信息系统由四大部件组成:信息源、信息处理器、信息用户和信息管理者。
其中,信息源是信息的产生地;信息处理器负责信息的传输、加工、保存等;信息用户是信息的使用者,并利用信息进行决策;信息管理者负责系统的设计、实现以及运行和协调。
第二章信息系统开发概述1、软件工程:P24软件工程师一门研究用工程化方法构建和维护有效的、实用的和高质量的软件学科。
系统辨识考试题最终

系统辨识考试题最终2009-2010 学年第二学期研究生课程考核(读书报告、研究报告)考核科目:系统辨识理论及应用学生所在院:电信学院学生所在学科:信号与信息系统姓名:学号:1. 简述系统辨识的基本概念、定义和主要步骤(15分)答:系统辨识的概念:根据系统的输入输出时间函数来确定描述系统行为的数学模型。
对系统分析大的主要问题是根据输入时间函数和系统的特性来确定输出信号。
对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
而系统辨识所研究的问题恰好是这些问题的逆问题。
系统辨识的定义:根据系统的输入输出时间函数来确定描述系统行为的数学模型,是现代控制理论中的一个分支。
对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。
对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
系统辨识的主要步骤:系统辩识包括结构辩识和参数估计两个主要内容。
辩识的一般步骤如下:(1)明确目的和获取先验知识首先要尽可能多的获取关于辨识对象的先验知识和明确辩识的目的。
明确目的和掌握尽可能多的先验知识往往是辨识结果好坏的重要先决条件。
(2)实验设计实验设计主要包括以下六个方面内容:a.选择观测点;b.输入信号的形状和幅度(可持续激励条件);c.采样间隔T0 ;d.开环和闭环辩识(闭环可辩识条件);e.在线和离线辩识;f.测量数据的存储和预处理。
(3)模型结构的确定(4)参数估计(Parameter Estimation)(5)模型验证模型精度是否可以接受?否则需要重复实验,重复辩识。
系统辩识的内容和步骤见后示意框图。
辩识目的与先知识验实验设计模型结构的确定输入/输出数据获取参数估计模型验证最终模型2. 简述相关辨识的基本原理和基于二进制伪随机序列的相关辩识方法。
(15分)答:相关辨识的基本原理如下图所示。
g(t)延时τ1/Tπ×x(t)w(τ)x(t-τ)y(t) ×(t-τ)kg(t)x(t) —输入(白噪声); y(t) —测量输出;w(τ) ω(t )—随机干扰(不可测)基于二进制伪随机序列的相关辩识方法:x(t)用二位式周期性伪随机信号,积分时间大大缩短()()xy 0R () 1/T x t y(t )dt g()Tτττ=+?? ()s T T >二位式信号使得乘法运算简化。
系统辨识理论及应用(课后题答案第三章3.2、3.3)国防工业出版社

1、系统辨识——连续系统传递函数——脉冲传递函数function h=Continuous_system_transferFcn(N,G,dt)% N——系统阶数% G——采样数据(个数大于等于2N+1)% G为一维行向量% dt——采样间隔if nargin<3errordlg('not enough input varibles','error hint');elseg_NN=zeros(N,N);for i=1:Ng_NN(i,:)=G(i+1:i+1+N-1);endg_N=-G(1:N)';a=inv(g_NN)*g_N;%% x的求解syms xfor i=1:NX(i)=x^i;endf=X*a+1;x=double(solve(f));%%极点的求解p=log(x)/dt;c_NN=zeros(N,N);for i=1:Nc_NN(i,:)=x.^(i-1);endc_N=G(1:N)';%%增益求解k=inv(c_NN)*c_N;pkz=zeros(1,N);p=p';k=k';Continuous_TransferFcn=0;for i=1:NContinuous_TransferFcn=Continuous_TransferFcn+zpk(z(i),p(i),k(i)); endContinuous_TransferFcnendend例题 3.1(P32)>>G=[0 0.1924 0.2122 0.1762];>> N=2;>> dt=1;>> Continuous_system_transferFcn(N,G,dt) p =-0.4934-0.7085k =1.6280-1.6280Continuous_TransferFcn =0.35024 s---------------------(s+0.4934) (s+0.7085)Continuous-time zero/pole/gain model.习题3.2(P34)>> G=[0 0.196 0.443 0.624 0.748 0.831]; >> N=3;>> dt=0.2;>> Continuous_system_transferFcn(N,G,dt) p =-0.0633-1.7846-11.1860k =1.1249-1.33990.2150Continuous_TransferFcn =-0.08507 s (s-253.1)-------------------------------(s+0.06329) (s+1.785) (s+11.19) Continuous-time zero/pole/gain model.2 系统辨识——离散系统传递函数——脉冲传递函数function h=Discrete_system_transferFcn(N,G,dt)% N——系统阶数% G——采样数据(个数大于等于2N+1)% G为一维行向量% dt——采样间隔if nargin<3errordlg('not enough input varibles','error hint');elseg_NN=zeros(N,N);for i=1:Ng_NN(i,:)=G(i+1:i+1+N-1);endg_N=-G(N+2:2*N+1)';a1=inv(g_NN)*g_N;a=zeros(N,1);for j=1:Na(j,1)=a1(N+1-j,1);endB=zeros(N+1,N+1);B=diag(linspace(1,1,N+1));for i=1:N+1for j=1:N+1if (i==j)&(i<N+1)&(j<N+1)B(i+1:N+1,j)=a(1:N+1-i,1);endendendg__N=G(1:N+1)';b=B*g__N;abnum=b';den=[1 a'];Discrete_TransferFcn=tf(num,den,dt);Discrete_TransferFcnendend例题 3.2(P33)>> G=[0 7.157039 9.491077 8.563839 5.930506 2.845972 0.144611]; >> N=3;>> dt=0.05;>> Discrete_system_transferFcn(N,G,dt)a =-2.23001.7606-0.4950b =7.1570-6.4691-0.0009Discrete_TransferFcn =7.157 z^2 - 6.469 z - 0.0008933--------------------------------z^3 - 2.23 z^2 + 1.761 z - 0.495Sample time: 0.05 secondsDiscrete-time transfer function.习题3.3(P34)>> G=[10 6.989 4.711 3.136 2.137 1.559 1.252 1.096 0.938 0.860]; >> N=3;>> dt=0.1;>> Discrete_system_transferFcn(N,G,dt)a =-2.19191.7166-0.4794b =10.0000-14.92956.55810.0139Discrete_TransferFcn =10 z^3 - 14.93 z^2 + 6.558 z + 0.01389--------------------------------------z^3 - 2.192 z^2 + 1.717 z - 0.4794Sample time: 0.1 secondsDiscrete-time transfer function.。
系统辨识复习提纲(答案版)

系统辨识复习提纲1.什么是系统?什么是系统辨识?系统泛指由一群有关联的个体组成,根据预先编排好的规则工作,能完成个别元 件不能单独完成的工作的群体。
即一群有相互关联的个体组成的集合称为系统。
系统辩识就是:利用对未知系统的试验数据或在线运行数据(输入/输出数据)以及原理和原则建立系统的(数学)模型的科学。
2.什么是宽平稳随机过程,其遍历定理容是什么?答:在数学中,平稳随机过程或者严平稳随机过程,又称狭义平稳过程,是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程:即随机过程的统计特性不随时间的推移而变化。
这样,数学期望和方差这些参数也不随时间和位置变化。
如果平稳随机过程()t x de 各集和平均值等于相对应的时间平均值x =μx ,()()τ+t x t x =Rx ()τ,式中x 伪随机过程()t x 的时间平均值;x μ为与以为 概率密度有关的数字特征量集合均值;Rx ()τ为自相关函数。
则称()t x 是各态遍历的平稳随机过程。
3.简述噪声模型及其分类。
P130噪声模型:)()()(111---=z C z D z H分类:1) 自回归模型,简称AR 模型,其模型结构为 )()()(1k v k e z C =- 2) 平均滑动模型,简称MA 模型,其模型结构为)()()(1k v z D k e -=3)自回归平均滑动模型,简称ARMA 模型,其模型结构为))()()()(11k v z D k e z C --=4.白噪声与有色噪声的区别是什么?答:辨识所用的数据通常含有噪声。
如果这种噪声相关性较弱或者强度很小,则可近似将其视为白噪声。
白噪声过程是一种最简单的随机过程。
严格地说,它是一种均值为零、谱密度为非零常数的平稳随机过程,或者说它是由一系列不相关的随机变量组成的一种理想化随机过程。
白噪声过程没有“记忆性”,也就是说t 时刻的数值与t 时刻以前的过去值无关,也不影响t 时刻以后的将来值。
08243 系统辩识基础

系统辨识基础复习资料(课程代码:08243)知识点汇总:1.所谓系统,按通常的意义去理解,就是按某种相互依赖关系联系在一起的客体的集合。
2.所谓系统辨识,利用对未知系统的试验数据或在线运行数据(输入/输出数据)以及原理和原则建立系统的(数学)模型的科学。
3.系统辨识的步骤:(1)先验知识和建模目的的依据;(2)实验设计;(3)结构辨识;(4)参数估计;(5)模型适用性检验。
4.系统的数学模型,描述系统输入与输出之间数量关系的数学表达式称为系统的数学模型。
5. 目前最流行的控制系统辅助工具是Matlab。
6.机理分析和系统辨识相结合建模方法也称为“灰箱问题”。
7.机理建模这种建模方法也称为“白箱问题”。
8.频谱覆盖宽、能量均匀分布是白噪声信号的特点。
9.最小二乘法辨识方法不属于系统辨识的经典方法。
10.关于多阶最小二乘法,描述错误的是计算简单,计算量小,只用五步基本的最小二乘法可获得较好的结果。
11.渐消记忆法是指对旧数据加上遗忘因子,按指数加权来使得旧数据的作用衰减。
12.脉冲响应数学模型属于非参数型。
13.检验模型的标准是模型的实际效果,检验应从不同的侧面检验其可靠性。
14.与周期测试信号相比,阶跃响应法不能够比较准确地反映对象的动态特性。
15.闭环系统前向通道的阶次不是可辨识的。
16.使辨识系统可被辨识的最低要求是辨识时间内系统的动态必须被输入信号持续激励。
17.观测数据内容不属于系统辨识的基本内容。
18.输入数据不属于系统辨识过程中的3大要素。
19.棕箱不属于按提供的实验信息分类的建模方法。
20.数学建模不属于现代控制论的三大支柱。
21.不属于传递函数辨识的时域方法的是时间图索法。
22.关于递推算法收敛性的结论错误的是递推辅助变量法收敛于非真值。
23.设A为n×n矩阵,B为n×m矩阵,C为m×n矩阵,并且A,A+BC和I+CA-1B都是非奇异矩阵,则下列等式横成立的是[A+BC] -1=A-1-A-1B[I+CA-1B]-1CA-1。
系统辨识总复习

通过辨识企业运营过程中的关键因素和变量关系,可以建立企业经营决策模型,实现企业资源的优化配 置和经济效益的最大化。
06
系统辨识的挑战和未来发展
系统辨识面临的挑战
复杂系统建模
对于具有高度非线性、时变 性和不确定性的复杂系统, 如何建立准确的数学模型是 一个重要挑战。
数据质量和数量
系统辨识的未来发展趋势
基于深度学习的系统辨识
利用深度学习强大的特征提取和表达 能力,提高系统辨识的准确性和效率。
数据驱动与模型驱动相结合
结合数据驱动和模型驱动的优势,发 展混合辨识方法,提高辨识精度和实 用性。
多源信息融合
利用多源信息进行系统辨识,提高辨 识结果的鲁棒性和可靠性。
实时在线辨识
针对动态变化的系统,发展实时在线 辨识技术,实现系统的实时状态监测 和性能评估。
缺点
对于非线性系统辨识效果较差,且对噪声和异常 值敏感。
梯度校正法
原理
应用
优点
缺点
梯度校正法是一种迭代 优化算法,它通过计算 目标函数的梯度并按照 一定的步长进行更新来 寻找最优解。
在系统辨识中,梯度校 正法常用于非线性系统 的参数估计。通过定义 合适的目标函数,如误 差平方和或似然函数, 并使用梯度校正法进行 迭代优化,可以得到系 统的参数估计值。
设计实验
根据被辨识对象的特性和辨识目的,设计合适的实验,包括输入信号 的选择、采样时间的选择、数据长度的确定等。
系统辨识的步骤
采集数据
按照实验设计进行数据采集,获取被辨识对象的输入输出数据。
数据预处理
对采集到的数据进行预处理,如去除噪声、异常值处理等,以提高数 据质量。
选择模型结构和参数估计方法
系统辨识习题解答(最新),DOC

系统辨识习题解答1-14、若一个过程的输入、输出关系可以用MA模型描述,请将由白噪声v(k)驱动的线性环节的输出,该线性环节称为成形滤波器,其脉冲传递函数可写成即)()()()(11k v z D k e z C --= 其中ccn n z c z c z C ---+++= 1111)(根据其结构,噪声模型可区分为以下三类:1-4-证明:(1)1)]()()1()(1)[()1()()(--+-=k k k k k k k k Λh P h h P h P τ (2)1)]()()()(1)[()()()1(--=-k k k k k k k k Λh P h h P h P τ,(3)1)]()()1()(1)[()1()()()()(--+-=k k k k k k k k k k Λh P h h P h h P h τττ,(4)1)]()()()(1)[()()()()1()( --=-k k k k k k k k k k Λh P h h P h h P h τττ, 解:(1)由于)1()]()([)(--=k k h k K I k τP P 声。
定义参数向量请利用增广最小二乘思想,写出模型参数θ的递推辨识算法。
解:令及⎪⎩⎪⎨⎧=--------=ττθ],,,,,,,,[)](,),1(),(,),1(),(,),1([)(111d b a n n n f d b f f a f f f d d b b a a n k v k v n k u k u n k z k z k h计概念出发,证明该模型的参数向量θτ=[,,,,]a a b b n n 11 的估计值 θ可以写成如下加权最小二乘算法的形式()θττ=-H H H z L L L L L L ΛΛ1,式中,H L 为数据矩阵,z L 为输出向量,加权矩阵取ΛL v=12στC C ,其中矩阵C 为是正定的对角阵,由加权因子)(k Λ构成ΛL=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ΛΛΛ)(000)2(000)1(L , 设WLSˆθ使得J (θ)最小,则有: 取加权阵C C v vL τσ211=∑=Λ-。
系统辨识复习题

一、概念题1. 请给系统辨识下个定义。
2. 如何获得适合辨识的观测数据?3. 系统辨识有哪些应用?4. 为何要将辨识数据标准化?如何标准化?5. 白噪声的定义是什么?6. 什么是M 序列?7. 线性系统的结构由哪些参量来描述? 8. 什么是预报误差模型? 二、计算与问答题9. 请用双线性变换将连续传递函数)2(1)(++=s s s s W 转换为离散传递函数(T=0.5s)。
10. 一被识系统的观测数据含有有色噪声E(k)。
拟选的参考模型为A(q -1)y(k)=B(q -1)u(k)+E(k)请问:1)用LS 能否得到A(q -1)和B(q -1)的无偏估计?为什么?2)如果将)()(ˆ)(ˆ)(ˆ11k u q Aq Bk y LSLS --=作为辅助变量,能否得到A(q -1)和B(q -1)的无偏估计?写出此时的计算公式。
11. 试述相关最小二乘二步法的适用条件和计算过程。
12. 已选择被识系统的参考模型为)()(1)()()()(111k w q C k u q A q B k y ---+=,其中w(k)为白色噪声。
为了进行递推辨识,请将模型改写为伪线性回归形式,并给出其中所有估计量的表达式。
13. 试述一种多步最小二乘法的适用条件和计算过程。
14. 已选择被识系统的参考模型为)()()()()()(111k w q D k u q A q B k y ---+=,其中w(k)为白色噪声。
为了进行递推辨识,请将模型改写为伪线性回归形式,并给出其中所有估计量的表达式。
15. 如果一个系统的部分参数已知(例如,A(q-1)y(k)=B(q-1)u(k)+w(k)中,A(q-1)已知,B(q-1)未知),你怎么去辨识其他未知参数?写出你的计算公式。
16. Matlab 中Rand 函数产生的随机数是不是白噪声?说出你的理由。
17. 逐步回归法辨识模型结构的原理是什么?18. 结构判断准则FPE 和AIC 的共同特点是什么? 三、选择题1)要辨识一个实际系统,正确的获得辨识数据的过程是:A 在实验室做模拟仿真B 在被辨识系统处于正常工况时采集数据C 通过施加激励信号,使被辨识系统处于非正常工况时采集数据D 在实验室做数字仿真2)过滤观测数据中的噪声,正确的方法是:A 对系统输出数据做低通滤波B 对系统输入数据做低通滤波C 对系统输入、输出数据做不同的滤波D 对系统输入、输出数据做相同的滤波3) 最小二乘法的适用模型是:A 带白色噪声的线性回归模型;B 带白色噪声的连续传递函数模型;C 带白色噪声的离散传递函数模型;D 带白色噪声的伪线性回归模型;4)辨识结果是否好的标准是:A 模型阶次是小的;B 参数估计误差是小的;C 输出估计误差是小的;D 模型是稳定的;5)对于模型A(q -1)y(k)=B(q -1)u(k)+E(q -1)w(k),A(q -1)、B(q -1)、E(q -1)均是多项式。
系统辨识答案
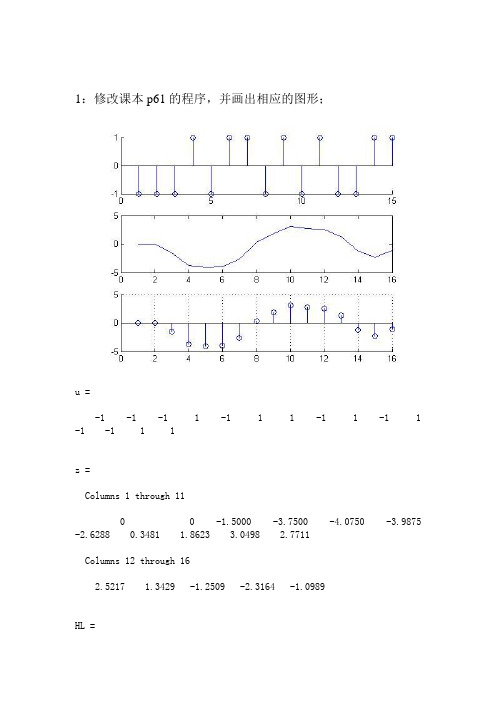
1:修改课本p61的程序,并画出相应的图形;u =-1 -1 -1 1 -1 1 1 -1 1 -1 1 -1 -1 1 1z =Columns 1 through 110 0 -1.5000 -3.7500 -4.0750 -3.9875 -2.6288 0.3481 1.8623 3.0498 2.7711Columns 12 through 162.5217 1.3429 -1.2509 -2.3164 -1.0989HL =0 0 -1.0000 -1.00001.5000 0 -1.0000 -1.00003.7500 1.5000 1.0000 -1.00004.0750 3.7500 -1.0000 1.0000 3.9875 4.0750 1.0000 -1.0000 2.6288 3.9875 1.0000 1.0000 -0.3481 2.6288 -1.0000 1.0000 -1.8623 -0.3481 1.0000 -1.0000 -3.0498 -1.8623 -1.0000 1.0000 -2.7711 -3.0498 1.0000 -1.0000 -2.5217 -2.7711 -1.0000 1.0000 -1.3429 -2.5217 -1.0000 -1.00001.2509 -1.3429 1.0000 -1.00002.3164 1.2509 1.0000 1.0000 ZL =-1.5000-3.7500-4.0750-3.9875-2.62880.34811.86233.04982.77112.52171.3429-1.2509-2.3164-1.0989c =-1.50000.70001.00000.5000a1 =-1.5000a2 =0.7000b1 =1b2 =0.50002:修改课本p63的程序,并画出相应的图形(V的取值范围为54-200);V = [54.3000, 61.8000, 72.4000, 88.7000, 118.6000, 194.0000]τP = [61.2000, 49.5000, 37.6000, 28.4000, 19.2000, 10.1000]τZL = [4.1141, 3.9020, 3.6270, 3.3464, 2.9549, 2.3125]τHL =-3.9945 1.0000-4.1239 1.0000-4.2822 1.0000-4.4853 1.0000-4.7758 1.0000-5.2679 1.0000c4 =1.40429.6786alpha = 1.4042beita = 1.5972e+0043:表1中是在不同温度下测量同一热敏电阻的阻值,根据测70时的电阻量值确定该电阻的数学模型,并求出当温度在C︒值。
系统辨识复习题

系统辨识复习题系统辨识复习题系统辨识是一门研究如何从实验数据中提取系统动态特性的学科。
它在工程领域中有着广泛的应用,例如控制系统设计、信号处理、模型预测控制等。
在这篇文章中,我们将回顾一些系统辨识的基本概念和方法,并通过一些复习题来帮助读者巩固对这门学科的理解。
1. 什么是系统辨识?系统辨识是通过实验数据推断和确定系统的动态特性,包括系统的传递函数、状态空间模型等。
它是一种基于观测数据的反问题求解方法,通过对输入输出数据的分析,建立数学模型以描述系统的行为。
2. 为什么需要系统辨识?系统辨识在工程领域中具有重要的意义。
通过对系统进行辨识,我们可以了解系统的特性,从而设计出更好的控制策略。
此外,系统辨识还可以用于故障诊断、信号处理等方面的应用。
3. 系统辨识的基本步骤是什么?系统辨识的基本步骤包括:数据采集、模型结构选择、参数估计和模型验证。
首先,需要采集到系统的输入输出数据。
然后,根据数据的特点选择合适的模型结构,例如ARX模型、ARMA模型等。
接下来,通过最小二乘法等方法估计模型的参数。
最后,通过模型验证来评估模型的准确性和预测性能。
4. 什么是参数辨识?参数辨识是系统辨识中的一个重要环节,它是指通过实验数据估计系统模型的参数。
参数辨识的目标是找到一组参数,使得模型的输出与实际系统的输出之间的误差最小。
5. 常用的参数辨识方法有哪些?常用的参数辨识方法包括最小二乘法、极大似然估计、频域法等。
最小二乘法是一种常用的线性参数辨识方法,它通过最小化实际输出与模型输出之间的误差平方和来估计模型的参数。
极大似然估计是一种常用的非线性参数辨识方法,它通过最大化观测数据出现的概率来估计模型的参数。
频域法则是通过对输入输出数据进行频谱分析来估计模型的参数。
6. 如何评估辨识模型的准确性?评估辨识模型的准确性可以使用拟合优度指标,例如决定系数R^2、均方根误差RMSE等。
决定系数R^2反映了模型对数据的拟合程度,取值范围在0到1之间,值越接近1表示模型拟合效果越好。
系统辨识复习整理

1.系统辨识的概念系统辨识是利用系统运行或实验过程中获取的系统输入-输出数据求得系统数学模型(传递函数)的方法和技术。
2.过程的概念通常泛指具有时间或空间上的跨度的对象。
具体的如:工程系统、生物系统或社会经济系统都可以称为过程3.模型的概念指过程运动规律的本质描述。
4.模型按照描述形式分类(1)直觉模型指过程的特性以非解析的形式直接存储在人脑中靠人的直觉控制过程地进行。
(2)物理模型实际过程的一种物理模拟。
(3)图表模型以图形式或表格的形式来表现过程的特性,也成为非参数模型。
(4)数学模型用数学结构的形式来反映实际过程的行为特点。
5.根据模型的特性,数学模型可以分为线性和非线性模型系统线性与关于参数空间线性本质线性与本质非线性动态和静态模型确定性和随机性模型宏观(积分方程)和微观(微分方程)模型等6.建立过程数学模型的两种主要方法(1)机理分析法通过分析过程的运动规律、应用一些已知的规律、定理和与原理建立过程的数学模型,这种方法也称为理论建模(2)测试法——辨识方法利用输入输出数据所提供的信息来建立过程的数学模型白箱——理论建模黑箱——辨识建模灰箱——理论建模与辨识建模结合7.辨识的定义辨识有三个要素- 数据、模型类和准则,辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型8.系统辨识的步骤(1)根据辨识目的,利用先验知识,初步确立模型结构 (2)采集数据(3)进行模型参数和结构辨识 (4)验证获得最终模型9. 随机过程无穷多个随机函数的总体称为随机过程。
两层含义:随机过程ξ(t)在任一时刻都是随机变量; 随机过程ξ(t)是大量样本函数的集合。
10. 各种随机过程计算公式 二维分布函数:二维概率密度函数:2212122121212(,;,)(,;,)F x x t t f x x t t x x ∂=∂⋅∂一维和n 维类推数学期望:反映了随机过程取值的集中位置)()()}({1t a x P x t E Ki i i ==∑=ξ(离散))()()}({t a dx x xf t E ==⎰∞∞-ξ(连续)方差:反映了随机过程的集中程度[]{}22[()]()()D t Et a t σξξ==-2[()()]()t a t f x dx ξ∞-∞=-⎰自协方差:用来衡量任意两个时刻上获得的随机变量的统计相关特性 )]}()()][()({[),(221121t a t t a t E t t B --=ξξ11222121212[()][()](,;,)x a t x a t f x x t t dx dx ∞∞-∞-∞=--⎰⎰自相关函数:⎰⎰∞∞-∞∞-==2121212212121),;,()]()([),(dx dx t t x x f x x t t E t t R ξξ二者关系:121212(,)(,)[()][()]B t t R t t E t E t ξξ=-⋅互协方差函数:)]}()()][()({[),(221121t a t t a t E t t B ηξξηηξ--=F 2(x 1,x 2; t 1,t 2)=P {ξ(t 1)≤x 1, ξ(t 2)≤x 2}互相关函数:)]()([),(2121t t E t t R ηξξη=特别的:()0R ξητ=表示两个随机过程是不相关(正交的随机过程)11. 平稳随机过程对于任意的正整数n 和任意实数t 1,t 2,...,t n ,τ,随机过程ξ(t)的n 维概率密度函数满足12121212(,,,;,,,)(,,,;,,,)n n n n n n f x x x t t t f x x x t t t τττ=+++则称ξ(t)为平稳随机过程(严平稳随机过程或狭义平稳随机过程)若随机过程ξ(t)的数学期望和方差与时间无关,自相关函数仅是τ的函数,则称它为宽平稳随机过程或广义平稳随机过程。
系统辨识与建模智慧树知到课后章节答案2023年下湘潭大学

系统辨识与建模智慧树知到课后章节答案2023年下湘潭大学湘潭大学第一章测试1. A system is a unity composed of various parts that are interconnectedconstrained and interacted with each other and have certain overallfunctions and comprehensive behaviors.()A:对 B:错答案:对2.Which one is not belong to modern control theory system?().A:System identification B:Modern control theory C:State estimationD:Automatic control答案:Automatic control3.建立数学模型的方法可大体分为:().A:观测法 B:理论分析法 C:测试法 D:实验法答案:理论分析法;测试法4.下列哪些属于非参数模型?()A:权序列模型 B:输入输出模型 C:状态空间模型 D:脉冲响应模型答案:权序列模型;脉冲响应模型5.针对水箱进行机理建模时,我们应该凭借哪种关系建立公式?().A:水箱流入量和流出量之差为流入水流量的增量 B:水箱流入量和流出量之差为液位的增量 C:水箱流入量和流出量之差为液体存储量的变化率 D:水箱流入量和流出量之差为流出水流量的增量答案:水箱流入量和流出量之差为液体存储量的变化率第二章测试1.下面哪些内容不属于系统辨识的基本内容?()A:观测数据 B:模型结构辨识 C:模型验证 D:模型参数辨识答案:观测数据2.白噪声过程没有“记忆性”,也就是说t时刻的数值与t时刻以前的值无关,也不影响t时刻以后的将来值。
()A:对 B:错答案:对3.关于白噪声的均匀分布计算问题,将产生的(0,1)均匀分布的随机数通通减去0.5,然后乘以存储器f中预置的系数,这里取f=2,从而得到新的分布()。
系统辨识作业及答案

系统辨识作业及答案一.问答题1. 介绍系统辨识的步骤。
答:(1)先验知识和建模目的的依据;(2)实验设计;(3)结构辨识;(4)参数估计;(5)模型适用性检验。
2. 考虑单输入单输出随机系统,状态空间模型[])()(11)()(11)(0201)1(k v k x k y k u k x k x +=+=+ 转换成ARMA 模型。
答:ARMA 模型的特点是u(k)=0,[])()(11)()(0201)1(k v k x k y k x k x +=??=+3. 设有一个五级移位寄存器,反馈取自第2级和第3级输出的模2加法和。
试说明:(1)其输出序列是什么?(2)是否是M 序列?(3)它与反馈取自第4级与第3级输出模2加法和所得的序列有何不同?(4)其逆M 序列是什么?答:(1)设设输入序列1 1 1 1 1111018110107101006010015100114001113011112111111)()()()()()()()(()()()()()()()01110161110115110101410100)13(0100112100111 10011110011109()()()()()()()001112401110)23(111012********* 010020010011910011180011117()()()()()()()()10011320011131011103000111291101028101002701001261001125 其输出序列为:1 1 1 1 1 0 0 1 0 1⑵不是M 序列⑶第4级与第3级模2相加结果100108001007010006100015000114001113011112111111)()()()()()()()(()()()()()()()11110161110115110101410101)13(0101112101101 10110010110019()()()()()()()110012410010)23(001002201000211 000120000111900111180111117()()()()()()()()01111321111031111013011010291010128010112710110260110025 不同点:第2级和第3级模二相加产生的序列,是从第4时刻开始,每隔7个时刻重复一次;第4级与第3级模2相加产生的,序列,是从第2时刻开始每隔15个时刻重复一次。
系统辨识考试答案

2.描述用随机信号测试线性系统的动态响应的原理与方法。
用伪随机噪声作为输入测试系统的动态响应:伪随机信号的自相关函数是周期为T 的周期函数,其互相关函数为:......)()(.....)()()()()(20+++=+-+-=⎰⎰ττσστσσστστT kg kg d R g d R g R TT x T x xy T >系统的脉冲响应时间时,)(τ+T g =0,…,则)()(ττkg R xy =,与白噪声作输入信号时结果相同,但此处)(τxy R 的计算只需在0~T 一个周期的时间内进行。
这就是采用伪随机信号测试系统动态特性的优越性。
用随机信号测试线性系统的动态响应的原理是相关滤波原理利用随机信号测试线性系统的动态特性的理论基础是维纳一霍夫积分方程,即 ⎰∞∞--=σστστd R g R x xy )()()( =)()(ττx R g *当系统输出端存在干扰)(t n 时,系统的实际输出y(t)与输入x(t)的互相关函数为:)()()]}()()[({)}()({)(ττττττxn xz xy R R t n t z t x E t y t x E R +=+++=+=为了测试系统的动态响应特性,选用与测量噪声n(t)无关的激励信号x(t),即x(t)与n(t)无关,故其互相关函数)(τxn R =0,所以)()(ττxz xy R R =,即实际输入与输出(带测量噪声)的互相关函数)(τxy R 等价于真实输入与输出(不带测量噪声)的互相关函数)(τxz R 。
这就是相关滤波原理。
利用相关滤波原理测试测试线性系统的动态响应的突出优点是抗干扰能力强。
用白噪声作为输入测试系统的动态响应:维纳一霍夫积分方程变为:)()()()()()(00τσστδσσστστkg d k g d R g R x xy =-=-=⎰⎰∞∞ 可见,当输入为自噪声时,系统输入输出的互相关函数)(τxy R 与脉冲响应函数)(τg 成正比。
系统辨识基础复习

第一章 绪论(一)系统辨识的基本概念
1、系统的定义 所谓“系统”,按通常的意义去理解,就是按某种 相互依赖关系联系在一起的客体的集合。 2、模型的定义 3、什么是系统的数学模型?简述建立系统数学模型 的两类基本方法。 描述系统输入与输出之间数量关系的数学表达式称 为系统的数学模型。 教材p2 4、系统辨识的定义、三要素及实用定义?p2 5、请介绍系统辨识的步骤。p10
一、最小二乘递推算法 1、说明什么是最小二乘一次完成算法和递推 算法,试比较优缺点?p72 二、最小二乘实时算法 什么叫递推最小二乘法的“数据饱和”现象? 采用什么算法可以解决这种现象?说明这些 算法的基本思想。P74-77
第四章 最小二乘法(三)有色噪声情 形下的最小二乘法
1、广义最小二乘法 2、增广最小二乘法 3、辅助变量法 4、多级最小二乘法
第七章 阶次的辨识 1、损失函数检验法及算例 2、F检验法 3、脉冲响应函数定阶法
第七章 阶次的辨识
• 用损失函数检验法对某系统进行阶次的辨识,根 据所观测到的系统的输入输出数据,计算出系统 模型的阶次与相应的残差平方和关系如表1,则 系统模型的阶次为 阶。
表 模型阶数 残差平方和 系统残差平方和与模型阶次关系表 1 2 3 4 5 228.336 122.552 21.668 21.551 21.541
第四章 最小二乘法(三)有色噪声情 形下的最小二乘法
1、若模型噪声为有色噪声,则可采用的辨识方法 为 、 、 和 。 2、广义最小二乘法针对噪声模型为的系统模型,这一点上与 相同。 3、在辅助变量法中,辅助变量的选取需满足的两个条件 是 ,且 。 4、增广最小二乘法是 的一种简单推广,只是扩 充了参数向量和数据向量的维数,它适用于噪声模型为 的系统模型。 5、系统辨识的三要素指 、 和 。 6、解决递推最小二乘法“数据饱和”现象可采 用 、 和 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统辨识复习提纲1.什么是系统?什么是系统辨识?系统泛指由一群有关联的个体组成,根据预先编排好的规则工作,能完成个别元 件不能单独完成的工作的群体。
即一群有相互关联的个体组成的集合称为系统。
系统辩识就是:利用对未知系统的试验数据或在线运行数据(输入/输出数据)以及原理和原则建立系统的(数学)模型的科学。
2.什么是宽平稳随机过程,其遍历定理内容是什么?答:在数学中,平稳随机过程或者严平稳随机过程,又称狭义平稳过程,是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程:即随机过程的统计特性不随时间的推移而变化。
这样,数学期望和方差这些参数也不随时间和位置变化。
如果平稳随机过程()t x de 各集和平均值等于相对应的时间平均值x =μx ,()()τ+t x t x =Rx ()τ,式中x 伪随机过程()t x 的时间平均值;x μ为与以为 概率密度有关的数字特征量集合均值;Rx ()τ为自相关函数。
则称()t x 是各态遍历的平稳随机过程。
3.简述噪声模型及其分类。
P130噪声模型:)()()(111---=z C z D z H分类:1) 自回归模型,简称AR 模型,其模型结构为 )()()(1k v k e z C =- 2) 平均滑动模型,简称MA 模型,其模型结构为)()()(1k v z D k e -=3)自回归平均滑动模型,简称ARMA 模型,其模型结构为))()()()(11k v z D k e z C --=4.白噪声与有色噪声的区别是什么?答:辨识所用的数据通常含有噪声。
如果这种噪声相关性较弱或者强度很小,则可近似将其视为白噪声。
白噪声过程是一种最简单的随机过程。
严格地说,它是一种均值为零、谱密度为非零常数的平稳随机过程,或者说它是由一系列不相关的随机变量组成的一种理想化随机过程。
白噪声过程没有“记忆性”,也就是说t 时刻的数值与t 时刻以前的过去值无关,也不影响t 时刻以后的将来值。
工程实际中数据所含的噪声往往是有色噪声。
所谓有色噪声指的是噪声序列中每一时刻的噪声和另一时刻的噪声是相关的。
5.设一个随机序列)},,2,1(),({L k k z ∈的均值是参数θ 的线性函数{()}()z k k τθ=E h其最小二乘估计为:L L L L L z H H H ΛΛθττ1WLS )(ˆ-=试给出其递推形式的详细推导过程,要求其最终其递推矩阵为保对称的。
P64在2n 阶“持续激励”输入信号的作用下,加权最小二乘法的解为L L L L L z H H H ΛΛθττ1WLS )(ˆ-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=∑∑=-=L i L i i z i i i i i 111)()()()()()(h h h ΛΛτ记k 时刻的参数估计值为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=∑∑=-=k i k i i z i i i i i k 111)()()()()()()(ˆh h h ΛΛτθ令∑==ki i h i h i k R 1)()()()(τΛ,并利用R h () ()()()()k k i i z i i k --==-∑1111θΛ,则有⎪⎩⎪⎨⎧+-=--+-=-)()()()1()()]1(ˆ)()()[()()()1(ˆ)(ˆT1k k k k k k k k z k k k k k h h R R h h R ΛΛθθθτ 又设R R ()()k kk =1,可导出如下的加权最小二乘估计递推算法,记作WRLS(Weighted Recursive Least Squares algorithm),⎪⎩⎪⎨⎧--+-=--+-=-)]1()()()([1)1()()]1(ˆ)()()[()()(1)1(ˆ)(ˆ1k k k k k k k k k k z k k k k k k R h h R R h h R ττθθθΛΛ 置[]11111)()()()1()()()()(1)(---=-Λ+-=⎥⎦⎤⎢⎣⎡Λ==∑k k k k i i i k k k k i ττh h P h h R P ,并利用矩阵反演公式111111)()(------+-=+A C C A C B C A A CBC A τττ ,令增益矩阵为:)()()()(k k k k Λ=h P K那么算法将演变成下面所示的另一种递推算法形式⎪⎪⎪⎩⎪⎪⎪⎨⎧--=⎥⎦⎤⎢⎣⎡+--=--+-=-)1()]()([)()(1)()1()()()1()()]1(ˆ)()()[()1(ˆ)(ˆ1k k k k k k k k k k k k k k z k k k P h K P h P h h P K h K τττθθθI Λ 6.简述在最小二乘估计问题中引入加权因子的作用。
P587.假如给出在不同温度下测量同一热敏电阻的阻值,根据测量值确定该电阻的数学模型,并求出当温度在t 时的电阻值。
(1)利用头两个数据给出00010(0)()()ˆ(0)(0)0T L L TL L L -⎧==⎪⎨=⎪⎩P P H H θP H z (2)写出最小二乘的递推公式;(3)计算ˆ()[(),()]T k a k b k =θ并要求在计算过程中给出矩阵(),()k k P K 的值。
老师给过示例7题:表1中是在不同温度下测量同一热敏电阻的阻值,根据测量值确定该电阻的数学模型,并求出当温度在C ︒70时的电阻值。
要求用递推最小二乘求解: (a )设观测模型为 利用头两个数据给出⎪⎩⎪⎨⎧===-0L T L L T L L z H P θH H P P 000)0()0(ˆ)()()0(10 (b )写出最小二乘的递推公式; (c )利用Matlab 计算表1 热敏电阻的测量值i i v bt a y ++=T k a k b k )](),([)(ˆ=θ并画出相应的图形。
解:首先写成[][]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=+==a b t a b h h a bt k k z k k 1)()(12θτh θL L H z =T L L z z ],...,[1=z ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1 (112)1L L t t t H ,⎥⎦⎤⎢⎣⎡=a b θ的形式。
利用头两个数据给出最小二乘的初值:,126120.50⎥⎦⎤⎢⎣⎡=L H ⎥⎦⎤⎢⎣⎡=7907650L z 这样可以算得⎪⎩⎪⎨⎧===-0L T L L T L L z H P θH H P P 000)0()0(ˆ)()()0(10 求得⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡==671.8182 4.5455 )0()0(ˆ36.2397 1.5372- 1.5372- 0.0661)()0(000L T L L z H P θP P 注意对于手工计算,可以直接用2阶矩阵求逆公式⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡-a c b d bc ad d c b a 11有了初值,可以写出递推公式:T 1032]1010 980 942 910 873 850 826 [=L z⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡= 1.0000 95.7000 1.0000 88.0000 1.000080.0000 1.0000 73.0000 1.0000 61.0000 1.0000 51.0000 1.0000 40.0000 1.000032.7000 L H ⎥⎦⎤⎢⎣⎡=1)(k t k h 这样可以根据公式进行计算。
⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡Λ+---=⎥⎦⎤⎢⎣⎡Λ+--=--+-=-)(1)()1()()()()1()()(1)()1()()()1()()]1(ˆ)()()[()1(ˆ)(ˆ1k k k k k k k k k k k k k k k k k k z k k k h P h K K P P h P h h P K h K ττττθθθ 算得:P(1) =0.0134 -0.3536 -0.3536 9.6685 P(2) =0.0047 -0.1397 -0.1397 4.4118 P(3) =0.0017 -0.0594 -0.0594 2.2224 P(4) =0.0008 -0.0327 -0.0327 1.4264 P(5) =0.0005 -0.0198 -0.0198 1.0025 P(6) =0.0003 -0.0143 -0.0143 0.8103 P(7) =0.0002 -0.0110-0.0110 0.6863 P(8) =0.0002 -0.0088 -0.0088 0.5986Tk ⎥⎦⎤⎢⎣⎡=702.7620 702.9683 705.3110 708.4127 702.9463 698.6728 675.2295 661.3131 3.4344 3.4292 3.3668 3.2778 3.4443 3.5878 4.4470 5.0134 )(ˆθ8.简述系统辨识中的模型、逆模型及广义模型的概念,Bayes 辨识和Kalman 滤波分别采用什么模型?● 模型的含义模型-把关于实际过程的本质的部分信息简缩成有用的描述形式。
它是用来描述过程的运动规律,是过程的一种客观写照或缩影,是分析、预报、控制过程行为的有力工具。
模型是实体的一种简化描述。
模型保持实体的一部分特征,而将其它特征忽略或者变化。
不同的简化方法得到不同的模型。
Bayes---最小二乘模型 Kalman---线性代数和隐马尔可夫模型9.在线辨识和离线辨识的差别是什么?如果系统的模型结构已经选好,阶数也已确定,在获得全部数据之后,用最小二乘法、极大似然法或其它估计方法,对数据进行集中处理后,得到模型参数的估计值,这种方法称为离线辨识。
离线辨识的优点是参数估计值的精度较高,缺点是需要存储大量数据,运算量也大,难以适用于实时控制 。
在线辨识时,系统的模型结构和阶数是事先确定好的。
当获得一部分新的输入输出数据后,在线采用估计方法进行处理,从而得到模型的新的估计值。
在线辨识的优点是所要求的计算机存储量较小,辨识计算时运算量较小,适合于实时控制,缺点是参数估计的精度较差。
为了实现自适应控制,必须采用在线辨识,要求在很短的时间内把参数辨识出来。
10.已知确定性问题的梯度校正参数辨识方法的参数估计递推公式为ˆˆˆ(1)()()()[()()()]k k k k y k k k τ+=+-h h θθR θ并且权矩阵)(k R 选取如下形式。
12()()[(),(),,()]N k c k diag k k k ΛΛΛ=R如果权矩阵满足以下条件。
(1)0(),(12)L i H k i N ΛΛΛ<≤≤=,,,; (2)N 个()i k Λ中存在一个()m k Λ,使得)()1()()()1()(k k k k k k i i i m m m ΛΛΛΛΛΛ+-≥+-(3)2120()()()Ni ii c k k h k Λ=<<∑;(4))(ˆ)(~0k k θθθ-=与)(k h 不正交。
