等腰直角三角形中的常用模型
八年级数学人教版(上册)小专题(十一)等腰直角三角形常见的解题模型

小专题(十一) 等腰直角三角形常见的解题模型
模型 1 等腰直角三角形+斜边的中点,常连接直角顶点和斜 边中点
如图,在等腰 Rt△ABC 中,D 为斜边的中点,则连接 AD⇒AD =BD=DC,∠B=∠DAF=45°.常结合已知条件,通过证明△BDE ≌△ADF 或△ADE≌△CDF 得出相关结论.
【变式】 将第 3 题中的“∠AEB=45°”改为“∠AEC= 135°”,第 3 题中的结论还成立吗?并说明理由.
解:第 3 题中的结论仍然成立. 理由:如图,过点 A 作 AF⊥AE,交 CE 的延长线于点 F, 则∠BAE=90°+∠CAE=∠CAF. ∵∠AEC=135°, ∴∠AEF=45°.
1.如图,在△ABC 中,∠A=90°,AB=AC,D 为 BC 的中点, E,F 分别是 AB,AC 上的点,且 BE=AF.求证:△DEF 为等腰直 角三角形.
证明:连接 AD, ∵AB=AC,∠BAC=90°,D 为 BC 的中点, ∴AD=BD=CD,且 AD 平分∠BAC. ∴∠BAD=∠CAD=45°=∠B.
模型 2 变式 等腰直角三角形及 8 字模型中只有一个直角,过 等腰直角三角形的顶点作垂线段构造直角
如图,已知等腰 Rt△ABC,∠AEB=45°,常过点 A 作 AF⊥ AE,则∠FAE=90°,∠1=∠2.
3.(T2 变式)如图,△ABC 为等腰直角三角形,∠BAC=90°, AB=AC,D 是 AC 上一点.若∠AEB=45°,求证:CE⊥BD.
∵∠BAD=∠CED=90°,∠ADB=∠EDC,
∴∠ABF=∠ACE. AB=AC,
在△ABF 和△ACE 中,∠ABF=∠ACE, BF=CE,
∴△ABF≌△ACE(SAS).
三角形中的重要模型-弦图模型、勾股树模型(学生版+解析版)

三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图,是中国古代数学家赵爽发现,既可以证明勾股定理,也可以以此命题,相关的题目有一定的难度,但解题方法也常常是不唯一的。
弦图之美,美在简约,然不失深厚,经典而久远,被誉为“中国数学界的图腾”。
弦图蕴含的割补思想,数形结合思想、图形变换思想更是课堂教学中数学思想渗透的绝佳载体。
一个弦图集合了初中平面几何线与形,位置与数量,方法与思想,小身板,大能量,它就是数学教育里的不老神话。
广受数学教师和数学爱好者研究,近年来也成为了各地中考的热点问题。
模型1、弦图模型(1)内弦图模型:如图1,在正方形ABCD中,AE⊥BF于点E,BF⊥CG于点F,CG⊥DH于点G,DH⊥AE于点H,则有结论:△ABE≌△BCF≌△CDG≌△DAH;S正方形ABCD =4S△EAB+S正方形EFGH。
图1图2图3(2)外弦图模型:如图2,在正方形ABCD中,E,F,G,H分别是正方形ABCD各边上的点,且四边形EFGH是正方形,则有结论:△AHE≌△BEF≌△CFG≌△DGH;S正方形ABCD =4S△EAB+S正方形EFGH。
(3)内外组合型弦图模型:如图3,2S正方形EFGH =S正方形ABCD+S正方形PQMN.1(2023秋·湖北·九年级校联考开学考试)如图,2002年8月在北京召开的国际数学家大会会标其原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成如.如果大正方形的面积是16,直角三角形的直角边长分别为a,b,且a2+b2=ab+10,那么图中小正方形的面积是()A.2B.3C.4D.52(2022·安徽安庆·八年级期末)汉代数学家赵爽为了证明勾股定理,构造了一副“弦图”,后人称其为“赵爽弦图”,如图,大正方形ABCD由四个全等的直角三角形和一个小正方形组成,若∠ADE=∠AED,AD =45,则△ADE的面积为()A.24B.6C.25D.2103(2023·山西八年级期末)如图,图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是()A.24B.52C.61D.764(2022·杭州九年级月考)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是()A.S1=2B.S2=3C.S3=6D.S1+S3=85(2023·广东·九年级专题练习)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》题时给出了“赵爽弦图”.将两个“赵爽弦图”(如图1)中的两个正方形和八个直角三角形按图2方式摆放围成正方形MNPQ,记空隙处正方形ABCD,正方形EFGH的面积分别为S1,S2S1>S2,则下列四个判断:①S1+S2=14S四边形MNPQ②DG=2AF;③若∠EMH=30°,则S1=3S2;④若点A是线段GF的中点,则3S1=4S2,其中正确的序号是模型2. 勾股树模型6(2022·福建·八年级期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,如果正方形A、B、C、D的边长分别为3,4,1,2.则最大的正方形E的面积是.7(2022·浙江·乐清市八年级期中)如图,在四边形ABCD中,∠B=∠D=90°,分别以AB,BC,CD,DA为一边向外作正方形甲、乙、丙、丁,若用S甲,S乙,S丙,S丁来表示它们的面积,那么下列结论正确的是()A.S 甲=S 丁B.S 乙=S 丙C.S 甲-S 乙=S 丁-S 丙D.S 甲+S 乙=S 丙+S 丁8(2022·河南八年级期末)如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2,⋯按照此规律继续下去,则S 9的值为()A.126B.127C.128D.1299(2023春·山东菏泽·八年级校考阶段练习)“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,如果第一个正方形面积为1,则第2023代勾股树中所有正方形的面积为.10(2023·浙江八年级期中)如图,以Rt △ABC 的三边为直径,分别向外作半圆,构成的两个月牙形面积分别为S 1、S 2,Rt △ABC 的面积S 3.若S 1=4,S 2=8,则S 3的值为.11(2022春·浙江温州·九年级校考开学考试)如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt △ABC 中,∠BAC =90°,以其三边为边分别向外作正方形,延长EC ,DB 分别交GF ,AH 于点N ,K ,连接KN 交AG 于点M ,若S 1S 2=916,则tan ∠ACB 为()A.12B.23C.34D.51212(2023·贵州遵义·统考二模)如图1,毕达哥拉斯树,也叫“勾股树”,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形.在图2中,∠ACB =90°,分别以Rt △ABC 的三条边为边向外作正方形,连接BE ,DG 、BE ,交AC 于点Q ,若∠BAC =30°,BC =2,则四边形EQGD 的面积是.13(2023秋·浙江·八年级专题练习)【背景阅读】勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了验证勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.【实践操作】(1)请叙述勾股定理;(2)验证勾股定理,人们已经找到了400多种方法,请从下列几种常见的验证方法中任选一种来验证该定理:(以下图形均满足验证勾股定理所需的条件)【探索发现】(3)如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有个;(4)如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1、S2,直角三角形面积为S3,请判断S1、S2、S3的关系并说明理由.课后专项训练1(2022·云南九年级一模)如图是按照一定规律“生长”的“勾股树”:经观察可以发现:图(1)中共有3个正方形,图(2)在图(1)的基础上增加了4个正方形,图(3)在图(2)的基础上增加了8个正方形,⋯⋯,照此规律“生长”下去,图(6)应在图(5)的基础上增加的正方形的个数是()A.12B.32C.64D.1282(2022·浙江初三期中)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为()图1图2A.42B.6C.254D.1323(2023·浙江·杭州八年级阶段练习)如图,Rt△ABC中,∠BAC=90°,分别以△ABC的三边为边作正方形ABDE,正方形BCFG,正方形ACHI,AI交CF于点J.三个正方形没有重叠的部分为阴影部分,设四边形BGFJ的面积为S1,四边形CHIJ的面积为S2,若S1-S2=12,S△ABC=4,则正方形BCFG的面积为()A.16B.18C.20D.224(2023春·湖北黄冈·八年级统考期中)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则EF 的长为()A.9B.92C.32D.35(2022·四川成都·模拟预测)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2.则图2中阴影部分面积等于()A.直角三角形的面积B.最大正方形的面积C.最大正方形与直角三角形的面积和D.较小两个正方形重叠部分的面积6(2023春·广东潮州·九年级校考期末)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着中国古代的数学成就.如图所示的“弦图”,是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.直角三角形的斜边长为13,一条直角边长为12,则小正方形ABCD 的面积的大小为()A.144B.100C.49D.257(2023春·湖北武汉·八年级统考期末)大约公元222年我国汉代数学家赵爽为《周髀算经》一书作序时介绍了“勾股圆方图”,亦称“赵爽弦图”,如图,四个全等的直角三角形拼成大正方形ABCD ,中空的部分是小正方形EFGH ,连接EG ,BD 相交于点O ,BD 与HC 相交于点P ,若GO =GP ,则直角三角形的边CG 与BG 之比是()A.12B.25C.2-1D.3-28(2023春·江苏泰州·七年级统考期末)大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(如图1).某数学兴趣小组类比“赵爽弦图”构造出图2:△ABC 为等边三角形,AD 、BE 、CF 围成的△DEF 也是等边三角形.已知点D 、E 、F 分别是BE 、CF 、AD 的中点,若△ABC 的面积为14,则△DEF 的面积是()A.1B.2C.3D.49(2023·河北石家庄·校考二模)如图1,毕达哥拉斯树,也叫“勾股树”,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形.在图2中,∠ACB=90°,分别以Rt△ABC的三条边为边向外作正方形,连接BE,DG,BE交AC于点Q.若∠BAC=30°,BC=2,则四边形EQGD的面积是()B.23C.53+3D.3A.53+3210(2023·江苏扬州·统考中考真题)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若b-a=4,c=20,则每个直角三角形的面积为.11(2022秋·四川成都·八年级校考期中)“勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在△ABC中,∠ACB=90°,分别以△ABC的三条边为边向外作正方形,连接EB,CM,DG,CM分别与AB,BE相交于点P,Q.若∠ABE=30°,则DGQM的值为.12(2022春·安徽合肥·八年级合肥市第四十二中学校考期中)如图①,在Rt△ACB中∠ACB=90°,分别以AC、BC、AB为边,向形外作等边三角形,所得的等边三角形的面积分别为S1、S2、S3,请解答以下问题:(1)S1、S2、S3满足的数量关系是.(2)现将△ABF向上翻折,如图②,若阴影部分的S甲=6、S乙=5、S丙=4,则S△ACB=.13(2023·湖北孝感·统考三模)“勾股树”是以正方形一边为斜边向外作直角三角形,再以直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为.14(2022·山东临沂·统考二模)中国古代的数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位尤其是三国时期的数学家赵爽,不仅最早对勾股定理进行了证明,而且创制了“勾股圆方图”,开创了“以形证数”的思想方法.在图中,小正方形ABCD的面积为1,如果把它的各边分别延长一倍得到正方形A1B1C1D1(如图1),则正方形的面积为;再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2(如图2),如此进行下去,得到的正方形A n B n C n D n的面积为(用含n的式子表示,n为正整数).15(2023·浙江台州·八年级校考期中)如图1,是一个封闭的勾股水箱,其中Ⅰ,Ⅱ,Ⅲ部分是可盛水的正方形,且相互联通,已知∠ACB=90°,AC=6,BC=8,开始时Ⅲ刚好盛满水,而Ⅰ,Ⅱ无水.(1)如图2摆放时,Ⅰ刚好盛满水,而Ⅱ无水,则Ⅲ中有水部分的面积为;(2)如图3摆放时,水面刚好经过Ⅲ的中心O(正方形两条对角线的交点),则Ⅱ中有水部分的面积为.16(2023·湖北黄冈·统考中考真题)如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b,连接AE,BE,若△ADE与△BEH的面积相等,则b2a2+a2b2=.17(2023·江苏徐州·统考二模)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连接AC,若AG平分∠CAD,且正方形EFGH的面积为2,则正方形ABCD的面积为.18(2023·陕西渭南·统考二模)魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.如图,四边形ABCD、四边形BFGH和四边形AFMN都是正方形,BF交CD于E,若DE=2,CE=4,则BF的长为.19(2022·宁夏吴忠·统考一模)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是17,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,则图2中最大的正方形的面积为31.试求图1中小正方形的面积是为.20(2023·山东济宁·统考二模)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.勾股定理内容为:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2.(1)如图2、3、4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有个;(2)如图5所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图6所示的“勾股树”.在如图7所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,回答下列问题:(结果可用含m的式子表示)①a2+b2+c2+d2=;②b与c的关系为,a与d的关系为.21(2022·湖南·八年级课时练习)如图①,美丽的弦图,蕴含着四个全等的直角三角形.(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图①,试验证勾股定理.(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长24,OC=3,求该飞镖状图案的面积.(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,求S2.22(2023·广东深圳·校联考三模)中华文明源远流长,如图①是汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称之为赵爽弦图,被誉为中国数学界的图腾.2002年北京国际数学家大会依据赵爽弦图制作了会标,该图有4个全等的直角三角形围成几个大正方形和中间一个小正方形,巧妙的证明了勾股定理.问题发现:如图①,若直角三角形的直角边BC=3,斜边AB=5,则中间小正方形的边长CD=,连接BD,△ABD的面积为.知识迁移:如图②,P是正方形ABCD内一点,连接PA,PB,PC,当∠BPC=90°,BP=10时,△PAB的面积为.拓展延伸:如图③,已知∠MBN=90°,以点B为圆心,适当长为半径画弧,交射线BM,BN分别于A,C两点.(1)已知D为线段AB上一个动点,连接CD,过点B作BE⊥CD,垂足为点E;在CE上取一点F,使EF=BE;过点F作GF⊥CD交BC于点G,试判断三条线段BE,DE,GF之间的数量关系,并说明理由.(2)在(1)的条件下,若D为射线BM上一个动点,F为射线EC上一点;当AB=10,CF=2时,直接写出线段DE的长.三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图,是中国古代数学家赵爽发现,既可以证明勾股定理,也可以以此命题,相关的题目有一定的难度,但解题方法也常常是不唯一的。
(完整版)等腰直角三角形中的常用模型

等腰直角三角形中的常用模型模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
1.如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△P AQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MBPC的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .G G B ACD E F (2)(1)FE D C B AF DAA(2)FEDC A A B C DE F (1)(2)(3)(1)DD EEC C EC A AAB变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD于点E ,交BC 于点F ,连接DF ,求证:∠1=∠2。
模型12 脚拉脚模型(解析版)-2023年中考数学重难点解题大招复习讲义-几何模型篇
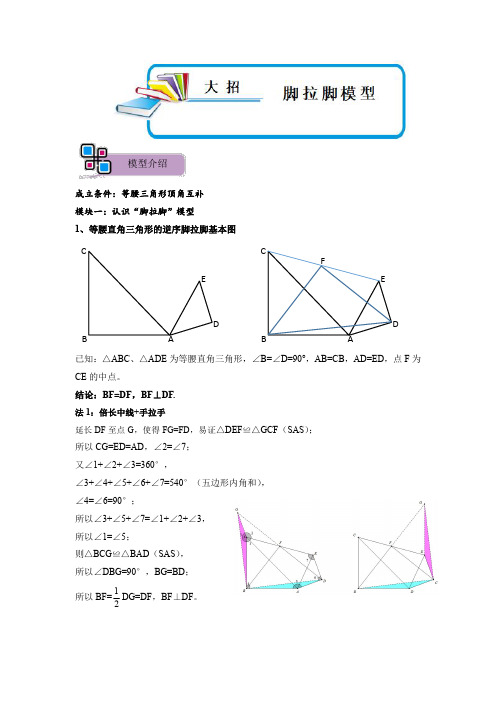
模型介绍成立条件:等腰三角形顶角互补模块一:认识“脚拉脚”模型1、等腰直角三角形的逆序脚拉脚基本图ABCEDABCEDF已知:△ABC 、△ADE 为等腰直角三角形,∠B=∠D=90°,AB=CB ,AD=ED ,点F 为CE 的中点。
结论:BF=DF ,BF ⊥DF.法1:倍长中线+手拉手延长DF 至点G ,使得FG=FD ,易证△DEF ≌△GCF (SAS );所以CG=ED=AD ,∠2=∠7;又∠1+∠2+∠3=360°,∠3+∠4+∠5+∠6+∠7=540°(五边形内角和),∠4=∠6=90°;所以∠3+∠5+∠7=∠1+∠2+∠3,所以∠1=∠5;则△BCG ≌△BAD (SAS ),所以∠DBG=90°,BG=BD ;所以BF=21DG=DF ,BF ⊥DF 。
由△BCF≌△GEF(SAS),得BC∥GH,由△DEF≌△GCF(SAS),得GH ∥DE,所以∠2=∠6=90°,则∠2=∠1,所以∠H+∠ADE=180°,即∠H=∠ADE=90°,在四边形ADEH中,∠1+∠2=180°,所以∠H=∠ABC=90°,则∠3+∠4=180°,又∠4+∠5=180°,所以∠1=∠2(8型转角),所以∠3=∠5所以∠3=∠4注意:选择“四边形对角互补”还是“8型转角”证明角相等取决原有等腰直角三角形底边与公共顶点的夹角(夹角小于45°:选择“四边形对角互补”;夹角大于45°:选择“8型转角”)法2:斜边中线+中位线取AC中点G,AE中点H,连接BG,FG,FH,DH。
由中位线定理可知:FG=21AE=DH ,FH=21AC=BG ,∠1=∠3=∠2,所以∠1+∠5=∠2+∠4,所以∠BGF=∠FHD ;则△BGF ≌△FHD (SAS ),所以BF=DF ,∠FBG=∠DFH ,∠BFG=∠FDH ;所以∠BFG+∠GFH+∠DFH=∠BFG+∠3+∠FBG =∠BFG+∠1+∠FBG ,又∠BFG+∠1+∠FBG+∠5=180°(三角形内角和),所以∠BFG+∠1+∠FBG=90°,所以BF ⊥DF 。
双等腰直角三角形模型及证明

双等腰直角三角形模型及证明
双等腰直角三角形是一种特殊的三角形,它既是等腰三角形,也是直角三角形。
下面我们将展示双等腰直角三角形的模型,并给出其证明。
双等腰直角三角形的模型可以使用两条等长的直线段和一条直线段垂直于这两条直线段构建。
具体步骤如下:
1. 首先,我们画一条水平直线段AB,作为等腰直角三角形的底边。
2. 接下来,我们从A、B两点相同的方向上,分别作两条与底边等长的直线段,分别记为AC和BD。
这两条直线段将与底边AB相交于
C、D两点。
3. 然后,我们将竖直地连接C和D两点,得到CD这条垂直于底边AB的直线段。
完成上述步骤后,我们可以观察到所构建的模型正好满足双等腰直角三角形的定义:即底边AB与两条斜边AC和BD等长,且直角CD 垂直于底边AB。
接下来我们对这个模型进行证明。
首先,我们可以通过观察得到AC和CD、BD和CD都是等长的,因为AC和BD与底边AB相交于C和D两点,所以它们与底边AB的长度必然相等。
同时,直角CD垂直于底边AB,与底边构成直角,因此CD也与AB等长。
其次,由于AC和CD、BD和CD等长,所以根据等腰三角形的性质,我们可以得到AC与BD等长。
最后,由于CD垂直于AB且与AB等长,根据直角三角形的性质,我们可以得到底边AB和直角CD构成直角。
综上所述,我们证明了双等腰直角三角形的模型确实满足双等腰直角三角形的定义。
解题技巧专题:利用等腰三角形的“三线合一”作辅助线压轴题三种模型全攻略(解析版)

解题技巧专题:利用等腰三角形的'三线合一'作辅助线压轴题三种模型全攻略【考点导航】目录【典型例题】【类型一等腰三角形中底边有中点时,连中线】【类型二等腰三角形中底边无中点时,作高线】【类型三巧用“角平分线+垂线合一”构造等腰三角形】【典型例题】【类型一等腰三角形中底边有中点时,连中线】1如图,在△ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,过D 作直线DE 交直线AB 与E ,过D 作直线DF ⊥DE ,并交直线AC 与F .(1)若E点在线段AB 上(非端点),则线段DE 与DF 的数量关系是;(2)若E 点在线段AB 的延长线上,请你作图(用黑色水笔),此时线段DE 与DF 的数量关系是,请说明理由.【答案】(1)DE =DF(2)图见解析,DE =DF ,理由见解析【分析】(1)连接AD ,先根据等腰直角三角形的性质可得AD =BD =CD ,∠B =∠DAF =45°,AD ⊥BC ,再根据垂直的定义、等量代换可得∠BDE =∠ADF ,然后根据三角形全等的判定证出△BDE ≅△ADF ,根据全等三角形的性质即可得出结论;(2)分①当点E 在线段AB 的延长线上,且在BC 的下方时,②当点E 在线段AB 的延长线上,且在BC 的上方时两种情况,参考(1)的思路,根据三角形全等的判定与性质即可得出结论.【详解】(1)解:如图,连接AD ,∵在△ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,∴AD =BD =CD ,∠B =∠DAF =45°,AD ⊥BC ,∴∠BDE +∠ADE =90°,∵DF ⊥DE ,∴∠ADF+∠ADE =90°,∴∠BDE =∠ADF ,在△BDE 和△ADF 中,∠B =∠DAFBD =AD ∠BDE =∠ADF,∴△BDE ≅△ADF ASA ,∴DE =DF ,故答案为:DE =DF .(2)解:DE =DF ,理由如下:①如图,当点E 在线段AB 的延长线上,且在BC 的下方时,如图,连接AD ,∵在△ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,∴AD =BD ,∠ABD =∠DAC =45°,AD ⊥BC ,∴∠DBE =∠DAF =135°,∠ADF +∠BDF =90°,∵DF ⊥DE ,∴∠BDE +∠BDF =90°,∴∠BDE =∠ADF ,在△BDE 和△ADF 中,∠DBE =∠DAFBD =AD ∠BDE =∠ADF,∴△BDE ≅△ADF ASA ,∴DE =DF ;②如图,当点E 在线段AB 的延长线上,且在BC 的上方时,如图,连接AD ,∵在△ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,∴AD =CD ,∠ACD =∠DAB =45°,AD ⊥BC ,∴∠DCF =∠DAE =135°,∠ADE +∠CDE =90°,∵DF ⊥DE ,∴∠CDF +∠CDE =90°,∴∠ADE =∠CDF ,在△ADE 和△CDF 中,∠DAE =∠DCFAD =CD ∠ADE =∠CDF,∴△ADE ≅△CDF ASA ,∴DE =DF ;综上,线段DE 与DF 的数量关系是DE =DF ,故答案为:DE =DF .【点睛】本题考查了等腰直角三角形的性质、三角形全等的判定与性质等知识点,通过作辅助线,构造全等三角形是解题关键.【变式训练】1如图,在等腰直角三角形ABC 中,∠C =90°,AC =a ,点E 为边AC 上任意一点,点D 为AB 的中点,过点D 作DF ⊥DE 交BC 于点F .求证:CE +CF为定值.【答案】证明见解析【分析】连接CD ,证明△CDE ≌△BDF ,得CE =BF ,进一步证明CE +CF =BC =AC =a ,从而得到结论.【详解】证明:连接CD ,如图,∵△ABC 是等腰直角三角形,且D 为AB 的中点,∴CD ⊥AB ,CD 平分∠ACB ,AD =BD =CD∴∠DCA =∠DCB =∠DBC =45°又DE ⊥DF∴∠EDC +∠FDC =90°而∠FDC +∠FDB =90°∴∠EDC =∠FDB在△CDE 和△BDF 中,∠DCE =∠DBFCD =CD∠EDC =∠BDF∴△CDE ≌△BDF∴CE =BF∵BC =AC =a ∴CE +CF =BE +CF =BC =AC =a ,故:CE +CF 为定值.【点睛】此题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,证明CE =BF 是解答此题的关键.2如图1,在Rt △ABC 中,∠C =90°,AC =BC ,点P 是斜边AB 的中点,点D ,E 分别在边AC ,BC 上,连接PD ,PE ,若PD ⊥PE.(1)求证:PD =PE ;(2)若点D ,E 分别在边AC ,CB 的延长线上,如图2,其他条件不变,(1)中的结论是否成立?并加以证明;(3)在(1)或(2)的条件下,△PBE 是否能成为等腰三角形?若能,请直接写出∠PEB 的度数(不用说理);若不能,请说明理由.【答案】(1)见解析(2)成立,见解析(3)能成为等腰三角形,此时∠PEB 的度数为22.5°或67.5°或90°或45°【分析】(1)连接PC ,根据等腰直角三角形的性质可得∠DCP =45°=∠B ,从而得到CP =BP ,再由PD ⊥PE ,可得∠DPC =∠EPB ,可证得△DPC ≌△EPB ,即可求证;(2)连接PC ,根据等腰直角三角形的性质可得∠ECP =45°=∠ABC =∠A =∠ACP ,从而得到CP =AP ,再由∵PD ⊥PE ,CP ⊥AB ,可得∠APD =∠CPE ,可证得△APD ≌△CPE ,即可;(3)根据等腰三角形的性质,分四种情况讨论,即可求解.【详解】(1)明∶连接PC,∵∠ACB =90°,AC =BC ,∴∠A =∠B =45°,∵P 为斜边AB 的中点,∴CP ⊥AB ,∴∠DCP =45°=∠B ,∴CP =BP ,∵PD ⊥PE ,∴∠DPC +∠CPE =∠CPE +∠EPB =90°,∴∠DPC =∠EPB ,在△DPC 和△EPB 中,∠DCP =∠BPC =PB ∠DPC =∠EPB,∴△DPC ≌△EPB ASA ,∴PD =PE ;(2)解:PD =PE 仍成立,理由如下:连接CP,∵∠C =90°,AC =BC ,∴∠A =∠ABC =45°,∵P 为斜边AB 的中点,∴CP ⊥AB ,∴∠ECP =45°=∠ABC =∠A =∠ACP ,∴CP =AP ,又∵PD ⊥PE ,CP ⊥AB ,∴∠DPE =∠CPA =90°,∴∠DPE +∠CPD =∠CPA +∠CPD ,∴∠APD =∠CPE ,在△APD 和△CPE 中,∠PAD =∠PCEPC =PA ∠APD =∠CPE,∴△APD ≌△CPE ASA ,∴PD =PE ;(3)解:△PBE 能成为等腰三角形,①当BE =BP ,点E 在CB 的延长线上时,则∠E =∠BPE ,又∵∠E +∠BPE =∠ABC =45°,∴∠PEB =22.5°;②当BE =BP ,点E 在CB 上时,则∠PEB =∠BPE =12180°-45° =67.5°;③当EP =EB 时,则∠B =∠BPE =45°,∴∠PEB =180°-∠B -∠BPE =90°;④当EP =PB ,点E 和C 重合,∴∠PEB =∠B =45°;综上所述,△PBE 能成为等腰三角形,∠PEB 的度数为22.5°或67.5°或90°或45°.【点睛】本题主要考查了等腰三角形的性质,全等三角形的判定和性质,熟练掌握等腰三角形的性质,全等三角形的判定和性质,利用分类讨论思想解答是解题的关键.3在Rt△ABC中,AC=BC,∠ACB=90°,点O为AB的中点.(1)若∠EOF=90°,两边分别交AC,BC于E,F两点.①如图1,当点E,F分别在边AC和BC上时,求证:OE=OF;②如图2,当点E,F分别在AC和CB的延长线上时,连接EF,若OE=6,则S△EOF=.(2)如图3,若∠EOF=45°,两边分别交边AC于E,交BC的延长线于F,连接EF,若CF=3,EF=5,试求AE的长.【答案】(1)①见解析;②18(2)2【分析】(1)①由“ASA”可证△AOE≌△COF,可得OE=OF;②由“ASA”可证△COE≌△BOF,可得OE=OF=6,即可求解;(2)由“ASA”可证△COF≌△AOH,可得CF=AH=3,OF=OH,由“SAS”可证△EOF≌△EOH.,可得EF=EH=5,即可求解.【详解】(1)①证明:如图1,连接OC,∵AC=BC,∠ACB=90°,∴∠=∠B=45°.∵点O为AB的中点,∴∠AOC=∠EOF=90°,∴△AOC和△BOC是等腰直角三角形,∴AO=CO=BO,∴∠AOE=∠COF,∴△AOE≌△COF(ASA),∴OE=OF;②解:如图2,连接OC,同理可证:AO=CO=BO,∠ABC=∠ACO=45°,∴∠OCE=∠OBF=135°,∵∠AOC=∠EOF=90°,∴∠COE=∠BOF,∴△COE≌△BOF(ASA),∴OE=OF=6,×OE⋅OF=18,∴SΔEOF=12故答案为:18;(2)解:如图3,连接CO,过点O作HO⊥FO,交CA的延长线于点H,∵AC=BC,∠ACB=90°,点O为AB的中点,∴AO=CO=B0,∠AOC=∠FOH=90°,∠BAC=∠BCO=45°,∴.∠COF=∠AOH,∠OCF=∠OAH=135°,∴△COF≌△AOH(ASA),∴CF=AH=3,OF=OH,∵∠EOF=45°,∠FOH=90°,∴∠EOF=∠EOH=45°,又∵OF=OH,EO=EO,∴△EOF≌△EOH(SAS),∴EF=EH=5,∴.AE=EH-AH=2.【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.【类型二等腰三角形中底边无中点时,作高线】1如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.(1)如图1,求证:BD=CE;(2)如图2,当AD=CD时,过点C作CM⊥AD于点M,如果DM=2,求CD-BD的值.【答案】(1)见解析(2)4【分析】(1)过A作AH⊥BC于点H,根据三线合一可得:BH=CH,DH=EH,即可证明;(2)过A作AH⊥BC于点H,易证△AHD≌△CMD,可得MD=DH,即可求解.【详解】(1)证明:如图过A作AH⊥BC于点H,∵AB=AC,AH⊥BC,∴BH=CH,∵AD=AE,∴DH=EH,∴BD=CE;(2)解:过A作AH⊥BC于点H,在△AHD 和△CMD 中,∠CDM =∠ADH∠CMD =∠AHD =90°CD =AD∴△AHD ≌△CMD AAS ,∴DH =MD ,∴CD -BD =CH +DH -BH -DH =2DH =2MD =4.【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质“三线合一”,熟练掌握全等三角形的判定方法是解题的关键.【变式训练】1如图,△ADB 与△BCA 均为等腰三角形,AD =AB =CB ,且∠ABC =90°,E 为DB 延长线上一点,∠DAB =2∠EAC.(1)若∠EAC =20°,求∠CBE 的度数;(2)求证:AE ⊥EC ;(3)若BE =a ,AE =b ,CE =c ,求△ABC 的面积(用含a ,b ,c 的式子表示).【答案】(1)20°(2)见解析(3)12a 2+12bc 【分析】(1)先,是等腰三角形性质与三角形内角和定理求出∠D =∠DBA =70°,即可由∠CBE =180°-∠DBA -∠ABC 求解;(2)过点A 作AF ⊥DE 于点F ,过点C 作CG ⊥DE 于点G ,证明△BAF ≌△CBG AAS ,得出AF =BG ,BF =CG ,进而求得∠AEF =∠ACB =45°,∠CEG =∠AEF =45°,即可得出∠AEC =90°,从而得出结论;(3)由(2)可知CG =BF ,AF =EF ,从而有CG =BF =EF -BE =AF -BE ,再根据S △ABC =S △AEB +S △AEC -S △BEC ,则有S △ABC =12BE ⋅AF +12AE ⋅EC -12BE ⋅CG =12BE AF -CG +12AE ⋅EC =12BE ⋅BE +12AE ⋅EC ,即可求解.【详解】(1)解:∵∠EAC =20°,∠DAB =2∠EAC ,∴∠BAD =40°,∵AD =AB ,∴∠D =∠DBA =12180°-∠BAD =12180°-40° =70°,又∵∠ABC =90°,∴∠CBE =180°-70°-90°=20°.(2)证明:过点A 作AF ⊥DE 于点F ,过点C 作CG ⊥DE 于点G ,∴∠AFB =∠ABC =∠CGB =90°,又∵AD =AB =CB ,∴∠BAC =∠ACB =45°,∠FAB =12∠DAB =∠CAE ,∵∠FAB +∠FBA =∠FBA +∠CBG =90°,∴∠FAB =∠CBG =∠CAE ,∴在△BAF 和△CBG 中,∠BAF =∠CBG∠AFB =∠CGB AB =BC,∴△BAF ≌△CBG AAS ,∴AF =BG ,BF =CG ,∵∠CBG =∠CAE ,设AE 、BC 交于点O ,则∠AEF =180°-∠CBG -∠BOE∠ACB =180°-∠CAE -∠AOC又∠BOE =∠AOC ,∴∠AEF =∠ACB =45°,∴AF =EF =BG ,BF =CG ,∴BF =EG =CG ,∴∠CEG =∠AEF =45°,∴∠AEC =90°,∴AE ⊥EC .(3)解:由(2)可知CG =BF ,AF =EF ,∴CG =BF =EF -BE =AF -BE ,∵S △ABC =S △AEB +S △AEC -S △BEC ,∴S △ABC =12BE ⋅AF +12AE ⋅EC -12BE ⋅CG .=12BE AF -CG +12AE ⋅EC =12BE ⋅BE +12AE ⋅EC =12a 2+12bc .【点睛】本题考查等腰三角形的性质与判定,等腰直角三角形的性质,三角形内角和,三角形外角性质,全等三角形的判定与性质,三角形面积,属三角形综合题目,难度适中.2已知OP 平分∠MON ,如图1所示,点B 在射线OP 上,过点B 作BA ⊥OM 于点A ,在射线ON 上取一点C ,使得BC =BO .(1)若线段OA =3cm ,求线段OC 的长;(2)如图2,点D 是线段OA 上一点,作∠DBE ,使得∠DBE =∠ABO ,∠DBE 的另一边交ON 于点E ,连接DE .①∠OBC =2∠DBE 是否成立,请说明理由;②请判断三条线段CE ,OD ,DE 的数量关系,并说明理由.【答案】(1)6cm(2)①∠OBC =2∠DBE 成立,理由见解析;②CE =OD +DE ,理由见解析【分析】(1)如图所示,过点B作BH⊥OC于H,由三线合一定理得到OC=2OH,由角平分线的定义得到∠BOA=∠BOH,进一步证明△BAO≌△BHO,得到OH=OA=3cm,则OC=2OH=6cm;(2)①如图所示,过点B作BH⊥OC于H,由三线合一定理得到∠OBC=2∠OBH,同(1)可得△BAO≌△BHO,则∠OBH=∠OBA,由∠DBE=∠ABO,即可推出∠OBC=2∠OBH=2∠DBE;②如图所示,在CE上截取CQ=OD,连接BQ,先证明∠BOD=∠BCQ,进而证明△BOD≌△BCQ,得到BD=BQ,∠OBD=∠CBQ,进一步证明∠EBQ=∠EBD,从而证明△EBD≌△EBQ,得到DE=QE,由CE=CQ+QE可证明CE=OD+DE.【详解】(1)解:如图所示,过点B作BH⊥OC于H,∵BC=OB,BH⊥OC,∴OH=CH,即OC=2OH,∵OP平分∠MON,∴∠BOA=∠BOH,∵BA⊥OM,BH⊥OC,∴∠BAO=∠BHO=90°,又∵OB=OB,∴△BAO≌△BHO AAS,∴OH=OA=3cm,∴OC=2OH=6cm(2)解:①∠OBC=2∠DBE成立,理由如下:如图所示,过点B作BH⊥OC于H,∵BC=OB,BH⊥OC,∴∠OBH=∠CBH,即∠OBC=2∠OBH,同(1)可得△BAO≌△BHO,∴∠OBH=∠OBA,∵∠DBE=∠ABO,∴∠DBE=∠OBH,∴∠OBC=2∠OBH=2∠DBE;②CE=OD+DE,理由如下:如图所示,在CE上截取CQ=OD,连接BQ,∵OB=BC,∴∠BOC=∠BCO,∵△BAO≌△BHO,∴∠BOA=∠BOH,∴∠BOD=∠BCQ,∴△BOD≌△BCQ SAS,∴BD=BQ,∠OBD=∠CBQ,∠OBC,∵∠DBE=12∠OBC,∴∠OBD+∠ODE=12∴∠CBQ+∠ODE=1∠OBC,∴∠EBQ =12∠OBC ,∴∠EBQ =∠EBD ,又∵EB =EB ,∴△EBD ≌△EBQ SAS ,∴DE =QE ,∵CE =CQ +QE ,∴CE =OD +DE .【点睛】本题主要考查了全等三角形的性质与判定,三线合一定理,正确作出辅助线构造全等三角形是解题的关键.【类型三巧用“角平分线+垂线合一”构造等腰三角形】1如图,在△ABC 中,AD 平分∠BAC ,E 是BC 的中点,过点E 作FG ⊥AD 交AD 的延长线于H ,交AB 于F ,交AC 的延长线于G .求证:(1)AF =AG ;(2)BF =CG .【答案】(1)见解析(2)见解析【分析】(1)根据ASA 证明△AHF ≌△AHG ,即可得出AF =AG ;(2)过点C 作CM ∥AB 交FG 于点M ,由△AHF ≌△AHG 可得∠AFH =∠G ,根据平行线的性质得出∠CMG =∠AFH ,可得∠CMG =∠G ,进而得出CM =CG ,再根据据ASA 证明△BEF ≌△CEM ,得出BF =CM ,等量代换即可得到BF =CG .【详解】(1)证明:∵AD 平分∠BAC ,∴∠FAH =∠GAH ,∵FG ⊥AH ,∴∠AHF =∠AHG =90°,在△AHF 和△AHG 中,∠FAH =∠GAHAH =AH ∠AHF =∠AHG,∴△AHF ≌△AHG ASA,∴AF =AG ;(2)证明:过点C 作CM ∥AB 交FG 于点M ,∵△AHF ≌△AHG ,∴∠AFH =∠G ,∵CM ∥AB ,∴∠CMG =∠AFH ,∴∠CMG =∠G ,∴CM =CG ,∵E 是BC 的中点,∴BE =CE ,∵CM ∥AB ,∴∠B =∠ECM ,在△BEF 和△CEM 中,∠B =∠ECMBE =CE ∠BEF =∠CEM,∴△BEF ≌△CEM ASA ,∴BF =CM ,∴BF =CG .【点睛】此题考查了全等三角形的判定与性质,等角对等边,平行线的性质,熟记全等三角形的判定定理、性质定理及作出合适的辅助线是解此题的关键.【变式训练】1如图所示,D 为△ABC 内一点,CD 平分∠ACB ,BD ⊥CD ,∠A =∠ABD ,若BD =1,BC =3,求:线段AC的长.【答案】5【分析】延长BD 交AC 于点E ,由题意可推出BE =AE ,依据等角的余角相等,即可得等腰三角形BCE ,可推出BC =CE ,AE =BE =2BD ,根据BD =1,BC =3,即可求出AC 的长度.【详解】解∶延长BD 交AC 于点E ,∵∠A =∠ABD ,∴BE =AE ,∵BD ⊥CD ,∴BE ⊥CD ,∴∠BDC =∠EDC =90°,∴∠BCD +∠EBC =∠ECD +∠BEC =90°,∵CD 平分∠ACB ,∴∠BCD =∠ECD ,∴∠EBC =∠BEC ,∴BC =CE,∵BE ⊥CD ,∴BE =2BD ,∵BD =1,BC =3,∴BE =2,CE =3,∴AE =BE =2,∴AC =AE +EC =2+3=5.【点睛】本题主要考查等腰三角形的判定与性质,解题的关键在于正确地作出辅助线,构建等腰三角形,通过等量代换,即可推出结论.2如图,AD 为△ABC的角平分线.(1)如图1,若CE ⊥AD 于点F ,交AB 于点E ,AB =8,AC =5.则BE =.(2)如图2,若∠C =2∠B ,点E 在AB 上,且AE =AC ,AB =a ,AC =b ,求CD 的长;(用含a 、b 的式子表示)(3)如图3,BG ⊥AD ,点G 在AD 的延长线上,连接CG ,若△ACG 的面积是7,求△ABC 的面积.【答案】(1)3(2)a -b(3)14【分析】(1)利用ASA 证明△AEF ≌△ACF ,得出AE =AC =5,再利用BE =AB -AE 即可求得答案;(2)利用SAS 证明△AED ≌△ACD ,得出∠AED =∠C ,ED =CD ,由题意可得出BE =AB -AE =a -b ,再利用等角对等边证得DE =BE ,即可得出答案;(3)延长AC 、BG 交于H ,先证明△ABG ≌△AHG ,得出:BG =GH ,S △ABG =S △AHG ,利用等底等高的两个三角形面积相等可得S △CBG =S △CGH ,设S △CBG =S △CGH =x ,即可得出答案.【详解】(1)解:∵AD 平分∠BAC ,∴∠EAF =∠CAF ,∵CE ⊥AD ,∴∠AFE =∠AFC =90°,在△AEF 和△ACF 中,∠EAF =∠CAFAF =AF ∠AFE =∠AFC,∴△AEF ≌△ACF ASA ∴AE =AC =5,∵AB =8,∴BE =AB -AE =8-5=3;故答案为:3.(2)解:∵AD 平分∠BAC ,∴∠EAD =∠CAD ,在△AED 和△ACD 中,AE =AC∠EAD =∠CAD AD =AD,∴△AED ≌△ACD SAS ,∴∠AED =∠C ,ED =CD ,∵AE =AC ,AB =a ,AC =b ,∴BE =AB -AE =a -b ,在△BDE 中,∠AED =∠B +∠BDE ,∴∠C =∠B +∠BDE ,∵∠C =2∠B ,∴∠B =∠BDE ,∴DE =BE =a -b ,∴CD =a -b ;(3)解:如图,延长AC 、BG 交于H ,∵AD 平分∠BAC ,∴∠BAG =∠HAG ,∵BG ⊥AD ,∴∠AGB =∠AGH =90°,在△ABG 和△AHG 中,∠BAG =∠HAGAG =AG ∠AGB =∠AGH,∴△ABG ≌△AHG ASA ,∴BG =GH ,S △ABG =S △AHG ,∴S △CBG =S △CGH ,设S △CBG =S △CGH =x ,∵S △ACG =7,∴S △AGH =S △ACG +S △CGH =7+x ,∴S △ABG =S △AHG =7+x ,∴S △ABH =27+x =14+2x ,∴S △ABC =S △ABH -S △CBG +S △CGH =14+2x -x +x =14.【点睛】本题考查了角平分线定义,三角形面积,全等三角形的判定和性质,等腰三角形判定和性质等,熟练掌握全等三角形的判定和性质是解题关键.3△ABC 中,∠ACB =90°,AC =BC ,点D 是BC 边上的一个动点,连接AD 并延长,过点B 作BF ⊥AD 交AD 延长线于点F.(1)如图1,若AD 平分∠BAC ,AD =6,求BF 的值;(2)如图2,M 是FB 延长线上一点,连接AM ,当AD 平分∠MAC 时,试探究AC 、CD 、AM 之间的数量关系并说明理由;(3)如图3,连接CF ,①求证:∠AFC =45°;②S △BCF =354,S △ACF =21,求AF 的值.【答案】(1)3(2)AC +CD =AM ,理由见解析(3)①证明见解析;②12【分析】(1)如图,分别延长AC ,BF 交于点E .证明△ADC ≌△BEC ASA ,得到BE =AD =6,再证明△ABF ≌△AEF ,即可得到BF =EF =12BE =3;(2)如图,分别延长BF ,AC 交于点E ,由(1)可得△ACD ≌△BCE ,得CD =CE ,再证△AFM ≌△AFE 得到AM =AE ,由此可得结论;(3)如图所示,在AD 上截取AH =BF ,证明△ACH ≌△BCF ,得到CH =CF ,∠ACH =∠BCF ,进一步证明∠HCF =90°,则∠CFH =∠CHF =180°-∠HCF 2=45°;②如图所示,过点C 作CG ⊥HF 于G ,则△CGH 、△CGF 都是等腰直角三角形,可得GH =GF =GC ,由全等三角形的性质得到S △ACH =S △BCF =354则S △CHF =S △ACF -S △ACH =494,据此求出HF =7,则CG =3.5,进一步求出AH =5则AF =AH +HF =12.【详解】(1)解:如图,分别延长AC ,BF 交于点E .∵BF ⊥AD ,∴∠AFB =∠ACB=90°,又∵∠ADC =∠BDF ,∴∠DAC =∠EBC .在△ADC 和△BEC 中,∠DAC =∠EBCAC =BC∠ACD =∠BCE =90°∴△ADC ≌△BEC ASA .∴BE =AD =6;∵BF ⊥AD ,∴∠AFB =∠AFE =90°,∵AD 平分∠BAC ,∴∠BAF =∠EAF .在△ABF 和△AEF 中,∠BAF =∠EAFAF =AF∠AFB =∠AFE∴△ABF ≌△AEF ASA .∴BF =EF =12BE =3;(2)解:AC +CD =AM ,理由如下:如图所示,延长MF ,AC 交于点E .由(1)可得,△ADC ≌△BCE ,∴CD =CE .∵BF ⊥AD ,∴∠AFM =∠AFE =90°,∵AF 平分∠MAE ,∴∠MAF =∠EAF .在△AMF 和△AEF 中,∠MAF =∠EAFAF =AF∠AFM =∠AFE∴△AFM ≌△AFE ASA .∴AM =AE .∵AE =AC +CE =AC +CD .∴AC +CD =AM .(3)解:①如图所示,在AD 上截取AH =BF ,在△ACH 和△BCF 中,AH =BF∠CAH =∠CBF AC =BC,∴△ACH ≌△BCF SAS ,∴CH =CF ,∠ACH =∠BCF ,∵∠ACH +∠BCH =90°,∴∠BCF +∠BCH =90°,即∠HCF =90°,∴∠CFH =∠CHF =180°-∠HCF 2=45°;②如图所示,过点C 作CG ⊥HF 于G ,∴∠GCH =GCF =45°,∴△CGH 、△CGF 都是等腰直角三角形,∴GH =GF =GC ,∵△ACH ≌△BCF ,∴S △ACH =S △BCF =354∴S △CHF=S △ACF -S △ACH =494,∴12HF ⋅CG =494,即12HF ⋅12HF =494,∴HF =7,∴CG=3.5,∴1 2AH×3.5=354,∴AH=5,∴AF=AH+HF=12.【点睛】本题主要考查了全等三角形的性质与判定,角平分线的定义,三角形内角和定理,三角形面积,等腰直角三角形的性质与判定等等,正确作出辅助线构造全等三角形是解题的关键.4(2022春·河北石家庄·八年级校考期中)(1)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分∠MON.点A为OM上一点,过点A作AC⊥OP,垂足为C,延长AC交ON于点B,可根据证明△AOC≌△BOC,则AO=BO,AC= BC(即点C为AB的中点).(2)【类比解答】如图2,在△ABC中,CD平分∠ACB,AE⊥CD于E,若∠EAC=63°,∠B=37°,通过上述构造全等的办法,可求得∠DAE=.(3)【拓展延伸】如图3,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论.(4)【实际应用】如图4是一块肥沃的三角形土地,其中AC边与灌渠相邻,李伯伯想在这块地中划出一块直角三角形土地进行水稻试验,故进行如下操作:①用量角器取∠ACB的角平分线CD;②过点A作AD⊥CD于D.已知BC=13,AC=10,△ABC面积为20,则划出的△ACD的面积是多少?请直接写出答案.【答案】(1)ASA(2)26°(3)BE=12CD,证明见解析(4)△ACD的面积是10013【分析】(1)证△AOC≌△BOC(ASA),得AO=BO,AC=BC即可;(2)延长AE交BC于点F,由问题情境可知,AC=FC,再由等腰三角形的性质得∠EFC=∠EAC=63°,然后由三角形的外角性质即可得出结论;(3)拓展延伸延长BE、CA交于点F,证△ABF≌△ACD(ASA),得BF=CD,再由问题情境可知,BE=FE =12BF ,即可得出结论;(4)实际应用延长AD 交BC 于E ,由问题情境可知,AD =ED ,EC =AC =10,则S △ACD =S △ECD ,再由三角形面积关系得S △ACE =1013S △ABC =20013,即可得出结论.【详解】(1)解:∵OP 平分∠MON ,∴∠AOC =∠BOC ,∵AC ⊥OP ,∴∠ACO =∠BCO ,∵OC =OC ,∴△AOC ≌△BOC (ASA ),∴AO =BO ,AC =BC ,故答案为:ASA ;(2)解:如图2,延长AE 交BC 于点F ,由可知,AC =FC ,∴∠EFC =∠EAC =63°,∵∠EFC =∠B +∠DAE ,∴∠DAE =∠EFC -∠B =63°-37°=26°,故答案为:26°;(3)解:BE =12CD ,证明如下:如图3,延长BE 、CA 交于点F ,则∠BAF =180°-∠BAC =90°,∵BE ⊥CD ,∴∠BED =90°=∠BAC ,∵∠BDC =∠ABF +∠BED =∠ACD +∠BAC ,∴∠ABF =∠ACD ,又∵AB =AC ,∴△ABF ≌△ACD (ASA ),∴BF =CD ,由问题情境可知,BE =FE =12BF ,∴BE =12CD ;(4)解:如图4,延长AD 交BC 于E ,由问题情境可知,AD =ED ,EC =AC =10,∴S △ACD =S △ECD ,∵S △ABC =20,∴S △ACE =1013S △ABC =20013,∴S △ACD =12S △ACE =10013,答:△ACD 的面积是10013.【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰三角形的性质、三角形的外角性质、角平分线定义以及三角形面积等知识,本题综合性强,熟练掌握等腰三角形的性质,证明三角形全等是解题的关键,属于中考常考题型.。
重难点拓展:等腰三角形中的半角模型两种常见题型解题技巧(学生版)
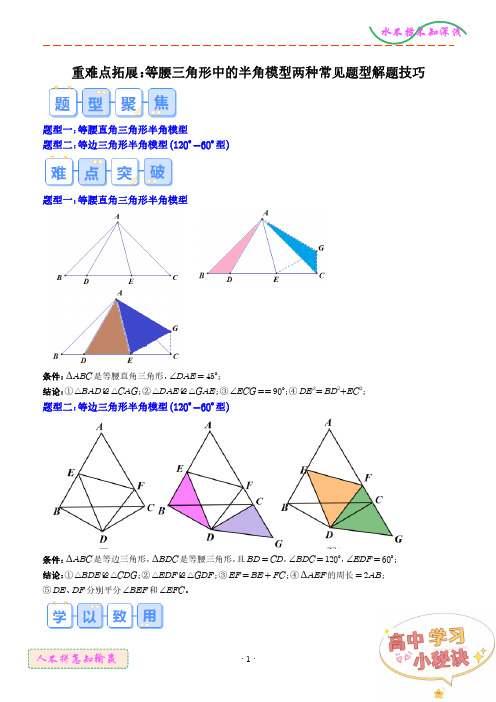
重难点拓展:等腰三角形中的半角模型两种常见题型解题技巧题型一:等腰直角三角形半角模型题型二:等边三角形半角模型(120°-60°型)题型一:等腰直角三角形半角模型条件:ΔABC是等腰直角三角形,∠DAE=45°;结论:①△BAD≌△CAG;②△DAE≌△GAE;③∠ECG==90°;④DE2=BD2+EC2;题型二:等边三角形半角模型(120°-60°型)条件:ΔABC是等边三角形,ΔBDC是等腰三角形,且BD=CD,∠BDC=120°,∠EDF=60°;结论:①△BDE≌△CDG;②△EDF≌△GDF;③EF=BE+FC;④ΔAEF的周长=2AB;⑤DE、DF分别平分∠BEF和∠EFC。
题型归纳题型一:等腰直角三角形半角模型1如图,已知△ABC中,∠BAC=90°,AB=AC,D,E是B C边上的点,将△ABD绕点A旋转,得到△ACD ,当∠DAE=45°时,求证:DE=D E;在(1)的条件下,猜想:BD2,DE2,CE2有怎样的数量关系?请写出,并说明理由.2(2022秋•原平市校级期中)如图,RtΔABC中AB=AC,D、E为BC边上两点,且∠DAE=45°,将ΔADC绕点A顺时针旋转90°后,得到ΔAFB,连接EF.下列4个结论:①ΔADC≅ΔAFB;②ΔABE≅ΔACD;③ΔAED≅ΔAEF;④BE+EF=BC-BF.正确的有( )个.A.1B.2C.3D.43(2023·浙江·八年级假期作业)如图,在Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,D、E是斜边BC上两点,且∠DAE=45°,若BD=3,CE=4,S△ADE=15,则△ABD与△AEC的面积之和为()A.36B.21C.30D.224(2023秋•九龙坡区校级期中)如图1,ΔABC为等边三角形,点D为BC的中点,连接AD,AE平分∠DAC,交BC于点E,点F在ΔABC外,连接FE,BF,AF,满足BF⎳AC,∠AFB=∠AEC.(1)求∠FAE的度数;(2)如图2,点G是AC上一点,连接EG,GF,GF与AE交于点K.若AK=EK,求证:CG=2CE.题型二:等边三角形半角模型(120°-60°型)1(2023秋•越秀区校级月考)在等边ΔABC的两边AB、AC所在直线上分别有两点M、N,D为ΔABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及ΔAMN的周长Q与等边ΔABC的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时Q L=;(2)如图2,点M、N边AB、AC上,且当DM≠DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;(3)如图3,当M、N分别在边AB、CA的延长线上时,若AN=x,则Q=(用x、L表示).2如图,ΔABC是边长为6的等边三角形,BD=CD,∠BDC=120°,以点D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连结MN,则ΔAMN的周长是.3如图,ΔABC是边长为4的等边三角形,BD=CD,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于点M.交AC于点N,连接MN,则ΔAMN的周长是.4(2022秋•宜丰县校级期中)如图1,ΔABC是正三角形,ΔBDC是等腰三角形,BD=CD,∠BDC= 120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.(1)探究BM、MN、NC之间的关系,并说明理由.(2)若ΔABC的边长为2,求ΔAMN的周长.过关检测一、单选题1如图所示,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后得到△AFB,连接EF,有下列结论:①BE=DC;②∠BAF=∠DAC;③∠FAE=∠DAE;④BF=DC.其中正确的有()A.①②③④B.②③C.②③④D.③④2(21-22八年级上·福建龙岩·期中)如图,在Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,D、E 是斜边BC上两点,且∠DAE=45°,若BD=3,CE=4,S△ADE=15,则△ABD与△AEC的面积之和为()A.36B.21C.30D.22二、解答题3在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN= 60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时Q L=;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.4如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,求△AMN的周长.5如图,△ABC是边长为2的等边三角形,△BDC是顶角为120°的等腰三角形,以点D为顶点作∠MDN=60°,点M、N分别在AB、AC上.(1)如图①,当MN⎳BC时,则△AMN的周长为;(2)如图②,求证:BM+NC=MN.6(21-22八年级上·浙江绍兴·期中)问题情境在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC= 120°,BD=DC.特例探究如图1,当DM=DN时,(1)∠MDB=度;(2)MN与BM,NC之间的数量关系为;归纳证明(3)如图2,当DM≠DN时,在NC的延长线上取点E,使CE=BM,连接DE,猜想MN与BM,NC之间的数量关系,并加以证明.拓展应用(4)△AMN的周长与△ABC的周长的比为.7如图,已知在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD ,连接D E.(1)当∠BAC=120°,∠DAE=60°时,求证:DE=D E;(2)当DE=D E时,∠DAE与∠BAC有怎样的数量关系?请写出,并说明理由.8(20-21七年级下·四川成都·期末)如图,CA=CB,CA⊥CB,∠ECF=45°,CD=CF,∠ACD=∠BCF.(1)求∠ACE+∠BCF的度数;(2)以E为圆心,以AE长为半径作弧;以F为圆心,以BF长为半径作弧,两弧交于点G,试探索△EFG的形状?是锐角三形,直角三角形还是钝角三角形?请说明理由.9(2020秋•西青区期末)已知在ΔABC中,AB=AC,D,E是BC边上的点,将ΔABD绕点A旋转,得到ΔACD ,连接D E.(Ⅰ)如图1,当∠BAC=120°,∠DAE=60°时,求证:DE=D E;(Ⅱ)如图2,当DE=D E时,请写出∠DAE与∠BAC的数量关系,并说明理由.10(2022春•林甸县期末)如图ΔABC为等边三角形,直线a⎳AB,D为直线BC上任一动点,将一60°角的顶点置于点D处,它的一边始终经过点A,另一边与直线a交于点E.(1)若D恰好在BC的中点上(如图1)求证:ΔADE是等边三角形;(2)若D为直线BC上任一点(如图2),其他条件不变,上述(1)的结论是否成立?若成立,请给予证明;若不成立,请说明理由.。
等腰直角三角形中的常用模型
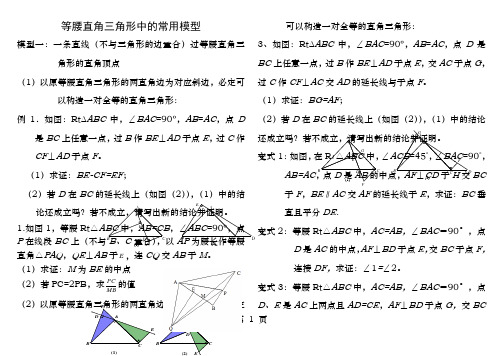
第 1 页等腰直角三角形中的常用模型模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
1.如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点 (2)若PC=2PB ,求MBPC 的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD 于点E ,交BC 于点F ,连接DF ,求证:∠1=∠2。
变式3:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 、E 是AC 上两点且AD=CE ,AF ⊥BD 于点G ,交BCGGBA CDEF(2)(1)FE DC B ADE F FED(1)CCABBA(2)FEDC B AAB C DE F(1)第 2 页于点F 连接DF ,求证:∠1=∠2。
(实用版)等腰直角三角形中的实际应用模型

(实用版)等腰直角三角形中的实际应用模型等腰直角三角形是一种具有特殊性质和应用价值的三角形。
在实际生活中,等腰直角三角形的模型被广泛应用于多个领域,包括建筑、工程、地理测量和天文学等等。
建筑领域的应用- 屋顶结构设计:等腰直角三角形的特殊性质使其成为建筑屋顶结构设计中的重要元素。
例如,在典型的尖顶房屋中,等腰直角三角形的形状使其具有良好的结构稳定性和承重能力。
屋顶结构设计:等腰直角三角形的特殊性质使其成为建筑屋顶结构设计中的重要元素。
例如,在典型的尖顶房屋中,等腰直角三角形的形状使其具有良好的结构稳定性和承重能力。
- 建筑布局规划:等腰直角三角形的对称性和刚性特点使其成为建筑布局规划中常用的基本单位。
例如,在城市规划中,可以利用等腰直角三角形构建高效的街道和街区布局模式。
建筑布局规划:等腰直角三角形的对称性和刚性特点使其成为建筑布局规划中常用的基本单位。
例如,在城市规划中,可以利用等腰直角三角形构建高效的街道和街区布局模式。
工程领域的应用- 桥梁设计:等腰直角三角形的稳定性和均匀的压力分布使其成为桥梁设计中的常用形式。
例如,在悬索桥的设计中,等腰直角三角形被广泛应用于桥梁塔台的结构。
桥梁设计:等腰直角三角形的稳定性和均匀的压力分布使其成为桥梁设计中的常用形式。
例如,在悬索桥的设计中,等腰直角三角形被广泛应用于桥梁塔台的结构。
- 测量和计算:等腰直角三角形的特殊关系使其在测量和计算中发挥重要作用。
例如,在三角测量中,可以利用等腰直角三角形的特性来测量远距离和高度。
测量和计算:等腰直角三角形的特殊关系使其在测量和计算中发挥重要作用。
例如,在三角测量中,可以利用等腰直角三角形的特性来测量远距离和高度。
地理测量和天文学中的应用- 方位测量:等腰直角三角形被用于方位测量,即确定一个点相对于一个参考点的方位角。
例如,在地理测量中,可以利用等腰直角三角形和其他测量工具来确定地球上的位置。
方位测量:等腰直角三角形被用于方位测量,即确定一个点相对于一个参考点的方位角。
等腰三角形中的分类讨论模型(解析版)--常见几何模型全归纳之模型解读

等腰三角形中的分类讨论模型模型1、等腰三角形中的分类讨论:【知识储备】凡是涉及等腰三角形边、角、周长、面积等问题,优先考虑分类讨论,再利用等腰三角形的性质与三角形三边关系解题即可。
1)无图需分类讨论①已知边长度无法确定是底边还是腰时要分类讨论;②已知角度数无法确定是顶角还是底角时要分类讨论;③遇高线需分高在△内和△外两类讨论;④中线把等腰△周长分成两部分需分类讨论。
2)“两定一动”等腰三角形存在性问题:即:如图:已知A,B两点是定点,找一点C构成等腰△ABC方法:两圆一线具体图解:①当AB=AC时,以点A为圆心,AB长为半径作⊙A,点C在⊙A上(B,C除外)②当AB=BC时,以点B为圆心,AB长为半径作⊙B,点C在⊙B上(A,E除外)③当AC=BC时,作AB的中垂线,点C在该中垂线上(D除外)1(2023秋·河北张家口·八年级统考期末)△ABC是等腰三角形,AB=5,AC=7,则△ABC的周长为()A.12B.12或17C.14或19D.17或19【答案】D【分析】根据等腰三角形的定义分两种情况:当腰为5与腰为7时,即可得到答案.【详解】解:当△ABC的腰为5时,△ABC的周长5+5+7=17;当△ABC的腰为7时,△ABC的周长5+7+7=19.故选:D.【点睛】本题主要考查等腰三角形的定义,掌握等腰三角形的定义是解题的关键.2(2023春·四川巴中·七年级统考期末)等腰三角形的周长为32cm,一边长为8cm,则其它两边长是()A.8cm,16cmB.12cm,12cmC.8cm,16cm或12cm,12cmD.12cm,8cm【答案】B【分析】根据等腰三角形的性质和构成三角形的条件即可得.【详解】解:∵等腰三角形的周长为32cm,一边长为8cm,∴①当底边长为8cm时,其它两边长是32-82=12(cm),②当腰长为8cm时,其它两边长是8cm或32-2×8=16(cm),8+8=16,此时三边不能构成三角形,综上,其它两边长是12cm,12cm,故选:B.【点睛】本题考查了等腰三角形,构成三角形的条件,解题的关键是掌握这些知识点.3(2023秋·广东八年级课时练习)若△ABC是等腰三角形,∠A=36°,则∠C的度数是()A.72°或108°B.36°或72°C.108°或36°D.36°或72°或108°【答案】D【分析】根据等腰三角形性质分情况讨论即可得到答案.【详解】解:∵△ABC是等腰三角形,∠A=36°,∴当∠A是顶角时,∠C=∠B=180°-36°2=72°;当∠A是底角时,①当∠B=∠A=36°时,则∠C=180°-2×36°=108°;②∠C=∠A=36°;综上所述,∠C的度数是36°或72°或108°,故选:D.【点睛】本题考查利用等腰三角形性质求角度,根据等腰三角形性质分类讨论是解决问题的关键.4(2022秋·江苏南通·八年级启东市长江中学校考阶段练习)等腰三角形一腰上的高与另一腰的夹角为60°,那么这个等腰三角形的顶角的度数为.【答案】30°或150°【分析】根据题意画出图形,分别从锐角三角形与钝角三角形分析求解即可求出答案.【详解】根据题意得:AB=AC,BD⊥AC,如图(1)所示,∠ABD=60°,则∠A=30°,即顶角为30°;如图(2)所示,∠ABD=60°,则∠DAB=30°,∴∠BAC=150°,即顶角为150°;故答案为:30°或150°.【点睛】本题考查等腰三角形的性质,注意掌握分类讨论思想和数形结合思想的应用是解题的关键.5(2023秋·江苏·八年级专题练习)在如图所示的网格中,在格点上找一点P,使△ABP为等腰三角形,则点P有()A.6个B.7个C.8个D.9个【答案】C【分析】分三种情况讨论:以AB为腰,点A为顶角顶点;以AB为腰,点B为顶角顶点;以AB为底.【详解】解:如图:如图,以AB为腰,点A为顶角顶点的等腰三角形有5个;以AB为腰,点B为顶角顶点的等腰三角形有3个;不存在以AB为底的等腰△ABP,所以合计8个.故选:C.【点睛】本题考查等腰三角形的定义,网格图中确定线段长度;在等腰三角形腰、底边待定的情况下,分类讨论是解题的关键.6(2023·重庆市八年级期中)如图1,一副直角三角板△ABC和△DEF,∠BAC=∠EDF=90°,∠B=45°,∠F=30°,点B、D、C、F在同一直线上,点A在DE上.如图2,△ABC固定不动,将△EDF绕点D逆时针旋转α(0°<α<135°)得△E′DF',当直线E′F′与直线AC、BC所围成的三角形为等腰三角形时,α的大小为.【答案】7.5°或75°或97.5°或120°【分析】设直线E′F′与直线AC、BC分别交于点P、Q,根据△CPQ为等腰三角形,分三种情况:①当∠PCQ为顶角时,∠CPQ=∠CQP,如图1,可求得α=7.5°;如图2,△CPQ为等腰三角形中,∠PCQ为顶角,可求得α=∠EDE′=90°+7.5°=97.5°;②当∠CPQ为顶角时,∠CQP=∠PCQ=45°,可得∠CPQ =90°,如图3,进而求得α=90°-15°=75°;③如图4,当∠CQP为顶角时,∠CPQ=∠PCQ=45°,可得∠CQP=90°,进而求得α=∠EDE′=∠EDQ+∠QDE′=90°+30°=120°.【详解】解:设直线E′F′与直线AC、BC分别交于点P、Q,∵△CPQ为等腰三角形,∴∠PCQ为顶角或∠CPQ为顶角或∠CQP为顶角,①当∠PCQ为顶角时,∠CPQ=∠CQP,如图1,∵∠BAC=∠EDF=90°,∠B=45°,∠F=30°,∴∠E′DF′=90°,∠ACB=45°,∠E′F′D=30°,∵∠CPQ+∠CQP=∠ACB=45°,∴∠CQP=22.5°,∵∠E′F′D=∠CQP+∠F′DQ,∴∠F′DQ=∠E′F′D-∠CQP=30°-22.5°=7.5°,∴α=7.5°;如图2,∵△CPQ为等腰三角形中,∠PCQ为顶角,∴∠CPQ=∠CQP=67.5°,∵∠E′DF′=90°,∠F′=30°,∴∠E′=60°,∴∠E′DQ=∠CQP-∠E′=67.5°-60°=7.5°,∴α=∠EDE′=90°+7.5°=97.5°;②当∠CPQ为顶角时,∠CQP=∠PCQ=45°,∴∠CPQ=90°,如图3,∵∠DE′F′=∠CQP+∠QDE′,∴∠QDE′=∠DE′F′-∠CQP=60°-45°=15°,∴α=90°-15°=75°;③如图4,当∠CQP为顶角时,∠CPQ=∠PCQ=45°,∴∠CQP=90°,∴∠QDF′=90°-∠DF′E′=60°,∴∠QDE′=∠E′DF′-∠QDF′=30°,∴α=∠EDE′=∠EDQ+∠QDE′=90°+30°=120°;综上所述,α的大小为7.5°或75°或97.5°或120°.故答案为:7.5°或75°或97.5°或120°.【点睛】本题考查了等腰三角形性质,直角三角形性质,旋转的性质,三角形内角和定理等,解题关键是运用数形结合思想和分类讨论思想思考解决问题.7(2022秋·江苏徐州·八年级校考期中)如图,∠AOB=70°,点C是边OB上的一个定点,点P在角的另一边OA上运动,当△COP是等腰三角形,∠OCP=°.【答案】40或70或55【分析】分三种情况讨论:①当OC=PC,②当PO=PC,③当OP=OC,根据等腰三角形的性质以及三角形内角和定理即可得到结论.【详解】解:如图,①当OC=PC时,∴∠COP=∠CPO=70°∴∠OCP=180°-∠OPC-∠COP=40°.②当PO=PC时,∠OCP=∠COP=70°;③当OP=OC时,∠OCP=180°-∠AOB2=55°;综上所述,∠OCP的度数为70°或40°或55°.故答案为:70或40或55.【点睛】本题考查了等腰三角形的性质以及三角形内角和定理,进行分类讨论是解题的关键.8(2023·安徽阜阳·八年级统考期末)在平面直角坐标系中,若点A0,4,B3,0,则AB=5.请在x轴上找一点C,使ΔABC是以AB为腰的等腰三角形,点C的坐标为.【答案】-3,0、-2,0或8,0【分析】分两种情况求解:①AB=AC,②AB=BC.【详解】解:①当AB=AC时,∵AO⊥BC,∴OC=BO=3,∴C(-3,0);②当AB=BC=5时,若点C在B点左侧,CO=BC-BO=2,此时点C的坐标为(-2,0);若点C在B点右侧,CO=BO+BC=8,此时点C的坐标为(8,0).综上所述,满足条件的点C有3个.故答案为:-3,0、-2,0或8,0.【点睛】本题考查了等腰三角形的性质、坐标与图形性质以及分类讨论,做题时需注意两点,一是注意点C 必须位于x轴上,二是注意不能漏解,应分AB=AC与AB=BC两种情况分别解答,难度适中.9(2023·江苏苏州·八年级校考期中)如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A-B-C-A运动,设运动时间为t秒(t>0).(1)若点P 在BC 上,且满足PA =PB ,求此时t 的值;(2)若点P 恰好在∠ABC 的角平分线上,求此时t 的值:(3)在运动过程中,当t 为何值时,△ACP 为等腰三角形.【答案】(1)6516(2)316或52(3)54或32或95或3【分析】(1)设PB =PA =xcm ,则PC =4-x cm ,利用勾股定理求出AC =3cm ,在Rt △ACP 中,依据AC 2+PC 2=AP 2,列方程求解即可得到t 的值.(2)如图所示,当点P 在AC 上时,过P 作PD ⊥AB 于D ,设PD =PC =ycm ,则AP =3-y cm ,在Rt △ADP 中,依据AD 2+PD 2=AP 2,列方程求解即可得到t 的值.当点P 与点B 重合时,点P 也在∠ABC 的角平分线上,此时,t =AB 2=52.(3)分四种情况:当P 在AB 上且AP =CP 时,当P 在AB 上且AP =CA =3cm 时,当P 在AB 上且AC =PC 时,当P 在BC上且AC =PC =3cm 时,分别依据等腰三角形的性质即可得到t 的值.【详解】(1)解:如图,设PB =PA =xcm ,则PC =4-x cm ,∵∠ACB =90°,AB =5cm ,BC =4cm ,∴AC =AB 2-BC 2=3cm ,在Rt △ACP 中,由勾股定理得AC 2+PC 2=AP 2,∴32+4-x 2=x 2,解得x =258,∴BP =258,∴t =AB +BP 2=5+2582=6516;(2)解:如图所示,当点P 在AC 上时,过P 作PD ⊥AB 于D ,∵BP 平分∠ABC ,∠C =90°,PD ⊥AB ∴PD =PC ,∠DBP =∠CBP ,在△BCP 与△BDP 中,∠BDP =∠BCP∠DBP =∠CBP BP =BP,∴△BDP ≌△BCP AAS∴BC =BD =4cm ,∴AD =5-4=1cm ,设PD =PC =ycm ,则AP =3-y cm ,在Rt △ADP 中,由勾股定理得AD 2+PD 2=AP 2,∴12+y2=3-y2,解得y=43,∴CP=43,∴t=AB+BC+CP2=5+4+432=316,当点P与点B重合时,点P也在∠ABC的角平分线上,此时,t=AB2=52.综上所述,点P恰好在∠ABC的角平分线上,t的值为316或52.(3)解:分四种情况:①如图,当P在AB上且AP=CP时,∴∠A=∠ACP,∵∠A+∠B=90°,∠ACP+∠BCP=90°,∴∠B=∠BCP,∴CP=BP=AP,∴P是AB的中点,即AP=12AB=52cm,∴t=AP2=54.②如图,当P在AB上且AP=CA=3cm时,∴t=AP2=32.③如图,当P在AB上且AC=PC时,过C作CD⊥AB于D,∵S△ABC=12AC⋅BC=12AB⋅CD,∴CD=AC⋅BCAB=125cm,在Rt△ACD中,由勾股定理得AD=AC2-CD2=32-1252=95cm,∴AP=2AD=185cm,∴t=AP2=95.④如图,当P在BC上且AC=PC=3cm时,则BP=4-3=1cm,∴t=AB+BP2=62=3.综上所述,当t的值为54或32或95或3时,△ACP为等腰三角形.【点睛】本题属于三角形综合题,考查了角平分线的性质,等腰三角形的性质以及勾股定理的综合运用.画出图形,利用分类讨论的思想是解第(3)题的关键.10(2022春·四川成都·八年级校考期中)如图,在平面直角坐标系内,点O为坐标原点,经过A-2,6的直线交x轴正半轴于点B,交y轴于点C,OB=OC,直线AD交x轴负半轴于点D,若△ABD的面积为27(1)求直线AB的表达式和点D的坐标;(2)横坐标为m的点P在线段AB上(不与点A、B重合),过点P 作x轴的平行线交AD于点E,设PE的长为y y≠0,求y与m之间的函数关系式并直接写出相应的m 取值范围;(3)在(2)的条件下,在x轴上是否存在点F,使△PEF为等腰直角三角形?若存在求出点F的坐标;若不存在,请说明理由.【答案】(1)y=-x+4,D-5,0(2)y=32m+3,-2<m<4(3)存在,点F的坐标为25,0或-165,0或-87,0【分析】(1)据直线AB交x轴正半轴于点B,交y轴于点C,OB=OC,设直线AB解析式为y=-x+n,把A的坐标代入求得n的值,从而求得B的坐标,再根据三角形的面积建立方程求出BD的值,求出OD 的值,从而求出D点的坐标;(2)直接根据待定系数法求出AD的解析式,先根据B、A的坐标求出直线AB的解析式,将P点的横坐标代入直线AB的解析式,求出P的纵坐标,将P的纵坐标代入直线AD的解析式就可以求出E的横坐标,根据线段的和差关系就可以求出结论;(3)要使△PEF为等腰直角三角形,分三种情况分别以点P、E、F为直角顶点,据等腰直角三角形的性质求出(2)中m的值,就可以求出F点的坐标.【详解】(1)解:∵OB=OC,∴设直线AB的解析式为y=-x+n,∵直线AB经过A-2,6,∴2+n=6,∴n=4,∴直线AB的解析式为y=-x+4,∴B4,0,∴OB=4,∵△ABD的面积为27,A-2,6,∴S△ABD=12×BD×6=27,∴BD=9,∴OD=5,∴D-5,0,∴直线AB的解析式为y=-x+4,D-5,0(2)解:设直线AD的解析式为y=ax+b,∵A-2,6,D-5,0∴-2a+b=6-5a+b=0,解得a=2b=10.∴直线AD的解析式为y=2x+10;∵点P在AB上,且横坐标为m,∴P m,-m+4,∵PE∥x轴,∴E的纵坐标为-m+4,代入y=2x+10得,-m+4=2x+10,解得x=-m-62,∴E-m-62,-m+4,∴PE的长y=m--m-62=3m2+3;即y=32m+3,-2<m<4;(3)解:在x轴上存在点F,使△PEF为等腰直角三角形,①当∠FPE=90°时,如图①,有PF=PE,PF=-m+4,PE=32m+3,∴-m+4=32m+3,解得m=25,此时F25,0;②当∠PEF=90°时,如图②,有EP=EF,EF的长等于点E的纵坐标,∴EF=-m+4,∴-m+4=32m+3,解得:m=25,∴点E的横坐标为x=-m-62=-165,∴F-165,0;③当∠PFE=90°时,如图③,有FP=FE,∴∠FPE=∠FEP.∵∠FPE+∠EFP+∠FEP=180°,∴∠FPE=∠FEP=45°.作FR⊥PE,点R为垂足,∴∠PFR=180°-∠FPE-∠PRF=45°,∴∠PFR=∠RPF,∴FR=PR.同理FR=ER,∴FR= 12PE.∵点R与点E的纵坐标相同,∴FR=-m+4,∴-m+4=1232m+3,解得:m=107,∴PR=FR=-m+4=-107+4=187,∴点F的横坐标为107-187=-87,∴F-87,0.综上,在x轴上存在点F使△PEF为等腰直角三角形,点F的坐标为25,0或-165,0或-87,0.【点睛】本题考查了等腰直角三角形的性质,三角形的面积公式的运用,待定系数法求一次函数的解析式的运用,解答本题时求出函数的解析式是关键.课后专项训练1(2023春·四川成都·七年级统考期末)等腰三角形的两边长分别为4cm和9cm,则这个三角形的周长为()A.22cmB.17cm或13cmC.13cmD.17cm或22cm【答案】A【分析】分4cm是腰长与底边长两种情况讨论求解.【详解】解:①4cm是腰长时,三角形的三边分别为4cm、4cm、9cm,因为4+4<9,故不能组成三角形;②4cm是底边长时,三角形的三边分别为4cm、9cm、9cm,能组成三角形,周长=4+9+9=22cm,综上所述,这个等腰三角形的周长是22cm.故选:A.【点睛】本题考查了等腰三角形的定义和三角形三边关系的应用,难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形.2(2023·浙江·八年级课堂例题)如图,P是射线ON上一动点,∠AON=30°,当△AOP为等腰三角形时,∠OAP的度数一定不可能是()A.120°B.75°C.60°D.30°【答案】C【分析】分AO=AP、AO=OP和OP=AP三种情况,利用等腰三角形的性质结合三角形的内角和定理解答即可.【详解】解:若△AOP为等腰三角形则有AO=AP、AO=OP和OP=AP三种情况,①当AO=AP时,则有∠O=∠APO=30°,故∠A=120°;②当AO=OP时,则∠A=∠APO=12180°-30°=75°;③当OP=AP时,则∠A=∠AON=30°,综上可知:∠A不可能为60°;故选:C.【点睛】本题考查了等腰三角形的性质和三角形的内角和定理,正确分类、熟练掌握等腰三角形的性质是解题的关键.3(2023·福建龙岩·八年级校考期中)在平面直角坐标系xOy中,点A2,0,B0,2,若点C在x轴上,且△ABC为等腰三角形,则满足条件的点C的个数为()A.1B.2C.3D.4【答案】D【分析】分为AB=AC、BC=BA,CB=CA三种情况画图判断即可.【详解】解:如图所示:当AB=AC时,符合条件的点有2个;当BC=BA时,符合条件的点有1个;当CB=CA,即当点C在AB的垂直平分线上时,符合条件的点有一个.故符合条件的点C共有4个.故选:D.【点睛】本题考查了等腰三角形的定义,线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解题的关键.4(2023·江苏八年级期中)如图,在正方形网格中,每个小正方形的边长都为1,点A、B都是格点(小正方形的顶点叫做格点),若△ABC为等腰三角形,且△ABC的面积为1,则满足条件的格点C有()A.0个B.2个C.4个D.8个【答案】C【分析】根据等腰三角形的性质和三角形的面积解答即可.【详解】解:如图所示:∵△ABC为等腰三角形,且△ABC的面积为1,∴满足条件的格点C有4个,故选C.【点睛】本题考查了等腰三角形的判定;熟练掌握等腰三角形的性质和三角形的面积是解决问题的关键5(2023·山东日照·八年级统考期末)如图,由8个全等的小长方形拼成一个大正方形,线段AB的端点都在小长方形的顶点上,若点C是某个小长方形的顶点,连接CA,CB,那么满足△ABC是等腰三角形的点C的个数是()A.3B.4C.5D.6【答案】D【分析】根据等腰三角形的判定即可得到结论.【详解】解:如图所示,使△ABP为等腰三角形的点P的个数是6,故选:D.【点睛】本题考查了等腰三角形的判定,正确的找出符合条件的点P是解题的关键.6(2022·山东青岛·统考二模)在平面直角坐标系中,O为坐标原点,点A的坐标为1,3,若M为x 轴上一点,且使得△MOA为等腰三角形,则满足条件的点M有()A.2个B.3个C.4个D.5个【答案】A【分析】分别以O、A为圆心,以OA长为半径作圆,与x轴交点即为所求点M,再作线段OA的垂直平分线,与坐标轴的交点也是所求的点M,作出图形,利用数形结合求解即可.【详解】解:如图,满足条件的点M的个数为2.故选A.【点睛】本题考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.7(2022·安徽淮北·九年级阶段练习)如图,在△ABC中,∠C=90°,BC=8,AC=6.若点P为直线BC上一点,且△ABP为等腰三角形,则符合条件的点P有( ).A.1个B.2个C.3个D.4个【答案】D【分析】根据勾股定理求出AB,分为三种情况:①AB=AP,②AB=BP,③AP=BP,得出即可.【详解】解:在△ABC中,∠B=90°,BC=8,AC=6,由勾股定理的:AC=AC2+BC2=62+82=10,如图,以点A为圆心,以10为半径画圆,交直线BC于两点,即点B和点P1;以点B为圆心,以10为半径画圆,交直线BC于两点,即点P2和P3;作线段AB的垂直平分线交直线BC与一点,即点P4;即共4个点,故选:D【点睛】本题考查了等腰三角形的判定和勾股定理的应用,关键要用分类讨论的思想.8(2022·黑龙江·哈尔滨八年级阶段练习)如图,在平面直角坐标系中,点A的坐标为1,1,在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P有()A.2个B.3个C.4个D.5个【答案】C【分析】先计算OA的长,再以OA为腰或底分别讨论,进而得出答案.【详解】解:如图,OA=12+12=2,当AO=OP1,AO=OP3时,P1(-2,0),P3(2,0),当AP2=OP2时,P2(1,0),当AO=AP4时,P4(2,0),故符合条件的点有4个.故选:C.【点睛】本题以平面直角坐标系为载体,主要考查了勾股定理和等腰三角形的定义,属于常考题型,全面分类、掌握解答的方法是关键.9(2022·四川广元·八年级期末)如图,在Rt△ABC中,∠ACB=90°,∠CAB=36°,以C为原点,C所在直线为y轴,BC所在直线为x轴建立平面直角坐标系,在坐标轴上取一点M使△MAB为等腰三角形,符合条件的M点有()A.6个B.7个C.8个D.9个【答案】C【分析】根据等腰三角形的判定,“在同一三角形中,有两条边相等的三角形是等腰三角形(简称:在同一三角形中,等边对等角)”分三种情况解答即可.【详解】解:如图,①以A为圆心,AB为半径画圆,交直线AC有二点M1,M2,交BC有一点M3,(此时AB=AM);②以B为圆心,BA为半径画圆,交直线BC有二点M5,M4,交AC有一点M6(此时BM=BA).③AB的垂直平分线交AC一点M7(MA=MB),交直线BC于点M8;∴符合条件的点有8个.故选:C.【点睛】本题考查了等腰三角形的判定;构造等腰三角形时本着截取相同的线段就能作出等腰三角形来,思考要全面,做到不重不漏.10(2023春·山东泰安·七年级统考期末)等腰三角形的一角为30°,则其顶角的大小是.【答案】120°或30°【分析】等腰三角形的一个内角是30°,则该角可能是底角,也可能是顶角,注意讨论即可.【详解】解:分两种情况:当30°的角是底角时,180°-30°×2=120°,则顶角度数为120°;当30°的角是顶角时,则顶角为30°;故答案为:120°或30°.【点睛】本题考查等腰三角形的性质,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.11(2023·四川凉山·八年级校考期中)等腰三角形一腰上的高与另一腰的夹角是36°,则底角是.【答案】27°或63°【分析】等腰三角形的高相对于三角形有三种位置关系:三角形的内部、三角形的边上、三角形的外部,根据条件可知第二种高在三角形的边上这种情况不成立,因而应分两种情况进行讨论即可得解.【详解】解:①当高在三角形内部时,如图:∵BD⊥AC,∴∠ADB=90°,∵∠ABD=36°,∴∠A=90°-∠ABD=54°,∴∠ABC=∠C=12180°-54°=63°;②当高在三角形外部时,如图:∵BD ⊥AC ,∴∠ADB =90°,∵∠ABD =36°,∴∠DAB =90°-36°=54°,∴∠ABC =∠C =12∠DAB =12×54°=27°.∴综上所述,底角是27°或63°.故答案是:27°或63°.【点睛】本题主要考查了与三角形的高有关的计算、直角三角形两锐角互余、三角形外角的性质三角形的分类以及等腰三角形的性质,熟记三角形的高相对于三角形的三种位置关系是解题的关键.12(2023春·四川达州·八年级校考阶段练习)我们规定:等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”,记作k .若k =2,则该等腰三角形的顶角为度.【答案】90【分析】根据等腰三角形的性质和三角形的内角和即可得到结论.【详解】解:∵k =2,∴设顶角=2α,则底角=α,∴α+α+2α=180°,∴α=45°,∴该等腰三角形的顶角为90°,故答案为:90.【点睛】本题考查了等腰三角形的性质,掌握等腰三角形的两底角相等是解题的关键.13(2023春·四川达州·八年级校考阶段练习)如果等腰三角形一腰上的中线将其周长分别为12和9两部分,那么这个等腰三角形的腰和底的长分别是.【答案】6,9或8,5【分析】根据等腰三角形一腰上的中线将其周长分别为12和9两部分得到底和要的差是12-9=3,再根据周长列式求解即可得到答案;【详解】解:∵等腰三角形一腰上的中线将其周长分别为12和9两部分,∴腰与底的差为:12-9=3,①当底边比腰长时,设腰为x ,则底为x +3,由题意可得,x +3+2x =12+9,解得:x =6,x +3=6+3=9,②当腰比底边长时,设腰为x ,则底为x -3,由题意可得,x -3+2x =12+9,解得:x =8,x -3=8-3=5,故答案为:6,9或8,5.【点睛】本题主要考查三角形中线有关计算,解题的关键是得到腰长与底边之差再分类讨论.14(2022·黑龙江哈尔滨·八年级期末)在平面直角坐标系xOy 中,已知A (1,2),在y 轴确定点P ,使△AOP 为等腰三角形,则符合条件的点P 有个.【答案】4.【分析】根据等腰三角形的判定得出可能OA 为底,可能OA 为腰两种情况,依此即可得出答案.【详解】①以A 为圆心,以OA 为半径作圆,此时交y 轴于1个点(O 除外);②以O 为圆心,以OA 为半径作圆,此时交y 轴于2个点;③作线段AO 的垂直平分线,此时交y 轴于1个点;共1+2+1=4.故答案为:4.【点睛】本题考查了等腰三角形的判定的应用,有两边相等的三角形是等腰三角形,注意要进行分类讨论.15(2022秋·江苏盐城·八年级校考阶段练习)如图,△ABC 中,∠ACB =90°,AB =10cm ,AC =8cm ,若点P 从点A 出发,以每秒1cm 的速度沿折线A -C -B -A 运动,设运动时间为t 秒t >0 ,当点P 在边AB 上,当t =s 时,△BCP 是等腰三角形.【答案】19或20或21.2【分析】利用等腰三角形的性质,依次画图,分类讨论即可.【详解】∵∠ACB =90°,AB =10cm ,AC =8cm ,∴由勾股定理得:BC =AB 2-AC 2=102-82=36=6(cm ),当P 在BA 上时,①当BC =BP =6cm 时,如图,∴t =8+6+6 ÷1=20s ;②当BC =CP =6cm 时,过CD ⊥PB 于点D ,如图,∴BD =DP =12BP ,∵S △ABC =12AC ∙BC =12AB ∙CD ,∴CD =AC ∙BC AB=6×810=4.8,在Rt △CBD 中,由勾股定理得:BD =BC 2-CD 2=62-4.82=3.6cm ,∴BP =2BD =2×3.6=7.2cm ,∴t =8+6+7.2 ÷1=21.2s ,③当BP =CP ,如图,∵∠ACB =90°,BP =CP ∴CP =BP =12AB =5cm ∴t =8+6+5 ÷1=19s 综上可知:t 的值为:19或20或21.2.,故答案为:19或20或21.2.【点睛】此题考查了等腰三角形的判定与性质、角平分线的性质、勾股定理,解题时需要作辅助线构造直角三角形以及等腰三角形,熟练掌握等腰三角形的判定与性质,进行分类讨论是解题的关键.16(2022秋·江苏扬州·八年级统考阶段练习)如图,在Rt △ABC 中,∠ACB =90°,AB =5cm ,AC =3cm ,动点P 从点B 出发,沿射线BC 以1cm/s 的速度运动,设运动时间为ts ,当t =s 时,△ABP 是以AB 为腰的等腰三角形.【答案】5或8【分析】△ABP 是以AB 为腰的等腰三角形时,分两种情况:①当AB =BP 时;②当AB =AP 时,分别求出BP 的长度,继而可求得t 值.【详解】解:在Rt △ABC 中,∠ACB =90°,AB =5cm ,AC =3cm ,∴BC =AB 2-AC 2=52-32=4cm ,①当AB =BP 时,如图1,则t =5;②当AB =AP 时,BP =2BC =8cm ,t =8故答案为:5或8.【点睛】本题考查了勾股定理以及等腰三角形的知识,解答本题的关键是掌握等腰三角形的性质,以及分情况讨论,注意不要漏解.17(2022·河南平顶山·八年级期末)如图,△ABC 中,∠C =90°,BC =6,∠ABC 的平分线与线段AC 交于点D ,且有AD =BD ,点E 是线段AB 上的动点(与A 、B 不重合),连接DE ,当△BDE 是等腰三角形时,则BE 的长为.【答案】4或43##43或4【分析】现根据已知条件得出∠CBD=∠ABD=∠BAD=30°,再根据BC=6,分别求出AB、AC、BD、AD、CD的长,然后分类讨论即可.【详解】解:∵△ABC中BD平分∠ABC,∴∠CBD=∠ABD,∵BD=AD,∴∠ABD=∠BAD,∴∠CBD=∠ABD=∠BAD,∵∠ACB=90°,∴∠CBD+∠ABD+∠BAD=90°,∴∠CBD=∠ABD=∠BAD=30°,∵BC=6,∴AB=2BC=12,AC=AB2-BC2=122-62=63,∵∠CBD=30°,且BC=6,∴BD=2CD,∵BD2=CD2+BC2,即(2CD)2=CD2+62,∴CD=23,BD=2CD=2×23=43=AD;(1)当BE=BD=43时,如图:(2)当BE=DE,如图:∵BE=DE,∴∠EDB=∠ABD=30°,∴∠AED=∠EDB+∠ABD=60°,∴∠ADE=180°-∠AED-∠A=180°-60°-30°=90°,∴△ADE为直角三角形,又∵∠A=30°且AD=43,∴DE=4,∴BE=4;(3)当BD=DE,时,点E与A重合,不符合题意;综上所述,BE为4或43.故答案为:4或43.【点睛】本题考查了等腰三角形的性质,直角三角形的性质和判定,勾股定理的应用,30°直角三角形的性质的应用,按三种不同的情况进行讨论是解题的关键.18(2023·上虞市初二月考)在如图所示的三角形中,∠A=30°,点P和点Q分别是边AC和BC上的两个动点,分别连接BP和PQ,把△ABC分割成三个三角形△ABP,△BPQ,△PQC,若分割成的这三个三角形都是等腰三角形,则∠C有可能的值有个.【答案】7【分析】①当AB=AP,BQ=PQ,CP=CQ时;②当AB=AP,BP=BQ,PQ=QC时;③当APB,PB =BQ,PQ=CQ时;④AP=PB,PB=PQ,PQ=QC时;根据等腰三角形的性质和三角形的内角和即可得到结论.【解析】解:如图所示,共有9种情况,∠C的度数有7个,分别为80°,40°,35°,20°,25°,100°,50°.①当AB=AP,BQ=PQ,CP=CQ时;②当AB=AP,BP=BQ,PQ=QC时,③当AP=AB,PQ=CQ,PB=PQ时.④当AP=AB,PQ=PC,BQ=PQ时,⑤当AP=BP,CP=CQ,QB=PQ时,⑥当AP=PB,PB=BQ,PQ=CQ时;⑦AP=PB,PB=PQ,PQ=QC时.⑧AP=PB,QB=PQ,PQ=CC时.⑨BP=AB,PQ=BQ,PQ=PC时.【点睛】本题考查了等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.19(2022·浙江·八年级专题练习)已知:如图,线段AC和射线AB有公共端点A.求作:点P,使点P在射线AB上,且ΔACP为等腰三角形.(利用无刻度的直尺和圆规作出所有符合条件的点P,不写作法,保留作图痕迹)【答案】见解析.【分析】分别作出①AP=CP;②AP=AC;③AC=CP即可.【详解】如图所示,点P1、P2、P3即为所求.【点睛】本题考查尺规作图-作等腰三角形.特别注意△ACP是等腰三角形的三种情况,避免漏答案.20(2022·山东·周村二中八年级期中)在同一平面内,若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形,则称点P是△ABC的巧妙点.(1)如图,求作△ABC的巧妙点P(尺规作图,不写作法,保留作图痕迹).(2)如图,在△ABC中,∠A=80°,AB=AC,若点P是△ABC的巧妙点,则符合条件的点P一共有几个?请直接写出每种情况下∠BPC的度数.(3)等边三角形的巧妙点的个数有()A.2个B.6个C.10个D.12个【答案】(1)见解析;(2)6个;∠BPC的度数为40°或160°或140°或80°;(3)C.【分析】(1)根据线段垂直平分线的性质,作AB、AC的垂直平分线,交点P即为所求;(2)分别以点B、C为圆心,BC为半径画圆,以点A、B为圆心画圆,作出BC、AB的垂直平分线,交于P5,图中P1、P2、P3、P4、P5、P6即为所求,根据等腰三角形的性质分别求出∠BPC的度数即可得答案;(3)根据(2)中作图方法画出图形,即可得答案.【详解】(1)点P为所求,(2)如图:分别以点B、C为圆心,BC为半径画圆,以点A、B为圆心画圆,作出BC、AB的垂直平分线,交于P5,图中P1、P2、P3、P4、P5、P6即为所求,共6个,∵∠BAC=80°,AB=AC,P1P6是BC的垂直平分线,∠BAC=40°,∴∠ABC=∠ACB=50°,∠BP1A=∠CP1A,∠BAP5=12∵AP1=AB,∴∠P1BA=∠BP1A,∴∠BAP5=2∠P1BA=40°∴∠P1BA=20°,∴∠BP1C=2∠P1BA=40°,∵AP2=AC,BP2=BC,∴∠AP2C=∠ACP2,∠BP2C=∠BCP2,∴∠AP2C+∠BP2C=∠ACP2+∠BCP2,∴∠BP2A=∠BCA=50°,∴∠ABP2=∠ABC=50°,∴∠P2BC=100°,(180°-∠P2BC)=40°,同理可得:∠BP3C=40°,∴∠BP2C=12∵∠BAP5=40°,AP5=BP5,∴∠ABP5=∠BAP5=40°∵∠ABP5=∠BAP5=40°,∴∠P5BC=∠ABC-∠ABP5=10°,∵BP5=CP5,∴∠BPC=180°-2∠P5BC=160°,∵AC=AP4,∠CAP4=40°,∴∠APC=70°,∴∠BPC=2∠APC=140°,∵AC=CP6,∴∠AP6C=∠CAP6=40°,∴∠BP6C=2∠AP6C=80°.综上所述:∠BPC的度数40°或80°或140°或160°.(3)如图所示,分别以等边三角形的三条边作其对应边的垂直平分线,再分别以等边三角形的三个顶点为圆心,等边三角形的边长为半径画圆,分别与三条边的垂直平分线的交点和三条垂直平分线的交点即为等边三角形的巧妙点,共有10个,故选:C.【点睛】本题主要考查垂直平分线的性质、等腰三角形的性质,构建等腰三角形的作法:定顶点,定圆心;定腰,定半径;以及等边三角形的性质等.熟练掌握相关性质是解题关键.21(2022·黑龙江密山·八年级期末)如图,直线MN与x轴、y轴分别相交于B、A两点,OA-6+OB-82=0.(1)求A,B两点的坐标;(2)若点O到AB的距离为245,求线段AB的长;(3)在(2)的条件下,x轴上是否存在点P,使△ABP是以AB为腰的等腰三角形,若存在请直接写出满足条件的点P的坐标.【答案】(1)A(0,6),B(8,0);(2)AB=10;(3)存在,(-8,0)、(-2,0)、(18,0).【分析】(1)由非负数的性质知OA=6,OB=8,据此可得点A和点B的坐标;(2)根据S△OAB=12AB∙d=1 2∙OA∙OB求解可得;(3)先设点P(a,0),根据A(0,6),B(8,0)得PA2=a2+62,PB2=a-82,AB2=102=100,再分PA=AB和AB=PB两种情况分别求解可得.(1)∵OA-6+OB-82=0∴OA-6=0OB-8=0∴OA=6OB=8则A点的坐标为A(0,6),B点的坐标为(8,0)(2)∵S△OAB=12AB∙d=12∙OA∙OB,d=245∴AB=OA∙OBd=6×8245=10(3)存在点P,使△ABP是以AB为腰的等腰三角形设点P(a,0),根据A(0,6),B(8,0)得PA2=a2+62,PB2=a-82,AB2=102=100①若PA=AB,则PA2=AB2,即a2+62=100,解得a=8(舍)或a=-8,此时点P(-8,0);②若AB=PB,即AB2=PB2,即100=a-82解得a=18或a=-2,此时点P(18,0)或(-2,0);综上,存在点P,使△ABP使以AB为腰的等腰三角形,其坐标为(-8,0)或(18,0)或(-2,0).【点睛】本题考察了非负数的性质、直角三角形的面积求法、勾股定理及等腰三角形的性质,分类讨论思想的运用是解决第3问的关键。
初中数学58种模型之角平分线+垂直构造等腰三角形

模型 3 角平分线+垂线构造等腰三角形
如图,P 是∠MON 的平分线上一点, AP⊥OP 于 P 点,延长 AP交ON于点 B。 结论:△AOB 是等腰三角形。
模型证明: 由已知可得 AP⊥OP,BP⊥OP,OP=OP,∠POA=∠ POB ∴△POA≌△POB ∴OA=OB ∴△AOB 是等腰三角形
模型分析 构造此模型可以利用等腰三角形的 “三线合一”,也可以得到两个全等 的直角三角形,进而得到对应边、对 应角相等。这个模型巧妙地把角平分 线 和三线合一联系了起来。
模型实例 如图,已知等腰直角三角形 ABC 中, ∠A=90°,AB=AC,BD 平分∠ABC, CE⊥BD,垂足为 E。求证: BD=2CE。
证明:如图延长BA、CE交于点F则有: ∠ABE=∠CBE,BE=BE ∴RT△BEF≌RT△BEC ∴CE=EF ∴CF=2CE 又∵∠ADB=∠CDE ∠DCE+∠CDE=∠DCE+∠F=90° ∴∠ADB=∠F 又AB=AC
∴RT△BAD≌RT△CAF ∴BD=CF ∴BD=2CE.
模型练习
1.如图,在△ABC 中,BE 是角平 分线,AD⊥BE,垂足为 D。 求证:∠2=∠1+∠C。
证明:如图延长AD交BC于点F则有 BD=BD,∠ABD=∠FBD ∴RT△ADB≌RT△FDB ∴∠2=∠BFD=∠1+∠C ∴∠2=∠1+∠C
2.如图,在△ABC 中,∠ABC=3∠C,AD 是 ∠BAC 的角平分线,BE⊥AD 于点 E。 求证:BE= ½(AC-AB)。
ቤተ መጻሕፍቲ ባይዱ
微专题 全等三角形的六种基本模型-2024年中考数学复习

21
全等三角形的六种基本模型
模型应用
8.如图17, △ 是边长为1的等边三角形, = ,
∠ = 120∘ ,点 , 分别在 , 上,且
∠ = 60∘ .求 △ 的周长.
提示:如图16,延长 至点 ,使 = ,连接 .
图6
= ,
在 △ 和 △ 中, ቐ∠ = ∠, ∴ △≌△ SAS .
= ,
∠ = ∠ = 50∘ .
7
全等三角形的六种基本模型
模型三 旋转型
模型剖析
如图7,将三角形绕着公共顶
点旋转一定角度后,两个三角形能
够完全重合,这两个三角形称为旋
图3
在 △ 和△ 中, ∵ ∠ = ∠ , ∠ = ∠ , = ,
∴ △ ≌ △ AAS .
∴ = .
4
全等三角形的六种基本模型
模型二 对称型
模型剖析
如图4、图5,将所给图形沿某一条直线折叠后,直线两旁的部分能
够完全重合,这两个三角形称为对称型全等三角形,其中重合的顶点就
= , ∴ △ ≌ △ SAS . ∴ = ,
图17
图16
22
全等三角形的六种基本模型
∠ = ∠. ∵ ∠ = 120∘ , ∠ = 60∘ , ∴ ∠ +
∠ = 60∘ . ∴ ∠ + ∠ = 60∘ . ∴ ∠ = ∠ =
∴ ∠ = ∠ + ∠ = 110∘ .
∴ ∠ = ∠ .
= ,
图9
在 △ 和 △ 中, ቐ∠ = ∠ , ∴ △ ≌ △ .
= ,
∴ = .
11
全等三角形的六种基本模型
关于两个等腰三角形的三个重要的几何模型之间的异同以及当三角形为等腰直角三角形时的特殊证法

关于两个等腰三角形的三个重要的几何模型之间的异同以及当三角形为等腰直角三角形时的特殊证法------手拉手、婆罗摩笈多模型、脚拉脚初中阶段,关于两个等腰三角形的问题,十分常见.我们可以归纳为大三类,为了介绍方便,分别取名为“手拉手模型、婆罗摩笈多模型、脚拉脚模型”.1.1 手拉手模型:两个等腰三角形的顶角顶点重合,且顶角相等.按逆时针顺序,把位置相同的底角顶点相连.简记为:共顶点,同顶角,左手拉左手.如图,两个等腰三角形△ABE 和△ACD ,∠BAE=∠CAD ,且AB=AE ,AC=AD ,连接BD ,CE.结论:(1)△ABD ≌△AEC ;(2)∠α+∠BOC=180°(位置相同的底角顶点相连,所成夹角等于顶角) ;(3)OA 平分∠BOC(第三边的交点与顶点连线平分第三边的夹角).证明:(1)由AB=AE ,AC=AD ,∠BAD=∠CAE ,易得△ABD ≌△AEC.(2) 因为△ABD ≌△AEC ,所以∠CEA=∠DBA ,又∠EOA+∠OEA=∠EAB+∠DBA ,所以∠OEA=∠α.(3)第3问的证明很巧妙,只需过A 点作BD ,CE 的垂线段.因为△ABD ≌△AEC ,所以对应边的高也相等.再由角平分线的判定,从而得到OA 平分∠BOC.1.2 手拉手模型的特殊情况:当两个等腰三角形是等腰直角三角形时,而且隐藏在正方形中,如下:变式1.如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H .问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?解析:(1)由,,,DC DA ADG CDE DG DE =∠=∠=得.)(≌△△SAS CDE ADG由.CE AG CDE ADG =∴≌△△(2) 设AG 与CD 相较于点P ,由GAD ECD CDE ADG ∠=∠∴≌△△又.90H CE AG CDA CHA APD GAD CPG ECD 于点⊥∴︒=∠=∠∴∠+∠=∠+∠(3) 过D 点作AG DM ⊥于M 点,EC DN ⊥于N 点DNDM CDE ADG =∴≌△△ HD ∴平分.AHE ∠2.1婆罗摩笈多模型:两个等腰三角形的顶角顶点重合,且顶角互补。
(基础版)等腰直角三角形中的基本模型

基础版)等腰直角三角形中的基本模型等腰直角三角形是一种特殊的三角形,具有两条边长度相等且与底边垂直的特点。
对于等腰直角三角形,我们可以有一些基本模型来帮助我们理解和解决相关问题。
1.基本定义等腰直角三角形具有以下特点:两条边的长度相等,称为腰;底边与两条腰垂直相交,形成一个直角。
2.边长关系设等腰直角三角形的腰长为 *a*,底边长为 *b*。
由勾股定理可知:a^2 + a^2 = b^2*,即 *2a^2 = b^2*;则 *a = \sqrt{\frac{b^2}{2}}*。
3.高的计算等腰直角三角形的高即为顶点到底边的垂直距离。
根据几何关系可知,高等于腰的一半,即高 *h* 和腰 *a* 的关系为:h = \frac{a}{2}*。
4.面积计算等腰直角三角形的面积可以通过底边长和高的关系来计算,即面积 *S* 和底边长 *b*、高 *h* 的关系为:S = \frac{b \cdot h}{2}*。
5.例题解析例题 1已知等腰直角三角形的底边长为 8 cm,求其面积。
解析:根据高的计算公式,高 *h* 等于底边长的一半,即 *h =\frac{8}{2} = 4*。
代入面积公式可得:S = \frac{8 \cdot 4}{2} = 16*。
所以,等腰直角三角形的面积为 16 平方厘米。
例题 2已知等腰直角三角形的腰长为 6 cm,求其底边长和面积。
解析:根据边长关系公式,底边长 *b* 等于 *a* 的平方根的两倍,即*b = 2 \cdot \sqrt{\frac{6^2}{2}} = 12*。
代入面积公式可得:S = \frac{12 \cdot \frac{6}{2}}{2} = 18*。
所以,等腰直角三角形的底边长为 12 厘米,面积为 18 平方厘米。
6.总结等腰直角三角形是一种特殊的三角形,在解题过程中可以利用基本定义、边长关系、高的计算和面积计算等基本模型来求解相关问题。
通过掌握这些基本模型,我们可以更好地理解和应用等腰直角三角形的概念和性质。
特殊三角形中的分类讨论模型—2024年中考数学常见几何模型全归纳之模型解读(全国通用)(解析版)

三角形中的重要模型-特殊三角形中的分类讨论模型 模型1、等腰三角形中的分类讨论模型【知识储备】凡是涉及等腰三角形边、角、周长、面积等问题,优先考虑分类讨论,再利用等腰三角形的性质与三角形三边关系解题即可。
1)无图需分类讨论①已知边长度无法确定是底边还是腰时要分类讨论;②已知角度数无法确定是顶角还是底角时要分类讨论; ③遇高线需分高在△内和△外两类讨论;④中线把等腰△周长分成两部分需分类讨论。
2)“两定一动”等腰三角形存在性问题:即:如图:已知A ,B 两点是定点,找一点C 构成等腰ABC △方法:两圆一线具体图解:①当AC AB =时,以点A 为圆心,AB 长为半径作⊙A ,点C 在⊙A 上(B ,C 除外)②当BC AB =时,以点B 为圆心,AB 长为半径作⊙B ,点C 在⊙B 上(A ,E 除外)③当BC AC =时,作AB 的中垂线,点C 在该中垂线上(D 除外)【答案】C【分析】由已知等式,结合非负数的性质求m 、n 的值,再根据m 、n 分别作为等腰三角形的腰,分类求解.【详解】解:()2350m n −+−=,30m −≥,()250n −≥,30m ∴−=,50n −=,解得:3m =,5n =,当3m =作腰时,三边为3,3,5,符合三边关系定理,周长为:33511++=,当5n =作腰时,三边为3,5,5,符合三边关系定理,周长为:35513++=,故选:C .【点睛】本题考查了等腰三角形的性质,三角形的三边关系,非负数的性质,关键是根据非负数的性质求m 、n 的值,再根据m 或n 作为腰,分类求解. 例2.(2023春·黑龙江佳木斯·八年级校考期中)一个等腰三角形的周长为18cm ,且一边长是4cm ,则它的腰长为( )A .4cmB .7cmC .4cm 或7cmD .全不对【答案】B【分析】根据等腰三角形的定义,两腰相等,结合三角形的三边关系,进行求解即可.【详解】解:当4cm 为腰长时,则底边长为182410−⨯=cm ,∵4410+<,不符合题意;∴4cm 为底边长,∴等腰三角形的腰长为:()11847cm 2⨯−=;故选B . 【点睛】本题考查等腰三角形的定义,三角形的三边关系.解题的关键是掌握等腰三角形的两腰相等,注意讨论时要根据三角形的三边关系,判断能否构成三角形.例3.(2023春·四川达州·八年级校考阶段练习)等腰三角形的一个角是80︒,则它顶角的度数是( )A .80︒B .80︒或20︒C .80︒或30︒D .20︒【答案】B【分析】根据三角形的内角和为180︒,进行分类讨论即可【详解】解:①当底角为80︒时,顶角18080220=︒−︒⨯=︒,②当顶角为80︒时,顶角度数80=︒,综上:顶角度数为80︒或20︒;故选:B .【点睛】本题考查了三角形的内角和为180︒,等腰三角形两底角相等,解题的关键是书熟练掌握相关内容. 例3.(2023·四川广安·八年级校考期中)等腰三角形的一个外角为100︒,则它的底角为( )A .55︒B .80︒C .55︒或80︒D .以上都不是 【答案】D【分析】等腰三角形的一个外角等于100︒,则等腰三角形的一个内角为80︒,但已知没有明确此角是顶角还是底角,所以应分两种情况进行分类讨论.【详解】∵等腰三角形的一个外角等于100︒,∴等腰三角形的一个内角为80︒,①当80︒为顶角时,其他两角都为50︒、50︒,②当80︒为底角时,其他两角为80︒、20︒,所以等腰三角形的底角可以是50︒,也可以是80︒.故选:D .【点睛】本题考查了等腰三角形的性质和三角形的内角和定理;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错. 例4.(2023·四川绵阳·八年级校考阶段练习)等腰三角形一腰上的高与另一腰的夹角为70︒,则等腰三角形的顶角度数为 .【答案】20︒或160︒【分析】要注意分类讨论,等腰三角形可能是锐角三角形也可能是钝角三角形,然后根据三角形的内角和以及三角形的外角的性质即可求解.【详解】解:若三角形为锐角三角形时,如图,AB AC =,70ACD ∠=︒,CD 为高,即90ADC ∠=︒,此时180A ACD ADC ∠+∠+∠=︒,∴180907020A =︒−︒−︒=︒,若三角形为钝角三角形时,如图,AB AC =,70ACD ∠=︒,CD 为高,即90ADC ∠=︒,此时9070160BAC D ACD ∠=∠+∠=︒+︒=︒,综上,等腰三角形的顶角的度数为20︒或160︒.故答案为:20︒或160︒. 【点睛】本题主要考查了等腰三角形的性质,三角形外角的性质,三角形内角和定理,解题的关键是根据题意画出图形,并注意分类讨论. 例5.(2023·山东滨州·八年级校考期末)我们称网格线的交点为格点.如图,在6行5⨯列的长方形网格中有两个格点A 、B ,连接AB ,在网格中再找一个格点C ,使得ABC 是等腰直角三角形,则满足条件的格点C 的个数是( )A .3B .4C .5D .6【答案】C 【分析】根据题意,结合图形,分两种情况讨论:①AB 为等腰直角ABC 底边;②AB 为等腰直角ABC 其中的一条腰.【详解】如图:分情况讨论:①AB 为等腰直角ABC 底边时,符合条件的格点C 点有2个;②AB 为等腰直角ABC 其中的一条腰时,符合条件的格点C 点有3个.故共有5个点,故选:C .【点睛】本题考查了等腰三角形的性质和判定;解答本题关键是根据题意,画出符合实际条件的图形,数形结合的思想是数学解题中很重要的解题思想.例6.(2023·北京·八年级期中)Rt △ABC 中,∠BAC =90°,AB =AC =2,以AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段BD 的长为____.【答案】4或【分析】根据题意分类讨论,①90CAD ∠=︒,②90ACD ∠=︒,③90ADC ∠=︒,分别作出图形,再结合已知条件勾股定理求解即可.【详解】解:①如图,当90CAD ∠=︒时,902BAC AB AC ∠=︒==,,ACD △是等腰直角三角形,2AC AD AB ∴===,180BAD BAC CAD ∠=∠+∠=︒,224BD AB AD ∴=+=+=;②如图,当90ACD ∠=︒时,过点D 作DE BC ⊥,交BC 的延长线于点E ,902BAC AB AC ∠=︒==,,ACD △,ABC 是等腰直角三角形,2CD AC AB ∴===,18045DCE ACD ACB ∠=︒−∠−∠=︒, 又DE BC ⊥,∴DEC 是等腰直角三角形,DE CE ∴=,在Rt DEC △中,22222DC CE DE DE =+=,∴2DE DC ==在Rt ABC 中,BC 在Rt BDE 中,BD =③如图,当90ADC ∠=︒时,902BAC AB AC ∠=︒==,ACD △,ABC 是等腰直角三角形, 2CD AD AC ∴===在Rt ABC 中,BC ==Rt BDC 中,BD =综上所述,BD 的长为:4或4或.【点睛】本题考查了勾股定理,等腰三角形的性质,分类讨论是解题的关键. 例7.(2023·福建南平·八年级校考期中)已知△ABC 中,如果过顶点B 的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC 的关于点B 的二分割线.如图1,Rt △ABC 中,显然直线BD 是△ABC 的关于点B 的二分割线.在图2的△ABC 中,∠ABC =110°,若直线BD 是△ABC 的关于点B 的二分割线,则∠CDB 的度数是 .【答案】40°或90°或140°【分析】分三种情况讨论,由等腰三角形的性质和直角三角形的性质可求解.【详解】解:①如图,当∠DBC=90°,AD=BD 时,直线BD 是△ABC 的关于点B 的二分割线,∵∠ABC=110°,∠DBC=90°,∴∠ABD=20°,∵AD=BD ,∴∠A=∠ABD=20°,∴∠CDB=∠A+∠ABD=40°;②如图,当∠BDC=90°,AD=BD 时,直线BD 是△ABC 的关于点B 的二分割线,或当∠BDC=90°,CD=BD 时,直线BD 是△ABC 的关于点B 的二分割线,;③如图,当∠ABD=90°,CD=BD 时,直线BD 是△ABC 的关于点B 的二分割线,∵∠ABC=110°,∠ABD=90°,∴∠DBC=20°,∵CD=BD ,∴∠C=∠DBC=20°,∴∠BDC=140°.综上所述:当∠BDC 的度数是40°或90°或140°时,直线BD 是△ABC 的关于点B 的二分割线.【点睛】本题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,理解二分割线是本题关键. 且ABP 为等腰三角形,则点【答案】(2,0)或(2,0)−或(64+或(6−【分析】根据等腰三角形的判定,分①AB=BP ;②AB=AP ;③AP=BP 三种情况求解即可.【详解】∵ABP 为等腰三角形,①当AB BP =时,如图①,∵AB ==∴BP =∵(6,0)B ,∴(6P +或(6P −;②当AB AP =时,如图② 作AC BP ⊥于C 点,则(2,0)C ,∵AB AP =,∴BC CP =,∵624BC =−=,∴4CP =,∴(2,0)P −.③当AP BP =时,如图③,作AP BP ⊥,∴4AP BP ==,∴(2,0)P .综上所述:点P 的坐标为(2,0)或(2,0)−或(6+或(6−,故答案为:(2,0)或(2,0)−或(6+或(6−.【点睛】本题考查了等腰三角形的判定与性质、勾股定理、坐标与图形,熟练掌握等腰三角形的判定与性质,灵活运用分类讨论的思想解决问题是解答的关键. 八年级校考期中)如图,ABC 中,A 【答案】(1)16(2)6或2(3)4或2或95或3【分析】(1)设cm PB PA x ==,则()4cm PC x =−,利用勾股定理求出3cm AC =,在Rt ACP 中,依据222AC PC AP +=,列方程求解即可得到t 的值.(2)如图所示,当点P 在AC 上时,过P 作PD AB ⊥于D ,设cm PD PC y ==,则()3cm AP y =−,在Rt ADP 中,依据222AD PD AP +=,列方程求解即可得到t 的值.当点P 与点B 重合时,点P 也在ABC ∠的角平分线上,此时,522AB t ==.(3)分四种情况:当P 在AB 上且AP CP =时,当P 在AB 上且3cm AP CA ==时,当P 在AB 上且AC PC =时,当P 在BC 上且3cm AC PC ==时,分别依据等腰三角形的性质即可得到t 的值.【详解】(1)解:如图,设cm PB PA x ==,则()4cm PC x =−,90ACB ∠=︒,5cm AB =,4cm BC =,3cm AC ∴,在Rt ACP 中,由勾股定理得222AC PC AP +=,()22234x x ∴+−=,解得258x =,258BP ∴=,2556582216AB BP t ++∴===;(2)解:如图所示,当点P 在AC 上时,过P 作PD AB ⊥于D ,BP 平分ABC ∠,90C ∠=︒,PD AB ⊥PD PC ∴=,DBP CBP ∠=∠,在BCP 与BDP △中,BDP BCP DBP CBP BP BP ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AAS BDP BCP ∴≌4cm BC BD ∴==,541cm AD ∴=−=,设cm PD PC y ==,则()3cm AP y =−,在Rt ADP 中,由勾股定理得222AD PD AP +=,()22213y y ∴+=−,解得43y =,43CP \=,454313226AB BC CP t ++++∴===,当点P 与点B 重合时,点P 也在ABC ∠的角平分线上,此时,522AB t ==. 综上所述,点P 恰好在ABC ∠的角平分线上,t 的值为316或52.(3)解:分四种情况:①如图,当P 在AB 上且AP CP =时,∴A ACP ∠=∠,∵A B ∠∠=︒+90,90ACP BCP ∠+∠=︒,B BCP ∴∠=∠,CP BP AP ∴==,P ∴是AB 的中点,即15cm 22AP AB ==,524AP t ∴==. ②如图,当P 在AB 上且3cm AP CA ==时,∴322AP t ==. ③如图,当P 在AB 上且AC PC =时,过C 作CD AB ⊥于D , ∵1122ABC S AC BC AB CD =⋅=⋅,∴12cm 5AC BC CD AB ⋅==,在Rt ACD △中,由勾股定理得9cm 5AD =,182cm 5AP AD ∴==,925AP t ∴==. ④如图,当P 在BC 上且3cm AC PC ==时,则431cm BP =−=,6322AB BP t +∴===. 综上所述,当t 的值为54或32或95或3时,ACP △为等腰三角形.【点睛】本题属于三角形综合题,考查了角平分线的性质,等腰三角形的性质以及勾股定理的综合运用.画出图形,利用分类讨论的思想是解第(3)题的关键. 例10.(2022春·四川成都·八年级校考期中)如图,在平面直角坐标系内,点O 为坐标原点,经过()26A−,的直线交x 轴正半轴于点B ,交y 轴于点C OB OC =,,直线AD 交x 轴负半轴于点D ,若ABD △的面积为27(1)求直线AB 的表达式和点D 的坐标;(2)横坐标为m 的点P 在线段AB 上(不与点A B 、重合),过点P 作x 轴的平行线交AD 于点E ,设PE 的长为()0y y ≠,求y 与m 之间的函数关系式并直接写出相应的m 取值范围;(3)在(2)的条件下,在x 轴上是否存在点F ,使PEF !为等腰直角三角形?若存在求出点F 的坐标;若不存在,请说明理由.【答案】(1)()450y x D =−+−,,(2)()33242y m m =+−<<,(3)存在,点F 的坐标为2,05⎛⎫ ⎪⎝⎭或16,05⎛⎫− ⎪⎝⎭或8,07⎛⎫− ⎪⎝⎭ 【分析】(1)据直线AB 交x 轴正半轴于点B ,交y 轴于点C ,OB OC =,设直线AB 解析式为y x n =−+,把A 的坐标代入求得n 的值,从而求得B 的坐标,再根据三角形的面积建立方程求出BD 的值,求出OD 的值,从而求出D 点的坐标; (2)直接根据待定系数法求出AD 的解析式,先根据B A 、的坐标求出直线AB 的解析式,将P 点的横坐标代入直线AB 的解析式,求出P 的纵坐标,将P 的纵坐标代入直线AD 的解析式就可以求出E 的横坐标,根据线段的和差关系就可以求出结论;(3)要使PEF !为等腰直角三角形,分三种情况分别以点P E F 、、为直角顶点,据等腰直角三角形的性质求出(2)中m 的值,就可以求出F 点的坐标.【详解】(1)解:OB OC =,∴设直线AB 的解析式为y x n =−+,∵直线AB 经过()26A −,,26n ∴+=,4n ∴=,∴直线AB 的解析式为4y x =−+,()40B ∴,,4OB ∴=,ABD 的面积为()2726A −,,,16272ABD S BD =⨯⨯=,9BD ∴=,5OD ∴=,()50D ∴−,,∴直线AB 的解析式为()450y x D =−+−,,(2)解:设直线AD 的解析式为y ax b =+,()26A −,,()50D −,∴2650a b a b −+=⎧⎨−+=⎩,解得210a b =⎧⎨=⎩.∴直线AD 的解析式为210y x =+;∵点P 在AB 上,且横坐标为m ,()4P m m ∴−+,,PE x ∥轴,∴E 的纵坐标为4m −+,代入210y x =+得,4=210m x −++,解得62m x −−=,6,42m E m −−⎛⎫∴−+ ⎪⎝⎭, PE ∴的长63322m m y m −−=−=+;即332y m =+,()24m −<<;(3)解:在x 轴上存在点F ,使PEF !为等腰直角三角形,①当90FPE ∠=︒时,如图①,有PF PE =,4PF m =−+,332PE m =+,3432m m ∴−+=+,解得25m =,此时2,05F ⎛⎫ ⎪⎝⎭; ②当90PEF ∠=︒时,如图②,有EP EF =,EF 的长等于点E 的纵坐标,4EF m ∴=−+,3432m m ∴−+=+,解得:25m =, ∴点E 的横坐标为61625m x −−==−,∴16,05F ⎛⎫− ⎪⎝⎭;③当90PFE ∠=︒时,如图③,有FP FE =,FPE FEP ∴∠=∠.180FPE EFP FEP ∠+∠+∠=︒,45FPE FEP ∴∠=∠=︒.作FR PE ⊥,点R 为垂足,18045PFR FPE PRF ∴∠=︒−∠−∠=︒,=PFR RPF ∴∠∠,=FR PR ∴.同理=FR ER ,12FR PE ∴=.∵点R 与点E 的纵坐标相同,4FR m ∴=−+,∴134322m m ⎛⎫−+=+ ⎪⎝⎭,解得:107m =, 10184477PR FR m ∴==−+=−+=,∴点F 的横坐标为10188777−=−,8,07F ⎛⎫∴− ⎪⎝⎭. 综上,在x 轴上存在点F 使PEF !为等腰直角三角形,点F 的坐标为2,05⎛⎫ ⎪⎝⎭或16,05⎛⎫− ⎪⎝⎭或8,07⎛⎫− ⎪⎝⎭.【点睛】本题考查了等腰直角三角形的性质,三角形的面积公式的运用,待定系数法求一次函数的解析式 模型2、直角三角形中的分类讨论模型【知识储备】凡是涉及直角三角形问题,优先考虑直角顶点(或斜边)分类讨论,再利用直角三角形的性质或勾股定理解题即可。
等腰直角三角形中的常用模型
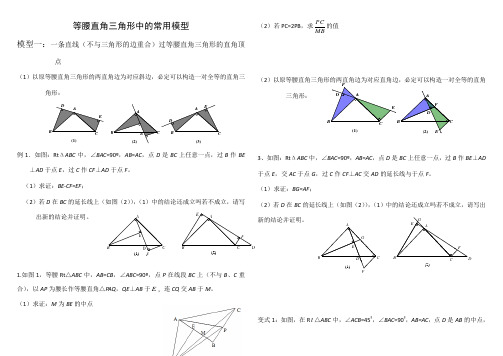
等腰直角三角形中的常用模型模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗若不成立,请写出新的结论并证明。
1.如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MBPC的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,GG BACDEF(2)(1)F EDCBADEF FED (2)(1)CCABBA(2)FEDC B AAB C D E F(1)(2)(3)(1)DDEECEAAABAF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE.变式2:等腰Rt△ABC中,AC=AB,∠BAC=90°,点D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF,求证:∠1=∠2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰直角三角形中的常用模型
模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶
点
(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三
角形:
例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作
BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;
(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,
请写出新的结论并证明。
1.如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△P AQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点
(2)若PC=2PB ,求
MB
PC
的值
(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角
三角形:
3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;
(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的
中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .
G G B A
C
D E F (2)(1)F
E D C B A
F D
A
A
(2)F
E
D
C A A B C D
E F (1)(2)(3)(1)D
D E
E
C C E
C A A
A
B
变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD
于点E ,交BC 于点F ,连接DF ,求证:∠1=∠2。
变式3:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 、E 是AC 上两点且AD=CE ,AF ⊥BD 于点G ,交BC 于点F 连接DF ,求证:∠1=∠2。
模型二:等腰直角三角形与另一个直角三角形共斜边
等腰直角三角形与另一个直角三角形有公共斜边,一定可以以两腰为对应边构造全等三角形
例1:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,E 是AC 上一点,过C 作CD ⊥BE
于D ,连接AD ,求证:∠ADB =45°。
变式1:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,E 是AC 上一点,点D 为BE
延长线上一点,且∠ADC =135°求证:BD ⊥DC 。
变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,BE 平分∠ABC 交AC 于E ,过C 作CD ⊥BE 于D ,DM ⊥AB 交BA 的延长线于点M ,
(1)求BC AB BM +的值;(2)求AB BC AM
-的值。
模型三:两个等腰直角三角形共一个顶点
(1)两个等腰直角三角形共直角顶点,必定含一对全等三角形:
例1、如图1,△ABC 、△BEF 都是等腰直角三角形,∠ABC =∠BEF =90º,连接
AF 、CF ,M 是AF 的中点,连ME ,将△BEF 绕点B 旋转。
猜想CF 与EM 的数量关系并证明;
E
B
A B C D E A B C D
E E D C
B A (1)(2)
(3)A B C D
E
F
(2)
(1)
F E D
C
B A
(2)两个等腰直角三角形共锐角顶点且直角开口方向相反,必定可利用平移构造含一对全等三角形:
如图,△ABC 和△EBD 都是等腰直角三角形,∠BAC =∠BED =90º。
把DE 平移到CF ,使E 与C 重合,连接AE 、AF ,则△AEB 与△AFC 全等(关键是利用平行证明∠ABE =∠ACF )
例.如图:两个直角三角形ABC 、ADE 的顶点A 重合,P 是线段BD 的中点,连PC 、
PE 。
(1)如图1,若∠BAC =∠DAE =45°,当A 、C 、D 在同一直线上时,线段PC 、PE 的关系是 ;
(2)如图2、3,将⊿BAC 绕A 旋转α度,(1)中的结论是否仍然成立?任意选择一个证明你的结论。
三【巩固练习】
1.已知:Rt ⊿ABC 中,AB=AC ,∠BAC =90°,若O 是BC 的中点,以O 为顶点作∠
MON ,交AB 、AC 于点M 、N 。
(1)若∠MON =90°(如图1),求证:OM=ON ; (2)若∠MON =45°(如图2),求证:①AM+MN =CN ;
2、如图,在平面直角坐标系中,△AOB 为等腰直角三角形,A (4,4)。
(1)若C 为x 轴正半轴上一动点,以AC 为直角边作等腰直角△ACD ,∠ACD=90°,连OD ,求∠AOD 的度数;
(2)过A 作y 轴的垂线交y 轴于E ,F 为x 轴负半轴上一点,G 在EF 的延长线上,以EG 为直角边作等腰Rt △EGH ,过A 作x 轴垂线交EH 于点M ,连FM ,等式
1=-OF
FM
AM 是否成立?若成立,请证明;若不成立,说明理由。
图2
N
M
O
C B
A
图1N
M
C B A
A B
C
D
E
P
图3A B C D E P 图2
图1
P E D C
B
A E
D A
(3)F
E D C B (2)
F (1)A D
E
3.在△ABC和△DCE中,AB=AC,DC=DE,∠BAC=∠EDC=90°,点E在AB上,连
AD,DF⊥AC于点F。
试探索AE、AF、AC的数量关系;并求出∠DAC的度数。
4.如图:等腰Rt△ABC和等腰Rt△EDB,AC=BC,DE=BD,∠ACB=∠EDB=90°,E为AB是一点,P为AE的中点。
⑴连接PC,PD;则PC,PD的位置关系是;数量关系是;
并证明你的结论。
⑵当E在线段AB上变化时,其它条件不变,作EF⊥BC于F,连接PF,试判断
△PCF的形状;在点E运动过程中,△PCF是否可为等边三角形?若可以,试求△ACB与△EDB的两直角边之比。
6.已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;(2)如图1,若CB=a,CE=2a,求BM,ME的长;(3)如图2,当∠BCE=45°时,求证:BM=ME.
7、如图,在平面直角坐标系中,A (4,0),B (0,4)。
点N为OA上一点,OM⊥BN
于M,且∠ONB=45°+∠MON。
(1)求证:BN平分∠OBA;
(2)求
BN
MN
OM
的值;
(3)若点P为第四象限内一动点,且∠APO=135°,问AP与BP是否存在某种确定的位置关系?请证明你的结论。
F
A D
B C
E
(2)。
