折叠问题涉及6种题型梳理
七年级折叠题知识点

七年级折叠题知识点在七年级数学学习中,折叠题是一个非常重要而且常见的题型。
学生们需要理解并掌握各种不同的折叠方法以及折叠后形状的变化,才能顺利解题。
以下是几个常见的折叠题知识点。
一、线段的平分线段的平分是折叠题中最基本的知识点。
当我们折叠纸张时,可以通过简单的折痕将一个线段平分成两半。
假设有一条长度为8cm的线段AB,我们需要将其平分为两段等长的线段。
我们可以在AB的中点C处将纸张折叠,从而将线段AB平分为两条等长的线段AC和CB。
当然,线段的平分不仅限于将一条线段平分为两半,我们还可以将线段平分为三等分、四等分等,具体方法可以根据题目来确定。
但在任何情况下,我们都需要通过折痕将纸张切分成若干个等长的部分,从而将线段平分。
二、正方形的变形正方形的变形也是折叠题中常见的知识点之一。
我们可以通过不同的折叠方式将正方形变形为其他形状,例如三角形、矩形等等。
假设有一个边长为6cm的正方形ABCD,我们需要将其折叠成一个等腰三角形。
首先将正方形沿着AC的中垂线折叠,使A点和C点重合。
然后再将D点向下折叠,使D点、B点、C点三点重合,此时ABCD就变成了一个等腰三角形。
如果题目要求我们将正方形变形为其他形状,我们需要根据题目给出的要求合理地折叠纸张,并通过计算来求解。
三、投影投影也是折叠题中常见的知识点之一。
我们可以通过折痕将立体图形的某一面投影到另一面上。
假设有一个长方体ABCDEF,我们需要将点F关于AB平面投影到DE上。
首先在BC和EF之间折叠一次,使点F移动到长方体内部,然后再将长方体按照AD所在的平面折叠,使点F的投影位置与DE重合。
注意,在进行投影时,需要保证折叠后所得到的形状与投影完全重合,否则就会影响计算结果。
四、平行四边形的变形平行四边形的变形也是折叠题中常见的知识点之一。
我们可以通过不同的折叠方式将一些平行四边形变形为其他平行四边形。
假设有一个边长为6cm、高为4cm的平行四边形ABCD,我们需要将其折叠成一个高为8cm、底边长度为10cm的平行四边形EFGH。
初中数学折叠问题(全)精品

初中数学中的折叠问题折叠问题(对称问题)是近几年来中考出现频率较高的一类题型,学生往往由于对折叠的实质理解不够透彻,导致对这类中档问题失分严重。
本文试图通过对在初中数学中经常涉及到的几种折叠的典型问题的剖析,从中抽象出基本图形的基本规律,找到解决这类问题的常规方法。
其实对于折叠问题,我们要明白: 1、折叠问题(翻折变换)实质上就是轴对称变换.2、折叠是一种对称变换,它属于轴对称.对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.3、对于折叠较为复杂的问题可以实际操作图形的折叠,在画图时,画出折叠前后的图形,这样便于找到图形之间的数量关系和位置关系.4、在矩形(纸片)折叠问题中,重合部分一般会是一个以折痕为底边的等腰三角形5、利用折叠所得到的直角和相等的边或角,设要求的线段长为x ,然后根据轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求解.一、矩形中的折叠1.将一张长方形纸片按如图的方式折叠,其中BC ,BD 为折痕,折叠后BG 和BH 在同一条直线上,∠CBD= 度.折叠前后的对应角相等2.如图所示,一张矩形纸片沿BC 折叠,顶点A 落在点A ′处,再过点A ′折叠使折痕DE ∥BC ,若AB=4,AC=3,则△ADE 的面积是 .对称轴垂直平分对应点的连线3.如图,矩形纸片ABCD 中,AB=4,AD=3,折叠纸片使AD 边与对角线BD 重合,得折痕DG ,求AG 的长.根据对称的性质得到相等的对应边和对应角,再在直角三角形中根据勾股定理列方程求解即可GA'C D4.把矩形纸片ABCD 沿BE 折叠,使得BA 边与BC 重合,然后再沿着BF 折叠,使得折痕BE 也与BC 边重合,展开后如图所示,则∠DFB 等于( )注意折叠前后角的对应关系5.如图,沿矩形ABCD 的对角线BD 折叠,点C 落在点E 的位置,已知BC=8cm ,AB=6cm ,求折叠后重合部分的面积.重合部分是以折痕为底边的等腰三角形6.将一张矩形纸条ABCD 按如图所示折叠,若折叠角∠FEC=64°,则∠1= 度;△EFG 的形状 三角形.对折前后图形的位置变化,但形状、大小不变,注意一般情况下要画出对折前后的图形,便于寻找对折前后图形之间的关系,注意以折痕为底边的等腰△GEF8.如图,正方形纸片ABCD 的边长为8,将其沿EF 折叠,则图中①②③④四个三角形的周长之和为折叠前后对应边相等321FEDCBA54132G D‘FC‘DBCAE9.如图,将边长为4的正方形ABCD 沿着折痕EF 折叠,使点B 落在边AD 的中点G 处,求四边形BCFE 的面积注意折叠过程中的变与不变,图形的形状和大小不变,对应边与对应角相等10.如图,将一个边长为1的正方形纸片ABCD 折叠,使点B 落在边AD 上 不与A 、D 重合.MN 为折痕,折叠后B’C’与DN 交于P .(1)连接BB’,那么BB’与MN 的长度相等吗?为什么? (2)设BM=y ,AB’=x ,求y 与x 的函数关系式;(3)猜想当B 点落在什么位置上时,折叠起来的梯形MNC’B’面积最小?并验证你的猜想.PC'NB CADMB'QPH C'N BCADM B'二、纸片中的折叠11.如图,有一条直的宽纸带,按图折叠,则∠α的度数等于()题考查的是平行线的性质,同位角相等,及对称的性质,折叠的角与其对应角相等,和平角为180度的性质,注意△EAB是以折痕AB为底的等腰三角形12.如图,将一宽为2cm的纸条,沿BC,使∠CAB=45°,则后重合部分的面积为在折叠问题中,一般要注意折叠前后图形之间的联系,将图形补充完整,对于矩形(纸片)折叠,折叠后会形成“平行线+角平分线”的基本结构,即重叠部分是一个以折痕为底边的等腰三角形ABC13.将宽2cm的长方形纸条成如图所示的形状,那么折痕PQ的长是注意掌握折叠前后图形的对应关系.在矩形(纸片)折叠问题中,会出现“平行线+角平分线”的基本结构图形,即有以折痕为底边的等腰三角形APQa2130°BEFACD14.如图a 是长方形纸带,∠DEF=20°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∠CFE 的度数是( )本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.由题意知∠DEF=∠EFB=20°图b ∠GFC=140°,图c 中的∠CFE=∠GFC -∠EFG15.将一张长为70 cm 的长方形纸片ABCD ,沿对称轴EF 折叠成如图的形状,若折叠后,AB 与CD 间的距离为60cm ,则原纸片的宽AB 是( )16.一根30cm 、宽3cm 的长方形纸条,将其按照图示的过程折叠(阴影部分表示纸条的反面),为了美观,希望折叠完成后纸条两端超出点P 的长度相等,则最初折叠时,求MA 的长图c 图b图aCDGFEAC GDFEAFDBCAEB BGE F D A EF D B C AB C60c m三、三角形中的折叠17.如图,把Rt△ABC(∠C=90°),使A,B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则CE:AE=(3)如图(3)把△CDE沿DE斜向上折叠,探求∠1、∠2、∠C的关系.(1)根据折叠前后的图象全等可知,∠1=180°-2∠CDE,∠2=180°-2∠CED,再根据三角形内角和定理比可求20.观察与发现:将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);在第一次折叠的基础上第二次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.实践与运用:(1)将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D’处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.在第一次折叠中可得到∠EAD = ∠FAD在第二次折叠中可得到EF是AD的垂直平分线,则AD⊥EF∴∠AEF = ∠AFE∴△AEF是等腰三角形(1)由折叠可知∠AEB = ∠FEB,∠DEG = ∠BEG而∠BEG = 45°+ ∠α因为∠AEB + ∠BEG + ∠DEG = 180°所以 45°+ 2(45°+∠α)= 180°∠α = 22.5°由于角平分线所在的直线是角的对称轴,所以在三角形中的折叠通常都与角平分线有关。
立体几何中的折叠问题题型归纳汇总

高考热点问题:立体几何中折叠问题一、考情分析立体几何中的折叠问题是历年高考命题的一大热点与难点,主要包括两个方面:一是平面图形的折叠问题,多涉及到空间中的线面关系、体积的求解以及空间角、距离的求解等问题;二是几何体的表面展开问题,主要涉及到几何体的表面积以及几何体表面上的最短距离等.二、经验分享(1)立体几何中的折叠问题主要包含两大问题:平面图形的折叠与几何体的表面展开.把一个平面图形按照某种要求折起,转化为空间图形,进而研究图形在位置关系和数量关系上的变化,这就是折叠问题.把一个几何体的表面伸展为一个平面图形从而研究几何体表面上的距离问题,这就是几何体的表面展开问题.折叠与展开问题是立体几何的两个重要问题,这两种方式的转变正是空间几何与平面几何问题转化的集中体现,展开与折叠问题就是一个由抽象到直观,由直观到抽象的过程.此类问题也是历年高考命题的一大热点. (2) 平面图形通过折叠变为立体图形,就在图形发生变化的过程中,折叠前后有些量(长度、角度等)没有发生变化,我们称其为“不变量”.求解立体几何中的折叠问题,抓住“不变量”是关键.(3)把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.三、题型分析(一) 平面图形的折叠解答折叠问题的关键在于画好折叠前后的平面图形与立体图形,抓住两个关键点:不变的线线关系、不变的数量关系.不变的线线关系,尤其是平面图形中的线线平行、线线垂直关系是证明空间平行、垂直关系的起点和重要依据;不变的数量关系是求解几何体的数字特征,如几何体的表面积、体积、空间中的角与距离等的重要依据.1. 折叠后的形状判断【例1】如下图,在下列六个图形中,每个小四边形皆为全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的是_____________(要求:把你认为正确图形的序号都填上)①②③④⑤⑥【分析】根据平面图形的特征,想象平面图形折叠后的图形进行判断.也可利用手中的纸片画出相应的图形进行折叠.【答案】①③⑥【解析】①③⑥可以.②把横着的小方形折起后,再折竖着的小方形,则最上方的小方形与正方体的一个侧面重合,导致正方体缺少一个侧面;④把下方的小方形折起后,则上方的小方形中的第1,2个重合,导致正方体的底面缺少,不能折成正方体;⑤把中间的小方形当成正方体的底面,则右下方的小方形折叠不起来,构不成正方体.【小试牛刀】下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后的图形是()A. B. C. D.【例2】将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四边形ABCD(如图2),则在空间四边形ABCD中,AD与BC的位置关系是( )图1 图2A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直【答案】C【解析】在图1中的等腰直角三角形ABC 中,斜边上的中线AD 就是斜边上的高,则AD ⊥BC ,折叠后如图2,AD 与BC 变成异面直线,而原线段BC 变成两条线段BD 、CD ,这两条线段与AD 垂直,即AD ⊥BD ,AD ⊥CD ,故AD ⊥平面BCD ,所以AD ⊥BC .【小试牛刀】如图,在正方形ABCD 中,点E,F 分别为边BC,AD 的中点,将沿BF 所在直线进行翻折,将沿DE 所在直线进行翻折,在翻折过程中( )A. 点A 与点C 在某一位置可能重合B. 点A 与点C 的最大距离为C. 直线AB 与直线CD 可能垂直D. 直线AF 与直线CE 可能垂直 3.折叠后几何体的数字特征折叠后几何体的数字特征包括线段长度、几何体的表面积与体积、空间角与距离等,设计问题综合、全面,也是高考命题的重点.解决此类问题的关键是准确确定折叠后几何体的结构特征以及平面图形折叠前后的数量关系之间的对应.【例3】(体积问题)如图所示,等腰ABC △的底边66AB =,高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF △的位置,使PE AE ⊥,记BE x =,()V x 表示四棱锥P ACFE −的体积.(1)求()V x 的表达式;(2)当x 为何值时,()V x 取得最大值?PED F B CA【解析】(1)由折起的过程可知,PE ⊥平面ABC,96ABC S ∆=,V(x)= (036x <<)(2),所以(0,6)x ∈时,'()0v x > ,V(x)单调递增;636x <<时'()0v x < ,V(x)单调递减;因此x=6时,V(x)取得最大值126.【小试牛刀】【河北省五个一名校联盟2019届高三下学期一诊】在平面四边形 中,AB=BC=2,AC=AD=2,现沿对角线AC 折起,使得平面DAC平面ABC ,则此时得到的三棱锥D-ABC外接球的表面积为( ) A .B .C .D .【例4】(空间角问题)如左图,矩形ABCD 中,12AB =,6AD =,E 、F 分别为CD 、AB 边上的点,且3DE =,4BF =,将BCE ∆沿BE 折起至PBE ∆位置(如右图所示),连结AP 、EF 、PF ,其中25PF =.(Ⅰ)求证:PF ⊥平面ABED ; (Ⅱ)求直线AP 与平面PEF 所成角的正弦值.【解析】(Ⅰ)由翻折不变性可知, , ,在PBF ∆中, ,所以PF BF ⊥ 在图1中,易得,在PEF ∆中, ,所以PF EF ⊥又,BF ⊂平面ABED ,EF ⊂平面ABED ,所以PF ⊥平面ABED .. .ACDBEF图图ABCD PEF(Ⅱ)方法一:以D 为原点,建立空间直角坐标系D xyz −如图所示,则()6,0,0A ,,()0,3,0E ,()6,8,0F ,所以, ,,设平面PEF 的法向量为(),,x y z =n ,则0FP EF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n ,即,解得560x y z ⎧=−⎪⎨⎪=⎩令6y =−,得,设直线AP 与平面PEF 所成角为θ,则81281427. 所以直线AP 与平面PEF 所成角的正弦值为81281427. 方法二:过点A 作AH EF ⊥于H ,由(Ⅰ)知PF ⊥平面ABED ,而AH ⊂平面ABED 所以PF AH ⊥,又,EF ⊂平面PEF ,PF ⊂平面PEF ,所以AH ⊥平面PEF ,所以APH ∠为直线AP 与平面PEF 所成的角. 在Rt APF ∆中,在AEF ∆中,由等面积公式得4861在Rt APH ∆中,所以直线AP 与平面PEF 所成角的正弦值为81281427. 【点评】折叠问题分析求解两原则:解法二图ABCD PEFHxy z 解法一图A BC D PEF(1)折叠问题的探究须充分利用不变量和不变关系;(2)折叠前后始终位于折线的同侧的几何量和位置关系保持不变.【小试牛刀】【广东省汕头市2019届高三上学期期末】如图,已知是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足,如图,将沿DE折成四棱锥,且有平面平面BCED.求证:平面BCED;记的中点为M,求二面角的余弦值.(二) 几何体的展开几何体表面展开问题是折叠问题的逆向思维、逆过程,一般地,涉及到多面体表面距离的问题,解题时不妨将它展开成平面图形试一试.1.展开后形状的判断【例5】把正方体的表面沿某些棱剪开展成一个平面图形(如右下图),请根据各面上的图案判断这个正方体是()解析:这是图③模型,在右图中,把中间的四个正方形围起来做“前后左右”四个面,有“空心圆”的正方形做“上面”,显然是正方体C的展形图,故选(C).【小试牛刀】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、“你”、“前”分别表示正方体的______________________.2.展开后的数字特征——表面上的最短距离问题【例6】如图,已知圆柱体底面圆的半径为2π,高为2,AB CD,分别是两底面的直径,AD BC,是母线.若一只小虫从A点出发,从侧面爬行到C点,求小虫爬行的最短路线的长度.【解析】如图,将圆柱的侧面展开,其中AB为底面周长的一半,即,2AD=.则小虫爬行的最短路线为线段AC.在矩形ABCD中,.所以小虫爬行的最短路线长度为22.【点评】几何体表面上的最短距离需要将几何体的表面展开,将其转化为平面内的最短距离,利用平面内两点之间的距离最短求解.但要注意棱柱的侧面展开图可能有多种展开图,如长方体的表面展开图等,要把不同展开图中的最短距离进行比较,找出其中的最小值.【小试牛刀】如图,在长方体中, ,求沿着长方体表面从A到1C的最短路线长.四、迁移运用1.【浙江省2019年高考模拟训练】已知四边形中,,,在将沿着翻折成三棱锥的过程中,直线与平面所成角的角均小于直线与平面所成的角,设二面角,的大小分别为,则()A. B. C.存在 D.的大小关系无法确定【答案】B【解析】如图,在三棱锥中,作平面于,连,则分别为与平面所成的角.∵直线与平面所成角的角均小于直线与平面所成的角,∴.过作,垂足分别为,连,则有,∴分别为二面角,的平面角,∴.在中,,设BD的中点为O,则为边上的中线,由可得点H在CO的左侧(如图所示),∴.又,∴.又为锐角, ∴.故选B .2.【四川省德阳市2018届高三二诊】以等腰直角三角形ABC 的斜边BC 上的中线AD 为折痕,将ABD ∆与ACD ∆折成互相垂直的两个平面,得到以下四个结论:①BD ⊥平面ACD ;②ABC ∆为等边三角形;③平面ADC ⊥平面ABC ;④点D 在平面ABC 内的射影为ABC ∆的外接圆圆心.其中正确的有( ) A. ①②③ B. ②③④ C. ①②④ D. ①③④ 【答案】C【解析】由于三角形ABC 为等腰直角三角形,故,所以BD ⊥平面ACD ,故①正确,排除B 选项.由于AD BD ⊥,且平面ABD ⊥平面ACD ,故AD ⊥平面BCD ,所以AD CD ⊥,由此可知,三角形为等比三角形,故②正确,排除D 选项.由于,且ABC ∆为等边三角形,故点D 在平面ABC 内的射影为ABC ∆的外接圆圆心, ④正确,故选C .3.已知梯形如下图所示,其中,,为线段的中点,四边形为正方形,现沿进行折叠,使得平面平面,得到如图所示的几何体.已知当点满足时,平面平面,则的值为( )A. B. C. D.【答案】C 【解析】因为四边形为正方形,且平面平面,所以两两垂直,且,所以建立空间直角坐标系(如图所示),又因为,,所以,则,,设平面的法向量为,则由得,取,平面的法向量为,则由得,取,因为平面平面,所以,解得.故选C.4.如图是棱长为1的正方体的平面展开图,则在这个正方体中,以下结论错误的是( )A .点M 到AB 的距离为22B .AB 与EF 所成角是90︒C .三棱锥C DNE −的体积是16D .EF 与MC 是异面直线 【答案】D【解析】根据正方体的平面展开图,画出它的立体图形如图所示,A 中M 到AB 的距离为222MC =,A 正确;AB 与EF 所成角是90︒,B 正确;三棱锥C DNE −的体积是,C 正确;//EF MC ,D 错误.5.把正方形ABCD 沿对角线AC 折起,当以四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为( )度A .90B .60C .45D .30 【答案】C【解析】折叠后所得的三棱锥中易知当平面ACD 垂直平面ABC 时三棱锥的体积最大.设AC 的中点为O ,则DBO ∠即为所求,而DOB ∆是等腰直角三角形,所以,故选C .6.【辽宁省辽阳市2018学届高三第一次模拟】如图,圆形纸片的圆心为O ,半径为6cm ,该纸片上的正方形ABCD 的中心为O , E , F , G , H 为圆O 上的点, ABE V , BCF V , CDG V , ADH V 分别以AB , BC , CD , DA 为底边的等腰三角形,沿虚线剪开后,分别以AB , BC , CD , DA 为折痕折起ABE V , BCF V , CDG V , ADH V ,使得E , F , G , H 重合,得到一个四棱锥,当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的体积为__________.【答案】500327π3cm【解析】如图:连接OE 交AB 于点I ,设E ,F ,G ,H 重合于点P ,正方形的边长为x ()0x >,则OI=2x , IE 62x =−. 因为该四棱锥的侧面积是底面积的2倍,所以,解得4x =,设该四棱锥的外接球的球心为Q ,半径为R ,则,,解得5R 3=,外接球的体积3cm7.【山东省济南市2019届高三上学期期末】在正方形中,点,分别为,的中点,将四边形沿翻折,使得平面平面,则异面直线与所成角的余弦值为__________.【答案】【解析】连接FC ,与DE 交于O 点,取BE 中点为N , 连接ON ,CN ,易得ON ∥BD ∴∠CON 就是异面直线与所成角设正方形的边长为2, OC=,ON=,CN=∴cos ∠CON==故答案为:8.如图所示,在四边形ABCD 中,,将四边形ABCD 沿对角线BD 折成四面体BCD A −',使平面⊥BD A /平面BCD ,则下列结论正确的是 .(1)BD C A ⊥'; (2);(3)A C '与平面BD A '所成的角为︒30; (4)四面体BCD A −'的体积为61. 【答案】(2)(4)【解析】平面⊥BD A /平面BCD CD ∴⊥平面'A BD ,/CA 与平面BD A /所成的角为'CA D ∠,四面体BCDA −/的体积为,,综上(2)(4)成立.9.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1AC 的中点,则在ADE ∆翻折过程中,下面四个选项中正确的是 (填写所有的正确选项)(1)||BM 是定值 (2)点M 在某个球面上运动(3)存在某个位置,使1DE AC ⊥ (4)存在某个位置,使//MB 平面1A DE 【答案】(1)(2)(4).【解析】取CD 中点F ,连接MF ,BF ,则1//MF DA ,//BF DE ,∴平面//MBF 平面1A DE , ∴//MB 平面1A DE ,故(4)正确;由,为定值,FB DE =为定值,由余弦定理可得,∴MB 是定值,故(1)正确;∵B 是定点,∴M 是在以B 为圆心,MB 为半径的圆上,故(2)正确;∵1AC 在平面ABCD 中的射影为AC ,AC 与DE 不垂直,∴存在某个位置,使1DE A C ⊥错误,故(3)错误.10.【四川省广元市高2018届第二次高考适应性统考】如图,在矩形ABCD 中, 4AB =, 2AD =, E 是CD 的中点,以AE 为折痕将DAE ∆向上折起, D 变为'D ,且平面'D AE ⊥平面ABCE .(Ⅰ)求证: 'AD EB ⊥; (Ⅱ)求二面角'A BD E −−的大小. 【答案】(Ⅰ)证明见解析;(Ⅱ) 90o . 【解析】(Ⅰ)证明:∵, AB 4=,∴,∴AE EB ⊥,取AE 的中点M ,连结MD ',则,∵ 平面D AE '⊥平面ABCE ,∴MD '⊥平面ABCE ,∴MD '⊥ BE , 从而EB ⊥平面AD E ',∴AD EB '⊥ (Ⅱ)如图建立空间直角坐标系,则()A 4,2,0、()C 0,0,0、()B 0,2,0、()D 3,1,2',()E 2,0,0,从而BA u u u v=(4,0,0),,.设为平面ABD '的法向量,则可以取设为平面BD E '的法向量,则可以取因此, 12n n 0⋅=u u v u u v ,有12n n ⊥u u v u u v,即平面ABD ' ⊥平面BD E ',故二面角的大小为90o .11.【福建省龙岩市2019届高三下学期教学质量检查】如图1,已知菱形的对角线交于点,点为线段的中点,,,将三角形沿线段折起到的位置,,如图2所示.(Ⅰ)证明:平面平面;(Ⅱ)求三棱锥的体积.【解析】(Ⅰ)折叠前,因为四边形为菱形,所以;所以折叠后,,, 又,平面,所以平面因为四边形为菱形,所以.又点为线段的中点,所以.所以四边形为平行四边形.所以.又平面,所以平面.因为平面,所以平面平面.(Ⅱ)图1中,由已知得,,所以图2中,,又所以,所以又平面,所以又,平面,所以平面,所以.所以三棱锥的体积为.12.【湖南省长沙市长郡中学2019届高三上学期第一次适应性考试(一模】如图,在多边形中(图1),为长方形,为正三角形,现以为折痕将折起,使点在平面内的射影恰好在上(图2).(Ⅰ)证明:平面;(Ⅱ)若点在线段上,且,当点在线段上运动时,求三棱锥的体积. 【解析】(Ⅰ)过点作,垂足为.由于点在平面内的射影恰好在上,∴平面.∴.∵四边形为矩形,∴.又,∴平面,∴.又由,,可得,同理.又,∴,∴,且,∴平面.(Ⅱ)设点到底面的距离为,则.由,可知,∴.又,∴.13.【江西省上饶市重点中学2019届高三六校第一次联考】如图所示,在边长为2的菱形中,,现将沿边折到的位置.(1)求证:;(2)求三棱锥体积的最大值.【解析】(1)如图所示,取的中点为,连接,易得,,又面(2)由(1)知,= ,当时,的最大值为1.14.【云南师范大学附属中学2019届高三上学期第一次月考】如图所示甲,在四边形ABCD中,,,是边长为8的正三角形,把沿AC折起到的位置,使得平面平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.求证:平面PON;求三棱锥的体积.【解析】如图所示,为正三角形,O为AC的中点,,平面平面ACD,平面平面,平面ACD,平面ACD,.,,,,即.,N分别为棱AC,AD的中点,,,又,平面PON;解:由,,,可得,点O、N分别是AC、AD的中点,,是边长为8的等边三角形,,又为PA的中点,点M到平面ANO的距离,.又,.15.【湖北省荆门市2019届高三元月调研】如图,梯形中,,过分别作,,垂足分别,,已知,将梯形沿同侧折起,得空间几何体,如图.1若,证明:平面;2若,,线段上存在一点,满足与平面所成角的正弦值为,求的长.【解析】1由已知得四边形ABFE是正方形,且边长为2,在图2中,,由已知得,,平面又平面BDE,,又,,平面2在图2中,,,,即面DEFC,在梯形DEFC中,过点D作交CF于点M,连接CE,由题意得,,由勾股定理可得,则,,过E作交DC于点G,可知GE,EA,EF两两垂直,以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系,则,.设平面ACD的一个法向量为,由得,取得,设,则m,,,得设CP与平面ACD所成的角为,.所以16.【山西省吕梁市2019届高三上学期第一次模拟】已知如图(1)直角梯形,,,,,为的中点,沿将梯形折起(如图2),使.(1)证明:平面;(2)求点到平面的距离.【解析】(1)由已知可得为直角三角形,所以.又,所以,所以平面.(2)因为平面,平面,所以,又因为,平面,平面,,所以,平面,又因为,所以平面,又因为平面,所以.在直角中,,设点到平面的距离为,由,则,所以.16.正△ABC的边长为4,CD是AB边上的高,,E F分别是AC和BC边的中点,现将△ABC沿CD翻折−−.成直二面角A DC B(1)试判断直线AB与平面DEF的位置关系,并说明理由;−−的余弦值;(2)求二面角E DF C(3)在线段BC 上是否存在一点P ,使AP DE ⊥?证明你的结论.【分析】(1)问可利用翻折之后的几何体侧面ABC ∆的中位线得到//AB EF ,便可由线面平行的判定定理证得;(2)先根据直二面角A DC B −−将条件转化为AD ⊥面BCD ,然后做出过点E 且与面BCD 垂直的直线EM ,再在平面BCD 内过M 作DF 的垂线即可得所求二面角的平面角;(3)把AP DE ⊥作为已知条件利用,利用ADC ∆中过A 与DE 垂直的直线确定点P 的位置.【解析】(1)如图:在△ABC 中,由E 、F 分别是AC 、BC 中点,得EF//AB,又AB ⊄平面DEF,EF ⊂平面DEF .∴AB ∥平面DEF .(2)∵AD ⊥CD,BD ⊥CD∴∠ADB 是二面角A —CD —B 的平面角∴AD ⊥BD ∴AD ⊥平面BCD取CD 的中点M,这时EM ∥AD ∴EM ⊥平面BCD过M 作MN ⊥DF 于点N,连结EN,则EN ⊥DF∴∠MNE 是二面角E —DF —C 的平面角,在Rt △EMN 中,EM=1,MN=23 ∴tan ∠MNE=233,cos ∠MNE=721(3)在线段BC 上存在点P,使AP ⊥DE. 证明如下:在线段BC 上取点P,使BC BP 31=,过P 作PQ ⊥CD 与点Q, ∴PQ ⊥平面ACD∵, 在等边△ADE 中,∠DAQ=30°,∴AQ ⊥DE ∴AP ⊥DE.。
折叠问题题型梳理

折叠问题题型梳理题型1 折痕为对角线1.如图,将▱ABCD 沿对角线AC 折叠,使点B 落在B ′处,若∠1=∠2=44°,则∠B 为A .66°B .104°C .114°D .124°【解析】∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠ACD =∠BAC ,由折叠的性质得:∠BAC =∠B′AC ,∴∠BAC =∠ACD =∠B′AC =12∠1=22°∴∠B =180°–∠2–∠BAC =180°–44°–22°=114°;选C . 2.如图,将▱ABCD 沿对角线BD 折叠,使点A 落在点E 处,交BC 于点F ,若ABD 48∠=,CFD 40∠=,则E ∠为( )A . 102B . 112C . 122D . 92 【解析】AD //BC ,ADB DBC ∠∠∴=,由折叠可得ADB BDF ∠∠=,DBC BDF ∠∠∴=,又DFC 40∠=,DBC BDF ADB 20∠∠∠∴===, 又ABD 48∠=, A 1802048112∠=--=,E A 112∠∠∴==,选B3.如图,在矩形ABCD 中,BC =6,CD =3,将△BCD 沿对角线BD 翻折,点C 落在点C 1处,BC 1交AD 于点E ,则线段DE 的长为( )A . 3B . 154C . 5D . 152【解析】根据题意易证BE =DE ,设ED =x ,则AE =8﹣x ,在△ABE 中根据勾股定理得到关于线段AB 、AE 、BE 的方程x 2=42+(8﹣x )2, 解方程得x =5,即ED =5,故选C .题型2 折痕过一顶点4.如图,在矩形ABCD 中,AB =4,BC =6,点E 为BC 的中点,将△ABE 沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则CF 的长为 .【解析】连接BF ,∵BC =6,点E 为BC 的中点,∴BE =3又∵AB =4,∴AE ==5,∴BH =,则BF =∵FE =BE =EC ,∴∠BFC =90°根据勾股定理得,CF ===5.如图,矩形纸片ABCD ,对角线为BD ,沿过点D 的直线折叠,使点A 落在对角线BD 上的点E 处,折痕DG ,若4,3AB BC ==,则AG 的长是( )A . 43B . 32C . 125D . 23【解析】根据题意可得:∠GDA =∠GDB ,AD =ED ,∵四边形ABCD 是矩形,∴∠A =90°,AD =BC =3,∴AG =EG ,ED =3,∵AB =4,BC =3,∠A =90°,∴BD =5,设AG =x ,则GE =x ,BE ==2,BG =4-x ,在Rt △BEG 中,EG 2+BE 2=BG 2,即:x 2+4=(4-x )2,解得:x =32,∴AG =32,选B . 6.如图,在平行四边形ABCD 中,E 为边CD 上一点,将ADE 沿AE 折叠至AD E '处,AD '与CE 交于点F .若54B ∠=︒,20DAE ∠=︒,则FED '∠的大小为( )A . 27°B . 32°C . 36°D . 40°【解析】∵四边形ABCD 是平行四边形,54B ∠=︒,∴54D B =∠=︒∠又∠DAE =20°,∴∠AED =180°-∠D -∠DAE =106°,根据折叠可得:106AED AED ∠=∠='︒ 又∠AEF =180°-∠AED =74°,∴32FED AED AEF ∠∠'=∠-='︒,选B7.如图,把正方形ABCD 沿对边中点所在的直线对折后展开,折痕为,MN 再过点B 折叠纸片,使点A 格在MN 上的点F 处,折痕为,BE 若AB 长为2,则EN 的长为(( )A . 3B . 3-C . 2D . 3【解析】∵四边形ABCD 为正方形,AB =2,过点B 折叠纸片,使点A 落在MN 上的点F 处,∴FB =AB =2,BM =12BC =1,BF =BA =2,∠BMF =90°,则在Rt △BMF 中,FM =∴2FN MN FM =-=设AE =FE =x ,则EN =1x -,∵Rt △EFN 中,222NE NF EF +=,∴()(22212x x -+=,解得:4x =-EN =13x -=,选A 8.如图,在正方形ABCD 中,E 为BC 上一点,将△ABE 沿AE 折叠至AB E '∆处,B E '与AC 交于点F ,若∠EFC =67°,则∠CAE 的度数为____.【解析】由正方形性质知:∠ACE =45°,∵∠EFC =67°,∴在△FEC 中,由外角定理有:∠BEF =∠EFC +∠ACE =67°+45°=112°,由折叠的性质可知:∠BEA =12∠BEF =56°,∴∠BAE =90°-∠BEA =90°-56°=34°, ∴∠EAC =45°-34°=11°.故答案为:11°.9.已知,如图:一张矩形纸片ABCD ,6AB =,8AD =,E 为AD 边上一动点,将矩形沿BE 折叠,要使点A 落在BC 上,则折痕BE 的长度是________;若点A 落在AC 上,则折痕BE 与AC 的位置关系是__________.若翻折后A 点的对应点是A '点,连接DA ',则在点E 运动的过程中,DA '的最小值是______.【解析】如图,由折叠的性质可知,,AB A B EAB BA E ''=∠=∠ ,∵四边形ABCD 是矩形,∴90ABA '∠=︒ ,∴四边形ABA E '是正方形,6AE AB ∴==,BE ∴==若点A 落在AC 上,根据折叠的性质可知,BE 垂直平分,所以折痕BE 与AC 的位置关系是垂直;如图,当A '在BD 上时,DA '的长度最小,6,8AB AD ==,10BD ∴== .6BA BA '== ,4DA BD BA ''∴=-= ,∴DA '的最小值是4.10..如图,在矩形ABCD 中,2,AB AD m ==,动点P 从点D 出发,沿射线DA 以每秒1个单位的速度向点A 方向运动,连接CP ,把PDC △沿PC 翻折,得到PEC .设点P 的运动时间为()t s .(1)若3m =,当P E B 、、三点在同一直线上时,求t 的值;(2)若点E 到直线BC 的距离等于1,求t 的值;(3)若AE 的最小值为1,直接写出m 的值.【解析】(1)如图1中,设PD =t .则P A =3-t∵P 、B 、E 共线,∴∠BPC =∠DP C ,∵AD ∥BC ,∴∠DPC =∠PCB ,∴∠BPC =∠PCB ,∴BP =BC =3,在Rt △ABP 中,∵AB 2+AP 2=BP 2,∴22+(3-t )2=32,∴t =3 +5(舍去)或3-5∴当t =3 P E B 、、三点在同一直线上.,2, 过点E 作MN ⊥BC ,交AD 于点M∵四边形ABCD 是矩形,MN ⊥BC ,∴MN ⊥AD∵点E 到直线BC 的距离等于1,∴EN =1,∵MN =AB =2, EC =CD =2,∴EN =MN -EN =2-1=1∴在Rt △ENC 中,NC MD = NC∵由题意得:MP =MD -PD -t ,ME =MN -EN =2-1=1,EP =PD =t∴在Rt △MPE 中,222=ME MP PE +,即:)2221=t +,解得:t ,3,如图,当点A ,点E ,点C 在同一条直线上时,AE 最短.由题意得:AE =1,EC =CD =AB =2,∴在Rt △ABC 中,BC∴m =AD =BC 题型3 不过顶点,折痕在内11.如图,将一个边长为4和8的长方形纸片ABCD 折叠,使C 点与A 点重合,则折痕EF 的长是( )A .B .C .D . 【解析】根据折叠的性质知,四边形AFEB 与四边形FDCE 全等,有EC =AF =AE ,由勾股定理得,AB 2+BE 2=AE 2即42+(8﹣AE )2=AE 2,解得,AE =AF =5,BE =3,作EG ,AF 于点G ,则四边形AGEB 是矩形,有AG =3,GF =2,GE =AB =4,由勾股定理得EF =D12.如图,在矩形ABCD 中,9,3,AD cm AB cm ==将其折叠,使点D 与点B 重合, 则重叠部分()BEF ∆的面积为( )2cmA . 15B . 152C . 6D . 5【解析】设DE =x .由翻折的性质可知D E =EB =x ,∠DEF =∠BEF ,则AE =(9﹣x )cm .由勾股定理得;BE 2=EA 2+AB 2,即x 2=(9﹣x )2+32,解得:x =5 ,DE =5cm ,,四边形ABCD 为矩形,,BC ∥AD .,∠BF E =∠DEF .,∠BFE =∠FEB , ,FB =BE =5cm .,,BEF 的面积=12BF •AB =12×3×5=152(cm 2),选B 13.如图,将矩形ABCD 沿EF 折叠,使点C 恰好落在AB 边的中点C '上,点D 落在D '处,C 'D '交AE 于点M .若AB =6,BC =9,求线段ED .【解析】如图,连接C 'E设DE =D'E =x ,∵在矩形ABCD 中,AB =6,BC =9∴CD =AB =6,AD =BC =9,∠A =∠D =90°,,AE =AD -DE =9-x∵折叠,∴∠D'=∠D =90°,C 'D '=CD =6,∵点C '为AB 边的中点∴AC '=12AB =3,在Rt ,AEC'中,C 'E 2=AE 2+AC '2=32+(9-x )2 在Rt △C'D'E 中,C 'E 2=C 'D '2+D 'E 2=62+x 2,∴32+(9-x )2=62+x 2,解得x =3 ∴线段ED 的长为3。
中考数学中的折叠问题精选全文

精选全中考数学中的折叠问题文完整版(可编辑修改)近年来,在各地中考数学命题时,十分重视对图形语言、文字语音、符号语言的理解运用及相互之间的关系,相互之间的转化能力以及动手操作能力的考查。
这样,图形的折叠问题就成为一个亮点,有关翻折的考题日趋增加。
翻折问题的解决方法,抓住翻折后与翻折的图形是以折痕为轴的轴对称图形这一关键,并运用代数方程,一般均可求得。
下面我们以中考题为例,谈谈翻折问题的几例类型及解法,供大家参考。
一、以矩形为母体的翻折这种类型最多,以折痕的不同位置又可分下面几种:1、沿对角线翻折例1、(2000年山西省)已知:如图1,将矩形ABCD沿直线BD折叠,使点C 落在C’处,BC’交AD于E,AD=8,AB=4,求△BED的面积。
分析:因为BD是对称轴,∴∠CBD=∠C’BD,又AD∥BC,∴∠CBD=∠ADB,得:∠C’BD=∠ADB,∴ED=EB设ED=x,∴AD=8-x在Rt△ABE中,AB2+AE2=BE2,即42+(8-x)2=x2,∴x=5,∴ED=EB=5又BD=∴S△BED==10方法2:过E作EF⊥BD,垂足F,在得到BE=5,BD=4后,在Rt△BEF中,EF=,得S△BED=BD×EF=×4×=10方法3:∵Rt△BEF∽Rt△BDC’,∴EF:DC’=BF:BC’,得EF==(以下略)2、沿一直线翻折,使一顶点落在对边上例2、(2000年山东省)已知矩形ABCD的两边AB与BC的比为4:5,E是AB 上一点,沿CE将△EBC向上翻折,若B点恰好落在边AD上的F点,如图2,则tg∠DCF=______。
A、B、C、D、分析:因为CF=CB,∴CF:CD=5:4,得CD:DF=4:3,∴tg∠DCF==,应选(A)。
例3、(1998年台州市)如图3,矩形ABCD的长、宽分别为5和3,将顶点C 折过来,使它落在AB上的C’点(DE为折痕),那么阴影部分的面积是______。
数学折叠问题初一

数学折叠问题初一
在初一的数学课程中,折叠问题是一个常见的话题。
这些问题通常涉及到几何形状,特别是多边形和纸张的折叠。
通过解决这些问题,学生可以锻炼他们的空间想象能力和几何推理能力。
以下是一些常见的初一数学折叠问题的类型和解决方法:
1. 角度计算
问题:一张纸被折叠一次,使得一个角与另一个角重合。
计算新形成的角度。
解决方法:首先理解折叠是轴对称的。
如果知道原始角度,可以通过减去或加上相应的角度来找到新角度。
2. 长度计算
问题:一张纸被折叠后,某一部分与另一部分重合。
计算重合部分的长度。
解决方法:利用相似三角形或全等三角形的性质来计算长度。
3. 面积计算
问题:一张纸被折叠后,形成一个新的形状。
计算新形状的面积。
解决方法:根据折叠后的形状,使用相应的面积公式进行计算。
4. 折叠模式识别
问题:描述一个特定的折叠过程,然后要求学生识别出最终的形状或模式。
解决方法:通过逻辑推理和空间想象来预测最终的形状或模式。
5.多步骤折叠
问题:一张纸经过多次折叠后形成一个复杂的形状。
要求学生描述或分析这个过程。
解决方法:分步骤进行,每次只关注一次折叠,然后逐步建立整体的理解。
解决这些问题时,建议学生使用实际的纸张进行模拟,这有助于他们更好地理解折叠过程并锻炼空间想象能力。
同时,也要鼓励学生多练习不同类型的折叠问题,以提高他们的解题技巧和速度。
北师大版九年级数学上学期题型全攻略专题01 特殊平行四边形中的折叠问题全梳理(解析版)

专题01特殊平行四边形中的折叠问题全梳理目录【方法归纳】 (1)【考法一、三角形翻折问题】 (1)【考法二、四边形翻折问题】 (16)【课后练习】 (28)【方法归纳】1.折叠的基本性质:翻折前后对应的边与角相等;2.对于翻折都不确定的情况,注意分类讨论,避免漏掉解;3.方程思想:灵活设未知数,通过勾股定理建立方程,解出答案4.综合性:把折叠性质与四边形性质相结合,建立边角之间的关系。
【考法一、矩形翻折问题】例.如图,在矩形OABC 中8AB =,4BC =,点D 为对角线OB 中点,点E 在OC 所在的直线上运动,连结DE ,把ODE 沿DE 翻折,点O 的对应点为点F ,连结BF .(1)当点F 在OC 下方时(如图1),求证:DE BF ∥.(2)当点F 落在矩形的对称轴上时,求EF 的长.(3)是否存在点E ,使得以D ,E ,F ,B 为顶点的四边形是平行四边形?若存在,求OE 的长;若不存在,请说明理由.当四边形△中,在Rt ABO222=+=OB AB AO8BC OC⊥∴∥,且D为OBDM BC中位线,DM∴为OCBOE EF BD DO ∴==,,25OE OD ∴==;如图,当四边形DEBF 为平行四边形时,DF OD BE ∴=,25BE ∴=,在Rt BEC △中,EC =826OE ∴=-=;DF OD BD DF == ,25BE OD ∴==,在Rt BCE 中,2CE BE =-在矩形ABCD 中,8AB =,6AD =,现将纸片折叠,点D 的对应点记为点P ,折痕为EF (点E 、F 是折痕与矩形的边的交点),再将纸片还原.【初步思考】(1)若点P落在矩形ABCD的边AB上(如图①)当点P与点A重合时,DEF∠=_____︒,当点E与点A重合时,DEF∠=______︒;【深入探究】(2)若点P落在矩形ABCD的内部(如图②),且点E、F分别在AD、DC边上,AP的最小值是______;【拓展延伸】(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图③)在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请求出线段AE的长度;若不存在,请说明理由.【答案】(1)90;45(2)2(3)存在某一情况,使得线段AM与线段DE的长度相等,线段AE的长度为65或4211【分析】(1)当点P与点A重合时,画出图形可得结论;当点E与点A重合时,则EF平分DAB∠,即可得出答案;(2)当F与C重合,点P在对角线AC上时,AP有最小值,根据折叠的性质求8CD PC==,由勾股定理求10AC=,即可得出结果;(3)分两种情况根据全等三角形的判定和性质以及勾股定理解答即可.【详解】解:(1)四边形ABCD是矩形,90DAB D∴∠=∠=︒,当点P与点A重合时,EF是AD的中垂线,90DEF∴∠=︒,当点E与点A重合时,如图,则EF平分DAB∠,==,则AF=设DF PF x当A,P,F在一直线上时,当x最大为8时,AP最小值为四边形ABCD是矩形,A ADC B∴∠=∠=∠=90∠由折叠的性质得:EPM ,AM DE=∴=,AM EP四边形ABCD是矩形,∴∠=∠=∠=︒,DAM ADC B90∠=∠由折叠的性质得:EPC ADC ∴∠=∠=︒,GAM GPE90变式2.【问题情境】折纸操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘,下面是折纸过程.【动手操作】步骤1:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,展平纸片;步骤2:点M 为边AD 上任意一点(与点A ,D 不重合),ABM 沿BM 折叠得到A BM '△,折痕BM 交EF 于点N .【问题探究】(1)如图1,当点A 的对称点A '落在EF 上时,连接AN .求证:四边形ANA M '为菱形;(2)已知2BC AB =,继续对折矩形纸片ABCD ,使AB 与DC 重合,折痕GH 与EF 交于点O .将ABM 沿BM 折叠,连接MO ,若点A 的对称点A '恰好落在线段MO 上,此时2AM =.①尺规作图:请在图2中用直尺和圆规,作点A 的对称点A '(保留作图痕迹,不写作法);②求AB 的长度;【拓展迁移】如图3,在矩形纸片ABCD 的边AB 上取一点P ,折叠纸片,使P ,B 两点重合,展平纸片,得到折痕EF ;点B '为EF 上任意一点(与点E ,F 不重合),折叠纸片使B ,B '两点重合,得到折痕l 及点P 的对应点P ',折痕l 交EF 于点K ,展平纸片,连接BP ',KP '.(3)猜想P B K ∠'与BC P '∠的数量关系,并证明.【答案】(1)见解析;(2)①见解析;②6AB =;(3)3P BC BP K ''∠∠=,理由见解析【分析】(1)根据折叠可得出NA NA '=,MA MA '=,AMB A MB '∠=∠,,证明AD EF ∥,利用平行线的性质得出AMB MNA '∠=∠,则A MB MNA ''∠=∠,利用等角对等边得出MA NA ''=,即可得证;(2)①以M 为圆心,MA 为半径画弧交MO 于A '即可;②利用折叠的性质,矩形的判定与性质可得出2BH AB A B AG OG '====,证明()HL OA B OHB ' ≌,得出OA OH OG '==,在Rt MGO △中,根据勾股定理,可求出OG ,进而求出AB ;(3)连接PK ,BK ,延长BK 交P B ''于点M ,可证明EB B MBB ''≌ ,得出BE B M '=,90FEB BMB '∠=∠=︒,由折叠可得BK PK P K B K ''===,利用等边对等角和三线合一的性质可得出P BK BP K ''∠=∠,KBB KB B ''∠=∠,MB MP ''=,利用线段垂直平分线的性质BP BB ''=,利用三线合一性质可得出P BK KBB ''∠=∠,则P BK BP K KBB KB B ''''∠=∠=∠=∠,由(1)中BC EF ∥,可得出B BC KB B ''∠=∠,即可得证.【详解】(1)证明:连接AA ',∵ABM 沿BM 折叠,得到A BM '△,∴BM 垂直平分AA ',∴NA NA '=,MA MA '=,AMB A MB '∠=∠,由折叠可知:AEF BEF ∠=∠,∵180AEF BEF ∠+∠=︒,∴90BEF ∠=︒,∵四边形ABCD 为矩形,∴90DAB ∠=︒,∴90BEF DAB ∠=∠=︒,∴AD EF ∥,∴AMB MNA '∠=∠,∴A MB MNA ''∠=∠,∴MA NA ''=,∴MA NA NA MA ''===,∴四边形ANA M '为菱形;点A'即为所求,解:连接BO,由折叠可知:AB A B'=,MA 由(1)得90∠=∠=︒GHB HGA∵l为折痕,∴P B B PBB'''∠=∠,BP B P''=,l ∴KP KP'=,=,KB KB'∴KBB KB B''∠=∠,∵B B BB''=,∴BE B M '=,90FEB BMB '∠=∠=︒,由折叠可知:KP KB =,EP EB =,90FEB ∠=︒,∴KP KB '=,KP KB ''=∴P BK BP K ''∠=∠,MB MP ''=∴BP BB ''=,∴P BK BP K KBB KB B ''''∠=∠=∠=∠,由(1)可知BC EF ∥,∴B BC KB B ''∠=∠,∴3P BC BP K ''∠=∠.【点睛】本题考查了矩形与折叠,等腰三角形的判定与性质,全等三角形的判定与性质,线段垂直平分线的性质等知识,明确题意,灵活运用所学知识解决问题是解题的关键.变式3.如图1,在矩形ABCD 中,点E 是边AB 上的一点,连接DE .(1)若DE 平分ADC ∠,点G 是CD 上的一点,连接EC ,EG ,且EC EG =.过点C 作CQ EG⊥于Q ,CQ 延长线交ED 于H ,过点H 作HP CD ⊥于P ,如图.①填空:AED △的形状是______三角形;②求证:PHC BEC△△≌(2)将图1的矩形ABCD 画在纸上,若DE 平分ADC ∠,沿过点E 的直线折叠,点C 恰好落在AD 上的点C '处,点B 落在点B '处,得到折痕EF ,B C ''交AB 于点M ,如图.求证:MC ME '=.(3)如图,延长DE 交CB 的延长线于点K 使得AB BK =,此时恰好BE BC =,连接AC 交DK 于点J ,连接BJ .请证明:KJ AJ BJ >+.【答案】(1)①等腰直角;②见解析(2)见解析(3)见解析【分析】(1)①根据矩形的性质和角平分线的性质可得45AED ADE ∠=∠=︒,进而得出结果;②可证得BCE PCH ∠=∠,EC HC =,90HPC B ︒∠=∠=,进而得出结论;(2)连接C E ',可证得Rt Rt EC A C EB ''' ≌,可得C EA EC B '''∠=∠,根据等角对等边即可得出结论;(3)在线段EK 上取点I ,使得KI AJ =,连接BI ,可证KBE ABC ≌△△,得BKE BAC ∠=∠,在证KBI ABJ ≌△△,得KBI ABJ ∠=∠,90IBJ KBA ︒∠=∠=,得出IJ BJ >,进一步得出结论.【详解】(1)① 四边形ABCD 是矩形,∴90A ADC ∠=∠=︒,DE 平分ADC ∠,∴1452ADE ADC ∠=∠=︒,∴9045AED ADE ∠=︒-∠=︒,∴AED ADE ∠=∠,∴AE DE =,∴AED △等腰直角三角形,故答案为:等腰直角②证明:如图,过点E 作EW CD ⊥于W .EC EG = ,EGC ECG ∴∠=∠,CH EG ⊥ ,90HCP EGC ∴∠+∠=︒,90BCE ECG ∠︒∠+= ,BCE PCH ∴∠=∠,45EDW DEW ∠︒∠== ,45EHC EDW PCH PCH ∴∠=∠︒+∠=+∠,DEC DEW CEW ∠=∠+∠,EW BC ∥,BCE CEW PCH ∴∠=∠=∠,DEC EHC ∴∠=∠,EC HC ∴=,90HPC B ∠=∠=︒PHC BEC ∴△△≌.(2)证明:如图,连接C E ',由(1)知,AED △为等腰直角三角形,AD AE ∴=,四边形ABCD 是矩形,AD BC ∴=,90EAC B '∠=∠=︒,由折叠知,B C BC ''=,B B '∠=∠,AE B C ''∴=,EAC B ''∠=∠,又EC C E ''=,在Rt EC A '△和Rt C EB ''△中,EC C E ''=,AE B C ''=,∴Rt Rt EC A C EB ''' ≌,C EA EC B '''∴∠=∠,MC ME '∴=.(3)如图,在线段EK 上取点I ,使得KI AJ =,连接BI ,在AJB 与KIB △中,BK AB =,ABC ABK ∠=∠,BE BC =,KBE ABC ∴△△≌,BKE BAC ∴∠=∠.KI AJ = ,BK AB =,BKE BAC ∠=∠,KBI ABJ ∴△△≌,KBI ABJ ∴∠=∠,90IBJ IBA ABJ IBA KBI KBA ∴∠=∠+∠=∠+∠=∠=︒,IBJ ∴△为直角三角形,IJ BJ ∴>,KJ AJ BJ ∴>+.【点睛】本题是四边形综合题,考查了等腰直角三角形的判定和性质,矩形的性质,全等三角形的判定和性质,轴对称的性质,准确添加常用辅助线,构造特殊三角形和证明全等三角形是解本题的关键。
七年级折叠问题知识点梳理

七年级折叠问题知识点梳理折叠问题是数学中的一种经典问题,也是考察对数学知识的理解和实际应用能力的重要领域。
在初中数学中,折叠问题也是一个重要的知识点,需要深入理解和掌握。
本文将对七年级折叠问题知识点进行梳理和整理,以帮助同学们更好地掌握这一知识点,从而在考试中取得更好的成绩。
一、基本概念折叠问题是指在平面图形上切割一条或数条线,然后将剩余部分按照指定的顺序进行折叠,并寻求可能出现的图形形态。
常出现的几何图形包括三角形、正方形、长方形等。
二、折叠的基本操作1. 折叠轴:指在平面图形上折叠的参考线,通常为直线。
2. 对称轴:指原图形和折叠后图形的对称轴,它们的交点处是折叠轴。
3. 折线:指从折叠轴起到图形边缘的折叠线段。
4. 折叠方向:指折叠时图形所向的方向,可以是向上、向下、向左或向右。
5. 折痕:指在图形上产生的折叠痕迹。
三、折叠问题的解题方法在解决折叠问题时,首先要对给定图形和折叠过程进行分析,然后选择合适的方法进行求解,一般有以下几种方法:1. 利用对称性:可以利用图形对称性进行折叠,其中对称轴可以作为折叠轴,而对称轴两侧的部分可以通过折叠得到图形的其他部分。
2. 利用折线的特性:根据折线的特性可以确定图形的边长和角度,从而得到图形的面积和形状。
3. 综合使用多种方法:在解决较为复杂的折叠问题时,可以综合使用多种方法,包括对称性、折线特性、面积等多个方面,灵活应用不同的方法。
四、折叠问题的实际应用折叠问题在实际生活中也有广泛的应用,例如在制作纸质建筑模型时,需要根据图纸进行折叠,从而得到复杂的建筑结构;在设计3D打印模型时,需要将平面图形折叠成三维立体模型,从而进行后续加工等。
总之,折叠问题是数学中非常重要的一个知识点,需要同学们用心理解和掌握,善于运用不同的方法解决问题,在实际应用中也能够得心应手。
希望本文对七年级学生们的学习有所帮助,祝愿大家在数学学习中取得更好的成绩。
折叠问题涉及6种解题方法梳理

折叠问题涉及6种解题方法梳理本文将概述折叠问题并介绍六种不涉及法律复杂性的解题方法。
折叠问题是指在纸张的折叠过程中,出现曲线和线段的交叉情况。
以下是六种常见的解题方法:1. 几何解法该方法通过几何定理和推导,分析折叠过程中的几何关系。
可以运用平行线的性质、相似三角形和直角三角形等知识,将折叠问题转换为几何问题进行求解。
2. 数学解法数学解法通过数学模型和方程求解折叠问题。
可以利用代数方程、函数关系和不等式等数学工具,建立数学模型,然后通过求解方程或优化函数得到折叠问题的答案。
3. 图论解法图论解法通过将折叠问题转化为图的问题进行求解。
可以将折叠过程中的曲线和线段抽象为图的节点和边,利用图论中的算法和定理,求解出最优的折叠方式。
4. 逻辑解法逻辑解法通过推理和演绎,分析折叠问题的逻辑关系。
可以从条件和前提出发,运用逻辑规则和推理方法,得出折叠问题的解答。
5. 模拟解法模拟解法通过计算机程序模拟折叠过程,通过迭代和模拟的方式求解折叠问题。
可以使用计算机编程语言编写程序,模拟纸张的折叠过程,并通过不断迭代求解最优的折叠方式。
6. 统计解法统计解法通过统计和分析大量的样本数据,得出折叠问题的概率和分布。
可以使用统计学方法,收集大量的折叠数据,并通过统计分析得出折叠问题的解答。
以上是六种不涉及法律复杂性的折叠问题解题方法。
每种方法都有其适用的场景和优势,可以根据具体问题的性质选择合适的方法进行求解。
希望这份文档对您有所帮助!。
初中折叠问题题型

初中数学中常见的折叠问题题型有以下几种:
折纸问题:给定一张矩形纸,将其沿着某些折痕折叠,问最后得到的图形是什么。
这类问题涉及到几何图形的变形和对称性质,需要掌握基本的折叠技巧和对称关系。
线段折叠问题:给定一条线段,将其沿着某些点折叠成一些角度,然后问折叠后的图形是什么。
这类问题涉及到三角函数和几何图形的变形,需要掌握基本的三角函数知识和折叠技巧。
立体图形折叠问题:给定一个立体图形的展开图,将其折叠成一个实体立体图形,然后问最终得到的图形是什么。
这类问题涉及到几何图形的空间变形和对称性质,需要掌握立体几何的基本概念和折叠技巧。
以上是初中数学中常见的折叠问题题型,需要注意的是,这些问题不仅考察计算能力,还要求学生具备一定的几何直观和空间想象能力。
矩形的折叠问题归类

矩形的折叠问题归类矩形的折叠问题是指在二维平面上,将一个矩形沿某一方向进行折叠,使得其中的某一条边与另一条边重合的问题。
这个问题可以分为以下几类。
1.水平折叠:在这种情况下,矩形按照水平方向进行折叠。
即将矩形的上边与下边进行折叠,使得它们重合。
这种情况下,折叠中心通常是矩形的中点。
2.垂直折叠:与水平折叠类似,垂直折叠是指将矩形的左边和右边进行折叠,使得它们重合。
折叠中心通常是矩形的中点。
3.对角线折叠:对角线折叠是指将矩形的一条对角线进行折叠,使得它与另一条对角线重合。
这种情况下,折叠中心就是矩形的中心点。
4.不对称折叠:不对称折叠是指将矩形沿任意一条线进行折叠,使得其中的两条边重合,但折叠中心不是矩形的对称中心。
这种类型的折叠通常需要一些几何推理和计算来求解。
5.多次折叠:在这种情况下,矩形可以进行多次折叠,使得多个边重合。
这种问题通常需要分析每次折叠的效果,并综合考虑到所有边的重合情况。
通过以上分类,我们可以看出矩形的折叠问题是一个几何学和空间想象力的结合。
解决这类问题通常需要从折叠后的形状入手,利用几何知识和计算方法,通过推理和计算找到解决方案。
例如,对于水平折叠问题,可以通过计算矩形的上边和下边的重合点来求解。
类似地,对于垂直折叠问题,可以计算矩形的左边和右边的重合点。
而对于对角线折叠问题,可以通过计算矩形的对角线的重合点来求解。
在不对称折叠问题中,可能需要通过几何推理来找到折叠点的位置,然后再进行计算。
这可能涉及到一些较为复杂的几何分析和角度计算。
在多次折叠问题中,可以通过类似的方法逐步解决每个折叠步骤,然后整合所有步骤的结果。
总之,矩形的折叠问题是一个有趣的几何学问题,需要运用数学和空间想象力来解决。
通过分类和分析不同类型的折叠问题,我们可以更好地理解和解决这类问题。
(完整版)七年级数学折叠问题总结(最新整理)
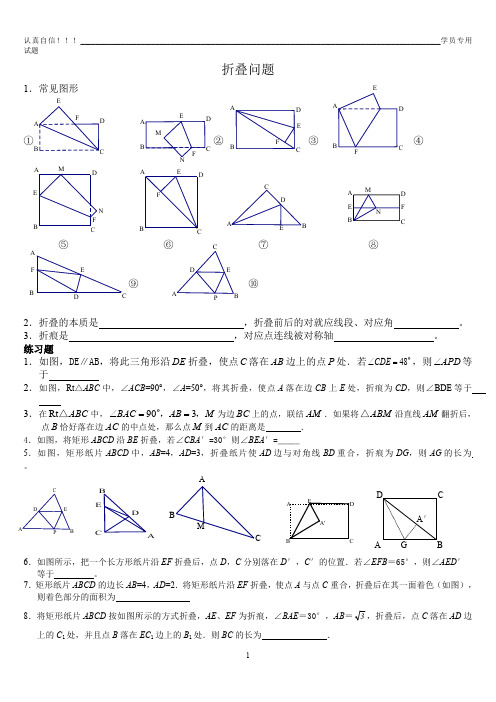
的长是 G
A
D
E
A
DD
FF
C
M F
D′
N
B
FC
C′
A
E
B
B
E
C
10.如图,梯形 ABCD 中,AD∥BC,DC⊥BC,将梯形沿对角线 BD 折叠,点 A 恰好落在 DC 边上的点 A´处,若
∠A´BC=20°,则∠A´BD 的度数为
.
11.如图,有一矩形纸片 ABCD,AB=10,AD=6,将纸片折叠,使 AD 边落在 AB 边上,折痕为 AE,再将△AED 以 DE 为折痕向
沿过点 E 的直线折叠,使点 D 落在 BE 上的点 M 处,折痕为 EG(如图②);再展平纸片(如图
③).则图③中∠1=
A
.
E
DA
E
DA
E D
M 1
B
CB F
FCB GC FG Nhomakorabea图①
图②
图③
2
右折叠,AE 与 BC 交于点 F,则△CEF 的面积为
12.已知边长为 5 的等边三角形 ABC 纸片,点 E 在 AC 边上,点 F 在 AB 边上,沿着 EF 折叠,使点 A 落在 BC 边上的点 D
的位置,且 ED BC ,则 CE 的长是
。
A
A
D
F
A
B
C
E
B
DC
13.将矩形纸片 ABCD 沿过点 B 的直线折叠,使点 A 落在 BC 边上的点 F 处,折痕为 BE(如图①);再
.
1
认 真 自 信 ! ! ! ________________________________________________________________________________________________学 员 专 用 试题
中考数学 折叠问题涉及6种题型梳理

折叠问题涉及6种题型梳理一、问题导读折叠型问题是近年中考的热点问题,通常是把某个图形按照给定的条件折叠,通过折叠前后图形变换的相互关系来命题。
折叠型问题立意新颖,变幻巧妙,对培养识图能力及灵活运用数学知识解决问题的能力非常有效。
这类问题的解法思路,常常会困扰同学们,同样是翻折类题目,条件不一样,问题不一样,用到的知识和方法也不尽相同,今天我们就一起来探究一下,遇到这类题目,如何找到突破口,如何用我们已经掌握的知识和方法来解答,继而发现这类问题特有的解题思维模式。
二、典例精析类型1直角三角形的翻折或翻折后产生直角三角形的问题例1.(2018秋昌平区期末)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC 折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的长为()【分析】设BN=x,则由折叠的性质可得DN=AN=9﹣x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.【解答】设BN=x,由折叠的性质可得DN=AN=9﹣x,∵D是BC的中点,∴BD=3,在Rt△NBD中,x+3=(9﹣x),解得x=4.即BN=4.故选:A.例1变式1.(2018秋平度市期中)如图,在Rt△ABC中,直角边AC=6,BC=8,将△ABC按如图方式折叠,使点B与点A重合,折痕为DE,则CD的长为()A.25/4B.22/3C.7/4D.5/3【解析】由题意得DB=AD;设CD=x,则AD=DB=(8﹣x),∵∠C=90°,∴AD﹣CD=AC,(8﹣x)﹣x=36,解得x=7/4;即CD=7/4.故选:C.例1变式2.(2018秋瑞安市期末)如图,矩形ABCD中,AB=4,AD=6,点E为BC 上一点,将△ABE沿AE折叠得到△AEF,点H为CD上一点,将△CEH沿EH折叠得到△EH G,且F落在线段E G上,当G F=G H时,则BE的长为_____.【解析】由折叠可得∠AEH=1/2∠BEC=90°,进而得出Rt△AEH中,AE+EH2=AH,设BE=x,则EF=x,CE=6﹣x=E G,再根据勾股定理,即可得到方程x+4+(6﹣x)+(6﹣2x)=(2x﹣2)+6,解该一元二次方程,即可得到BE的长.BE的长为2.【点评】本题主要考查的是翻折的性质、矩形的性质、勾股定理以及解一元二次方程的综合运用,解决问题的关键是连接AH构造直角三角形AEH,这种折叠问题常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.方法策略模式:在折叠后产生的直角三角形中,把某条边设成未知数根据勾股定理列方程求解。
初二数学折叠经典题型

初二数学折叠经典题型
初二数学折叠经典题型:
一、折线图问题
折线图是常考的试题,也是比较容易理解的一类试题。
折线图一般由
坐标轴及其上的点组成,通过观察折线图能够清楚地了解关于某一特
征数据的变化规律。
有时,折线图中会带有该变化属性的数据,要求
求出某个特定点对应的数据。
在考查过程中,要注意时间连续性、跨
度大小、跨度的变化趋势等。
二、圆弧(圆周率)问题
圆弧问题,即求圆周率、圆面积、弦长、弦夹角等问题。
一般情况下,圆的概念都是以圆心为中心,而弦夹角一般是以原点(O)为参照物,
两点之间的夹角角α如果在第一象限,则α=OA1+A2O,如果在第四象限,则α=360-OA1+A2O。
三、函数的表示、求解及应用问题
函数的概念不难理解,但是在求解中却很复杂。
函数在学习中,可以
把函数理解为把某种特定的变化规律用一种简单的形式表示出来的叫
函数,而函数的求解,就是对函数中的变量做出合理的特定值,使函
数满足某种给定的要求,而函数的应用,则是在理解函数形式和性质
的基础上,把函数运用到实际中,解决实际问题。
四、直线方程及课本问题
直线方程是一种统一的表达式,可以用来表示两个变量直接的关系,
而课本问题则是一种特殊的直线方程应用,是用来探讨几何形体某一
特性的变化规律,并在此基础上求出其特性的特定值。
2019中考数学复习必考知识点总结突破策略:折叠问题中必考的七大题型无答案

2019中考数学复习必考知识点突破策略:折叠问题中必考的七大题型图形的“折叠问题”是近年中考数学中每年必考的热点问题。
折叠的对象也往往有三角形、矩形、正方形等;考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;解题时,灵活运用轴对称性质和背景图形性质。
轴对称性质——折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。
一.利用折叠问题求折线长例1.将三角形纸片(a ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B',折痕为EF,已知AB=AC=3, BC=4,若以点B', F, C为顶点的三角形与4ABC相似,那么BF的长度是 .练习:1.在Rt A ABC中,/BAC = 90°, AB = 3, M为边BC上的点,联结AM(如图 3所示).如果将^ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是.二.利用折叠问题求折纸边长周长例1.在4ABC中,AB=12, AC=10, BC=9, AD是BC边上的高.将^ABC按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则4DEF 的周长为( )B. 10.5C. 11D. 15.5 练习: 矩形纸片ABCD 中,AB =4, AD =3,折叠纸片使AD 边与对角线4 3A . 1B . 4C . -D . 22三.利用折叠问题求重叠面积例1.如图,已知一个三角形纸片ABC , BC 边的长为8, BC 边上的高为6 , Z B 和Z C 都为锐角,M 为AB 一动点(点M 与点A 、B 不重合),过点M 作 MN 〃 BC ,交AC 于点N ,在△ AMN 中,设MN 的长为1 , MN 上的高为h .(1)请你用含1的代数式表示h .(2)将4AMN 沿MN 折叠,使4AMN 落在四边形BCNM 所在平面,设点A 落 在平面的点为A , △ AMN 与四边形BCNM 重叠部分的面积为 >,当i 为何值时,1 1J 最大,最大值为多少?1.如图BD 重合, 折痕为DG ,贝。
七年级折叠问题知识点

七年级折叠问题知识点折叠问题是数学中的一个经典问题。
在数学竞赛和考试中,被认为是一种基本函数,是考察数学运算能力和思维逻辑的基本题型之一。
而在七年级的数学课中,也会接触到一些折叠问题。
本文将介绍七年级折叠问题的知识点,供大家参考。
一、折纸图形的平移、旋转和对称在折叠问题中,图形的平移、旋转和对称是常见的变换方式。
因此,掌握这些变换的基本概念及性质是十分重要的。
1.平移变换平移变换指的是保持图形形状不变的情况下,将整个图形沿着某一方向移动一定距离后得到的新图形。
平移变换的性质是:对于平面上任意两点A和B,其平移后的位置A'和B'可以由向量AB和A'B'相等得到。
2.旋转变换旋转变换指的是保持图形形状不变的情况下,将整个图形绕给定的点(旋转中心)顺时针或逆时针旋转一定角度后得到的新图形。
旋转变换的性质是:任何平面上的图形旋转一周后均回到原来的位置。
3.对称变换对称变换指的是保持图形形状不变的情况下,将整个图形绕某条直线对称后得到的新图形。
对称变换的性质是:对称变换前后的图形具有相等的形状和大小。
二、折纸图形的叠合和重合折叠问题中,叠合和重合是两个核心概念。
只有掌握了这些概念,才能更好地解决折叠问题。
1.叠合叠合指的是将两个相同的图形重叠在一起,使它们完全重合的过程。
叠合要求两个图形的形状和大小完全相同。
2.重合重合指的是将两个不完全相同但有一定相似之处的图形重合在一起,使它们重合的程度最大。
重合要求两个图形的形状和大小不需要完全相同。
三、折纸图形的解析与构造折叠问题通常需要进行图形的解析和构造。
下面介绍两个基本的解析和构造方法。
1.解析方法解析方法指的是通过观察图形特征,确定图形各个部分的位置、大小和形状的方法。
解析方法的关键在于观察,要将图形各个部分的位置、大小和形状仔细观察、分析和比较,找出它们之间的关系,以便在后续的折叠中更好地处理图形。
2.构造方法构造方法指的是通过折叠纸张的方式,得到所需的图形的方法。
七年级物理折叠问题总结

七年级物理折叠问题总结本文旨在总结七年级物理学中的折叠问题,并提供一些简单有效的解决策略。
折叠问题是物理学中的基础概念之一,在几何学和力学方面有着重要的应用。
折叠是指将一物体的部分或全部重叠起来,使其形成新的形状或结构的过程。
折叠问题常涉及折纸、衣物、地图等对象,对学生的空间想象力、几何概念和手工技能有一定的要求。
1.折纸问题:将一张纸折叠成特定的形状,如折纸飞机、折纸鹤等。
2.衣物折叠问题:如何将一件衣物折叠成最小的体积,便于储存和携带。
3.地图折叠问题:如何将大面积的地图折叠成适合携带的小纸张。
1.理解几何概念:了解几何学中的基本形状、角度和对称性等概念,有助于理解和解决折叠问题。
2.掌握折纸技巧:学会基本的折叠技巧,如折线、折点、折痕等,可以帮助解决复杂的折叠问题。
3.分析问题:仔细观察和分析给定的折叠问题,确定需要达到的目标形状,并思考如何通过折叠实现这个目标。
4.反复实践:通过多次实践和尝试,探索不同的折叠方法和策略,在错误中找到正确的解决方案。
1.注意纸张的质量和厚度:纸张的质量和厚度会影响折叠的难度和结果,选择适合的纸张可以提高解决问题的效果。
2.注意折叠的精度和规范性:折叠过程中需要保持精确的折叠角度和折痕,以确保最终形状的准确性和稳定性。
折叠问题是七年级物理学中的一个重要内容,通过研究和解决折叠问题,不仅可以培养学生的空间想象力和几何概念,还可以锻炼学生的观察力和手工技能。
掌握解决折叠问题的基本策略,将有助于学生在物理研究中取得更好的成绩和应用。
折叠问题是七年级物理学中的一个重要内容,通过学习和解决折叠问题,不仅可以培养学生的空间想象力和几何概念,还可以锻炼学生的观察力和手工技能。
掌握解决折叠问题的基本策略,将有助于学生在物理学习中取得更好的成绩和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
折叠问题涉及6种题型梳理
一、问题导读
折叠型问题是近年中考的热点问题,通常是把某个图形按照给定的条件折叠,通过折叠前后图形变换的相互关系来命题。
折叠型问题立意新颖,变幻巧妙,对培养识图能力及灵活运用数学知识解决问题的能力非常有效。
这类问题的解法思路,常常会困扰同学们,同样是翻折类题目,条件不一样,问题不一样,用到的知识和方法也不尽相同,今天我们就一起来探究一下,遇到这类题目,如何找到突破口,如何用我们已经掌握的知识和方法来解答,继而发现这类问题特有的解题思维模式。
二、典例精析
类型1 直角三角形的翻折或翻折后产生直角三角形的问题
例1.(2018秋昌平区期末)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC 折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的长为()
【分析】设BN=x,则由折叠的性质可得DN=AN=9﹣x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.
【解答】设BN=x,由折叠的性质可得DN=AN=9﹣x,
∵D是BC的中点,∴BD=3,在Rt△NBD中,x +3 =(9﹣x),
解得x=4.即BN=4.故选:A.
例1变式1.(2018秋平度市期中)如图,在Rt△ABC中,直角边AC=6,BC=8,将△ABC按如图方式折叠,使点B与点A重合,折痕为DE,则CD的长为()
A.25/4 B.22/3 C.7/4 D.5/3
【解析】由题意得DB=AD;设CD=x,则AD=DB=(8﹣x),
∵∠C=90°,∴AD﹣CD=AC ,(8﹣x)﹣x=36,
解得x=7/4;即CD=7/4.故选:C.
例1变式2.(2018秋瑞安市期末)如图,矩形ABCD中,AB=4,AD=6,点E为BC 上一点,将△ABE沿AE折叠得到△AEF,点H为CD上一点,将△CEH沿EH折叠得到△EH G,且F落在线段E G上,当G F=G H时,则BE的长为_____.
【解析】由折叠可得∠AEH=1/2∠BEC=90°,进而得出Rt△AEH中,AE+EH2 =AH,设BE=x,则EF=x,CE=6﹣x=E G,再根据勾股定理,即可得到方程x+4 +(6﹣x)+(6﹣2x)=(2x﹣2)+6 ,解该一元二次方程,即可得到BE的长.BE的长为2.
【点评】本题主要考查的是翻折的性质、矩形的性质、勾股定理以及解一元二次方程的综合运用,解决问题的关键是连接AH构造直角三角形AEH,这种折叠问题常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.
方法策略模式:在折叠后产生的直角三角形中,把某条边设成未知数根据勾股定理列方程求解。
类型2 翻折前有平行线这一条件的问题
例2.(2018秋宜兴市期中)如图,在长方形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若OC=5cm,则CD的长为()
A.6cm B.7cm C.8cm D.10cm
【分析】由折叠的性质可得:∠BAC=∠EAC=∠ACD,可得AO=CO=5cm,根据勾股定理可求DO的长,即可求CD的长.
【解答】∵折叠,∴∠BAC=∠EAC,
∵四边形ABCD是矩形,∴AB∥CD,∴∠BAC=∠ACD,
∴∠EAC=∠ACD,∴AO=CO=5cm,
在直角三角形ADO中,利用勾股定理可求得DO=3cm,
∴CD=DO+CO=3+5=8cm.故选:C.
例2变式.(2018春南岗区校级月考)如图,矩形纸片ABCD中,AB=4,BC=8,现将A、C重合,使纸片折叠压平,设折痕为EF,则图形中重叠部分△AEF的面积为_____.
【解析】设AE=x,由折叠可知,EC=x,BE=8﹣x,
在Rt△ABE中,AB +BE=AE,即4 +(8﹣x)=x,解得:x=5,
由折叠可知∠AEF=∠CEF,
∵AD∥BC,∴∠CEF=∠AFE,∴∠AEF=∠AFE,即AE=AF=5,
∴S△AEF=1/2×AF×AB=1/2×5×4=10.
故答案为:10.
方法策略模式:图形折叠后,相当于出现了角平分线,有角平分线,有平行,就会产生等腰三角形,我们去找那个等腰三角形一般就会使得问题得到解决。
