直线和平面平行与平面与平面平行证明题专题训练
高中数学必杀1-4线面平行与面面平行的判定及性质
专题4 线面平行与面面平行的判定及性质一、直线与平面平行下列条件中,能判断两个平面平行的是()A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面【解析】由面面平行的定义可知选D.【例2】若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直【解析】A错误,a与α内的直线平行或异面.【例3】已知不重合的直线a ,b 和平面α,①若a ∥α,b ⊂α,则a ∥b ;②若a ∥α,b ∥α,则a ∥b ;③若a ∥b ,b ⊂α,则a ∥α;④若a ∥b ,a ∥α,则b ∥α或b ⊂α,上面命题中正确的是________(填序号).【解析】 ①中a 与b 可能异面;②中a 与b 可能相交、平行或异面;③中a 可能在平面α内,④正确.【例4】已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,α⊄n ,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且α⊄n ,β⊄n ,则n ∥α且n ∥β其中正确命题的个数是( )A .1B .2C .3D .4【解析】对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,故选B.【例5】已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题: ①n m n m //⇒⎩⎨⎧⊥⊥αα;①αα//n n m m ⇒⎩⎨⎧⊥⊥;①n m n m ⊥⇒⎩⎨⎧⊥αα//其中真命题的个数为( ) A .0 B .1 C .2 D .3【解析】若⎩⎨⎧⊥⊥ααn m ,则m ①n ,即命题①正确;若⎩⎨⎧⊥⊥n m m α,则n ①α或n ①α,即命题①不正确;若⎩⎨⎧⊥αα//n m ,则m ①n ,即命题①正确;综上可得,真命题共有2个.故选C .【例6】已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是( ) A .m ∥β且l 1∥α B .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2【解析】由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.【例7】在下列条件中,可判断平面α与β平行的是( ) A .α、β都平行于直线l B .α内存在不共线的三点到β的距离相等C .l 、m 是α内两条直线,且l ①β,m ①βD .l 、m 是两条异面直线,且l ①α,m ①α,l ①β,m ①β【解析】排除法,A 中α、β可以是相交平面;B 中三点可面平面两侧;C 中两直线可以不相交.故选D ,也可直接证明.【例8】经过平面外的两点作该平面的平行平面可以作( )A .0个B .1个C .0个或1个D .1个或2个【解析】这两点可以是在平面同侧或两侧.故选C .达标训练11.(2019•延安一模)已知m ,n 表示两条不同的直线,α表示平面.下列说法正确的是( )A .若//m α,//n α,则//m nB .若m α⊥,n α⊥,则//m nC .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥ 2.(2019•湖北期中)平面α与平面β平行的条件可以是( )A .α内有无数多条直线都与β平行B .直线a α⊂,b β⊂,且//a β,//b αC .直线//a α,//a β,且直线a 不在α内,也不在β内D .一个平面α内两条不平行的直线都平行于另一个平面β3.(2019•深圳二模)己知正方体1111ABCD A B C D -,P 为棱1CC 的动点,Q 为棱1AA 的中点,设直线m 为平面BDP 与平面11B D P 的交线,以下关系中正确的是( ) A .1//m D Q B .//m 平面11B D QC .1m B Q ⊥D .m ⊥平面11ABB A4.(2019•聊城二模)在长方体1111ABCD A B C D -中,F ,F ,G ,H 分别为棱11A B ,1BB ,1CC ,11C D 的中点,则下列结论中正确的是( )A .1//AD 平面EFGHB .1//BD GHC .//BD EFD .平面//EFGH 平面11A BCD5.(2019•汕头月考)如图,在正方体1111ABCD A B C D -中,M ,N 分别是1BC ,1CD 的中点,则下列判断错误的是( ) A .1MN CC ⊥B .MN ⊥平面11ACC AC .//MN 平面ABCDD .11//MN A B6.(2019•大连一模)已知m ,n 为两条不重合直线,α,β为两个不重合平面,下列条件中,可以作为//αβ的充分条件的是( ) A .//m n ,m α⊂,n β⊂ B .//m n ,m α⊥,n β⊥ C .m n ⊥,//m α,//n βD .m n ⊥,m α⊥,n β⊥7.(2019•汕头一模)在正方体1111ABCD A B C D -中,点O 是四边形ABCD 的中心,关于直线1A O ,下列说法正确的是( )A .11//AO D C B .1AO BC ⊥C .1//A O 平面11B CDD .1A O ⊥平面11AB D8.(2019•青云月考)如图,四棱锥P ABCD -中,M ,N 分别为AC ,PC 上的点,且//MN 平面PAD ,则( ) A .//MN PD B .//MN PAC .//MN ADD .以上均有可能9.(2019•上饶一模)设m ,n 表示不同的直线,α,β表示不同的平面,且m ,n α⊂.则“//αβ”是“//m β且//n β”的( ) A .充分但不必要条件 B .必要但不充分条件C .充要条件D .既不充分又不必要条件10.(2018•沧州一模)如图,在下列四个正方体中,P ,R ,Q ,M ,N ,G ,H 为所在棱的中点,则在这四个正方体中,阴影平面与PRQ 所在平面平行的是( )A .B .C .D .11.(2017•洛南期末)已知平面//α平面β,直线m α⊂,直线n β⊂,下列结论中不正确的是( ) A .//m βB .//n αC .//m nD .m 与n 不相交12.(2018•杭州期中)如图,四棱锥P ABCD -的底面ABCD 是平行四边形,M 、N 分别为线段PC 、PB 上一点,若:3:1PM MC =,且//AN 平面BDM ,则:PN NB =( )A .4:1B .3:1C .3:2D .2:113.(2018•厦门二模)如图,在正方体1111ABCD A B C D -中,M ,N ,P 分别是11C D ,BC ,11A D 的中点,则下列命题正确的是( )A .//MN APB .1//MN BDC .//MN 平面11BBD DD .//MN 平面BDP14.(2018•辛集期中)在四棱锥P ABCD -中,底面ABCD 为菱形,60BAD ∠=︒,Q 为AD 的中点,点M 在线段PC 上,PM tPC =,//PA 平面MQB ,则实数t 的值为( ) A .15B .14 C .13D .1215.(2018•四川模拟)如图是某几何体的平面展开图,其中四边形ABCD 为正方形,E ,F 分别为PA ,PD 的中点.在此几何体中,以下结论一定成立的是( ) A .直线//BE PFB .直线//EF 平面PBCC .平面BCE ⊥平面PAD D .直线PB 与DC 所成角为60︒16.(2017•万州期末)平面α与ABC ∆的两边AB ,AC 分别交于点D ,E ,且::AD DB AE EC =,如图,则BC 与α的位置关系是( )A .异面B .相交C .平行或相交D .平行17.(2018•桃城模拟)如图,各棱长均为1的正三棱柱111ABC A B C -,M ,N 分别为线段1A B ,1B C 上的动点,且//MN 平面11ACC A ,则这样的MN 有( )A .1条B .2条C .3条D .无数条18.(2018•雁江月考)已知P 为ABC ∆所在平面外一点,平面//α平面ABC ,且α交线段PA ,PB ,PC 于点A ',B ',C ',若:2:3PA AA ''=,则:A B C ABC S S '''=△△( )A .2:3B .2:5C .4:9D .4:2519.(2018•香坊四模)对于不重合的两个平面α和β,给定下列条件: ①存在直线l ,使得l α⊥,且l β⊥; ①存在平面γ,使得αγ⊥且βγ⊥; ①α内有不共线的三点到β的距离相等;①存在异面直线l ,m ,使得//l α,//l β,//m α,//m β. 其中,可以判定α与β平行的条件有( ) A .1个B .2个C .3个D .4个20.(2018•西城期末)在直三棱柱111ABC A B C -中,D 为1AA 中点,点P 在侧面11BCC B 上运动,当点P 满足条件 时,1//A P 平面BCD (答案不唯一,填一个满足题意的条件即可达标训练21.(2017•新课标①)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )A .B .C .D .2.(2011•浙江)若直线l 不平行于平面α,且l α⊂/,则( ) A .α内存在直线与l 异面 B .α内存在与l 平行的直线C .α内存在唯一的直线与l 平行D .α内的直线与l 都相交 3.(2010•浙江)设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是( ) A .若l m ⊥,m α⊂,则l α⊥ B .若l α⊥,//l m ,则m α⊥C .若//l α,m α⊂,则//l mD .若//l α,//m α,则//l m 4.(2010•江西)如图,M 是正方体1111ABCD A B C D -的棱1DD 的中点,给出下列命题 ①过M 点有且只有一条直线与直线AB 、11B C 都相交; ①过M 点有且只有一条直线与直线AB 、11B C 都垂直; ①过M 点有且只有一个平面与直线AB 、11B C 都相交; ①过M 点有且只有一个平面与直线AB 、11B C 都平行. 其中真命题是( ) A .①①①B .①①①C .①①①D .①①①5.(2008•湖南)已知直线m 、n 和平面α、β满足m n ⊥,m α⊥,αβ⊥,则( ) A .n β⊥ B .//n β,或n β⊂ C .n α⊥D .//n α,或n α⊂6.(2007•北京)平面//α平面β的一个充分条件是( ) A .存在一条直线a ,//a α,//a β B .存在一条直线a ,a α⊂,//a βC .存在两条平行直线a ,b ,a α⊂,b β⊂,//a β,//b αD .存在两条异面直线a ,b ,a α⊂,b β⊂,//a β,//b α7.(2011•福建)如图,正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在CD 上,若//EF 平面1AB C ,则线段EF 的长度等于 .。
直线与平面平行经典题目

9.2 直线与平面平行●知识梳理1.直线与平面的位置关系有且只有三种,即直线与平面平行、直线与平面相交、直线在平面内.2.直线与平面平行的判定:如果平面外的一条直线与平面内的一条直线平行,那么这条直线与这个平面平行.3.直线与平面平行的性质:如果一条直线与一个平面平行,经过这条直线的平面与已知平面相交,那么这条直线与交线平行.●点击双基1.设有平面α、β和直线m 、n ,则m ∥α的一个充分条件是 A.α⊥β且m ⊥β B.α∩β=n 且m ∥n C.m ∥n 且n ∥α D.α∥β且m β 答案:D2.设m 、n 是两条不同的直线,α、β、γ是三个不同的平面.给出下列四个命题,其中正确命题的序号是①若m ⊥α,n ∥α,则m ⊥n ②若α∥β,β∥γ,m ⊥α,则m ⊥γ ③若m ∥α,n ∥α,则m ∥n ④若α⊥γ,β⊥γ,则α∥β A.①② B.②③ C.③④ D.①④解析:①②显然正确.③中m 与n 可能相交或异面.④考虑长方体的顶点,α与β可以相交. 答案:A3.一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是 A.异面 B.相交 C.平行 D.不能确定 解析:设α∩β=l ,a ∥α,a ∥β, 过直线a 作与α、β都相交的平面γ, 记α∩γ=b ,β∩γ=c , 则a ∥b 且a ∥c , ∴b ∥c .又b ⊂α,α∩β=l ,∴b ∥l .∴a ∥l .答案:C4.(06重庆卷)对于任意的直线l 与平同a ,在平面a 内必有直线m ,使m 与l A.平行 B.相交 C.垂直 D.互为异面直线解析:对于任意的直线l 与平面α,若l 在平面α内,则存在直线m ⊥l ;若l 不在平面α内,且l ⊥α,则平面α内任意一条直线都垂直于l ,若l 不在平面α内,且l 于α不垂直,则它的射影在平面α内为一条直线,在平面α内必有直线m 垂直于它的射影,则m 与l 垂直, 综上所述,选C.5.已知平面βα,和直线,给出条件:①α//m ;②α⊥m ;③α⊂m ;④βα⊥;⑤βα//. (i )当满足条件 ③⑤ 时,有β//m ;(ii )当满足条件 ②⑤ 时,有β⊥m .(填所选条件的序号)●典例剖析【例1】 如下图,两个全等的正方形ABCD 和ABEF 所在平面相交于AB ,M ∈AC ,N ∈FB 且AM =FN ,求证:MN ∥平面BCE .QB CDMP FE N证法一:过M 作MP ⊥BC ,NQ ⊥BE ,P 、Q 为垂足(如上图),连结PQ . ∵MP ∥AB ,NQ ∥AB ,∴MP ∥NQ .又NQ =22 BN =22CM =MP ,∴MPQN 是平行四边形. ∴MN ∥PQ ,PQ ⊂平面BCE .而MN ⊄平面BCE ,∴MN ∥平面BCE . 证法二:过M 作MG ∥BC ,交AB 于点G (如下图),连结NG .GBCDM FE N∵MG ∥BC ,BC ⊂平面BCE ,MG ⊄平面BCE ,∴MG ∥平面BCE .又GA BG =MA CM =NFBN,∴GN ∥AF ∥BE ,同样可证明GN ∥平面BCE . 又面MG ∩NG =G ,∴平面MNG ∥平面BCE .又MN ⊂平面MNG .∴MN ∥平面BCE . 特别提示证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,通过“面面”平行,证得“线面”平行.【例2】 已知正四棱锥P —ABCD 的底面边长及侧棱长均为13,M 、N 分别是PA 、BD 上的点,且PM ∶MA =BN ∶ND =5∶8.BD E OMNP(1)求证:直线MN ∥平面PBC ;(2)求直线MN 与平面ABCD 所成的角. (1)证明:∵P —ABCD 是正四棱锥,∴ABCD 是正方形.连结AN 并延长交BC 于点E ,连结PE . ∵AD ∥BC ,∴EN ∶AN =BN ∶ND . 又∵BN ∶ND =PM ∶MA ,∴EN ∶AN =PM ∶MA . ∴MN ∥PE .又∵PE 在平面PBC 内,∴MN ∥平面PBC .(2)解:由(1)知MN ∥PE ,∴MN 与平面ABCD 所成的角就是PE 与平面ABCD 所成的角. 设点P 在底面ABCD 上的射影为O ,连结OE ,则∠PEO 为PE 与平面ABCD 所成的角. 由正棱锥的性质知PO =22OB PB -=2213. 由(1)知,BE ∶AD =BN ∶ND =5∶8, ∴BE =865. 在△PEB 中,∠PBE =60°,PB =13,BE =865, 根据余弦定理,得PE =891. 在Rt △POE 中,PO =2213,PE =891,∴sin ∠PEO =PEPO =724.故MN 与平面ABCD 所成的角为arcsin 724.【例3】如图, 在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AA 1=4,点D 是AB 的中点,(I )求证:AC ⊥BC 1; (II )求证:AC 1//平面CDB 1; (III )求异面直线 AC 1与 B 1C 所成角的余弦值.解析:(I )直三棱柱ABC -A 1B 1C 1,底面三边长AC=3,BC=4,AB=5,∴ AC ⊥BC ,且BC 1在平面ABC 内的射影为BC ,∴ AC ⊥BC 1;(II )设CB 1与C 1B 的交点为E ,连结DE ,∵ D 是AB 的中点, E 是BC 1的中点,∴ DE//AC 1, ∵ DE ⊂平面CDB 1,AC 1⊄平面CDB 1, ∴ AC 1//平面CDB 1;(III )∵ DE//AC 1,∴ ∠CED 为AC 1与B 1C 所成的角,在△CED 中, ED=21AC 1=25,CD=21AB=25,CE=21CB 1=22, ∴ 8cos 5522CED∠==⋅, ∴ 异面直线AC 1与 B 1C 所成角的余弦值5. ●闯关训练夯实基础1. (07福建理)已知m 、n 为两条不同的直线,为两个不同的平面,则下列命题中正确的是A. m n m ,,α⊂α⊂∥β,n ∥β⇒ α∥βB. α∥β,α⊂α⊂n m ,,⇒m ∥nC. m ⊥α,m ⊥n ⇒n ∥α D . n ∥m,n ⊥α⇒m ⊥α解析:A 中m 、n 少相交条件,不正确;B 中分别在两个平行平面的两条直线不一定平行,不正确;C 中n 可以在α内,不正确,选D2.(06福建卷)对于平面α和共面的直线m 、n ,下列命题中真命题是 A.若m ⊥α,m ⊥n ,则n ∥α B.若m ∥α,n ∥α,则m ∥nC.若m ⊂α,n ∥α,则m ∥nD.若m 、n 与α所成的角相等,则n ∥m 解:对于平面α和共面的直线m 、,n 真命题是“若,m n αα⊂∥,则m ∥n ”, 选C. 3.(06湖南卷)过平行六面体ABCD-A 1B 1C 1D 1任意两条棱的 中点 作直线,其中与平面DBB 1D 1平行的直线共有 ( ) A. 4条 B.6条 C.8条 D.12条解:如图,过平行六面体1111D C B A ABCD -任意两条棱的中点作直线, 其中与平面11D DBB 平行的直线共有12条,选D.4.(06重庆卷)若P 是平面α外一点,则下列命题正确的是A.过P 只能作一条直线与平面α相交B.过P 可作无数条直线与平面α垂直C.过P 只能作一条直线与平面α平行D.过P 可作无数条直线与平面α平行 解析:过平面外一点有且只有一个平面与已知平面平行, 且这个平面内的任一条直线都与已知平面平行。
直线与平面平行的判定及其性质 测试题(答案)

直线与平面平行的判定和性质年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共26题,题分合计130分)1.直线a //平面M ,直线b ⊂/M ,那么a //b 是b //M 的 条件. A.充分而不必要 B.必要而不充分 C.充要 D.不充分也不必要2.已知l 、m 、n 为两两垂直且异面的三条直线,过l 作平面α与m 垂直,则直线n 与平面α的关系是A.n //αB.n //α或n ⊂αC.n ⊂α或n 不平行于αD.n ⊂α3.能保证直线a 与平面α平行的条件是A.b a b a //,,αα⊂⊄B.b a b //,α⊂C.c a b a c b //////,,,αα⊂D.b D b C a B a A b ∈∈∈∈⊂,,,,α且BD AC =4.如果直线a 平行于平面α,则A.平面α内有且只有一直线与a 平行B.平面α内无数条直线与a 平行C.平面α内不存在与a 平行的直线D.平面α内的任意直线与直线a 都平行5.如果两直线a ∥b ,且a ∥平面α,则b 与α的位置关系A.相交B.α//bC.α⊂bD.α//b 或α⊂b6.下列命题正确的个数是(1)若直线l 上有无数个点不在平面α内,则l ∥α(2)若直线l 与平面α平行,则l 与平面α内的任意一直线平行(3)两条平行线中的一条直线与一个平面平行,那么另一条也与这个平面平行 (4)若一直线a 和平面α内一直线b 平行,则a ∥α A.0个 B.1个 C.2个 D.3个7.若直线a ⊥b ,且a ∥平面α,则直线b 与平面α的位置关系是A.b ⊂αB.b ∥αC.b ⊂α或b ∥αD.b 与α相交或b ∥α或b ⊂α都有可能8.已知α、β是两个不同的平面,在下列条件中,可判断平面α与平面β平行的是A.α、β都垂直于平面γB.a 、b 是α内两条直线,且a ∥β,b ∥βC.α内不共线的三个点到β的距离相等D.a 、b 为异面直线,且a ∥α,b ∥α,a ∥β,b ∥β9.下列命题正确的个数是①若直线l 上有无数个点不在平面α内,则l ∥α②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行 ④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点 A.0个 B.1个 C.2个 D.3个10.b 是平面α外的一条直线,下列条件中可得出b ∥α是A.b 与α内的一条直线不相交B.b 与α内的两条直线不相交C.b 与α内的无数条直线不相交D.b 与α内的所有直线不相交11.已知直线l 1、l 2,平面α,l 1∥l 2,l 1∥α,则l 2与α的位置关系是A.l 2∥αB.l 2⊂αC.l 2∥α或l 2⊂αD.l 2与α相交12.已知两条相交直线a 、b ,a ∥平面α,则b 与α的位置关系A.b ∥αB.b 与α相交C.b ⊂αD.b ∥α或b 与α相交13.下列命题中正确的是①过一点,一定存在和两条异面直线都平行的平面②垂直于同一条直线的一条直线和一个平面平行③若两条直线没有公共点,则过其中一条直线一定有一个平面与另一条直线平行 A.① B.③ C.①③ D.①②③14.a、b为平面M外的两条直线,在a∥M的前提下,a∥b是b∥M的A.充要条件B.充分条件C.必要条件D.以上情况都不15.α和β是两个不重合的平面,在下列条件中可判定平面α与β平行的是A.α、β都垂直于平面γB.α内不共线的三点到β的距离相等C.l,m是α平面内的直线,且l∥β,m∥βD.l、m是两条异面直线且l∥α,m∥α,m∥β,l∥β16.在空间中,下述命题正确的A.若直线a∥平面M,直线b⊥直线a,则直线b⊥平面MB.若平面M∥平面N,则平面M内任意一条直线a∥平面NC.若平面M与平面N的交线为a,平面M内的直线b⊥直线a,则直线b⊥平面ND.若平面N内的两条直线都平行于平面M,则平面N∥平面M17.设直线a在平面M内,则直线M平行于平面N是直线a平行于平面N的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件18.设a、b是平面α外的任意两条直线,则"a、b长相等"是"a、b在平面α内的射影长相等"的A.既不充分也不必要条件B.充分必要条件C.必要但不充分条件D.充分但不必要条件19.如果平面α和直线l满足l和α内两条平行直线垂直,则A.l αB.l∥αC.l与α相交D.以上都不对20.如果一条直线和一个平面平行,为了使夹在它们之间的两条线段的长相等,以下结论正确的是A.其充分条件是这两条线段平行B.其必要条件是这两条线段平行C.其充要条件是这两条线段平行D.其必要条件是这两条线段平行21.直线a∥平面α,平面α内有n条直线交于一点,那么这几条直线中与直线a平行的A.至少有一条B.至多有一条C.有且只有一条D.不可能有22.若直线m平面α,则“平面α∥平面β”是“直线m∥平面β”的A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件23.平行于同一个平面的两条直线的位置关系是A.平行B.相交C.异面D.平行或相交或异面24.下列四个命题中假命题的个数是①两条直线都和同一个平面平行,则这两条直线平行②两条直线没有公共点,则这两条直线平行③两条直线都和第三条直线垂直,则这两条直线平行④一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行A.4B.3C.2D.125.如果一条直线和一个平面平行,为了使夹在它们之间的两条线段的长相等,以下结论正确的是A.其充分条件是这两条线段平行B.其必要条件是这两条线段平行C.其充要条件是这两条线段平行D.其必要条件是这两条线段平行26.直线与平面平行的充要条件是这条直线与平面内的A.一条直线不相交B.两条直线不相交C.任意一条直线都不相交D.无数条直线不相交二、填空题(共6题,题分合计25分)1.如图,空间四边形ABCD 中,E 、H 分别是AB 、AD 的中点,F 、G 分别是CB 、CD 上的点.且32==CD CG CB CF ,若BD =6 cm ,梯形EFGH 的面积为28 cm 2,则平行线EH 与FG 间的距离为_______.2.一条直线与平面α相交于点A ,在平面α内不过A 点的直线与这条直线所成角的最大值为_________.3.正方体ABCD -A 1B 1C 1D 1中,E 为DD 1的中点,则BD 1与过点A 、E 、C 的平面的位置关系是__________.4.几何体ABCD -A 1B 1C 1D 1是棱长为A 的正方体,M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =31a ,过P 、M 、N 的平面交上底面于PQ ,Q 在CD 上,则PQ =___________.5.如果两条直线a 与b 互相平行,且a ∥平面α,那么b 与α的位置关系是 .6.直线a ∥平面α,直线b 、c 都在α 内且a ∥b ∥c ,若a 到b , c 的距离分别为d 1、d 2,且d 1>d 2,则直线a 到α 的距离d 的取值范围是___________.三、解答题(共12题,题分合计112分)1.求证:若直线l与平面α有一个公共点,且l平行于α内的一条直线,则l α..2.如图,P是△ABC所在平面外一点,M∈PB,试过AM作一平面平行于BC,并说明画法的理论依据Array3.设AB、CD为夹在两个平行平面α、β之间线段,且直线AB、CD为异面直线,М、P分别为AB、CD的中点,求证:MP ∥α.4.ABCD-A1B1C1D1是棱长为a的正方体,(1)画出过A、C、B1的平面与下底面的交线l;(2)求l与直线AC的距离.5.正方体ABCD-A1B1C1D1中,侧面对角线AB1、BC1分别有E、F,且B1E=C1F,求证:EF∥平面ABCD.6.平面外的两条平行直线中的一条平行于这个平面,那么另一条直线也平行于这个平面.7.设a、b是异面直线,自AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点.8.求证:如果一条直线和两个相交的平面都平行,那么这条直线和它们的交线平行.9.α∩β=c,α∩γ=b,β∩γ=a,若直线a∥直线b,你能得到什么结论?10.如图,正方体ABCD-A1B1C1D1中,E在AB1上,F在BD上,且B1E=BF.求证:EF∥平面BB1C1C.11.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.求证:MN∥平面AA1B1B.12.如图,平面EFGH分别平行于CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.(1)求证:EFGH是矩形.(2)点E在什么位置时,EFGH的面积最大.直线与平面平行的判定和性质答案一、选择题(共26题,合计130分)1.答案:A2.答案:A3.答案:A4.答案:B5.答案:D6.答案:A7.答案:D8.答案:B9.答案:B10.答案:D11.答案:C12.答案:D13.答案:B14.答案:B15.答案:D16.答案:B17.答案:A18.答案:A19.答案:D20.答案:A21.答案:B22.答案:A23.答案:D24.答案:A25.答案:A26.答案:C二、填空题(共6题,合计25分)1.答案:8 cm2.答案:90°3.答案:BD1∥平面AEC4.答案:a2 325.答案:b∥α或b α6.答案:) ,0(2 d三、解答题(共12题,合计112分)1.答案:见注释2.答案:见注释3.答案:见注释4.答案:. 26 a5.答案:见注释6.答案:见注释7.答案:见注释8.答案:见注释9.答案:见注释10.答案:见注释11.答案:见注释12.答案:(1)见注释(2)E为BD的中点时。
高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:a αb β => a∥αa∥b●知能训练一.选择题1.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n2.若直线l不平行于平面α,且l⊄α,则()A.α内存在直线与l异面B.α内存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交3.如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交;②过M点有且只有一条直线与直线AB、B1C1都垂直;③过M点有且只有一个平面与直线AB、B1C1都相交;④过M点有且只有一个平面与直线AB、B1C1都平行.其中真命题是()A.②③④B.①③④C.①②④D.①②③4.正方体ABCD-A1B1C1D1中M,N,Q分别是棱D1C1,A1D1,BC的中点.P在对角线BD1上,且BP=BD1,给出下面四个命题:(1)MN∥面APC;(2)C1Q∥面APC;(3)A,P,M三点共线;(4)面MNQ∥面APC.正确的序号为()A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4)5.在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中,任取两点连成直线,所连的直线中与A1BC1平行的直线共有()A.12条B.18条C.21条D.24条6.直线a∥平面α,P∈α,那么过P且平行于a的直线()A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内7.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交8.如图在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是()A.DD1B.A1D1C.C1D1D.A1D9.如图,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1上的一点,若BC1∥平面AB1D1,则等于()A.1/2B.1 C.2 D.310.下面四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是()A.①②B.①④C.②③D.③④11.如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=,则下列结论中错误的是()A.AC⊥BEB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值二.填空题12.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H,M分别是棱AD,DD1,D1A1,A1A,AB的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件时,就有MN⊥A1C1;当N只需满足条件时,就有MN∥平面B1D1C.13.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于.三.解答题14.如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB 1∥平面BC1D;(2)若BC=3,求三棱锥D-BC1C的体积.2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
高中数学练习题 线面、面面平行的判定与性质

线面、面面平行的判定与性质基础巩固强化1.已知l是直线,α、β是两个不同平面,下列命题中的真命题是()A.若l∥α,l∥β,则α∥βB.若α⊥β,l∥α,则l⊥βC.若l⊥α,l∥β,则α⊥βD.若l∥α,α∥β,则l∥β2.已知m、n是两条直线,α、β是两个平面,给出下列命题:①若n⊥α,n⊥β,则α∥β;②若平面α上有不共线的三点到平面β的距离相等,则α∥β;③若n、m为异面直线,n⊂α,n∥β,m⊂β,m∥α,则α∥β.其中正确命题的个数是()A.3个B.2个C.1个D.0个一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:①AB⊥EF②AB与CM成60°③EF与MN是异面直线④MN∥CD其中正确的是()A.①②B.③④C.②③D.①③3.已知平面α∩β=l,m是α内不同于l的直线,那么下列命题中错误..的是()A.若m∥β,则m∥l B.若m∥l,则m∥βC.若m⊥β,则m⊥l D.若m⊥l,则m⊥β4.设a、b是两条不同的直线,α、β是两个不同的平面,则下列命题错误的是()A.若a⊥α,b∥α,则a⊥bB.若a⊥α,b∥a,b⊂β,则α⊥βC.若a⊥α,b⊥β,α∥β,则a∥bD.若a∥α,a∥β,则α∥β对于平面α和共面的直线m、n,下列命题是真命题的是()A.若m,n与α所成的角相等,则m∥n B.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n5.设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中真命题是() A.若a∥α,b∥α,则a∥b B.若a∥α,b∥β,a∥b,则α∥βC.若a⊥α,b⊥β,a∥b,则α∥βD.若a、b在平面α内的射影互相垂直,则a⊥b 6.设两个平面α、β,直线l,下列三个条件:①l⊥α;②l∥β;③α⊥β.若以其中两个作为前提,另一个作为结论,则可构成三个命题,这三个命题中正确命题的个数为()A .3B .2C .1D .07.正方体ABCD -A 1B 1C 1D 1的棱长为1cm ,过AC 作平行于对角线BD 1的截面,则截面面积为________.8.在空间中,有如下命题:①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线; ②若平面α∥平面β,则平面α内任意一条直线m ∥平面β;③若平面α与平面β的交线为m ,平面α内的直线n ⊥直线m ,则直线n ⊥平面β; ④若平面α内的三点A 、B 、C 到平面β的距离相等,则α∥β. 其中正确命题的序号为________.9.已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题: ①若m ∥α,n ∥α,m ∥β,n ∥β,则α∥β; ②若α⊥γ,β⊥γ,α∩β=m ,n ⊂γ,则m ⊥n ; ③若m ⊥α,α⊥β,m ∥n ,则n ∥β; ④若n ∥α,n ∥β,α∩β=m ,那么m ∥n . 其中正确命题的序号是________.10.如图,直三棱柱ABC -A ′B ′C ′,∠BAC =90°,AB =AC =2,AA ′=1,点M 、N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面A ′ACC ′;(2)求三棱锥A ′-MNC 的体积(锥体体积公式V =13Sh ,其中S 为底面面积,h 为高).如图,在侧棱垂直底面的四棱柱ABCD -A 1B 1C 1D 1中,AD ∥BC ,AD ⊥AB ,AB =2,AD =2,BC =4,AA 1=2,E 是DD 1的中点,F是平面B1C1E与直线AA1的交点.(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF;(2)求BC1与平面B1C1EF所成角的正弦值.能力拓展提升11.如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()A.不存在B.有1条C.有2条D.有无数条12.如图,若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确...的是()A.EH∥FG B.四边形EFGH是矩形C.Ω是棱柱D.Ω是棱台下列命题中,是假命题的是()A.三角形的两条边平行于一个平面,则第三边也平行于这个平面B.平面α∥平面β,a⊂α,过β内的一点B有唯一的一条直线b,使b∥aC.α∥β,γ∥δ,α、β与γ、δ的交线分别为a、b和c、d,则a∥b∥c∥dD.一条直线与两个平面成等角是这两个平面平行的充要条件13.(2012·南昌二模)若P是两条异面直线l、m外的任意一点,则下列命题中假命题的序号是________.①过点P有且仅有一条直线与l、m都平行;②过点P有且仅有一条直线与l、m都垂直;③过点P有且仅有一条直线与l、m都相交;④过点P有且仅有一条直线与l、m都异面.14.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是______(写出所有符合要求的图形序号).15.(2011·广东揭阳一模)如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G、H分别是DF、BE的中点.(1)求证:GH∥平面CDE;(2)若CD=2,DB=42,求四棱锥F-ABCD的体积.[解析](1)证法1:∵EF∥AD,AD∥BC,∴EF∥BC.又EF=AD=BC,∴四边形EFBC是平行四边形,∴H为FC的中点.又∵G是FD的中点,∴GH∥CD.∵GH⊄平面CDE,CD⊂平面CDE,∴GH∥平面CDE.证法2:连接EA,∵ADEF是正方形,∴G是AE的中点.∴在△EAB中,GH∥AB.又∵AB∥CD,∴GH∥CD.∵HG⊄平面CDE,CD⊂平面CDE,∴GH∥平面CDE.(2)∵平面ADEF⊥平面ABCD,交线为AD,且F A⊥AD,∴F A⊥平面ABCD.∵AD=BC=6,∴F A=AD=6.又∵CD=2,DB=42,CD2+DB2=BC2,∴BD⊥CD. ∵S▱ABCD=CD·BD=82,∴V F-ABCD=13S▱ABCD·F A=13×82×6=16 2.(理)如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;(3)求四面体B-DEF的体积.[解析](1)证明:设AC与BD交于点G,联结EG、GH.则G为AC中点,∵H是BC中点,∴GH綊12AB,又∵EF綊12AB,∴四边形EFHG为平行四边形.∴FH∥EG.又EG⊂平面EDB,而FH⊄平面EDB,∴FH∥平面EDB.(2)证明:∵EF∥AB,EF⊥FB.∴AB⊥FB.又四边形ABCD为正方形,∴AB⊥BC,又FB∩BC=B,∴AB⊥平面BFC.∵FH⊂平面BFC,∴AB⊥FH.又∵FB=FC,H是BC中点,∴FH⊥BC.又AB∩BC=B,∴FH⊥平面ABCD,∴FH⊥AC. 又EG∥FH,∴EG⊥AC,又AC⊥BD,BD∩EG=G,∴AC⊥平面EDB.(3)∵EF⊥BF,BF⊥FC且EF∩FC=F,∴BF⊥平面CDEF,∴BF 为四面体B —DEF 的高. 又∵BC =AB =2,∴BF =FC = 2.四边形CDEF 为直角梯形,且EF =1,CD =2. ∴S △DEF =12(1+2)×2-12×2×2=22∴V B —DEF =13×22×2=13. 16.(2012·辽宁大连市、沈阳市联考)如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,四边形ABCD 为长方形,AD =2AB ,点E 、F 分别是线段PD 、PC 的中点.(1)证明:EF ∥平面P AB ;(2)在线段AD 上是否存在一点O ,使得BO ⊥平面P AC ,若存在,请指出点O 的位置,并证明BO ⊥平面P AC ;若不存在,请说明理由.[解析] (1)证明:∵EF ∥CD ,CD ∥AB ,∴EF ∥AB , 又∵EF ⊄平面P AB ,AB ⊂平面P AB ,(2)在线段AD上存在一点O,使得BO⊥平面P AC,此时点O为线段AD的四等分点,且AO=14AD,∵P A⊥底面ABCD,∴P A⊥BO,又∵长方形ABCD中,AD=2AB,∴△ABO△DAC,∴∠ABO+∠BAC=∠DAC+∠BAC=90°,∴AC⊥BO,又∵P A∩AC=A,∴BO⊥平面P AC.1.(2012·四川文,6)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行[答案] C[解析]本题考查了线面角,面面垂直,线面平行,面面平行等位置关系的判定与性质,对于A选项,两条直线也可相交,B选项若三点在同一条直线上,平面可相交.D选项这两个平面可相交(可联系墙角),而C项可利用线面平行的性质定理,再运用线面平行的判定与性质可得.本题需要我们熟练掌握各种位置关系的判定与性质.2.(2012·石家庄二模)三棱锥的三组相对的棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等,且长分别为2、m 、n ,其中m 2+n 2=6,则该三棱锥体积的最大值为( )A.12B.8327 C.33 D.23[答案] D[解析] 令m =n ,由m 2+n 2=6得m =n =3,取AB 的中点E ,则BE =22,PB =3,∴PE =102,CE =102,∴EF =2,∴V P -ABC =13S △PEC ·AB =13×(12×2×2)×2=23,∵23>12,∴23>33,23>8327,故选D.3.如图,正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,AB =1,M ,N 分别在AD 1、BC 上移动,且始终保持MN ∥平面DCC 1D 1,设BN =x ,MN =y ,则函数y =f (x )的图象大致是( )[答案] C[解析] 过M 作ME ⊥AD 于E ,连接EN ,则平面MEN ∥平面DCC 1D 1,所以BN =AE =x (0≤x <1),ME =2x ,MN 2=ME 2+EN 2,则y 2=4x 2+1,y 2-4x 2=1(0≤x <1,y >0),图象应是焦点在y 轴上的双曲线的一部分.故选C.4.(2012·东营市期末)设m 、n 是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:①若m ⊥n ,m ⊥α,n ⊄α,则n ∥α;②若α⊥β,α∩β=m ,n ⊥m ,则n ⊥α或n ⊥β; ③若m ⊥β,α⊥β,则m ∥α; ④若m ⊥n ,m ⊥α,n ⊥β,则α⊥β. 其中真命题的序号是________. [答案] ①④⎭⎪⎬⎪⎫ ⎭⎪⎬⎪⎫[解析] m ⊥n m ⊥α⇒n ∥α或n ⊂α n ⊄α⇒n ∥α,故①真; 正方体ABCD -A 1B 1C 1D 1中,平面ABCD 与ADD 1A 1分别取作平面α,β,其交线AD 为m ,取直线AB 1为n ,则满足n ⊥m ,知②错;m ⊥β,α⊥β时,可能m ∥α,也可能m ⊂α,知③错;⎭⎬⎫ ⎭⎪⎬⎪⎫m ⊥n m ⊥α⇒n ∥α或n ⊂αn ⊥β⇒α⊥β,故④真.。
直线和平面平行与平面与平面平行证明题专题训练
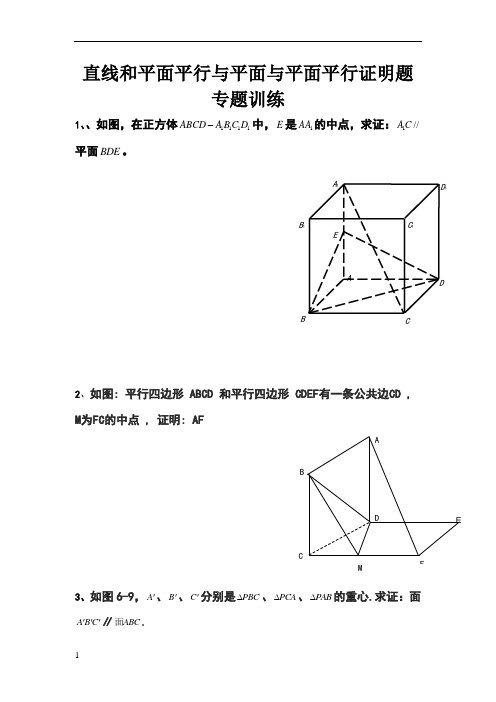
直线和平面平行与平面与平面平行证明题专题训练1、、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,求证:1//A C 平面BDE 。
2、如图: 平行四边形 ABCD 和平行四边形 CDEF 有一条公共边CD ,M 为FC 的中点 , 证明: AF3、如图6-9,A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证:面A B C '''∥ABC 面.A 1ED 1C 1B 1DCBAM ABCDEFv1.0 可编辑可修改4、 在长方体ABCD —A1B1C1D1中. (1)作出过直线AC 且与直线BD1平行的 截面,并说明理由.(2)设E ,F 分别是A1B 和B1C 的中点,求证直线EF5、、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EHABCC 1DA 1B 1D 1∥FG.求证:EH∥BD. (12分)6、P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证://PC平面BDQ.(自己作图)HG FEDBACv1.0 可编辑可修改7、如图,α//a ,A 是α的另一侧的点,a D C B ∈,,,线段AB ,AC ,AD 交α于E ,F ,G ,若4=BD ,4=CF ,5=AF ,则EG =___________.8、求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.。
平行的判定和性质专题及答案

平行的判定和性质专题平行的判断方法及性质汇总:一、判定两线平行的方法1、平行于同一直线的两条直线互相平行2、垂直于同一平面的两条直线互相平行3、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行4、如果两个平行平面同时和第三个平面相交,那么它们的交线平行5、在同一平面内的两条直线,可依据平面几何的定理证明二、判定线面平行的方法1、据定义:如果一条直线和一个平面没有公共点2、如果平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行3、两面平行,则其中一个平面内的直线必平行于另一个平面4、平面外的两条平行直线中的一条平行于平面,则另一条也平行于该平面5、平面外的一条直线和两个平行平面中的一个平面平行,则也平行于另一个平面三、判定面面平行的方法1、定义:没有公共点2、如果一个平面内有两条相交直线都平行于另一个平面,则两面平行3 垂直于同一直线的两个平面平行4、平行于同一平面的两个平面平行四、面面平行的性质1、两平行平面没有公共点2、两平面平行,则一个平面上的任一直线平行于另一平面3、两平行平面被第三个平面所截,则两交线平行4、垂直于两平行平面中一个平面的直线,必垂直于另一个平面专题训练一.选择题:1.两直线a, b平行于平面α,那么a, b的位置关系是 D(A)平行(B)相交(C)异面(D)平行、相交或异面2.两条直线a//b,b在平面α内,则a与α的位置关系是C(A)a//α(B)a与α相交(C)a//α或a在α内(D)a在α内3.直线l与平面α平行,在平面α内,与l平行的直线有 C(A)1条(B)2条(C)无数条(D)n条(n是一正整数)4.若一直线和一平面平行,夹在直线和平面间的两条线段相等,那么这两条线段所在的直线的位置关系是 D(A)平行(B)相交(C)异面(D)平行、相交或异面5.若a, b是异面直线,a//平面α,那么b与α的位置关系是 D(A)b//α(B)b与α相交(C)b在α内(D)不确定6.若直线a//平面α,且点A∈α,则过点A且a与平行的直线 B(A)只有一条,但不一定在α内(B)只有一条,且在α内(C)有无数条,但都不在α内(D)有无数条,且都在α内7.能够保证直线a∥平面β的条件是…………………………………(C )(A)β⊂b,a∥b (B)a∥b∥c,β⊂b,β⊂c(C)β⊄a,β⊂b,a∥b (D)β⊂b,BDACbDCaBA=∈∈,,,,8.如果l∥α,则l平行于α内的( B )(A)全部直线(B)过l的平面与α的交线(C)任一直线(D)唯一确定地直线9.如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是 C(A)平行(B)相交(C)平行或相交(D)无法确定10.在下列条件中,可判定平面α与平面β平行的是( D )(A)α、β都垂直于平面γ(B)α内不共线的三个点到β的距离相等(C)l、m是α内两条直线,且l∥β,m∥β(D)l、m是两异面直线且l∥α,m∥α,且l∥β,m∥β11.若两条直线m, n分别在平面α、β内,且α//β,则m, n的关系一定是(D )(A)平行(B)相交(C)异面(D)平行或异面12.已知直线l和平面α:(1)若直线l与平面α内无数条直线平行,则l//α;(2)若直线l与平面α内任意一直线都不平行,则直线l与平面α相交;(3)若l⊄α,则直线l与平面α内某些直线平行;(4)若直线l∩平面α=A,则存在α内的直线b,使b⊥l. 其中正确命题的个数是 C(A)0 (B)1 (C)2 (D)313.能保证直线a与平面α平行的条件是 A(A)a⊄α, b⊂α, a//b (B)b⊂α, a//b(C)b⊂α, c//α, a//b, a//c (D)b⊂α, A∈a, B∈a, C∈b, D∈b, 且AC=BD14.若直线m不平行于平面α,且m⊄α,则下列结论成立的是 B(A)α内的所有直线与m异面(B)α内不存在与m平行的直线(C)α内存在惟一的直线与m平行(D)α内的直线与m都相交15.如果两条直线a//b,且直线a//平面α,则b与α的位置关系是 D(A)相交(B)b//α (C)b⊂α (D)b//α或b⊂α16.设直线a与平面M平行,则必有 D(A)在平面M内不存在与a垂直的直线(B)在平面M内存在与a垂直的惟一直线(C)在平面M内有且只有一条直线与a平行(D)在平面M内有无数条直线与a平行17.已知∠ABC=90°,BC//平面M,AB与平面M斜交,那么∠ABC在平面M内的射影是B(A)锐角(B)直角(C)锐角或直角(D)锐角或直角或钝角18.在正方体ABCD-A1B1C1D1中,点E, F分别是AA1与AB的中点,O1为正方形A1B1C1D1的中心,则EF与BO1所成的角为 A(A)30°(B)45°(C)60°(D)90°19.已知A, B, C, D是空间不共面的四点,它们到平面α的距离之比依次为1 : 1 : 1 : 2,则满足条件的平面α的个数是 C(A)3 (B)4 (C)7 (D)820.下列命题中正确的是 C(A)经过两条异面直线中的一条且与另一条平行的平面至少有一个(B)若两条直线在同一平面内的射影平行,则这两条直线也平行(C)若a, b是异面直线,则一定存在平面α与a, b所成的角相等(D)与两条异面直线都平行的平面只有一个二.填空题:1.过直线外一点且与这条直线平行的平面有无数个。
直线和平面平行与平面与平面平行证明题专题训练
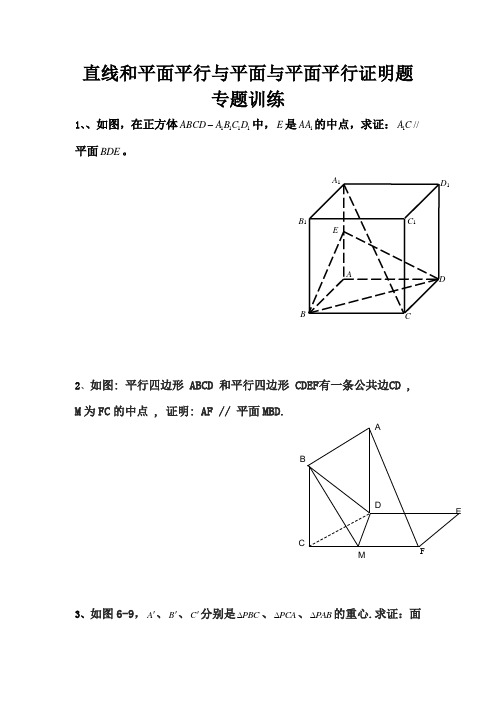
直线和平面平行与平面与平面平行证明题专题训练1、、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,求证:1//A C 平面BDE 。
2、如图: 平行四边形 ABCD 和平行四边形 CDEF 有一条公共边CD ,M 为FC 的中点 , 证明: AF // 平面MBD.3、如图6-9,A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证:面A 1ED 1C 1B 1DCBAMABCDEFA B C '''∥ABC 面.4、 在长方体ABCD —A1B1C1D1中.(1)作出过直线AC 且与直线BD1平行的 截面,并说明理由.(2)设E ,F 分别是A1B 和B1C 的中点, 求证直线EF//平面ABCD.5、、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG.ABCC 1DA 1B 1D 1求证:EH∥BD. (12分)6、P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证://PC平面BDQ.(自己作图)HG FEDBAC7、如图,α//a ,A 是α的另一侧的点,a D C B ∈,,,线段AB ,AC ,AD 交α于E ,F ,G ,若4=BD ,4=CF ,5=AF ,则EG =___________.8、求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
直线、平面平行的判定及性质及详细答案
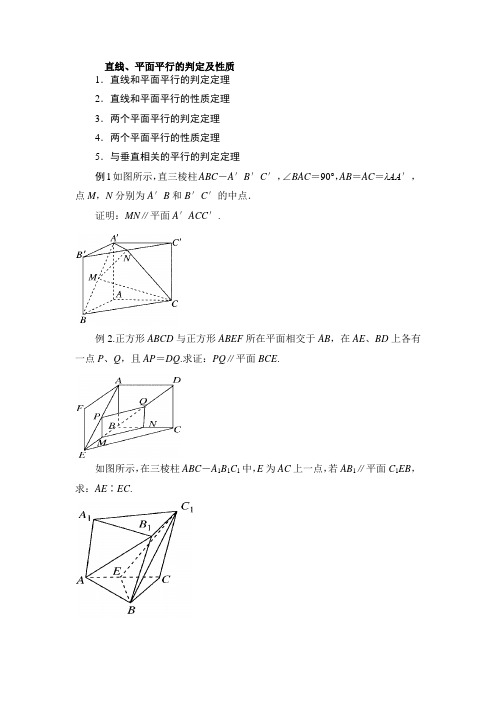
直线、平面平行的判定及性质1.直线和平面平行的判定定理2.直线和平面平行的性质定理3.两个平面平行的判定定理4.两个平面平行的性质定理5.与垂直相关的平行的判定定理例1如图所示,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点.证明:MN∥平面A′ACC′.例2.正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ∥平面BCE.如图所示,在三棱柱ABC-A1B1C1中,E为AC上一点,若AB1∥平面C1EB,求:AE∶EC.例3如图所示,正方体ABCD—A1B1C1D1中,M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点.求证:平面AMN∥平面EFDB.例4如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E、F分别在线段AB,CD上,且AE∶EB=CF∶FD.求证:EF∥β.练习题:1.(课本习题改编)给出下列四个命题:①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行;②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行;③若平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行;④若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行.其中正确命题的个数是________个.1.下列命题中正确的是________.①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.2.(2014·合肥一检)给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.1.已知两条不同直线l1和l2及平面α,则直线l1∥l2的一个充分条件是() A.l1∥α且l2∥αB.l1⊥α且l2⊥αC.l1∥α且l2⊄αD.l1∥α且l2⊂α答案 B解析l1⊥α且l2⊥α⇒l1∥l2.2.(2012·四川)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行答案 C解析若两条直线和同一平面所成的角相等,则这两条直线可平行、可异面、可相交,A项不正确;如果到一个平面距离相等的三个点在同一条直线上或在这个平面的两侧,那么经过这三个点的平面与这个平面相交,B项不正确.3.(2013·浙江)设m,n是两条不同的直线,α,β是两个不同的平面() A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β答案 C解析A项中,直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B项中,α与β也可能相交,此时直线m平行于α,β的交线;D 项中,m也可能平行于β.故选C项.4.设α,β表示平面,m,n表示直线,则m∥α的一个充分不必要条件是()A .α⊥β且m ⊥βB .α∩β=n 且m ∥nC .m ∥n 且n ∥αD .α∥β且m ⊂β答案 D解析 若两个平面平行,其中一个面内的任一直线均平行于另一个平面,故选D.5.若空间四边形ABCD 的两条对角线AC 、BD 的长分别是8、12,过AB 的中点E 且平行于BD 、AC 的截面四边形的周长为( )A .10B .20C .8D .4答案 B解析 设截面四边形为EFGH ,F 、G 、H 分别是BC 、CD 、DA 的中点,∴EF =GH =4,FG =HE =6.∴周长为2×(4+6)=20.6.在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是( )A .相交B .平行C .垂直D .不能确定答案 B解析 连接CD 1,在CD 1上取点P ,使D 1P =2a3,∴MP ∥BC ,PN ∥AD 1. ∴MP ∥面BB 1C 1C ,PN ∥面AA 1D 1D . ∴面MNP ∥面BB 1C 1C ,∴MN ∥面BB 1C 1C .7.如图所示,四个正方体图形中,A 、B 为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出AB ∥面MNP 的图形的序号是________(写出所有符合要求的图形序号).答案①③8. 棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,P A⊥底面ABCD,E为PC的中点,则BE与平面P AD的位置关系为________.答案平行解析取PD的中点F,连接EF.在△PCD中,EF綊12CD.又∵AB∥CD且CD=2AB,∴EF=12CD且CD=2AB.∴EF綊AB,∴四边形ABEF是平行四边形,∴EB∥AF.又∵EB⊄平面P AD,AF⊂平面P AD,∴BE∥平面P AD.9. 如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1、B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.答案22 3a解析 如图所示,连接AC ,易知MN ∥平面ABCD .∴MN ∥PQ .又∵MN ∥AC ,∴PQ ∥AC . 又∵AP =a 3,∴PD AD =DQ CD =PQ AC =23. ∴PQ =23AC =232a =223a .10.考查下列三个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中l 、m 为直线,α、β为平面),则此条件为________.①⎭⎬⎫m ⊂αl ∥m⇒l ∥α;②⎭⎬⎫l ∥m m ∥α⇒l ∥α;③⎭⎬⎫l ⊥βα⊥β⇒l ∥α. 答案 l ⊄α解析 ①体现的是线面平行的判定定理,缺的条件是“l 为平面α外的直线”,即“l ⊄α”,它也同样适合②③,故填l ⊄α.11.在四面体ABCD 中,M 、N 分别是面△ACD 、△BCD 的重心,则四面体的四个面中与MN 平行的是________.答案 平面ABC 和平面ABD解析 连接AM 并延长交CD 于E ,连接BN 并延长交CD 于F .由重心的性质可知,E 、F 重合为一点,且该点为CD 的中点E .由EM MA =EN NB =12,得MN ∥AB .因此MN ∥平面ABC 且MN ∥平面ABD .12.过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,其中与平面ABB 1A 1平行的直线共有________条.答案 6解析 过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,记AC ,BC ,A 1C 1,B 1C 1的中点分别为E ,F ,E 1,F 1,则直线EF ,EF 1,EE 1,FF 1,E 1F ,E 1F 1均与平面ABB1A 1平行,故符合题意的直线共6条.13. 如图所示,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E、B、F、D1四点共面;(2)求证:平面A1GH∥平面BED1F.答案(1)略(2)略解析(1)连接FG.∵AE=B1G=1,∴BG=A1E=2.∴BG綊A1E,∴A1G∥BE.又∵C1F綊B1G,∴四边形C1FGB1是平行四边形.∴FG綊C1B1綊D1A1.∴四边形A1GFD1是平行四边形.∴A1G綊D1F,∴D1F綊EB.故E、B、F、D1四点共面.(2)∵H是B1C1的中点,∴B1H=32.又B1G=1,∴B1GB1H=23.又FCBC=23,且∠FCB=∠GB1H=90°,∴△B1HG∽△CBF.∴∠B1GH=∠CFB=∠FBG,∴HG∥FB.又由(1)知,A1G∥BE,且HG∩A1G=G,FB∩BE=B,∴平面A1GH∥平面BED1F.14. 如图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:P A∥平面EFG;(2)求三棱锥P—EFG的体积.答案(1)略(2)1 6解析(1)如图所示,取AD的中点H,连接GH,FH.∵E,F分别为PC,PD的中点,∴EF∥CD.∵G,H分别是BC,AD的中点,∴GH∥CD.∴EF∥GH,∴E,F,H,G四点共面.∵F,H分别为DP,DA的中点,∴P A∥FH.∵P A⊄平面EFG,FH⊂平面EFG,∴P A∥平面EFG.(2)∵PD⊥平面ABCD,CG⊂平面ABCD,∴PD⊥CG.又∵CG⊥CD,CD∩PD=D,∴GC⊥平面PCD.∵PF =12PD =1,EF =12CD =1, ∴S △PEF =12EF ·PF =12. 又GC =12BC =1,∴V P —EFG =V G —PEF =13×12×1=16.15.一个多面体的直观图和三视图如图所示(其中M ,N 分别是AF ,BC 中点).(1)求证:MN ∥平面CDEF ; (2)求多面体A —CDEF 的体积. 答案 (1)略 (2)83解析 (1)证明 由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB =BC =BF =2,DE =CF =22,∴∠CBF =90°.取BF 中点G ,连接MG ,NG ,由M ,N 分别是AF ,BC 中点,可知:NG ∥CF ,MG ∥EF .又MG ∩NG =G ,CF ∩EF =F ,∴平面MNG ∥平面CDEF ,∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ,由于三棱柱ADE —BCF 为直三棱柱,∴AH ⊥平面CDEF ,且AH = 2.∴V A -CDEF =13S 四边形CDEF ·AH =13×2×22×2=83.16. 如图所示,三棱柱ABC -A 1B 1C 1,底面为正三角形,侧棱A 1A ⊥底面ABC ,点E 、F 分别是棱CC 1、BB 1上的点,点M 是线段AC 上的动点,EC =2FB .当点M 在何位置时,BM ∥平面AEF?答案当M为AC中点时,BM∥平面AEF.解析方法一:如图所示,取AE的中点O,连接OF,过点O作OM⊥AC 于点M.∵侧棱A1A⊥底面ABC,∴侧面A1ACC1⊥底面ABC.∴OM⊥底面ABC.又∵EC=2FB,∴OM∥FB綊12EC.∴四边形OMBF为矩形.∴BM∥OF.又∵OF⊂面AEF,BM⊄面AEF,故BM∥平面AEF,此时点M为AC的中点.方法二:如图所示,取EC的中点P,AC的中点Q,连接PQ、PB、BQ. ∴PQ∥AE.∵EC=2FB,∴PE綊BF,PB∥EF.∴PQ∥平面AEF,PB∥平面AEF.又PQ∩PB=P,∴平面PBQ ∥平面AEF .又∵BQ ⊂面PQB ,∴BQ ∥平面AEF .故点Q 即为所求的点M ,此时点M 为AC 的中点.17. (2013·福建)如图所示,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,BC =5,DC =3,AD =4,∠P AD =60°.(1)当正视方向与向量AD →的方向相同时,画出四棱锥P -ABCD 的正视图(要求标出尺寸,并写出演算过程);(2)若M 为P A 的中点,求证:DM ∥平面PBC ;(3)求三棱锥D -PBC 的体积.答案 (1)略 (2)略 (3)8 3解析 方法一:(1)在梯形ABCD 中,过点C 作CE ⊥AB ,垂足为E ,由已知得,四边形ADCE 为矩形,AE =CD =3,在Rt △BEC 中,由BC =5,CE =4,依勾股定理,得BE =3,从而AB =6.又由PD ⊥平面ABCD ,得PD ⊥AD .从而在Rt △PDA 中,由AD =4,∠P AD =60°,得PD =4 3.正视图如图所示.(2) 取PB 中点N ,连接MN ,CN .在△P AB 中,∵M 是P A 中点,∴MN ∥AB ,MN =12AB =3.又CD ∥AB ,CD =3,∴MN ∥CD ,MN =CD .∴四边形MNCD 为平行四边形.∴DM ∥CN .又DM ⊄平面PBC ,CN ⊂平面PBC ,∴DM ∥平面PBC .(3)V D -PBC =V P -DBC =13S △DBC ·PD ,又S △DBC =6,PD =43,所以V D -PBC =8 3.方法二:(1)同方法一.(2) 取AB 的中点E ,连接ME ,DE .在梯形ABCD 中,BE ∥CD ,且BE =CD ,∴四边形BCDE 为平行四边形.∴DE ∥BC .又DE ⊄平面PBC ,BC ⊂平面PBC ,∴DE∥平面PBC.又在△P AB中,ME∥PB,ME⊄平面PBC,PB⊂平面PBC,∴ME∥平面PBC.又DE∩ME=E,∴平面DME∥平面PBC.又DM⊂平面DME,∴DM∥平面PBC.(3)同方法一.。
直线与平面平行的判定和性质经典练习及详细答案

平面平行的判定及其性质羄直线、1.2.薂下列命题中,正确命题的是④.;肇①若直线I上有无数个点不在平面:.内,则I // :•芆②若直线I与平面「平行,则I与平面「内的任意一条直线都平行;莁③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;④若直线I与平面「平行,则I与平面:.内的任意一条直线都没有公共点3.4. 芀下列条件中,不能判断两个平面平行的是____________ (填序号)肇①一个平面内的一条直线平行于另一个平面蚆②一个平面内的两条直线平行于另一个平面膃③一个平面内有无数条直线平行于另一个平面聿④一个平面内任何一条直线都平行于另一个平面答案①②③5.5. 腿对于平面和共面的直线m n,下列命题中假命题是________________ (填序号)肇①若mL用,m丄n,贝V n / 、丄薁②若mil :- , n // :•,贝V m// n膂③若m二:z , n// :•,贝U m// n芇④若m n与:•所成的角相等,则m// n 答案①②④7.6. 膄已知直线a, b,平面「,则以下三个命题:芃①若a // b, b二:乂,则a //⑶袁②若a // b, a //芒,贝U b //芒;莆③若 a // :•, b // :-,则 a // b.薅其中真命题的个数是答案09.7. 羅直线a//平面M直线b M那么a// b是b〃M的条件.蚀A.充分而不必要 B.必要而不充分 C.充要 D.不充分也不必要11.12.蒆能保证直线a与平面〉平行的条件是, a// b p bu a, a//b肆A. a 広a, b u a, c//a,a//b,a//c蒃C. b u a£a,C^b, D e b 且AC=BD葿D. b u 口,A^a,B13.14. 薆如果直线a平行于平面?,则 _________a平行 B.平面〉内无数条直线与a平行蒇A.平面?内有且只有一直线与a平行的直线 D.平面〉内的任意直线与直线a都平行膅C.平面〉内不存在与15.15. 蒂如果两直线a// b,且a//平面〉,则b与〉的位置关系__________蚆A.相交B. b〃° c.匕匚口D.b〃°或b u°17.16. 薄下列命题正确的个数是______19.17. 蚃(1)若直线I上有无数个点不在平面a内,则I // al与平面a平行,则l与平面a内的任意一直线平行芁(2)若直线,那么另一条也与这个平面平行蚆(3)两条平行线中的一条直线与一个平面平行a和平面a内一直线b平行,则a // a羅(4 )若一直线莄A.0个 B.1个 C.2个 D.3个21.22. 罿b是平面a外的一条直线,下列条件中可得出b/ a是肀A. b与a内的一条直线不相交 B. b与a内的两条直线不相交莅C.b与a内的无数条直线不相交 D.b与a内的所有直线不相交23.23. 螂已知两条相交直线a、b, a//平面a ,则b与a的位置关系肂A. b / a B.b与a相交 C.b」a D.b/ a或b与a相交25.24. 膀如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC, SGSAB上的高,D E、F分别是AC BC SC的中点,试判断SG与平面DEF的位置关系,并给予证明.螆解SG//平面DEF证明如下:薄方法一:三角形中位线连接CG交螁••• DE是厶ABC的中位线,芀••• DE// AB.腿在△ ACG中, D是AC的中点,羂且DH// AG薀• H为CG的中点.艿• FH是厶SCG的中位线,芄• FH// SG蚄又SG亿平面DEF FHU平面DEF,荿••• SG//平面DEF荿方法二:平面平行的性质蚅••• EF为厶SBC的中位线,• EF/ SB膂••• EF伉平面SAB SBu平面SAB莂• EF//平面SAB葿同理可证,DF//平面SAB EF A DF=F ,肆.••平面SAB/平面DEF,又SG二平面SAB • SG//平面DEF27.25. 袄如图所示,在正方体ABC—ABC1D1中,E、F、G H分别是BC CG、賺CD、A1A的中点.求证:蕿(1)BF/ HD;蒇(2)EG//平面BBDD;莁(3)平面BDF/平面BDH袀证明平行四边形的性质,平行线的传递性虿(1 )如图所示,取BB的中点M易证四边形蚄又••• MC/ BF,「. BF/ HD.肃(2)取BD的中点0,连接E0, D0,贝U OE^蚈又DG& I DC• OE^ DG2蝿.••四边形OEGD是平行四边形,• GE// DO.肄又D 0-平面BB D D, • EG/平面BBD D.蒁(3)由(1)知DH// BF,又BD// BD, BD、HD =平面HBD, BF、BH 平面BDF,且BD A HD=D, DBA BF=B,「.平面BDF// 平面B D H.29.26. 螁如图所示,在三棱柱ABC-A i B C中,M N分别是BC和A i B i的中点. 衿求证:MN//平面AACC.蒅证明方法一:平行四边形的性质膃设AC中点为F,连接NF, FC,蒀••• N为A i B i中点,衿••• NF// BQ,且NF=^B C i,2祎又由棱柱性质知B i C i庄BC蚁又M是BC的中点,艿• NF MC羈.••四边形NFCM^平行四边形.芇• MIN/ CF,又CF 平面AA C i, MN二平面AA C ,• MIN/平面AAC C. 莃方法二:三角形中位线的性质节连接AM交C C于点P,连接A i P, 肇T M是BC的中点,且MC/ B i C i,莄• M是B i P的中点,肅又••• N为A B中点,肁• MN// A P,又 A PU 平面AA C , MW 平面AAC,:MIN/平面AACC.膈方法三:平面平行的性质 螅设BiG 中点为Q 连接NQ MQ ,薃•••M Q 是BG BG 的中点,袀•••MQ CG ,又 CGu 平面 AAGC, MQ 伉平面 AAGC, 芈•••MQ/平面 AA C i C.膆•••N 、Q 是A B i 、B i C 的中点,芅• NQ 二 AQ ,又 A i C 二平面 AAC C, NQ 二平面 AAC C, 蕿• NQ//平面 AA C i C.莈又••• MQ P NQB ,「.平面 MNQ 平面 AAC C, 薇又MN 二平面MNQ. MIN/平面AA C C.3 i .32.螂如图所示,正方体 ABC — A B i C D 中,侧面对角线 AB , BC 上分 别有两点 E , F ,且B E=C F. 蚁求证: EF //平面 ABCD 蒈方法一:平行四边形的性质螃过E 作ES// BB 交AB 于S,过F 作FT // BB 交BC 于 T ,蒄连接ST ,则-AE 更,且AB i B i B BC i C i C莀T B i E=C F , B A=CB,. AE=BF蒈•••旦,••• ES=FTB i B CC i膄又••• ES// B B// FT ,.四边形 EFTS 为平行四边形Bl ______ G袂•••EF// ST ,又 ST=平面 ABCD EFC :平面 ABCD : EF//平面 ABCD腿方法二:相似三角形的性质 薈连接BF 交BC 于点Q 连接AQ薅••• BQ // BC, • B 1L =圧BQ C 1B膂• EF // AQ 又 AQ=平面 ABCD EF 二平面 ABCD •- EF//平面 ABCD 蚇方法三:平面平行的性质 羆过E 作EG/ AB 交BB 于G,肂连接GF,则B 11史£ ,B 1A B 1B羁 TB i E=C i F , BA=CB ,螇••• C i E =B i G , • FG // B l C i // BC C 1B B i B 莇又 EG A FG P G , AB A BC=B ,螄.••平面 EFG/平面 ABCD 而EF 二平面EFG螀• EF//平面ABCD33.34.袇如图所示,在正方体 ABC — A B i C D 中,O 为底面ABCD 的中心,P 是DD 的中点,设薄T B i E=C i F , BiA=GB,B L E B ,FB 1D B i QQ是CC上的点,问:当点Q在什么位置时,平面DBQ// 平面PAO蒄解面面平行的判定节当Q为CC的中点时,A B葿平面 DBQ//平面PAO羇••• Q 为CG 的中点,P 为DD 的中点,••• QB// PA袅:P 、O 为 DD 、DB 的中点,• DB// PO羄又 PO P PA=P , DB A QB=B , 薂DB //平面PAO QB//平面 PAO 肇.••平面 DBQ//平面PAO芆直线与平面平行的性质定理35.EFGH 为空间四边形ABCD 勺一个截面,若截面为平行四边形芀(1)求证:AB//平面 EFGH CD//平面 EFGH肇(2)若AB=4, CD=6,求四边形EFGH 周长的取值范围 蚆(1)证明•••四边形EFGH 为平行四边形,• EF// HG膃•••HX 平面 ABD • EF//平面 ABD 聿•••EF 平面 ABC 平面 ABD A 平面 ABCAB腿• EF// AB. • AB//平面 EFGH 肇同理可证,CD//平面EFGH薁⑵ 解 设EF=x (O v x v 4),由于四边形 EFGH 为平行四边形,膂•••CF=x 则 FG = B F = B C -C F =1- x .从而 F G=6- 1 2 3x . •••四边形 EFGH 的周长 CB 4 6 BC BC 4 21 =2(x+6-5)=12- x.又0v x v 4,则有8v l v 12, •四边形 EFGH 周长的取值范围是(8,212) 37.36.莁如图所示,四边形 AC38.芇如图所示,平面:• //平面[,点A € :. , C €「,点B € 1 , D € [,点E , F 分别在线 段 AB CD 上,且 AE : EB=CF : FD薆••• AC// DH, •••四边形 ACDH 是平行四边形, 蒇在AH 上取一点 G,使AG : GH=CF : FD,膅又••• AE : EB=CF : FD, • GF// HD EG// BH 蒂又EG A GFG, •平面 EFG//平面-蚆•••EF 平面 EFG •- EF / l 综上,EF// I薄(2)解三角形中位线膄(1)求证:EF / -; :. / :,:.门平面 ACDHAC,蚃 如图所示,连接 AD,取AD 的中点 M 连接 ME MF.芁••• E , F 分别为AB, CD 的中点,蚆••• ME// BD, MF// AC,羅且 M ^Z BGB , MF=LAC=2,2 2莄•••/ EMF 为AC 与BD 所成的角(或其补角),罿EMF=60。
高考专题练习: 直线、平面平行的判定与性质

1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与这个平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)因为l∥a,a⊂α,l⊄α,所以l∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)因为l∥α,l⊂β,α∩β=b,所以l∥b2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)因为a∥β,b∥β,a∩b=P,a⊂α,b⊂α,所以α∥β性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行因为α∥β,α∩γ=a,β∩γ=b,所以a∥b常用结论1.三种平行关系的转化线线平行、线面平行、面面平行的相互转化是解决与平行有关的证明题的指导思想.2.平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.(2)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.(3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)直线l平行于平面α内的无数条直线,则l∥α.()(2)若直线l在平面α外,则l∥α.()(3)若直线l∥b,直线b⊂α,则l∥α.()(4)若直线l∥b,直线b⊂α,那么直线l平行于平面α内的无数条直线.()答案:(1)×(2)×(3)×(4)√二、易错纠偏常见误区|(1)对空间平行关系的相互转化条件理解不够;(2)忽略线面平行、面面平行的条件.1.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线都不相交解析:选D.因为a∥平面α,直线a与平面α无公共点,因此a和平面α内的任意一条直线都不相交,故选D.2.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为________.解析:因为平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,所以EF∥HG.同理EH∥FG,所以四边形EFGH 是平行四边形.答案:平行四边形与线、面平行相关命题的判定(师生共研)(1)设m,n表示不同直线,α,β表示不同平面,则下列结论中正确的是()A.若m∥α,m∥n,则n∥αB.若m⊂α,n⊂β,m∥β,n∥α,则α∥βC.若α∥β,m∥α,m∥n,则n∥βD.若α∥β,m∥α,n∥m,n⊄β,则n∥β(2)(2020·沈阳市教学质量监测(一))已知a,b为两条不同的直线,α,β,γ为三个不同的平面,则下列说法中正确的是()①若a∥α,α∥β,则a∥β;②若α∥β,β∥γ,则α∥γ;③若a⊥α,b⊥α,则a∥b;④若α⊥γ,β⊥γ,则α⊥β.A.①③B.②③C.①②③D.②③④【解析】(1)A错误,n有可能在平面α内;B错误,平面α可能与平面β相交;C错误,n也有可能在平面β内;D正确,易知m∥β或m⊂β,若m⊂β,又n∥m,n⊄β,所以n∥β,若m∥β,过m作平面γ交平面β于直线l,则m∥l,又n∥m,所以n∥l,又n⊄β,l⊂β,所以n∥β.(2)若a∥α,α∥β,则a可能平行于β,也可能在β内,故①不正确;若α∥β,β∥γ,则由面面平行的性质知α∥γ,故②正确;若a⊥α,b⊥α,则由线面垂直的性质知a∥b,故③正确;若α⊥γ,β⊥γ,则α与β可能平行也可能相交,故④不正确.综上所述,②③正确,故选B.【答案】(1)D(2)B解决线、面平行关系应注意的问题(1)注意判定定理与性质定理中易忽视的条件,如线面平行的条件中线在面外易被忽视.(2)结合题意构造或绘制图形,结合图形作出判断.(3)会举反例或用反证法推断命题是否正确.1.下列命题中正确的是()A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥α解析:选D.A错误,a可能在经过b的平面内;B错误,a与α内的直线平行或异面;C错误,两个平面可能相交;D正确,由a∥α,可得a平行于经过直线a的平面与α的交线c,即a∥c,又a∥b,所以b∥c,b⊄α,c⊂α,所以b∥α.2.设α,β为两个平面,则α∥β的充要条件是()A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面解析:选B.对于A,C,D选项,α均有可能与β相交,故排除A,C,D 选项,选B.线面平行的判定与性质(多维探究)角度一线面平行的证明在正方体ABCD-A1B1C1D1中,E,F,G,H分别是BC,CC1,C1D1,A1A的中点.求证:(1)BF∥HD1;(2)EG∥平面BB1D1D.【证明】(1)如图所示,取BB1的中点M,连接MH,MC1,易证四边形HMC 1D 1是平行四边形,所以HD 1∥MC 1.又因为在平面BCC 1B 1中,BM ∥=FC 1, 所以四边形BMC 1F 为平行四边形, 所以MC 1∥BF ,所以BF ∥HD 1. (2)取BD 的中点O ,连接EO ,D 1O , 则OE ∥DC 且OE =12DC ,又D 1G ∥DC 且D 1G =12DC ,所以OE ∥=D 1G , 所以四边形OEGD 1是平行四边形,所以GE ∥D 1O . 又D 1O ⊂平面BB 1D 1D ,GE ⊄平面BB 1D 1D , 所以EG ∥平面BB 1D 1D .证明直线与平面平行的常用方法(1)利用线面平行的定义.(2)利用线面平行的判定定理:关键是找到平面内与已知直线平行的直线,可先直观判断题中是否存在这样的直线,若不存在,则需作出直线,常考虑利用三角形的中位线、平行四边形的对边平行或过已知直线作一平面,找其交线进行证明.角度二 线面平行性质定理的应用如图,在五面体ABCDFE 中,底面ABCD 为矩形,EF ∥AB ,过BC的平面交棱FD 于点P ,交棱F A 于点Q .证明:PQ ∥平面ABCD .【证明】 因为底面ABCD 为矩形,所以AD ∥BC ,⎭⎪⎬⎪⎫AD ∥BCAD ⊂平面ADF BC ⊄平面ADF ⇒BC ∥平面ADF ,⎭⎪⎬⎪⎫BC ∥平面ADFBC ⊂平面BCPQ 平面BCPQ ∩平面ADF =PQ ⇒BC ∥PQ ,⎭⎪⎬⎪⎫PQ ∥BCPQ ⊄平面ABCD BC ⊂平面ABCD ⇒PQ ∥平面ABCD .应用线面平行的性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面来确定交线.该定理的作用是由线面平行转化为线线平行.1.(一题多解)(2021·河南中原名校联考)如图,已知点P 是平行四边形ABCD 所在平面外的一点,E ,F 分别是P A ,BD 上的点且PE ∶EA =BF ∶FD ,求证:EF ∥平面PBC .证明:方法一:如图,连接AF ,并延长交BC 于点G ,连接PG ,因为BC ∥AD ,所以FG F A =FBFD , 又因为PE EA =BFFD ,所以PE EA =GFF A ,所以EF ∥PG .又因为PG ⊂平面PBC ,EF ⊄平面PBC , 所以EF ∥平面PBC .方法二:如图,过点F 作FM ∥AD ,交AB 于点M ,连接EM ,因为FM ∥AD ,AD ∥BC ,所以FM ∥BC ,又因为FM ⊄平面PBC ,BC ⊂平面PBC , 所以FM ∥平面PBC . 由FM ∥AD 得BM MA =BFFD ,又因为PE EA =BF FD ,所以PE EA =BMMA ,所以EM ∥PB . 因为PB ⊂平面PBC ,EM ⊄平面PBC , 所以EM ∥平面PBC ,因为EM ∩FM =M ,EM ,FM ⊂平面EFM ,所以平面EFM∥平面PBC,因为EF⊂平面EFM,所以EF∥平面PBC.2.如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.证明:(1)取BD的中点O,连接CO,EO.由于CB=CD,所以CO⊥BD.又EC⊥BD,EC∩CO=C,又因为CO,EC⊂平面EOC,所以BD⊥平面EOC,因此BD⊥EO,又O为BD的中点,所以BE=DE.(2)取AB的中点N,连接DN,MN,因为M是AE的中点,N是AB的中点,所以MN∥BE.又MN⊄平面BEC,BE⊂平面BEC,所以MN∥平面BEC.因为△ABD为正三角形,所以∠BDN=30°,又CB=CD,∠BCD=120°,因此∠CBD=30°,所以DN∥BC.又DN⊄平面BEC,BC⊂平面BEC,所以DN∥平面BEC.又MN∩DN=N,故平面DMN∥平面BEC,又DM⊂平面DMN,所以DM∥平面BEC.面面平行的判定与性质(典例迁移)如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EF A1∥平面BCHG.【证明】(1)因为G,H分别是A1B1,A1C1的中点,所以GH∥B1C1,又B1C1∥BC,所以GH∥BC,所以B,C,H,G四点共面.(2)在△ABC中,E,F分别为AB,AC的中点,所以EF∥BC,因为EF⊄平面BCHG,BC⊂平面BCHG,所以EF∥平面BCHG.又因为G,E分别为A1B1,AB的中点,所以A1G∥=EB,所以四边形A1EBG是平行四边形,所以A1E∥GB.因为A1E⊄平面BCHG,GB⊂平面BCHG,所以A1E∥平面BCHG.又因为A1E∩EF=E,所以平面EF A1∥平面BCHG.【迁移探究1】(变条件)在本例条件下,若D为BC1的中点,求证:HD∥平面A1B1BA.证明:如图所示,连接HD,A1B,因为D为BC1的中点,H为A1C1的中点,所以HD∥A1B,又HD⊄平面A1B1BA,A1B⊂平面A1B1BA,所以HD∥平面A1B1BA.【迁移探究2】(变条件)在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.证明:如图所示,连接A1C交AC1于点M,因为四边形A1ACC1是平行四边形,所以M是A1C的中点,连接MD,因为D为BC的中点,所以A1B∥DM.因为A1B⊂平面A1BD1,DM⊄平面A1BD1,所以DM∥平面A1BD1.又由三棱柱的性质知,D1C1∥=BD,所以四边形BDC1D1为平行四边形,所以DC1∥BD1.又DC1⊄平面A1BD1,BD1⊂平面A1BD1,所以DC1∥平面A1BD1,又因为DC1∩DM=D,DC1,DM⊂平面AC1D,所以平面A1BD1∥平面AC1D.1.如图,AB∥平面α∥平面β,过点A,B的直线m,n分别交α,β于点C,E和点D,F,若AC=2,CE=3,BF=4,则BD的长为()A.65B.75C.85D.95解析:选C.由AB∥α∥β,易证ACCE=BDDF.即AC AE =BDBF,所以BD=AC·BFAE=2×45=85.2.(一题多解)如图,四边形ABCD是正方形,ED⊥平面ABCD,AF⊥平面ABCD.证明:平面ABF∥平面DCE.证明:方法一:因为DE⊥平面ABCD,AF⊥平面ABCD,所以DE∥AF.因为AF⊄平面DCE,DE⊂平面DCE,所以AF∥平面DCE.因为四边形ABCD是正方形,所以AB∥CD.因为AB⊄平面DCE,CD⊂平面DCE,所以AB∥平面DCE.因为AB∩AF=A,AB⊂平面ABF,AF⊂平面ABF,所以平面ABF∥平面DCE.方法二:因为DE⊥平面ABCD,AF⊥平面ABCD,所以DE∥AF.因为四边形ABCD为正方形,所以AB∥CD.又AF∩AB=A,DE∩DC=D,所以平面ABF∥平面DCE.方法三:因为DE⊥平面ABCD,所以DE⊥AD,在正方形ABCD中,AD⊥DC.又DE∩DC=D,所以AD⊥平面DEC.同理AD⊥平面ABF.所以平面ABF∥平面DCE.[A级基础练]1.已知α,β表示两个不同的平面,直线m是α内一条直线,则“α∥β”是“m∥β”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选A.由α∥β,m⊂α,可得m∥β;反过来,由m∥β,m⊂α,不能推出α∥β.综上,“α∥β”是“m∥β”的充分不必要条件.2.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是()A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面解析:选D.A项,α,β可能相交,故错误;B项,直线m,n的位置关系不确定,可能相交、平行或异面,故错误;C项,若m⊂α,α∩β=n,m∥n,则m∥β,故错误;D项,假设m,n垂直于同一平面,则必有m∥n,所以原命题正确,故D项正确.3.(2021·合肥模拟)已知a,b,c为三条不同的直线,α,β,γ为三个不同的平面,则下列说法正确的是()A.若a∥b,b⊂α,则a∥αB.若a⊂α,b⊂β,a∥b,则α∥βC.若α∥β,a∥α,则a∥βD.若α∩β=a,β∩γ=b,α∩γ=c,a∥b,则b∥c解析:选D.若a∥b,b⊂α,则a∥α或a⊂α,故A不正确;若a⊂α,b ⊂β,a∥b,则α∥β或α与β相交,故B不正确;若α∥β,a∥α,则a∥β或a⊂β,故C不正确;如图,由a∥b可得b∥α,又b⊂γ,α∩γ=c,所以b∥c,故D正确.4.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()解析:选A.对于选项B,如图所示,连接CD,因为AB∥CD,M,Q分别是所在棱的中点,所以MQ∥CD,所以AB∥MQ,又AB⊄平面MNQ,MQ⊂平面MNQ,所以AB∥平面MNQ.同理可证选项C,D中均有AB∥平面MNQ.故选A.5.如图,在三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于DE,则DE与AB的位置关系是()A.异面B.平行C.相交D.以上均有可能解析:选B.在三棱柱ABC-A1B1C1中,AB∥A1B1.因为AB⊂平面ABC,A1B1⊄平面ABC,所以A1B1∥平面ABC.因为过A1B1的平面与平面ABC交于DE,所以DE∥A1B1,所以DE∥AB.6.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度为________.解析:因为EF∥平面AB1C,EF⊂平面ABCD,平面ABCD∩平面AB1C=AC,所以EF∥AC,所以点F为DC的中点.故EF=12AC= 2.答案: 27.在棱长为2的正方体ABCD-A1B1C1D1中,M是棱AA1的中点,过C,M,D1作正方体的截面,则截面的面积是________.解析:由面面平行的性质知截面与平面AB1的交线MN是△AA1B的中位线,所以截面是梯形CD1MN,其面积为12×(2+22)×(5)2-⎝⎛⎭⎪⎫222=92.答案:9 28.如图所示,在正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件________时,就有MN∥平面B1BDD1.(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)解析:连接HN,FH,FN,则FH∥DD1,HN∥BD,FH∩HN=H,DD1∩BD =D,所以平面FHN∥平面B1BDD1,只需M∈FH,则MN⊂平面FHN,所以MN∥平面B1BDD1.答案:点M在线段FH上(或点M与点H重合)9.如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,P A⊥平面ABCD,P A=2,AB=1.设M,N分别为PD,AD的中点.(1)求证:平面CMN∥平面P AB;(2)求三棱锥P-ABM的体积.解:(1)证明:因为M,N分别为PD,AD的中点,所以MN∥P A,又MN⊄平面P AB,P A⊂平面P AB,所以MN∥平面P AB.在Rt△ACD中,∠CAD=60°,CN=AN,所以∠ACN=60°.又∠BAC=60°,所以CN∥AB.因为CN⊄平面P AB,AB⊂平面P AB,所以CN∥平面P AB.又CN∩MN=N,所以平面CMN∥平面P AB.(2)由(1)知,平面CMN∥平面P AB,所以点M到平面P AB的距离等于点C到平面P AB的距离.因为AB=1,∠ABC=90°,∠BAC=60°,所以BC=3,所以三棱锥P-ABM的体积V=V MP AB=V CP AB=V PABC=13×12×1×3×2=33.10.如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,AB=2,AF=1,M是线段EF的中点.(1)求证:AM∥平面BDE;(2)若平面ADM∩平面BDE=l,平面ABM∩平面BDE=m,试分析l与m 的位置关系,并证明你的结论.解:(1)证明:如图,记AC与BD的交点为O,连接OE.因为O,M分别是AC,EF的中点,四边形ACEF是矩形,所以四边形AOEM是平行四边形,所以AM∥OE.又因为OE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.(2)l∥m,证明如下:由(1)知AM∥平面BDE,又AM⊂平面ADM,平面ADM∩平面BDE=l,所以l∥AM,同理,AM∥平面BDE,又AM⊂平面ABM,平面ABM∩平面BDE=m,所以m ∥AM ,所以l ∥m .[B 级 综合练]11.如图,在四面体ABCD 中,若截面PQMN 是正方形,则在下列说法中,错误的为( )A .AC ⊥BDB .AC =BD C .AC ∥截面PQMND .异面直线PM 与BD 所成的角为45° 解析:选B .因为截面PQMN 是正方形, 所以PQ ∥MN ,QM ∥PN ,则PQ ∥平面ACD ,QM ∥平面BDA , 所以PQ ∥AC ,QM ∥BD ,由PQ ⊥QM 可得AC ⊥BD ,故A 正确; 由PQ ∥AC 可得AC ∥截面PQMN ,故C 正确; 由BD ∥PN ,所以∠MPN 是异面直线PM 与BD 所成的角,且为45°,D 正确; 由上面可知:BD ∥PN ,MN ∥AC . 所以PN BD =AN AD ,MN AC =DN AD ,而AN 与DN 关系不确定,PN =MN , 所以BD 与AC 关系不确定.B 错误.故选B .12.在正四棱柱ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,则点Q 满足条件________时,有平面D 1BQ ∥平面P AO .解析:如图所示,设Q 为CC 1的中点,因为P 为DD 1的中点,所以QB ∥P A .连接DB ,因为P ,O 分别是DD 1,DB 的中点,所以D 1B ∥PO ,又D 1B ⊄平面P AO ,QB ⊄平面P AO ,PO ⊂平面P AO ,P A ⊂平面P AO ,所以D 1B ∥平面P AO ,QB ∥平面P AO ,又D 1B ∩QB =B ,所以平面D 1BQ ∥平面P AO .故Q 为CC 1的中点时,有平面D 1BQ ∥平面P AO .答案:Q 为CC 1的中点13.(2021·烟台模拟)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =AD =2,AA 1=1.一平面截该长方体,所得截面为OPQRST ,其中O ,P 分别为AD ,CD 的中点,B 1S =12,则AT =________.解析:设AT =x ,则A 1T =1-x ,由面面平行的性质得,PO ∥SR ,TO ∥QR ,TS ∥PQ , 所以△DOP ∽△B 1RS .因为DP =OD =1,所以B 1S =B 1R =12, 所以A 1S =C 1R =32.由△ATO ∽△C 1QR ,可得AO AT =C 1RC 1Q ,即1x =32C 1Q ,故C 1Q =3x2.由△A 1TS ∽△CQP ,可得CQ CP =A 1TA 1S ,即1-3x 21=1-x 32,解得x =25.答案:2514.(2020·高考全国卷Ⅱ)如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点.过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1//MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心.若AO =AB =6,AO //平面EB 1C 1F ,且∠MPN =π3,求四棱锥B -EB 1C 1F 的体积.解:(1)证明:因为M ,N 分别为BC ,B 1C 1的中点,所以MN ∥CC 1.又由已知得AA 1∥CC 1,故AA 1∥MN .因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 1N .又B 1C 1⊥MN ,故B 1C 1⊥平面A 1AMN .又因为B 1C 1⊂平面EB 1C 1F ,所以平面A 1AMN ⊥平面EB 1C 1F .(2)AO ∥平面EB 1C 1F ,AO ⊂平面A 1AMN ,平面A 1AMN ∩平面EB 1C 1F =PN ,故AO ∥PN .又AP ∥ON ,故四边形APNO 是平行四边形,所以PN =AO =6,AP=ON =13AM =3,PM =23AM =23,EF =13BC =2.因为BC ∥平面EB 1C 1F ,所以四棱锥B -EB 1C 1F 的顶点B 到底面EB 1C 1F 的距离等于点M 到底面EB 1C 1F 的距离.如图,作MT ⊥PN ,垂足为T ,则由(1)知,MT ⊥平面EB 1C 1F ,故MT =PM sin ∠MPN =3.底面EB 1C 1F 的面积为12×(B 1C 1+EF )·PN =12×(6+2)×6=24.所以四棱锥B -EB 1C 1F 的体积为13×24×3=24.[C 级 提升练]15.如图,四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB ∥CD ,AB ⊥AD ,AB =2CD =2AD =4,侧面P AB 是等腰直角三角形,P A =PB ,平面P AB ⊥平面ABCD ,点E ,F 分别是棱AB ,PB 上的点,平面CEF ∥平面P AD .(1)确定点E ,F 的位置,并说明理由;(2)求三棱锥F -DCE 的体积.解:(1)因为平面CEF ∥平面P AD ,平面CEF ∩平面ABCD =CE ,平面P AD ∩平面ABCD =AD ,所以CE ∥AD ,又AB ∥DC ,所以四边形AECD 是平行四边形,所以DC =AE =12AB ,即点E 是AB 的中点.因为平面CEF ∥平面P AD ,平面CEF ∩平面P AB =EF ,平面P AD ∩平面P AB =P A ,所以EF ∥P A ,又点E 是AB 的中点,所以点F 是PB 的中点.综上,E ,F 分别是AB ,PB 的中点.(2)连接PE ,由题意及(1)知P A =PB ,AE =EB ,所以PE ⊥AB ,又平面P AB ⊥平面ABCD ,平面P AB ∩平面ABCD =AB , 所以PE ⊥平面ABCD .又AB ∥CD ,AB ⊥AD ,所以V F DEC =12V P DEC =16S △DEC ×PE =16×12×2×2×2=23.。
直线与平面、平面与平面平行的判定(附答案)
直线与平面、平面与平面平行的判定[学习目标]1。
理解直线与平面平行、平面与平面平行判定定理的含义.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用。
3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题。
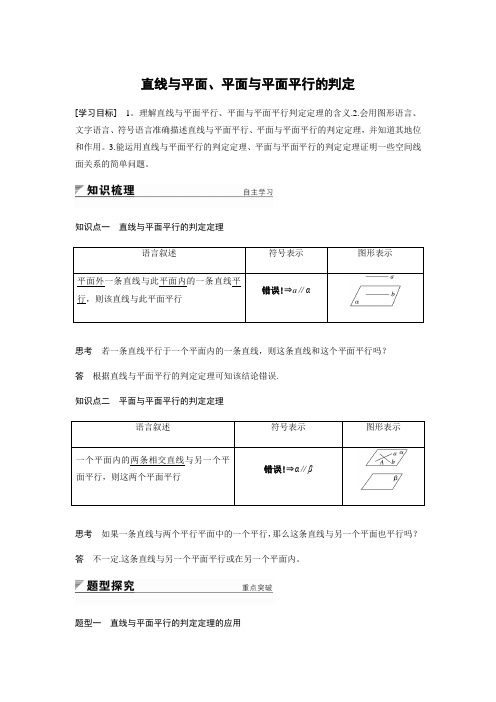
知识点一直线与平面平行的判定定理语言叙述符号表示图形表示平面外一条直线与此平面内的一条直线平错误!⇒a∥α行,则该直线与此平面平行思考若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗?答根据直线与平面平行的判定定理可知该结论错误.知识点二平面与平面平行的判定定理语言叙述符号表示图形表示一个平面内的两条相交直线与另一个平错误!⇒α∥β面平行,则这两个平面平行思考如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗?答不一定.这条直线与另一个平面平行或在另一个平面内。
题型一直线与平面平行的判定定理的应用例1如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:(1)EH∥平面BCD;(2)BD∥平面EFGH。
证明(1)∵EH为△ABD的中位线,∴EH∥BD。
∵EH⊄平面BCD,BD⊂平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊄平面EFGH,EH⊂平面EFGH,∴BD∥平面EFGH.跟踪训练1在四面体A-BCD中,M,N分别是△ABD和△BCD的重心,求证:MN∥平面ADC。
证明如图所示,连接BM,BN并延长,分别交AD,DC于P,Q两点,连接PQ。
因为M,N分别是△ABD和△BCD的重心,所以BM∶MP=BN∶NQ=2∶1。
所以MN∥PQ.又因为MN⊄平面ADC,PQ⊂平面ADC,所以MN∥平面ADC。
题型二面面平行判定定理的应用例2如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1。
直线与平面平行的判定和性质经典练习及详细答案

直线、平面平行的判定及其性质1. 下列命题中,正确命题的是 ④ . ①若直线l 上有无数个点不在平面α内,则l ∥α;②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行;③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点. 2. 下列条件中,不能判断两个平面平行的是 (填序号). ①一个平面内的一条直线平行于另一个平面 ②一个平面内的两条直线平行于另一个平面 ③一个平面内有无数条直线平行于另一个平面④一个平面内任何一条直线都平行于另一个平面 答案 ①②③3. 对于平面α和共面的直线m 、n ,下列命题中假命题是 (填序号). ①若m ⊥α,m ⊥n ,则n ∥α ②若m ∥α,n ∥α,则m ∥n ③若m ⊂α,n ∥α,则m ∥n④若m 、n 与α所成的角相等,则m ∥n 答案 ①②④ 4. 已知直线a ,b ,平面α,则以下三个命题: ①若a ∥b ,b ⊂α,则a ∥α; ②若a ∥b ,a ∥α,则b ∥α; ③若a ∥α,b ∥α,则a ∥b .其中真命题的个数是 . 答案 05. 直线a //平面M ,直线b ⊂/M ,那么a //b 是b //M 的 条件. A .充分而不必要 B.必要而不充分 C.充要 D.不充分也不必要6. 能保证直线a 与平面α平行的条件是 A.b a b a //,,αα⊂⊄ B.b a b //,α⊂ C.c a b a c b //////,,,αα⊂D.b D b C a B a A b ∈∈∈∈⊂,,,,α且BD AC =7. 如果直线a 平行于平面α,则A.平面α内有且只有一直线与a 平行B.平面α内无数条直线与a 平行C.平面α内不存在与a 平行的直线D.平面α内的任意直线与直线a 都平行 8. 如果两直线a ∥b ,且a ∥平面α,则b 与α的位置关系 A.相交 B.α//b C.α⊂b D .α//b 或α⊂b 9. 下列命题正确的个数是10.(1)若直线l上有无数个点不在平面α内,则l∥α(2)若直线l与平面α平行,则l与平面α内的任意一直线平行(3)两条平行线中的一条直线与一个平面平行,那么另一条也与这个平面平行(4)若一直线a和平面α内一直线b平行,则a∥αA.0个B.1个C.2个D.3个11.b是平面α外的一条直线,下列条件中可得出b∥α是A.b与α内的一条直线不相交B.b与α内的两条直线不相交C.b与α内的无数条直线不相交D.b与α内的所有直线不相交12.已知两条相交直线a、b,a∥平面α,则b与α的位置关系A.b∥αB.b与α相交C.b⊂αD.b∥α或b与α相交13.如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.解SG∥平面DEF,证明如下:方法一:三角形中位线连接CG交DE于点H,如图所示.∵DE是△ABC的中位线,∴DE∥AB.在△ACG中,D是AC的中点,且DH∥AG.∴H为CG的中点.∴FH是△SCG的中位线,∴FH∥SG.又SG⊄平面DEF,FH⊂平面DEF,∴SG∥平面DEF.方法二:平面平行的性质∵EF为△SBC的中位线,∴EF∥SB.∵EF⊄平面SAB,SB⊂平面SAB,∴EF∥平面SAB.同理可证,DF∥平面SAB,EF∩DF=F,∴平面SAB∥平面DEF,又SG⊂平面SAB,∴SG∥平面DEF.14.如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是BC、CC1、C1D1、A1A的中点.求证:(1)BF∥HD1;(2)EG∥平面BB1D1D;(3)平面BDF∥平面B1D1H.证明平行四边形的性质,平行线的传递性(1)如图所示,取BB1的中点M,易证四边形HMC1D1是平行四边形,∴HD1∥MC1.又∵MC1∥BF,∴BF∥HD1.(2)取BD 的中点O ,连接EO ,D 1O ,则OE 21DC ,又D 1G 21DC ,∴OED 1G ,∴四边形OEGD 1是平行四边形,∴GE ∥D 1O . 又D 1O ⊂平面BB 1D 1D ,∴EG ∥平面BB 1D 1D .(3)由(1)知D 1H ∥BF ,又BD ∥B 1D 1,B 1D 1、HD 1⊂平面HB 1D 1,BF 、BD ⊂平面BDF ,且B 1D 1∩HD 1=D 1,DB ∩BF =B ,∴平面BDF ∥平面B 1D 1H .15. 如图所示,在三棱柱ABC —A 1B 1C 1中,M 、N 分别是BC 和A 1B 1的中点. 求证:MN ∥平面AA 1C 1C.证明 方法一:平行四边形的性质 设A 1C 1中点为F ,连接NF ,FC , ∵N 为A 1B 1中点,∴NF ∥B 1C 1,且NF =21B 1C 1,又由棱柱性质知B 1C 1 BC , 又M 是BC 的中点,∴NF MC ,∴四边形NFCM 为平行四边形.∴MN ∥CF ,又CF ⊂平面AA 1C 1,MN ⊄平面AA 1C 1,∴MN ∥平面AA 1C 1C. 方法二:三角形中位线的性质 连接AM 交C 1C 于点P ,连接A 1P , ∵M 是BC 的中点,且MC ∥B 1C 1, ∴M 是B 1P 的中点, 又∵N 为A 1B 1中点,∴MN ∥A 1P ,又A 1P ⊂平面AA 1C 1,MN ⊄平面AA 1C 1,∴MN ∥平面AA 1C 1C. 方法三:平面平行的性质设B 1C 1中点为Q ,连接NQ ,MQ , ∵M 、Q 是BC 、B 1C 1的中点,∴MQ CC 1,又CC 1⊂平面AA 1C 1C , MQ ⊄平面AA 1C 1C , ∴MQ ∥平面AA 1C 1C .∵N 、Q 是A 1B 1、B 1C 1的中点,∴NQ A 1C 1,又A 1C 1⊂平面AA 1C 1C ,NQ ⊄平面AA 1C 1C , ∴NQ ∥平面AA 1C 1C .又∵MQ ∩NQ=B ,∴平面MNQ ∥平面AA 1C 1C , 又MN ⊂平面MNQ ∴MN ∥平面AA 1C 1C.16. 如图所示,正方体ABCD —A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E =C 1F . 求证:EF ∥平面ABCD .方法一:平行四边形的性质过E 作ES ∥BB 1交AB 于S ,过F 作FT ∥BB 1交BC 于T ,连接ST ,则11AE ES AB B B =,且11BF FT BC C C =∵B 1E =C 1F ,B 1A =C 1B ,∴AE=BF∴11ES FT B B CC =,∴ES=FT 又∵ES ∥B 1B ∥FT ,∴四边形E FTS 为平行四边形.∴EF ∥ST ,又ST ⊂平面ABCD ,EF ⊄平面ABCD ,∴EF ∥平面ABCD . 方法二:相似三角形的性质连接B 1F 交BC 于点Q ,连接AQ , ∵B 1C 1∥BC ,∴1111B F C F B Q C B =∵B 1E =C 1F ,B 1A =C 1B ,∴1111B E B FB D B Q=∴EF ∥AQ ,又AQ ⊂平面ABCD ,EF ⊄平面ABCD ,∴EF ∥平面ABCD . 方法三:平面平行的性质 过E 作EG ∥AB 交BB 1于G , 连接GF ,则BB GB A B E B 1111=, ∵B 1E =C 1F ,B 1A =C 1B , ∴BB GB BC E C 1111=,∴FG ∥B 1C 1∥BC , 又EG ∩FG =G ,AB ∩BC =B ,∴平面EFG ∥平面ABCD ,而EF ⊂平面EFG , ∴EF ∥平面ABCD .17. 如图所示,在正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q是CC 1上的点,问:当点Q 在什么位置时,平面D 1BQ ∥平面PAO ? 解 面面平行的判定 当Q 为CC 1的中点时, 平面D 1BQ ∥平面PAO .∵Q 为CC 1的中点,P 为DD 1的中点,∴QB ∥PA . ∵P 、O 为DD 1、DB 的中点,∴D 1B ∥PO . 又PO ∩PA =P ,D 1B ∩QB =B ,D 1B ∥平面PAO ,QB ∥平面PAO , ∴平面D 1BQ ∥平面PAO . 直线与平面平行的性质定理18. 如图所示,四边形EFGH 为空间四边形ABCD 的一个截面,若截面为平行四边形.(1)求证:AB ∥平面EFGH ,CD ∥平面EFGH .(2)若AB =4,CD =6,求四边形EFGH 周长的取值范围. (1)证明 ∵四边形EFGH 为平行四边形,∴EF ∥HG . ∵HG ⊂平面ABD ,∴EF ∥平面ABD .∵EF ⊂平面ABC ,平面ABD ∩平面ABC =AB , ∴EF ∥AB .∴AB ∥平面EFGH . 同理可证,CD ∥平面EFGH . (2)解 设EF =x (0<x <4),由于四边形EFGH 为平行四边形, ∴4x CB CF =.则6FG =BC BF =BC CF BC -=1-4x .从而FG =6-x 23.∴四边形EFGH 的周长l =2(x +6-x 23)=12-x .又0<x <4,则有8<l <12,∴四边形EFGH 周长的取值范围是(8,12).19. 如图所示,平面α∥平面β,点A ∈α,C ∈α,点B ∈β,D ∈β,点E ,F 分别在线段AB ,CD 上,且AE ∶EB =CF ∶FD . (1)求证:EF ∥β;(2)若E ,F 分别是AB ,CD 的中点,AC =4,BD =6,且AC ,BD 所成的角为60°,求EF 的长.(1)证明 两个平行平面同时与第三个平面相交,则交线平行;平行线分线段成比例方法① 当AB ,CD 在同一平面内时, 由α∥β,平面α∩平面ABDC =AC ,平面β∩平面ABDC =BD ,∴AC ∥BD , ∵AE ∶EB =CF ∶FD ,∴EF ∥BD ,又EF ⊄β,BD ⊂β,∴EF ∥β.方法② 当AB 与CD 异面时, 设平面ACD ∩β=DH ,且DH =AC . ∵α∥β,α∩平面ACDH =AC ,∴AC ∥DH ,∴四边形ACDH 是平行四边形,在AH 上取一点G ,使AG ∶GH =CF ∶FD , 又∵AE ∶EB =CF ∶FD ,∴GF ∥HD ,EG ∥BH , 又EG ∩GF =G ,∴平面EFG ∥平面β.∵EF ⊂平面EFG ,∴EF ∥β.综上,EF ∥β.(2)解三角形中位线如图所示,连接AD ,取AD 的中点M ,连接ME ,MF . ∵E ,F 分别为AB ,CD 的中点, ∴ME ∥BD ,MF ∥AC , 且ME =21BD =3,MF =21AC =2,∴∠EMF 为AC 与BD 所成的角(或其补角), ∴∠EMF =60°或120°,∴在△EFM 中由余弦定理得,EF =EMF MF ME MF ME ∠∙∙-+cos 222=212322322⨯⨯⨯±+=613±, 即EF =7或EF =19.20. 正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP =DQ . 求证:PQ ∥平面BCE .证明 方法一:平行四边形的性质 如图所示,作PM ∥AB 交BE 于M ,作QN ∥AB 交BC 于N ,连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ,∴AE =BD . 又∵AP =DQ ,∴PE =QB , 又∵PM ∥AB ∥QN , ∴AEPE AB PM =,BD BQ DC QN =,DC QNAB PM =,∴PM QN ,∴四边形PMNQ 为平行四边形,∴PQ ∥MN .又MN ⊂平面BCE ,PQ ⊄平面BCE , ∴PQ ∥平面BCE .方法二:相似三角形的性质如图所示,连接AQ ,并延长交BC 于K ,连接EK ,∵AE =BD ,AP =DQ , ∴PE =BQ , ∴PE AP =BQDQ① 又∵AD ∥BK ,∴BQ DQ =QKAQ②由①②得PE AP =QKAQ,∴PQ ∥EK .又PQ ⊄平面BCE ,EK ⊂平面BCE , ∴PQ ∥平面BCE .方法三:平面平行的性质 如图所示,在平面ABEF 内,过点P 作PM ∥BE ,交AB 于点M , 连接QM .∵PM ∥BE ,PM ⊄平面BCE , 即PM ∥平面BCE , ∴PE AP =MBAM①又∵AP =DQ ,∴PE =BQ ,∴PE AP =BQDQ②由①②得MB AM =BQDQ,∴MQ ∥AD , ∴MQ ∥BC ,又∵MQ ⊄平面BCE ,∴MQ ∥平面BCE . 又∵PM ∩MQ =M ,∴平面PMQ ∥平面BCE , PQ ⊂平面PMQ ,∴PQ ∥平面BCE .21. 如图所示,正四棱锥P —ABCD 的各棱长均为13,M ,N 分别为PA ,BD 上的点,且PM ∶MA =BN ∶ND =5∶8.(1)求证:直线MN ∥平面PBC ; (2)求线段MN 的长.(1)证明:方法一: 相似三角形的性质 连接AN 并延长交BC 于Q , 连接PQ ,如图所示.∵AD ∥BQ ,∴△AND ∽△QNB , ∴NQ AN =NB DN =BQ AD =58, 又∵MA PM =ND BN =85, ∴MP AM =NQ AN =58,∴MN ∥PQ , 又∵PQ ⊂平面PBC ,MN ⊄平面PBC , ∴MN ∥平面PBC .方法二:平行四边形的性质如图所示,作MQ ∥AB 交P B 于Q ,作NR ∥AB 交BC 于R ,连接QR.∵MQ ∥AB ∥NR , ∴PM MQ PAAB=,NR BN DCBD=,又∵PM BNMA ND=,∴MQ NR , ∴四边形MNRQ 为平行四边形,∴MN ∥QR.又QR ⊂平面P BC ,MN ⊄平面P BC , ∴MN ∥平面P BC .方法三:平面平行的性质如图所示,在平面ABP 内,过点M 作MN ∥P B ,交AB 于点O , 连接ON.∵MO ∥P B ,MO ⊄平面P BC ,PB ⊂平面P BC 即MO ∥平面P BC ,∴AM AP=AO AB又∵MA PM =ND BN =85, ∴AO AB=DN DB,∴NO ∥AD ,∴NO ∥BC ,又∵NO ⊄平面P BC ,BC ⊂平面P BC ∴NO ∥平面P BC . 又∵MO ∩NO=O ,∴平面MNO ∥平面P BC , MN ⊂平面MNO ,∴MN ∥平面P BC .(2)解 在等边△PBC 中,∠PBC =60°,在△PBQ 中由余弦定理知 PQ 2=PB 2+BQ 2-2PB ·BQ cos ∠PBQ=132+2865⎪⎭⎫⎝⎛-2×13×865×21=642818,∴PQ =891,∵MN ∥PQ ,MN ∶PQ =8∶13,∴MN =891×138=7.。
直线、平面平行的判定与性质知识点+典型例题及答案解析

2.2 直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定1、直线和平面的位置关系一条直线和一个平面的位置关系有且只有以下三种 位置关系 直线在平面内 直线与平面相交 直线与平面平行 公共点 有无数个公共点有且只有一个公共点没有公共点 符号表示a ⊂αa ∩α=Aa||α 图形表示注:直线和平面相交或平行的情况统称为直线在平面外 2、直线和平面平行(1)定义:直线和平面没有公共点,则称此直线L 和平面α平行,记作L ||α。
(2)判定定理:如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
简记为:线线平行,则线面平行.符号表示:,////a b a b a ααα⊄⊂⇒、.2.2.2 平面与平面平行的判定1、定义:没有公共点的两个平面叫做平行平面。
符号表示为:平面α、平面β,若a ∩β=∅,则a ∥β2、判定定理:1..性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行. 简记为:线面平行,则线线平行.判定文字描述如果两个平面无公共点,责成这两个平面平行一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行.如果两个平面同时垂直于一条直线,那么这两个平面垂直。
图形条件=αβ∅α,b ⊂β,α∩b =P α∥α,b ∥α ⇒β∥αl ⊥α l ⊥β ⇒β∥α结论//αβ //αβ //αβ符号表示:若//,,,//a a b a b αβαβ⊂=则.2.2.4 平面与平面平行的性质性质文字描述如果两个平行平面同时和第三平面相交,那么他们的交线平行 如果两个平行平面中有一个垂直于一条直线,那么另一个平面也垂直于这条直线 如果两个平面平行,那么其中一个平面内的直线平行于另一个平面 图形条件 α∥β β∩γ=b α∩γ=a α∥β l ⊥α α∥β a ⊂β结论a ∥bl ⊥βa ∥α1. 解题方法(1) 证明直线与平面平行的常用方法:2.利用定义,证明直线与平面没有公共点。
平面与平面平行的判定与性质试题及答案

平面与平面平行的判定与性质一、选择题1.平面α∥平面β,点A 、C ∈α,点B 、D ∈β,则直线AC ∥直线B D 的充要条件是( )A .AB ∥CD B .AD ∥CBC .AB 与CD 相交 D .A 、B 、C 、D 四点共面2.“α内存在着不共线的三点到平面β的距离均相等”是“α∥β”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要的条件3.平面α∥平面β,直线a ⊂α,P ∈β,则过点P 的直线中( )A .不存在与α平行的直线B .不一定存在与α平行的直线C .有且只有—条直线与a 平行D .有无数条与a 平行的直线4.下列命题中为真命题的是( )A .平行于同一条直线的两个平面平行B .垂直于同一条直线的两个平面平行C .若—个平面内至少有三个不共线的点到另—个平面的距离相等,则这两个平面平行.D .若三直线a 、b 、c 两两平行,则在过直线a 的平面中,有且只有—个平面与b ,c 均平行.5.已知平面α∥平面β,且α、β间的距离为d ,l ⊂α,l ′⊂β,则l 与l ′之间的距离的取值范围为( )A .(d ,∞)B .(d ,+∞)C .{d}D .(0,∞)6.已知直线a 、b 、c ⊂α,且a ∥β、b ∥β、c ∥β,则“a 、b 、c 到平面β的距离均相等”是“α∥β”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要的条件7.给出以下命题:①夹在两个平行平面间的线段,较长的与平面所成的角较小;②夹在两个平行平面间的线段,如果它们的长度相等,则它们必平行;③夹在两个平行平面间的线段,如果它的长度相等,则它们与平面所成的角也相等; ④在过定点P 的直线中,被两平行平面所截得的线段长为d 的直线有且只有一条,则两平行平面间的距离也为d其中假命题共有( )A .1个B .2个C .3个D .4个8.设α∥β,P ∈α,Q ∈β当P 、Q 分别在平面α、β内运动时,线段PQ 的中点X 也随着运动,则所有的动点X ( )A .不共面B .当且仅当P 、Q 分别在两条平行直线上移动时才共面C .当且仅当P 、Q 分别在两条互相垂直的异面直线上移动时才共面D .无论P 、Q 如何运动都共面二、填空题9.已知α∥β且α与β间的距离为d ,直线a 与α相交于点A 与β相交于B ,若d AB 332=,则直线a 与α所成的角=___________.10.过两平行平面α、β外的点P 两条直线AB 与CD ,它们分别交α于A 、C 两点,交β于B 、D 两点,若P A =6,AC =9,PB =8,则BD 的长为__________.11.已知点A 、B 到平面α的距离分别为d 与3d ,则A 、B 的中点到平面α的距离为________.12.已知平面α内存在着n 个点,它们任何三点不共线,若“这n 个点到平面β的距离均相等”是“α∥β”的充要条件,则n 的最小值为_________.三、解答题13.已知平面α∥平面β直线a ∥α,a β,求证:a ∥β.14.如图,平面α∥平面β,A 、C ∈α,B 、D ∈β,点E 、F 分别在线段A B、CD 上,且FD CF EB AE =,求证:EF ∥平面β.15.P 是△A BC 所在平面外一点,A ′,B ′,C ′分别是△P BC 、△PCA 、△P A B的重心,(1)求证:平面A ′B′C ′∥平面A BC ;(2)求S △A ′B′C ′∶S △A BC .16.如图已知平面α∥平面β,线段A B分别交α、β于M 、N ,线段AD 分别交α、β于C 、D ,线段BF 分别交α,β于F 、E ,若AM =m ,BN =n ,MN =P ,求△END 与△FMC 的面积之比.17.如图,已知:平面α∥平面β,A 、C ∈α,B 、D ∈β,AC 与BD 为异面直线,AC =6,BD =8,A B=CD =10,A B与CD 成60°的角,求AC 与BD 所成的角.参考答案一、选择题1.D 2.B 3.C 4.B 5.B 6.C 7.A 8.D二、填空题9.60° 10.12 11.d 或2d 12.5三、解答题13.证明:取平面α内一定点A ,则直线a 与点A 确定平面γ,设γ∩α=b ,γ∩β=c , 则由a ∥α得a ∥b ,由α∥β得b ∥c ,于是a ∥c .又∵a ⊄β,∴a ∥β.14.证明:(1)若直线AB 和CD 共面,∵α∥β,平面ABDC 与α、β分别交于AC 、BC 两直线,∴AC ∥BD .又∵EB AE =FD CF,∴EF ∥AC ∥BD ,∴EF ∥平面β.(2)若AB 与CD 异面,连接BC 并在BC 上取一点G ,使得EB AE =GB CG,则在△BAC 中,EG ∥AC ,AC ⊂平面α,∴EG ∥α.又∵α∥β,∴EG ∥β;同理可得:GF ∥BD ,而BD ⊂β,又∵GF ∥β.∵EG ∩GF =G ,∴平面EGF ∥β,又∵EF ⊂平面EGF ,∴EF ∥β.综合(1)(2)得EF ∥β.15.证明:(1)连接P A ′、PB ′、PC ′,分别交BC 、CA 、AB 于K 、G 、H ,连接GH 、KG 、HK .∵B ′、C ′均为相应三角形的重心,∴G 、H 分别为AC 、AB 的中点,且PG B P '=PH C P '=32,∴B ′C ′∥GH ,同理A ′B ′∥KG ,A ′B ′∩B ′C ′=B ′且GH ∩KG =G ,从而平面A ′B ′C ′∥平面ABC .(2)由(1)知△A ′B ′C ′∽△KGH , ∴KGH C B A S S ∆'''∆=2)(GH C B ''=94,又∵S △KGH =41S △ABC ,∴S △A ′B ′C ′=91S △ABC ,∴S △A ′B ′C ′∶S △ABC =1∶9.16.证明:∵α∥β,平面AND 分别交α,β于MC 、ND ,∴由面面平行的性质定理知,MC ∥ND ,同理MF ∥NE ;又由等角定理:“一个角的两边分别平行于另一角的两边且方向相同,则两角相等”知:∠END =∠FMC ,从而ND MC =AN AM ,MF NE =BM BN,∴ND =AM AN ·MC =m p m +·MC ,NE =BM BN·MF =p n n +·MF .∴S △END =21ND ·NE ·sin ∠END=21·m pm +·p n n +·MC ·MF ·sin ∠FMC=)+()+(p n m p m n ·S △FMC .∴FMC END S S ∆∆=)+()+(p n m p m n .即:△END 与△FMC 的面积之比为)+()+(p n m p m n .17.由α∥β作BE ∥=AC ,连结CE ,则ABEC 是平行四边形.∠DBE 是AC 与BD 所成的角.∠DCE 是AB 、CD 所成的角,故∠DCE =60°.由AB =CD =10,知CE =10,于是△CDE 为等边三角形, ∴DE =10.又∵BE =AC =6,BD =8,∴∠DBE =90°.∴AC 与BD 所成的角为90°.。
高考数学二轮复习考点知识讲解与练习47---直线、平面平行的判定与性质

高考数学二轮复习考点知识讲解与练习第47讲直线、平面平行的判定与性质考点知识:1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理;2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题.知识梳理1.直线与平面平行(1)直线与平面平行的定义直线l与平面α没有公共点,则称直线l与平面α平行.(2)判定定理与性质定理文字语言图形表示符号表示判定定理平面外一条直线与此平面内的一条直线平行,则该直线平行于此平面a⊄α,b⊂α,a∥b⇒a∥α性质定理一条直线和一个平面平行,则过这条直线的任一平面与此平面a∥α,a⊂β,α∩β=b⇒a∥b的交线与该直线平行2.平面与平面平行(1)平面与平面平行的定义没有公共点的两个平面叫做平行平面.(2)判定定理与性质定理文字语言图形表示符号表示判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行a⊂α,b⊂α,a∩b=P,a∥β,b∥β⇒α∥β性质定理两个平面平行,则其中一个平面内的直线平行于另一个平面α∥β,a⊂α⇒a∥β如果两个平行平面同时和第三个平面相交,那么它们的交线平行α∥β,α∩γ=a,β∩γ=b⇒a∥b1.平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.(2)平行于同一平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.(3)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.2.三种平行关系的转化诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)若一条直线和平面内一条直线平行,那么这条直线和这个平面平行.( )(2)若直线a∥平面α,P∈α,则过点P且平行于直线a的直线有无数条.( )(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( )(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( )答案(1)×(2)×(3)×(4)√解析(1)若一条直线和平面内的一条直线平行,那么这条直线和这个平面平行或在平面内,故(1)错误.(2)若a∥α,P∈α,则过点P且平行于a的直线只有一条,故(2)错误.(3)如果一个平面内的两条直线平行于另一个平面,则这两个平面平行或相交,故(3)错误.2.下列说法中,与“直线a∥平面α”等价的是( )A.直线a上有无数个点不在平面α内B.直线a与平面α内的所有直线平行C.直线a与平面α内无数条直线不相交D.直线a与平面α内的任意一条直线都不相交答案 D解析因为a∥平面α,所以直线a与平面α无交点,因此a和平面α内的任意一条直线都不相交,故选D.3.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为________.答案平行四边形解析∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.4.(2021·太原质检)平面α∥平面β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α答案 D解析若α∩β=l,a∥l,a⊄α,a⊄β,a∥α,a∥β,故排除A;若α∩β=l,a⊂α,a∥l,则a∥β,故排除B;若α∩β=l,a⊂α,a∥l,b⊂β,b∥l,则a∥β,b∥α,故排除C;故选D.5.(2022·长春调研)已知α,β表示两个不同的平面,直线m是α内一条直线,则“α∥β”是“m∥β”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件答案 A解析由α∥β,m⊂α,可得m∥β;反过来,由m∥β,m⊂α,不能推出α∥β.综上,“α∥β”是“m∥β”的充分不必要条件.6.(2021·衡水中学检测)如图,四棱锥P-ABCD中,AB=BC=12AD,∠BAD=∠ABC=90°,E是PD的中点.则CE与平面PAB的关系是________.答案平行解析取PA的中点F,连接EF,BF,∵E 是PD 中点,知EF 綉12AD ,又∠BAD =∠ABC =90°,BC =12AD ,∴BC 綉12AD ,从而BC 綉EF ,则四边形BCEF 为平行四边形,故CE ∥AF , 又BF ⊂平面PAB ,CE ⊄平面PAB , 所以CE ∥平面PAB .考点一 与线、面平行相关命题的判定1.(2019·全国Ⅱ卷)设α,β为两个平面,则α∥β的充要条件是( ) A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线 D .α,β垂直于同一平面 答案 B解析 若α∥β,则α内有无数条直线与β平行,当α内无数条直线互相平行时,α与β可能相交;若α,β平行于同一条直线,则α与β可以平行也可以相交;若α,β垂直于同一个平面,则α与β可以平行也可以相交,故A ,C ,D 中条件均不是α∥β的充要条件.根据两平面平行的判定定理知,若一个平面内有两条相交直线与另一个平面平行,则两平面平行,反之也成立.因此B 中条件是α∥β的充要条件. 2.(2021·西安质检)设a ,b 为两条不同直线,α,β,γ为三个不同平面,则下列命题正确的是( )A.若a∥α,b∥α,则a∥bB.若a⊂α,b⊂β,α∥β,则a∥bC.若a∥α,a∥β,则α∥βD.若α∥β,α∩γ=a,β∩γ=b,则a∥b答案 D解析A不正确:a∥b或a与b相交或异面;B不正确,a∥b或a与b是异面直线;C不正确,α∥β或平面α与β相交.D正确,根据面面平行的性质,可得a∥b.3.在正方体ABCD-A1B1C1D1中,下列结论正确的是________(填序号).①AD1∥BC1;②平面AB1D1∥平面BDC1;③AD1∥DC1;④AD1∥平面BDC1.答案①②④解析如图,因为AB綉C1D1,所以四边形AD1C1B为平行四边形.故AD1∥BC1,从而①正确;易证BD∥B1D1,AB1∥DC1,又AB1∩B1D1=B1,BD∩DC=D,1故平面AB1D1∥平面BDC1,从而②正确;由图易知AD1与DC1异面,故③错误;因为AD1∥BC1,AD1⊄平面BDC1,BC1⊂平面BDC1,所以AD1∥平面BDC1,故④正确.感悟升华直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理,并注意定理中易忽视的条件.(2)结合题意构造或绘制图形,结合图形作出判断.(3)利用实物进行空间想象,比较判断.(4)熟记一些常见结论,如垂直于同一条直线的两个平面平行等.考点二直线与平面平行的判定与性质角度1 直线与平面平行的判定【例1】(2019·全国Ⅰ卷)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.(1)证明如图,连接B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=12B1C.又因为N为A1D的中点,所以ND=12A1D.由题设知A1B1綉DC,可得B1C綉A1D,故ME綉ND,因此四边形MNDE为平行四边形,所以MN∥ED.又MN⊄平面C1DE,DE⊂平面C1DE,所以MN∥平面C1DE.(2)解过点C作C1E的垂线,垂足为H.由已知可得DE⊥BC,DE⊥C1C,又BC∩C1C=C,BC,C1C⊂平面C1CE,所以DE⊥平面C1CE,故DE⊥CH.所以CH⊥平面C1DE,故CH的长即为点C到平面C1DE的距离.由已知可得CE=1,C1C=4,所以C1E=17,故CH=417 17.从而点C到平面C1DE的距离为417 17.感悟升华 1.利用线面平行的判定定理证明直线与平面平行的关键是在平面内找到一条与已知直线平行的直线.2.利用面面平行的性质证明线面平行时,关键是构造过该直线与所证平面平行的平面,这种方法往往借助于比例线段或平行四边形.【训练1】如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:GH∥平面PAD.证明如图,连接AC交BD于点O,连接MO,因为四边形ABCD是平行四边形,所以O是AC的中点.又M是PC的中点,所以AP∥OM.根据直线和平面平行的判定定理,则有PA∥平面BMD.因为平面PAHG∩平面BMD=GH,根据直线和平面平行的性质定理,所以PA∥GH.因为GH⊄平面PAD,PA⊂平面PAD,所以GH∥平面PAD.角度2 线面平行的性质定理的应用【例2】(2021·河南、江西五岳联考)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,AB=BC=PA=12AD=2,E为PB的中点,F是PC上的点.(1)若EF∥平面PAD,证明:F为PC的中点;(2)求点C到平面PBD的距离.(1)证明因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD.因为P∈平面PBC,P∈平面PAD,所以可设平面PBC∩平面PAD=PM,又因为BC⊂平面PBC,所以BC∥PM,因为EF∥平面PAD,EF⊂平面PBC,所以EF∥PM,从而得EF∥BC.因为E为PB的中点,所以F为PC的中点.(2)解因为PA⊥底面ABCD,∠DAB=90°,AB=BC=PA=12AD=2,所以PB=PA2+AB2=22,PD=PA2+AD2=25,BD=BA2+AD2=25,所以S △DPB =12PB ·DP 2-⎝ ⎛⎭⎪⎫12PB 2=6.设点C 到平面PBD 的距离为d ,由V C -PBD =V P -BCD ,得13S △DPB ·d =13S △BCD ·PA =13×12×BC ×AB ×PA ,则6d =12×2×2×2,解得d =23.感悟升华 在应用线面平行的性质定理进行平行转化时,一定注意定理成立的条件,通常应严格按照定理成立的条件规范书写步骤,如:把线面平行转化为线线平行时,必须说清经过已知直线的平面和已知平面相交,这时才有直线与交线平行.【训练2】 如图所示,已知四边形ABCD 是正方形,四边形ACEF 是矩形,M 是线段EF 的中点.(1)求证:AM ∥平面BDE ;(2)若平面ADM ∩平面BDE =l ,平面ABM ∩平面BDE =m ,试分析l 与m 的位置关系,并证明你的结论.(1)证明 如图,记AC 与BD 的交点为O ,连接OE .因为O ,M 分别为AC ,EF 的中点,四边形ACEF 是矩形, 所以四边形AOEM 是平行四边形,所以AM ∥OE .又因为OE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.(2)解l∥m,证明如下:由(1)知AM∥平面BDE,又AM⊂平面ADM,平面ADM∩平面BDE=l,所以l∥AM,同理,AM∥平面BDE,又AM⊂平面ABM,平面ABM∩平面BDE=m,所以m∥AM,所以l∥m.考点三面面平行的判定与性质【例3】(经典母题)如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A 1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.证明(1)∵G,H分别是A1B1,A1C1的中点,∴GH是△A1B1C1的中位线,则GH∥B1C1.又∵B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.(2)∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1綉AB,∴A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又∵A1E∩EF=E,∴平面EFA1∥平面BCHG.【迁移1】在本例中,若将条件“E,F,G,H分别是AB,AC,A1B1,A1C1的中点”变为“D1,D分别为B1C1,BC的中点”,求证:平面A1BD1∥平面AC1D.证明如图所示,连接A1C交AC1于点M,∵四边形A1ACC1是平行四边形,∴M是A1C的中点,连接MD,∵D为BC的中点,∴A1B∥DM.∵A1B⊂平面A1BD1,DM⊄平面A1BD1,∴DM∥平面A1BD1,又由三棱柱的性质及D ,D 1分别为BC ,B 1C 1的中点知,D 1C 1綉BD , ∴四边形BDC 1D 1为平行四边形,∴DC 1∥BD 1. 又DC 1⊄平面A 1BD 1,BD 1⊂平面A 1BD 1, ∴DC 1∥平面A 1BD 1,又DC 1∩DM =D ,DC 1,DM ⊂平面AC 1D , 因此平面A 1BD 1∥平面AC 1D .【迁移2】 在本例中,若将条件“E ,F ,G ,H 分别是AB ,AC ,A 1B 1,A 1C 1的中点”变为“点D ,D 1分别是AC ,A 1C 1上的点,且平面BC 1D ∥平面AB 1D 1”,试求ADDC的值. 解 连接A 1B 交AB 1于O ,连接OD 1. 由平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BC 1D =BC 1, 平面A 1BC 1∩平面AB 1D 1=D 1O , 所以BC 1∥D 1O ,则A 1D 1D 1C 1=A 1OOB=1. 又由题设A 1D 1D 1C 1=DC AD, ∴DC AD =1,即ADDC=1. 感悟升华 1.判定面面平行的主要方法 (1)利用面面平行的判定定理.(2)线面垂直的性质(垂直于同一直线的两平面平行).2.面面平行条件的应用(1)两平面平行,分别构造与之相交的第三个平面,交线平行.(2)两平面平行,其中一个平面内的任意一条直线与另一个平面平行.提醒利用面面平行的判定定理证明两平面平行,需要说明是在一个平面内的两条直线是相交直线.【训练3】(2021·成都五校联考)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA =PD,AB=AD,PA⊥PD,AD⊥CD,∠BAD=60°,M,N分别为AD,PA的中点.(1)证明:平面BMN∥平面PCD;(2)若AD=6,求三棱锥P-BMN的体积.(1)证明连接BD,如图所示.∵AB=AD,∠BAD=60°,∴△ABD为正三角形.∵M为AD的中点,∴BM⊥AD.∵AD⊥CD,CD,BM⊂平面ABCD,∴BM∥CD.又BM⊄平面PCD,CD⊂平面PCD,∴BM∥平面PCD.∵M,N分别为AD,PA的中点,∴MN∥PD. 又MN⊄平面PCD,PD⊂平面PCD,∴MN∥平面PCD.又BM,MN⊂平面BMN,BM∩MN=M,∴平面BMN∥平面PCD.(2)解在(1)中已证BM⊥AD.∵平面PAD⊥平面ABCD,BM⊂平面ABCD,∴BM⊥平面PAD.又AD=6,∠BAD=60°,∴BM=3 3.∵PA=PD,PA⊥PD,AD=6,∴PA=PD=32AD=32,∵M,N分别为AD,PA的中点,∴S△PMN=14S△PAD=14×12×(32)2=94.∴三棱锥P-BMN的体积V=V B-PMN=13S△PMN·BM=13×94×33=934.A级基础巩固一、选择题1.下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥α答案 D解析A中,a可以在过b的平面内;B中,a与α内的直线也可能异面;C中,两平面可相交;D中,由直线与平面平行的判定定理知b∥α,正确.2.如果AB,BC,CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是( )A.平行 B.相交C.AC在此平面内 D.平行或相交答案 A解析把这三条线段放在正方体内可得如图,显然AC∥EF,AC⊄平面EFG,∵EF⊂平面EFG,故AC∥平面EFG,故选A.3.(2021·重庆联考)如图,四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且DEEB=DFFD1=12,G在CC1上且平面AEF∥平面BD1G,则CGCC1=( )A.12B.13C.23D.14答案 B解析如图所示,延长AE交CD于H,连接FH,则△DEH∽△BEA,所以DHAB=DEEB=12.因为平面AEF∥平面BD1G,平面AEF∩平面CDD1C=FH,平面BD1G∩平面CDD1C1=D1G,所以FH∥D1G.又四边形CDD1C1是平行四边形,所以△DFH∽△C1GD1,所以DFC1G=DHC1D1,因为DHC1D1=DHAB=12,所以DFC1G=12,因为DFFD1=12,所以FD1=C1G,DF=CG,所以CGCC1=13,故选B.4. (2021·兰州诊断)如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于DE,则DE与AB的位置关系是( )A.异面 B.平行 C.相交 D.以上均有可能答案 B解析在三棱柱ABC-A1B1C1中,AB∥A1B1,∵AB⊂平面ABC,A1B1⊄平面ABC,∴A1B1∥平面ABC.∵过A1B1的平面与平面ABC交于DE,∴DE∥A1B1,∴DE∥AB.5.(2021·河南名校联考)在正方体ABCD-A1B1C1D1中,E,F,G分别是BB1,DD1,A1B1的中点,则下列说法错误的是( )A.B1D∥平面A1FC1 B.CE∥平面A1FC1C.GE∥平面A1FC1 D.AE∥平面A1FC1答案 C解析作出图形如图所示,观察可知,B1D∥FO,CE∥A1F,AE∥C1F,又FO⊂平面A1FC1,A 1F⊂平面A1FC1,C1F⊂平面A1FC1,B1D⊄平面A1FC1,CE⊄平面A1FC1,AE⊄平面A1FC1,所以选项A,B,D正确;因为GE∥A1B,所以GE与平面A1FC1相交,所以选项C错误,故选C.6.若平面α截三棱锥所得截面为平行四边形,则该三棱锥中与平面α平行的棱有( ) A.0条 B.1条 C.2条 D.1条或2条答案 C解析如图所示,平面α即平面EFGH,则四边形EFGH为平行四边形,则EF∥GH.∵EF⊄平面BCD,GH⊂平面BCD,∴EF∥平面BCD.又∵EF⊂平面ACD,平面BCD∩平面ACD=CD,∴EF∥CD.又EF⊂平面EFGH,CD⊄平面EFGH.∴CD∥平面EFGH,同理,AB∥平面EFGH,所以与平面α(平面EFGH)平行的棱有2条.二、填空题7.如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF=________.答案 2解析根据题意,因为EF∥平面AB1C,EF⊂平面ACD,平面ACD∩平面AB1C=AC,所以EF ∥AC.又E是AD的中点,所以F是CD的中点.因为在Rt△DEF中,DE=DF=1,故EF= 2. 8.设α,β,γ是三个不同的平面,m,n是两条不同的直线,在命题“α∩β=m,n⊂γ,且________,则m∥n”中的横线处填入下列三组条件中的一组,使该命题为真命题.①α∥γ,n⊂β;②m∥γ,n∥β;③n∥β,m⊂γ.可以填入的条件有________(填序号).答案①或③解析由面面平行的性质定理可知,①正确;当m∥γ,n∥β时,n和m可能平行或异面,②错误;当n∥β,m⊂γ时,n和m在同一平面内,且没有公共点,所以m∥n,③正确.9.如图所示,在正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件________时,就有MN∥平面B1BDD1(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况).答案点M在线段FH上(或点M与点H重合)解析连接HN,FH,FN,则FH∥DD1,HN∥BD,且FH∩HN=H,D1D∩BD=D,∴平面FHN∥平面B1BDD1,只需M∈FH,则MN⊂平面FHN,∴MN∥平面B1BDD1.三、解答题10.(2021·绵阳诊断)如图,四边形ABCD是正方形,PA⊥平面ABCD,点E、F分别是线段AD,PB的中点,PA=AB=2.(1)证明:EF∥平面PCD;(2)求三棱锥F-PCD的体积.(1)证明取PC的中点G,连接DG,FG.∵四边形ABCD为正方形,且DE綉12BC,FG∥BC,且FG=12BC,∴DE∥FG且DE=FG,∴四边形DEFG为平行四边形,∴EF∥DG,又∵EF⊄平面PCD,DG⊂平面PCD,∴EF∥平面PCD.(2)解∵EF∥平面PCD,∴F到平面PCD的距离等于E到平面PCD的距离,∴V F-PCD=V E-PCD=12VA-PCD=12VP-ACD.∵PA⊥平面ABCD,∴V P-ACD=13×S△ACD×PA=13×12×22×2=43.∴V F-PCD=12VP-ACD=23.11.如图,四边形ABCD与四边形ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:(1)BE∥平面DMF;(2)平面BDE∥平面MNG.证明(1)如图,连接AE,则AE必过DF与GN的交点O,因为四边形ADEF为平行四边形,所以O为AE的中点.连接MO,则MO为△ABE的中位线,所以BE∥MO,又BE⊄平面DMF,MO⊂平面DMF,所以BE∥平面DMF.(2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN,又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG.因为M为AB的中点,N为AD的中点,所以MN为△ABD的中位线,所以BD∥MN,又BD⊄平面MNG,MN⊂平面MNG,所以BD∥平面MNG,又DE与BD为平面BDE内的两条相交直线,所以平面BDE∥平面MNG.B级能力提升12.如图,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1D1,A1B1的中点,过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )A. 2 B.98C. 3 D.62答案 B解析如图1,分别取B1C1,C1D1的中点E,F,连接EF,BE,DF,B1D1,ME,易知EF∥B1D1∥BD,AB∥ME,AB=EM,所以四边形ABEM为平行四边形,则AM∥BE,又BD和BE为平面BDFE内的两条相交直线.图1 图2所以平面AMN∥平面BDFE,即平面BDFE为平面α,BD=2,EF=12B1D1=22,得四边形BDFE为等腰梯形,DF=BE=5 2,在等腰梯形BDFE如图2中,过E,F作BD的垂线,则四边形EFGH为矩形,∴其高FG=DF2-DG2=54-18=324,故所得截面的面积为12×⎝ ⎛⎭⎪⎫22+2×324=98.13.在正四棱柱ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,则点Q 满足条件________时,有平面D 1BQ ∥平面PAO . 答案 Q 为CC 1的中点解析 如图所示,设Q 为CC 1的中点,因为P 为DD 1的中点,所以QB ∥PA .连接DB ,因为P ,O 分别是DD 1,DB 的中点,所以D 1B ∥PO ,又D 1B ⊄平面PAO ,QB ⊄平面PAO ,PO ⊂平面PAO ,PA ⊂平面PAO ,所以D 1B ∥平面PAO ,QB ∥平面PAO ,又D 1B ∩QB =B ,所以平面D 1BQ ∥平面PAO .故Q 为CC 1的中点时,有平面D 1BQ ∥平面PAO .14.(2021·西安调研)如图,在三棱柱ABC -A 1B 1C 1中,侧棱垂直于底面,E ,F 分别是BC ,A 1C 1的中点,△ABC 是边长为2的等边三角形,AA 1=2AB .(1)求证:EF ∥平面ABB 1A 1; (2)求点C 到平面AEF 的距离.(1)证明 如图,取AB 的中点D ,连接DE ,A 1D . 因为E 是BC 的中点,所以DE ∥AC ,且DE =12AC .由三棱柱的性质知AC ∥A 1C 1. 因为F 是A 1C 1的中点, 所以A 1F ∥AC ,且A 1F =12AC ,所以A 1F ∥DE ,且A 1F =DE , 所以四边形DEFA 1是平行四边形. 所以EF ∥DA 1.又因为EF ⊄平面ABB 1A 1,DA 1⊂平面ABB 1A 1, 所以EF ∥平面ABB 1A 1.(2)解 由题可得V F -ACE =13×AA 1×S △ACE =13×4×12×34×22=233.在△AEF 中,易求得AE =3,AF =17,EF =17, AE 边上的高为17-⎝ ⎛⎭⎪⎫322=652,所以S △AEF =12×652×3=1954.设点C 到平面AEF 的距离为h ,则V C-AEF=13×h×S△AEF=233,解得h=865 65.。
2023年高考数学一轮复习第七章立体几何与空间向量4空间直线平面的平行练习含解析

空间直线、平面的平行考试要求 1.理解空间中直线与直线、直线与平面、平面与平面的平行关系,并加以证明.2.掌握直线与平面、平面与平面平行的判定与性质,并会简单应用.知识梳理1.线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行错误!⇒a∥α性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行错误!⇒a∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行错误!⇒β∥α性质定理两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行错误!⇒a∥b常用结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.(2)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.(3)垂直于同一个平面的两条直线平行,即a⊥α,b⊥α,则a∥b.(4)若α∥β,a⊂α,则a∥β.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.( ×)(2)若直线a∥平面α,P∈α,则过点P且平行于直线a的直线有无数条.( ×)(3)若直线a⊂平面α,直线b⊂平面β,a∥b,则α∥β.( ×)(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( √)教材改编题1.下列说法中,与“直线a∥平面α”等价的是( )A.直线a上有无数个点不在平面α内B.直线a与平面α内的所有直线平行C.直线a与平面α内无数条直线不相交D.直线a与平面α内的任意一条直线都不相交答案 D解析因为a∥平面α,所以直线a与平面α无交点,因此a和平面α内的任意一条直线都不相交.2.已知不重合的直线a,b和平面α,则下列选项正确的是( )A.若a∥α,b⊂α,则a∥bB.若a∥α,b∥α,则a∥bC.若a∥b,b⊂α,则a∥αD.若a∥b,a⊂α,则b∥α或b⊂α答案 D解析若a∥α,b⊂α,则a∥b或异面,A错;若a∥α,b∥α,则a∥b或异面或相交,B错;若a∥b,b⊂α,则a∥α或a⊂α,C错;若a∥b,a⊂α,则b∥α或b⊂α,D对.3.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为______.答案平行四边形解析∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.题型一 直线与平面平行的判定与性质 命题点1 直线与平面平行的判定例1 如图,在四棱锥P -ABCD 中,底面ABCD 是平行四边形,E ,F 分别是BC ,PD 的中点,求证:(1)PB ∥平面ACF ;(2)EF ∥平面PAB .证明 (1)如图,连接BD 交AC 于O ,连接OF ,∵四边形ABCD 是平行四边形, ∴O 是BD 的中点,又∵F 是PD 的中点,∴OF ∥PB , 又∵OF ⊂平面ACF ,PB ⊄平面ACF , ∴PB ∥平面ACF .(2)取PA 的中点G ,连接GF ,BG . ∵F 是PD 的中点, ∴GF 是△PAD 的中位线, ∴GF 綉12AD ,∵底面ABCD 是平行四边形,E 是BC 的中点, ∴BE 綉12AD ,∴GF 綉BE ,∴四边形BEFG 是平行四边形, ∴EF ∥BG ,又∵EF ⊄平面PAB ,BG ⊂平面PAB , ∴EF ∥平面PAB .命题点2 直线与平面平行的性质例2 如图所示,在四棱锥P-ABCD中,四边形ABCD是平行四边形,M是PC的中点,在DM 上取一点G,过G和PA作平面交BD于点H.求证:PA∥GH.证明如图所示,连接AC交BD于点O,连接OM,∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴PA∥OM,又OM⊂平面BMD,PA⊄平面BMD,∴PA∥平面BMD,又平面PAHG∩平面BMD=GH,∴PA∥GH.教师备选如图,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.证明∵四边形ABCD为矩形,∴BC∥AD.∵AD⊂平面PAD,BC⊄平面PAD,∴BC∥平面PAD.∵平面BCFE∩平面PAD=EF,BC⊂平面BCFE,∴BC∥EF.∵AD=BC,AD≠EF,∴BC≠EF,∴四边形BCFE是梯形.思维升华(1)判断或证明线面平行的常用方法①利用线面平行的定义(无公共点).②利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).③利用面面平行的性质(α∥β,a⊂α⇒a∥β).④利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).(2)应用线面平行的性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面确定交线.跟踪训练1 如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,M是线段EF的中点.(1)求证:AM∥平面BDE;(2)若平面ADM∩平面BDE=l,平面ABM∩平面BDE=m,试分析l与m的位置关系,并证明你的结论.(1)证明如图,记AC与BD的交点为O,连接OE.因为O,M分别为AC,EF的中点,四边形ACEF是矩形,所以四边形AOEM是平行四边形,所以AM∥OE.又因为OE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.(2)解l∥m,证明如下:由(1)知AM∥平面BDE,又AM⊂平面ADM,平面ADM∩平面BDE=l,所以l∥AM,同理,AM∥平面BDE,又AM⊂平面ABM,平面ABM∩平面BDE=m,所以m∥AM,所以l∥m.题型二平面与平面平行的判定与性质例3 如图所示,在三棱柱ABC-A1B1C1中,过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合).(1)求证:BC∥GH;(2)若E,F,G分别是AB,AC,A1B1的中点,求证:平面EFA1∥平面BCHG.证明(1)∵在三棱柱ABC-A1B1C1中,∴平面ABC∥平面A1B1C1,又∵平面BCHG∩平面ABC=BC,且平面BCHG∩平面A1B1C1=HG,∴由面面平行的性质定理得BC∥GH.(2)∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1綉AB,∴A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又∵A1E∩EF=E,A1E,EF⊂平面EFA1,∴平面EFA1∥平面BCHG.延伸探究在本例中,若将条件“E,F,G分别是AB,AC,A1B1的中点”变为“点D,D1分别是AC,A1C1上的点,且平面BC1D∥平面AB1D1”,试求ADDC的值.解如图,连接A1B交AB1于O,连接OD1.由平面BC 1D ∥平面AB 1D 1, 且平面A 1BC 1∩平面BC 1D =BC 1, 平面A 1BC 1∩平面AB 1D 1=D 1O , 所以BC 1∥D 1O ,则A 1D 1D 1C 1=A 1OOB=1. 又由题设A 1D 1D 1C 1=DC AD, 所以DC AD=1,即AD DC=1. 教师备选如图,在三棱柱ABC -A 1B 1C 1中,E ,F ,G 分别为B 1C 1,A 1B 1,AB 的中点.(1)求证:平面A 1C 1G ∥平面BEF ;(2)若平面A 1C 1G ∩BC =H ,求证:H 为BC 的中点. 证明 (1)∵E ,F 分别为B 1C 1,A 1B 1的中点, ∴EF ∥A 1C 1,∵A 1C 1⊂平面A 1C 1G ,EF ⊄平面A 1C 1G , ∴EF ∥平面A 1C 1G ,又F ,G 分别为A 1B 1,AB 的中点, ∴A 1F =BG , 又A 1F ∥BG ,∴四边形A 1GBF 为平行四边形, 则BF ∥A 1G ,∵A 1G ⊂平面A 1C 1G ,BF ⊄平面A 1C 1G , ∴BF ∥平面A 1C 1G ,又EF ∩BF =F ,EF ,BF ⊂平面BEF , ∴平面A 1C 1G ∥平面BEF .(2)∵平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,平面A1C1G与平面ABC有公共点G,则有经过G的直线,设交BC于点H,如图,则A1C1∥GH,得GH∥AC,∵G为AB的中点,∴H为BC的中点.思维升华证明面面平行的常用方法(1)利用面面平行的判定定理.(2)利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β⇒α∥β).(3)利用面面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(α∥β,β∥γ⇒α∥γ).跟踪训练2 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形.(1)证明:平面A1BD∥平面CD1B1;(2)若平面ABCD∩平面CD1B1=直线l,证明:B1D1∥l.证明(1)由题设知BB1綉DD1,所以四边形BB1D1D是平行四边形,所以BD∥B1D1.又BD⊄平面CD1B1,B1D1⊂平面CD1B1,所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC,所以四边形A1BCD1是平行四边形,所以A1B∥D1C.又A1B⊄平面CD1B1,D1C⊂平面CD1B1,所以A1B∥平面CD1B1.又因为BD∩A1B=B,BD,A1B⊂平面A1BD,所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1,又平面ABCD∩平面CD1B1=直线l,平面ABCD∩平面A1BD=直线BD,所以直线l∥直线BD,在四棱柱ABCD-A1B1C1D1中,四边形BDD1B1为平行四边形,所以B 1D 1∥BD ,所以B 1D 1∥l .题型三 平行关系的综合应用例4 如图,在正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别为对角线BD ,CD 1上的点,且CQ QD 1=BP PD =23.(1)求证:PQ ∥平面A 1D 1DA ;(2)若R 是AB 上的点,AR AB的值为多少时,能使平面PQR ∥平面A 1D 1DA ?请给出证明. (1)证明 连接CP 并延长,与DA 的延长线交于M 点,如图,连接MD 1,因为四边形ABCD 为正方形, 所以BC ∥AD ,故△PBC ∽△PDM , 所以CP PM =BP PD =23,又因为CQ QD 1=BP PD =23, 所以CQ QD 1=CP PM =23, 所以PQ ∥MD 1.又MD 1⊂平面A 1D 1DA ,PQ ⊄平面A 1D 1DA , 故PQ ∥平面A 1D 1DA .(2)解 当AR AB 的值为35时,能使平面PQR ∥平面A 1D 1DA .如图,证明如下:因为AR AB =35,即BR RA =23, 故BR RA =BP PD. 所以PR ∥DA .又DA ⊂平面A 1D 1DA ,PR ⊄平面A 1D 1DA , 所以PR ∥平面A 1D 1DA ,又PQ ∥平面A 1D 1DA ,PQ ∩PR =P ,PQ ,PR ⊂平面PQR , 所以平面PQR ∥平面A 1D 1DA . 教师备选如图,四边形ABCD 与ADEF 均为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.求证:(1)BE ∥平面DMF ; (2)平面BDE ∥平面MNG .证明 (1)如图,连接AE ,则AE 必过DF 与GN 的交点O ,连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO . 又BE ⊄平面DMF ,MO ⊂平面DMF , 所以BE ∥平面DMF .(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点,所以DE ∥GN , 又DE ⊄平面MNG ,GN ⊂平面MNG , 所以DE ∥平面MNG . 又M 为AB 的中点,所以MN 为△ABD 的中位线,所以BD ∥MN , 又MN ⊂平面MNG ,BD ⊄平面MNG , 所以BD ∥平面MNG ,又DE ,BD ⊂平面BDE ,DE ∩BD =D ,所以平面BDE ∥平面MNG .思维升华 证明平行关系的常用方法熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键.面面平行判定定理的推论也是证明面面平行的一种常用方法.跟踪训练3 如图所示,四边形EFGH 为空间四边形ABCD 的一个截面,若截面为平行四边形. (1)求证:AB ∥平面EFGH ;(2)若AB =4,CD =6,求四边形EFGH 周长的取值范围.(1)证明 ∵四边形EFGH 为平行四边形, ∴EF ∥HG .∵HG ⊂平面ABD ,EF ⊄平面ABD , ∴EF ∥平面ABD . 又∵EF ⊂平面ABC , 平面ABD ∩平面ABC =AB , ∴EF ∥AB ,又∵AB ⊄平面EFGH ,EF ⊂平面EFGH , ∴AB ∥平面EFGH . (2)解 设EF =x (0<x <4), 由(1)知EF ∥AB , ∴CF CB =EF AB =x4, 与(1)同理可得CD ∥FG , ∴FG CD =BF BC, 则FG 6=BF BC=BC -CF BC =1-x4, ∴FG =6-32x .∴四边形EFGH 的周长L =2⎝⎛⎭⎪⎫x +6-32x =12-x .又∵0<x <4,∴8<L <12,故四边形EFGH 周长的取值范围是(8,12).课时精练1.(2022·宁波模拟)下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a⊂α,b⊄α,则b∥α答案 D解析A中,a可以在过b的平面内;B中,a与α内的直线也可能异面;C中,两平面可能相交;D中,由直线与平面平行的判定定理知b∥α,正确.2.(2022·呼和浩特模拟)设a,b是两条不同的直线,α,β是两个不同的平面,则α∥β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α答案 D解析对于A,一条直线与两个平面都平行,两个平面不一定平行,故A不正确;对于B,一个平面中的一条直线平行于另一个平面,两个平面不一定平行,故B不正确;对于C,两个平面中的两条直线平行,不能保证两个平面平行,故C不正确;对于D,如图,在直线b上取点B,过点B和直线a确定一个平面γ,交平面β于a′,因为a∥β,所以a∥a′,又a′⊄α,a⊂α,所以a′∥α,又因为b∥α,b∩a′=B,b⊂β,a′⊂β,所以β∥α.3.(2022·广州模拟)如图,在三棱柱ABC-A1B1C1中,AM=2MA1,BN=2NB1,过MN作一平面分别交底面△ABC的边BC,AC于点E,F,则( )A.MF∥EBB.A1B1∥NEC.四边形MNEF为平行四边形D.四边形MNEF为梯形答案 D解析由于B,E,F三点共面,F∈平面BEF,M∉平面BEF,故MF,EB为异面直线,故A错误;由于B1,N,E三点共面,B1∈平面B1NE,A1∉平面B1NE,故A1B1,NE为异面直线,故B错误;∵在平行四边形AA1B1B中,AM=2MA1,BN=2NB1,∴AM∥BN,AM=BN,故四边形AMNB为平行四边形,∴MN∥AB.又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB,显然在△ABC中,EF≠AB,∴EF≠MN,∴四边形MNEF为梯形,故C错误,D正确.4.(2022·杭州模拟)已知P为△ABC所在平面外一点,平面α∥平面ABC,且α交线段PA,PB,PC于点A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC等于( )A.2∶3B.2∶5C.4∶9D.4∶25答案 D解析∵平面α∥平面ABC,∴A′C′∥AC,A′B′∥AB,B′C′∥BC,∴S△A′B′C′∶S△ABC=(PA′∶PA)2,又PA′∶AA′=2∶3,∴PA′∶PA=2∶5,∴S△A′B′C′∶S△ABC=4∶25.5.(多选)(2022·济宁模拟)如图,在下列四个正方体中,A,B为正方体的两个顶点,D,E,F为所在棱的中点,则在这四个正方体中,直线AB与平面DEF平行的是( )答案AC解析对于A,AB∥DE,AB⊄平面DEF,DE⊂平面DEF,∴直线AB与平面DEF平行,故A正确;对于B,如图,取正方体所在棱的中点G,连接FG并延长,交AB延长线于H,则AB与平面DEF相交于点H,故B错误;对于C,AB∥DF,AB⊄平面DEF,DF⊂平面DEF,∴直线AB与平面DEF平行,故C正确;对于D,AB与DF所在平面的正方形对角线有交点B,DF与该对角线平行,∴直线AB与平面DEF相交,故D错误.6.(多选)如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器一边AB 于地面上,再将容器倾斜,随着倾斜程度的不同,有下面几个结论,其中正确的是( )A .没有水的部分始终呈棱柱形B .水面EFGH 所在四边形的面积为定值C .随着容器倾斜程度的不同,A 1C 1始终与水面所在平面平行D .当容器倾斜如图(3)所示时,AE ·AH 为定值 答案 AD解析 根据棱柱的特征(有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行),结合题中图形易知A 正确;由题图可知水面EFGH 的边EF 的长保持不变,但邻边的长却随倾斜程度而改变,可知B 错误;因为A 1C 1∥AC ,AC ⊂平面ABCD ,A 1C 1⊄平面ABCD ,所以A 1C 1∥平面ABCD ,当平面EFGH 不平行于平面ABCD 时,A 1C 1不平行于水面所在平面,故C 错误;当容器倾斜如题图(3)所示时,因为水的体积是不变的,所以棱柱AEH -BFG 的体积V 为定值,又V =S △AEH ·AB ,高AB 不变,所以S △AEH 也不变,即AE ·AH 为定值,故D 正确.7.考查①②两个命题,①⎭⎪⎬⎪⎫m ⊂αl ∥m ⇒l ∥α;②⎭⎪⎬⎪⎫l ∥m m ∥α ⇒l ∥α,它们都缺少同一个条件,补上这个条件就可以使其构成真命题(其中l ,m 为直线,α为平面),则此条件为__________. 答案 l ⊄α解析 ①由线面平行的判定定理知l ⊄α;②由线面平行的判定定理知l ⊄α.8.如图所示,在正四棱柱ABCD —A 1B 1C 1D 1中,E ,F ,G ,H 分别是棱CC 1,C 1D 1,D 1D ,DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 只需满足条件______,就有MN ∥平面B 1BDD 1.(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)答案 点M 在线段FH 上(或点M 与点H 重合) 解析 连接HN ,FH ,FN (图略), 则FH ∥DD 1,HN ∥BD ,∴平面FHN ∥平面B 1BDD 1,只需M ∈FH , 则MN ⊂平面FHN ,∴MN ∥平面B 1BDD 1.9.如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G ,H 分别是BC ,CC 1,C 1D 1,AA 1的中点,求证:(1)BF ∥HD 1; (2)EG ∥平面BB 1D 1D ; (3)平面BDF ∥平面B 1D 1H . 证明 如图.(1)取B 1B 的中点M ,连接HM ,MC 1,易证四边形HMC 1D 1是平行四边形, ∴HD 1∥MC 1. 又MC 1∥BF , ∴BF ∥HD 1.(2)取BD 的中点O ,连接OE ,OD 1, 则OE 綉12DC .又D 1G 綉12DC ,∴OE 綉D 1G .∴四边形OEGD 1是平行四边形, ∴EG ∥D 1O .又D 1O ⊂平面BB 1D 1D ,EG ⊄平面BB 1D 1D , ∴EG ∥平面BB 1D 1D .(3)由(1)知BF ∥HD 1,由题意易证B 1D 1∥BD .又B 1D 1,HD 1⊂平面B 1D 1H ,BF ,BD ⊂平面BDF ,且B 1D 1∩HD 1=D 1,DB ∩BF =B , ∴平面BDF ∥平面B 1D 1H .10.如图,在四棱锥P -ABCD 中,AD ∥BC ,AB =BC =12AD ,E ,F ,H 分别为线段AD ,PC ,CD 的中点,AC 与BE 交于O 点,G 是线段OF 上一点.(1)求证:AP ∥平面BEF ; (2)求证:GH ∥平面PAD . 证明 (1)如图,连接EC , 因为AD ∥BC ,BC =12AD ,所以BC ∥AE ,BC =AE ,所以四边形ABCE 是平行四边形, 所以O 为AC 的中点. 又因为F 是PC 的中点, 所以FO ∥AP , 因为FO ⊂平面BEF ,AP ⊄平面BEF ,所以AP ∥平面BEF .(2)连接FH ,OH ,因为F ,H 分别是PC ,CD 的中点, 所以FH ∥PD ,因为PD ⊂平面PAD ,FH ⊄平面PAD , 所以FH ∥平面PAD .又因为O 是BE 的中点,H 是CD 的中点, 所以OH ∥AD ,因为AD ⊂平面PAD ,OH ⊄平面PAD , 所以OH ∥平面PAD .又FH ∩OH =H ,FH ,OH ⊂平面OHF , 所以平面OHF ∥平面PAD . 又因为GH ⊂平面OHF , 所以GH ∥平面PAD .11.(多选)已知α,β是两个平面,m,n是两条直线.下列命题正确的是( )A.如果m∥n,n⊂α,那么m∥αB.如果m∥α,m⊂β,α∩β=n,那么m∥nC.如果α∥β,m⊂α,那么m∥βD.如果α⊥β,α∩β=n,m⊥n,那么m⊥β答案BC解析如果m∥n,n⊂α,那么m∥α或m⊂α,故A不正确;如果m∥α,m⊂β,α∩β=n,那么m∥n,这就是线面平行推得线线平行的性质定理,故B正确;如果α∥β,m⊂α,那么m∥β,这就是利用面面平行推线面平行的性质定理,故C正确;缺少m⊂α这个条件,故D不正确.12.(2022·福州检测)如图所示,正方体ABCD-A1B1C1D1中,点E,F,G,P,Q分别为棱AB,C1D1,D1A1,D1D,C1C的中点,则下列叙述中正确的是( )A.直线BQ∥平面EFGB.直线A1B∥平面EFGC.平面APC∥平面EFGD.平面A1BQ∥平面EFG答案 B解析过点E,F,G的截面如图所示(H,I分别为AA1,BC的中点),连接A1B,BQ,AP,PC,易知BQ与平面EFG相交于点Q,故A错误;∵A1B∥HE,A1B⊄平面EFG,HE⊂平面EFG,∴A1B∥平面EFG,故B正确;AP⊂平面ADD1A1,HG⊂平面ADD1A1,延长HG与PA必相交,故C错误;易知平面A1BQ与平面EFG有交点Q,故D错误.13.(多选)(2022·临沂模拟)如图1,在正方形ABCD 中,点E 为线段BC 上的动点(不含端点),将△ABE 沿AE 翻折,使得二面角B -AE -D 为直二面角,得到图2所示的四棱锥B -AECD ,点F 为线段BD 上的动点(不含端点),则在四棱锥B -AECD 中,下列说法正确的有( )图1 图2A .B ,E ,C ,F 四点不共面 B .存在点F ,使得CF ∥平面BAE C .三棱锥B -ADC 的体积为定值D .存在点E 使得直线BE 与直线CD 垂直 答案 AB解析 对于A ,假设直线BE 与直线CF 在同一平面上,所以E 在平面BCF 上, 又因为E 在折前线段BC 上,BC ∩平面BCF =C ,所以E 与C 重合,与E 异于C 矛盾, 所以直线BE 与直线CF 必不在同一平面上,即B ,E ,C ,F 四点不共面,故A 正确; 对于B ,如图,当点F 为线段BD 的中点,EC =12AD 时,直线CF ∥平面BAE ,证明如下:取AB 的中点G ,连接GE ,GF , 则EC ∥FG 且EC =FG ,所以四边形ECFG 为平行四边形, 所以FC ∥EG ,又因为EG ⊂平面BAE , 则直线CF 与平面BAE 平行,故B 正确;对于C ,在三棱锥B -ADC 中,因为点E 的移动会导致点B 到平面ACD 的距离发生变化,所以三棱锥B -ADC 的体积不是定值,故C 不正确;对于D ,过D 作DH ⊥AE 于H ,因为平面BAE ⊥平面AECD ,平面BAE ∩平面AECD =AE ,所以DH ⊥平面BAE ,所以DH ⊥BE ,若存在点E 使得直线BE 与直线CD 垂直,DH ⊂平面AECD ,且DC ⊂平面AECD ,DH ∩DC =D ,所以BE ⊥平面AECD ,所以BE ⊥AE ,与△ABE 是以B 为直角的三角形矛盾,所以不存在点E 使得直线BE 与直线CD 垂直,故D 不正确.14.如图,在长方体ABCD -A 1B 1C 1D 1中,AD =DD 1=1,AB =3,E ,F ,G 分别是AB ,BC ,C 1D 1的中点,点P 在平面ABCD 内,若直线D 1P ∥平面EFG ,则线段D 1P 长度的最小值是________.答案72解析 如图,连接D 1A ,AC ,D 1C .因为E ,F ,G 分别为AB ,BC ,C 1D 1的中点, 所以AC ∥EF ,又EF ⊄平面ACD 1,AC ⊂平面ACD 1, 则EF ∥平面ACD 1.同理可得EG ∥平面ACD 1,又EF ∩EG =E ,EF ,EG ⊂平面EFG ,所以平面ACD 1∥平面EFG . 因为直线D 1P ∥平面EFG , 所以点P 在直线AC 上.在△ACD 1中,易得AD 1=2,AC =2,CD 1=2, 所以1AD C S △=12×2×22-⎝⎛⎭⎪⎫222=72, 故当D 1P ⊥AC 时,线段D 1P 的长度最小,最小值为7212×2=72.15.(2022·合肥市第一中学模拟)正方体ABCD -A 1B 1C 1D 1的棱长为1,点M ,N 分别是棱BC ,CC 1的中点,动点P 在正方形BCC 1B 1(包括边界)内运动,且PA 1∥平面AMN ,则PA 1的长度范围为( )A.⎣⎢⎡⎦⎥⎤1,52B.⎣⎢⎡⎦⎥⎤324,52C.⎣⎢⎡⎦⎥⎤324,32 D.⎣⎢⎡⎦⎥⎤1,32答案 B解析 取B 1C 1的中点E ,BB 1的中点F ,连接A 1E ,A 1F ,EF , 取EF 的中点O ,连接A 1O ,如图所示,∵点M ,N 分别是棱长为1的正方体ABCD -A 1B 1C 1D 1中棱BC ,CC 1的中点, ∴AM ∥A 1E ,MN ∥EF ,∵AM ∩MN =M ,A 1E ∩EF =E ,AM ,MN ⊂平面AMN ,A 1E ,EF ⊂平面A 1EF , ∴平面AMN ∥平面A 1EF ,∵动点P 在正方形BCC 1B 1(包括边界)内运动, 且PA 1∥平面AMN ,∴点P 的轨迹是线段EF ,∵A 1E =A 1F =12+⎝ ⎛⎭⎪⎫122=52,EF =1212+12=22,∴A 1O ⊥EF ,∴当P 与O 重合时,PA 1的长度取最小值A 1O , A 1O =⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫242=324,当P 与E (或F )重合时,PA 1的长度取最大值A 1E 或A 1F ,A 1E =A 1F =52.∴PA 1的长度范围为⎣⎢⎡⎦⎥⎤324,52.16.如图,正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为AB 1,A 1C 1上的点,A 1N =AM .(1)求证:MN ∥平面BB 1C 1C ;(2)求MN 的最小值.(1)证明 如图,作NE ∥A 1B 1交B 1C 1于点E ,作MF ∥AB 交BB 1于点F ,连接EF , 则NE ∥MF .∵NE ∥A 1B 1,∴NEA 1B 1=C 1NA 1C 1.又MF ∥AB ,∴MF AB =B 1MAB 1,∵A 1C 1=AB 1,A 1N =AM ,∴C 1N =B 1M .∴NE A 1B 1=MF AB,又AB =A 1B 1,∴NE =MF .∴四边形MNEF 是平行四边形,∴MN ∥EF , 又MN ⊄平面BB 1C 1C ,EF ⊂平面BB 1C 1C , ∴MN ∥平面BB 1C 1C .(2)解 设B 1E =x ,∵NE ∥A 1B 1, ∴B 1E B 1C 1=A 1NA 1C 1.又∵MF ∥AB ,∴B 1F BB 1=B 1M AB 1,∵A 1N =AM ,A 1C 1=AB 1=2a ,B 1C 1=BB 1=a ,B 1E =x ,∴B 1E B 1C 1+B 1F BB 1=A 1N A 1C 1+B 1MAB 1,∴x a +B 1F a =1,∴B 1F =a -x ,从而MN =EF =B 1E 2+B 1F 2 =x 2+a -x2 =2⎝ ⎛⎭⎪⎫x -a 22+⎝ ⎛⎭⎪⎫a 22, ∴当x =a 2时,MN 的最小值为22a .。
直线与平面、平面与平面平行的判定(附答案)

直线与平面、平面与平面平行的判定[学习目标] 1.理解直线与平面平行、平面与平面平行判定定理的含义.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用.3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题.知识点一直线与平面平行的判定定理语言叙述符号表示图形表示平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行⎭⎪⎬⎪⎫a⊄αb⊂αa∥b⇒a∥α思考若一条直线平行于一个平面内的一条直线,则这条直线和这个平面平行吗答根据直线与平面平行的判定定理可知该结论错误.知识点二平面与平面平行的判定定理语言叙述符号表示图形表示一个平面内的两条相交直线与另一个平面平行,则这两个平面平行⎭⎪⎬⎪⎫a⊂α,b⊂αa∩b=Aa∥β,b∥β⇒α∥β思考如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面也平行吗答不一定.这条直线与另一个平面平行或在另一个平面内.题型一直线与平面平行的判定定理的应用例1 如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)EH∥平面BCD;(2)BD∥平面EFGH.证明(1)∵EH为△ABD的中位线,∴EH∥BD.∵EH⊄平面BCD,BD⊂平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊄平面EFGH,EH⊂平面EFGH,∴BD∥平面EFGH.跟踪训练1 在四面体A-BCD中,M,N分别是△ABD和△BCD的重心,求证:MN∥平面ADC.证明如图所示,连接BM,BN并延长,分别交AD,DC于P,Q两点,连接PQ.因为M,N分别是△ABD和△BCD的重心,所以BM∶MP=BN∶NQ=2∶1.所以MN∥PQ.又因为MN⊄平面ADC,PQ⊂平面ADC,所以MN∥平面ADC.题型二面面平行判定定理的应用例2 如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.证明由棱柱性质知,B1C1∥BC,B1C1=BC,又D,E分别为BC,B1C1的中点,所以C1E綊DB,则四边形C1DBE为平行四边形,因此EB∥C1D,又C1D⊂平面ADC1,EB⊄平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1綊BD,所以四边形EDBB1为平行四边形,则ED綊B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED綊A1A,则四边形EDAA1为平行四边形,所以A1E∥AD,又A1E⊄平面ADC1,AD⊂平面ADC1,所以A1E∥平面ADC1.由A1E∥平面ADC1,EB∥平面ADC1,A1E⊂平面A1EB,EB⊂平面A1EB,且A1E∩EB=E,所以平面A1EB∥平面ADC1.跟踪训练2 已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,点G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.求证:(1)E,B,F,D1四点共面;(2)平面A1GH∥平面BED1F.证明(1)∵AE=B1G=1,∴BG=A1E=2.又∵BG∥A1E,∴四边形A1EBG是平行四边形,∴A1G∥BE.连接FG.∵C1F=B1G,C1F∥B1G,∴四边形C1FGB1是平行四边形,∴FG=C1B1=D1A1,FG∥C1B1∥D1A1,∴四边形A1GFD1是平行四边形,∴A1G∥D1F,∴D1F∥EB.故E,B,F,D1四点共面.(2)∵H是B1C1的中点,∴B1H=32 .又∵B 1G =1,∴B 1G B 1H =23.又FC BC =23,且∠FCB =∠GB 1H =90°, ∴△B 1HG ∽△CBF ,∴∠B 1GH =∠CFB =∠FBG ,∴HG ∥FB .又由(1)知,A 1G ∥BE ,且HG ∩A 1G =G ,FB ∩BE =B , ∴平面A 1GH ∥平面BED 1F .题型三 线面平行、面面平行判定定理的综合应用例3 在正方体ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点.问:当点Q 在什么位置时,平面D 1BQ ∥平面PAO 请说明理由.解 当Q 为CC 1的中点时,平面D 1BQ ∥平面PAO .理由如下:连接PQ .∵Q 为CC 1的中点,P 为DD 1的中点, ∴PQ ∥DC ∥AB ,PQ =DC =AB ,∴四边形ABQP 是平行四边形,∴QB ∥PA .又∵O为DB的中点,∴D1B∥PO.又∵PO∩PA=P,D1B∩QB=B,∴平面D1BQ∥平面PAO.跟踪训练3 如图,三棱柱ABC-A1B1C1的底面为正三角形,侧棱A1A⊥底面ABC,E,F分别是棱CC1,BB1上的点,EC=是线段AC上的动点,当点M在何位置时,BM∥平面AEF请说明理由.解当M为AC中点时,BM∥平面AEF.理由如下:方法一如图1,取AE的中点O,连接OF,OM.∵O,M分别是AE,AC的中点,∴OM∥EC,OM=12 EC.又∵BF∥CE,EC=2FB,∴OM∥BF,OM=BF,∴四边形OMBF为平行四边形,∴BM∥OF.又∵OF⊂面AEF,BM⊄面AEF,∴BM∥平面AEF.方法二如图2,取EC的中点P,连接PM,PB.∵PM是△ACE的中位线,∴PM∥AE.∵EC=2FB=2PE,CC1∥BB1,∴PE=BF,PE∥BF,∴四边形BPEF是平行四边形,∴PB∥EF.又∵PM⊄平面AEF,PB⊄平面AEF,∴PM∥平面AEF,PB∥平面AEF.又∵PM∩PB=P,∴平面PBM∥平面AEF.又∵BM⊂面PBM,∴BM∥平面AEF.面面平行的判定例4 已知在正方体ABCD-A′B′C′D′中,M,N分别是A′D′,A′B′的中点,在该正方体中是否存在过顶点且与平面AMN平行的平面若存在,试作出该平面,并证明你的结论;若不存在,请说明理由.分析根据题意画出正方体,根据平面AMN的特点,试着在正方体中找出几条平行于该平面的直线,然后作出判断,并证明.解如图,与平面AMN平行的平面有以下三种情况:下面以图①为例进行证明.如图①,取B′C′的中点E,连接BD,BE,DE,ME,B′D′,可知四边形ABEM是平行四边形,所以BE∥AM.又因为BE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.因为MN是△A′B′D′的中位线,所以MN∥B′D′.因为四边形BDD′B′是平行四边形,所以BD∥B′D′.所以MN∥BD.又因为BD⊂平面BDE,MN⊄平面BDE,所以MN∥平面BDE.又因为AM⊂平面AMN,MN⊂平面AMN,且AM∩MN=M,所以由平面与平面平行的判定定理可得,平面AMN∥平面BDE.1.过直线l外两点,作与l平行的平面,则这样的平面( )A.不可能作出B.只能作出一个C.能作出无数个D.上述三种情况都存在2.经过平面α外两点,作与α平行的平面,则这样的平面可以作( )个或2个个或1个个个3.若线段AB,BC,CD不共面,M,N,P分别为线段AB,BC,CD的中点,则直线BD与平面MNP的位置关系是( )A.平行B.直线在平面内C.相交D.以上均有可能4.在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是( )A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G5.梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α的位置关系是________.一、选择题1.下列说法正确的是( )①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;④若一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.A.①③B.②④C.②③④D.③④2.平面α与平面β平行的条件可以是( )A.α内有无穷多条直线与β平行B.直线a∥α,a∥β,且直线a不在α与β内C.直线a⊂α,直线b⊂β,且b∥α,a∥βD.α内的任何直线都与β平行3.六棱柱的表面中,互相平行的平面最多有( )对对对对4.如果直线a平行于平面α,那么下列命题正确的是( )A.平面α内有且只有一条直线与a平行B.平面α内有无数条直线与a平行C.平面α内不存在与a平行的直线D.平面α内的任意直线与直线a都平行5.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )∥平面EFG,且四边形EFGH是平行四边形∥平面BCD,且四边形EFGH是梯形∥平面ABD,且四边形EFGH是平行四边形∥平面ADC,且四边形EFGH是梯形6.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为( )A.平行B.相交C.平行或相交D.可能重合7.已知直线l,m,平面α,β,下列命题正确的是( )∥β,l⊂α⇒α∥β∥β,m∥β,l⊂α,m ⊂α⇒α∥β∥m,l⊂α,m⊂β⇒α∥β∥β,m∥β,l⊂α,m⊂α,l∩m=M⇒α∥β二、填空题8.三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的关系为________.9.如图是正方体的平面展开图.在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是________.10.右图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面五个结论:①平面EFGH∥平面ABCD;②PA∥平面BDG;③EF∥平面PBC;④FH∥平面BDG;⑤EF∥平面BDG;其中正确结论的序号是________.三、解答题11.如图,在已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.12.如图,在正四棱柱ABCD-A1B1C1D1中,M是棱AB的中点,点N在侧面AA1D1D上运动,点N满足什么条件时,MN∥平面BB1D1D当堂检测答案1.答案D解析设直线外两点为A、B,若直线AB∥l,则过A、B可作无数个平面与l平行;若直线AB与l异面,则只能作一个平面与l平行;若直线AB与l相交,则过A、B没有平面与l平行.2.答案B解析①当经过两点的直线与平面α平行时,可作出一个平面β使β∥α.②当经过两点的直线与平面α相交时,由于作出的平面又至少有一个公共点,故经过两点的平面都与平面α相交,不能作出与平面α平行的平面.故满足条件的平面有0个或1个.3.答案A解析连接NP,因为N、P分别是BC、CD的中点,M是AB的中点,AB、BC、CD不共面,所以直线BD不在平面MNP上.∴直线BD与平面MNP平行.4.答案A解析如图,∵EG∥E1G1,EG⊄平面E1FG1,E1G1⊂平面E1FG1,∴EG∥平面E1FG1,又G1F∥H1E,同理可证H1E∥平面E1FG1,又H1E∩EG=E,∴平面E1FG1∥平面EGH1.5.答案CD∥α解析因为AB∥CD,AB⊂平面α,CD⊄平面α,由线面平行的判定定理可得CD∥α.课时精练答案一、选择题1.答案D解析如图,长方体ABCD-A1B1C1D1中,在平面ABCD内,在AB上任取一点E,过点E作EF∥AD,交CD于点F,则由线面平行的判定定理,知EF,BC都平行于平面ADD1A1,用同样的方法可以在平面ABCD内作出无数条直线都与平面ADD1A1平行,但是平面ABCD与平面ADD1A1不平行,因此①②都错;③正确,事实上,因为一个平面内任意一条直线都平行于另一个平面,所以这两个平面必无公共点(要注意“任意一条直线”与“无数条直线”的区别);④是平面与平面平行的判定定理,正确.2.答案D解析 对于A 项,当α与β相交时,α内也有无数条直线都与交线平行,故A 错误;对于B 项,当a 平行于α与β的交线时,也能满足,但此时α与β相交,故B 错误;对于C 项,当a 和b 都与α与β的交线平行时,也能满足,但此时α与β相交,故C 错误;对于D 项,α内的任何直线都与β平行,故在一个平面内存在两条相交直线平行于另一平面,故D 正确. 3.答案 C解析 侧面中有3对,对面相互平行,上下两底面也相互平行. 4.答案 B解析 如图,直线B 1C 1∥平面ABCD ,B 1C 1∥BC ,B 1C 1∥AD ,B 1C 1∥EF (E ,F 为中点)等,平面ABCD 内平行于BC 的所有直线均与B 1C 1平行.但AB与B 1C 1不平行.5.答案 B解析 易证EF ∥平面BCD .由AE ∶EB =AF ∶FD ,知EF ∥BD ,且EF =15BD .又因为H ,G 分别为BC ,CD 的中点,所以HG∥BD,且HG=12BD.综上可知,EF∥HG,EF≠HG,所以四边形EFGH是梯形,且EF∥平面BCD.6.答案C解析若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交.7.答案D解析如图所示,在长方体ABCDA1B1C1D1中,AB∥CD,则AB∥平面DC1,AB⊂平面AC,但是平面AC与平面DC1不平行,所以A错误;取BB1的中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面⊂平面BC1,B1C1⊂平面BC1,但是平面AC与平面BC1不平行,所以B错误;可证AD∥B1C1,AD⊂平面AC,B1C1⊂平面BC1,又平面AC与平面BC1不平行,所以C错误;很明显D是面面平行的判定定理,所以D正确.二、填空题8.答案平行解析如图,延长AG交BC于F,连接SF,则由G为△ABC的重心知AG∶GF=2,又AE∶ES=2,∴EG∥SF,又SF⊂平面SBC,EG⊄平面SBC,∴EG∥平面SBC.9.答案①②③④解析以ABCD为下底面还原正方体,如图:则易判定四个命题都是正确的.10.答案①②③④解析把图形还原为一个四棱锥,然后根据线面、面面平行的判定定理判断即可.三、解答题11.证明因为PM∶MA=BN∶ND=PQ∶QD,所以MQ∥AD,NQ∥BP.因为BP⊂平面PBC,NQ⊄平面PBC,所以NQ∥平面PBC.又因为底面ABCD为平行四边形,所以BC∥AD,所以MQ∥BC.因为BC⊂平面PBC,MQ⊄平面PBC,所以MQ∥平面PBC.又因为MQ∩NQ=Q,所以根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.12.解如图,在正四棱柱ABCD-A1B1C1D1中,分别取棱A1B1,A1D1,AD的中点E,F,G,连接ME,EF,FG,GM.因为M是AB的中点,所以ME∥AA1∥FG,且ME=AA1=FG.所以四边形MEFG是平行四边形.因为ME∥BB1,BB1⊂平面BB1D1D,ME⊄平面BB1D1D,所以ME∥平面BB1D1D.在△A1B1D1中,因为EF∥B1D1,B1D1⊂平面BB1D1D,EF⊄平面BB1D1D,所以EF∥平面BB1D1D.又因为ME∩EF=E,且ME⊂平面MEFG,EF⊂平面MEFG,所以平面MEFG∥平面BB1D1D.在FG上任取一点N,连接MN,所以MN⊂平面MEFG.所以MN与平面BB1D1D无公共点.所以MN∥平面BB1D1D.总之,当点N在平面AA1D1D内的直线FG上(任意位置)时,都有MN∥BB1D1D,即当点N在矩形AA1D1D中过A1D1与AD的中点的直线上运动时,都有MN∥平面BB1D1D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线和平面平行与平面与平面平行证明题
专题训练
1、、如图,在正方体1111ABCD A B C D 中,E 是1AA 的中点,求证:1//
A C 平面BDE 。
2、如图: 平行四边形 ABCD 和平行四边形 CDEF 有一条公共边
CD ,
M 为FC 的中点 , 证明: AF // 平面MBD.
A 1
E
D 1
C 1
B 1
D
C
B
A
M
A
B
C
D
E
F
3、如图6-9,A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证:
面A B C '''∥ABC 面.
4、 在长方体ABCD —A1B1C1D1中. (1)作出过直线AC 且与直线BD1平行的 截面,并说明理由.
(2)设E ,F 分别是A1B 和B1C 的中点, 求证直线EF//平面ABCD.
A
B
C
C 1
D
A 1
B 1
D 1
5、、已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,且EH∥FG.
求证:EH∥BD. (12分)
6、
P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证://
PC平面BDQ.(自己作图)
H
G F
E
D
B
A
C
7、
如图,α//a ,A 是α的另一侧的点,a D C B ∈,,,线段AB ,AC ,AD 交α
于E ,F ,G ,若4=BD ,4=CF ,5=AF ,则EG =___________.
8、求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.。
