人教版初中数学中考复习专题 四点共圆巧解中考题(28张ppt)
人民教育出版社九级数学上册 第二十四章 数学活动 探究四点共圆的条件(共19张PPT)

数学活动
探究四点共圆的条件
创设情境,发现问题
四个学生正在做投圈游戏,他们呈“一”字 型排开,这样的队形对每个人公平吗?
创设情境,发现问题
你认为他们应当排成什么样的队形?
∴过A、B、C、D四点可以作一个圆 ∵四边形ABCD内接于⊙O (圆的内接四边形的对角互补) ∵BF与BE 的和小于一个圆周 ∠CAD=16°,则∠ABD的度数为________ 那么过A、B、C三点作圆,则点D在圆外 ③ 任意三点都不在同一条直线上的四点 (圆的内接四边形的对角互补) 求证:过点A、B、C、D可作一个圆。 ∵BF与BE 的和小于一个圆周 你能利用圆周角与其所对弧的大小关系证明吗? 如果四名学生站在固定的四个位置,目标物应放在哪,游戏才公平? ∵BF与BE 的和小于一个圆周 如果∠A与∠C所对的弧组成了一个圆周,则∠A+ ∠C=180 ° ③ 任意三点都不在同一条直线上的四点
(能画一个圆)
创设情境,发现问题 不在同一条直线上的三个点确定一个圆
创设情境,发现问题
经过四点画圆
① 都在同一条直线上的四点
分类讨论
(不能画圆)
② 只有三点在同一条直线上的四点 (不能画圆)
③ 任意三点都不在同一条直线上的四点
?
合作探究,获得猜想
过下列四边形的四个顶点能作一个圆吗?试着画 一画
本节课的学习,你有什么收获?
① 都在同一条直线上的四点
在同圆或等圆中,圆周角与其所对弧的大小关系
∵BF与BE 的和小于一个圆周
(圆的内接四边形的对角互补)
一个定理 ② 只有三点在同一条直线上的四点
对角互补的四边形四个顶点共圆。
3、如图,在四边形ABCD 中,∠ABC=∠ADC=90°
2024年云南省人教版九年级中考数学二轮复习课件专题四 圆的证明与计算(35张PPT)

∴∠ODF=30°.∴∠DOF=60°.
∵AB⊥DC,∴DF=FC.
∵BF=OF,AB⊥DC,
∴S△CFB=S△CFO=S△DFO.
×
∴S 阴影部分=S 扇形 BOD=
= π.
[典型例题2] (2023北京)如图所示,圆内接四边形ABCD的对角线AC,BD
交于点E,BD平分∠ABC,∠BAC=∠ADB.
∵CP与☉O相切,∴OC⊥PC.∴∠PCB+∠OCB=90°.
∵AB⊥DC,∴∠PAD+∠ADF=90°.∴∠PCB=∠PAD.
(2)若☉O的直径为4,弦DC平分半径OB,求图中阴影部分的面积.
(2)解:如图②所示,连接 OD,
∵弦 DC 平分半径 OB,∴BF=OF.
在 Rt△ODF 中,OF= OD.
∵AC为☉O的直径,∴∠ABC=90°.
∵BD是∠ABC的平分线,∴∠ABD=∠DBE=45°.
∴∠DOC=2∠DBE=90°.
∵AC∥DE,∴∠ODE=90°,即OD⊥DE.
∵OD是☉O的半径,∴DE是☉O的切线
(2)探究线段BE,CE,DE之间有何数量关系?写出你的结论,并证明.
2
(2)解:DE =CE·BE.证明如下:
2
又∵
2
=
,∴ =
.解得 CE=
2
.
2
2.如图所示,☉O的半径为1,A,P,B,C是☉O上的四个点,
∠APC=∠CPB=60°.
(1)判断△ABC的形状,并说明理由.
解:(1)△ABC是等边三角形.理由如下:
∵∠APC=∠CPB=60°,
专题3.8 四点共圆(隐圆压轴五)(解析版)

∴DG=CG﹣CD= = ,
在 Rt△ADG 中,由勾股定理得
=
=
,
∴
=
=
.
故答案为:6,
.
【变式 1-5】如图,AB⊥BC,AB=5,点 E、F 分别是线段 AB、射线 BC 上的动 点,以 EF 为斜边向上作等腰 Rt△DEF,∠D=90°,连接 AD,则 AD 的最 小值为 .
【答案】 . 【解答】解:连接 BD 并延长,如图,
模型解读:
模型 1:对角互补型: 若∠A+∠C=180º或∠B+∠D=180º, 则 A、B、C、D 四点共圆 模型 2:同侧等角型 (1)若∠A=∠C, 则 A、B、C、D 四点共圆
(2)手拉手(双子型)中的四点共圆 条件:△OCD∽△OAB 结论:①△OAC∽△OBD ②AC 与 BD 交于点 E,必有∠AEB=∠AOB; ③点 E 在△OAB 的外接圆上,即 O、A、B、E 四点共圆.同理:ODCE 也四点共圆.
∴S△ABC=
=
=300 km2.
则当△ADC 的面积最大时,四边形 ABCD 的面积最大.
当 AD=CD 时,DF 最大,此时四边形 ABCD 的面积最大.
在 Rt△ACE 中,AC=
=10 km,AF= AC=5
km,
∵∠ADF=
=30°,
∴DF= AF=5 km,
∴S△ADC=
Hale Waihona Puke ==925 km2.
C.15
【答案】C
【解答】解:∵∠BAC=60°,∠BDC=120°,
∴A、E、D、F 四点共圆,
∵AD 平分∠BAC,
∴∠DAE=∠DAF,
∴DE=DF=6,
2020年九年级中考数学总复习课件:圆 %28共34张PPT%29

第 5页
二 圆心角、弧、弦、弦心距之间的关系
1.圆心角定理 在同圆或等圆中,相等的圆心角所对的⑪__弧____相等、所对的 ⑫__弦____相等、所对的⑬___弦__心__距___相等.如图,在⊙O 中,若∠
︵︵
AOB=∠COD,则AB =CD ,AB=CD,OM=ON. 2.圆心角定理的推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一
第 4页
(1)对称性:圆既是中心对称图形(圆心是对称中心),也 是轴对称图形(任何一条直径所在的直线都是它的对称 轴).
(2)旋转对称性:圆是旋转对称图形(绕圆心旋转任何一 个角度都与原图形重合).
(3)同圆或等圆的半径相等. (4)圆的直径等于同圆或等圆半径的2倍. (5)弧的度数等于它所对圆心角的度数.
(D)
A.4
B.2 2
C. 3
D.2 3
第 17 页
7.(2019·江苏连云港中考)如图,点A、B、C在⊙O上,BC= 6,∠BAC=30°6,则⊙O的半径为_____.
第 18 页
8.(2019·湖南娄底中考)如图,C、D两点在以AB为直径的圆 上,AB=2,∠ACD=30°,则AD=__1___.
第 2页
(1)圆:圆是到定点的距离等于定长的点的集合,这个 定点叫做①__圆__心____,这个定长叫做②__半_径_____.圆心确 定圆的③_位_置______,半径确定圆的④___大_小____.
(2)弧:圆上任意两点间的部分叫做弧;圆上任意一条 直径的两个端点把圆分成两条弧,每一条弧都叫做半 圆.小于半圆的弧叫做⑤___劣_弧____,大于半圆的弧叫 做⑥__优__弧____.
推 周角是 ○23 __9_0_°____; ___9_0_°___;
中考数学复习 PPT课件 (圆与其它知识的联系等64个) 人教版57

•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
19、就算生活让你再蛋疼,也要笑着学会忍。
•
20、当你能飞的时候就不要放弃飞。
•
21、所有欺骗中,自欺是最为严重的。
•
22、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。
•
•
67、心中有理想 再累也快乐
•
68、发光并非太阳的专利,你也可以发光。
•
69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。
•
70、当你的希望一个个落空,你也要坚定,要沉着!
•
71、生命太过短暂,今天放弃了明天不一定能得到。
•
72、只要路是对的,就不怕路远。
•
73、如果一个人爱你、特别在乎你,有一个表现是他还是有点怕你。
,
x y
x2 y2
.
【例5】 已知,关于x的方程(n-1)x2+mx+1=0①有两个 相等的实数根.
(1)求证:关于y的方程m2y2-2my-m2-2n2+3=0②必有两 个不相等的实数根;
(2)若方程①的一根的相反数恰好是方程②的一个根,求 代数式m2n+12n的值. 14
方法小结:
•
4、当你能梦的时候就不要放弃梦。
•
5、龙吟八洲行壮志,凤舞九天挥鸿图。
•
6、天下大事,必作于细;天下难事,必作于易。
•
7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。
•
8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。
•
2024年中考数学常见几何模型全归纳(全国通用)专题31 圆中的重要模型之四点共圆模型(解析版)

专题31圆中的重要模型之四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
【答案】2【分析】首先连接OE,由角器上对应的读数.【详解】解:连接OE,A .13B .52∵在ABC 中,90BAC【答案】30【分析】连接AC 与BD 又易知在Rt ACD △中,【详解】解:连接AC 与∵四边形形ABCD 是矩形,12OA OB OC OD AC又∵DE BF 于E ,即是直角三角形,∴12OE BD ,∴OA OC OD OE ,∴点A B 、、,由旋转的性质可知:AF AB ,【答案】122【分析】(1)根据条件,证明AOD COD△△△△,代入推断即可.(2)通过AOG ABC证明ODF CBF△△,代入推断即可.又∵∵CE CF∴CEF CFE模型2、定边对双直角共圆模型C同侧型异侧型1)定边对双直角模型(同侧型)条件:若平面上A、B、C、D四个点满足90ABD ACD,结论:A、B、C、D四点共圆,其中AD为直径。
2)定边对双直角模型(异侧型)条件:若平面上A、B、C、D四个点满足90ABC ADC,结论:A、B、C、D四点共圆,其中AC为直径。
【点睛】本题考查了圆的直径所对的圆周角为【点睛】此题主要考查圆内接四边形,直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点,解答此题的关键是添加辅助线构造特殊三角形,求出线段.模型3、定边对定角共圆模型条件:如图1,平面上A 、B 、C 、D 四个点满足ADB ACB ,结论:A 、B 、C 、D 四点共圆.条件:如图2,AC 、BD 交于H ,AH CH BH DH ,结论:A B C D 、、、四点共圆.例1.(2023·江苏·九年级假期作业)如图,在Rt ABC 中,∠BAC =90°,∠ABC =40°,将 ABC 绕A 点顺时针旋转得到 ADE ,使D 点落在BC 边上.(1)求∠BAD 的度数;(2)求证:A 、D 、B 、E 四点共圆.【答案】(1)10°;(2)见解析【分析】(1)由三角形内角和定理和已知条件求得∠C 的度数,由旋转的性质得出AC =AD ,即可得出∠ADC =∠C ,最后由外角定理求得∠BAD 的度数;(2)由旋转的性质得到∠ABC =∠AED ,由四点共圆的判定得出结论.【详解】解:(1)∵在Rt ABC 中,∠BAC =90°,∠ABC =40°,∴∠C =50°,∵将 ABC 绕A 点顺时针旋转得到 ADE ,使D 点落在BC 边上,∴AC =AD ,∴∠ADC =∠C =50°,∴∠ADC =∠ABC +∠BAD =50°,∴∠BAD =50°-40°=10°证明(2)∵将 ABC 绕A 点顺时针旋转得到 ADE ,∴∠ABC =∠AED ,∴A 、D 、B 、E 四点共圆.【点睛】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定,解题的关键是理解旋转后的图形与原图形对应边相等,对应角相等.例3.(2022·江苏无锡·中考真题)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=________°;现将△DCE 绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是________.【答案】804##4【分析】利用SAS 证明△BDC ≌△AEC ,得到∠DBC =∠EAC =20°,据此可求得∠BAF 的度数;利用全等三角形的性质可求得∠AFB =60°,推出A 、B 、C 、F 四个点在同一个圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,此时线段AF 长度有最小值,据此求解即可.【详解】解:∵△ABC 和△DCE 都是等边三角形,∴AC =BC ,DC =EC ,∠BAC =∠ACB =∠DCE =60°,∴∠DCB +∠ACD =∠ECA +∠ACD =60°,即∠DCB =∠ECA ,在△BCD 和△ACE 中,CD CE BCD ACE BC AC,∴△ACE ≌△BCD (SAS ),∴∠EAC =∠DBC ,∵∠DBC =20°,∴∠EAC =20°,∴∠BAF =∠BAC +∠EAC =80°;设BF 与AC 相交于点H,如图:∵△ACE ≌△BCD ∴AE =BD ,∠EAC =∠DBC ,且∠AHF =∠BHC ,∴∠AFB =∠ACB =60°,∴A 、B 、C 、F 四个点在同一个圆上,∵点D 在以C 为圆心,3为半径的圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,∴此时线段AF 长度有最小值,在Rt △BCD 中,BC =5,CD =3,∴BD 4,即AE =4,∴∠FDE =180°-90°-60°=30°,∵∠AFB =60°,∴∠FDE =∠FED =30°,∴FD =FE ,过点F 作FG ⊥DE 于点G ,∴DG =GE =32,∴FE =DF =cos 30DG∴AF =AE -FE 80;【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.例4.(2022·贵州遵义·统考中考真题)探究与实践:“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.提出问题:如图1,在线段AC 同侧有两点B ,D ,连接AD ,AB ,BC ,CD ,如果B D ,那么A ,B ,C ,D 四点在同一个圆上.探究展示:如图2,作经过点A ,C ,D 的O ,在劣弧AC 上取一点E (不与A ,C 重合),连接AE ,CE 则180AEC D (依据1)B D ∵180AEC B点A ,B ,C ,E 四点在同一个圆上(对角互补的四边形四个顶点共圆)点B ,D 在点A ,C ,E 所确定的O 上(依据2)点A ,B ,C ,E 四点在同一个圆上(1)反思归纳:上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:__________;依据2:__________.(2)图3,在四边形ABCD 中,12 ,345 ,则4 的度数为__________.(3)拓展探究:如图4,已知ABC 是等腰三角形,AB AC ,点D 在BC 上(不与BC 的中点重合),连接AD .作点C 关于AD 的对称点E ,连接EB 并延长交AD 的延长线于F ,连接AE ,DE .①求证:A ,D ,B ,E与判定,掌握以上知识是解题的关键.模型4、对角互补共圆模型P条件:如图1,平面上A、B、C、D四个点满足ABC ADC,结论:A、B、C、D四点共圆.条件:如图2,BA、CD的延长线交于P,PA PB PD PC,结论:A、B、C、D四点共圆.A.2B.22【答案】A【分析】先根据等腰三角形的性质可得,,,A B E D四点共圆,在以BE为直径的圆上,连接【答案】43/113【分析】过点B作BH AM交F,点A,M,B,C四点共圆,得法求解,12AMBS AM DE△【详解】解析:过点B作BH 于点,如图所示:【答案】52 2【分析】连接BD并延长,利用四点共圆的判定定理得到的性质和圆周角定理得到DBF性质解答即可得出结论.(1)求证:A ,E ,B ,D 四点共圆;(2)如图2,当AD CD 时,O 是四边形AEBD O 的切线;(3)已知1206BC ,,点M 是边BC 的中点,此时P 是四边形出圆心P 与点M 距离的最小值.【答案】(1)证明见解析(2)证明见解析(3)32(3)解:如图所示,作线段AB 的垂直平分线,分别交∵120AB AC BAC ,,∴B课后专项训练1.(2023秋·河北张家口·九年级校考期末)如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为()A.2B.3C.4D.6【答案】D【分析】根据两个直角三角形公共斜边时,四个顶点共圆,结合图形求解可得.【详解】解:如图,以AH为斜边的两个直角三角形,四个顶点共圆(A、F、H、E),以BH为斜边的两个直角三角形,四个顶点共圆(B、F、H、D),以CH为斜边的两个直角三角形,四个顶点共圆(C、D、H、E),以AB为斜边的两个直角三角形,四个顶点共圆(A、E、D、B),以BC为斜边的两个直角三角形,四个顶点共圆(B、F、E、C),以AC为斜边的两个直角三角形,四个顶点共圆(A、F、D、C),共6组.故选D.【点睛】本题考查四点共圆的判断方法.解题的关键是明确有公共斜边的两个直角三角形的四个顶点共圆.,.下2.(2023·安徽合肥·校考一模)如图,O是AB的中点,点B,C,D到点O的距离相等,连接AC BD列结论不一定成立的是()A .12B .3=4C .180ABC ADCD .AC 平分BAD【答案】D 【分析】以点O 为圆心,OA 长为半径作圆.再根据圆内接四边形的性质,圆周角定理逐项判断即可.【详解】如图,以点O 为圆心,OA 长为半径作圆.由题意可知:OA OB OC OD .即点A 、B 、C 、D 都在圆O 上.A .∵ AB AB ,∴12 ,故A 不符合题意;B .∵ BCBC ,∴3=4 ,故B 不符合题意;C .∵四边形ABCD 是O 的内接四边形,∴180ABC ADC ,故C 不符合题意;D .∵ BC 和CD不一定相等,∴BAC 和DAC 不一定相等,∴AC 不一定平分BAD ,故D 符合题意.故选:D .【点睛】本题考查圆周角定理及其推论,充分理解圆周角定理是解答本题的关键.3.(2023·江苏宿迁·九年级校考期末)如图,在Rt ABC △中,90ACB ,3BC ,4AC ,点P 为平面内一点,且CPB A ,过C 作CQ CP 交PB 的延长线于点Q ,则CQ 的最大值为()【点睛】本题考查相似三角形的判定和性质以及四点共圆,掌握同圆或等圆中,同弧所对的圆周角相等确定四点共圆,利用相似三角形性质得到线段间等量关系是解题关键.4.(2023·北京海淀·九年级校考期中)如图,点接AC,BD.请写出图中任意一组互补的角为【答案】DAB【分析】首先判断出点【答案】130【分析】根据题意得到四边形【详解】解:由题意得到∴四边形ABCD为圆∵∠ABC=50°,∴∠【点睛】此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.6.(2023·浙江金华·A.3B.1∵PE AB 于点E ,PD AC 于点,∴90AEP ADP ,∴180AEP ADP ,∴A 、E 、D 四点共圆,PA 是直径,在Rt PDC 中,45C ,∴△是等腰直角三角形,45APD ∴APD △也是等腰直角三角形,45PAD ,∴PED PAD ∴45AED ,∴AED C ,∵EAD CAB ,∴AED ∽设2AD x ,则2PD DC x ,22x ,如图2,取AP 的中点O 则2AO OE OP x ,∵604515EAP BAC PAD ,过E 作EM AP 于M ,则EM x,cos30OM OE ,∴36222OM x x ,∴6226222AM x x x ,由勾股定理得: 222226222AE AM EM x x +【答案】3632 /323 【分析】数形结合,根据动点的运动情况判断点【详解】解:如图旋转,连接以BC 为直径作O ,以AE 为半径作在ABD △和ACE △中AB AC AD AE BAD CAEPBC PBA ACB PBC 90BAC BPC EAD ∵,122AB ∵,A 的半径为62∴又∵90BAC EAD ,CAD,∵33BC ,OP BC∵MQ,MC与圆O相切,1QOM COM COP 【答案】(1)见详解(2)证明:如下图所示由题意可知AC 逆时针旋转90得到边AE ,90E ACB ,则90ACB ∵,AE BF ∥,90 ∵,90EFC ,,F ,E 四点共圆..∵四边形ABCD是菱形,AC,且 GOC GCO90==∵, 点90DHC DOC=BDF OCH=,且BF OM ∵, 点==90AED AOD尝试应用如图2,点D 为等腰Rt ABC △外一点,AB AC ,BD CD ,过点A 的直线分别交DB 的延长线和CD 的延长线于点N ,M ,求证:12ABN ACM S S AN AM △△.问题拓展如图3,ABC 中,AB AC ,点D ,E 分别在边AC ,BC 上,60BDA BEA ,AE ,BD ,直接写出BE 的长度(用含a ,b 的式子)∵ABC 为等腰直角三角形,∴AB AC , 又∵BD CD ,即:=90BDC ,∴A 、B 在ABN 与ACE △中,AB AC ABN ACE BN CE,∴∴BAN BAE CAE BAE BAC ∴1122AME AMC S AE AM AN AM S S △△∴60AFB BAF ABF ,AB AF AC ,∵60BDA BEA ,∴A 、D 、E 、B 、F 五点共圆,则:13 ,24 ,60BEF AEB ,【答案】问题情境:见解析;问题解决:(1)102;(2)13522【分析】[问题情境]连结AC ,取AC 的中点O ,连结OB 、OD ,根据直角三角形斜边上的中线等于斜边的一半,可得OD OA OC OB ,以此即可证明;[问题解决](1)根据题意可得225AE AD DE ,由[问题情境]结论可知A 、D 、E 、据圆周角定理以及正方形的性质可得45PDE PAE ,则PAE △为等腰直角三角形,设AP 长为a ,根据勾股定理列出方程,求解即可;(2)由[问题情境]结论可知A 、D 、E 、P 四点共圆,过点O 作OG AD 于点G ,作OH 接OB 交O 于点P ,连接PB ,根据题意可得四边形MBNP 为矩形,则要求MN 的最小值,即求值,根据平行线的性质和中点的定义可得OG 为ADE V 的中位线,得1AG ,12OG ,同理可证四边形1【翻折】(1)如图1,将DEF 沿线段AB 翻折,连接CF ,下列对所得四边形ACBF 的说法正确的是平分CBF 、CAF ,②AB 、CF 互相平分,③12ACBF S AB CF 四边形,④A 、C 、B 、F 四点共圆.AB 垂直平分CF ,故②ABC ABF ACBF S S S 四边形1122AB AB FG 12AB CG 取AB 的中点O ,连接CO FO ,ABC ABF △、△均为直角三角形,∴OB OC OA OF ,∴A 、B 、F 四点共圆,故()沿线段向左平移,∴AB CF ,CF BE 的中点,∴BE BD BF特殊情况分析:(1)如图1,正方形ABCD 中,点P 为对角线时针旋转ADC 的度数,交直线BC 于点Q .小明的思考如下:连接DQ ,∵AD CQ ∥,90ADC DCQ ,∴ACQ DAC ∵90DPQ ,∴180DPQ DCQ ,∴点D P Q 、、PDQ PCQ DQP PCD∵在菱形ABCD 中BC AD ∥,180ADC DCQ ,DPQ ADC ,∵180DPQ DCQ ,∴点P C Q 、、、共圆,∴DQP ACD ,ACB PDQ ,∵AC 为菱形ABCD 的对角线,ACB ACD ,∴PDQ DQP ,∴ DP PQ ;(3)解:3PQ 或3.由于点P 为对角线AC 上一个动点,分两类情况讨论如下:所示:180302ADC ACD,。
中考数学复习 PPT课件 (圆与其它知识的联系等64个) 人教版17

•
80、乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。
•
67、心中有理想 再累也快乐
•
68、发光并非太阳的专利,你也可以发光。
•
69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。
•
70、当你的希望一个个落空,你也要坚定,要沉着!
•
71、生命太过短暂,今天放弃了明天不一定能得到。
•
72、只要路是对的,就不怕路远。
•
73、如果一个人爱你、特别在乎你,有一个表现是他还是有点怕你。
•
3、现在决定未来,知识改变命运。
•
4、当你能梦的时候就不要放弃梦。
•
5、龙吟八洲行壮志,凤舞九天挥鸿图。
•
6、天下大事,必作于细;天下难事,必作于易。
•
7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。
•
8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。
•
9、永远不要逃避问题,因为时间不会给弱者任何回报。
(3)求出总运费最低的调运方案,最低运费 是多少?
三、甲、乙两个仓库要向A、B两地运送水泥,已知甲库可调出 100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨 水泥,两库到A、B两地的路程和运费如下表(表中运费栏“元/ 吨·千米”表示每吨水泥运送1千米所需人民币):
路程(千米)
运费(元/吨·千米)
甲库
乙库
甲库 乙库
A地
20
15
12
12
B地
25
20
10
8
(1)设甲库运往A地水泥x吨,求总运费y(元)关于 x(吨)的函数关系式,
(2)当甲乙两库各运往A、B两地多少吨水泥时,总运费 最省?最省的总运费是多少 ?
中考数学几何模型专题11四点共圆模型(学生版) 知识点+例题

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题11四点共圆模型若四个点到一个定点的距离相等,则这四个点共圆.如图,若OA =OB =OC =OD ,则A ,B ,C ,D 四点在以点O 为圆心、OA 为半径的圆上.模型2:对角互补共圆模型2.若一个四边形的一组对角互补,则这个四边形的四个顶点共圆.如图,在四边形ABCD 中, 若∠A +∠C =180°(或∠B +∠D =180°)则A ,B ,C ,D 四点在同一个圆上.拓展:若一个四边形的外角等于它的内对角,则这个四边形的四个顶点共圆.如图,在四边形ABCD 中,∠CDE 为外角,若∠B =∠CDE ,则A ,B ,C ,D 四点在同一个圆上.模型3:定弦定角共圆模型若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆如图,点A ,D 在线段BC 的同侧,若∠A =∠D ,则A ,B ,C ,D 四点在同一个圆上.12cm 的正方形ABCD 中,点E 从点D 出发,沿边DC 以1cm/s 的速度向点C 运动,同时,点F 从点C 出发,沿边CB 以1cm/s 的速度向点B 运动,当点E 达到点C 时,两点同时停止运动,连接AE 、DF 交于点P ,设点E .F DDD运动时间为t秒.回答下列问题:(1)如图1,当t为多少时,EF的长等于4√5cm?(2)如图2,在点E、F运动过程中,①求证:点A、B、F、P在同一个圆(①O)上;①是否存在这样的t值,使得问题①中的①O与正方形ABCD的一边相切?若存在,求出t值;若不存在,请说明理由;①请直接写出问题①中,圆心O的运动的路径长为_________.【例2】(2022·吉林白山·八年级期末)(1)如图①,△OAB、△OCD的顶点O重合,且∠A+∠B+∠C+∠D=180°,则①AOB+①COD=______°;(直接写出结果)(2)连接AD、BC,若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.①如图①,如果∠AOB=110°,那么∠COD的度数为_______;(直接写出结果)①如图①,若∠AOD=∠BOC,AB与CD平行吗?为什么?【例3】(2020·四川眉山·一模)问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=12∠BAC=60°,于是BCAB=2BDAB=√3;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.①求证:△ADB≌△AEC;①请直接写出线段AD,BD,CD之间的等量关系式;拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM 的对称点E,连接AE并延长交BM于点F,连接CE,CF.①证明△CEF是等边三角形;①若AE=5,CE=2,求BF的长.【例4】(2022·全国·九年级课时练习)定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.已知四边形ABCD是圆美四边形.(1)求美角∠A的度数;(2)如图1,若⊙O的半径为5,求BD的长;(3)如图2,若CA平分∠BCD,求证:BC+CD=AC.一、解答题1.(2022·辽宁葫芦岛·一模)射线AB与直线CD交于点E,①AED=60°,点F在直线CD 上运动,连接AF,线段AF绕点A顺时针旋转60°得到AG,连接FG,EG,过点G作GH⊥AB 于点H.(1)如图1,点F和点G都在射线AB的同侧时,EG与GH的数量关系是______;(2)如图2,点F和点G在射线AB的两侧时,线段EF,AE,GH之间有怎么样的数量关系?并证明你的结论;(3)若点F和点G都在射线AB的同侧,AE=1,EF=2,请直接写出HG的长.2.(2022·上海宝山·九年级期末)如图,已知正方形ABCD,将AD绕点A逆时针方向旋转n°(0<n<90)到AP的位置,分别过点C、D作CE⊥BP,DF⊥BP,垂足分别为点E、F.(1)求证:CE=EF;(2)联结CF,如果DPCF =13,求∠ABP的正切值;(3)联结AF,如果AF=√22AB,求n的值.3.(2022·重庆市育才中学九年级期末)在等边△ABC中,D是边AC上一动点,连接BD,将BD绕点D顺时针旋转120°,得到DE,连接CE.。
(完整版)初三上专题四点共圆
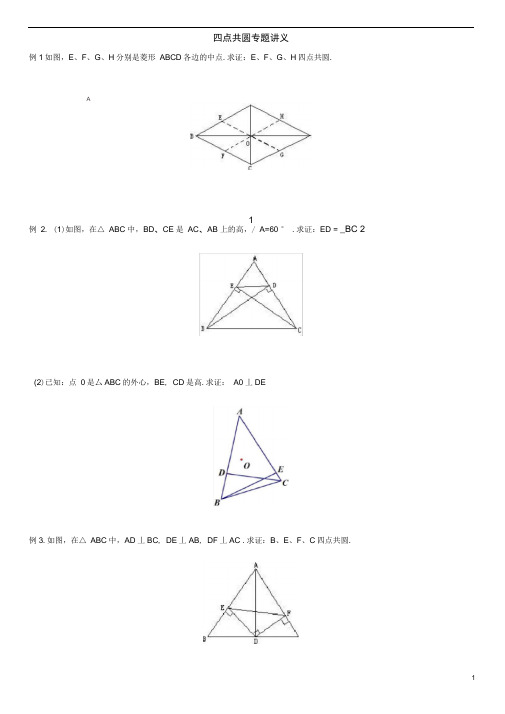
四点共圆专题讲义例1如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.A1例2. (1)如图,在△ ABC 中,BD、CE 是AC、AB 上的高,/ A=60 ° .求证:ED = _BC 2(2)已知:点0是厶ABC的外心,BE, CD是高.求证:A0丄DE例3.如图,在△ ABC中,AD丄BC, DE丄AB, DF丄AC .求证:B、E、F、C四点共圆.〔、〈* ---- 空R;°7、 / f —*ff A OA=OB=OC/ ADC= / ABC=90°/ ACD= / ABD=90°/ B+ / D=180。
或/A+ / BCD=180。
或/A= / DCE/ A= / D 或/ B= /C1. ______________________________________________________2. _______________________________________________________3.________________________________________________________4.例4•求证:圆内接四边形对边乘积的和等于对角线的乘积,即图中练习1.在△ ABC中,BA BC , BAC , M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2得到线段PQ .(1)若60且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,请补全图形,并写出/ CDB 的度数;(2)在图2中,点P不与点B, M重合,线段CQ的延长线与射线BM交于点D,猜想/ CDB的大小(用含的代数式表示),并加以证明;(3)对于适当大小的,当点P在线段BM上运动到某一位置(不与点B, M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ = QD,请直接写出的范围.AB • CD + BC • AD=AC • BD .练习2.在△ ABC中,/ A=30°, AB=2j3,将△ ABC绕点B顺时针旋转(0° < <90°),得到△ DBE,其中点A的对应点是点D,点C的对应点是点E,AC、DE相交于点F,连接BF.(1)如图1,若=60°,线段BA绕点B旋转得到线段BD.请补全△ DBE,并直接写出/ AFB的度数;(2)如图2,若=90°,求/ AFB的度数和BF的长;(3)如图3,若旋转(0 ° < <90 °),请直接写出/ AFB的度数及BF的长(用含的代数式表示)•练习3 .已知,点P是/ MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON 于点B,且使/ APB+ / MON=180°.(1)利用图1,求证:PA=PB ;(2)如图2,若点C是AB与OP的交点,当S APOB=3S APCB时,求PB与PC的比值;图1(3)若/ MON=60°, OB=2,射线AP交ON于点D,且满足且/ PBD = Z ABO,请借助图3补全图形,并求OP长. 练习4 .已知,在△ABC中,AB=AC .过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角0, 直线a交BC边于点P (点P不与点B、点C重合),A RMN的边MN始终在直线a上(点M在点N的上方),且BM = BN,连接CN .(1)当/ BAC=Z MBN=90°时,①如图a,当0=45°时,/ ANC的度数为___________ ;②如图b,当0工45时,①中的结论是否发生变化?说明理由;(2)如图C,当/ BAC= / MBN丰90时,请直接写出/ ANC与/ BAC之间的数量关系,不必证明.练习5.已知:Rt A A'BC'和Rt A ABC 重合,A'C'B = / ACB=90° , BA'C' = / BAC=30° ,现将Rt A A'BC'绕点B按逆时针方向旋转角 a (60°w a 90°),设旋转过程中射线C'C'和线段AA'相交于点D,连接BD .(1)当a=60时时,A'B过点C,如图1所示,判断BD和AA'之间的位置关系,不必证明;(2)当a=90 °时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;(3)如图3,对旋转角a (60°v av90° ),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.图1 图2 图3练习6 .在等边厶ABC 外侧作直线 AP ,点B 关于直线AP 的对称点为D ,连接AD , BD , CD ,其中CD 交直线AP 于点 E .设/ PAB = ,/ ACE = ,/ AEC =. (1)依题意补全图1 ;(2)若 =15°,直接写出 和 的度数;⑶ 如图2,若60° < <120。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∵∠DBE=∠DBE,∴△BOF∽△BED. ∴BBOE=ODFE=130 5. ∵DE=4,∴OF=56 5.
∴BF=59 10.
课堂精讲
方法二:如图,∵∠BOC=∠BFC=90°,
∴B,C,F,O 四点共圆.
∴∠1=∠2=45°.
∵∠2=∠3=45°,∴∠1=∠3=45°.
∵∠DBE=∠FBO,∴△BOF∽△BED.
中考·数学
2020版
第一部分 系统复习
专题9 四点共圆巧解中考题
考点解读
四点共圆在圆内接四边形综合问题的求解中占据 了重要地位,都是在大题中结合题目的几何背景进行 综合考查,重在考查学生对知识的应用能力.考查的 基本类型有:利用四点共圆证相似,利用四点共圆求 最值,这些问题大都利用转化思想,将几何问题转化 为四点共圆问题,使题目能简单求解.
课堂精讲
【解】方法一:∵CF⊥BE, ∴∠BCF=∠EBC=90°. ∵∠EBC+∠BEC=90°, ∴∠BEC=∠BCF.
9 ∴BBFD=56
120=130
5,BBOE=23 120=130
5.
∴BBFD=BBOE.
∵∠BCE=∠BFC=90°, BC BF
∴△BCF∽△BEC.∴BE=BC. ∵BC=6,CE=2, ∴BE= BC2+CE2=2 10.
课堂精讲
例2 如图,正方形ABCD的边长为6,点O是对 角线AC,BD的交点,点E在CD上,且DE=2CE,过点 C作CF⊥BE,垂足为F,连接OF,求OF的长.
课堂精讲
【分析】方法一:∵正方形 ABCD 的边长为 6,点 O 是 对角线 AC,BD 的交点.∴△AOB,△AOD,△BOC,△COD 为 等腰直角三角形,且 AO=BO=CO=DO=3 2.∵DE=2CE, ∴CE=2,DE=4.∴BE=2 10(在 Rt△BCE 中用勾股定理求 得).然后利用△BCF∽△BEC,求得 BF.利用BBFD=BBEO,易证 △BOF∽△BED,根据比例求解 OF 即可.
方法提炼
1.四点共圆 如果同一平面内的四个点在同一个圆上,则称这四 个点共圆,一般简称为“四点共圆”. 2.四点共圆的性质 (1)共圆的四个点所连成同侧共底的两个三角形的 顶角相等. (2)圆内接四边形的对角互补. (3)圆内接四边形的一个外角等于它的内对角.
方法提炼
3.四点共圆的判定 (1)用“角”判定: ①一组对角互补的四边形的四个顶点在同一个圆上; ②一个外角等于它的内对角的四边形的四个顶点在同一个圆上; ③如果两个三角形有一条公共边,且位于公共边同侧的两个角 相等,则这两个三角形的四个顶点在同一个圆上. (2)“等线段”判定: 四顶点到同一点的距离相等,若OA=OB=OC=OD,则A,B,C, D四点共圆. (3)用“比例线段”判定: 若线段AB,CD(或其延长线)交于点P,且PA·PC=PB·PD,则A, B,C,D四点共圆.
∴BBOE=ODFE=130 5.
答案图
∵DE=4,∴OF=56 5.
【方法归纳】求线段长常用的方法就是两种:利用相似中的
比例线段求线段长或者利用直角三角形中的勾股定理求线段长.
课后精练
1.(2019·镇江)如图,四边形 ABCD 是半圆的内接 四边形,AB 是直径,D︵C=C︵B.若∠C=110°,则∠ABC
【答案】C
答案图
课堂精讲
【方法归纳】若已知圆上四点,常常使用四点 共圆的性质,找角之间的转化关系.本题考查了圆 周角定理:在同圆或等圆中,同弧或等弧所对的圆 周角相等,都等于这条弧所对的圆心角的一半.推 论:半圆(或直径)所对的圆周角是直角,90°的圆 周角所对的弦是直径,用“四点共圆”的思想进行 角的数量代换,有助于我们更好地解题.
的度数等于( A )
A.55°
第 1 题图 B.60° C.65°
D.70°
课后精练 2.(2018·邵阳)如图,四边形ABCD为⊙O的内接 四边形,∠BCD=120°,则∠BOD的大小是( B )
第2题图 A.80° B.120° C.100° D.90°
课后精练
3.(2019·天水)如图,四边形ABCD是菱形,⊙O经过点A, C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的 度数为( C )
课堂精讲
方法二:我们观察这个图形可以发现点 B,C,F,O 这四点是共圆的,故∠1=∠2=45°(圆中同弧所对圆周 角相等),所以∠1=∠3=45°,加上公共角∠DBE,就能 得到△BOF∽△BED,这样的方法是利用几何图形中的变换 得到所要的结论,少了许多计算.这道题的方法还有很多, 还可以过点 O 向 BE 作垂线,垂足为 M,然后利用勾股定理 求解.
第3题图 A.20° B.25° C.30° D.35°
课后精练
4.如图,以 Rt△ABC 的斜边 BC 为一边在△ABC 的同 侧作正方形 BCEF,设正方形的中心为点 O,连接 AO,如果
AB=4,AO=6 2,那么 AC 的长等于___1_6___.
第 4 题图
课后精练
5.已知△ABC 为等腰直角三角形,∠C 为直 角,延长 CA 至点 D,以 AD 为直径作圆,连接 BD 与⊙O 交于点 E,连接 CE,CE 的延长线交⊙O 于
BD 另一点 F,那么CF的值等于______.
第 5 题图
课后精练 6.如图,AB为圆的直径,AD,BC为圆的两条弦, 且BD与AC相交于点E.求证:AC·AE+BD·BE=AEF⊥AB于点F. ∵∠EFB=90°,∠C=90°, ∴∠EFB+∠C=180°. ∴B,C,E,F四点共圆. ∴AE·AC=AF·AB.① ∵∠EFA=90°,∠D=90°, ∴∠EFA+∠D=180°. ∴A,D,E,F四点共圆. ∴BE·BD=BF·AB.② ①+②,得 AE·AC+BE·BD=AF·AB+BF·AB. ∵AF+BF=AB,∴AE·AC+BE·BD=AB2.
课堂精讲
例 1 (2019·潍坊)如图,四边形 ABCD 内接于⊙O,AB
为直径,AD=CD,过点 D 作 DE⊥AB 于点 E,连接 AC 交 DE 于
点 F.若 sin∠CAB=35,DF=5,则 BC 的长为(
)
A.8
B.10 C.12 D.16
课堂精讲
【分析】连接BD,如图,先利用圆周角定理证明 ∠ADE=∠DAC得到FD=FA=5,再根据正弦的定义计算 出EF=3,则AE=4,DE=8,接着证明△ADE∽△DBE, 利用相似比得到BE=16,所以AB=20,然后在Rt△ABC 中利用正弦定义计算出BC的长.
