pascal 基本算法
Pascal的算术运算

100
trunc(-100.5) -100
trunc(-100.4) -100
結果 2.75
2 3
單元減法~
將負號放在數字前的運算稱為否定,這種運算只需要一 個操作數。 例如:-7的意思是7的負數
運算的優先順序~
優先次序 最高 高 低
運算符 - (單元減法或否定)
* / div mod +-
1~較高優先次序的運算會在較低的運算之前執行 2~具有相同優先次序的運算符會從左至加順序執行 3~括號可以改變運算的次序,括號內的表達式會首先運算~
運算 加法 減法或單元減法 乘法 實數除法 整數除法 模數
加法和減法~
由普通的加號[+]和減號[-]來表示,運算的方式與 數學的相同。
乘法~
乖法時,必須使用[*],例子:A乘B時應寫成A*B [+]~ [-]~ [*]可以在實數或整數數據中使用,當所
有操作數都是整數時,結果亦是整數。另外, 當操作數是實數,結果也是實數。
我們可以將In和exp組成一條公式,以計算答案。
Xy:=exp(y*In(x))
其中x必須是正的實數或整數
函數調用
結果
trunc (x) 截斷函數trunc回送實數變元的整數部份, 並以整數表示,任合小部份都會被截去。 變元實際上會被捨入至最接近零的整數。
trunc (100.5但是即使在無需要時,我們亦可以使用拾號~ 目的只是為了使優先次序更清晰,但不會改變這次序~
●~賦值語句~○
語法----<變量> := <表達式>
<變量>是用來表示值的標識符。 <表達式>可以是(1)常量值
(2)已經貯有值的另一個變量 (3)將要計算的公式 [:=]稱為賦值符號,意思是[取其值],而在兩個符號中間是沒有空格的。 在一句賦值語句中,被賦值的變量必須放在賦值符號的左邊,放在友邊 的表達式會被首先運算,然後結果會貯在左邊的變量中。 例子: A:=5;
pascal经典算法28页PPT

经典算法
语言与计算机
• 递归调用 • 向前引用 • 随机化 • 指针类型 • 按位运算
排序(一)
• 冒泡排序(起泡排序) • 选择排序 • 插入排序 • ★ Shell排序 • 快速排序
排序(二)
• 线性时间排序 • 查找第k大元素 • 带第二关键字的排序
数论(一)
• 素性判断 • 筛选建立素数表 • 分解质因数 • 进制转换 • 二分取幂 • ★二分求解线性递推方程
贪心
• 最优装载问题 • 部分背包问题 • 独立区间的选择 • 覆盖区间的选择 • 区间的最小点覆盖 • 点的最小区间覆盖
递推
• Fibonacci数的若干应用 • Catalan数的若干应用 • 拆分数 • 差分序列
• ★网络流 • ★置换群 • ★KMP算法
其它
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
数据结构(二)
• ★平衡二叉树 • ★树状数组 • ★线段树 • ★块状链表
排列与组合
• 生成所有排列 • 生成所有组合 • 生成下一个排列 • 生成下一个组合
计算几何(一)
• 计算斜率 • 计算点积 • 计算余弦 • 计算平面两点的距离 • 计算空间两点的距离 • ★计算广义空间两点的距离 • 判断三点是否共线
动态规划(一)
• 0-1背包 • 完全背包 • 乘法问题 • 数塔问题 • 装箱问题
动态规划(二)
• 最长上升序列(LIS) • 最长公共子串(LCM) • 最小代价子母树
PASCAL算法

算法设计题集第一章算法初步第一节程序设计与算法一、算法算法是解决问题方法的精确描述,但是并不是所有问题都有算法,有些问题经研究可行,则相应有算法,但这并不是说问题就有结果。
上述的“可行”,是指对算法的研究。
1.待解问题的描述待解问题表述应精确、简练、清楚,使用形式化模型刻划问题是最恰当的。
例如,使用数学模型刻划问题是最简明、严格的,一旦问题形式化了,就可依据相应严格的模型对问题求解。
2.算法设计算法设计的任务是对各类具体问题设计良好的算法及研究设计算法的规律和方法。
常用的算法有:穷举搜索法、递归法、回溯法、贪心法、分治法等。
3.算法分析算法分析的任务是对设计出的每一个具体的算法,利用数学工具,讨论各种复杂度,以探讨某种具体算法适用于哪类问题,或某类问题宜采用哪种算法。
算法的复杂度分时间复杂度和空间复杂度。
.时间复杂度:在运行算法时所耗费的时间为f(n)(即n的函数)。
.空间复杂度:实现算法所占用的空间为g(n)(也为n的函数)。
称O(f(n))和O(g(n))为该算法的复杂度。
二、程序设计1.程序程序是对所要解决的问题的各个对象和处理规则的描述,或者说是数据结构和算法的描述,因此有人说,数据结构+算法=程序。
2.程序设计程序设计就是设计、编制和调试程序的过程。
3.结构化程序设计结构化程序设计是利用逐步求精的方法,按一套程式化的设计准则进行程序的设计。
由这种方法产生的程序是结构良好的。
所谓“结构良好”是指:(1)易于保证和验证其正确性;(2)易于阅读、易于理解和易于维护。
按照这种方法或准则设计出来的程序称为结构化的程序。
“逐步求精”是对一个复杂问题,不是一步就编成一个可执行的程序,而是分步进行。
.第一步编出的程序最为抽象;.第二步编出的程序是把第一步所编的程序(如过程、函数等)细化,较为抽象;.…….第i步编出的程序比第i-1步抽象级要低;.…….直到最后,第n步编出的程序即为可执行的程序。
所谓“抽象程序”是指程序所描述的解决问题的处理规则,是由那些“做什么”操作组成,而不涉及这些操作“怎样做”以及解决问题的对象具有什么结构,不涉及构造的每个局部细节。
pascal常用算法代码

//求无向图割顶的算法,割顶:若在图的dfs树上,i 存在儿子节点 s ,使得 s 及 s 的所有子孙的后向边不指向 i 的祖先(可以指向i),输出的是一个点I,尝试写成过程,然后找到其应用
ary(多进制2-16转十进制).pas
program ary;
var a:array [1..10000] of longint;
program ary;
var a:array [1..10000] of longint;
k:array [1..10000] of char;
s,j,b,t:longint;
begin
readln(s);
readln(b);
while s<>0 do
begin
'B':a[j]:=11;
'C':a[j]:=12;
'D':a[j]:=13;
'E':a[j]:=14;
'F':a[j]:=15;
end;
inc(j);
end;
for i:=1 to j do
if a[i]>=b then
for k:=1 to n do if (i<>k)and(j<>k)then
if (a[i,j]<>maxlongint)and(d[i]<>maxlongint)and(d[j]>d[i]+a[i,j])then
d[j]:=d[i]+a[i,j];
for i:=1 to n do
begin
case a[j] of
pascal算法讲义-第十一讲

第十一讲 动态规划一、动态规划总述动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
1957年出版了他的名著《Dynamic Programming》,这是该领域的第一本著作。
跟分治法一样,动态规划也是通过组合子问题的解而解决整个问题的。
分治法可以把问题划分成一些独立的子问题,递归的求解各个子问题,然后合并子问题的解而得到原问题的解。
与此不同,动态规划适用于子问题不独立的情况,也就是各子问题包含公共的子子问题。
这种情况下,分治法就会有大量的重复计算,即重复求解公共子子问题。
动态规划对每个子子问题只求解一次,将结果存在一张表里,从而避免每次遇到各个子问题时重新计算答案。
动态规划通常应用于最优化问题。
此类问题一般有很多很多种可行解,每个解有一个值,而我们希望找出一个具有最优(最大或最小)值的解。
称这样的解为该问题的最优解(而不是确定的最优解),因为可能存在多个取值最优的解。
动态规划算法的设计可以分为如下4个步骤:1)描述最优解的结构2)递归定义最优解的值,这个递归方程称为状态转移方程3)按自底向上的方式计算最优解的值4)由计算结果构造一个最优解(一般竞赛时无需构造,如果有要求则有时需要在第三步的计算中记录一些附加信息)。
下面介绍一些术语,希望读者在阅读完整节内容后进行理解:阶段:把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同.描述阶段的变量称为阶段变量。
Pascal算法

算法:
算法是程序的基础。
有了一个好的算法,再进行编码,把算法转换成任何一个程序设计语言所表示的程序。
算法就是解题步骤。
例题:求1——100这一百个相继整数的和S。
解法一:s=1+2+3+……+100 【需要100-1次加法】
解法二:s=(1+100)*50 【需要加法、乘法、除法各一次】不同的算法,对计算的工作量造成重大影响,还要考虑算法对精确度的影响。
程序质量的高低,主要取决于算法。
结构化程序特点:
1按功能相对独立原则划分若干模块。
2 单入口、单出口。
3 强调三种基本结构组成(顺序、选择、循环性)。
4 书写格式清晰。
5 不包含无限循环(即执行时间是有限的)
6 没有死语句(即程序中所有语句都能得到执行的机会)
设计结构化程序方法:
1 自顶向下
2 逐步细化。
3 按“功能单一”原则划分模块。
pascal排序算法资料重点

program maopaosort;
可见,其时间复杂度也是O(n2)
const mx=10000; var
d:array[1..mx]of longint;
的。不难发现,如果某趟排序 中没有发生交换,就意味着任
n,i,j,k:longint; begin
readln(n);
意两个相邻元素都是有序的, 那么全部元素就已经有序了。
此时第n个数据已经是最大的了,下面对前N-1个数据重复 这个过程,又将次大的数据放到了第n-1个位置。一般地,第i 趟冒泡排序是对第1个到第n-i+1个数据进行操作,选出原序列 第i大的数据放到数组的第n-i+1位置。重复这个过程,直到i=n1为止。
初始关键字:[225 220 41 190 242 185 42 231] 第一趟排序后:[220 41 190 225 185 42 231] 242 第二趟排序后:[41 190 220 185 42 225] 231 242 第三趟排序后:[41 190 185 42 220] 225 231 242 第四趟排序后:[41 185 42 190] 220 225 231 242 第五趟排序后:[41 42 185] 190 220 225 231 242 第六趟排序后:[41 42] 185 190 220 225 231 242 第七趟排序后:[41] 42 185 190 220 225 231 242
排序算法
1、选择排序 2、冒泡排序 3、插入排序 4、快速排序
什么是排序? 排序是处理数据过程中一种很常用的运算,是将一
组原本无序的数据元素,通过一定的方法,按照某个域 的值(关键字)递增或递减的次序重新排列的过程。
下面主要讨论几种常见的内排序算法: 选择排序、冒泡排序、插入排序、快速排序。
pascal算法讲义第九讲

第九讲 分治算法一、分治思想分治思想融入于常见算法的各个角落,简单点说,所谓的分治,实际上是将一个问题拆成若干个小问题,将它们分别解决后,就等价于解决了整个问题。
二、快速幂算法与分治思想(底下部分的^表示乘方)求2^233(mod 1,000,000,007)这个问题我们可以这么考虑2^233 = 2^116 * 2^116 * 2那么原来问题就转化为求2^116(mod 1,000,000,007)就这样下去,我们只要求得2^52即可,也就是说2^26即可换句话说,我们求得2^13即可,也就是说2^6 * 2^6 * 22^6 = 2^3 * 2^32^3 = 2^1 * 2^1 * 2 = 8所以2^6 = 8*8=642^13 = 2^6 * 2^6 * 2 = 64 * 64 * 2 = 8192就这样…我们逐步回推,可以得到2^233当然注意要取模*你可以说这个算法是递归,但是这个也可以说是”拆成若干个小问题”*三、一道NOIP2007的例题本题摘自NOIP 2007 普及组初赛(完善程序第二题) 大家可以暂时思考一下本题中,我们只要求构造一种方案所以,这个题我们可以采取分治的策略来解决首先,我们思考一下,这一题的特殊条件1,我们用的是2的k次方*2的k次方的格子2,这一题中,有一个”-1”的存在那么,我们就可以用一种特殊的策略首先,如果k=0,那么……就不用构造了,皆大欢喜所以,我们想办法将2^k改为2^(k-1)即可我们可以将原来的正方形切成四个,如右图所以,这时候,我们可以将三个”1”当作-1,带入到右上,右下,左下处理,将”-1”依旧留在左上角这样,问题就转化成了一个2^(k-1)规模的然后..(本图中为了较为清晰的显示,将13~16与18~21略去了)所以,这样就将原来问题分治出来了那么,这一个问题就得到了解决四、一道来自codeforces的例题这一题摘自Codeforces 321C题面:英文版:C. Ciel the Commandertime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard outputNow Fox Ciel becomes a commander of Tree Land. Tree Land, like its name said, has n cities connected byn - 1 undirected roads, and for any two cities there always exists a path between them.Fox Ciel needs to assign an officer to each city. Each officer has a rank — a letter from 'A' to 'Z'. So there will be 26 different ranks, and 'A' is the topmost, so 'Z' is the bottommost.There are enough officers of each rank. But there is a special rule must obey: if x and y are two distinct cities and their officers have the same rank, then on the simple path between x and y there must be a city z that has an officer with higher rank. The rule guarantee that a communications between same rank officers will be monitored by higher rank officer.Help Ciel to make a valid plan, and if it's impossible, output "Impossible!".InputThe first line contains an integer n (2 ≤ n ≤ 105) — the number of cities in Tree Land.Each of the following n - 1 lines contains two integers a and b (1 ≤ a, b ≤ n, a ≠ b) — they mean that there will be an undirected road between a and b. Consider all the cities are numbered from 1 to n.It guaranteed that the given graph will be a tree.OutputIf there is a valid plane, output n space-separated characters in a line — i-th character is the rank of officer in the city with number i.Otherwise output "Impossible!".Examplesinput41 21 31 4outputA B B Binput101 22 33 44 55 66 77 88 99 10outputD C B A D C B D C DNoteIn the first example, for any two officers of rank 'B', an officer with rank 'A' will be on the path between them. So it is a valid solution.中文题意:给你n个点,求构造一个方案,使得每个点存在一个’A’到’Z’的权值任意两个权值为x(x从’A’到’Z’)的点之间,一定存在至少一个权值比x大的点如果无解,输出”Impossible!”注意:’A’比’B’~’Z’大,’B’比’C’~’Z’大……’Y’比’Z’大如果不懂,可以观察样例所以,这道题我们该怎么做呢?我们仔细观察‘A’是最大的,也就是说,最多只有一个’A’那么我们每次选一个点,将它当作最大的点,然后,将它的其他部分”解离”也就是说,将它的其他部分分开处理这样,就可以解决了这题红点为A,然后将绿色点当B/C*但是,怎么找这个点呢*我们可以在这个树里面,随机一个点,但是是有可能得出无解我们这时候,只要找出”树的重心”即可这个树的重心可以百度得到……。
Pascal相关知识备忘

Pascal相关知识备忘(以free Pascal2.04为语言载体)熟练掌握并灵活使用以下Pascal语言相关知识:(一)、常用运算:1、算术运算:+、-、*、/、DIV、MOD2、字符串运算:+(字符串连接)3、集合运算:+(并集)、*(交集)、一(差集)、in2、关系运算:>、<、=、<>、>=、<=3、逻辑运算:NOT、AND、OR、XOR(二)、常用子程序1、求绝对值函数abs(x)如:abs(3)返回值为3;abs(-3.1)返回值为:3.12、取整函数int(x)定义:function Int(X:Real):Real;如int(3.6)返回值为:3.0;int(-3.6)返回值为:-3.03、截尾函数trunc(x)定义:function Trunc(X:Real):Longint如trunc(3.6)返回值为:3;trunc(-3.6)返回值为:-34、四舍五入函数round(x)如R:=round(123.456);{123}R:=round(12.56);{13}R:=round(-123.456);{-123}R:=round(-12.56);{-13}5、取小数函数frac(x)如R:=Frac(123.456);{0.456};R:=Frac(-123.456);{-0.456}6、求平方根函数sqrt(x)和平方函数sqr(x)如:R:=sqrt(4);{2.0};R:=sqr(4);{16}7、随机数函数function random[(range:word)]:<same type>randomize随机数初始化语句random返回)1,0[之间的随机实数,0[range随机整数如:random(5)返回0、1、2、3、4共5个数random(range)返回)8、求字符x对应序号函数ord(x)如R:=ord(‘A’);{65}9、求序号x对应字符函数chr(x)如R:=chr(65);{‘A’}10、将字符串小写转换为大写函数upcase(st)如R:=upcase(‘AbcD’);{‘ABCD’}11、求前趋函数pred(x)如R:=pred(‘B’);{‘A’}12、求后继函数succ(x)如R:=succ(‘B’);{‘C’}13、判断x是否为奇数函数odd(x)如R:=odd(7);{TRUE};如R:=odd(8);{FALSE}14、字符转换为数值过程val(str,a,b)如,执行语句val(‘2.4’,a,b);后,a值为:2.4执行语句val(‘2c4’,a,b);后,a为:0,b为:215、数值转换为字符过程Str(a,st)如,执行语句str(12,st);后,st值为:’12’16、求字串st长度函数length(st)如R:=length(‘ABC’);{3}17、函数Pos(st1,st):查找st1在st里的起始位置,整型。
Pascal基础算法

1.快排procedure quicksort(l,r:longint);{从L到R排序}vari,j,mid:longint;begini:=l;{首标记}j:=r;{尾标记}mid:=a[ (l+r) div 2];{中间值}repeatwhile a[i]<mid do inc(i);{找到不合顺序的a[i]}while a[j]>mid do dec(j);{找到不合顺序的a[j]}if i<=j then begin{交换}swap(a[i],a[j]);inc(i);dec(j);end;until i>j;if l<j then quicksort(l,j);{递归,排L到j之间的数}if i<r then quicksort(i,r);{递归,排L到j之间的数}end;2.高精度加法:typehp=array[0..200] of longint;procedure g_jia_g(a,b:hp;var c:hp);varlen,i:longint;beginfillchar(c,sizeof(c),0);if a[0]>b[0] then len:=a[0] else len:=b[0];{len=答案的长度}for i:=1 to len do{加的过程}beginc[i]:=a[i]+b[i]+c[i];if c[i]>=10 then begin{进位}c[i]:=c[i]-10;c[i+1]:=c[i+1]+1;end;end;c[0]:=len+1;{判断最高位是否进位}f c[len+1]=0 then c[0]:=c[0]-1;end;3.压位高精度加法typehp=array[0..200] of longint; {每个单位存100000000之内的数(1*10^8,即1后8个0)}procedure init;{读入的过程}begina[0]:=(l1-1) div 8+1;{第一个加数的长度}b[0]:=(l2-1) div 8+1;{第二个加数的长度}for i:=1 to l1 do{读入加数a的过程}a[(l1-i) div 8+1]:= a[(l1-i) div 8+1]*10+ord(s1[i])-48;for i:=1 to l2 do{读入加数b的过程}b[(l2-i) div 8+1]:=b[(l2-i) div 8+1]*10+ord(s2[i])-48;end;procedure hiadd(a,b:hp;var c:hp);beginfillchar(c,sizeof(c),0);if a[0]>b[0] then c[0]:=a[0] else c[0]:=b[0];{加数长度}for i:=1 to c[0] do{加的过程}c[i]:=c[i]+a[i]+b[i];for i:=1 to c[0] do{进位}begininc(c[i+1],c[i] div 100000000);c[i]:=c[i] mod 100000000;end;if c[c[0]+1]>0 then inc(c[0]);{判断最高位是否有进位}end;procedure print;{输出过程}beginwrite(c[c[0]]);{输出最高位}for i:=c[0]-1 downto 1 dobeginif c[i] div 10000000=0 then write(0);if c[i] div 1000000=0 then write(0);if c[i] div 100000=0 then write(0);if c[i] div 10000=0 then write(0);if c[i] div 1000=0 then write(0);if c[i] div 100=0 then write(0);if c[i] div 10=0 then write(0);write(c[i]);end;end;4.高精度乘法typehp=array[0..200] of longint;procedure g_cheng_g(a,b:hp;var c:hp);varlen,i,j:longint;beginfillchar(c,sizeof(c),0);for i:=1 to a[0] do{累乘+进位过程}for j:=1 to b[0] dobeginc[i+j-1]:=c[i+j-1]+a[i]*b[j];c[i+j]:=c[i+j]+c[i+j-1] div 10;c[i+j-1]:=c[i+j-1] mod 10;end;len:=a[0]+b[0]+1;{结果长度}while (c[len]=0) and (len>1) do dec(len);{判断最高位是否为零} c[0]:=len;end;5.压位高精度乘法typehp=array[0..200] of longint;procedure init;{读入过程}begina[0]:=(l1-1)div 4+1;{加数a的长度}b[0]:=(l2-1)div 4+1;{加数b的长度}for i:=1 to l1 do{读入a}a[(l1-i)div 4+1] :=a[(l1-i)div 4+1]*10+ord(s1[i])-48;for i:=1 to l2 do{读入b}b[(l2-i)div 4+1] :=b[(l2-i)div 4+1]*10+ord(s2[i])-48;end;procedure yacheng(a,b:hp;var c:hp);beginfillchar(c,sizeof(c),0);for i:=1 to a[0] do{累乘+进位过程}for j:=1 to b[0] dobeginc[i+j-1]:=c[i+j-1]+a[i]*b[j];c[i+j]:=c[i+j]+c[i+j-1] div 10000;c[i+j-1]:=c[i+j-1] mod 10000;end;c[0]:=a[0]+b[0]-1;{最高位是否进位}while c[c[0]+1]>0 dobegininc(c[0]);c[c[0]+1]:=c[c[0]+1]+c[c[0]] div 10000;c[c[0]]:=c[c[0]] mod 10000;end;end;procedure print;{输出过程}beginwrite(c[c[0]]);for i:=c[0]-1 downto 1 dobeginif c[i] div 1000=0 then write(0);if c[i] div 100=0 then write(0);if c[i] div 10=0 then write(0);write(c[i]);end;end;6.二分法查找procedure found(x,top,last:longint);{从top与last之间找x(a数组必须有序)} beginif top<=last thenbeginmid:=(top+last) div 2;{中间的下标}if x=a[mid] then writeln(mid){找到了}else if x<a[mid] then found(x,top,mid-1){在前面}else found(x,mid+1,last);{在后面} endelse writeln('not found');{a中没有x}end;7.斐波那契数列function f(x:longint):longint;{输出斐波那契中的第x项}beginif x=0 then f:=0else if x=1 then f:=1else if x=2 then f:=1else f:=f(x-1)+f(x-2);end;8.判断素数function pdss(x:longint):boolean;vari:longint;beginif (x=0) or (x=1) then exit(false);{0和1不是素数}if (x=2) or (x=3) then exit(true);{2和3是素数}for i:=2 to trunc(sqrt(x)) doif x mod i =0 then exit(false);exit(true);end;9.分解质因数成表格形式{2——2 3——1 5——1 =2*2*3*5=60}procedure fat(x:longint;var a:arr;var s:longint);begini:=1; {最小的因子}s:=0;repeatinc(i);{因子加1}if x mod i=0 thenbegininc(s);{标记加1}a[s,1]:=i;{因子}a[s,2]:=0;{因子个数清零}while x mod i=0 do begin inc(a[s,2]); x:=x div i; end;{去除该因子} end;until x=1;end;10.十进制化二进制procedure s_e(n:longint);{除2取余法}vari:longint;begin{1770}read(n);i:=0;while n<>0 dobegina[i]:=n mod 2;i:=i+1;n:=n div 2;end;end.11.最大公约数function gcd(a,b:integer):integer;beginif b=0 then gcd:=aelse gcd:=gcd (b,a mod b);{辗转相除法}end;12.最小公倍数function lcm(a,b:integer):integer;beginif a<b then swap(a,b);lcm:=a;while lcm mod b>0 do inc(lcm,a);end;13.全排列procedure solve(dep:integer);var i:integer;beginif dep=n+1 thenbeginwriteln(s);exit;end;for i:=1 to n doif not used[i] thenbegins:=s+chr(i+ord('0'));used[i]:=true;solve(dep+1);s:=copy(s,1,length(s)-1);used[i]:=false;end;end;14.背包DPprogram bb2;varxk,n,i,j:longint;w,c:array[1..100] of longint;f:array[0..101,0..100001] of longint;function max(x,y:longint):longint;beginif x>y then exit(x) else exit(y);end;beginassign(input,'bb2.in');assign(output,'bb2.out');reset(input);rewrite(output);readln(xk,n);for i:=1 to n doreadln(w[i],c[i]);{f[i,j] 第i个物品,重量是j 的最大价值}fillchar(f,sizeof(f),0);for i:=1 to n dofor j:=1 to xk doif j>=w[i] then f[i,j]:=max( f[i-1,j] , f[i-1,j-w[i]]+c[i] )else f[i,j]:=f[i-1,j];write(f[n,xk]);close(input);close(output);end.。
pascal常见算法整理

3、归并排序
program gbpx;
const maxn=7;
type arr=array[1..maxn] of integer;
var a,b,c:arr;
i:integer;
procedure merge(r:arr;l,m,n:integer;var r2:arr);
a[i+d]:=t;
end;
end;
write('output data:');
for i:=1 to n do write(a[i]:6);
writeln;
end.
程序2:(子序列是冒泡排序)
program xepx;
const n=7;
type
arr=array[1..n] of integer;
while (i<n) and bool do
begin
bool:=false;
for j:=n downto i+1 do
if a[j-1]<a[j] then
begin t:=a[j-1];a[j-1]:=a[j];a[j]:=t;bool:=true end;
for i:=1 to n do write(a[i]:6);
writeln;
end.
i,j,k,t:integer;
begin
write('Enter date:');
for i:= 1 to n do read(a[i]);
writeln;
for i:=2 to n do
begin
k:=a[i];j:=i-1;
Pascal的运算符及表达式
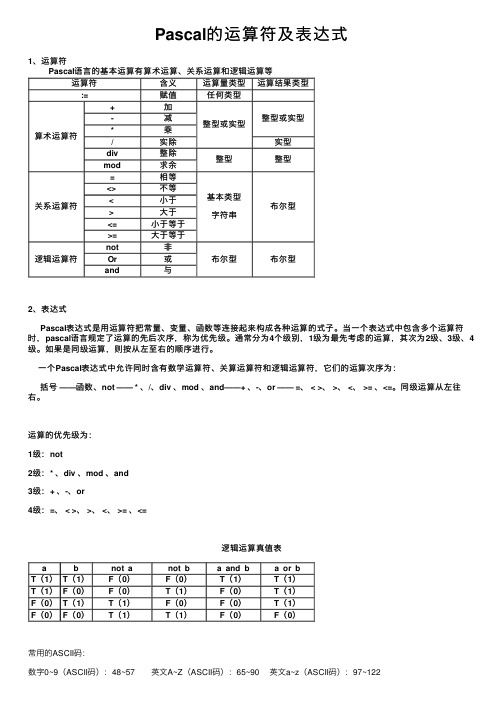
Pascal的运算符及表达式1、运算符Pascal语⾔的基本运算有算术运算、关系运算和逻辑运算等运算符含义运算量类型运算结果类型:=赋值任何类型算术运算符+加整型或实型整型或实型-减*乘/实除实型div整除整型整型mod求余关系运算符=相等基本类型字符串布尔型<> 不等< ⼩于> ⼤于<=⼩于等于>=⼤于等于逻辑运算符not⾮布尔型布尔型Or或and与2、表达式Pascal表达式是⽤运算符把常量、变量、函数等连接起来构成各种运算的式⼦。
当⼀个表达式中包含多个运算符时,pascal语⾔规定了运算的先后次序,称为优先级。
通常分为4个级别,1级为最先考虑的运算,其次为2级、3级、4级。
如果是同级运算,则按从左⾄右的顺序进⾏。
⼀个Pascal表达式中允许同时含有数学运算符、关算运算符和逻辑运算符,它们的运算次序为:括号 ——函数、not —— * 、/、div 、mod 、and——+ 、-、or ——=、 < >、 >、 <、 >= 、<=。
同级运算从左往右。
运算的优先级为:1级:not2级:* 、div 、mod 、and3级:+ 、-、or4级:=、 < >、 >、 <、 >= 、<=逻辑运算真值表a b not a not b a and b a or bT(1)T(1)F(0)F(0)T(1)T(1)T(1)F(0)F(0)T(1)F(0)T(1)F(0)T(1)T(1)F(0)F(0)T(1)F(0)F(0)T(1)T(1)F(0)F(0)常⽤的ASCII码:数字0~9(ASCII码):48~57 英⽂A~Z(ASCII码):65~90 英⽂a~z(ASCII码):97~122。
Pascal算法-3.递推算法

图20 倒推到第二步
为了在I=2处贮藏1000公升汽油,卡车至少从I=3处开三趟满载油的 车至I=2处。所以I=3处至少贮有3*500公升汽油,即oil[3]=500*3=1500。 加上I=2至I=3处的二趟返程空车,合计5次。路途耗油亦应500公升,即 d23=500/5, Way[3]=Way[2]+d23=Way[2]+500/5; 此时的状况如图21所示。
(1 n) * (1 m) * n * m s=(1+2+┉┉+n)*( 1+2+┉┉+m)= 4
3.长宽不等的长方形个数s2 显然,s2=s-s1
(1 n) * (1 m) * n * m = 4
min{m, n}1 i 0
(n i ) * (m i )
由此得出算法: program ex7_3; var m,n,m1,n1,s1,s2:longint; begin readln(m,n); m1:=m;n1:=n; s1:=m1*n1; while (m1<>0)and(n1<>0)do begin m1:=m1-1;n1:=n1-1; s1:=s1+m1*n1; end; s2:=((m+1)*(n+1)*m*n) div 4-s1; writeln(s1,' ',s2); end.
//计算正方形的个数s1
// 计算长方形的个数s2
【例4】贮油点
一辆重型卡车欲穿过1000公里的沙漠,卡车耗汽油为1升/公里,卡车总载油 能力为500公升。显然卡车装一次油是过不了沙漠的。因此司机必须设法在沿途 建立若干个贮油点,使卡车能顺利穿过沙漠。试问司机如怎样建立这些贮油点? 每一贮油点应存储多少汽油,才能使卡车以消耗最少汽油的代价通过沙漠?(结 果保留小数点后两位) 编程计算及打印建立的贮油点序号,各贮油点距沙漠边沿出发的距离以及存 油量。格式如下: No. Distance(k.m.) Oil(litre)
pascal-经典算法

动态规划(一)
• 0-1背包 • 完全背包 • 乘法问题 • 数塔问题 • 装箱问题
动态规划(二)
• 最长上升序列(LIS) • 最长公共子串(• 归并排序 • 最近点对问题 • 求最大子序列和的O(nlogn)算法 • Hanoi塔问题及其变种 • 棋盘覆盖问题 • 循环赛日程表问题
贪心
• 最优装载问题 • 部分背包问题 • 独立区间的选择 • 覆盖区间的选择 • 区间的最小点覆盖 • 点的最小区间覆盖
递推
• Fibonacci数的若干应用 • Catalan数的若干应用 • 拆分数 • 差分序列
数据结构(二)
• ★平衡二叉树 • ★树状数组 • ★线段树 • ★块状链表
排列与组合
• 生成所有排列 • 生成所有组合 • 生成下一个排列 • 生成下一个组合
计算几何(一)
• 计算斜率 • 计算点积 • 计算余弦 • 计算平面两点的距离 • 计算空间两点的距离 • ★计算广义空间两点的距离 • 判断三点是否共线
语言与计算机
• 递归调用 • 向前引用 • 随机化 • 指针类型 • 按位运算
排序(一)
• 冒泡排序(起泡排序) • 选择排序 • 插入排序 • ★ Shell排序 • 快速排序
排序(二)
• 线性时间排序 • 查找第k大元素 • 带第二关键字的排序
数论(一)
• 素性判断 • 筛选建立素数表 • 分解质因数 • 进制转换 • 二分取幂 • ★二分求解线性递推方程
图论:二分图
• 验证二分图 • 匈牙利算法 • ★KM算法 • ★稳定婚姻系统
树
• 求树的最短链 • 二叉树的四种遍历 • 已知先序中序求后序 • 已知中序后序求先序 • ★已知先序后序求中序 • ★LCA问题的Tarjan离线算法 • ★Huffman编码
pascal排序算法

排序查找算法排序算法:我们在前面学过的排序算法有选择排序、冒泡排序等,它们的时间复杂性为O(n2),稳定性比较好,但速度比较慢另外的一些排序算法:插入排序、希尔(Shell)排序、快速排序、归并(合并)排序插入排序:其思想与打牌时,当手中的一手牌已排好序,又摸起一张新的牌插入这一手牌中时差不多算法的基本思想:1)设n个数据已经按照顺序排列好(假定已按从小到大的顺序排序,并存放在数组a中)2)输入一个数据x,将其按有序顺序,放入适当的位置上,从而使整个数据序列仍然保持有序顺序;a)将x与n个数比较,寻找应当插入x的位置:i:=1;while x>a[i]do i:=i+1;b)j:=i;c)将a数组中从j位置开始的元素向后移动:for k:=n+1downto1do a[k]:=a[k-1];a)a[j]:=x;3、输出已经插入完毕的有序数列。
算法(最坏情况下)的复杂性:O(n2)适用于:原先的数据已经过了排序、又插入了一个新数据项的情况Shell排序(希尔排序)此算法是Shell于1959年提出的,又称缩小增量排序算法,其基本思想是:1)发现当n不大时,插入排序的性能是不错的。
因此,将大量的插入排序划分为小组的、少量数据的插入排序;2)设法先取小于n的一个增量d1,将第1、1+d1、1+2d1…个元素作为第一组,将第2、2+d1、2+2d1…个元素作为第二组,将d1、d1+d1、d1+2d1…个元素作为第d1组,并在各组之内运用插入排序。
3)然后,再取d2<d1,重复进行上述过程,直到增量di=1时为止。
进行Shell排序时要考虑的问题:增量的个数、大小应如何选取?无明确的规则,只能凭经验。
该算法是一种不稳定的排序算法,其时间复杂性为O(n1.3)。
思考:与插入排序相比,Shell排序的性能为什么能有一定的改善?快速排序(Quick sort)是冒泡排序算法的改进,它是目前所有常用排序方法中最快的一种(为什么?)在冒泡排序中,数据的比较和交换是在相邻单元中进行的,每次的交换只能上移或下移一个单元,因而总的比较次数多在快速排序中,数据的比较和交换是从两端向中间进行的,一次就可以交换定位两个单元中的数据,因而总的比较次数和交换次数比较少快速排序算法设有n个数存放在数组s中;在s[1..n]中任取一个元素作为比较的基准点(亦称为支点)元素,例如取t=s[1],其目的是定出t应在排序结果中的位置k,并将排序的元素交换成:s[1...k-1]<=s[k]<=s[k+1..n]3)利用分治策略,可以进一步对s[1...k-1]和s[k+1..n]中的两组数据进行快速排序,直到分组对象只有一个数据时为止。
Pascal递归算法

第七讲递归算法【递归的定义】为了描述问题的某一状态,必须用到它的上一状态,而描述上一状态,又必须用到它的上一状态……这种用自已来定义自己的方法,称为递归定义。
例如:定义函数f(n)为:则当n<>0时,须用f(n-1)来定义f(n),用f(n-1-1)来定义f(n-1)……当n=0时,f(n)=1。
由上例我们可看出,递归定义有两个要素:(1)递归边界条件。
也就是所描述问题的最简单情况,它本身不再使用递归的定义。
如上例,当n=0时,f(n)=1,不使用f(n-1)来定义。
(2)递归定义:使问题向边界条件转化的规则。
递归定义必须能使问题越来越简单。
如上例:f(n)由f(n-1)定义,越来越靠近f(0),也即边界条件。
最简单的情况是f(0)=1。
递归算法的效率往往很低, 费时和费内存空间. 但是递归也有其长处, 它能使一个蕴含递归关系且结构复杂的程序简介精炼, 增加可读性. 特别是在难于找到从边界到解的全过程的情况下, 如果把问题推进一步没其结果仍维持原问题的关系, 则采用递归算法编程比较合适.递归按其调用方式分为:1. 直接递归, 递归过程P直接自己调用自己;2. 间接递归, 即P包含另一过程D, 而D又调用P。
递归算法适用的一般场合为:1. 数据的定义形式按递归定义.如裴波那契数列的定义: f(n)=f(n-1)+f(n-2); f(0)=1; f(1)=2.对应的递归程序为:Function fib(n : integer) : integer;Beginif n = 0 then fib := 1 { 递归边界 }else if n = 1 then fib := 2 { 递归边界 }else fib := fib(n-2) + fib(n-1) { 递归 }End;这类递归问题可转化为递推算法, 递归边界作为递推的边界条件.2. 数据之间的关系(即数据结构)按递归定义. 如树的遍历, 图的搜索等.3. 问题解法按递归算法实现. 例如回溯法等.【举例】例1:楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,编一程序计算共有多少种不同的〖问题分析〗:设n阶台阶的走法数为f(n),显然有:例2:求m与n的最大公约数。
PASCAL讲义

第一章 PASCAL 基础一、PASCAL 介绍PASCAL 语言是由瑞士的沃斯教授于1971年提出来的,它的命名是为了纪念法国数学家Pascal 。
1、语言的特点:(1)它是世界上第一个结构化程序设计语言。
结构化:主张在程序中去掉goto 语句,所有的程序都由三种基本结构(顺序结构,选择结构、循环结构)组成,后来有人把函数和过程作为第四种基本结构。
(2)功能强、应用广广泛用于编写各种系统软件和应用软件。
(3)编译和运行效率高。
去掉了一些影响效率的因素。
(例如去掉了乘幂运算、字符串运算,去掉了动态数组等。
)使pascal 语言编译和运行效率都较高。
(4)可移植性、易推广。
用pascal 语言写的源程序可以在各种具有pascal 编译的机器上运行。
2、基本符号:(1)大小写英文字母:A ,B ,C ,D ,E ,F ,G ,H ,I ,J ,K ,L ,M ,N ,O ,P ,Q ,R ,S ,T ,U ,V ,W ,X ,Y ,Za ,b ,c ,d ,e ,f ,g ,h ,i ,j ,k ,l ,m ,n ,o ,p ,q ,r ,s ,t ,u ,v ,w ,x ,y ,z(2)数字:0,1,2,3,4,5,6,7,8,9(3)其它符号:+,-,*,/,=,<>,<=,>=,<,>,(,),[,] ,{,},: =,,,;,·,:,′,↑ 注意:pascal 语言除了能使用以上规定的基本符号外,不得使用任何其他符号。
例如:Ω,,,,πγβα等都不得到pascal 语言中使用。
3、保留字:在pascal语言中,有些具有特定的含义。
用户必须了解其含义,以便正确的使用,否则会造成错误。
这些具有特定含义的词被称为保留字。
保留字一共有35个,它们是:AND,ARRAY,BEGIN,CASE,CONST,DIV,DO,DOWNTO,ELSE,END,FILE,FOR,FUNCTION,GOTO,IF,IN,LABEL,MOD,NIL,NOT,OF,OR,RACKED,PROCEDURE,PROGRAM,RECORD,REPEAT,SET,THEN,TO,TYPE,UNTIL,V AR,WHILE,WITH保留字不得另作它用。
第2讲 pascal基本数据类型介绍及表达式运算(pascal程序语言基础)

2、构造类型
包括数组类型,集合类型,记录类型和文件类型 3、指针类型 指针类型属于动态数据类型
二、整型
用来表示整数数据的数据类型
Turbo pascal中五种预定义的整型
类型 Shorint Integer Longint 取值范围 -128...127 -32768...32767 -2147483648... 2147483647 占字节数 1 2 4 格式 带符号8位 带符号16位 带符号32位
作业:
1、将下列的数学表达式改写成PASCAL表达式: b2-4ac
2、求下列表达式的值: 20 mod 19 15 mod 9 7 div 8 19 div 3 (4>5) and (7<8) (8>9) or ( 9<10) 2 and ((3=3) or (3<7))
3、给一个数,利用ROUND()或TRUNC() 函数,在屏幕上输出该实数本身、整数部分、小 数部分(保留小数点后3位)。
4、输入一个四位整数,把它的各位数字倒序 输出。(提示:用MOD和DIV运算完成)
例:
11 div 2=5 -4 div 3= -1 11 mod 2=1 -4 mod 3= -1
4 div -3= -1
4 mod -3=1
A mod B=A - (A div B) * B mod运算的符号总是和被除数相同。
整型的运算 思考: 怎样判断一个数A是否能被数B整除?
比较运算:
( > , >= , < , <= , = , <> )
比较运算: (> , >= , < , <= , = , <> )
相关函数(如:abs(x),sqr(x),int(x)……)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本算法模块对于NOIP,基础是相当重要的,在3个小时之内做完4道题,那么就要求我们有相当快的速度。
特别是对于一些简单的、常用的算法模块,一定要要熟练掌握并灵活运用。
由于NOIP是一个比较基础的比赛,因此基本算法的掌握尤为重要,所以要求能够把这些基本的模块快速、准确的移植到不同的程序中,才能在稳中取胜。
基本算法模块中最重要的是基本程序框架,也就是说,要养成适合于自己的程序风格,这样对于程序编写的速度与程序的准确度都有较大的提高。
模块目录一、排序1.选择排序2.插入排序3.冒泡排序4.快速排序5.堆排序6.归并排序7.线性时间排序二、高精度1.高精度比较2.高精度加法3.高精度减法4.单精度乘法5.高精度乘法6.单精度除法7.高精度除法8.进制转换三、数论1.欧几里德算法2.扩展欧几里德3.求最小公倍数4.求解线形同余方程5.素数的判断6.素数的生成四、排列组合1.排列生成算法2.组合生成算法3.排列按序生成法4.排列字典序生成法五、图论1.图的读入2.深度优先搜索3.广度优先搜索4.强连同分量5.拓扑排序6.最小生成树7.最短路径六、背包问题1.装满背包2.一维价值最大背包3.二位价值最大背包一、排序算法vara:array[1..maxn]of longint;——排序对象1.选择排序——Select_sortprocedure select_sort;beginfor i:=1to n-1dofor j:=i+1to n doif a[i]>a[j]thenbegin temp:=a[i];a[i]:=a[j];a[j]:=temp;end;end;2.插入排序——Insert_sortprocedure insert_sort;beginfor i:=2to n dobeginkey:=a[i];j:=i-1;while(key<a[j])and(j>0)do begin a[j+1]:=a[j];dec(j);end;a[j+1]:=key;end;end;3.冒泡排序——Bubble_sortprocedure bubble_sort;beginfor i:=1to n-1dofor j:=n downto i+1doif a[j]<a[j-1]thenbegin temp:=a[j];a[j]:=a[j-1];a[j-1]:=temp;end;end;4.快速排序——Quick_sortprocedure qsort(s,t:longint);vari,j,x:longint;begini:=s;j:=t;x:=a[(i+j)div2];repeatwhile a[i]<x do inc(i);{找左边比他大的}while a[j]>x do dec(j);{找右边比他小的}if i<=j then{交换}begintemp:=a[i];a[i]:=a[j];a[j]:=temp;inc(i);dec(j);end;until i>j;if s<j then qsort(s,j);if i<t then qsort(i,t);end;5.堆排序——Heap_sortprocedure heap(i,n:longint);{将第i个元素向下筛}varj,x:longint;beginj:=i*2;x:=a[i];while j<=n dobeginif(j<n)and(a[j]<a[j+1])then inc(j);if x<a[j]then begina[i]:=a[j];i:=j;j:=i*2;endelse j:=n+1;end;a[i]:=x;end;procedure heap_sort;beginfor i:=n div2downto1do heap(i,n);for i:=n downto2dobegintemp:=a[i];a[i]:=a[1];a[1]:=temp;heap(1,i-1);end;end;6.归并排序——Merge_sortprocedure mergesort(s,t:longint);varm,i,j,k:longint;beginif t-s=0then exit;m:=(s+t)div2;mergesort(s,m);mergesort(m+1,t);for i:=1to m-s+1do b[i]:=a[s+i-1];for j:=m+1to t do c[j-m]:=a[j];i:=1;j:=1;b[m-s+2]:=max;c[t-m+1]:=max;for k:=s to t doif b[i]<c[j]then begin a[k]:=b[i];inc(i);endelse begin a[k]:=c[j];inc(j);end;end;7.线性时间排序——基数排序、计数排序、桶排序二、高精度算法——High_precisionconstmaxcount=进制位maxlen=记录高精度数组大小typebignum=array[0..maxlen]of longint;0为位数1.高精度比较function compare(a,b:bignum):longint;beginwhile a[a[0]]=0do dec(a[0]);{检查位数是否正确}while b[b[0]]=0do dec(b[0]);while a[a[0]+1]>0do inc(a[0]);while b[b[0]+1]>0do inc(b[0]);if a[0]>b[0]then exit(1);if a[0]<b[0]then exit(-1);for i:=a[0]downto1dobeginif a[i]>b[i]then exit(1);if a[i]<b[i]then exit(-1);end;exit(0);end;2.高精度加法procedure add(a,b:bignum;var c:bignum);vari:longint;beginfillchar(c,sizeof(c),0);c[0]:=1;if a[0]>b[0]then c[0]:=a[0]else c[0]:=b[0];for i:=1to a[0]do inc(c[i],a[i]);for i:=1to b[0]do inc(c[i],b[i]);for i:=1to c[0]dobegininc(c[i+1],c[i]div maxcount);c[i]:=c[i]mod10;end;while c[c[0]+1]>0dobegininc(c[0]);inc(c[c[0]+1],c[c[0]]div maxcount);c[c[0]]:=c[c[0]]mod maxcount;end;end;3.高精度减法procedure minus(a,b:bignum;var c:bignum);vari:longint;beginfillchar(c,sizeof(c),0);c[0]:=a[0];for i:=1to c[0]do c[i]:=a[i]-b[i];for i:=1to c[0]doif c[i]<0thenbegindec(c[i+1]);inc(c[i],maxcount);end;while(c[0]>1)and(c[c[0]]=0)do dec(c[0]);end;4.单精度乘法procedure mulnum(a:bignum;x:longint,var c:bignum);vari:longint;beginfillchar(c,sizeof(c),0);c[0]:=a[0];for i:=1to c[0]do c[i]:=a[i]*x;for i:=1to c[0]dobegininc(c[i+1],c[i]div maxcount);c[i]:=c[i]mod10;end;while c[c[0]+1]>0dobegininc(c[0]);inc(c[c[0]+1],c[c[0]]div maxcount);c[c[0]]:=c[c[0]]mod maxcount;end;end;5.高精度乘法procedure mul(a,b:bignum;var c:bignum);vari,j:longint;beginfillchar(c,sizeof(c),0);c[0]:=a[0]+b[0]-1;for i:=1to a[0]dofor j:=1to b[0]doinc(c[i+j-1],a[i]*b[j]);for i:=1to c[0]dobegininc(c[i+1],c[i]div maxcount);c[i]:=c[i]mod10;end;while c[c[0]+1]>0dobegininc(c[0]);inc(c[c[0]+1],c[c[0]]div maxcount);c[c[0]]:=c[c[0]]mod maxcount;end;end;6.单精度除法function divnum(a:bignum;x:longint;var c:bignum):longint;vari,temp:longint;beginfillchar(c,sizeof(c),0);c[0]:=a[0];temp:=0;for i:=a[0]downto1dobegintemp:=temp*maxcount+a[i];c[i]:=temp div x;temp:=temp mod x;end;while(c[o]>1)and(c[c[0]]=0)do dec(c[0]);exit(temp);end;7.高精度除法procedure div(a,b:bignum;var c,d:bignum);vari:longint;beginfillchar(c,sizeof(c),0);c[0]:=a[0]-b[0]+1;fillchar(d,sizeof(d),0);d[0]:=1;for i:=c[0]downto1dobeginc[i]:=maxcount;repeatdec(c[i]);mul(c,b,temp);until compare(a,temp)>=0;end;while(c[o]>1)and(c[c[0]]=0)do dec(c[0]);minus(a,temp,d);end;8.进制转换10进制数用bignum记,maxcount=10k进制数用string记constrepchar:array[0..35]ofstring=(‘0’,‘1’,’2’,……,’a’,’b’,……,’z’);——数码对应的字符repnum:array[48..122]of longint=(0,1,2……,34,35);——字符的ASCCI码对应的数码k进制转十进制:procedure change_to_ten(s:string;k:longint):bignum;vari,l:longint;temp:bignum;beginl:=length(s);temp[0]:=1;temp[1]:=repnum[ord(s[l])];for i:=1to l-1dobegininc(temp[1],repnum[ord(s[l-i])]);mulnum(temp,k);end;exit(temp);end;十进制转k进制:procedure change_to_k(num:bignum;k:longint):string;vari,temp:longint;s:string;beginif(num[0]=1)and(num[1]=0)then exit(‘0’);while not((num[0]=1)and(num[1]=0))dobegintemp:=divnum(num,k,num);s:=repchar[temp]+s;end;exit(s);end;三、数论算法1.求最大公约数——gcd(欧几里德算法)递归(recursion):function gcd(a,b:longint):longint;beginif b=0then exit(a);exit(gcd(b,a mod b));end;非递归(iterative):function gcd(a,b:longint):longint;vart:longint;beginwhile b<>0dobegint:=a;a:=b;b:=t mod b;end;exit(a);end;2.扩展欧几里德算法function extended_euclid(a,b:longint;var x,y:longint):longint;varp,q:longint;beginif b=0thenbeginx:=1;y:=0;exit(a);end;p:=extended_euclid(b,a mod b,x,y);q:=x;x:=y;y:=q-a div b*y;exit(p);end;3.求最小公倍数k:=a*b div gcd(a,b);4.求解线性同余方程typeansnode=recordansnum:longint;——解的个数num:array[1..maxnnum]of longint;——解end;procedure modular_linear_equation(a,b,n:longint;var ans:ansnode);vard,i,x,y,temp:longint;begind:=extended_euclid(a,n,x,y);if b mod d<>0then ans.ansnum:=0else beginans.ansnum:=d;temp:=(x*(b div d))mod n;for i:=1to d do ans.num[i]:=(temp+i*(n div d))mod n;end;end;5.素数的判断function prime_bool(x:longint):boolean;vari:longint;beginfor i:=2to trunc(sqrt(x))doif x mod i=0then exit(false);exit(true);end;6.素数的生成maxnum=生成质数的范围maxprime=对应范围中的质数个数varprime:array[0..maxprime]of longint;——存储质数bool:array[1..maxnnum]of boolean;——存储每个数是不是质数procedure prime_make;vari,j:longint;beginfillchar(bool,sizeof(bool),0);i:=2;while i<=maxnnum dobeginif not p[i]thenbeginj:=2*i;while i<=maxnnum dobeginp[j]:=true;inc(j,i);end;inc(prime[0]);prime[prime[0]]:=i;end;inc(i);end;end;四、排列组合算法1.排列生成算法——m的n排列vara:array[0..maxn]of longint;——排列方案b:array[0..maxm]of boolean;——每个数是否被用过递归(recursion):procedure make_permutation_recursion(t:longint)vari:longint;beginif t=n+1thenbeginwrite(a[1]);for i:=2to n do write(‘‘,a[i]);writeln;exit;end;for i:=1to m doif not b[i]thenbeginb[i]:=true;a[t]:=i;make(t+1);b[i]:=false;end;end;非递归(iterative):procedure make_permutation_iterative(m,n:longint);vari,j:longint;begini:=1;a[1]:=0;repeatj:=a[i]+1;while(j<=m)and(b[j])do inc(j);if j<=mthen begina[i]:=j;b[j]:=true;if i=nthen beginwrite(a[1]);for j:=2to n do write(‘‘,a[j]);writeln;b[a[n]]:=false;endelse begininc(i);a[i]:=0;end;endelse begindec(i);b[a[i]]:=false;end;until i=0;end;2.组合生成算法——m的n组合procedure make_combination(t:longint)vari:longint;beginif t=n+1thenbeginwrite(a[1]);for i:=2to n do write(‘‘,a[i]);writeln;exit;end;for i:=a[t-1]to m doif not b[i]thenbeginb[i]:=true;a[t]:=i;make(t+1);b[i]:=false;end;end;3.排列按序生成法constpower:array[1..maxn]of longint=(…);power[i]为i的阶乘typepermutationnode=array[1..maxn]of longint;——排列方案求n的全排的字典序:function get_number(n:longint;a:permutationnode):longint;varb:array[1..maxn]of longint;i,j,s:longint;beginfor i:=1to n do b[i]:=i-1;s:=0;for i:=1to n-1dobegininc(s,b[a[i]]*power[n-i]);for j:=a[i]+1to n do dec(b[j]);end;exit(s+1);end;求字典序为m的n的全排:function get_permutation(m,n:longint;):permutationnode;varuse:array[1..maxn]of boolean;a:array[0..maxn]of longint;temp:permutationnode;begindec(m);for i:=1to n-1dobegina[i]:=m mod(i+1);m:=m div(i+1);end;a[0]:=0;for i:=1to n dobeginj:=0;for k:=1to a[n-i]+1dobegininc(j);while use[j]do inc(j);end;temp[i]:=j;use[j]:=true;end;exit(temp);end;4.排列字典序生成法——求n的某个全排的下m个字典序排列procedure make_next(n,m:longint;a:permutationnode):permutationnode;vari,j,k,t,temp:longint;beginfor t:=1to m dobegini:=n;while(i>1)and(a[i]<a[i-1])do dec(i);j:=n;while a[j]<a[i-1]do dec(j);temp:=a[i-1];a[i-1]:=a[j];a[j]:=temp;for k:=i to(i+n)div2dobegintemp:=a[k];a[k]:=a[n+i-k];a[n+i-k]:=temp;end;end;exit(a);end;五、图论算法1.图的读入以点为基础读入(没有特殊说明,一般以此方法读入):varvetex:array[1..maxn,0..maxn]of longint;——邻接表,记录与那些点相连map:array[1..maxn,1..maxn]of longint;——邻接矩阵,记录点点之间的距离procedure initgraph;vari,u,v,c:longint;beginreadln(n,e);for i:=1to e dobeginreadln(u,v,c);inc(vetex[u,0]);vetex[u,vetex[u,0]]:=v;map[u,v]:=c;end;end;以边为基础读入:typenode=recordu,v,w:longint;——u为起点,v为终点,w为权end;varvetex:array[1..maxe]of node;——记录边procedure initgraph;vari:longint;beginreadln(n,e);for i:=1to e dowith vetex[i]do readln(u,v,w);end;2.深度优先搜索——DFSvartime:longint;——时间flag:array[1..maxn]of boolean;——是否标记procedure DFS(t:longint);vari:longint;begininc(time);gettime[t]:=time;flag[t]:=true;for i:=1to vetex[t,0]doif not flag[vetex[t,i]]thenbeginfrom[vetex[t,i]]:=t;dep[vetex[t,i]]:=dep[t]+1;DFS(vetex[t,i]);end;inc(time);finishtime[t]:=time;end;3.广度优先搜索——BFSprocedure BFS(t:longint);vartime,open,closed,i,v:longint;flag:array[1..maxn]of boolean;x0:array[1..maxn]of longint;beginfillchar(flag,sizeof(flag),0);open:=0;closed:=1;x0[1]:=t;dep[t]:=0;time:=1;flag[t]:=true;flagtime[t]:=1;repeatinc(open);v:=x0[open];inc(time);finishtime[v]:=time;for i:=1to vetex[v,0]doif not flag[vetex[v,i]]thenbegininc(closed);x0[closed]:=vetex[v,i];flag[vetex[v,i]]:=true;dep[vetex[v,i]]:=dep[v]+1;inc(time);gettime[vetex[v,i]]:=time;end;until open>=closed;end;4.强连通分量varconnected:array[1..maxn,0..maxn]of longint;——connect[i,0]为此分量包含的节点数total:longint;——强连同分量的个数procedure strongly_connected;vari,time:longint;flag:array[1..maxn]of boolean;sign:array[1..maxn]of longint;procedure sort1(t:longint);vari:longint;beginflag[t]:=true;for i:=1to n doif(map[t,i]<>0)and(not flag[i])thensort1(i);inc(time);sign[time]:=t;end;procedure sort2(t:longint);vari:longint;beginflag[t]:=true;for i:=1to n doif(not flag[i])and(map[i,t]<>0)thensort2(i);inc(connected[total,0]);connected[total,conneted[total,0]]:=t;end;beginfillchar(flag,sizeof(flag),0);for i:=1to n doif not flag[i]thensort1(i);for i:=n downto1doif not flag[sign[i]]thenbegininc(total);sort(sign[i]);end;end;5.拓扑排序procedure topological_sort;vari,open,closed:longint;flag:array[1..maxn]of boolean;beginopen:=0;closed:=0;for i:=1to n doif inv[i]=0thenbegininc(closed);flag[i]:=true;AOV[closed]:=i;end;if closed=0then exit{error};repeatinc(open);v:=AOV[open];for i:=1to vetex[v,0]doif not flag[vetex[v,i]]thenbegindec(inv[vetex[v,i]]);if inv[vetex[v,i]]=0thenbegininc(closed);AOV[closed]:=vetex[v,i];flag[vetex[v,i]]:=true;end;end;until open=closed;if closed<n then exit{error};end;6.最小生成树Prime:procedure prime_normal;vari,j,min,mj:longint;flag:array[1..maxn]of boolean;lowcost:array[1..maxn]of longint;beginfillchar(lowcost,sizeof(lowcost),$5F);lowcost[1]:=0;flag[1]:=true;for i:=1to v[1,0]dolowcost[v[1,i]]:=map[1,v[1,i]];for i:=2to n dobeginmin:=maxlongint;for j:=1to n doif(not flag[j])and(lowcost[j]<min)thenbeginmin:=lowcost[j];mj:=j;end;flag[mj]:=true;inc(totallen,min);for j:=1to v[mj,0]doif(not flag[v[mj,j]])and(lowcost[v[mj,j]]>map[mj,v[mj,j]])thenlowcost[v[mj,j]]:=map[mj,v[mj,j]];end;end;Kruskal——以边为基础读入:procedure kruskal;varset1,set2,vetex_pointer,last_set_num:longint;function find(x:longint):longint;beginif father[x]=x then find:=father[x]else begin father[x]:=find(father[x]);find:=father[x];end;end;beginqsort(1,e);——对vetex以w为关键字从小到大排序for i:=1to n do father[i]:=i;vetex_pointer:=1;last_set_num:=n;while(last_set_num>1)and(vetex_pointer<=e)dobeginset1:=find(vetex[vetex_pointer].u);set2:=find(vetex[vetex_pointer].v);if set1<>set2thenbegininc(totallen,vetex[vetex_pointer].w);dec(last_set_num);father[set1]:=set2;end;inc(vetex_pointer);end;writeln(totallen);end;7.最短路径Dijktra:procedure Dijkstra(s:longint);vari,j,min,mi:longint;beginfillchar(shortest,sizeof(shortest),$5F);shortest[s]:=0;for i:=1to n dobeginmin:=max;for j:=1to n doif(not flag[j])and(shortest[j]<min)thenbegin min:=shortest[j];mi:=j;end;flag[mi]:=true;for j:=1to vetex[mi,0]doif(not flag[vetex[mi,j]])and(shortest[vetex[mi,j]]>min+map[mi,vetex[mi,j]])thenshortest[vetex[mi,j]]:=min+map[mi,vetex[mi,j]];end;end;Floyd:procedure Floyd;vari,j,k:longint;beginfillchar(len,sizeof(len),$5F);for i:=1to n dobeginlen[i,i]:=0;for j:=1to vetex[i,0]dolen[i,vetex[i,j]]:=map[i,vetex[i,j]];end;for k:=1to n dofor i:=1to n dofor j:=1to n doif len[i,k]+len[k,j]<len[i,j]thenlen[i,j]:=len[i,k]+len[k,j];end;Bellman-ford——以边为基础读入:procedure Bellman-ford(s:longint);vari,j:longint;bool:boolean;beginfillchar(shortest,sizeof(shortest),$5F);shortest[s]:=0;bool:=true;for i:=1to n-1doif bool thenbeginbool:=false;for j:=1to e doif shortest[vetex[j].v]>shortest[vetex[j].u]+vetex[j].w thenbeginshortest[vetex[j].v]:=shortest[vetex[j].u]+vetex[j].w;bool:=true;end;end;for j:=1to e doif shortest[vetex[j].v]>shortest[vetex[j].u]+vetex[j].w thenexit(flase);exit(true);end;SPFA:procedure SPFA(s:longint);varu,i:longint;x0:array[1..maxn]of longint;beginfillchar(shortest,sizeof(shortest),$5f);fillchar(flag,sizeof(flag),0);open:=0;closed:=1;x0[1]:=s;shortest[s]:=0;flag[s]:=true;repeatinc(open);u:=x0[open];for i:=1to vetex[u,0]doif shortest[vetex[u,i]]<shortest[u]+map[u,vetex[u,i]]thenbeginshortest[vetex[u,i]]:=shortest[u]+map[u,vetex[u,i]];if not flag[vetex[u,i]]thenbegininc(closed);x0[closed]:=vetex[u,i];flag[vetex[u,i]]:=true;end;end;flag[u]:=false;until open>=closed;end;六、背包问题1.尽量把容量为w的箱子装满varf:array[0..maxw]of boolean;weight:array[1..maxn]of longint;function p1:longint;vari,j:longint;beginfillchar(f,sizeof(f),0);f[0]:=true;for i:=1to n dofor j:=w downto weight[i]dof[j]:=f[j]or f[j-weight[j]];i:=w;while not f[i]do dec(i);exit(i);end;2.在容量为w的箱子中装入物品使总价值最高varf:array[0..maxw]of longint;weight,value:array[1..maxn]of longint;function p2:longint;vari,j:longint;beginfillchar(f,sizeof(f),$FF);f[0]:=0;for i:=1to n dofor j:=w downto weight[i]doif f[j-weight[i]]<>-1thenf[j]:=max(f[j],f[j-weight[i]]+value[i]);j:=0;for i:=0to w do j:=max(j,f[i]);exit(j);end;3.在满足两个量的限制(w,h)条件下使总价值最高typenode=recordw,h:longint;value:longint;end;varf:array[0..maxw,0..maxh]of longint;num:array[1..maxn]of node;function p3:longint;vari,j:longint;beginfillchar(f,sizeof(f),$FF);f[0,0]:=0;for i:=1to n dofor j:=w downto num[i].w dofor k:=h downto num[i].h doif f[j-num[i].w,k-num[i].h]<>-1thenf[j,k]:=max(f[j,k],f[j-num[i].w,k-num[i].h]+num[i].value);i:=0;for j:=0to w dofor k:=0to h do i:=max(i,f[j,k]);exit(i);end;。
