特勒根定理ppt课件

合集下载

第8讲电阻电路的分析-特勒根定理、互易定理

支路 1
(a) 2 3 1 2 2 3 4 2 2 5 1 4 -1 6 1 5 6 -2 1 -1 -3 7 2 8 -4
∑u i
k =1 6
6
(b)
k k
= −15 + 3 + 4 − 4 − 2 + 14 = 0
ˆi ∑u
k =1 6
k =1 6
k k
= −21 + 2 + 10 − 6 − 1 + 16 = 0
uS1
1 2 1' 2'
1.定理陈述 1.定理陈述
N
N
i22'
22 '
11'
S1
S2
^ i 11'
1
1'
N
2 ^S2 u 2'
S1
S2
22 '
11'
§2-12 互易定理
§2-12 互易定理
2.证明互易定理 2.证明互易定理
ˆ u22 ' u = 11' ˆS 2 iS1 i
⑵
1 1'
1
iS1
1'
N N
k k k =1
b
k k
=0
3 3 6 0
^ ^ 1 ' 2 ^ 1 ^ 5
^ ^ 4 2' ^ ^ 3 3' ^ 6 ^' 0
∑u i
k =1
k k
=0
证明：证明：设两个电路如图1 设两个电路如图1、图2
k =1
) ∑ uk ik = 0
b
(5)
1
图1 图2 对图1 对图1电路，电路，应用KVL 应用KVL写出节点电压表示的各支路电压表示式 KVL写出节点电压表示的各支路电压表示式对图2 对图2电路，电路，应用KCL 应用KCL写出各节点电流代数和表示式 KCL写出各节点电流代数和表示式

电路(特勒根互易定理)

(b)
则两个支路中电压电流有如下关系: 则两个支路中电压电流有如下关系:
u2 u1 = iS1 iS 2
当
或 u1 i S 1 = u2 i S 2
时,u2 = u1
返回上页下页
iS1 = iS2
情况3 情况3
激励
图a 图b
电流源电压源响应线性电阻网络 NR
图a 图b
电流电压
a iS1 b
线性电阻网络 NR
c i2 d
a + u1 – b
c + – d uS2
(a)
(b)
则两个支路中电压电流在数值上有如下关系: 则两个支路中电压电流在数值上有如下关系:
i2 u1 = i S 1 uS 2
当
或 u1 i S 1 = uS 2 i2
时,i2 = u1
返回上页下页
1. 互易定理
对于一个仅含线性电阻且只有一个激励的电路, 对于一个仅含线性电阻且只有一个激励的电路,在保持电路将独立源置零后电路拓扑结构不变的条件下, 电路将独立源置零后电路拓扑结构不变的条件下,当激励与响应互换位置后,响应与激励的比值保持不变. 响应互换位置后,响应与激励的比值保持不变.
返回
上页
下页
情况1 情况1 a uS1 + – b
激励线性电阻网络 NR
电压源
响应线性电阻网络 NR
电流
c i2 d i1
a
c + – d uS2
(a)
b
(b)
则两个支路中电压电流有如下关系: 则两个支路中电压电流有如下关系:
当
uS1 = uS2
时,i2 = i1

特勒根与互易定理.ppt

0
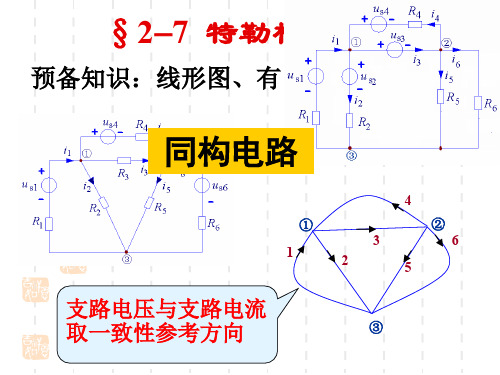
以④节点作为电位参考点，则 ①、②、③节点的电位分别为 v1、v2、v3
i1 i4 i6 0 i2 i4 i5 0 i3 i5 i6 0
u1 v1, u2 v2 , u3 v3 ,

u4

v1

v2 , u5

v2

v3 , u6

v3

v1

对于任一具有nt = n+1个节点、b条支路的电路，其支路电流、支路电压分别为( i1，i2 ，···，ib )、 ( u1，u2 ，···， ub )，且各支路电压与电流参考方向相关联，则在任意时刻t，均有
b
ukik 0
k 1
该定理表明，在任意电路中，在任何瞬时t，各支路吸收功率的代数和恒等于零。也就是说，电路中各独立源供给功率的总和，等于其余各支路吸收功率的总和，满足功率守恒。
注意：
（1）该定理要求u(或 uˆ )和i(或 iˆ)应分别满足KVL和KCL。
特勒根定理适用于任何（线性或非线性、有源或无源、时变或非时变）集中参数网络。特勒根定理只与考虑电路的联接形式，与元件特性无关。
（2）每一个支路的电流、电压均取一致的参考方向。
（3）特勒根定理既可用于两个具有相同有向图的不同网络，k Rkikiˆk
k 1
k 1
b
b
Rkiˆkik uˆkik
k 1
k 1
u11iˆ11 u22iˆ22 uˆ11i11 uˆ22i22
互易定理的第一种形式
因为则故
u11 us , u22 0 uˆ22 us , uˆ11 0
I2

2-7特勒根定理

b
有
∑u i
k =1
k k
=0
(2) 证明: 证明:
§27 特勒根定理
b
∑u i
k =1
k k
=0
令v4=0 支路电压用节点电压表示 u1= - v1 u2= - v2
k =1
∑ uk ik = u1i1 + u2i2 + u3i3 + u4i4 + u5i5 + u6i6
=-v1i1 +(-v )i2 +(-v )i3 +(v-v2 )i4 +(v2-v )i5 +(v3-v )i6 2 3 1 3 1
6
=v1(i1 +i4 i6) +v2(i2 i4 +i5) +v3(i3 i5 +i6 =0 )
§27 特勒根定理
将这一结论推广到任一具有n个节点, 条支路的将这一结论推广到任一具有个节点,b条支路的个节点 b 电路, 电路,则有这就是特勒根功率定理(Tellegen′s power theorem) ′ 这就是特勒根功率定理的数学表达式.该定理表明, 的数学表达式.该定理表明,在任意集中参数电路中, 在任何瞬时t, 路中 , 在任何瞬时 t , 各支路吸收功率之和恒等于零.也就是说, 于零.也就是说,电路中各独立源供给功率的总等于其余各支路吸收功率的总和. 和,等于其余各支路吸收功率的总和条支路在t时刻吸收的功率 (3)物理意义 uk (t)ik (t) = 第k条支路在时刻吸收的功率 )物理意义: 条支路在表整个电路在t时刻各支路吸收功率之和守恒( 表整个电路在时刻各支路吸收功率之和守恒(为时刻各支路吸收功率之和守恒又叫瞬时功率守恒定理. 瞬时功率守恒定理零), 所以又叫瞬时功率守恒定理.

特勒根与互易定理

上页
下页

2A + –

+ 无源 4V 电阻 – 网络
b
1A + 2V –
3A +
(5 / 4)U 2

+ 无源 4.8V 电阻 – – 网络

+
U2
–
b
ˆ ˆ U1 ( I 1 ) U 2 I 2 Rk I k I k U 1 ( I1 ) U 2 I 2 Rk I k I k
un1 (i1 i2 i4 ) un 2 (i4 i5 i6 ) un 3 (i2 i3 i6 ) 0
2. 特勒根定理2
2
4
1 2 3 6
5
4 3
1 任何时刻，对于两个具有n个结点和b条支路的集总电路，当它们具有相同的图，但由内容不同的支路构成，在支路电流和电压取关联参考方向下，满足:
k 1

b
u
k 1
b
k
i k u1 i 1 u2 i 2 uk i k
k 3

b

u1 i 1 u2 i 2 Rk ik i k 0
bFra biblioteku
k 1
b

k k
i u1 i1 u 2 i2 u k ik
k 3

k 3 b
u1 i1 u 2 i2 Rk ik i k 0
返回
上页
下页
* 4.6
互易定理
互易性是一类特殊的线性网络的重要性质。一个具有互易性的网络在输入端（激励）与输出端（响应）互换位置后，同一激励所产生的响应并不改变。具有互易性的网络叫互易网络，互易定理是对电路的这种性质所进行的概括，它广泛的应用于网络的灵敏度分析和测量技术等方面。

第6章特勒根定理

+
~ I1
~ I2
JS
若网络互易，必有
2010-11-4
~ V2 = V1
第6章特勒根定理 7
互易定义2 端口网络互易）二、互易定义（n端口网络互易）端口网络互易
一个P端口时不变网络，或者一个端元件，一个端口时不变网络，或者一个P+1端元件，如果存在：端口时不变网络端元件
k =1
则有： ∆Vb = Z b ∆I b + ∆Z b I b + ∆Z b ∆I b 上式略去二阶小量后，得
∆Vb = Z b ∆I b + ∆Z b I b
2010-11-4 第6章特勒根定理 18
设网络N的伴随网络为 ~ ~ VbT I b − VbT I b = 0
T
~ N
则有：
网络N参数变化前的变量网络N参数变化后的变量
2010-11-4 第6章特勒根定理 16
交互互易定理在灵敏度分析中的应用 ~ 相互伴随，若网络 N 和 N 相互伴随，
则对于非独立电源支路集合b，必有：则对于非独立电源支路集合，必有：
l =1
~ ~ ∑ (Vl I l − Vl I l ) = 0
b
或写作矩阵形式
T~ Vb I b
~T − Vb I b = 0
T~ Vb I b
~T − Vb I b = 0
=
T T I b (Z b
~ − Z b )I b = 0
上式恒为零，只有
Zb =
T Zb
1）互易性也存在着伴随网络，只不过伴随网络就是网络N本身 2）交互互易性意义更广泛，它可以应用于任意网络，只需构造出伴随网络。（由节点导纳矩阵或回路阻抗矩阵看，若是互易元件组成的，由于是对称矩阵，伴随网络的矩阵就是原网络相应矩阵本身），（若含非互易元件，伴随网络的矩阵取相应矩阵的转置即可）。因此伴随网络的选择非常容易。

课件：第3.4节特勒根定理

电路
刘洪臣哈尔滨工业大学电气及自动化学院
3.4 特勒根定理
基本要求：理解特勒根定理的内容、证明过程、物理意义和普遍适用性。
1. 定理
uk ,ik
N
(a)
uk , ik
N
(b)
结 (1) 节点数与支路数分别相同；构 (2) 节点与支路的连接关系也分别相同；相 (3) 节点与支路的编号也相同；
b
因为 i i ukik
(un i un i )
k 1
所有支路
N
(a)
uk , ik
对于整个电路存在 un i
N
(b)
b
i 0 ukik 0 同样可以证明第二种表达形式
k 1
3.4 特勒根定理
如果将特勒根定理用于一个电路N（即Nˊ也是N），便
得到
b
ukik 0
k 1
同 (4) 对应的支路具有相同的u，i 关联参考方向。
3.4 特勒根定理
特勒根定理: 电路N中各支路电压uk与电路 N 中对
应支路电流 i的k 乘积之和等于零，即
b
b
ukik 0 同样
ukik 0
k 1
k 1
uk ,ik
证明： ukik (un un )ik (un un )i
【例题3.20】图示电路中N为纯二端电阻网络，
在图(a)中 U1 4V, R2 2, I1 1A, I2 0.5A ；
在图(b)中 I1 2A, R2 4,U2 3.2V 求等效电阻 Ri 。
I1
I2
I1
I2
U1
N
R2 U2
U1
N
R2 勒根定理得 U1I1 U2I2 U1I1 U2I2

特勒根定理ppt课件

uˆ1i1 uˆ 2i2 uˆ k ik 0
uk iˆk Rk ik iˆk ( Rk iˆk )ik uˆ k ik 5
k3
证明：设共有b条支路， u1 uS , u2 0;uˆ1 0, uˆ 2 uˆ S
b
u1iˆ1 u2iˆ2 uk iˆk 0
uk Rkik uˆ k Rk iˆk
( un3 un1 )i4 un2i5 un3i6
un1( i1 i2 i4 ) un2 ( i2 i3 i5 ) un3 ( i3 i4 i6 )
0
KCL：
能量守恒是特勒根定理1的特例
i1 i2 i4 0
二、特勒根定理2：
i2 i3 i5 0 i3 i4 i6 0
2.6 特勒根定理
一、特勒根定理1：
对于一个n个结点，b条支路的网络，令向量i=(i1，i2…..，ib) 和u=(u1，u2…..，ub)分别表示支路电流和支路电压，并规定
支路电压和支路电流为关联参考方向，有：
证明： 4
b
ukik 0
k 1
KCL：
①
②
③
2
3
15
6
0
i1 i2 i4 0 i2 i3 i5 0 i3 i4 i6 0
u ( u1 ,u2 ,...........,ub )
iˆ ( iˆ1 ,iˆ2 ,...........,iˆb ) uˆ ( uˆ1 ,uˆ 2 ,...........,uˆ b ) 来表示
并规定所有支路电压和支路电流为关联参考方向, 则有：
b
ukiˆk 0
k 1
b
uˆ kik 0
即
uS i2
uˆ S iˆ1
特殊 uS uˆ S , 则 i2 iˆ1

特勒根定理

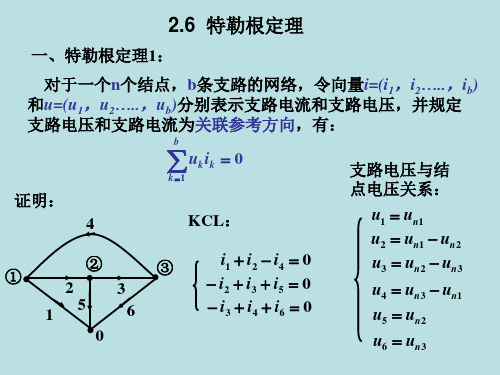
线性电阻网络 N
(b) ˆ ˆ = 0, u2 = uS
ˆ ˆ uk = Rk ik
ˆ ˆ u1 i1 + u2 i2 + ˆ ˆ u1 i1 + u2 i2 +
b
∑ u iˆ
k =3 b
k k
=0 =0
∵ uk = Rk ik
ˆ ∑u i
k =3
k k
ˆ ˆ ˆ ˆ ∴ uk ik = Rk ik ik = ( Rk ik )ik = uk ik
i = ( i1 ,i2 ,...........,ib )
u = ( u1 ,u2 ,...........,ub )
ˆ ˆ ˆ ˆ i = ( i1 , i2 ,..........., ib )
ˆ ˆ ˆ ˆ u = ( u1 ,u2 ,...........,ub ) 来表示
并规定所有支路电压和支路电流为关联参考方向则有：并规定所有支路电压和支路电流为关联参考方向, 则有：关联参考方向
b k=1
b
∑
ˆ uk ik = 0
ˆ ∑u i
k=1
k k
=0
KCL、KVL和特勒根定理合称为拓扑约束，适、合称为拓扑约束和特勒根定理合称为拓扑约束，用于任何集总电路用于任何集总电路例4-8 已知如图 , 求电流 ix 。 i1 + ix 10V 1A R N 解：设电流 i1和 i2 ，方向如图所示。方向如图所示。由特勒根定理2 由特勒根定理2，得： 5V + i2
2.6 特勒根定理
一、特勒根定理1：特勒根定理：对于一个n个结点，条支路的网络令向量i=(i 条支路的网络，对于一个个结点，b条支路的网络，令向量 1，i2…..，ib) 个结点分别表示支路电流和支路电压，和u=(u1，u2…..，ub)分别表示支路电流和支路电压，并规定分别表示支路电流和支路电压支路电压和支路电流为关联参考方向关联参考方向，支路电压和支路电流为关联参考方向，有：

讲义第十六章

Z 参数也称开路阻抗参数
【注】 (4)无源（可逆）等效电路——T型等效
例：求图示双口网络吸收的功率 P N 。解：法一
法二
短路导纳参数 Y
两端口的 Y 参数矩阵。矩阵中的元素称为 Y 参数 Y 参数属于导纳性质
例:求图示双口网络的导纳参数矩阵 Y 解：列方程为
例:求图示双口网络的导纳参数矩阵 Y 解：【法一】节点方程为
•
I2
•
U2
§16-5 二端口的连接
一个复杂二端口网络可以看作是由若干简单的二端口按某种方式联接而成，这将使电路分析得到简化。两端口的级联 (链联) 、并联、串联
有载双口网络的分析:当双口网络的两个端口分别联接上其他元件或支路时，称为有载双口网络。
例：如图所示双口网络的T参数矩阵为：
[Y
]1
II12
[Z
]
I1 I2
传输参数 T
在许多工程实际问题中，往往希望找到一个端口的电压、电流与另一个端口的电压、电流之间的直接关系。 T 参数用来描绘两端口网络的输入和输出或始端和终端的关系
T 参数的物理意义及计算和测定
端口2开路时端口1与端口2的电压比，称转移电压比；
端口2短路时端口1的电压与端口2的电流比，称短路转移阻抗；
T
D
C
D
B D
双口网络的等效电路
•
I1
Z1
Z3
•
a. 若双口网络内部不
I 2 含受控源，则该双口网
络可以用T型电路或型
•
U1
Z2
•
U2
电路等效
T 型电路
•
•
U 1 Z1 I 1 Z2
••
I1 I2

特勒根定理

特勒根定理
特勒根定理
特勒根定理（Tellegen’s theorem）是在克希霍夫定律的基础上发展起来的网络定理。

它与网络元件的特性无关，对非线性参数以及时变参数的网络都适用。

4.4.1 特勒根功率定理
一、内容
在一个具有n个节点、b条支路的网络N中，假设各个支路的电压与支路电流分别为(u1,u2....)和(i1,i2....) ，它们取关联参考方向，则对任意时间t，有
二、定理的证明
本教材中给出了一个实际的例子进行说明，有助于大家理解。

证明的依据是克希霍夫定律，以及电路的节点电压与各个支路电压的关系。

具体的严格证明过程同学们可以参见相关参考文献。

三、意义
在任意网络N中，在任意瞬时t，各个支路吸收的功率的代数和恒等于零。

也就是说，该定理实质上是功率守恒的具体体现。

4.4.2 特勒根拟功率定理
一、内容
两个具有n个节点、b条支路的网络N，它们由不同的元件组成，但它们的拓扑结构完全相同。

假设两个网络中对应的各个支路的电压与电流取关联参考方向，分别为
则对任意时间t，有
这个和式中的每一项，都仅仅是一个数学量，没有实际物理意义，定义它为“拟功率”。

特勒根定理 (2)ppt课件

k 3
k 3
故： u1i1'u2i2 ' u1'i1 u2 'i2
10
+ +i1
i2 + +
i1' +
i2' +
3v -
u-1
NR 4Ω u-2
3v -
u' 1 NR 8Ω u' 2
-
-
3i1'4i2 i2' 3i1 8i2'i2
i1＝-2A， i2＝1A， i1‘＝-1.8A代入
3(1.8) 41 i2' 3(2) 8i2'1 i2' 0.15A
特勒根定理
特勒根第一定理(功率守恒)：
任意一个具有b条支路、n个节点的
集总参数网络，设它的各支路电压和电
流分别为uk 和 ik (k＝1、2、3、…b)，
且各支路电压和电流取关联参考方向，
则有
b
uk ik 0
k 1
1
特勒根第二定理(似功率守恒)：
N
有向图相同 N’
支路电压 uk 支路电流 ik
6
uk 'ik = 4×3＋0×(-2)＋4×1＋
k1 8×1＋4×4＋(-8)×5＝0
这就验证了特勒根第二定理。
特勒根定理适用于任意集总参数电路
6
特勒根第二定理的证明：
设 N和N’两网络均有n个节点b条支；。各支路电压、电流的参考方向关联且相同。则N网络的KCL方程为
i12 i13 i1n 0 i21 i23 i2n 0 in1 in2 inn1 0 将上式分别乘以N’网络的相应电压， 7
i1'＝2A， i2'＝0A， i3'＝－2A， i4'＝2A， i5'＝0A， i6'ik ' 4×2＋0×0＋4×(-2)＋

特勒根

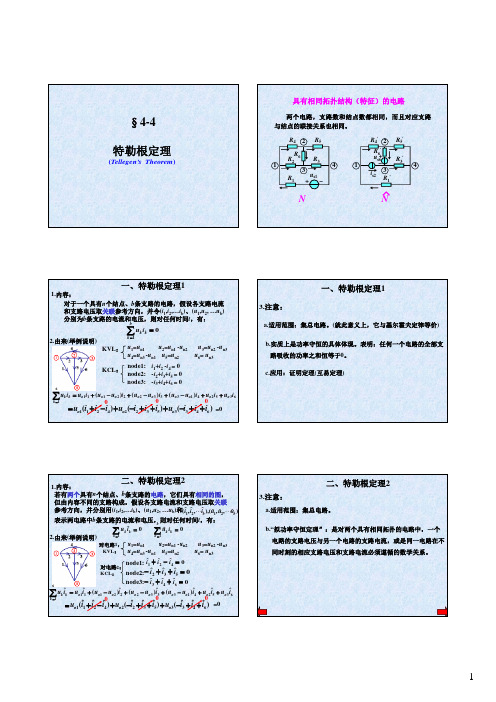
u i
2.由来(举例说明)
k 1
b
k k
0
u3=un2 -un3 u6= un3
u2=un1 -un2 KVL： u1=un1 u4=un3 -un1 u5=un2 node1: i1+i2 -i4 = 0 KCL： node2: -i2+i3+i5 = 0 node3: -i3+i4+i6 = 0
由图(a)、(b)：
k 3 k3 b
b
N R , N R 内部为线性电阻 ˆ R (k 3,4,b) ˆ i u i R u
k k k k kຫໍສະໝຸດ k(a)ˆ u i ˆ ˆ ˆ u1 i 1 2 2 u1 i1 u2 i 2
由图(a)、(b)：
0
-is
-is
0
(b)
ˆ u i ˆ ˆ ˆ u1 i 1 2 2 u1 i1 u2 i 2
具有相同拓扑结构（特征）的电路
§4-4 特勒根定特勒根定理
(Tellegen’s Theorem)
两个电路，支路数和结点数都相同，而且对应支路与结点的联接关系也相同。 R4 R2 R1 R6 3 + 2 R5 R3 us1 – R4 ' 2 R6 + us6 – is2
'
R5 ' R3 '
1
4
1
u i
k 1
6
k k
un1i1 ( un1 un 2 )i2 ( un 2 un 3 )i3 ( un 3 un1 )i4 un 2 i5 un 3 i6 0 0 0 un1(i1 i2 i4 ) un2 (i2 i3 i5 ) un3 (i3 i4 i6 ) =0

§3-6 特勒根定理

ˆ uk ik = 0 ∑
ˆ ∑u i
k= k=1
b
k=1 b
k k
=0
(5)
(4)
似功率平衡定理
u1 = 9V 例题1 已知例题 u2 = 0V
i1 = 4.5A i2 = 1A
ˆ i1
，ˆ 2 = u1 = 9V u
ˆ i2
ˆ 求 u1 = −2i1 = ? ˆ
i1 + u1
−
i2
NR
i2
+ u2
−
b
+ ˆ u1 R = 2 N R
−
−+ ˆ u2 Nhomakorabea解： uk iˆk ∑
k =1
b
ˆ ˆ = - u1i1 + u2i2 + ∑k ik = 0 uˆ
ˆ ˆ = - u1i1 + u2i2 + ˆ u ∑i
k=3
ˆ ∑u i
k =1
b
k=3 b
k k
k k
=0
ˆ uk ˆ uk ik = uk Rk uk ˆ ˆ uk ik = uk Rk
ˆ设对网络 N ：
支路电流 ik 支路电压 uk
k = 1,2,Lb k = 1,2,Lb
取关联参考方向
ˆ 支路电流ik k = 1,2,Lb 取关联参考方向 ˆ 支路电压 uk k = 1,2,Lb
特勒根定理( 特勒根定理(Tellegen’s Theorem) )
则有：则有：
X
解（续）
ˆ Q∑k ik = ∑k ik uˆ u
k=3 k=3 b b
??????
ˆ ˆ ˆ ˆ ∴− u1i1 + u2i2 = −u1i1 + u2i2

特勒根定理

在稳态情况下，线性电容及电感为互易元件
~ ~ ~ ~ V1I1 V1I1 ZI1I1 ZI1I1 0
不是所有元件都是互易元件，如晶体管，回转器，独立电源等等
2015-1-15 第6章特勒根定理 9
互易定理：由互易元件组成的P端口网络一定是互易的
I1

Ip
V1

~ I1
Vp
~ Ip
由特勒根定理得：
b
~ V I k k 0
k 1
b
所有支路（变化前）所有支路（变化后）
k 1 b
~ (Vk Vk ) I k 0
~ V I k k 0
k 1
~ Vk ( I k I k ) 0
b
k 1
nb
b ~ ~ V I V I k k k k 0 k 1
由基尔霍夫电流定律 Ka I b 0
故必有
T Vb I b
0
K b：回路－支路关联矩阵
功率守恒
T 由网络的关联性可知 Ib Kb Im
T VbT Ib VbT ( Kb Im ) ( KbVb ) Im
T
由基尔霍夫电压定律故必有
2015-1-15
KbVb 0
VbT I b 0
T T ( I b Zb T T ~ I b Zb ) I b
Vb ZbI b Zb I b
~T Vb I b ~T T T~ T~ I b Z b I b ( I b Vb Vb I b ) T T~ I b Zb I b
T~ ( I b Vb
则称
2015-1-15
N
~ 互为伴随网络 N

电路原理4.5.1特勒根定理 - 特勒根定理

返回上页下页
电路定理
2.具有相同拓扑结构（特征）的电路：
两个电路，支路数和结点数都相同，而且对应支路与结点的连接关系也相同。
N
1
R4 2 R5
R2R6
R3
4
3
R1
uS1 +–
N
1
R4' 2 R5'
RuS6+6' –
R3' 4
iS2
3 R1'
故两个电路具有相同拓扑结构，即它们的拓扑图
（图）完全相同。
互易定理有的三种不同形式，其中激励和响应可能是电压或电流而有所不同，当激励和响应互换位置时，将不改变同一激励所产生的响应。
返回上页下页
电路定理
应用互易定理时应注意： (1)互易定理适用于线性网络在单一电源激励下，
两个支路的电压电流关系。 (2)激励为电压源时，响应为电流电压与电流互易
激励为电流源时，响应为电压
(3)电压源激励，互易时原电压源处短路，电压源串入另一支路；电流源激励，互易时原电流源处开路，电流源并入另一支路的两个结点间。
(4)互易要注意电源与电压(电流)的方向。 (5)含有受控源的网络，互易定理一般不成立。
返回上页下页
利用特勒根定理2（注意电压与电流的方向），可知：
U1( - I1 ) + U2 I 2 U1 ( - I1 ) + U 2 I2
-4 3 + 21.25Uˆ2 -4.8 2 + Uˆ2 1
Uˆ 2
2.4/1.5 1.6V 返回上页下页
电路定理
例2 已知：U1=10V, I1=5A, U2=0, I2=1A ；U 2 10V

电路定理-特勒根定理互易定理和对偶定理 ppt课件

对应元素互换，两个方程可以彼此转换，两个电路互为对偶。
电阻 R 电压源 us 网孔电流 il KVL 串联网孔电导 G 电流源 is 节点电压 un KCL 并联节点
ppt课件
18
例2 i1 R1
+
us1
il1
–
R3 R2 il2
+
is1
rm i1
–
un1 G2 un2
+
u1 G1
G3
–
gm u1
电路定理
第三讲（总第十四讲）
特勒根定理
互易定理
对偶原理
ppt课件
1
特勒根定理(Tellegen’s Theorem)
一、具有相同拓扑结构的电路
2
1 3
N
+–
2
2
13
14
5 3
6
2
+
-
4
1
3
41
ppt课件
2
2
13
4
5 3
6
4 N
4
2
2
2
例:
2
2
13
13
14
5 3
4
14
5 3
4
N6
6
N
*对应支路取相同的参考方向
(1) 惯例网孔电流取顺时针方向，节点电压极性对地为正。每个网孔对应一个节点，外网孔对应参考节点。
(2) 电源方向（在按惯例选取网孔电流和节点电压方向的前提下）
原回路中所包含的电压源如果沿顺时针方向电压升高，则在对偶电路中电流源的电流方向应指向该网孔对应的独立节点。
I1
+ us

10-特勒根定理、互易定理和对偶原理newrevPPT课件

关联参考
对偶
线性电路
两电路
所有元素对偶后，新电路 -特性与原电路完全相同
16
作业-1
2A
3A
I
6V
N
3V
N
2V
N为纯电阻网络，求I
-
17
作业-2
12
2A
1A
1 N
2V
1
I
N
2A 12V
12
N为纯电阻网络，求I
-
18
作业-3
R1
R2
R1
R2
2
2A
R3
R4
2
2A
R3
R4
10V
I
求I
-
19
-
14
如何得到对偶电路-例题
2A
3mH
5F
4
2V
3mF 5H
4S
求对偶电路
-
15
各定理之比较
适用条件
相互关系
内容
注意事项
叠加线性电路
总=各独立源单独作用之和
含受控源时保持不动
齐性
线性电路叠加的推论
所有独立源变K 倍，响应也变K倍
替代
线性非线性
一元件
已知支路电压或电流，可用同值电压源或电流源替代
-
9
特勒根定理2和互易定理的应用
1A
2
2A
I
N
2
N
4
Hale Waihona Puke 3A4N为纯电阻网络，求I
答案: I=-12A
-
10
特勒根定理2和互易定理的应用
4
0.5A
4
5V

特勒根定理ppt课件

第8讲 电阻电路的分析-特勒根定理、互易定理

电路(特勒根互易定理)

特勒根与互易定理.ppt

2-7特勒根定理

特勒根与互易定理

第6章 特勒根定理

课件：第3.4节 特勒根定理

特勒根定理ppt课件

特勒根定理

讲义第十六章

特勒根定理

特勒根定理 (2)ppt课件

特勒根

§3-6 特勒根定理

特勒根定理

电路原理4.5.1特勒根定理 - 特勒根定理

电路定理-特勒根定理互易定理和对偶定理 ppt课件

10-特勒根定理、互易定理和对偶原理newrevPPT课件

第8讲电阻电路的分析-特勒根定理、互易定理

第6章特勒根定理

课件：第3.4节特勒根定理