广州市初中数学青年教师解题比赛试卷
广州市首届青年教师解题能力比赛初赛试题

一、填空题(请将答案填在答题卷指定的位置)【第1~6题每小题5分,第7~12题每小题10分,本大题共计90分】1. 将1~8-2.计算(答数用分数表示):741301.103237.0409÷⨯⎪⎭⎫ ⎝⎛+ = 。
3.甲用40秒可绕一环形跑道跑一圈。
乙反方向跑,每隔15秒与甲相遇一次。
求乙跑一圈所用的时间是 秒。
4.有一只小蚂蚁在一根弹性充分好的橡皮筋上的A 点,以每秒1厘米的速度向前爬行。
从小蚂蚁开始爬行的时候算起,橡皮筋在第2秒、第4秒、第6秒、第8秒、第10秒、……时均匀的伸长为原来的2倍。
那么,在第9秒时,这只小蚂蚁离A 点 厘米。
5.有一次考试共20题,记分方法是:做对第K 题得K (K =1、2、3、…、20)分;做错第K 题则倒扣K 分。
小华做了所有题,得分为100分。
那么小华至多做对了 题。
6.某工厂加工配套的机器零件要经过三道工序。
第一道工序平均每人每小时做20件,第二道工序平均每人每小时做16件,第三道工序平均每人每小时做24件。
现有1332名工人,要使各工序安排合理,那么,第一道工序应安排 名工人。
7.如右图是两个正方形,其边长分别为8cm 和4cm ,问:阴影部分的面积是 。
8.一列火车全长800米,行驶速度为每小时72千米。
铁路上有两个隧道,列车通过第一个隧道用了2分钟,通过第二个隧道用了3分钟,从车头进入第一个隧道到车尾离开第二个隧道共用了6分钟。
两个隧道之间的路程是 米。
9.两个盒子中各有12个大小一样的小球,且都是红、黄、绿色各4个。
闭上眼睛,然后先从第一盒中拿出尽可能少且至少有两个颜色一样的球放入第二个盒中,再从第二个盒中拿出尽可能少的球放入第一个盒中,要使第一个盒中每种颜色的球不少于3个,这时,第一个盒中有 个球,第二个盒中有 个球。
10.如右图是长、宽、高分别为5,4,3的立方体,把这个长方体从上向下切4刀,从左向右切2刀,从前向后切3刀(每个方向上切的几刀都是平行于侧面的,)问:(1)一共切成 个小长方体。
广州市荔湾区初中数学青年教师解题比赛及答案

19、(本题满分 10 分) . 等差数列 an 中,公差为 d, a4 84 ,前 n 项和为 Sn ,且 S10 >0, S11 <0, 求 d 的取值范围 .
20、(本题满分 10 分) 如图 3,在 ABC 中,以 BC 为直径的⊙ O 交 AB 于 D,交 AC 于 E,BD=CE,求证: AB=AC (要求:用多种方法证明 .详写其中一种证明, 其余证明则略写 .用三种方法证明结论成立的满分)
24. (本题满分 14 分)
如图 4 直线 y
3 x 3 分别与 x 轴、 y 轴交于点 A、 B,⊙ E 经过原点 O
3
及 A、B 两点.
(1)C 是⊙ E 上一点,连结 BC交 OA于点 D,若∠ COD=∠ CBO,求点 A、B、
2、已知集合 M { x | 2 x 2}, N { x | x2 2x 3 0}, 则集合 M N ( * ).
(A){ x | x 2} (B){ x | x 3} (C){ x | 2 x 3} (D){ x | 1 x 3}
3、已知函数 y
f (2 x ) 的定义域是 [ -1,1] ,则函数 y
( A)4 (B)6 (C)10 (D)12
第 II 卷(非选择题,共 106 分)
二、填空题( 本大题共 5 小题 ,每小题 4 分,共 20 分)
12、在实数范围内把多项式 x2 y 2xy y 分解因式所得的结果是 __* __.
13、已知函数 f (x)
4 log 3( x
2 ) ,则方程 f 1 ( x)
4 的解 x
___*__.
2
14、设 x、 y、 z 满足关系式 x- 1= y 1 = z 2 ,
2
广州青教师初中数学解题比赛决赛试卷

2005年广州市青年教师初中数学解题比赛决赛试卷本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷.请将选择题和填空题地答案做在第3页地答卷上.全卷共三大题25小题,满分150分,考试时间120分钟.第I 卷(选择题,共44分)一、选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确地答案代号填在第3页地答题卷上)1、a 是任意实数,下列判断一定正确地是(). (A )a a ->(B )a a<2(C )23a a >(D )02≥a 2、已知集合},032|{},4|{22<--=<=x x x N x x M 则集合=⋂N M ( ). (A )}2|{-<x x (B )}3|{>x x (C )}21|{<<-x x (D )}32|{<<x x 3、若二次函数2y ax bx c =++地图象如图所示,则点(a +b ,ac )在( ). (A )第一象限(B )第二象限 (C )第三象限(D )第四象限4、同圆地内接正十边形和外切正十边形地周长之比等于( ).(A )cos18°(B )sin18°(C )cos36°(D )sin36°5、用黑白两种颜色地正六边形地面砖按如下所示地规律,拼成若干个图案:则第8个图案中有白色地面砖()块.(A)34(B)36(C)38(D)406、将正方形地四边四等分,包括顶点共有16个点,这16个点可得到地 直线条数是( ). (A)120 (B)84 (C)82 (D)807、如图,⊙O 中,弦AD ∥BC ,DA =DC ,∠AOC =160°, 则∠BCO 等于( ).(A )20° (B )30° (C )40° (D )50°8、如果y x ,为实数,且,0)1(22=-+-y x x 则x 地取值范围是(). (A)任意实数 (B)负实数(C)210≤<x (D)10≤≤x 9、方程012=-+x x 所有实数根地和等于( ).(A)1-(B)1 (C)0 (D)510、将四个完全相同地矩形(长是宽地3倍),用不同地方式拼成一个大矩形, 设拼得地大矩形面积是四个小矩形地面积和,则大矩形周长地值只可能是( ). (A)1种(B)2种(C)3种(D)4种 11、一次函数b ax x f +=)((a 为整数)地图象经过点(98,19),它与x 轴 地交点为(p,0),它与y 轴地交点为(0,q ),若p 是质数,q 为正整数,则满 足条件地所有一次函数地个数为().(A)0 (B)1(C)2 (D)大于2地整数第II 卷(非选择题,共106分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在第三页地答题卷上) 12、函数x y lg =在定义域上是函数(填奇或偶);在区间上是增加地.13、如图,有两个同心圆,大圆地弦AB 与小圆相切于点P , 大圆地弦CD 经过点P ,且CD =13,PD =4,两圆组成地圆 环地面积是.14、已知t bac a c b c b a =+=+=+,那么直线t tx x f +=)(一定通过第象限. 15、已知上的点,为上的点,为内一定点,为ON B OM A MON P MON ∠=∠,400则当PAB ∆地周长取最小值时,的度数为APB ∠. 16、已知实数b a ,满足t b a ab t b ab a 那么且,,12222--==++地取值范围是OC B AD .ABCDO17、若c b a ,,为实数,且,2,0==++abc c b a 那么c b a ++地最小值可达到. 三、解答题(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程) 18、(本题8分)若直线0=+-a y x 与圆122=+y x 相交,求实数a 地取值范围.19、(本题8分)菱形ABCD 地边AB=5,对角线BD=6,且AC 与BD 相 交于点O ,沿BD 折叠得四面体ABCD ,已知该四面体地体积等于8, 求二面角A-BD-C 地大小.20、(本题8分)设,0,12≠=++a a x x x求1242++x x x 地值.21、(本题8分)某商场计划销售一批运动衣后可获总利润12000元. 在进行市场调查后,为了促销降低了定价,使得每套运动衣少获利润10元,结果实际销售比计划增加了400套,总利润比计划多了4000元,问实际销售运动衣多少套?每套运动衣实际利润多少元?22、(本题10分)已知任意三角形ABC,其面积为S. 作BC地平行线与1AB、AC分别交于D、E . 设三角形BDE地面积为M,求证:M≤S423、(本题11分)已知:如图,在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b 厘米,a >b ,且a 、b 是方程2(1)40x m x m --++=地两根,⑴求a 和b 地值;⑵△'''C B A 与△ABC 开始时完全重合,然后让△ABC 固定不动,将 △'''C B A 以1厘米/秒地速度沿BC 所在地直线向左移动.ⅰ)设x 秒后△'''C B A 与△ABC 地重叠部分地面积为y 平方厘米,求y 与x 之间地函数关系式,并写出x 地取值范围; ⅱ)几秒后重叠部分地面积等于38平方厘米?24、(本题11分)已知:如图,⊙O 与⊙P 相交于A 、B 两点,点P 在⊙O 上,⊙O 地弦AC 切⊙P 于点A ,CP 及其延长线交⊙P 于D 、E ,经过E 作EF ⊥CE 交CB 地延长线于F.⑴ 求证:BC 是⊙P 地切线;⑵ 若CD =2,CB =22,求EF 地长;⑶ 若设k =PE:CE,是否存在实数k,使△PBD 恰好是等边三角形?若存在,求出k 地值;若不存在,请说明理由. 25、(本题12分)如图,EFGH 是正方形ABCDA MA'地内接四边形,两条对角线EG 和FH 相交于点O ,且它们所夹地锐角为θ,CFH BEG ∠∠与都是锐角,已知,,l FH k EG ==四边形EFGH 地面积为S ,(1) 求证:klS 2sin =θ (2) 试用S l k 、、来表示正方形ABCD 地面积.25、 (1)证明:θθθθθθθθsin 21sin 21sin 21sin 21sin 21sin 21sin 021sin 021⋅=⋅⋅=⋅⋅+⋅⋅=⋅⋅+⋅⋅+⋅⋅+⋅⋅=+++=+=∆∆∆∆∆∆kl FH EG OH EG OF EG OH GO OH EO F GO F EO S S S S S S S GOH EOH GOF EOF EHGEFG 所以klS2sin =θ(2)解:PQRT DA CD BC AB H G F E 的垂线,得矩形、、、分别作、、、过.设正方形ABCD 地边长为a,2222,,,a l c a k b c QR b PQ -=-===则, 由PEF BEF TEH AEH S S S S ∆∆∆∆==,, RGH DGH QFG GFC S S S S ∆∆∆∆==, 得S S S PQRT ABCD 2=+,S a l a k a S bc a 2,2222222=-⋅-+=+∴即,2222224)4(S l k a S l k -=-+∴,由(1)知S kl l k S Skl 42,2sin 222>≥+>=所以θ, 故Sl k S l k a S ABCD44222222-+-==2005年广州市青年教师初中数学解题比赛决赛参考答案2005-3-20一、选择题答案(每小题4分,共44分)二、填空题答案(每小题5分,共30分)三、解答题(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程) 18、解:(代数方法)由题意,⎩⎨⎧=+-=+0122a y x y x⇒012222=-++a ax x直线与圆相交,∴0>∆即0)2(4)1(84222>--=--=∆a a a则022<-a ,即22<<-a 时,有0>∆直线与圆相交(此题可有几何方法,相应评分)19、解: AO=OC=435BO AB 2222=-=-,易得 θ = ∠ ⊥ ⊥AOC , BD OC , BD AO 为二面角A-BD-C 地平面角. .sin 166sin 38BDS 31V ,sin 8sin 421AOC sin OC AO 21S AOC ABCD 2AOC θ=⋅θ=⋅=θ=θ⋅=∠⋅=∆∆依题意,8sin 16=θ得21sin =θ,又πθ<<0, 656ππθ或所以=, 故所求二面角地大小为656ππ或20、解:分析 已知式和要求值地式子都是分母比分子复杂,不妨考查它们地倒数.因为,0,12≠=++a a x x x故 2 3 4 5 678 9 10 11 C DAABB DC CA区 学校 姓名 考号,0,112≠=++a a x x x 即x+111-=a x , 又11122224++=++x x x x x 222211)11(1)1(a a a x x -=--=-+=所以 aa x x x 2112242-=++21、解:设实际销售运动衣x 套,每套运动衣实际利润为y 元.则 ⎩⎨⎧==+-16000xy 12000)10y )(400x ( 解得.20y ,800x 11⎩⎨⎧== 及⎩⎨⎧-=-=20y 800x 22 (舍去) 答:实际销售运动衣800套,每套运动衣实际利润20元22、()也是等高三角形,故与又是等高的三角形,故与由于证明:ABE ADE 11ADABAD AD -AB AD BD S M BDE ADEADE ∆∆-===∆∆∆ ()()x ,设此比值为,故又同理,ACAEAB AD BC ||DE 3ACAES S 2AB ADS S ABE ABE ADE ===∆∆∆()()()()S M x x x S M M Sx x x x 4141)21(41)1S 41M 04SM S 0S,1S MAB ADAB AD -1AC AE AB AD 1-AD AB S M3,2,1 222≤⇒≤--=-=≤≥-=∆=+--=⎪⎭⎫ ⎝⎛=⋅⋅⎪⎭⎫ ⎝⎛=(法二:由解之得有实根,故法一:展开得即式相乘,得将23、解:(1)∵△ABC 是Rt △且BC=a ,AC=b ,AB=5 (a>b )又a 、b 是方程地两根∴⎪⎪⎩⎪⎪⎨⎧=+>+=⋅>-=+>+--=∆2504010)4(4)1(222b a m b a m b a m m ∴(a+b)2-2ab=25 (m-1)2-2(m+4)=25 推出 (m-8)(m+4)=0…………. 得m 1=8 m 2=-4 经检验m=-4不合舍去 ∴m=8…………∴x 2-7x+12=0 x 1=3 x 2=4 ∴a=4,b=3(2)∵△'''C B A 以1厘米/秒地速度沿BC 所在直线向左移动. ∴x 秒后BB ′=x 则B ′C ′=4-x ∵C ′M ∥AC ∴△BC ′M ∽△BCA ∴AC C M BC C B '='∴)4(43x C M -=' ∴)4(43)4(21x x y S M C B --=='∆ 即2)4(83x y -=∴y=63832+-x x (0≤x ≤4)当y=83时 2)4(83x -=83x 1=3 x 2=5(不合舍去)ABCMA'B'C'∴经过3秒后重叠部分地面积等于83平方厘米.24、(1)证明:连结PA 、PB ,∵AC 切⊙P 于A ,PA 是⊙P 地半径,∴AC ⊥PA ,即∠PAC=900,又∵四边形PACB 内接于⊙O ,∴∠PBC+∠PAC=1800.∴∠PBC=900,即PB ⊥CB.又∵PB 是⊙P 地半径,∴BC 是⊙P 地切线.(2)解:由切割线定理,得BC 2=CD*CE. ∴42)22(22===CD BC CE DE=CE-CD=4-2=2. ∴PB=1,在Rt △EFC 和Rt △BPC 中,∠ECF=∠BCP ,∴Rt △EFC ∽Rt △BPC ,22241,=⨯=⋅==∴CB CE BP EF CB CE BP EF . (3)解:存在实数k=31时,△PBD 为等边三角形. 下面证明:分,,,,)知道而由(,,又,11为等边三角形60219012233100 。
2007年广州市初中数学青年教师解题比赛试题-新人教

2007年广州市初中数学青年教师解题比赛决 赛 试 卷 2007-4-15本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷.请将选择题和填空题的答案做在第3页的答卷上.全卷共三大题25小题,满分150分,考试时间120分钟.第I 卷(选择题,共44分)一、选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在第3页的答题卷上.)1.对于实数a ,下列运算正确的是( ).(A ))2(121a a ÷=- (B )3232a a a =+(C )623)(a a a -=⋅- (D )422)()(a a a -=-⨯-2.给出以下三个命题:①两个无理数的和一定是无理数;②两个无理数的和有可能是有理数;③两个无理数的和一定是实数.其中正确的命题是( ).(A )①和②(B )①和③(C )②和③(D )③3.已知等差数列}{n a 的前n 项和为n S ,且,7,384==S S 则12S 的值是 ( ) .(A )8 (B )11 (C )12(D )154.如果b a ,为实数,则“b a =”是“直线2)()222=-+-+=b y a x x y 与圆(相切” 的( ) . (A )充分不必要条件 (B )必要不充分条件(C ) 充要条件(D )既不充分又不必要条件5.已知AB 是圆O 的直径,弦AD 和BC 相交于点P , 那么ABCD等于( ). (A )BPD ∠sin (B )cos BPD ∠ (C )tan BPD ∠ (D )cot ∠6要使第三个天平也保持平衡,则需在它的右盘中放置( ).(3)(2)(1)(A )3个球 (B )4个球 (C )5个球 (D )6个球7.如图是一个正方体的表面展开图,已知正方体的每一个面上都有一个实数,且相对面上的两个数互为倒数,那么代数式b ca-的值等于( ). (A )43- (B )6- (C )43(D )6 8.已知集合}3,2,0{=A ,},,|{A b a ab x x B ∈==且,则集合B 的子集的个数是( ).(A )4 (B )8 (C )15 (D )16第5题图 第7题图9.如图,ABC ∆的角,,A B C 所对边分别为,,a b c , 点是O ABC ∆的外心,,于,于E AC OE D BC OD ⊥⊥,于F AB OF ⊥ 则OD OE OF =∶∶( ) .(A )a b c ∶∶ (B )cb a 1:1:1(C )C B A cos :cos :cos (D )C B A sin :sin :sin10.设a b >,在同一平面直角坐标系内,一次函数a bx y +=与b ax y +=的图象最有可能的是( ).(A )13- (B )12- (C )-1 (D )-2第II 卷(非选择题,共106分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上.)12.随机掷一枚均匀的正方体骰子(正方体骰子的六个面上的点数分别为1,2,3,4,5,6),每次实验掷两次,则每次实验中掷两次骰子的点数之和为6的概率是__________. 13.如果关于x 的方程()012122=++++a x a x 有一个小于1的正数根,那么实数a 的取值范围是 .14.在矩形ABCD 中,已知两邻边AD =12,AB =5,P 是AD 边上异于D A 和的任意一点,且BD PE ⊥,F E AC PF 、,⊥分别是垂足,那么=+PF PE ___________.15.已知012=--x x ,那么代数式123+-x x 的值是 .16.已知z y x ,,为实数,且3,5=++=++zx yz xy z y x ,则z 的取值范围为 .17.已知正方形ABCD 的面积35平方厘米, E 、F 分别为边AB 、BC 上的点, AF 和CE 相交于点G ,并且ABF ∆的面积为5平方厘米,BCE ∆的面积为14平方厘米,那么四边形BEGF 的面积是___________平方厘米.y第9题图第11题图第14题图第17题图2007年广州市初中数学青年教师解题决赛答题卷2007-4-1512. 13. 14.15. 16. 17.三、解答题(共8小题,满分76分.解答应写出必要的文字说明、演算步骤或证明过程.)18.(本小题8分)已知01<<-a ,21a A +=,21a B -=,aC +=11,试比较A 、B 、C 的大小,并说明理由.19.(本小题8分)设)(x f 是奇函数,)(x g 是偶函数,并且x x x g x f -=-2)()(,求)(x f 和)(x g .区 学校 姓 考PA矩形ABCD所在平面,20.(本小题10分)已知⊥M、N分别是AB、PC的中点.MN⊥;(1)求证:CD∠PDA45°,求证MN⊥面PCD.(2)若=第20题图21.(本小题10分)在ABC ∆中,,60,40==AC AB 以A 为圆心,AB 的长为半径作圆交BC 边于D ,若DC BD 和的长均为正整数,求BC 的长.第21题图22.(本小题10分)如图,在等腰直角三角形ABC 中,1=AB ,=∠A 900,点E 为腰AC 的中点,点F 在底边BC 上,且BE FE ⊥,求CEF ∆的面积.23.(本小题10分)在正实数范围内,只存在一个数是关于x 的方程k x x kx x +=-++3132的解,求实数k 的取值范围.第22题图24.(本小题10分)如图,在梯形PMNQ 中,MN PQ //,对角线MQ PN 和相交于点O ,并把梯形分成四部分,记这四部分的面积分别为4321S S S S 、、、.试判断21S S +和43S S +的大小关系,并证明你的结论.第24题图25.(本小题10分)已知42++=m m y ,若m 为整数,在使得y 为完全平方数的所有m 的值中,设m 的最大值为a ,最小值为b ,次小值为c .(注:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数.) (1)求c b a 、、的值;(2)对c b a 、、下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2007?证明你的结论.密封线 密封线2007年广州市初中数学青年教师解题决赛试题参考答案及评分标准3.选C [解析]:∵{a n }等差数列,∴2(S 8 -S 4)= S 4+(S 12-S 8),且S 4=3,S 8=7,则S 12=12. 4.选A [解析]: 若a =b ,则直线与圆心的距离为22|2|=+-a a 等于半径,∴)()222=-+-+=b y a x x y 与圆(相切.若2)()222=-+-+=b y a x x y 与圆(相切,则22|2|=+-b a ,∴40-=-=-b a b a 或.故“a =b ”是“直线2)()222=-+-+=b y a x x y 与圆(相切”的充分不必要条件.8.选C [解析]:如果b a ,中至少有1个为零,则0=ab ;如果2==b a ,则4=ab ;如果3==b a ,则9=ab ;如果2332a ab b ==⎧⎧⎨⎨==⎩⎩或,则6=ab ,于是B ={0,4,6,9},∴B 有42=16个子集.10.选B [解析]:由方程组⎩⎨⎧+=+=b ax y abx y 的解知两直线的交点为),1(b a +,而图A 中交点横坐标是负数,故图A 不对;图C 中交点横坐标是2≠1,故图C 不对;图D 中交点纵坐标是大于a ,小于b 的数,不等于b a +,故图D 不对;故选B.11.选 B [解析]:设),0,(),0,(21x B x A 由,22=++c bn an 且222AB BQ AQ =+,得21-=a .二、填空题答案(每小题5分,共6小题,共30分)12.365. 13. 211-<<-a . 因式分解得()()0121=+++a x x ,因此“小于1的正数根”是12--a .由1120<--<a 得211-<<-a .14.1360. 如图,过A 作AG ⊥BD 于G .因为等腰三角形底边上的任意一点到两腰距离的和等于腰上的高,所以PE +PF =AG .因为AD =12,AB =5,所以BD =13,所 以,136013512=⨯=AG 所以1360=+PF PE .15. 2.2)1()(122233+--+--=+-x x x x x x x 22)1()1(22=+--+--=x x x x x .16. 3131≤≤-z . 3,5=++--=zx yz xy z x y 代入由,得0)35()5(22=+-+-+z z x z x ,因为x 为实数,所以0≥∆,解得3131≤≤-z . 17.27204.∵72==∆∆ABC ABF S S BC BF ,同理54=BA BE ,如图,连BG . 记a S AGE =∆,b S EGB =∆,c S BGF =∆,d S FGC =∆. 由已知 5=++c b a ,14=++d c b ,解之得2728=b ,27100=c . ∴)(2720427128平方厘米==+=c b S BEGF .三、解答题答案(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程) 18.解:它们的大小关系为C A B <<. ………………………2分 由01<<-a 得01>+a ,02)1()1(222>=--+=-a a a B A 得B A >, (4)分143)21(1)1()1(11222>+⎥⎦⎤⎢⎣⎡++-=+++-=+-+=-aa a a a a a a a A C ,得A C >, ………………6分即得C A B <<. ………………8分19.解: )(x f 为奇函数 )()(x f x f -=-∴)(x g 为偶函数 )()(x g x g =-∴ …………………2分由x x x g x f x x x g x f +=---∴-=-22)()( )()(…………………4分 从而 x x x g x f x x x g x f --=++=--22)()(,)()( …………………6分2007年广州市初中数学青年教师解题比赛决赛试题 第 11 页 共 13 页⎩⎨⎧-=-=⇒⎩⎨⎧--=+-=-222)()()()()()(x x g x x f x x x g x f x x x g x f …………………8分20.证明: 分平面平面面平面为平行四边形,四边形且又则中点为,又、连中点取5.//,//,21,//.21,//,,)1( CD MN AE CD ADP AE ADP CD AD CD PA CD ABCD CD ABCD PA AE MN AMNE NE AM NE AM CD AM CD AM CD NE CD NE PC N AE NE E PD ⊥∴⊥⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊂⊥∴∴=∴==分平面又则为等腰直角三角形时当10.,,//,,45)2( PCD MN DCD PD PD MN AE MN PD AE PAD Rt PDA ⊥∴=⋂⊥∴⊥∆=∠21.设BD =a ,CD =b ,(a ,b 为正整数)作AE ⊥BD ,垂足为E ,则AB =AD =40,BE =DE =2a . ∵ 222)2(40aAE -=,222)2(60b a AE +-=, ∴ 2222)2(60)2(40b a a+-=-, ∴ 34522000)(⨯==+b b a , …………………6分∵ 20<b a +<100,∴ 只有⎪⎩⎪⎨⎧⨯=⨯=+,52,5232b b a 或⎪⎩⎪⎨⎧=⨯=+.5,5224b b a ………………9分 故BC 的长为50或80. …………………10分22.解法1:如图,过C 作CD ⊥CE 与EF 的延长线交于D . …… ……2分 因为∠ABE +∠AEB =90°,∠CED +∠AEB =90°,所以∠ABE =∠CED .于是Rt △ABE ∽Rt △CED , …………………4分所以2412====∆∆AE AB CD CE AB CE S S EAB CDE ,)(. ………………6分 又∠ECF=∠DCF=45°,所以CF 是∠DCE 的平分线,点F 到CE 和CD 的距离相等,2007年广州市初中数学青年教师解题比赛决赛试题 第 12 页 共13 页所以2==∆∆CDCE S S CDF CEF . ……………8分 所以241214132413232=⨯⨯=⨯==∆∆∆∆ABC ABE CDE CEF S S S S .………10分 解法2: 如图,作FH ⊥CE 于H ,设FH=h . ………………2分因为∠ABE +∠AEB =90°,∠FEH+∠AEB=90°,所以 ∠ABE=∠FEH ,于是Rt △EHF ∽Rt △BAE . (4)分因为,即h EH AE AB FH EH 2.== 所以h HC 221-=. 又因为,FH HC =所以,61,221=-=h h h …………………8分 所以24161212121=⨯⨯=⨯=∆FH EC S CEF . ………………10分 23.解:原方程可化为0)3(322=+--k x x ,① …………………1分(1)当△=0时,833-=k ,4321==x x 满足条件; …………………2分(2)若1=x 是方程①的根,得0)3(13122=+-⨯-⨯k ,4-=k .此时方程①的另一个根为21,故原方程也只有一根21=x ; …………………4分 (3)当方程①有异号实根时,02)3(21<+-=k x x ,得3->k ,此时原方程也只有一个正实数根;………7分 (4)当方程①有一个根为0时,3-=k ,另一个根为23=x ,此时原方程也只有一个正实根. …………9分综上所述,满足条件的k 的取值范围是833-=k 或4-=k 或3-≥k . …………………10分24.解:设,,n MN m PQ == PMN ∆ 和QMN ∆同底等高,Q MN PMN S S ∆∆=∴,,2423S S S S +=+∴ , 即:43S S =. (2)2007年广州市初中数学青年教师解题比赛决赛试题 第 13 页 共 13 页 分POQ ∆ ∽NOM ∆,,:):(:22221n m OM OQ S S ==∴1222S m n S ⋅=∴. ………………4分,:::31n m OM OQ S S == 13S mn S ⋅=∴. ……………6分 1122143212)()(S m n S m n S S S S S ⋅⋅-⋅+=+-+∴21221)1()21(m n S m n mn S -=⋅-+= .…………9分43212,0)1(S S S S m n +>+∴>- . …………………10分(本题只写对结论而没有过程的只得1分)25. 解:(1)设224k m m =++(k 为非负整数),则有0422=-++k m m , (1)分由m 为整数知其△为完全平方数(也可以由△的公式直接推出), …………………2分即22)4(41p k =--(p 为非负整数),得,15)2)(2(=-+p k p k 显然:p k p k ->+22,所以21521k p k p +=-=⎧⎨⎩或2523k p k p +=-=⎧⎨⎩,解得7=p 或1=p , 所以12p m -±=,得:1,0,4,34321-==-==m m m m , …………………5分所以1,4,3-=-==c b a . …………………6分(2)因为222222a b a b c a b c ++=+++-, ………………8分 即操作前后,这三个数的平方和不变, 而222222200620052004)1()4(3++≠-+-+. ………………9分所以,对c b a 、、进行若干次操作后,不能得到2004,2005,2006这三个数.………10分。
2018年广州市白云区初中数学青年教师解题比赛(含答案)

2018年广州市白云区初中数学青年教师解题比赛试 卷学校 姓名 考号 得分本试卷分选择题和非选择题两部分,共三大题24小题,共4页,满分150分.考试时间120分钟.注意事项:1.答卷前,请务必填写上自己所在的学校、姓名及考号. 2.用黑色字迹的钢笔或签字笔作答.第I 卷(选择题,共44分)一、选择题1、a 是负实数,下列判断正确的是( ). (A )a a -> (B )a a<2(C )23a a > (D )20a > 2、已知集合2{|22},{|230},M x x N x x x =-<<=--<则集合M N =( ).(A )}2|{-<x x (B )}3|{>x x (C ){|23}x x -<< (D ){|13}x x -<<3、已知函数)2(x f y =的定义域是[-1,1],则函数)(log 2xf y =的定义域是( ). (A) (0,+∞) (B) (0,1) (C) [1,2] (D) [2,4]4、函数224)(1++=+x x x f 的值域是( ).(A ) ),1[+∞ (B )),2(+∞ (C )),3(+∞ (D)),4[+∞5、如果1x 、2x 是两个不相等的实数,且满足21120061x x -=,22220061x x -=, 那么 x 1+x 2=( ).(A )2006 (B )-2006 (C ) 1 (D )-1 6、已知0a b c -+=, 930a b c ++=, 则二次函数2y ax bx c =++ 的图象的顶点可能在( ).(A)第一或第四象限 (B)第三或第四象限(C)第一或第二象限 (D)第二或第三象限7、如图1,⊙O 中,弦AD ∥BC ,DA =DC ,∠BCO =15°,则∠AOC 等于( ).(A )120° (B )130° (C )140° (D )150° 8、已知a 、b 是不全为零的实数,则关于x 的方程222()0x a b x a b ++++=的根的情况为( ).(A ) 有两个负根 (B )有两个正根 (C )有两个异号的实根 (D )无实根9、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案: 则第( )个图案中有白色地面砖38块.(A)8 (B)9 (C)10 (D)1110、甲、乙、丙三位同学进行立定跳远比赛,每人轮流跳一次称为一轮,每轮按名次从高到低分别得3分、2分、1分(没有并列名次),他们一共进行了五轮比赛,结果甲共得14分;乙第一轮得3分,第二轮得1分,且总分最低.那么丙得到的分数是( ).(A)8分 (B)9分 (C)10分 (D)11分11、一个围棋盘由18×18个边长为1的正方形小方格组成,一块边长为1.5的正方形卡片放在棋盘上,被这块卡片覆盖了一部分或全部的小方格共有n 个,则n 的最大值是( ).( A)4 (B)6 (C)10 (D)12第II 卷(非选择题,共106分)二、填空题(本大题共5小题,每小题4分,共20分)12、在实数范围内把多项式22x y xy y --分解因式所得的结果是___________________.13、已知函数)24(log )(3+=xx f ,则方程4)(1=-x f 的解=x _________. 14、设x 、y 、z 满足关系式 x -1=21+y =32-z , 则x 2+y 2+z 2的最小值为 .15、不等边三角形ABC 的两条高的长度分别为4和12,若第三条高也为整数,O C BA D图1那么它的长度最大可能是_____ .16、已知:如图2,正方形ABCD 的边长为8,M 在CD 上,且DM=2,N 是AC 上的一个动点,则DN+MN 的最小值为 .三、解答题(共7小题,满分86分.解答应写出必要文字说明、演算步骤和证明过程) 17、(本题满分9分)已知⎩⎨⎧<-≥=1,11,1)(x x x f ,求不等式3)1()1(≤+++x x f x 的解集.18、(本题满分9分)求圆064422=++-+y x y x 截直线x -y -5=0所得的弦长?19、(本题满分10分).等差数列{n a }中,公差为d ,484a =,前n 项和为n s ,且10s >0,11s <0, 求d 的取值范围.20、(本题满分10分)如图3,在⊿ABC 中,以BC 为直径的⊙O 交AB 于D ,交AC 于E ,BD=CE ,求证:AB=AC(要求:用多种方法证明.详写其中一种证明, 其余证明则略写.用三种方法证明结论成立的满分)21、 (本通满分10分)已知:不论k 取什么实数,关于x 的方程 1632=--+bkx a kx (a 、b 是常数)的根总是x =1, 试求a 、b 的值.22(本题满分10分)已知m为整数,且12<m<40,试求m为何值时,关于未知数x的方程22--+-+=有两个整数根.x m x m m2(23)4148023 (本题满分14分)已知抛物线y=-x2+mx-m+2.(1)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB 求m的值;(2)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且△MNC的面积等于27,试求m的值.24. (本题满分14分) 如图4直线333+-=x y 分别与x 轴、y 轴交于点A 、B ,⊙E 经过原点O 及A 、B 两点.(1)C 是⊙E 上一点,连结BC 交OA 于点D ,若∠COD=∠CBO ,求点A 、B 、C 的坐标;(2)求经过O 、C 、A 三点的抛物线的解析式: (3)若延长BC 到P ,使DP =2,连结AP ,试判断直线PA 与⊙E 的位置关系,并说明理由.图42006年广州市白云区初中数学青年教师解题比赛参考答案第I 卷(选择题,共44分)二、 选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在答题卷上)第II 卷(非选择题,共106分)二、填空题(本大题共5小题,每小题4分,共20分)三、解答题17、解:当0x ≥时(1)1f x +=则不等式变为(1)3,1x x x ++≤≤解得当0x ≤时(1)1f x+=-则不等式变为(1)3,x x x -++≤解得为任意实数 不等式3)1()1(≤+++x x f x 的解集是{}1|≤x x 18、解:解法1:先求交点坐标,设A 1122(,),(,)x y B x y064422=++-+y x y xx -y -5=0 弦长==把x=y+5代入064422=++-+y x y x 中得2210110y y ++= 所以22212121211()()4(5)432y y y y y y -=+-=--⨯= 同理得22121212()()43x x x x x x -=+-=152-+225252x y -+=--=弦长221212()()336x x y y -+-=+=解法3:由064422=++-+y x y x 得圆心(2,-22 圆心到直线的距离2222522211d +-===+ 根据勾股定理弦长AB=22262(2)()262-== 19、解:⑴由 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⨯+⨯+=+021011110291010843111<>d a d a d a 解之得 -56<d <-4220、解:21、解:把x =1代入原方程并整理得(b +4)k =7-2a要使等式(b +4)k =7-2a 不论k 取什么实数均成立,只有⎩⎨⎧=-=+02704a b解之得 27=a ,4-=b22、解:08144)32(222=+-+--m m x m x []22=2(23)-4414884m m m m ---++()=(23)x m -±又12<m <40所以59,且m得m=2423、解: (1)A(x 1,0),B (x 2,0) . 则x 1 ,x 2是方程 x 2-mx +m -2=0的两根.∵x 1 + x 2 =m , x 1·x 2 =m -2 <0 即m <2 ;又AB =∣x 1 — x 2,∴m 2-4m +3=0 .解得:m =1或m =3(舍去) , ∴m 的值为1 . (2)M (a ,b ),则N (-a ,-b ) . ∵M 、N 是抛物线上的两点,∴222,2.a ma m b a ma m b ⎧-+-+=⎪⎨---+=-⎪⎩①②①+②得:-2a 2-2m +4=0 . ∴a 2=-m +2 . ∴当m <2时,才存在满足条件中的两点M 、N .∴a = .这时M 、N 到y轴的距离均为 又点C 坐标为(0,2-m ),而S △M N C = 27 ,∴2×12×(2-m.∴解得m =-7 .24、解:(1)连结EC 交x 轴于点N (如图). ∵ A 、B 是直线333+-=x y 分别与x 轴、y 轴的交点.∴ A (3,0),B )3,0(. 又∠COD =∠CBO . ∴ ∠CBO =∠ABC .∴ C 是的中点. ∴ EC ⊥OA .∴ 232,2321====OB EN OA ON . 连结OE .∴ 3==OE EC . ∴ 23=-=EN EC NC .∴ C 点的坐标为(23,23-). (2)设经过O 、C 、A 三点的抛物线的解析式为()3-=x ax y . ∵ C (23,23-). ∴)323(2323-⋅=-a .∴ 392=a . ∴ x x y 8329322-=为所求. (3)∵ 33tan =∠BAO , ∴ ∠BAO =30°,∠ABO =60°. 由(1)知∠OBD =∠ABD .∴ ︒=︒⨯-∠=∠30602121ABO OBD .∴ OD =OB ·tan30°=1.∴ DA =2.∵ ∠ADC =∠BDO =60°,PD =AD =2.∴ △ADP 是等边三角形. ∴ ∠DAP =60°.∴ ∠BAP =∠BAO +∠DAP =30°+60°=90°.即 PA ⊥AB . 即直线PA 是⊙E 的切线.。
历年各地初中数学青年教师解题竞赛试题及参考答案(上)

1. 20XX 年秋季广州市初中数学青年教师解题比赛试题及解答2. 常州市武进区初中数学教师解题竞赛试题及参考答案3. 20XX 年广州市初中数学青年教师解题比赛试题4.20XX 年武进区初中数学教师解题竞赛试题初中数学青年教师解题竞赛试卷一、填空(本题共有10小题,每小题4分,共40分) 1.函数112-+-=x x y 中,自变量x 的取值范围是 . 2.圆锥的母线长为5cm ,高为3 cm ,在它的侧面展开图中,扇形的圆心 角是 度.3.已知3=xy ,那么yxyx y x+的值是 . 4.△ABC 中,D 、E 分别是AB 、AC 上的点,DE//BC ,BE 与CD 相交 于点O ,在这个图中,面积相等的三角形有 对.5.不等式x x 4115≥+的正整数解的共有 个. 6.函数13++=x x y 的图象在 象限.7.在△ABC 中,AB =10,AC =5,D 是BC 上的一点,且BD :DC =2:3,则AD 的取值范围是 .8.关于自变量x 的函数c bx ax y ++=2是偶函数的条件是 . 9.若关于未知数x 的方程x p x =-有两个不相等的实数根,则实数p 的取值范围是 .10.AB 、AC 为⊙O 相等的两弦,弦AD 交BC 于E ,若AC =12,AE =8, 则AD = . 二、(本题满分12分)11.如图,已知点A 和点B ,求作一个圆⊙O , 和一个三角形BCD ,使⊙O 经过点A ,且使所作的 图形是对称轴与直线AB 相交的轴对称图形.(要求 写出作法,不要求证明)三、(本题满分12分)12.梯子的最高一级宽33cm ,最低一级宽110cm ,中间还有10级,各级 的宽成等差数列,计算与最低一级最接近的一级的宽. 四、(本题满分13分)13.已知一条曲线在x 轴的上方,它上面的每一点到点A (0,2)的距离减去它到x 轴的距离的差都是2,求这条曲线的方程. 五、(本通满分13分)14.池塘中竖着一块碑,在高于水面1米的地方观测,测得碑顶的仰角为︒20,测得碑顶在水中倒影的俯角为︒30(研究问题时可把碑顶及其在水中的倒影所在的直线与水平线垂直),求水面到碑顶的高度(精确到0.01米,747.270tan ≈︒). 六、(本题满分14分).15.若关于未知数x 的方程022=-+q px x (p 、q 是实数)没有实数根,..AB求证:41<+q p . 七、(本题满分14分)16.如果⊙O 外接于正方形ABCD ,P 为劣弧AD 上的一个任意点,求:PBPCPA +的值. 八、(本题满分16分)17.试写出m 的一个数值,使关于未知数x 的方程08242=+--m x x 的 两根中一个大于1,另一个小于1. 九、(本题满分16分)18.点P 在锐角△ABC 的边上运动,试确定点P 的位置,使P A +PB +PC 最小,并证明你的结论.参考答案一、1. 2≤x 且1≠x 2.288 3. 32± 4.4 5.6 .一、二、三 7. 4<AD <8 8.b =0 9. 410<≤p 10.18. 二、作法:11.1、作直线OB 与直线AB 相交于点B ;2、以O 为圆心,OA 为半径作⊙O ;3、过点O 作直线CD ⊥OB 交⊙O 于 点C 和点D ;4、分别连结CB 和DB .则⊙O 和△BCD 就是所求. 三、12.解:用{}n a 表示题中的等差数列,由已知条件有12,110,33121===n a a ().1133即110,112112d d a a +=-+=解得 7=d..A BDCO().1037033111111=+=-+=∴d a a答:与最低一级最接近的一级的宽103cm.四、13.解:设点M (x ,y )是曲线上的任一点,MB ⊥x 轴,垂足为B , 那么点M 属于集合{}2=-=MB MA M P . 由距离公式,得()2222=---y y x ,化简,得281x y =. 曲线在x 轴的上方,y >0,∴所求的曲线的方程是()0812≠=x x y 五、14.解:如图,DE 表示水面,A 表示观测点,B 为碑顶,B '在水中的倒影,由题意: ()m 13020=︒='∠︒=∠,AD AC B ,BAC︒='∠︒=∠∴60,70B B设x BE =,则.1,1+='-=x C B x BC在Rt △ABC 中,()︒-=⋅=70tan 1tan x B BC AC ○1 在Rt △A B 'C 中,()︒+='⋅'=60tan 1tan x B C B AC ○2 由○1、○2得()()︒+=︒-60tan 170tan 1x x ()︒+︒=︒-︒∴60tan 70tan 60tan 70tan x 41.4479.4015.1≈∴=x x 米答:水面到碑顶的高度4.41米.六、15. 证:由题意,令0442<-=∆q p得2p q -<B 'EA BC D41412122≤+⎪⎭⎫ ⎝⎛--=+-<+p pp q p即41<+q p七、16.解:如图,BP 平分直角APC ∠,︒=∠=∠∴4521在△APB 中,由余弦定理,得:2222AB PB PA PB PA =⋅-+同理,在△BPC 中,有2222BC PC PB PC PB =⋅-+22222AC PC AP BC AB =+=+().20222=+∴=+-∴PB PCPA PC PA PB PB 当点P 与点A 或点D 重合时.2=+PBPCPA 八、17.解法1:设()()062=-+x x ,则01242=--x x ,令1282-=+-m ,得10=m ,∴当10=m 时,所给方程两根中,一个大于1,另一个小于1.解法2:设21,x x 是方程的两根,则m x ,x x x 2842121-=⋅=+,依题意,()()()()⎪⎪⎩⎪⎪⎨⎧>>⇒⎩⎨⎧<-->---=∆.25,21.011,02844212m m x x m 解得:25>m .∴当3=m 时,所给的方程的两根中,一个大于1,另一个小于1. 九、18.解:当点P 在锐角△ABC 最短边上的高的垂足的位置时,P A +PB +PC 最小.ABCDP12证明:如图,P 为△ABC 一边BC 边 上的高的垂足,而Q 为BC 边上的任一点,+++=++QB QA PC PA PC PB PA , QA PA BC QA QC <+=,QC QB QA PC PB PA ++<++∴又设AC 为△ABC 最短边,作这边上的高P B '(如图),可知AP P B >'.在P B '上截取AP P B o =',在BC 上截 取AC C B =',作AC P B o ⊥'.垂足为o P ,连 结o B B '.APC ∆Rt ≌=∴'∆AP C P B o RtP B P B o o '='. 四边形o o P P B B ''是矩形,︒='∠∴90B B B o ,在B B B o '∆中,+='+'+'>'o o BB C P B P A P BB B BAC AP +,PC PB PA C P B P A P AP AC B B PC PB PA ++<'+'+'∴++'=++.20XX 年广州市初中数学青年教师解题比赛试卷2002.04.07一、填空(本题共有10小题,每小题4分,共40分) 1.函数1142-+-=x x y 中,自变量x 的取值范围是 . 2.若一个半径为32㎝的扇形面积等于一个半径为2㎝的圆的面积,则扇形的圆心角为 . 3.分式方程11-x -()11-x x =2的解是 . 4.代数式x 2-2xy +3y 2―2x ―2y +3的值的取值范围是 .5.⊙O 1、⊙O 2的半径分别为2和3,O 1O 2=9,则平面上半径为4且与⊙O 1、⊙O 2都相切的圆有 个.6、若关于未知数x 的方程+++++=()0522=++++m x m x 的两根都是正数,则m 的取值范围ABCPoP B 'oB P 'ABCP是 .7.在Rt △ABC 中,AD 是斜边BC 上的高,如果BC =a a BC =,=βB =∠,则AD = . 8.平面内一个圆把平面分成两部分,现有5个圆,其中每两个圆都相交,每三个圆都不共点,那么这5个圆则把平面分成 部分.9.在平坦的草地上有甲、乙、丙三个小球.若已知甲球与乙球相距5米,乙球与丙球相距3米,问甲球与丙球距离的取值范围?答: .10.计算12003200220012000+⨯⨯⨯所得的结果是 .二、(本题满分12分)11.如图,已知A 是直线l 外的一点,B 是l 上的一点. 求作:(1)⊙O ,使它经过A ,B 两点,且与l 有交点C ; (2)锐角△BCD ,使它内接于⊙O .(说明:只要求作出符合条件的一个圆和一个三角形,要求写出作法,不要求证明)三、(本题满分12分)12.如图,己知正三棱锥S —ABC 的高SO =h ,斜高SM =l .求经过SO 的中点平行于底面的截面△A ´B ´C ´的面积.四、(本题满分13分)13.证明:与抛物线的轴平行的直线和抛物线只有一个交点. 五、(本题满分13分)14.甲、乙两船从河中A 地同时出发,匀速顺水下行至某一时刻,两船分别到达B 地和C 地.已知河中各处水流速度相同,且A 地到B 地的航程大于A 地到C 地的航程.两船在各自动力不变情况下,分别从B 地和C 地驶回A 地所需的时间为t 1和t 2.试比较t 1和t 2的大小关系. 六、(本题满分14分)15.如图,在锐角θ内,有五个相邻外切的不等圆,它们都与θ角的边相切, 且半径分别为r 1、r 2、r 3、r 4、r 5.若最小的半径r 1=1,最大的半径r 5=81。
广州市初中数学青年教师解题比赛决赛试卷

广州市初中数学青年教师解题比赛决赛试卷本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷.请将选择题和填空题的答案做在第3页的答卷上.全卷共三大题25小题,满分150分,考试时间120分钟.第I 卷(选择题,共44分)一、选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在第3页的答题卷上.)1.对于实数a ,下列运算正确的是( ).(A ))2(121a a÷=- (B )3232a a a =+(C )623)(a a a -=⋅- (D )422)()(a a a -=-⨯-2.给出以下三个命题:①两个无理数的和一定是无理数;②两个无理数的和有可能是有理数;③两个无理数的和一定是实数.其中正确的命题是( ).(A )①和②(B )①和③(C )②和③(D )③3.已知等差数列}{n a 的前n 项和为n S ,且,7,384==S S 则12S 的值是( ) .(A )8 (B )11 (C )12(D )154.如果b a ,为实数,则“b a =”是“直线2)()222=-+-+=b y a x x y 与圆(相切” 的( ) . (A )充分不必要条件 (B )必要不充分条件(C ) 充要条件(D )既不充分又不必要条件5.已知AB 是圆O 的直径,弦AD 和BC 相交于点P , 那么ABCD等于(). (A )BPD ∠sin (B )cos BPD ∠ (C )tan BPD ∠ (D )cot 6.如图,三个天平的托盘中相同的物体质量相等.图⑴、三个天平也保持平衡,则需在它的右盘中放置( ).(3)(2)(1)(A )3个球 (B )4个球 (C )5个球 (D )6个球7.如图是一个正方体的表面展开图,已知正方体的每一个面上都有一个实数,且相对面上的两个数互为倒数,那么代数式b ca-的值等于( ). (A )43- (B )6- (C )43(D )6 8.已知集合}3,2,0{=A ,},,|{A b a ab x x B ∈==且,则集合B 的子集的个数是( ).(A )4 (B )8 (C )15 (D )16 9.如图,ABC ∆的角,,A B C 所对边分别为,,a b c , 点是O ABC ∆的外心,,于,于E AC OE D BC OD ⊥⊥,于F AB OF ⊥ 则OD OE OF =∶∶( ) .第5题图第7题图(A )a b c ∶∶ (B )cb a 1:1:1 (C )C B A cos :cos :cos (D )C B A sin :sin :sin10.设a b >,在同一平面直角坐标系内,一次函数a bx y +=与b ax y +=的图象最有可能的是( ).(A )13- (B )12- (C )-1 (D )-2第II 卷(非选择题,共106分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上.)12.随机掷一枚均匀的正方体骰子(正方体骰子的六个面上的点数分别为1,2,3,4,5,6),每次实验掷两次,则每次实验中掷两次骰子的点数之和为6的概率是__________. 13.如果关于x 的方程()012122=++++a x a x 有一个小于1的正数根,那么实数a 的 取值范围是 .14.在矩形ABCD 中,已知两邻边AD =12,AB =5,P 是AD 边上异于D A 和的任意一点,且BD PE ⊥,F E AC PF 、,⊥分别是垂足,那么=+PF PE ___________.15.已知012=--x x ,那么代数式123+-x x 的值是 .16.已知z y x ,,为实数,且3,5=++=++zx yz xy z y x ,则z 的取值范围为 .17.已知正方形ABCD 的面积35平方厘米, E 、F 分别为边AB 、BC 上的点, AF 和CE 相交于点G ,并且ABF ∆的面积为5平方厘米,BCE ∆的面积为14平方厘米,那么四边形BEGF 的面积是___________平方厘米.y第9题图第11题图第14题图第17题图2007年广州市初中数学青年教师解题决赛答题卷2007-4-1512. 13. 14.15. 16. 17.三、解答题(共8小题,满分76分.解答应写出必要的文字说明、演算步骤或证明过程.)18.(本小题8分)已知01<<-a ,21a A +=,21a B -=,aC +=11,试比较A 、B 、C 的大小,并说明理由.19.(本小题8分)设)(x f 是奇函数,)(x g 是偶函数,并且x x x g x f -=-2)()(,求)(x f 和)(x g .区 学校 姓 考20.(本小题10分)已知⊥PA 矩形ABCD所在平面,M 、N 分别是AB 、PC 的中点. (1)求证:CD MN ⊥;(2)若=∠PDA 45°,求证MN ⊥面PCD .21.(本小题10分)在ABC ∆中,,60,40==AC AB 以A 为圆心,AB 的长为半径作圆交BC 边于D ,若DC BD 和的长均为正整数,求BC 的长.第20题图第21题图22.(本小题10分)如图,在等腰直角三角形ABC 中,1=AB ,=∠A 900,点E 为腰AC 的中点,点F 在底边BC 上,且BE FE ⊥,求CEF ∆的面积.23.(本小题10分)在正实数范围内,只存在一个数是关于x 的方程k x x kx x +=-++3132的解,求实数k 的取值范围.第22题图24.(本小题10分)如图,在梯形PMNQ 中,MN PQ //,对角线MQ PN 和相交于点O ,并把梯形分成四部分,记这四部分的面积分别为4321S S S S 、、、.试判断21S S +和43S S +的大小关系,并证明你的结论.第24题图25.(本小题10分)已知42++=m m y ,若m 为整数,在使得y 为完全平方数的所有m 的值中,设m 的最大值为a ,最小值为b ,次小值为c .(注:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数.) (1)求c b a 、、的值;(2)对c b a 、、另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2007?证明你的结论.密封线 密封线2007年广州市初中数学青年教师解题决赛试题参考答案及评分标准3.选C [解析]:∵{a n }等差数列,∴2(S 8 -S 4)= S 4+(S 12-S 8),且S 4=3,S 8=7,则S 12=12. 4.选A [解析]: 若a =b ,则直线与圆心的距离为22|2|=+-a a 等于半径,∴2)()222=-+-+=b y a x x y 与圆(相切.若2)()222=-+-+=b y a x x y 与圆(相切,则22|2|=+-b a ,∴40-=-=-b a b a 或.故“a =b ”是“直线2)()222=-+-+=b y a x x y 与圆(相切”的充分不必要条件.8.选C [解析]:如果b a ,中至少有1个为零,则0=ab ;如果2==b a ,则4=ab ;如果3==b a ,则9=ab ;如果2332a ab b ==⎧⎧⎨⎨==⎩⎩或,则6=ab ,于是B ={0,4,6,9},∴B 有42=16个子集. 10.选B [解析]:由方程组⎩⎨⎧+=+=bax y abx y 的解知两直线的交点为),1(b a +,而图A 中交点横坐标是负数,故图A 不对;图C 中交点横坐标是2≠1,故图C 不对;图D 中交点纵坐标是大于a ,小于b 的数,不等于b a +,故图D 不对;故选B.11.选B [解析]:设),0,(),0,(21x B x A 由,22=++c bn an 且222AB BQ AQ =+,得21-=a . 二、填空题答案(每小题5分,共6小题,共30分)12.365. 13. 211-<<-a . 因式分解得()()0121=+++a x x ,因此“小于1的正数根”是12--a.由1120<--<a 得211-<<-a .14.1360. 如图,过A 作AG ⊥BD 于G .因为等腰三角形底边上的任意一点到两腰距离的和等于腰上的高,所以PE +PF =AG .因为AD =12,AB =5,所以BD =13,所以,136013512=⨯=AG 所以1360=+PF PE . 15. 2. 2)1()(122233+--+--=+-x x x x x x x 22)1()1(22=+--+--=x x x x x .16. 3131≤≤-z . 3,5=++--=zx yz xy z x y 代入由,得0)35()5(22=+-+-+z z x z x ,因为x 为实数,所以0≥∆,解得3131≤≤-z . 17.27204.∵72==∆∆ABC ABF S S BC BF ,同理54=BA BE ,如图,连BG . 记a S AGE =∆,b S EGB =∆,c S BGF =∆,d S FGC =∆. 由已知 5=++c b a ,14=++d c b ,解之得2728=b ,27100=c . ∴)(2720427128平方厘米==+=c b S BEGF .三、解答题答案(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程)18.解:它们的大小关系为C A B <<. ………………………2分 由01<<-a 得01>+a ,02)1()1(222>=--+=-a a a B A 得B A >,…………4分 0143)21(1)1()1(11222>+⎥⎦⎤⎢⎣⎡++-=+++-=+-+=-aa a a a a a a a A C ,得A C >, ………………6分即得C A B <<. (8)分19.解: )(x f 为奇函数 )()(x f x f -=-∴)(x g 为偶函数 )()(x g x g =-∴ …………………2分由x x x g x f x x x g x f +=---∴-=-22)()( )()(…………………4分从而 x x x g x f x x x g x f --=++=--22)()(,)()( …………………6分⎩⎨⎧-=-=⇒⎩⎨⎧--=+-=-222)()()()()()(x x g xx f x x x g x f x x x g x f …………………8分20.证明:分平面平面面平面为平行四边形,四边形且又则中点为,又、连中点取5.//,//,21,//.21,//,,)1(CD MN AE CD ADP AE ADP CD AD CD PA CD ABCD CD ABCD PA AE MN AMNE NE AM NE AM CD AM CD AM CD NE CD NE PC N AE NE E PD ⊥∴⊥⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊂⊥∴∴=∴==分平面又则为等腰直角三角形时当10.,,//,,45)2( PCD MN D CD PD PD MN AE MN PD AE PAD Rt PDA ⊥∴=⋂⊥∴⊥∆=∠21.设BD =a ,CD =b ,(a ,b 为正整数)作AE ⊥BD ,垂足为E ,则AB =AD =40,BE =DE =2a . ∵ 222)2(40a AE -=,222)2(60b aAE +-=, ∴ 2222)2(60)2(40b aa +-=-, ∴ 34522000)(⨯==+b b a , …………………6分 ∵ 20<b a +<100,∴ 只有⎪⎩⎪⎨⎧⨯=⨯=+,52,5232b b a 或⎪⎩⎪⎨⎧=⨯=+.5,5224b b a ………………9分 故BC 的长为50或80. …………………10分22.解法1:如图,过C 作CD ⊥CE 与EF 的延长线交于D . …… ……2分因为∠ABE +∠AEB =90°,∠CED +∠AEB =90°,所以∠ABE =∠CED . 于是Rt △ABE ∽Rt △CED , …………………4分 所以2412====∆∆AE AB CD CE AB CE S S EAB CDE ,)(. ………………6分又∠ECF=∠DCF=45°,所以CF 是∠DCE 的平分线,点F 到CE 和CD 的距离相等, 所以2==∆∆CDCES S CDF CEF . ……………8分 所以241214132413232=⨯⨯=⨯==∆∆∆∆ABC ABE CDE CEF S S S S .………10分 解法2: 如图,作FH ⊥CE 于H ,设FH=h . ………………2分因为∠ABE +∠AEB =90°,∠FEH+∠AEB=90°,所以 ∠ABE=∠FEH ,于是Rt △EHF ∽Rt △BAE . (4)分 因为,即h EH AE AB FH EH 2.== 所以h HC 221-=. 又因为,FH HC =所以,61,221=-=h h h …………………8分 所以24161212121=⨯⨯=⨯=∆FH EC S CEF . ………………10分 23.解:原方程可化为0)3(322=+--k x x ,① …………………1分(1)当△=0时,833-=k ,4321==x x 满足条件; …………………2分 (2)若1=x 是方程①的根,得0)3(13122=+-⨯-⨯k ,4-=k .此时方程①的另一个根为21,故原方程也只有一根21=x ; …………………4分 (3)当方程①有异号实根时,02)3(21<+-=k x x ,得3->k ,此时原方程也只有一个正实数根;………7分(4)当方程①有一个根为0时,3-=k ,另一个根为23=x ,此时原方程也只有一个正实根. …………9分综上所述,满足条件的k 的取值范围是833-=k 或4-=k 或3-≥k .…………………10分 24.解:设,,n MN m PQ == PMN ∆ 和QMN ∆同底等高,Q MN PMN S S ∆∆=∴,,2423S S S S +=+∴ , 即:43S S =. ………2分POQ ∆ ∽NOM ∆,,:):(:22221n m OM OQ S S ==∴1222S m n S ⋅=∴.………4分 ,:::31n m OM OQ S S == 13S mn S ⋅=∴. ……………6分 1122143212)()(S m n S m n S S S S S ⋅⋅-⋅+=+-+∴21221)1()21(m n S m n mn S -=⋅-+= .…9分43212,0)1(S S S S m n +>+∴>- . …………………10分(本题只写对结论而没有过程的只得1分)25. 解:(1)设224k m m =++(k 为非负整数),则有0422=-++k m m ,…………1分 由m 为整数知其△为完全平方数(也可以由△的公式直接推出), …………………2分 即22)4(41p k =--(p 为非负整数),得,15)2)(2(=-+p k p k 显然:p k p k ->+22,所以21521k p k p +=-=⎧⎨⎩或2523k p k p +=-=⎧⎨⎩,解得7=p 或1=p , 所以12pm -±=,得:1,0,4,34321-==-==m m m m , …………………5分 所以1,4,3-=-==c b a . …………………6分(2)因为222222a b a b c a b c ++=+++-, ………………8分 即操作前后,这三个数的平方和不变, 而222222200620052004)1()4(3++≠-+-+. ………………9分所以,对c b a 、、进行若干次操作后,不能得到2004,2005,2006这三个数.………10分。
2006年广州市天河区初中数学青年教师解题比赛试题评分标准

2006年广州市天河区初中数学青年教师解题比赛试题评分标准第I 卷(选择题,共44分)一、 选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在答题卷上)第II 卷(非选择题,共106分)二、填空题(本大题共5小题,每小题4分,共20分)三、解答题17、解:当0x ≥时(1)1fx +=则不等式变为(1)3,1x x x ++≤≤解得当0x ≤时(1)1f x+=-则不等式变为(1)3,x x x -++≤解得为任意实数 不等式3)1()1(≤+++x x f x 的解集是{}1|≤x x 18、解:解法1:先求交点坐标,设A 1122(,),(,)x y B x y064422=++-+y x y xx -y -5=0 弦长==把x=y+5代入064422=++-+y x y x 中得2210110y y ++= 所以22212121211()()4(5)432y y y y y y -=+-=--⨯= 同理得22121212()()43x x x x x x -=+-=1152x y -+==2252x y =-=弦长==解法3:由064422=++-+y x y x 得圆心(2,-2圆心到直线的距离2d === 根据勾股定理弦长AB=22=⨯=19、解:⑴由 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⨯+⨯+=+021011110291010843111<>d a d a d a 解之得 -56<d <-4220、解:21、解:把x =1代入原方程并整理得(b +4)k =7-2a要使等式(b +4)k =7-2a 不论k 取什么实数均成立,只有⎩⎨⎧=-=+02704a b解之得 27=a ,4-=b22、解:08144)32(222=+-+--m m x m x []22=2(23)-4414884m m m m ---++ ()=(23)x m -±又12<m <40所以59,且m得m=2423、解: (1)A(x 1,0),B (x 2,0) . 则x 1 ,x 2是方程 x 2-mx +m -2=0的两根.∵x 1 + x 2 =m , x 1·x 2 =m -2 <0 即m <2 ;又AB =∣x 1 — x 2,∴m 2-4m +3=0 .解得:m =1或m =3(舍去) , ∴m 的值为1 . (2)M (a ,b ),则N (-a ,-b ) . ∵M 、N 是抛物线上的两点,∴222,2.a ma m b a ma m b ⎧-+-+=⎪⎨---+=-⎪⎩ ①②①+②得:-2a 2-2m +4=0 . ∴a 2=-m +2 . ∴当m <2时,才存在满足条件中的两点M 、N .∴a = .这时M 、N 到y, 又点C 坐标为(0,2-m ),而S △M N C = 27 ,∴2×12×(2-m=27 .∴解得m =-7 .24、解:(1)连结EC 交x 轴于点N (如图). ∵ A 、B 是直线333+-=x y 分别与x 轴、y 轴的交点.∴ A (3,0),B )3,0(. 又∠COD =∠CBO . ∴ ∠CBO =∠ABC .∴ C 是的中点. ∴ EC ⊥OA .∴ 232,2321====OB EN OA ON . 连结OE .∴ 3==OE EC . ∴ 23=-=EN EC NC .∴ C 点的坐标为(23,23-). (2)设经过O 、C 、A 三点的抛物线的解析式为()3-=x ax y . ∵ C (23,23-). ∴)323(2323-⋅=-a .∴ 392=a .∴ 293y x x =-为所求. (3)∵ 33tan =∠BAO , ∴ ∠BAO =30°,∠ABO =60°. 由(1)知∠OBD =∠ABD .∴ ︒=︒⨯-∠=∠30602121ABO OBD .∴ OD =OB ·tan30°=1.∴ DA =2.∵ ∠ADC =∠BDO =60°,PD =AD =2.∴ △ADP 是等边三角形. ∴ ∠DAP =60°.∴ ∠BAP =∠BAO +∠DAP =30°+60°=90°.即 PA ⊥AB . 即直线PA 是⊙E 的切线.另也可用高中知识:直线斜率k 1k 2=-1证明PA ⊥AB .。
广州市初中数学青年教师解题比赛决赛试卷

的取值范围为
.
17.已知正方形 ABCD 的面积 35 平方厘米 , E、F 分别为边 AB、BC 上的点 , AF 和 CE 相交于点 G,并且 ABF 的面积为 5 平方厘 米 , BCE 的面积为 14 平方厘米 ,那么四边形 BEGF 的面积是
___________ 平方厘米.
第 17 题图
OF AB于 F,则 OD ∶ OE ∶OF (
).
( A) a ∶b ∶c ( C) cos A : cos B : cosC
111 (B) : :
abc (D ) sin A : sin B : sin C
第 9 题图
10.设 b a ,在同一平面直角坐标系内,一次函数
是( ).
y bx a 与 y ax b 的图象最有可能的
).
2 相切 ”
的(
).
(A )充分不必要条件
( B )必要不充分条件
(C) 充要条件
( D )既不充分又不必要条件
CD
5.已知 AB 是圆 O 的直径,弦 AD 和 BC 相交于点 P , 那么
等于(
AB
(A ) sin BPD ( B) cos BPD ( C) tan BPD (D ) cot
.)
考
18.(本小题 8 分)已知 1 a 0 , A 1 a 2 , B 1 a2 , C 1 ,试比较 A、B、C 的
1a
大小,并说明理由.
名 姓 校 学
19.(本小题 8 分)设 f (x) 是奇函数, g( x) 是偶函数,并且 f ( x) g(x) x2 x ,求 f (x) 和 g( x) .
区
20.(本小题 10 分)已知 PA 矩形 ABCD 所在平面, M 、 N 分别是 AB 、 PC 的中点. ( 1)求证: MN CD ; ( 2)若 PDA 45°,求证 MN ⊥面 PCD .
历年各地初中数学青年教师解题竞赛试题及参考答案(下)

1. 20XX 年初中数学青年教师解题竞赛试卷2. 20XX 年中山市第二届初中数学教师解题比赛试卷3. 20XX 年广州市白云区初中数学青年教师解题比赛及答案4.20XX 年广州市初中数学青年教师解题比赛决赛试卷2007-4-15初中数学青年教师解题竞赛试卷一、填空(本题共有8小题,每小题5分,共40分)1.把多项式y xy y x 922+-分解因式所得的结果是___________________.2.如果不等边三角形各边长均为整数,且周长小于13,那么这样的三角形共有_________个. 3.函数223x x y -+=中,自变量x 的取值范围是_____________.4.若关于未知数x 的一元二次方程032)1(22=-+++-m m x x m 有一个根为0,则m 的________.5.条件P :1=x 或2=x ,条件q :11-=-x x 中,P 是q 的_______________条件.(填充分不必要、必要不充分、充要、既不充分也不必要中的一个)6.两个等圆相交于A 、B 两点,过B 作直线分别交两圆于点C 、D .那么 △ACD 一定是 ____________三角形.(要求以边或角的分类作答)7.一直角三角形的斜边长为c ,它的内切圆的半径是r ,则内切圆的面积与三角形的面积的____________.8.不等边三角形ABC 的两条高的长度分别为4和12,若第三条高也为整数,那么它的长度最大可能是_____________.二、(本题满分12分)9.如图,已知点A 在⊙O 上,点B 在⊙O 外, 求作一个圆,使它经过点B ,并且与⊙O 相切于点A . (要求写出作法,不要求证明)三、(本题满分12分)10.一次选拔考试的及格率为25%,及格者的平均分数比规定的及格分数多15分,不及格者的平均分数比规定的及格分数少25分,又知全体考生的平均分数是60分,求这次考试规定的及格分数是多少?四、(本题满分13分)11.有30根水泥电线杆,要运往1000米远的地方开始安装,在1000米处放一根,以后每50米放一根,一辆汽车每次只能运3根,如果用一辆汽车完成这项任务,这辆汽车的行程共有多少千米?五、(本题满分13分)12.正实数a 、b 满足a b =b a ,且a <1,求证:a =b. 六、(本题满分14分)13.已知m 为整数,且12<m <40,试求m 为何值时,关于未知数x 的方程08144)32(222=+-+--m m x m x 有两个整数根.七、(本题满分14分)14.如图,已知A 、B 是锐角α的OM 边上的 两个定点,P 在ON 边上运动.问P 点在什么位置 时,22PB PA +的值最小?八、(本题满分16分)15.已知抛物线c bx ax y ++=2的顶点在直线x y =上,且这个顶点到原点的距离为2,又·A·B·O·A·BMNOα知抛物线与x 轴两交点横坐标之积等于1 ,求此抛物线的解析式.九、(本题满分16分)16.已知△ABC 是锐角三角形. ⑴求证:2sin A >cos B +cos C ;⑵若点M 在边AC 上,作△ABM 和△CBM 的外接圆,则当M 在什么位置时,两外接圆的公共部分面积最小?一、编写客观题内容:根据二次根式的性质“2a =│a │”编写一组填空题和选择题。
2019年广州市初中数学青年教师解题决赛试题含答案
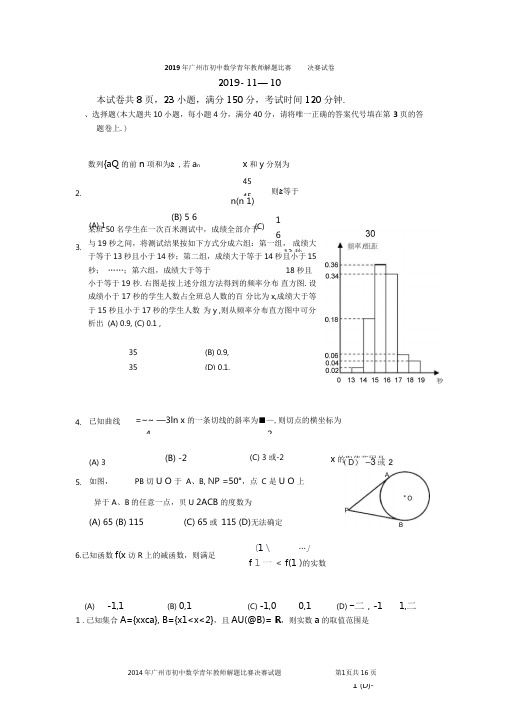
2.数列{aQ 的前n 项和为& ,若a nn(n 1)则&等于3.(B) 5 6某班50名学生在一次百米测试中,成绩全部介于与19秒之间,将测试结果按如下方式分成六组:第一组, 成绩大于等于13秒且小于14秒;第二组,成绩大于等于 14秒且小于15秒; ……;第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布 直方图.设成绩小于 17秒的学生人数占全班总人数的百 分比为x,成绩大于等于15秒且小于17秒的学生人数 为y ,则从频率分布直方图中可分析出 (A) 0.9, (C) 0.1 ,(A) 1 (C) 1 613秒35 35(B) 0.9, (D) 0.1,x 和y 分别为45 454. 已知曲线=~~ —3ln x 的一条切线的斜率为■—,则切点的横坐标为 425. (A) 3 如图,(B) -2(C) 3 或-2PB 切U O 于 A 、B, N P =50°,点 C 是U O 上异于A 、B 的任意一点,贝U 2ACB 的度数为(A) 65 (B) 115 (C) 65或 115 (D)无法确定6.已知函数f(x 访R 上的减函数,则满足(1 \…」f 1一 < f(1 )的实数x 的取值范围是(A)-1,1 (B) 0,1 (C) -1,0 0,1(D) -二,-1 1,二2019年广州市初中数学青年教师解题比赛 决赛试卷2019- 11— 10本试卷共8页,23小题,满分150分,考试时间120分钟.、选择题(本大题共10小题,每小题4分,满分40分,请将唯一正确的答案代号填在第 3页的答题卷上.)1 .已知集合A={xxca}, B={x1<x<2},且AU(@B)= R ,则实数a 的取值范围是7 .设m是不小于-1的实数,使得关于x的方程x2 ^2(m-2)x + m2-3m+3 =0有两个不相等的实数根x1、x2.若x2 +x22 =6,贝U m的值是(A) 5-'、17 517(B) ------------ 2(D) -1MPN 取最大值时,点 P 的横坐标是10.已知a 、b 值等于(A) 11.)8.如图是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm).将它们拼成如图的新几何体,则该新几何体的体积为(D) 2c 为正整数,且a 2 +b 2 + c 2 —ab —bc —ac = 19 ,那么a + b + c 的最小(B) 10(C) 8(D) 6、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上... 1 0 ..、一 ............. ...11.函数y= ------------ +(x —2)中,自变重 x 的取值氾围是lg(x-3)fx —y +3 » 0,I12.设变量x, y 满足约束条件<x +y » 0,则目标函数2x + y 的最小值为 ________[-2 < x < 3,13. 已知甲盒内有大小相同的 1个红球和3个黑球,乙盒内有大小相同的 2个红球和4个黑 球.现从甲、乙两个盒内各任取 2个球.则取出的4个球均为黑球的概率是 .14. 如图,平行四边形 ABCD 中,AM ± BC 于M, AN±CD 于 N,已知AB=10,BM=6, MC=3,贝U MN 的长为.215. 若f(x)表示x+3和2x —8x+3中较大者,则函数f(x) 的最小值是.16. 将杨辉三角中的奇数换成 1,偶数换成0,得到如图所示的0-1三角数表.从上往下数,第 1次全行的数都为1的是第1行,第2次全行的数都为1的是第 3行,•第 n 次全行的数都为1的是第 __________ 行;第61行中1的个数 (A)(B)-4(C) 1(D) 60 n是第1行11第2行101第3行1 1 11第4行 1 000 1第5行110 0 1 12019年广州市初中数学青年教师解题决赛答题卷2018-11 10、选择题答案(每小题4分,共40分)、填空题答案(每小题5分,共30分)l 11. 12. 13.号考14. 15. 16.三、角牟答题(共7小题,满分80分.解答应写出必要的文字说明、演算步骤或证明过程.)17.(本小题满分8分)已知y = f(x )是定义在R上且关于y轴对称的函数,当xN0时,f (x) = x2— 2x — 3 .(1)用分段函数形式写出y = f(x)的解析式;名(2)求y = f (x)的单调区间及函数的最值.姓校学18.(本小题满分8分)已知向量m = (T3cosx-sinx,1), n = (2cosx,a-73),x,a元R*为常数.区(1)求y= m n关于x的函数关系式y = f (x);(2)若x w |0,身时,f (x)的最小值为一2,求a的值.1 2 J19.(本小题满分12分)如图,四边形ABCD为矩形,DA_L平面ABE,AE = EB = BC=2 , BF _L平面ACE 于点F ,且点F在CE上,点M是线段AB的中点.(1)求证:AE _L BE ;(2)求三棱锥D -AEC的体积;(3)试在线段CE上确定一点N,使得MN //平面DAE .[来20.(本小题满分12分)正方形ABCD中,点P为边AD上的一点,DE ±CP于E,延长CP到F,使得CE=EF ,连结DF、AF,过点D作Z ADF的角平分线,交CF于H,连结BH.(1)求证:DE=EH ;(2)求证:BH // AF.21.(本小题满分12分)如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90的扇形.(1)求这个扇形的面积(结果保留兀).(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.(3)当LJO的半径R(R》0)为任意值时,(2)中的结论是否仍然成立?请说明理由.,O 为坐标原点,直线 OA 交22. (本小题满分14分)k -已知A 是双曲线y =_( k >0)在第一象限的图象上的一点X双曲线于另一点 C.. ...... .................. ,一 ,3 ........................ .... ..................... ...............(1)当OA 在第一象限的角平分线上时,将OA 向上平移3个单位后与双曲线在第一象限的2OA图象父于点 M,父y 轴于点N,右---------- =2 (如图1),求k 的值;MN(2)若k =1,点B 在双曲线的第一象限的图象上运动,点D 在双曲线的第三象限的图象上运动,且使得ABCD 是凸四边形时(如图 2),求证:Z BCD=Z23.(本小题满分14分)如图,已知A(—1,0) E(0,—手),以点A为圆心,以AO长为半径的圆交x轴于另一点B, 过点B作BFII AE交_ A于点F,直线FE交x轴于点C .(1)求证:直线FC是_ A的切线;(2)求点C的坐标及直线FC的解析式;(3)有一个半径与_ A的半径相等,且圆心在x轴上运动的_ P .若L P与直线FC相交于M , N两点,是否存在这样的点P,使^ PMN是直角三角形.若存在,求出点P的坐标;若不存在,请说明理由.*y2019年广州市初中数学青年教师解题决赛试题参考答案及评分标准、选择题答案(每小题4分,共10小题,共40分)题号12345678910答案D二B厂A P A P C C C D厂B「注:9 .选C [解析]:设直线MN (l MN : y = x+3 )交x轴于点A,则点P,必须满足2AP =AM AN ,易计算得,XA=—3, AP=4.10.选B [解析]:不妨设a芝b芝c, a—b=m , b—c = n , m、n为非负整数,2 2a—c = m+n, m +mn+n —19 = 0,由△ a0,可得,n <6 ,当n = 0, 1, 4, 5 时,m无解,n = 2时,m = 3 ;n = 3时,m = 2 ,①当n=2 , m=3 时,a = 3 + b, c=b—2 芝1, b 芝3 , a 芝6, a+b+c=3b+1 芝10 ,此时,取a=6, b=3 , c = 1 时,a+b+c = 10 最小;②当n=3 , m =2 时,同理可求,得a+b+c = 11, a = 6 , b=4, c=1,综上,最小值a + b + c = 10 .二、填空题答案(每小题5分,共6小题,共30分)11. (3,4) U(4, +" . 12.- 3 .13. 1. 14. 4 73.作MH ± AN 于5 5H, AH 245,HN =1232,MH =三、解答题答案(共7小题,满分80分.解答应写出必要文字说明、演算步骤和证明过程)17.解:(1)由已知得当x<0 时,f (x) =x2+2x—3 .•••2_L x -2x -3, x _ 0,f(x)=[x2+2x-3, x<0. ................................................................................................................... ......................... 3分(2 )单调递减区间是(_8,_1],[0,1], 单调递增区间是[―1,0],[1,危)• ................................... 6 分最小值是-4 , 没有最大值. .............................................................. 8分18. 解:( 1 )f (x) = (、、3cos x - sin x) 2cos x a -、3 = 2、3cos2x- 2sin xcosx a - 3=\/3cos2x-sin 2x+a =2cos(2x + 兰)+a . ...................................................6.................. 4分■■:'•7二二、3(2) . x w [0,—],二一<2x +—< —,二一1Mcos(2x + —)M —,2 6 6 6 6 2二a—2 壬 f (x) M 右+a. ...................................................................................... ............................... 6分f (x)min =a—2 , 由题意得a —2 = —2 二a=0. ................................................................................................... 8 分19 .解:(1)证明:由AD _L平面ABE及AD // BC. . BC 上加ABE , . .AE _L BC .而BF _L 平面ACE ,BF _L AE,又BC 计BF = B ,••• AE平面 B C , 又BEU 平面B CA JE . ........................................................................................ 3 分(2)连接EM , M 为AB 中点,AE=EB=2, EM _L AB .又DA _L 平面ABE, EM u ABE 平面,•. DA _L EM ,15. 3.16. 2n —1, 32 .2014年广州市初中数学青年教师解题比赛决赛试题 第12页共16页所 以 EM 上平 面A • ................................................................................................................................................... 5 分由已知及(1)得 EM =; AB = J2,S A DC =2^2 .2 -、2 ::V D _AEC =VE HDCJ2=—3(3)取BE 中点G ,连接MG,GF,FM .. BF _L 平面ACE , . . BF _LCE ,又EB = BC,所以 F 为CE 中点,GF//BC.又.• BC//AD, GF//AD .所以GF //平面ADE . ........................................................ 9分同理MG //平面ADE,所以平面GMF //平面ADE .又MF u 平面M G , 贝U MF //A ,D ............................................................................................................................... 12 分20.证明:(1)••• DC=DF ,.DE±CP且CE=EF ,/ — 1 /FDE=— z匕FDC ,2Z FDH = 1 Z FDC- 1 Z FDA= 12 2 2/ HDE =/ FDE-45 ° • ............................................................................................ 4 分Z ADC =EHD =HDE =45° ..... ......................................................................................................................... ....... 5分••• DE=EH .⑵延长DH交AF于点O, 将^ DEC绕点C逆时针旋转90°到△ BMC的位置,连结ME.△ DEC 9 △ BMC .••• DE=BM , Z DCE=Z BCM,. Z DCE+Z ECB=90°,•••Z BCM + Z ECB=90° .••• BM // CH. .......................................................................................... 8 分在^ EMC 中,Z ECM =90° , MC=CE ,•••Z CEM =45° .由(1)知,DE=EH=BM , 「.BMEH 为平行四边形.二BH // EM .又由(1)知DC=DF,贝U DA=DF , DO为Z ADF的角平分线,第20题DO ±AF.又对顶角/ EHD=Z FHO ,••• Z AFH=Z HDE=45° .Z AFH = Z MEC=45° .••• AF // ME.AFBH.……••…12分21. 解:(1 ) 连接BC ,由勾股定理求得:AB=AC =J22 』c n 二R 1s = ----- =—二.360 2(2)连接AO并延长,与弧BC和O交于E, F ,EF = AF —AE =2 —龙,弧BC的长:|=飒=巫兀.180 2设圆锥的底面半径为r.'2,2「:r = —■■:,2圆锥的底面直第21题2r 为 : 6分锥. ;2一、22.•.不能在余料③中剪出一个圆作为底面与此扇形围成 ................................................................................. 8分(3 )由勾股定理求得AB=AC=J2R,弧 BC 的长:|=邱=寸2!^,180 2:2町=匝职,2二圆锥的底面直径为:2r=J2R , EF =AF — AE=2R —J2R=(2—J2)R.2二(2 — J2)R <X2R,即无论半径R为何值,EF<2r.2二不能在余料③中剪出一个圆作为底面与此扇形围成圆锥. .................................... 12分22,解:(1) 3 根据题息,可碍直线 MN 的解析式为y = x+—.2=xk ,可得点A 的坐标(Jk, Jk).................................................................. k OA 设点M 的坐标为(x1, y1),所以——= ------------ x 1 MN =2. 八、、E 3,线万程 y = x+- 中 2x1 - i k2 k =1. •… (2)过点B 作BE± x 轴,交 AD 于E,过点D 作DH ± x 轴, 交BC 于点H, 设点A 、B 的坐标分别为 A( a , — )、B( b ,—),点C 、D 的坐标分别为C (b 代入直 D ( d —), d BE 交 直 线 AC 1 y = =x, ................................. a AC 解析式为.••点F 的坐标为(b , g ). a2 , 1 1、2 -2 (a —b)(—-) a b AB a 2(a 2b 2 1) b 2(a 4 1)l AF T (a-b)2 +([-与)2a a21 12 (a b) ()222a b = a (a b 1) (a b)2 (1b2)2一 aBC 2 CF AB 2 即—— AF |BC |2FTAB AFBC CF2 4 b (a 1)BFABC. .......................................同理,DH 平分Z ADC,12分.••在△ ABE 和△ 0DH 中,/ ABE=Z EB0= / DH0 , / AEB= / ADH= / 0DH ,BCD=BAD.- …14分 23. (1)证明:连结AF . TAE II BF 一N 1 =匕3, /4=/2 . 又'「AB=AF ,二23 =匕4 .二4 =22 . 又 了 AO =AF, AE =AE , . △ AOE AFE .,・.2AFE =/AOE =90’ . ,•■FC 是_ O 画切线. ............... 3分 2 (2)万法 1:由(1)知 EF =OE =、_ . 2 * yOF MN CBAQPxAC CE f AE II BF ,二 ----- =—. ---------- AB EF 0C+1 CE ,心-竭+史. 一2 ' 22 又’「OE 2 +pC 2 =CE 2, .•.CE 2 由 OC =2 , OC = 0… … 2 扫直线FC 经过E 0,-— 2 ,0(2,0)两点.设FC 的解析式:y=kx+b. 2 k =— 4一「2b =-— 2 线 2k b =0( 龙解得ib =- 2 2F02 y =4x 方法 2: CF 切 L A 于点 F , ,•WAFC =£EOC =90’ .OE 2+OC=CE>+co 2 .由CO =2 .(求FC 的解析式同上)0).CO =0方法3: |V AEII BFAC CE ABEFOC +1 CE「.CE =2!_CO27 FC 切L A 于点F ,/.ZAFC =ZCOE =90:' . /.ZACE =ZOCE , ;r ACOE^ACFA .OE CO AF "CF ,笠2〒一 CE+虫CO:.CE壬 C 。
广州初中数学青教师解题比赛

秒2011年广州市初中数学青年教师解题比赛决赛试卷 2011-4-10本试卷共8页,23小题,满分150分,考试时间120分钟.一、选择题(本大题共10小题,每小题4分,满分40分,请将唯一正确地答案代号填在第3页地答题卷上.) 1.已知集合{}{12}A x x a B x x =<=<<,,且()UA B =R ð,则实数a 地取值范围是(A )1a ≤(B )a ≥1(C )a ≤2(D )2a ≥ 2.数列{}n a 地前n 项和为n S ,若1(1)n a n n =+,则5S 等于(A )1 (B )56(C )16(D )1303.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于 14秒且小于15秒;……;第六组,成绩大于等于18秒且 小于等于19秒.右图是按上述分组方法得到地频率分布 直方图.设成绩小于17秒地学生人数占全班总人数地百分比为x ,成绩大于等于15秒且小于17秒地学生人数 为y ,则从频率分布直方图中可分析出x 和y 分别为 (A )0.9,35 (B )0.9,45 (C )0.1,35(D )0.1,454.已知曲线23ln 4x y x =-地一条切线地斜率为12,则切点地横坐标为 (A )3(B )2-(C )3或2-(D )3-或25. 如图,P A 、PB 切O 于A 、B ,50P ∠=,点C 是O 上异于A 、B 地任意一点,则ACB ∠地度数为 (A )65(B )115(C )65或115(D )无法确定 6.已知函数()x f 为R 上地减函数,则满足()11f x f <⎪⎪⎭⎫⎝⎛地实数x 地取值范围是 (A)()1,1- (B)()1,0 (C)()()1,00,1 - (D)()()+∞-∞-,11,7.设m 是不小于1-地实数,使得关于x 地方程222(2)330x m x m m +-+-+=有两个不相等地实数根1x 、2x .若22126x x +=,则m 地值是(A(B(C(D )1-8.如图是三个直立于水平面上地形状完全相同地几何体(下底面为圆面,单位:cm ).将它们拼成如图地新几何体,则该新几何体地体积为 ( ) cm 3.(A )48π(B )50π(C )58π(D )60π9.给定点M (-1, 2),N (1,4),点P 在x 轴上移动,当∠MPN 取最大值时,点P 地横坐标是(A)21 (B) 43(C)1 (D)2 10.已知a 、b 、c 为正整数,且19222=---++ac bc ab c b a ,那么c b a ++地最小值等于(A)11 (B) 10 (C) 8 (D)6二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上.)11.函数0)2()3lg(1-+-=x x y 中,自变量x 地取值范围是______.12.设变量x y ,满足约束条件30023x y x y x -+⎧⎪+⎨⎪-⎩≥,≥,≤≤,则目标函数2x y +地最小值为.13.已知甲盒内有大小相同地1个红球和3个黑球,乙盒内有大小相同地2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.则取出地4个球均为黑球地概率是__________.14.如图,平行四边形ABCD 中,AM ⊥BC 于M , AN ⊥CD 于N ,已知AB =10,BM =6, MC =3,则MN 地长为_________.15.若()f x 表示3x +和2283x x -+中较大者,则函数()f x 地最小值是.16.将杨辉三角中地奇数换成1,偶数换成0,得到如图所示地0-1三角数表.从上往下数,第1次全行地数都为1地是第1行,第2次全行地数都为1地是第3行,…,第n 次全行地数都为1地是第行;第61行中1地个数是.第1行 1 1 第2行 1 0 1 第3行 1 1 1 1 第4行 1 0 0 0 1 第5行 1 1 0 0 1 1 ……………………………………………2011年广州市初中数学青年教师解题决赛答题卷2011-4-1011. 12.13.14.15. 16.三、解答题(共7小题,满分80分.解答应写出必要地文字说明、演算步骤或证明过程.)17.(本小题满分8分)已知)(x f y =是定义在R 上且关于y 轴对称地函数,当0≥x 时,32)(2--=x x x f . (1)用分段函数形式写出=y )(x f 地解析式; (2)求)(x f y =地单调区间及函数地最值. 18.(本小题满分8分)已知向量m sin ,1)x x =-,n (2cos ,,,x a x a a =∈R 为常数. (1)求y=m ⋅n 关于x 地函数关系式()y f x =;(2)若0,2x π⎡⎤∈⎢⎥⎣⎦时,()f x 地最小值为-2,求a 地值.区 学校 姓 考19.(本小题满分12分)如图,四边形ABCD 为矩形,DA ⊥平面ABE ,2AE EB BC ===,BF ⊥平面ACE 于点F ,且点F 在CE 上,点M 是线段AB 地中点. (1)求证:AE BE ⊥;(2)求三棱锥D AEC -地体积;(3)试在线段CE 上确定一点N ,使得//MN 平面DAE .20.(本小题满分12分)正方形ABCD 中,点P 为边AD 上地一点,DE ⊥CP 于E ,延长CP 到F ,使得CE=EF ,连结DF 、AF ,过点D 作∠ADF 地角平分线,交CF 于H ,连结BH .(1)求证:DE=EH ; (2)求证: BH ∥AF .D A 第20题 密封线 密封线21.(本小题满分12分)如图,从一个直径是2地圆形铁皮中剪下一个圆心角为90地扇形.(1)求这个扇形地面积(结果保留π).(2)在剩下地三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.R R>为任意值时,(2)中地结论是否仍然成立?请说明理由.(3)当O地半径(0)③密封线 密封线交A 于点F 是A 地切线;地坐标及直线FC 地解析式;有一个半径与A 地半径相等,轴上运动地P .若P 与直线两点,是否存在这样地点是直角三角形.若存在,求出点坐标;若不存在,请说明理由.评分标准9.选C [解析]:设直线MN (MN l :3+=x y )交x 轴于点A,则点P ,必须满足AN AM AP ⋅=2,易计算得,3-=A x ,4=AP .10.选B [解析]:不妨设c b a ≥≥,m b a =-,n c b =-,m 、n 为非负整数,yn m c a +=-, 01922=-++n mn m ,由Δ≥0,可得,6<n ,当0=n ,1,4,5时,m 无解,2=n 时,m 3=;3=n 时,2=m ,①当2=n ,m 3=时,b a +=3,2-=b c 1≥,3≥b ,6≥a ,1013≥+=++b c b a ,此时,取6=a ,3=b ,1=c 时,10=++c b a 最小; ②当3=n ,2=m 时,同理可求,得,11=++c b a 6=a ,4=b ,1=c , 综上,最小值10=++c b a .二、填空题答案(每小题5分,共6小题,共30分)11.3,4)(4,)+∞(.12.23-. 13.51. 14. 5734.作MH ⊥AN 于H ,AH =524,HN =512,MH =532.15. 3.16.21n -,32.三、解答题答案(共7小题,满分80分.解答应写出必要文字说明、演算步骤和证明过程)17. 解:(1)由已知得当0x <时,2()23f x x x =+-. ∴2223,0,()23,0.x x x f x x x x ⎧--≥⎪=⎨+-<⎪⎩……………………………………………………………………………………3分(2)单调递减区间是]1,0[],1,(--∞,单调递增区间是),1[],0,1[+∞-.…………………………………………6分最小值是4-,没有最大值.…………………………………………………………………………………8分 18. 解:(1)2()sin )2cos 2sin cos f x x x x a x x x a =-⋅+=-+-2sin 22cos(2)6x x a x a π=-+=++.……………………………………………4分(2)7[0,],2,1cos(2)266662x x x πππππ∈∴≤+≤∴-≤+≤,2()a f x a ∴-≤≤.……………………………………………………………………………………6分min ()2f x a ∴=-,由题意得22a -=-0a ∴=.……………………………………………………………8分19.解:(1)证明:由AD ⊥平面ABE 及//AD BC ,∴BC ⊥平面ABE ,∴AE BC ⊥.而BF ⊥平面ACE ,∴BF AE ⊥,又BC BF B =,∴AE ⊥平面B C ,又BE ⊂平面B C ,∴A E⊥.………………………………………………3分(2)连接EM ,∵M 为AB 中点,AE =EB =2,∴AB EM ⊥.又⊥DA 平面⊂EM ABE ,ABE 平面,∴EM DA ⊥, 所以⊥EM 平面A.……………………………………………………………………………………5分 由已知及(1)得22,221===∆ADC S AB EM .故1433D AECE ADC V V --==⨯=.……………………………………………………………………7分(3)取BE 中点G ,连接FM GF MG ,,.∵BF ⊥平面ACE ,∴CE BF ⊥,又BC EB =,所以F 为CE 中点,∴GF //BC . 又∵BC //AD ,∴GF //AD .所以GF //平面ADE .………………………………9分 同理//MG 平面ADE ,所以平面GMF //平面ADE .又⊂MF 平面M G ,则//MF 平面AD.………………………………………………………………12分20. 证明: (1) ∵DE ⊥CP 且CE=EF , ∴DC=DF , ∠FDE =21∠FDC , ∠HDE =∠FDE -∠FDH =21∠FDC -21∠FDA =21∠ADC =45°.………………………………………………4分∴∠EHD =∠HDE =45°.……………………………………………………………………………………………5分∴ DE=EH .(2)延长DH 交AF 于点O , 将ΔDEC 绕点C 逆时针旋转90°到ΔBMC 地位置,连结ME . ∴ΔDEC ≌ΔBMC . ∴DE=BM , ∠DCE =∠BCM ,∵∠DCE +∠ECB =90°, ∴∠BCM +∠ECB =90°.∴BM ∥CH . …………………………………………………8分在ΔEMC 中,∠ECM =90°,MC=CE ,∴∠CEM =45°.由(1)知, DE=EH=BM ,∴BMEH 为平行四边形 ∴BH ∥EM .又由(1)知DC=DF ,则DA=DF ,DO 为∠ADF 地角平分线,∴ DO ⊥AF .又对顶角∠EHD =∠FHO , ∴∠AFH =∠HDE =45°. ∴∠AFH =∠MEC =45°. ∴AF ∥ME . ∴AF ∥BH .………………………………………………………………………………………………………12分A C D 第20题21. 解:(1)连接BC ,由勾股定理求得:AB AC ==,213602n R S π==π. ……………………………3分(2)连接AO 并延长,与弧BC 和O 交于E F ,,2EF AF AE =-=弧BC地长:1802n R l π==π. 设圆锥地底面半径为r .222r π=π, ∴圆锥地底面直径为:2r =6分22-<, ∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.…………………………………………………8分(3)由勾股定理求得:AB AC ==,弧BC地长:180n R l R π==,222rR π=π, 第21题∴圆锥地底面直径为:2r R =,2(2EF AF AE R R =-==. 22-<且0R >, (22R R ∴<,即无论半径R 为何值,2EF r <. ∴不能在余料③中剪出一个圆作为底面与此扇形围成圆22.解:(1由方程组y y =⎧⎪⎨=⎪⎩设点M k x 211=1=k (2)过点B 设点A 、B D (d ,d1)BE交直x ay 21=∴点FxP 'N '∴)1()1()1()()11()(422222222222++=-+--+-=a b b a a a b a b a b a b a AF AB , )1()1()1()()11()(422222222222++=++++++=a b b a a ab a b a b a b a CF BC , 即2222CFBC AFAB =,∴CFBC AFAB =,∴BF 平分∠ABC .……………………………………………………………………………12分 同理,DH 平分∠ADC , ∴在ΔABE 和ΔCDH 中,∠ABE =∠EBC =∠DHC ,∠AEB=∠ADH=∠CDH , ∴∠BCD =∠BAD .…………………………………………………………………………………………………14分 AE BF ∥又AB AF =又AO AF =AOE ∴△≌△90. FC 是O 地切线.…………………)方法1:由(AE BF ∥AC 11OC +∴又2+OE OC①2OC=,……………………………………………………………………………直线:CF切A于点F90.∴△=∠,COEACF OCE:AEFC切A于点F90.∴∠OE CO∴=,∴AF CF90,过点90MPN∠=,PM2cos452 PM⨯=AF FC⊥PH CPAF CA∴=90,版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.y6v3A。
2007年广州市初中数学青年教师解题比赛试题-新人教

2007年广州市初中数学青年教师解题比赛决 赛 试 卷 2007-4-15本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷.请将选择题和填空题的答案做在第3页的答卷上.全卷共三大题25小题,满分150分,考试时间120分钟.第I 卷(选择题,共44分)一、选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在第3页的答题卷上.)1.对于实数a ,下列运算正确的是( ).(A ))2(121a a ÷=- (B )3232a a a =+(C )623)(a a a -=⋅- (D )422)()(a a a -=-⨯-2.给出以下三个命题:①两个无理数的和一定是无理数;②两个无理数的和有可能是有理数;③两个无理数的和一定是实数.其中正确的命题是( ).(A )①和②(B )①和③(C )②和③(D )③3.已知等差数列}{n a 的前n 项和为n S ,且,7,384==S S 则12S 的值是 ( ) .(A )8 (B )11 (C )12(D )154.如果b a ,为实数,则“b a =”是“直线2)()222=-+-+=b y a x x y 与圆(相切” 的( ) . (A )充分不必要条件 (B )必要不充分条件(C ) 充要条件(D )既不充分又不必要条件5.已知AB 是圆O 的直径,弦AD 和BC 相交于点P , 那么ABCD等于( ). (A )BPD ∠sin (B )cos BPD ∠ (C )tan BPD ∠ (D )cot BPD ∠6.如图,三个天平的托盘中相同的物体质量相等.图⑴、⑵所示的两个天平处于平衡状态要使第三个天平也保持平衡,则需在它的右盘中放置( ).(A )3个球 (B )4个球 (C )5个球 (D )6个球7.如图是一个正方体的表面展开图,已知正方体的每一个面上都有一个实数,且相对面上的两个数互为倒数,那么代数式b ca-的值等于( ). (A )43- (B )6- (C )43 (D )6 8.已知集合}3,2,0{=A ,},,|{A b a ab x x B ∈==且,则集合B 的子集的个数是( ).(A )4 (B )8 (C )15 (D )16 9.如图,ABC ∆的角,,A B C 所对边分别为,,a b c , 点是O ABC ∆的外心,,于,于E AC OE D BC OD ⊥⊥,于F AB OF ⊥ 则OD OE OF =∶∶( ) .第5题图第7题图(A )a b c ∶∶ (B )cb a 1:1:1 (C )C B A cos :cos :cos (D )C B A sin :sin :sin10.设a b >,在同一平面直角坐标系内,一次函数a bx y +=与b ax y +=的图象最有可能的是( ).(A )13- (B )12-(C )-1 (D )-2 第II 卷(非选择题,共106分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上.)12.随机掷一枚均匀的正方体骰子(正方体骰子的六个面上的点数分别为1,2,3,4,5,6),每次实验掷两次,则每次实验中掷两次骰子的点数之和为6的概率是__________. 13.如果关于x 的方程()012122=++++a x a x 有一个小于1的正数根,那么实数a 的取值范围是 .14.在矩形ABCD 中,已知两邻边AD =12,AB =5,P 是AD 边上异于D A 和的任意一点,且BD PE ⊥,F E AC PF 、,⊥分别是垂足,那么=+PF PE ___________.15.已知012=--x x ,那么代数式123+-x x 的值是 .16.已知z y x ,,为实数,且3,5=++=++zx yz xy z y x ,则z 的取值范围为 .17.已知正方形ABCD 的面积35平方厘米, E 、F 分别为边AB 、BC 上的点, AF 和CE 相交于点G ,并且ABF ∆的面积为5平方厘米,BCE ∆的面积为14平方厘米,那么四边形BEGF 的面积是___________平方厘米.2007年广州市初中数学青年教师解题决赛答题卷第9题图第11题图第14题图第17题图2007-4-1512. 13. 14. 15. 16. 17.三、解答题(共8小题,满分76分.解答应写出必要的文字说明、演算步骤或证明过程.)18.(本小题8分)已知01<<-a ,21a A +=,21a B -=,aC +=11,试比较A 、B 、C 的大小,并说明理由.19.(本小题8分)设)(x f 是奇函数,)(x g 是偶函数,并且x x x g x f -=-2)()(,求)(x f 和)(x g .20.(本小题10分)已知⊥PA 矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点. (1)求证:CD MN ⊥;(2)若=∠PDA 45°,求证MN ⊥面PCD .21.(本小题10分)在ABC ∆中,,60,40==AC AB 以A 为圆心,AB 的长为半径作圆交BC 边于D ,若DC BD 和的长均为正整数,求BC 的长.22.(本小题10分)如图,在等腰直角三角形ABC 中,1=AB ,=∠A 900,点E 为腰AC 的中点,点F 在底边BC 上,且BE FE ⊥,求CEF ∆的面积. 23.(本小题10分)在正实数范围内,只存在一个数是关于x 的方程k x x kx x +=-++3132的解,求实数k 的取值范围. 24.(本小题10分)如图,在梯形PMNQ 中,MN PQ //,对角线MQ PN 和相交于点O ,并把梯形分成四部分,记这四部分的面积分别为4321S S S S 、、、.试判断21S S +和43S S +的大小关系,并证明你的结论.25.(本小题10分)已知42++=m m y ,若m 为整数,在使得y 为完全平方数的所有m 的值中,设m 的最大值为a ,最小值为b ,次小值为c .(注:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数.) (1)求c b a 、、的值;第20题图第21题图第22题图第24题图(2)对c b a 、、下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2007?证明你的结论.2007年广州市初中数学青年教师解题决赛试题参考答案及评分标准3.选C [解析]:∵{a n }等差数列,∴2(S 8 -S 4)= S 4+(S 12-S 8),且S 4=3,S 8=7,则S 12=12. 4.选A [解析]: 若a =b ,则直线与圆心的距离为22|2|=+-a a 等于半径,∴2)()222=-+-+=b y a x x y 与圆(相切.若2)()222=-+-+=b y a x x y 与圆(相切,则22|2|=+-b a ,∴40-=-=-b a b a 或.故“a =b ”是“直线2)()222=-+-+=b y a x x y 与圆(相切”的充分不必要条件.8.选C [解析]:如果b a ,中至少有1个为零,则0=ab ;如果2==b a ,则4=ab ;如果3==b a ,则9=ab ;如果2332a ab b ==⎧⎧⎨⎨==⎩⎩或,则6=ab ,于是B ={0,4,6,9},∴B 有42=16个子集.10.选B [解析]:由方程组⎩⎨⎧+=+=bax y abx y 的解知两直线的交点为),1(b a +,而图A 中交点横坐标是负数,故图A 不对;图C 中交点横坐标是2≠1,故图C 不对;图D 中交点纵坐标是大于a ,小于b 的数,不等于b a +,故图D 不对;故选B.11.选 B [解析]:设),0,(),0,(21x B x A 由,22=++c bn an 且222AB BQ AQ =+,得21-=a .二、填空题答案(每小题5分,共6小题,共30分)12.365. 13. 211-<<-a . 因式分解得()()0121=+++a x x ,因此“小于1的正数根”是12--a .由1120<--<a 得211-<<-a . 14.1360. 如图,过A 作AG ⊥BD 于G .因为等腰三角形底边上的任意一点到两腰距离的和等于腰上的高,所以PE +PF =AG .因为AD =12,AB =5,所以BD =13,所 以,136013512=⨯=AG 所以1360=+PF PE . 15. 2.2)1()(122233+--+--=+-x x x x x x x 22)1()1(22=+--+--=x x x x x .16. 3131≤≤-z . 3,5=++--=zx yz xy z x y 代入由,得0)35()5(22=+-+-+z z x z x ,因为x 为实数,所以0≥∆,解得3131≤≤-z . 17.27204.∵72==∆∆ABC ABF S S BC BF ,同理54=BA BE ,如图,连BG . 记a S AGE =∆,b S EGB =∆,c S BGF =∆,d S FGC =∆. 由已知 5=++c b a ,14=++d c b ,解之得2728=b ,27100=c . ∴)(2720427128平方厘米==+=c b S BEGF . 三、解答题答案(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程)18.解:它们的大小关系为C A B <<. ………………………2分由01<<-a 得01>+a ,02)1()1(222>=--+=-a a a B A 得B A >,…………4分143)21(1)1()1(11222>+⎥⎦⎤⎢⎣⎡++-=+++-=+-+=-aa a a a a a a a A C ,得A C >, ………………6分即得C A B <<. ………………8分19.解:Θ)(x f 为奇函数 )()(x f x f -=-∴Θ)(x g 为偶函数 )()(x g x g =-∴ …………………2分由x x x g x f x x x g x f +=---∴-=-22)()( )()(…………………4分 从而 x x x g x f x x x g x f --=++=--22)()(,)()( …………………6分⎩⎨⎧-=-=⇒⎩⎨⎧--=+-=-222)()()()()()(x x g xx f x x x g x f x x x g x f …………………8分20.证明:21.设BD =a ,CD =b ,(a ,b 为正整数)作AE ⊥BD ,垂足为E ,则AB =AD =40,BE =DE =2a. ∵ 222)2(40a AE -=,222)2(60b aAE +-=, ∴ 2222)2(60)2(40b aa +-=-, ∴ 34522000)(⨯==+b b a , …………………6分 ∵ 20<b a +<100,∴ 只有⎪⎩⎪⎨⎧⨯=⨯=+,52,5232b b a 或⎪⎩⎪⎨⎧=⨯=+.5,5224b b a ………………9分故BC 的长为50或80. …………………10分22.解法1:如图,过C 作CD ⊥CE 与EF 的延长线交于D . …… ……2分因为∠ABE +∠AEB =90°,∠CED +∠AEB =90°,所以∠ABE =∠CED . 于是Rt △ABE ∽Rt △CED , …………………4分所以2412====∆∆AEAB CD CE AB CE S S EAB CDE ,)(. ………………6分 又∠ECF=∠DCF=45°,所以CF 是∠DCE 的平分线,点F 到CE 和CD 的距离相等, 所以2==∆∆CDCES S CDF CEF . ……………8分所以241214132413232=⨯⨯=⨯==∆∆∆∆ABC ABE CDE CEF S S S S .………10分 解法2: 如图,作FH ⊥CE 于H ,设FH=h . ………………2分 因为∠ABE +∠AEB =90°,∠FEH+∠AEB=90°,所以 ∠ABE=∠FEH ,于是Rt △EHF ∽Rt △BAE . ………………4分 因为,即h EH AE AB FH EH 2.== 所以h HC 221-=. 又因为,FH HC =所以,61,221=-=h h h …………………8分 所以24161212121=⨯⨯=⨯=∆FH EC S CEF . ………………10分23.解:原方程可化为0)3(322=+--k x x ,① …………………1分 (1)当△=0时,833-=k ,4321==x x 满足条件; …………………2分(2)若1=x 是方程①的根,得0)3(13122=+-⨯-⨯k ,4-=k .此时方程①的另一个根为21,故原方程也只有一根21=x ; …………………4分(3)当方程①有异号实根时,02)3(21<+-=k x x ,得3->k ,此时原方程也只有一个正实数根;………7分(4)当方程①有一个根为0时,3-=k ,另一个根为23=x ,此时原方程也只有一个正实根. …………9分综上所述,满足条件的k 的取值范围是833-=k 或4-=k 或3-≥k . …………………10分24.解:设,,n MN m PQ == PMN ∆Θ和QMN ∆同底等高,QMN PMN S S ∆∆=∴,,2423S S S S +=+∴ , 即:43S S =. ……………2分POQ ∆Θ∽NOM ∆,,:):(:22221n m OM OQ S S ==∴1222S mn S ⋅=∴. (4)分,:::31n m OM OQ S S ==Θ13S mnS ⋅=∴. ……………6分 1122143212)()(S m n S m n S S S S S ⋅⋅-⋅+=+-+∴21221)1()21(m nS m n mn S -=⋅-+= .…………9分43212,0)1(S S S S mn +>+∴>-Θ . …………………10分(本题只写对结论而没有过程的只得1分)25. 解:(1)设224k m m =++(k 为非负整数),则有0422=-++k m m , (1)分由m 为整数知其△为完全平方数(也可以由△的公式直接推出), …………………2分即22)4(41p k =--(p 为非负整数), 得,15)2)(2(=-+p k p k 显然:p k p k ->+22,所以21521k p k p +=-=⎧⎨⎩或2523k p k p +=-=⎧⎨⎩,解得7=p 或1=p ,所以12p m -±=,得:1,0,4,34321-==-==m m m m , (5)分 所以1,4,3-=-==c b a . …………………6分(2)因为222222a b a b c a b c ++=+++-, ………………8分即操作前后,这三个数的平方和不变,而222222200620052004)1()4(3++≠-+-+. ………………9分 所以,对c b a 、、进行若干次操作后,不能得到2004,2005,2006这三个数.………10分。
年广州市青年教师初中数学解题比赛决赛试卷答案

年广州市青年教师初中数学解题比赛决赛参考答案-3-20 题号 1 2 3 4 5 6 7 8 9 10 11 答案 D C D A A B B D C C A12. 偶 ,),0(+∞ 13. 36π 14. 二、三15. 0100 16.313-≤≤-t 17. 4三、解答题(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程) 18、解:(代数方法)由题意,⎩⎨⎧=+-=+0122a y x y x⇒012222=-++a ax x直线与圆相交,∴0>∆即0)2(4)1(84222>--=--=∆a a a则022<-a ,即22<<-a 时,有0>∆直线与圆相交(此题可有几何方法,相应评分)19、解: AO=OC=435BO AB 2222=-=-,易得 θ = ∠ ⊥ ⊥AOC , BD OC , BD AO 为二面角A-BD-C 的平面角。
.sin 166sin 38BDS 31V ,sin 8sin 421AOC sin OC AO 21S AOC ABCD 2AOC θ=⋅θ=⋅=θ=θ⋅=∠⋅=∆∆依题意,8sin 16=θ得21sin =θ,又πθ<<0, 656ππθ或所以=, 故所求二面角的大小为656ππ或20、解:分析 已知式和要求值的式子都是分母比分子复杂,不妨考查它们的倒数。
区 学校 姓名 考号因为,0,12≠=++a a x x x故 ,0,112≠=++a a x x x 即x+111-=a x , 又11122224++=++x x x x x222211)11(1)1(a a ax x -=--=-+=所以 aa x x x 2112242-=++ 21、解:设实际销售运动衣x 套,每套运动衣实际利润为y 元.则 ⎩⎨⎧==+-16000xy 12000)10y )(400x ( 解得.20y ,800x 11⎩⎨⎧== 及⎩⎨⎧-=-=20y 800x 22 (舍去) 答:实际销售运动衣800套,每套运动衣实际利润20元22、()也是等高三角形,故与又是等高的三角形,故与由于证明:ABE ADE 11ADABAD AD -AB AD BD S M BDE ADEADE ∆∆-===∆∆∆ ()()x ,设此比值为,故又同理,ACAEAB AD BC ||DE 3ACAES S 2AB ADS S ABE ABE ADE ===∆∆∆()()()()S M x x x S M M Sx x x x 4141)21(41)1S 41M 04SM S 0S,1S MAB ADAB AD -1AC AE AB AD 1-AD AB S M3,2,1 222≤⇒≤--=-=≤≥-=∆=+--=⎪⎭⎫ ⎝⎛=⋅⋅⎪⎭⎫ ⎝⎛=(法二:由解之得有实根,故法一:展开得即式相乘,得将23、解:(1)∵△ABC 是Rt △且BC=a ,AC=b ,AB=5 (a>b )又a 、b 是方程的两根∴⎪⎪⎩⎪⎪⎨⎧=+>+=⋅>-=+>+--=∆2504010)4(4)1(222b a m b a m b a m m ∴(a+b)2-2ab=25 (m-1)2-2(m+4)=25 推出 (m-8)(m+4)=0…………. 得m 1=8 m 2=-4 经检验m=-4不合舍去∴m=8 ………… ∴x 2-7x+12=0 x 1=3 x 2=4 ∴a=4,b=3(2) ∵△'''C B A 以1厘米/秒的速度沿BC 所在直线向左移动。
广州市初中青年数学教师解题比赛决赛试题与答案

20XX 年广州市初中数学青年教师解题决赛试题参考答案及评分标准9.选C [解析]:设直线MN (MN l :3+=x y )交x 轴于点A,则点P ,必须满足AN AM AP ⋅=2,易计算得,3-=A x ,4=AP .10.选B [解析]:不妨设c b a ≥≥,m b a =-,n c b =-,m 、n 为非负整数,n m c a +=-, 01922=-++n mn m ,由Δ≥0,可得,6<n ,当0=n ,1,4,5时,m 无解,2=n 时,m 3=;3=n 时,2=m ,① 当2=n ,m 3=时,b a +=3,2-=b c 1≥,3≥b ,6≥a ,1013≥+=++b c b a ,此时,取6=a ,3=b ,1=c 时,10=++c b a 最小; ②当3=n ,2=m 时,同理可求,得,11=++c b a 6=a ,4=b ,1=c , 综上,最小值10=++c b a .二、填空题答案(每小题5分,共6小题,共30分)11.3,4)(4,)+∞U (. 12. 23-. 13.51. 14. 5734.作MH ⊥AN 于H ,AH =524,HN =512,MH =532.15. 3. 16.21n -,32 .三、解答题答案(共7小题,满分80分.解答应写出必要文字说明、演算步骤和证明过程) 17. 解:(1)由已知得当0x <时,2()23f x x x =+-.∴2223,0,()23,0.x x x f x x x x ⎧--≥⎪=⎨+-<⎪⎩……………………………………………………………………………………3分(2)单调递减区间是]1,0[],1,(--∞,单调递增区间是),1[],0,1[+∞-.…………………………………………6分最小值是4-,没有最大值.…………………………………………………………………………………8分18. 解:(1)2()sin )2cos 2sin cos f x x x x a x x x a =-⋅+=-+-2sin 22cos(2)6x x a x a π=-+=++.……………………………………………4分(2)7[0,],2,1cos(2)26666x x x πππππ∈∴≤+≤∴-≤+≤Q2()a f x a ∴-≤≤.……………………………………………………………………………………6分min ()2f x a ∴=-,由题意得22a -=-0a ∴=.……………………………………………………………8分19.解:(1)证明:由AD ⊥平面ABE 及//AD BC ,∴BC ⊥平面ABE ,∴AE BC ⊥. 而BF ⊥平面ACE ,∴BF AE ⊥,又BC BF B =I ,∴AE ⊥平面BCE ,又BE ⊂平面BCE ,∴AE BE ⊥.………………………………………………3分(2)连接EM ,∵M 为AB 中点,AE =EB =2,∴AB EM ⊥.又⊥DA 平面⊂EM ABE ,ABE 平面,∴EM DA ⊥,所以⊥EM 平面ACD .……………………………………………………………………………………5分由已知及(1)得22,221===∆ADC S AB EM .故1422233D AECE ADCV V --==⨯=.……………………………………………………………………7分 (3)取BE 中点G ,连接FM GF MG ,,.∵BF ⊥平面ACE ,∴CE BF ⊥,又BC EB =,所以F 为CE 中点,∴GF //BC . 又∵BC //AD ,∴GF //AD .所以GF //平面ADE .………………………………9分 同理//MG 平面ADE ,所以平面GMF //平面ADE .又⊂MF 平面MGF ,则//MF 平面ADE .………………………………………………………………12分20. 证明: (1) ∵DE ⊥CP 且CE=EF ,∴ DC=DF , ∠FDE =21∠FDC , ∠HDE =∠FDE -∠FDH =21∠FDC -21∠FDA =21∠ADC = 45°.………………………………………………4分∴∠EHD =∠HDE =45°.……………………………………………………………………………………………5分∴ DE=EH .(2)延长DH 交AF 于点O , 将ΔDEC 绕点C 逆时针旋转90°到ΔBMC 的位置,连结ME . ∴ΔDEC ≌ΔBMC . ∴ DE=BM , ∠DCE =∠BCM ,∵∠DCE +∠ECB =90°, ∴∠BCM +∠ECB =90°.∴ BM ∥CH . …………………………………………………8分在ΔEMC 中,∠ECM =90°,MC=CE ,∴∠CEM =45°.由(1)知, DE=EH=BM , ∴BMEH 为平行四边形 ∴ BH ∥EM .又由(1)知DC=DF ,则DA=DF ,DO 为∠ADF 的角平分线,∴ DO ⊥AF .又对顶角∠EHD =∠FHO , ∴ ∠AFH =∠HDE =45°. ∴ ∠AFH =∠MEC =45°. ∴ AF ∥ME .∴ AF ∥BH . ………………………………………………………………………………………………………12分A D 第20题21. 解:(1)连接BC ,由勾股定理求得:2AB AC ==,213602n R S π==π. ……………………………3分 (2)连接AO 并延长,与弧BC 和O e 交于E F ,,22EF AF AE =-=-,弧BC 的长:21802n R l π==π. 设圆锥的底面半径为r .22r π=πQ , ∴圆锥的底面直径为:22r =.……………………………………………………………………………6分 2222-<Q , ∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.…………………………………………………8分(3)由勾股定理求得:2AB AC R ==,弧BC 的长:2180n R l R π==π,22r R π=πQ , ∴圆锥的底面直径为:22r R =,22(22)EF AF AE R R R =-=-=-. 2222-<Q 且0R >, 2(22)2R R ∴-<,即无论半径R 为何值,2EF r <. ∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.………………………………………………12分第21题∠ABE=∠EBC=∠DHC,∠AEB=∠ADH=∠CDH,∴∠BCD=∠BAD. …………………………………………………………………………………………………14分xyABCO P F MEH NQP 'N 'M '1 23423. (1)证明:连结AF .AE BF Q ∥,1342∴∠=∠∠=∠,. 又AB AF =Q ,34∴∠=∠.12∴∠=∠. 又AO AF AE AE ==Q ,,AOE AFE ∴△≌△.90AFE AOE ∴∠=∠=o . FC ∴是O e 的切线.…………………3分(2)方法1:由(1)知22EF OE ==. AE BF Q ∥,AC CEAB EF∴=. 1122OC CE+∴=,2222CE CO ∴=+. ① 又222OE OC CE +=Q ,22222CE CO ⎛⎫∴=+ ⎪ ⎪⎝⎭. ② 由①②解得0OC =(舍去)或2OC =,……………………………………………………………………………5分 Q 直线FC 经过202E ⎛⎫- ⎪ ⎪⎝⎭,,(20)C ,两点. 设FC 的解析式:y kx b =+. 2022k b b +=⎧⎪∴⎨=-⎪⎩解得2422k b ⎧=⎪⎪⎨⎪=-⎪⎩. ∴直线FC 的解析式为2242y x =-.……………………………………………………………………………7分 方法2:CF Q 切A e 于点F ,90AFC EOC ∴∠=∠=o . 又ACF OCE ∠=∠,COE CFA ∴△∽△,OE COAF CF∴=.22122CO CE ∴=+.即222CE CO =-. ① 又222OE OC CE +=,22222CE CO ⎛⎫∴=+ ⎪ ⎪⎝⎭. ② 由①②解得0CO =(舍去)或2CO =. (20)C ∴, .………………………………………………………5分 (求FC 的解析式同上). 方法3:Q AE BF ∥,AC CEAB EF ∴=.1122OC CE +∴=. 2222CE CO ∴=+. ① FC Q 切A e 于点F ,90AFC COE ∴∠=∠=o .ACE OCE ∴∠=∠,COE CFA ∴△∽△.。
2004年广州市番禺区初中数学青年教师解题比赛试题参考答案

2004年广州市番禺区初中数学青年教师解题比赛试题参考答案一、共6小题,每小题5分,共30分)9.3 10. 60 11. 64 12. 32π 13. 212-<<-a c三、解答题14. 解: 由于26810b b -+=,则0b ≠,则211()860b b-⨯+=(1分)当1a b ≠时,,则a ,1b 为方程0682=+-x x 的两个根(3分),不妨设1x a =,21x b=,则128x x +=,126x x =,(5分),所以21212122112()2164122663x x x x x x ab ab x x x x +--+=+===(7分) 当1a b =时,即1=ab ,因此1ab ab+=2.(10分) 综上:当1a b ≠时,1ab ab + =326; 当1a b =时, 1ab ab+=2(10分)注:没有综述但其它均正确者不扣分.另直接求出a,b 的值再计算也可以15. 解:设n a 表示制糖厂第n 年的制糖量(1分),则51=a ,1.152⨯=a ,231.15⨯=a ,…11.15-⨯=n n a (5分),显然{}n a 是公比为1.1的等比数列(7分),设n 年内的总产量达到30万吨,则301.11)1.11(5=--n (9分),则6.11.1=n,所以5=n (11分),答:经过5年可使总产量达到30万吨.(12分)16. 解: 当∠A 090≤时,显然∠BOC=2∠A,(1分) ∠BIC=1800-∠IBC -∠ICB=1800-21(∠ABC+∠ACB)= 1800-21(1800-∠A)=900+21∠A (2分) 由于∠A+∠BIC+∠BOC=3980,则∠A+900+21∠A+2∠A=3980 (3分) 解之得∠A=880 (4分)∴∠BOC=2∠A=1760(5分) ∠BIC=900+21∠A=1340 (6分)当∠A 为钝角时,∠BOC=2(1800-∠A )=3600-2∠A(7分),∠BIC=900+21∠A (8分),则∠A+900+21∠A+3600-2∠A=3980,解得∠A=1040(9分),∠BOC=3600-2∠A=1520(10分),∠BIC=900+21∠A=1420(11分)故∠A=880,∠BOC=1760, ∠BIC=1340或∠A=1040,∠BOC=1520, ∠BIC=1420(12分)注:只有一个正确结果者扣6分. 17.解: (1) 依题意得⎩⎨⎧+=+=+24242b a b a ,(2分)解之得⎩⎨⎧==11b a (4分)即函数解析式为2y x x =+(6分).(2)当10033≥-y x 时方能收回投资并开始赢利(8分),即2321000x x -+≤(8分),显然3=x 不是不等式的解,而4=x 是不等式的解(11分),因此投产后,这个企业在第4年就能收回投资并开始赢利.(12分)18.(1) 证明:过A 作两圆的内公切线,交BC 于D,则由切线的性质知DB=DA=DC ,则三角形ABC 为直角三角形.即AB ⊥AC (3分)(2)猜想:∠BAC+ ∠BAD=1800(4分)证明:过点A 作两圆的内公切线,交BC 于E ,由切线的性质得, ∠BAC=∠BAE+∠EAC=∠ABC+∠ADC (7分),因此 ∠BAC+∠BAD=∠ABC+∠ADC+∠BAD=1800(8分) (3)猜想:∠BAC+ ∠BDC=1800(9分),连结AD ,由于BC 是它们的一条外公切线,由切线的性质得, 则∠BAC=∠BAD+∠DAC=∠DBC+∠DCB (12分),所以∠BAC+∠BDC=∠DBC+∠DC B+∠BDC =1800(13分).19.解:(1)∠APC=12∠AOC=12(180060-0)=600,它不会随着点P 的变化而变化.(3分) (2)解法1:设AP 与CD 交于M ,PC 与AB 交于N ,连结BC ,易证ΔAMO ≌ΔCNB ,∴AM=CN ,MO=NB ,(5分)又∠AOD=∠APN ,∠MAO=∠NAP=600,∴ΔAMO ∽ΔANP ,∴APAOAN AM =,即AN AO AP AM ⋅=⋅①(7分)同理CM CO CP CN ⋅=⋅,亦即CM AO CP AM ⋅=⋅②(9分),①+②得,311(1)()(=+++=+++⨯=+⋅=+⋅NB ON OM CO ON AO CM AN AO PC PA AM ,∴ AM PC PA 3=+(11分),而≤23AM 1≤(12分),因此3≤PA+PC ≤故PA+PC 的值会随着点P 的变化而变化,其变化范围为3≤PA+PC ≤分)解法2:由于三角形AOC 为等腰三角形,且∠AOC=1200,AO=OC=1,因此(5分),在ΔAPC 中,由余弦定理得:2222cos60AC AP PC APPC =+-,即223AP PC AP PC +-= ,因此2()33AP PC AP PC +=+ (8分),要确定AP+PC 有无变化或其变化范围,只需研究AP PC 的值有无变化或其变化范围,而01sin 602APC S AP PC ∆=,故只需ΔAPC 的面积有无变化或其变化范围.由于底边AC 为定值,点P 在 DB上运动,则点P 到AC 的距离是变化的,因此ΔAPC 的面积是变化的,从而AP PC 的值也是变化的,且随点P 到AC 的距离的增大而增大(10分),由于点P 到AC 的距离的最大值为32,此时点P 为 DB 的中点,三角形APC 为正三角形,PA+PC的值为(11分).点P 到AC 的距离的最小值为1,此时点P 与点D 或点B 重合,PA+PC 的值为3(12分),因此,PA+PC 值的变化范围为3≤PA+PC ≤13分)注: 1、本题能得出结果但不能证明者扣分.2、本题还可以用O 、M 、P 、N 四点共圆、高中解析几何方法等方法证明20.解:设函数2y x ax b =++与x 轴的两个交点坐标分别为A )0,(1x ,B )0,(2x 且21x x <(1分),函数2y x bx a =++与x 轴的两个交点坐标分别为C )0,(3x ,D )0,(4x ,且43x x <(2分),则,021≤-=+a x x ,021<=b x x 则01<x ,02>x (4分),同理,043>-=+b x x ,043≥=a x x 则03≥x ,04>x (6分),则A 、B 、C 、D 在x 轴上的左右顺序为A ,B ,C ,D 或A ,C ,B ,D 或A ,C ,D ,B (7分)若按A ,C ,D ,B 的顺序排列,则AC=CD=DB ,则有2413x x x x -=-,即4321x x x x +=+,即b a -=-,与假设(0)a b ≥>矛盾,此不可能.(9分)若按A 、B 、C 、D 的顺序排列,则233412x x x x x x -=-=-,由于2422,1ba a x -±-=,2424,3ab b x -±-=,则a b b a 4422-=-∴0)4)((=++-b a b a ,而b a >, ∴ 04=++b a ,又4232x x x +=,则2424242222ab b b a a a b b -+-+-+-=---⨯, 化简得:b a a b b a 44322-+-=+,即444322-=-+-b a a b ,此不可能(11分) 若按A 、C 、B 、D 的顺序排列,则243213x x x x x x -=-=-,则有3412x x x x -=-,且2213x x x +=,因此a b b a 4422-=-,∴0)4)((=++-b a b a ,而b a >,∴04=++b a ,又1232x x x +=,则a ab b -=---⨯2422,解之得0=a 或4-=a (13分),而0≥a ,∴0=a ,4-=b ,经经验,0=a ,4-=b 满足题设要求.故0=a ,4-=b 为所求(14分).以上各题还有其它方法,请另制定评分标准!答案错误难免,请批评指正!。
第三届广东省中小学青年教师教学能力大赛 初中数学题目

第三届广东省中小学青年教师教学能力大赛初中数
学题目
1、现有一条直径为12厘米的圆柱形铅柱,若要铸造12只直径
为12厘米的铅球,应截取多长的铅柱(损耗不计)?(球的体积公
式R2,R为球半径)
2、直径为30厘米,高为50厘米的圆柱形瓶里存满了饮料,现
把饮料倒入底面直径为10厘米的圆柱形小杯中,刚好倒满20杯,求小杯子的高。
3、用60米长的篱笆,围成一个长方形的花圃,若长比宽的2倍少3米,则长方形的面积是多少?
4、将一个长、宽、高分别为15厘米、12厘米和8厘米的长方
体钢块,锻造成一个底面边长为12厘米的正方形的长方体零件钢坯。
试问是锻造前长方体钢块的表面积大,还是锻造后的长方体零件钢坯的表面积大?请计算回答。
5、某车间原计划每周装配36台机床,预计若干周完成任务。
在装配了三分之一以后,改进操作技术,工效提高了一倍,结果提前一周半完成了任务.求这次任务需要装配机床总台数。
6、公民每月工资不超过1600元,不需要交税,超过1600元的
部分为全月应纳税所得额,但根据超过部分的多少按不同的税率交税,税表如下:全月应纳税所得额税率不超过500元部分5%500元至2000元部分1000元至5000元部分15%某人3月份应纳税款为117.10元,求他当月的工资是多少?。
2007年广州市初中数学青年教师解题比赛试题-新人教

2007年广州市初中数学青年教师解题比赛决 赛 试 卷 2007-4-15本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷.请将选择题和填空题的答案做在第3页的答卷上.全卷共三大题25小题,满分150分,考试时间120分钟.第I 卷(选择题,共44分)一、选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在第3页的答题卷上.)1.对于实数a ,下列运算正确的是( ).(A ))2(121a a ÷=- (B )3232a a a =+(C )623)(a a a -=⋅- (D )422)()(a a a -=-⨯-2.给出以下三个命题:①两个无理数的和一定是无理数;②两个无理数的和有可能是有理数;③两个无理数的和一定是实数.其中正确的命题是( ).(A )①和②(B )①和③(C )②和③(D )③3.已知等差数列}{n a 的前n 项和为n S ,且,7,384==S S 则12S 的值是 ( ) .(A )8 (B )11 (C )12(D )154.如果b a ,为实数,则“b a =”是“直线2)()222=-+-+=b y a x x y 与圆(相切” 的( ) . (A )充分不必要条件 (B )必要不充分条件(C ) 充要条件(D )既不充分又不必要条件5.已知AB 是圆O 的直径,弦AD 和BC 相交于点P , 那么ABCD等于( ). (A )BPD ∠sin (B )cos BPD ∠ (C )tan BPD ∠ (D )cot BPD ∠6.如图,三个天平的托盘中相同的物体质量相等.图⑴、⑵所示的两个天平处于平衡状态要使第三个天平也保持平衡,则需在它的右盘中放置( ).(A )3个球 (B )4个球 (C )5个球 (D )6个球7.如图是一个正方体的表面展开图,已知正方体的每一个面上都有一个实数,且相对面上的两个数互为倒数,那么代数式b ca-的值等于( ). (A )43- (B )6- (C )43 (D )6 8.已知集合}3,2,0{=A ,},,|{A b a ab x x B ∈==且,则集合B 的子集的个数是( ).(A )4 (B )8 (C )15 (D )16 9.如图,ABC ∆的角,,A B C 所对边分别为,,a b c , 点是O ABC ∆的外心,,于,于E AC OE D BC OD ⊥⊥,于F AB OF ⊥ 则OD OE OF =∶∶( ) .第5题图第7题图(A )a b c ∶∶ (B )cb a 1:1:1 (C )C B A cos :cos :cos (D )C B A sin :sin :sin10.设a b >,在同一平面直角坐标系内,一次函数a bx y +=与b ax y +=的图象最有可能的是( ).(A )13- (B )12-(C )-1 (D )-2 第II 卷(非选择题,共106分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上.)12.随机掷一枚均匀的正方体骰子(正方体骰子的六个面上的点数分别为1,2,3,4,5,6),每次实验掷两次,则每次实验中掷两次骰子的点数之和为6的概率是__________. 13.如果关于x 的方程()012122=++++a x a x 有一个小于1的正数根,那么实数a 的取值范围是 .14.在矩形ABCD 中,已知两邻边AD =12,AB =5,P 是AD 边上异于D A 和的任意一点,且BD PE ⊥,F E AC PF 、,⊥分别是垂足,那么=+PF PE ___________.15.已知012=--x x ,那么代数式123+-x x 的值是 .16.已知z y x ,,为实数,且3,5=++=++zx yz xy z y x ,则z 的取值范围为 .17.已知正方形ABCD 的面积35平方厘米, E 、F 分别为边AB 、BC 上的点, AF 和CE 相交于点G ,并且ABF ∆的面积为5平方厘米,BCE ∆的面积为14平方厘米,那么四边形BEGF 的面积是___________平方厘米.2007年广州市初中数学青年教师解题决赛答题卷第9题图第11题图第14题图第17题图2007-4-1512. 13. 14. 15. 16. 17.三、解答题(共8小题,满分76分.解答应写出必要的文字说明、演算步骤或证明过程.)18.(本小题8分)已知01<<-a ,21a A +=,21a B -=,aC +=11,试比较A 、B 、C 的大小,并说明理由.19.(本小题8分)设)(x f 是奇函数,)(x g 是偶函数,并且x x x g x f -=-2)()(,求)(x f 和)(x g .20.(本小题10分)已知⊥PA 矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点. (1)求证:CD MN ⊥;(2)若=∠PDA 45°,求证MN ⊥面PCD .21.(本小题10分)在ABC ∆中,,60,40==AC AB 以A 为圆心,AB 的长为半径作圆交BC 边于D ,若DC BD 和的长均为正整数,求BC 的长.22.(本小题10分)如图,在等腰直角三角形ABC 中,1=AB ,=∠A 900,点E 为腰AC 的中点,点F 在底边BC 上,且BE FE ⊥,求CEF ∆的面积. 23.(本小题10分)在正实数范围内,只存在一个数是关于x 的方程k x x kx x +=-++3132的解,求实数k 的取值范围. 24.(本小题10分)如图,在梯形PMNQ 中,MN PQ //,对角线MQ PN 和相交于点O ,并把梯形分成四部分,记这四部分的面积分别为4321S S S S 、、、.试判断21S S +和43S S +的大小关系,并证明你的结论.25.(本小题10分)已知42++=m m y ,若m 为整数,在使得y 为完全平方数的所有m 的值中,设m 的最大值为a ,最小值为b ,次小值为c .(注:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数.) (1)求c b a 、、的值;第20题图第21题图第22题图第24题图(2)对c b a 、、下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2007?证明你的结论.2007年广州市初中数学青年教师解题决赛试题参考答案及评分标准3.选C [解析]:∵{a n }等差数列,∴2(S 8 -S 4)= S 4+(S 12-S 8),且S 4=3,S 8=7,则S 12=12. 4.选A [解析]: 若a =b ,则直线与圆心的距离为22|2|=+-a a 等于半径,∴2)()222=-+-+=b y a x x y 与圆(相切.若2)()222=-+-+=b y a x x y 与圆(相切,则22|2|=+-b a ,∴40-=-=-b a b a 或.故“a =b ”是“直线2)()222=-+-+=b y a x x y 与圆(相切”的充分不必要条件.8.选C [解析]:如果b a ,中至少有1个为零,则0=ab ;如果2==b a ,则4=ab ;如果3==b a ,则9=ab ;如果2332a ab b ==⎧⎧⎨⎨==⎩⎩或,则6=ab ,于是B ={0,4,6,9},∴B 有42=16个子集.10.选B [解析]:由方程组⎩⎨⎧+=+=bax y abx y 的解知两直线的交点为),1(b a +,而图A 中交点横坐标是负数,故图A 不对;图C 中交点横坐标是2≠1,故图C 不对;图D 中交点纵坐标是大于a ,小于b 的数,不等于b a +,故图D 不对;故选B.11.选 B [解析]:设),0,(),0,(21x B x A 由,22=++c bn an 且222AB BQ AQ =+,得21-=a .二、填空题答案(每小题5分,共6小题,共30分)12.365. 13. 211-<<-a . 因式分解得()()0121=+++a x x ,因此“小于1的正数根”是12--a .由1120<--<a 得211-<<-a . 14.1360. 如图,过A 作AG ⊥BD 于G .因为等腰三角形底边上的任意一点到两腰距离的和等于腰上的高,所以PE +PF =AG .因为AD =12,AB =5,所以BD =13,所 以,136013512=⨯=AG 所以1360=+PF PE . 15. 2.2)1()(122233+--+--=+-x x x x x x x 22)1()1(22=+--+--=x x x x x .16. 3131≤≤-z . 3,5=++--=zx yz xy z x y 代入由,得0)35()5(22=+-+-+z z x z x ,因为x 为实数,所以0≥∆,解得3131≤≤-z . 17.27204.∵72==∆∆ABC ABF S S BC BF ,同理54=BA BE ,如图,连BG . 记a S AGE =∆,b S EGB =∆,c S BGF =∆,d S FGC =∆. 由已知 5=++c b a ,14=++d c b ,解之得2728=b ,27100=c . ∴)(2720427128平方厘米==+=c b S BEGF . 三、解答题答案(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程)18.解:它们的大小关系为C A B <<. ………………………2分由01<<-a 得01>+a ,02)1()1(222>=--+=-a a a B A 得B A >,…………4分143)21(1)1()1(11222>+⎥⎦⎤⎢⎣⎡++-=+++-=+-+=-aa a a a a a a a A C ,得A C >, ………………6分即得C A B <<. ………………8分19.解:Θ)(x f 为奇函数 )()(x f x f -=-∴Θ)(x g 为偶函数 )()(x g x g =-∴ …………………2分由x x x g x f x x x g x f +=---∴-=-22)()( )()(…………………4分 从而 x x x g x f x x x g x f --=++=--22)()(,)()( …………………6分⎩⎨⎧-=-=⇒⎩⎨⎧--=+-=-222)()()()()()(x x g xx f x x x g x f x x x g x f …………………8分20.证明:21.设BD =a ,CD =b ,(a ,b 为正整数)作AE ⊥BD ,垂足为E ,则AB =AD =40,BE =DE =2a. ∵ 222)2(40a AE -=,222)2(60b aAE +-=, ∴ 2222)2(60)2(40b aa +-=-, ∴ 34522000)(⨯==+b b a , …………………6分 ∵ 20<b a +<100,∴ 只有⎪⎩⎪⎨⎧⨯=⨯=+,52,5232b b a 或⎪⎩⎪⎨⎧=⨯=+.5,5224b b a ………………9分故BC 的长为50或80. …………………10分22.解法1:如图,过C 作CD ⊥CE 与EF 的延长线交于D . …… ……2分因为∠ABE +∠AEB =90°,∠CED +∠AEB =90°,所以∠ABE =∠CED . 于是Rt △ABE ∽Rt △CED , …………………4分所以2412====∆∆AEAB CD CE AB CE S S EAB CDE ,)(. ………………6分 又∠ECF=∠DCF=45°,所以CF 是∠DCE 的平分线,点F 到CE 和CD 的距离相等, 所以2==∆∆CDCES S CDF CEF . ……………8分所以241214132413232=⨯⨯=⨯==∆∆∆∆ABC ABE CDE CEF S S S S .………10分 解法2: 如图,作FH ⊥CE 于H ,设FH=h . ………………2分 因为∠ABE +∠AEB =90°,∠FEH+∠AEB=90°,所以 ∠ABE=∠FEH ,于是Rt △EHF ∽Rt △BAE . ………………4分 因为,即h EH AE AB FH EH 2.== 所以h HC 221-=. 又因为,FH HC =所以,61,221=-=h h h …………………8分 所以24161212121=⨯⨯=⨯=∆FH EC S CEF . ………………10分23.解:原方程可化为0)3(322=+--k x x ,① …………………1分 (1)当△=0时,833-=k ,4321==x x 满足条件; …………………2分(2)若1=x 是方程①的根,得0)3(13122=+-⨯-⨯k ,4-=k .此时方程①的另一个根为21,故原方程也只有一根21=x ; …………………4分(3)当方程①有异号实根时,02)3(21<+-=k x x ,得3->k ,此时原方程也只有一个正实数根;………7分(4)当方程①有一个根为0时,3-=k ,另一个根为23=x ,此时原方程也只有一个正实根. …………9分综上所述,满足条件的k 的取值范围是833-=k 或4-=k 或3-≥k . …………………10分24.解:设,,n MN m PQ == PMN ∆Θ和QMN ∆同底等高,QMN PMN S S ∆∆=∴,,2423S S S S +=+∴ , 即:43S S =. ……………2分POQ ∆Θ∽NOM ∆,,:):(:22221n m OM OQ S S ==∴1222S mn S ⋅=∴. (4)分,:::31n m OM OQ S S ==Θ13S mnS ⋅=∴. ……………6分 1122143212)()(S m n S m n S S S S S ⋅⋅-⋅+=+-+∴21221)1()21(m nS m n mn S -=⋅-+= .…………9分43212,0)1(S S S S mn +>+∴>-Θ . …………………10分(本题只写对结论而没有过程的只得1分)25. 解:(1)设224k m m =++(k 为非负整数),则有0422=-++k m m , (1)分由m 为整数知其△为完全平方数(也可以由△的公式直接推出), …………………2分即22)4(41p k =--(p 为非负整数), 得,15)2)(2(=-+p k p k 显然:p k p k ->+22,所以21521k p k p +=-=⎧⎨⎩或2523k p k p +=-=⎧⎨⎩,解得7=p 或1=p ,所以12p m -±=,得:1,0,4,34321-==-==m m m m , (5)分 所以1,4,3-=-==c b a . …………………6分(2)因为222222a b a b c a b c ++=+++-, ………………8分即操作前后,这三个数的平方和不变,而222222200620052004)1()4(3++≠-+-+. ………………9分 所以,对c b a 、、进行若干次操作后,不能得到2004,2005,2006这三个数.………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市初中数学青年教师解题比赛试卷
一、填空(本题共有10小题,每小题4分,共40分) 1.函数1
1
42-+
-=x x y 中,自变量x 的取值范围是 . 2.若一个半径为32㎝的扇形面积等于一个半径为2㎝的圆的面积,则扇形的圆心角为 . 3.分式方程
1
1
-x -()11-x x =2的解是 . 4.代数式x 2-2xy +3y 2―2x ―2y +3的值的取值范围是 .
5.⊙O 1、⊙O 2的半径分别为2和3,O 1O 2=9,则平面上半径为4且与⊙O 1、⊙O 2都相切的圆有 个. 6、若关于未知数x 的方程+++++=()0522=++++m x m x 的两根都是正数,则m 的取值范围是 .
7.在Rt △ABC 中,AD 是斜边BC 上的高,如果BC =a a BC =,=βB =∠,则AD = .
8.平面内一个圆把平面分成两部分,现有5个圆,其中每两个圆都相交,每三个圆都不共点,那么这5个圆则把平面分成 部分.
9.在平坦的草地上有甲、乙、丙三个小球.若已知甲球与乙球相距5米,乙球与丙球相距3米,问甲球与丙球距离的取值范围?答: .
10.计算12003200220012000+⨯⨯⨯所得的结果是 . 二、(本题满分12分)
11.如图,已知A 是直线l 外的一点,B 是l 上的一点. 求作:(1)⊙O ,使它经过A ,B 两点,且与l 有交点C ; (2)锐角△BCD ,使它内接于⊙O .
(说明:只要求作出符合条件的一个圆和一个三角形,要求写出作法,不要求证明)
三、(本题满分12分) 12.如图,己知正三棱锥S —ABC 的高SO =h ,斜高SM =l . 求经过SO 的中点平行于底面的截面△A ´B ´C ´的面积. 四、(本题满分13分)
13.证明:与抛物线的轴平行的直线和抛物线只有一个交点. 五、(本题满分13分)
14.甲、乙两船从河中A 地同时出发,匀速顺水下行至某一时刻,两船分别到达B 地和C 地.已知河中各处水流速度相同,且A
地到B 地的航程大于A 地到C 地的航程.两船在各自动力不变情况下,分别从B 地和C 地驶回A 地所需的时间为t 1和t 2.试比较t 1和t 2的大小关系. 六、(本题满分14分)
15.如图,在锐角θ内,有五个相邻外切的不等圆,它们都与θ角的边相切, 且半径分别为r 1、r 2、r 3、r 4、r 5.若最 小的半径r 1=1,最大的半径r 5=81。
求θ. 七、(本题满分16分) 16.过半径为r 的圆O 的直径AB 上一点P ,作PC ⊥AB 交圆周于C .若要以P A 、PB 、PC 为边作三角形,求OP 长的范围.
八、(本题满分16分)
17.设关于未知数x 的方程x 2―5x ―m 2+1=0的实根为α、β,试确定实数m 的取值范围,使|α|+|β|≤6成立. 九、(本题满分16分)
18.在重心为G 的钝角△ABC 中,若边BC =1,∠A =300,,且D 点平分BC .当A 点变动,B 、C 不动时,求DG 长度的取值范围. 2002年广州市初中数学青年教师解题比赛试卷
参考答案
一、填空(本题共有10小题,每小题4分,共40分)
1.22≤≤-x 且1±≠x 2.60° 3.2
1
=
x 4.[)+∞,0 5.3 6.45-≤<-m 7.ββcos sin a 8.22 9.相距大于等于2米而小于等于8米 10.4006001
二、(本题满分12分)
·
· l
A
B
θ
·
A '
B '
C '
A B
C
M
O S
(1)作法:
① 在l 上取点C ,(使∠CAB ≠90°) ② 经过A 、B 、C 作⊙O ,则⊙O 就是 所求.
(2)作法:
① 过O 作BC 的垂线交优弧BC 于D , ② 连结DC 、DB 、AB ,则△BCD 就是 所求.
三、(本题满分12分)
解:连结OM 、OA ,在Rt △SOM 中,
22h l OM -=.
因为棱锥S —ABC 正棱锥,所以O 是等边
△ABC 的中心.
223260tg 22h l OM AM AB -⋅=︒⋅⋅==,
()()
2222233344
3
43h l h l AB S ABC -=-⨯⨯==
∆
4
1=∆'''∆ABC C B A S S
()
22
4
3341h l S S ABC C B A -==
∴∆'''∆ 四、(本题满分13分)
证明:设抛物线方程为px y 22=,平行于抛物线的轴的直线方程为()0≠=b b y .
解方程组⎩⎨⎧==,,22
b y px y 得⎪⎩
⎪⎨⎧==
,
,22
b y p b x
故抛物线方程为px y 22=与平行于其轴的直线()0≠=b b y 只有一个交点. 五、(本题满分13分)
解:若以1S 、2S 、t 、x 、y 、a 分别表示A ~B 航程、A ~C 航程、下行时间、在静水中甲船航速、乙船航速和水
流速度,则有:
(),2111t a x a a x t a x a x S t ⎪⎭⎫ ⎝
⎛-+=-+=-=
(),2122t a y a a y t a y a y S t ⎪⎪⎭
⎫
⎝⎛-+=-+=-=
a y a x a t S S >>>>>,,0,0,21
y x >∴,从而.1
1,
a
y a x a y a x -<-->- A
B
C
l
O
D
A '
B '
C '
O '
A B C
S
O
M
21t t <∴
六、(本题满分14分)
解:545
445452
sin
12sin 12
sin
12sin 12sin r r r r r r r r ⋅+-=
⇒+-=⇒=+-θ
θθ
θθ
同理,52
3432sin 12sin 12sin 12sin 1r r r r ⋅⎪⎪⎪⎪
⎭⎫ ⎝
⎛
+-=⇒⋅+-=θθθθ
同理可得,5
4
12sin 12sin 1r r ⋅⎪
⎪⎪⎪
⎭⎫ ⎝
⎛
+-=θθ
212sin 312sin 12sin 18112sin 12sin 14
=⇒=+-⇒=⎪
⎪⎪⎪
⎭⎫
⎝
⎛
+-∴θθθθθ
︒=︒=∴
60,302
θθ
七、(本题满分16分)
解:不失一般性,令P 在OB 上,且0>=OP x ,
则有AP >BP ,AP >PC . 若以AP 、BP 、PC 为边作三角形,结合上面条件, 只须BP +PC>AP ,即x x r x r PC 2=+-+>, 又()1,4,0022x PC ,x PC >∴≥>
又()()222x r x r x r BP AP PC -=-+=⋅=.代入(1)得2224x x r >-,
解得:r x r 5
555<<-
. ∴OP 的取值范围是r x 5
5
0<≤. 八、(本题满分16分)
解:∵△()214145222+=-+=m m ∴不论m 取何值,所给的方程都有两个不相等的实根. ∵6,152≤+-==+βααββαm ,,
∴36222≤++αββα,即()36222
≤+-+αβαββα.
∴()
3612122522≤-+--m m 当012≥-m 时,3625≤成立, ∴11≤≤-m . (1)
当012<-m 时,得()3614252≤--m ,
· A
B
C O
P
x
∴2
15215≤≤-
m . (2) 由(1)、(2)得2
15
215≤≤-
m . 九、(本题满分16分)
解:在图中30°的弓形弧BC ,令MB ⊥BC ,NC ⊥BC , 由题意知,A 点在不含端点的BM 、CN 上. 且BD <AD <DM ,
故33DM
DG BD ≤
≤,
但21321==,DM BD ,
6
1361<<∴
DG .
·
A
B C
D
M
N
G。
