马尔可夫信源
合集下载
第二章-信息论基本概念（3）
H ( X m1 / X1 X 2 X m )
这表明：m阶马尔可夫信源的极限熵H 就等于m阶条件熵，记为H m 1
akm )
设状态 Ei (ak1 ak2 akm ),信源处于状态Ei时，再发出下一个符号akm1
此时，符号序列 (ak2 ak3 a ) km1 就组成了新的信源状态
Ej (ak2 ak3 a ) km1 ，这时信源所处的状态由 Ei 转移到 Ej
状态转移图(香农线图)
0:0.5 E1
1:0.5 E3
1
0:0.6
E2
1:0.4
【注】E1、E2、E3是三种状态，箭头是指从一个状态转移到另
一个状态，旁边的数字代表发出的某符号和条件概率p(ak/Ei) 。 这就是香农提出的马尔可夫状态转移图，也叫香农线图。
二、马尔可夫信源
若信源输出的符号和信源所处的状态满足以下两个条 件，则称为马尔可夫信源：
a1 a2
p(sl
E2
/ xl
a3
sl1 E1 ) 0 sl1 E1 ) 1 sl1 E1 ) 1 sl1 E1 ) 0
可求得状态的一步转移概率：
1
2
1 4
0
1 4
0
0
1 2
1 2
0
0
p(E j
/
Ei
)
0
3
1
0
0
44
0
0
0
0
1
0
0
0
3 4
1 4
此信源满足马尔可夫的 两个条件，所以是马尔可夫 信源，并且是齐次马尔可夫 信源。
对于这个随机序列，若有：
p(xn Sin | xn1 Sin1 ,..., x1 Si1 ) p(xn Sin | xn1 S ) in1
马尔科夫信源课件
马尔科夫信源在物联网中的应用前景
1 2
物联网通信
探讨马尔科夫信源在物联网通信中的应用前景， 分析其在物联网通信中的优势和局限性。
低功耗设计
研究如何在保证性能的同时降低马尔科夫信源的 功耗，以满足物联网设备低功耗的需求。
3
跨领域应用
探讨马尔科夫信源在其他领域的应用前景，如生 物信息学、医学影像处理等，分析其在这些领域 的适用性和优势。
进行计算。
应用
03
状态转移概率是马尔科夫信源的重要参数，用于描述信源的动
态特性，是进行信息编码和数据压缩的重要依据。
平稳状态分布
01
定义
平稳状态分布是指马尔科夫信源在无限长时间内的状态概率分布。
02
计算方法
平稳状态分布可以通过迭代计算得到，也可以通过数学模型进行推导。
03
应用
平稳状态分布是马尔科夫信源的重要参数，用于描述信源的统计特性，
如果马尔科夫链的状态转移是稳定的，那么信源的统计特性就可以被视为具有长期一致性，从而在编 码时可以利用这些信息来提高压缩效率。相反，如果状态转移是不稳定的，那么信源的统计特性就可 能具有较大的波动，需要采用不同的编码策略来处理。
03 马尔科夫信源的编码与解码
CHAPTER
编码原理
统计特性
马尔科夫信源的编码原理基于信源的统计特性，通过对概率较大符号的压缩，以及对概率较小符号的冗余编码，实现 数据压缩。
计算复杂度
编码与解码过程中的计算复杂度也是衡量效率的重要因素，计算复 杂度越低，表示实现越简单，效率越高。
04 马尔科夫信源的应用场景
CHAPTER
自然语言处理
语言模型
马尔科夫链蒙特卡洛方法可以用于构 建语言模型，通过训练大量文本数据 ，预测给定前一个词的情况下下一个 词的概率分布。
第2章_2.7马尔可夫信源
在状态E2时， 以0.8的概率发出符号 1，状态仍然为 E2； 以0.2的概率发出符号 0，状态转移到 E1
19
马尔可夫信源－状态转移图
为什么马尔可夫信源是非平稳的信源： 初始概率为： p(0) p(1) 0.5 进入 E1 或 E 2 两个状态。之后无论在哪个状态， 下一个输出的符号有80％的可能性是1，转移 到 E 2 ，有20％的可能性是0，转移到 E1 ，所以 p(0) 0.2; p(1) 0.8 ，与初始概率不同， 不满足平稳信源的定义 。
jE
iE
6
1,...,k步转移概率
定义k步转移概率为
(k ) pij (m) P{Sm k j | Sm i}
i, j E
它表示在时刻m时，Xm的状态为i的条件下， 经过k步转移到达状态j的概率。 性质：
(k ) 1、pij (m) 0
i, j E iE
2、 pij( k ) (m) 1
21
m阶马尔可夫信源
m阶马尔可夫信源：在任何时刻l，输出 分量的概率分布只与前面m个分量的输出有 关。
可以把前面m个分量组成的序列做为l时 刻信源所处的状态 。
如果信源的符号集是 A a1
m q 则信源的状态共有个
a2 aq
22
m阶马尔可夫信源
例2.9 二元二阶马尔可夫信源。二元指信源 可能的输出有2种取值，如0，1； 马尔可夫信源共有个 q m 2 2 4 状态， 前两个分量可能取值的排列
E0 E1 E2 ，其中设为 该马尔可夫信源有三个状态： E0 初始状态，初始概率为 p(0) p(1) 0.5 ，等概率的 转移到 E1和E2 这两个状态
18
马尔可夫信源－状态转移图
马尔科夫信源
x3 0 1 00 0.4 0.6 01 0.2 0.8 10 0.3 0.7 11 0.4 0.6
• 从第四单位时间开始，随机变量Xi只与前面二 个单位时间的随机变量Xi-2Xi-1有依赖关系: p(xi| xi-1 xi-2…x2 x1) = p(xi| xi-1 xi-2) (i＞3) 且 p(xi| xi-1 xi-2) = p(x3| x2x1) (i＞3) 求：⑴信源状态转移情况和相应概率； ⑵画出完整的二阶马尔可夫信源状态转移图； ⑶求平稳分布概率； （4）马尔科夫信源达到稳定后，0和1的分布 概率。
s1 00; s2 01; s3 10; s4 11
由于信源只可能发出0或者1，所以信源下一时刻只 可能转移到其中的两种状态之一。如目前所处状态 为00，那么下一时刻信源只可转移到00或者01。而不 12 会转到10或者11状态。
p( s1 | s1 ) p( s4 | s4 ) 0.8, p( s3 | s2 ) p( s1 | s3 ) p( s4 | s2 ) p( s4 | s2 ) p( s2 | s3 ) 0.5; p( s2 | s1 ) p( s3 | s4 ) 0.2
区 别
p11 p1n P p( x j | si ) pQ1 pQn
7
马尔可夫信源
• 状态转移图
–齐次马尔可夫链可以用其 状态转移图(香农线图)表示 –每个圆圈代表一种状态 –状态之间的有向线代表某 一状态向另一状态的转移 –有向线一侧的符号和数字 分别代表发出的符号和条 件概率
• 解: • 设信源开始处于s0状态,并以 等概率发出符号0和1,分别 到达状态s1和s2 : s0 • 若处于s1 ,以0.3和0.7的概率 发出0和1到达s3和s4 • 若处于s2,以0.4和0.6的概率 发出0和1到达s5和s6
• 从第四单位时间开始，随机变量Xi只与前面二 个单位时间的随机变量Xi-2Xi-1有依赖关系: p(xi| xi-1 xi-2…x2 x1) = p(xi| xi-1 xi-2) (i＞3) 且 p(xi| xi-1 xi-2) = p(x3| x2x1) (i＞3) 求：⑴信源状态转移情况和相应概率； ⑵画出完整的二阶马尔可夫信源状态转移图； ⑶求平稳分布概率； （4）马尔科夫信源达到稳定后，0和1的分布 概率。
s1 00; s2 01; s3 10; s4 11
由于信源只可能发出0或者1，所以信源下一时刻只 可能转移到其中的两种状态之一。如目前所处状态 为00，那么下一时刻信源只可转移到00或者01。而不 12 会转到10或者11状态。
p( s1 | s1 ) p( s4 | s4 ) 0.8, p( s3 | s2 ) p( s1 | s3 ) p( s4 | s2 ) p( s4 | s2 ) p( s2 | s3 ) 0.5; p( s2 | s1 ) p( s3 | s4 ) 0.2
区 别
p11 p1n P p( x j | si ) pQ1 pQn
7
马尔可夫信源
• 状态转移图
–齐次马尔可夫链可以用其 状态转移图(香农线图)表示 –每个圆圈代表一种状态 –状态之间的有向线代表某 一状态向另一状态的转移 –有向线一侧的符号和数字 分别代表发出的符号和条 件概率
• 解: • 设信源开始处于s0状态,并以 等概率发出符号0和1,分别 到达状态s1和s2 : s0 • 若处于s1 ,以0.3和0.7的概率 发出0和1到达s3和s4 • 若处于s2,以0.4和0.6的概率 发出0和1到达s5和s6
第8讲Markov信源
p(0 | s1) = 1 p(1| s1) = 1 2 2 p(0 | s ) = 1 p(1| s2 ) = 2 2 3 3 p(0 | s3) = 14 p(1| s3) = 34 p(0 | s4 ) = 1 p(1| s4 ) = 4 5 5
得 状 态 转 移 概 率
其他状态转移概率均为零
二阶平稳Markov信源的例子解答 二阶平稳Markov信源的例子解答 Markov
根据上述状态转移概率结果画出状态转移图如下
1/2 s1:00 1/2 1/4 s4:11 4/5 1/5 s3:10 1/3 3/4 2/3 s2:01
由Markov链知识可得出信源的状态转移概率矩阵， P=[pij]=[p(sj|si)]，以及达到平稳状态以后，处于sj 的 概率p(sj) .即：
设信源符号集X={a1, …,ar}，所处状态空间 设信源符号集 ，所处状态空间S={s1, …,sj}，在初 ， 始状态下，设信源每发出一个符号产生一种新的状态， 始状态下，设信源每发出一个符号产生一种新的状态，若符号 序列和状态序列满足： 序列和状态序列满足： 某时刻发出符号仅与当前信源状态有关，而与更前无关； (1). 某时刻发出符号仅与当前信源状态有关，而与更前无关； (2). 某时刻信源所处的状态仅与前一时刻所处的状态和当前符 号有关。 号有关。 则称该信源为Markov信源。 则称该信源为Markov信源。 Markov信源
这样由三元信 X ∈{0,1,2}得到的状态空间 e1, e2 , e3}和 源 { 相应的一步转 移概率构成的一阶 马尔可夫信源模型 为 ee2e3 1 p(ej / ei ) i, j =1,2,3 且∑(ej / ei ) =1
j =1 3
得 状 态 转 移 概 率
其他状态转移概率均为零
二阶平稳Markov信源的例子解答 二阶平稳Markov信源的例子解答 Markov
根据上述状态转移概率结果画出状态转移图如下
1/2 s1:00 1/2 1/4 s4:11 4/5 1/5 s3:10 1/3 3/4 2/3 s2:01
由Markov链知识可得出信源的状态转移概率矩阵， P=[pij]=[p(sj|si)]，以及达到平稳状态以后，处于sj 的 概率p(sj) .即：
设信源符号集X={a1, …,ar}，所处状态空间 设信源符号集 ，所处状态空间S={s1, …,sj}，在初 ， 始状态下，设信源每发出一个符号产生一种新的状态， 始状态下，设信源每发出一个符号产生一种新的状态，若符号 序列和状态序列满足： 序列和状态序列满足： 某时刻发出符号仅与当前信源状态有关，而与更前无关； (1). 某时刻发出符号仅与当前信源状态有关，而与更前无关； (2). 某时刻信源所处的状态仅与前一时刻所处的状态和当前符 号有关。 号有关。 则称该信源为Markov信源。 则称该信源为Markov信源。 Markov信源
这样由三元信 X ∈{0,1,2}得到的状态空间 e1, e2 , e3}和 源 { 相应的一步转 移概率构成的一阶 马尔可夫信源模型 为 ee2e3 1 p(ej / ei ) i, j =1,2,3 且∑(ej / ei ) =1
j =1 3
信息论马尔科夫信源
x
xk N ) log p(
xk N
xk N m xk N 1
)}
p( xk1 xkm1 )
xk1 xkm
)
H(
X m1
X1 X m
) H m1
p( xkm1 / xk1 xk2 xkm ) p( xk / si ) p( s j / si ) H H m1 p( si ) p( s j / si ) log 2 p( s j / si )
输出状态序列：S1S2 Sl 1Sl
1
2
某时刻输出符号仅与此刻信源所处的状态有关；
某时刻所处状态由当前输出符号和前一时刻信源状态 唯一确定。
设l时刻信源处于si , 输出xk
pl (
pl (
xk
si
si
) p(
X l xk
Sl si
)
)
sj
) p(
Sl s j
Sl 1 si
则由信源输出符号的条件概率
p( xim1 / xi1 xi2 ... xim )
可以确定状态转移概率p(sj/si)，i，j∈{1,2,…,nm} 马尔可夫信源的状态空间
s1...si ...s j ...sn m p( s / s ) j i
例：设一个二元一阶马尔可夫信源，信源符号集为 X={0,1}，信源输出符号的条件概率为 p(0/0)=0.25，p(0/1)=0.50，p(1/0)=0.75，p(0/1)=0.50， 求状态转移概率。 解：由于信源符号数n=2，因此二进制一阶信源仅有2个状 态：s1=0，s2=1。由条件概率求得信源状态转移概率为 p(s1/s1)=0.25，p(s1/s2)=0.50，p(s2/s1)=0.75，p(s2/s2)=0.50
3.4_马尔可夫信源
信息论与编码技术电子信息工程专业主讲：孙静机械电子工程系3.4 马尔可夫信源离散信源中有一类特殊的信源，其信源输出的符号序列中符号之间的依赖关系是有限的，并且满足马尔可夫链的性质，因此可用马尔可夫链来处理。
任何时刻信源符号发生的概率只与前面已经发生过的若干个符号有关，而与更前面的符号无关。
3.5.2课上要求：课本P641.【定义】若离散平稳信源在某时刻发出的符号仅与在此之前发出的有限个符号有关，而与更早些时刻发出的符号无关，这类信源称为马尔可夫（MovKov）信源。
2.【数学描述】如果随机变量序列X 中的任一时刻(n +1)的随机变量X n +1只依赖于前面已经发生的n 个随机变量X 1X 2…X n ，与更前面的随机变量无关，则称这种信源为n 阶马尔可夫信源。
其概率分布表示为：)|()|(21211221n i i i i i i i i n i i x x x x p x x x x x x x x p ---++---=3.【特殊说明】①n阶马尔可夫信源只与前面发出的n个符号有关，即关联长度为n+1。
②当n=1时，即任何时刻信源符号发生的概率只与前面一个符号有关，则称为一阶马尔可夫信源。
二、相关概念1.状态【定义】把排在指定符号前面与它相关联的n个符号定义为该符号的状态。
【数目】n阶马尔可夫信源可以有q n种不同的状态。
当前时刻输出的符号1.状态【举例】序列的状态是由信源的符号构成的。
•比如二元二阶马尔可夫信源有四个状态：{0，1} {00，01，10，11}前一时刻输出的符号2.状态转移设离散平稳有记忆信源的状态集为S={S1,S2,…,S J}，在每一状态下输出的符,a2,…,a q}，并认为每一时刻号X∈A={a1，当信源发出一个符号后，信源所处的状态将会发生转移。
【注意】本课程只研究时齐马尔可夫信源，即状态转移过程与时间无关。
1.前提假设信源输出符号序列为：x 1, x 2, … , x l -1, x l , …。
马尔可夫信源和剩余度
BUPT Press
举例
BUPT Press
BUPT Press
BUPT Press
信源熵的相对率
H H0
信源的剩余度（冗余度）
1 1
H H0 1 H log q
英文的冗余度
1
1.4 0.71 4.76
信息变差
BUPT Press
BUPT Press
BUPT Press
BUPT Press
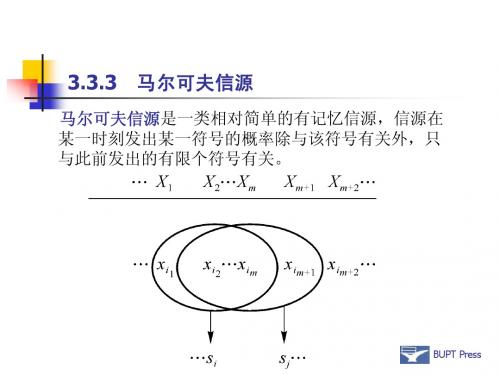
3.3.3
马尔可夫信源
马尔可夫信源是一类相对简单的有记忆信源，信源在 某一时刻发出某一符号的概率除与该符号有关外，只 与此前发出的有限个符号有关。
BUPT Press
3.3.3
马尔可夫信源
我们把前面若干个符号看作 一个状态，可以认为信源在 某一时刻发出某一符号的概 率除了与该符号有关外，只 与该时刻信源所处的状态有 关，而与过去的状态无关。 信源发出一个符号后，信源 所处的状态即发生改变，这 些状态的变化组成了马氏链。
BUPT Press
BUPT Press
BUPT Press
BUPT Press
BUPT Press
例
BUPT Press
BUPT Press
BUPT Press
一步转移概率矩阵
BUPT Press
BUPT Press
m阶马尔可夫信源的条件概率
m阶马尔可夫信源的极限熵
BUPT Press
BUPT Press
BUPT Press
BUPT Press
例3.5 设有一个二元2阶马尔可夫信源，其信源符号集为
BUPT Press
解得 计算极限熵
BUPT Press
ch06马尔可夫信源
Review of the last lecture
问题2&3:
• H(X)/矢量熵= H(X1X2…XN-1XN)/联合熵表示平均发一个消息 （由N个符号组成）提供的信息量。 • 平均符号熵：信源平均每发一个符号提供的信息量为
H N (X ) =
1 N
H (X1X 2 … X N )
• 极限熵：当N→∞时，平均符号熵取极限值称之为极限熵 或极限信息量。用H∞表示，即
• 这里利用了m阶马尔可夫信源“有限记忆长度”的根本特 性，使无限大参数N变为有限值m，把求极限熵的问题变 成了一个求m阶条件熵的问题。 • 状态一步转移概率p(ej /ei)是给定或测定的。求解Hm+1条件 熵的关键就是要得到p(ei)(i=1,2,…,nm) 。 p(ei)是马尔可夫 信源稳定后(N→∞)各状态的极限概率。 • 有限状态的马尔可夫链：状态空间的状态是有限的。 • 可列状态的马尔可夫链：状态空间I是{0,±1,±2,…}。
k =1
由图中看出： P( S = e / X = x , S = e ) = 0 ⎧ l 2 l 1 l −1 1
⎪ P( S = e / X = x , S = e ) = 1 l 1 l 1 l −1 1 ⎪ ⎪ ⎨ P( S l = e2 / X l = x2 , S l −1 = e1 ) = 1 ⎪ P( S = e / X = x , S = e ) = 0 l 3 l 2 l −1 1 ⎪ ⎪ ⎩
H ∞ = lim
N →∞
1 N
H (X1X 2 … X N )
Review of the last lecture
• 极限熵的存在性：当离散有记忆信源是平稳信源时，从 数学上可以证明，极限熵是存在的，且等于关联长度 N→∞时，条件熵H(XN/X1X2…XN-1)的极限值，即
信息论之马尔可夫信源
k =1
q
( k, k −1 = 1, 2K, q )
其马尔科夫链的状态空间也为 得 P ( ak | Ei ) = P ( ak | ak −1 )( k , = 1, 2K, q; i = k −1 = 1, 2,K, q )
而状态极限概率Q ( Ei ) = Q ( ak −1 )( i = k −1 = 1,2,K, q ) 因此，一阶马尔科夫信源的信息熵
对q元m阶马尔可夫信源来说只有状态极限概率j12?q离散平稳信源m阶马尔可夫信源一阶马尔可夫信源实际信源离散无记忆信散无记忆信源1关于离散信源熵实际信源可能是非平稳离散有记忆随机序列信源其信息熵不一定存在
第二章 离散信源及其信息测度
2.7 马尔可夫信源 2.8 信源剩余度与自然语言的熵 *2.9 信息意义和加权熵
∑ K∑ ∑ Q( a Ka )P( a
q q q km =1 km+1 =1 k1 km
km+1
| ak1 Kakm log P akm+1 | ak1 Kakm
)
(
)
= H ( Xm+1 | X1 X2 KXm )
由此得时齐、遍历的m阶马尔可夫信源的熵等于有限记忆长度为 m的条件熵。但必须注意它不同于有限记忆长度为m的离散平稳 信源。时齐、遍历的m阶马尔可夫信源并非是记忆长度为m的离 散平稳信源。只有当时间N足够长以后，信源所处的状态链达到 稳定，这时由m个符号组成的各种可能的状态达到一种稳定分布 后，才可将时齐、遍历的m阶马尔可夫信源作为记忆长度为m的 离散平稳信源。
P (1| 00 ) = P ( 0 |11) = 0.2
根据给定的条件概率，可以求得状态 之间的转移概率 ( 一步转移概率 ) 为 P ( E1 | E1 ) = P ( E4 | E4 ) = 0.8
q
( k, k −1 = 1, 2K, q )
其马尔科夫链的状态空间也为 得 P ( ak | Ei ) = P ( ak | ak −1 )( k , = 1, 2K, q; i = k −1 = 1, 2,K, q )
而状态极限概率Q ( Ei ) = Q ( ak −1 )( i = k −1 = 1,2,K, q ) 因此，一阶马尔科夫信源的信息熵
对q元m阶马尔可夫信源来说只有状态极限概率j12?q离散平稳信源m阶马尔可夫信源一阶马尔可夫信源实际信源离散无记忆信散无记忆信源1关于离散信源熵实际信源可能是非平稳离散有记忆随机序列信源其信息熵不一定存在
第二章 离散信源及其信息测度
2.7 马尔可夫信源 2.8 信源剩余度与自然语言的熵 *2.9 信息意义和加权熵
∑ K∑ ∑ Q( a Ka )P( a
q q q km =1 km+1 =1 k1 km
km+1
| ak1 Kakm log P akm+1 | ak1 Kakm
)
(
)
= H ( Xm+1 | X1 X2 KXm )
由此得时齐、遍历的m阶马尔可夫信源的熵等于有限记忆长度为 m的条件熵。但必须注意它不同于有限记忆长度为m的离散平稳 信源。时齐、遍历的m阶马尔可夫信源并非是记忆长度为m的离 散平稳信源。只有当时间N足够长以后，信源所处的状态链达到 稳定，这时由m个符号组成的各种可能的状态达到一种稳定分布 后，才可将时齐、遍历的m阶马尔可夫信源作为记忆长度为m的 离散平稳信源。
P (1| 00 ) = P ( 0 |11) = 0.2
根据给定的条件概率，可以求得状态 之间的转移概率 ( 一步转移概率 ) 为 P ( E1 | E1 ) = P ( E4 | E4 ) = 0.8
第二篇基本信息论4_马尔可夫信源
p( X t xk / St ej , X t1 xk1, St1 ei ,...) pt (xk / ej ) 若信源时齐，则pt ( xk / ei ) p( xk / ei ) 不论何时，在状态ei下发生符号xk的概率不变。
2）信源某时刻 t 所处的状态，由当前的输出符号 和前一时刻 (t-1) 信源所处的状态唯一确定。
态一步转移概率矩
阵，可写出：
e2 01
0: 0.8
00 e1
0: 0.5
0: 0.5 1: 0.5
10 e3
1: 0.5 当信源处于状态e1 00时：
0: 0.2
11 e4
1: 0.8
p(0 / 00) p( x1 / e1) p(e1 / e1) 0.8
p(1/ 00) p( x2 / e1) p(e2 / e1) 0.2
2.4 马尔可夫信源
一、马尔可夫链
设信源所处的状态为：S e1,e2,...,enm
信源每一状态下可能输出的符号：X x1, x2,..., xn
每一时刻信源发出一个符号后，所处的状态发生 转移
信源输出的随机符号序列为： X1, X 2 ,..., X t1, X t ,... 信源所处的状态序列为： S1, S2 ,..., St1, St ,...
若马尔可夫信源的状态数为m， 则称为m阶马尔可夫信源
m阶马尔可夫信源的熵：
H
lim
N
H
(
X
N
/
X1X 2...X N1)
Hm1 H ( X m1 / X1 X 2...X m )
nn
n
...
p( xk1 xk2 ...xkm1 ) lb p( xkm1 / xk1 xk2 ...xkm )
2）信源某时刻 t 所处的状态，由当前的输出符号 和前一时刻 (t-1) 信源所处的状态唯一确定。
态一步转移概率矩
阵，可写出：
e2 01
0: 0.8
00 e1
0: 0.5
0: 0.5 1: 0.5
10 e3
1: 0.5 当信源处于状态e1 00时：
0: 0.2
11 e4
1: 0.8
p(0 / 00) p( x1 / e1) p(e1 / e1) 0.8
p(1/ 00) p( x2 / e1) p(e2 / e1) 0.2
2.4 马尔可夫信源
一、马尔可夫链
设信源所处的状态为：S e1,e2,...,enm
信源每一状态下可能输出的符号：X x1, x2,..., xn
每一时刻信源发出一个符号后，所处的状态发生 转移
信源输出的随机符号序列为： X1, X 2 ,..., X t1, X t ,... 信源所处的状态序列为： S1, S2 ,..., St1, St ,...
若马尔可夫信源的状态数为m， 则称为m阶马尔可夫信源
m阶马尔可夫信源的熵：
H
lim
N
H
(
X
N
/
X1X 2...X N1)
Hm1 H ( X m1 / X1 X 2...X m )
nn
n
...
p( xk1 xk2 ...xkm1 ) lb p( xkm1 / xk1 xk2 ...xkm )
信息论汇总马尔科夫信源ppt培训课件
字母有关外,只与此前发出的有限个字母有 关
• m阶马尔可夫信源：
– 信源输出某一符号的概率仅与以前的m个符 号有关，而与更前面的符号无关。
• 条件概率 p ( x L |x L 1 , x 1 ) p ( x L |x L 1 , x L m )
4
马氏链的基本概念
• 一阶马尔可夫信源：
p(0|0)=0.25, p(0|1)=0.5, p(1|0)=0.75, p(1|1)=0.5 求状态转移概率，画出状态转移图。
q2,m1,qm2
s10;s21 p(s1|s1)0.25,p(s1|s2)0.5;p(s2|s1)0.75,p(s2|s2)0.5
1 0.5 0 0.25
：
0
1：0.75
1
：
0：0.5
12
• 例3 设有一个二元二阶马尔科夫信源，其信源 符号集X={0,1}，信源输出符号的条件概率为
P(0|00)=p(1|11)=0.8, p(1|00)=0.2
p(0|01)=p(0|10)=p(1|01)=p(1|10)=0.5 求状态转移概率矩阵，画出状态转移图
• 引入状态变量的好处：使得高阶马尔科夫过程 可以转化为一阶马尔科夫过程处理。
5
马氏链的基本概念
• 令si = (xi1, xi2, …xim) xi1,,xi2, …xim ∈(a1, a2, …an) • 状态集S ={ s1,s2,…,sQ} Q = nm • 信源输出的随机符号序列为：x1, x2,…xi-1, xi … • 信源所处的随机状态序列为：s1, s2,…si-1 , si … • 例：二元序列为…01011100… • 考虑m = 2，Q = nm =22= 4
• m阶马尔可夫信源：
– 信源输出某一符号的概率仅与以前的m个符 号有关，而与更前面的符号无关。
• 条件概率 p ( x L |x L 1 , x 1 ) p ( x L |x L 1 , x L m )
4
马氏链的基本概念
• 一阶马尔可夫信源：
p(0|0)=0.25, p(0|1)=0.5, p(1|0)=0.75, p(1|1)=0.5 求状态转移概率，画出状态转移图。
q2,m1,qm2
s10;s21 p(s1|s1)0.25,p(s1|s2)0.5;p(s2|s1)0.75,p(s2|s2)0.5
1 0.5 0 0.25
：
0
1：0.75
1
：
0：0.5
12
• 例3 设有一个二元二阶马尔科夫信源，其信源 符号集X={0,1}，信源输出符号的条件概率为
P(0|00)=p(1|11)=0.8, p(1|00)=0.2
p(0|01)=p(0|10)=p(1|01)=p(1|10)=0.5 求状态转移概率矩阵，画出状态转移图
• 引入状态变量的好处：使得高阶马尔科夫过程 可以转化为一阶马尔科夫过程处理。
5
马氏链的基本概念
• 令si = (xi1, xi2, …xim) xi1,,xi2, …xim ∈(a1, a2, …an) • 状态集S ={ s1,s2,…,sQ} Q = nm • 信源输出的随机符号序列为：x1, x2,…xi-1, xi … • 信源所处的随机状态序列为：s1, s2,…si-1 , si … • 例：二元序列为…01011100… • 考虑m = 2，Q = nm =22= 4
2.4马尔可夫信源
2.4马尔可夫信源如果信源的前个不同的序列值，决定信源下一时刻发送某个符号的概率，这类信源输出符号时不仅与信源的符号集有关（与普通信源类似），而且还与信源状态有关（即前m 个符号有关）,所以要引入信源状态的概念。
设信源所处的状态为：}{ej e e S ,...2,1∈在信源每一状态下可能输出的符号为：{}n x x x X ,...2,1∈而且一般每一时刻信源发出一个符号后，所处的状态发生转移，信源输出的随机符号序列为：X1,X2,…X t-1, X t ,…信源所处的状态序列为： S1,S2,…S t-1, S t ,…设在第时刻信源处于状态时，输出符号的概率给定（在马尔可夫信源中这是已知值）为： p t (x k /e i )= p(X t =x k /S t =e i )另外设信源在的前一时刻时刻处于状态，而在时刻转移到的状态，转移概率为：p t(e j/e i)= p(S t=e j/S t-1=e i)如果信源输出的符号和所处的状态满足下面两条，则称为马尔可夫信源:1．某时刻信源输出哪个符号只与此时信源所处的状态有关，而与以前的状态以及以前的输出符号均无关。
2．信源某时刻所处的状态，由当前的输出符号和前一时刻信源的状态唯一确定。
可见状态的转移依赖于发出的信源符号和此时的信源序列的状态，因为条件概率是已经给定的，所以状态的转移必以一定的概率进行。
在确定的情况下，原状态转换到下一状态，则显然状态的一步转移概率与有下列关系：p(e j/e i)= p t(x k/e i)可以用状态转移图，条件概率矩阵以及状态的一步转移概率矩阵描述马尔可夫信源特性。
各态历经定理：所谓各态历经性是指经过若干时间后，处于各状态的概率与初始状态无关，即稳定下来了。
具有各态历经性的阶马尔可夫信源，其状态极限概率可由式（2.4.3）求出，再进一步和已知的据式（2.4.2）求出阶马尔可夫信源的熵。
[例2.4.1]马尔可夫信源（在稳定后）是用状态概率分布及各状态下发出符号的概率作为已知条件来研究信源的熵，其状态概率只有在稳定以后才是确定的，也就是说马尔可夫信源的状态转移图（例如图2.4.1）原来是变的，经过一定时间才稳定下来（成为稳定的图），而马尔可夫信源各状态的概率，在起始时与到了后来稳定时完全可以不相同。
马尔科夫信源
∑ P (m, m + n) = 1, i = 1, 2,…
j =1 ij
∞
当Pij(m,m+n)与m无关时，称马尔科夫链 (m,m+n)与 为齐次马尔科夫链，通常说的马尔科夫 齐次马尔科夫链，通常说的马尔科夫 链都是指齐次马尔科夫链。
马尔可夫信源
例：二阶马尔可夫信源，原始符号集为{1,0}， 条件概率定为：P(0|00)=P(1|11)=0.8 P(1|00)=P(0|11)=0.2 P(0|01)=P(0|10)=P(1|01)=P(1|10)=0.5 由此可见，信源共有2^2=4种状态 E：{e1=00,e2=01,e3=10,e4=11} 状态之间有转移概率， p(e2/e1)=p(e3/e4)=0.2 p(e2/e4)=p(e1/e3)=p(e2/e3)=p(e3/e2)=0.5 P(e1/e1)=p(e4/e4)=0.8
多符号离散平稳信源
根据信息熵的定义，可得： （1）联合熵
H ( X 1 X 2 ) = −∑∑ P(ai a j ) logP(ai a j )
i =1 j =1Fra bibliotekqq
可以表征信源输出长度为2的平均不确定性，或所含 有的信息量。因此可以用 1/ 2 H ( X 1 X 2 )作为二维平稳信 源的信息熵的近似值
e2 0 e3 0 e4 1 e5 1 4
1
1 2
1 4 1 2 3 4
0
1 4
0 1 2
1 4 1 2 1 4
e1
e2
e3
e4
e5
e1 1 1 0 1 0 2 4 4 e2 0 1 1 0 0 2 2 e3 0 3 1 0 0 4 4 e4 由图中可得状态的一步转移概率： 由图中可得状态的一步转移概率： 0 0 0 0 1 e5 0 0 0 3 1 4 4 该信源满足马尔可夫信源定义。 该信源满足马尔可夫信源定义。
例4二元2阶马尔可夫信源
第五节 离散平稳信源 根据信息熵的定义，可得： （1）联合熵
H ( X1 X 2 ) P(ai a j ) logP(ai a j )
i 1 j 1
q
q
可以表征信源输出长度为2的平均不确定性，或所含 有的信息量。因此可以用 1/ 2H ( X1 X 2 )作为二维平稳信 源的信息熵的近似值
A1=a1a1
A4=a2a1 A7=a3a1
A2=a1a2 A5=a2a2 A8=a3a2
A3=a1a3 A6=a2a3 A9=a3a3
第四节 离散无记忆的扩展信源 其概率关系为 :
A1
A2
A3
A4
A5 1/4
A6 1/8
A7
A8
A9 1/16
1/16 1/8
1/16 1/8
1/16 1/8
计算可知 H ( X 2 ) 3bit
第四节 离散无记忆的扩展信源
其中：
P(i ) P(ai1 ) P(ai 2 )...P(aiN )
根据信息熵的定义：
H ( X N ) P( X N )log P( X N )
XN
可以证明，对于离散无记忆的扩展信源
H ( X N ) NH ( X )
第四节 离散无记忆的扩展信源 例: 离散无记忆信源的N次扩展信源 离散无记忆信源为：X:{a1,a2,a3}; P(X):{1/4, 1/2, 1/4} 2次扩展信源为：X2:{A1…A9} 信源的9个符号为：
第二节 离散信源的信息熵 例：天气预报，有两个信源
X 1 a1, p( x) 1/ 4,
则：
a2 X 2 a1, 3/ 4 p( x) 1/ 2,
马尔可夫信源
从而得到马尔可夫信源状态空间
e1
e2
...
enm
p ej / ei
13
HUST --- Information and Coding Theory
马尔可夫信源与马尔可夫链
其状态e由（x
i
i1
,
xi2
,
L
, xim）唯一确定，
因此p(xkm1 xkm ,L , xk1 ) p(xkm1 ei ) 信源发出xkm1 ,状态变为ej ,
其意义是： 系统在现在时刻n 1处于状态Sin 1，那么将来时刻n的状态Sin 与过去时刻n 2, n 3,...,1的状态Sin 2,..., Si1无关， 仅与现在时刻n 1的状态Sin 1有关。 即，已知系统的现在，那么系统的将来与过去无关。 这种特性称为马尔可夫特性。
2
HUST --- Information and Coding Theory
基本（一步）转移概率
当n m 1时，pij(m, m 1)即为一步转移概率。 一般， 把pij(m, m 1)记为pij(m)，m 0, 称为基本转移概率。
pij(m)=P X m1 j | X m i i, j S
pij(m)中m表示基本转移概率与时刻m有关。
4
HUST --- Information and Coding Theory
18
HUST --- Information and Coding Theory
马尔可夫信源-例题
例 设有一个二进制二阶马尔可夫信源， 信源符号集为{0,1}，条件概率为 p(0 00) p(111) 0.8， p(1 00) p(0 11) 0.2， p(0 01) p(0 10) p(1 01) p(110) 0.5 试求其平稳分布和极限熵。
信息论与编码马尔可夫信源
2.2.4 马尔可夫信源
(1) 马尔可夫信源的定义 (2) m阶马尔可夫信源 (3) 举例
(1) 马尔可夫信源的定义
① 信源的状态和符号集 ② 马尔可夫信源定义 ③ 举例
① 信源的状态和符号集
有一类信源， 有一类信源，输出的符号序列中符号之间的依赖关系 是有限的， 是有限的，即任何时刻信源符号发生的概率只与前面 已经发出的若干个符号有关， 已经发出的若干个符号有关，而与更前面发出的符号 无关。 无关。 设符号集为X和状态为S 设符号集为X和状态为S。信源输出的信息符号还与 信源所处的状态有关。 信源所处的状态有关。 状态S ,…,e 状态S∈{e1,e2,…,ej} 符号X …,x 符号X∈{x1,x2, …,xn} 每一时刻信源发出一个符号后， 每一时刻信源发出一个符号后，所处的状态将发生 转移。 转移。 …,X 信源输出的随机符号序列为 X1,X2, …,Xl-1,Xl, … 信源所处的随机状态序列为 S1,S2, …,Sl-1,Sl, … …,S
k m+1
)
（或写成 。
p ( xkm+1 / xk1 xk 2 L xkm ) = p ( xk / ei ) = p (e j / ei )
nm nm i =1 j =1
H ∞ = H m +1 = −∑∑ p (ei ) p(e j / ei ) log 2 p(e j / ei )
其中p )(i=1,2,…,n 其中p(ei)(i=1,2,…,nm)是m阶马尔可夫信源稳定后的状 阶马尔可夫信源稳定后 稳定后的状 态极限概率， 是一步转移概率。 态极限概率， p(ej /ei)是一步转移概率。
② m阶马尔可夫信源的极限 熵
m阶马尔可夫信源的极限熵
H ∞ = lim H ( X N / X 1 X 2 … X N −1 )
(1) 马尔可夫信源的定义 (2) m阶马尔可夫信源 (3) 举例
(1) 马尔可夫信源的定义
① 信源的状态和符号集 ② 马尔可夫信源定义 ③ 举例
① 信源的状态和符号集
有一类信源， 有一类信源，输出的符号序列中符号之间的依赖关系 是有限的， 是有限的，即任何时刻信源符号发生的概率只与前面 已经发出的若干个符号有关， 已经发出的若干个符号有关，而与更前面发出的符号 无关。 无关。 设符号集为X和状态为S 设符号集为X和状态为S。信源输出的信息符号还与 信源所处的状态有关。 信源所处的状态有关。 状态S ,…,e 状态S∈{e1,e2,…,ej} 符号X …,x 符号X∈{x1,x2, …,xn} 每一时刻信源发出一个符号后， 每一时刻信源发出一个符号后，所处的状态将发生 转移。 转移。 …,X 信源输出的随机符号序列为 X1,X2, …,Xl-1,Xl, … 信源所处的随机状态序列为 S1,S2, …,Sl-1,Sl, … …,S
k m+1
)
（或写成 。
p ( xkm+1 / xk1 xk 2 L xkm ) = p ( xk / ei ) = p (e j / ei )
nm nm i =1 j =1
H ∞ = H m +1 = −∑∑ p (ei ) p(e j / ei ) log 2 p(e j / ei )
其中p )(i=1,2,…,n 其中p(ei)(i=1,2,…,nm)是m阶马尔可夫信源稳定后的状 阶马尔可夫信源稳定后 稳定后的状 态极限概率， 是一步转移概率。 态极限概率， p(ej /ei)是一步转移概率。
② m阶马尔可夫信源的极限 熵
m阶马尔可夫信源的极限熵
H ∞ = lim H ( X N / X 1 X 2 … X N −1 )
分布函数ff与马尔可夫信源的关系
分布函数ff与马尔可夫信源的关系马尔可夫信源是一种特殊的离散随机过程，它的输出符号只依赖于前一个符号，而与其他符号无关。
以此类推，输出符号的概率只与前一个符号相关，而不受其他符号的影响，因此，马尔可夫信源的输出概率可以由一个分布函数ff来描述。
本文将探究分布函数ff与马尔可夫信源的关系。
一、马尔可夫信源的定义及特点马尔可夫信源是一种随机变量序列，其输出符号只与前一个符号有关。
具有以下特点：1. 符号集合有限；2. 输出符号的概率只与前一个符号相关；3. 输出符号的概率具有稳定性和不变性。
二、分布函数ff的定义及性质分布函数ff指的是符号集合中每个符号出现的概率，它可以由离散离散的条件概率pp来计算。
具有以下性质：1. 值的范围在[0,1]之间；2. ff的和为1；3. 可以描述信源的统计特性。
三、分布函数ff与马尔可夫信源的关系马尔可夫信源的输出概率只与前一个符号相关，因此该信源的概率可以由一个一阶Markov链来描述，而Markov链对应的转移矩阵可以通过分布函数ff来表示。
具体来说，设s_{i}和s_{j}是马尔可夫信源中的两个符号，则它们之间的转移概率可以由如下公式计算：p_{ij}＝P(s_{t+1}=j|s_{t}=i)而分布函数ff可以定义为：f(i)＝P(s=i)如果分布函数ff满足如下条件，则称其为可逆分布：∀{i,j}，f(i)p_{ij}＝f(j)p_{ji}对于可逆分布，可以通过修改转移矩阵的值来得到新的转移矩阵，使得该新矩阵仍然满足概率转移矩阵的性质。
四、结论分布函数ff可以描述马尔可夫信源的输出概率，而转移矩阵则可以通过分布函数ff来定义。
分布函数ff与马尔可夫信源的关系可以通过转移概率公式来描述，而可逆分布则可以通过修改转移矩阵来得到新的转移矩阵。
这一关系为信源在数据传输和处理中提供了理论支持和重要参考。
马尔可夫信源概率分布
马尔可夫信源概率分布
马尔可夫信源概率分布是概率论中的一个重要概念，泛指一个随
时间变化的信源，其输出符号的概率分布会随着时间变化而变化，但
这些变化是依赖于先前符号的概率分布而展示。
本文将围绕这一概念，分步骤阐述其含义与应用。
第一步，先了解什么是信源。
信源是指在设定的符号集中，向外
发出符号串的物理实体。
在通信系统中，信源可以是汉字、数字、语音、图像等各类载体。
马尔可夫信源是指这个信源在时间轴上符号的
出现是依据某个时刻的前一次的发生而定的。
简单来说，在一个符号
序列中，当前的符号的出现概率仅与前一次的符号发生概率有关。
第二步，就是对于马尔可夫信源概率分布的阐述。
对于一个随机
变量，它的概率分布可以描述它在不同取值下的概率。
对于马尔可夫
信源，随机变量是因其前一个符号而产生的当前符号，其概率分布也
是随机的，并且在时间上呈现出有序性的结构。
如果设P（x_i|x_j）
表示在当前x_i之前，前一个符号的取值是x_j的条件下，x_i的概率，则可以得出马尔可夫信源的概率分布。
第三步，是阐述马尔可夫信源在实际应用中的作用。
马尔可夫信
源概率分布的应用可以很广泛，例如在自然语言处理中，可以用于抽
取文本的特征，对文本进行分类、聚类、切分等处理；在模拟系统领域，可以用于模拟真实世界中的许多机制，如金融市场、天气预报、
股票价格等预测等。
总之，马尔可夫信源概率分布是概率统计领域中一项重要的概念，在各领域的应用下，可以帮助我们更好地了解和处理时变的信息，将
信息转化为有用的知识，以推进科学技术的进步，助力人类社会的发展。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
设在第L时刻信源处于状态 E i 时，输出符号 ak 的概率给定为：
P xl ak | sl Ei
另外，假设在第 l 1 时刻信源处于Ei状态，下一时刻转移到Ej 状态的转移概率为： P {sl E j | sl 1 Ei ) ij (l ) P 称此信源的随机状态服从马尔可夫链
1 2 q
P
P(akm1 | ak1 ak2 akm )
1
2
m
m 1
并满足
0 P(akm1 | ak1 ak2 akm ) 1 且
km1 1
P( a
q
km1
| ak1 ak2 akm ) 1
(k1 , k2 ,, km , km1 1, 2,, q)
p(0 / 01) p(1 / 01) p(0 / 10) p(1 / 10) 0.5
电子信息工程学院
信息论
2. 6 马尔可夫信源
若当这些概率和时刻L无关，既满足
P( xl ak | sl Ei ) P ak | Ei
Pij P E j | Ei
则成为时齐的或齐次的。此时，信源的状态序列服从时齐马 尔可夫链。
若时齐马尔可夫链对一切 Ei , E j存在不依赖于Ei 的极限
M=1时，称为一阶马尔可夫信源。
电子信息工程学院
信息论
2. 6 马尔可夫信源
m 阶马尔可夫信源在任何时刻L，符号发生概率只于前M个 符号有关，所以可设状态Ei ak ak ak 。由于 k1, k2 ,, km 均可 取1, 2,, q ,的信源状态集 E E1, E2 ,, EJ , J qm , 则已知的 条件概率可变换成下式。
则称其具有遍历性，Pj 称为 平稳分布，其中Pj 为该马尔可夫链的初始分布。
N
i 0 j
lim Pij Pj ，且满足
Pj 0; Pj Pij ; Pj 1
电子信息工程学院
信息论
2. 6 马尔可夫信源
2.6.1(1) 马尔可夫信源定义
马尔可信源的输出的符号序列和信源所处的状态满 足下列两个条件：
电子信息工程学院
信息论
2. 6 马尔可夫信源
注：条件②表明，若信源处于某一状态 Ei ，当它输出一个 符号后，所处的状态就变了，一定从状态 Ei 转移到另一状 态。显然，状态的转移依赖于输出的信源符号，因此任何 时刻信源处于什么状态完全由前一时刻的状态和输出的符 号决定。 这种信源的状态序列在数学模型上可以作为时齐马尔可夫 链来处理。因而可用马尔可夫链的状态转移图来描述信源。 马尔可夫链的状态转移图：每个圆圈代表一种状态，状态 之间的有向线代表某一状态向另一状态转移。有向线一侧 的符号和数字分别代表发出的符号和条件概率。
设信源所处的状态为：S E E1, E2 ,, EJ
信源每个状态下可能输出的符号： X A a1 , a2 ,, aq
每一时刻信源发出一个符号后，所处的状态发生转移 信源输出的随机符号序列为： x1，x2 ,, xl 1, xl ,
, sl 1 , sl , 信源所处的随机状态序列为： s1，s2，
km1 i
m1 m1 m1
2 3 m1
k 1, 2,, q; i 1, 2,, J
2
3
m1
电子信息工程学院
信息论
2. 6 马尔可夫信源
p(0 / 00) p(1 / 11) 0.8
p(1 / 00) p(0 / 11 ) 0.2,
[例2-9] 给定二元二阶马氏源，符号集A:{0,1}，符号转移概率分 别为:
(1) P( xl ak | sl) P( xl ak | sl Ei )
(2) P ( sl E j | xl ak sl 1 Ei ) 0 1 Ei , E j E ak A
信息论
2. 6 马尔可夫信源
非平稳离散信源：描述信源输出消息的随机序列X 是非平稳的随机序列——马尔可夫信源 输出的随机序列X中各随机变量之间有依赖关系。 但记忆长度有限且满足马尔可夫链的性质，因此可 以用马尔科夫链来处理。 本节将讨论这类信源及其信息熵。
电子信息工程学院
信息论
2. 6 马尔可夫信源
1 2 m
P akm1 | ak1 ak2 akm P akm1 | Ei P ak | Ei
条件概率 P a | E 则表示任何L时刻信源处在状态 Ei 时输出符 号 ak 的概率。而ak 可以取 a1, a2 ,, aq 之一，所以可以简化 成 ak 表示。而且当在 L时刻，信源输出符号 ak 后，由符 号序列 ak ak ak 组成了新的信源状态E j ak ak ak E ， 信源所处的状态也由 Ei 转移到E j 。
电子信息工程学院
信息论
2. 6 马尔可夫信源
注：条件②表明，若信源处于某一状态 Ei ，当它输出一个 符号后，所处的状态就变了，一定从状态 Ei 转移到另一状 态。显然，状态的转移依赖于输出的信源符号，因此任何 时刻信源处于什么状态完全由前一时刻的状态和输出的符 号决定。 这种信源的状态序列在数学模型上可以作为时齐马尔可夫 链来处理。因而可用马尔可夫链的状态转移图来描述信源。 马尔可夫链的状态转移图：每个圆圈代表一种状态，状态 之间的有向线代表某一状态向另一状态转移。有向线一侧 的符号和数字分别代表发出的符号和条件概率。
电子信息工程学院
信息论
2. 6 马尔可夫信源
2.6.1(2) m阶马尔可夫信源定义
m阶马尔可夫信源符号集共有q个符号，则信源共有 q 不同状态，对应于 q 个长度为m的不同符号序列。
m
m
个
定义 m阶有记忆离散信源的数学模型可由一组信源符号集 X a , a , , a 和一组条件概率确定： (k , k , , k , k 1, 2, , q)