随机信号分析理论的应用综述

合集下载

通信原理第2章-随机信号分析

1 1 2
f ( x)dx f ( x)dx
a
2
在点 a 处取极大值: 1
2
■ a f x 左右平移
f x宽窄
a
x
37
二、正态分布函数
积分无法用闭合形式计算，要设法把这个积分式和可以在数学手册上查出积分值的特殊函数联系起来，常引入误差函数和互补误差函数表示正态分布函数。
38
三、误差函数和互补误差函数
39
40
四、为了方便以后分析，给出误差函数和互补误差函数的主要性质：
41
42
2.5.4 高斯白噪声
43
这种噪声称为白噪声，是一种理想的宽带随机过程。式子是一个常数，单位是瓦/赫兹。白噪声的自相关函数：
说明，白噪声只有在＝0 时才相关，而在任意
两个时刻上的随机变量都是不相关的。白噪声的功率谱和自相关函数如图。
F1 x1 ,
x1
t1
f1 x1 ,
t1
则称 f1 x1 , t1 为 (t的) 一维概率密度函数。
显然，随机过程的一维分布函数或一维概率密度函数仅仅描述了随机过程在各个孤立时刻的统计特性，没有说明随机过程在不同时刻取值之间的内在联系，因此需要在足够多的时间上考虑随机过程的多维分布函数
60
用示波器观察一个实现的波形，如图所示，是一个频率近似为fc，包络和相位随机缓变的正弦波。
Df －fc
s(t)
S( f )
O (a) 缓慢变化的包络[a(t)]
O
频率近似为 fc (b)
窄带过程的频谱和波形示意
61
Df
fc
f
t
因此，窄带随机过程ξ(t)可表示成:

《随机信号分析与处理》教学大纲

《随机信号分析与处理》教学⼤纲《随机信号分析与处理》教学⼤纲（执笔⼈：罗鹏飞教授学院：电⼦科学与⼯程学院）课程编号：070504209英⽂名称：Random Signal Analysis and Processing预修课程：概率论与数理统计、信号与系统、数字信号处理学时安排：60学时，其中讲授54学时，实践6学时学分：3⼀、课程概述（⼀）课程性质地位本课程是电⼦⼯程、通信⼯程专业的⼀门学科基础课程。

该课程系统地介绍随机信号的基本概念、随机信号的统计特性分析⽅法以及随机信号通过系统的分析⽅法；介绍信号检测、估计、滤波等信号处理理论的基本原理和信息提取⽅法。

其⽬的是使学⽣通过本课程的学习，掌握随机信号分析与处理的基本概念、基本原理和基本⽅法，培养学⽣运⽤随机信号分析与处理的理论解决⼯程实际问题的能⼒，提⾼综合素质，为后续课程的学习打下必要的理论基础。

本课程是电⼦信息技术核⼼理论基础。

电⼦信息系统中的关键技术是信息获取、信息传输、信息处理，这些技术的理论基础就是随机信号的分析、检测、估计、滤波等理论，这正是本课程的主要内容。

因此，本课程内容是电⼦信息类应⽤型⼈才知识结构中不可或缺的必备知识。

⼆、课程⽬标（⼀）知识与技能通过本课程的学习，掌握随机信号分析与处理基本概念和基本分析⽅法。

内容包括：1.理解和掌握随机过程基本概念和统计描述；2.掌握随机过程通过线性和⾮线性系统分析⽅法3.理解和掌握典型随机过程的特点及分析⽅法；4.掌握参数估计的概念、规则和性能分析⽅法；5.掌握信号检测的概念、规则和性能分析⽅法；6.掌握⾼斯⽩噪声中最佳检测器的结构和性能分析。

通过本课程的学习，要达到的能⼒⽬标是：1.具有正确地理解、阐述、解释⽣活中的随机现象的能⼒，即培养统计思维能⼒；2.运⽤概率、统计的数学⽅法和计算机⽅法分析和处理随机信号的能⼒；3.初步具备雷达、通信、导航等技术领域的信号处理系统的分析、设计、仿真的科学研究能⼒；4.培养⾃主学习能⼒；5.培养技术交流能⼒（包括论⽂写作和⼝头表达）；6.培养协作学习的能⼒；（⼆）过程与⽅法依托“理论、实践、第⼆课堂”三个基本教学平台，通过课堂教学、概念测试、课堂研讨、案例研究、作业、实验、课程论⽂、⽹络教学等多种教学形式，采⽤研究型、案例式、互动研讨、基于团队学习、基于MATLAB的教学以及基于多媒体的教学等多种教学⽅法和⼿段，使学⽣加深对随机信号分析与处理的基本概念、基本原理以及应⽤的理解，并使学⽣通过⾃主学习、⼩组作业、案例研究、实验、课题论⽂等主动学习形式，培养⾃学能⼒和协同学习的能⼒，使学⽣不仅获得知识、综合素质得到提⾼。

随机信号分析与处理

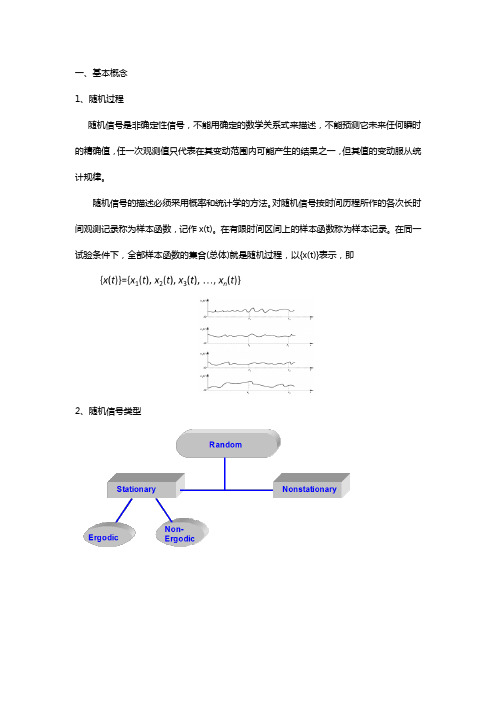
一、基本概念1、随机过程随机信号是非确定性信号，不能用确定的数学关系式来描述，不能预测它未来任何瞬时的精确值，任一次观测值只代表在其变动范围内可能产生的结果之一，但其值的变动服从统计规律。

随机信号的描述必须采用概率和统计学的方法。

对随机信号按时间历程所作的各次长时间观测记录称为样本函数，记作x(t)。

在有限时间区间上的样本函数称为样本记录。

在同一试验条件下，全部样本函数的集合(总体)就是随机过程，以{x(t)}表示，即2、随机信号类型3、平稳随机过程平稳随机过程就是统计特征参数不随时间变化而改变的随机过程。

例如，对某一随机过程的全部样本函数的集合选取不同的时间t进行计算，得出的统计参数都相同，则称这样的随机过程为平稳随机过程，否则就是非平稳随机过程。

如采样记录的均值不随时间变化4、各态历经随机过程若从平稳随机过程中任取一样本函数，如果该单一样本在长时间内的平均统计参数(时间平均)和所有样本函数在某一时刻的平均统计参数(集合平均)是一致的，则称这样的平稳随机过程为各态历经随机过程。

显然，各态历经随机过程必定是平稳随机过程，但是平稳随机过程不一定是各态历经的。

各态历经随机过程是随机过程中比较重要的一种，因为根据单个样本函数的时间平均可以描述整个随机过程的统计特性，从而简化了信号的分析和处理。

但是要判断随机过程是否各态历经的随机过程是相当困难的。

一般的做法是，先假定平稳随机过程是各态历经的，然后再根据测定的特性返回到实际中分析和检验原假定是否合理。

由大量事实证明，一般工程上遇到的平稳随机过程大多数是各态历经随机过程。

虽然有的不一定是严格的各态历经过程，但在精度许可的范围内，也可以当作各态历经随机过程来处理。

事实上，一般的随机过程需要足够多的样本(理论上应为无限多)才能描述它，而要进行大量的观测来获取足够多的样本函数是非常困难或做不到的。

在测试工作中常以一个或几个有限长度的样本记录来推断整个随机过程，以其时间平均来估计集合平均。

随机信号分析理论的应用综述

随机信号分析理论的应用综述结课论文学院：系别：电子信息工程班级：姓名：学号：指导老师：目录第一章概述随机信号分析的研究背景随机信号分析的主要研究问题第二章随机信号分析的主要内容随机信号分析的主要研究内容随机信号分析的基本研究方法第三章随机信号分析的应用实例均匀分布白噪声通过低通滤波器语音盲分离系统辨识基于bartlett的周期图法估计功率谱基于MATLAB_GUI的Kalman滤波程序第四章展望参考文献第一章概述随机信号分析的研究背景在一般的通信系统中,所传输的信号都具有一定的不确定性,因此都属于随机信号,否则不可能传递任何信息,也就失去了通信的意义;随机信号是一种不能用确定的数学关系式来描述的、无法预测未来时刻精准值的信号,也无法用实验的方法重复实现;随机信号是客观上广泛存在的一类信号,它是持续时间无限长,能量无限大的功率信号,这类信号的分析与处理主要是研究它们在各种变化域中的统计规律,建立相应的数学模型,以便定性和定量的描述其特性,给出相关性能指标,并研究如何改善对象的动静态性能等;随机信号分析内容涉及线性系统与信号、时间序列分析、数字信号处理、自适应滤波理论、快速算法、谱估计等方面的知识;我们所学的是从工程应用的角度讨论随机信号的理论分析和研究方法,主要以分析随机信号与系统的相互作用为主要内容;近年来,随着现代通讯和信息理论的飞速发展,对随机信号的研究已渗透到的各个科学技术领域,随机信号的处理是现代信号处理的重要理论基础和有效方法之一;主要研究问题对随机过程信号的分析来讲,我们往往不是对一个实验结果一个实现或一个具体的函数波形感兴趣,而是关心大量实验结果的某些平均量统计特性,因而随机过程信号的描述方式以及推演方式都应以统计特性为出发点;这样,尽管从个别的实现看不出什么规律性的东西,但从统计的角度却表现出一定的规律性,即统计规律性,它是本门学科一个最根本的概念;随机信号分析重点研究一般化抽象化的系统干扰和信号,往往仅给出他们的系统函数模型和数学模型,而不是讨论具体的系统,更不会局限于一些具体的电路系统上;概率论与数理统计随机过程理论等只是处理本命学科有关问题的一种工具因而学习本门课程除了注意处理问题的方法,更重要的是对一数学推演的结果和结论的物理意义有深入的理解;随机信号通过线性、非线性系统统计特件的变化；在通信、雷达和其他电子系统中常见的一些典型随机信号,如白噪声、窄带随机过程、高斯随机过程、马尔可夫过程等;第二章随机信号分析的主要内容随机信号分析与处理时研究随机信号的特点及其处理方法的专业基础课程,是目标检测、估计、滤波等信号处理的理论基础,在学习过程中,我们需要学会三个概念,统计的概念、模型的概念和物理概念,学习时既要理论联系实际,又要学会数学模型的抽象思维方法;一随机信号分析的主要研究内容：随机过程的基本概念和基本特征,它是学习随机信号分析的基础；随机信号的平稳性,平稳随机过程的数字特征、相关函数的性质;掌握平稳随机序列的期望、自相关序列的求解等；功率谱密度以及它的性质、互谱密度及性质等；随机信号两种统计特性的描述方法,重点研究数字特征,均值、方差、相关函数、相干函数、功率谱密度;平稳随机过程：将随机过程划分为平稳和非平稳有重要的实际意义,因为过程若属于平稳的可使问题的分析变得简单;随机信号的功率谱密度：利用傅里叶变换,研究随机过程的频域分析的功率谱密度并讨论其频率结构带宽以及系统的相互作用;随机信号通过线性系统：当输入信号为随机过程时,线性,稳定,时不变系统输出的统计特性,讨论系统的冲激响应ht是实函数的情况;功率谱估值：基于傅里叶变换的经典法和基于随机信号模型的现代谱估值法,前者称为非参数谱估值法,后者称为参数谱估值法;窄带随机过程：建立窄带过程的物理模型和数学模型以及分析窄带信号和系统的重要工具希尔伯特变换,来分析窄带随机过程的统计特性及其一些重要性质;讨论窄带随机过程经包络检波器和平方律检波器后统计特性的变换;随机信号通过非线性系统：当动态非线性系统可分时,分为线性系统与无记忆的非线性系统的级联,一般用多项式和伏特拉级数的方法;马尔可夫过程：一随机过程 {Xt,t∈T},其值域状态可以连续取值,也可以离散取值,如果他的条件概率满足下列关系：PXtn+1<=Xn+1 Xtn=xn,Xtn-1=xn-1,...,Xto=xo=PXtn+1<=xn+1 Xtn=xn 则Xt为马尔可夫过程;基于假设检验的信号检测：信号的统计检测是随机信号分析与处理的重要内容,应用统计方法来导出判决和估值的步骤,是合乎情理的;二随机信号分析理论的基本研究方法：在学习随机信号分析这一门课程时除了注意处理随机信号的方法外,更重要的是深入理解数学推演结果、结论的物理意义;对一些复杂的数学推演的中间步骤不必死记硬背,更不必深究其数学上的严密性,重在弄清楚来龙去脉,掌握分析的思路与方法;利用计算机为工具,对特定随机过程产生的数据进行统计分析,也是研究随机过程的重要方法,以及利用现代分析手段去分析,研究随机信号用来解决工程应用中的实际问题;第三章随机信号分析的应用实例均匀分布白噪声通过低通滤波器matlab环境下%%%%均匀分布白噪声通过低通滤波器xn=rand1,500; hn=fir150,;f,xi=ksdensityxn; plotxi,f;title'均匀分布白噪声概率密度';yn=filterhn,1,xn;t,xi=ksdensityyn;figure; plotxi,t;title'均匀分布白噪声通过低通滤波器后的概率密度';均匀分布白噪声概率均匀分布白噪声通过低通滤波器后的概率密度语音盲分离语音信号的盲源就是在源信号和源信号如何混合都未知的情况下,从观测到的混合信号中恢复出未知源信号;语音信号盲分离技术被成功地用在了通信、医学、图像和语音信号处理等领域;我们所要研究的混合语音信号盲分离问题就是用麦克风阵列或多个麦克风阵列来模仿人的耳朵,采集得到相互干扰的混叠语音信号,然后通过分离算法将混叠的语音信号相互分离开来,提取我们所感兴趣的信号;举个例子就是在多人同时说话的嘈杂环境下,我们能够辨识感兴趣人的说话声的能力;然后把它分辨出来;系统辨识根据系统的输入输出时间函数来确定描述系统行为的数学模型;通过辨识建立数学模型的目的是估计表征系统行为的重要参数,建立一个能模仿真实系统行为的模型,用当前可测量的系统的输入和输出预测系统输出的未来演变,以及设计控制器;对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号;对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求;而系统辨识所研究的问题恰好是这些问题的逆问题;通常,预先给定一个模型类μ={M},一类输入信号u和等价准则J=Ly,yM；然后选择使误差函数J达到最小的模型,作为辨识所要求的结果;系统辨识包括两个方面：结构辨识和参数估计;在实际的辨识过程中,随着使用的方法不同,结构辨识和参数估计这两个方面并不是截然分开的,而是可以交织在一起进行的;基于bartlett的周期图法估计功率谱功率谱估计是随机信号分析中的一个重要内容;从介绍功率谱的估计原理入手分析经典谱估计和现代谱估计两类估计方法的原理、各自特点及在Matlab中的实现方法;经典功率谱估计的方差大、谱分辨率差,分辨率反比于有效信号的长度,但现代谱估计的分辨率不受此限制;给出了功率谱估计的应用;基于MATLAB_GUI的Kalman滤波程序MATLAB_GUI为Kalman滤波器的研究和应用提供了一个直观、高效、便捷的利器;它以矩阵运算为基础,把计算、可视化、仿真以及设计融合到一个交互式的工作环境中;本文基于MATLAB_GUI对Kalman滤波器进行设计和仿真;第四章展望电子信息工程是一门应用计算机等现代化技术进行电子信息控制和信息处理的学科,主要研究信息的获取与处理,电子设备与信息系统的设计、开发、应用和集成;现在,电子信息工程已经涵盖了社会的诸多方面,像电话交换局里怎么处理各种电话信号,手机是怎样传递我们的声音甚至图像的,我们周围的网络怎样传递数据,甚至信息化时代军队的信息传递中如何保密等都要涉及电子信息工程的应用技术;我们可以通过一些基础知识的学习认识这些东西,并能够应用更先进的技术进行新产品的研究和开发;中国IT行业起步至今有十年,很年轻;新鲜的事物、朝阳的产业总是备受注目;正是这个原因,计算机专业迅速成为高校的热门专业,不少同学削尖又再削尖了脑袋往这个象牙塔里的象牙顶钻,或为兴趣,或为谋生掌握一门技能,或为前途更好更快地发展;在学习随机信号分析这一门课程时,应能掌握随机过程的基本概念、其统计特性的描述、随机信号通过系统分析以及电子系统中常见的窄带、正态随机信号的分析,而数字技术的发展使得离散随机信号分析成为本课程的重点要求掌握内容,其在电子信息技术中所占比重及重要性将得到进一步加强;随机信号理论在它形成的初期,便在通信、雷达、导航以及密码学等领域中获得了广泛的应用;近年来,随着对随机信号理论研究的进一步深入,人们对随机信号有了更多的认识,随机信号的实际应用也越来越多;其应用范围从上述领域扩展到自动控制、计算机、声学和光学测量、数字式跟踪和测距系统以及数字网络系统的故障检测等方面;参考文献：1“随机信号分析与处理”研究型教学总结谢明霞,罗鹏飞,张文明,徐振海3基于局域波法和盲源分离的故障诊断方法应用郝治华 20054概率论与数理统计第二版盛骤等北京高等教育出版社 2001.5非平稳随机信号分析与处理王宏禹国防工业出版社1999.6非平稳信号的一种ARMA模型参数估计法.信号处理王文华,王宏禹 19987Electronic Design EngineeringGao Hai Ning,YUAN Lei Ming,L of signal processing module of agricultural products based on acoustic resonance. 20128随机信号分析与应用刘磊 20139随机信号分析与处理0课程设计案例张文明,罗鹏飞长沙：电气电子教学学报,201010随机信号分析赵淑清,郑薇哈尔滨：哈尔滨工业大学出版社,1999。

随机信号分析实验报告

一、实验名称微弱信号的检测提取及分析方法二、实验目的1．了解随机信号分析理论如何在实践中应用2．了解随机信号自身的特性，包括均值、方差、相关函数、频谱及功率谱密度等3．掌握随机信号的检测及分析方法三、实验原理1．随机信号的分析方法在信号与系统中，我们把信号分为确知信号和随机信号。

其中随机信号无确定的变化规律，需要用统计特新进行分析。

这里我们引入随机过程的概念，所谓随机过程就是随机变量的集合，每个随机变量都是随机过程的一个取样序列。

随机过程的统计特性一般采用随机过程的分布函数和概率密度来描述，他们能够对随机过程作完整的描述。

但由于在实践中难以求得，在工程技术中，一般采用描述随机过程的主要平均统计特性的几个函数，包括均值、方差、相关函数、频谱及功率谱密度等来描述它们。

本实验中算法都是一种估算法，条件是N要足够大。

2．微弱随机信号的检测及提取方法因为噪声总会影响信号检测的结果，所以信号检测是信号处理的重要内容之一，低信噪比下的信号检测是目前检测领域的热点，而强噪声背景下的微弱信号提取又是信号检测的难点。

噪声主要来自于检测系统本身的电子电路和系统外空间高频电磁场干扰等，通常从以下两种不同途径来解决①降低系统的噪声，使被测信号功率大于噪声功率。

②采用相关接受技术，可以保证在信号功率小于噪声功率的情况下，人能检测出信号。

对微弱信号的检测与提取有很多方法，常用的方法有：自相关检测法、多重自相法、双谱估计理论及算法、时域方法、小波算法等。

对微弱信号检测与提取有很多方法，本实验采用多重自相关法。

多重自相关法是在传统自相关检测法的基础上，对信号的自相关函数再多次做自相关。

即令：式中，是和的叠加；是和的叠加。

对比两式，尽管两者信号的幅度和相位不同，但频率却没有变化。

信号经过相关运算后增加了信噪比，但其改变程度是有限的，因而限制了检测微弱信号的能力。

多重相关法将当作x（t），重复自相关函数检测方法步骤，自相关的次数越多，信噪比提高的越多，因此可检测出强噪声中的微弱信号。

随机信号分析李晓峰

随机信号分析李晓峰引言随机信号分析是一门研究信号及其性质的学科，其在现代通信、图像处理、生物医学工程等领域中具有重要的应用价值。

本文将介绍随机信号分析的基本概念、常见的分析方法以及李晓峰教授在随机信号分析领域的研究成果。

随机信号的定义随机信号是指在某个时间段内具有随机性质的信号。

其特点是信号的取值在时间和幅度上都是不确定的，只能通过概率统计的方法来描述。

一个随机信号可以用一个概率密度函数来描述其取值的分布情况。

随机信号有两种基本的分类方式：离散随机信号和连续随机信号。

离散随机信号是在离散的时间点上进行取样的信号，连续随机信号则是在连续的时间上变化的信号。

随机信号分析方法统计特性分析统计特性分析是随机信号分析的基本方法之一，它通过对信号进行统计分析，从而得到信号的数学特性。

常见的统计特性包括均值、方差、自相关函数和谱密度等。

均值是衡量随机信号集中程度的一个指标，它表示信号的中心位置。

方差则用来衡量信号的离散程度，方差越大表示信号的波动性越大。

自相关函数描述了信号在不同时间点之间的相关性，而谱密度则表示信号在不同频率上的能量分布情况。

概率密度函数分析随机信号的概率密度函数描述了信号取值的概率分布情况。

常见的概率密度函数包括高斯分布、均匀分布和指数分布等。

高斯分布是最常用的概率密度函数之一，其形状呈钟型曲线，具有对称性。

均匀分布则表示信号的取值在一个区间上是均匀分布的，而指数分布则表示信号的取值在一个时间段内的分布服从指数规律。

谱分析谱分析是通过对随机信号进行频域分析来研究其频率成分的分析方法。

常见的谱分析方法有功率谱密度分析和相关函数分析。

功率谱密度分析可以用来分析信号在不同频率上的能量分布情况，通过功率谱密度分析可以得到信号的频谱图。

相关函数分析则是通过对信号进行自相关操作，得到信号的相关函数，从而分析信号在不同频率上的相关性。

李晓峰教授的研究成果李晓峰教授是我国著名的随机信号分析专家，他在随机信号分析领域做出了许多重要的研究成果。

随机信号分析

随机信号分析随机信号是在时间或空间上具有随机性质的信号，其数学模型采用随机过程来描述。

随机信号的分析是信号与系统理论中的重要内容，其应用广泛涉及通信、控制、电力系统等领域。

本文将从随机信号的基本特性、常见的随机过程以及随机信号分析的方法等方面进行阐述。

随机信号的基本特性包括：平均性、相关性和功率谱密度。

首先，平均性是指随机信号的统计平均等于其数学期望值。

随机信号的平均性是通过计算信号在一定时间或空间范围内的平均值来描述的。

其次，相关性是指随机信号在不同时刻或不同空间位置上的取值之间存在一定程度的相关性。

相关性可以描述信号之间的相似度和相关程度，常用相关函数来表示。

最后，功率谱密度是用来描述信号在频域上的分布特性，它表示了随机信号在不同频率上所占的功率份额。

随机信号的常见模型主要有白噪声、随机行走、随机震荡等。

其中，白噪声是指功率谱密度在整个频率范围内均匀分布的信号，其在通信领域中应用广泛。

随机行走模型是一种随机过程，它描述了随机信号在不同时刻之间的步长是独立同分布的。

随机震荡模型是一种具有振荡特性的随机过程，常用于描述具有周期性或周期性变化的信号。

对于随机信号的分析方法，主要包括时间域分析和频域分析两种。

时间域分析是通过观察信号在时间上的波形和变化规律来分析随机信号的特性，常用的方法有自相关函数和互相关函数等。

频域分析是将信号转换为频率域上的功率谱密度来分析信号的频谱特性，常用的方法有傅里叶变换和功率谱估计等。

在实际应用中，随机信号的分析对于信号处理和系统设计具有重要意义。

在通信系统中，随机信号的噪声特性是衡量系统性能的关键因素之一，因此通过对随机信号的分析可以有效地优化通信系统的传输质量。

此外，在控制系统和电力系统中，随机信号的分析也能帮助我们进行系统建模和性能预测，从而实现系统的稳定性和可靠性。

综上所述，随机信号的分析是信号与系统理论中的重要内容，其对于各个领域的应用具有重要的意义。

通过对随机信号的基本特性、常见的随机过程以及分析方法的了解，可以为我们深入理解和应用随机信号提供帮助。

随机信号分析-估计理论

主讲教师:罗鹏飞教授
估计理论
举例：高斯白噪声中的DC电平估计
zi A vi
i 1,..., N
vi 是独立同分布的高斯随机变量，均值为零，方差为 v2
A ~ N ( A , )
2 A
f ( A | z)
f (z | A) f ( A)

f (z | A) f ( A)dA
z
v exp[( x a)2 / 2] exp[( x a) 2 / 2 2[Q( x a) Q( x a)]
a A0 / v
x z / v
主讲教师:罗鹏飞教授
估计理论
估计量 A0
ˆ A ml
ˆ A map
ˆ A ms
-A0 A0
z
-A0 估计图形
主讲教师:罗鹏飞教授
估计理论
1 1 2 ( zi A) exp 2 A A 2 i 1 2 A 2 A 1 1 1 1 N 2 2 2 ( zi A) exp 2 A A dA (22 ) N / 2 exp 2 2 i 1 2 A 2 A 1 1 exp 2 2 N /2 (2 ) 2
生物医学
自动控制
地震学
这些应用都有一个共同的目标：要能够确定感兴趣的事件在什么时候发生，以及该事件中更多的一些信息，前者是一个检测问题，或者称为统计判决问题，后者是参数的估计问题。
主讲教师:罗鹏飞教授
估计理论
主讲教师:罗鹏飞教授
估计理论
数字源
0或1
调制器
信道
解调器
检测器
主讲教师:罗鹏飞教授

随机信号在通信系统的应用

随机信号分析与处理在通信系统抗噪声性能的应用分析学院：信息与电气工程学院专业：电子信息工程班级：电子信息工程3班姓名：田浪绪论在通信系统的分析中，随机过程是非常重要的数学工具。

因为通信系统中的信号与噪声都具有一定的随机性，需要用随机过程来描述。

发送信号必须有一定的不可预知性，或者说随机性，否则信号就失去了传输的价值。

另外,介入系统中的干扰与噪声、信道特性的起伏，也是随机变化的。

通信系统中的热噪声就是这样的一个例子，热噪声是由电阻性元器件中的电子因热扰动而产生的。

另一个例子是在进行移动通信时，电磁波的传播路径不断变化，接收信号也是随机变化的。

因此,通信中的信源、噪声以及信号传输特性都可使用随机过程来描述。

在对无线电传输的信息进行调制和解调时，可以知道发射的载波的频率很高，而传输过程的带宽却很小，正是用了这样的特性从而滤除其他的干扰因素对传输的影响，但是不可能完全的滤除掉噪声对传输信号的影响。

信号进入带通滤波器之前是正弦波，经过带通滤波器后是正弦波和窄带高斯噪声的混合波形，而这些噪声是随机性的。

另外由于传输媒质的物理性质以及传输媒质的差异对信号传输的影响，而产生的加性噪声也是不能避免的。

所以在通信系统中，对信号的调制解调抗噪声的研究就显得必不可少。

由于这个过程满足窄带随机过程的条件，可以利用窄带随机过程的特性和方法来讨论抗噪声性能。

随机信号分析与处理在通信系统抗噪声性能的应用如果一个随机过程的功率谱集中在某一中心频率附近的一个很小的频带内，且该频带又远小于其中心频率，这样的随机过程称为窄带随机过称。

而通信系统中的调制信号是典型的窄带随机过程。

信号在信道中传输会叠加上一定的信道噪声，因此调制系统的抗噪声性能分析非常重要。

在一般无线电接收系统中通常都有髙频或中频放大器,它们的通频带往往远小于中心频率，即：所以，无线电接收系统为窄带系统，研究时可当作窄带系统研究。

当系统的输入端加入白噪声或宽带噪声时，由于系统的带通特性，输出的功率谱集中在为中心的一个很小的频带内,其窄带过程表现为具有载波角频率，但相对于载波而言幅度和相位是慢变化的正弦振荡形式，可表示为：其中为中心频率，是慢变化的随机过程，因此此公式称为窄带随机过程的准正弦振荡表示形式。

随机信号分析

随机信号是一种不能用确定的数学关系式来描述的、无法预测未来时刻精确值的信号，也无法用实验的方法重复再现。

换言之，随机信号是指不能用确定性的时间函数来描述，只能用统计方法研究的信号。

其统计特性：概率分布函数、概率密度函数。

统计平均：均值、方差、相关。

随机信号分为平稳和非平稳两大类。

平稳随机信号又分为各态历经和非各态历经。

1）各态历经信号——指无限个样本在某时刻所历经的状态，等同于某个样本在无限时间里所经历的状态的信号。

2）平稳随机信号——其均值和相关不随时间变化。

注：各态历经信号一定是随机信号，反之不然。

工程上的随机信号通常都按各态历经平稳随机信号来处理。

仅在离散时间点上给出定义的随机信号称为离散时间随机信号，即随机信号序列。

平稳随机信号在时间上的无限的，故其能量是无限的，只能用功率谱密度来描述随机信号的频域特性。

1. 随机信号的数字特征均值、均方值、方差若连续随机信号x(t)是各态历经的，则随机信号x(t)的均值可表示为：⎰→∞==TT x dt t x Tt x E 0)(1lim)]([μ均值描述了随机信号的静态分量（直流）。

随机信号x(t)的均方值表达式为：dt t x TTT x)(1lim22⎰→∞=ψ2xψ表示信号的强度或功率。

随机信号x(t)的均方根值表示为：⎰→∞=T T x dt t x T 02)(1limψ x ψ也是信号能量的一种描述。

随机信号x(t)的方差表达式为：⎰-==-→∞Tx T x x dx t x Tx E 0222])([1lim])[(μσμ2xσ是信号的幅值相对于均值分散程度的一种表示，也是信号纯波动分量（交流）大小的反映。

随机信号x(t)的均方差（标准差）可表示为⎰-=→∞T x T x dx t x T 02])([1limμσ 它和2x σ意义相同。

平稳随机过程统计特征的计算要求信号x(t)无限长，而实际上只能用一个样本即有限长序列来计算。

第5章随机信号分析

Rxy () 0
R xy ( )
0 的最大峰值一般不在处。
3. 估计

直接方法：
1 R ( m ) x ( n ) y ( n m ) xy N mn 0
^
N 1 m
1 R ( m ) y ( n ) x ( n m ) yx N mn 0
求傅立叶变换，得
N 1 ^
N 1N 1 1 j m j m R ( m ) e x ( n ) x ( n m ) e x N N N m ( N 1 ) m ( N 1 ) n 0
N 1 N 1 1 j m x ( n ) x ( n m ) e N N N n 0 m ( N 1 )
^
4 自相关函数的应用

检测淹没在随机噪声中的周期信号
x ( t ) x sin( t ) 0
T / 2 1 2 R ( ) lim x sin( t ) sin[ ( t ) ] dt x 0 T / 2 T T

t 令(
) ,则 dt 1 d
R 0 )R m ) X( X(

性质3
周期平稳过程的自相关函数必是周期函数，且与过程的周期相同。
E[ X 2 (n)]

性质4
性质5
2 R ( 0 ) = EX [ ( n ) ] X

不包含任何周期分量的非周期平稳过程满足
m 2 lim R ( m ) R ( ) X X X

平稳随机过程
均值和时间无关，是常数；自相关函数与时间的起点无关，只与两点的时间差有关。

随机信号分析与处理第一讲

随机信号分析与处理第一讲目录一、内容概述 (2)1. 课程介绍与背景 (2)2. 课程内容及结构介绍 (3)二、随机信号概述 (4)1. 随机信号定义与分类 (5)2. 随机信号的基本特性 (5)三、随机过程基础 (7)1. 随机过程的概念与分类 (8)2. 随机过程的数学描述方法 (9)3. 概率分布与统计特征 (10)四、随机信号分析方法和工具 (11)1. 随机信号的统计特性分析方法 (12)2. 随机信号的信号处理工具介绍 (13)3. 频谱分析与信号处理工具箱的应用 (14)五、随机信号处理基础 (15)1. 随机信号处理概述 (16)2. 信号滤波与平滑处理 (18)3. 信号检测与估计理论 (20)六、应用实例与案例分析 (21)1. 通信系统中的随机信号处理应用实例 (22)2. 图像处理中的随机信号处理案例分析 (23)3. 控制系统中的随机信号处理案例分析 (24)七、课程展望与复习要点 (25)一、内容概述随机信号分析与处理是通信、电子、信息等工程领域中不可或缺的核心理论基础。

本课程将带领同学们系统地探索随机信号的生成原理、特性分析方法以及处理技术。

从基础的随机过程概念入手，逐步深入到信号的分解、估计与滤波，最终实现信号的重建与识别。

通过本讲的学习，同学们将能够掌握随机信号分析与处理的基本框架和思路，为后续的专业学习和工作实践奠定坚实的基础。

1. 课程介绍与背景随着信息技术的迅猛发展，信号处理作为通信、电子、计算机等学科的核心基础，其在现代科学实验和工程技术中的应用日益广泛。

而随机信号作为信号处理领域的一个重要分支，其分析方法与处理技术对于揭示信号的内在规律、提高信号处理性能具有重要意义。

本门课程《随机信号分析与处理》旨在系统介绍随机信号的基本理论、分析方法以及处理技术。

课程内容涵盖了随机信号的建模、统计特性分析、功率谱估计、滤波器设计、信号分解与重构等多个方面。

通过本课程的学习，学生将能够掌握随机信号处理的基本原理和方法，为在通信、雷达、声纳、生物医学工程等领域中的应用打下坚实基础。

随机信号分析及应用教学设计

随机信号分析及应用教学设计前言随机信号是工程领域中广泛应用的基础概念之一，它在噪声处理、信号估计、信号处理等方面都有着重要的应用。

而对于学生而言，掌握随机信号的基础知识及分析方法，不仅提高了他们理论课知识的掌握度，还有利于他们将所学的知识应用到实际的工程中去。

因此，本教学设计旨在通过对随机信号的分析及应用进行详细的说明，帮助学生巩固理论基础，掌握相关实践技能。

完整学习目标在本教学设计中，学生应该能够：•掌握随机信号的基础知识，包括随机过程、随机变量、高斯随机变量等；•学习随机信号的主要分析方法，包括功率谱、自相关函数等；•实践应用所学的分析方法，应用于噪声处理、信号估计等领域；•增强团队合作能力及实际操作技能。

教学内容及设计1. 随机信号基础知识学生在本部分将掌握随机信号的基本概念，包括随机过程及随机变量等。

教学重点主要包括：•随机过程的定义及主要性质；•随机变量的概念及分类；•概率密度函数与分布函数。

对于这部分的教学，我们主要采用理论课授课形式，注重图表及实例的引入，增加教学生动感。

同时，学生也需要在课后进行相关习题练习。

2. 总体功率谱分析本部分是随机信号最常用的分析方法之一，主要包括总体功率谱、信号的自相关函数等。

主要内容包括：•总体功率谱的定义及计算公式；•信号自相关函数的定义及计算方式；•实践应用所学方法。

对于这部分的教学，我们采取理论与实践相结合的方式，通过合理设计实例及应用，帮助学生更深入理解相关分析方法。

3. 应用领域本部分主要针对随机信号分析方法在噪声处理、信号估计等领域的实际应用进行说明。

主要内容包括：•基于功率谱的噪声处理方法；•基于自相关函数的信号估计方法；•实践应用。

对于这部分的教学，我们将通过项目式教学方式让学生利用所学的方法进行实际操作，以便于他们更好的领悟相关的应用领域。

4. 团队合作在本部分，我们主要考虑到学生团队合作能力的培养，设计了一些相关的合作实践。

主要内容包括：•团队分工及协作方式；•团队时间管理方法；•团队成果展示。

随机信号分析课程应用实例

随机信号分析课程应用实例通过随机信号分析课程学习到的概念，去寻找相应的应用实例，以加深学习知识的理解。

内容包括1）概念和理论知识分析；2）举出实际应用实例；3）正确应用理论于实际、应用方法：4）Matlab 仿真结果；5）小结；6）参考文献。

一随机信号均值、方差及相关函数 09722 随机信号的平稳性； 09728 随机信号的各态历经性；09724随机信号功率谱、互功率谱； 09723 二随机信号通过线性系统 09722 窄带随机过程 09728 随机信号通过非线性系统 09724 特殊随机过程 09723 示范：随机信号的相关函数：自相关函数；协方差函数；互相关函数互相关函数（1）互相关函数的定义：设有两个随机信号()X t 和()Y t ，它们在任意两个时刻1t 和2t 的状态分别为1()X t 和2()Y t ，则随机信号()X t 和()Y t 的互相关函数定义为121212(,)[()()](,;,)XY XY R t t E X t Y t xyf x y t t dxdy +∞+∞-∞-∞==⎰⎰（2）互相关分析就是分析两个随机信号在不同的时刻的相似性。

为了便于分析其规律，通常固定时刻1t ，让2t 变化，讨论两个信号的相关性变化。

此时有21t t τ=+1211(,)(,)XY XY R t t R t t τ=+11[()()]E X t Y t τ=+特别地，令 10t =有(0,)()[(0)()]xy xy R R E X Y τττ==对其采样得（均采样为N 个点，s T 为采样周期）11()()()N XY n R m X n Y n m N-==+∑（3）应用上式互相关分析可测量汽车车速在汽车前后轮的一侧各安装加速度传感器，测量垂直振动的加速度波形，如图1所示图1 汽车前后轮的加速度传感器一般车辆前、后轮距大致相等（设为l ），后轮必然走过前轮走的路程，因此测量到的前、后轮的振动波形()X n 、()Y n 大致相似，且()Y n 滞后()X n ，即0()()Y n X n n =-。

基于雨课堂的随机信号分析理论实践

学科探素Disciplines Exploration ffll基于雨课堂的随机信号分析理论实践汪飞徐文俊（南京航空航天大学江苏•南京211106）摘要理论与实践统一是教学模式发展的必然趋势。

作为大学工科的专业基础课，随机信号分析是大学基础课程与专业课程的关键纽带。

理论教学的同时融入具体实践是提升教学效果的重中之重。

雨课堂不仅体现了互联网+的教学模式，而且雨课堂的教学数据恰好具有典型的随机信号特征。

随机信号分析的核心基础是概率论与随机过程。

课堂中全体同学回答选择题的正确率分布正是随机信号分析中概率论的典型实践；课堂中每位同学在整个教学过程的表现正是随机信号分析中随机过程的典型实践。

实时利用雨课堂及其教学数据不仅能够有意提高本科生的课堂注意率，而且能够实时将随机信号分析理论与实践相统一，达到学以致用的教学效果。

关键词雨课堂互联网+随机信号中图分类号:TN911文献标识码:A DOIilO.l6400/ki.kjdks.2020」0.019 Theory and Practice of Random Signal Analysis Based on Rain ClassWANG Fei,XU Wenjun(Nanjing University of Aeronautics and Astronautics,Nanjing,Jiangsu211106) Abstract The unity of theory and practice is the inevitable trend of the development of teaching mode.As a professional basic course of engineering,stochastic signal analysis is the key link between basic courses and professional courses.The most important thing to improve the teaching effect is to integrate the theory teaching with the concrete practice.Rain classroom not only embodies the Internet plus teaching mode,but also has typical random signal characteristics in the rain classroom teaching data.The core foundation of stochastic signal analysis is probability theory and stochastic process.The distribution of the correct rate of all students answering multiple-choice questions in class is the typical practice of probability theory in random signal analysis;the performance of each student in the whole teaching process is the typical practice of random process in random signal analysis.The real-time use of rain class and its teaching data can not only improve the attention rate of undergraduates, but also unify the theory and practice of random signal analysis in real time,so as to achieve the teaching effect of applying what they have learned.Keywords rain class;Internet+;random signal0引言随机信号分析是大学本科电子信息类必修的专业基础课，以随机过程作为学习与研究对象,概率与数理统计中随机变量的基础知识是其先导课程。

随机信号分析第一章

02
随机信号的统计描
述
概率密度函数
定义
概率密度函数（PDF）是描述随机信号在各个时刻取值概率分布的函数。
性质
概率密度函数具有非负性、归一化性质，即概率密度函数在全域上的积分等于1。
计算方法
可以通过直方图法、核密度估计法等方法计算概率密度函数。
概率分布函数
定义
概率分布函数（CDF）是描述随机信号取值小于或等于某个值的概率的函数。
随机信号的特性
统计特性
随机信号的统计特性包括均值、方差、概率分布等，这些特性描述了信号的平均行为和不确定性。
时间特性
随机信号的时间特性包括自相关函数、互相关函数、功率谱密度等，这些特性描述了信号在不同时间点的相关性以及频率成分。
随机信号的应用
通信
在通信领域，随机信号可用于扩频通信、无线通信等领域，以提高通信的抗干扰能力和保密性。
05
随机信号的采样定
理
采样定理的内容
采样定理定义
对于一个时间连续的模拟信号，如果以不高于其最高频率分量的频率进行采样，则可以无失真地恢复原始信号。
采样定理的数学表达式
如果信号的最高频率为Fmax，则采样频率应不小于2Fmax。
采样定理的意义
采样定理是数字信号处理的基础，它确保了从离散样本中能够准确重建原始信号。
雷达与声呐
在雷达与声呐领域，随机信号可用于目标检测、测距、定位等方面，以提高探测的精度和可靠性。
地球物理学
在地球物理学领域，随机信号可用于地震勘探、矿产资源探测等方面，以揭示地球内部结构和物质分布。
金融与经济
在金融与经济领域，随机信号可用于股票价格分析、市场预测等方面，以揭示市场动态和经济发展趋势。

随机信号分析理论的应用综述

欢迎共阅随机信号分析理论的应用综述（结课论文）学院：3.1均匀分布白噪声通过低通滤波器3.2语音盲分离3.3系统辨识3.4基于bartlett的周期图法估计功率谱3.5基于MATLAB_GUI的Kalman滤波程序第四章展望参考文献第一章概述1.1随机信号分析的研究背景在一般的通信系统中，所传输的信号都具有一定的不确定性，因此都属于随机信号，否则不可能传递任何信息，也就失去了通信的意义。

随机信号是一种不能用确定的数学关系式来描述的、无法预测未来时刻精准值的信号，也无法用实定的规律性，即统计规律性，它是本门学科一个最根本的概念。

随机信号分析重点研究一般化（抽象化）的系统干扰和信号，往往仅给出他们的系统函数模型和数学模型，而不是讨论具体的系统，更不会局限于一些具体的电路系统上。

概率论与数理统计随机过程理论等只是处理本命学科有关问题的一种工具因而学习本门课程除了注意处理问题的方法，更重要的是对一数学推演的结果和结论的物理意义有深入的理解。

随机信号通过线性、非线性系统统计特件的变化；在通信、雷达和其他电子系统中常见的一些典型随机信号，如白噪声、窄带随机过程、高斯随机过程、马尔可夫过程等。

第二章随机信号分析的主要内容随机信号分析与处理时研究随机信号的特点及其处理方法的专业基础课程，是目标检测、估计、滤波等信号处理的理论基础，在学习过程中，我们需要学会统的重要工具希尔伯特变换，来分析窄带随机过程的统计特性及其一些重要性质。

讨论窄带随机过程经包络检波器和平方律检波器后统计特性的变换。

随机信号通过非线性系统：当动态非线性系统可分时，分为线性系统与无记忆的非线性系统的级联，一般用多项式和伏特拉级数的方法。

马尔可夫过程：一随机过程 {X(t),t∈T}，其值域（状态）可以连续取值，也可以离散取值，如果他的条件概率满足下列关系：P[X(tn+1)<=Xn+1 X(tn)=xn,X(tn-1)=xn-1,...,X(to)=xo]=P[X(tn+1)<=xn+1 X(tn)=xn] 则X（t）为马尔可夫过程。

关于《随机信号分析》的教学实践与思考

关于《随机信号分析》的教学实践与思考摘要：《随机信号分析》是一门理论性较强的课程。

针对学生初学这门课程时，往往会感到模糊、难懂、不易学，因此讲授这门课程必须从它的特点出发，采用不同的教学方法才能对本课程有较好的把握。

本文就《随机信号分析》教学的基本内容和应把握好的几个问题，进行了实践和有益的思考。

关键词：随机信号分析教学思考中图分类号：tn929.11 文献标识码：a 文章编号：1674-098x （2012）08（c）-0158-03《随机信号分析》课程是通信工程、电子信息工程、测控技术与仪器、自动化等多个专业方向所共有的一门非常重要的专业基础课。

其研究对象为随机信号，区别于我们以往课程的研究对象。

以往电子类的基础课和专业基础课的研究对象为确定信号，其主要特征是有确定的数学表达式对信号的变化过程进行描述。

而本门课程中的随机信号作为一个全新的概念被提出和研究，随机信号主要特征是没有确定的变化形式，对其进行的观测结果没有确定的变化规律。

随机信号相比于确定信号要复杂得多，研究其要困难得多，但由于日常生活中有很多现象都是随机的，通俗得讲，就是随机信号广泛地作用于我们所见的环境和事物。

比如说，每天的天气情况，学生考试成绩的分布等等，都是随机信号，所以这门课程的理论与工程实际应用与我们的日常生活紧密相联。

为了研究和进一步了解、改善我们的日常生活环境，我们必须教好和学好这门课程。

本课程要求学生通过本课程学习并掌握随机信号的基本理论与特性、随机信号的基本分析方法以及用其分析问题和解决问题的能力。

该课程主要内容包括随机信号的基本概念，随机信号的概率分析与矩分析方法，随机过程的严格平稳性、广义平稳性、周期平稳性及随机过程的均值各态历经性，随机过程的功率谱分析，随机信号与噪声通过线性系统，高斯与窄高斯随机过程分析。

本课程48学时，大三上学期开出。

该课程的先修课程为《概率论》、《电路分析》、《信号与系统》等。

1 《随机信号分析》课程特点[1][2]1.1 统计的概念[3]分析随机信号，往往不是对其一个实验结果感兴趣，而是关心其大量的实验结果的某些统计特性，因而随机信号的描述方式以及推演方式都应以其统计特性为出发点。

关于《随机信号分析》的教学实践与思考

关于《随机信号分析》的教学实践与思考《随机信号分析》是一门应用数学课程，它主要研究随机信号的统计特性和分析方法，对于电子信息工程、通信工程等领域的学生来说具有重要的理论和实践应用价值。

在这门课程的教学实践中，我进行了以下思考和实践。

首先，教材选择。

《随机信号分析》的内容较为复杂，学生对于概率与统计的基础知识要求较高。

因此，在教学过程中我选择了一本系统完整、理论与实践相结合的教材，既能够让学生理解抽象概念，又能够帮助他们掌握具体的计算方法。

其次，教学方法。

在教学过程中，我注重理论与实践相结合的实践教学方法。

我通过理论讲解、案例分析和实验操作等方式，使学生能够充分理解随机信号的基本概念和分析方法，并在实践中掌握具体的计算技巧。

通过实践教学，学生能够更好地理解和应用所学知识。

另外，我注重培养学生的问题解决能力。

在课堂上，我鼓励学生提问，引导他们分析问题、思考解决方法，并在讨论中培养他们的逻辑思维和创新能力。

通过问题解决的实践训练，学生能够更好地理解《随机信号分析》的核心概念和分析方法，并能够灵活运用到实际问题中。

此外，我还注重课堂互动和实践操作。

在教学过程中，我通过提问、讨论和小组活动等方式，积极引导学生参与课堂互动，激发学生的学习兴趣和合作精神。

同时，我还设计了一些实践操作环节，让学生能够亲自动手实践，巩固所学知识，提高应用能力。

最后，我还注重评价和反馈。

在教学过程中，我定期布置作业和实验报告，评价学生对于随机信号分析的理解和应用能力。

同时，我还及时给予学生反馈，指导他们改正错误和提高学习效果。

通过评价和反馈，学生能够清楚了解自己的学习水平，并及时调整学习策略。

总之，《随机信号分析》是一门理论与实践相结合的课程，我在教学实践中注重培养学生的理论思维和实践能力。

通过选择合适的教材、采用有效的教学方法、培养学生的问题解决能力、促进课堂互动和实践操作、定期评价和反馈等手段，我努力使学生能够深入理解随机信号分析的内容和方法，并能够运用到实际问题中。